Abstract
In December 2019, a new outbreak in Wuhan, China has attracted world-wide attention, the virus then spread rapidly in most countries of the world, the objective of this paper is to investigate the mathematical modelling and dynamics of a novel coronavirus (COVID-19) with Caputo-Fabrizio fractional derivative in the presence of quarantine and isolation strategies. The existence and uniqueness of the solutions for the fractional model is proved using fixed point iterations, the fractional model are shown to have disease-free and an endemic equilibrium point.We construct a fractional version of the four-steps Adams-Bashforth method as well as the error estimate of this method. We have used this method to determine the numerical scheme of this model and Matlab program to illustrate the evolution of the virus in some countries (Morocco, Qatar, Brazil and Mexico) as well as to support theoretical results. The Least squares fitting is a way to find the best fit curve or line for a set of points, so we apply this method in this paper to construct an algorithm to estimate the parameters of fractional model as well as the fractional order, this model gives an estimate better than that of classical model.
Keywords: Caputo-Fabrizio derivative, COVID-19, SEIR epidemic model, Fractional differential equations, Fractional Adams–Bashforth method
Introduction
In December 2019, an unidentified virus was found in Wuhan, Hubei province, China. The responsible virus was later confirmed as a new coronavirus [23]. The World Health Organization (WHO) temporarily named the virus as the novel coronavirus 2019 (2019-nCoV), and the disease as coronavirus disease 2019 (COVID-19) on 11 February 2020. The first confirmed case of the virus was discovered on 17 November 2019 in Hubei. As of 5 July 2020, more than 11.1 million cases have been reported in 188 countries in the world, which resulted in more than 528,000 deaths. Over 6.03 million people recovered [57].
The progress of fractional calculus in the last few years has been very rapid due to its applicability in many fields, such as physical problems [15, 23, 51, 58], engineering mechanics [9], epidemiological models [6, 14, 17, 18, 26, 29, 44, 45, 47], image processing [28, 59], chaos theory [10, 52] and others. There are in the literature several definitions of the fractional derivative, the most famous of these is the definition of Caputo, Riemann-Liouville, Grünwald–Letnikov and Hadamard derivative, the new operators with non-singular kernels appear in this domain of mathematics, namely the Caputo-Fabrizio derivative [19] and the Atangana-Baleanu-Caputo derivative [8].
A number of epidemiological models with fractional derivative have been developed to understand the transmission dynamics of COVID-19 and other infectious diseases outbreak from various aspects. We mention them, Kumar et al. [33] have been studied fractional SIRS-SI model describing the transmission of malaria disease by using the Caputo–Fabrizio fractional operator. Tuan et al. [53] studied a mathematical model for COVID-19 transmission by using the Caputo fractional derivative. Singh et al. [49] studied the numerical solution of SEIAR model with Grünwald-Leitnikov derivative. Abdo et al. [1] have investigated the mathematical model of novel coronavirus (COVID-19) depending of fourteen nonlinear FDEs with Atangana-Baleanu-Caputo fractional derivative. Peter et al. [42] investigated a fractional order mathematical model of COVID-19 in Nigeria using Atangana-Aaleanu derivative. Ahmad et al. [2] Studied the fractional model and dynamics of COVID-19 in Pakistan using Atangana Baleanau operators. Nisar et al. [41] Proposed a SIRD model of COVID-19 with Caputo fractional derivative. Rezapour et al. [44] presented a new mathematical model for the transmission of Zika virus between humans as well as between humans and mosquitoes using Caputo derivative. Baleanu et al. [16] proposed a new fractional model for human liver involving Caputo– Fabrizio derivative. Rezapour et al. [43] studied the fractional-order model for the anthrax disease between animals based on the Caputo–Fabrizio derivative. Dokuyucu and Dutta [26] examined the Ebola virus model using the fractional derivative and the integral operator proposed by Caputo and Fabrizio. Area et al. [6] have been studied the classical and Caputo fractional order SEIR (susceptible, exposed, infections, removed) Ebola epidemic model and its comparison with real data. Tulu et al. [54] developed the Caputo fractional mathematical model of the Ebola virus with a quarantine strategy and the presence of the vaccine, using both the Euler method and one of the top ten most influential algorithms known as Markov Chain Monte Carlo (MCMC) method. Singh et al. [48] have been studied the fractional epidemiological model for computer viruses using Caputo-Fabrizio fractional derivative. Singh et al. [47] studied the diabetes model and its complications with the CF-fractional derivative. Mohammadi et al. [38] used Caputo–Fabrizio fractional derivative to model hearing loss in children caused by the mumps virus. Higazy [30] suggested a SIDARTHE model for COVID-19 pandemic by using Caputo fractional derivative. Zhang et al. [63] applied the fractional SEIRD Model to the real data of the COVID-19 for China using Caputo fractional derivative. Some other outstanding studies of COVID-19 by fractional derivative have been made in [4, 5, 7, 24, 31, 34, 37, 46, 60, 62].
Always when a new virus appears, researchers look for effective ways to control the virus, including vaccination, isolation, and quarantine. In the absence of the vaccine, the isolation and quarantine strategies remain effective to mitigate and eliminate the impact of the virus (see [12, 20–22, 27, 64]). In this current study, we modify the general SEIR epidemiological model for the effects of isolation and quarantine strategies on COVID-19 transmission, to become a fractional order model of type Caputo-Fabrezio fractional derivative. The main objective in this work is to provide a new discussion and new tools for developing epidemiological models with Caputo-Fabrizio derivative, this work is motivated by all these results that prove the efficiency of fractional derivative, to our best knowledge, such problem has never been studied previously for the fractional case. We will start this article in the theoretical part by proving the existence and uniqueness of the solutions, then we will determine the equilibrium and the basic reproduction number of the model. We construct a fractional version of the four-steps Adams-Bashforth method as well as the error estimate of this method.
In machine learning, the Least squares fitting is a way to find the best fit curve or line for a set of points, so we apply this method in this paper to construct an algorithm to estimate the parameters of fractional model as well as the fractional order, this model gives an estimate better than that of classical model. The paper is organized as follows. In Section 2, we present the basic theory of the Caputo-Fabrizio derivative. The clasical and fractional model are formulated in Section 3. The basic roprodoction number and the disease-free equilibrium are given in Section 4. The fixed point iterations is applied to prove existence and uniqueness results in Section 5. Using fractional m-step Adams-Bashforth scheme with derivative, the numerical solution of the proposed model is obtained in Section 6. Simulation results are presented in Section 7. Finally, the present work is concluded in Section 8.
Preliminaries
Recalled here some background material for the Caputo-Fabrizio fractional derivatives, see [3, 19, 32] for details.
Definition 1
([19]) Let the time fractional Caputo-Fabrizio fractional differential operator is defined by
where M is a normalization function which depends on and gives , where if u is a constant function. The definition is also written if the function does not belong to
The corresponding integral was described by Jorge and Juan [32].
Definition 2
([32]) Let 0 , then the CF fractional integral operator of order given by
Model Formulation
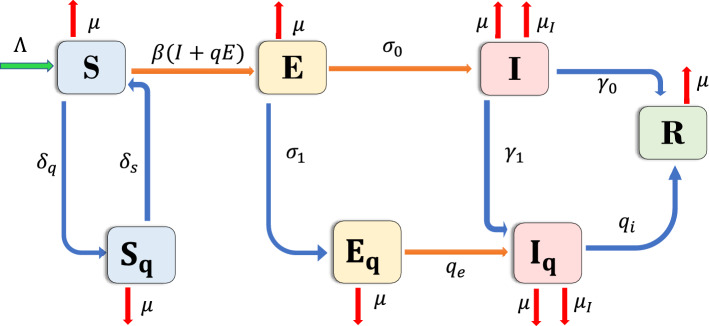
In more detail, we have studied a fractional SEIR epidemiological model with quarantine and isolation strategies. The total population is divided into seven groups, namely susceptible (S), exposed (E), infectious but not yet symptomatic, infectious with symptoms (I) and recovered (R) compartments, as well as quarantined susceptible quarantined exposed and isolated infected compartments. Where susceptible individuals can be quarantined at a rate of and then returned to the pool of susceptible individuals once it is determined they are uninfected at a rate of . The unquarantined susceptible individuals, if infected, move to the compartment E at a rate of where is the transmission incidence rate and q is the fraction of transmission rate for exposed, also the exposed individuals develop symptoms at a rate and are assumed to be quarantined at a rate not only-but also the exposed quarantined individuals can be isolated at rate they also recover after isolation at rate . Likewise the infected symptomatically individuals develop symptoms and can be isolated at rate , in addition they recover from the disease at rates , finally is the recruitment rate, represent natural death rate and show the death rate of infected human individuals with the coronavirus disease 2019.
The transfer diagram for this model is described by Fig. 1 and the classical version of this model formulated by the following system of ODEs:
| 1 |
Fig. 1.
Schematic diagram of the model compartments and parameters
Fractional Model
Now replacing the classical derivative in (1) by Caputo-Fabrizio derivative we obtain by moment closure, the following system of fractional ODEs :
| 2 |
with the initial conditions and is the Caputo-Fabrizio fractional operator of order .
The total population . Then
In the absence of the disease, , this shows that the population size tends to carrying capacity
Quarantine Reproductive Number and Existence of Equilibrium
The epidemic model (2) has a family of disease-free equilibrium, obtained by setting the right hand side of the equations in (2) to zero, given by
where and
| 3 |
Now using the notation in [56], the non-negative matrix, F, for the new infection terms and the non-singular M -matrix, V, for the remaining transfer terms are given by
| 4 |
| 5 |
Thus
| 6 |
where
The effective reproduction number (or quarantine-isolation reproduction number), denoted by is given by where denotes the spectral radius. It follows that
| 7 |
The system (2) has a unique endemic steady state
where
Existence and Uniqueness of a System of Solutions
In this section, we prove the existence of the system of solutions by applying the fixed-point theorem.
Let , and C(J) be a Banach space of continuous valued functions on the interval J with the norm
where denote the supremum norm in C(J).
Now using the integral operator of fractional order introduced by Losada and Nieto Jorge and Juan [32] on the system (2), we get
For simplicity,
To prove the following theorems, we will assume that and where , are some positive constants. Denote
Theorem 3
The kernels , satisfy the Lipschitz condition and contraction if the inequality given below holds
| 8 |
Proof
Let and be two functions, then
Thus
| 9 |
Hence, for the Lipschitz condition is obtained. Similarly for , and the Lipschiz condition can be easily verified and given below:
Now we write the system (2) in the following recursive form:
| 10 |
The initial conditions are
, , , , , and
Then we get the following expressions for the difference between the successive terms:
| 11 |
| 12 |
| 13 |
| 14 |
| 15 |
| 16 |
| 17 |
Taking the norm on both side of the Eq. (11), applying triangular inequality and using the Lipschitz condition proved in (9) we obtained
Then, we have
| 18 |
Similarly, for the remaining equations of the system, we obtain the following results:
| 19 |
| 20 |
| 21 |
| 22 |
| 23 |
| 24 |
Immediately, in view of the above results, we state the following theorem.
Theorem 4
The solution of the CF—fractional model given in (2) will exist and be unique if we can find some such that
| 25 |
Proof
As the functions and are bounded and fulfill Lipschitz condition. So, by considering Eqs. (18)–(24), we obtain the following relations:
Thus, the proof the existence and continuity of the solutions is completed. To show that the above functions are solutions of system (2), we set as follows:
Therefore, we have
| 26 |
On using this process recursively, it yields
where is a positive constant. Then at we have
Now taking the limit as n tends to infinity, we get
Repeating the same procedure we obtain
Hence, proof of existence is verified.
Next to show the uniqueness of the solution of the model (2), suppose on the contrary that there exists another set of solutions , , , , , and then
Applying norm in the above equation, we get
By employing the Lipschitz condition of kernel, we have
It gives
Clearly if
| 27 |
Employing the same procedure, we get
and
Hence the solution is unique if condition (25) is satisfied.
Numerical Scheme
In this Section, we present a numerical solution of the fractional order model (2). Then The numerical simulations are obtained using the proposed scheme for Adams-Bashforth. For this purpose we use the fractional m-step Adams Bashforth method to approximate the CF-fractional integral operator and to obtain an iterative scheme,
Consider the Caputo-Fabrizio fractional differential equation
| 28 |
Now applying the fractional integral to system (28) we get:
At , and for , we have
| 29 |
and
| 30 |
Subtracting (30) from (29), the following equation obtained
The function can be approximated over for and using the interpolation polynomial of Lagrange of degree m, we have
where are the Lagrange functions on the points and given by
Therefore, the integral becomes
Thus
This method is known as m-step Adams–Bashforth method, for we obtain the CF-fractional second-order Adams-Bashforth method (see also [11])
For we obtain the CF-fractional three-order Adams-Bashforth method (see also Moore et al. [39])
For we obtain the CF-fractional four-order Adams-Bashforth method
It should be noted that when this method reduces to the classical Adams–Bashforth m-step method.
The truncation error for the m-step formula can be estimated by using the error estimate for the Lagrange interpolating polynomial, namely,
Then we have
a simple calculation shows that the last quantity is bounded by
where c is a constant only depends on f and m.
Now using 4-step fractional Adams–Bashforth scheme to obtain numerical solutions of the fractional model (2) we get for the first equation in (2) the following scheme:
where
| 31 |
similarly for the other equations, thus, desired numerical approach is obtained for CF-fractional model.
Numerical Simulation and Calibration of the Model
In this Section, we illustrate the numerical results for the fractional model (2) for different values of fractional order to analyze the influence of fractional order on the disease dynamics. Some numerical simulations with the Caputo–Fabrizio operator for the fractional COVID-19 virus model are presented using the fractional version of Adams-Bashforth four-step method.
Estimation of Model Parameters and Best Fit of Fractional Orders
The model calibration problem seeks to estimate the model parameters which, to some extent, make the model response as close as possible to the observed values (real data), for that using the Least Squares method to predict the model parameters.
We consider the model solution depending on the vector of parameters excepting and N, which are kept fixed, and the vector X of the observation data at given times Let be the function computing the numerical solution u of the fractional differential system (2), the vector of parameters is restricted to be on the convex set of admissible values such as lb and ub are lower and upper vector bounds for the model parameter respectively.
The estimation of the parameter is obtained by solving the following non linear least squares problem by finding a vector of parameter such that:
The aim is to minimize the objective function
subject to and Equation (2) to obtain the best estimate of parameters and the fractional order . For more details about least squares method, see for example [25, 36]. Now using 4-steps Adams-Bashforth method we get the optimization problem
| 32 |
to obtain the best estimate of parameters and the vector of fractional orders , where
the values of are given in (31) and the function f is the right-hand side of the model (2).
Impact of Fractional Order Derivative
Based on numerical scheme derived in Section 6, we present the graphical results of the proposed CF fractional model (2) in Figs. 2, 3, 4 and 5 to analyze the influence of fractional order. We have considered the initial conditions , , and .
Fig. 2.
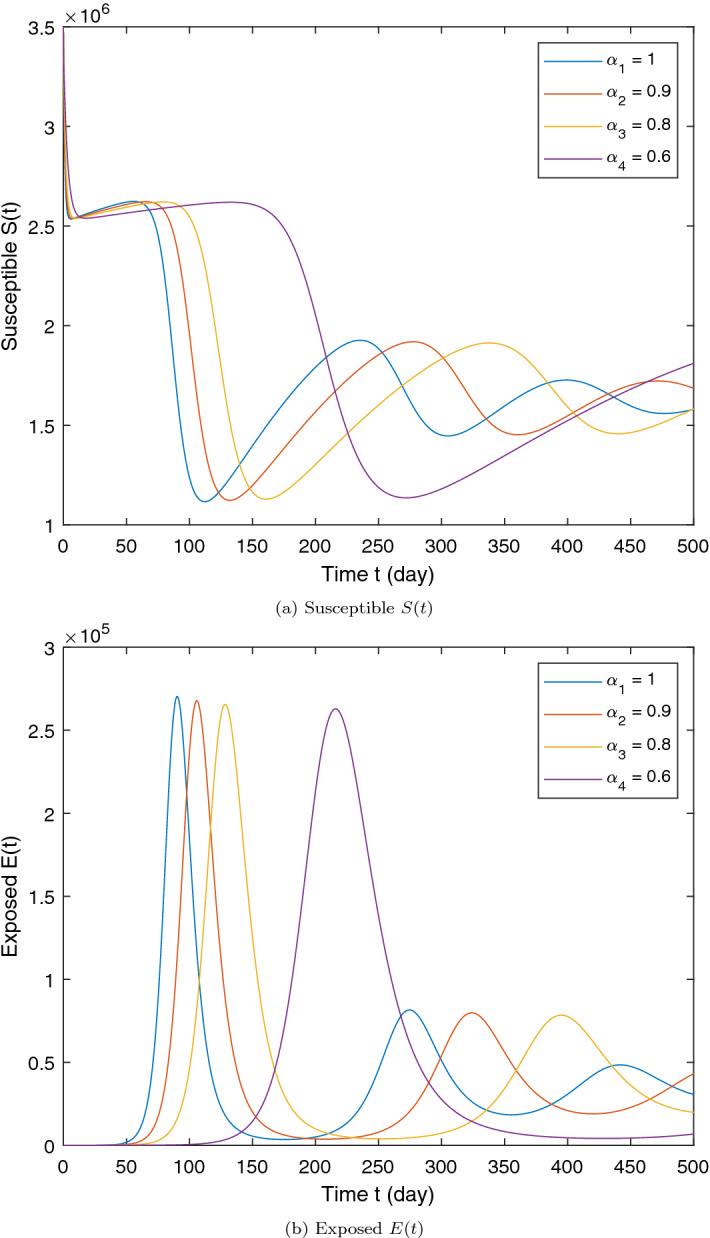
Graphical representation of numerical solution for susceptible S(t) and Exposed E(t) at various fractional order of the considered model. Parameter values used are as given in Table 1
Fig. 3.
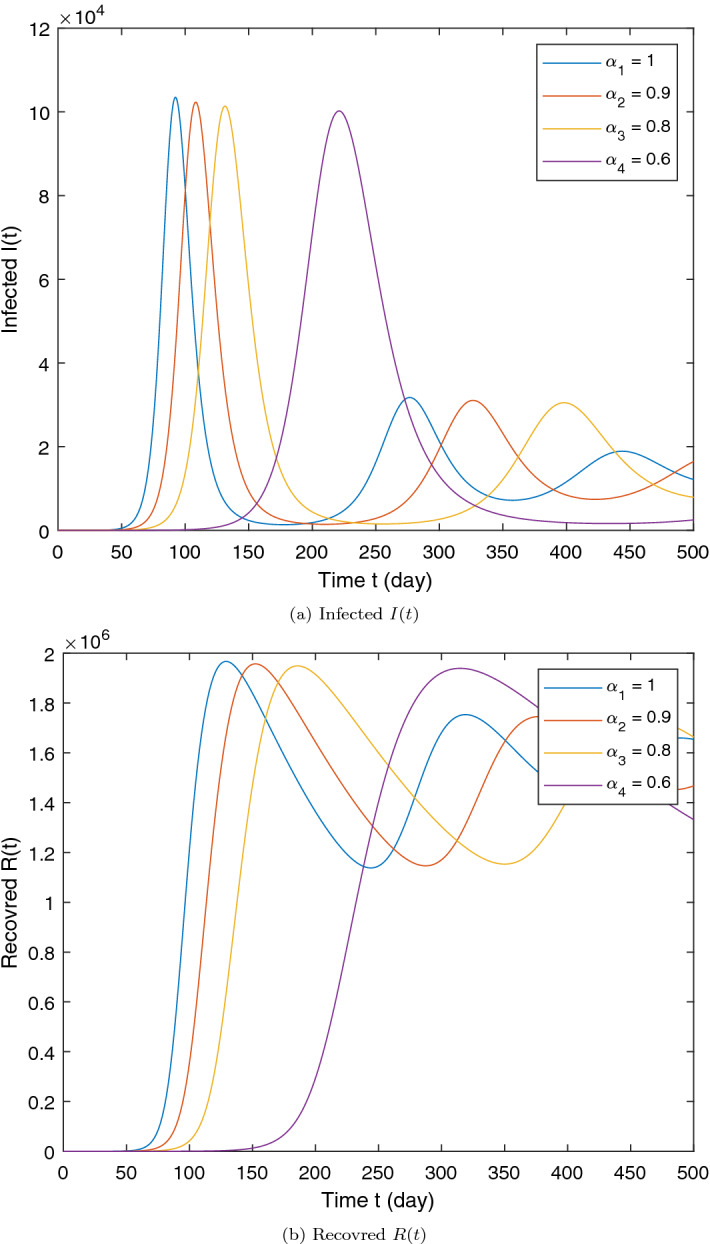
Graphical representation of numerical solution for Infected I(t) and Recovered R(t) at various fractional order of the considered model. Parameter values used are as given in Table 1
Fig. 4.
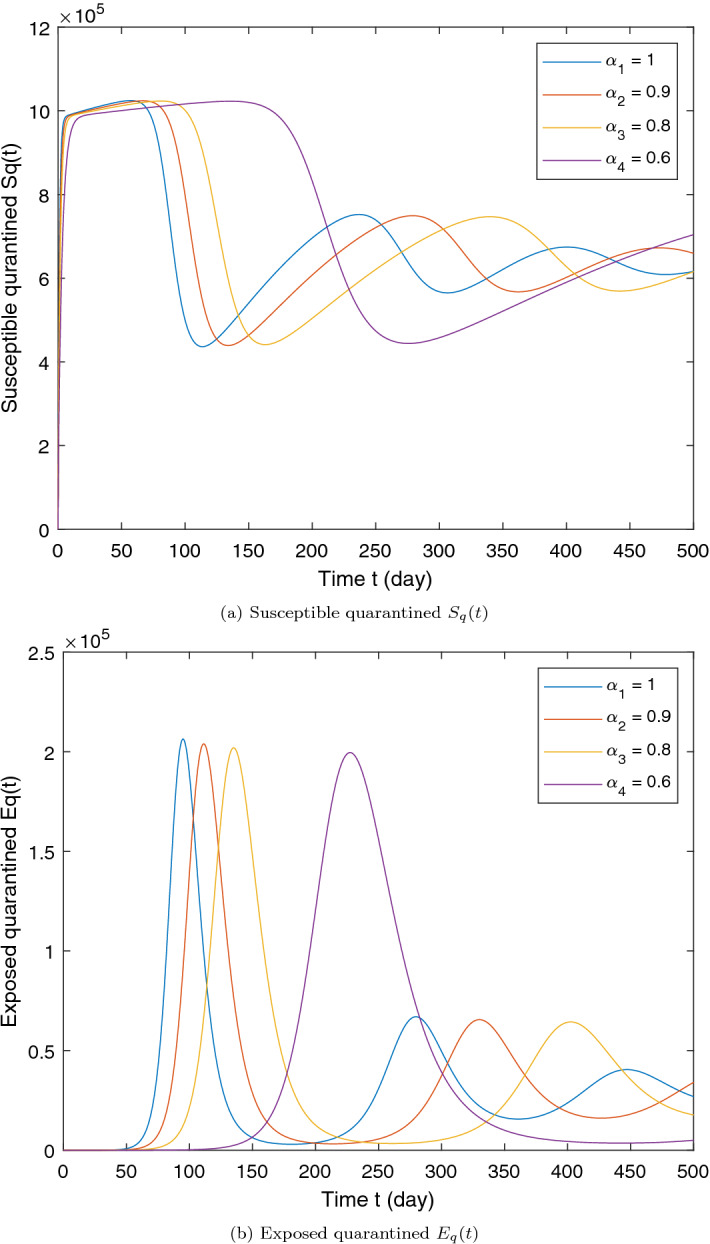
Graphical representation of numerical solution for Susceptible quarantined and Exposed quarantined at various fractional order of the considered model. Parameter values used are as given in Table 1. The initial conditions are the same of the Section 7.2
Fig. 5.
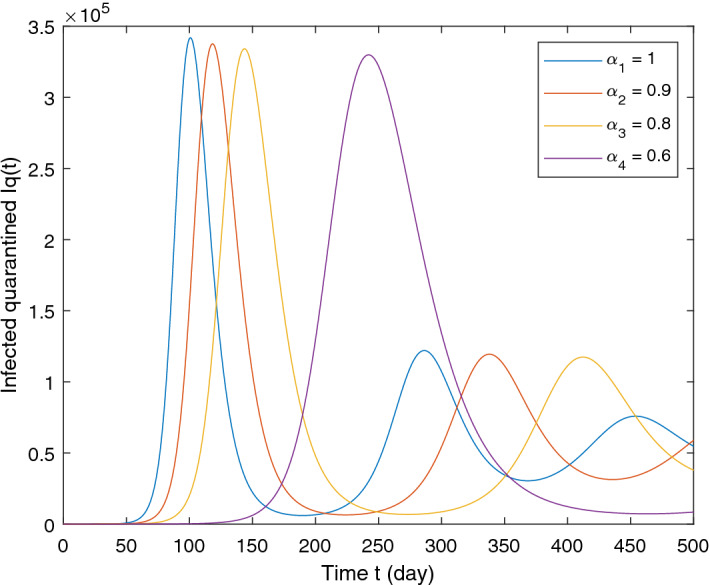
Graphical representation of numerical solution for Infected isolated at various fractional order of the considered model. Parameter values used are as given in Table 1. The initial conditions are the same of the Section 7.2
From the analysis of the obtained graphs, we notice that the population of the infected class decreases significantly by decreasing the order of the fractional derivative and the endemic state of the disease goes to the disease-free state in all the cases studied. In addition, the graphical results of the CF-derivative model reveal that this operator is more significant in exploring the dynamics of the model and providing more biologically feasible results.
Impact of Quarantined and Isolation Parameters
It is well known that the effective reproduction number of the fractional model is a very important parameter in the infectious disease, which determines whether the could spread. In our model, is determined by the parameters given in (3) and (7). In order to identify the impacts of these parameters on COVID-19 transmission and prevalence, we will discuss the change in the number of infected individuals with the COVID-19 virus when we change the values of the controlled parameters, transmission rate (), quarantine rate of susceptible (), isolation rate of infected individuals () and quarantine rate of exposed (). All parameter values for the simulation in this section are given in Table 1.
Table 1.
Parameter of the model used in the simulation
| Parameters | Description | Value | Confidence interval | Source |
|---|---|---|---|---|
| Recruitment rate | 0.008 N | − | Assumed | |
| Transmission incidence rate | 0.74 | [0.2, 2] | Assumed | |
| Quarantine rate of susceptible | 0.28 | [0, 1] | [61] | |
| Rate which quarantined susceptible return to S | 0.071 | [0, 1] | [40] | |
| q | The fraction of transmission rate for exposed | 0.63 | [0,1] | [61] |
| Recovery rate of infected | 0.33 | [0, 1] | [50] | |
| Recovery rate of isolated infected | 0.12 | [0, 1] | [50] | |
| COVID-19 Death rate | 0.001 | - | Assumed | |
| Natural death rate | 0.007 | - | [55] | |
| isolation rate of infected | 0.13 | [0,1] | [50] | |
| Quarantine rate of exposed | 0.16 | [0, 1] | Assumed | |
| Rate of exposed individuals to the infected | 0.183 | [1/14, 1/2] | [13, 35, 64, 65] | |
| Rate exposed individuals to the isolated class | 0.183 | [1/14, 1/2] | [13, 35, 64, 65] |
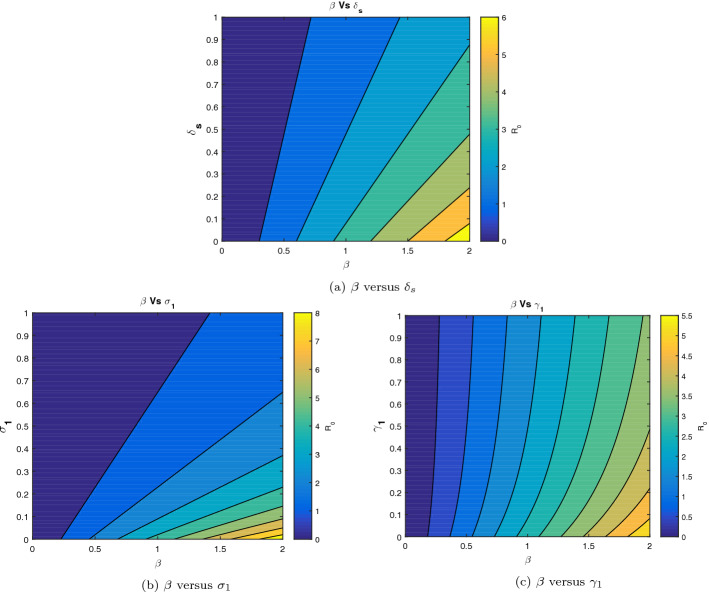
Firstly, to determine the dependence of the attack rate on the controllable model parameters, fixing two of and at the specific value (given in Table 1) and varying the other two parameters (one of the previous four parameters with ), the contour plots of the quarantine reproduction number are illustrated in Fig. 6.
Fig. 6.
Contour shows the variation of for different parameter values: a shows the variation of for different values for and , b shows the variation of for different values for and and the lower heat map c shows the variation of for different values for and
Figure 6a and 6b show that higher quarantine rate and will reduce , then will help bring , thus prevent the outbreak from happening. On the other hand Fig. 6c shows that the isolation rate is effective when the transmission rate is high, this is natural since infected people are those who carry the virus and transmit it to other people in the population.
In order to compare the effectiveness of quarantine and isolation to reduce the spread of a virus COVID-19, the model is simulated the impact of using quarantine only as well as isolation interventions only for a range of values of quarantine and isolation parameters.
Figures 7,8, 9 and 10 show the effectiveness of the quarantine strategy, similarly Figs. 11 and 12 show the effectiveness of the isolation of infected cases to control the evolution of viruses.
Fig. 7.
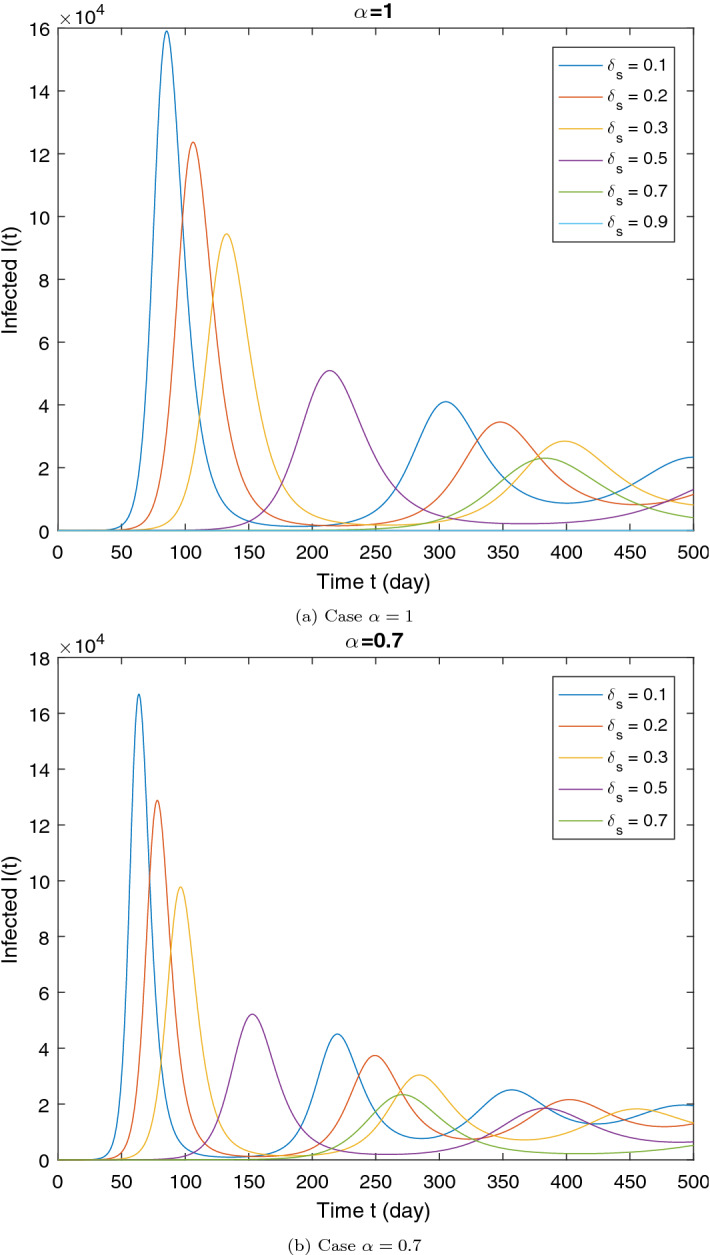
Illustration of the impact of quarantine rate on the dynamics of the infected (I) for two values of . All other parameters are given in the Table 1. The initial conditions are the same of the Section 7.2
Fig. 8.
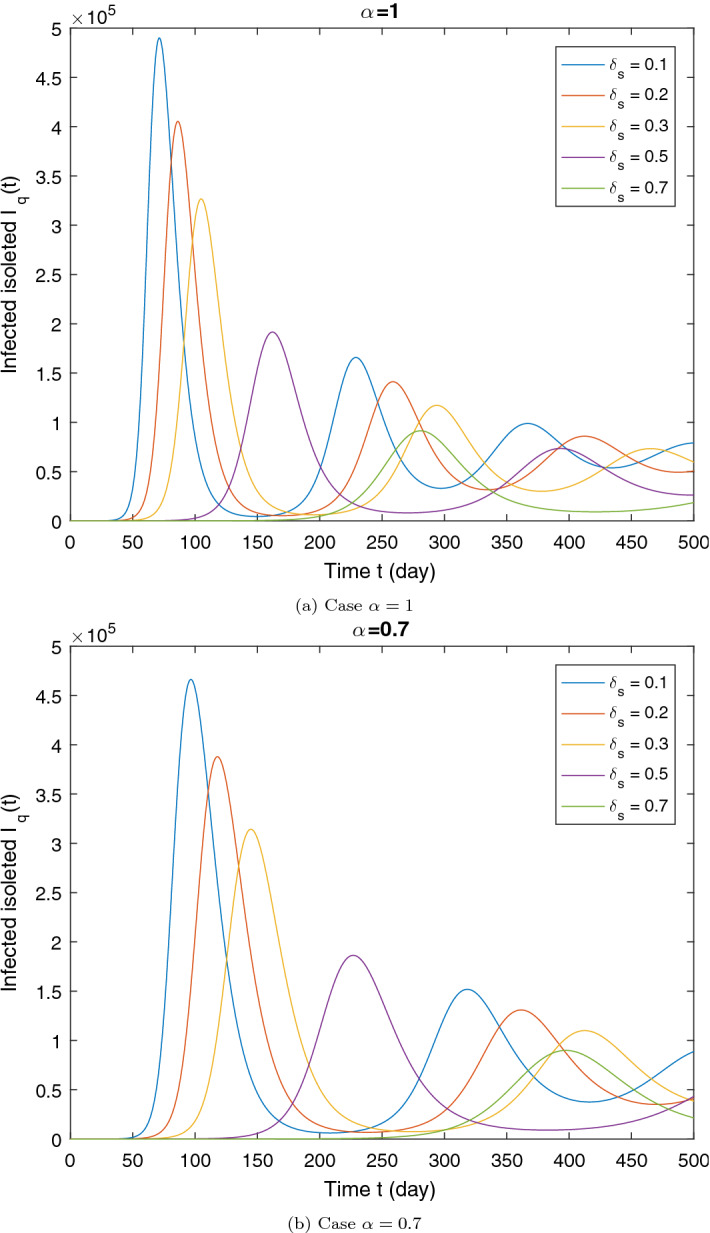
Illustration of the impact of quarantine rate on the dynamics of the infected quarantined () for two values of . All other parameters are given in the Table 1. The initial conditions are the same of the Section 7.2
Fig. 9.
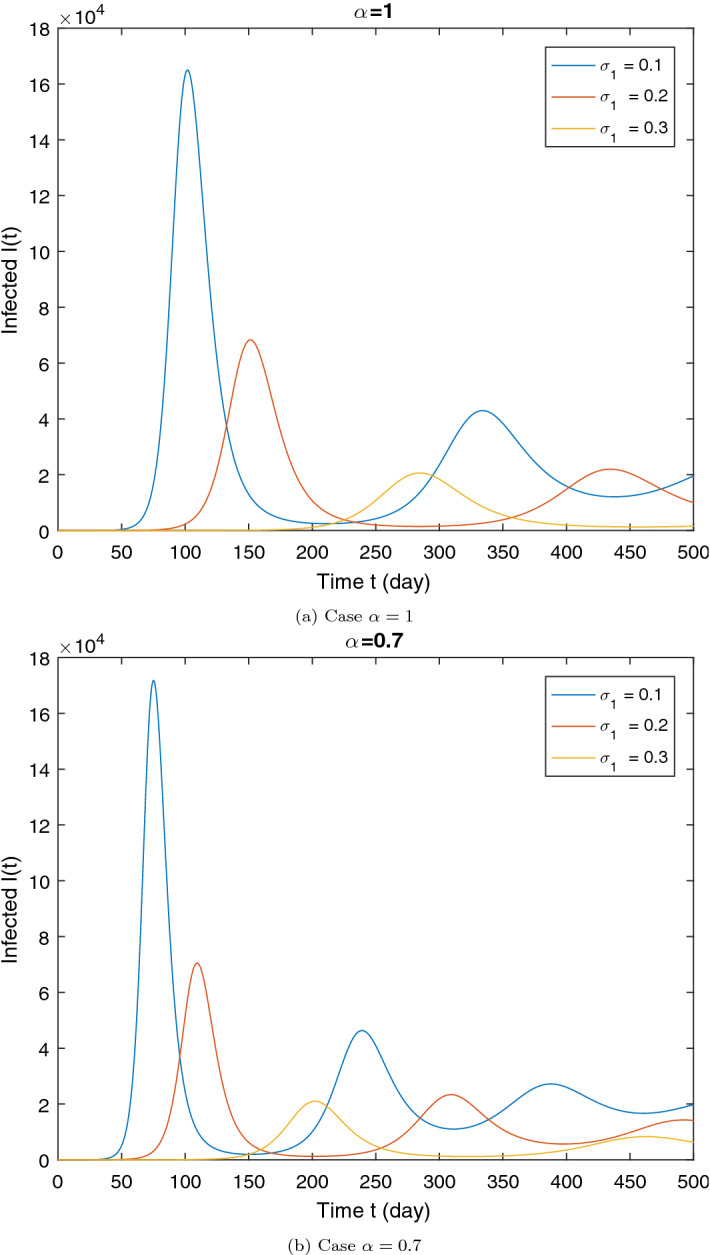
Illustration of the impact of quarantine rate on the dynamics of the infected (I) for two values of . All other parameters are given in the Table 1. The initial conditions are the same of the Section 7.2
Fig. 10.
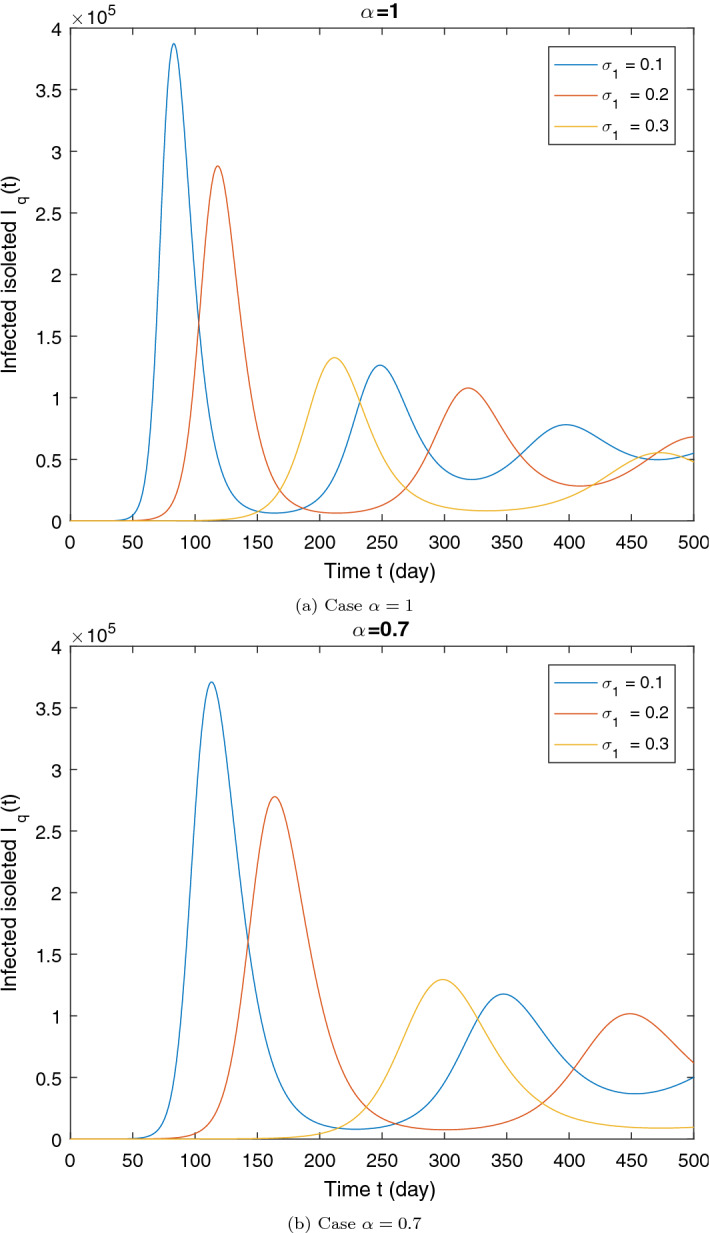
Illustration of the impact of quarantine rate on the dynamics of the infected quarantined () for two values of . All other parameters are given in the Table 1. The initial conditions are the same of the Section 7.2
Fig. 11.
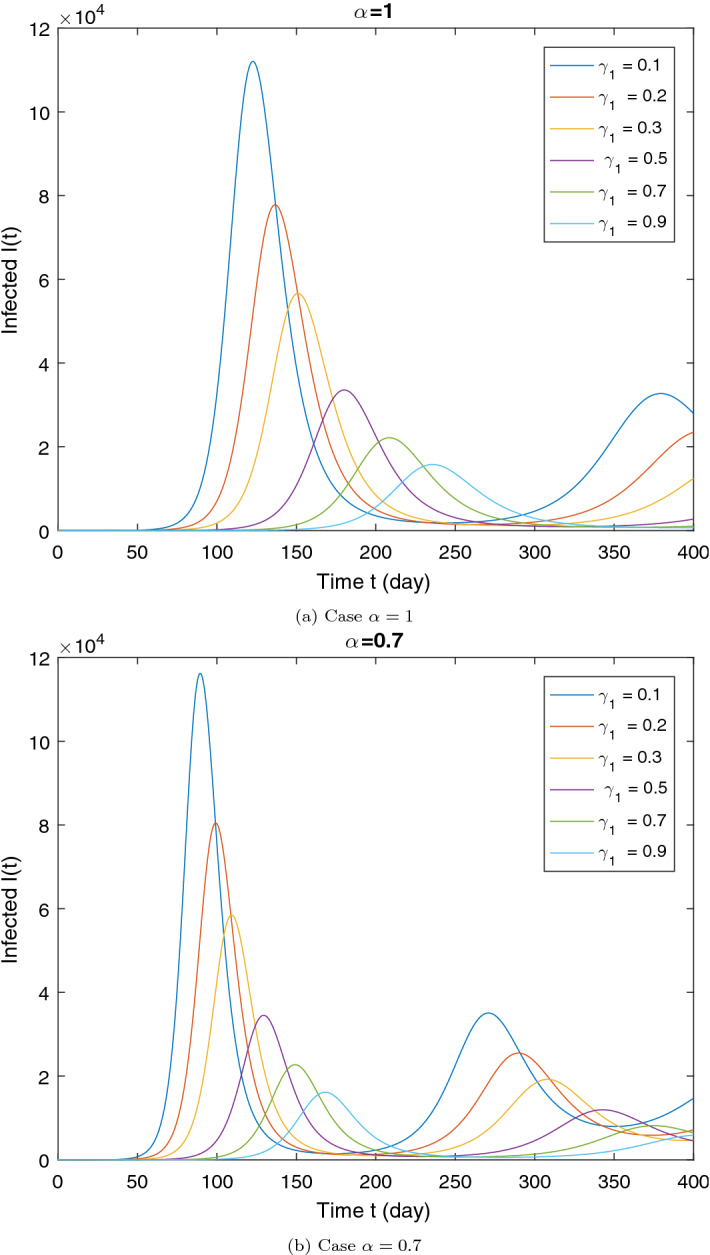
Illustration of the impact of isolation rate on the dynamics of the infected (I) for two values of . All other parameters are given in the Table 1. The initial conditions are the same of the Section 7.2
Fig. 12.
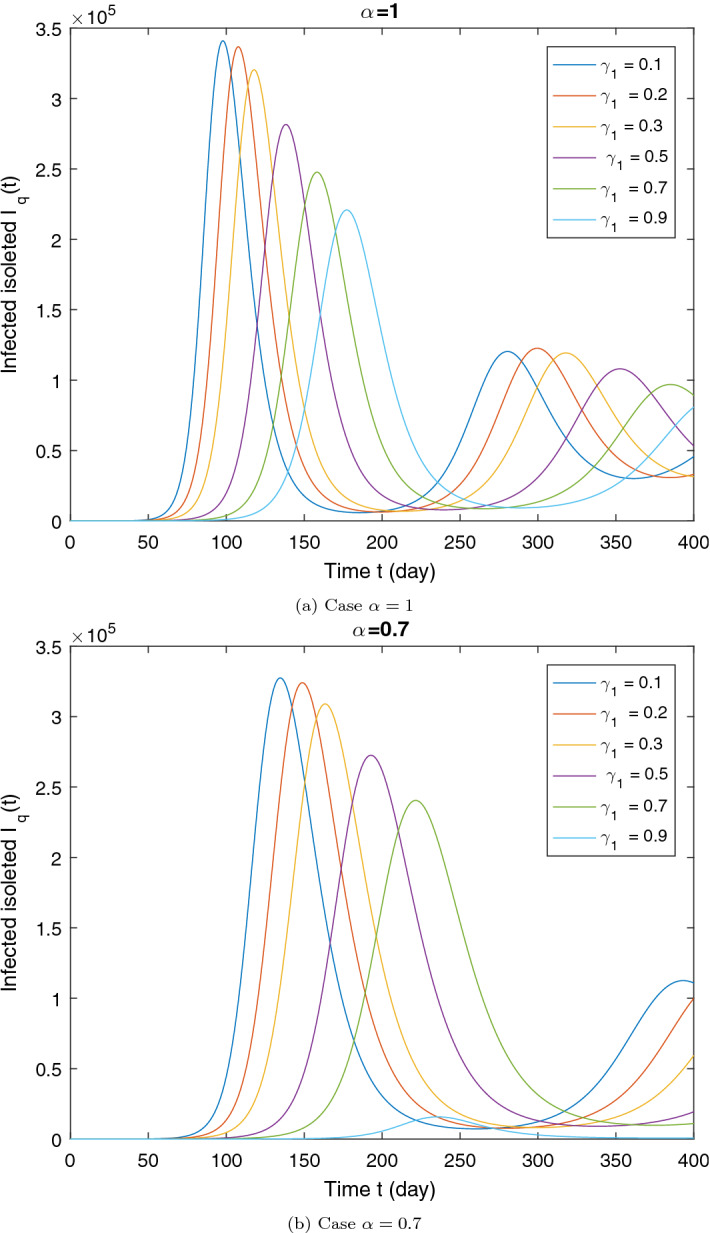
Illustration of the impact of isolation rate on the dynamics of the infected quarantined () for two values of . All other parameters are given in the Table 1. The initial conditions are the same of the Section 7.2
Fitting Model to Real Data
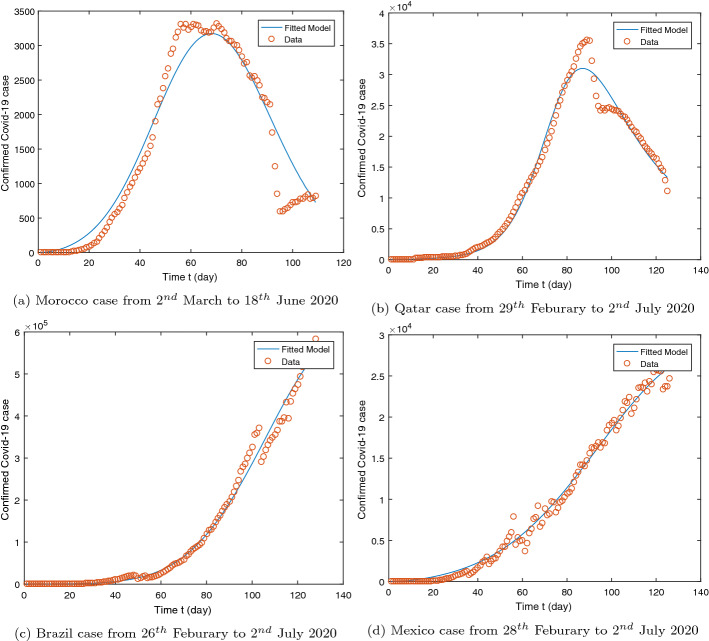
In this present section we have estimated the important model parameters and the fractional order using the infection cases (that are found on the WHO web-page) in Morocco, Qatar, Brazil and Mexico. The initial conditions used are given in the Table 4, we estimated the value of the fractional order for the four countries and we found 0.9533 for the Morocco model, 0.9418 for Qatar, 0.9906 for Brazil and 0.822 for Mexico. These values show the importance of the fractional order in the COVID-19 considered model and its influence to decrease the error of the of least squares method. In addition to making the proposed model more realistic and obtaining the average values of the acceptable parameters.
Table 4.
Initial values using in Fig. 13
| Country | N(0) [57] | S(0) | E(0) | I(0) | R(0) | |||
|---|---|---|---|---|---|---|---|---|
| Morocco | 36029093 | 9 | 1 | 0 | 3029079 | 3 | 1 | |
| Qatar | 2881053 | 58 | 15 | 0 | 880978 | 1 | 1 | |
| Mexico | 128929303 | 900 | 1 | 0 | 8928398 | 3 | 1 | |
| Brazil | 212569392 | 227 | 9 | 0 | 195805154 | 1 | 1 |
Now by analyzing the curves presented in Fig. 13, the importance role of quarantine and isolation in Morocco and Qatar in reducing the impact of the COVID-19, whilst Mexico and Brazil did not succeed in applying the quarantine well, which caused an increase in the number of people infected with the virus. Finally these values are kept low compared to potential values in the absence of a quarantine and isolation strategy (see Fig. 6, Tables 2 and 3 )
Fig. 13.
Fitting model to data in Morocco, Qatar, Brazil and Mexico (Real data source: WHO report of COVID-19)
Table 2.
Different values of quarantine reproduction number according to quarantine rate of susceptible individuals
| Values of | 0.1 | 0.2 | 0.3 | 0.5 | 0.7 | 0.9 |
|---|---|---|---|---|---|---|
| Values of () | 2.1652 | 1.9290 | 1.7394 | 1.4535 | 1.2484 | 1.0940 |
| Values of () | 1.3778 | 1.2276 | 1.1069 | 0.9250 | 0.7944 | 0.6962 |
Table 3.
Different values of quarantine reproduction number according to quarantine rate of exposed individuals
| Vlues of | 0.1 | 0.2 | 0.3 | 0.5 | 0.7 | 0.9 |
|---|---|---|---|---|---|---|
| Values of () | 2.1413 | 1.5923 | 1.2673 | 0.9000 | 0.6977 | 0.5697 |
Conclusion
In this manuscript, a Caputo–Fabrizio fractional differential equation model for COVID-19 with quarantine (of susceptible and exposed cases) and isolation (of symptomatic cases) has been investigate and the effect of each of them was studied. The existence and uniqueness of the system of solutions of the Caputo-Fabrizio model are established using a fixed-point theorem and an Picard iterative method. The m-step Adams-Bashforth approach is proposed to numerically approximate the solutions of the fractional model. We have compared the numerical simulations with respect to different values of the fractional order . Finally, The Method of Least Squares is used to determine the best fit to real data (real data for Morocco, Qatar, Brazil and Mexico). The paper gives an example of the use of the Caputo–Fabrizio fractional derivative as a model for real world problems (especially epidemiological problems).
Acknowledgements
The authors would like to thank the anonymous reviewers for their insightful suggestions and careful reading of the manuscript.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Abdo MS, Shah K, Wahash HA, Panchal SK. On a comprehensive model of the novel coronavirus (COVID-19) under Mittag-Leffler derivative. Chaos Solitons Fractals. 2020;135:109867. doi: 10.1016/j.chaos.2020.109867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ahmad Z, Arif M, Ali F, Khan I, Nisar KS. A report on covid-19 epidemic in pakistan using seir fractional model. Sci. Rep. 2020;10(1):1–14. doi: 10.1038/s41598-020-79405-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Alaoui AL, Azroul E, Hamou AA. Monotone iterative technique for nonlinear periodic time fractional parabolic problems. Adv. Theory Nonlinear Anal. Appl. 2020;4(3):194–213. [Google Scholar]
- 4.Alkahtani BST, Alzaid SS. A novel mathematics model of covid-19 with fractional derivative stability and numerical analysis. Chaos, Solitons Fractals. 2020;138:110006. doi: 10.1016/j.chaos.2020.110006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Alshomrani AS, Ullah MZ, Baleanu Dumitru. Caputo sir model for covid-19 under optimized fractional order. Adv. Differ. Equ. 2021;2021(1):1–17. doi: 10.1186/s13662-021-03345-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Area I, Batarfi H, Losada J, Nieto JJ, Shammakh W, Torres Á. On a fractional order Ebola epidemic model. Adv. Differ. Equ. 2015;2015(1):278. doi: 10.1186/s13662-015-0613-5. [DOI] [Google Scholar]
- 7.Atangana A. Modelling the spread of COVID-19 with new fractal-fractional operators: Can the lockdown save mankind before vaccination? Chaos Solitons Fractals. 2020;136:109860. doi: 10.1016/j.chaos.2020.109860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Atangana A, Baleanu D. New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. Therm. Sci. 2016 doi: 10.2298/TSCI160111018A. [DOI] [Google Scholar]
- 9.Atangana A, Baleanu D. Caputo-fabrizio derivative applied to groundwater flow within confined aquifer. J. Eng. Mech. 2017;143(5):D4016005. doi: 10.1061/(ASCE)EM.1943-7889.0001091. [DOI] [Google Scholar]
- 10.Atangana A, Koca I. Chaos in a simple nonlinear system with atangana-baleanu derivatives with fractional order. Chaos Solitons Fractals. 2016;89:447–454. doi: 10.1016/j.chaos.2016.02.012. [DOI] [Google Scholar]
- 11.Atangana A, Owolabi KM. New numerical approach for fractional differential equations. Math. Model. Nat. Phenom. 2018;13(1):3. doi: 10.1051/mmnp/2018010. [DOI] [Google Scholar]
- 12.Baba IA, Yusuf A, Nisar KS, Abdel-Aty AH, Nofal TA. Mathematical model to assess the imposition of lockdown during covid-19 pandemic. Results Phys. 2021;20:103716. doi: 10.1016/j.rinp.2020.103716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Backer JA, Klinkenberg D, Wallinga J. Incubation period of 2019 novel coronavirus (2019-nCoV) infections among travellers from Wuhan, China, 20–28 january 2020. Eurosurveillance. 2020;25(5):2000062. doi: 10.2807/1560-7917.ES.2020.25.5.2000062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Baleanu D, Aydogn SM, Mohammadi H, Rezapour S. On modelling of epidemic childhood diseases with the Caputo-Fabrizio derivative by using the Laplace Adomian decomposition method. Alex. Eng. J. 2020;59(5):3029–3039. [Google Scholar]
- 15.Baleanu D, Etemad S, Rezapour S. A hybrid caputo fractional modeling for thermostat with hybrid boundary value conditions. Bound. Value Probl. 2020;2020(1):1–16. [Google Scholar]
- 16.Baleanu D, Jajarmi A, Mohammadi H, Rezapour S. A new study on the mathematical modelling of human liver with caputo-fabrizio fractional derivative. Chaos Solitons Fractals. 2020;134:109705. [Google Scholar]
- 17.Baleanu D, Mohammadi H, Rezapour S. Analysis of the model of HIV-1 infection of CD4 T-cell with a new approach of fractional derivative. Adv. Differ. Equ. 2020;2020(1):1–17. [Google Scholar]
- 18.Boudaoui A, ElhadjMoussa Y, Hammouch Z, Ullah S. A fractional-order model describing the dynamics of the novel coronavirus (covid-19) with nonsingular kernel. Chaos Solitons Fractals. 2021;146:110859. doi: 10.1016/j.chaos.2021.110859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Caputo M, Fabrizio MD. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015;1(2):1–13. [Google Scholar]
- 20.Castillo-Chavez C, Castillo-Garsow CW, Yakubu A. Mathematical models of isolation and quarantine. JAMA. 2003;290(21):2876–2877. doi: 10.1001/jama.290.21.2876. [DOI] [PubMed] [Google Scholar]
- 21.Cheema, S.A., Kifayat, T., Rahman, A.R., Khan, U., Zaib, A., Khan, I., Nisar, K.S.: Is social distancing, and quarantine effective in restricting covid-19 outbreak? statistical evidences from Wuhan, China. Comput. Mater. Contin. 66(2) (2020)
- 22.Chimmalee B, Sawangtong W, Wiwatanapataphee B. The effects of community interactions and quarantine on a complex network. Cogent Math. 2016;3(1):1249141. doi: 10.1080/23311835.2016.1249141. [DOI] [Google Scholar]
- 23.Cohen J. New SARS-like virus in China triggers alarm. Science. 2020;367(6475):234–235. doi: 10.1126/science.367.6475.234. [DOI] [PubMed] [Google Scholar]
- 24.Danane J, Allali K, Hammouch Z, Nisar KS. Mathematical analysis and simulation of a stochastic covid-19 lévy jump model with isolation strategy. Results Phys. 2021;23:103994. doi: 10.1016/j.rinp.2021.103994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Dantas E, Tosin M, Cunha A., Jr Calibration of a SEIR-SEI epidemic model to describe the Zika virus outbreak in brazil. Appl. Math. Comput. 2018;338:249–259. doi: 10.1016/j.amc.2018.06.024. [DOI] [Google Scholar]
- 26.Dokuyucu MA, Dutta H. A fractional order model for Ebola virus with the new Caputo fractional derivative without singular kernel. Chaos Solitons Fractals. 2020;134:109717. doi: 10.1016/j.chaos.2020.109717. [DOI] [Google Scholar]
- 27.Erdem M, Safan M, Castillo-Chavez C. Mathematical analysis of an SIQR influenza model with imperfect quarantine. Bull. Math. Biol. 2017;79(7):1612–1636. doi: 10.1007/s11538-017-0301-6. [DOI] [PubMed] [Google Scholar]
- 28.Ghanbari B, Atangana A. A new application of fractional atangana-baleanu derivatives: Designing abc-fractional masks in image processing. Phys. A. 2020;542:123516. doi: 10.1016/j.physa.2019.123516. [DOI] [Google Scholar]
- 29.Hamou, A.A., Azroul, E.H., Hammouch, Z., Alaoui, A.L.: A fractional multi-order model to predict the COVID-19 outbreak in Morocco. Appl. Comput. Math. 20(1), 177–203 (2020)
- 30.Higazy M. Novel fractional order SIDARTHE mathematical model of COVID-19 pandemic. Chaos Solitons Fractals. 2020;138:110007. doi: 10.1016/j.chaos.2020.110007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hussain G, Khan T, Khan A, Inc M, Zaman G, Nisar KS, Akgül A. Modeling the dynamics of novel coronavirus (covid-19) via stochastic epidemic model. Alex. Eng. J. 2021;60(4):4121–4130. doi: 10.1016/j.rinp.2021.104004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Jorge, L., Nieto, J.J.: Properties of a new fractional derivative with out singular kernel. Prog. Fract. Differ. Appl. Int. J. 87–92 (2015). http://www.naturalspublishing.com/files/published/2j1ns3h8o2s789.pdf
- 33.Kumar D, Singh J, Al Qurashi M, Baleanu D. A new fractional SIRS-SI malaria disease model with application of vaccines, antimalarial drugs, and spraying. Adv. Differ. Equ. 2019;2019(1):278. doi: 10.1186/s13662-019-2199-9. [DOI] [Google Scholar]
- 34.Kumar S, Cao J, Abdel-Aty M. A novel mathematical approach of COVID-19 with non-singular fractional derivative. Chaos Solitons Fractals. 2020;139:110048. doi: 10.1016/j.chaos.2020.110048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lauer Stephen A, Grantz Kyra H, Bi Qifang, Jones Forrest K, Zheng Qulu, Meredith Hannah R, Azman Andrew S, Reich Nicholas G, Lessler Justin. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Ann. Intern. Med. 2020;172(9):577–582. doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Li MY. An Introduction to Mathematical Modeling of Infectious Diseases. New York: Springer; 2018. [Google Scholar]
- 37.Logeswari, K., Ravichandran, C., Nisar, K.S.: Mathematical model for spreading of covid-19 virus with the mittag–leffler kernel. Numer. Methods Partial Differ. Equ. (2020) [DOI] [PMC free article] [PubMed]
- 38.Mohammadi H, Kumar S, Rezapour S, Etemad S. A theoretical study of the caputo-fabrizio fractional modeling for hearing loss due to mumps virus with optimal control. Chaos Solitons Fractals. 2021;144:110668. [Google Scholar]
- 39.Moore EJ, Sirisubtawee S, Koonprasert S. A caputo-fabrizio fractional differential equation model for HIV/AIDS with treatment compartment. Adv. Diff. Equ. 2019;2019(1):200. doi: 10.1186/s13662-019-2138-9. [DOI] [Google Scholar]
- 40.National Health Commission of the People’s Republic of China: Accessed: (23 January 2020). http://www.nhc.gov.cn/xcs/xxgzbd/gzbd_index.shtml [DOI] [PMC free article] [PubMed]
- 41.Nisar KS, Ahmad S, Ullah A, Shah K, Alrabaiah H, Arfan M. Mathematical analysis of sird model of covid-19 with caputo fractional derivative based on real data. Results Phys. 2021;21:103772. doi: 10.1016/j.rinp.2020.103772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Peter, O.J., Shaikh, A.S., Ibrahim, M.O., Nisar, K.S., Baleanu, D., Khan, I., Abioye A.I.: Analysis and dynamics of fractional order mathematical model of covid-19 in nigeria using atangana-baleanu operator. Comput. Mater. Contin. 66(2), (2020)
- 43.Rezapour S, Etemad S, Mohammadi H. A mathematical analysis of a system of Caputo-Fabrizio fractional differential equations for the anthrax disease model in animals. Adv. Differ. Equ. 2020;2020(1):1–30. [Google Scholar]
- 44.Rezapour S, Mohammadi H, Jajarmi A. A new mathematical model for Zika virus transmission. Adv. Differ. Equ. 2020;2020(1):1–15. [Google Scholar]
- 45.Sahoo P, Mondal HS, Hammouch Z, Abdeljawad T, Mishra D, Reza M. On the necessity of proper quarantine without lock down for 2019-ncov in the absence of vaccine. Results Phys. 2021;25:104063. doi: 10.1016/j.rinp.2021.104063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Shaikh AS, Shaikh IN, Nisar KS. A mathematical model of covid-19 using fractional derivative: outbreak in india with dynamics of transmission and control. Adv. Differ. Equ. 2020;2020(1):1–19. doi: 10.1186/s13662-020-02834-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Singh J, Kumar D, Baleanu D. On the analysis of fractional diabetes model with exponential law. Adv. Differ. Equ. 2018;2018(1):1–15. doi: 10.1186/s13662-018-1680-1. [DOI] [Google Scholar]
- 48.Singh J, Kumar D, Hammouch Z, Atangana A. A fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl. Math. Comput. 2018;316:504–515. doi: 10.1016/j.amc.2017.08.048. [DOI] [Google Scholar]
- 49.Singh H, Srivastava HM, Hammouch Z, Nisar KS. Numerical simulation and stability analysis for the fractional-order dynamics of covid-19. Results Phys. 2021;20:103722. doi: 10.1016/j.rinp.2020.103722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Tang B, Wang X, Li Q, Bragazzi NL, Tang S, Xiao Y, Jianhong W. Estimation of the transmission Risk of the 2019-nCoV and its implication for public health interventions. J. Clin. Med. 2020;9(2):462. doi: 10.3390/jcm9020462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Thabet STM, Etemad S, Rezapour S. On a new structure of the pantograph inclusion problem in the Caputo conformable setting. Bound. Value Probl. 2020;2020(1):1–21. [Google Scholar]
- 52.Toufik M, Atangana A. New numerical approximation of fractional derivative with non-local and non-singular kernel: application to chaotic models. Eur. Phys. J. Plus. 2017;132(10):444. doi: 10.1140/epjp/i2017-11717-0. [DOI] [Google Scholar]
- 53.Tuan NH, Mohammadi H, Rezapour S. A mathematical model for covid-19 transmission by using the caputo fractional derivative. Chaos Solitons Fractals. 2020;140:110107. doi: 10.1016/j.chaos.2020.110107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Tulu TW, Tian B, Zunyou W. Modeling the effect of quarantine and vaccination on Ebola disease. Adv. Differ. Equ. 2017;2017(1):1–14. doi: 10.1186/s13662-017-1225-z. [DOI] [Google Scholar]
- 55.United Nations Population Division: UNdata: Crude death rate per 1000 population, Accessed: (17 June 2020). http://data.un.org/Data.aspx?q=world+death+rate&d=PopDiv&f=variableID%3a65%3bcrID%3a1802%2c900
- 56.Van den Driessche P, Watmough J, Pauline W. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002;180(1–2):29–48. doi: 10.1016/S0025-5564(02)00108-6. [DOI] [PubMed] [Google Scholar]
- 57.Worldometer: International team of developers, researchers and volunteers, Accessed: (5 July 2020). https://www.worldometers.info/world-population
- 58.Yang XJ, Baleanu D. Fractal heat conduction problem solved by local fractional variation iteration method. Therm. Sci. 2013;17(2):625–628. doi: 10.2298/TSCI121124216Y. [DOI] [Google Scholar]
- 59.Yang Q, Chen D, Zhao T, Chen YQ. Fractional calculus in image processing: a review. Fract. Calc. Appl. Anal. 2016;19(5):1222–1249. doi: 10.1515/fca-2016-0063. [DOI] [Google Scholar]
- 60.Zamir M, Nadeem F, Abdeljawad T, Hammouch Z. Threshold condition and non pharmaceutical interventions’s control strategies for elimination of covid-19. Results Phys. 2021;20:103698. doi: 10.1016/j.rinp.2020.103698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Zengyun H, Cui Q, Han J, Wang X, Wei EI, Teng Z. Evaluation and prediction of the COVID-19 variations at different input population and quarantine strategies, a case study in guangdong province, china. Int. J. Infectious Dis. 2020;95:231–240. doi: 10.1016/j.ijid.2020.04.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Zhang Z. A novel covid-19 mathematical model with fractional derivatives: Singular and nonsingular kernels. Chaos Solitons Fractals. 2020 doi: 10.1016/j.chaos.2020.110060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Zhang Y, Xiangnan Y, Sun HG, Tick GR, Wei W, Jin B. Applicability of time fractional derivative models for simulating the dynamics and mitigation scenarios of COVID-19. Chaos Solitons Fractals. 2020;138:109959. doi: 10.1016/j.chaos.2020.109959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Zhao S, Lin Q, Ran J, Musa SS, Yang G, Wang W, Lou Y, Gao D, Yang L, He D, Wang MH. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: a data-driven analysis in the early phase of the outbreak. Int. J. Infectious Dis. 2020;92:214–217. doi: 10.1016/j.ijid.2020.01.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Zhao S, Musa SS, Lin Q, Ran J, Yang G, Wang W, Lou Y, Yang L, Gao D, He D, et al. Estimating the unreported number of novel coronavirus (2019-nCoV) cases in China in the first half of january 2020: A data-driven modelling analysis of the early outbreak. J. Clin. Med. 2020;9(2):388. doi: 10.3390/jcm9020388. [DOI] [PMC free article] [PubMed] [Google Scholar]