Evaluation of government strategies against COVID-19 pandemic using q-rung orthopair fuzzy TOPSIS method

Abstract

The COVID-19 outbreak, which emerged in China and continues to spread rapidly all over the world, has brought with it increasing numbers of cases and deaths. Governments have suffered serious damage and losses not only in the field of health but also in many other fields. This has directed governments to adopt and implement various strategies in their communities. However, only a few countries succeed partially from the strategies implemented while other countries have failed. In this context, it is necessary to identify the most important strategy that should be implemented by governments. A decision problem based on the decisions of many experts, with some contradictory and multiple criteria, should be taken into account in order to evaluate the multiple strategies implemented by various governments. In this study, this decision process is considered as a multi-criteria decision making (MCDM) problem that also takes into account uncertainty. For this purpose, q-rung orthopair fuzzy sets (q-ROFSs) are used to allow decision-makers to their assessments in a wider space and to better deal with ambiguous information. Accordingly, two different Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) approaches are recommended under the q-ROFS environment and applied to determine the most appropriate strategy. The results of the proposed approaches determine the A1 — Mandatory quarantine and strict isolation strategy as the best strategy. Comparisons with other q-rung orthopair fuzzy MCDM methods and intuitionistic fuzzy TOPSIS method are also presented for the validation of the proposed methods. Besides, sensitivity analyses are conducted to check the robustness of the proposed approaches and to observe the effect of the change in the q parameter.

1. Introduction

Coronaviruses are enveloped non-segmented positive-sense RNA viruses and broadly infected in mainly humans and other mammals. Although the coronavirus infections in most humans are mild, the epidemics of the two betacoronaviruses, severe acute respiratory syndrome coronavirus (SARS-CoV) and Middle East respiratory syndrome coronavirus (MERS-CoV) have resulted in numerous deaths [1]. The high prevalence and wide distribution of coronaviruses have the potential to reveal newer and severe events [1], [2].

In December 2019, a series of patients with pneumonia of unexplained cause associated with the 2019 novel coronavirus (2019-nCoV) has emerged in Wuhan, China [1]. The epidemic starting in China has been spread to other countries such as Italy, Japan, ABD, England, Spain, Turkey and many cases have confirmed. Furthermore, this epidemic has resulted in the death of many cases worldwide. The COVID-19 virus, which continues to spread very easily and sustainably among people, has been described as a pandemic by the World Health Organization (WHO) on 11 March. Data published by WHO as of November 9, 2020, contain information that the epidemic has spread to 219 countries, there are more than 50 million confirmed cases and more than 1.2 million confirmed deaths globally [3].

The number of studies on such a serious epidemic, the cause of which is not yet known and has no cure, has increased continuously in a short time. Ebrahim et al. [4] proposed several strategies that could reduce the spread of COVID-19 over the community. They stressed that country-specific timing is a critical determinant to reduce the effects of the outbreak. Anderson et al. [5] emphasized that various measures should be taken to improve the inevitable economic decline of governments due to the epidemic and what these measures could be. Whang et al. [6] provided information on the protection of medical personnel in China and the reassignment of their medical resources. Marcel et al. [7] explained the importance of testing, contact tracing, and self-isolation until vaccination or treatments are available to prevent the COVID-19 epidemic in Switzerland. Fang et al. [8] simulated the spread dynamics of the COVID-19 epidemic and the effect of different control measures, conducted a sensitivity analysis to identify the key factor. There are several other important studies on modeling the spread of the COVID-19 pandemic (Parè et al. [9]; Rahimi et al. [10]; Carli et al. [11]; Giordano et al. [12]).

The COVID-19 epidemic has caused many effects such as economic, social, and psychological, in addition to its serious and great impact on health worldwide and this has directed the researchers to carry out more studies on this epidemic. 936 studies have been published in just three months according to the Scopus database and many reports are published daily by WHO. The rapid spread of the COVID-19 epidemic has prompted countries to adopt various strategies by directing to take many measures. For example, countries such as China, Italy have imposed the curfew, countries such as Turkey, France, and Belgium have imposed partial curfew, England has released its people to gain immunity. Due to the COVID-19 epidemic which negatively affects countries in all respects and becomes a major threat, it is necessary to determine the most effective strategy for governments by considering variety of criteria, however, there is no study in the literature that can help governments in this topic.

The assessment of governmental strategies involves several conflicting criteria such as cost minimization and digital technology purchase, which you must handle by a multiple criteria decision-making method. MCDM methods, an effective method in dealing with complex problems simultaneously evaluate various criteria by including the opinion of multiple decision-makers (DMs). Therefore, MCDM methods can be successfully used in determining the best strategy for governments. Dotoli et al. [13] present a taxonomy on multi criteria group decision making under uncertainty. They perform a comparative analysis among some selected well-known MCDM techniques, namely the Analytic Hierarchy Process (AHP), the Preference Ranking Organization METHod for Enrichment of Evaluations (PROMETHEE), the Multi Attribute Utility Theory (MAUT), and the Data Envelopment Analysis (DEA) to show how they can properly support the specific decision-making process of Public Procurement (PP) tenders. A comparison analysis is extended to the fuzzy counterparts of AHP and DEA, showing that these methods can be effectively applied to the PP sector under uncertainty. There are available numerous MCDM methods such as AHP [14], Analytic Network Process (ANP) [15], Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) [16], Vise Kriterijumska Optimizacija I Kompromisno Resenje (VIKOR) [17], Elimination and Choice Translating Reality English (ELECTRE) [18] in the literature. TOPSIS method, which is a simple and useful MCDM method, is a distance-based method aiming to choose the best alternative with the shortest distance from the positive ideal solution (PIS) and the farthest distance from the negative ideal solution (NIS) [19].

The choice of the model under uncertainty depends on availability of data. The data are obtained from the experts’ knowledge based on a very short period of time since there is not yet much information about COVID-19 pandemic. If sufficient observations had been handled, stochastic modeling could be used. Although decision-makers express their opinions as a crisp value in the classical TOPSIS method, when uncertain and vague information takes into account in decision making, these crisp values are often insufficient and inadequate for the solution of real decision-making problems [20]. To handle such type of vagueness, Zadeh [21] introduced the fuzzy set theory in 1965. Ordinary fuzzy sets represented with a membership function that has a value between zero and one have been developed several extensions of its to determine a clear solution in more complex decision-making problems [20]. After were introduced type-2 fuzzy sets by Zadeh [22] in 1975, Atanassov [23] extended the fuzzy sets into the intuitionistic fuzzy sets (IFSs) represented with membership and non-membership degrees including the hesitancy of decision-makers [24]. Hesitant fuzzy sets (HFSs) introduced by Torra [25] are the extension of fuzzy sets allowing a set of values that are many potential degrees of membership of an element [24]. After intuitionistic type-2 fuzzy sets (IFS2) proposed by Atannasov [26] in 1999, Yager [27] called them as Pythagorean fuzzy sets (PFSs) in 2013. PFSs are characterized by a membership degree and a non-membership degree providing the condition that the square sum of membership and non-membership degrees is equal to one at most. Later, Yager [28] introduced q-rung orthopair fuzzy sets (q-ROFSs) representing a general class of IFSs and PFSs. q-ROFSs are characterized with both membership and non-membership degrees of an element in a fuzzy set and the sum of their qth power has to at most equal to 1. Yager expressed that as q increases the range of acceptable orthopairs increases and thus enables the experts more freedom than the other fuzzy set extensions in expressing their belief about membership grade [28]. The recent extensions of ordinary fuzzy sets such as PFSs and fermatean fuzzy sets (FFSs) are based on the certain powers of membership and non-membership degrees, which all aim at enlarging the domain area for the assignment of these degrees and almost have the same theoretical basis that is not so different. An inclusive fuzzy set extension of PFSs and FFSs is q-ROFSs, which is a generalization of intuitionistic fuzzy sets. Thus, we prefer q-ROFSs by considering the liberty of choosing the degree of power. This study aims at proposing a q-rung orthopair fuzzy (q-ROF) MCDM method for better handling of vagueness and imprecise information.

The contribution of our study is to develop a decision support system (DSS) for the assessment of governmental strategies against COVID-19 pandemic. In the developed DSS, the originalities of our study are as follows. It is known that in the literature there is no study evaluating the government strategies for a new type of coronavirus with a MCDM method. Due to this lack of literature, the main motivation of our study is to assess by using fuzzy-based MCDM method the strategies of governments for the COVID-19 epidemic, which is currently a major threat. The developed two methods are the linguistic q-ROF TOPSIS methods, based on the linguistic scales proposed by us in the literature, one scale for weighting the criteria and another one for the evaluations in the decision matrix. The weights are produced by an aggregation operator in the first method whereas we employ an entropy based weighted criteria in the second one. Comparisons with other q-ROF MCDM methods and intuitionistic fuzzy TOPSIS method are also presented for the validation of the proposed methods. A sensitivity analysis is conducted on the changes in the values of the q parameter to show and verify how the attitude of the decision maker has a change on the results. Additionally, we applied a scenario analysis to show the dynamic structure of our proposed methods on the considered problem.

In the study, q-ROFSs are used as it provides a stronger definition of uncertainty and thus more accurate management of the decision-making process by allowing decision makers to make an assessment in a wider area due to the uncertainties that arise in the problems addressed and the lack of information and inconsistencies between expert groups. The criteria and alternatives to be used in the study are determined by examining the papers and reports in the literature and taking into account the expert opinions.

The rest of this paper is organized as follows. A literature review on COVID-19 and its MCDM methodologies and q-ROF MCDM methods is presented in Section 2. The preliminaries of IFSs, PFSs, and q-ROFSs, are given in Section 3. The details of the proposed approaches based on q-ROF TOPSIS are presented in Section 4. Application of the approaches, sensitivity analysis and comparative analysis are presented in Section 5. Finally, the study is concluded in Section 6.

2. Literature review

Our literature review is divided into two subsections. In the first subsection of the “literature review”, MCDM methods on COVID-19 problems are summarized and in the second subsection q-ROFSs based MCDM methods are analyzed.

2.1. Literature review: MCDM on COVID-19 problems

COVID-19, caused by a new coronavirus, is a respiratory pandemic spreading from person to person. Although the number of studies conducted on this epidemic that spread rapidly in a very short time is very high, studies using MCDM methods are limited in the literature. These studies have been briefly summarized in the following.

Majumder et al. [29] proposed a new TOPSIS approach in identifying the most important risk factor for COVID-19. In the proposed method, first time supremum metric for ideal solution is used instead of Euclidean distance. Mohammed et al. [30] developed an integrated MCDM method to evaluate the different diagnostic models for COVID19 according to the determined criteria. In the proposed approach, the entropy method is used for determining the criteria weights and the TOPSIS method is used for the ranking of the COVID-19 diagnostic models. Yang et al. [31] introduced a decision support algorithm based on the novel concept of the spherical normal fuzzy (SpNoF) set. In the study, the new score and accuracy function, the SpNoF Bonferroni mean operator and the weighted Bonferroni mean operator are developed. A multi-criteria decision-making method is established for antivirus mask selection over the COVID-19 pandemic based on the proposed SpNoF operators. The sensitivity and comparative analyses are conducted to check the availability and superiority of the proposed method. Albahri et al. [32] proposed an intelligence-integrated concept in the determination of the most suitable convalescent plasma and the prioritization of patients with COVID-19 for helping doctors hasten treatments. In the study, a new MCDM method called subjective and objective decision by opinion score method (SODOSM) is proposed, which consists of integrating several MCDM methods. Requia et al. [33] presented a MCDM model based on the AHP method for ranking how each community attribute may influence the spread or control of COVID-19 at the municipal level. Albahri et al. [34] developed an integrated AHP and VIKOR approach for evaluation and benchmarking AI techniques used in the classification of COVID-19 medical images.

2.2. Literature review: MCDM based on q-ROFSs

q-ROFSs have been used in MCDM methods recently. Studies applying a MCDM method based on q-ROFSs have been briefly analyzed in the following.

Banerjee et al. [35] developed a closeness index-based q-ROF qualitative flexible (QUALIFLEX) methodology. Pinar and Boran [36] introduced q-ROF TOPSIS and q-ROF ELECTRE based on the group decision-making approach for the supplier selection problem. Joshi and Gegov [37] used them in a MCDM problem by proposing some q-ROF aggregation operators. Wang et al. [38] introduced the q-ROF multi-attributive border approximation area comparison (MABAC) model to solve multiple attribute group decision making (MAGDM) problems. Liu and Wang [39] proposed the q-ROF weighted averaging operator and the q-ROF weighted geometric operator to handle the multi-attribute decision making (MADM) problems under the fuzzy environment. Krishankumar et al. [40] proposed the q-ROF complex proportional assessment (COPRAS) method for a renewable energy source prioritization problem. Wang et al. [41] proposed a new q-ROF linguistic method to handle the supplier selection problem. Hussain et al. [42] proposed a new hybrid q-ROF approach covering rough set and TOPSIS. Xu et al. [43] presented a new MADM approach by developing interval-valued q-rung dual hesitant fuzzy sets and also proposed new aggregation operators based on fuzzy sets developed. Deng et al. [44] combined a q-ROFS with the multiplicative multi-objective optimization by ratio analysis method and introduced an optimization-based consensus model. Li et al. [45] proposed q-rung picture linguistic set (q-RPLS) to solve MAGDM problems and introduced new aggregation operators based on the proposed q-RPLS. Mi et al. [46] introduced q-ROF VIKOR method integrated with the best worst method based on the proposed new score function. Huang and Wei [47] developed the interval-valued q-rung orthopair fuzzy (IVq-ROF) method. Liu et al. [48] proposed IVq-ROF multi-objective optimization based on ratio analysis plus the full multiplicative form (IVq-ROF-MULTIMOORA) method. Darko and Liang [49] introduced some q-ROF Hamacher aggregation operators and demonstrated their application by developing q-ROF Evaluation Based on Distance from Average Solution (EDAS) method.

3. Q-rung orthopair fuzzy sets: Preliminaries

In this section, basic notions and operations of IFSs, PFSs, and q-ROFSs are briefly reviewed.

3.1. Intuitionistic fuzzy sets

Intuitionistic fuzzy sets as an extension of the ordinal fuzzy set theory was introduced by Atanassov in 1986. IFSs are characterized by membership degree and non-membership degree that their sum is one or less than one. It is demonstrated as given in Definition 3.1 [23].

Definition 3.1

Let $X$ be a fixed set. An IFS $\tilde{I}$ in $X$ is an object having the form given by:

$$\tilde{I}=\left\{\left(x,{\mu }_{\tilde{I}}\left(x\right),{\vartheta }_{\tilde{I}}\left(x\right)\right)|x\epsilon X\right\}$$ (1)

where the function ${\mu }_{\tilde{I}}:X\to \left[0,1\right]$ and ${\vartheta }_{\tilde{I}}:X\to \left[0,1\right]$ defines the degree of membership and the degree of non-membership of an element to the sets $\tilde{I}$, respectively, with the condition that

$$0\le {\mu }_{\tilde{I}}\left(x\right)+{\vartheta }_{\tilde{I}}\left(x\right)\le 1,for\forall x\epsilon X$$ (2)

The degree of hesitancy is calculated as follows:

$${\pi }_{\tilde{I}}\left(x\right)=1-{\mu }_{\tilde{I}}\left(x\right)-{\vartheta }_{\tilde{I}}\left(x\right)$$ (3)

Definition 3.2

Let $\tilde{A}=\left({\mu }_{\tilde{A}},{\vartheta }_{\tilde{A}}\right)$ and $\tilde{B}=\left({\mu }_{\tilde{B}},{\vartheta }_{\tilde{B}}\right)$ be two intuitionistic fuzzy numbers (IFNs), then the addition and multiplication operations on these two IFNs were defined by Atanassov as follows:

$$\tilde{A}\oplus \tilde{B}=\left({\mu }_{\tilde{A}}+{\mu }_{\tilde{B}}-{\mu }_{\tilde{A}}{\mu }_{\tilde{B}},{\vartheta }_{\tilde{A}}{\vartheta }_{\tilde{B}}\right)$$ (4)

$$\tilde{A}\otimes \tilde{B}=\left({\mu }_{\tilde{A}}{\mu }_{\tilde{B},}{\vartheta }_{\tilde{A}}+{\vartheta }_{\tilde{B}}-{\vartheta }_{\tilde{A}}{\vartheta }_{\tilde{B}}\right)$$ (5)

3.2. Pythagorean fuzzy sets

Pythagorean fuzzy sets have been introduced by Yager [27] as an extension of the intuitionistic fuzzy set. PFSs are characterized by two membership degrees named as membership and non-membership. In PFSs unlike IFSs, the sum of membership degree and non-membership degree assigned by decision-makers may be more than 1, but the sum of their squares has to be at most 1. PFSs are described as given in Definition 3.3.

Definition 3.3

Let $X$ be a fixed set. A Pythagorean fuzzy set $\tilde{P}$ in $X$ is an object having the form [50]:

$$\tilde{P}=\left\{〈x,{\mu }_{\tilde{P}}\left(x\right),{\vartheta }_{\tilde{P}}\left(x\right)〉|x\epsilon X\right\}$$ (6)

where the function ${\mu }_{\tilde{P}}:X\to \left[0,1\right]$ defines the degree of membership and ${\vartheta }_{\tilde{P}}:X\to \left[0,1\right]$ defines the degree of non-membership of the element $x\epsilon X$ to $\tilde{P}$, respectively, and for every $x\epsilon X$, it holds that:

$$0\le {\left({\mu }_{\tilde{P}}\left(x\right)\right)}^2+{\left({\vartheta }_{\tilde{P}}\left(x\right)\right)}^2\le 1$$ (7)

The degree of hesitancy is calculated as follows:

$${\pi }_{\tilde{P}}\left(X\right)=\sqrt{1-{\mu }_{\tilde{P}}{\left(x\right)}^2-{\vartheta }_{\tilde{P}}{\left(x\right)}^2}$$ (8)

Definition 3.4

Let ${\tilde{P}}_1=\left({{\mu }_{\tilde{P}}}_1,{{\vartheta }_{\tilde{P}}}_1\right)$ and ${\tilde{P}}_2=\left({{\mu }_{\tilde{P}}}_2,{{\vartheta }_{\tilde{P}}}_2\right)$ be two Pythagorean fuzzy numbers (PFNs), then the operations of these two PFNs are defined as follows [50]:

$${\tilde{P}}_1\oplus {\tilde{P}}_2=\left(\sqrt{{{{\mu }_{\tilde{P}}}_1}^2+{{{\mu }_{\tilde{P}}}_2}^2-{{{\mu }_{\tilde{P}}}_1}^2{{{\mu }_{\tilde{P}}}_2}^2},{{\vartheta }_{\tilde{P}}}_1{{\vartheta }_{\tilde{P}}}_2\right)$$ (9)

$${\tilde{P}}_1\otimes {\tilde{P}}_2=\left({{\mu }_{\tilde{P}}}_1{{\mu }_{\tilde{P}}}_2,\sqrt{{{{\vartheta }_{\tilde{P}}}_1}^2+{{{\vartheta }_{\tilde{P}}}_2}^2-{{{\vartheta }_{\tilde{P}}}_1}^2{{{\vartheta }_{\tilde{P}}}_2}^2}\right)$$ (10)

3.3. Q-rung orthopair fuzzy sets

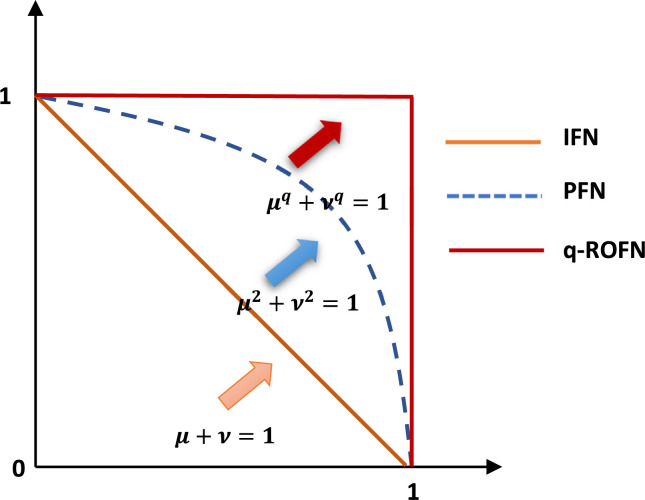
q-rung orthopair fuzzy sets introduced by Yager [28] in 2018 are represented with the degree of membership and non-membership. In q-ROFSs, the sum of the qth power of the membership and non-membership degrees must be at most equal to one [51]. In Fig. 1, it is easily observed that q ROFSs have an acceptable membership grade space larger than of IFSs and PFSs. q-ROFSs are described as demonstrate in Definition 3.5.

Fig. 1.

Geometric space range of IFNs, PFNs, and q-ROFNs.

Definition 3.5

A q-ROFS $\tilde{Q}$ in a finite universe of discourse X is defined as follows by Yager [51].

$$\tilde{Q}=\left\{\left(x,{\mu }_{\tilde{Q}}\left(x\right),{\vartheta }_{\tilde{Q}}\left(x\right)\right)|x\epsilon X\right\}$$ (11)

where the function ${\mu }_{\tilde{Q}}:X\to \left[0,1\right]$ denotes the degree of membership and ${\upsilon }_{\tilde{Q}}:X\to \left[0,1\right]$] denotes the degree of non-membership of the element x $\varepsilon$ X to the set $\tilde{Q}$, respectively, with the condition that $0\le {\mu }_{\tilde{Q}}\left(x\right)+{\vartheta }_{\tilde{Q}}\left(x\right)\le 1$, for every $x\epsilon X$. The degree of indeterminacy is given as ${\pi }_{\tilde{Q}}\left(x\right)=\sqrt[q]{1-{\mu }_{\tilde{Q}}{\left(x\right)}^q-{\vartheta }_{\tilde{Q}}{\left(x\right)}^q}$ [52].

Definition 3.6

Let $\tilde{Q}=\left({\mu }_{\tilde{Q}},{\vartheta }_{\tilde{Q}}\right)$, ${\tilde{Q}}_1=\left({\mu }_{{\tilde{Q}}_1},{\vartheta }_{{\tilde{Q}}_1}\right)$ and ${\tilde{Q}}_2=\left({\mu }_{{\tilde{Q}}_2},{\vartheta }_{{\tilde{Q}}_2}\right)$ be three q-rung orthopair fuzzy numbers (q-ROFNs), then their operations can be defined as follows [51].

$${\tilde{Q}}_1\cap {\tilde{Q}}_2=\left(min\left\{{\mu }_{{\tilde{Q}}_1},{\mu }_{{\tilde{Q}}_2}\right\},max\left\{{\vartheta }_{{\tilde{Q}}_1},{\vartheta }_{{\tilde{Q}}_2}\right\}\right)$$ (12)

$${\tilde{Q}}_1\cup {\tilde{Q}}_2=\left(max\left\{{\mu }_{{\tilde{Q}}_1},{\mu }_{\tilde{Q}}\right\},min\left\{{\vartheta }_{{\tilde{Q}}_1},{\vartheta }_{\tilde{Q}}\right\}\right)$$ (13)

$${\tilde{Q}}_1\oplus {\tilde{Q}}_2=\left({\left({{{\mu }_{\tilde{Q}}}_1}^q+{{{\mu }_{\tilde{Q}}}_2}^q-{{{\mu }_{\tilde{Q}}}_1}^q{{{\mu }_{\tilde{Q}}}_2}^q\right)}^{\frac{1}{q}},{{\vartheta }_{\tilde{Q}}}_1{{\vartheta }_{\tilde{Q}}}_2\right)$$ (14)

$${\tilde{Q}}_1\otimes {\tilde{Q}}_2=\left({{\mu }_{\tilde{Q}}}_1{{\mu }_{\tilde{Q}}}_2,{\left({{{\vartheta }_{\tilde{Q}}}_1}^q+{{{\vartheta }_{\tilde{Q}}}_2}^q-{{{\vartheta }_{\tilde{Q}}}_1}^q{{{\vartheta }_{\tilde{Q}}}_2}^q\right)}^{\frac{1}{q}}\right)$$ (15)

$$\lambda \tilde{Q}=\left({\left(1-{\left(1-{{\mu }_{\tilde{Q}}}^q\right)}^{\lambda }\right)}^{\frac{1}{q}},{{\vartheta }_{\tilde{Q}}}^{\lambda }\right),\lambda >0$$ (16)

$${\tilde{Q}}^{\lambda }=\left({{\mu }_{\tilde{Q}}}^{\lambda },{\left(1-{\left(1-{{\vartheta }_{\tilde{Q}}}^q\right)}^{\lambda }\right)}^{\frac{1}{q}}\right),\lambda >0$$ (17)

Definition 3.7

Let $\tilde{Q}=\left({\mu }_{\tilde{Q}},{\vartheta }_{\tilde{Q}}\right)$ be a q-ROFN, then the score function $S\left(\tilde{Q}\right)$ and accuracy function $H\left(\tilde{Q}\right)$ of $\tilde{Q}$ can be defined as in Eqs. (18), (19), respectively [51].

$$S\left(\tilde{Q}\right)={{\mu }_{\tilde{Q}}}^q-{{\vartheta }_{\tilde{Q}}}^q$$ (18)

$$H\left(\tilde{Q}\right)={{\mu }_{\tilde{Q}}}^q+{{\vartheta }_{\tilde{Q}}}^q$$ (19)

Definition 3.8

Let ${\tilde{Q}}_i=\left({\mu }_{{\tilde{Q}}_i},{\vartheta }_{{\tilde{Q}}_i}\right)$ $\left(i=1,2,\dots ..,n\right)$ be a set of q-ROFNs and $w={(w_1,w_2,\dots .,w_n)}^T$ be weight vector of ${\tilde{Q}}_i$ with ${\sum }_{i=1}^n{w}_i=1$, then a q-rung orthopair fuzzy weighted average $\left(q-\mathit{ROFWA}\right)$ operator is [51]:

$$q-\mathit{ROFWA}\left({\tilde{Q}}_1,{\tilde{Q}}_2,\dots .,{\tilde{Q}}_n\right)=\left({\left(1-\prod _{i=1}^n{\left(1-{\mu }_{{\tilde{Q}}_i}^q\right)}^{w_i}\right)}^{\frac{1}{q}},\prod _{i=1}^n{\vartheta }_{{\tilde{Q}}_i}^{w_i}\right)$$ (20)

Definition 3.9

Let ${\tilde{Q}}_i=\left({\mu }_{{\tilde{Q}}_i},{\vartheta }_{{\tilde{Q}}_i}\right)$ $\left(i=1,2,\dots ..,n\right)$ be a set of q-ROFNs and $w={(w_1,w_2,\dots .,w_n)}^T$ be weight vector of ${\tilde{Q}}_i$ with ${\sum }_{i=1}^n{w}_i=1$, then a q-rung orthopair fuzzy weighted geometric $\left(q-\mathit{ROFWG}\right)$ operator is [51]:

$$q-\mathit{ROFWG}\left({\tilde{Q}}_1,{\tilde{Q}}_2,\dots .,{\tilde{Q}}_n\right)=\left(\prod _{i=1}^n{\mu }_{{\tilde{Q}}_i}^{w_i},{\left(1-\prod _{i=1}^n{\left(1-{\vartheta }_{{\tilde{Q}}_i}^q\right)}^{w_i}\right)}^{\frac{1}{q}}\right)$$ (21)

4. Proposed methodologies

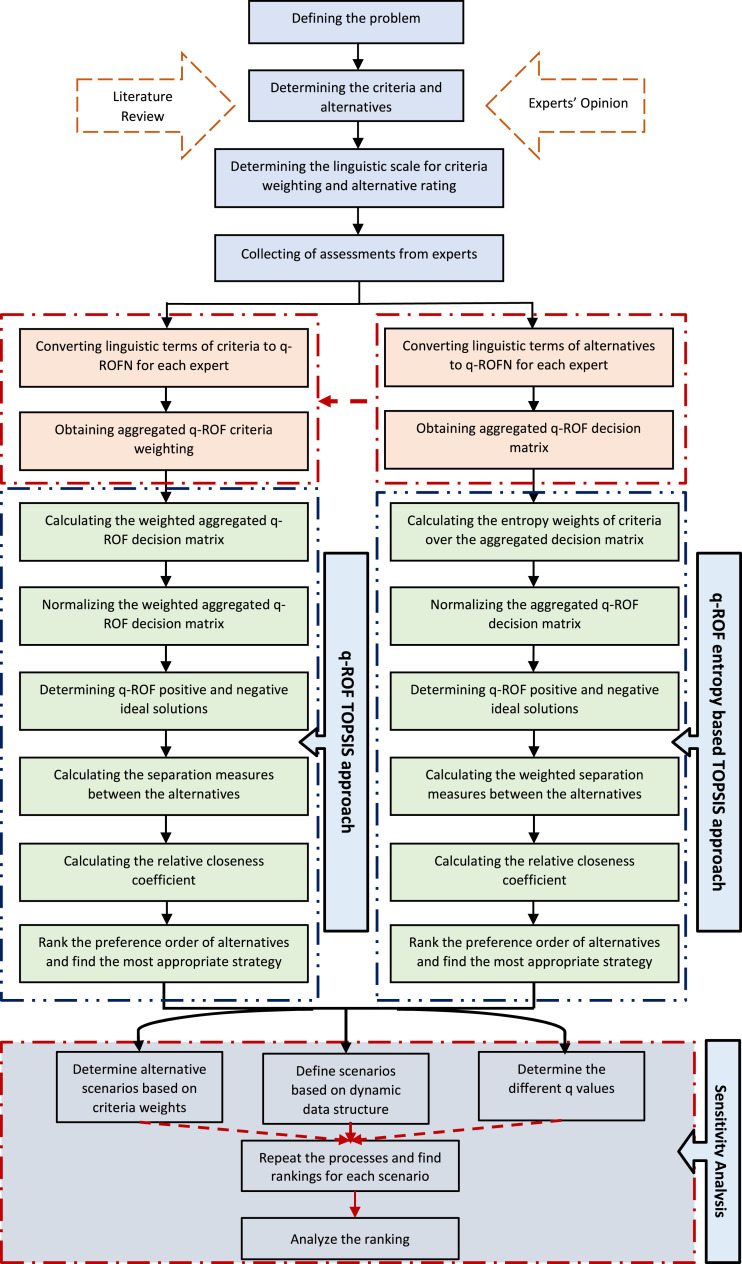
In this section, two different new approaches of q-ROF TOPSIS method have been proposed to select the best COVID-19 strategy and rank strategies with their details. The framework of the proposed approaches has been given in the flowchart in Fig. 2.

Fig. 2.

Framework of the proposed approaches.

Method-I

The details of the first proposed method are as follows.

Step 1. Determine the alternatives, relevant criteria, and decision-makers (DMs) to construct the proposed approach. The set $A_i=\left\{A_1,A_2,\dots ..,A_m\right\}$ having $i=1,2,\dots .,m$ alternatives, is assessed by $n$ decision criteria of set $C_j=\left\{C_1,C_2,\dots ..,C_n\right\}$, with $j=1,2,\dots .,n$. Let $w=(w_1,w_2,\dots .,w_n)$ be the vector set used for defining the criteria weights, where $w_j>0$ and ${\sum }_{j=1}^n{w}_j=1$.

Step 2. Construct the q-ROF decision matrices $\left(D_k\right)$ with respect to experts’ opinions by using the scale given in Table 1. The q-ROF decision matrix based on Expert $\left(k\right)$ to evaluate the alternatives in terms of each criterion is presented in Table 2. Here, ${\tilde{D}}_k={\left({\tilde{d}}_{ijk}\right)}_{nxm}$ in which ${\tilde{d}}_{ijk}=\left[{\mu }_{ijk},{\vartheta }_{ijk}\right]$ is constructed by utilizing the linguistic terms scale given in Table 1. Accordingly, ${\tilde{d}}_{ijk}$ indicates the performance of alternative $A_i$ in terms of criterion $C_j$ of $kth$ expert.

Table 1.

Linguistic scale for ratings of alternatives.

Linguistic terms	q-ROFN for alternatives
	$\mu$	$\vartheta$
Certainly high value $-$ (CHV)	0.99	0.11
Very high value $-$ (VHV)	0.88	0.22
High value $-$ (HV)	0.77	0.33
Above average value $-$ (AAV)	0.66	0.44
Average value $-$ (AV)	0.55	0.55
Under average value $-$ (UAV)	0.44	0.66
Low value $-$ (LV)	0.33	0.77
Very low value $-$ (VLV)	0.22	0.88
Certainly low value $-$ (CLV)	0.11	0.99

Table 2.

The decision matrix based on q-rung orthopair fuzzy number with respect to expert k.

Criteria	Alternatives
	$A_1$	$A_2$	……	$A_m$
$C_1$	$〈\left[{\mu }_{11k},{\vartheta }_{11k}\right]〉$	$〈\left[{\mu }_{12k},{\vartheta }_{12k}\right]〉$	……	$〈\left[{\mu }_{1mk},{\vartheta }_{1mk}\right]〉$
$C_2$	$〈\left[{\mu }_{21k},{\vartheta }_{21k}\right]〉$	$〈\left[{\mu }_{22k},{\vartheta }_{22k}\right]〉$	……	$〈\left[{\mu }_{2mk},{\vartheta }_{2mk}\right]〉$
$⋮$	$⋮$	$⋮$	$\ddots$	$⋮$
$C_n$	$〈\left[{\mu }_{n1k},{\vartheta }_{n1k}\right]〉$	$〈\left[{\mu }_{n2k},{\vartheta }_{n2k}\right]〉$	……	$〈\left[{\mu }_{nmk},{\vartheta }_{nmk}\right]〉$

Step 3. Compute the aggregated q-ROF decision matrix. The individual decision matrices are aggregated in one decision matrix using $q-\mathit{ROFWG}$ given in Eq. (21). Aggregated q-ROF decision matrix $\left(\tilde{D}\right)$ is constructed as in Table 3. Here, $\tilde{D}={\left({\tilde{d}}_{ij}\right)}_{nxm}$ in which ${\tilde{d}}_{ij}=\left[{\mu }_{ij},{\vartheta }_{ij}\right]$ is used to indicate the aggregated q-ROFN of $ith$ alternative with respect to $jth$ criterion.

Table 3.

Aggregated q-ROF decision matrix.

Criteria	Alternatives
	$A_1$	$A_2$	……	$A_m$
$C_1$	$〈\left[{\mu }_{11},{\vartheta }_{11}\right]〉$	$〈\left[{\mu }_{12},{\vartheta }_{12}\right]〉$	……	$〈\left[{\mu }_{1m},{\vartheta }_{1m}\right]〉$
$C_2$	$〈\left[{\mu }_{21},{\vartheta }_{21}\right]〉$	$〈\left[{\mu }_{22},{\vartheta }_{22}\right]〉$	……	$〈\left[{\mu }_{2m},{\vartheta }_{2m}\right]〉$
$⋮$	$⋮$	$⋮$	$\ddots$	$⋮$
$C_n$	$〈\left[{\mu }_{n1},{\vartheta }_{n1}\right]〉$	$〈\left[{\mu }_{n2},{\vartheta }_{n2}\right]〉$	……	$〈\left[{\mu }_{nm},{\vartheta }_{nm}\right]〉$

Step 4. Determine the q-ROF weights of criteria for each expert $\left(\tilde{W}\right)$ using the linguistic scale given in Table 4. Here, ${\tilde{W}}_k={\left(w_{jk}\right)}_{1xn}$ indicates q-ROFN of $kth$ expert with respect to $jth$ criterion.

Table 4.

Linguistic scale for weighting of the criteria.

Linguistic terms	q-ROFN for criteria
	$\mu$	$\vartheta$
Certainly high importance $-$ (CHI)	0.99	0.11
Very high importance $-$ (VHI)	0.88	0.22
High importance $-$ (HI)	0.77	0.33
Above average importance $-$ (AAI)	0.66	0.44
Average importance $-$ (AI)	0.55	0.55
Under average importance $-$ (UAI)	0.44	0.66
Low importance $-$ (LI)	0.33	0.77
Very low importance $-$ (VLI)	0.22	0.88
Certainly low importance $-$ (CLI)	0.11	0.99

Step 5. Aggregate the assessments on criteria weights. The individual assessments are aggregated in the criteria weight matrix $\left(\tilde{W}\right)$ using $q-\mathit{ROFWG}$ given in Eq. (21). Here, $\tilde{W}={\left(w_j\right)}_{1xn}$ shows the q-ROF weight of $jth$ criterion.

Step 6. Calculate the weighted aggregated q-ROF decision matrix $\left(\tilde{R}\right)$. After the weights of the criteria and the ratings of the alternatives are determined, the weighted aggregated q-ROF decision matrix $\left(\tilde{R}\right)$ is obtained by multiplying the q-ROF weights vector $\left(w_j\right)$ with the aggregated q-ROF decision matrix $\left(\tilde{D}\right)$ by utilizing Eqs. (22), (23) as follows:

$$\tilde{R}={\left({\tilde{r}}_{ij}\right)}_{nxm}$$ (22)

$${\tilde{r}}_{ij}=w_j\otimes {\tilde{d}}_{ij}$$ (23)

where ${\tilde{r}}_{ij}=\left[{\mu }_{r_{ij}},{\vartheta }_{r_{ij}}\right]$ shows the weighted aggregated q-ROFN of $ith$ alternative with respect to $jth$ criterion. Table 5 indicates the weighted aggregated q-ROF decision matrix.

Table 5.

Weighted aggregated q-ROF decision matrix.

Criteria	Alternatives
	$A_1$	$A_2$	……	$A_m$
$C_1$	$〈\left[{\mu }_{r_{11}},{\vartheta }_{r_{11}}\right]〉$	$〈\left[{\mu }_{r_{12}},{\vartheta }_{r_{12}}\right]〉$	……	$〈\left[{\mu }_{r_{1m}},{\vartheta }_{r_{1m}}\right]〉$
$C_2$	$〈\left[{\mu }_{r_{21}},{\vartheta }_{r_{21}}\right]〉$	$〈\left[{\mu }_{r_{22}},{\vartheta }_{r_{23}}\right]〉$	……	$〈\left[{\mu }_{r_{2m}},{\vartheta }_{r_{2m}}\right]〉$
$⋮$	$⋮$	$⋮$	$\ddots$	$⋮$
$C_n$	$〈\left[{\mu }_{r_{n1}},{\vartheta }_{r_{n1}}\right]〉$	$〈\left[{\mu }_{r_{n2}},{\vartheta }_{r_{n2}}\right]〉$	……	$〈\left[{\mu }_{r_{nm}},{\vartheta }_{r_{nm}}\right]〉$

Step 7. Normalize the weighted aggregated q-ROF decision matrix. If the criterion is benefit type, then do nothing; if the criterion is a cost type, then the cost type criterion should be converted into a benefit type criterion. The normalized q-ROF decision matrix $\left(\tilde{A}\right)$ is shown as follows:

$$\tilde{A}={\tilde{a}}_{ij}=\left({\mu }_{ij},{\vartheta }_{ij}\right)=\left\{\begin{array}{cc}\left({\mu }_{ij},{\vartheta }_{ij}\right),\hfill & for\mathit{benefit}type{C}_j\hfill \\ \left({\vartheta }_{ij},{\mu }_{ij}\right),\hfill & forcosttype{C}_j\hfill \end{array}\right)$$ (24)

Step 8. Determine q-ROF positive ideal solution (q-ROFPIS) and q-ROF negative ideal solution (q-ROFNIS) given in Eqs. (25), (27) by using score function and accuracy function based on the normalized decision matrix.

$${\tilde{A}}_j^{\ast }=max\left\{S\left(A_{1j}\right),S\left(A_{2j}\right),\dots .,S\left(A_{mj}\right)\right\}j=1,2,\dots ..,n$$ (25)

or

$${\tilde{A}}^{\ast }=\left\{〈C_1,\left({\mu }_1^{\ast },{\vartheta }_1^{\ast }\right)〉,〈C_2,\left({\mu }_2^{\ast },{\vartheta }_2^{\ast }\right)〉,\dots .,〈C_n,\left({\mu }_n^{\ast },{\vartheta }_n^{\ast }\right)〉\right\}$$ (26)

where $S\left(\tilde{A}\right)$ is the score function of q-ROFN and $\left({\mu }_j^{\ast },{\vartheta }_j^{\ast }\right)$ is the maximum q-ROFN with the highest score value among alternatives for $jth$ criterion. If the value $S\left(A_{1j}\right)=S\left(A_{2j}\right)=\cdots ...=S\left(A_{mj}\right)$, then the values of the accuracy function are compared.

$${\tilde{A}}_j^{-}=min\left\{S\left(A_{1j}\right),S\left(A_{2j}\right),\dots .,S\left(A_{mj}\right)\right\}j=1,2,\dots ..,n$$ (27)

or

$${\tilde{A}}^{-}=\left\{〈C_1,\left({\mu }_1^{-},{\vartheta }_1^{-}\right)〉,〈C_2,\left({\mu }_2^{-},{\vartheta }_2^{-}\right)〉,\dots .,〈C_n,\left({\mu }_n^{-},{\vartheta }_n^{-}\right)〉\right\}$$ (28)

where $S\left(\tilde{A}\right)$ is the score function of q-ROFN and $\left({\mu }_j^{-},{\vartheta }_j^{-}\right)$ is the minimum q-ROFS with the lowest score value among alternatives for $j^{th}$ criterion. If the value $S\left(A_{1j}\right)=S\left(A_{2j}\right)=\cdots ...=S\left(A_{mj}\right)$, then the values of the accuracy function are compared.

Step 9. Obtain the separation measures by calculating the distances for each alternative according to positive-ideal $\left({\tilde{A}}^{\ast }\right)$ and negative-ideal solutions $\left({\tilde{A}}^{-}\right)$. Distance between each alternative, and positive-ideal solution $\left({\tilde{A}}^{\ast }\right)$ as well as negative-ideal solution $\left({\tilde{A}}^{-}\right)$ are calculated based on normalized Euclidean distance as in Eqs. (29), (30), respectively.

$$d\left(A_i,A^{\ast }\right)={\left(\frac{1}{2n}\sum _{j=1}^n\left({|{\mu }_{ij}^q-{\left({\mu }_j^{\ast }\right)}^q|}^2+{|{\vartheta }_{ij}^q-{\left({\vartheta }_j^{\ast }\right)}^q|}^2\right)\right)}^{1/2}$$ (29)

$$d\left(A_i,A^{-}\right)={\left(\frac{1}{2n}\sum _{j=1}^n\left({|{\mu }_{ij}^q-{\left({\mu }_j^{-}\right)}^q|}^2+{|{\vartheta }_{ij}^q-{\left({\vartheta }_j^{-}\right)}^q|}^2\right)\right)}^{1/2}$$ (30)

Step 10. Calculate the relative closeness coefficient $\left(C{C}_i\right)$ of alternatives by using the following:

$$C{C}_i=\frac{d\left(A_i,A^{-}\right)}{d\left(A_i,A^{-}\right)+d\left(A_i,A^{+}\right)}$$ (31)

Step 11. Rank the alternatives according to final scores. The best alternative(s) are selected based on the descending order of the values of the relative closeness coefficient $\left(C{C}_i\right)$.

Method-II

The second proposed method is constructed based on the entropy of q-ROFSs developed by Liu et al. [53], and the TOPSIS method based on q-ROFSs developed by Liu et al. [54]. The steps of the proposed method are as follows.

Steps 1, 2, and 3: The first three steps contain the same steps as the first proposed method.

Step 4. Obtain the entropy values of each q-ROFN in the aggregated decision matrix by using the following:

$$K{E}_{q,ij}\left(x\right)=\frac{1}{\sqrt{2}}\sqrt{{\left({\left(\mu \left(x\right)\right)}^q\right)}^2+{\left({\left(\vartheta \left(x\right)\right)}^q\right)}^2+{\left({\left(\mu \left(x\right)\right)}^q+{\left(\vartheta \left(x\right)\right)}^q\right)}^2}$$ (32)

$$E{N}_{q,ij}\left(x\right)=1-K{E}_{q,ij}\left(x\right)=1-\frac{1}{\sqrt{2}}\sqrt{{\left({\left(\mu \left(x\right)\right)}^q\right)}^2+{\left({\left(\vartheta \left(x\right)\right)}^q\right)}^2+{\left({\left(\mu \left(x\right)\right)}^q+{\left(\vartheta \left(x\right)\right)}^q\right)}^2}$$ (33)

Step 5. Calculate the weights of criteria. The weights of criteria are calculated based on entropy values by using the following:

$$w_j=\frac{1-{\xi }_j}{\sum _{j=1}^n\left(1-{\xi }_j\right)};j=1,2,\dots ..,n$$ (34)

where ${\xi }_j=\frac{{\sum }_{i=1}^{m}E{N}_{q,ij}}{{\sum }_{i=1}^m{\sum }_{j=1}^{n}E{N}_{q,ij}}$ indicates the q-ROF entropy value.

Step 6. Normalize the q-ROF aggregated decision matrix. The aggregated decision matrix is normalized by transforming cost types of criteria to the benefit type as given in Eq. (24).

Step 7. Determine q-ROFPIS ${\tilde{A}}^{\ast }=\left\{{\tilde{A}}_1^{\ast },{\tilde{A}}_2^{\ast },\dots .,{\tilde{A}}_n^{\ast }\right\}$ and q-ROFNIS ${\tilde{A}}^{-}=\left\{{\tilde{A}}_1^{-},{\tilde{A}}_2^{-},\dots .,{\tilde{A}}_n^{-}\right\}$ calculated by the score and accuracy functions as given in Eqs. (18), (19), respectively.

Step 8. Determine separation measures by calculating the weighted distances for each alternative according to positive-ideal $\left({\tilde{A}}^{\ast }\right)$ and negative-ideal solutions $\left({\tilde{A}}^{-}\right)$. Distance between each alternative, and positive-ideal solution $\left({\tilde{A}}^{\ast }\right)$ as well as negative-ideal solution $\left({\tilde{A}}^{-}\right)$ are calculated by utilizing Euclidean distance as given in Eqs. (35), (36), respectively.

$$d\left(A_i,A^{\ast }\right)={\left(\frac{1}{2}\sum _{j=1}^n{w}_j\left({|{\mu }_{ij}^q-{\left({\mu }_j^{\ast }\right)}^q|}^2+{|{\vartheta }_{ij}^q-{\left({\vartheta }_j^{\ast }\right)}^q|}^2\right)\right)}^{1/2}$$ (35)

$$d\left(A_i,A^{-}\right)={\left(\frac{1}{2}\sum _{j=1}^n{w}_j\left({|{\mu }_{ij}^q-{\left({\mu }_j^{-}\right)}^q|}^2+{|{\vartheta }_{ij}^q-{\left({\vartheta }_j^{-}\right)}^q|}^2\right)\right)}^{1/2}$$ (36)

Step 9. Calculate the closeness coefficient $\left(C{C}_i\right)$ of alternative ${\tilde{A}}_i$ by using Eq. (31) given in the first proposed method.

Step 10. Determine the optimal alternative(s) by ranking in descending order the alternative(s). In this step, we compare our two proposed methods to control its reliability and robustness.

5. Application

5.1. Problem definition

COVID-19, caused by a new coronavirus, is a respiratory pandemic spreading from person to person in many countries. This epidemic, which has various symptoms, is to continue its course according to the age of the persons and the diseases they have, and mortality rates are to vary depending on these situations. COVID-19 is to spread rapidly among people and cause serious effects if the necessary precautions are not taken. Therefore, the rapid spread of the COVID-19 epidemic has prompted countries to adopt various strategies by directing them to take many measures. Due to the COVID-19 epidemic which negatively affects countries in all respects and becomes a major threat, it is necessary to determine the most effective strategy for governments by considering certain criteria. MCDM methods can be successfully used in determining the best strategy for governments. Therefore, in this section, the COVID-19 strategies of governments are evaluated by using the proposed new approaches and it is aimed to select the best strategy among several alternatives.

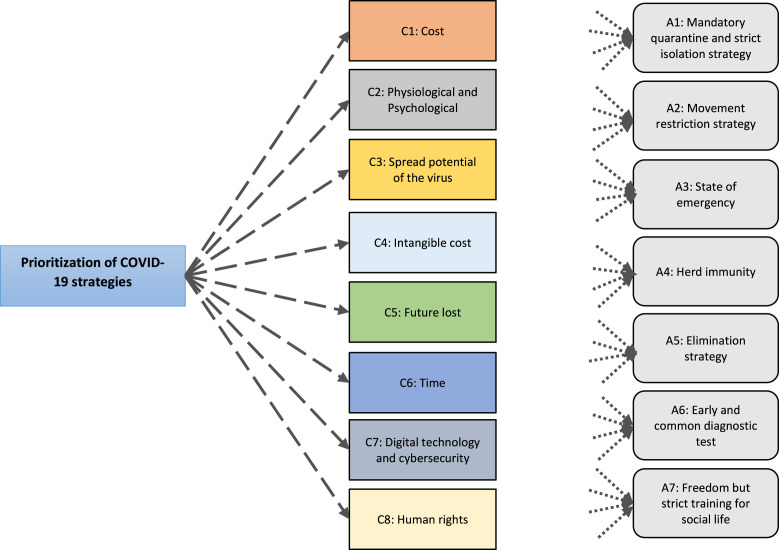
In the group of decision makers consisting of three experts which are abbreviated as DM1, DM2, and DM3, there is a professor advising in the health sector, a lecturer advising on strategies and policies in the ministry of health, and a professor who has carried out many projects on multi-criteria decision making. The weights of these decision-makers who have different experience levels are 0.4, 0.3, and 0.3, respectively. The strategies applied by the governments and the criteria that affect these strategies are determined as 7 alternatives and 8 criteria as given in Fig. 3 as a result of the expert opinions and evaluation of the studies in the literature.

Fig. 3.

Hierarchical structure of the problem.

5.2. COVID-19 strategies and selection criteria

Brief descriptions of the COVID-19 strategies considered are as follows:

Mandatory quarantine and strict isolation strategy (A1): This strategy includes stopping the social interactions of the whole society, tighter restrictions on travel or mandatory home lockdowns and self-isolation, and also applying rapid screening and contact tracing of infected individuals [55], [56]. The mandatory quarantine and strict isolation strategy have been implemented in China, Singapore, Japan, and Hong Kong [56].

Movement restriction strategy (A2): Several different methods are preferred in this strategy. This strategy includes isolating suspicious cases in their own homes and quarantine their relatives, and removing and protecting the elderly and chronic ill people from social life in the risk group [57]. In this strategy, governments impose curfews either in cities with a high number of infections or at certain times of a day or at certain days of the week or based on risk groups. Due to COVID-19, several countries such as Turkey, Belgium, Spain, Ireland, Germany, France, Cyprus, Tunisia, and Libya have imposed various curfews [58].

State of emergency (A3): The state of emergency stems from a government declaration in response to a state of emergency that poses a major threat to the country.  A government can declare such a situation during an armed action against the state by civil unrest, a natural disaster, a medical epidemic, a financial or economic crisis [59]. Countries such as Finland, Hungary, Portugal, Romania, Bulgaria, and Spain have implemented the state of emergency because of COVID-19 [60].

Herd immunity (A4): Herd immunity stems from the effects of individual immunity scaled to the level of the population. It means the indirect conservation from infection conferred to sensitive individuals when enough great ratio of immune individuals exists in a population. The aim is to provide that the virus spreads in a controlled manner. The herd immunity strategy has been implemented in the UK and Sweden [61], [62].

Elimination strategy (A5): This strategy applied  in New Zealand refers to reducing new cases in a defined geographical area, in this case New Zealand, to zero (or a very low defined target rate). The two primary aims of a COVID-19 elimination strategy are to eliminate transmission chains in New Zealand and to forbid the emergence of new transmission chains caused by cases that arrive from outside the country. The basics of the strategy are based on border controls, robust case detection, surveillance, effective contact tracing, and strong community support of control measures [63].

Early and common diagnostic test (A6): By testing the vast population as free as possible in South Korea, after determining in which regions the disease is most concentrated, it has isolated the infected patients and quarantined them by monitoring their contact. In this way, there is no need to take measures such as curfew, quarantine, and restriction of movement. In this strategy, South Korea has disclosed real-time information about COVID-19 through special websites, mass media, telephone messages, and mobile applications [56], [62].

Freedom but strict training for social life (A7): In this strategy, individuals can move freely, except for strict rules that must be followed in their social lives. If the mandatory rules are not followed, individuals are exposed to various financial penalties.

The criteria that are effective in prioritizing the strategies are as follows:

Cost (C1): Along with COVID-19, many sectors, from the agricultural sector to the manufacturing sector, could not perform their activities and suffered serious economic losses. Besides, the increase in consumption rate and decrease in productivity lead to serious material losses. Besides, the epidemic brings with it a decrease in growth rate, increase in the unemployment rate and inflation rate, the balance of payments and deterioration in budget balance, and external financing difficulties. Moreover, the tests used for the epidemic, treatment, therapy, medication, medical equipment, medical staff time, resources used for care, and access also lead to extra financial losses.

Physiological and Psychological (C2): The difficulties, risks, and uncertainties due to the coronavirus, which is declared as a pandemic worldwide, are to affect many people both physiologically and psychologically. With COVID-19, individuals feel seedy, bored, and tired, experience fear and anxiety about their health and the health of their loved ones, increase or decrease in eating and sleep patterns, and experience disconnection from social relationships, helplessness, sadness, anxiety, and anger. Besides, individuals are to experience difficulties in concentrating and gathering attention.

Spread potential of the virus (C3): The virus is transmitted very easily among people and the number of deaths caused by the virus is increasing day by day. Therefore, the potential for spreading the virus has an important effect on determining the most appropriate strategy. Governments should adopt a strategy to minimize disease spread.

Intangible cost (C6): Changing customer expectations with COVID-19 will lead to a reduction in customer satisfaction for many sectors and this will cause serious material losses depending on the loss of the customer. Besides, the loss of morale of employees and the decrease in the will to work will lead to a decrease in the productivity rate. COVID-19, which causes intangible costs like these, carries the risk of long-term financial losses and is, therefore, one of the important criteria to be considered in determining the most suitable strategy.

Future lost (C5): For a certain period of time, COVID-19 will cause employees to face a loss of skills and abilities, many industries not to be preferred by customers, and individuals to move away from social groups. Therefore, this criterion should be taken into consideration in determining the most appropriate strategy.

Time (C6): The least possible damage and overcoming of the epidemic is the primary target of all governments. Therefore, the time factor constitutes an important place in determining the most suitable strategy.

Digital technology and cybersecurity (C7): With digital technology and cybersecurity, another important criterion in determining the strategy, governments need to adopt the appropriate strategy where they can benefit more from technology. It is important to consider these two criteria together in determining the most appropriate strategy for the governments because of their potential to be exposed to too many cybersecurity attacks while making maximum use of technology.

Human rights (C8): The most appropriate strategy that requires human beings to be at the center should be determined against human rights violations experiencing in combating the epidemic.

5.3. Problem solution

For the first proposed q-ROF TOPSIS approach,

Step 1. An expert group of three decision-makers is defined in Section 5.1, strategies and criteria are defined in Section 5.2. The expert group evaluates strategies in line with the defined objectives and criteria.

Step 2. The linguistic decision matrix created based on the evaluations of experts using the scale in Table 1 is presented in Table 6. Then, the linguistic evaluations of DMs are converted to the corresponding q-ROFNs based on the scale in Table 1.

Table 6.

Linguistic decision matrix for each expert.

	DM1								DM2								DM3
	A1	A2	A3	A4	A5	A6	A7		A1	A2	A3	A4	A5	A6	A7		A1	A2	A3	A4	A5	A6	A7
C1	VLV	AV	AV	VHV	AAV	VLV	LV		VLV	LV	LV	VHV	AAV	VLV	UAV		CLV	LV	LV	CHV	AV	VLV	AAV
C2	AAV	AAV	VHV	AAV	AV	UAV	VLV		LV	LV	LV	VHV	AAV	HV	LV		VLV	LV	UAV	VHV	AV	AAV	UAV
C3	VLV	LV	LV	VHV	AAV	CLV	VLV		CHV	VHV	VHV	VLV	HV	VHV	HV		VHV	HV	HV	VLV	AAV	HV	VHV
C4	AV	AAV	AV	VHV	UAV	VLV	LV		CLV	LV	UAV	VHV	AV	HV	LV		VLV	UAV	LV	CHV	UAV	HV	UAV
C5	CLV	LV	VLV	HV	AV	VLV	VLV		CLV	VLV	LV	VHV	AV	AV	AAV		CLV	LV	VLV	VHV	UAV	AV	AV
C6	VLV	LV	VLV	HV	AV	CLV	VLV		VHV	HV	HV	VLV	AAV	VHV	AV		VHV	HV	HV	VLV	AAV	HV	AV
C7	VHV	AAV	AAV	LV	AAV	CLV	VLV		VHV	HV	HV	VLV	AAV	VHV	LV		CHV	VHV	HV	VLV	AAV	VHV	VLV
C8	VHV	VHV	VHV	AAV	AV	VHV	HV		AAV	AAV	AV	HV	AAV	VHV	HV		HV	HV	AV	VHV	HV	VHV	AAV

Step 3. Individual q-ROF decision matrices are aggregated to obtain the collective decision matrix using Eq. (21). In this process, the parameter determination stage requires scientific formulation or estimation. The parameter q can be given any value reflecting their optimistic and pessimistic attitudes by the group of experts. For the illustrative purpose, we present the results of q = 5 to provide a stronger definition of uncertainty, and to express information more flexibly, which indicates that the expert group has a relatively optimistic attitude. The aggregated q-ROF decision matrix is constructed as shown in Table 7.

Table 7.

Aggregated decision matrix.

	A1	A2	A3	A4	A5	A6	A7
C1	$\left[0.179,0.947\right]$	$\left[0.405,0.717\right]$	$\left[0,405,0.717\right]$	$\left[0.912,0.205\right]$	$\left[0.625,0.485\right]$	$\left[0.22,0.88\right]$	$\left[0.443,0.691\right]$
C2	$\left[0.386,0.774\right]$	$\left[0.435,0.708\right]$	$\left[0.533,0.661\right]$	$\left[0.784,0.370\right]$	$\left[0.580,0.526\right]$	$\left[0.588,0.566\right]$	$\left[0.306,0.812\right]$
C3	$\left[0.524,0.763\right]$	$\left[0,571,0.654\right]$	$\left[0,571,0.654\right]$	$\left[0.383,0.816\right]$	$\left[0.0.691,0.418\right]$	$\left[0.368,0.931\right]$	$\left[0.486,0.764\right]$
C4	$\left[0.258,0.927\right]$	$\left[0.475,0.667\right]$	$\left[0.441,0.679\right]$	$\left[0.912,0.205\right]$	$\left[0.470,0.635\right]$	$\left[0.467,0.764\right]$	$\left[0.359,0.745\right]$
C5	$\left[0.11,0.99\right]$	$\left[0.292,0.815\right]$	$\left[0.248,0.857\right]$	$\left[0,834,0,285\right]$	$\left[0.514,0.593\right]$	$\left[0.381,0.776\right]$	$\left[0.403,0.772\right]$
C6	$\left[0.505,0.764\right]$	$\left[0.549,0.655\right]$	$\left[0,467,0.764\right]$	$\left[0.363,0.817\right]$	$\left[0.614,0.496\right]$	$\left[0.368,0.931\right]$	$\left[0.381,0.776\right]$
C7	$\left[0.912,0.205\right]$	$\left[0.754,0.380\right]$	$\left[0.724,0.389\right]$	$\left[0.259,0.848\right]$	$\left[0.66,0.44\right]$	$\left[0.383,0.931\right]$	$\left[0.248,0.857\right]$
C8	$\left[0.776,0.364\right]$	$\left[0.775,0.364\right]$	$\left[0.664,0.498\right]$	$\left[0.754,0.380\right]$	$\left[0.643,0.484\right]$	$\left[0.88,0.22\right]$	$\left[0.735,0.378\right]$

Steps 4 and 5. The linguistic evaluations of the criteria assigned by DMs using the scale in Table 4 and their aggregated results based on q-ROFNs using Eq. (21) are shown in Table 8.

Table 8.

Linguistic evaluations of criteria for each expert and aggregated criterion weights based on the first approach.

Criterion	DM1	DM2	DM3	Aggregated results	Type
					Cost	Benefit
C1	HI	VHI	CHI	$\left[0.864,0.280\right]$	✓
C2	AAI	AAI	AI	$\left[0.625,0.485\right]$	✓
C3	CHI	CHI	CHI	$\left[0.99,0.11\right]$	✓
C4	HI	AI	HI	$\left[0.696,0.448\right]$	✓
C5	VHI	AAI	VHI	$\left[0.807,0.351\right]$	✓
C6	HI	VHI	VHI	$\left[0.834,0.285\right]$	✓
C7	AI	AI	UAI	$\left[0.514,0.593\right]$		✓
C8	AAI	AI	UAI	$\left[0.553,0.570\right]$		✓

Step 6. The weighted aggregated q-ROF decision matrix is constructed by multiplying the q-ROF weights vector with the aggregated q-ROF decision matrix by using Eq. (15) as given in Table 9.

Table 9.

Weighted aggregated decision matrix based on the first approach.

	A1	A2	A3	A4	A5	A6	A7
C1	$\left[0.154,0.947\right]$	$\left[0.35,0.718\right]$	$\left[0.35,0.718\right]$	$\left[0.788,0.291\right]$	$\left[0.540,0.491\right]$	$\left[0.190,0.880\right]$	$\left[0.383,0.692\right]$
C2	$\left[0.241,0785\right]$	$\left[0.272,0.725\right]$	$\left[0.333,0.684\right]$	$\left[0.490,0.507\right]$	$\left[0.363,0.581\right]$	$\left[0.367,0.608\right]$	$\left[0.191,0.820\right]$
C3	$\left[0.518,0.763\right]$	$\left[0.565,0.654\right]$	$\left[0.565,0.654\right]$	$\left[0.379,0.816\right]$	$\left[0.684,0.418\right]$	$\left[0.364,0.931\right]$	$\left[0.481,0.764\right]$
C4	$\left[0.179,0.928\right]$	$\left[0.330,0.682\right]$	$\left[0.307,0.693\right]$	$\left[0.635,0.50\right]$	$\left[0.327,0.654\right]$	$\left[0.324,0.772\right]$	$\left[0.250,0.754\right]$
C5	$\left[0.089,0.990\right]$	$\left[0.236,0.817\right]$	$\left[0.20,0.858\right]$	$\left[0.673,0.373\right]$	$\left[0.308,0.778\right]$	$\left[0.308,0.778\right]$	$\left[0.325,0.774\right]$
C6	$\left[0.422,0.764\right]$	$\left[0.458,0.657\right]$	$\left[0.389,0.765\right]$	$\left[0.303,0.817\right]$	$\left[0.307,0.932\right]$	$\left[0.307,0.932\right]$	$\left[0.318,0.777\right]$
C7	$\left[0.469,0.594\right]$	$\left[0.388,0.605\right]$	$\left[0.372,0.606\right]$	$\left[0.133,0.863\right]$	$\left[0.197,0.937\right]$	$\left[0.197,0.937\right]$	$\left[0.128,0.871\right]$
C8	$\left[0.429,0.581\right]$	$\left[0.429,0.581\right]$	$\left[0.367,0.617\right]$	$\left[0.417,0.584\right]$	$\left[0.487,0.571\right]$	$\left[0.487,0.571\right]$	$\left[0.407,0.583\right]$

Step 7. The weighted aggregated decision matrix is normalized by converting the cost type criterion to benefit type using Eq. (24) if the criterion is a cost type. The normalized decision matrix is as shown in Table 10.

Table 10.

Normalized decision matrix based on the first approach.

	A1	A2	A3	A4	A5	A6	A7
C1	$\left[0.947,0.154\right]$	$\left[0.718,0.35\right]$	$\left[0.718,0.35\right]$	$\left[0.291,0.788\right]$	$\left[0.491,0.540\right]$	$\left[0.880,0.190\right]$	$\left[0.692,0.383\right]$
C2	$\left[0785,0.241\right]$	$\left[0.725,0.272\right]$	$\left[0.684,0.333\right]$	$\left[0.507,0.490\right]$	$\left[0.581,0.363\right]$	$\left[0.608,0.367\right]$	$\left[0.820,0.191\right]$
C3	$\left[0.763,0.518\right]$	$\left[0.654,0.565\right]$	$\left[0.654,0.565\right]$	$\left[0.816,0.379\right]$	$\left[0.418,0.684\right]$	$\left[0.931,0.364\right]$	$\left[0.764,0.481\right]$
C4	$\left[0.928,0.179\right]$	$\left[0.682,0.330\right]$	$\left[0.693,0.307\right]$	$\left[0.50,0.635\right]$	$\left[0.654,0.327\right]$	$\left[0.772,0.324\right]$	$\left[0.754,0.250\right]$
C5	$\left[0.990,0.089\right]$	$\left[0.817,0.236\right]$	$\left[0.858,0.20\right]$	$\left[0.373,0.673\right]$	$\left[0.778,0.308\right]$	$\left[0.778,0.308\right]$	$\left[0.774,0.325\right]$
C6	$\left[0.764,0.422\right]$	$\left[0.657,0.458\right]$	$\left[0.765,0.389\right]$	$\left[0.817,0.303\right]$	$\left[0.932,0.307\right]$	$\left[0.932,0.307\right]$	$\left[0.777,0.318\right]$
C7	$\left[0.469,0.594\right]$	$\left[0.388,0.605\right]$	$\left[0.372,0.606\right]$	$\left[0.133,0.863\right]$	$\left[0.197,0.937\right]$	$\left[0.197,0.937\right]$	$\left[0.128,0.871\right]$
C8	$\left[0.429,0.581\right]$	$\left[0.429,0.581\right]$	$\left[0.367,0.617\right]$	$\left[0.417,0.584\right]$	$\left[0.487,0.571\right]$	$\left[0.487,0.571\right]$	$\left[0.407,0.583\right]$

Step 8. After score values for each q-ROFN in the normalized decision matrix are calculated using Eq. (18), the positive ideal solution and negative ideal solutions are obtained by using Eqs. (25), (27) as shown in Table 11.

Table 11.

Positive and negative ideal solutions based on the first approach.

Criterion	q-ROF positive ideal solution	q-ROF negative ideal solution
C1	$\left[0.947,0.154\right]$	$\left[0.291,0.788\right]$
C2	$\left[0.820,0.191\right]$	$\left[0.507,0.490\right]$
C3	$\left[0.931,0.364\right]$	$\left[0.418,0.684\right]$
C4	$\left[0.928,0.179\right]$	$\left[0.450,0.635\right]$
C5	$\left[0.990,0.089\right]$	$\left[0.373,0.673\right]$
C6	$\left[0.932,0.307\right]$	$\left[0.502,0.512\right]$
C7	$\left[0.469,0.594\right]$	$\left[0.197,0.937\right]$
C8	$\left[0.487,0.571\right]$	$\left[0.367,0.617\right]$

Step 9. The separation measures for each alternative according to the positive-ideal and negative-ideal solutions are calculated using the Euclidean distance in Eqs. (29), (30) as given in Table 12.

Table 12.

Separation measures of the alternatives based on the first approach.

	A1	A2	A3	A4	A5	A6	A7
$\mathit{d}\left({\mathit{A}}_{\mathit{i}},{\mathit{A}}^{\mathit{\ast }}\right)$	0.1573	0.32308	0.29854	0.39895	0.408	0.27079	0.31303
$\mathit{d}\left({\mathit{A}}_{\mathit{i}},{\mathit{A}}^{\mathit{-}}\right)$	0.40761	0.21887	0.23477	0.14011	0.17883	0.30502	0.18856

Step 10. The closeness coefficient of each alternative is calculated using Eq. (31) as shown in Table 13.

Table 13.

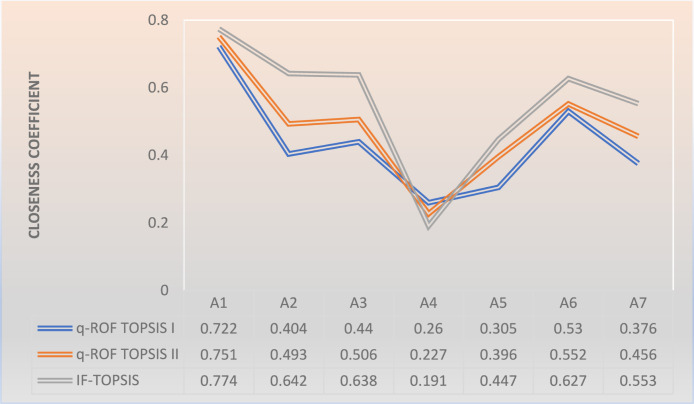
Closeness coefficient and ranks of the alternatives.

	A1	A2	A3	A4	A5	A6	A7
${\mathit{CC}}_{\mathit{i}}$	0.7215	0.4039	0.4402	0.2599	0.3047	0.5297	0.3759
Rank	1	4	3	7	6	2	5

Step 11. The closeness coefficients indicate that the ranking order of the alternatives are A1 > A6 > A3 > A2 > A7 > A5 > A4.

Now, we propose a new approach by applying different criteria weighting method. We compare the proposed two new approaches based on different criteria weighting methods on the results.

For the second proposed q-ROF entropy-based TOPSIS approach,

Step 1. To be valid and reliable of the results of the proposed methods, the same set of decision-makers, criteria and alternatives mentioned in the first proposed approach is used.

Steps 2 and 3. For this proposed approach, the scale given in Table 1 and the linguistic decision matrix in Table 6 created based on this scale are used. Besides, the aggregated decision matrix in Table 7, which is based on the linguistic decision matrices in the first proposed method, is used in the same way. The parameter q can be given any value by the group of experts. For the illustrative purpose, we present the results of q = 5.

Steps 4 and 5. After the entropy values of each q-ROFN in the aggregated decision matrix are obtained using Eqs. (32), (33), respectively, the weight of each criterion is calculated based on Entropy values using Eq. (34). The weights of criteria are as shown in Table 14.

Table 14.

Weights of criteria based on the second approach.

Criterion	Weight of criterion	Type
		Cost	Benefit
C1	0.12628	✓
C2	0.1205	✓
C3	0.12452	✓
C4	0.12479	✓
C5	0.12723	✓
C6	0.12404	✓
C7	0.12797		✓
C8	0.12467		✓

Step 6. The aggregated decision matrix is normalized as given in Eq. (24). The normalized decision matrix is determined as in Table 15.

Table 15.

Normalized decision matrix based on the second approach.

	A1	A2	A3	A4	A5	A6	A7
C1	$\left[0.947,0.179\right]$	$\left[0.717,0.405\right]$	$\left[0.717,0.405\right]$	$\left[0.205,0.912\right]$	$\left[0.485,0.625\right]$	$\left[0.88,0.22\right]$	$\left[0.691,0.443\right]$
C2	$\left[0.774,0.386\right]$	$\left[0.708,0.435\right]$	$\left[0.661,0.523\right]$	$\left[0.370,0.784\right]$	$\left[0.526,0.581\right]$	$\left[0.566,0.588\right]$	$\left[0.812,0.306\right]$
C3	$\left[0.763,0.524\right]$	$\left[0.654,0.571\right]$	$\left[0.654,0.571\right]$	$\left[0.816,0.383\right]$	$\left[0.418,0.691\right]$	$\left[0.931,0.368\right]$	$\left[0.764,0.486\right]$
C4	$\left[0.927,0.258\right]$	$\left[0.667,0.475\right]$	$\left[0.679,0.441\right]$	$\left[0.205,0.912\right]$	$\left[0.635,0.470\right]$	$\left[0.764,0.467\right]$	$\left[0.745,0.360\right]$
C5	$\left[0.99,0.11\right]$	$\left[0.815,0.292\right]$	$\left[0.857,0.248\right]$	$\left[0.249,0.834\right]$	$\left[0.593,0.514\right]$	$\left[0.776,0.381\right]$	$\left[0.772,0.403\right]$
C6	$\left[0.764,0.505\right]$	$\left[0.655,0.549\right]$	$\left[0.764,0.467\right]$	$\left[0.817,0.363\right]$	$\left[0.496,0.614\right]$	$\left[0.931,0.368\right]$	$\left[0.776,0.381\right]$
C7	$\left[0.912,0.205\right]$	$\left[0.754,0.380\right]$	$\left[0.724,0.389\right]$	$\left[0.259,0.848\right]$	$\left[0.66,0.44\right]$	$\left[0.383,0.931\right]$	$\left[0.248,0.857\right]$
C8	$\left[0.776,0.364\right]$	$\left[0.776,0.364\right]$	$\left[0.664,0.498\right]$	$\left[0.754,0.380\right]$	$\left[0.643,0.484\right]$	$\left[0.88,0.22\right]$	$\left[0.735,0.378\right]$

Step 7. After score values for each q-ROFN in the normalized decision matrix are calculated using Eq. (18), the positive ideal and negative ideal solutions are determined with the help of Eqs. (25), (27) as shown in Table 16.

Table 16.

Positive and negative ideal solutions based on the second approach.

Criterion	q-ROF positive ideal solution	q-ROF negative ideal solution
C1	$\left[0.947,0.178\right]$	$\left[0.205,0.912\right]$
C2	$\left[0.812,0.306\right]$	$\left[0.370,0.784\right]$
C3	$\left[0.931,0.368\right]$	$\left[0.418,0.691\right]$
C4	$\left[0.927,0.258\right]$	$\left[0.205,0.912\right]$
C5	$\left[0.990,0.11\right]$	$\left[0.285,0.834\right]$
C6	$\left[0.931,0.368\right]$	$\left[0.496,0.614\right]$
C7	$\left[0.912,0.205\right]$	$\left[0.383,0.931\right]$
C8	$\left[0.88,0.22\right]$	$\left[0.643,0.484\right]$

Step 8. Separation measures for each alternative based on the positive ideal and negative ideal solutions are calculated using the Euclidean distance given in Eqs. (29), (30) as in Table 17.

Table 17.

Separation measures of the alternatives based on the second approach.

	A1	A2	A3	A4	A5	A6	A7
$\mathit{d}\left({\mathit{A}}_{\mathit{i}},{\mathit{A}}^{\mathit{\ast }}\right)$	0.16886	0.34544	0.33496	0.50209	0.44413	0.32309	0.36436
$\mathit{d}\left({\mathit{A}}_{\mathit{i}},{\mathit{A}}^{\mathit{-}}\right)$	0.50817	0.33643	0.34267	0.1478	0.29088	0.39784	0.30581

Step 9. The closeness coefficient $\left(C{C}_i\right)$ of each alternative is determined using Eq. (31) as shown in Table 18.

Table 18.

Closeness coefficient and ranks of the alternatives based on the second approach.

	A1	A2	A3	A4	A5	A6	A7
${\mathit{CC}}_{\mathit{i}}$	0.75059	0.49339	0.50569	0.22742	0.39575	0.55184	0.45631
Rank	1	4	3	7	6	2	5

Step 10. Taking into account the closeness values, ranks of the alternatives are as in Table 18. Results indicate that the ranking of alternatives are A1 > A6 > A3 > A2 > A7 > A5 > A4.

The results show that A1 — Mandatory quarantine and strict isolation strategy is the most important strategy because of having a greater closeness coefficient for both the proposed approaches. Besides, it can be seen that the ranking of order for both the proposed approaches is the same in Table 13, Table 18. This can clearly show that the proposed methods are effective.

5.4. Sensitivity analysis

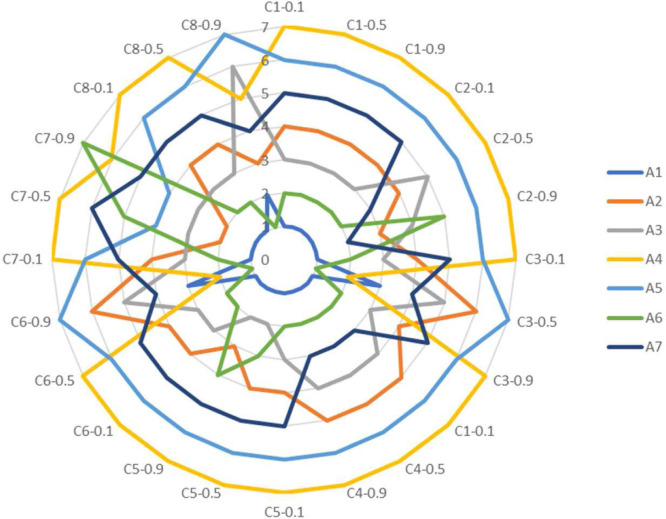
In this section, sensitivity analyses are performed to measure the robustness of the results of the proposed methods. For the proposed approaches based on q-ROF TOPSIS, the sensitivity analyses are first conducted to emphasize various scenarios in decision-makers’ priorities on criterion weights that might alter the result of the proposed methods. In this analysis, we change the linguistic weights assigned by each decision-maker to a certain criterion, from CHI to CLI, respectively, while keeping the linguistic weights of other criteria constant. On the other hand, for the second proposed approach, q-ROF entropy-based TOPSIS, three different scenarios for each criterion are conducted. In this analysis, the entropy weight of each criterion is changed as 0.1, 0.5, and 0.9, respectively, while the others are proportionally kept constant. Using these new criteria weights, the closeness coefficients of alternatives are recalculated. The sum of the weights equals 1 in each case. For example, if the weight of C1 is changed to 0.1, the others are arranged as 0.129. Thus, the effects of the changes on alternative ranks are observed with both analyses. The outputs of each analysis are presented in Fig. 4, Fig. 5, respectively. In Fig. 4, it can be seen that A1 — Mandatory quarantine and strict isolation strategy is determined as the best alternative for strategy selection since it is superior to the six alternatives in all sensitivity analyses. This shows that our first proposed method’s decisions are robust and effective. The changes in the ranks of alternatives occurred when the weight of C7 criterion changes. Besides, the closeness coefficients change for each different criterion weight. This also proves the first proposed approach is sensitive to the changes in the criteria’ weights.

Fig. 4.

Results of sensitivity analysis for the first proposed approach based on the criteria weights.

Fig. 5.

Results of sensitivity analysis for the second proposed approach based on the criteria weights.

When the results are examined for the second proposed approach as seen in Fig. 5, the changes made on C3- Spread potential of the virus, C6- Time, and C8- Human rights change the best alternative, unlike the others. When the entropy weight is increased to 0.5 for C3 criterion, and to 0.9 for C6 and C8, A6- Early and common diagnostic test is determined as the best alternative. C3, C6, and C8 are the most effective criteria for A6 since the value of C3, C6, and C8 criteria and the rank of A6 alternative increase. In all other cases, A1- Mandatory quarantine and strict isolation strategy is the best alternative for our second proposed approach. Besides, the other sensitivity analysis results can be summarized as follows:

When the entropy weight of C2 and C4 criteria are increased, they are the most effective criteria for A7 since the value of C2 and C4 criteria and the rank of A7 alternative increase. However, the order of A1 does not change.

When the entropy weight of C5 criterion is increased, it is the most effective criteria for A3 since the value of C5 criterion and the rank of A3 alternative increase. However, the order of A1 does not change.

When the entropy weight of C7 criterion is increased, it is the most effective criteria for A2 since the value of C7 criterion and the rank of A2 alternative increase. However, the order of A2 does not change.

These results show that our second method’s decisions are robust, and results are sensitive, as well.

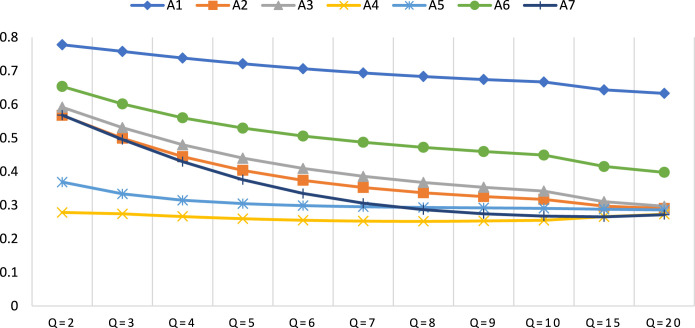
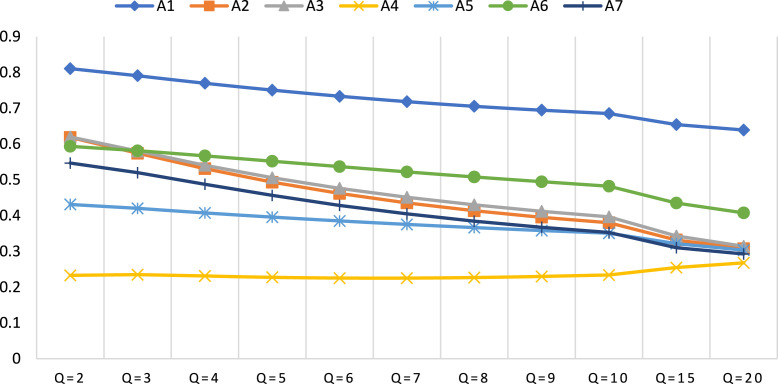
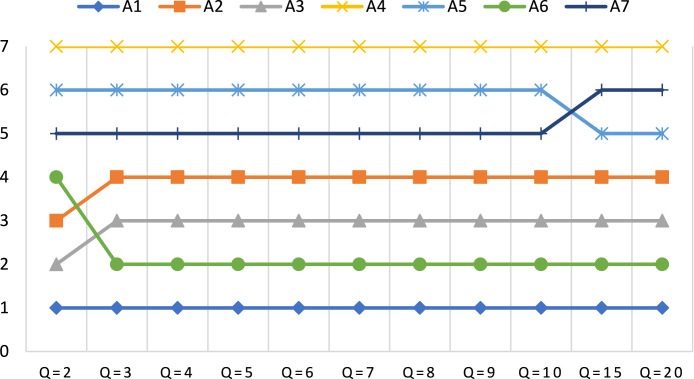
The proposed approaches allow decision-makers to expand their decision evaluation spaces based on the parameter q. The parameter q, which has a significant impact on the results, is very important for the proposed approaches. Therefore, to analyze the flexibility and sensitivity of the parameter q, we investigated the effect of different values of the parameter $q$ on the decision results. For this, we re-calculated the closeness coefficients for each alternative by re-applying the steps of the proposed approaches based on each change in the value of q. The ranking results of strategies for both proposed approaches are as given in Table 19. The changes of closeness coefficients values of strategies for the first and second proposed approaches are given in Fig. 6, Fig. 7, respectively.

Table 19.

Ranking results for proposed approaches.

q	Ranking for the first proposed approach	Ranking for the second proposed approach
q $=$ 2	$A1>A6>A3>A7>A2>A5>A4$	$A1>A3>A2>A6>A7>A5>A4$
q $=$ 3	$A1>A6>A3>A2>A7>A5>A4$	$A1>A6>A3>A2>A7>A5>A4$
q $=$ 4	$A1>A6>A3>A2>A7>A5>A4$	$A1>A6>A3>A2>A7>A5>A4$
q $=$ 5	$A1>A6>A3>A2>A7>A5>A4$	$A1>A6>A3>A2>A7>A5>A4$
q $=$ 6	$A1>A6>A3>A2>A7>A5>A4$	$A1>A6>A3>A2>A7>A5>A4$
q $=$ 7	$A1>A6>A3>A2>A7>A5>A4$	$A1>A6>A3>A2>A7>A5>A4$
q $=$ 8	$A1>A6>A3>A2>A5>A7>A4$	$A1>A6>A3>A2>A7>A5>A4$
q $=$ 8	$A1>A6>A3>A2>A5>A7>A4$	$A1>A6>A3>A2>A7>A5>A4$
q $=$ 9	$A1>A6>A3>A2>A5>A7>A4$	$A1>A6>A3>A2>A7>A5>A4$
q $=$ 10	$A1>A6>A3>A2>A5>A7>A4$	$A1>A6>A3>A2>A7>A5>A4$
q $=$ 15	$A1>A6>A3>A2>A5>A4>A7$	$A1>A6>A3>A2>A5>A7>A4$
q $=$ 20	$A1>A6>A3>A2>A5>A4>A7$	$A1>A6>A3>A2>A5>A7>A4$

Fig. 6.

Closeness coefficient values of alternatives based on the first proposed approach in different values of q.

Fig. 7.

Closeness coefficient values of alternatives based on the second proposed approach in different values of q.

In Table 19, Figs. 8, and Fig. 9 for both proposed approaches, it can be seen differences in the ranking order when the q parameter changes between 2 and 20. There have been minor changes in the ranking order for different values of parameter q. In both proposed approaches, when the q parameter is 2, i.e. PFSs, different ranking orders have been obtained. Furthermore, for the first proposed approach, when the q parameter is between 3 and 7, the ranking order is the same, while more different ranking orders have been obtained for the q parameter values greater than 7. For the second proposed approach, different ranking orders have been also obtained at the relatively larger values of the q parameter. However, no matter how the parameter q changes, the alternative A1 — Mandatory quarantine and strict isolation strategy has the biggest value of closeness coefficient in all cases for both approaches which means the alternative A1 is always the best choice. Besides, when the value of the parameter q is relatively small (from 2 to 5), the closeness coefficients are relatively larger and with the increase of q value (greater than 5), it has been observed that the closeness coefficients were generally smaller (see Fig. 6, Fig. 7). These results show that the q parameter has an influence on the decision results. Therefore, decision-makers should choose a suitable value of the q parameter according to their preferences.

Fig. 8.

Sensitivity analysis results of q parameter for the first proposed approach.

Fig. 9.

Sensitivity analysis results of q parameter for the second proposed approach.

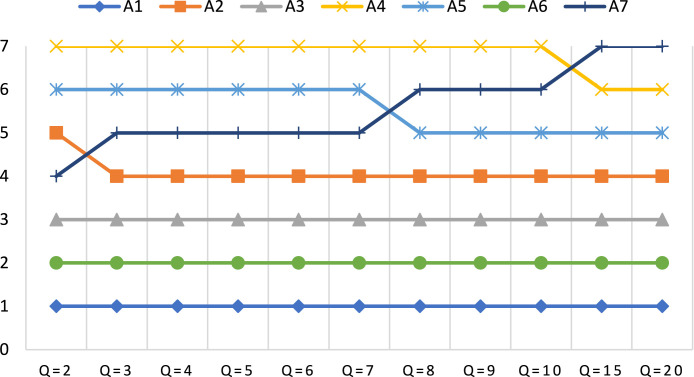
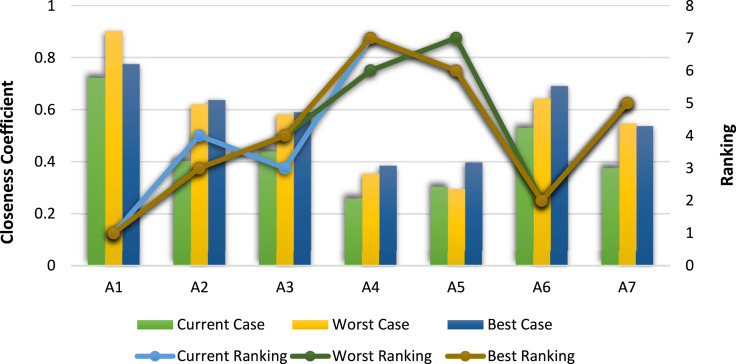
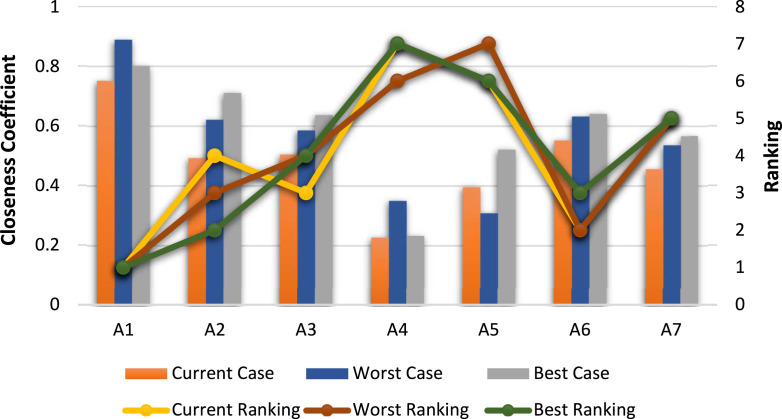
In the study, the evaluations obtained by experts in the current situation may vary according to the course of the pandemic, and this may cause a change in the rank of strategies that can be implemented. Therefore, to show the applicability of the developed methods, the evaluations considered need to be analyzed dynamically. In line with this scope, a scenario-based evaluation analysis is applied in the study. Since small changes in course of the pandemic did not cause a change in the results, experts were asked to make their evaluations by taking into account the worst and best cases in which the pandemic’s course could occur. After obtaining the best and worst-case evaluations from the experts, the proposed methods have been rerun and the results obtained for both methods have been presented in Fig. 10, Fig. 11.

Fig. 10.

Results of scenario analysis for the first proposed method.

Fig. 11.

Results of scenario analysis for the second proposed method.

According to the results obtained from Fig. 10, when the effect of the change in expert evaluations in the worst case of the pandemic is analyzed, it is seen that the closeness coefficient scores vary without causing a big change in the ranking results. It has been observed that the alternatives A1 — Mandatory quarantine and strict isolation strategy and A6 — Early and common diagnostic test that should be considered as the first and second in the current situation are in the first and second rank in the worst case of the pandemic. According to the current situation, it is observed that the alternatives A3 — State of emergency and A2 — Movement restriction strategy, which ranked third and fourth, replaced each other, while the fifth-ranked alternative A7 — Freedom but strict training for social life does not change. Besides, the alternatives A5 — Elimination strategy and A4 — Herd immunity, which ranks sixth and seventh according to the current situation, are also observed to be replaced with each other. When considering the expert evaluations for the best case in which the course of pandemic could happen, it is observed that the closeness coefficient scores vary without causing a big change in the ranking results. According to the results obtained, it is seen that the ranking of the best alternative A1 — Mandatory quarantine and strict isolation strategy does not change again. When the rest of the ranking is examined, it is seen that only the alternatives A3 — State of emergency and A2 — Movement restriction strategy in the third and fourth ranks replace each other.

According to the scenario-based analysis results performed on the second proposed method as shown in Fig. 11, it is observed that the changes in the expert evaluations for the worst case of the pandemic vary the closeness coefficient scores without causing a big change in the ranking results and it gives the same ranking results as the first method proposes. When considering the expert evaluations for the best case in which the course of pandemic could happen, it is seen that the closeness coefficient scores vary without causing a big change in the ranking results. It is observed that the A1 — Mandatory quarantine and strict isolation strategy alternative, which should be considered first in the current situation, is also in the first place for the best situation in which the course of the pandemic could happen. According to the current situation, it is seen that the alternative A6 — Early and common diagnostic test which is in the second place is ranked third, the alternative A3 — State of emergency which is in the third place is ranked fourth, and the alternative A2 — Movement restriction strategy which is in the fourth place is ranked second. It is observed that the rankings of the alternatives A7 — Freedom but strict training for social life, A5 — Elimination strategy, and A4 — Herd immunity which are ranked fifth, sixth and seventh, respectively, does not change.

As a conclusion, the scenario analysis applied on both methods change the final weights of the alternatives, but this change does not cause a major change in the final ranking order. It is seen that the strategy A1, which should be dealt with first in the methods proposed for all cases, does not change and still ranks first.

5.5. Comparative analysis

Various MCDM methods and approaches in fuzzy environment have been discussed by many researchers in the literature. Researchers tend to select the right MCDM method by considering many factors such as the required effort, desired accuracy, calculation time, users’ skills and knowledge, and assumptions in their studies. In this study, TOPSIS method, which is a distance-based MCDM technique, is taken into consideration because of its simple and understandable content, strong computational ability and simple mathematical process with low calculation times, without needing high user skills and knowledge for the relationship between decision alternatives, as well as the ranking of the alternatives considering their relative proximity to the best solution.

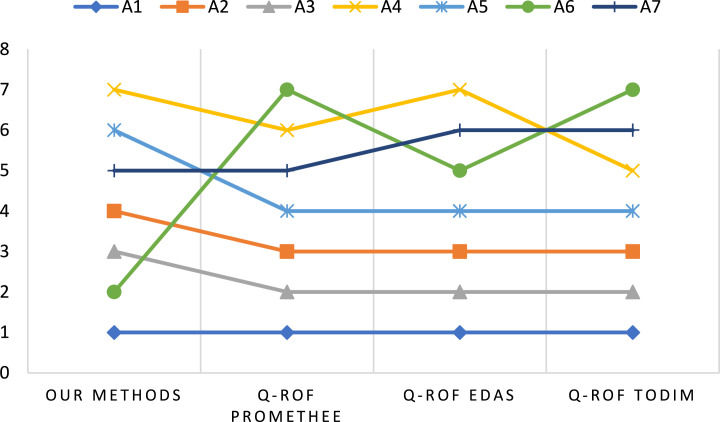
In order to compare our proposed methods with other MCDM methods which are not based on distance measurement, we selected three different q-ROF-based MCDM methods to validate our results. The comparative analysis is conducted with q-ROF-PROMETHEE II [64] with q = 5, which is based on outranking relations and q-ROF-EDAS [65] with q = 5, which is based on average solutions and q-ROF-TODIM [66] with q = 5, which is based on the prospect theory. The ranking results of the comparative analyses conducted by using q-ROF-based MCDM methods are shown in Fig. 12. Based on the obtained results, it is seen that there are differences in the ranking order obtained between the proposed methods and other methods. However, it is seen that the rank of alternative A1 in all methods does not change, which is the first strategy to be considered.

Fig. 12.

Comparative analysis on q-ROF-based MCDM methods.

In addition to comparisons with q-ROF MCDM methods, we compare our proposed q-ROF TOPSIS method with the intuitionistic fuzzy (IF) TOPSIS method proposed by Boran et al. [67]. The scales used for q-ROF TOPSIS are converted to intuitionistic fuzzy scale developed by Boran et al. [67] for the comparison purpose. In the proposed scale, we modified the linguistic terms as given in Table 20, Table 21 and we used the same scale both in the ratings of alternatives and in the weighting of criteria for a reliable comparison. We also used the same weights of decision-makers given in our proposed approach.

Table 20.

Linguistic scale for ratings of alternatives.

Linguistic terms	IF number for alternatives
	$\left(\mu ,\vartheta ,\pi \right)$
Very very high $-$ (VVH)	$\left(0.9,0.1,0\right)$
Very high $-$ (VH)	$\left(0.8,0.1,0.1\right)$
High $-$ (H)	$\left(0.7,0.2,0.1\right)$
Medium high $-$ (MH)	$\left(0.6,0.3,0.1\right)$
Medium $-$ (M)	$\left(0.5,0.4,0.1\right)$
Medium Low $-$ (ML)	$\left(0.4,0.5,0.1\right)$
Low $-$ (L)	$\left(0.25,0.6,0.15\right)$
Very low $-$ (VL)	$\left(0.2,0.75,0.15\right)$
Very very low $-$ (VVL)	$\left(0.1,0.9,0.1\right)$

Table 21.

Linguistic scale for weighting of criteria.

Linguistic terms	IF number for criteria
	$\left(\mu ,\vartheta ,\pi \right)$
Certainly high importance $-$ (CHI)	$\left(0.9,0.1,0\right)$
Very high importance $-$ (VHI)	$\left(0.8,0.1,0.1\right)$
High importance $-$ (HI)	$\left(0.7,0.2,0.1\right)$
Above average importance $-$ (AAI)	$\left(0.6,0.3,0.1\right)$
Average importance $-$ (AI)	$\left(0.5,0.4,0.1\right)$
Under average importance $-$ (UAI)	$\left(0.4,0.5,0.1\right)$
Low importance $-$ (LI)	$\left(0.25,0.6,0.15\right)$
Very low importance $-$ (VLI)	$\left(0.2,0.75,0.15\right)$
Certainly low importance $-$ (CLI)	$\left(0.1,0.9,0.1\right)$

The assessments of each decision-maker transformed from q-ROF values to IF values have been presented together with the aggregated criterion weights in Table 22. Besides, the weighted aggregated decision matrix consisting of IF values are constructed as shown in Table 23.

Table 22.

IF values of criteria for each expert and aggregated IF criterion weights.

Criterion	DM1	DM2	DM3	Aggregated values
C1	$\left(0.7,0.2,0.1\right)$	$\left(0.8,0.1,0.1\right)$	$\left(0.9,0.1,0\right)$	$\left(0.809,0.132,0.059\right)$
C2	$\left(0.6,0.3,0.1\right)$	$\left(0.6,0.3,0.1\right)$	$\left(0.5,0.4,0.1\right)$	$\left(0.572,0.327,0.101\right)$
C3	$\left(0.9,0.1,0\right)$	$\left(0.9,0.1,0\right)$	$\left(0.9,0.1,0\right)$	$\left(0.9,0.1,0\right)$
C4	$\left(0.7,0.2,0.1\right)$	$\left(0.5,0.4,0.1\right)$	$\left(0.7,0.2,0.1\right)$	$\left(0.65,0.246,0.104\right)$
C5	$\left(0.8,0.1,0.1\right)$	$\left(0.6,0.3,0.1\right)$	$\left(0.8,0.1,0.1\right)$	$\left(0.754,0.139,0.107\right)$
C6	$\left(0.7,0.2,0.1\right)$	$\left(0.8,0.1,0.1\right)$	$\left(0.8,0.1,0.1\right)$	$\left(0.765,0.132,0.103\right)$
C7	$\left(0.5,0.4,0.1\right)$	$\left(0.5,0.4,0.1\right)$	$\left(0.4,0.5,0.1\right)$	$\left(0.472,0.428,0.1\right)$
C8	$\left(0.6,0.3,0.1\right)$	$\left(0.5,0.4,0.1\right)$	$\left(0.4,0.5,0.1\right)$	$\left(0.517,0.381,0.102\right)$

Table 23.

Weighted aggregated decision matrix for IF values.

	A1	A2	A3	A4
C1	$\left(0.081,0.82,0.099\right)$	$\left(0.293,0.575,0.132\right)$	$\left(0.293,0.575,0.132\right)$	$\left(0.678,0.218,0.104\right)$
C2	$\left(0.22,0.654,0.126\right)$	$\left(0.239,0.633,0.128\right)$	$\left(0.335,0.514,0.151\right)$	$\left(0.421,0.431,0.147\right)$
C3	$\left(0.633,0.301,0.065\right)$	$\left(0.555,0.327,0.118\right)$	$\left(0.555,0.327,0.118\right)$	$\left(0.456,0.401,0.142\right)$
C4	$\left(0.188,0.711,0.102\right)$	$\left(0.296,0.571,0.134\right)$	$\left(0.262,0.61,0.127\right)$	$\left(0.545,0.322,0.134\right)$
C5	$\left(0.075,0.914,0.011\right)$	$\left(0.157,0.691,0.152\right)$	$\left(0.111,0743,0.146\right)$	$\left(0576,0.253,0.171\right)$
C6	$\left(0.486,0.326,0.188\right)$	$\left(0.434,0.401,0.164\right)$	$\left(0.408,0.427,0.165\right)$	$\left(0.321,0.516,0.163\right)$
C7	$\left(0.395,0.485,0.12\right)$	$\left(0.331,0.537,0.132\right)$	$\left(0.313,0.562,0.125\right)$	$\left(0.077,0.82,0.103\right)$
C8	$\left(0.373,0.487,0.14\right)$	$\left(0.373,0.487,0.14\right)$	$\left(0.337,0.523,0.139\right)$	$\left(0.362,0.499,0.138\right)$
	A5	A6	A7
C1	$\left(0.463,0.416,0.121\right)$	$\left(0.081,0.783,0.136\right)$	$\left(0.339,0.532,0.128\right)$
C2	$\left(0.305,0.574,0.121\right)$	$\left(0.325,0.546,0.128\right)$	$\left(0.140,0.745,0.114\right)$
C3	$\left(0.57,0.339,0.091\right)$	$\left(0.529,0.367,0.104\right)$	$\left(0.529,0.348,0.123\right)$
C4	$\left(0.281,0.599,0.120\right)$	$\left(0.347,0.502,0.150\right)$	$\left(0.194,0.674,0.131\right)$
C5	$\left(0.356,0507,0.137\right)$	$\left(0.277,0.582,0.141\right)$	$\left(0.308,0.545,0.147\right)$
C6	$\left(0.43,0.424,0.146\right)$	$\left(0.449,0.389,0.161\right)$	$\left(0.281,0.578,0.141\right)$
C7	$\left(0.283,0.599,0.117\right)$	$\left(0.3,0.566,0.135\right)$	$\left(0.07,0.829,0.101\right)$
C8	$\left(0.31,0.566,0.125\right)$	$\left(0.414,0.443,0.143\right)$	$\left(0.347,0.521,0.131\right)$

The positive ideal and negative ideal solutions consisting of IF values are determined as shown in Table 24. After separation measures for each alternative are calculated as given in Table 25, the closeness coefficient $\left(C{C}_i\right)$ of each alternative is determined as shown in Table 26. Results of the IF-TOPSIS are as given in Table 26.

Table 24.

Positive and negative ideal solutions of the alternatives for IF-TOPSIS.

Criterion	IF positive ideal solution	IF negative ideal solution
C1	$\left(0.081,0.82,0.099\right)$	$\left(0.678,0.219,0.104\right)$
C2	$\left(0.141,0.745,0.114\right)$	$\left(0.421,0.431,0.147\right)$
C3	$\left(0.456,0.401,0.142\right)$	$\left(0.633,0.301,0.065\right)$
C4	$\left(0.188,0.711,0.102\right)$	$\left(0.545,0.322,0.134\right)$
C5	$\left(0.075,0.913,0.011\right)$	$\left(0.576,0.253,0.171\right)$
C6	$\left(0.281,0.578,0.141\right)$	$\left(0.486,0.326,0.188\right)$
C7	$\left(0.395,0.485,0.12\right)$	$\left(0.07,0.829,0.101\right)$
C8	$\left(0.414,0.443,0.14\right)$	$\left(0.31,0.566,0.125\right)$

Table 25.

Separation measures of the alternatives for IF-TOPSIS.

	A1	A2	A3	A4	A5	A6	A7
$\mathit{d}\left({\mathit{A}}_{\mathit{i}},{\mathit{A}}^{\mathit{\ast }}\right)$	0.104	0.141	0.147	0.364	0.219	0.159	0.194
$\mathit{d}\left({\mathit{A}}_{\mathit{i}},{\mathit{A}}^{\mathit{-}}\right)$	0.357	0.253	0.259	0.086	0.177	0.267	0.240

Table 26.

Closeness coefficient and ranks of the alternatives for IF-TOPSIS.

	A1	A2	A3	A4	A5	A6	A7
${\mathit{CC}}_{\mathit{i}}$	0.774	0.642	0.638	0.191	0.447	0.627	0.553
Rank	1	2	3	7	6	4	5

The results indicate that A1 is the best alternative in both q-ROF TOPSIS and IF-TOPSIS methodologies as shown in Fig. 13 and the overall ranking obtained with IF-TOPSIS is A1, A2, A3, A6, A7, A5, and A4, respectively. Although these results give the same result with the best alternative determined by our proposed method, the ranking of the A2 and A6 alternatives have changed. Besides, it seems that the differences between the weights of the alternatives are more distinct in our proposed method. This is indicative of the advantage of q-ROFS, which enables the uncertainties that arise in decision-making problems and the lack of information and inconsistencies between expert groups to be represented in a wider area.

Fig. 13.

Results of comparative analyses.

6. Conclusion

COVID-19 is an epidemic that has not yet been approved, emerging in China and spreading all over the world. The severity of the epidemic increasing day by day has brought various difficulties to the governments. Although governments take various measures to prevent the spread of the epidemic in their communities, these measures are insufficient and therefore, it is necessary to ensure that the epidemic is managed most correctly with the most appropriate strategy. Almost all governments have adopted a strategy and implemented it in their communities. However, the implemented strategies have either failed to benefit many countries sufficiently or became harmful rather than beneficial. Some countries have been exposed to harmful effects socially or environmentally, while some countries have experienced harmful effects economically. Therefore, the strategies implemented by governments need to be evaluated and compared. At this point, the problem becomes an MCDM problem, where multiple alternatives should be evaluated under more than one criterion. However, due to uncertainties arising in the problem addressed and the lack of information and inconsistencies between expert groups, q-ROFSs that allow decision-makers to evaluate in a wider space should be addressed. Since q-ROFSs provide a stronger ability to contain broader information by expressing information more flexibly, it is more powerful to address problems in vague and uncertain environments. Particularly, using q-ROFSs in MCDM approaches, ambiguity and uncertainty are defined more strongly and thus the decision-making process can be managed more accurately. Based on this advantage, two different TOPSIS methods based on q-ROFSs have been proposed in this paper for the selection of the best strategy that can be implemented by governments. Alternatives and criteria have been determined in the light of the opinions of the experts and the information in the literature. According to the results of two different proposed approaches, A1 — Mandatory quarantine and strict isolation strategy has been determined as the most important strategy that should be implemented by governments. On the other hand, the strategies that can be implemented by the governments have been found to be A6, A3, A2, A7, A5, and A4, respectively, in order of importance in both proposed approaches.

In the study, sensitivity analysis has been conducted out on different criteria weights and q parameters. Sensitivity analysis conducted on criterion weights has shown that the results of the proposed approaches are robust and reliable. On the other hand, when the value of the q parameter changes, there have been minor differences in the ranking order for some values of q. However, the best strategy to be preferred by the governments in both approaches has not changed in all cases. In addition, in both proposed approaches, when the q parameter is 2, i.e. PFSs, different ranking orders have been obtained and this has indicated the real advantage of using q-ROFS in TOPSIS. Besides, it has been proven for both proposed approaches that decision-makers have a more optimistic attitude due to the higher closeness coefficients obtained for the relatively smaller values of the q parameter. It has been proven for both proposed approaches that decision-makers have a more pessimistic attitude due to the lower closeness coefficients obtained for relatively larger values of the q parameter. Furthermore, to show the applicability of the developed methods, the evaluations obtained by decision-makers have been analyzed dynamically. For this, a scenario-based evaluation analysis has applied for changes that may occur in the course of the pandemic. According to the results, it has been observed that the best strategy was again A1 — Mandatory quarantine and strict isolation strategy in cases where the pandemic’s course is the best and the worst.

The comparative analyses have been also conducted with other q-ROF MCDM methods and the IF-TOPSIS method. It has been seen that the TOPSIS method compared with other MCDM techniques in fuzzy environment is a simple mathematical process with low computation time and strong computational capability. On the other hand, it has been revealed that our proposed approaches exhibit results involving more detailed and more comprehensive information in uncertain decision-making environments in the second comparison analysis.

For further study, triangular q-ROFSs, trapezoidal q-ROFSs, or interval-valued q-ROFSs instead of singleton q-ROFSs can be used in the proposed q-ROF TOPSIS methods. The proposed approaches can be extended to other types of ordinary fuzzy sets, such as type-2 fuzzy sets, hesitant fuzzy sets, and neutrosophic sets. Different MCDM methods based on q-ROFSs can be developed to compare with our proposed approaches.

CRediT authorship contribution statement

Nurşah Alkan: Conceptualization, Methodology, Validation, Investigation, Visualization, Writing - review & editing. Cengiz Kahraman: Conceptualization, Methodology, Validation, Supervision, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.