Abstract
Although the interpersonal distance represents an important parameter affecting the risk of infection due to respiratory viruses, the mechanism of exposure to exhaled droplets remains insufficiently characterized. In this study, an integrated risk assessment is presented for SARS-CoV-2 close proximity exposure between a speaking infectious subject and a susceptible subject. It is based on a three-dimensional transient numerical model for the description of exhaled droplet spread once emitted by a speaking person, coupled with a recently proposed SARS-CoV-2 emission approach. Particle image velocimetry measurements were conducted to validate the numerical model.
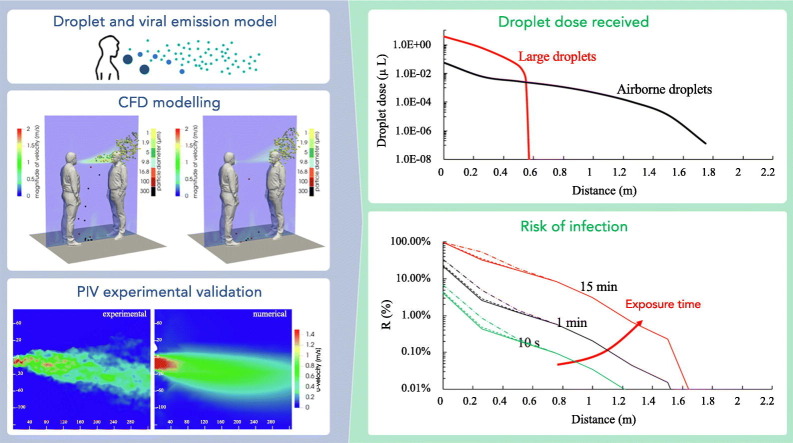
The contribution of the large droplets to the risk is barely noticeable only for distances well below 0.6 m, whereas it drops to zero for greater distances where it depends only on airborne droplets. In particular, for short exposures (10 s) a minimum safety distance of 0.75 m should be maintained to lower the risk below 0.1%; for exposures of 1 and 15 min this distance increases to about 1.1 and 1.5 m, respectively. Based on the interpersonal distances across countries reported as a function of interacting individuals, cultural differences, and environmental and sociopsychological factors, the approach presented here revealed that, in addition to intimate and personal distances, particular attention must be paid to exposures longer than 1 min within social distances (of about 1 m).
Keywords: CFD analysis, Virus transmission, Close proximity, PIV, SARS-CoV-2, Droplets
Graphical abstract
1. Introduction
The COVID-19 pandemic has highlighted the key role of droplets exhaled during respiratory activities (such as oral breathing, speaking, sneezing, coughing) as potential virus carriers leading to risk of infections and/or diseases (Morawska and Cao, 2020). Three possible routes of transmission are generally considered: the fomite, and large droplet and airborne droplet routes (Li, 2021a).
The large droplet route has been incorrectly considered to be the primary route for most respiratory infections since the beginning of the last century (Chapin, 1912; Flügge, 1897), and the associated protective measure of social distancing of 1–2 m (varying in each country as a function of activities) is known and imposed worldwide. The large droplet route is commonly identified with close proximity during which an infectious bacterium or virus can be transmitted effectively via specific routes, as discussed below. Despite the importance, a recent search of the literature revealed that the characterization of exposure to droplets exhaled at different interpersonal distances remains surprisingly unexplored. We point out that the term of “droplets” in this paper refers to all sizes, from the smallest droplets of sub-micron size to the largest ones with dimensions of hundreds of microns; moreover, we adopted the term “close proximity” instead of “close contact” (also used in the scientific literature) in order to avoid misinterpretation implying transmission by some sort of contact. Recent studies have identified two major routes for close proximity transmission (Chen et al., 2020): the large droplet route and the airborne droplet route. The large droplet route concerns the deposition of large droplets from the infected subject on the mucous membranes (lips, eyes, nostrils) of the susceptible subject (Gallo et al., 2021; Lu et al., 2020). According to Xie et al. (2007), who revisited previous guidelines by Wells (1934) with improved evaporation and settling models, droplets larger than about 100 μm in diameter rapidly settle out of the air by gravity, with the infective range being within a short distance of the source. In contrast, the airborne droplet route involves droplets smaller than about 100 μm in diameter that, as soon they are exhaled, decrease their diameter by evaporation and can be inhaled by the receiving host as interconnected multiphase flow processes (Balachandar et al., 2020). In fact, the surrounding ambient air enables the exhaled droplets to evaporate and rapidly shrink to droplet nuclei, reaching a final size that is governed by the initial amount of non-volatiles. As an example, by considering the average peak value of exhaled air velocity for breathing and speaking and the evaporation time, a droplet with a 50 μm diameter would shrink to a droplet nucleus before it reached a nearby person (Zhang et al., 2020a).
Recently Chen et al. (2020), using a simple mathematical model of exhaled flows and both droplet deposition and inhalation phenomena, found the airborne droplet route to dominate in the social distancing range of 1–2 m during both speaking and coughing. The large droplet route (> 100 μm) only dominates when the distance is lower than 0.2 m while talking or 0.5 m while coughing, whereas when the subjects are more than 0.3 m apart, the large droplet route can be neglected even while coughing.
Although the work of Chen et al. (2020) represents a novel analysis in the investigation of infection transmission in close proximity, it has limitations mainly associated with the simplicity of the proposed analytical model, i.e. adopting steady state conditions, not considering the fluid dynamics connected to the breathing of the subjects, and using corrective coefficients to simulate the inhalation process. In this regard, thermo-fluid dynamic modeling represents a more advanced approach to solve complex flow behaviors (i.e. three-dimensional, transient) typical of respiratory activities, and of the related droplet emission and inhalation, which are not possible with ordinary calculus. However, to date, most of the thermo-fluid dynamic analyses performed on this very complex subject are limited to non-pathogen carrying droplet emission and/or simulate simplified conditions (e.g. constant emission, steady-state analyses) (Ai et al., 2019; Ai and Melikov, 2018).
A further limitation of the analysis proposed by Chen et al. (2020) is that it estimates the fluid dynamics of droplets but does not investigate the issues related to host-to-host viral airborne transmission, which is fundamental in an infectious risk assessment. To this end, the authors recently presented an approach to evaluate the viral load emitted by infected individuals (Buonanno et al., 2020b) that takes into account the effect of other parameters such as inhalation rate, type of respiratory activity, and activity level. Such an approach has been applied to prospective and retrospective cases (Buonanno et al., 2020a), and then extended to viruses other than SARS-CoV-2 (Mikszewski et al., 2021), adopting a simplified zero-dimensional model and allowing the risk of infection due to airborne droplets to be estimated in different indoor scenarios involving people sharing room air and maintaining distancing. Nonetheless, the well-mixed hypothesis of such an approach cannot be applied when it comes to evaluating the risk of infection in close proximity scenarios.
On the basis of the abovementioned approach allowing evaluation of the viral load emitted, in this paper the authors present an integrated approach aimed at assessing the close proximity risk of infection from SARS-CoV-2. For this purpose, a numerical approach has been developed to estimate the volume of the droplets and the corresponding viral load received by a susceptible subject (through inhalation and deposition) at different distances in close proximity scenarios (distance less than 2 m). Particle image velocimetry (PIV) measurements were conducted to characterize the air flow exhaled during human expiratory activities to validate the modeling results. Therefore, on the basis of the integrated approach between thermo-fluid dynamic modeling of exhaled droplets and viral load, an infectious risk assessment is presented for a close proximity scenario represented by a speaking infected subject (emitter) and a susceptible subject (receiver) in the case of a face-to-face orientation and stagnant air conditions.
2. Materials and methods
The proposed SARS-CoV-2 infectious risk assessment is characterized by an integrated approach, based on the following main steps: (i) development of a three-dimensional Eulerian-Lagrangian numerical model to describe droplet spread once emitted by a speaking person in transient conditions; this is based on an Eulerian-Lagrangian approach, in which the continuum equations are solved for the air flow and Newton's equation of motion is solved for each droplet (2.1, 2.2); (ii) PIV measurements to define the boundary conditions and to validate the numerical model (Section 2.3); iii) definition of a droplet emission model including droplet diameters from 0.5 μm to 800 μm emitted by an adult while speaking (Section 2.4); and iv) infectious SARS-CoV-2 risk assessment in a close proximity scenario by considering the contributions of the large droplet and airborne droplet routes as well as the distance between the speaking infected subject and a susceptible subject (Section 2.5). The assessment has been performed in stagnant air conditions, which clearly represents the worst scenario in terms of virus spread as it could occur also in outdoor environments with negligible wind speed.
2.1. Eulerian-Lagrangian based model to simulate the droplet dynamics at as function of the interpersonal distance
The Computational Fluid Dynamics (CFD) technique has been adopted for numerical description of velocity, pressure, and temperature fields, along with the motion and interaction of the droplets with the fluid. The fully open source finite volume based openFOAM software has been employed. This choice was dictated by the need to have a fully open and flexible tool with complete control over the solved partial differential equations (PDEs), boundary conditions, and correlations employed for SARS-CoV-2 risk assessment. The substantial complexity of the adopted approach has paid off by allowing detailed description in space and time of thermo-fluid dynamic fields and associated droplet motion. Additionally, the use of the openFoam software offered the ability to directly access the source code, so modifying available mathematical models, boundary conditions, and thermophysical models is possible, as well as implementing new ones if necessary.
From a mathematical point of view, the droplet motion inside the air flow has been modeled by employing the Lagrangian particle tracking (LPT) approach, based on a dispersed dilute two-phase flow. In particular, the spacing between droplets in the exhaled air plume is sufficiently large and the volume fraction of the droplets sufficiently low (<10−3) to justify the use of a Eulerian-Lagrangian approach, in which the continuum equations are solved for the air flow (continuous phase) and Newton's equation of motion is solved for each droplet. The continuum equations solved for an unsteady incompressible Newtonian fluid are widely described in the available scientific literature (Arpino et al., 2014; Massarotti et al., 2006; Scungio et al., 2013) and are not reported here for brevity. Since the flow regime associated to breathing activity is laminar, no turbulence has been considered in the numerical investigations. The droplet motion has been described using a solving approach based on the following LPT equation:
| (1) |
and
| (2) |
where m d (kg) is the mass of the droplet; represents the droplet velocity; t (s) is the time; F D (N) and F g(N) are, respectively, the drag and gravity forces acting on the droplet; and x d (m) represents the trajectory of the droplet. The drag force is given by Crowe (2011):
| (3) |
In Eq. (3), , d d(m) and Re d represent, respectively, the density, diameter and Reynolds number of the droplet. The droplet density has been considered constant and equal to 1200 kg m−3 as representative of the density of non-volatile components carried by respiratory droplets (McCombs and Rawls, 1968; Pattison et al., 1975; Ritchie et al., 1973). The Re d is calculated as:
| (4) |
where is the air density, whereas the drag coefficient, C D, in Eq. (3) is evaluated as a function of the droplet Reynolds number:
| (5) |
Droplet collisions are considered to be elastic, and the equations of motion for the droplets are solved assuming a two-way coupling: the flow field affects the droplet motion and vice-versa. Finally, numerical simulations were performed adopting the following thermophysical properties of air: air heat capacity of 1004.5 J/(kg K), air dynamic viscosity of 1.8 × 10−5 Pa s, and Prandtl number of 0.71.
2.2. Scenario analyzed: close proximity during speaking
The Eulerian-Lagrangian based model described in Section 2.1 has been applied to the analysis of droplet dispersion in close proximity during speaking. In particular, face-to-face interactions between two subjects (infected emitter and susceptible receiver) of the same height, located at different distances in the range 0.25–1.75 m, were studied. The susceptible subject was considered to be a mouth-breather, thus airborne droplets were inhaled through the mouth. Moreover, because oral, nasal (Gallo et al., 2021), and ocular mucosa (Lu et al., 2020) have been recognized as possible transmission routes for respiratory viruses, large droplet deposition onto mouth, ocular and nostril surfaces due to their inertial trajectories was estimated through the Eulerian-Lagrangian numerical model.
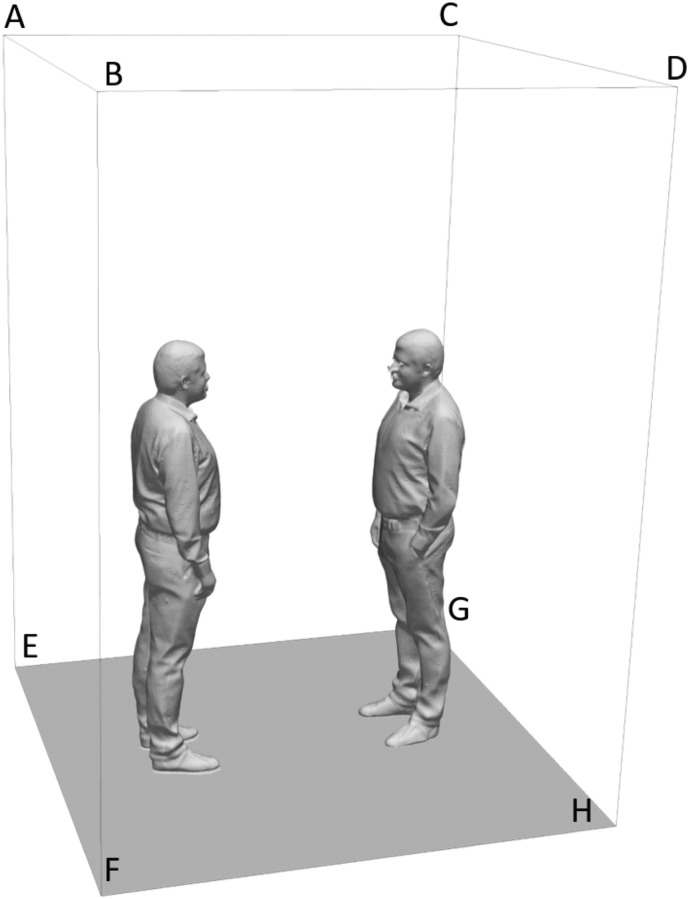
In Fig. 1 , the computational domain including the external surfaces, the emitter, and the receiver is illustrated. The cad file for emitter and receiver was obtained as an opensource file by the website “gradcad.com”. The mathematical model described in Section 2.1 was numerically solved using the open source openFOAM software, based on the finite volume technique, under the boundary conditions presented in Table 1 .
Fig. 1.
Computational domain in which the emitter (on the left), the receiver (on the right), and the external surfaces have been highlighted.
Table 1.
Boundary conditions (BC) adopted for the external surfaces of the computational domain and for the subjects.
| Surface | BC for velocity | BC for pressure | BC for temperature |
|---|---|---|---|
| ABEF | u = 0 | ||
| CDGH | u = 0 | ||
| BDFH | u = 0 | ||
| ACEG | u = 0 | ||
| ABCD | p = 101325 Pa | T = 293.15 K | |
| Emitter mouth | See Fig. 2 | T = 308.15 K | |
| Receiver mouth | u = A ∙ sin (2πft) | T = 308.15 K |
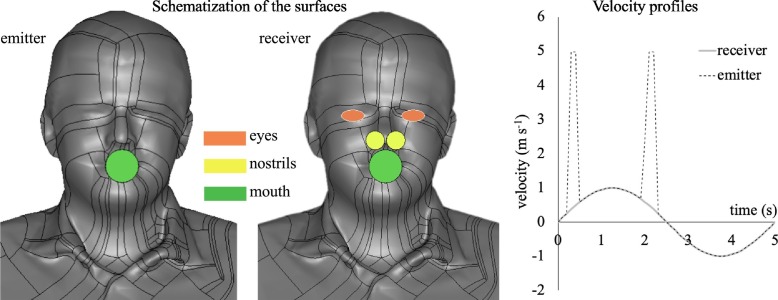
In Fig. 2 , the schematization of the surfaces of interest of the two subjects is presented: the emitter and receiver mouths were modeled as circular surfaces with a diameter of 2 cm, the nostrils were modeled as circular surfaces with a diameter of 1.13 cm, and the eyes were modeled as ellipses with axes of 2.76 and 1.38 cm, respectively (Chao et al., 2009; Chen et al., 2020).
Fig. 2.
Schematization of the surfaces of interest for emitter and receiver (eyes, nostrils, and mouth) and the transient velocity profile adopted as a boundary condition at the emitter and receiver mouths.
In Fig. 2, the boundary condition in terms of air velocity at the mouths of the emitter and receiver is also graphed; in particular, a sinusoidal approximation of breathing is adopted to realistically simulate a real interaction between two subjects. The volumetric flow rates were selected as the average values amongst those indicated by Abkarian et al. (2020): 1 L s−1 for speaking and 0.45 L s−1 for mouth breathing. In particular, the transient sinusoidal velocity profile applied at the receiver mouth presents an amplitude of 1 m s−1 and a frequency of 0.2 s−1, assuming a time period of 5 s for a full breath. The amplitude value was selected on the basis of the PIV measurement results reported in Section 3.1. Velocity peaks of 5 m s−1 mounted on the sinusoidal velocity profile were considered for the emitter during speaking, as confirmed by Abkarian et al. (2020) and by the PIV experimental analysis for speaking (see PIV results in Section 3.1). As concerns the velocity vector direction from the emitter's mouth, a conical jet flow was considered, adopting a cone angle equal to 22° with random velocity directions in intervals of 0.1 s. This adopted angle was calculated by Abkarian et al. (2020) to enclose 90% of the particles in a cone passing through the mouth exit, and was verified to remain stable with time after the initial cycles. Finally, as concern the boundary conditions of the droplets, the Lagrangian particle tracking was solved applying an escape boundary condition over all the surfaces of the computational domain including the emitter and the receiver subjects (see Fig. 1). In other words, the droplets touching the external surfaces (of the domain and of the subjects) disappear and cannot re-enter the computational domain, thus avoiding accumulation of viral load in the environment.
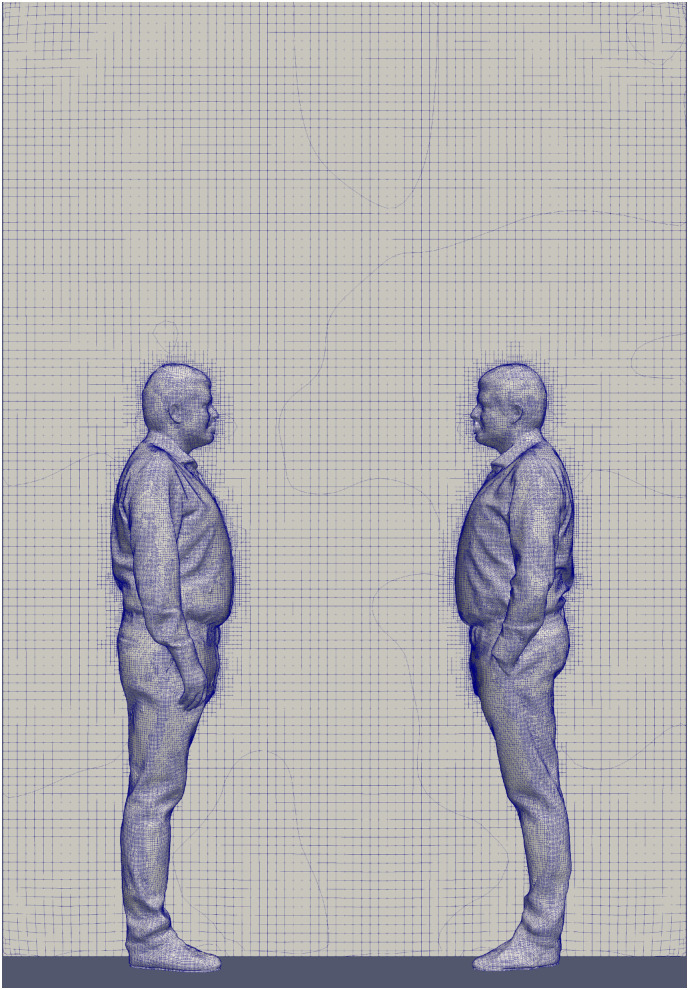
Careful attention was paid to the computational mesh construction: simulations were performed employing hexahedral-based unstructured computational grids, and realized employing the open source snappyHexMesh algorithm, chosen on the basis of a proper mesh sensitivity analysis. In particular, three meshes were selected: Mesh 1 composed of 687,380 elements, Mesh 2 composed of 1,801,060 elements, and Mesh 3 composed of 3,023,827 elements. The average percent deviation amongst the velocity fields obtained comparing Mesh 1 and Mesh 2 was equal to 6.56%, while comparing Mesh 2 and Mesh 3 resulted in an average percent deviation equal to 1.93%. Because the percent deviation amongst the velocity fields obtained between Mesh 2 and Mesh 3 was low (lower than 5%), the simulations were carried out adopting Mesh 2. As an example, Fig. 3 shows the computational grid employed (Mesh 2) to simulate droplet spread in the case of an interpersonal distance of 0.76 m. The grid is refined in correspondence of the solid surfaces, where a boundary layer region is added to better capture the viscous region gradients, and presents a maximum non-orthogonality value of about 50.
Fig. 3.
Computational grid employed (Mesh 2, 1,801,060 elements) to simulate droplet spread in the case of an interpersonal distance of 0.76 m.
2.3. Particle image velocimetry experimental investigations
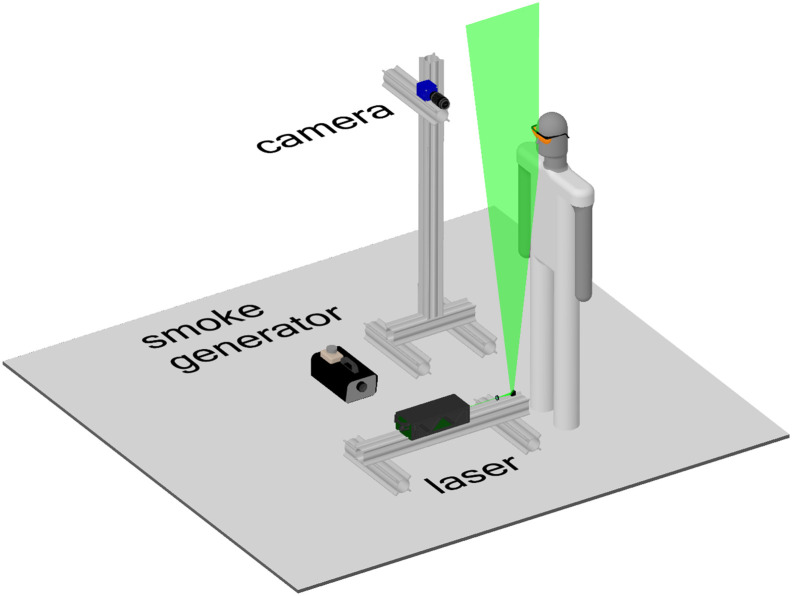
PIV measurements, aimed at validating the fluid-dynamic simulation results, were performed at TU Delft's laboratories to study the air flow exhaled during human expiratory activities. The experimental setup (Fig. 4 ) consists of an sCMOS camera from LaVision (2560 × 2160 px) coupled with a Nikon objective lens (35 mm focal length), an Nd:YAG Quantel laser (Evergreen, 200 mJ per pulse) and a smoke generator. The laser sheet (2–3 mm thickness) was formed from below the mouth, and passed through the subject's mid-plane, whereas the sCMOS camera was positioned approximately at the subject's mouth height, at a distance of 80 cm from the laser sheet, with the objective's axis perpendicular to it. The image magnification was 0.05, rendering a field of view of 30 cm (height) × 36 cm (width), while the resolution was 0.14 mm px−1. Images were acquired in frame-straddling mode (double frame, single exposure) at 10 Hz, with a time interval of 500 μs between frames.
Fig. 4.
Particle image velocimetry experimental setup.
The subject (male, 32 years old, 1.84 m, 80 kg) was protected against the laser light by safety goggles and a black screen positioned in front of him (not shown), with a 5 cm diameter opening for the mouth-exhaled air. A 3 cm long cylinder of the same diameter was placed at the opening to help position the head and to block the laser light from below. The head was positioned with the subject's nose slightly touching the upper surface of the cylinder; therefore, inhalation and exhalation through the nose did not influence the measured flow velocities. The entire setup, including the subject, was encompassed by a black tent (about 15 m3), whose main objective was to contain the smoke. The entire tent was filled with smoke by turning the smoke generator on for about 2 s with the tent closed, and waiting for about 10 min for the smoke to become homogeneously spread and the flow disturbances due to the smoke generator to become negligible.
Three different respiratory activities were investigated: inhaling through the nose and exhaling from the mouth, inhaling through and exhaling from the mouth, and speaking. Each activity was recorded for a duration of 50 s (500 images), which comprised about five respiratory cycles. The speaking activity consisted of reciting an excerpt from the rainbow passage (Fairbanks, 1941), a speech often used for the study of voice and articulation and representative of the multiple sounds of the English language: “When the sunlight strikes raindrops in the air, they act as a prism and form a rainbow. The rainbow is a division of white light into many beautiful colours. These take the shape of a long round arch, with its path high above, and its two ends apparently beyond the horizon. There is, according to legend, a boiling pot of gold at one end. People look, but no one ever finds it. When a man looks for something beyond his reach, his friends say he is looking for the pot of gold at the end of the rainbow.”
The images were processed via cross-correlation analysis, using the software DaVis 8.4 from LaVision. The final interrogation window was 48 × 48 px (7 × 7 mm2) with 75% overlap, yielding about 160 × 200 vectors per image. Typical uncertainty of a PIV displacement measurement is 0.1 px (Raffel et al., 2018); because the velocity magnitude close to the mouth varied in the range of 1–5 m s−1 (3–18 px), the uncertainty of the instantaneous velocity is estimated to be within 0.5%–3%.
2.4. Droplet emission
The number of droplets exhaled by the infected subject as a function of the diameter per unit time, i.e. the droplet number emission rate (ERN, droplet s−1), was estimated starting from the number distribution of the droplets emitted by an adult person provided by Johnson et al. (2011) and Morawska et al. (2009). They measured the droplet distribution from 0.5 μm to about 1000 μm in close proximity of an adult person's mouth while speaking, in order to consider negligible the droplet evaporation phenomenon. Such measurement was extremely challenging; indeed, the experimental analysis was performed in a purpose-built wind tunnel (named the expired droplet investigation system, EDIS) applying two separate measurement techniques to cover the entire size range: an aerodynamic particle sizer (up to 20 μm) and a droplet deposition analysis (20–1000 μm). For the sake of brevity, the experimental analyses performed in that study are not exhaustively described here: interested readers can refer to the original papers for further details.
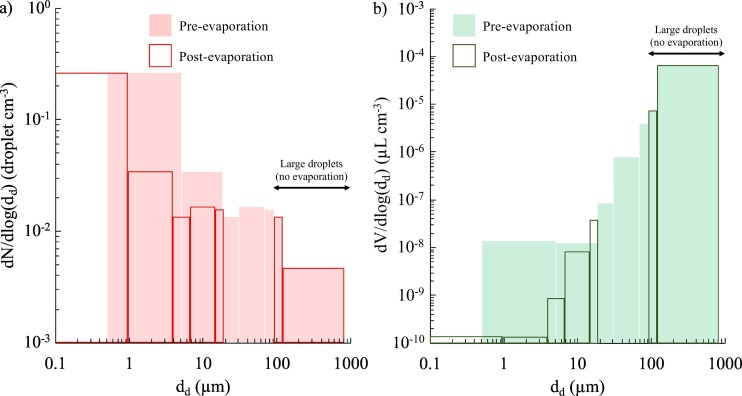
To make the simulations affordable, the droplet distributions (Johnson et al., 2011; Morawska et al., 2009) were fitted through a simplified distribution. In particular, from the number distribution provided by Johnson et al. (2011) and Morawska et al. (2009), the volume distribution was calculated considering spherical droplets, then both number and volume distributions were fitted through simplified distributions made up of seven diameters (i.e. seven size ranges). Because the evaporation phenomenon occurs quickly as soon as the droplets are emitted (Balachandar et al., 2020; Xie et al., 2007), in the present paper the post-evaporation number and volume distributions were considered in the simulation. To this end, the volume droplet distribution before evaporation (i.e. as emitted) was reduced to that resulting from the quick evaporation, which is the volume fraction of non-volatiles in the initial droplet, here considered equal to 1% (Balachandar et al., 2020). Therefore, the droplet shrinkage due to evaporation reduces the droplet diameter to about 20% of the initial emitted size. Additionally, the shrinking effect is not homogeneous for the entire size range. In particular, as reported in the scientific literature (Balachandar et al., 2020; Xie et al., 2007), the evaporation is slow for very small droplets (<1 μm) and quite negligible for large droplets. Therefore, we (i) grouped all the droplets <1 μm after the evaporation (i.e. droplets <4.6 μm at emission) in a single size interval labelled as 1 μm droplet diameter; (ii) considered the droplet nuclei resulting from the evaporation process for droplets with an initial diameter of 4.6–90 μm (reduced to droplets with a diameter of 1–19.2 μm after evaporation); and (iii) neglected the evaporation for droplets >90 μm at emission. The resulting number and volume distributions are summarized in Table 2 and in Fig. 5 . In Table 2 the resulting droplet number (ERN) and volume (ERV, pre-evaporation) emission rates are also reported, calculated by multiplying the number (or volume) concentration at each size by the expiration flow rate of a speaking subject while standing (1.0 L s−1, average value measured for an adult by Abkarian et al., 2020). The total droplet number and volume concentrations are reported in Table 2: the total droplet number concentration (0.25 droplet cm−3) is the same before and after evaporation, whereas a small variation was recognizable for the volume concentration (6.27 × 10−5 and 6.19 × 10−5 μL cm−3 before and after evaporation, respectively) due to shrinkage of droplets initially <90 μm. In terms of the number concentration (or emission rate), the contribution of the airborne droplets is 98%, whereas it is only 1% and 0.01% in terms of volume concentration (or emission rate) before and after evaporation, respectively, thus confirming that a reduced number of large droplets mostly contributes to the total volume emitted.
Table 2.
Droplet number and volume distributions pre- and post-evaporation (fitted by seven size ranges) adopted in the simulations. Droplet diameters and corresponding ranges before and after evaporation are also reported, as well as droplet number and volume emission rates. Airborne and large droplets were separately identified.
| Type of droplets | Pre-evaporation |
Post-evaporation |
||||||
|---|---|---|---|---|---|---|---|---|
| Droplet diameter, dd (μm) |
dN/dlog(dd) (droplet cm−3) |
dV/dlog(dd) (μL cm−3) |
ERN (droplet s−1) |
ERV (μL s−1) |
Droplet diameter, dd (μm) |
dN/dlog(dd) (droplet cm−3) |
dV/dlog(dd) (μL cm−3) |
|
| Airborne droplets | 4.6 μm (<0.5 to 4.6 μm) |
0.266 | 1.39 × 10−10 | 217.6 | 1.14 × 10−7 | 1 μm (< 1 μm) |
0.266 | 1.39 × 10−8 |
| 9.0 μm (4.6 to 17.7 μm) |
0.035 | 1.33 × 10−10 | 20.3 | 7.80 × 10−8 | 1.9 μm (1.0 to 3.8 μm) |
0.035 | 1.33 × 10−8 | |
| 23.2 μm (17.7 to 30.4 μm) |
0.013 | 8.74 × 10−10 | 3.1 | 2.05 × 10−7 | 5 μm (3.8 to 6.6 μm) |
0.013 | 8.74 × 10−8 | |
| 45.5 μm (30.4 to 68.2 μm) |
0.016 | 8.08 × 10−9 | 5.7 | 2.83 × 10−6 | 9.8 μm (6.6 to 14.7 μm) |
0.016 | 8.08 × 10−7 | |
| 78 μm (68 to 90 μm) |
0.015 | 3.83 × 10−8 | 1.8 | 4.48 × 10−6 | 16.8 μm (14.7 to 19.2 μm) |
0.015 | 3.83 × 10−6 | |
| Large droplets | 100 μm (90 to 120 μm) |
0.014 | 7.09 × 10−6 | 1.6 | 8.29 × 10−4 | 100 μm (90 to 120 μm) |
0.014 | 7.09 × 10−6 |
| 300 μm (120 to 800 μm) |
0.005 | 6.53 × 10−5 | 4.3 | 6.11 × 10−2 | 300 μm (120 to 800 μm) |
0.005 | 6.53 × 10−5 | |
| Total | 0.254 | 6.27 × 10−5 | 254.5 | 6.19 × 10−2 | 0.254 | 6.19 × 10−5 | ||
Fig. 5.
Droplet number (a) and volume (b) distributions adopted in the simulations as fitted through seven size ranges; in particular, distributions pre- and post-evaporation are reported to show how airborne and large droplets are affected by the evaporation phenomenon.
2.5. Estimation of the dose received by the susceptible subject and infectious risk assessment
The viral load carried by the droplets exhaled by the infected subject was evaluated as the product of the droplet volume (discussed in the previous section) and the corresponding viral load. The viral load of an infected subject, c v, can vary significantly (several orders of magnitude) (Buonanno et al., 2020a, Buonanno et al., 2020b; Mikszewski et al., 2021); thus, to achieve a proper infection risk assessment of an exposed subject, all the possible viral load data should be considered. In other words, when calculating the dose of RNA copies received by the susceptible subject (through inhalation or deposition), the probability distribution function of c v values should be considered, which is the probability of occurrence of each c v value. Data of the viral load in sputum so far available in the scientific literature (Fajnzylber et al., 2020; Pan et al., 2020; Wölfel et al., 2020) can be fitted through a log-normal distribution characterized by average and standard deviation c v values of log10 5.6 and log10 1.2 RNA copies mL−1 (Mikszewski et al., 2021), i.e. 1st, 50th, and 99th percentiles equal to 6.4 × 102, 4.0 × 105, and 2.5 × 108 RNA copies mL−1, respectively.
The large and airborne droplet doses of RNA copies (D large and D airborne) received by the susceptible subject for each c v value were calculated as:
| (6) |
where V d-large(t) and V d-airborne-pre(t) are the doses of airborne droplets inhaled and large droplets deposited as a function of the exposure time (t), and T is the total exposure time. The authors point out that the viral load carried by the droplet is related to the initial droplet volume (i.e. before evaporation), and evaporation leads to a reduction in the droplet volume, whereas the RNA copies do not evaporate; thus, the V d-airborne-pre term refers to the dose of airborne droplets calculated with the initial (pre-evaporation) volume. Therefore, assuming an instantaneous evaporation turns out to be a conservative assumption since smaller droplets can reach longer distances carrying the same amount of RNA copies. The V d-airborne-pre term has been adopted to distinguish it from the actual doses of airborne droplets inhaled (V d-airborne-post), i.e. droplets with the actual volume at the time of inhalation (i.e. post-evaporation). The total dose of RNA copies received by the exposed subject for each c v value was then evaluated by summing up the deposition and inhalation contributions, i.e. D total(c v) = D large(c v) + D airborne(c v).
Nonetheless, when assessing the doses of RNA copies received by the exposed subject, two further aspects need to be considered: i) the different pathogen concentrations as a function of the droplet diameter, ii) the different effectiveness of the two transmission routes in causing infection. As regards the first aspect, a review study (Fennelly, 2020) showed that the viral load is not equally concentrated for all the droplet sizes: pathogens predominate in airborne droplets with values depending on the type of virus and expiratory activity, reaching contributions >90%. As concerns the effectiveness of the transmission routes, Bixler et al. (2021) recently recognized that a roughly 100-fold higher dose of SARS-CoV-2 should be instilled (i.e. deposited) in macaques' mucosa to obtain the same physiological response related to the inhalation route. An even larger difference amongst inhalation and deposition routes was also previously measured in humans in case of flu (Little et al., 1979). Combining these two effects, the equivalent dose of RNA copies related to the large droplet deposition process results at least one hundredth of the airborne droplet inhaled. In the paper, since no experimental data are already available for SARS-CoV-2 virus concentration as a function of the droplet size and for pathological response to SARS-CoV-2 virus instilled in humans' mucosa, we have adopted a parametric analysis considering a dose of RNA copies related to the deposition of large droplets of one hundredth, one thousandth, and negligible (i.e. no large droplet contribution) with respect to inhalation of airborne droplets.
From the dose of RNA copies, the probability of infection (P I) of the exposed subject for each c v was calculated adopting a well-known exponential dose–response model (Haas, 1983; Sze To and Chao, 2010; Watanabe et al., 2010):
| (7) |
where HID 63 represents the human infectious dose for 63% of susceptible subjects, i.e. the number of RNA copies needed to initiate the infection with a probability of 63%. For SARS-CoV-2, a HID 63 value of 7 × 102 RNA copies was adopted based on the thermodynamic-equilibrium dose–response model developed by Gale (2020).
The individual risk of infection (R) of the exposed person was then calculated by integrating, for all the possible c v values, the product between the conditional probability of the infection for each c v (P I(c v)) and the probability of occurrence of each c v value (Pcv):
| (8) |
The authors point out that in the present analysis an equal amount of RNA copies received by inhalation of airborne droplets or by deposition of large droplets was considered to cause the same effect in terms of infection.
3. Results and discussion
3.1. Particle image velocimetry measurements and numerical results
As mentioned in the methodology section, PIV measurement results for a mouth breathing case study provided the required information to choose the velocity boundary conditions employed in the computational fluid dynamics (CFD) numerical simulations summarized in Section 2.2.
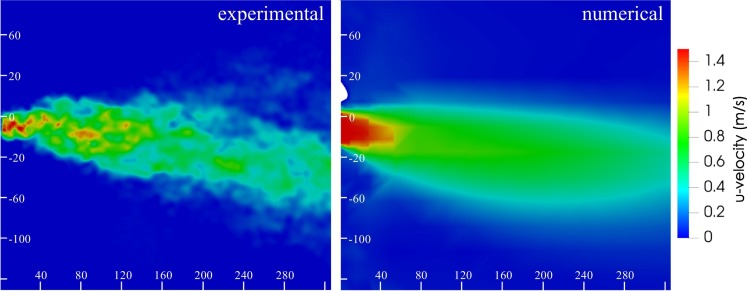
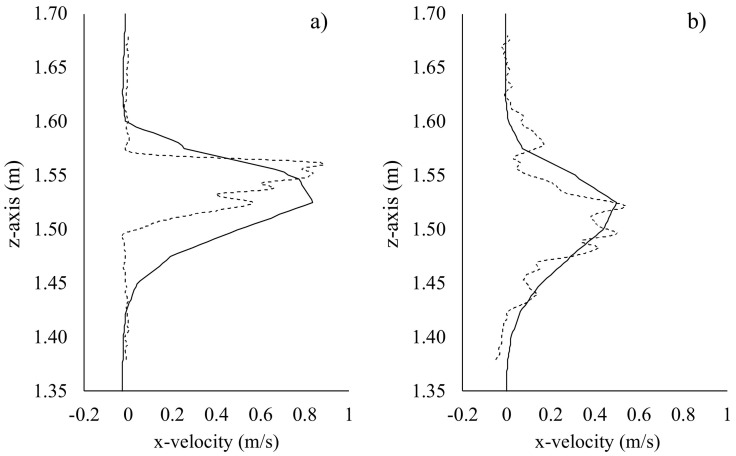
In particular, the adopted boundary condition for the mouth-breathing receiver was verified by comparing numerical results with PIV data in terms of velocity profiles obtained at different distances from the mouth of the emitter. This comparison also provided a rough confirmation of the numerical velocity field. To this end, experimental (PIV) and numerical (CFD) velocity contours obtained in the sagittal plane, by synchronizing the instant of time for breathing at which the maximum velocity values are reached, are presented in Fig. 6 , whereas PIV and CFD vertical velocity profiles in sagittal plane at a distance from the emitter mouth equal to 0.10 m and 0.32 m are compared in Fig. 7 . The peak numerical and experimental peak velocities differ by 6% and 7% at interpersonal distances of 0.10 m and 0.32 m, respectively, thus validating the numerical solutions obtained through the CFD analyses.
Fig. 6.
Experimental and CFD velocity contours obtained in a sagittal plane by synchronizing the instant of time for breathing at which the maximum velocity values are reached. Scales bars are reported in mm.
Fig. 7.
Experimental (particle image velocimetry, dotted lines) and CFD (solid lines) velocity profile comparison obtained in a sagittal plane at a distance from the emitter mouth equal to 0.10 m (a) and 0.32 m (b).
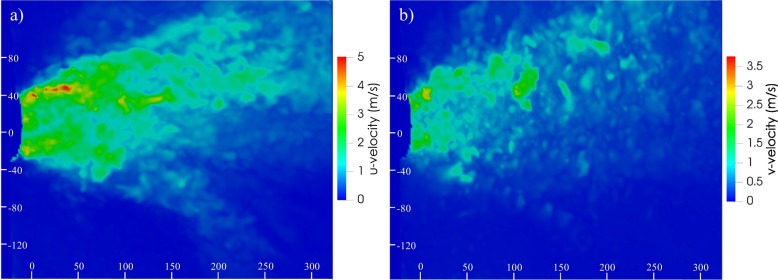
The emitter velocity peaks of 5 m s−1 adopted in the simulations were confirmed by the experimental analysis related to the speaking expiratory activity. Amongst the 500 recorded images obtained in the 50 s of the experiment (see Section 2.3), the time instant giving the maximum u-velocity and v-velocity values were selected and illustrated for a cross-section plane at the height of the mouth: u-velocity peaks of 5 m s−1 are clearly recognizable in Fig. 8a.
Fig. 8.
Instantaneous u-velocity (a) and v-velocity (b) contours for a cross-section plane at the height of the mouth obtained by particle image velocimetry during reading of the excerpt from the rainbow passage. Scales bars are reported in mm.
3.2. Droplet dose received by the susceptible subject
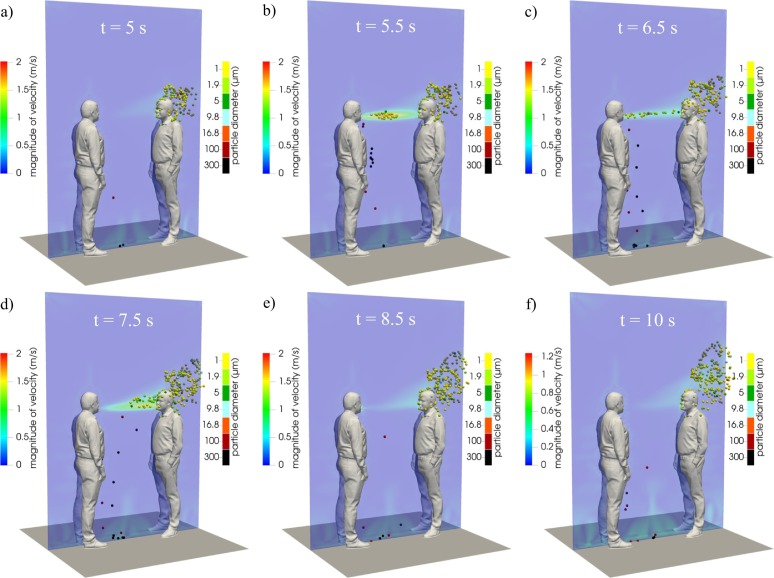
As an illustrative example of the droplet trajectories and flow fields obtained from the simulations, Fig. 9 shows the velocity contours and droplet positions for a 5-s breathing period (at computational times of 5, 5.5, 6.5, 7.5, 8.5, and 10 s) in the case of an interpersonal distance of 0.76 m between the injector and receiver mouths. For this distance, large droplets fall to the ground without reaching the susceptible surfaces of the receiver, while the airborne droplets are partly inhaled by the receiver. Indeed, airborne droplets are transported by the air velocity field, reach the receiver, and then are spread while rising in a vertical direction due to the effect of buoyancy forces. In fact, from the analysis of the three dimensional transient air velocity field shown in Fig. 9, it can be observed that when the air velocity from the emitter is low (Fig. 9a, d, e, f), the effect of buoyancy is evident, while forced convection dominates when the air velocity from the emitter is high (Fig. 9b, c).
Fig. 9.
Numerical velocity contours during a single breath at a distance of 0.76 m between people: six selected computational times (5, 5.5, 6.5, 7.5, 8.5, and 10 s) are shown.
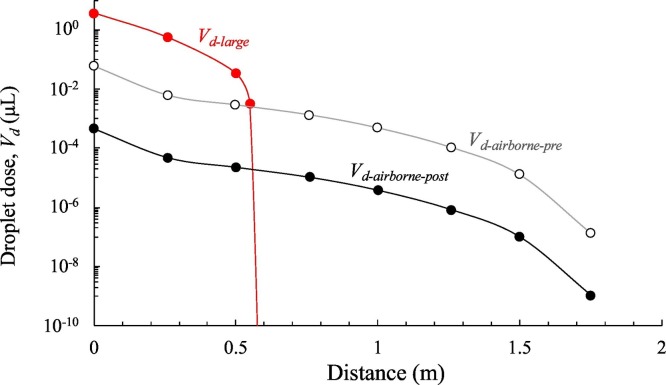
Fig. 10 shows airborne and large droplet doses (i.e. V d-airborne-pre, V d-airborne-post, and V d-large, μL) as a function of distance for an exposure time of 1 min. Data were obtained by performing numerical simulations of 15 min and averaging the obtained volumes over an observation time equal to 1 min. The trends show that the large droplet dose dominates up to a distance of <0.6 m but, beyond this distance, a step-decrease is observed because the large droplets cannot reach the deposition surfaces of the susceptible subject due to their inertial trajectories. As mentioned above, Chen et al. (2020) in their simplified mathematical model, recognized a dominant contribution of the large droplets while talking just up to 0.2 m; such a difference could be partly due to the different size distribution of exhaled droplets adopted (they used the one provided by Duguid (1946)), but more likely, to the different velocity profiles applied at the emitter mouth (e.g. once again we have adopted a sinusoidal profile with peaks at 5 m s−1, whereas Chen et al. (2020) adopted a constant velocity of 3.9 m s−1) and to the ability of the CFD methods to capture more in details the dynamic of the droplets with respect to simplified mathematical models. Fig. 10 also shows the dose of non-evaporated airborne droplets (V d-airborne-pre): this information is useful because infectivity (and therefore the risk) is directly related to this metric. For distances >0.6 m, only the airborne droplet contribution to the total dose received by the infected subject is observed. While the trajectory of large droplets is mostly affected by their inertia, and the related effect is negligible for distances >0.6 m, the spread of airborne droplets is affected by the spread angle of the exhaled flow. In particular, we recognized that at short interpersonal distances (roughly <0.76 m) from the emission point, where the exhaled air flow angle is still narrow, the dose of airborne droplets decays following the 1/L rule (with L representing the interpersonal distance), whereas for interpersonal distances in the range of 0.76–1.75 m, where the exhaled air flow angle becomes wider, the dose of airborne droplets decays following the 1/L2 rule as recognized for passive tracer-gas decay and reported by Li (2021b). The authors point out that the higher contribution of the large droplets to the dose received by susceptible persons must not mislead the reader regarding the risk of infection; indeed, as described in details in the Section 2.5, the risk of infection is also strongly affected by the different pathogen concentrations as a function of the droplet diameter, and the different effectiveness of the two transmission routes in causing infection. These two effects, as reported in the Section 3.3, strongly mitigate the higher contribution to the dose of the large droplets: in fact, as hereinafter explained, the contribution of airborne droplets to the risk received by the susceptible subject is dominant even for distance <0.6 m.
Fig. 10.
1-min large (Vd-large) and airborne droplet doses (Vd-airborne-pre and Vd-airborne-post) received by the susceptible subject (by deposition and inhalation, respectively) as a function of the distance between the two subjects.
3.3. Risk assessment as a function of the interpersonal distance
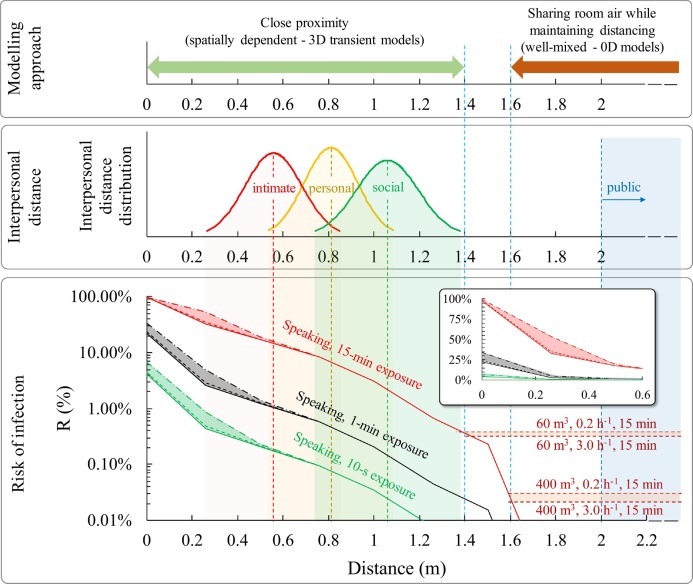
Fig. 11 shows the infection risk (R) as a function of the interpersonal distance between the speaking infected subject and the susceptible subject for different exposure times (10 s, 1 min, 15 min). The contributions of both deposited large droplets and inhaled airborne droplets are shown; in particular, the risk contribution of the dose of RNA copies related to the deposition of large droplets is shown considering such deposited dose equal to one hundredth, one thousandth, and negligible (i.e. no large droplet contribution) with respect to dose of RNA copies due to the inhalation of airborne droplets (as reported in the Section 2.5).
Fig. 11.
Infection risk (R, %) of a susceptible subject as a function of the time of exposure and interpersonal distance from the infected subject; infection risk trends at short and long distances are highlighted as well as the modeling approaches to be applied. The contributions of both deposited large droplets and inhaled airborne droplets are reported; in particular the risk contribution of the large droplets by deposition is shown considering a contribution of the dose of RNA copies related to the deposition of large droplets of one hundredth (dash-dotted line), one thousandth (dashed line), and negligible (solid line) with respect to inhalation of airborne droplets; the risk for distance <0.6 m was also zoomed to highlight the different relative contributions of the large droplets in these three different assumptions.
For distances less than 0.6 m between infected and exposed subjects, i.e. where the large droplets dominate the total droplet dose received by the susceptible subject (Fig. 10), the infection risk is extremely high for 15-min exposures as it ranges from >90% at few centimeters to >10% at 0.6 m. In particular, the risk is also affected by the equivalent dose of RNA copies due to the large droplet deposition: as an example, for 15-min exposure, at a distance of 30 cm the risk ranges from 30% (in case of negligible contribution of the dose of RNA copies related to the deposition of large droplets) to about 50% (in case of a contribution of the dose of RNA copies related to the deposition of large droplets equal to one hundredth of the airborne droplets). Thus, the airborne droplets represent the dominant contribution to the infection risk received also for distances well lower than 0.6 m. This is a key finding of the paper, indeed, it clearly highlights that performing infectious risk assessments just based on the fluid dynamics of droplets could be extremely misleading as they predict an erroneous dominant contribution of the large droplets for distances <0.6 m; on the contrary, the proposed integrated approach able to take into account for the viral load carried by the droplets, the droplet evaporation, the different pathogen concentrations as a function of the droplet diameter, and the different effectiveness of the transmission routes, clearly demonstrates the dominant role, in terms of risk of infection, of the airborne droplets also at short distances.
For shorter exposures, the risk at a distance of <0.6 m is still not negligible as it ranges from 1% to 30% in case of 1-min exposure and from about 0.1% to 7% for 10-s exposures, respectively; once again the main contribution to such risk is due to the inhalation of airborne droplets. Beyond 0.6 m, where there is only the contribution of airborne droplets (inhaled dose), the risk of infection can be reduced by several orders of magnitude as a function of the exposure duration and interpersonal distance as well. As an example, Fig. 11 shows that the distance to be adopted to achieve a risk lower than 0.1% in the case of an exposure time of 15 min is around 1.5 m (reducing to 1.1 m for an exposure time of 1 min and 0.75 m for a 10-s exposure), thus confirming the effectiveness of the six feet rule suggested by the US Centers for Disease and Control Prevention (CDC) but also highlighting the limited effectiveness of the 1-m physical distance adopted in most of the countries worldwide and suggested by the WHO. Once again, we point out that the estimated infection risk value is related to an outdoor environment with stagnant air or to an indoor environment without the contribution due to the accumulation of viral load in the environment itself. Nonetheless, when people share indoor air maintaining distancing because of airborne droplets, an infection risk can still be present. For example, in Fig. 11 the infection risk is estimated when sharing room air and maintaining distancing on the basis of the zero-dimensional well-mixed approach reported in Buonanno et al., 2020a, Buonanno et al., 2020b and Mikszewski et al. (2021) in small (60 m3, e.g. offices, classrooms) and large volumes (400 m3, e.g. restaurants, conference rooms). The simulations were performed for an exposure time of 15 min for typical ventilation rates (0.2–3.0 h−1) occurring in indoor environments (Frattolillo et al., 2021; Stabile et al., 2019). The 15-min close proximity (spatially-dependent) infection risk merges into the constant (not spatially dependent) sharing room air infection risks at interpersonal distances of about 1.4–1.6 m (depending on the volume and the ventilation rate) as also indicated in Li (2021b); this distance is representative of the boundary of simplified well-mixed model applicability. Thus, for the investigated scenario, infection risk assessments through complex three-dimensional and transient CFD models are essential for interpersonal short distances (<1.4–1.6 m), whereas simplified zero-dimensional well-mixed models can be applied for longer distances.
When applying these findings, an obvious question arises regarding the typical exposure duration and distance data. To address this issue, Zhang et al. (2020b) monitored and analyzed indoor human behavior in a graduate student office using automatic devices. They measured a median duration of close proximity of 15 s and an average interpersonal distance of 0.81 m during such close proximities. Adopting such median exposure durations, the corresponding infection risk is negligible (i.e. less than 0.1%, adopted as the threshold value by Buonanno et al. (2020a)), reaching 0.5% for exposure times of 1 min. Only with long exposure times (15 min) the risk would become significantly higher than 1%. Therefore, even though Zhang et al. (2020b) verified that 9.7% of employees' time in offices was in close proximity (with 4.0 close contacts h−1), an interpersonal distance of 0.81 cm is sufficient to have a limited risk for the measured exposure times (<1 min) in the analyzed common occupational scenario. Apart from workplace scenarios, the interpersonal distance is an essential feature of individuals' social behavior more broadly in relation to their physical environment and social interactions (Hall, 1966). On the basis of the classical proxemic theory (Hall, 1966), interpersonal distances are classified as (i) public distance (>2 m), (ii) social distance, during more formal interactions, (iii) personal distance, during interactions with friends, and (iv) intimate distance, maintained in close relationships, with Southern European, Latin American, and Arabian countries being the so-called “contact cultures”, and North America, Northern Europe, and Asian populations being the “noncontact cultures” (Hall, 1966). Sorokowska et al. (2017) reported significant variability in preferred interpersonal distances across countries as a function of certain characteristics of interacting individuals (such as gender or age), cultural differences, and environmental and sociopsychological factors. They reported worldwide interpersonal distance distributions of 0.56 ± 0.13 m, 0.81 ± 0.12 m, and 1.06 ± 0.14 m for intimate, personal and social distance, respectively, which are included in Fig. 11 for discussion. In the case of intimate distance, the average infection risk (i.e. the risk corresponding to the average distance value, i.e. 0.56 m) is >1%, starting from exposure times of 1 min, whereas for short exposures (10 s) it is about 0.2%. For personal distances, the average infection risk is negligible for short exposures (<0.1%), limited for 1-min exposures (<1%), and high for 15-min exposures. Finally, in the case of social distances, the average infection risk becomes significant only for 15-min exposures.
The authors highlight that the approach and the results presented here provide an important insight into potential virus transmission over short distances that could help regulatory authorities and air quality experts in implementing and imposing proper mitigation solutions as a function of the microenvironment and the type of contact expected. The paper also provides information about choosing the proper modeling approach for infection risk assessments. Despite the value of these findings, the authors acknowledge the simplified hypothesis and limitations of this study that should be addressed in future development of this research. First, the results obtained through the CFD approach were compared to the experimental data only in terms of the velocity field and only one subject; second, the effect of turbulence should be investigated for velocity peaks associated to speaking activity; third, the study was limited to mouth-breather subjects; fourth, transmission through surfaces (fomites) was not considered. Moreover, a further limitation worthy of mention regards the validation of the absolute values of infection risk. Such values are based on a viral load emission approach and a dose-response model that can be validated through experiments. Anyway, the exponential dose–response model here adopted (which is a stochastic non-threshold dose–response model) was recognized as one of the most biologically plausible (Sze To and Chao, 2010; Watanabe et al., 2010); moreover, even if a proper validation is not practically feasible, in our previous paper (Buonanno et al., 2020a) we adopted the same viral emission approach and dose-response model in retrospective applications and they were able to reproduce documented outbreaks in terms of attack rate.
4. Conclusions
The paper presents an integrated risk assessment for SARS-CoV-2 combining thermo-fluid dynamic modeling and infectious risk assessment to investigate close proximity exposure scenarios.
The results show that the contribution of airborne droplets (<100 μm) to the risk received by the susceptible subject is dominant even for an interpersonal distance <0.6 m, which means highly influential on the infection risk also at intimate interpersonal distances (average distance of 0.56 m). The contribution of the large droplets to the risk is appreciable only for distances well below 0.6 m, whereas it drops to zero for greater distances since the large droplets quickly settle on the ground. In fact, in the case of personal (0.81 m) and social (1.06 m) distancing, the only contribution to the risk of infection comes from airborne droplets. In addition to the distance, the exposure time plays a key role in the risk of infection: indeed, the average infection risk is not negligible even for short exposures (10 s) in the case of intimate distance, whereas in the case of social distances only long exposures (15 min) can lead to a not negligible risk.
A possible threshold value to be adopted as a safe distance in close proximity is around 1.5 m, which lowers the infection risk to 0.1% order of magnitude even with prolonged exposure times (15 min). Such a threshold value also represents the boundary distance beyond which simplified well-mixed approaches can be adopted instead of complex spatially dependent three-dimensional transient CFD analyses. Indeed, we have shown that the same infection risk values for short (close proximity) and long distances (sharing room air while maintaining distancing) can be obtained for a typical indoor environment for interpersonal distances in the range of 1.4–1.6 m, thus confirming that 1.5 m can be adopted as the typical distance for close proximity.
CRediT authorship contribution statement
G. Cortellessa: Methodology, Data curation, Formal analysis, Writing – original draft. L. Stabile: Methodology, Data curation, Formal analysis, Writing – original draft. F. Arpino: Methodology, Data curation, Formal analysis, Writing – review & editing. D.E. Faleiros: Methodology, Data curation. W. van den Bos: Methodology, Data curation. L. Morawska: Conceptualization, Supervision, Writing – review & editing. G. Buonanno: Conceptualization, Supervision, Writing – review & editing.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors would like to thank Prof. Jose Luis Jimenez (University of Colorado, Boulder, USA) for his valuable suggestions and discussions.
Editor: Pavlos Kassomenos
References
- Abkarian M., Mendez S., Xue N., Yang F., Stone H.A. Speech can produce jet-like transport relevant to asymptomatic spreading of virus. Proc. Natl. Acad. Sci. 2020;117:25237. doi: 10.1073/pnas.2012156117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ai Z.T., Melikov A.K. Airborne spread of expiratory droplet nuclei between the occupants of indoor environments: a review. Indoor Air. 2018;28:500–524. doi: 10.1111/ina.12465. [DOI] [PubMed] [Google Scholar]
- Ai Z., Hashimoto K., Melikov A.K. Influence of pulmonary ventilation rate and breathing cycle period on the risk of cross-infection. Indoor Air. 2019;29:993–1004. doi: 10.1111/ina.12589. [DOI] [PubMed] [Google Scholar]
- Arpino F., Cortellessa G., Dell’Isola M., Massarotti N., Mauro A. High order explicit solutions for the transient natural convection of incompressible fluids in tall cavities. Numer. Heat Transf. Part Appl. 2014;66:839–862. doi: 10.1080/10407782.2014.892389. [DOI] [Google Scholar]
- Balachandar S., Zaleski S., Soldati A., Ahmadi G., Bourouiba L. Host-to-host airborne transmission as a multiphase flow problem for science-based social distance guidelines. Int. J. Multiphase Flow. 2020;132:103439. doi: 10.1016/j.ijmultiphaseflow.2020.103439. [DOI] [Google Scholar]
- Bixler S.L., Stefan C.P., Jay A., Rossi F., Ricks K.M., Shoemaker C.J., Moreau A.M., Zeng X., Hooper J.W., Dyer D., Frick O., Koehler J.W., Kearney B., DiPinto N., Liu J., Tostenson S., Clements T.L., Smith J.M., Johnson J.A., Berrier K., Esham H., Delp K.L., Coyne S.R., Bloomfield H., Kuehnert P., Akers K., Gibson K., Minogue T.D., Nalca A., Pitt M.L.M. Aerosol exposure of cynomolgus macaques to SARS-CoV-2 results in more severe pathology than existing models. bioRxiv. 2021 doi: 10.1101/2021.04.27.441510. [DOI] [Google Scholar]
- Buonanno G., Morawska L., Stabile L. Quantitative assessment of the risk of airborne transmission of SARS-CoV-2 infection: prospective and retrospective applications. Environ. Int. 2020;145:106112. doi: 10.1016/j.envint.2020.106112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buonanno G., Stabile L., Morawska L. Estimation of airborne viral emission: quanta emission rate of SARS-CoV-2 for infection risk assessment. Environ. Int. 2020;141:105794. doi: 10.1016/j.envint.2020.105794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chao C.Y.H., Wan M.P., Morawska L., Johnson G.R., Ristovski Z.D., Hargreaves M., Mengersen K., Corbett S., Li Y., Xie X., Katoshevski D. Characterization of expiration air jets and droplet size distributions immediately at the mouth opening. J. Aerosol Sci. 2009;40:122–133. doi: 10.1016/j.jaerosci.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chapin C.V. J. Wiley & Sons; [etc., etc.], New York: 1912. The sources and modes of infection. [Google Scholar]
- Chen W., Zhang N., Wei J., Yen H.-L., Li Y. Short-range airborne route dominates exposure of respiratory infection during close contact. Build. Environ. 2020;176:106859. doi: 10.1016/j.buildenv.2020.106859. [DOI] [Google Scholar]
- Crowe T.C. CRC Press; 2011. Multiphase Ows With Droplets and Particles. [Google Scholar]
- Duguid J.P. The size and the duration of air-carriage of respiratory droplets and droplet-nuclei. J. Hyg. (Lond.) 1946;44:471–479. doi: 10.1017/s0022172400019288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fairbanks G. The Laryngoscope, Harper and Brothers. vol. 51. 1941. Voice and articulation drillbook; p. 1141. [DOI] [Google Scholar]
- Fajnzylber J., Regan J., Coxen K., Corry H., Wong C., Rosenthal A., Worrall D., Giguel F., Piechocka-Trocha A., Atyeo C., Fischinger S., Chan A., Flaherty K.T., Hall K., Dougan M., Ryan E.T., Gillespie E., Chishti R., Li Y., Jilg N., Hanidziar D., Baron R.M., Baden L., Tsibris A.M., Armstrong K.A., Kuritzkes D.R., Alter G., Walker B.D., Yu X., Li J.Z., Abayneh B.A. (Betty), Allen P., Antille D., Balazs A., Bals J., Barbash M., Bartsch Y., Boucau J., Boyce S., Braley J., Branch K., Broderick K., Carney J., Chevalier J., Choudhary M.C., Chowdhury N., Cordwell T., Daley G., Davidson S., Desjardins M., Donahue L., Drew D., Einkauf K., Elizabeth S., Elliman A., Etemad B., Fallon J., Fedirko L., Finn K., Flannery J., Forde P., Garcia-Broncano P., Gettings E., Golan D., Goodman K., Griffin A., Grimmel S., Grinke K., Hartana C.A., Healy M., Heller H., Henault D., Holland G., Jiang C., Jordan H., Kaplonek P., Karlson E.W., Karpell M., Kayitesi C., Lam E.C., LaValle V., Lefteri K., Lian X., Lichterfeld M., Lingwood D., Liu H., Liu J., Lopez K., Lu Y., Luthern S., Ly N.L., MacGowan M., Magispoc K., Marchewka J., Martino B., McNamara R., Michell A., Millstrom I., Miranda N., Nambu C., Nelson S., Noone M., Novack L., O'Callaghan C., Ommerborn C., Osborn M., Pacheco L.C., Phan N., Pillai S., Porto F.A., Rassadkina Y., Reissis A., Ruzicka F., Seiger K., Selleck K., Sessa L., Sharpe A., Sharr C., Shin S., Singh N., Slaughenhaupt S., Sheppard K.S., Sun W., Sun X., Suschana E. (Lizzie), Talabi O., Ticheli H., Weiss S.T., Wilson V., Zhu A., The Massachusetts Consortium for Pathogen Readiness SARS-CoV-2 viral load is associated with increased disease severity and mortality. Nat. Commun. 2020;11:5493. doi: 10.1038/s41467-020-19057-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fennelly K.P. Particle sizes of infectious aerosols: implications for infection control. Lancet Respir. Med. 2020;8:914–924. doi: 10.1016/S2213-2600(20)30323-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flügge C. Ueber Luftinfection. Z. Für Hyg. Infekt. 1897;25:179–224. doi: 10.1007/BF02220473. [DOI] [Google Scholar]
- Frattolillo A., Stabile L., Dell’Isola M. Natural ventilation measurements in a multi-room dwelling: critical aspects and comparability of pressurization and tracer gas decay tests. J. Build. Eng. 2021;42:102478. doi: 10.1016/j.jobe.2021.102478. [DOI] [Google Scholar]
- Gale P. Thermodynamic equilibrium dose-response models for MERS-CoV infection reveal a potential protective role of human lung mucus but not for SARS-CoV-2. Microb. Risk Anal. 2020;16:100140. doi: 10.1016/j.mran.2020.100140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallo O., Locatello L.G., Mazzoni A., Novelli L., Annunziato F. The central role of the nasal microenvironment in the transmission, modulation, and clinical progression of SARS-CoV-2 infection. Mucosal Immunol. 2021;14:305–316. doi: 10.1038/s41385-020-00359-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haas C.N. Estimation of risk due to low doses of microorganisms: a comparison of alternative methodologies. Am. J. Epidemiol. 1983;118:573–582. doi: 10.1093/oxfordjournals.aje.a113662. [DOI] [PubMed] [Google Scholar]
- Hall E.T. Doubleday, New York; New York: 1966. The Hidden Dimension. [Google Scholar]
- Johnson G.R., Morawska L., Ristovski Z.D., Hargreaves M., Mengersen K., Chao C.Y.H., Wan M.P., Li Y., Xie X., Katoshevski D., Corbett S. Modality of human expired aerosol size distributions. J. Aerosol Sci. 2011;42:839–851. doi: 10.1016/j.jaerosci.2011.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y. Basic routes of transmission of respiratory pathogens—a new proposal for transmission categorization based on respiratory spray, inhalation, and touch. Indoor Air. 2021;31:3–6. doi: 10.1111/ina.12786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y. The respiratory infection inhalation route continuum. Indoor Air. 2021;31:279–281. doi: 10.1111/ina.12806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Little J.W., Gordon R.D., Hall W.J., Jr., Roth F.K. Attenuated influenza produced by experimental intranasal inoculation. J. Med. Virol. 1979;3:177–188. doi: 10.1002/jmv.1890030303. [DOI] [PubMed] [Google Scholar]
- Lu C.-W., Liu X.-F., Jia Z.-F. 2019-nCoV transmission through the ocular surface must not be ignored. Lancet Lond. Engl. 2020;395:e39. doi: 10.1016/S0140-6736(20)30313-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Massarotti N., Arpino F., Lewis R.W., Nithiarasu P. Explicit and semi-implicit CBS procedures for incompressible viscous flows. Int. J. Numer. Methods Eng. 2006;66:1618–1640. doi: 10.1002/nme.1700. [DOI] [Google Scholar]
- McCombs R.M., Rawls W.E. Density gradient centrifugation of rubella virus. J. Virol. 1968;2:409–414. doi: 10.1128/JVI.2.5.409-414.1968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mikszewski A., Stabile L., Buonanno G., Morawska L. The airborne contagiousness of respiratory viruses: a comparative analysis and implications for mitigation. medRxiv. 2021 doi: 10.1101/2021.01.26.21250580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morawska L., Cao J. Airborne transmission of SARS-CoV-2: the world should face the reality. Environ. Int. 2020;139:105730. doi: 10.1016/j.envint.2020.105730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morawska L., Johnson G.R., Ristovski Z.D., Hargreaves M., Mengersen K., Corbett S., Chao C.Y.H., Li Y., Katoshevski D. Size distribution and sites of origin of droplets expelled from the human respiratory tract during expiratory activities. J. Aerosol Sci. 2009;40:256–269. doi: 10.1016/j.jaerosci.2008.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan Y., Zang D., Yang P., Poon L.M., Wang Q. Viral load of SARS-CoV-2 in clinical samples Yang Pan Daitao Zhang Peng Yang Leo L M Poon Quanyi Wang. Lancet. 2020;20(4):411–412. doi: 10.1016/S1473-3099(20)30113-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pattison M., Alexander D.J., Harkness J.W. Purification and preliminary characterisation of a pathogenic strain of infectious bursal disease virus. Avian Pathol. J. WVPA. 1975;4:175–187. doi: 10.1080/03079457509353864. [DOI] [PubMed] [Google Scholar]
- Raffel M., Willert C.E., Scarano F., Kähler C., Wereley S.T., Kompenhans J. 3rd ed. Springer International Publishing; 2018. Particle Image Velocimetry. A Practical Guide. [Google Scholar]
- Ritchie A.E., Deshmukh D.R., Larsen C.T., Pomeroy B.S. Electron microscopy of coronavirus-like particles characteristic of turkey bluecomb disease. Avian Dis. 1973;17:546–558. doi: 10.2307/1589153. [DOI] [PubMed] [Google Scholar]
- Scungio M., Arpino F., Stabile L., Buonanno G. Numerical simulation of ultrafine particle dispersion in urban street canyons with the spalart-allmaras turbulence model. Aerosol Air Qual. Res. 2013;13:1423–1437. doi: 10.4209/aaqr.2012.11.0306. [DOI] [Google Scholar]
- Sorokowska A., Sorokowski P., Hilpert P., Cantarero K., Frackowiak T., Ahmadi K., Alghraibeh A.M., Aryeetey R., Bertoni A., Bettache K., Blumen S., Błażejewska M., Bortolini T., Butovskaya M., Castro F.N., Cetinkaya H., Cunha D., David D., David O.A., Dileym F.A., Domínguez Espinosa A. de C., Donato S., Dronova D., Dural S., Fialová J., Fisher M., Gulbetekin E., Hamamcıoğlu Akkaya A., Hromatko I., Iafrate R., Iesyp M., James B., Jaranovic J., Jiang F., Kimamo C.O., Kjelvik G., Koç F., Laar A., de Araújo Lopes F., Macbeth G., Marcano N.M., Martinez R., Mesko N., Molodovskaya N., Moradi K., Motahari Z., Mühlhauser A., Natividade J.C., Ntayi J., Oberzaucher E., Ojedokun O., Omar-Fauzee M.S.B., Onyishi I.E., Paluszak A., Portugal A., Razumiejczyk E., Realo A., Relvas A.P., Rivas M., Rizwan M., Salkičević S., Sarmány-Schuller I., Schmehl S., Senyk O., Sinding C., Stamkou E., Stoyanova S., Šukolová D., Sutresna N., Tadinac M., Teras A., Tinoco Ponciano E.L., Tripathi R., Tripathi N., Tripathi M., Uhryn O., Yamamoto M.E., Yoo G., Pierce J.D. Preferred interpersonal distances: a global comparison. J. Cross-Cult. Psychol. 2017;48:577–592. doi: 10.1177/0022022117698039. [DOI] [Google Scholar]
- Stabile L., Massimo A., Canale L., Russi A., Andrade A., Dell’Isola M. The effect of ventilation strategies on indoor air quality and energy consumptions in classrooms. Buildings. 2019;9 doi: 10.3390/buildings9050110. [DOI] [Google Scholar]
- Sze To G.N., Chao C.Y.H. Review and comparison between the Wells–Riley and dose-response approaches to risk assessment of infectious respiratory diseases. Indoor Air. 2010;20:2–16. doi: 10.1111/j.1600-0668.2009.00621.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanabe T., Bartrand T.A., Weir M.H., Omura T., Haas C.N. Development of a dose-response model for SARS coronavirus. Risk Anal. Off. Publ. Soc. Risk Anal. 2010;30:1129–1138. doi: 10.1111/j.1539-6924.2010.01427.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wells W.F. On airborne infection: study II. Droplets and droplet nuclei. Am. J. Epidemiol. 1934;20:611–618. doi: 10.1093/oxfordjournals.aje.a118097. [DOI] [Google Scholar]
- Wölfel R., Corman V.M., Guggemos W., Seilmaier M., Zange S., Müller M.A., Niemeyer D., Jones T.C., Vollmar P., Rothe C., Hoelscher M., Bleicker T., Brünink S., Schneider J., Ehmann R., Zwirglmaier K., Drosten C., Wendtner C. Virological assessment of hospitalized patients with COVID-2019. Nature. 2020;581:465–469. doi: 10.1038/s41586-020-2196-x. [DOI] [PubMed] [Google Scholar]
- Xie X., Li Y., Chwang A.T.Y., Ho P.L., Seto W.H. How far droplets can move in indoor environments—revisiting the Wells evaporation-falling curve. Indoor Air. 2007;17:211–225. doi: 10.1111/j.1600-0668.2007.00469.x. [DOI] [PubMed] [Google Scholar]
- Zhang N., Chen W., Chan P.-T., Yen H.-L., Tang J.W.-T., Li Y. Close contact behavior in indoor environment and transmission of respiratory infection. Indoor Air. 2020;30:645–661. doi: 10.1111/ina.12673. [DOI] [PubMed] [Google Scholar]
- Zhang N., Su B., Chan P.-T., Miao T., Wang P., Li Y. Infection spread and high-resolution detection of close contact behaviors. Int. J. Environ. Res. Public Health. 2020;17 doi: 10.3390/ijerph17041445. [DOI] [PMC free article] [PubMed] [Google Scholar]