Mixed convection of Casson fluid in a differentially heated bottom wavy wall

Abstract

Numerical simulations of mixed convection of Casson fluid with a heated bottom wavy wall in a trapezoidal enclosure are performed. The enclosure's left and right sidewalls are assumed to be cold temperatures, while the enclosure's bottom and top walls are kept at hot temperatures and thermally insulated, respectively. The top wall is supposed to slide at a constant speed $U_0$ from left to right. After transforming the governing equations into a non-dimensional form, the finite element method is employed to solve them and modeled with Comsol-Multiphysics. The effect of non-dimensional parameters such as the Richardson number $(Ri=0.1,1,10)$, Casson fluid parameters $(\varphi =0.1,0.5,1)$, and the number of oscillations $(N=0,1,2,3)$ on flow and thermal fields, as well as the heat transfer rate has been studied. Furthermore, the results for the Average Nusselt number over the heated bottom wavy wall under the influence of the Rayleigh number and Casson parameter are depicted. The results showed that as the Richardson number increases, so does the average Nusselt number for all Casson fluid parameter values.

Casson fluid; Mixed convection; Trapezoidal cavity; Wavy wall; Finite element method.

1. Introduction

The study of heat transfer and fluid flow analysis is an interesting research topic because of its wide range of applications in applied sciences, engineering, and industries. For instance, heat exchangers, thermal designing of buildings, cooling of microelectronic and electronic components, solar collectors, nuclear reactors, food processing, and float glass production, etc. Natural and forced convection flow combine to form mixed convection flow in any enclosure. Natural convection is induced by buoyancy flow caused by thermal non-homogeneity inside the enclosure, while forced convection is caused by shear flow caused by the movement of one or two wall of a cavity. The study of transfer of heat in mixed convection in different geometries using efficient methods has piqued the interest of a number of researchers.

Fatin et al. [1] conducted one of the earliest studies on mixed convection inside a double lid-driven cavity with a heated bottom wavy wall. Their numerical results revealed that the velocity of the fluid and the distribution of the temperature are dependent on Reynolds number and the velocity of the fluid increase as the Reynolds number increase. In another study, Fatin et al. [2] numerically investigated nanofluids mixed convection flow in a wavy bottom cavity with a solid inner body. They discovered that a high Reynolds number produces better fluid flow and a reasonable convective heat transfer rate. Wubshet and Mohammed [3] employed finite element method to simulate the flow dynamics in a trapezoidal cavity which exposed to non-uniform temperature at its lower base. Wang et al. [4] computed the lid-driven cavity with fin of porous surface exposed to mixed convection. Their study revealed that the transfer of heat in the cavity was greatly affected by the velocity of the lid and the oscillating frequency. Also, Geridonmez and Oztop [5] studied lid-driven square cavity with the application of magnetic body force to understand temperature distribution and flow of streamlines within the cavity when the lid moves back and forth. Lamarti et al. [6] discussed on the mixed convection in a periodically oscillating lid driven with numerical simulation of Lattice Boltzmann. Their results showed that varying Grashof and Reynolds numbers has an effect on the drag force and temperature distribution depending on the velocity cycle's conduct. Later, Chamkha and Abu-Nada [7] developed a computational simulation for mixed convection heat transfer in lid driven enclosure with a wavy wall utilizing a finite volume technique of second order accuracy. They discovered that having a wavy wall improves heat transfer. Alsabery et al. [8] simulated numerically combined convection heat transfer in a lid driven enclosure with a flexible side wall and a rotating cylinder. They discovered that the Rayleigh number enhances the rate of heat transfer and is greatest when the cylinder is rotated counterclockwise.

Non-Newtonian fluids have recently piqued the interest of engineers and scientists due to their engineering and scientific applications in comparison to Newtonian fluids. A non-Newtonian fluid is one that does not obey Newton's law of viscosity [9], which states that viscosity remains constant regardless of stress. Researchers proposed various flow models from time to time to better understand the mechanisms involved in the flow of non-Newtonian fluids. Some of the proposed models of non-Newtonian fluids are, Casson Models [10], Jeffrey fluid model [11], power-law model [12, 13], Maxwell fluid model [14], and viscoplastic fluid models. Casson fluid models are the most commonly used of these models because most materials behave as shear thinning fluids. Food industries are now using the Casson fluid model to illustrate the rheological behavior of chocolates. As a result, researchers are focusing on the numerical investigation of this model. These are the literatures [15, 16, 17, 18, 19, 20, 21, 22] containing an investigation of the Casson fluid model in different geometries. Mohammed et al. [17] numerically studied the characteristics of combined convection flow in a square cavity having solid obstacle with magnetic field effect. They found that increased Reynolds number accelerates heat transfer with Casson fluid parameter, whereas higher Hartmann number has the opposite effect. The mechanism of natural convection flow containing casson fluid in trapezoidal cavity heated partially at the bottom waal was reported by Hamid et al. [15]. They discovered that average Nusselt increases with increasing Casson fluid parameter, Rayleigh number, and heater length. Pop and Sheremet [23] investigated free convection of Casson fluid under the effects of viscous dissipation and thermal radiation. Their findings were revealed that the Casson fluid parameter increases the heat transfer rate and flow. For higher values of the Casson fluid parameter, the heat transfer rate is accelerated due to variation in Prandtl number. Madhu et al. [16] used finite element method to solve numerically the natural convection of Casson fluid in a porous cavity. The findings of their study showed that increasing the Darcy number and Casson fluid parameter increases flow circulation and heat transfer. They are also discovered that conduction dominates heat transfer for low Darcy numbers over a wide range of Rayleigh numbers.

The purpose of this paper is to provide a thorough investigation of mixed convection of Casson fluid with a heated bottom wavy wall in a trapezoidal enclosure, as well as a solution procedure based on the finite element method. The advantages of using the finite element method in this study is that it offers great freedom within the selection of discretization, both within the elements which will be wont to discretize space and basis functions. Another advantage is that its well-developed theory. The reason for this is that the weak formulation and the numerical formulation of the PDE problem are inextricably linked. For example, when the numerical model equations are solved on a computer, the theory provides useful error estimates.

2. Mathematical and physical formulation

A schematic diagram of the work is a trapezoidal cavity which is differentially heated wavy enclosure at the bottom of length $L$ depicted in Figure 1. The shape of the bottom wavy wall is assumed to mimic the pattern $y=1-\text{cos}\left(2N\pi x\right),$ where $N$ is the number of oscillations. The cavity filled with Casson fluid and the laminar mixed convection flow is considered with the heated from the bottom wavy wall and cooled from the left and right side at uniform temperatures of $T_h$ and $T_c$, respectively. The upper wall of the enclosure is supposed to be thermally insulated and moving at a constant speed $U_0$ from left to right. It is assumed to be all sides of the cavity are rigid and impermeable. The governing equations of Casson fluid mixed convection heat transfer problem in dimensional coordinates system are given as [15, 24].

$$\nabla \cdot u=0\text{,}$$ (1)

$$u\cdot \nabla u=-\frac{1}{\rho }\nabla p+\nu \left(1+\frac{1}{\varphi }\right){\nabla }^{2}u+g\beta (T-T_c)e\text{,}$$ (2)

$$u\cdot \nabla T=\alpha {\nabla }^{2}T\text{,}$$ (3)

where $e=\left(\mathrm{0,1}\right)$ is unit vector. The variables $p,T,$ and $u=(u,v)$ are pressure, temperature, and velocity vector, respectively. $\nu ,g,\beta$ and $\alpha =\frac{\kappa }{\rho c}$ are kinematic viscosity, acceleration due to gravity, coefficient of fluid thermal expansion, and thermal diffusivity. respectively. $\rho$ is density, $\kappa$ is the thermal conductivity, and $c$ is the specific heat capacity. Now, the system described above has been simplified to the following non-dimensional form:

$$\nabla \cdot U=0\text{,}$$ (4)

$$U\cdot \nabla U=-\nabla P+\frac{1}{Re}\left(1+\frac{1}{\varphi }\right){\nabla }^{2}U+\frac{Gr}{R{e}^2}\theta e\text{,}$$ (5)

$$U\cdot \nabla \theta =\frac{1}{RePr}{\nabla }^2\theta \text{,}$$ (6)

where $U=\left(U,V\right)=\frac{\left(uL,vL\right)}{\alpha },P=\frac{p{L}^2}{\rho {\alpha }^2},\left(T-T_c\right)=\left(T_h-T_c\right)\theta ,Pr=\frac{\nu }{\alpha },Gr=\frac{g\beta \left(T_h-T_c\right)}{{\nu }^2}{L}^3,$ and $Re=\frac{U_{0}L}{\nu }$. The dimensionless variables $P,\theta ,$ and $U=(U,V)$ are non-dimensional pressure, temperature, and velocity vector, respectively. The parameters $Pr,Gr,$ and $Re$ are Prandtl, Grashof, and Reynolds number respectively.

Figure 1.

Schematic diagram.

The Boundary conditions associated with the set of Eqs. (4), (5), and (6) are listed below:

• On the bottom wavy wall: $\theta =1,V=U=0$.

• On the left and right side walls: $V=U=0,\theta =0,$

• On the top wall $V=0,U=1,\frac{\partial \theta }{\partial Y}=0.$

The local rate of transfer of heat at the heated bottom wavy wall can be evaluated by the local Nusselt numbers given as:

$$Nu=-L\frac{\partial \theta }{\partial n}\text{,}$$ (7)

where $\frac{\partial \theta }{\partial n}=\frac{1}{L}\sqrt{{\left(\frac{\partial \theta }{\partial Y}\right)}^2+{\left(\frac{\partial \theta }{\partial Y}\right)}^2}$. The average rate of heat transfer at the heated bottom wavy wall can be evaluated by the average Nusselt numbers defined as:

$$N{u}_{avg}=-\frac{1}{H}\underset{0}{\overset{H}{\int }}NudH$$ (8)

3. Finite element analysis

The Galerkin weighted residual finite element numerical approach has been implemented to solve the nonlinear and coupled Eqs. (4), (5), and (6) with the associated boundary conditions. It follows that, Eq. (4) and equation $P=-\gamma \nabla \cdot U$ are used to remove the pressure term $P$, whereas Eq. (4) is fulfilled for higher values of $\gamma ={10}^7$. Then by substituting the pressure term into the Eq. (5) and its reduced to

$$U\cdot \nabla U=\gamma \nabla \cdot \nabla U+\frac{1}{Re}\left(1+\frac{1}{\varphi }\right){\nabla }^{2}U+\frac{Gr}{R{e}^2}\theta e\text{.}$$ (9)

Expanding the temperature $\left(\theta \right)$ and velocity vector $U=(U,V)$ using the basis set ${\left\{{\text{Φ}}_r\right\}}_{r=1}^M$ as,

$$\theta \approx \sum _{r=1}^M{\text{Φ}}_r{\theta }_r,U\approx \sum _{r=1}^M{\text{Φ}}_r{U}_r,andV\approx \sum _{r=1}^M{\text{Φ}}_r{V}_r\text{.}$$ (10)

Then, for Eqs. (9) and (6) the Galerkin finite element technique produces the nonlinear residual equations shown below:

$$\begin{array}{l}{R}_j^{\left(1\right)}=\sum _{r=1}^M{U}_r{\int }_{\Omega }\left[\left(\sum _{r=1}^M{\Phi }_r{U}_r\right)\frac{\partial {\Phi }_r}{\partial X}+\left(\sum _{r=1}^M{\Phi }_r{V}_r\right)\frac{\partial {\Phi }_r}{\partial Y}\right]\Phi {}_{j}dXdY\\ +Y\left[\sum _{r=1}^M{U}_k{\int }_{\Omega }\frac{\partial {\Phi }_j}{\partial X}\frac{\partial {\Phi }_r}{\partial Y}dXdY+\sum _{r=1}^M{V}_r{\int }_{\Omega }\frac{\partial {\Phi }_j}{\partial X}\frac{\partial {\Phi }_r}{\partial Y}dXdY\right]\\ +\frac{1}{Re}\left(1+\frac{1}{\varphi }\right)\sum _{r=1}^M{U}_r{\int }_{\Omega }\left[\frac{\partial {\Phi }_j}{\partial X}\frac{\partial {\Phi }_r}{\partial X}+\frac{\partial {\Phi }_j}{\partial Y}\frac{\partial {\Phi }_r}{\partial Y}\right]dXdY\text{,}\end{array}$$ (11)

$$\begin{array}{l}{R}_j^{\left(2\right)}=\sum _{r=1}^M{V}_r{\int }_{\Omega }\left[\left(\sum _{r=1}^M{\Phi }_r{U}_r\right)\frac{\partial {\Phi }_r}{\partial X}+\left(\sum _{r=1}^M{\Phi }_r{V}_r\right)\frac{\partial {\Phi }_r}{\partial Y}\right]\Phi {}_{j}dXdY\\ +\left[\sum _{r=1}^M{U}_r{\int }_{\Omega }\frac{\partial {\Phi }_j}{\partial X}\frac{\partial {\Phi }_r}{\partial Y}dXdY+\sum _{r=1}^M{V}_r{\int }_{\Omega }\frac{\partial {\Phi }_j}{\partial X}\frac{\partial {\Phi }_k}{\partial Y}dXdY\right]\\ +\frac{1}{Re}\left(1+\frac{1}{\varphi }\right)\sum _{r=1}^M{V}_r{\int }_{\Omega }\left[\frac{\partial {\Phi }_j}{\partial X}\frac{\partial {\Phi }_r}{\partial X}+\frac{\partial {\Phi }_j}{\partial Y}\frac{\partial {\Phi }_r}{\partial Y}\right]dXdY\\ -\frac{Gr}{R{e}^2}{\int }_{\Omega }\left(\sum _{r=1}^M{\Phi }_r{\Theta }_r\right){\Phi }_{j}dXdY\text{,}\end{array}$$ (12)

and

$$\begin{array}{l}{R}_j^{\left(3\right)}=\sum _{r=1}^M{\Theta }_r{\int }_{\Omega }\left[\left(\sum _{r=1}^M{\Phi }_r{U}_r\right)\frac{\partial {\text{Φ}}_r}{\partial X}+\left(\sum _{r=1}^M{\Phi }_r{V}_r\right)\frac{\partial {\text{Φ}}_r}{\partial Y}\right]{\Phi }_{j}dXdY\\ +\frac{1}{RePr}\sum _{r=1}^M{\Theta }_r{\int }_{\Omega }\left[\frac{\partial {\text{Φ}}_j}{\partial X}\frac{\partial {\text{Φ}}_r}{\partial X}+\frac{\partial {\text{Φ}}_j}{\partial Y}\frac{\partial {\text{Φ}}_r}{\partial Y}\right]dXdY\text{.}\end{array}$$ (13)

The set of non-linear algebraic Eqs. (11), (12), and (13) are solved using reduced integration technique and Newton Raphson method. At every iteration $m$, the linear system:

$$R\left(b^m\right)=J\left(b^m\right)[b^m-b^{m+1}]\text{,}$$ (14)

is solved. The derivatives of the residual equations with regard to the temperature ${\left({\theta }_i\right)}^{\prime }s$ and the components of velocity ${\left(U_i\right)}^{\prime }s,{\left(V_i\right)}^{\prime }s$ are included in the elements of the Jacobian matrix, $J\left(b^n\right)$ and $R\left(b^n\right)$ is the residuals vector. The iteration of the present study is assumed to be convergence solution when the corresponding error of each variable less than or equals ${10}^{-6}$. Finite element meshes with non-uniform triangular components are used to discretize the solution domain. Different types of mesh elements, and boundary elements were achieved to test the grid sensitivity for the current model, as shown in Table 1. Variation of average Nusselt number at the hot bottom wavy wall with $\varphi =1,N=3$ and $Ri=1$ was considered. It was tasted by evaluating percentage error in non dimensional average Nusselt number $\left(N{u}_{avg}\right)$ variation of the hot bottom wavy wall. To find the desired result, the less percentage error $0.03$ is chosen at an extremely fine mesh with $18881$ elements and $551$ boundary elements. Figure 2 depicts the suggested grid layout for this study.

Table 1.

Grid independency study for $Ri=1,N=3$, and $\varphi =1$.

Mesh size	Mesh elements	Boundary elements	$N{u}_{avg}$	Percentage error $\left(\text{\%}\right)$
Normal	1540	130	9.1572
Fine	2280	160	9.4310	2.9
Finer	5155	285	9.6738	2.5
Extra fine	13653	551	10.580	9.3
Extremely fine	18881	551	10.576	0.03

Figure 2.

Mesh of the trapezoidal cavity with a differentially heated bottom wavy wall.

To demonstrate the accuracy of the numerical procedure, a comparison was made with existing results for mixed convection in a driven cavity from Iwestu et al. [25]. Table 2 shows a comparison of the current results with the comparable results. It can be seen a very good agreement among the existing data.

Table 2.

Comparison of the numerical procedure with [25].

$Ri$	[25]	This study
0.01	1.94	1.203
1	1.34	1.36
10	1.02	1.02

4. Results and discussion

This section conducted a thorough investigation of the results and provides meaningful physical interpretations through graphs and tables. In this context, a detailed analysis of the effect on streamlines and isotherms of the Richardson number, Casson fluid parameters, and the number of oscillations are performed. During the simulations, the Prandtl number and Reynolds number are kept set at $Pr=4.623$ and $Re=100$ respectively. The nature of average and local Nusselt numbers is also taken into account due to the variation of different parameters.

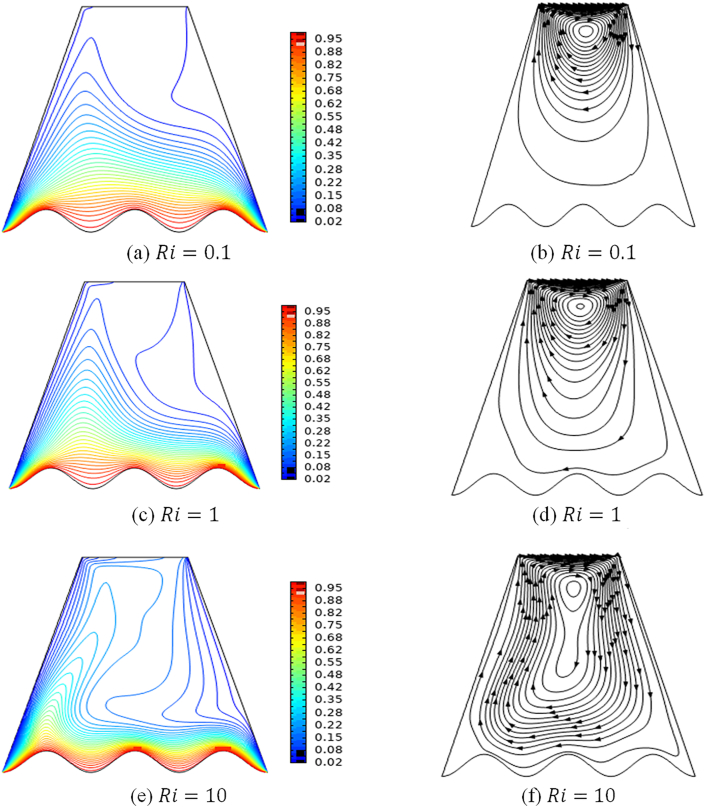
Figure 3 exhibited significant behavior against various values of Richardson number on temperature contours and streamlines with Casson fluid parameter $\varphi =0.5$ and number of oscillation $N=3$. The Richardson number is defined as $Ri=\frac{Gr}{R{e}^2}$ and indicates the importance of thermal natural convection forces versus mechanically induced lid-driven forced convection. The considered values of $Ri$ is ranged from $0.1$ to $10$. The small value of the Richardson number $Ri=0.1$ is obtained if $Gr={10}^3$. In this case the cavity's system is dominated by forced convection. The temperature contours shown in Figure 3a showed that the heated symmetric temperatures built up on the undulating bottom wall, while both vertical walls remained cold. The fluid began to convey at the enclosure left wall, according to the definition of transfer of heat by conduction. The transfer of heat pattern appears to be plume-shaped as the Richardson number increases as observed in Figure 3e. It also starts to compress at the hot bottom wavy wall due to the influence of low density, where the transfer of heat by convective is the major mode of heat transmission. Figure 3b,d,f shows a streamlines plot for various Richardson numbers with a moving lid velocity of $U=1$ at the top wall. A single clockwise rotating vortex is formed for all values of Richardson number as the top wall is moved at a constant speed from left to right, forced nearly all of the fluids into the cavity. The main circulation cell tends to move closer to moving top wall at $Ri=0.01$ as shown in Figure 3b, with the streamline plot is more concentrated around the top wall of the enclosure than bottom wall of the enclosure. When the Richardson number increases to $Ri=1$, the flow profiles changed from forced to mixed convection heat transfer, with both the moving lid and the buoyancy force contributing to the flow profiles. More vortices are produced when a strong buoyancy force is present at a high Richardson number as revealed in Figure 3d,f, which enhances the flow fluid and enables the cavity's system is to be dominated by natural convection.

Figure 3.

Plots showing the effect of Richardson number isotherms and streamlines with Casson fluid parameter ϕ = 0.5 and number of oscillations N = 3.

For higher values of Richardson number $Ri=10$, the clockwise rotating vortex extends horizontally taking a more elliptical shape and it shrinks towards the wavy wall as shown in Figure 3f.

The effect of Casson fluid parameters on temperature contours and streamlines with Richardson number $Ri=1$ and oscillation number $N=3$ are shown in Figure 4. For different values of the casson fluid parameter the streamlines plot is almost identical, but as the casson fluid parameter is increased the flow circulations inside the cavity become more intense. The parameter $1+\frac{1}{\varphi }$ attached to ${\nabla }^{2}U$ in the continuity equation of the governing equation indicate the additional viscosity of the fluid. Thus the fluid effective viscosity progressively decreases as the parameter of Casson fluid increases. As a result, the small value $\varphi =0.1$ of the Casson fluid parameter implies a significant effect of viscosity. For high values of Casson fluid parameter with the heated wavy bottom wall, the temperature contours imply a crucial interaction between layers of thermal boundary. It is important to remember that as the Casson fluid parameter is increased, the thickness of the thermal boundary layers and velocity progressively decreases.

Figure 4.

Plots showing the effect of Casson parameter isotherms and streamlines with Richardson number $Ri=1$ and number of oscillations $N=3$.

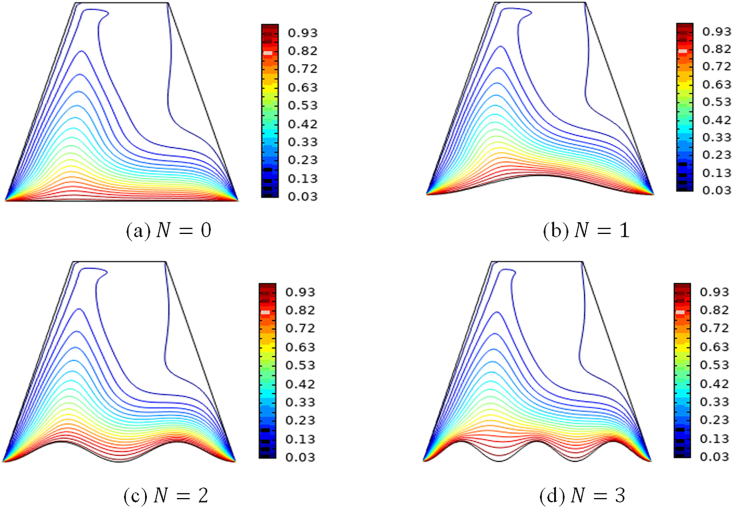
The effects of the length of the number of oscillations on isotherms and streamlines with Richardson number $Ri=1$ and Casson fluid parameter $\varphi =1$ are presented in Figures 5 and 6 respectively. It is observed from the figures that both the thermal fields and velocity are nearly identical across the cavity with the exception of the region near the bottom wavy wall, where both temperature contours and streamlines conform to the wavy wall profile.

Figure 5.

Plots of stream lines for different values of number of oscillations with Richardson number $Ri=1$ and Casson fluid parameter $\varphi =1$.

Figure 6.

Plots of isotherms for different values of number of oscillations with Richardson number $Ri=1$ and Casson fluid parameter $\varphi =1$.

Figure 7 presents the local rate of heat transfer in terms of the local Nusselt number. Figure 7a showed the effect of Richardson number on the local Nusselt number at the bottom wavy wall for $\varphi =1$ and $N=3$. The figure showed that a higher value of Richardson number has a dominant effect at the middle of the cavity. It is also observed that, near the side walls there is no dominance. The same behaviour is observed for the effect of Casson fluid parameter on local Nusselt number as the effect of Richardson number on the local Nusselt number as shown in Figure 7b.

Figure 7.

Plots showing local heat transfer rate in terms of local Nusselt number.

Figure 8 depicts the heat transfer rate in terms of the average Nusselt number. Figure 8a and Table 3 shows the effect Richardson number on the average Nusselt number for various values of Casson fluid parameter with $N=3$. It is observed from the figure for all values of Casson fluid parameter the average Nusselt number increases as the Richardson number increases. Figure 8b depicts the effect of the number of oscillation on the average Nusselt number for various Richardson numbers. The results show that as the considered values of the Richardson number increase, so does the average Nusselt number. At $Ri=10$, an interesting phenomenon is observed in which the average Nusselt number peaks at $N=1$ and then decreases, reflecting the high heat transfer rate at $Ri=10$ and $N=1$ as we can observe in Figure 8b and Table 4.

Figure 8.

Plots showing heat transfer rate in terms of average Nusselt number.

Table 3.

Table of values showing the average Nusselt number with Richardson number $Ri$ on the heated bottom wavy wall for different values $\varphi$.

$\varphi$	$Ri$	$N{u}_{avg}$	$\varphi$	$Ri$	$N{u}_{avg}$
0.1	$0.1$	9.8778	0.5	$10$	12.069
0.1	$1$	9.9432	1	$0.01$	9.9027
0.1	$10$	11.018	1	$1$	10.576
0.5	$0.1$	9.8916	1	$10$	12.512
0.5	$1$	10.35

Table 4.

Table of values showing the average Nusselt number with number of oscillation $N$ on the heated bottom wavy wall for different values $Ri$.

$N$	$Ri$	$N{u}_{avg}$	$N$	$Ri$	$N{u}_{avg}$
0	$0.1$	8.9854	2	$0.1$	9.7401
0	$1$	9.7582	2	$1$	10.367
0	$10$	12.128	2	$10$	12.220
1	$0$	9.4778	3	$0.1$	9.8916
1	$1$	10.046	3	$1$	10.350
1	$10$	12.507	3	$10$	12.069

5. Conclusion

The mixed convection of Casson fluid with a heated bottom wavy wall in a trapezoidal cavity is investigated for various non-dimensional parameters in this study. The effect of the Richardson number, Casson fluid parameters, and number of oscillations on temperature and velocity profiles has been studied in terms of isotherms and streamlines, respectively. The following are brief summaries of the inquiry outcomes:

• •As the Richardson number increases the clockwise rotating vortex extends horizontally taking a more elliptical shape and it shrinks towards the wavy wall in the streamline.
• •When the Richardson number is high, the isotherms become more distorted, and convection dominates.
• •The presence of oscillations in the bottom wall reduces the intensity of the flow circulation and increases the dominance of the conduction effect.
• •Under the effect of the Richardson number and the Casson fluid parameter, the average Nusselt number increases, whereas at high values of the Richardson number, it becomes a peak and then decreases as the number of oscillations increases.

Declarations

Author contribution statement

Mohammed Hirpho: Conceived and designed the analysis; Analyzed and interpreted the data; Contributed analysis tools or data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

No data was used for the research described in the article.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.