Abstract
Non-pharmaceutical interventions (NPIs) are important to mitigate the spread of infectious diseases as long as no vaccination or outstanding medical treatments are available. We assess the effectiveness of the sets of non-pharmaceutical interventions that were in place during the course of the Coronavirus disease 2019 (Covid-19) pandemic in Germany. Our results are based on hybrid models, combining SIR-type models on local scales with spatial resolution. In order to account for the age-dependence of the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), we include realistic prepandemic and recently recorded contact patterns between age groups. The implementation of non-pharmaceutical interventions will occur on changed contact patterns, improved isolation, or reduced infectiousness when, e.g., wearing masks. In order to account for spatial heterogeneity, we use a graph approach and we include high-quality information on commuting activities combined with traveling information from social networks. The remaining uncertainty will be accounted for by a large number of randomized simulation runs. Based on the derived factors for the effectiveness of different non-pharmaceutical interventions over the past months, we provide different forecast scenarios for the upcoming time.
Keywords: SARS-CoV-2, Covid-19, Coronavirus disease, Mitigation, Non-pharmaceutical interventions, Forecast
1. Introduction
With more than 2.2 million reported deaths [1], the coronavirus disease 2019 (Covid-19) remains one of the most pressing issues for the whole globe. Already in October, WHO officials estimated that 10% of the world’s population had been infected [2] and vaccination of the population will still take a considerable amount of time. Since exposing people is highly unethical [3], the only interim solution is to mitigate the spread of the disease by the application of non-pharmaceutical interventions.
The assessment of non-pharmaceutical interventions and prediction by simulation has to be based on reliable models; cf. [4], [5], [6], [7], [8], [9], [10], [11] for the spread of SARS-CoV-2 (severe acute respiratory syndrome coronavirus 2) and other infectious diseases. Only then, the most effective interventions can be determined as a basis for informed political decisions.
The aim of our study is to assess non-pharmaceutical interventions and to provide a reliable forecast of the Covid-19 pandemic in Germany based on four principles. First, we account for the age-dependence of SARS-CoV-2 [12], [13], [14]. Second, we include realistic contact patterns between different age groups [15], [16], [17], [18], [19]. Third, we include high-quality, spatially resolved information on commuting activities [20], [21] combined with traveling information based on the social network Twitter. Fourth, we combine all information and account for the remaining uncertainty by Monte-Carlo Ensemble runs. To our knowledge, such an in-depth study is not accounted for in the literature so far.
The remainder of this paper is structured as follows. We first present our mathematical model and its numerical solution approach. Then, we present the social and non-pharmaceutical parameters used in our model and we discuss afterwards the epidemiological parameters obtained by extensive analyses. Our results are presented and discussed in the following.
2. Materials and methods
2.1. Model and solver
There are various models to forecast the spread of infectious diseases across a country or community. Besides the well known SIR-type ODE models [22], [23], there are integro-differential models [22], [24], Bayesian Monte Carlo approaches [11], or agent-based models [25], [26]. While SIR-type models are praised for their simplicity and understandability, they lack for a good representation of spatial heterogeneity.
To combine the advantages of a SIR model without loss of spatial resolution, we use multiple SIR-type models on a fine local scale and connect the compartments and age groups by graphs that represent traveling; cf. [27] among others. These SIR-type models can be easily exchanged by agent-based models due to the generic implementation of our graphs. This is integrated as part of our high performance modular epidemics simulation software MEMILIO that is continuously under development [28].
2.1.1. Age-resolved SIR-type model
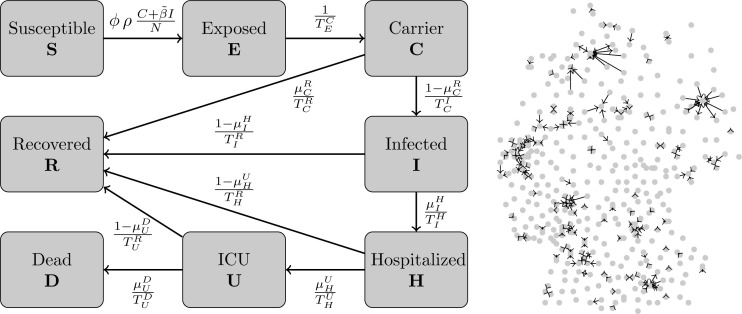
The base of our SIR-type model can be found in the first version of [9]. Our model consists of the compartments Susceptible (S), healthy individuals without immune memory of SARS-CoV-2; Exposed (E), who carry the virus but are not yet infectious to others; Carrier (C), who carry the virus and are infectious to others but do not yet show symptoms (they may be pre- or asymptomatic); Infected (I), who carry the virus, are infectious and show symptoms; Hospitalized (H), who experience a severe development of the disease; In Intensive Care Unit (U); Dead (D); and Recovered (R), who cannot be infected again. To resolve age-specific disease parameters, we divide the totality of people into different age groups. We then have .
For each age group , the transmission risk is denoted by and the proportion of infected people not isolated or quarantined is denoted by ; see Table 1, Table 2 for details. Infection results from contact with people from different age groups. We introduce the contact frequency matrix
| (1) |
where represents the (mean) daily contacts of a person of age group with people from age group . We refer to [29] which states that “the resulting matrix is not symmetric due to the different number of individuals in each age-group”. So due to the particularly chosen age groups and the demography of Germany, these contact matrices will be non-symmetric in our case.
Table 1.
Description of parameters and main resources for their derivation.
| Param. | Description | Reference | Resources |
|---|---|---|---|
| age-dependent transmission risk | Eq. (14),(2),(3) | [30], [31], [32], [33], [34], [35], [36] | |
| seasonality parameter | Eq. (15), (14) | [37], [38], [39], [40] | |
| proportion of not isolated or quarantined symptomatic individuals | Eq. (2), (3) | Assumption. | |
| period of latent non-infectious stage | Eq. (3), (4) | [9], [41], [42] | |
| proportion of mild, asymptomatic cases | Eq. (4), (5), (8) | [35], [43], [44], [45], [46] | |
| period of asymptomatic stage before recovery | Eq. (4), (8) | [9] | |
| period of latent infectious stage | Eq. (4), (5) | [9], [41], [42] | |
| proportion of symptomatic cases needing hospitalization | Eq. (5), (6), (8) | [14], [47],[48, Report of Sept. 15] | |
| period of mild symptoms for individuals requiring hospitalization later on | Eq. (5), (6), Suppl. Mat. | [49], [50], [51] | |
| period of mild symptoms for individuals not requiring hospitalization later on | Eq. (5), (8) | [9], [52] | |
| proportion of hospitalized individuals getting ICU treatment | Eq. (6), (7), (8) | [47], [53], [54] | |
| period of hospitalization before ICU treatment (of critical cases) | Eq. (6), (7), Suppl. Mat. | [49], [50] | |
| period of hospitalization before recovery (of non-critical cases) | Eq. (6), (8), Suppl. Mat | [9] | |
| proportion of individuals in ICU care that die | Eq. (7), (8), (9), Fig. 4 | [54], [55] | |
| period of ICU treatment before recovery | Eq. (7), (8), Suppl. Mat | [9], [50], [56] | |
| period of ICU treatment before death | Eq. (7), (9), Suppl. Mat | [9], [50] |
Table 2.
Summary of the age-dependency of parameters and their ranges.
| Range in age group | ||||||
|---|---|---|---|---|---|---|
| Param. | 0–4 | 5–14 | 15–34 | 35–59 | 60–79 | 80+ |
| sigmoidal curve from to | ||||||
| [0.20,0.30] | [0.15,0.25] | |||||
| sampled with and (16), incubation period = 5.2 | ||||||
| [0.006,0.009] | [0.015,0.023] | [0.049,0.074] | [0.15,0.18] | [0.20,0.25] | ||
| [9,12] | [5,7] | |||||
| [5.6,8.4] | ||||||
| [0.05,0.10] | [0.10,0.20] | [0.25,0.35] | [0.35,0.45] | |||
| [3,7] | ||||||
| [4,6] | [5,7] | [7,9] | [9,11] | [13,17] | ||
| [0.00,0.10] | [0.10,0.18] | [0.3,0.5] | [0.5,0.7] | |||
| [5,9] | [14,21] | [10,15] | ||||
| [4,8] | [15,18] | [10,12] | ||||
The naming convention for the remaining parameters can be understood as follows: We use the variables for the time spent in state before moving to state . For example, represents the time an individual in age group spent in the hospital before returning home due to recovery from the disease. Accordingly, represents the probability of a patient to transit to state when that patient is currently in state .
The model, as expressed in Fig. 1, is
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
Fig. 1.
SIR-type model and strongest inter-county commuter activities. SIR-type model for one German county, based the on first version of [9] (left). We omit the age-dependence index for clarity; see Table 1, Table 2 for a description of the parameters. Graph with center points of all German counties as nodes and edges according to commuter activity (right). Edges only shown where more than 10 000 workers commute on a daily basis.
The Eqs. (2)–(9) represent the transition of people from one state to another. Note that people in an age group cannot transit to another group for . In the section of the epidemiological parameters, we will discuss in detail which of the parameters we assume to be age-dependent and how this is included in our model. These findings are summarized in Table 1, Table 2.
2.1.2. Spatial resolution
While SIR-type models are straightforward to apply and interpret, they lack the possibility of modeling local effects or spatial heterogeneity. In order to avoid averaging over important effects such as infection clusters, we assign one particular age-resolved model to each county. We represent each county by a node of a (directed) graph. The edges of the graph represent the connections between the different counties and are weighted with the number of people commuting daily and traveling on average. The edges do not only hold single values (weights) for how many people daily commute between different counties but also coefficients to determine the proportion of people of different age groups and compartments that commute or travel. Doing so, we can restrict travel activities to healthy or only mildly infected individuals.
Let be the number of counties (nodes of the graph). Then, for two nodes and , , the weight on edge represents the proportion of people going daily from to .
2.1.3. Numerical solver
Common numerical solvers for the system of nonlinear ordinary differential Eqs. (2)–(9) are semi-implicit or adaptive explicit. While the former allow for larger time steps, the latter allow adaptive time steps to prevent large numerical errors. We have implemented an adaptive Runge–Kutta -Fehlberg45 (RKF45) method [57] that uses methods of 4th and 5th order and solves the equations without excessively small time steps.
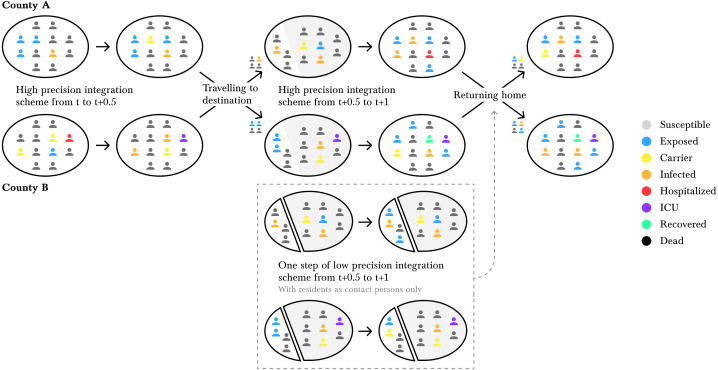
The numerical procedure becomes more challenging when we also resolve the equations spatially. For this, we define a commuter as a person who travels from county to , and back again within one day (whether it is work or free time related). Given start values from day , we advance our adaptive RKF45 solver for 0.5 days. Next, we allow people to commute or travel. Their amount is defined by the commuter rate between two counties, namely the weights introduced in the previous section and further specified in following section. Note that commuting also depends on the infection state since hospitalized individuals cannot commute and infected individuals will travel less than healthy ones. For the latter, we assume the same level of isolation or quarantine as on county level. With the updated population, we again advance our adaptive solver for 0.5 days.
Additionally, we conduct an auxiliary step with step size of 0.5 days with an explicit Euler solver where we only consider the in-commuters, using the county’s population as contact population only. This step is executed since, after the high precision scheme from to , we do not know the updated state of our commuters (e.g., susceptible may have become exposed or carriers have become symptomatic). This is due to the nature of the SIR model (2)–(9) that does not keep track of individuals. Still, the commuters have to go back to their home county, and we need to know their most likely infection state. We use the results from the explicit Euler step, to quantify the proportion of individuals of the different compartments that return. With this estimation, we start the returning process. These considerations are summarized in Fig. 2.
Fig. 2.
Illustration of our numerical scheme for spatial heterogeneity. The individuals represent the size of the compartments in our SIR-type model (2)–(9). First, we evolve County A and County B separately, resulting in updated compartments in both counties. Then, a proportion of the county’s population commutes. We solve the SIR model for another half day including the in-commuters and excluding the out-commuters. Additionally, we do one step of an auxiliary low order scheme (with residents as contact persons only) to estimate the updated states of the in-commuters (shown in the dashed box). Then, the commuters return home.
2.2. Social and non-pharmaceutical parameters
The spread of SARS-CoV-2 depends on many parameters. While some of these parameters are inherent to the virus, others depend on social contact patterns and non-pharmaceutical interventions introduced by decision makers. In this section, we will focus on non-pharmaceutical interventions and their influence on contact patterns and commuter rates in our model.
2.2.1. Inter-county travel
Let us first continue with the spatial resolution of our model and focus on how we specify the rate of work or leisure commuters between different counties and . To estimate on the edge that connects both counties, we use statistics from the German Federal Employment Agency [20] complemented with geo-referenced Twitter data.
From [20], we have for each county the number of incoming commuters from each other county. However, it is not specified if commuting takes place on a daily basis. We assume that any commuting activity with a linear distance of 100–200 km only happens twice a week and for a distance of over 200 km, we assume that it happens only once a week. We thus scale the corresponding off-diagonal matrix entries by 0.5 and 0.2, respectively. After this smoothing procedure, we remain with about 11.8 million daily commuting activities. These values are then divided by the approximate population size in working age. This results in the work commuting population , which is only taken from age groups and compartments that commute for work. For the geometry of complex and network-driven contagion phenomena, we also refer to [59].
Motivated by [60], [61], we also analyzed a totality of about 2.8 million geo-referenced tweets obtained from the Twitter API [62] between January 1, 2018 and January 31, 2020. Since [20] is biased towards the working population, the geo-referenced tweets act as a “counterpart” with a bias towards the younger population, student commuters, and leisure traveling individuals. From the totality of tweets, we first removed all tweets from users with more than 1000 tweets in the considered period to waive statistical anomalies introduced by bots or hyperactive users. For each pair of consecutive user tweets in the considered period, we then count one travel action from to if the first tweet happened from and the second happened from , . In order to further reduce the influence of the most active users, we remove the 300 users with the most travels. Then, there remain about 36 000 active users from which 11 000 had five or more travel activities. In total, we have about 235 700 travel activities. In 95% of the nontrivial matrix entries, one unique user adds only two activities on average.
Although different in scale, the remaining tweets show similar travel patterns as obtained from [20]; see supplementary figures for a comparison. Note, however, that a certain amount of deviation is to be expected since both sources are biased towards either the working or the student population. In twitter mobility, for instance, we observe relatively strong connections to bigger cities like Hamburg, Hannover, Cologne, or Stuttgart.
Assuming that the mobility obtained from Twitter accounts for 20% of all travel activities (work commuting, student commuting, leisure travel etc.), we scale the twitter matrix accordingly. The resulting values are divided by the population size and the result will be denoted by , .
The amount of mobility in our model is given be the edge weights of the graph. These weights are derived from the matrix for the work commuters and from for the ‘Twitter’ activities. The weights also depend on the implementation of non-pharmaceutical interventions. In particular, they depend on the NPI related parameters for work and for “other” places related measures that mainly affect free-time activities. Here, and are the corresponding age groups; see the corresponding section and Table 3 for details on these parameters.
Table 3.
Summary of different non-pharmaceutical interventions and implementations in simulations.
| Intervention | Implementation | Factor ranges | Comment |
|---|---|---|---|
| working | weak | ||
| from | intermediate | ||
| home | strong | ||
| partial school | none | ||
| closures and | weak | ||
| remote | intermediate | ||
| schooling | complete | ||
| gathering bans, | weak | additional increase of | |
| (partial) closing | rather weak | by 0.05 to 0.20, | |
| of bars, | intermediate | according to strictness; | |
| restaurants, | strong | cf. corresp. section | |
| cinemas etc. | very strong | ||
| face masks, | weak | ||
| distancing, | rather weak | ||
| regular | intermediate | ||
| ventilation of | strong | ||
| closed spaces | very strong | ||
The commuter matrices contain many insignificant coefficients close to zero. These are due to loosely coupled regions where only a very limited number of individuals commute on a daily basis (e.g., 1 or 2). To reduce the computational effort, we eliminate edges where and . The cutoff values are chosen so only 1% of information is dropped and that more than 99% of travels are included. We also paid attention to reflect the above assumption that Twitter data represents 20% of travels. With this procedure, the number of edges is reduced by approximately 60% and the computational efficiency is increased significantly.
2.2.2. Contact patterns in Germany
In the following, we focus on the intra-county contact patterns. In this section, we derive a baseline, prepandemic contact matrix and a minimum contact matrix for a simulated strict lockdown in Germany.
As SARS-CoV-2 transmission occurs mainly during human-to-human interaction, reducing contacts can efficiently slow down the spread of the disease; cf. [15], [16], [17], [63] for literature on contacts and the spread of infectious diseases. However, lockdowns which effectively reduce contacts to a minimum should be avoided due to their profound negative impact on many individuals and communities [3]. Therefore, the challenge for today’s decision makers is to find the most appropriate and effective interventions for the actual developments.
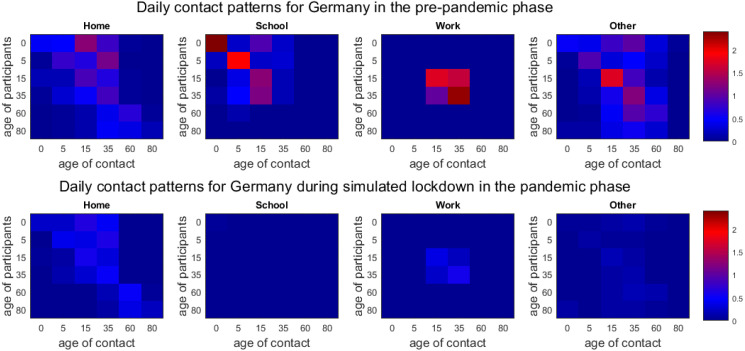
Prepandemic patterns. In order to quantify the potential of transmission reduction by contact pattern changes, good prepandemic as well as recent data is needed. From [15] and its projections [17], we use realistic contact patterns for Germany split up into the categories “Home”, “School”, “Work”, and “Other”. In [15], contacts are defined as skin-to-skin contact, or where at least three words were exchanged.
For the particular case of school contacts, the mean numbers of contacts recorded in [15] are rather low for Germany. Given the fact of aerosol transmission risk in closed spaces, we suggest to assume slightly higher contact rates for a conservative estimate on the spread of the disease. Further information is offered by the demography-based school contact matrix in [16]. We use the quotient of the maximum eigenvalues between both matrices to scale the contact matrix of [17] which then results in a larger number of school contacts.
The combination of baseline contacts for “Home”, “Work”, and “Other” from [15], [17] and for “School” based on the comparison of [16], [17] results in the contact matrix ; cf. Fig. 3 (top).
Fig. 3.
Inter-age group contact patterns. Combined prepandemic contact patterns of [16], [17] for Germany interpolated to age intervals as provided by [58] (top). Extrapolated, pandemic contact patterns for simulated lockdown phase for Germany (as of end March in the UK; based on contact study [18]) (bottom).
SARS-CoV-2-related minimum patterns. The potential of possible contact reduction is limited by the minimum number of necessary contacts that keep essential sectors of the society running. To assess this, we consider the contact study [18], that started during the lockdown phase in the United Kingdom. By the end of March, many ‘non-essential’ parts of the economy were shut down and social interaction was limited to a minimum [64]. This study yields the minimum contact matrix .
The matrix is missing values since only individuals aged 18 or older participated in [18]. In order to fill out the missing information, we follow a strategy similar to [65]. We employ the prepandemic/baseline contact matrix from [17]. We scale this matrix by the ratio of the dominant eigenvalues and of the lower-right, square matrices , . Then, we use this scaled version to fill out the missing subset
| (10) |
We aim at deriving a minimum contact matrix for a simulated strictest lockdown in Germany. We consider the number of contacts in the UK by the end of March to be a minimum that we can achieve in a SARS-CoV-2-related lockdown. From the UK data, we consider the quotient of contact reduction
| (11) |
and apply these factors to the matrices derived from [16], [17]
| (12) |
In Fig. 3, the minimum is shown at the bottom. Note that the single entries given in the bottom row of Fig. 3 are not required to be smaller than the ones in the top row. The minimum of contacts during lockdown is to be understood as the minimum of total contacts of all individuals. Locally, for one location and the interaction of two age groups, the mean contacts could even increase slightly. The difference between the top and bottom of Fig. 3 defines realistic boundaries for all non-pharmaceutical interventions that could possibly be implemented. To assess uncertainty, we allow for a 5–10% deviance of the given values in our ensemble runs. From [66], we have an estimated contact reduction during spring lockdown in Germany of 63%, taking the minimum values here, we could achieve a contact reduction of 76%.
2.2.3. Contact-related interventions
There are two ways to reduce potentially dangerous contacts, namely, to avoid the contacts (first level of reduction) at all or to wear masks, keep distance and ventilate closed spaces (second level).
While the mean number of daily contacts in Germany is lower than in many other European countries, a relatively large percentage of contacts happens at workplaces [15]. Hence, many transmissions can be avoided by working from home whenever possible. From a recent analysis of Germany [21], up to 40–50% of the population could work from home if necessary. We suppose that in the prepandemic phase “home office” was only used by 5% with as much as 20–35% working from home during different phases of the pandemic [21, pp. 96–101]. Further contact reduction is induced by people who stop working altogether, so these values have to be subtracted from the prepandemic matrix. We know that about 20% of the population stopped working in March and April [21, p. 96]. For the less strict interventions, we assume values of 5–10%.
While working from home is feasible for a larger part of the population, global school closures and the resulting home schooling “present an unprecedented risk to children’s education, protection and well-being” [67]. Apart from school closures, contacts in schools can be reduced by smaller classes where possible, fixed seating arrangements, regular ventilation, or pooled testing [68]. There are a number of further locations where contact reductions are feasible such as bars, restaurants, supermarkets, or public transport.
We here include the effect of interventions such as face masks, distancing etc. In many studies such as [38], [69], face coverings and ejected air flows while breathing, speaking, or coughing are studied. The meta analyses in [70] and [71] find (large) protective effects of face masks for SARS-CoV-2 transmission such as 40% or even a pooled odds ratio of 0.35. In particular, the protective effect of community-wide masks is shown in [72]. We will consider different risk reduction ranges for wearing masks combined with keeping distance and regular ventilation of closed spaces.
In the predictive analysis of the spread of infectious diseases, not only non-pharmaceutical interventions and one-time contact changes but also adherence to interventions is important. While there is a small decrease in adherence to preventive measures observed in [19], [73] after months of the pandemic, the adherence is still large and rather stable with an even increasing number of people wearing masks [73] (e.g., 93% wear them often or always). In the consequence, we do not include these opposing effects in our simulations.
In the results section, we vary the strictness of the interventions according to the political decisions and Table 3.
2.2.4. Deducing contact patterns from interventions
In this section, we provide the influence of the NPIs on the contact patterns and commuter rates. Let and denote the mean daily contacts as shown in Fig. 3 in the top and bottom row, respectively, with for the age groups and for the locations.
Since different interventions like working from home and face masks reduce the mean contacts by sequentially applied multiplicative factors to the remaining contacts, we use a multiplicative definition. For two intervention levels , e.g., for gathering bans and for face masks and distancing, we introduce factors with and . For the modeling of events such as carnival, we could also have .
We define the resulting contact patterns as
| (13) |
The factors corresponding to each intervention are summarized in Table 3. If all factors are set to zero, the baseline contact rate is obtained.
Note that a third level could be used to, e.g., implement particular awareness of senior population. In our simulations, however, including additional parameters for senior contact reduction always led to underestimations of the number of deaths.
2.3. Epidemiological parameters
In this section, we provide interval ranges for the epidemiological parameters used in our model. The main references for each parameter are given in the corresponding subsection. For certain parameters, we also refer to the derivation in [9]. Furthermore, we derive different parameters in the clinical section of our model (stages and transitions between , , , , and ) from the LEOSS study [74]. Some recent results from LEOSS can also be found in [75]. Based on 3 265 hospitalized patients with Covid-19, we provide age-specific mean values and confidence intervals for the probabilities and . For the time spans , , , , and , we use median values and uniform distributions. We further provide distribution fits to the age-resolved data in the supplementary figures which are of larger interest when using agent-based models. We considered gamma, Weibull, lognormal, normal, and exponential distributions and fitted according to the lowest Pearson’s cumulative test statistic.
2.3.1. Transmission risk, secondary attack rate
We denote the transmission risk , . As mortality is clearly found to be age-specific for Covid-19 [13], age-dependent susceptibility or transmission is less clear and under discussion [46]. There is, however, evidence showing odds ratios smaller than 0.5 for children below 15 years compared to adults [34], [35], [36], with an odds ratio of about 0.34 for children compared to adults and 1.47 of seniors above 65 years compared to adults. The meta analysis of [33] also showed higher susceptibility in adults than in children.
From [30], we find the number of second generation infections divided by the number of close contacts of the first generation as . From [31], we know that the secondary attack rate in households was found to be lower than 20% (in most of the studies) and thus even lower in general (non-household) settings. From [32] and the first cases of Germany, we have a secondary attack rate of 5–10%. The meta analysis in [33] found a pooled secondary attack rate in household settings of 18% and of 0–5% in workplace, school or social settings. Taking relative susceptibility as described before into account and adding uncertainty, we have , , , . From the mortality for Germany, we derived that a slightly larger had to be used to account for many infection clusters in residential homes for the elderly [48, Report of Dec. 16]. Then, we define
| (14) |
with the seasonality factor given in the next section in Eq. (15). By this parameter, we take the influence of seasons into account, a factor that is still under discussion in the literature [37], [76]. We will allow for a slight variation of the infection rate with the seasons as detailed in the next subsection.
2.3.2. Influence of the seasons
As Covid-19 raged all over the world and did not disappear in the summer months, only reduced seasonality can be expected. The analysis of over 100 articles in [37] found only a “weak modulation effect” so far, with more evidence only to be expected in 2021.
Another important aspect of seasons is the transition from outdoor to indoor contacts. While counter-strategies like face masks [38], [71], [72] or adapted air flows [69], or both [77], [78] are studied, it is reasonable to assume that they cannot fully waive the risk of indoor infections. In [39], the large majority of considered clusters appeared in closed environments, while [40] even quantified the risk of indoor infections 18.7 times larger than the risk of open-air infections. As we do not distinguish between contacts in closed spaces and in outdoor spaces, we allow the infection rate (cf. (14)) to vary slightly with the seasons by using
| (15) |
where is the day of the year and . The chosen parameter will yield scenarios with modest seasonal influences. From the simulation results, we will see that the implemented seasonality is capable of reproducing low and only modestly increasing numbers of infections to the end of the summer period. On the other hand, we can also correctly model the recent horizontal development of detected cases in autumn and beginning of winter scenarios. For more details, see the results section.
Recently, our choice of has been validated by an empirical global study [79] and a modeling study [80], particularly for Germany. Our mean value realizes peak values of and in summer and winter, respectively. Similar values have been used by [80] and [79] found a % increase in total infections in the Southern Hemisphere during the cold period and a % decrease in total infections in the Northern Hemisphere during the warm period.
2.3.3. Quarantine and isolation
Note that we use the parameter (or ) differently than the in the most recent version of [9]. In the latter, represents the risk of infection from the detected and infected symptomatic patients not yet effectively isolated.
The parameter in our model additionally represents the share of infected people that are not detected. For comparison, suppose , i.e. the infected are the sum of the undetected , those later hospitalized and those that recover on their own . Then, our and in [9] are related by
A value of could then mean that the number of unreported cases equals the number of reported cases , and reported cases are perfectly quarantined from the first moment of infection () while unreported cases move freely for the whole time of infection. Of course this is only the very unlikely edge case.
The decrease of is what the national strategy [81] of test, trace, and isolate majorly contributes to [82]. Unfortunately, we already faced “no longer traceable transmission chains” [48, Report of Oct. 28]. Since it is difficult to quantify how phases of relative transmission control or “diffuse spread” [48, Report of Oct. 28] influence , we assume and consider different scenarios. Thereby, we let increase along a sigmoidal (cosine) curve from the minimum in to the maximum value in . We assume the minimum for phases with less than 50 infections per 100 000 individuals increasing smoothly to the maximum for about 250 infections per 100 000 individuals.
2.3.4. Exposure, carrier, and infection transition
denotes the time elapsed between exposure and carrier state and the time between the beginning of carrier state and the onset of symptoms. We assume that these parameters do not depend on age. represents the time an individual remains in a latent non-infectious stage following the transmission. The incubation period is the time between exposure and when symptoms are first apparent, i.e.
| (16) |
We use an incubation period of 5.2 days and assume that infections occur randomly during the infectious period [9]; for more details, see [9], [41], [42]. We allow for . Hence, by median, and .
2.3.5. Asymptomatic individuals
During the early outbreak in Germany, a proportion of 22% of infections was reported to be asymptomatic [83]. Two recent meta analyses [44], [45] found ranges of asymptomatic cases from 3–67% with an overall estimate of 17% and 20%, respectively. The role of children is still heavily under discussion, and the number of asymptomatic cases in children is even less clear [35], [43], [44], [46]. For instance the studies [35], [46] considered children diagnosed with SARS-CoV-2 infection. The former found 28% of asymptomatic cases compared to 12% in adults, and the latter found 19% with another 25% of mild cases. We thus consider for and for .
While the asymptomatic individual remains infectious, we assume ; for more details, we refer to [9].
2.3.6. Symptomatic individuals
Symptomatic cases are divided into those with mild symptoms not requiring hospitalization and those where an initially mild stage becomes severe. From [48, Report of Sept. 15], we have a range of 5% to 22% of hospitalized cases with respect to the reported number of cases in Germany. The highest number in the report occurs during a time of presumed huge underreporting and when also many elderly people were infected. In [14] and its adjusted version for Great Britain [47] the symptomatic cases range from about 0% for age group 0–9 to 18% and 27%, respectively, for people older than 80 years. We range our samples accordingly and allow for a deviance of up to 20% from the mean or median; see Table 2.
For the recovery time of mild cases, we take a median of about seven days [9], [52] With a deviance of up to 20%, we consider a range . For the time span of initially mild symptoms becoming severe and where hospitalization is needed, we assume for patients aged 0–34 years and for individuals older than 35 years. In [9], we refer to some earlier studies [49], [50], [51] providing a median period of 4, 4.9 and 7 days, respectively. From [74] and 3 265 patients, we have a median time of known infection to hospitalization of 9 days for age group 0–14 and 12 days for age group 15–34, and 6 days for 35–65 years, 7 days for 65–75 years, and 5 days for 75+ years; see supplementary figures. Note that the time of known infection, however, only provides a lower bound for the time of symptoms onset to hospitalization.
2.3.7. Hospitalized individuals and transfer to intensive care
In our model, there are essentially two possibilities for patients which are admitted to a hospital. Either individuals recover directly in the hospital or individuals are transferred to intensive care units with probability .
In an early study [53], 26% of hospitalized patients needed intensive care which comes close to the 25% reported in [54]. In our analysis of LEOSS [74], we see an increase from no cases or only a few for the youngest individuals to 37% for the age group 66–75 years, with a surprising slight decrease to 24% for the age group 80+. The latter could be explained by personal decisions to refuse intensive care treatment but the data lacks a qualified explanation. In contrast, [47] provides a monotonous curve from 5% to 70%. Combining the results, we let range from 0.05 to 0.45 for the different age groups; see Table 2 for details.
The median time from symptoms onset to intensive care () is estimated to be 9 and 9.8 days in [49], [50] (with a median of 4 and 4.9 days from symptoms onset to hospitalization, i.e., ). From [74], we derive hospital stays for patients admitted to ICU (and recovering later on) of 11.3 to 8.4 days on average (median 13 to 5 days). This includes, however, days before and after intensive care; see supplementary figures. Combining these results, we consider a range of 3 to 7 days for for all age groups.
For the time of individuals recovering in the hospital without needing intensive care, we refer to our reasoning in [9] where 7–16 days were considered. From [74] and our supplementary figures, we have median recovery time spans of 4 to 6 days for age groups 0–14 and 15–35 years, respectively. This value rises to 8 days for 36–65 years, 10 days for 66–75 years, and 15 days for 76 years and older.
2.3.8. Intensive care, recovery and death
At last, we have to determine the mortality of patients in intensive care and the patients’ average time spans to either recovery () or death ().
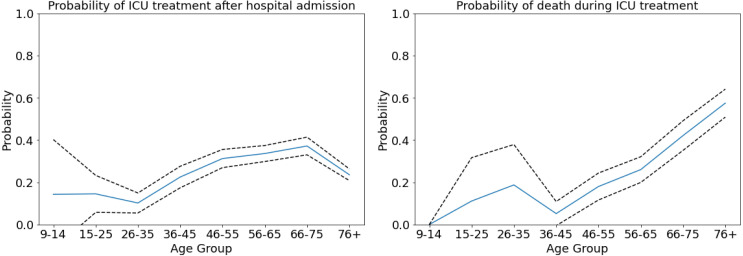
For , we use the ranges as presented in Table 2 based on a combination of the following findings: In [55], the overall ICU mortality is estimated as 41%. The mortality among mechanically ventilated patients is considered in [54] and ranges from 28% to 72% from the youngest to the oldest age group. For non-ventilated patients, these numbers range from 1% to 34%. From the LEOSS survey [74], we have ICU mortalities of 0%, no cases, or large confidence intervals around low values for the youngest individuals, increasing up to 57% for patients aged 76 years and older; cf. Fig. 4.
Fig. 4.
Age-specific probabilities. Age-specific probability to need intensive care once hospitalized (left). Age-specific probability to die once intensive care was necessary (right). Mean value shown in blue, 95% confidence interval shown in dashed black lines. Graphs derived from LEOSS [74].
The recovery time for severe or critical cases can take up to 3–6 weeks [9], [56]. In [50], the pooled median from symptoms onset to recovery was 18.3 days. However, this also potentially includes mild cases. From the LEOSS survey [74], we have mean recovery time spans of 6 and 11 days (median: 7 and 7 days) for people between 0–14 and 15-35 years. For older people, the average time spans are 17, 21, and 15 days (median: 14, 18, and 9 days); see Table 2 for the ranges used in our simulations.
The pooled time span from symptoms onset to death is estimated as 15.9 days in [50]. In our database from [74], no death is observed for individuals aged 0–14 years. For the age groups, 15–35, 36–65, 66–75, and 76 and more years we have mean values of 12, 18, 18, and 12 (median: 15, 16, 15, 9). In [9], we also assume to be slightly shorter than . For the ranges finally considered in our simulations, see Table 2.
2.4. Results and discussion
In this section, we present different scenarios based on the course of the pandemic in Germany. Four of these scenarios are retrospective and start at June 1, July 15, September 1, and October 10, respectively, and they last for a period of 45 days. Twelve scenarios are considered for the time span of December 12 to January 10. Our aim is to qualitatively capture the trend of infections and their time-dependent distribution across Germany. We use the same set of epidemiological parameters for every scenario without adapting them for the specific situation. We implement different sets of interventions that lead to different rates of contact reductions. The mean effectiveness of the sets of NPIs is derived from the development of SARS-CoV-2 infections and Covid-19-related deaths in Germany.
2.4.1. Aims and expectations
Our first aim is to qualitatively capture the infection trends and death rates for all scenarios without tweaking specific parameters for a better local fit. These local fits are often achieved by a daily fitting of contact patterns which often result in overfitting and less generalizable results. We thus do not expect to exactly predict the number of deaths or infections for all scenarios. We rather expect slight under- and overshoots depending on the scenario and the quality of the underlying data. The simulation times in the retrospective scenarios are rather long and we know that predictions for many weeks become increasingly less reliable. We do not expect that this is different for our model. What we want to see here is that our model reproduces the main trend.
The prediction of SARS-CoV-2 infections or related deaths is a challenging task and heavily depends on the input data. Our model is age-resolved, but some of the input data is not. While already relatively good data is available from RKI [58] and DIVI [84], additional data may be necessary to further validate our simulations. For the deaths reported with age resolution, only the dates of the assumed infection are available in the repository [58], and we thus have to extrapolate the time of death from the time of infection in the real data. This is then only an approximation to the real life situation. The overall number in the situation reports, however, is not age-resolved. ICU occupancy also lacks age resolution, so we have to extrapolate intensive care for the different age groups.
A further approximation in our model is that people can only die after they were in intensive care first; cf. Fig. 1. In real life, and in particular in times of high infection rates, Covid-19-related deaths can also happen in, e.g., residential homes for elderly care. This leads to an overestimation of ICU occupancy in our model.
Our second aim is to capture the regional spread of the infection across Germany. Our model must be able to predict the spread of the virus along the routes provided by our mobility data. Our model is only calibrated with real data once at the beginning. Local effects are very hard to capture in the simulation. For example, in the real world, the implemented local NPIs in regions with very high incidence might differ considerably in their effectiveness. A further local driving mechanism of the infection are super-spreading events. As these events are by nature random, we expect regional deviations between the simulated scenarios and the extrapolated real data that may, of course, also influence the global infection spread. However, if local hot spots are already contained in the initial data, we expect to see their effects.
Our third and main aim is to assess the mean effectiveness of mitigation strategies. We implement local dynamic NPIs to control hot spots with more than 200 infections per 100 000 inhabitants. These are used carefully to avoid overfitting and to not distort the image of the country-wide mitigation strategy. By variation of the country-wide contact reduction over a large number of simulations runs, the comparison with the extrapolated real data will yield the effective contact reduction of implemented mitigation strategy.
2.4.2. Retrospective scenarios
For all simulations, we use the ranges for the epidemiological parameters in Table 2. We run sets of 1000 Monte Carlo runs with different levels of mitigation as in Table 3. We then identify ranges for the effective mitigation in the different scenarios by comparing our simulation results to the real data.
In all scenarios, school holidays are implemented for the corresponding dates for all federal states. Furthermore, we group the most relevant interventions on state level to single dates and consider their mean effectiveness over periods of multiple weeks. In the following, for better readability, we drop the indices and of the NPI-related parameters ; cf. Table 3.
Set of NPIs for June to October. For the time span of June 1 to September 30, we model rather weak effective contact reductions — in accordance with the lifting of many interventions in the summer period as described in [85], [86] – to reproduce the slow spread of the disease. We assume contact reductions in the range of 0 to 20% in home and other locations, a working from home percentage between 20 and 30%, up to 5% of people who stopped working altogether (also cf. [21]) as well as an additional contact reduction in all locations by wearing masks and distancing of up to 20%. These considerations translate to , with , with , ; see the corresponding section.
In addition, by averaging we implement the partial school closures and remote schooling () from June 1 until June 15 for all states; after that, schools operate as usual with (except for the school holidays on federal level, where ).
From our simulations runs, we assess the effectiveness of the mitigation strategies in this period on the overall contact reduction by 15% with schools open and by 30% during school holidays.
Set of NPIs for October. From October 1 to October 30 we assume slightly stricter contact reductions than in the summer based, e.g., on the call to further attentiveness end of September [87]. We identify slightly increased values for contact reduction at home (20 to 40%, i.e., ) with increased values for protective interventions such as wearing masks, regular ventilation of closed spaces, or distancing (20 to 40%, i.e., , ). All other NPIs are kept in place as before. The NPIs’ effect on the median overall contact reduction that we obtained from our simulations is about 31%.
Set of NPIs for November. For the time span of November 1 to November 30, stronger restrictions are in place [88]. We assume contact reduction in homes by 40 to 60%, a proportion of non-working individuals of 0 to 10% plus a proportion of home-working individuals of 20 to 30%. Since restaurants, bars, and most leisure-related facilities were closed, we model a contact reduction in other locations by 60 to 80%. Additional protective effects to avoid contacts are estimated as 20 to 40% in homes and schools (since face masks are less worn in private situations [18], [73] and since school contacts are more difficult to reduce than work or other contacts) and 40 to 60% in work and other situations. Through our simulations runs, we assess the effectiveness of the mitigation strategies in this scenario on the overall contact reduction with 50%. This is slightly larger than the estimation of 43% by [66] but still far from the reported reduction in spring (63%) that may have been necessary to substantially mitigate the spread of the virus. Note however, that, in our simulations, wearing masks and keeping distance is modeled as contact reduction such that the values we present are slightly larger than in cases were this is not considered a contact reduction.
To summarize, we set , with , and . We further assume , and , .
Dynamic and local non-pharmaceutical interventions. In order to mitigate the spread in local hot spots, we dynamically implement a set of strict non-pharmaceutical interventions. Once 200 infections per 100 000 inhabitants and county are reached, an enforced contact reduction is implemented for 14 days. The parameters of this local set of interventions are the sames as the NPIs for November described above with the following modifications: , with , since additional facilities may be closed on a local scale, and , , which is a quite strong measure for distancing, face masks and other interventions.
Simulation. Our initial conditions are derived from the age-resolved case data provided by [58]. We take confirmed cases around the start date of our simulation from which we extrapolate the compartments in Eq. (2)–(9) by using the parameters in Table 2. Based on [84] and our parameters, we extrapolate age-resolved ICU data. In order to obtain age-resolved ICU data, we slightly reduce the initial extrapolation of 80+ intensive care cases since too large death rates occur in the beginning part of the simulation otherwise. We refrain from further correction of initial values without having more reliable data.
Given positive rates of 1% or less during summer [48, Report of Aug. 26], we assume that the number of unknown symptomatic infections was small. Therefore, we start our simulations on June 1, July 15, and September 1 directly from the number of confirmed cases. Given the increased proportion of positive tests up to mid of October, we start the simulations with a twofold of the confirmed cases. For each scenario, we run 1000 Monte Carlo runs such that we have a reliable set of parameters sampled in the given ranges. For the runs, we provide the median values as well as the percentiles obtained from the simulation runs. We use a seven day moving average of real world data and extrapolate the day of death, using the parameters from Table 2.
2.4.3. Discussion of retrospective scenarios
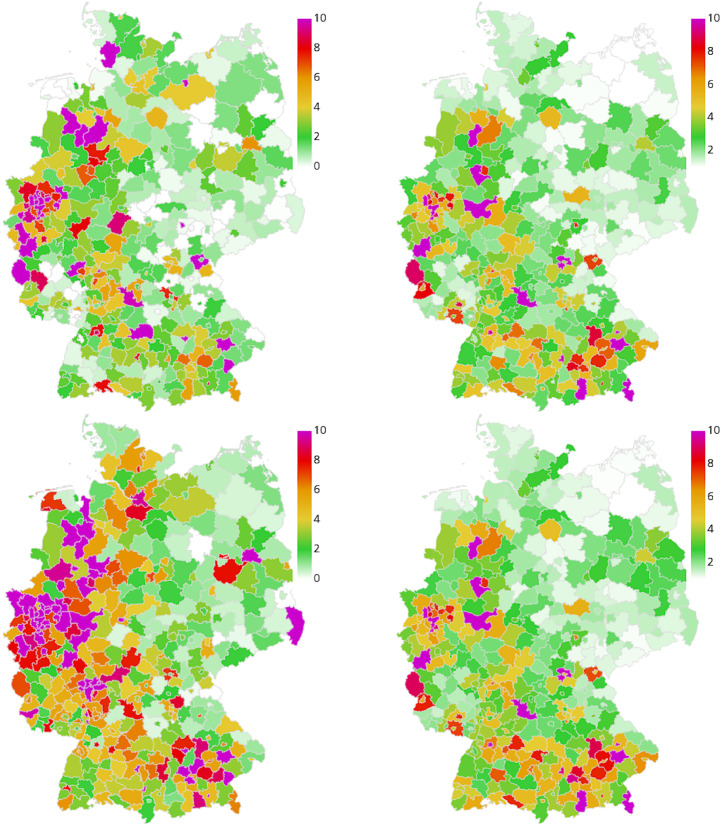
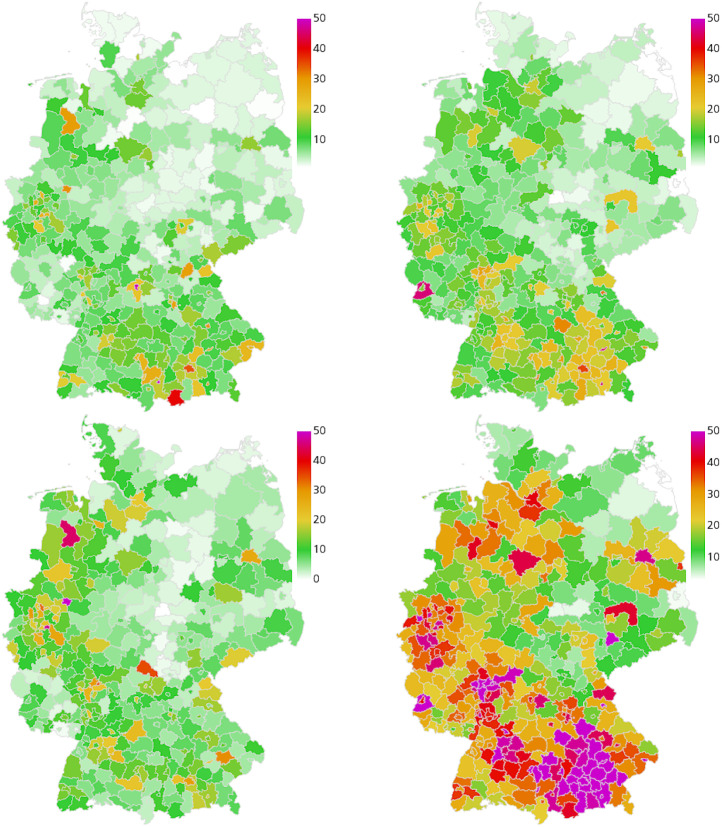
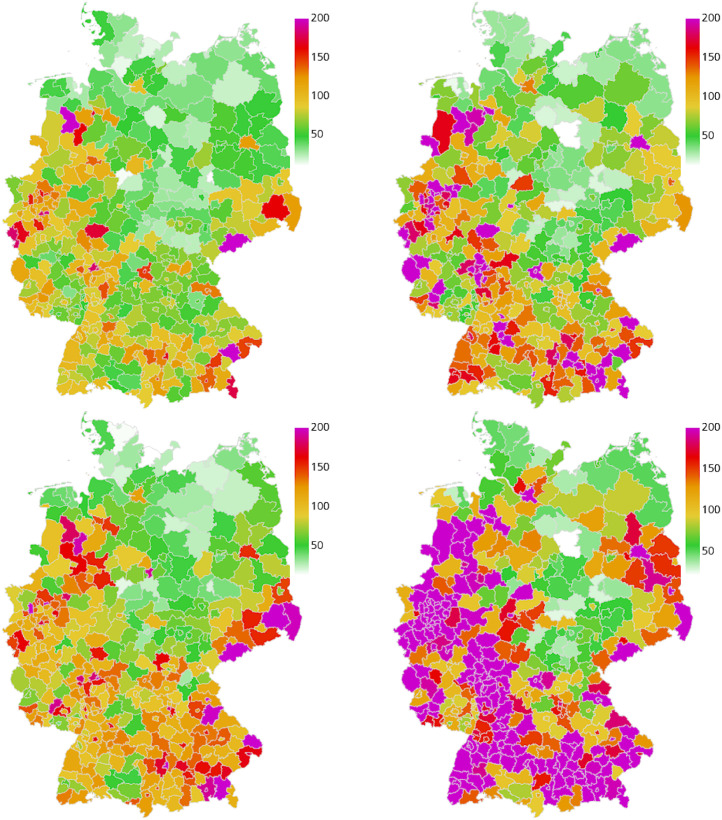
In the following, we discuss the results of the four different retrospective scenarios with the described sets of implemented NPIs over time. We compare the overall and the age-resolved death rates with the extrapolated real data. We also compare the overall infection rates and the ICU occupancy. In the corresponding Figs. 5, 7, 9, and 11, we present the median (percentile p50) and the percentiles ranges from (p05 and p95) as well as p25 and p75 as explained above. Additionally, in the maps of Figs. 6, 8, 10, and 12, we show two snapshots of the regional spread of the infection, where we compare the extrapolated real data on the left with our simulation on the right. Note that the scaling of the color bars differs for the scenarios and represents the relative number of infections per 100 000 inhabitants.
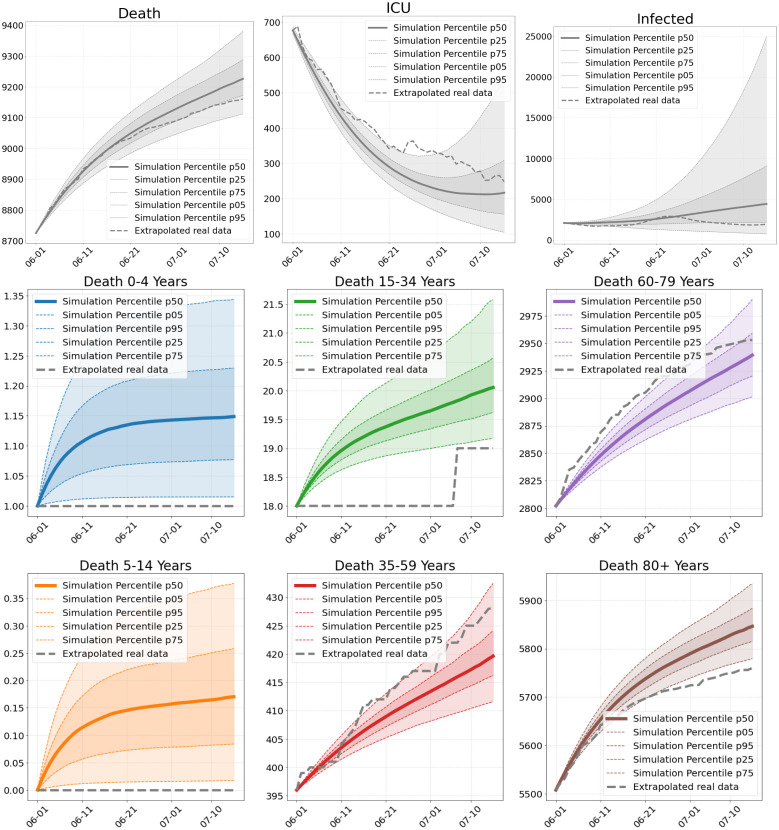
Fig. 5.
Number of deaths, ICU patients and infections in Scenario 1. Total numbers (top) and deaths per age group (center and bottom), as of our simulations compared to extrapolated real world data from June 1 to July 15.
Fig. 7.
Number of deaths, ICU patients and infections in Scenario 2. Total numbers (top) and deaths per age group (center and bottom), as of our simulations compared to real world data from July 15 to August 29.
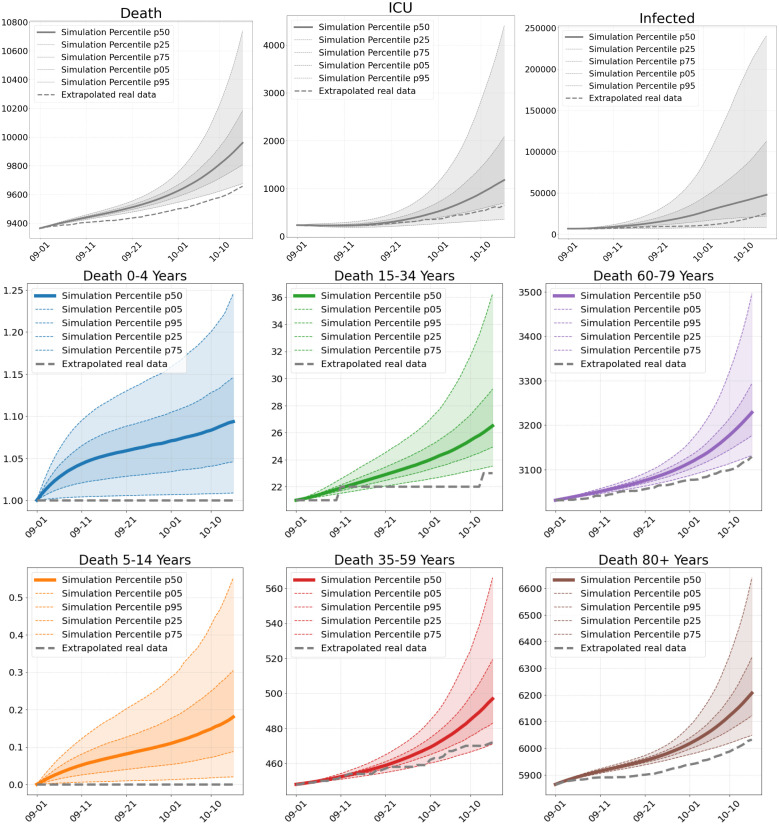
Fig. 9.
Number of deaths, ICU patients and infections in Scenario 3. Total numbers (top) and deaths per age group (center and bottom), as of our simulations compared to extrapolated real world data from September 1 to October 15.
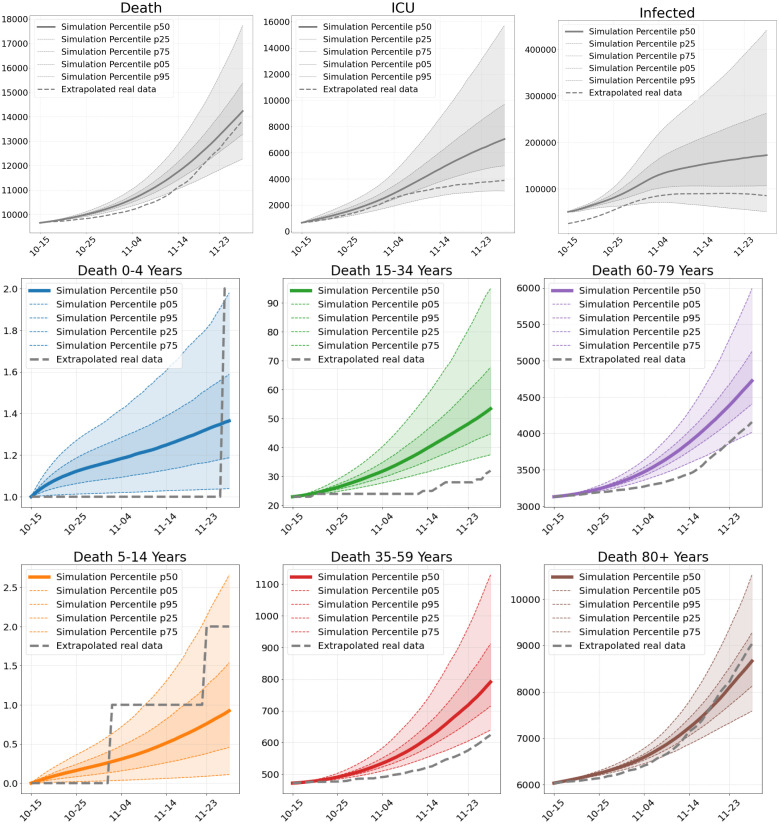
Fig. 11.
Number of deaths, ICU patients and infections in Scenario 4. Total numbers (top) and deaths per age group (center and bottom), as of our simulations compared to extrapolated real world data from October 15 until November 30.
Fig. 6.
Geographic spread of the disease in Scenario 1. Extrapolated real world data (left) and simulated number of infections (right), relative per 100 000 inhabitants, on June 15 (top), and June 30 (bottom). On average we have 0.4 exceedances of 200 infections per 100 000 inhabitants where stricter local NPIs are implemented.
Fig. 8.
Geographic spread of the disease in Scenario 2. Extrapolated real world data (left) and simulated number of infections (right), relative per 100 000 inhabitants, on July 30 (top), and August 14 (bottom). On average we have 0.03 exceedances of 200 infections per 100 000 inhabitants where stricter local NPIs are implemented.
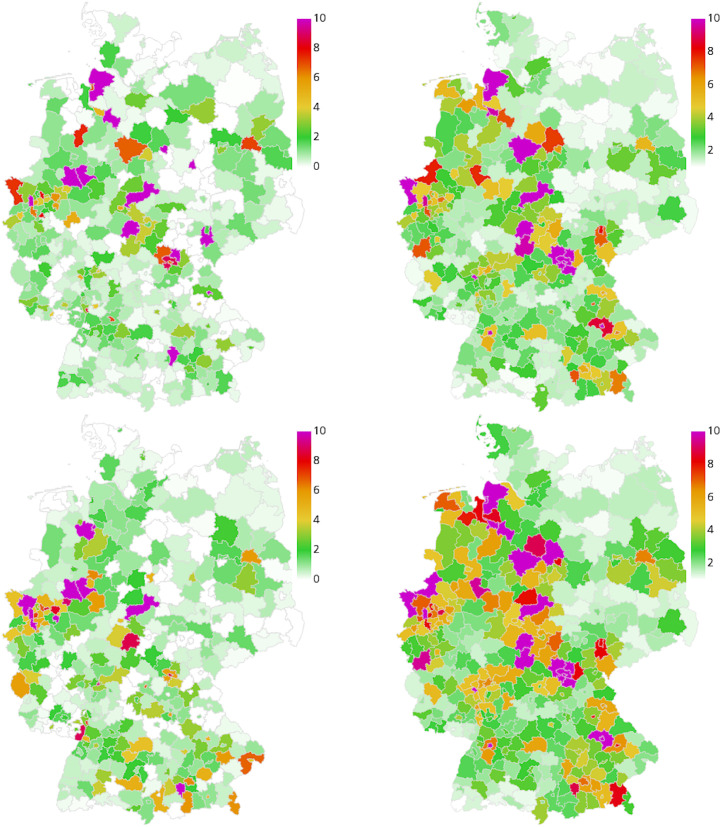
Fig. 10.
Geographic spread of the disease in Scenario 3. Extrapolated real world data (left) and simulated number of infections (right), relative per 100 000 inhabitants, on September 15 (top) and September 30 (bottom). On average we have 44 exceedances of 200 infections per 100 000 inhabitants where stricter local NPIs are implemented.
Fig. 12.
Geographic spread of the disease in Scenario 4. Extrapolated real world data (left) and simulated number of infections (right), relative per 100 000 inhabitants, on October 30 (top) and November 14 (bottom). On average we have 371 exceedances of 200 infections per 100 000 inhabitants where stricter local NPIs are implemented.
Scenario 1. Our first scenario (S1) is computed 45 days from June 1 onward. During the summer months, we observe only a slow rise in the infections in the RKI data and a decrease of ICU occupancy from DIVI (Fig. 5). Both are captured well with the median of our simulations. The small elevation in the number of infections in June is due to an outbreak of Covid-19 in a slaughterhouse in Gütersloh. As expected, we cannot capture such a stochastic event.
Focusing on the first part of June (see Fig. 6, top), we observe further regions that are underestimated by our simulation and some where it is the other way around. Overall, however, a larger incidence in the RKI data mostly corresponds to a larger incidence in the simulation data. Note that over- and underestimating also happens due to a different strictness of local interventions. Worth mentioning is the spread of infections into neighboring regions which we can see for Berlin from the middle to the bottom. Due to the inclusion of mobility, we see that the infection spreads into the near regions in our simulation (right) as in the extrapolated real data (left). Due to the longer simulation time, the results on the bottom show further deviation from the data.
In Fig. 5, we plot the median death rate, the percentiles and the extrapolated real data for the different age groups. Our model is quite close to the overall death rate. The age group 60–79 years is captured very well and the age groups below are also captured well. We are a little less close for the age group 80+ years. The deviations are to be expected since we aim for an overall good fit of our model without tweaking it for the individual scenarios. Additionally, we lack age-resolved ICU occupancy data and have to extrapolate the intensive care input data for the different age groups. This then also affects the simulated death rates. Note that the age groups below 15 years only contribute marginally to the death rate. The deviance with simulation seems large, but due to the small numbers (0 or 1), we are actually close to the real world value.
Scenario 2. Our second scenario (S2) is computed 45 days from July 15 onward. The results of this Scenario are very similar to the results of S1. This holds for the overall death rates and the death rates in the different age groups as depicted in Fig. 7. A main difference is the influence of travel returners [48, Report of Aug. 9] that might be responsible for the rise of infected in the beginning of August with a plateau reached at the end of that month; cf. Fig. 7. Such an influence is not considered in our simulation which contributes to the underestimation of infections. Similarly, we underestimate the number of ICU occupancy.
In addition to travelers, many smaller outbreaks in a number of administrative districts in various settings (social, industrial, etc.) are reported [48, Report of Aug. 9]. There is an increasing trend in 7-day incidences in North Rhine-Westfalia (NRW) and Hamburg and higher-than-average 7-day incidences in Hesse and Berlin, as well as a Covid-19 related outbreak in the Bavarian district of Dingolfing–Landau (DL) with cases. This is what we observe in the map of the extrapolated real world data in Fig. 8 (left).
In our simulation (Fig. 8, right), NRW still seems to be a little underrepresented, but interestingly, we catch the outbreak in DL with our input data from July 15, as well as its spread to neighboring regions that we observe in the real data. Hesse and Berlin are regions of higher infection rates in our simulation as well. Some local hot spots, maybe due to weddings in that time, are again missed due to their stochastic nature. The qualitative regional infection spread is however captured well.
Scenario 3. Our third scenario (S3) is computed 45 days from September 1 onward. Compared to S1 and S2, we overestimate the number of deaths for all age-groups (Fig. 9) compared to the extrapolated real data. However, by the end of this period, on October 15, we also have 9710 deaths reported in the [48, Report of Oct. 15]. This means that some of the infected died earlier then we could extrapolate from the assumed day of infection in [58]. 9710 deaths is then already much closer to the prediction of our simulation.
The slight overestimation of deaths is consistent with the projected infection numbers and ICU occupancy that are overestimated as well. As the proportion of positive tests grew considerably from 0.7% to 5.6% in the considered period, we assume that there might have been a larger number of undetected cases at the end of this scenario which are not reflected in the real data yet. As explained in Section 2.4.1, we expect our model to rather overestimate ICU occupancy in phases of high infection rates. This might also already contribute to the overestimation we observe in Fig. 9.
Our simulations from September 1 predict larger incidences in West and Southern Germany with lower incidence in the center and North-Eastern Germany; see Fig. 10 (right). Although we have a qualitatively similar picture in the extrapolated real data, the number of reported cases are substantially below the predicted values; see Fig. 10 (left). However, we see that these and even much higher incidences are to be found in the real data in October in these precise regions; see Fig. 12. This suggests a larger number of undetected cases in the infections that are not captured in the real data in Fig. 10 (left).
Scenario 4. Our fourth scenario (S4) is computed 45 days from October 15 onward. Due to the increased proportion of positive tests, we start this simulation with the assumption of twice as many confirmed cases, which is also the reason for the difference between the infected in the real data and the simulation data in the initial phase depicted in Fig. 11. We see that the curve of predicted deaths is steeper in the beginning while the extrapolated real data curve becomes steeper towards the end of the scenario; see 12. As in the last scenario, the situation reports already yields 16 248 deaths at the end of November [48, Report of Nov. 15], but again the corresponding age-resolved data that we need to compare to is not directly available. In this scenario, we overestimate the sum of the extrapolated deaths while we still underestimate the overall number of 16 248 in the situation report.
While we see a slight decrease in reported cases towards the end of November, our model instead predicts a slight but further increase of infections; see Fig. 11. This predicted increase is however consistent with the increasing number of confirmed cases in the beginning of December; cf. [48, Report of Dec. 16].
The slight decrease in confirmed cases end of November is likely to be a statistical artifact obtained due to a changed test strategy that has been in place in Germany since November 11 [48, Report of Nov. 18]. After that, the conducted PCR tests fell by around 200,000, while the positive rate rose. Again, the curve of predicted intensive care patients lies above the extrapolated data. Our model thus shows the expected behavior in times of higher infections.
Summary of retrospective results. All in all, we have reached our aims: The median of our death and infection rates is close to the extrapolated real data without further adaptations for each individual scenario. We can identify the mean effectiveness of the sets of non-pharmaceutical interventions during different phases of the pandemic in Germany. Although we have no mechanism to predict local stochastic super-spreading events, we see how commuter activities lead to the spread of the disease along the routes visualized in Fig. 1 (right). We can predict regions with larger incidence over time spans of several weeks.
2.4.4. Predictive scenario
On December 18, we submitted twelve prospective scenarios for Germany from December 12 to January 10 to the preprint server. In these scenarios, we assess different strictness and compliance levels in relation to the recently announced lockdown [89]. We assume that the strictness of the lockdown, the strictness of the partial lifting over Christmas, and the number of infected individuals (detected & undetected) will have the most influence on the effective mitigation and prediction of the spread of SARS-CoV-2 in that period.
We assume an effective contact reduction of this lockdown of 74% or 67%. From December 12 to December 16, we use the same contact reduction (50%) as in our November scenario in retrospective section. In our scenarios the lockdown restrictions are lifted for December 24–26 with contact reductions as given in Fig. 13. Our predictions are based on an assumed initial number of undetected cases on December 12, namely 50% and 150%. Since the effects on the number of deaths through contact reduction in this period will only be seen from mid of January onward, we do not provide predictions for the number of deaths.
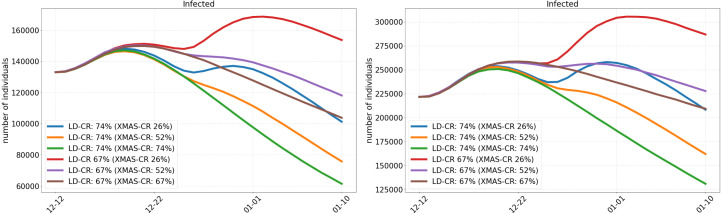
Fig. 13.
Prediction of the infected individuals in Germany from December 12 to January 10. Application of a strict lockdown (LD) from December 16 and based on different potential numbers of undetected cases on December 12 (50% left and 150% right). Lifting of the lockdown restrictions for December 24–26 (XMAS) with lower contact reductions (CR) as presented.
2.4.5. Discussion of predictive scenarios
In Fig. 13, we present scenarios considering contact reductions of 74% and 67% during lockdown with different increases in contact rates over Christmas. The scenarios on the left assume 50% of undetected infections while the scenarios on the right assume 150% of undetected infections on December 12.
Qualitatively, the curves in Fig. 13 are similar for both proportions, 50% (left) and 150% (right), of undetected infections. We see that the strictest measures with 74% contact reduction (CR) during lockdown and 74% (green) or 52% (orange) reduction over Christmas lead to the lowest number of infections by January 10. With a contact reduction of 67% during the lockdown and over Christmas (brown), the number of infections also declines, but not to the same extent. The purple curve (52% CR over Christmas) behaves to the brown scenario as the orange to the green scenario. With only 26% contact reduction over Christmas (blue or red), there is a substantial new rise of the number of infections before the lockdown can take its effect.
We observe that only slight additional contact reductions during lockdown can substantially change the speed of infection mitigation. Considering a lifting of restrictions over Christmas to allow for a mean of 7.2 daily contacts (CR 26%) could throw back the containment of the virus for weeks. Note that these 7.2 daily contacts cannot be directly translated to persons in a room but highly depend on further parameters like (the type of) masks, distancing, ventilation etc. Considering the contact reduction of 52% which may be closer to the NPIs in place over Christmas, we see that they contribute far less to the spread the virus than the 26% scenario.
2.5. Conclusion
We have extended the model [9] by age-resolution and added a model to resolve spatial heterogeneity using mobility data from the German Federal Employment Agency [20] and Twitter [62]. A numerical solution approach for the regional models was also introduced. One important future achievement will be the release of our modular epidemics simulation software MEMILIO [28] which uses the presented model and data. Our open-source software will also be available via a front-end that can be used by the public and decision makers.
We have collected extensive data on epidemiological parameters and conducted own analyses based on patient-specific data. While age-resolved incidence data is a good starting point, further data such as daily number of tests per age group, age-resolved hospitalization and intensive care data would be valuable information to further validate our model.
We have run experiments with different contact reduction factors and thus have identified parameters for the effectiveness of mitigation during different phases of the pandemic in Germany. In the retrospective scenarios the trends of infections have been reproduced well with the derived factors on the effective mitigation strategy in Germany. Local stochastic events such as super-spreading, which are naturally random, cannot be predicted. However, once infection information is included in the starting data, we see how commuter activities lead to increased infections also in surrounding counties. On the other hand, we see that less affected regions like the center of Germany or North-Eastern Germany are also predicted to be less affected by our simulations. Infection clusters as, e.g., appeared in large areas of Southern and Western Germany from beginning of autumn could be reproduced.
Funding
The work of M. Häberle and X. Zhu is supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. [ERC-2016-StG-714087], Acronym: So2Sat). This work has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 101003480 and by the Initiative and Networking Fund of the Helmholtz Association. It was supported by German Federal Ministry of Education and Research for the project CoViDec (FKZ: 01KI20102). The funding bodies had no role in the design of the study, collection, analysis, and interpretation of the results, or writing the manuscript.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
We thank Valerie Grappendorf, a student at the Hochschule für Gestaltung Schwäbisch Gmünd, for contributing Fig. 2. We express our deep gratitude to all study teams supporting the LEOSS study. The LEOSS study group contributed at least 5 per mille to the analyses of this study: C. Spinner, S. Rieg, F. Hanses, S. Borgmann, M. Hower, M. Vehreschild, M. M. Rüthrich, L. Tometten, C. Piepel, S. Dolff, K. Wille, J. Lanzster, M. von Bergwelt-Baildon, U. Merle, C. Römmele, C. Degenhardt, J. Fürst, S. Dalin, N. Isberner, B. Grüner, N. Jung, H. Haake, K. Hellwig, W. Rimili, C. Raichle, L. Eberwein, S. Grunwald, M. Akova, A. Friedrichs, D. Rauschning, C. Wyen, B. Jensen, K. de With, W. Guggemos, J. Kielstein, B. Schultheis, J. Trauth, R. Bals, P. Markart, S. Stieglitz, I. Atkin, M. Milovanovic, K. Rothfuss, J. Rüddel, J. Nattermann, D. Heigener, L. Walter, J. Schubert, J. Voigt, G. Müller-Jörger, C. Riedel, M. Worm. The LEOSS study infrastructure group: J. J. Vehreschild, L. Pilgram, M. Stecher, M. Schons, C. E. M. Jakob, A. Claßen, S. M. Nunes de Miranda, S. Fuhrmann, B. Franke, N. Schulze, F. Praßer and M. Lablans. The LEOSS study was supported by the German Center for Infection Research (DZIF) and the Willy Robert Pitzer Foundation .
Footnotes
Supplementary material related to this article can be found online at https://doi.org/10.1016/j.mbs.2021.108648.
Appendix A. Supplementary data
The following is the Supplementary material related to this article.
Estimation of age-resolved disease parameters and inter-regional mobility from official sources and social media.
References
- 1.JHU Center for Systems Science and Engineering . 2021. ArcGIS Dashboards. https://www.arcgis.com/apps/opsdashboard/index.html#bda7594740fd40299423467b48e9ecf6. [Google Scholar]
- 2.Deutsche Welle Coronavirus: WHO estimates 10% of global population infected with COVID-19. DW.COM. 2020 https://www.dw.com/en/coronavirus-who-estimates-10-of-global-population-infected-with-covid-19/a-55162783. [Google Scholar]
- 3.World Health Organization . 2020. Coronavirus disease (COVID-19): Herd immunity, lockdowns and COVID-19. https://www.who.int/news-room/q-a-detail/herd-immunity-lockdowns-and-covid-19. [Google Scholar]
- 4.Banholzer N., Weenen E.v., Kratzwald B., Seeliger A., Tschernutter D., Bottrighi P., Cenedese A., Salles J.P., Vach W., Feuerriegel S. Impact of non-pharmaceutical interventions on documented cases of COVID-19. MedRxiv. 2020 doi: 10.1101/2020.04.16.20062141. 2020.04.16.20062141. [DOI] [Google Scholar]
- 5.Barbarossa M.V., Fuhrmann J., Meinke J.H., Krieg S., Varma H.V., Castelletti N., Lippert T. Modeling the spread of COVID-19 in Germany: Early assessment and possible scenarios. PLoS One. 2020;15(9):1–22. doi: 10.1371/journal.pone.0238559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cauchemez S., Ferguson N.M., Wachtel C., Tegnell A., Saour G., Duncan B., Nicoll A. Closure of schools during an influenza pandemic. Lancet Infect. Dis. 2009;9(8):473–481. doi: 10.1016/S1473-3099(09)70176-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Desvars-Larrive A., Dervic E., Haug N., Niederkrotenthaler T., Chen J., Di Natale A., Lasser J., Gliga D.S., Roux A., Sorger J., Chakraborty A., Ten A., Dervic A., Pacheco A., Jurczak A., Cserjan D., Lederhilger D., Bulska D., Berishaj D., Tames E.F., Alvarez F.S., Takriti H., Korbel J., Reddish J., Grzymala-Moszczynska J., Stangl J., Hadziavdic L., Stoeger L., Gooriah L., Geyrhofer L., Ferreira M.R., Bartoszek M., Vierlinger R., Holder S., Haberfellner S., Ahne V., Reisch V., Servedio V.D.P., Chen X., Pocasangre-Orellana X.M., Garncarek Z., Garcia D., Thurner S. A structured open dataset of government interventions in response to COVID-19. Sci. Data. 2020;7(1):1–9. doi: 10.1038/s41597-020-00609-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ferretti L., Wymant C., Kendall M., Zhao L., Nurtay A., Abeler-Dörner L., Parker M., Bonsall D., Fraser C. Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science. 2020;368(6491) doi: 10.1126/science.abb6936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Khailaie S., Mitra T., Bandyopadhyay A., Schips M., Mascheroni P., Vanella P., Lange B., Binder S., Meyer-Hermann M. Development of the reproduction number from coronavirus SARS-CoV-2 case data in Germany and implications for political measures. MedRxiv. 2020 doi: 10.1101/2020.04.04.20053637. 2020.04.04.20053637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ngonghala C.N., Iboi E., Eikenberry S., Scotch M., MacIntyre C.R., Bonds M.H., Gumel A.B. Mathematical assessment of the impact of non-pharmaceutical interventions on curtailing the 2019 novel coronavirus. Math. Biosci. 2020;325 doi: 10.1016/j.mbs.2020.108364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Stojanovic O., Leugering J., Pipa G., Ghozzi S., Ullrich A. A Bayesian Monte Carlo approach for predicting the spread of infectious diseases. PLoS One. 2019;14(12) doi: 10.1371/journal.pone.0225838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Poletti P., Tirani M., Cereda D., Trentini F., Guzzetta G., Marziano V., Buoro S., Riboli S., Crottogini L., Piccarreta R., Piatti A., Grasselli G., Melegaro A., Gramegna M., Ajelli M., Merler S. Age-specific SARS-CoV-2 infection fatality ratio and associated risk factors, Italy, February to April 2020. Eurosurveillance. 2020;25(31) doi: 10.2807/1560-7917.ES.2020.25.31.2001383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Levin A.T., Hanage W.P., Owusu-Boaitey N., Cochran K.B., Walsh S.P., Meyerowitz-Katz G. Assessing the age specificity of infection fatality rates for Covid-19: systematic review, meta-analysis, and public policy implications. MedRxiv. 2020 doi: 10.1101/2020.07.23.20160895. 2020.07.23.20160895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Verity R., Okell L.C., Dorigatti I., Winskill P., Whittaker C., Imai N., Cuomo-Dannenburg G., Thompson H., Walker P.G.T., Fu H., Dighe A., Griffin J.T., Baguelin M., Bhatia S., Boonyasiri A., Cori A., Cucunubá Z., FitzJohn R., Gaythorpe K., Green W., Hamlet A., Hinsley W., Laydon D., Nedjati-Gilani G., Riley S., Elsland S.v., Volz E., Wang H., Wang Y., Xi X., Donnelly C.A., Ghani A.C., Ferguson N.M. Estimates of the severity of coronavirus disease 2019: a model-based analysis. Lancet Infect. Dis. 2020;20(6):669–677. doi: 10.1016/S1473-3099(20)30243-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mossong J., Hens N., Jit M., Beutels P., Auranen K., Mikolajczyk R., Massari M., Salmaso S., Tomba G.S., Wallinga J., Heijne J., Sadkowska-Todys M., Rosinska M., Edmunds W.J. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Med. 2008;5(3) doi: 10.1371/journal.pmed.0050074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fumanelli L., Ajelli M., Manfredi P., Vespignani A., Merler S. Inferring the structure of social contacts from demographic data in the analysis of infectious diseases spread. Salathé M., editor. PLoS Comput. Biol. 2012;8(9) doi: 10.1371/journal.pcbi.1002673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Prem K., Cook A.R., Jit M. Projecting social contact matrices in 152 countries using contact surveys and demographic data. PLoS Comput. Biol. 2017;13(9) doi: 10.1371/journal.pcbi.1005697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jarvis C.I., Van Zandvoort K., Gimma A., Prem K., Auzenbergs M., O’Reilly K., Medley G., Emery J.C., Houben R.M.G.J., Davies N., Nightingale E.S., Flasche S., Jombart T., Hellewell J., Abbott S., Munday J.D., Bosse N.I., Funk S., Sun F., Endo A., Rosello A., Procter S.R., Kucharski A.J., Russell T.W., Knight G., Gibbs H., Leclerc Q., Quilty B.J., Diamond C., Liu Y., Jit M., Clifford S., Pearson C.A.B., Eggo R.M., Deol A.K., Klepac P., Rubin G.J., Edmunds W.J., CMMID COVID-19 working group Quantifying the impact of physical distance measures on the transmission of COVID-19 in the UK. BMC Med. 2020;18(1):124. doi: 10.1186/s12916-020-01597-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jit M., Cook A.R., Prem K., Eggo R., Edmunds J., Gimma A. Contact matrices for the COVID-19 era. LSHTM. 2020 https://www.lshtm.ac.uk/newsevents/events/contact-matrices-covid-19-era. [Google Scholar]
- 20.BMAS M. Pendlerverflechtungen der sozialversicherungspflichtig Beschäftigten nach Kreisen - Deutschland (Jahreszahlen) Www.Bmas.de. 2019 https://statistik.arbeitsagentur.de/SiteGlobals/Forms/Suche/Einzelheftsuche_Formular.html?nn=20934&topic_f=beschaeftigung-sozbe-krpend. [Google Scholar]
- 21.Bonin H., Eichhorst W., Kaczynska J., Kümmerling A., Rinne U., Scholten A., Steffes S. Verbreitung und Auswirkungen von mobiler Arbeit und Homeoffice. Www.Bmas.de. 2020 https://www.bmas.de/DE/Service/Medien/Publikationen/Forschungsberichte/fb-549-verbreitung-auswirkungen-mobiles-arbeiten.html. [Google Scholar]
- 22.Kermack W.O., McKendrick A.G., Walker G.T. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A. 1927;115(772):700–721. doi: 10.1098/rspa.1927.0118. [DOI] [Google Scholar]
- 23.Anderson R.M., May R.M. Population biology of infectious diseases: Part I. Nature. 1979;280(5721):361–367. doi: 10.1038/280361a0. [DOI] [PubMed] [Google Scholar]
- 24.Keimer A., Pflug L. Friedrich-Alexander-Universität Erlangen-Nr̈nberg; 2020. Modeling Infectious Diseases Using Integro-Differential Equations: Optimal Control Strategies for Policy Decisions and Applications in COVID-19: Technical report. [DOI] [Google Scholar]
- 25.Kim Y., Ryu H., Lee S. Agent-based modeling for super-spreading events: A case study of MERS-CoV transmission dynamics in the Republic of Korea. Int. J. Environ. Res. Public Health. 2018;15(11):2369. doi: 10.3390/ijerph15112369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Bicher M.R., Rippinger C., Urach C., Brunmeir D., Siebert U., Popper N. Agent-based simulation for evaluation of contact-tracing policies against the spread of SARS-CoV-2. MedRxiv. 2020 doi: 10.1101/2020.05.12.20098970. 2020.05.12.20098970. [DOI] [PubMed] [Google Scholar]
- 27.Adamu Y., Abdulganiyu A., Aisha A., Gana U.M. Modelling the direction and pattern of spread of infectious disease on a contagious multi-city network. Unique Res. J. Math. Phys. Sci. 2016;1(1):007–018. [Google Scholar]
- 28.Abele D., Kühn M.J., Koslow W., Siggel M., Klitz M., Rack K., Spataro L., Gilg J., Kleinert J., Mitra T., Abedi M., Khailaie S., Binder S., Meyer-Hermann M., Basermann A. 2021. MEMILIO - a high performance modular epidemics simulation software. [Google Scholar]
- 29.Arregui S., Aleta A., Sanz J., Moreno Y. Projecting social contact matrices to different demographic structures. PLoS Comput. Biol. 2018;14(12):1–18. doi: 10.1371/journal.pcbi.1006638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.He D., Zhao S., Lin Q., Zhuang Z., Cao P., Wang M.H., Yang L. The relative transmissibility of asymptomatic COVID-19 infections among close contacts. Intl. J. Infect. Dis. 2020;94:145–147. doi: 10.1016/j.ijid.2020.04.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Shah K., Saxena D., Mavalankar D. Secondary attack rate of COVID-19 in household contacts: a systematic review. QJM. 2020 doi: 10.1093/qjmed/hcaa232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Böhmer M.M., Buchholz U., Corman V.M., Hoch M., Katz K., Marosevic D.V., Böhm S., Woudenberg T., Ackermann N., Konrad R., Eberle U., Treis B., Dangel A., Bengs K., Fingerle V., Berger A., Hörmansdorfer S., Ippisch S., Wicklein B., Grahl A., Pörtner K., Muller N., Zeitlmann N., Boender T.S., Cai W., Reich A., an der Heiden M., Rexroth U., Hamouda O., Schneider J., Veith T., Mühlemann B., Wölfel R., Antwerpen M., Walter M., Protzer U., Liebl B., Haas W., Sing A., Drosten C., Zapf A. Investigation of a COVID-19 outbreak in Germany resulting from a single travel-associated primary case: a case series. Lancet Infect. Dis. 2020;20(8):920–928. doi: 10.1016/S1473-3099(20)30314-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Koh W.C., Naing L., Chaw L., Rosledzana M.A., Alikhan M.F., Jamaludin S.A., Amin F., Omar A., Shazli A., Griffith M., Pastore R., Wong J. What do we know about SARS-CoV-2 transmission? A systematic review and meta-analysis of the secondary attack rate and associated risk factors. PLoS One. 2020;15(10) doi: 10.1371/journal.pone.0240205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zhang J., Litvinova M., Liang Y., Wang Y., Wang W., Zhao S., Wu Q., Merler S., Viboud C., Vespignani A., Ajelli M., Yu H. Changes in contact patterns shape the dynamics of the COVID-19 outbreak in China. Science. 2020;368(6498):1481–1486. doi: 10.1126/science.abb8001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dattner I., Goldberg Y., Katriel G., Yaari R., Gal N., Miron Y., Ziv A., Hamo Y., Huppert A. The role of children in the spread of COVID-19: Using household data from Bnei Brak, Israel, to estimate the relative susceptibility and infectivity of children. MedRxiv. 2020 doi: 10.1101/2020.06.03.20121145. 2020.06.03.20121145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Fontanet A., Tondeur L., Madec Y., Grant R., Besombes C., Jolly N., Pellerin S.F., Ungeheuer M.-N., Cailleau I., Kuhmel L., Temmam S., Huon C., Chen K.-Y., Crescenzo B., Munier S., Demeret C., Grzelak L., Staropoli I., Bruel T., Gallian P., Cauchemez S., van der Werf S., Schwartz O., Eloit M., Hoen B. Social Science Research Network; Rochester, NY: 2020. Cluster of COVID-19 in Northern France: A Retrospective Closed Cohort Study: SSRN Scholarly Paper ID 3582749. https://papers.ssrn.com/abstract=3582749. [Google Scholar]
- 37.Smit A.J., Fitchett J.M., Engelbrecht F.A., Scholes R.J., Dzhivhuho G., Sweijd N.A. Winter is coming: A southern hemisphere perspective of the environmental drivers of SARS-CoV-2 and the potential seasonality of COVID-19. Int. J. Environ. Res. Public Health. 2020;17(16):5634. doi: 10.3390/ijerph17165634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Viola I.M., Peterson B., Pisetta G., Pavar G., Akhtar H., Menoloascina F., Mangano E., Dunn K.E., Gabl R., Nila A., Molinari E., Cummins C., Thompson G., McDougall C.M., Lo T.Y.M., Denison F.C., Digard P., Malik O., Dunn M.J.G., Mehendale F. 2020. Face coverings, aerosol dispersion and mitigation of virus transmission risk. arXiv:2005.10720 [Physics] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Qian H., Miao T., Liu L., Zheng X., Luo D., Li Y. Indoor transmission of SARS-CoV-2. MedRxiv. 2020 doi: 10.1101/2020.04.04.20053058. [DOI] [PubMed] [Google Scholar]
- 40.Nishiura H., Oshitani H., Kobayashi T., Saito T., Sunagawa T., Matsui T., Wakita T., Team M.C.-.R., Suzuki M. Closed environments facilitate secondary transmission of coronavirus disease 2019 (COVID-19) MedRxiv. 2020 doi: 10.1101/2020.02.28.20029272. 2020.02.28.20029272. [DOI] [Google Scholar]
- 41.Nishiura H., Linton N.M., Akhmetzhanov A.R. Serial interval of novel coronavirus (COVID-19) infections. Intl. J. Infect. Dis. 2020;93:284–286. doi: 10.1016/j.ijid.2020.02.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zhao S., Gao D., Zhuang Z., Chong M.K.C., Cai Y., Ran J., Cao P., Wang K., Lou Y., Wang W., Yang L., He D., Wang M.H. Estimating the serial interval of the novel coronavirus disease (COVID-19): A statistical analysis using the public data in Hong Kong from january 16 to february 15, 2020. Front. Phys. 2020;8:347. doi: 10.3389/fphy.2020.00347. [DOI] [Google Scholar]
- 43.Jones T.C., Mühlemann B., Veith T., Biele G., Zuchowski M., Hoffmann J., Stein A., Edelmann A., Corman V.M., Drosten C. An analysis of SARS-CoV-2 viral load by patient age. MedRxiv. 2020 doi: 10.1101/2020.06.08.20125484. 2020.06.08.20125484. [DOI] [Google Scholar]
- 44.Byambasuren O., Cardona M., Bell K., Clark J., McLaws M.-L., Glasziou P. Estimating the extent of asymptomatic COVID-19 and its potential for community transmission: systematic review and meta-analysis. MedRxiv. 2020 doi: 10.1101/2020.05.10.20097543. 2020.05.10.20097543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Buitrago-Garcia D.C., Egli-Gany D., Counotte M.J., Hossmann S., Imeri H., Ipekci A.M., Salanti G., Low N. Asymptomatic SARS-CoV-2 infections: a living systematic review and meta-analysis. MedRxiv. 2020 doi: 10.1101/2020.04.25.20079103. 2020.04.25.20079103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Zhen-Dong Y., Gao-Jun Z., Run-Ming J., Zhi-Sheng L., Zong-Qi D., Xiong X., Guo-Wei S. Clinical and transmission dynamics characteristics of 406 children with coronavirus disease 2019 in China: A review. J. Infect. 2020;81(2):e11–e15. doi: 10.1016/j.jinf.2020.04.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Ferguson N.M., Laydon D., Nedjati-Gilani G., Imai N., Ainslie K., Baguelin M., Bhatia S., Boonyasiri A., Cucunubá Z., Cuomo-Dannenburg G., Dighe A., Dorigatti I., Fu H., Gaythorpe K., Green W., Hamlet A., Hinsley W., Okell L.C., van Elsland S., Thompson H., Verity R., Volz E., Wang H., Wang Y., Walker P.G., Walters C., Winskill P., Whittaker C., Donnelly C.A., Riley S., Ghani A.C. Imperial College; 2020. Impact of Non-Pharmaceutical Interventions (Npis) to Reduce COVID-19 Mortality and Healthcare Demand: Technical report. https://www.gov.uk/government/publications/impact-of-non-pharmaceutical-interventions-npis-to-reduce-covid-19-mortality-and-healthcare-demand-16-march-2020. [Google Scholar]
- 48.Robert Koch Institute N.M. Robert Koch Institut; 2020. Coronavirus disease 2019 - daily situation report of the Robert Koch Institute. https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Situationsberichte/ [Google Scholar]
- 49.Dreher M., Kersten A., Bickenbach J., Balfanz P., Hartmann B., Cornelissen C., Daher A., Stöhr R., Kleines M., Lemmen S.W., et al. The characteristics of 50 hospitalized COVID-19 patients with and without ARDS. Dtsch. Ärzteblatt Intl. 2020;117(10):271. doi: 10.3238/arztebl.2020.0271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Khalili M., Karamouzian M., Nasiri N., Javadi S., Mirzazadeh A., Sharifi H. Epidemiological characteristics of COVID-19: a systematic review and meta-analysis. Epidemiol. Infect. 2020;148 doi: 10.1017/S0950268820001430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Huang C., Wang Y., Li X., Ren L., Zhao J., Hu Y., Zhang L., Fan G., Xu J., Gu X., Cheng Z., Yu T., Xia J., Wei Y., Wu W., Xie X., Yin W., Li H., Liu M., Xiao Y., Gao H., Guo L., Xie J., Wang G., Jiang R., Gao Z., Jin Q., Wang J., Cao B. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet (London, England) 2020;395(10223):497–506. doi: 10.1016/S0140-6736(20)30183-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Wölfel R., Corman V.M., Guggemos W., Seilmaier M., Zange S., Müller M.A., Niemeyer D., Jones T.C., Vollmar P., Rothe C., Hoelscher M., Bleicker T., Brünink S., Schneider J., Ehmann R., Zwirglmaier K., Drosten C., Wendtner C. Virological assessment of hospitalized patients with COVID-2019. Nature. 2020;581(7809):465–469. doi: 10.1038/s41586-020-2196-x. [DOI] [PubMed] [Google Scholar]
- 53.Wang D., Hu B., Hu C., Zhu F., Liu X., Zhang J., Wang B., Xiang H., Cheng Z., Xiong Y., et al. Clinical characteristics of 138 hospitalized patients with 2019 novel coronavirus–infected pneumonia in Wuhan, China. JAMA. 2020;323(11):1061–1069. doi: 10.1001/jama.2020.1585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Karagiannidis C., Mostert C., Hentschker C., Voshaar T., Malzahn J., Schillinger G., Klauber J., Janssens U., Marx G., Weber-Carstens S., Kluge S., Pfeifer M., Grabenhenrich L., Welte T., Busse R. Case characteristics, resource use, and outcomes of 10 021 patients with COVID-19 admitted to 920 German hospitals: an observational study. Lancet Respiratory Med. 2020;8(9):853–862. doi: 10.1016/S2213-2600(20)30316-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Armstrong R.A., Kane A.D., Cook T.M. Outcomes from intensive care in patients with COVID-19: a systematic review and meta-analysis of observational studies. Anaesthesia. 2020;75(10):1340–1349. doi: 10.1111/anae.15201. [DOI] [PubMed] [Google Scholar]
- 56.World Health Organization R.A. 2020. Report of the WHO-China joint mission on coronavirus disease 2019 (COVID-19) https://www.who.int/publications-detail-redirect/report-of-the-who-china-joint-mission-on-coronavirus-disease-2019-(covid-19) [Google Scholar]
- 57.Fehlberg E. National aeronautics and space administration; 1969. Low-Order Classical Runge-Kutta Formulas with Stepsize Control and their Application to Some Heat Transfer Problems, vol. 315. [Google Scholar]
- 58.Institut R.K. 2020. RKI Covid-19 Germany. https://experience.arcgis.com/experience/478220a4c454480e823b17327b2bf1d4. [Google Scholar]
- 59.Brockmann D., Helbing D. The hidden geometry of complex, network-driven contagion phenomena. Science. 2013;342(6164):1337–1342. doi: 10.1126/science.1245200. arXiv:https://science.sciencemag.org/content/342/6164/1337.full.pdf, https://science.sciencemag.org/content/342/6164/1337. [DOI] [PubMed] [Google Scholar]
- 60.Jurdak R., Zhao K., Liu J., AbouJaoude M., Cameron M., Newth D. Understanding human mobility from Twitter. PLoS One. 2015;10(7) doi: 10.1371/journal.pone.0131469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.McNeill G., Bright J., Hale S.A. Estimating local commuting patterns from geolocated Twitter data. EPJ Data Sci. 2017;6(1):1–16. doi: 10.1140/epjds/s13688-017-0120-x. [DOI] [Google Scholar]
- 62.Twitter G. 2020. Twitter docs. https://developer.twitter.com/ [Google Scholar]
- 63.Glass R.J., Glass L.M., Beyeler W.E., Min H.J. Targeted social distancing designs for pandemic influenza. Emerg. Infect. Diseases. 2006;12(11):1671–1681. doi: 10.3201/eid1211.060255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.GOV.UK R.J. Prime minister’s statement on coronavirus (COVID-19): 23 march 2020. GOV.UK. 2020 https://www.gov.uk/government/speeches/pm-address-to-the-nation-on-coronavirus-23-march-2020. [Google Scholar]
- 65.Klepac P., Kucharski A.J., Conlan A.J., Kissler S., Tang M., Fry H., Gog J.R. Contacts in context: large-scale setting-specific social mixing matrices from the BBC Pandemic project. MedRxiv. 2020 doi: 10.1101/2020.02.16.20023754. 2020.02.16.20023754. [DOI] [Google Scholar]
- 66.Christian Drosten P. NDR Info Podcast Coronavirus-Update; 2020. Coronavirus-update: Harter lockdown jetzt? https://www.ndr.de/nachrichten/info/68-Coronavirus-Update-Harter-Lockdown-jetzt,podcastcoronavirus272.html. [Google Scholar]
- 67.UNESCO P. 2020. Framework for reopening schools. https://unesdoc.unesco.org/ark:/48223/pf0000373348. [Google Scholar]
- 68.Sunjaya A.F., Sunjaya A.P. Pooled testing for expanding COVID-19 mass surveillance. Disaster Med. Public Health Preparedness. 2020;14(3):e42–e43. doi: 10.1017/dmp.2020.246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Bhagat R.K., Wykes M.S.D., Dalziel S.B., Linden P.F. Effects of ventilation on the indoor spread of COVID-19. J. Fluid Mech. 2020;903 doi: 10.1017/jfm.2020.720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Liang M., Gao L., Cheng C., Zhou Q., Uy J.P., Heiner K., Sun C. Efficacy of face mask in preventing respiratory virus transmission: A systematic review and meta-analysis. Travel Med. Infect. Dis. 2020;36 doi: 10.1016/j.tmaid.2020.101751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Reiner R.C., Barber R.M., Collins J.K., Zheng P., Adolph C., Albright J., Antony C.M., Aravkin A.Y., Bachmeier S.D., Bang-Jensen B., Bannick M.S., Bloom S., Carter A., Castro E., Causey K., Chakrabarti S., Charlson F.J., Cogen R.M., Combs E., Dai X., Dangel W.J., Earl L., Ewald S.B., Ezalarab M., Ferrari A.J., Flaxman A., Frostad J.J., Fullman N., Gakidou E., Gallagher J., Glenn S.D., Goosmann E.A., He J., Henry N.J., Hulland E.N., Hurst B., Johanns C., Kendrick P.J., Khemani A., Larson S.L., Lazzar-Atwood A., LeGrand K.E., Lescinsky H., Lindstrom A., Linebarger E., Lozano R., Ma R., Mansson J., Magistro B., Herrera A.M.M., Marczak L.B., Miller-Petrie M.K., Mokdad A.H., Morgan J.D., Naik P., Odell C.M., O’Halloran J.K., Osgood-Zimmerman A.E., Ostroff S.M., Pasovic M., Penberthy L., Phipps G., Pigott D.M., Pollock I., Ramshaw R.E., Redford S.B., Reinke G., Rolfe S., Santomauro D.F., Shackleton J.R., Shaw D.H., Sheena B.S., Sholokhov A., Sorensen R.J.D., Sparks G., Spurlock E.E., Subart M.L., Syailendrawati R., Torre A.E., Troeger C.E., Vos T., Watson A., Watson S., Wiens K.E., Woyczynski L., Xu L., Zhang J., Hay S.I., Lim S.S., Murray C.J.L., IHME COVID-19 Forecasting Team Modeling COVID-19 scenarios for the United States. Nat. Med. 2020:1–12. doi: 10.1038/s41591-020-1132-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Cheng V.C.-C., Wong S.-C., Chuang V.W.-M., So S.Y.-C., Chen J.H.-K., Sridhar S., To K.K.-W., Chan J.F.-W., Hung I.F.-N., Ho P.-L., Yuen K.-Y. The role of community-wide wearing of face mask for control of coronavirus disease 2019 (COVID-19) epidemic due to SARS-CoV-2. J. Infect. 2020;81(1):107–114. doi: 10.1016/j.jinf.2020.04.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Betsch C., Korn L., Felgendreff L., Eitze S., Schmid P., Sprengholz P., Wieler L., Schmich P., Stollorz V., Ramharter M., Bosnjak M., Omer S.B., Thaiss H., De Bock F., von Rüden U., Schmid-Küpke N.K., Scholz S. COSMO Konsortium; 2020. COVID-19 Snapshot Monitoring (COSMO Germany) - Wave 23: Technical report. https://projekte.uni-erfurt.de/cosmo2020/web/summary/23/ [Google Scholar]
- 74.LEOSS C. 2020. Lean open survey on SARS-CoV-2 infected patients. https://leoss.net/ [Google Scholar]
- 75.Jakob C.E., Borgmann S., Duygu F., Behrends U., Hower M., Merle U., Friedrichs A., Tometten L., Hanses F., Jung N., et al. First results of the L̈ean European Open Survey on SARS-CoV-2-Infected Patients (LEOSS) Infection. 2020:1–11. doi: 10.1007/s15010-020-01499-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Chen B., Liang H., Yuan X., Hu Y., Xu M., Zhao Y., Zhang B., Tian F., Zhu X. Roles of meteorological conditions in COVID-19 transmission on a worldwide scale. MedRxiv. 2020 doi: 10.1101/2020.03.16.20037168. 2020.03.16.20037168. [DOI] [Google Scholar]
- 77.Buonanno G., Stabile L., Morawska L. Estimation of airborne viral emission: Quanta emission rate of SARS-CoV-2 for infection risk assessment. Environ. Int. 2020;141 doi: 10.1016/j.envint.2020.105794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Buonanno G., Morawska L., Stabile L. Quantitative assessment of the risk of airborne transmission of SARS-CoV-2 infection: Prospective and retrospective applications. Environ. Int. 2020;145 doi: 10.1016/j.envint.2020.106112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Liu X., Huang J., Li C., Zhao Y., Wang D., Huang Z., Yang K. The role of seasonality in the spread of COVID-19 pandemic. Environ. Res. 2021;195 doi: 10.1016/j.envres.2021.110874. https://www.sciencedirect.com/science/article/pii/S0013935121001687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Bauer S., Contreras S., Dehning J., Linden M., Iftekhar E., Mohr S.B., Olivera-Nappa A., Priesemann V. 2021. Relaxing restrictions at the pace of vaccination increases freedom and guards against further COVID-19 waves in Europe. ArXiv, arXiv:2103.06228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Robert Koch Institut S. Robert Koch Institut; 2020. Nationale Teststrategie - wer wird in Deutschland auf das Vorliegen einer SARS-CoV-2 Infektion getestet?: Technical report. https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Teststrategie/Nat-Teststrat.html?nn=13490888. [Google Scholar]
- 82.Contreras S., Dehning J., Loidolt M., Spitzner F.P., Urrea-Quintero J.H., Mohr S.B., Wilczek M., Zierenberg J., Wibral M., Priesemann V. 2020. The challenges of containing SARS-CoV-2 via test-trace-and-isolate. arXiv:2009.05732 [Q-Bio] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Streeck H., Schulte B., Kuemmerer B., Richter E., Hoeller T., Fuhrmann C., Bartok E., Dolscheid R., Berger M., Wessendorf L., Eschbach-Bludau M., Kellings A., Schwaiger A., Coenen M., Hoffmann P., Noethen M., Eis-Huebinger A.-M., Exner M., Schmithausen R., Schmid M., Hartmann G. Infection fatality rate of SARS-CoV-2 infection in a german community with a super-spreading event. MedRxiv. 2020 doi: 10.1101/2020.05.04.20090076. 2020.05.04.20090076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.2020. Deutsche Interdisziplinäre Vereinigung für Intensiv- und Notfallmedizin (DIVI), DIVI Intensivregister Tagesreport. https://www.divi.de/divi-intensivregister-tagesreport-archiv. [Google Scholar]
- 85.Bundesregierung H. Bundesregierung; 2020. Beschluss zur Telefonschaltkonferenz der Bundeskanzlerin am 6. Mai 2020. https://www.bundesregierung.de/resource/blob/975226/1750986/fc61b6eb1fc1d398d66cfea79b565129/2020-05-06-mpk-beschluss-data.pdf. [Google Scholar]
- 86.Bundesregierung H. Bundesregierung; 2020. Beschluss zur Besprechung der Bundeskanzlerin am 17. Juni 2020. https://www.bundeskanzlerin.de/resource/blob/656734/1761548/94bdb647e1b03200d8430ee22e504ea9/2020-06-17-infektionen-data.pdf. [Google Scholar]
- 87.Bundesregierung H. Bundesregierung; 2020. Beschluss zur Videoschaltkonferenz der Bundeskanzlerin am 29. September 2020. https://www.bundesregierung.de/resource/blob/975226/1792238/bbe262252712bf09bbb85f93effa9b15/2020-08-29-beschluss-mpk-data.pdf. [Google Scholar]
- 88.Bundesregierung H. Bundesregierung; 2020. Beschluss zur Videokonferenz der Bundeskanzlerin am 28. Oktober 2020. https://www.bundesregierung.de/resource/blob/975232/1805024/5353edede6c0125ebe5b5166504dfd79/2020-10-28-mpk-beschluss-corona-data.pdf. [Google Scholar]
- 89.Bundesregierung H. Bundesregierung; 2020. Beschluss zur Telefonkonferenz der Bundeskanzlerin am 13. Dezember 2020. https://www.bundesregierung.de/resource/blob/975226/1827366/69441fb68435a7199b3d3a89bff2c0e6/2020-12-13-beschluss-mpk-data.pdf. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Estimation of age-resolved disease parameters and inter-regional mobility from official sources and social media.