Accelerated MR spectroscopic imaging—a review of current and emerging techniques

Wolfgang Bogner; Ricardo Otazo; Anke Henning

doi:10.1002/nbm.4314

. 2020 May 12;34(5):e4314. doi: 10.1002/nbm.4314

Accelerated MR spectroscopic imaging—a review of current and emerging techniques

Wolfgang Bogner ^1,^✉, Ricardo Otazo ², Anke Henning ^3,⁴

PMCID: PMC8244067 PMID: 32399974

Abstract

Over more than 30 years in vivo MR spectroscopic imaging (MRSI) has undergone an enormous evolution from theoretical concepts in the early 1980s to the robust imaging technique that it is today. The development of both fast and efficient sampling and reconstruction techniques has played a fundamental role in this process. State‐of‐the‐art MRSI has grown from a slow purely phase‐encoded acquisition technique to a method that today combines the benefits of different acceleration techniques. These include shortening of repetition times, spatial‐spectral encoding, undersampling of k‐space and time domain, and use of spatial‐spectral prior knowledge in the reconstruction. In this way in vivo MRSI has considerably advanced in terms of spatial coverage, spatial resolution, acquisition speed, artifact suppression, number of detectable metabolites and quantification precision. Acceleration not only has been the enabling factor in high‐resolution whole‐brain ¹H‐MRSI, but today is also common in non‐proton MRSI (³¹P, ²H and ¹³C) and applied in many different organs. In this process, MRSI techniques had to constantly adapt, but have also benefitted from the significant increase of magnetic field strength boosting the signal‐to‐noise ratio along with high gradient fidelity and high‐density receive arrays. In combination with recent trends in image reconstruction and much improved computation power, these advances led to a number of novel developments with respect to MRSI acceleration. Today MRSI allows for non‐invasive and non‐ionizing mapping of the spatial distribution of various metabolites’ tissue concentrations in animals or humans, is applied for clinical diagnostics and has been established as an important tool for neuro‐scientific and metabolism research. This review highlights the developments of the last five years and puts them into the context of earlier MRSI acceleration techniques. In addition to ¹H‐MRSI it also includes other relevant nuclei and is not limited to certain body regions or specific applications.

Keywords: acceleration, acquisition, compressed sensing, MR spectroscopic imaging, parallel imaging, reconstruction, spatial‐spectral encoding, undersampling

This review summarizes the progress in fast MR spectroscopic imaging (MRSI) of the last five years and puts it into the context of earlier MRSI acceleration techniques. It highlights emerging techniques for time‐efficient sampling of MRSI data including repetition time reduction, spatial‐spectral encoding, k‐space undersampling, and use of spatial‐spectral prior knowledge. In addition to ¹H‐MRSI it also includes other relevant nuclei and is not limited to certain body regions or specific applications.

graphic file with name NBM-34-e4314-g004.jpg

Abbreviations

B₀: static magnetic field strength
B₁⁺: transmit RF field
CAIPIRINHA: controlled aliasing in parallel imaging results in higher acceleration
CRT: concentric ring trajectory
CS: compressed sensing
CSDE: chemical shift displacement error
EPI: echo planar imaging
EPSI: echo‐planar spectroscopic imaging
FID: free induction decay
FIDLOVS: FID acquisition localized by outer volume suppression
GRAPPA: generalized autocalibrating partially parallel acquisition
GSLIM: generalized series approach to MR spectroscopic imaging
IDEAL: iterative decomposition of water and fat with echo asymmetry and least‐squares estimation
LASER: localization by adiabatic selective refocusing
MRSI: MR spectroscopic imaging
OVS: outer volume suppression
PEPSI: proton EPSI
PI: parallel imaging
PRESS: point resolved spectroscopy
SAR: specific absorption rate
SBW: spectral bandwidth
SE: spin echo
SENSE: sensitivity encoding
SLAM: spectroscopy with linear algebraic modeling
SLIM: spectral localization by imaging
SLOOP: spectral localization with optimal pointspread function;
SMS: simultaneous multi‐slice
SNR: signal‐to‐noise ratio
SNR/t: SNR per unit time
SPICE: spectroscopic imaging by exploiting spatiospectral correlation
SRF: spatial response function
SSE: spatial‐spectral encoding
SSFP: steady‐state free precession
T_E: echo time
T_R: repetition time
UHF: ultra‐high field

1. INTRODUCTION

Shortly after the introduction of in vivo MRI and non‐localized in vivo MRS, in vivo MR spectroscopic imaging (MRSI) was demonstrated in the early 1980s. Two distinct acquisition methods were suggested: (i) “NMR chemical shift imaging in three dimensions” in 1982 by Brown et al. ¹ and “Spatially resolved high‐resolution spectroscopy by 4‐dimensional NMR” by Maudsley et al. ² in 1983 as well as (ii) “Spatial mapping of the chemical shift in NMR” in 1984 by Mansfield. ³ While (i) corresponds to classical phase‐encoded and thus non‐accelerated MRSI, (ii) represents the very first description of the most popular spatial‐spectral MRSI acceleration method, echo‐planar spectroscopic imaging (EPSI). ⁴ In these early days hardware limitations such as gradient strength and fidelity as well as static magnetic field strength (B ₀) and homogeneity hindered the translation of these theoretical concepts into the excellent results that we can obtain today. However, during the last 30 years in vivo MRSI has undergone an enormous evolution in terms of spatial coverage, spatial resolution, acquisition speed, artifact suppression, number of detectable metabolites, and quantification accuracy and precision. Today it allows for non‐invasive and non‐ionizing whole‐organ (e.g., brain) mapping of various metabolites’ tissue concentrations in animals and humans (e.g., up to 12 brain metabolites ⁵ and nine macromolecular compounds ⁶ ), up to 300 times faster than conventional phase‐encoded ¹H‐MRSI. ⁷ While mainly conventional point resolved spectroscopy (PRESS)‐localized Cartesian‐sampled MRSI is currently applied for clinical diagnostics, ⁸ basic and advanced MRSI protocols have been established as important tools for neuro‐scientific and metabolism research. ⁸

Due to the need to encode the chemical shift along with spatial information, classical MRSI utilizes phase encoding along all directions, which is intrinsically slow. Another complication is the very low signal intensity of metabolites. In comparison to ¹H‐MRI of tissue water, ¹H‐MRSI of tissue metabolites is about 10 000 times less sensitive due to the concentration difference between water and metabolites. In addition, abundant water and fat signals lead to much stricter needs to control related artifacts. MRSI of other nuclei such as ³¹P, ²H or ¹³C is yet another order of magnitude less sensitive and lacks the possibility to use anatomical images as reference and to generate prior knowledge, which further restricts the acceleration options. Hyperpolarized ¹³C‐MRSI has sufficiently high signal‐to‐noise ratio (SNR) and only a few metabolite peaks, but suffers from acquisition time restrictions. Thus, hyperpolarized ¹³C‐MRSI has benefitted particularly from the development of fast MRSI encoding techniques in the past, achieving nowadays time resolutions needed for assessing real‐time metabolic fluxes in clinical settings. ⁹

While the basic principles of ¹H‐MRI acceleration are applicable to ¹H‐ and non‐proton MRSI as well, they usually need substantial adaptation to encode chemical shift, work robustly in a low‐SNR regime and in the presence of strong nuisance signals (e.g., water, fat) or meet the scan time restrictions in hyperpolarized ¹³C‐MRSI.

There are four main principles for accelerating MRSI: (i) short repetition times (T _R), (ii) acquisition of multiple k‐space points per T _R, (iii) k‐space undersampling and (iv) data reconstruction using spectral or spatial prior knowledge. Reports on the short‐T _R principle range from moderately short T _R values to true steady‐state free precession (SSFP). The acquisition of multiple k‐space points per T _R can be accomplished by either multi‐spin‐echo sampling or more commonly spatial‐spectral encoding (SSE) including EPSI or non‐Cartesian k‐space trajectories. In a broad sense “k‐space undersampling” methods include widely available methods such as elliptical k‐space shuttering ¹⁰ or MRS pre‐localization (i.e., allowing field‐of‐view reduction with fewer required k‐space points). “Real” k‐space undersampling approaches include parallel imaging (PI), multi‐band acquisition, and compressed sensing (CS). Finally, there are reconstruction techniques that use prior knowledge from high‐resolution anatomical images and spectral priors, and combinations with low‐rank reconstruction. All these acceleration principles are complementary and can be combined. A detailed introduction of k‐space formalism and filtering is outside the scope of this review. We refer the interested reader to two excellent books that provide a general introduction, before continuing with the more specific sections detailed below. ¹⁰ , ¹¹

Related MRSI encoding methods have been reviewed by a number of previous review papers and book chapters ¹² , ¹³ , ¹⁴ , ¹⁵ , ¹⁶ that either cover mostly literature from before 2014 or have a limited coverage with respect to acceleration methods or applications. Recent progress in MRSI encoding has significantly benefitted from ultra‐high field (UHF) systems, high gradient fidelity and high‐density receive coil arrays. In addition, a number of dedicated acceleration methods for hyperpolarized ¹³C‐MRSI have been demonstrated. In combination with emerging trends in image reconstruction and much improved computation power, these advances led to a number of novel developments with respect to MRSI acceleration. Hence, this review highlights the developments of the last 5 years and puts them into the context of earlier techniques. In addition to ¹H‐MRSI it also includes other relevant nuclei and is not limited to certain body regions or specific applications. Thus, this review paper represents the most comprehensive and most up to date one of its kind.

2. SHORT T _R/T _E

The most straightforward way to speed up MRSI is by either shortening the T _R, ¹⁷ , ¹⁸ , ¹⁹ or acquiring multiple spin echoes (SEs) per T _R. ¹⁴ , ¹⁵ This approach has its roots in the early 2000s, when highly SNR‐efficient SSFP as well as turbo‐SE sequences were proposed for MRSI. ¹⁷ , ¹⁸ , ¹⁹ , ²⁰ , ²¹ These sequences benefit either from fast point‐by‐point sampling of the k‐space with short T _R, ¹⁷ , ¹⁸ , ¹⁹ or from sampling of multiple k‐space points per T _R in the case of multiple SEs ²⁰ , ²¹ (ie, their relative contribution is a function of the T ₁/T ₂ ratio and flip angles). Both methods restrict the acquisition time for the spectral readout to the inter‐pulse delay. Due to the resulting reduced spectral resolution, ²¹ , ²² SSFP‐MRSI was initially confined to well separated resonances (e.g., fat/water mapping, only the singlets of NAA, Cr and Cho in ¹H‐MRSI, or ³¹P/¹³C‐MRSI) ¹⁹ , ²³ , ²⁴ and animal studies (i.e., featuring faster encoding gradients and higher spectral resolution due to available high‐B ₀ MR scanners). ¹⁷ , ¹⁸ This changed when improved hardware became available also for human whole‐body MR systems and enabled the acquisition of true SSFP‐based ¹H‐MRSI (T _R < 200 ms) of the human brain with sufficiently high spatial and spectral resolution. ²⁵ , ²⁶ , ²⁷ Although SSFP‐based MRSI yields the highest possible SNR efficiency, major downsides include the low spectral resolution, limited water suppression, potential banding artifacts and strongly T ₁‐/T ₂‐weighted metabolite signals, which make metabolic maps highly qualitative without relaxation corrections, and interpretation of the exact neurochemical underpinnings in pathologies challenging. Recent implementations overcome problems with banding artifacts by using balanced SSFP with either a very narrow pass‐band frequency selective excitation and frequency sweeping ²⁸ or successive measurements with phase increments to achieve the spectral separation in a similar manner to the Dixon approach ²⁹

Albeit not as SNR efficient as SSFP‐MRSI, the lack of undesired T ₂‐weighting or J‐coupling effects has made pulse‐acquire or free induction decay (FID)‐MRSI sequences with Ernst angle excitation and gradient spoiling after each T _R (Figure 1) an increasingly popular alternative, not only for ³¹P‐MRSI ³⁰ , ³¹ , ³² , ³³ , ³⁴ and ¹³C‐MRSI, ²⁴ , ³⁵ , ³⁶ , ³⁷ , ³⁸ but also recently for ¹H‐MRSI. ⁵ , ³⁹ , ⁴⁰ , ⁴¹ , ⁴² The FIDLOVS (FID acquisition localized by outer volume suppression) sequence ⁴³ had still a fairly complicated design with a large number of outer volume suppression (OVS) pulses causing high specific absorption rate (SAR) demands at 7 T and consequently long T _R values, but it motivated simpler ¹H‐FID‐MRSI approaches that allowed for much shorter T _R values of a few hundred milliseconds by confining the sequence to water suppression and excitation pulses. ³⁹ , ⁴⁴ The T _R‐shortening of this type of sequence is only limited by a possible compromise in water suppression quality, T ₁‐weighting and spectral resolution (a side‐effect of reducing the FID sampling). Some implementations have even completely abandoned all suppression pulses and replaced these by retrospective nuisance removal. ⁴⁵ In particular at UHF ¹H‐FID‐MRSI overcomes critical limitations in SAR, chemical shift displacement error (CSDE), B ₁ ⁺‐inhomogeneity, T ₂‐weighting, J‐evolution and coverage of cortical regions in comparison with traditional MRSI. On the other hand, ¹H‐FID‐MRSI lacks high‐quality volume selection to reduce nuisance signals (e.g., extracranial lipids) and macromolecule signals are enhanced. While this makes accurate metabolite quantification challenging, it has enabled the high‐resolution mapping of macromolecules. ⁶ , ⁴⁶ , ⁴⁷ , ⁴⁸ Since then, FID‐MRSI acquisitions with short T _R values (~60 to 600 ms) have become an integral part of many UHF ¹H‐MRSI sequences at 7 T (References 41, 48, 49, 50, 51, 52, 53) and 9.4 T (References 5, 40, 54, 55, 56, 57) (Figure 2) and an increasing number of 3 T MRSI implementations. ⁵¹ , ⁵⁴ , ⁵⁸ FID‐MRSI is also the method of choice for ³¹P‐MRSI ³⁰ , ³¹ , ³² , ³³ , ³⁴ due to the fast T ₂ relaxation of most ³¹P‐MRS signals, and for ²H‐MRSI ⁵⁹ due to the absence of water and fat suppression modules. FID‐MRSI applications are so far limited mostly to the human brain but also for the investigation of skeletal muscles and ³¹P‐MRSI, ³⁰ , ⁴² where volume pre‐selection is secondary. First clinical examples have been demonstrated in patients with brain tumors, ⁷ , ³¹ , ⁴⁹ multiple sclerosis ⁷ , ⁵⁰ , ⁶⁰ and mild cognitive impairment. ⁶¹ , ⁶²

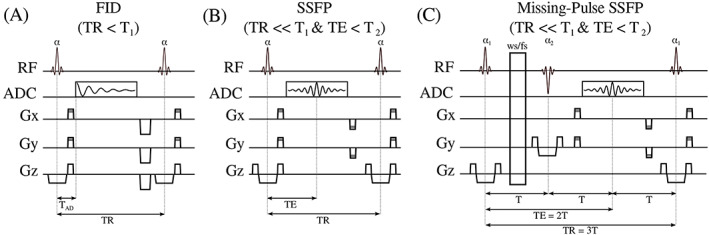
Comparison of different MRSI sequence types that make use of short T _R values for acceleration. A, FID‐MRSI sequences acquire an FID signal after an Ernst excitation pulse followed by a gradient spoiler to eliminate any remaining transverse magnetization. B, C, In contrast, SSFP‐MRSI sequences revert the phase‐encoding after signal sampling, so that the remaining transversal magnetization can be reused and the steady‐state condition can be established. Using this magnetization the next RF pulse creates an echo. This transversal magnetization continues to be refocused until the signal decays to zero. Therefore, each sampling interval collects the sum signal of multiple echoes, the relative contributions of which are determined by their T ₂. Because of the short T _R, the signal is additionally T ₁ weighted. The mix of T ₁/T ₂‐weighting is specific for each resonance (not metabolite) and depends also on the local excitation flip angle. C, As a more robust alternative missing‐pulse SSFP has been proposed to allow detection of complete SEs (eliminating the need for phasing, mitigating truncation artifacts and improving spectral resolution) and enabling the incorporation of improved spatial localization as well as water/fat suppression pulses. Courtesy of Philipp A. Moser

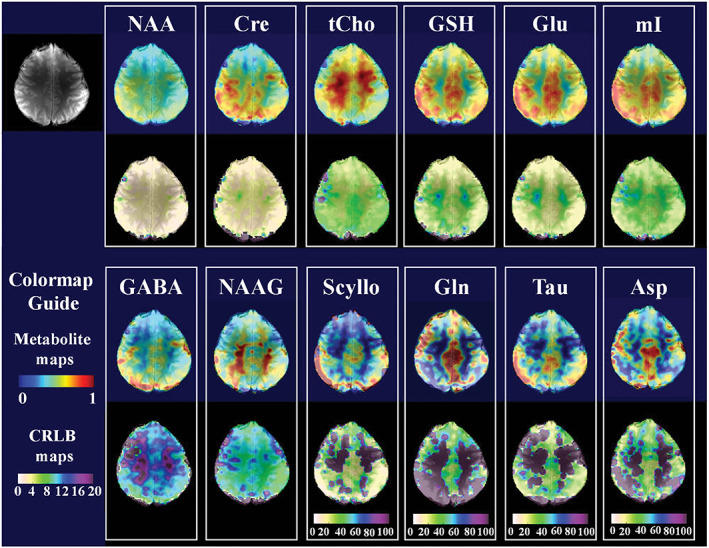
Ultra‐high resolution (128 × 128) metabolite maps for 12 different metabolites along with the anatomical reference scan (top left) obtained via FID‐MRSI at 9.4 T using a short T _R of 220 ms and acquisition delay of 1.5 ms. The CRLB maps are shown below the metabolite map in each box. Note the different scaling of the CRLB maps in the last four metabolites (Scyllo, Gln, Tau and Asp). Reproduced from the work of Nassirpour et al ⁵

In principle, also SE‐MRSI sequences can be used with shorter T _R, but this is uncommon, since SSFP‐MRSI is more efficient and especially the high bandwidth and SAR demands of refocusing pulses tailored for UHF (e.g., adiabatic RF pulses in particular) are a major constraint.

While the acquisition time saving associated with T _R reduction does not match that of common SSE approaches, the achievable acceleration factors are nevertheless good (~2‐ to 20‐fold) compared with typical undersampling techniques and come with only minor side effects (e.g., T ₁‐weighting, possible FID truncation), while benefitting among other advantages from a slight boost in SNR per unit time (SNR/t). ³⁹ Combinations with other acceleration methods, which all have the tendency to reduce SNR efficiency, are straightforward. Successful combinations have been shown with PI, ⁴¹ , ⁵¹ , ⁵² , ⁵⁵ , ⁵⁶ CS, ⁵⁷ SSE ⁶³ , ⁶⁴ or several approaches at once to enable high‐resolution rapid whole‐brain MRSI ⁷ , ⁶⁴ or dynamic 2D‐MRSI with high temporal resolution. ⁶⁵

3. SPATIAL‐SPECTRAL ENCODING

Even higher accelerations can be achieved using SSE. The basic principle of SSE was introduced by Mansfield ³ in 1984, but early implementations were limited by gradient hardware imperfections. ⁶⁶ , ⁶⁷ It took decades until SSE developed into the robust metabolic imaging tool that it is today. ⁶⁸ , ⁶⁹ , ⁷⁰ , ⁷¹

In contrast to phase‐encoded MRSI, where spatial and spectral encoding are strictly separated, SSE utilizes high‐slew‐rate gradient waveforms to sample spatial information (by sampling along k‐space trajectories) simultaneously with spectral information (by repeating the same trajectory a few hundred times per T _R) (Figure S1). This is possible since the encoding of the spectral dimension (sampling period in ms) is a slow process compared with the encoding of spatial dimensions (sampling period in μs). SSE enables highly efficient and about 25 to 170 times faster MRSI scans than pure phase‐encoding. ⁷² The SNR/t is similar to that of conventional phase‐encoding, provided that the most efficient sampling (e.g., ramp sampling for EPSI) is used. ⁷³ , ⁷⁴

SSE can employ a variety of different Cartesian or non‐Cartesian trajectories that have very different gradient requirements and k‐space densities (Figure 3), with EPSI ⁷⁵ and spiral‐based MRSI ⁷⁶ being the most prominent examples. However, gradient hardware limitations and the need for higher spectral bandwidth (SBW)/spatial resolution at higher B ₀, ⁷³ , ⁷⁷ , ⁷⁸ as well as the desire to reduce voxel bleeding by an improved spatial response function (SRF) (i.e., to mitigate extracranial lipid artifacts), have made alternative SSE strategies increasingly attractive ⁷⁹ , ⁸⁰ , ⁸¹ , ⁸² Overall, the use of SSE becomes challenging at UHF (i.e., the SNR efficiency suffers) since the maximum time permitted for one trajectory repetition (i.e., spectral dwelltime) is inverse proportional to the SBW, and trajectory repetitions become challenging for the higher spatial resolutions at UHF (Figure 4). Although temporal interleaving can somewhat alleviate this otherwise hard limit at the cost of measurement speed, the number of temporal interleaves is limited to three or less for ¹H‐MRSI, while it is freely adjustable for multi‐nuclear MRSI. ⁷ , ³⁰ , ⁶³ , ⁸³ The reason is that for more than three temporal interleaves high unsuppressed water signal lead to spectral aliasing artifacts in the spectral range of interest (e.g., between water and lipid signals), the intensity of which scales with temporal instabilities between temporal interleaves and cannot be easily removed. ¹⁵ A completely different approach is reduction of acquisition time using partition of the signal decay in spectroscopic imaging (RAPID‐SI), ⁸⁴ which is similar to an approach shown earlier by Cao et al for hyperpolarized ¹³C‐MRSI. ⁸⁵ Both speed up MRSI acquisition along a phase‐encoding direction approximately 2‐ to 16‐fold by separating the acquired FID into equidistant fractions via blipped phase‐encoding gradients (this resamples jumping from one k‐space point to the next during FID readout rather than moving along a continuous trajectory).

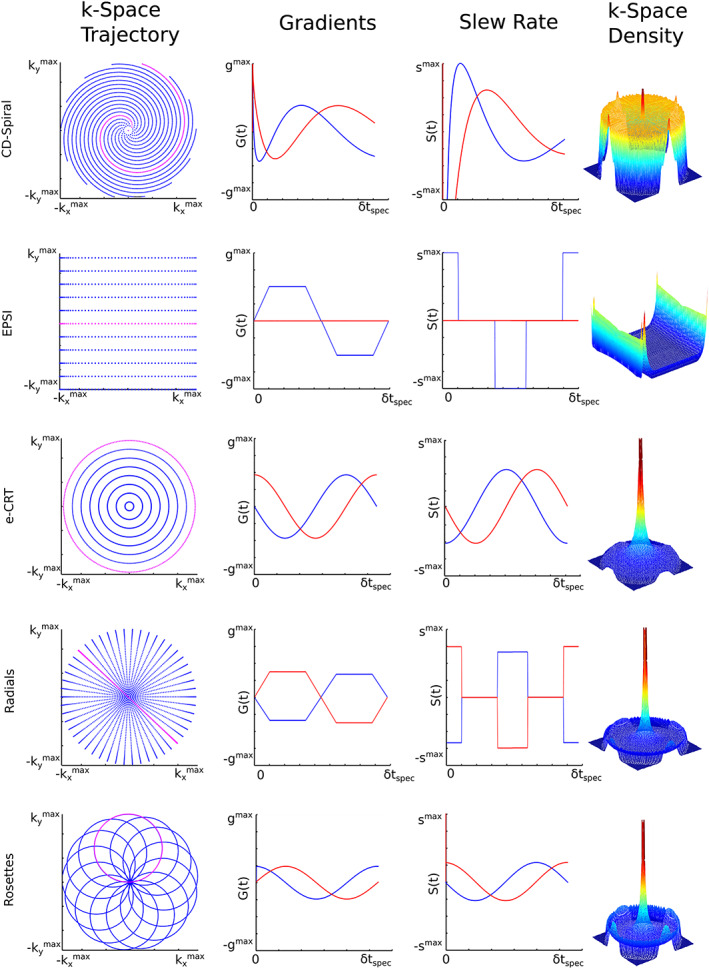
Qualitative side‐by‐side comparison of the most common SSE strategies (i.e., constant‐density spirals, symmetric EPSI, equidistant CRT, radial EPSI and rosettes) for encoding of a 2D k‐space (left column). In all cases a single k‐space trajectory, which is repeated several hundred times for a single T _R, is highlighted in pink while all remaining trajectories to fill the k‐space are displayed in blue. The time evolution of gradient strength and slew rate are displayed for x‐ and y‐gradients (blue and red, respectively) (middle columns). The achieved k‐space density as derived by simulations is illustrated by color‐coded surface plots. Courtesy of Lukas Hingerl

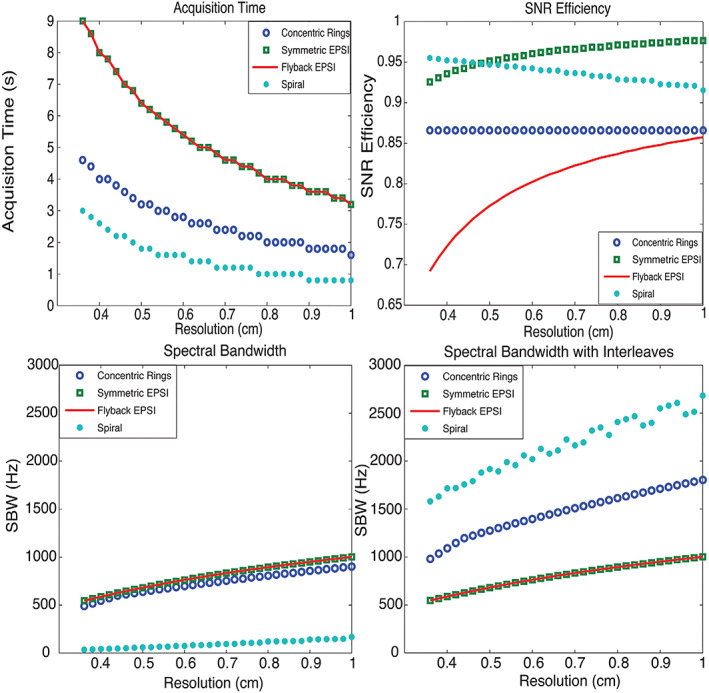
Comparison of concentric rings, EPSI and spiral spectroscopic imaging: top left, acquisition time; top right, SNR efficiency; bottom left, bottom right, SBW and SBW with spectral interleaves. CRT requires half of the total acquisition time compared with EPSI trajectories, offers about 87% SNR efficiency and provides much wider spectral bandwidth than flyback‐EPSI and symmetric EPSI. Although nominally spirals are the most efficient trajectories, offering the best acquisition time and SBW benefit while sacrificing the least SNR, they are limited by susceptibility to gradient infidelities. All designs assumed a gradient amplitude limit of 40 mT/m and maximum slew rate of 150 mT/m/ms. Top right, SNR efficiency of different trajectories for various resolutions. The SNR loss for flyback EPSI is mostly due to its low duty cycle. The finer the resolution is, the lower the duty cycle will be, and SNR efficiency decreases as the flyback portion requires more time. Although the duty cycle for symmetric EPSI with ramp sampling is 100%, the non‐uniform ramp sampling reduces SNR efficiency. For the constant slew rate spiral trajectories, SNR efficiency decreases as the resolution becomes coarser with a fixed FOV, since there is proportionally less outer k‐space sampling where spirals are more uniform. Non‐uniformity causes most of the SNR loss of spirals, while duty cycle results in a smaller fraction of the loss. Benefitting from the design of constant slew rate, the spiral trajectories provide even better SNR efficiency than flyback EPSI and CRT. CRT offers a constant SNR efficiency, which is better than flyback EPSI with the chosen prescriptions. The loss of SNR efficiency for CRT is caused by the non‐uniformity. Note that the SNR efficiency depends on the targeted k‐space density. Here a constant density k‐space was targeted. Given the same traversing velocity, the achieved SBWs for EPSI, CRT and spirals are decreasing (bottom left) without interleaves. To exploit the maximum SBW, both symmetric EPSI and flyback EPSI result in the same waveform, thus achieving the same SBW. They are only slightly better than CRT, since flyback EPSI requires flyback time and symmetric EPSI does not critically exploit the whole SBW. However, CRT and spiral trajectories are more scan‐time efficient compared with EPSI. If we take advantage of scan‐time efficiency by applying temporal interleaves, we can increase SBW. Bottom right, SBW of all trajectories was computed by accounting for the temporal interleaves constrained for the same total acquisition time. For this tradeoff, spirals offer the best SBW, while CRT's SBW is doubled compared with EPSI. The non‐monotonicity of the spiral trajectory SBW with respect to resolution in this analysis is due to using an integer number of interleaves. Reproduced from the work of Jiang et al. ⁸⁶

Since EPSI is in principle equivalent to multi‐echo MRI with extremely short echo spacing (i.e., spectral dwelltime in MRSI), Dixon‐based spectral separation can be considered an extreme case of SSE with very few (i.e., originally two), sometimes non‐equidistantly distributed, echoes. To quantify a few well‐separated spectral resonances (e.g., water and fat ⁸⁷ , ⁸⁸ or four resonances in ¹³C‐MRSI ⁸⁹ ), only a few echoes (i.e., EPSI lines or any other SSE trajectories) must be acquired. The basic idea is to exploit the difference in precession frequency between two or multiple resonances. For instance, to separate fat and water, two images with slightly different T _E values are acquired. For the first image the T _E is adjusted to show fat and water signals in phase, while the T _E for the second image is adjusted by a few milliseconds to have fat and water signals out of phase. Adding the two images leads to a water image and subtracting the two images to a fat image. The Dixon method and the related iterative decomposition of water and fat with echo asymmetry and least‐squares estimation (IDEAL) can be extended to the separation of multiple resonances by using multiple spin or gradient echoes. IDEAL has been combined with spiral and echo planar imaging (EPI) readouts as well as k‐t undersampling approaches for hyperpolarized ¹³C‐MRSI ⁸⁹ , ⁹⁰ , ⁹¹ , ⁹² , ⁹³ (the processing pipeline is shown in Figure 5) and ¹²⁹Xe‐MRSI. ⁹⁴

Diagram of the ¹³C data reconstruction steps with intermediate results. The IDEAL reconstruction transforms the seven echoes per dynamic into the five metabolites (pyruvate, lactate, bicarbonate, pyruvate hydrate and alanine) per dynamic. EPI ghost correction is performed using additionally acquired ¹H data. k‐t principal component analysis (k‐t PCA) or k‐t CS (k‐t SPARSE) is then applied and the data are transformed to image space. A surface coil sensitivity correction map acquired from a ¹³C‐urea phantom is applied to compensate for the reduced sensitivity in the inferior segment of the heart. Finally, the data are zero‐filled. The example images show data from a k‐t PCA scan and the lactate signal of a single dynamic. Reproduced from the work of Wespi et al ⁹³

Apart from the maximum possible acceleration factor and SNR efficiency, a main criterion for choosing the right SSE technique is the limitations imposed by the available gradient system. The targeted spatial resolutions are much lower in MRSI than in MRI. Hence, maximum gradient amplitudes do not impose any limitations, but a high gradient slew rate is critical to allow gradient trajectories to remain short and be repeated rapidly. This is necessary to cover the target spectral range (increasing with B ₀) and traverse a sufficiently large k‐space (otherwise limiting spatial resolution). ⁶³ The extent to which different SSE trajectories are susceptible to or induce gradient imperfections varies substantially. Generally, k‐space trajectory errors are more problematic for spirals, rosettes and radial EPSI than for other SSE alternatives ⁶⁷ , ⁸⁶ , ⁹⁵ , ⁹⁶ (see below and Table 1), but these deviations between actual and real trajectories can be measured and considered during MRSI reconstruction. ⁶⁷

TABLE 1.

List of major MRSI acceleration methods (without combinations). Methods listed in different categories can be combined. We differentiate three ranges of acceleration (~1.5 to 8, low; ~8 to 20, moderate; 20 and above, high) and encoding methods that additionally increase (SNR/t gain) or decrease (SNR/t loss) SNR per time efficiency as compared against a current clinical standard ¹H‐MRSI protocol (Cartesian sampling, T _R = 1500 ms, T _E = 30 ms), respectively

3.1. Cartesian SSE

Cartesian SSE techniques acquire one spatial dimension and the spectral dimension simultaneously in a single readout via a series of periodically inverted readout gradients. Each semi‐period encodes one line in k‐space and the progression of gradient pulses encodes the spectral dimension. Symmetric‐EPSI and flyback‐EPSI are most commonly used (Figure S1).

3.1.1. EPSI

The original EPSI technique, also known as symmetric EPSI or proton EPSI (PEPSI), uses a series of alternating positive and negative trapezoidal gradients to produce a zig‐zag trajectory in k _x‐t space. ³ Ideally, the acquired k _x‐t data can be sorted into a matrix after phase correction of the negative echo data and reconstructed using Fourier transform. In practice, the positive and negative echo data are not equivalent due to asymmetries in gradient switching and eddy currents, and direct Fourier transform reconstruction of combined positive and negative echoes would lead to ghosting artifacts in the spectral domain. One way to avoid spectral ghosting is to perform a separate Fourier transform for positive and negative echoes followed by combination after phase correction, at the expense of halving the SBW. ⁷⁵ If data are acquired during the gradient ramps, there is only a small penalty in SNR/t compared with phase‐encoded MRSI, despite the significant acceleration (e.g., 32‐fold). ⁷³ , ⁷⁴ Figure 6 shows PEPSI results in the human brain. Alternatively, shift correction between positive and negative echo data can be performed using an interlaced Fourier transform approach to exploit the full SBW. ⁹⁷ Center‐out EPSI readout, where the upper half of k‐space is acquired during the first segment and the lower half of k‐space during the second segment, has also been proposed to passively prevent formation of ghosting artifacts and optimize SBW, by computing the shift correction between positive and negative echo data directly from the differences between upper‐half and lower‐half k‐space data. ⁹⁸

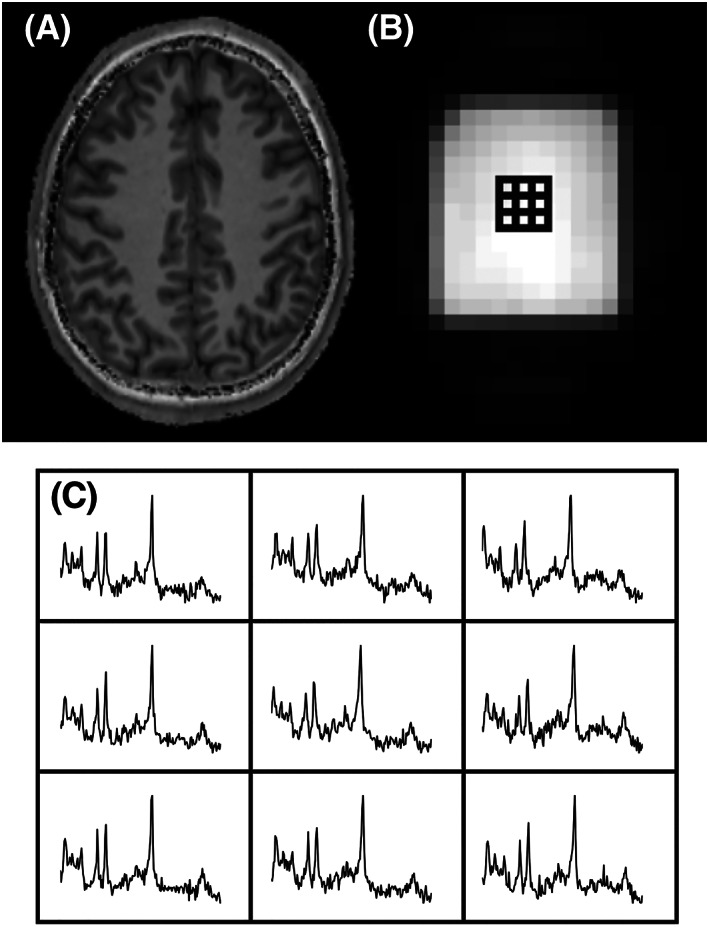
2D‐PEPSI in the human brain at 3 T using T _R 2 s, spatial matrix 32 × 32, scan time 64 s. The anatomical reference image (A) and an additional water image (B; from a separate non‐water‐suppressed acquisition) show the location of the multi‐voxel spectra (C)

EPSI implementations have been shown for various pre‐localization schemes including PRESS, ⁷⁹ semi‐LASER (localization by adiabatic selective refocusing), ⁷⁸ whole slice with OVS ⁹⁹ and slab‐selection. ¹⁰⁰

MRSI techniques that require multiple repetitions with different parameter settings benefit particularly from EPSI. This includes diffusion‐weighted MRSI, the first implementation of which was shown in 1995, ¹⁰¹ followed by more robust versions recently, ¹⁰² with some even enabling diffusion tensor imaging of metabolites. ¹⁰³ Combining MRSI with encoding of two frequency dimensions simultaneously (e.g., J‐resolved or correlation spectroscopy) is even more time consuming and has therefore been an active field of research. Correlated MRS (COSY)‐EPSI has been predominantly used to map muscle metabolism, ¹⁰⁴ , ¹⁰⁵ , ¹⁰⁶ , ¹⁰⁷ , ¹⁰⁸ while J‐resolved EPSI has been applied to prostate ¹⁰⁹ and investigations in the human brain. ¹¹⁰ , ¹¹¹ , ¹¹² , ¹¹³ , ¹¹⁴ Spectrally edited MRSI requires subtraction of one spectrum from another, which doubles the scan time and prohibits short T _R, and hence can be efficiently accelerated by EPSI. ¹¹⁵ Other less common applications include rapid temperature ¹¹⁶ and metabolite T ₂ mapping. ¹¹⁷

Unquestionably, the most common application of EPSI is to enable time‐efficient whole‐brain MRSI, ¹⁰⁰ which has reached a high level of sophistication and automation after many optimization steps. ¹¹⁸ , ¹¹⁹ It is used in clinical investigations for various brain disorders such as brain tumors, ¹²⁰ , ¹²¹ , ¹²² , ¹²³ amyotrophic lateral sclerosis, ¹²⁴ schizophrenia ¹²⁵ or dyslexia. ¹²⁶ Applications outside the brain, including MRSI of the breast, ¹²⁷ , ¹²⁸ liver ¹²⁹ and calf muscle, ¹³⁰ have been proposed as well.

3.1.2. Flyback‐EPSI and more

To reduce SBW limitations, the flyback‐EPSI technique uses only the positive gradient part for spatial encoding and short gradient pulses with maximum slew rate for refocusing. The flyback‐EPSI readout also mitigates eddy current effects and ghosting significantly, but at the loss of SNR due to gaps in data acquisition. ¹³¹ Other less common approaches to increase the SBW are temporal interleaving and repeating the acquisition with reversed readout gradients, which double both the SBW and the scan time. ⁷⁹ , ¹³² Another solution that doubles the SBW of EPSI without prolonging the scan time is coherent k‐t space EPSI. ⁸² , ¹³³ Finally, multi‐shot EPSI was proposed, which samples not only a single k‐space line along k _x, but a complete echo‐planar trajectory to cover a large fraction of the k _x‐k _y plane with gaps in k _y and time being filled up by the following shots, but this caused significant spectral aliasing artifacts and imposes SBW limitations. ¹³⁴ Flyback‐EPSI has been applied clinically in brain tumors, ¹³⁵ , ¹³⁶ prostate cancer ¹³⁷ and multi‐nuclear MRSI (i.e., hyperpolarized ¹³C‐MRSI ¹³⁸ and ³¹P‐MRSI ¹³⁹ of the calf muscle).

3.2. Non‐Cartesian SSE

Non‐Cartesian SSE techniques accelerate in two k‐space dimensions and the spectral dimension simultaneously with only a few exceptions. ¹⁴⁰ The most prominent examples are spirals, ⁷⁶ concentric ring trajectories (CRTs), ⁸⁰ rosettes ⁸¹ and radial EPSI. ⁹⁶ The most common reconstruction approach for non‐Cartesian trajectories is to perform a non‐uniform fast Fourier transform (NUFFT) in the spatial domain and conventional fast Fourier transform (FFT) along the temporal domain.

3.2.1. Spirals

Historically, the first non‐Cartesian SSE k‐space trajectory was the spiral. ⁷⁶ This was motivated by the early application of spirals in MRI and the fact that nominally constant‐density spirals are the most efficient trajectories, offering the best acquisition time and SBW benefit while sacrificing the least SNR, but they are also more susceptible to gradient infidelities than other SSE techniques, ⁸⁶ which requires corrections. ⁶⁷ For small matrix sizes and lower SBW (e.g at 1.5 T), spirals can acquire spectroscopic data in a single shot, but single‐shot approaches are usually not practical due to SBW limitations imposed by the time required to complete the spiral trajectory. In practice, spiral MRSI is, therefore achieved via spectral (Figure 7A) and spatial interleaves (Figure 7B) (i.e., acquiring only a fraction of the k‐space or FID, respectively, per T _R). ¹⁴¹

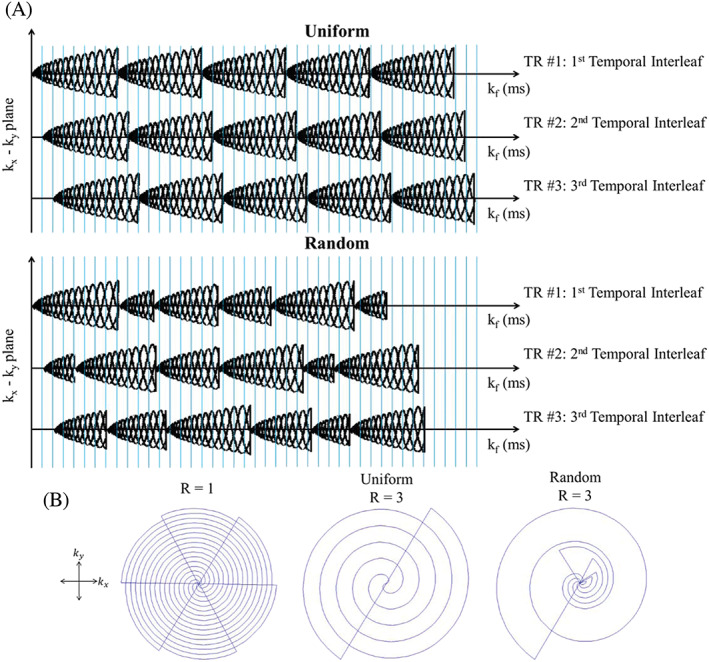
a: Two types of spiral‐based k‐space acquisition schemes illustrate the concept of spectral interleaves: Uniformly (top) and randomly (bottom) undersampled spiral k‐space acquisition schemes. The blue vertical lines represent the time at which a sample is acquired. b: The projections of possible k‐space trajectories onto the k_x‐k_y plane illustrate the concept of spatial (angular) interleaves. The projection from fully sampled (all six spatial interleaves), uniformly undersampled (R = 3, only two of six spatial interleaves), and randomly undersampled (R = 3) acquisition are shown from left to right, respectively. Reproduced from Chatnuntawech et al ¹⁴²

With these properties, spirals are ideal for application in hyperpolarized ¹³C studies, where speed is critical to minimize T ₁ relaxation‐related SNR losses, ³⁷ , ¹⁴³ , ¹⁴⁴ , ¹⁴⁵ , ¹⁴⁶ , ¹⁴⁷ but also more recently in dynamic ³¹P‐MRSI in muscles, ³⁰ , ¹⁴⁸ where a high temporal resolution is essential. Spiral SSE is also playing an increasingly important role in ¹H‐MRSI of the brain ⁷¹ , ¹⁴⁹ , ¹⁵⁰ , ¹⁵¹ , ¹⁵² , ¹⁵³ , ¹⁵⁴ , ¹⁵⁵ , ¹⁵⁶ , ¹⁵⁷ , ¹⁵⁸ and prostate ¹⁴¹ , ¹⁵⁹ , ¹⁶⁰ to reach clinically attractive scan times. At 3 T fully scanner‐integrated solutions for spiral MRSI ¹⁵⁴ , ¹⁵⁶ have recently facilitated a stronger clinical use for brain tumor, ¹⁵⁰ , ¹⁵² , ¹⁵³ neurodegenerative ¹⁵¹ , ¹⁶¹ and demyelinating disorders, ¹⁶¹ as well as psychiatric research. ¹⁴⁹ , ¹⁶³

Since the evolution of ¹H‐MRSI towards whole‐brain coverage ⁷⁶ , ¹⁶⁴ there is an increased need for mitigation of extra‐cranial lipid bleeding artifacts. This has led to the development of variable‐density spirals, which improve the SRF during the acquisition in an SNR‐efficient manner without the need for inefficient post‐processing k‐space filters. ¹⁴² , ¹⁶⁵ , ¹⁶⁶ , ¹⁶⁷ , ¹⁶⁸ This is frequently augmented by preprocessing to remove (lipid) artifacts even further. ¹⁶⁶ , ¹⁶⁷ , ¹⁶⁸ , ¹⁶⁹ , ¹⁷⁰

However, due to limitations imposed by common whole‐body gradients the efficiency of spirals suffers with increasing spatial resolution and SBW, which is typical for high‐field MRSI. ⁵ , ⁴¹ For SSE the same trajectory must be repeated several hundred times to sample an FID, but gradient slew rate limitations do not allow return to the k‐space center after each spiral sufficiently fast. All data acquired during such gradient rewinders (i.e., similar to flyback‐EPSI gradients) are unused, which lowers the SNR. ¹⁶ This makes “closed loop”‐trajectories without such a deadtime attractive for SSE. In‐out spirals feature such self‐rewinding properties, but they are only efficient for strong animal gradient systems, ¹⁷¹ , ¹⁷² not for whole‐body systems, where additional limitations on maximum SBW would be imposed.

3.2.2. Concentric rings

These problems have triggered the development of inherently closed SSE trajectories without deadtimes, which are not merely translations of existing MRI trajectories, but rather tailored for the needs of MRSI. CRTs are the best example of this. They were originally proposed for hyperpolarized ¹³C‐MRSI, ⁸⁰ , ⁸⁶ but were rapidly adapted for ¹H‐MRSI with high spatial resolution and SBW. ⁷ , ⁶³ , ⁶⁴ , ¹⁷³ , ¹⁷⁴ , ¹⁷⁵ , ¹⁷⁶ Via CRTs an N × N matrix resulting from a k _N × k _N k‐space is covered by k _N/2 equidistant rings, which makes CRT‐based SSE exactly twice as fast as EPSI (i.e., it requires k _N lines). For equidistant CRTs the acquired k‐space is inherently 1/k _r weighted, but the weighting can be optimized (e.g Hanning weighting) at the expense of reduced acceleration. ⁶³ , ¹⁷³ The constant‐angular‐velocity properties of CRTs make them robust to gradient timing imperfections and eddy current delays, ⁸⁶ and PI reconstruction is considerably simplified. ⁶⁴ A unique feature of CRTs is that scan time/SNR efficiency can be further improved by acquiring a variable number of temporal interleaves (one temporal interleave/circumnavigation is sufficient in the k‐space center, while in the k‐space periphery gradient slew rate limits demand two or three temporal interleaves). ⁷ This makes high‐resolution whole‐brain ¹H‐MRSI clinically feasible even at UHF (Figure 8).

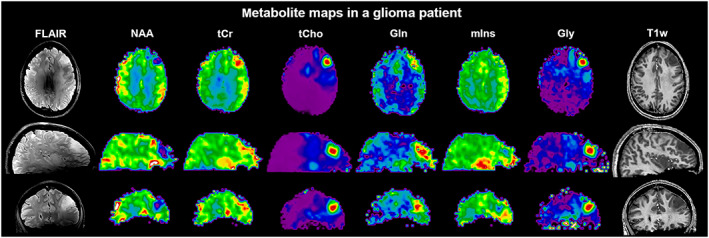
Sample maps of six major metabolites obtained in a brain tumor patient (30‐year‐old female; anaplastic astrocytoma grade 3 with suspected progression into glioblastoma) along with conventional T ₁‐ and T ₂‐weighted MRI displayed in transversal, sagittal and coronal planes. Whole‐brain FID‐MRSI data were acquired at 7 T in 15 min using a 3D CRT sequence with variable temporal interleaves, T _R 450 ms, acquisition delay 1.3 ms, spatial resolution 3.4 × 3.4 × 3.4 mm³, 64 × 64 × 39 matrix and SBW 2778 Hz. The T ₂‐weighted FLAIR image is strongly affected by B ₁ inhomogeneities, while this is less of a problem for gradient‐echo‐based images such as the T ₁‐weighted MRI and metabolic maps. Courtesy of Gilbert Hangel

3.2.3. Rosettes

Rosettes are the other class of closed non‐Cartesian SSE trajectories. ⁸¹ , ¹⁷⁷ , ¹⁷⁸ , ¹⁷⁹ A main feature of rosettes is their design flexibility, which allows tailoring of the trajectories for desirable features such as speed, low‐gradient performance, repeated sampling of the k‐space center or adapting the k‐space weighting. Depending on the parameter settings, rosettes can become identical to rings, in‐out spirals or radial EPSI. ¹⁷⁹ The ability to tailor rosette trajectories for low‐gradient performance and reduced acoustic noise could make them useful in the regime of very high SBW/spatial resolution. MRI results indicate that rosettes can be more incoherently undersampled than other non‐Cartesian trajectories, which may be a benefit for CS reconstruction. ¹⁸⁰

3.2.4. Radial EPSI

Finally, MRSI based on radial EPSI (again originally proposed for hyperpolarized ¹³C‐MRSI ⁹⁶ ) is a fairly young field. Only recently have preliminary experimental reports in ¹H‐MRSI and ³¹P‐MRSI been published. ¹⁸¹ , ¹⁸² Like spirals, radial EPSI trajectories return to the k‐space center, which offers in principle the possibility for self‐navigation (i.e., correction by phase/magnitude alignment of consecutive trajectories). This can be used to reduce instabilities (e.g., motion) between different k‐space interleaves (Figure S2), ¹⁸² , ¹⁸³ while other SSE techniques (e.g., EPSI) require interleaved navigators for this. ¹⁸⁴

4. UNDERSAMPLED MRSI

k‐space undersampling is the third major acceleration method for MRSI. For an unambiguous signal allocation by gradient encoding, the distance between all adjacent k‐space points must be less than 1/object size (i.e., Nyquist criterion). Conventional phase‐encoded MRSI at the Nyquist rate (i.e., full k‐space sampling) is very time consuming. In undersampled MRSI, fewer k‐space points are acquired below the Nyquist rate to speed up the acquisition using coherent and incoherent undersampling patterns (Figure 9). Complementary information other than gradient encoding, which includes sensitivity maps, spatial‐spectral sparsity or prior knowledge, is employed to reconstruct the undersampled data sets without aliasing.

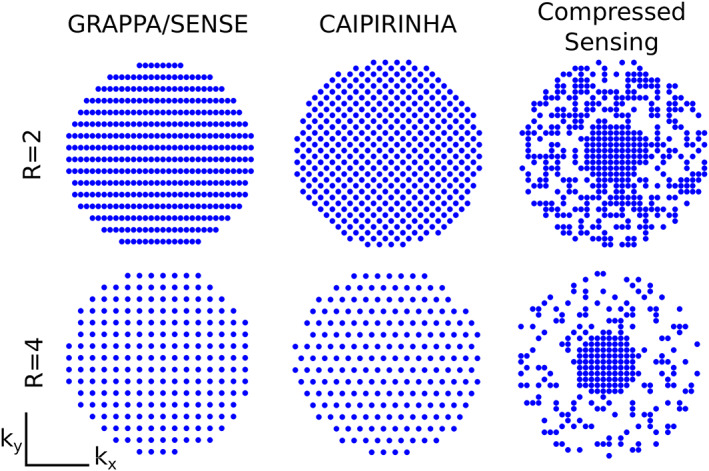
Illustration of different 2D k‐space undersampling schemas for two‐fold acceleration (R = 2) and four‐fold acceleration (R = 4). GRAPPA/SENSE can reconstruct coherently sampled k‐space data (e.g., entire rows or columns are not acquired), while CAIPIRINHA can reconstruct even coherently undersampled data with any other patter and benefits from controlled aliasing. All of them use information about sensitivity profiles of the individual receive channels to remove spatial aliasing either in the image (e.g., SENSE) or k‐space domain (e.g ., GRAPPA, CAIPIRINHA). This translates into better reconstruction with lower g‐factors (e.g ., less lipid aliasing and higher SNR). In contrast, CS can reconstruct incoherently (e.g., random‐like) undersampled k‐space data without knowledge about the coil receive profiles of the individual receive channels. Courtesy of Lukas Hingerl

4.1. Parallel imaging

A common group of methods for reconstruction of k‐space undersampled MRI data is PI. ¹⁸⁵ , ¹⁸⁶ , ¹⁸⁷ In classic implementations, k‐space undersampling is performed in a uniformly equidistant manner across k‐space (i.e., regular pattern), yielding a larger distance between sampled k‐space points. This in turn leads to a field‐of‐view reduction to below the dimensions of the object and thus to aliasing (folding) of image information. To reconstruct the missing k‐space points or to unfold the aliased image additional information on the spatial signal origin is derived from sensitivity profiles of receive coil arrays. There are two major reconstruction approaches in PI that have found widespread application: (i) sensitivity encoding (SENSE) ¹⁸⁷ and (ii) generalized autocalibrating partially parallel acquisition (GRAPPA). ¹⁸⁶ SENSE solves the image reconstruction problem in the image domain by unfolding the aliased images, and requires explicit sensitivity maps of each coil element to form an overdetermined system of linear equations. Both the k‐space encoding trajectory and receiver coil sensitivity patterns are input to the algorithm. GRAPPA solves the same problem in k‐space domain, and typically only undersamples the outer parts of the k‐space to derive a reconstruction kernel that predicts the missing k‐space points from the central fully sampled part of k‐space. Both principles are widely applied in MRI and have been demonstrated for ¹H‐MRSI as well. PI is generally also compatible with SSE and incoherent k‐space undersampling (see Section 5).

4.1.1. SENSE

Sensitivity‐encoded ¹H‐MRSI was introduced shortly after the invention of SENSE‐MRI in 2001 and was combined with different localization schemes such as PRESS, ¹⁸⁸ slice‐selective adiabatic SE localization, ¹⁸⁹ SE‐ or FID‐MRSI with OVS ¹⁹⁰ , ¹⁹¹ , ¹⁹² , ¹⁹³ or FID‐MRSI without OVS. ⁵⁵ This pre‐localization was necessary because the original SENSE‐MRSI implementation suffered from residual lipid aliasing artifacts introduced by imperfections of the sensitivity maps and insufficient control of the SRF. The ESPIRIT approach ⁵⁵ , ¹⁹² , ¹⁹⁴ , ¹⁹⁵ to derive reliable sensitivity maps enhanced the robustness and applicability of SENSE‐MRSI since it is free of residual bias fields or image contrasts, is compatible with transceiver arrays and is free of interpolation errors towards the edge of the object of interest. Several methods to further reduce lipid aliasing were presented, and include direct optimization of the SRF, overdiscrete or superresolution reconstruction and retrospective lipid removal. ⁵⁵ , ¹⁹³ , ¹⁹⁶ , ¹⁹⁷ , ¹⁹⁸ SENSE was also utilized for an overdiscrete B ₀‐correction that enhances the SNR of MRSI data. ⁵⁵ , ¹⁹² Figure 10 illustrates controls of SRF, resulting lipid artifacts, and SNR increase. SENSE‐MRSI was combined with alternative acceleration methods such as elliptical k‐space sampling, ¹⁹⁹ multi‐echo MRSI, ²⁰ , ²¹ EPSI, ¹⁹⁰ , ¹⁹¹ , ²⁰⁰ spiral MRSI, ¹⁴² CS, ⁵⁷ low‐rank reconstruction ⁵⁸ and partial Fourier imaging. ²⁰¹ SENSE‐MRSI was also used to accelerate the acquisition of unsuppressed water maps for internal water referencing ²⁰² and a phantom‐based external referencing for quantitative SENSE‐MRSI compatible with receive arrays. ²⁰³ SENSE‐MRSI was applied to clinical studies in brain tumor patients, ¹⁹⁶ , ²⁰⁴ and shortly after its introduction SENSE‐MRSI was also implemented as a commercial option by a major vendor and is utilized in clinical diagnostics today on a regular basis. SENSE‐MRSI is not easily applicable to ³¹P‐, ¹³C‐ and ²H‐MRSI due to the lack of a high‐SNR reference standard (e.g., water in ¹H‐MRI/MRSI) that allows for generation of high‐quality sensitivity maps. Nevertheless, applications of SENSE to hyperpolarized ¹³C‐MRSI have been demonstrated ²⁰¹ , ²⁰⁵ sensitivity maps have been derived either by self‐calibration exploiting the high SNR of in vivo pyruvate and a fully sampled k‐space center ²⁰⁵ or by using an oil phantom. ²⁰¹ , ²⁰⁶

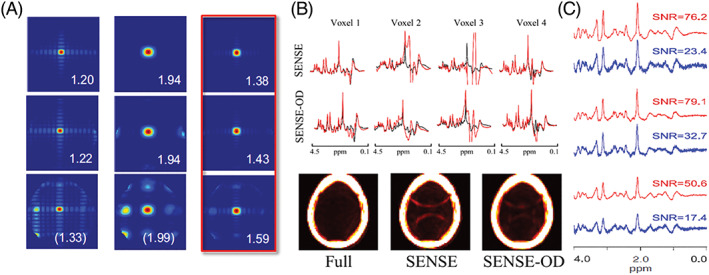
Lipid aliasing control by overdiscrete SENSE MRSI reconstruction. A, SRFs for different acceleration factors (top row ‐ R=1; middle row ‐ R=2; bottom row ‐ R=2x2) after standard SENSE reconstruction (left column), a Hamming filtered version of it (middle column) and an overdiscrete, spatial‐response function target based SENSE reconstruction (right column). B, Spectra and lipid maps from fully sampled, SENSE and SENSE‐OD reconstruction (2 × 2 acceleration each) of ¹H‐FID‐MRSI data from 9.4 T. C, SNR after SENSE (blue) and SENSE‐OD (red) reconstruction of 7 T ¹H‐FID‐MRSI data. Reproduced from the work of Kirchner et al. ¹⁹² , ¹⁹³ and Nassirpour et al ⁵⁵

4.1.2. GRAPPA

The earliest description of GRAPPA‐accelerated ¹H‐MRSI stems from 2006. ²⁰⁷ Implementations have been demonstrated that relied on PRESS pre‐localization, ²⁰⁴ , ²⁰⁷ slice‐selective or volumetric SE‐ ⁶⁵ , ²⁰⁸ and FID‐MRSI. ⁵² , ⁵⁶ , ⁶⁴ , ²⁰⁹ To reduce lipid aliasing in SE‐ or FID‐MRSI, lipid suppression by either OVS or double inversion recovery were presented, ¹⁹⁰ , ²⁰⁹ but both options limit the acquisition speed by demanding higher T _R values due to SAR. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA)‐MRSI encoding in combination with retrospective lipid removal yielded significantly better metabolite maps. ⁵² , ¹⁶⁷ Finally, training neural networks for GRAPPA reconstruction on MRI data ⁵⁶ or acquiring the reference data for GRAPPA reconstruction interleaved ⁶⁴ reduced lipid aliasing to a negligible level. GRAPPA‐MRSI was combined with alternative acceleration methods such as elliptical k‐space sampling, ²¹⁰ EPSI, ⁶⁵ , ²⁰⁸ , ²¹¹ CRT, ⁶⁴ and spirals. ²¹² Recently, through‐time/through‐k‐space GRAPPA was presented, which simultaneously yields an unsuppressed water reference scan. ⁶⁴ The impact of GRAPPA‐accelerated EPSI on diagnostic sensitivity in traumatic brain injury patients was investigated and identical metabolic changes were found. ²¹¹ GRAPPA is generally compatible with non‐proton MRSI, but preliminary ³¹P‐MRSI implementations were limited by low SNR. ²¹³ A simultaneous auto‐calibrating and k‐space estimation (SAKE) variant was applied to hyperpolarized ¹³C‐MRSI. ¹⁹⁵ , ²¹⁴ , ²¹⁵

Early implementations of SENSE‐MRSI and GRAPPA‐MRSI have been compared, and favorable results have been obtained for conventional GRAPPA due to SNR advantages and lower lipid aliasing. ²⁰⁴ SENSE‐MRSI was also compared against elliptical k‐space shuttering and EPSI, and it was concluded that all three methods are applicable to clinical diagnostics of brain tumors with individual advantages and disadvantages. ²¹⁶ However, the full potentials of neither SENSE nor GRAPPA have been exploited in these studies, and a more thorough comparison of state‐of‐the‐art SENSE and GRAPPA reconstruction algorithms and alternative sampling schemes has yet to be performed.

4.2. Multi‐band/simultaneous multi‐slice

Another possibility to exploit the sensitivity profiles of multi‐channel receive coils for MRI acceleration is simultaneous multi‐slice (SMS) imaging. ²¹⁷ SMS makes efficient use of simultaneous excitation of several slices by one multi‐band RF pulse ²¹⁸ in combination with controlled aliasing ²¹⁹ and reconstructs the individual slices using the PI concept (Figure 11). The achievable acceleration factors are fairly low (~2 to 4) and can therefore only be used as an add‐on to either undersampling ⁵² or SSE techniques, ⁸² , ²²⁰ as shown for preliminary ¹H‐MRSI ⁸² , ²²⁰ studies. The excitation of multiple slices via SMS should be not confused with multi‐band spectral‐spatial excitation (ie exciting different frequency bands simultaneously), which has been employed for rapid ¹³C‐MRSI. ³⁸ , ⁹² , ²²¹ , ²²²

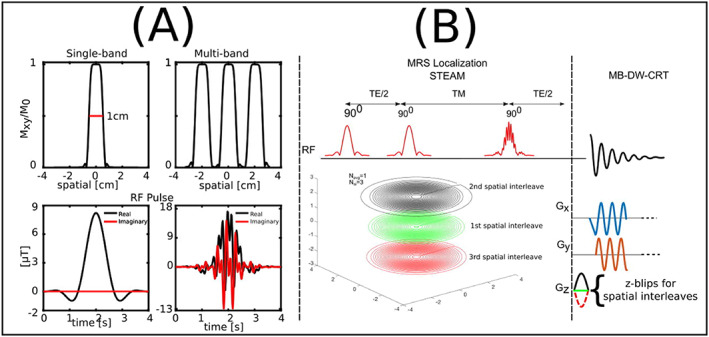
A, RF pulse and corresponding slice excitation profiles of single‐band and multi‐band pulses. The phase modulation of the multi‐band pulse reduced the peak B ₁ ⁺ while keeping the bandwidth of each band and pulse duration the same. B, The proposed multi‐band density‐weighted CRT MRSI method using the third STEAM pulse as a multi‐band excitation pulse. 96 rings with different radii are distributed evenly in three sets of rings with different z‐blip gradients. The single‐slice sequence has the same 96 rings in the k _x‐k _y plane without encoding with z‐blip gradients. Reproduced from the work of Xia et al ²²⁰

4.3. Compressed sensing

CS‐MRI relies on a combination of non‐uniform k‐space undersampling and the assumption of spatial and/or spectral sparsity. ²²³ Spatial or spectral sparsity means that there are relatively few significant voxels or spectral points with non‐zero values. During the image reconstruction, a wavelet and/or other compression transformation such as total variation or principal component analysis is performed to yield a sparse representation of the data similar to data compression in JPEG. k‐space undersampling must be incoherent to yield a noise‐like distribution of nuisance signals, which can be removed by a non‐linear reconstruction algorithm that enforces sparsity in the transformation domain (e.g., wavelet space) and is consistent with the acquired data.

The first implementation of CS‐MRSI was demonstrated in 2008 with application in hyperpolarized ¹³C‐MRSI, ³⁶ which still yields the majority of publications utilizing this MRSI acceleration method. ³⁵ , ³⁶ , ³⁸ , ⁸⁵ , ²²⁴ , ²²⁵ , ²²⁶ , ²²⁷ , ²²⁸ , ²²⁹ , ²³⁰ , ²³¹ CS is ideal for hyperpolarized ¹³C‐MRSI due to its intrinsic spectral sparsity, which allows for additional acceleration along the spectral dimension. CS can be combined with SSE to further accelerate the metabolic imaging readout for hyperpolarized ¹³C‐MRSI to reach sufficient coverage and resolution in the presence of strict time limits, ³⁵ , ³⁶ , ⁸⁵ , ²²⁸ , ²³¹ and was demonstrated for flyback‐EPSI, a custom designed incoherent spatial‐spectral undersampling scheme and EPI with frequency selective excitation. Other acceleration methods that have been combined with CS for hyperpolarized ¹³C‐MRSI are multi‐band encoding, ³⁸ multi‐point Dixon encoding ²²⁷ , ²³⁰ and balanced SSFP. ²²⁹ Applications of CS in ¹³C‐hyperpolarization studies have focused mainly on cancer imaging. ³⁵ , ²²⁴ , ²²⁵ , ²²⁶

Similarly, ³¹P‐MRSI is well suited for this acceleration approach due to well separated spectral lines and the absence of large nuisance signals. The first CS ³¹P‐MRSI implementation was shown in 2012 and was based on simulated 2D‐MRSI data. ²³² An actual 2D implementation for human brain ³¹P‐MRSI was shown in 2017. ¹⁴⁸ , ²³³ , ²³⁴ CS has been recently combined with flyback‐EPSI for highly accelerated ³¹P‐MRSI, ⁶² and two distinct reconstruction schemes—L1‐norm minimization and low‐rank Hankel matrix completion—have been compared. ¹³⁸

The application of CS to ¹H‐MRSI is complicated due to large water and lipid nuisance signals, which can mislead the reconstruction algorithm to exclude the lower‐intensity metabolite peaks by misadjusted thresholding. In addition, ¹H spectra are not sparse (short‐T _E MRS in particular), making acceleration along the spectral dimension more challenging. The first CS ¹H‐MRSI implementation was shown in 2009 in vitro ²³⁵ and 2012 in vivo via retrospective undersampling. ²³⁶ Several studies investigated the dependence of the SRF on the SNR and sampling pattern in CS‐accelerated ¹H‐MRSI using phantom data. ²³⁷ , ²³⁸ , ²³⁹ In vivo applications of CS ¹H‐MRSI were combined with either PRESS ¹⁴² , ²³⁶ , ²⁴⁰ , ²⁴¹ or semi‐LASER ⁸⁵ pre‐localization or slice‐selective ¹H‐FID‐MRSI ⁵⁷ , ⁵⁸ (Figure 12). CS was used to further accelerate 3D J‐resolved EPSI for ¹H‐MRSI prostate applications. ²⁴⁰ , ²⁴¹ In addition the combination of CS with SENSE, ⁵⁷ CS with SENSE and incoherently undersampled spiral trajectories ¹⁴² as well as CS and a low‐rank constrained reconstruction scheme have been demonstrated for ¹H‐MRSI. ⁵⁸

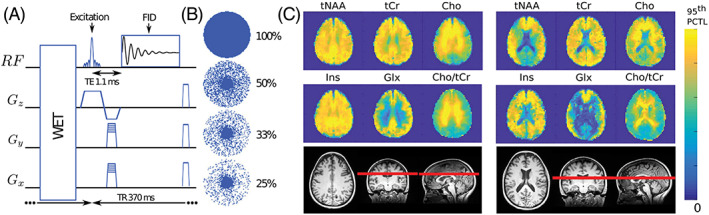
A, Diagram of the FID‐MRSI sequence with RF signal and gradient intensities along z, y and x directions (G _z, G _y, G _x) and B, illustration of the elliptical incoherent k‐space sampling schemes corresponding to acceleration factors 1, 2, 3 and 4 . C, Metabolite distributions from two healthy volunteers reconstructed with a low‐rank Total Generalized Variation model with optimal regularization parameter (λ = 10⁻³) and rank K = 20 without acceleration. The maximum of the scale was set to the 95th percentile of each metabolite image separately. Reproduced from the work of Klauser et al ⁵⁸

5. JOINT FORCES—COMBINING SSE, UNDERSAMPLING AND SHORT T _R

Even though SSE by itself can provide up to two magnitudes of acceleration compared with pure phase encoding, this is often not sufficient for reaching the desired target temporal resolution ³⁸ , ²⁰⁰ or volume coverage (e.g., whole brain) with sufficiently high spatial resolution. ⁶⁴ , ²⁰⁸ , ²¹¹ In such cases, SSE techniques can be combined with PI, ⁶⁴ , ⁸⁰ , ¹⁹⁰ , ²⁰⁸ , ²¹¹ CS ³⁵ , ³⁶ , ³⁸ , ²²⁸ or a mixture of the two techniques. ¹⁴² Such undersampling can be performed in spatial (k _x, k _y), spectral (t) and dynamic (frame) dimensions. The possibility to undersample in multiple dimensions in an entangled fashion (e.g., both k‐space and time domain) is highly beneficial for reconstruction efficiency. ²⁴² The high sparsity in the spectral dimension is particularly appealing for CS and can be efficiently exploited in conjunction with SSE by using a different k‐space undersampling for each FID point to introduce spectral incoherence (e.g., by adding random phase‐encoding blips). ¹⁴²

5.1. Cartesian

EPSI techniques simultaneously encode one spatial dimension and the spectral dimension, but the other spatial dimensions are still acquired using conventional phase encoding, and thus the scan time increases proportionally. PI can be used to regularly undersample the phase‐encoding dimensions of EPSI and exploit differences in coil sensitivities to reconstruct unaliased spectroscopic images. 1D‐SENSE ¹⁹¹ and 1D‐GRAPPA ⁶⁵ were employed to accelerate 2D‐EPSI in the brain twofold for an 8‐channel coil array and threefold for a 32‐channel array, resulting in acquisition times below 1 min for a 32 × 32 spatial matrix and T _R of 2 s. Acceleration in PI is limited by noise amplification due to a reduced number of phase‐encoding points and instability in the inverse reconstruction produced by overlapping coil sensitivities (the so‐called g‐factor). Higher accelerations are feasible with the use of 2D undersampling for 3D imaging and a coil array with a large number of elements to enable 2D‐SENSE, which reduce the g‐factor. For example, 2D‐SENSE using a 32‐channel soccer ball head coil array enabled an acceleration factor of 2 × 2 for 3D‐PEPSI with no additional degradation in spatial‐spectral quality beyond the expected SNR decrease of sqrt(R), resulting in acquisition times of 2 min for a 32 × 32 × 8 spatial matrix (Figure S3). ¹⁹⁰

An alternative approach to undersample the phase‐encoding dimensions of EPSI is CS, which can exploit the natural sparsity along the spectral dimension in long‐T _E acquisitions or transform sparsity for short‐T _E acquisitions. The application of typical sparsifying transforms, such as wavelets and principal component analysis, along the spectral dimension can lead to combined spatial‐spectral sparse representations of short‐T _E data. For 2D‐EPSI, spatial‐spectral incoherent sampling can be achieved by using phase‐encoding blips, which result in a different k _y‐undersampling pattern for each time point ⁹⁵ (Figure 13). To increase the acceleration rate, CS can be combined with PI to enforce joint coil sensitivity sparsity in the reconstruction. SPARSE‐SENSE, which combines CS and SENSE, was applied to 2D‐PEPSI to achieve fourfold acceleration with significant improvements compared with standard SENSE. ²⁴³ CS was also applied to T _E‐averaged EPSI of glutamate to compensate for the increased scan time required to acquire at multiple T _E values. ²⁴⁴ CS is also a natural candidate for acceleration of J‐resolved MRSI, given the substantial correlations in the high‐dimensional data. CS with fourfold acceleration was demonstrated for 4D echo‐planar correlated spectroscopic imaging to reduce the scan time to 5 min. ²⁴⁵

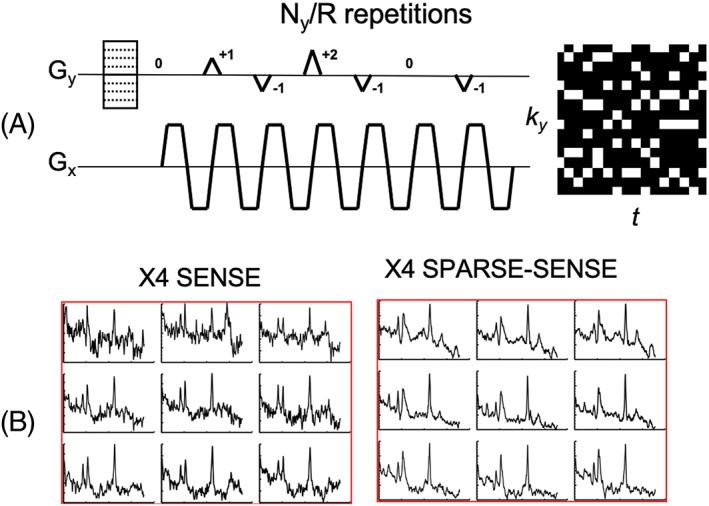
A, CS acquisition scheme for 2D‐PEPSI, based on random k _y‐t undersampling using phase‐encoding blips. Each time point is undersampled with a different random k _y pattern to achieve spatial‐spectral incoherence. B, Comparison of real spectra obtained with fourfold acceleration for 2D‐EPSI using SENSE (PI) and SPARSE‐SENSE (combination of CS and PI). SPARSE‐SENSE jointly exploits sparsity in the spectral wavelet domain and coil SENSE by enforcing joint multi‐coil sparsity in the reconstruction to achieve significantly higher spectral quality and noise reduction compared with standard SENSE due to regularization. Reproduced from the work of Otazo et al ²⁴³

5.2. Non‐Cartesian

It is well known from MRI that non‐Cartesian trajectories, such as those also used for radial EPSI, spirals and CRTs, can be more efficiently accelerated via PI than Cartesian trajectories, meaning that the g‐factor‐related SNR penalty is lower. ²⁴⁶ This is a consequence of the less structured aliasing artifacts that are obtained via non‐Cartesian sampling, which translates into more efficient reconstruction compared with Cartesian counterparts. ²⁴² This has also been suggested experimentally for MRSI using spirals ²¹² , ²⁴⁷ and CRTs (non‐Cartesian k‐space undersampling and reconstruction approaches illustrated in Figure 14). ⁶⁴ , ⁸⁰ SMS, which exploits sensitivity profiles as well, can therefore also be more efficiently combined with non‐Cartesian SSE (e.g., CRTs). ²²⁰ Additionally, CS reconstruction benefits from variable‐density k‐space sampling, ²²³ which can be easily achieved via non‐Cartesian spatial encoding.

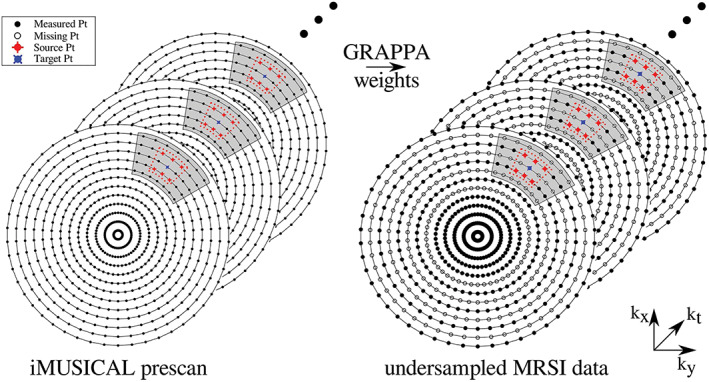
A schematic diagram of the through‐time/through‐k‐space GRAPPA method applied to concentric‐ring MRSI. The figure shows a fully sampled calibration dataset on the left and a two‐fold variable‐density undersampled MRSI k‐space on the right: the center of the k‐space is fully sampled (solid points), followed by constant two‐fold undersampling (empty points). For calibration, a segment (shaded area) was used around each target point for the through‐k‐space GRAPPA part with a kernel size of 3 × 2 (red dotted lines), i.e., six source points. The kernel was slid through the segment of the calibration data to gather all the through‐k‐space kernel repetitions. Twenty‐one calibration time points (through‐time kernel repetitions) were used. After calculating the GRAPPA weights using the calibration data, the weights are used to reconstruct missing k‐space points in the undersampled MRSI data (right). Reproduced from the work of Moser et al ⁶⁴

Despite this evidence, the number of reports that have combined non‐Cartesian SSE with undersampling is still limited compared with Cartesian SSE. This is partially related to the more complicated and often time‐consuming reconstructions (e.g., iterative). ²⁴⁶ , ²⁴⁸ With its excess SNR, hyperpolarized MRSI is a prime candidate to benefit from undersampled non‐Cartesian MRSI. On the other hand, there is a lack of good multi‐channel multi‐nuclear coils that would be necessary to perform PI efficiently for hyperpolarized ¹³C‐MRSI, leaving CS—in particular in the spectral domain—the only option for further acceleration. In fact, spectral aliasing due to undersampling may not necessarily have to be undone for hyperpolarized ¹³C‐MRSI as long as it does not cause major spectral overlap of important metabolite resonances. ²⁴⁹ In this context, it should be noted that spectral aliasing due to undersampling is more problematic for ¹H‐MRSI data. Short‐T _E MR spectra are far less sparse (i.e., many strongly overlapping resonances) and there can be strong contamination by large nuisance signals (i.e., unsuppressed water or extra‐cranial lipids). This is not a problem for ¹³C‐ or ³¹P‐MRSI. ¹⁴⁸ , ²³⁴ Nevertheless, highly efficient combination of variable density spirals and an entangled SENSE and CS reconstruction has so far been shown only for ¹H‐MRSI at 3 T using PRESS. ¹⁴² However, with an increasing number of better rapid non‐Cartesian reconstruction algorithms emerging for MRI, ²⁵⁰ the interest in undersampled non‐Cartesian SSE for ¹H‐MRSI is increasing.

6. USING PRIOR KNOWLEDGE

A promising approach to improve the results of highly accelerated MRSI is the incorporation of spatial (e.g., from high‐resolution anatomical MRI) and spectral (e.g., spectral components and their relaxation times) prior knowledge as well as bias field maps (B ₀ maps, B ₁ ⁺ maps) to reconstruct data with incoherent k‐space undersampling. More recently, low‐rank reconstruction schemes were combined with corresponding prior knowledge. The following paragraphs review the evolution of acquisition and reconstruction approaches based on prior knowledge.

6.1. Spatial prior knowledge and bias field maps: SLIM, SLOOP and SLAM

The utilization of prior knowledge derived from high‐resolution anatomical images for reconstruction of MRSI data with substantial k‐space undersampling was suggested as early as 1988, when the concept of spectral localization by imaging (SLIM) ²⁵¹ was introduced by Hu et al. The basic idea behind SLIM is to use a structural image to identify several compartments, each of which is assumed to be spatially uniform with regard to its metabolism. Hence, SLIM was originally used to derive spectra from a few arbitrarily shaped spatial compartments. For instance, a ¹H‐MR image of a limb may show three regions containing muscle, fat and bone marrow. ²⁵¹ In principle, only three phase encoding steps are required to reconstruct three spectra from these three compartments. Applications of SLIM were reported for ¹H and ³¹P‐MRS of tissue samples, ²⁵² perfused organs ²⁵³ and in vivo skeletal muscle. ²⁵¹ , ²⁵⁴ In 1991 spectral localization with optimal pointspread function (SLOOP) as an improvement to SLIM was suggested, which minimizes contaminations from other compartments by optimizing the k‐space sampling scheme, ²⁵⁵ SLOOP was developed further to include additional prior knowledge on B ₁ ⁺, T ₁ and sequence parameters to optimize the SNR for human application of 3D‐encoded ³¹P‐MRS in the human myocardium. ²⁵⁶ A further development step was the utilization of additional non‐linear gradients for the encoding of the SLOOP compartments. ²⁵⁷ In vivo ³¹P‐SLOOP was mainly performed to characterize human cardiac muscle metabolism. ²⁵⁷ , ²⁵⁸ , ²⁵⁹ , ²⁶⁰ , ²⁶¹ , ²⁶² , ²⁶³

SLIM developed into a metabolic imaging method, with the first report being the generalized series approach to MR spectroscopic imaging (GSLIM). ²⁶⁴ , ²⁶⁵ GSLIM allows for spatial variations inside the compartments (e.g., metabolite concentrations and B ₀ inhomogeneity), which are estimated from the data itself; the ill‐posedness of the problem is dealt with by using regularization techniques. GSLIM and natural linewidth chemical shift imaging (NL‐CSI) compensate for the sensitivity of SLIM to B ₀ inhomogeneity across the predefined compartments by incorporating prior knowledge from additional B ₀ maps into the reconstruction. ²⁶⁶ , ²⁶⁷ Static and radiofrequency‐compensated SLIM (STARSLIM) even incorporates prior knowledge about B ₀ and B ₁ ⁺ inhomogeneity. ²⁶⁸ B ₀‐adjusted and sensitivity‐encoded spectral localization by imaging (BASE‐SLIM) incorporated B ₀ and sensitivity maps into the SLIM reconstruction. ²⁶⁹ Finally, spectroscopy with linear algebraic modeling (SLAM) ²⁷⁰ , ²⁷¹ was introduced, which substitutes the compartments in SLIM by a set of coalesced MRSI voxels with the same concentrations. Similar to SLOOP, SLAM chooses an optimized set of the same number of low‐gradient k‐space vectors as final compartments to maximize SNR and to minimize signal bleeding. SLAM has been combined with SENSE. Initial applications are ³¹P‐MRS in human skeletal muscle and myocardium ²⁷¹ and hyperpolarized ¹³C‐MRSI. ²⁷² A recent review paper gives a more comprehensive overview of all derivatives of SLIM and its applications in brain MRSI. ²⁷³

An alternative reconstruction approach unrelated to SLIM incorporates B ₀ inhomogeneity as an additional encoding process together with the use of anatomical prior knowledge in a regularization term ²⁷⁴ to improve MRSI reconstruction of undersampled data. Finally, the consideration of image prior knowledge as a direct constraint of the SRF along with B ₀ inhomogeneity correction has also been demonstrated for SENSE‐MRSI to better control lipid artifacts. ²⁷⁵

6.2. Spatial‐spectral prior knowledge and low‐rank reconstruction: toward SPICE

In addition to spatial prior knowledge, spectral prior knowledge has been used to reconstruct accelerated MRSI data. The first reported use of spectral priors in MRSI reconstruction relates to B ₀ inhomogeneity correction by reference deconvolution using a spectral line shape model reflecting the B ₀ inhomogeneity distribution and aims at the improvement of the spectral linewidth. ²⁷⁶ , ²⁷⁷ , ²⁷⁸ Early spatial‐spectral modeling in MRSI reconstruction combined the conventional gradient encoding data consistency term with additional regularization terms considering a combined spectral and baseline model term as well as a total variation term ²⁷⁹ , ²⁸⁰ and considered B ₀ inhomogeneity as an encoding mechanism. ²⁸¹ Another spatial‐spectral reconstruction approach aimed at controlling lipid spread and combined the usual consistency term that minimizes the difference between the gradient encoding data model and the data with a regularization or penalty term that includes a spatial‐spectral lipid model. ¹⁶⁷

Another important development step was the use of low‐rank approximation approaches in MRSI reconstruction, ⁵⁸ , ¹⁶⁸ , ²⁸² , ²⁸³ , ²⁸⁴ , ²⁸⁵ the main idea of which is to remove basis vectors related to noise to yield higher‐SNR spectroscopic images. Following an initial application in denoising of MRSI data, ²⁸⁴ low‐rank filtering was integrated with B ₀ inhomogeneity correction ²⁸³ and additional image prior knowledge on tissue type boundaries ²⁸² for a more robust reconstruction of fully sampled Cartesian MRSI. Shortly afterwards, low‐rank approximation was combined with balanced‐SSFP or dynamic spiral hyperpolarized ¹³C‐MRSI with incoherent k‐space sampling ²⁸⁵ , ²⁸⁶ and ¹H‐FID‐MRSI accelerated by short T _R and a combined SENSE and CS acceleration. ⁵⁸ Low‐rank reconstruction was also used together with a spatiotemporal lipid prior that assumes orthogonality of spatiotemporal metabolite versus lipid signals and applied to lipid‐unsuppressed dual‐density spiral ¹H‐MRSI. ¹⁶⁸

A recent approach to reach very high acceleration factors and SNR in MRSI is the combination of the idea of “spatiotemporal imaging with partially separable functions” ²⁸⁷ that separates temporal and spatial basis vectors with spectral prior knowledge and low‐rank approximation. The resulting MRSI acceleration method SPICE (spectroscopic imaging by exploiting spatiospectral correlation) ²⁸⁸ represents the high‐dimensional spectroscopic imaging data as a union or superposition of subspaces (Figure 15). In practice, four subspaces are used, including metabolites, lipids, water and macromolecules. ⁴⁷ The premise of SPICE is that the existence of spatial and temporal correlations will result in a low‐dimensional representation given by the union of subspaces. Each subspace is represented using a low‐rank tensor, whose basis is estimated from training data given by a fully sampled high‐spectral‐resolution and low‐spatial‐resolution acquisition to capture spectral correlations (Figure S4). Once the basis sets have been determined, undersampled data acquired with high spatial and spectral resolution can be reconstructed by enforcing the pre‐computed union of subspaces model, which will remove aliasing artifacts and separate the spectroscopic imaging data into metabolites, lipids, water and macromolecules. The main advantage of SPICE is to learn an efficient model to represent spectroscopic images using training data, which goes beyond the handcrafted models used in CS and can enable access to higher spatial resolution and direct separation of nuisance signals. Recent implementations have eliminated the need for subject‐specific navigator data to facilitate practical application. ⁴⁵ Initial applications were shown for ¹H‐MRSI of the human brain. ²⁸⁹ , ²⁹⁰ Simultaneous readouts of SPICE‐accelerated ¹H‐MRSI with QSM ²⁹¹ and functional MRI ²⁹² of the human brain have been demonstrated. Other applications include mapping of brain macromolecules ⁴⁷ and dynamic ³¹P‐MRSI in skeletal muscle ²⁹³ and hyperpolarized ¹³C‐MRSI. ²⁹⁴ The development of using prior knowledge in image reconstruction from SLIM to SPICE is described in a recent book chapter. ²⁹⁵

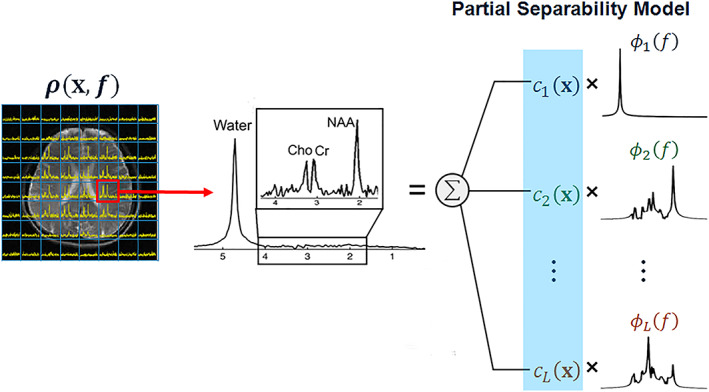
An illustration of the SPICE approach. Each voxel spectra in the high‐dimensional spatiospectral function of interest (ρ(x,f), the image on the left) is modeled as a linear combination of a small number of spectral basis functions $({\{φ_{l} (f)\}}_{l = 1}^{L}$ , rightmost column). This implies that the high‐dimensional signals reside in a low‐dimensional subspace (spanned by {φ_l(f)}). With the subspace predetermined (from training data), the imaging problem is transformed into the estimation of a set of spatial coefficients ( ${\{c_{l} (x)\}}_{l = 1}^{L}$ ) with much lower dimensions than the original spatiospectral function. Different subspaces can be constructed for different signal components, i.e., water, lipids and metabolites

6.3. Super‐resolution reconstruction

Another acceleration approach is the use of interpolation ²⁹⁶ to yield higher‐resolution metabolite maps from lower‐resolution MRSI data. The most simple approach is k‐space zero filling. ¹⁰ Alternatively, the SENSE reconstruction framework uses additional spatial information on coil sensitivity to yield super‐resolution MRSI data. ⁵⁵ , ¹⁹² , ¹⁹³ , ¹⁹⁷ , ¹⁹⁸ A recently presented sophisticated interpolation method is the patch‐based super‐resolution approach that uses image prior knowledge to enforce smooth transitions inside a tissue compartment and sharp tissue boundaries in interpolated metabolite images. It assumes the existence of image redundancy in the form of metabolically identical patches of voxels and thus compartments. It was applied to enhance ¹H‐MRSI of multiple sclerosis ⁶⁰ and glioma patients. ⁴⁹ For hyperpolarized ¹³C‐MRSI super‐resolution reconstruction in the spatiotemporal dimension was proposed in combination with an alternative spatial encoding without the necessity for time‐varying SSE gradients. ²⁹⁷ , ²⁹⁸ , ²⁹⁹ Finally, deep learning in combination with semi‐synthetic training data is utilized to yield super‐resolution MRSI data. ³⁰⁰

6.4. Spectral‐spatial excitation

Finally, another common strategy to accelerate metabolic imaging is to use prior knowledge about the resonance frequency of spectrally well separated signals for frequency‐selective excitation. This is applied especially to hyperpolarized ¹³C‐MRI by combining spectral‐spatial pulses with fast MRI readouts ²⁸⁶ , ³⁰¹ , ³⁰² , ³⁰³ , ³⁰⁴ , ³⁰⁵ , ³⁰⁶ , ³⁰⁷ , ³⁰⁸ , ³⁰⁹ but has been shown also for ³¹P‐MRI. ³¹⁰ , ³¹¹ Using a narrow‐band spectral‐spatial pulse to excite only a single metabolite resonance line makes the need for chemical shift encoding obsolete and enables conventional fast MRI readouts such as SSFP, echo‐planar or spiral MRI that can be further accelerated via coherent/incoherent undersampling. The application of spectral‐spatial pulses to different offset frequencies in successive MRI readouts enables fast hyperpolarized ¹³C‐MRI of multiple resonance lines and even dynamic readouts for all metabolites if applied in an interleaved manner.

7. SUMMARY AND OUTLOOK ON EMERGING TECHNOLOGIES

In the long history of MRSI, time‐efficient data acquisition was quickly identified as one of the main obstacles to high‐spatial‐resolution whole‐organ metabolic mapping. Although a number of alternative approaches to SSE have been proposed, SSE will certainly remain the workhorse of fast MRSI encoding, especially for ¹H‐MRSI at 3 T and hyperpolarized ¹³C‐MRSI. However, while whole‐brain MRSI today predominantly relies on different SSE strategies, it is increasingly challenged by other means of acceleration especially at UHF, where the increased SBW and spatial resolution demands have led to performance limitations for SSE with respect to speed and SNR efficiency. ⁶³ , ⁸⁶ These have complicated the use of purely SSE‐based MRSI on common whole‐body gradient systems, especially since the targeted spatial resolutions have gradually increased over time. ⁵ , ⁴¹ To make efficient use of the excess SNR available at UHF (e.g., by either shortening scans or increasing resolution) and to benefit from high‐resolution strategies to minimize intra‐voxel B ₀ inhomogeneities, ³¹² , ³¹³ , ³¹⁴ it will become critical to not only adapt SSE strategies, but also combine them efficiently with other means of acceleration and reconstruction algorithms. This will allow the benefits of high fields to be fully exploited. ⁶⁴ , ¹⁴² , ¹⁴⁸ , ¹⁹⁰ , ²³⁴ As the performance of k‐space undersampling increases (i.e., g‐factors improve with higher B ₀) and short‐T _R FID‐MRSI remains efficient (i.e., negligible SAR and CSDE at high B ₀) while the efficiency of SSE (i.e., increasing SBW and spatial resolution demand for higher gradient slew rates) decrease with increasing B ₀, we can expect to find an optimal balance between such combinations to slowly shift away from SSE alone to additional undersampling in the future. Depending on the application, such an efficient balance will include a reasonable compromise between short T _R (increased relaxation weighting and possibly reduced spectral resolution), undersampling (increased lipid artifacts and motion sensitivity) and SSE (increased gradient imperfections and scanner drift). ¹⁸⁴

The addition of spatial‐spectral prior knowledge in the reconstruction algorithm appears to be another promising way to circumvent these limits. ²⁹⁰ , ²⁹⁵ New reconstruction algorithms with more complex models have recently become feasible due to the constant increase in performance of computational hardware and software. However, critically questioning what kind of prior knowledge and how much regularization is truly justified to avoid bias remains an important concern. In this respect, it is also expected that deep‐learning‐based reconstruction, which has shown promising results for MRI/MRSI, ⁴⁵ , ⁵⁶ , ³¹⁵ , ³¹⁶ , ³¹⁷ , ³¹⁸ will play an increasingly important role in the near future with the potential to substantially speed up the time‐demanding reconstruction process of large multi‐channel whole‐brain MRSI datasets.

Another important step in the dissemination of fast MRSI techniques will therefore also be the progress in rapid automated spectral analysis tools tailored for whole‐brain MRSI. ³¹⁹ A number of well‐established and freely available MRSI processing pipelines already exist for application studies (e.g., MIDAS package for whole‐brain EPSI+GRAPPA; a comprehensive list of open‐source MRSI processing software is provided in the appendix). However, by no means all MRSI acceleration and reconstruction approaches described herein are available as user friendly freeware tools and hence are not yet ready for larger application studies. We anticipate that it is just a matter of time for a larger number of open‐source MRSI packages and full scanner integration of advanced MRSI methods to become available. To accelerate this process the developer community is encouraged to make MRSI sequences, reconstruction pipelines, and processing and visualization tools freely available to the scientific community. A more widespread dissemination of state‐of‐the art MRSI methodology is also needed for cross‐validation of different approaches.

Although several attempts to compare different MRSI acceleration strategies—mostly via simulations rather than experimental validation—are documented, ⁷⁴ , ⁸⁶ , ²¹⁶ , ³²⁰ , ³²¹ , ³²² , ³²³ a comprehensive comparison of all major SSE trajectories and undersampling techniques is not straightforward and has so far not been performed.

Considering the different and frequently hardware‐specific artifact behavior of different encoding approaches, simulations alone can only give rough guidelines. In addition, the choice of specific reconstruction pipelines and parameters have a major influence on the resulting data quality and novel forms of reconstruction (e.g., based on neuronal networks or comprehensive low‐rank models) may shift advantages/disadvantages in favor of currently more artifact‐prone, but otherwise more efficient, acquisition schemes. Hence only a qualitative comparison of the major categories of MRSI acceleration methods is provided in Table 1. It includes important considerations such as acceleration factor, SNR efficiency, typical artifacts and limitations, and suggests typical applications for each method. It is important to mention that the maximum possible acceleration factors that a particular acceleration method can achieve (Table 1) cannot be fully exploited in the case of SNR limitations. Another important factor to consider is the SRF that describes the source of the signal displayed in a given voxel. In particular, non‐Cartesian k‐space sampling and incoherent k‐space undersampling easily allow tailoring of the k‐space sampling density pattern (compare Table 1) and thus shaping of the SRF already during the acquisition. This allows trading the effective spatial resolution against higher SNR and better nuisance signal suppression (i.e., lipids in ¹H‐MRSI). SRF optimization is still possible during the reconstruction, but comes at the cost of SNR efficiency.

In line with the approach taken herein, a recent consensus effort on ¹H‐MRSI of the human brain ³²⁴ also includes only qualitative guidelines on the application‐dependent choice of MRSI sequence parameters and describes minimal standards for a wide range of influence factors including calibration, data acquisition, quantification and visualization. This is in contrast to a recent consensus on the standardized use of semi‐LASER for clinical single‐voxel MRS at 3 T, where the benefits over PRESS are unquestionable. ³²⁵ For MRSI, currently well‐established Cartesian SSE methods with standard k‐space undersampling and multi‐slice/3D options are strongly encouraged for clinical application. ³²⁴ However, this is certainly only the most practical short‐term solution, since multi‐vendor scanner integration is already available for these methods, which is critical for clinical acceptance. The application of different encoding strategies on standardized MRSI phantoms or the same group of people in multi‐center trials is needed to provide valuable experimental evidence that will help to come up with a true consensus on which MRSI acceleration methods should be implemented by manufacturers for future clinical use.

The development of methods with both time‐efficient acquisition and reconstruction is, therefore, still ongoing and equally important for enabling clinical implementation of high‐resolution whole‐brain MRSI (or large‐organ coverage), and possibly time‐resolved MRSI such as for hyperpolarized and functional MRSI.

FUNDING INFORMATION

The preparation of this manuscript was supported by the Austrian Science Fund (FWF)(projects KLI 718 and P 30701), the ERC starting grant 679927 / SYNAPLAST MR, Horizon 2020 ‐ H2020‐EU.3.1.6. / grant 634541 / CDS_QUAMRI and CPRIT established investigator award RR180056.

Supporting information

Figure S1: K‐space trajectories of EPSI, spiral and concentric rings spectroscopic imaging: the arrows illustrate the readout directions for both symmetric EPSI and flyback EPSI; for symmetric EPSI, we use different‐colored arrows to differentiate the odd/even echoes for reconstruction. Reproduced from Jiang et al.⁹⁵

Click here for additional data file.^{(3.6MB, tif)}

Figure S2: a. Measured radial EPSI k‐space trajectories for eight projection angles (different colors). b. Magnified view of k‐space origin for selected echoes (1, 16, and 32), showing unit Δk circle reference. Sampling errors are small with respect to Δk. c. Distance from k‐space trajectory to origin for all echoes. Note that measured trajectories from late echoes contain additional noise due to T2* relaxation. Reproduced from Ramirez et al.⁹⁷

Click here for additional data file.^{(5.8MB, tif)}

Figure S3: EPSI readout with (a) 2D‐SENSE undersampling scheme for 2 × 2 acceleration (black = acquired, grey = non‐acquired). (b) NAA concentration maps using LCModel spectral fitting for the fully‐sampled data (8 min scan time) and 2 × 2 accelerated data (2 min scan time). (c) Spectrum (black) and LCModel fit (red) corresponding to a white‐matter voxel. Reproduced from Otazo et al.¹⁹²

Click here for additional data file.^{(2.5MB, tif)}

Figure S4: SPICE (SPectroscopic Imaging by exploiting spatiospectral CorrElation) sequence for 3D encoding of ¹H‐MRSI: (a) the dual‐density, dual‐speed EPSI sequence with the slow EPSI component (left) to acquire D ₁and the rapid EPSI component to acquire D ₂ (right). Acquiring these complimentary data sets allows for determining the subspace with its spectral information and the spatial information with high spectral resolution and high SNR. τ denotes the timing for the echo shifts that can be used for additional spectral encodings; (b) the corresponding (k, t)‐space trajectories generated by the sequence in (a).²⁹²

Click here for additional data file.^{(6.8MB, tif)}

ACKNOWLEDGEMENTS

We thank Philipp A. Moser, Lukas Hingerl and Gilbert Hangel for their support with the preparation of Figures 1, 4, 6, and 8 as well as Zhi‐Pei Liang and Fan Lam for providing Figure 15.

APPENDIX A.

Open‐source MRS/MRSI processing tools (in alphabetical order).

BrICS (https://brainimaging.emory.edu/brics/)—mainly display of metabolic maps and spectra.
CSItools (https://hci.iwr.uni-heidelberg.de/hci/softwares/csitools)—MRSI processing and display.
FID‐A (https://github.com/CIC-methods/FID-A)—simulation and processing of MRS(I) data.
Gannet (http://www.gabamrs.com/)—edited MRS processing.
INSPECTOR (http://innovation.columbia.edu/technologies/cu17130_inspector)—simulation and processing of MRS(I) data.
jMRUI (http://www.jmrui.eu/)—simulation, processing and display of MRS(I) data.
jSIPRO (https://www.sites.google.com/site/jsiprotool/)—processing and display of MRSI data.
MIDAS (http://mrir.med.miami.edu:8000/midas/)—acquisition, processing and display of whole‐brain MRSI data.
MRSItoolbox (https://cds-quamri.eu/index.php)—processing and display of MRSI data.
OXSA (https://github.com/oxsatoolbox/oxsa)—processing of MRS(I) data.
ProFit (https://mrtm.ethz.ch/research/mr-spectroscopy/physiological-projects/profit.html)—quantification of MRS(I) data.
SIVIC (http://sourceforge.net/projects/sivic/)—processing and display of MRS(I) data.
TARQUIN (http://tarquin.sourceforge.net/)—processing and display of MRSI data.

Bogner W, Otazo R, Henning A. Accelerated MR spectroscopic imaging—a review of current and emerging techniques. NMR in Biomedicine. 2021;34:e4314. 10.1002/nbm.4314

REFERENCES

1. Brown TR, Kincaid BM, Ugurbil K. NMR chemical shift imaging in three dimensions. Proc Natl Acad Sci U S A. 1982;79(11):3523‐3526. [DOI] [PMC free article] [PubMed] [Google Scholar]
2. Maudsley AA, Hilal SK, Perman WH, Simon HE. Spatially resolved high‐resolution spectroscopy by 4‐dimensional NMR. J Magn Reson. 1983;51(1):147‐152. [Google Scholar]
3. Mansfield P. Spatial mapping of the chemical shift in NMR. Magn Reson Med. 1984;1(3):370‐386. [DOI] [PubMed] [Google Scholar]
4. Sabati M, Sheriff S, Gu M, et al. Multivendor implementation and comparison of volumetric whole‐brain echo‐planar MR spectroscopic imaging. Magn Reson Med. 2015;74(5):1209‐1220. [DOI] [PMC free article] [PubMed] [Google Scholar]
5. Nassirpour S, Chang P, Henning A. High and ultra‐high resolution metabolite mapping of the human brain using H‐1 FID MRSI at 9.4T. NeuroImage. 2018;168:211‐221. [DOI] [PubMed] [Google Scholar]
6. Povazan M, Strasser B, Hangel G, et al. Simultaneous mapping of metabolites and individual macromolecular components via ultra‐short acquisition delay H‐1 MRSI in the brain at 7T. Magn Reson Med. 2018;79(3):1231‐1240. [DOI] [PMC free article] [PubMed] [Google Scholar]
7. Hingerl L, Strasser B, Moser P, et al. Clinical high‐resolution 3D‐MR spectroscopic imaging of the human brain at 7 tesla. Invest Radiol. 2019;55(4):239‐248. [DOI] [PubMed] [Google Scholar]
8. Oz G, Alger JR, Barker PB, et al. Clinical proton MR spectroscopy in central nervous system disorders. Radiology. 2014;270(3):658‐679. [DOI] [PMC free article] [PubMed] [Google Scholar]
9. Kurhanewicz J, Vigneron DB, Ardenkjaer‐Larsen JH, et al. Hyperpolarized ¹³C MRI: path to clinical translation in oncology. Neoplasia. 2019;21(1):1‐16. [DOI] [PMC free article] [PubMed] [Google Scholar]
10. Bernstein MA, King KF, Zhou XJ. Handbook of MRI Pulse Sequences. Burlington, MA: Elsevier; 2004. [Google Scholar]
11. de Graaf RA. In Vivo NMR Spectroscopy—2nd Edition: Principles and Techniques. New York, NY: Wiley; 2007. [Google Scholar]
12. Shankar RV, Chang JC, Hu HCH, Kodibagkar VD. Fast data acquisition techniques in magnetic resonance spectroscopic imaging. NMR Biomed. 2019;32(3):1‐22:e4046. [DOI] [PubMed] [Google Scholar]
13. Oun A, Lechner‐Scott J, Ribbons K, Ramadan S. Fast magnetic resonance spectroscopic imaging techniques in human brain‐applications in multiple sclerosis. J Biomed Sci. 2017;24:1‐19. [DOI] [PMC free article] [PubMed] [Google Scholar]
14. Nelson SJ, Ozhinsky E, Li Y, Park IW, Crane J. Strategies for rapid in vivo H‐1 and hyperpolarized C‐13 MR spectroscopic imaging. J Magn Reson. 2013;229:187‐197. [DOI] [PMC free article] [PubMed] [Google Scholar]
15. Posse S, Otazo R, Dager SR, Alger J. MR spectroscopic imaging: principles and recent advances. J Magn Reson Imaging. 2013;37(6):1301‐1325. [DOI] [PubMed] [Google Scholar]
16. Posse S, Hu XP. High‐speed spatial‐spectral encoding with PEPSI and spiral MRSI. eMagRes. 2015;4(3):587‐600. [Google Scholar]
17. Althaus M, Dreher W, Geppert C, Leibfritz D. Fast 3D echo planar SSFP‐based H‐1 spectroscopic imaging: demonstration on the rat brain in vivo. Magn Reson Imaging. 2006;24(5):549‐555. [DOI] [PubMed] [Google Scholar]
18. Dreher W, Geppert C, Althaus M, Leibfritz D. Fast proton spectroscopic imaging using steady‐state free precession methods. Magn Reson Med. 2003;50(3):453‐460. [DOI] [PubMed] [Google Scholar]
19. Speck O, Scheffler K, Hennig J. Fast P‐31 chemical shift Imaging using SSFP methods. Magn Reson Med. 2002;48(4):633‐639. [DOI] [PubMed] [Google Scholar]
20. Dydak U, Pruessmann KP, Weiger M, Tsao J, Meier D, Boesiger P. Parallel spectroscopic imaging with spin‐echo trains. Magn Reson Med. 2003;50(1):196‐200. [DOI] [PubMed] [Google Scholar]
21. Dydak U, Meier D, Lamerichs R, Boesiger P. Trading spectral separation at 3T for acquisition speed in multi spin‐echo spectroscopic imaging. Am J Neuroradiol. 2006;27(7):1441‐1446. [PMC free article] [PubMed] [Google Scholar]
22. Dydak U, Schar M. MR spectroscopy and spectroscopic imaging: comparing 3.0 T versus 1.5 T. Neuroimaging Clin N Am. 2006;16(2):269‐283. [DOI] [PubMed] [Google Scholar]
23. Leupold J, Wieben O, Mansson S, et al. Fast chemical shift mapping with multiecho balanced SSFP. Magn Reson Mater Phys Biol Med. 2006;19(5):267‐273. [DOI] [PubMed] [Google Scholar]
24. Leupold J, Mansson S, Petersson JS, Hennig J, Wieben O. Fast multiecho balanced SSFP metabolite mapping of H‐1 and hyperpolarized C‐13 compounds. Magn Reson Mater Phys Biol Med. 2009;22(4):251‐256. [DOI] [PubMed] [Google Scholar]
25. Schuster C, Dreher W, Geppert C, Leibfritz D. Fast 3D H‐1 spectroscopic imaging at 3 tesla using spectroscopic missing‐pulse SSFP with 3D spatial preselection. Magn Reson Med. 2007;57(1):82‐89. [DOI] [PubMed] [Google Scholar]
26. Schuster C, Dreher W, Stadler J, Bernarding J, Leibfritz D. Fast three‐dimensional ¹H MR spectroscopic imaging at 7 tesla using "spectroscopic missing pulse—SSFP". Magn Reson Med. 2008;60(5):1243‐1249. [DOI] [PubMed] [Google Scholar]
27. Dreher W, Erhard P, Leibfritz D. Fast three‐dimensional proton spectroscopic imaging of the human brain at 3 T by combining spectroscopic missing pulse steady‐state free precession and echo planar spectroscopic imaging. Magn Reson Med. 2011;66(6):1518‐1525. [DOI] [PubMed] [Google Scholar]
28. Guo JY, Patay Z, Reddick WE. Fast frequency‐sweep spectroscopic imaging with an ultra‐low flip angle. Sci Rep. 2016;6:1‐12. [DOI] [PMC free article] [PubMed] [Google Scholar]
29. Varma G, Wang XE, Vinogradov E, et al. Selective spectroscopic imaging of hyperpolarized pyruvate and its metabolites using a single‐echo variable phase advance method in balanced SSFP. Magn Reson Med. 2016;76(4):1102‐1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
30. Valkovic L, Chmelik M, Meyerspeer M, et al. Dynamic P‐31‐MRSI using spiral spectroscopic imaging can map mitochondrial capacity in muscles of the human calf during plantar flexion exercise at 7 T. NMR Biomed. 2016;29(12):1825‐1834. [DOI] [PMC free article] [PubMed] [Google Scholar]
31. Mirkes C, Shajan G, Chadzynski G, Buckenmaier K, Bender B, Scheffler K. P‐31 CSI of the human brain in healthy subjects and tumor patients at 9.4 T with a three‐layered multi‐nuclear coil: initial results. Magn Reson Mater Phys Biol Med. 2016;29(3):579‐589. [DOI] [PubMed] [Google Scholar]
32. Lei H, Zhu XH, Zhang XL, Ugurbil K, Chen W. In vivo P‐31 magnetic resonance spectroscopy of human brain at 7 T: an initial experience. Magn Reson Med. 2003;49(2):199‐205. [DOI] [PubMed] [Google Scholar]
33. Chmelik M, Povazan M, Krssak M, et al. In vivo ³¹P magnetic resonance spectroscopy of the human liver at 7 T: an initial experience. NMR Biomed. 2014;27(4):478‐485. [DOI] [PubMed] [Google Scholar]
34. van der Velden TA, Italiaander M, van der Kemp WJM, et al. Radiofrequency configuration to facilitate bilateral breast P‐31 MR spectroscopic imaging and high‐resolution MRI at 7 tesla. Magn Reson Med. 2015;74(6):1803‐1810. [DOI] [PubMed] [Google Scholar]
35. Hu S, Lustig M, Balakrishnan A, et al. 3D compressed sensing for highly accelerated hyperpolarized C‐13 MRSI with in vivo applications to transgenic mouse models of cancer. Magn Reson Med. 2010;63(2):312‐321. [DOI] [PMC free article] [PubMed] [Google Scholar]
36. Hu S, Lustig M, Chen AP, et al. Compressed sensing for resolution enhancement of hyperpolarized C‐13 flyback 3D‐MRSI. J Magn Reson. 2008;192(2):258‐264. [DOI] [PMC free article] [PubMed] [Google Scholar]
37. Josan S, Spielman D, Yen YF, Hurd R, Pfefferbaum A, Mayer D. Fast volumetric imaging of ethanol metabolism in rat liver with hyperpolarized [1‐¹³C]pyruvate. NMR Biomed. 2012;25(8):993‐999. [DOI] [PMC free article] [PubMed] [Google Scholar]
38. Larson PEZ, Hu S, Lustig M, et al. Fast dynamic 3D MR spectroscopic imaging with compressed sensing and multiband excitation pulses for hyperpolarized C‐13 studies. Magn Reson Med. 2011;65(3):610‐619. [DOI] [PMC free article] [PubMed] [Google Scholar]
39. Boer VO, Siero JCW, Hoogduin H, van Gorp JS, Luijten PR, Klomp DWJ. High‐field MRS of the human brain at short TE and TR. NMR Biomed. 2011;24(9):1081‐1088. [DOI] [PubMed] [Google Scholar]
40. Chadzynski GL, Bause J, Shajan G, Pohmann R, Scheffler K, Ehses P. Fast and efficient free induction decay MR spectroscopic imaging of the human brain at 9.4 Tesla. Magn Reson Med. 2017;78(4):1281‐1295. [DOI] [PubMed] [Google Scholar]
41. Hangel G, Strasser B, Povazan M, et al. Ultra‐high resolution brain metabolite mapping at 7 T by short‐TR Hadamard‐encoded FID‐MRSI. NeuroImage. 2018;168:199‐210. [DOI] [PubMed] [Google Scholar]
42. Kukurova IJ, Valkovic L, Bogner W, et al. Two‐dimensional spectroscopic imaging with combined free induction decay and long‐TE acquisition (FID echo spectroscopic imaging, FIDESI) for the detection of intramyocellular lipids in calf muscle at 7 T. NMR Biomed. 2014;27(8):980‐987. [DOI] [PubMed] [Google Scholar]
43. Henning A, Fuchs A, Murdoch JB, Boesiger P. Slice‐selective FID acquisition, localized by outer volume suppression (FIDLOVS) for H‐1‐MRSI of the human brain at 7 T with minimal signal loss. NMR Biomed. 2009;22(7):683‐696. [DOI] [PubMed] [Google Scholar]
44. Bogner W, Gruber S, Trattnig S, Chmelik M. High‐resolution mapping of human brain metabolites by free induction decay ¹H MRSI at 7 T. NMR Biomed. 2012;25(6):873‐882. [DOI] [PubMed] [Google Scholar]
45. Lam F, Li Y, Guo R, Clifford B, Liang ZP. Ultrafast magnetic resonance spectroscopic imaging using SPICE with learned subspaces. Magn Reson Med. 2019;83(2):377‐390. [DOI] [PMC free article] [PubMed] [Google Scholar]
46. Heckova E, Povazan M, Strasser B, et al. Effects of different macromolecular models on reproducibility of FID‐MRSI at 7T. Magn Reson Med. 2019;83(1):12‐21. [DOI] [PMC free article] [PubMed] [Google Scholar]
47. Lam F, Li YD, Clifford B, Liang ZP. Macromolecule mapping of the brain using ultrashort‐TE acquisition and reference‐based metabolite removal. Magn Reson Med. 2018;79(5):2460‐2469. [DOI] [PubMed] [Google Scholar]
48. Povazan M, Hangel G, Strasser B, et al. Mapping of brain macromolecules and their use for spectral processing of H‐1‐MRSI data with an ultra‐short acquisition delay at 7 T. NeuroImage. 2015;121:126‐135. [DOI] [PubMed] [Google Scholar]
49. Hangel G, Jain S, Springer E, et al. High‐resolution metabolic mapping of gliomas via patch‐based super‐resolution magnetic resonance spectroscopic imaging at 7T. NeuroImage. 2019;191:587‐595. [DOI] [PMC free article] [PubMed] [Google Scholar]
50. Heckova E, Strasser B, Hangel GJ, et al. 7 T magnetic resonance spectroscopic imaging in multiple sclerosis: how does spatial resolution affect the detectability of metabolic changes in brain lesions? Invest Radiol. 2019;54(4):247‐254. [DOI] [PMC free article] [PubMed] [Google Scholar]
51. Gruber S, Heckova E, Strasser B, et al. Mapping an extended neurochemical profile at 3 and 7 T using accelerated high‐resolution proton magnetic resonance spectroscopic imaging. Invest Radiol. 2017;52(10):631‐639. [DOI] [PubMed] [Google Scholar]
52. Strasser B, Povazan M, Hangel G, et al. (2+1)D‐CAIPIRINHA accelerated MR spectroscopic imaging of the brain at 7T. Magn Reson Med. 2017;78(2):429‐440. [DOI] [PMC free article] [PubMed] [Google Scholar]
53. Strasser B, Chmelik M, Robinson SD, et al. Coil combination of multichannel MRSI data at 7 T: MUSICAL. NMR Biomed. 2013;26(12):1796‐1805. [DOI] [PMC free article] [PubMed] [Google Scholar]
54. Chang P, Nassirpour S, Avdievitch N, Henning A. Non‐water‐suppressed H‐1 FID‐MRSI at 3T and 9.4T. Magn Reson Med. 2018;80(2):442‐451. [DOI] [PubMed] [Google Scholar]
55. Nassirpour S, Chang P, Kirchner T, Henning A. Over‐discretized SENSE reconstruction and B ₀ correction for accelerated non‐lipid‐suppressed ¹H FID MRSI of the human brain at 9.4 T. NMR Biomed. 2018;31(12):1‐14:e4014. [DOI] [PubMed] [Google Scholar]
56. Nassirpour S, Chang P, Henning A. MultiNet PyGRAPPA: multiple neural networks for reconstructing variable density GRAPPA (a ¹H FID MRSI study). NeuroImage. 2018;183:336‐345. [DOI] [PubMed] [Google Scholar]
57. Nassirpour S, Chang P, Avdievitch N, Henning A. Compressed sensing for high‐resolution nonlipid suppressed H‐1 FID MRSI of the human brain at 9.4T. Magn Reson Med. 2018;80(6):2311‐2325. [DOI] [PubMed] [Google Scholar]
58. Klauser A, Courvoisier S, Kasten J, et al. Fast high‐resolution brain metabolite mapping on a clinical 3T MRI by accelerated H‐1‐FID‐MRSI and low‐rank constrained reconstruction. Magn Reson Med. 2019;81(5):2841‐2857. [DOI] [PubMed] [Google Scholar]
59. De Feyter HM, Behar KL, Corbin ZA, et al. Deuterium metabolic imaging (DMI) for MRI‐based 3D mapping of metabolism in vivo. Sci Adv. 2018;4(8):1‐11:eaat7314. [DOI] [PMC free article] [PubMed] [Google Scholar]
60. Jain S, Sima DM, Nezhad FS, et al. Patch‐based super‐resolution of MR spectroscopic images: application to multiple sclerosis. Front Neurosci. 2017;11:1‐12. [DOI] [PMC free article] [PubMed] [Google Scholar]
61. Schreiner SJ, Kirchner T, Narkhede A, et al. Brain amyloid burden and cerebrovascular disease are synergistically associated with neurometabolism in cognitively unimpaired older adults. Neurobiol Aging. 2018;63:152‐161. [DOI] [PubMed] [Google Scholar]
62. Schreiner SJ, Kirchner T, Wyss M, et al. Low episodic memory performance in cognitively normal elderly subjects is associated with increased posterior cingulate gray matter N‐acetylaspartate: a ¹H MRSI study at 7 Tesla. Neurobiol Aging. 2016;48:195‐203. [DOI] [PubMed] [Google Scholar]
63. Hingerl L, Bogner W, Moser P, et al. Density‐weighted concentric circle trajectories for high resolution brain magnetic resonance spectroscopic imaging at 7T. Magn Reson Med. 2018;79(6):2874‐2885. [DOI] [PMC free article] [PubMed] [Google Scholar]
64. Moser P, Bogner W, Hingerl L, et al. Non‐Cartesian GRAPPA and coil combination using interleaved calibration data—application to concentric‐ring MRSI of the human brain at 7T. Magn Reson Med. 2019;82(5):1587‐1603. [DOI] [PMC free article] [PubMed] [Google Scholar]
65. Tsai SY, Otazo R, Posse S, et al. Accelerated proton echo planar spectroscopic imaging (PEPSI) using GRAPPA with a 32‐channel phased‐array coil. Magn Reson Med. 2008;59(5):989‐998. [DOI] [PubMed] [Google Scholar]
66. Posse S, Tedeschi G, Risinger R, Ogg R, Lebihan D. High‐speed H‐1 spectroscopic imaging in human brain by echo‐planar spatial‐spectral encoding. Magn Reson Med. 1995;33(1):34‐40. [DOI] [PubMed] [Google Scholar]
67. Kim DH, Spielman DM. Reducing gradient imperfections for spiral magnetic resonance spectroscopic imaging. Magn Reson Med. 2006;56(1):198‐203. [DOI] [PubMed] [Google Scholar]
68. Tsai SY, Lin YR, Wang WC, Niddam DM. Short‐ and long‐term quantitation reproducibility of brain metabolites in the medial wall using proton echo planar spectroscopic imaging. NeuroImage. 2012;63(3):1020‐1029. [DOI] [PubMed] [Google Scholar]
69. Ding XQ, Maudsley AA, Sabati M, Sheriff S, Dellani PR, Lanfermann H. Reproducibility and reliability of short‐TE whole‐brain MR spectroscopic imaging of human brain at 3T. Magn Reson Med. 2015;73(3):921‐928. [DOI] [PMC free article] [PubMed] [Google Scholar]
70. Maudsley AA, Domenig C, Sheriff S. Reproducibility of serial whole‐brain MR Spectroscopic Imaging. NMR Biomed. 2010;23(3):251‐256. [DOI] [PMC free article] [PubMed] [Google Scholar]
71. Hnilicova P, Povazan M, Strasser B, et al. Spatial variability and reproducibility of GABA‐edited MEGA‐LASER 3D‐MRSI in the brain at 3T. NMR Biomed. 2016;29(11):1656‐1665. [DOI] [PMC free article] [PubMed] [Google Scholar]
72. Gagoski B. Magnetic Resonance Spectroscopic Imaging using Parallel Transmission at 7T. Cambridge, MA: Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology; 2011.
73. Otazo R, Mueller B, Ugurbil K, Wald L, Posse S. Signal‐to‐noise ratio and spectral linewidth improvements between 1.5 and 7 tesla in proton echo‐planar spectroscopic imaging. Magn Reson Med. 2006;56(6):1200‐1210. [DOI] [PubMed] [Google Scholar]
74. Pohmann R, von Kienlin M, Haase A. Theoretical evaluation and comparison of fast chemical shift imaging methods. J Magn Reson. 1997;129(2):145‐160. [DOI] [PubMed] [Google Scholar]
75. Posse S, Decarli C, Lebihan D. 3‐dimensional echo‐planar MR spectroscopic imaging at short echo times in the human brain. Radiology. 1994;192(3):733‐738. [DOI] [PubMed] [Google Scholar]
76. Adalsteinsson E, Irarrazabal P, Topp S, Meyer C, Macovski A, Spielman DM. Volumetric spectroscopic imaging with spiral‐based k‐space trajectories. Magn Reson Med. 1998;39(6):889‐898. [DOI] [PubMed] [Google Scholar]
77. Ebel A, Maudsley AA, Weiner MW, Schuff N. Achieving sufficient spectral bandwidth for volumetric H‐1 echo‐planar spectroscopic imaging at 4 Tesla. Magn Reson Med. 2005;54(3):697‐701. [DOI] [PMC free article] [PubMed] [Google Scholar]
78. Coello E, Noeske R, Burns BL, et al. High‐resolution echo‐planar spectroscopic imaging at ultra‐high field. NMR Biomed. 2018;31(11):1‐10:e3950. [DOI] [PubMed] [Google Scholar]
79. An ZX, Tiwari V, Ganji SK, et al. Echo‐planar spectroscopic imaging with dual‐readout alternated gradients (DRAG‐EPSI) at 7 T: application for 2‐hydroxyglutarate imaging in glioma patients. Magn Reson Med. 2018;79(4):1851‐1861. [DOI] [PMC free article] [PubMed] [Google Scholar]
80. Furuyama JK, Wilson NE, Thomas MA. Spectroscopic imaging using concentrically circular echo‐planar trajectories in vivo. Magn Reson Med. 2012;67(6):1515‐1522. [DOI] [PubMed] [Google Scholar]
81. Schirda CV, Tanase C, Boada FE. Rosette spectroscopic imaging: optimal parameters for alias‐free, high sensitivity spectroscopic imaging. J Magn Reson Imaging. 2009;29(6):1375‐1385. [DOI] [PubMed] [Google Scholar]
82. Schmidt R, Seginer A, Tal A. Combining multiband slice selection with consistent k‐t‐space EPSI for accelerated spectral imaging. Magn Reson Med. 2019;82(3):867‐876. [DOI] [PMC free article] [PubMed] [Google Scholar]
83. Korzowski A, Bachert P. High‐resolution P‐31 echo‐planar spectroscopic imaging in vivo at 7T. Magn Reson Med. 2018;79(3):1251‐1259. [DOI] [PubMed] [Google Scholar]
84. Bhaduri S, Clement P, Achten E, Serrai H. Reduction of Acquisition time using Partition of the signal Decay in Spectroscopic Imaging technique (RAPID‐SI). PLoS ONE. 2018;13(11):e0207015. [DOI] [PMC free article] [PubMed] [Google Scholar]
85. Cao P, Shin PJ, Park I, et al. Accelerated high‐bandwidth MR spectroscopic imaging using compressed sensing. Magn Reson Med. 2016;76(2):369‐379. [DOI] [PMC free article] [PubMed] [Google Scholar]
86. Jiang WW, Lustig M, Larson PEZ. Concentric rings K‐space trajectory for hyperpolarized ¹³C MR spectroscopic imaging. Magn Reson Med. 2016;75(1):19‐31. [DOI] [PMC free article] [PubMed] [Google Scholar]
87. Dixon WT. Simple proton spectroscopic imaging. Radiology. 1984;153(1):189‐194. [DOI] [PubMed] [Google Scholar]
88. Reeder SB, Pineda AR, Wen ZF, et al. Iterative decomposition of water and fat with echo asymmetry and least‐squares estimation (IDEAL): application with fast spin‐echo imaging. Magn Reson Med. 2005;54(3):636‐644. [DOI] [PubMed] [Google Scholar]
89. Reeder SB, Brittain JH, Grist TM, Yen YF. Least‐squares chemical shift separation for C‐13 metabolic imaging. J Magn Reson Imaging. 2007;26(4):1145‐1152. [DOI] [PubMed] [Google Scholar]
90. Wiesinger F, Weidl E, Menzel MI, et al. IDEAL spiral CSI for dynamic metabolic MR imaging of hyperpolarized [1‐¹³C]pyruvate. Magn Reson Med. 2012;68(1):8‐16. [DOI] [PubMed] [Google Scholar]
91. Gordon JW, Niles DJ, Fain SB, Johnson KM. Joint spatial‐spectral reconstruction and k‐t spirals for accelerated 2D spatial/1D spectral imaging of ¹³C dynamics. Magn Reson Med. 2014;71(4):1435‐1445. [DOI] [PMC free article] [PubMed] [Google Scholar]
92. Sigfridsson A, Weiss K, Wissmann L, et al. Hybrid multiband excitation multiecho acquisition for hyperpolarized C‐13 spectroscopic imaging. Magn Reson Med. 2015;73(5):1713‐1717. [DOI] [PubMed] [Google Scholar]
93. Wespi P, Steinhauser J, Kwiatkowski G, Kozerke S. High‐resolution hyperpolarized metabolic imaging of the rat heart using k‐t PCA and k‐t SPARSE. NMR Biomed. 2018;31(2):1‐11:e3876. [DOI] [PubMed] [Google Scholar]
94. Zanette B, Santyr G. Accelerated interleaved spiral‐IDEAL imaging of hyperpolarized Xe‐129 for parametric gas exchange mapping in humans. Magn Reson Med. 2019;82(3):1113‐1119. [DOI] [PubMed] [Google Scholar]
95. Mani M, Magnotta V, Jacob M. A general algorithm for compensation of trajectory errors: application to radial imaging. Magn Reson Med. 2018;80(4):1605‐1613. [DOI] [PMC free article] [PubMed] [Google Scholar]
96. Ramirez MS, Lee J, Walker CM, et al. Radial spectroscopic MRI of hyperpolarized [1‐C‐13] pyruvate at 7 tesla. Magn Reson Med. 2014;72(4):986‐995. [DOI] [PMC free article] [PubMed] [Google Scholar]
97. Metzger G, Hu XP. Application of interlaced Fourier transform to echo‐planar spectroscopic imaging. J Magn Reson. 1997;125(1):166‐170. [DOI] [PubMed] [Google Scholar]
98. Labadie C, Hetzer S, Schulz J, Mildner T, Aubert‐Frecon M, Moller HE. Center‐out echo‐planar spectroscopic imaging with correction of gradient‐echo phase and time shifts. Magn Reson Med. 2013;70(1):16‐24. [DOI] [PubMed] [Google Scholar]
99. Chu A, Alger JR, Moore GJ, Posse S. Proton echo‐planar spectroscopic imaging with highly effective outer volume suppression using combined presaturation and spatially selective echo dephasing. Magn Reson Med. 2003;49(5):817‐821. [DOI] [PubMed] [Google Scholar]
100. Maudsley AA, Domenig C, Govind V, et al. Mapping of brain metabolite distributions by volumetric proton MR spectroscopic imaging (MRSI). Magn Reson Med. 2009;61(3):548‐559. [DOI] [PMC free article] [PubMed] [Google Scholar]
101. Bito Y, Hirata S, Nabeshima T, Yamamoto E. Echo‐planar diffusion spectroscopic imaging. Magn Reson Med. 1995;33(1):69‐73. [DOI] [PubMed] [Google Scholar]
102. Bito Y, Hirata K, Ebisu T, et al. Diffusion‐weighted line‐scan echo‐planar spectroscopic imaging technique to reduce motion artifacts in metabolite diffusion imaging. Magn Reson Med Sci. 2015;14(1):43‐50. [DOI] [PubMed] [Google Scholar]
103. Fotso K, Dager SR, Landow A, et al. Diffusion tensor spectroscopic imaging of the human brain in children and adults. Magn Reson Med. 2017;78(4):1246‐1256. [DOI] [PMC free article] [PubMed] [Google Scholar]
104. Ye QM, Chen L, Qiu WQ, et al. Accelerating two‐dimensional nuclear magnetic resonance correlation spectroscopy via selective coherence transfer. J Chem Phys. 2017;146(1):1‐12:014202. [DOI] [PubMed] [Google Scholar]
105. Furuyama JK, Nagarajan R, Roberts CK, Lee CC, Hahn TJ, Thomas MA. A pilot validation of multi‐echo based echo‐planar correlated spectroscopic imaging in human calf muscles. NMR Biomed. 2014;27(10):1176‐1183. [DOI] [PMC free article] [PubMed] [Google Scholar]
106. Wilson NE, Burns BL, Iqbal Z, Thomas MA. Correlated spectroscopic imaging of calf muscle in three spatial dimensions using group sparse reconstruction of undersampled single and multichannel data. Magn Reson Med. 2015;74(5):1199‐1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
107. Nagarajan R, Carpenter CL, Lee CC, et al. Assessment of lipid and metabolite changes in obese calf muscle using multi‐echo echo‐planar correlated spectroscopic imaging. Sci Rep. 2017;7:1‐10. [DOI] [PMC free article] [PubMed] [Google Scholar]
108. Lipnick S, Verma G, Ramadan S, Furuyama J, Thomas MA. Echo planar correlated spectroscopic imaging: implementation and pilot evaluation in human calf in vivo. Magn Reson Med. 2010;64(4):947‐956. [DOI] [PMC free article] [PubMed] [Google Scholar]
109. Furuyama JK, Wilson NE, Burns BL, Nagarajan R, Margolis DJ, Thomas MA. Application of compressed sensing to multidimensional spectroscopic imaging in human prostate. Magn Reson Med. 2012;67(6):1499‐1505. [DOI] [PubMed] [Google Scholar]
110. Sarma MK, Nagarajan R, Iqbal Z, Macey PM, Thomas MA. Echo‐planar J‐resolved spectroscopic imaging using dual read‐outs: implementation and quantitation of human brain metabolites. Sci Rep. 2017;7:1‐11. [DOI] [PMC free article] [PubMed] [Google Scholar]
111. Sarma MK, Macey PM, Nagarajan R, Aysola R, Harper RM, Thomas MA. Accelerated echo planar J‐resolved spectroscopic imaging of putamen and thalamus in obstructive sleep apnea. Sci Rep. 2016;6:1‐10. [DOI] [PMC free article] [PubMed] [Google Scholar]
112. Sarma MK, Nagarajan R, Macey PM, et al. Accelerated echo‐planar J‐resolved spectroscopic imaging in the human brain using compressed sensing: a pilot validation in obstructive sleep apnea. Am J Neuroradiol. 2014;35(6):S81‐S89. [DOI] [PMC free article] [PubMed] [Google Scholar]
113. Iqbal Z, Wilson NE, Thomas MA. Prior‐knowledge fitting of accelerated five‐dimensional echo planar J‐resolved spectroscopic imaging: effect of nonlinear reconstruction on quantitation. Sci Rep. 2017;7:1‐12. [DOI] [PMC free article] [PubMed] [Google Scholar]
114. Iqbal Z, Wilson NE, Keller MA, et al. Pilot assessment of brain metabolism in perinatally HIV‐infected youths using accelerated 5D echo planar J‐resolved spectroscopic imaging. PLoS ONE. 2016;11(9):e0162810. [DOI] [PMC free article] [PubMed] [Google Scholar]
115. Magnusson PO, Boer VO, Marsman A, Paulson OB, Hanson LG, Petersen ET. Gamma‐aminobutyric acid edited echo‐planar spectroscopic imaging (EPSI) with MEGA‐sLASER at 7T. Magn Reson Med. 2019;81(2):773‐780. [DOI] [PMC free article] [PubMed] [Google Scholar]
116. McDannold N, Barnes AS, Rybicki FJ, et al. Temperature mapping considerations in the breast with line scan echo planar spectroscopic imaging. Magn Reson Med. 2007;58(6):1117‐1123. [DOI] [PubMed] [Google Scholar]
117. Tsai SY, Posse S, Lin YR, et al. Fast mapping of the T ₂ relaxation time of cerebral metabolites using proton echo‐planar spectroscopic imaging (PEPSI). Magn Reson Med. 2007;57(5):859‐865. [DOI] [PubMed] [Google Scholar]
118. Tsai SY, Wang WC, Lin YR. Comparison of sagittal and transverse echo planar spectroscopic imaging on the quantification of brain metabolites. J Neuroimaging. 2015;25(2):167‐174. [DOI] [PubMed] [Google Scholar]
119. Lecocq A, Le Fur Y, Maudsley AA, et al. Whole‐brain quantitative mapping of metabolites using short echo three‐dimensional proton MRSI. J Magn Reson Imaging. 2015;42(2):280‐289. [DOI] [PMC free article] [PubMed] [Google Scholar]
120. Verma G, Chawla S, Mohan S, et al. Three‐dimensional echo planar spectroscopic imaging for differentiation of true progression from pseudoprogression in patients with glioblastoma. NMR Biomed. 2019;32(2):1‐10:e4042. [DOI] [PMC free article] [PubMed] [Google Scholar]
121. Maudsley AA, Roy B, Gupta RK, et al. Association of metabolite concentrations and water diffusivity in normal appearing brain tissue with glioma grade. J Neuroimaging. 2014;24(6):585‐589. [DOI] [PMC free article] [PubMed] [Google Scholar]
122. Chawla S, Wang SM, Kim S, et al. Radiation injury to the normal brain measured by 3D‐echo‐planar spectroscopic imaging and diffusion tensor imaging: initial experience. J Neuroimaging. 2015;25(1):97‐104. [DOI] [PubMed] [Google Scholar]
123. Maudsley AA, Gupta RK, Stoyanova R, et al. Mapping of glycine distributions in gliomas. Am J Neuroradiol. 2014;35(6):S31‐S36. [DOI] [PMC free article] [PubMed] [Google Scholar]
124. Verma G, Woo JH, Chawla S, et al. Whole‐brain analysis of amyotrophic lateral sclerosis by using echo‐planar spectroscopic imaging. Radiology. 2013;267(3):851‐857. [DOI] [PMC free article] [PubMed] [Google Scholar]
125. Bustillo JR, Chen HJ, Gasparovic C, et al. Glutamate as a marker of cognitive function in schizophrenia: a proton spectroscopic imaging study at 4 tesla. Biol Psychiatry. 2011;69(1):19‐27. [DOI] [PMC free article] [PubMed] [Google Scholar]
126. Richards TL, Berninger VW, Aylward EH, et al. Reproducibility of proton MR spectroscopic imaging (PEPSI): comparison of dyslexic and normal‐reading children and effects of treatment on brain lactate levels during language tasks. Am J Neuroradiol. 2002;23(10):1678‐1685. [PMC free article] [PubMed] [Google Scholar]
127. Zhao CG, Bolan PJ, Royce M, et al. Quantitative mapping of total choline in healthy human breast using proton echo planar spectroscopic imaging (PEPSI) at 3 Tesla. J Magn Reson Imaging. 2012;36(5):1113‐1123. [DOI] [PMC free article] [PubMed] [Google Scholar]
128. Medved M, Ivancevic MK, Olopade OI, Newstead GM, Karczmar GS. Echo‐planar spectroscopic imaging (EPSI) of the water resonance structure in human breast using sensitivity encoding (SENSE). Magn Reson Med. 2010;63(6):1557‐1563. [DOI] [PMC free article] [PubMed] [Google Scholar]
129. Lin YR, Chiu JJ, Tsai SY. Feasibility and reproducibility of echo planar spectroscopic imaging on the quantification of hepatic fat. PLoS ONE. 2014;9(12):e114436. [DOI] [PMC free article] [PubMed] [Google Scholar]
130. Weis J, Bruvold M, Ortiz‐Nieto F, Ahlstrom H. High‐resolution echo‐planar spectroscopic imaging of the human calf. PLoS ONE. 2014;9(1):e87533. [DOI] [PMC free article] [PubMed] [Google Scholar]
131. Cunningham CH, Vigneron DB, Chen AP, et al. Design of flyback echo‐planar readout gradients for magnetic resonance spectroscopic imaging. Magn Reson Med. 2005;54(5):1286‐1289. [DOI] [PubMed] [Google Scholar]
132. Morgan PS, Bowtell RW, McIntyre DJO, Worthington BS. Correction of spatial distortion in EPI due to inhomogeneous static magnetic fields using the reversed gradient method. J Magn Reson Imaging. 2004;19(4):499‐507. [DOI] [PubMed] [Google Scholar]
133. Webb P, Spielman D, Macovski A. A fast spectroscopic imaging method using a blipped phase encode gradient. Magn Reson Med. 1989;12(3):306‐315. [DOI] [PubMed] [Google Scholar]
134. Tyszka JM, Mamelak AN. Volumetric multishot echo‐planar spectroscopic imaging. Magn Reson Med. 2001;46(2):219‐227. [DOI] [PubMed] [Google Scholar]
135. Park I, Chen AP, Zierhut ML, Ozturk‐Isik E, Vigneron DB, Nelson SJ. Implementation of 3 T lactate‐edited 3D H‐1 MR spectroscopic imaging with flyback echo‐planar readout for gliomas patients. Ann Biomed Eng. 2011;39(1):193‐204. [DOI] [PMC free article] [PubMed] [Google Scholar]
136. Li Y, Larson P, Chen AP, et al. Short‐echo three‐dimensional H‐1 MR spectroscopic imaging of patients with glioma at 7 tesla for characterization of differences in metabolite levels. J Magn Reson Imaging. 2015;41(5):1332‐1341. [DOI] [PMC free article] [PubMed] [Google Scholar]
137. Chen AP, Cunningham CH, Ozturk‐Isik E, et al. High‐speed 3T MR spectroscopic imaging of prostate with flyback echo‐planar encoding. J Magn Reson Imaging. 2007;25(6):1288‐1292. [DOI] [PubMed] [Google Scholar]
138. Cunningham CH, Chen AP, Albers MJ, et al. Double spin‐echo sequence for rapid spectroscopic imaging of hyperpolarized C‐13. J Magn Reson. 2007;187(2):357‐362. [DOI] [PubMed] [Google Scholar]
139. Santos‐Diaz A, Obruchkov SI, Schulte RF, Noseworthy MD. Phosphorus magnetic resonance spectroscopic imaging using flyback echo planar readout trajectories. Magn Reson Mater Phys Biol Med. 2018;31(4):553‐564. [DOI] [PubMed] [Google Scholar]
140. Uribe S, Guesalaga A, Mir R, Guarini M, Irarrazaval P. A 3D trajectory for undersampling k‐space in MRSI applications. Magn Reson Imaging. 2007;25(3):350‐358. [DOI] [PubMed] [Google Scholar]
141. Kim DH, Henry R, Spielman DM. Fast multivoxel two‐dimensional spectroscopic imaging at 3 T. Magn Reson Imaging. 2007;25(8):1155‐1161. [DOI] [PMC free article] [PubMed] [Google Scholar]
142. Chatnuntawech I, Gagoski B, Bilgic B, Cauley SF, Setsompop K, Adalsteinsson E. Accelerated ¹H MRSI using randomly undersampled spiral‐based k‐space trajectories. Magn Reson Med. 2015;74(1):13‐24. [DOI] [PubMed] [Google Scholar]
143. Levin YS, Mayer D, Yen YF, Hurd RE, Spielman DM. Optimization of fast spiral chemical shift imaging using least squares reconstruction: application for hyperpolarized C‐13 metabolic imaging. Magn Reson Med. 2007;58(2):245‐252. [DOI] [PubMed] [Google Scholar]
144. Park JM, Josan S, Jang T, et al. Volumetric spiral chemical shift imaging of hyperpolarized [2‐¹³C]pyruvate in a rat C6 glioma model. Magn Reson Med. 2016;75(3):973‐984. [DOI] [PMC free article] [PubMed] [Google Scholar]
145. Wang JX, Merritt ME, Sherry D, Malloy CR. A general chemical shift decomposition method for hyperpolarized C‐13 metabolite magnetic resonance imaging. Magn Reson Chem. 2016;54(8):665‐673. [DOI] [PMC free article] [PubMed] [Google Scholar]
146. Khegai O, Schulte RF, Janich MA, et al. Apparent rate constant mapping using hyperpolarized [1‐C‐13]pyruvate. NMR Biomed. 2014;27(10):1256‐1265. [DOI] [PubMed] [Google Scholar]
147. Xu T, Mayer D, Gu M, et al. Quantification of in vivo metabolic kinetics of hyperpolarized pyruvate in rat kidneys using dynamic C‐13 MRSI. NMR Biomed. 2011;24(8):997‐1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
148. Santos‐Diaz A, Harasym D, Noseworthy MD. Dynamic 31P spectroscopic imaging of skeletal muscles combining flyback echo‐planar spectroscopic imaging and compressed sensing. Magn Reson Med. 2019;81(6):3453‐3461. [DOI] [PubMed] [Google Scholar]
149. Bogner W, Gagoski B, Hess AT, et al. 3D GABA imaging with real‐time motion correction, shim update and reacquisition of adiabatic spiral MRSI. NeuroImage. 2014;103:290‐302. [DOI] [PMC free article] [PubMed] [Google Scholar]
150. Andronesi OC, Arrillaga‐Romany IC, Ly KI, et al. Pharmacodynamics of mutant‐IDH1 inhibitors in glioma patients probed by in vivo 3D MRS imaging of 2‐hydroxyglutarate. Nat Commun. 2018;9:1‐9. [DOI] [PMC free article] [PubMed] [Google Scholar]
151. Heckova E, Povazan M, Strasser B, et al. Real‐time correction of motion and imager instability artifacts during 3D gamma‐aminobutyric acid‐edited MR spectroscopic imaging. Radiology. 2018;286(2):666‐675. [DOI] [PMC free article] [PubMed] [Google Scholar]
152. Jafari‐Khouzani K, Loebel F, Bogner W, et al. Volumetric relationship between 2‐hydroxyglutarate and FLAIR hyperintensity has potential implications for radiotherapy planning of mutant IDH glioma patients. Neuro‐Oncology. 2016;18(11):1569‐1578. [DOI] [PMC free article] [PubMed] [Google Scholar]
153. Andronesi OC, Loebel F, Bogner W, et al. Treatment response assessment in IDH‐mutant glioma patients by noninvasive 3D functional spectroscopic mapping of 2‐hydroxyglutarate. Clin Cancer Res. 2016;22(7):1632‐1641. [DOI] [PMC free article] [PubMed] [Google Scholar]
154. Bogner W, Hess AT, Gagoski B, et al. Real‐time motion‐ and B₀‐correction for LASER‐localized spiral‐accelerated 3D‐MRSI of the brain at 3 T. NeuroImage. 2014;88:22‐31. [DOI] [PMC free article] [PubMed] [Google Scholar]
155. Kim DH, Gu M, Cunningham C, et al. Fast 3D H‐1 MRSI of the corticospinal tract in pediatric brain. J Magn Reson Imaging. 2009;29(1):1‐6. [DOI] [PMC free article] [PubMed] [Google Scholar]
156. Andronesi OC, Gagoski BA, Sorensen AG. Neurologic 3D MR spectroscopic imaging with low‐power adiabatic pulses and fast spiral acquisition. Radiology. 2012;262(2):647‐661. [DOI] [PMC free article] [PubMed] [Google Scholar]
157. Pfefferbaum A, Adalsteinsson E, Sullivan EV. Cortical NAA deficits in HIV infection without dementia: influence of alcoholism comorbidity. Neuropsychopharmacology. 2005;30(7):1392‐1399. [DOI] [PubMed] [Google Scholar]
158. Yazbek S, Prabhu SP, Connaughton P, Grant PE, Gagoski B. Comparison of accelerated 3‐D spiral chemical shift imaging and single‐voxel spectroscopy at 3T in the pediatric age group. Pediatr Radiol. 2015;45(9):1417‐1422. [DOI] [PubMed] [Google Scholar]
159. Steinseifer IK, Philips BWJ, Gagoski B, Weiland E, Scheenen TWJ, Heerschap A. Flexible proton 3D MR spectroscopic imaging of the prostate with low‐power adiabatic pulses for volume selection and spiral readout. Magn Reson Med. 2017;77(3):928‐935. [DOI] [PubMed] [Google Scholar]
160. Kim DH, Margolis D, Xing L, Daniel B, Spielman D. In vivo prostate magnetic resonance spectroscopic imaging using two‐dimensional J‐resolved PRESS at 3 T. Magn Reson Med. 2005;53(5):1177‐1182. [DOI] [PubMed] [Google Scholar]
161. Adalsteinsson E, Sullivan EV, Kleinhans N, Spielman DM, Pfefferbaum A. Longitudinal decline of the neuronal marker N‐acetyl aspartate in Alzheimer's disease. Lancet. 2000;355(9216):1696‐1697. [DOI] [PubMed] [Google Scholar]
162. Adalsteinsson E, Langer‐Gould A, Homer RJ, et al. Gray matter‐N‐acetyl aspartate deficits in secondary progressive but not relapsing‐remitting multiple sclerosis. Am J Neuroradiol. 2003;24(10):1941‐1945. [PMC free article] [PubMed] [Google Scholar]
163. Spurny B, Seiger R, Moser P, et al. Hippocampal GABA levels correlate with retrieval performance in an associative learning paradigm. NeuroImage. 2019;10(204):116‐244. [DOI] [PMC free article] [PubMed] [Google Scholar]
164. Gu M, Kim DH, Mayer D, Sullivan EV, Pfefferbaum A, Spielman DM. Reproducibility study of whole‐brain H‐1 spectroscopic imaging with automated quantification. Magn Reson Med. 2008;60(3):542‐547. [DOI] [PMC free article] [PubMed] [Google Scholar]
165. Kim DH, Adalsteinsson E, Spielman DM. Simple analytic variable density spiral design. Magn Reson Med. 2003;50(1):214‐219. [DOI] [PubMed] [Google Scholar]
166. Adalsteinsson E, Star‐Lack J, Meyer CH, Spielman DM. Reduced spatial side lobes in chemical‐shift imaging. Magn Reson Med. 1999;42(2):314‐323. [DOI] [PubMed] [Google Scholar]
167. Bilgic B, Gagoski B, Kok T, Adalsteinsson E. Lipid suppression in CSI with spatial priors and highly undersampled peripheral k‐space. Magn Reson Med. 2013;69(6):1501‐1511. [DOI] [PMC free article] [PubMed] [Google Scholar]
168. Bhattacharya I, Jacob M. Compartmentalized low‐rank recovery for high‐resolution lipid unsuppressed MRSI. Magn Reson Med. 2017;78(4):1267‐1280. [DOI] [PMC free article] [PubMed] [Google Scholar]
169. Bhave S, Eslami R, Jacob M. Sparse spectral deconvolution algorithm for noncartesian MR spectroscopic imaging. Magn Reson Med. 2014;71(2):469‐476. [DOI] [PubMed] [Google Scholar]
170. Sarkar S, Heberlein K, Hu XP. Truncation artifact reduction in spectroscopic imaging using a dual‐density spiral k‐space trajectory. Magn Reson Imaging. 2002;20(10):743‐757. [DOI] [PubMed] [Google Scholar]
171. Mayer D, Yen YF, Takahashi A, et al. Dynamic and high‐resolution metabolic imaging of hyperpolarized [1‐C‐13]‐pyruvate in the rat brain using a high‐performance gradient insert. Magn Reson Med. 2011;65(5):1228‐1233. [DOI] [PMC free article] [PubMed] [Google Scholar]
172. Hiba B, Faure B, Lamalle L, Decorps M, Ziegler A. Out‐and‐in spiral spectroscopic imaging in rat brain at 7 T. Magn Reson Med. 2003;50(6):1127‐1133. [DOI] [PubMed] [Google Scholar]
173. Chiew M, Jiang WW, Burns B, et al. Density‐weighted concentric rings k‐space trajectory for ¹H magnetic resonance spectroscopic imaging at 7T. NMR Biomed. 2018;31(1):1‐14:e3838. [DOI] [PMC free article] [PubMed] [Google Scholar]
174. Emir UE, Burns B, Chiew M, Jezzard P, Thomas MA. Non‐water‐suppressed short‐echo‐time magnetic resonance spectroscopic imaging using a concentric ring k‐space trajectory. NMR Biomed. 2017;30(7):1‐12:e3714. [DOI] [PMC free article] [PubMed] [Google Scholar]
175. Moser P, Hingerl L, Strasser B, et al. Whole‐slice mapping of GABA and GABA thorn at 7T via adiabatic MEGA‐editing, real‐time instability correction, and concentric circle readout. NeuroImage. 2019;184:475‐489. [DOI] [PMC free article] [PubMed] [Google Scholar]
176. Steel A, Chiew M, Jezzard P, et al. Metabolite‐cycled density‐weighted concentric rings k‐space trajectory (DW‐CRT) enables high‐resolution 1 H magnetic resonance spectroscopic imaging at 3‐Tesla. Sci Rep. 2018;8:1‐10. [DOI] [PMC free article] [PubMed] [Google Scholar]
177. Noll DC. Multishot rosette trajectories for spectrally selective MR imaging. IEEE Trans Med Imaging. 1997;16(4):372‐377. [DOI] [PubMed] [Google Scholar]
178. Schirda CV, Zhao TJ, Yushmanov VE, et al. Fast 3D rosette spectroscopic imaging of neocortical abnormalities at 3 T: assessment of spectral quality. Magn Reson Med. 2018;79(5):2470‐2480. [DOI] [PMC free article] [PubMed] [Google Scholar]
179. Schirda CV, Zhao TJ, Andronesi OC, et al. In vivo brain rosette spectroscopic imaging (RSI) with LASER excitation, constant gradient strength readout, and automated LCModel quantification for all voxels. Magn Reson Med. 2016;76(2):380‐390. [DOI] [PMC free article] [PubMed] [Google Scholar]
180. Li Y, Yang R, Zhang CS, Zhang JX, Jia S, Zhou ZY. Analysis of generalized rosette trajectory for compressed sensing MRI. Med Phys. 2015;42(9):5530‐5544. [DOI] [PubMed] [Google Scholar]
181. Ludwig D, Korzowski A, Ruhm L, Ladd ME, Bachert P. Three‐dimensional ³¹P radial echo‐planar spectroscopic imaging in vivo at 7T. Paper presented at: ISMRM 25th Annual Meeting and Exhibition; April 22‐27, 2017; Honolulu, HI.
182. Boer VO. Metabolite diffusion‐weighted imaging with golden angle radial echo planar spectroscopic imaging. Paper presented at: ISMRM Workshop on Ultrahigh Field Magnetic Resonance; March 31‐April 3, 2019; Dubrovnik, Croatia.
183. Kim DH, Adalsteinsson E, Spielman DM. Spiral readout gradients for the reduction of motion artifacts in chemical shift imaging. Magn Reson Med. 2004;51(3):458‐463. [DOI] [PubMed] [Google Scholar]
184. Ebel A, Maudsley AA. Detection and correction of frequency instabilities for volumetric H‐1 echo‐planar spectroscopic imaging. Magn Reson Med. 2005;53(2):465‐469. [DOI] [PubMed] [Google Scholar]
185. Hamilton J, Franson D, Seiberlich N. Recent advances in parallel imaging for MRI. Prog Nucl Magn Reson Spectrosc. 2017;101:71‐95. [DOI] [PMC free article] [PubMed] [Google Scholar]
186. Griswold MA, Breuer F, Blaimer M, et al. Autocalibrated coil sensitivity estimation for parallel imaging. NMR Biomed. 2006;19(3):316‐324. [DOI] [PubMed] [Google Scholar]
187. Pruessmann KP. Encoding and reconstruction in parallel MRI. NMR Biomed. 2006;19(3):288‐299. [DOI] [PubMed] [Google Scholar]
188. Dydak U, Weiger M, Pruessmann KP, Meier D, Boesiger P. Sensitivity‐encoded spectroscopic imaging. Magn Reson Med. 2001;46(4):713‐722. [DOI] [PubMed] [Google Scholar]
189. Zhu H, Soher BJ, Ouwerkerk R, Schar M, Barker PB. Spin‐echo magnetic resonance spectroscopic imaging at 7 T with frequency‐modulated refocusing pulses. Magn Reson Med. 2013;69(5):1217‐1225. [DOI] [PMC free article] [PubMed] [Google Scholar]
190. Otazo R, Tsai SY, Lin FH, Posse S. Accelerated short‐TE 3D proton echo‐planar spectroscopic Imaging using 2D‐SENSE with a 32‐channel array coil. Magn Reson Med. 2007;58(6):1107‐1116. [DOI] [PubMed] [Google Scholar]
191. Lin FH, Tsai SY, Otazo R, et al. Sensitivity‐encoded (SENSE) proton echo‐planar spectroscopic imaging (PEPSI) in the human brain. Magn Reson Med. 2007;57(2):249‐257. [DOI] [PubMed] [Google Scholar]
192. Kirchner T, Fillmer A, Henning A. Mechanisms of SNR and line shape improvement by B ₀ correction in overdiscrete MRSI reconstruction. Magn Reson Med. 2017;77(1):44‐56. [DOI] [PubMed] [Google Scholar]
193. Kirchner T, Fillmer A, Tsao J, Pruessmann KP, Henning A. Reduction of voxel bleeding in highly accelerated parallel H‐1 MRSI by direct control of the spatial response function. Magn Reson Med. 2015;73(2):469‐480. [DOI] [PubMed] [Google Scholar]
194. Lustig M, Pauly JM. SPIRiT: iterative self‐consistent parallel imaging reconstruction from arbitrary k‐space. Magn Reson Med. 2010;64(2):457‐471. [DOI] [PMC free article] [PubMed] [Google Scholar]
195. Uecker M, Lai P, Murphy MJ, et al. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med. 2014;71(3):990‐1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
196. Ozturk‐Isik E, Crane JC, Cha SM, Chang SM, Berger MS, Nelson SJ. Unaliasing lipid contamination for MR spectroscopic imaging of gliomas at 3T using sensitivity encoding (SENSE). Magn Reson Med. 2006;55(5):1164‐1169. [DOI] [PubMed] [Google Scholar]
197. Sanchez‐Gonzalez J, Tsao J, Dydak U, Desco M, Boesiger P, Pruessmann KP. Minimum‐norm reconstruction for sensitivity‐encoded magnetic resonance spectroscopic imaging. Magn Reson Med. 2006;55(2):287‐295. [DOI] [PubMed] [Google Scholar]
198. Otazo R, Lin FH, Wiggins G, Jordan R, Sodickson D, Posse S. Superresolution parallel magnetic resonance imaging: application to functional and spectroscopic imaging. NeuroImage. 2009;47(1):220‐230. [DOI] [PMC free article] [PubMed] [Google Scholar]
199. Ozturk‐Isik E, Chen AP, Crane JC, et al. 3D sensitivity encoded ellipsoidal MR spectroscopic imaging of gliomas at 3T. Magn Reson Imaging. 2009;27(9):1249‐1257. [DOI] [PMC free article] [PubMed] [Google Scholar]
200. Posse S, Otazo R, Tsai SY, Yoshimoto AE, Lin FH. Single‐shot magnetic resonance spectroscopic imaging with partial parallel imaging. Magn Reson Med. 2009;61(3):541‐547. [DOI] [PMC free article] [PubMed] [Google Scholar]
201. Ohliger MA, Larson PEZ, Bok RA, et al. Combined parallel and partial Fourier MR reconstruction for accelerated 8‐channel hyperpolarized carbon‐13 in vivo magnetic resonance spectroscopic imaging (MRSI). J Magn Reson Imaging. 2013;38(3):701‐713. [DOI] [PMC free article] [PubMed] [Google Scholar]
202. Birch R, Peet AC, Arvanitis TN, Wilson M. Sensitivity encoding for fast H‐1 MR spectroscopic imaging water reference acquisition. Magn Reson Med. 2015;73(6):2081‐2086. [DOI] [PubMed] [Google Scholar]
203. Bonekamp D, Smith MA, Zhu H, Barker PB. Quantitative SENSE‐MRSI of the human brain. Magn Reson Imaging. 2010;28(3):305‐313. [DOI] [PMC free article] [PubMed] [Google Scholar]
204. Ozturk E, Banerjee S, Majumdar S, Nelson SJ. Partially parallel MR spectroscopic imaging of gliomas at 3T. In: 2006 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. New York City, New York: IEEE; 2006:493‐496. [DOI] [PubMed] [Google Scholar]
205. Arunachalam A, Whitt D, Fish K, et al. Accelerated spectroscopic imaging of hyperpolarized C‐13 pyruvate using SENSE parallel imaging. NMR Biomed. 2009;22(8):867‐873. [DOI] [PubMed] [Google Scholar]
206. Tropp J, Lupo JM, Chen A, et al. Multi‐channel metabolic imaging, with SENSE reconstruction, of hyperpolarized [1‐C‐13] pyruvate in a live rat at 3.0 tesla on a clinical MR scanner. J Magn Reson. 2011;208(1):171‐177. [DOI] [PMC free article] [PubMed] [Google Scholar]
207. Banerjee S, Ozturk‐Isik E, Nelson SJ, Majumdar S. Fast magnetic resonance spectroscopic imaging at 3 Tesla using autocalibrating parallel technique. In: 2006 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. New York City, New York: IEEE; 2006:1866‐1869. [DOI] [PubMed] [Google Scholar]
208. Zhu XP, Ebel A, Ji JX, Schuff N. Spectral phase‐corrected GRAPPA reconstruction of three‐dimensional echo‐planar spectroscopic imaging (3D‐EPSI). Magn Reson Med. 2007;57(5):815‐820. [DOI] [PubMed] [Google Scholar]
209. Hangel G, Strasser B, Povazan M, et al. Lipid suppression via double inversion recovery with symmetric frequency sweep for robust 2D‐GRAPPA‐accelerated MRSI of the brain at 7T. NMR Biomed. 2015;28(11):1413‐1425. [DOI] [PMC free article] [PubMed] [Google Scholar]
210. Banerjee S, Ozturk‐Isik E, Nelson SJ, Majumdar S. Elliptical magnetic resonance spectroscopic imaging with GRAPPA for imaging brain tumors at 3 T. Magn Reson Imaging. 2009;27(10):1319‐1325. [DOI] [PubMed] [Google Scholar]
211. Sabati M, Zhan JP, Govind V, Arheart KL, Maudsley AA. Impact of reduced k‐space acquisition on pathologic detectability for volumetric MR spectroscopic imaging. J Magn Reson Imaging. 2014;39(1):224‐234. [DOI] [PMC free article] [PubMed] [Google Scholar]
212. Gu M, Liu CL, Spielman DM. Parallel spectroscopic imaging reconstruction with arbitrary trajectories using k‐space sparse matrices. Magn Reson Med. 2009;61(2):267‐272. [DOI] [PMC free article] [PubMed] [Google Scholar]
213. Raghavan RS, Panda A, Valette J, et al. ³¹P spectroscopic imaging with GRAPPA. Proc Int Soc Magn Reson Med. 2009;17:4317.
214. Shin PJ, Larson PEZ, Ohliger MA, et al. Calibrationless parallel imaging reconstruction based on structured low‐rank matrix completion. Magn Reson Med. 2014;72(4):959‐970. [DOI] [PMC free article] [PubMed] [Google Scholar]
215. Gordon JW, Hansen RB, Shin PJ, Feng Y, Vigneron DB, Larson PEZ. 3D hyperpolarized C‐13 EPI with calibrationless parallel imaging. J Magn Reson. 2018;289:92‐99. [DOI] [PMC free article] [PubMed] [Google Scholar]
216. Zierhut ML, Ozturk‐Isik E, Chen AP, Park I, Vigneron DB, Nelson SJ. H‐1 spectroscopic imaging of human brain at 3 tesla: comparison of fast three‐dimensional magnetic resonance spectroscopic imaging techniques. J Magn Reson Imaging. 2009;30(3):473‐480. [DOI] [PMC free article] [PubMed] [Google Scholar]
217. Feinberg DA, Setsompop K. Ultra‐fast MRI of the human brain with simultaneous multi‐slice imaging. J Magn Reson. 2013;229:90‐100. [DOI] [PMC free article] [PubMed] [Google Scholar]
218. Larkman DJ, Hajnal JV, Herlihy AH, Coutts GA, Young IR, Ehnholm G. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited. J Magn Reson Imaging. 2001;13(2):313‐317. [DOI] [PubMed] [Google Scholar]
219. Breuer FA, Blaimer M, Heidemann RM, Mueller MF, Griswold MA, Jakob PM. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi‐slice imaging. Magn Reson Med. 2005;53(3):684‐691. [DOI] [PubMed] [Google Scholar]
220. Xia P, Chiew M, Zhou X, Thomas MA, Dydak U, Emir UE. Density‐weighted concentric ring trajectory using simultaneous multi‐band acceleration: 3D metabolite‐cycled magnetic resonance spectroscopy imaging at 3T. BioRXiv. 2019. [Google Scholar]
221. Larson PEZ, Bok R, Kerr AB, et al. Investigation of tumor hyperpolarized [1‐C‐13]‐pyruvate dynamics using time‐resolved multiband RF excitation echo‐planar MRSI. Magn Reson Med. 2010;63(3):582‐591. [DOI] [PMC free article] [PubMed] [Google Scholar]
222. Larson PEZ, Kerr AB, Chen AP, et al. Multiband excitation pulses for hyperpolarized 13C dynamic chemical‐shift imaging. J Magn Reson. 2008;194(1):121‐127. [DOI] [PMC free article] [PubMed] [Google Scholar]
223. Lustig M, Donoho D, Pauly JM. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6):1182‐1195. [DOI] [PubMed] [Google Scholar]
224. Dafni H, Ronen SM. Dynamic nuclear polarization in metabolic imaging of metastasis: common sense, hypersense and compressed sensing. Cancer Biomark. 2010;7(4‐5):189‐199. [DOI] [PubMed] [Google Scholar]
225. Park I, Hu S, Bok R, et al. Evaluation of heterogeneous metabolic profile in an orthotopic human glioblastoma xenograft model using compressed sensing hyperpolarized 3D ¹³C magnetic resonance spectroscopic imaging. Magn Reson Med. 2013;70(1):33‐39. [DOI] [PMC free article] [PubMed] [Google Scholar]
226. von Morze C, Larson PEZ, Hu S, et al. Investigating tumor perfusion and metabolism using multiple hyperpolarized C‐13 compounds: HP001, pyruvate and urea. Magn Reson Imaging. 2012;20(3):305‐311. [DOI] [PMC free article] [PubMed] [Google Scholar]
227. Wiens CN, Friesen‐Waldner LJ, Wade TP, Sinclair KJ, McKenzie CA. Chemical shift encoded imaging of hyperpolarized C‐13 pyruvate. Magn Reson Med. 2015;74(6):1682‐1689. [DOI] [PubMed] [Google Scholar]
228. Geraghty BJ, Lau JYC, Chen AP, Cunningham CH. Accelerated 3D echo‐planar imaging with compressed sensing for time‐resolved hyperpolarized C‐13 studies. Magn Reson Med. 2017;77(2):538‐546. [DOI] [PubMed] [Google Scholar]
229. Milshteyn E, von Morze C, Reed GD, et al. Development of high resolution 3D hyperpolarized carbon‐13 MR molecular imaging techniques. Magn Reson Imaging. 2017;38:152‐162. [DOI] [PMC free article] [PubMed] [Google Scholar]
230. Wang JX, Merritt ME, Sherry AD, Malloy CR. Accelerated chemical shift imaging of hyperpolarized C‐13 metabolites. Magn Reson Med. 2016;76(4):1033‐1038. [DOI] [PMC free article] [PubMed] [Google Scholar]
231. Chen HY, Larson PEZ, Gordon JW, et al. Technique development of 3D dynamic CS‐EPSI for hyperpolarized C‐13 pyruvate MR molecular imaging of human prostate cancer. Magn Reson Med. 2018;80(5):2062‐2072. [DOI] [PMC free article] [PubMed] [Google Scholar]
232. Askin NC, Atis B, Ozturk‐Isik E. Accelerated phosphorus magnetic resonance spectroscopic imaging using compressed sensing. In: 2012 34th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. San Diego, California: IEEE; 2012:1106‐1109. [DOI] [PubMed] [Google Scholar]
233. Hatay GH, Yildirim M, Ozturk‐Isik E. Considerations in applying compressed sensing to in vivo phosphorus MR spectroscopic imaging of human brain at 3T. Med Biol Eng Comput. 2017;55(8):1303‐1315. [DOI] [PubMed] [Google Scholar]
234. Santos‐Diaz A, Noseworthy MD. Comparison of compressed sensing reconstruction algorithms for P‐31 magnetic resonance spectroscopic imaging. Magn Reson Imaging. 2019;59:88‐96. [DOI] [PubMed] [Google Scholar]
235. Fu Y, Ijare O, Thomas G, Fazel‐Rezai R, Serrai H. Implementation of wavelet encoding spectroscopic imaging technique on a 3 tesla whole body MR scanner: in vitro results. In: 2009 31st Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Minneapolis, Minnesota: IEEE; 2009:2688‐2691. [DOI] [PubMed] [Google Scholar]
236. Geethanath S, Baek HM, Ganji SK, et al. Compressive sensing could accelerate H‐1 MR metabolic imaging in the clinic. Radiology. 2012;262(3):985‐994. [DOI] [PMC free article] [PubMed] [Google Scholar]
237. Heikal AA, Wachowicz K, Fallone BG. Effect of the k‐space sampling pattern on the MTF of compressed sensing MRSI. Med Phys. 2012;39(7):4623‐4623. [Google Scholar]
238. Heikal AA, Wachowicz K, Fallone BG. MTF behavior of compressed sensing MR spectroscopic imaging. Med Phys. 2013;40(5):052302. [DOI] [PubMed] [Google Scholar]
239. Heikal AA, Wachowicz K, Fallone BG. Correlation between k‐space sampling pattern and MTF in compressed sensing MRSI. Med Phys. 2016;43(10):5626‐5634. [DOI] [PubMed] [Google Scholar]
240. Thomas MA, Nagarajan R, Huda A, et al. Multidimensional MR spectroscopic imaging of prostate cancer in vivo. NMR Biomed. 2014;27(1):53‐66. [DOI] [PubMed] [Google Scholar]
241. Nagarajan R, Iqbal Z, Burns B, et al. Accelerated echo planar J‐resolved spectroscopic imaging in prostate cancer: a pilot validation of non‐linear reconstruction using total variation and maximum entropy. NMR Biomed. 2015;28(11):1366‐1373. [DOI] [PMC free article] [PubMed] [Google Scholar]
242. Breuer FA, Blaimer M, Mueller MF, et al. Controlled aliasing in volumetric parallel imaging (2D CAIPIRINHA). Magn Reson Med. 2006;55(3):549‐556. [DOI] [PubMed] [Google Scholar]
243. Otazo R, Sodickson DK, Yoshimoto A, Posse S. Accelerated proton echo‐planar spectroscopic imaging using parallel imaging and compressed sensing. Proc Int Soc Magn Reson Med. 2009;17:331.
244. Iqbal Z, Wilson NE, Thomas MA. 3D spatially encoded and accelerated TE‐averaged echo planar spectroscopic imaging in healthy human brain. NMR Biomed. 2016;29(3):329‐339. [DOI] [PubMed] [Google Scholar]
245. Burns B, Wilson NE, Furuyama JK, Thomas MA. Non‐uniformly under‐sampled multi‐dimensional spectroscopic imaging in vivo: maximum entropy versus compressed sensing reconstruction. NMR Biomed. 2014;27(2):191‐201. [DOI] [PubMed] [Google Scholar]
246. Wright KL, Hamilton JI, Griswold MA, Gulani V, Seiberlich N. Non‐Cartesian parallel imaging reconstruction. J Magn Reson Imaging. 2014;40(5):1022‐1040. [DOI] [PMC free article] [PubMed] [Google Scholar]
247. Mayer D, Kim DH, Spielman DM, Bammer R. Fast parallel spiral chemical shift imaging at 3T using iterative SENSE reconstruction. Magn Reson Med. 2008;59(4):891‐897. [DOI] [PMC free article] [PubMed] [Google Scholar]
248. Baron CA, Dwork N, Pauly JM, Nishimura DG. Rapid compressed sensing reconstruction of 3D non‐Cartesian MRI. Magn Reson Med. 2018;79(5):2685‐2692. [DOI] [PMC free article] [PubMed] [Google Scholar]
249. Mayer D, Yen YF, Tropp J, Pfefferbaum A, Hurd RE, Spielman DM. Application of subsecond spiral chemical shift imaging to real‐time multislice metabolic imaging of the rat in vivo after injection of hyperpolarized C‐13(1)‐pyruvate. Magn Reson Med. 2009;62(3):557‐564. [DOI] [PMC free article] [PubMed] [Google Scholar]
250. Zhu B, Liu JZ, Cauley SF, Rosen BR, Rosen MS. Image reconstruction by domain‐transform manifold learning. Nature. 2018;555(7697):487‐492. [DOI] [PubMed] [Google Scholar]
251. Hu XP, Levin DN, Lauterbur PC, Spraggins T. SLIM—spectral localization by imaging. Magn Reson Med. 1988;8(3):314‐322. [DOI] [PubMed] [Google Scholar]
252. Kmiecik JA, Gregory CD, Liang ZP, Hrad DE, Lauterbur PC, Dawson MJ. Quantitative lactate‐specific MR imaging and H‐1 spectroscopy of skeletal muscle at macroscopic and microscopic resolutions using a zero‐quantum/double‐quantum coherence filter and SLIM/GSLIM localization. Magn Reson Med. 1997;37(6):840‐850. [DOI] [PubMed] [Google Scholar]
253. Xu S, Yang YH, Gregory CD, Vary JC, Liang ZP, Dawson MJ. Biochemical heterogeneity in hysterectomized uterus measured by P‐31 NMR using SLIM localization. Magn Reson Med. 1997;37(5):736‐743. [DOI] [PubMed] [Google Scholar]
254. Dong ZC, Hwang JH. Lipid signal extraction by SLIM: application to H‐1 MR spectroscopic imaging of human calf muscles. Magn Reson Med. 2006;55(6):1447‐1453. [DOI] [PubMed] [Google Scholar]
255. von Kienlin M, Mejia R. Spectral localization with optimal pointspread function. J Magn Reson. 1991;94(2):268‐287. [Google Scholar]
256. Loffler R, Sauter R, Kolem H, Haase A, von Kienlin M. Localized spectroscopy from anatomically matched compartments: improved sensitivity and localization for cardiac P‐31 MRS in humans. J Magn Reson. 1998;134(2):287‐299. [DOI] [PubMed] [Google Scholar]
257. Meininger M, Landschutz W, Beer M, et al. Concentrations of human cardiac phosphorus metabolites determined by SLOOP P‐31 NMR spectroscopy. Magn Reson Med. 1999;41(4):657‐663. [DOI] [PubMed] [Google Scholar]
258. Pohmann R, Rommel E, von Kienlin M. Beyond k‐space: spectral localization using higher order gradients. J Magn Reson. 1999;141(2):197‐206. [DOI] [PubMed] [Google Scholar]
259. Kostler H, Landschutz W, Koeppe S, et al. Age and gender dependence of human cardiac phosphorus metabolites determined by SLOOP P‐31 MR spectroscopy. Magn Reson Med. 2006;56(4):907‐911. [DOI] [PubMed] [Google Scholar]
260. Landschutz W, Meininger M, Beer M, et al. Concentration of human cardiac ³¹P‐metabolites determined by SLOOP ³¹P‐MRS. Magn Reson Mater Phys Biol Med. 1998;6(2/3):155‐156. [PubMed] [Google Scholar]
261. Geier O, Weng AM, Toepell A, et al. Acquisition‐weighted chemical shift imaging improves SLOOP quantification of human cardiac phosphorus metabolites. Z Med Phys. 2014;24(1):49‐54. [DOI] [PubMed] [Google Scholar]
262. Beer M, Seyfarth T, Sandstede J, et al. Absolute concentrations of high‐energy phosphate metabolites in normal, hypertrophied, and failing human myocardium measured noninvasively with P‐31‐SLOOP magnetic resonance spectroscopy. J Am Coll Cardiol. 2002;40(7):1267‐1274. [DOI] [PubMed] [Google Scholar]
263. von Kienlin M, Beer M, Greiser A, et al. Advances in human cardiac P‐31‐MR spectroscopy: SLOOP and clinical applications. J Magn Reson Imaging. 2001;13(4):521‐527. [DOI] [PubMed] [Google Scholar]
264. Liang ZP, Lauterbur PC. A generalized series approach to MR spectroscopic imaging. IEEE Trans Med Imaging. 1991;10(2):132‐137. [DOI] [PubMed] [Google Scholar]
265. Kmiecik JA, Gregory CD, Liang ZP, Lauterbur PC, Dawson MJ. Lactate quantitation in a gerbil brain stroke model by GSLIM of multiple‐quantum‐filtered signals. J Magn Reson Im aging. 1999;9(4):539‐543. [DOI] [PubMed] [Google Scholar]
266. Bashir A, Yablonskiy DA. Natural linewidth chemical shift imaging (NL‐CSI). Magn Reson Med. 2006;56(1):7‐18. [DOI] [PMC free article] [PubMed] [Google Scholar]
267. Khalidov I, Van de Ville D, Jacob M, Lazeyras F, Unser M. BSLIM: spectral localization by imaging with explicit B ₀ field inhomogeneity compensation. IEEE Trans Med Imaging. 2007;26(7):990‐1000. [DOI] [PubMed] [Google Scholar]
268. Passeri A, Mazzuca S, Del Bene V. Radiofrequency field inhomogeneity compensation in high spatial resolution magnetic resonance spectroscopic imaging. Phys Med Biol. 2014;59(12):2913‐2934. [DOI] [PubMed] [Google Scholar]
269. An L, Warach S, Shen J. Spectral localization by imaging using multielement receiver coils. Magn Reson Med. 2011;66(1):1‐10. [DOI] [PMC free article] [PubMed] [Google Scholar]
270. Zhang Y, Gabr RE, Zhou JY, Weiss RG, Bottomley PA. Highly‐accelerated quantitative 2D and 3D localized spectroscopy with linear algebraic modeling (SLAM) and sensitivity encoding. J Magn Reson. 2013;237:125‐138. [DOI] [PMC free article] [PubMed] [Google Scholar]
271. Zhang Y, Gabr RE, Schar M, Weiss RG, Bottomley PA. Magnetic resonance Spectroscopy with Linear Algebraic Modeling (SLAM) for higher speed and sensitivity. J Magn Reson. 2012;218:66‐76. [DOI] [PMC free article] [PubMed] [Google Scholar]
272. Farkash G, Markovic S, Novakovic M, Frydman L. Enhanced hyperpolarized chemical shift imaging based on a priori segmented information. Magn Reson Med. 2019;81(5):3080‐3093. [DOI] [PubMed] [Google Scholar]
273. Lee P, Adany P, Choi IY. Imaging based magnetic resonance spectroscopy (MRS) localization for quantitative neurochemical analysis and cerebral metabolism studies. Anal Biochem. 2017;529:40‐47. [DOI] [PMC free article] [PubMed] [Google Scholar]
274. Peng X, Nguyen H, Haldar J, Hernando D, Wang XP, Liang ZP. Correction of field inhomogeneity effects on limited k‐space MRSI data using anatomical constraints. In: 2010 32nd Annual International Conference of the Ieee Engineering in Medicine and Biology Society. Buenos Aires, Argentina: IEEE; 2010:883‐886. [DOI] [PubMed] [Google Scholar]
275. Kirchner T, Eisenring L, Pruessmann KP, Henning A. Inherent reduction of residual lipid aliasing in SENSE‐accelerated ¹H MRSI at 7T by spatially selective SRF optimization. Proc Int Soc Magn Reson Med. 2013;21:2007.
276. Dong Z, Peterson BS. Spectral resolution amelioration by deconvolution (SPREAD) in MR spectroscopic imaging. J Magn Reson Imaging. 2009;29(6):1395‐1405. [DOI] [PMC free article] [PubMed] [Google Scholar]
277. Halse ME, Callaghan PT. Imaged deconvolution: a method for extracting high‐resolution NMR spectra from inhomogeneous fields. J Magn Reson. 2007;185(1):130‐137. [DOI] [PubMed] [Google Scholar]
278. Dong ZC, Zhang YD, Liu F, Duan YS, Kangarlu A, Peterson BS. Improving the spectral resolution and spectral fitting of H‐1 MRSI data from human calf muscle by the SPREAD technique. NMR Biomed. 2014;27(11):1325‐1332. [DOI] [PubMed] [Google Scholar]
279. Eslami R, Jacob M. Robust reconstruction of MRSI data using a sparse spectral model and high resolution MRI priors. IEEE Trans Med Imaging. 2010;29(6):1297‐1309. [DOI] [PubMed] [Google Scholar]
280. Eslami R, Jacob M. Spatial spectral modeling for robust MRSI. In: 2009 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. New York City, New York: IEEE; 2009:6663‐6666. [DOI] [PubMed] [Google Scholar]
281. Eslami R, Jacob M. Correction of B ₀ inhomogeneity distortion in magnetic resonance spectroscopic imaging. In: 34th International Conference on Acoustics, Speech, and Signal Processing (ICASSP). Taipei, Taiwan: IEEE; 2009:405‐408. [Google Scholar]
282. Liu Y, Ma C, Clifford BA, Lam F, Johnson CL, Liang ZP. Improved low‐rank filtering of magnetic resonance spectroscopic imaging data corrupted by noise and B ₀ field inhomogeneity. IEEE Trans Biomed Eng. 2016;63(4):841‐849. [DOI] [PubMed] [Google Scholar]
283. Liu Y, Ma C, Clifford B, Lam F, Johnson CL, Liang ZP. Field‐inhomogeneity‐corrected low‐rank filtering of magnetic resonance spectroscopic imaging data. Eng Med Biol. 2014:6422‐6425. [DOI] [PubMed]
284. Nguyen HM, Peng X, Do MN, Liang ZP. Spatiotemporal denoising of MR spectroscopic imaging data by low‐rank approximations. In: 2011 8th IEEE International Symposium on Biomedical Imaging: From Nano to Macro. Chicago, IL, USA: IEEE; 2011:857‐860. [Google Scholar]
285. DeVience SJ, Mayer D. Speeding up dynamic spiral chemical shift imaging with incoherent sampling and low‐rank matrix completion. Magn Reson Med. 2017;77(3):951‐960. [DOI] [PMC free article] [PubMed] [Google Scholar]
286. Milshteyn E, von Morze C, Reed GD, et al. Using a local low rank plus sparse reconstruction to accelerate dynamic hyperpolarized C‐13 imaging using the bSSFP sequence. J Magn Reson. 2018;290:46‐59. [DOI] [PMC free article] [PubMed] [Google Scholar]
287. Liang ZP. Spatiotemporal imaging with partially separable functions. In: 2007 Joint Meeting of the Sixth International Symposium on Noninvasive Functional Source Imaging of the Brain and Heart and the International Conference on Functional Biomedical Imaging. Hangzhou, China: IEEE; 2007:356‐357. [Google Scholar]
288. Lam F, Liang ZP. A subspace approach to high‐resolution spectroscopic imaging. Magn Reson Med. 2014;71(4):1349‐1357. [DOI] [PMC free article] [PubMed] [Google Scholar]
289. Ma C, Lam F, Ning Q, Johnson CL, Liang ZP. High‐resolution ¹H‐MRSI of the brain using short‐TE SPICE. Magn Reson Med. 2017;77(2):467‐479. [DOI] [PMC free article] [PubMed] [Google Scholar]
290. Lam F, Ma C, Clifford B, Johnson CL, Liang ZP. High‐resolution H‐1‐MRSI of the brain using SPICE: data acquisition and image reconstruction. Magn Reson Med. 2016;76(4):1059‐1070. [DOI] [PMC free article] [PubMed] [Google Scholar]
291. Peng X, Lam F, Li YD, Clifford B, Liang ZP. Simultaneous QSM and metabolic imaging of the brain using SPICE. Magn Reson Med. 2018;79(1):13‐21. [DOI] [PMC free article] [PubMed] [Google Scholar]
292. Guo R, Zhao YB, Li YD, Li Y, Liang ZP. Simultaneous metabolic and functional imaging of the brain using SPICE. Magn Reson Med. 2019;82(6):1993‐2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
293. Ma C, Clifford B, Liu YC, et al. High‐resolution dynamic P‐31‐MRSI using a low‐rank tensor model. Magn Reson Med. 2017;78(2):419‐428. [DOI] [PMC free article] [PubMed] [Google Scholar]
294. Lee H, Song JE, Shin J, et al. High resolution hyperpolarized C‐13 MRSI using SPICE at 9.4T. Magn Reson Med. 2018;80(2):703‐710. [DOI] [PubMed] [Google Scholar]
295. Ma C, Lam F, Liang ZP. Encoding and decoding with prior knowledge: from SLIM to SPICE. eMagRes. 2015;4(2):535‐542. [Google Scholar]
296. Mahmoudzadeh AP, Kashou NH. Evaluation of interpolation effects on upsampling and accuracy of cost functions‐based optimized automatic image registration. Int J Biomed Imaging. 2013;2013:395915. [DOI] [PMC free article] [PubMed] [Google Scholar]
297. Schmidt R, Laustsen C, Dumez JN, et al. In vivo single‐shot C‐13 spectroscopic imaging of hyperpolarized metabolites by spatiotemporal encoding. J Magn Reson. 2014;240:8‐15. [DOI] [PMC free article] [PubMed] [Google Scholar]
298. Schmidt R, Frydman L. In vivo 3D spatial/1D spectral imaging by spatiotemporal encoding: a new single‐shot experimental and processing approach. Magn Reson Med. 2013;70(2):382‐391. [DOI] [PubMed] [Google Scholar]
299. Zhang ZY, Frydman L. MRSI via fully‐refocused spatiotemporal encoding with polychromatic spectral pulses. J Magn Reson. 2015;259:24‐31. [DOI] [PMC free article] [PubMed] [Google Scholar]
300. Iqbal Z, Nguyen D, Hangel G, et al. Super‐Resolution ¹H Magnetic Resonance Spectroscopic Imaging Utilizing Deep Learning. Front Oncol. 2019;9:1‐13:1010. [DOI] [PMC free article] [PubMed] [Google Scholar]
301. Larson PEZ, Kerr AB, Chen AP, et al. Multiband excitation pulses for hyperpolarized C‐13 dynamic chemical‐shift imaging. J Magn Reson. 2008;194(1):121‐127. [DOI] [PMC free article] [PubMed] [Google Scholar]
302. Lau AZ, Chen AP, Ghugre NR, et al. Rapid multislice imaging of hyperpolarized C‐13 pyruvate and bicarbonate in the heart. Magn Reson Med. 2010;64(5):1323‐1331. [DOI] [PubMed] [Google Scholar]
303. Singh M, Josan S, Zhu MJ, Jhajharia A, Mayer D. Dynamic metabolic imaging of copolarized [2‐C‐13]pyruvate and [1,4‐C‐13(2)]fumarate using 3D‐spiral CSI with alternate spectral band excitation. Magn Reson Med. 2019;81(5):2869‐2877. [DOI] [PMC free article] [PubMed] [Google Scholar]
304. Miller JJ, Lau AZ, Tyler DJ. Susceptibility‐induced distortion correction in hyperpolarized echo planar imaging. Magn Reson Med. 2018;79(4):2135‐2141. [DOI] [PMC free article] [PubMed] [Google Scholar]
305. Lau JYC, Geraghty BJ, Chen AP, Cunningham CH. Improved tolerance to off‐resonance in spectral‐spatial EPI of hyperpolarized [1‐C‐13]pyruvate and metabolites. Magn Reson Med. 2018;80(3):925‐934. [DOI] [PubMed] [Google Scholar]
306. Weiss K, Sigfridsson A, Wissmann L, et al. Accelerating hyperpolarized metabolic imaging of the heart by exploiting spatiotemporal correlations. NMR Biomed. 2013;26(11):1380‐1386. [DOI] [PubMed] [Google Scholar]
307. Cunningham CH, Chen AP, Lustig M, et al. Pulse sequence for dynamic volumetric imaging of hyperpolarized metabolic products. J Magn Reson. 2008;193(1):139‐146. [DOI] [PMC free article] [PubMed] [Google Scholar]
308. Schulte RF, Sperl JI, Weidl E, et al. Saturation‐recovery metabolic‐exchange rate imaging with hyperpolarized [1‐¹³C] pyruvate using spectral‐spatial excitation. Magn Reson Med. 2013;69(5):1209‐1216. [DOI] [PubMed] [Google Scholar]
309. von Morze C, Reed G, Shin P, et al. Multi‐band frequency encoding method for metabolic imaging with hyperpolarized [1‐C‐13]pyruvate. J Magn Reson. 2011;211(2):109‐113. [DOI] [PMC free article] [PubMed] [Google Scholar]
310. Schmid AI, Meyerspeer M, Robinson SD, et al. Dynamic PCr and pH imaging of human calf muscles during exercise and recovery using P‐31 gradient‐echo MRI at 7 tesla. Magn Reson Med. 2016;75(6):2324‐2331. [DOI] [PubMed] [Google Scholar]
311. Greenman RL, Wang XE, Smithline HA. Simultaneous acquisition of phosphocreatine and inorganic phosphate images for Pi:PCr ratio mapping using a RARE sequence with chemically selective interleaving. Magn Reson Imaging. 2011;29(8):1138‐1144. [DOI] [PMC free article] [PubMed] [Google Scholar]
312. Ebel A, Maudsley AA, Schuff N. Correction of local B ₀ shifts in 3D EPSI of the human brain at 4 T. Magn Reson Imaging. 2007;25(3):377‐380. [DOI] [PMC free article] [PubMed] [Google Scholar]
313. Ebel A, Maudsley AA. Improved spectral quality for 3D MR spectroscopic imaging using a high spatial resolution acquisition strategy. Magn Reson Imaging. 2003;21(2):113‐120. [DOI] [PubMed] [Google Scholar]
314. Motyka S, Moser P, Hingerl L, et al. The influence of spatial resolution on the spectral quality and quantification accuracy of whole‐brain MRSI at 1.5T, 3T, 7T, and 9.4T. Magn Reson Med. 2019;82(2):551‐565. [DOI] [PMC free article] [PubMed] [Google Scholar]
315. Wang SS, Su ZH, Ying L, et al. Accelerating magnetic resonance imaging via deep learning. In: 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI). Prague, Czech Republic: IEEE; 2016:514‐517. [DOI] [PMC free article] [PubMed] [Google Scholar]
316. Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated MRI data. Magn Reson Med. 2018;79(6):3055‐3071. [DOI] [PMC free article] [PubMed] [Google Scholar]
317. Wang G, Ye JC, Mueller K, Fessler JA. Image reconstruction is a new frontier of machine learning. IEEE Trans Med Imaging. 2018;37(6):1289‐1296. [DOI] [PubMed] [Google Scholar]
318. Lam F, Li Y, Peng X. Constrained magnetic resonance spectroscopic imaging by learning nonlinear low‐dimensional models. Magn Reson Med. 2020;39(3):545‐555. 10.1109/TMI.2019.2930586. Epub 2019 Jul 23. [DOI] [PubMed] [Google Scholar]
319. Ebel A, Soher BJ, Maudsley AA. Assessment of 3D proton MR echo‐planar spectroscopic imaging using automated spectral analysis. Magn Reson Med. 2001;46(6):1072‐1078. [DOI] [PubMed] [Google Scholar]
320. Nassirpour S, Chang P, Henning A. Comparison of different acceleration methods for high‐resolution metabolite mapping using 1H FID MRSI at 9.4T. Poster presented at: 25th Annual Meeting and Exhibition of the International Society for Magnetic Resonance in Medicine (ISMRM 2017); April 22‐27, 2017; Honolulu, HI.
321. Strasser B, Hingerl L, Gagoski B, et al. Comparison of acceleration methods for brain MRSI at 7T. Paper presented at: ISMRM 25th Annual Meeting and Exhibition; April 22‐27, 2017; Honolulu, HI.
322. Durst M, Koellisch U, Frank A, et al. Comparison of acquisition schemes for hyperpolarised C‐13 imaging. NMR Biomed. 2015;28(6):715‐725. [DOI] [PubMed] [Google Scholar]
323. Lee BY, Zhu XH, Chen W. Quantitative analysis of spatial averaging effect on chemical shift imaging SNR and noise coherence with k‐space sampling schemes. Magn Reson Imaging. 2019;60:85‐92. [DOI] [PMC free article] [PubMed] [Google Scholar]
324. Maudsley AA, Andronesi OC, Barker PB, et al. Advanced magnetic resonance spectroscopic neuroimaging: experts' consensus. NMR Biomed. 2020. accepted. [DOI] [PMC free article] [PubMed] [Google Scholar]
325. Wilson M, Andronesi O, Barker PB, et al. Methodological consensus on clinical proton MRS of the brain: review and recommendations. Magn Reson Med. 2019;82(2):527‐550. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file.^{(3.6MB, tif)}

Click here for additional data file.^{(5.8MB, tif)}

Click here for additional data file.^{(2.5MB, tif)}

Click here for additional data file.^{(6.8MB, tif)}

[nbm4314-bib-0001] 1. Brown TR, Kincaid BM, Ugurbil K. NMR chemical shift imaging in three dimensions. Proc Natl Acad Sci U S A. 1982;79(11):3523‐3526. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0002] 2. Maudsley AA, Hilal SK, Perman WH, Simon HE. Spatially resolved high‐resolution spectroscopy by 4‐dimensional NMR. J Magn Reson. 1983;51(1):147‐152. [Google Scholar]

[nbm4314-bib-0003] 3. Mansfield P. Spatial mapping of the chemical shift in NMR. Magn Reson Med. 1984;1(3):370‐386. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0004] 4. Sabati M, Sheriff S, Gu M, et al. Multivendor implementation and comparison of volumetric whole‐brain echo‐planar MR spectroscopic imaging. Magn Reson Med. 2015;74(5):1209‐1220. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0005] 5. Nassirpour S, Chang P, Henning A. High and ultra‐high resolution metabolite mapping of the human brain using H‐1 FID MRSI at 9.4T. NeuroImage. 2018;168:211‐221. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0006] 6. Povazan M, Strasser B, Hangel G, et al. Simultaneous mapping of metabolites and individual macromolecular components via ultra‐short acquisition delay H‐1 MRSI in the brain at 7T. Magn Reson Med. 2018;79(3):1231‐1240. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0007] 7. Hingerl L, Strasser B, Moser P, et al. Clinical high‐resolution 3D‐MR spectroscopic imaging of the human brain at 7 tesla. Invest Radiol. 2019;55(4):239‐248. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0008] 8. Oz G, Alger JR, Barker PB, et al. Clinical proton MR spectroscopy in central nervous system disorders. Radiology. 2014;270(3):658‐679. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0009] 9. Kurhanewicz J, Vigneron DB, Ardenkjaer‐Larsen JH, et al. Hyperpolarized ¹³C MRI: path to clinical translation in oncology. Neoplasia. 2019;21(1):1‐16. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0010] 10. Bernstein MA, King KF, Zhou XJ. Handbook of MRI Pulse Sequences. Burlington, MA: Elsevier; 2004. [Google Scholar]

[nbm4314-bib-0011] 11. de Graaf RA. In Vivo NMR Spectroscopy—2nd Edition: Principles and Techniques. New York, NY: Wiley; 2007. [Google Scholar]

[nbm4314-bib-0012] 12. Shankar RV, Chang JC, Hu HCH, Kodibagkar VD. Fast data acquisition techniques in magnetic resonance spectroscopic imaging. NMR Biomed. 2019;32(3):1‐22:e4046. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0013] 13. Oun A, Lechner‐Scott J, Ribbons K, Ramadan S. Fast magnetic resonance spectroscopic imaging techniques in human brain‐applications in multiple sclerosis. J Biomed Sci. 2017;24:1‐19. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0014] 14. Nelson SJ, Ozhinsky E, Li Y, Park IW, Crane J. Strategies for rapid in vivo H‐1 and hyperpolarized C‐13 MR spectroscopic imaging. J Magn Reson. 2013;229:187‐197. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0015] 15. Posse S, Otazo R, Dager SR, Alger J. MR spectroscopic imaging: principles and recent advances. J Magn Reson Imaging. 2013;37(6):1301‐1325. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0016] 16. Posse S, Hu XP. High‐speed spatial‐spectral encoding with PEPSI and spiral MRSI. eMagRes. 2015;4(3):587‐600. [Google Scholar]

[nbm4314-bib-0017] 17. Althaus M, Dreher W, Geppert C, Leibfritz D. Fast 3D echo planar SSFP‐based H‐1 spectroscopic imaging: demonstration on the rat brain in vivo. Magn Reson Imaging. 2006;24(5):549‐555. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0018] 18. Dreher W, Geppert C, Althaus M, Leibfritz D. Fast proton spectroscopic imaging using steady‐state free precession methods. Magn Reson Med. 2003;50(3):453‐460. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0019] 19. Speck O, Scheffler K, Hennig J. Fast P‐31 chemical shift Imaging using SSFP methods. Magn Reson Med. 2002;48(4):633‐639. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0020] 20. Dydak U, Pruessmann KP, Weiger M, Tsao J, Meier D, Boesiger P. Parallel spectroscopic imaging with spin‐echo trains. Magn Reson Med. 2003;50(1):196‐200. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0021] 21. Dydak U, Meier D, Lamerichs R, Boesiger P. Trading spectral separation at 3T for acquisition speed in multi spin‐echo spectroscopic imaging. Am J Neuroradiol. 2006;27(7):1441‐1446. [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0022] 22. Dydak U, Schar M. MR spectroscopy and spectroscopic imaging: comparing 3.0 T versus 1.5 T. Neuroimaging Clin N Am. 2006;16(2):269‐283. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0023] 23. Leupold J, Wieben O, Mansson S, et al. Fast chemical shift mapping with multiecho balanced SSFP. Magn Reson Mater Phys Biol Med. 2006;19(5):267‐273. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0024] 24. Leupold J, Mansson S, Petersson JS, Hennig J, Wieben O. Fast multiecho balanced SSFP metabolite mapping of H‐1 and hyperpolarized C‐13 compounds. Magn Reson Mater Phys Biol Med. 2009;22(4):251‐256. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0025] 25. Schuster C, Dreher W, Geppert C, Leibfritz D. Fast 3D H‐1 spectroscopic imaging at 3 tesla using spectroscopic missing‐pulse SSFP with 3D spatial preselection. Magn Reson Med. 2007;57(1):82‐89. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0026] 26. Schuster C, Dreher W, Stadler J, Bernarding J, Leibfritz D. Fast three‐dimensional ¹H MR spectroscopic imaging at 7 tesla using "spectroscopic missing pulse—SSFP". Magn Reson Med. 2008;60(5):1243‐1249. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0027] 27. Dreher W, Erhard P, Leibfritz D. Fast three‐dimensional proton spectroscopic imaging of the human brain at 3 T by combining spectroscopic missing pulse steady‐state free precession and echo planar spectroscopic imaging. Magn Reson Med. 2011;66(6):1518‐1525. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0028] 28. Guo JY, Patay Z, Reddick WE. Fast frequency‐sweep spectroscopic imaging with an ultra‐low flip angle. Sci Rep. 2016;6:1‐12. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0029] 29. Varma G, Wang XE, Vinogradov E, et al. Selective spectroscopic imaging of hyperpolarized pyruvate and its metabolites using a single‐echo variable phase advance method in balanced SSFP. Magn Reson Med. 2016;76(4):1102‐1115. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0030] 30. Valkovic L, Chmelik M, Meyerspeer M, et al. Dynamic P‐31‐MRSI using spiral spectroscopic imaging can map mitochondrial capacity in muscles of the human calf during plantar flexion exercise at 7 T. NMR Biomed. 2016;29(12):1825‐1834. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0031] 31. Mirkes C, Shajan G, Chadzynski G, Buckenmaier K, Bender B, Scheffler K. P‐31 CSI of the human brain in healthy subjects and tumor patients at 9.4 T with a three‐layered multi‐nuclear coil: initial results. Magn Reson Mater Phys Biol Med. 2016;29(3):579‐589. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0032] 32. Lei H, Zhu XH, Zhang XL, Ugurbil K, Chen W. In vivo P‐31 magnetic resonance spectroscopy of human brain at 7 T: an initial experience. Magn Reson Med. 2003;49(2):199‐205. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0033] 33. Chmelik M, Povazan M, Krssak M, et al. In vivo ³¹P magnetic resonance spectroscopy of the human liver at 7 T: an initial experience. NMR Biomed. 2014;27(4):478‐485. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0034] 34. van der Velden TA, Italiaander M, van der Kemp WJM, et al. Radiofrequency configuration to facilitate bilateral breast P‐31 MR spectroscopic imaging and high‐resolution MRI at 7 tesla. Magn Reson Med. 2015;74(6):1803‐1810. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0035] 35. Hu S, Lustig M, Balakrishnan A, et al. 3D compressed sensing for highly accelerated hyperpolarized C‐13 MRSI with in vivo applications to transgenic mouse models of cancer. Magn Reson Med. 2010;63(2):312‐321. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0036] 36. Hu S, Lustig M, Chen AP, et al. Compressed sensing for resolution enhancement of hyperpolarized C‐13 flyback 3D‐MRSI. J Magn Reson. 2008;192(2):258‐264. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0037] 37. Josan S, Spielman D, Yen YF, Hurd R, Pfefferbaum A, Mayer D. Fast volumetric imaging of ethanol metabolism in rat liver with hyperpolarized [1‐¹³C]pyruvate. NMR Biomed. 2012;25(8):993‐999. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0038] 38. Larson PEZ, Hu S, Lustig M, et al. Fast dynamic 3D MR spectroscopic imaging with compressed sensing and multiband excitation pulses for hyperpolarized C‐13 studies. Magn Reson Med. 2011;65(3):610‐619. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0039] 39. Boer VO, Siero JCW, Hoogduin H, van Gorp JS, Luijten PR, Klomp DWJ. High‐field MRS of the human brain at short TE and TR. NMR Biomed. 2011;24(9):1081‐1088. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0040] 40. Chadzynski GL, Bause J, Shajan G, Pohmann R, Scheffler K, Ehses P. Fast and efficient free induction decay MR spectroscopic imaging of the human brain at 9.4 Tesla. Magn Reson Med. 2017;78(4):1281‐1295. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0041] 41. Hangel G, Strasser B, Povazan M, et al. Ultra‐high resolution brain metabolite mapping at 7 T by short‐TR Hadamard‐encoded FID‐MRSI. NeuroImage. 2018;168:199‐210. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0042] 42. Kukurova IJ, Valkovic L, Bogner W, et al. Two‐dimensional spectroscopic imaging with combined free induction decay and long‐TE acquisition (FID echo spectroscopic imaging, FIDESI) for the detection of intramyocellular lipids in calf muscle at 7 T. NMR Biomed. 2014;27(8):980‐987. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0043] 43. Henning A, Fuchs A, Murdoch JB, Boesiger P. Slice‐selective FID acquisition, localized by outer volume suppression (FIDLOVS) for H‐1‐MRSI of the human brain at 7 T with minimal signal loss. NMR Biomed. 2009;22(7):683‐696. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0044] 44. Bogner W, Gruber S, Trattnig S, Chmelik M. High‐resolution mapping of human brain metabolites by free induction decay ¹H MRSI at 7 T. NMR Biomed. 2012;25(6):873‐882. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0045] 45. Lam F, Li Y, Guo R, Clifford B, Liang ZP. Ultrafast magnetic resonance spectroscopic imaging using SPICE with learned subspaces. Magn Reson Med. 2019;83(2):377‐390. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0046] 46. Heckova E, Povazan M, Strasser B, et al. Effects of different macromolecular models on reproducibility of FID‐MRSI at 7T. Magn Reson Med. 2019;83(1):12‐21. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0047] 47. Lam F, Li YD, Clifford B, Liang ZP. Macromolecule mapping of the brain using ultrashort‐TE acquisition and reference‐based metabolite removal. Magn Reson Med. 2018;79(5):2460‐2469. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0048] 48. Povazan M, Hangel G, Strasser B, et al. Mapping of brain macromolecules and their use for spectral processing of H‐1‐MRSI data with an ultra‐short acquisition delay at 7 T. NeuroImage. 2015;121:126‐135. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0049] 49. Hangel G, Jain S, Springer E, et al. High‐resolution metabolic mapping of gliomas via patch‐based super‐resolution magnetic resonance spectroscopic imaging at 7T. NeuroImage. 2019;191:587‐595. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0050] 50. Heckova E, Strasser B, Hangel GJ, et al. 7 T magnetic resonance spectroscopic imaging in multiple sclerosis: how does spatial resolution affect the detectability of metabolic changes in brain lesions? Invest Radiol. 2019;54(4):247‐254. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0051] 51. Gruber S, Heckova E, Strasser B, et al. Mapping an extended neurochemical profile at 3 and 7 T using accelerated high‐resolution proton magnetic resonance spectroscopic imaging. Invest Radiol. 2017;52(10):631‐639. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0052] 52. Strasser B, Povazan M, Hangel G, et al. (2+1)D‐CAIPIRINHA accelerated MR spectroscopic imaging of the brain at 7T. Magn Reson Med. 2017;78(2):429‐440. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0053] 53. Strasser B, Chmelik M, Robinson SD, et al. Coil combination of multichannel MRSI data at 7 T: MUSICAL. NMR Biomed. 2013;26(12):1796‐1805. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0054] 54. Chang P, Nassirpour S, Avdievitch N, Henning A. Non‐water‐suppressed H‐1 FID‐MRSI at 3T and 9.4T. Magn Reson Med. 2018;80(2):442‐451. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0055] 55. Nassirpour S, Chang P, Kirchner T, Henning A. Over‐discretized SENSE reconstruction and B ₀ correction for accelerated non‐lipid‐suppressed ¹H FID MRSI of the human brain at 9.4 T. NMR Biomed. 2018;31(12):1‐14:e4014. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0056] 56. Nassirpour S, Chang P, Henning A. MultiNet PyGRAPPA: multiple neural networks for reconstructing variable density GRAPPA (a ¹H FID MRSI study). NeuroImage. 2018;183:336‐345. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0057] 57. Nassirpour S, Chang P, Avdievitch N, Henning A. Compressed sensing for high‐resolution nonlipid suppressed H‐1 FID MRSI of the human brain at 9.4T. Magn Reson Med. 2018;80(6):2311‐2325. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0058] 58. Klauser A, Courvoisier S, Kasten J, et al. Fast high‐resolution brain metabolite mapping on a clinical 3T MRI by accelerated H‐1‐FID‐MRSI and low‐rank constrained reconstruction. Magn Reson Med. 2019;81(5):2841‐2857. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0059] 59. De Feyter HM, Behar KL, Corbin ZA, et al. Deuterium metabolic imaging (DMI) for MRI‐based 3D mapping of metabolism in vivo. Sci Adv. 2018;4(8):1‐11:eaat7314. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0060] 60. Jain S, Sima DM, Nezhad FS, et al. Patch‐based super‐resolution of MR spectroscopic images: application to multiple sclerosis. Front Neurosci. 2017;11:1‐12. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0061] 61. Schreiner SJ, Kirchner T, Narkhede A, et al. Brain amyloid burden and cerebrovascular disease are synergistically associated with neurometabolism in cognitively unimpaired older adults. Neurobiol Aging. 2018;63:152‐161. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0062] 62. Schreiner SJ, Kirchner T, Wyss M, et al. Low episodic memory performance in cognitively normal elderly subjects is associated with increased posterior cingulate gray matter N‐acetylaspartate: a ¹H MRSI study at 7 Tesla. Neurobiol Aging. 2016;48:195‐203. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0063] 63. Hingerl L, Bogner W, Moser P, et al. Density‐weighted concentric circle trajectories for high resolution brain magnetic resonance spectroscopic imaging at 7T. Magn Reson Med. 2018;79(6):2874‐2885. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0064] 64. Moser P, Bogner W, Hingerl L, et al. Non‐Cartesian GRAPPA and coil combination using interleaved calibration data—application to concentric‐ring MRSI of the human brain at 7T. Magn Reson Med. 2019;82(5):1587‐1603. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0065] 65. Tsai SY, Otazo R, Posse S, et al. Accelerated proton echo planar spectroscopic imaging (PEPSI) using GRAPPA with a 32‐channel phased‐array coil. Magn Reson Med. 2008;59(5):989‐998. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0066] 66. Posse S, Tedeschi G, Risinger R, Ogg R, Lebihan D. High‐speed H‐1 spectroscopic imaging in human brain by echo‐planar spatial‐spectral encoding. Magn Reson Med. 1995;33(1):34‐40. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0067] 67. Kim DH, Spielman DM. Reducing gradient imperfections for spiral magnetic resonance spectroscopic imaging. Magn Reson Med. 2006;56(1):198‐203. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0068] 68. Tsai SY, Lin YR, Wang WC, Niddam DM. Short‐ and long‐term quantitation reproducibility of brain metabolites in the medial wall using proton echo planar spectroscopic imaging. NeuroImage. 2012;63(3):1020‐1029. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0069] 69. Ding XQ, Maudsley AA, Sabati M, Sheriff S, Dellani PR, Lanfermann H. Reproducibility and reliability of short‐TE whole‐brain MR spectroscopic imaging of human brain at 3T. Magn Reson Med. 2015;73(3):921‐928. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0070] 70. Maudsley AA, Domenig C, Sheriff S. Reproducibility of serial whole‐brain MR Spectroscopic Imaging. NMR Biomed. 2010;23(3):251‐256. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0071] 71. Hnilicova P, Povazan M, Strasser B, et al. Spatial variability and reproducibility of GABA‐edited MEGA‐LASER 3D‐MRSI in the brain at 3T. NMR Biomed. 2016;29(11):1656‐1665. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0072] 72. Gagoski B. Magnetic Resonance Spectroscopic Imaging using Parallel Transmission at 7T. Cambridge, MA: Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology; 2011.

[nbm4314-bib-0073] 73. Otazo R, Mueller B, Ugurbil K, Wald L, Posse S. Signal‐to‐noise ratio and spectral linewidth improvements between 1.5 and 7 tesla in proton echo‐planar spectroscopic imaging. Magn Reson Med. 2006;56(6):1200‐1210. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0074] 74. Pohmann R, von Kienlin M, Haase A. Theoretical evaluation and comparison of fast chemical shift imaging methods. J Magn Reson. 1997;129(2):145‐160. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0075] 75. Posse S, Decarli C, Lebihan D. 3‐dimensional echo‐planar MR spectroscopic imaging at short echo times in the human brain. Radiology. 1994;192(3):733‐738. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0076] 76. Adalsteinsson E, Irarrazabal P, Topp S, Meyer C, Macovski A, Spielman DM. Volumetric spectroscopic imaging with spiral‐based k‐space trajectories. Magn Reson Med. 1998;39(6):889‐898. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0077] 77. Ebel A, Maudsley AA, Weiner MW, Schuff N. Achieving sufficient spectral bandwidth for volumetric H‐1 echo‐planar spectroscopic imaging at 4 Tesla. Magn Reson Med. 2005;54(3):697‐701. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0078] 78. Coello E, Noeske R, Burns BL, et al. High‐resolution echo‐planar spectroscopic imaging at ultra‐high field. NMR Biomed. 2018;31(11):1‐10:e3950. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0079] 79. An ZX, Tiwari V, Ganji SK, et al. Echo‐planar spectroscopic imaging with dual‐readout alternated gradients (DRAG‐EPSI) at 7 T: application for 2‐hydroxyglutarate imaging in glioma patients. Magn Reson Med. 2018;79(4):1851‐1861. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0080] 80. Furuyama JK, Wilson NE, Thomas MA. Spectroscopic imaging using concentrically circular echo‐planar trajectories in vivo. Magn Reson Med. 2012;67(6):1515‐1522. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0081] 81. Schirda CV, Tanase C, Boada FE. Rosette spectroscopic imaging: optimal parameters for alias‐free, high sensitivity spectroscopic imaging. J Magn Reson Imaging. 2009;29(6):1375‐1385. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0082] 82. Schmidt R, Seginer A, Tal A. Combining multiband slice selection with consistent k‐t‐space EPSI for accelerated spectral imaging. Magn Reson Med. 2019;82(3):867‐876. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0083] 83. Korzowski A, Bachert P. High‐resolution P‐31 echo‐planar spectroscopic imaging in vivo at 7T. Magn Reson Med. 2018;79(3):1251‐1259. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0084] 84. Bhaduri S, Clement P, Achten E, Serrai H. Reduction of Acquisition time using Partition of the signal Decay in Spectroscopic Imaging technique (RAPID‐SI). PLoS ONE. 2018;13(11):e0207015. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0085] 85. Cao P, Shin PJ, Park I, et al. Accelerated high‐bandwidth MR spectroscopic imaging using compressed sensing. Magn Reson Med. 2016;76(2):369‐379. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0086] 86. Jiang WW, Lustig M, Larson PEZ. Concentric rings K‐space trajectory for hyperpolarized ¹³C MR spectroscopic imaging. Magn Reson Med. 2016;75(1):19‐31. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0087] 87. Dixon WT. Simple proton spectroscopic imaging. Radiology. 1984;153(1):189‐194. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0088] 88. Reeder SB, Pineda AR, Wen ZF, et al. Iterative decomposition of water and fat with echo asymmetry and least‐squares estimation (IDEAL): application with fast spin‐echo imaging. Magn Reson Med. 2005;54(3):636‐644. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0089] 89. Reeder SB, Brittain JH, Grist TM, Yen YF. Least‐squares chemical shift separation for C‐13 metabolic imaging. J Magn Reson Imaging. 2007;26(4):1145‐1152. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0090] 90. Wiesinger F, Weidl E, Menzel MI, et al. IDEAL spiral CSI for dynamic metabolic MR imaging of hyperpolarized [1‐¹³C]pyruvate. Magn Reson Med. 2012;68(1):8‐16. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0091] 91. Gordon JW, Niles DJ, Fain SB, Johnson KM. Joint spatial‐spectral reconstruction and k‐t spirals for accelerated 2D spatial/1D spectral imaging of ¹³C dynamics. Magn Reson Med. 2014;71(4):1435‐1445. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0092] 92. Sigfridsson A, Weiss K, Wissmann L, et al. Hybrid multiband excitation multiecho acquisition for hyperpolarized C‐13 spectroscopic imaging. Magn Reson Med. 2015;73(5):1713‐1717. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0093] 93. Wespi P, Steinhauser J, Kwiatkowski G, Kozerke S. High‐resolution hyperpolarized metabolic imaging of the rat heart using k‐t PCA and k‐t SPARSE. NMR Biomed. 2018;31(2):1‐11:e3876. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0094] 94. Zanette B, Santyr G. Accelerated interleaved spiral‐IDEAL imaging of hyperpolarized Xe‐129 for parametric gas exchange mapping in humans. Magn Reson Med. 2019;82(3):1113‐1119. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0095] 95. Mani M, Magnotta V, Jacob M. A general algorithm for compensation of trajectory errors: application to radial imaging. Magn Reson Med. 2018;80(4):1605‐1613. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0096] 96. Ramirez MS, Lee J, Walker CM, et al. Radial spectroscopic MRI of hyperpolarized [1‐C‐13] pyruvate at 7 tesla. Magn Reson Med. 2014;72(4):986‐995. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0097] 97. Metzger G, Hu XP. Application of interlaced Fourier transform to echo‐planar spectroscopic imaging. J Magn Reson. 1997;125(1):166‐170. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0098] 98. Labadie C, Hetzer S, Schulz J, Mildner T, Aubert‐Frecon M, Moller HE. Center‐out echo‐planar spectroscopic imaging with correction of gradient‐echo phase and time shifts. Magn Reson Med. 2013;70(1):16‐24. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0099] 99. Chu A, Alger JR, Moore GJ, Posse S. Proton echo‐planar spectroscopic imaging with highly effective outer volume suppression using combined presaturation and spatially selective echo dephasing. Magn Reson Med. 2003;49(5):817‐821. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0100] 100. Maudsley AA, Domenig C, Govind V, et al. Mapping of brain metabolite distributions by volumetric proton MR spectroscopic imaging (MRSI). Magn Reson Med. 2009;61(3):548‐559. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0101] 101. Bito Y, Hirata S, Nabeshima T, Yamamoto E. Echo‐planar diffusion spectroscopic imaging. Magn Reson Med. 1995;33(1):69‐73. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0102] 102. Bito Y, Hirata K, Ebisu T, et al. Diffusion‐weighted line‐scan echo‐planar spectroscopic imaging technique to reduce motion artifacts in metabolite diffusion imaging. Magn Reson Med Sci. 2015;14(1):43‐50. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0103] 103. Fotso K, Dager SR, Landow A, et al. Diffusion tensor spectroscopic imaging of the human brain in children and adults. Magn Reson Med. 2017;78(4):1246‐1256. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0104] 104. Ye QM, Chen L, Qiu WQ, et al. Accelerating two‐dimensional nuclear magnetic resonance correlation spectroscopy via selective coherence transfer. J Chem Phys. 2017;146(1):1‐12:014202. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0105] 105. Furuyama JK, Nagarajan R, Roberts CK, Lee CC, Hahn TJ, Thomas MA. A pilot validation of multi‐echo based echo‐planar correlated spectroscopic imaging in human calf muscles. NMR Biomed. 2014;27(10):1176‐1183. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0106] 106. Wilson NE, Burns BL, Iqbal Z, Thomas MA. Correlated spectroscopic imaging of calf muscle in three spatial dimensions using group sparse reconstruction of undersampled single and multichannel data. Magn Reson Med. 2015;74(5):1199‐1208. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0107] 107. Nagarajan R, Carpenter CL, Lee CC, et al. Assessment of lipid and metabolite changes in obese calf muscle using multi‐echo echo‐planar correlated spectroscopic imaging. Sci Rep. 2017;7:1‐10. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0108] 108. Lipnick S, Verma G, Ramadan S, Furuyama J, Thomas MA. Echo planar correlated spectroscopic imaging: implementation and pilot evaluation in human calf in vivo. Magn Reson Med. 2010;64(4):947‐956. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0109] 109. Furuyama JK, Wilson NE, Burns BL, Nagarajan R, Margolis DJ, Thomas MA. Application of compressed sensing to multidimensional spectroscopic imaging in human prostate. Magn Reson Med. 2012;67(6):1499‐1505. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0110] 110. Sarma MK, Nagarajan R, Iqbal Z, Macey PM, Thomas MA. Echo‐planar J‐resolved spectroscopic imaging using dual read‐outs: implementation and quantitation of human brain metabolites. Sci Rep. 2017;7:1‐11. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0111] 111. Sarma MK, Macey PM, Nagarajan R, Aysola R, Harper RM, Thomas MA. Accelerated echo planar J‐resolved spectroscopic imaging of putamen and thalamus in obstructive sleep apnea. Sci Rep. 2016;6:1‐10. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0112] 112. Sarma MK, Nagarajan R, Macey PM, et al. Accelerated echo‐planar J‐resolved spectroscopic imaging in the human brain using compressed sensing: a pilot validation in obstructive sleep apnea. Am J Neuroradiol. 2014;35(6):S81‐S89. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0113] 113. Iqbal Z, Wilson NE, Thomas MA. Prior‐knowledge fitting of accelerated five‐dimensional echo planar J‐resolved spectroscopic imaging: effect of nonlinear reconstruction on quantitation. Sci Rep. 2017;7:1‐12. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0114] 114. Iqbal Z, Wilson NE, Keller MA, et al. Pilot assessment of brain metabolism in perinatally HIV‐infected youths using accelerated 5D echo planar J‐resolved spectroscopic imaging. PLoS ONE. 2016;11(9):e0162810. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0115] 115. Magnusson PO, Boer VO, Marsman A, Paulson OB, Hanson LG, Petersen ET. Gamma‐aminobutyric acid edited echo‐planar spectroscopic imaging (EPSI) with MEGA‐sLASER at 7T. Magn Reson Med. 2019;81(2):773‐780. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0116] 116. McDannold N, Barnes AS, Rybicki FJ, et al. Temperature mapping considerations in the breast with line scan echo planar spectroscopic imaging. Magn Reson Med. 2007;58(6):1117‐1123. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0117] 117. Tsai SY, Posse S, Lin YR, et al. Fast mapping of the T ₂ relaxation time of cerebral metabolites using proton echo‐planar spectroscopic imaging (PEPSI). Magn Reson Med. 2007;57(5):859‐865. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0118] 118. Tsai SY, Wang WC, Lin YR. Comparison of sagittal and transverse echo planar spectroscopic imaging on the quantification of brain metabolites. J Neuroimaging. 2015;25(2):167‐174. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0119] 119. Lecocq A, Le Fur Y, Maudsley AA, et al. Whole‐brain quantitative mapping of metabolites using short echo three‐dimensional proton MRSI. J Magn Reson Imaging. 2015;42(2):280‐289. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0120] 120. Verma G, Chawla S, Mohan S, et al. Three‐dimensional echo planar spectroscopic imaging for differentiation of true progression from pseudoprogression in patients with glioblastoma. NMR Biomed. 2019;32(2):1‐10:e4042. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0121] 121. Maudsley AA, Roy B, Gupta RK, et al. Association of metabolite concentrations and water diffusivity in normal appearing brain tissue with glioma grade. J Neuroimaging. 2014;24(6):585‐589. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0122] 122. Chawla S, Wang SM, Kim S, et al. Radiation injury to the normal brain measured by 3D‐echo‐planar spectroscopic imaging and diffusion tensor imaging: initial experience. J Neuroimaging. 2015;25(1):97‐104. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0123] 123. Maudsley AA, Gupta RK, Stoyanova R, et al. Mapping of glycine distributions in gliomas. Am J Neuroradiol. 2014;35(6):S31‐S36. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0124] 124. Verma G, Woo JH, Chawla S, et al. Whole‐brain analysis of amyotrophic lateral sclerosis by using echo‐planar spectroscopic imaging. Radiology. 2013;267(3):851‐857. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0125] 125. Bustillo JR, Chen HJ, Gasparovic C, et al. Glutamate as a marker of cognitive function in schizophrenia: a proton spectroscopic imaging study at 4 tesla. Biol Psychiatry. 2011;69(1):19‐27. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0126] 126. Richards TL, Berninger VW, Aylward EH, et al. Reproducibility of proton MR spectroscopic imaging (PEPSI): comparison of dyslexic and normal‐reading children and effects of treatment on brain lactate levels during language tasks. Am J Neuroradiol. 2002;23(10):1678‐1685. [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0127] 127. Zhao CG, Bolan PJ, Royce M, et al. Quantitative mapping of total choline in healthy human breast using proton echo planar spectroscopic imaging (PEPSI) at 3 Tesla. J Magn Reson Imaging. 2012;36(5):1113‐1123. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0128] 128. Medved M, Ivancevic MK, Olopade OI, Newstead GM, Karczmar GS. Echo‐planar spectroscopic imaging (EPSI) of the water resonance structure in human breast using sensitivity encoding (SENSE). Magn Reson Med. 2010;63(6):1557‐1563. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0129] 129. Lin YR, Chiu JJ, Tsai SY. Feasibility and reproducibility of echo planar spectroscopic imaging on the quantification of hepatic fat. PLoS ONE. 2014;9(12):e114436. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0130] 130. Weis J, Bruvold M, Ortiz‐Nieto F, Ahlstrom H. High‐resolution echo‐planar spectroscopic imaging of the human calf. PLoS ONE. 2014;9(1):e87533. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0131] 131. Cunningham CH, Vigneron DB, Chen AP, et al. Design of flyback echo‐planar readout gradients for magnetic resonance spectroscopic imaging. Magn Reson Med. 2005;54(5):1286‐1289. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0132] 132. Morgan PS, Bowtell RW, McIntyre DJO, Worthington BS. Correction of spatial distortion in EPI due to inhomogeneous static magnetic fields using the reversed gradient method. J Magn Reson Imaging. 2004;19(4):499‐507. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0133] 133. Webb P, Spielman D, Macovski A. A fast spectroscopic imaging method using a blipped phase encode gradient. Magn Reson Med. 1989;12(3):306‐315. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0134] 134. Tyszka JM, Mamelak AN. Volumetric multishot echo‐planar spectroscopic imaging. Magn Reson Med. 2001;46(2):219‐227. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0135] 135. Park I, Chen AP, Zierhut ML, Ozturk‐Isik E, Vigneron DB, Nelson SJ. Implementation of 3 T lactate‐edited 3D H‐1 MR spectroscopic imaging with flyback echo‐planar readout for gliomas patients. Ann Biomed Eng. 2011;39(1):193‐204. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0136] 136. Li Y, Larson P, Chen AP, et al. Short‐echo three‐dimensional H‐1 MR spectroscopic imaging of patients with glioma at 7 tesla for characterization of differences in metabolite levels. J Magn Reson Imaging. 2015;41(5):1332‐1341. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0137] 137. Chen AP, Cunningham CH, Ozturk‐Isik E, et al. High‐speed 3T MR spectroscopic imaging of prostate with flyback echo‐planar encoding. J Magn Reson Imaging. 2007;25(6):1288‐1292. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0138] 138. Cunningham CH, Chen AP, Albers MJ, et al. Double spin‐echo sequence for rapid spectroscopic imaging of hyperpolarized C‐13. J Magn Reson. 2007;187(2):357‐362. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0139] 139. Santos‐Diaz A, Obruchkov SI, Schulte RF, Noseworthy MD. Phosphorus magnetic resonance spectroscopic imaging using flyback echo planar readout trajectories. Magn Reson Mater Phys Biol Med. 2018;31(4):553‐564. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0140] 140. Uribe S, Guesalaga A, Mir R, Guarini M, Irarrazaval P. A 3D trajectory for undersampling k‐space in MRSI applications. Magn Reson Imaging. 2007;25(3):350‐358. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0141] 141. Kim DH, Henry R, Spielman DM. Fast multivoxel two‐dimensional spectroscopic imaging at 3 T. Magn Reson Imaging. 2007;25(8):1155‐1161. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0142] 142. Chatnuntawech I, Gagoski B, Bilgic B, Cauley SF, Setsompop K, Adalsteinsson E. Accelerated ¹H MRSI using randomly undersampled spiral‐based k‐space trajectories. Magn Reson Med. 2015;74(1):13‐24. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0143] 143. Levin YS, Mayer D, Yen YF, Hurd RE, Spielman DM. Optimization of fast spiral chemical shift imaging using least squares reconstruction: application for hyperpolarized C‐13 metabolic imaging. Magn Reson Med. 2007;58(2):245‐252. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0144] 144. Park JM, Josan S, Jang T, et al. Volumetric spiral chemical shift imaging of hyperpolarized [2‐¹³C]pyruvate in a rat C6 glioma model. Magn Reson Med. 2016;75(3):973‐984. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0145] 145. Wang JX, Merritt ME, Sherry D, Malloy CR. A general chemical shift decomposition method for hyperpolarized C‐13 metabolite magnetic resonance imaging. Magn Reson Chem. 2016;54(8):665‐673. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0146] 146. Khegai O, Schulte RF, Janich MA, et al. Apparent rate constant mapping using hyperpolarized [1‐C‐13]pyruvate. NMR Biomed. 2014;27(10):1256‐1265. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0147] 147. Xu T, Mayer D, Gu M, et al. Quantification of in vivo metabolic kinetics of hyperpolarized pyruvate in rat kidneys using dynamic C‐13 MRSI. NMR Biomed. 2011;24(8):997‐1005. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0148] 148. Santos‐Diaz A, Harasym D, Noseworthy MD. Dynamic 31P spectroscopic imaging of skeletal muscles combining flyback echo‐planar spectroscopic imaging and compressed sensing. Magn Reson Med. 2019;81(6):3453‐3461. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0149] 149. Bogner W, Gagoski B, Hess AT, et al. 3D GABA imaging with real‐time motion correction, shim update and reacquisition of adiabatic spiral MRSI. NeuroImage. 2014;103:290‐302. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0150] 150. Andronesi OC, Arrillaga‐Romany IC, Ly KI, et al. Pharmacodynamics of mutant‐IDH1 inhibitors in glioma patients probed by in vivo 3D MRS imaging of 2‐hydroxyglutarate. Nat Commun. 2018;9:1‐9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0151] 151. Heckova E, Povazan M, Strasser B, et al. Real‐time correction of motion and imager instability artifacts during 3D gamma‐aminobutyric acid‐edited MR spectroscopic imaging. Radiology. 2018;286(2):666‐675. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0152] 152. Jafari‐Khouzani K, Loebel F, Bogner W, et al. Volumetric relationship between 2‐hydroxyglutarate and FLAIR hyperintensity has potential implications for radiotherapy planning of mutant IDH glioma patients. Neuro‐Oncology. 2016;18(11):1569‐1578. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0153] 153. Andronesi OC, Loebel F, Bogner W, et al. Treatment response assessment in IDH‐mutant glioma patients by noninvasive 3D functional spectroscopic mapping of 2‐hydroxyglutarate. Clin Cancer Res. 2016;22(7):1632‐1641. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0154] 154. Bogner W, Hess AT, Gagoski B, et al. Real‐time motion‐ and B₀‐correction for LASER‐localized spiral‐accelerated 3D‐MRSI of the brain at 3 T. NeuroImage. 2014;88:22‐31. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0155] 155. Kim DH, Gu M, Cunningham C, et al. Fast 3D H‐1 MRSI of the corticospinal tract in pediatric brain. J Magn Reson Imaging. 2009;29(1):1‐6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0156] 156. Andronesi OC, Gagoski BA, Sorensen AG. Neurologic 3D MR spectroscopic imaging with low‐power adiabatic pulses and fast spiral acquisition. Radiology. 2012;262(2):647‐661. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0157] 157. Pfefferbaum A, Adalsteinsson E, Sullivan EV. Cortical NAA deficits in HIV infection without dementia: influence of alcoholism comorbidity. Neuropsychopharmacology. 2005;30(7):1392‐1399. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0158] 158. Yazbek S, Prabhu SP, Connaughton P, Grant PE, Gagoski B. Comparison of accelerated 3‐D spiral chemical shift imaging and single‐voxel spectroscopy at 3T in the pediatric age group. Pediatr Radiol. 2015;45(9):1417‐1422. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0159] 159. Steinseifer IK, Philips BWJ, Gagoski B, Weiland E, Scheenen TWJ, Heerschap A. Flexible proton 3D MR spectroscopic imaging of the prostate with low‐power adiabatic pulses for volume selection and spiral readout. Magn Reson Med. 2017;77(3):928‐935. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0160] 160. Kim DH, Margolis D, Xing L, Daniel B, Spielman D. In vivo prostate magnetic resonance spectroscopic imaging using two‐dimensional J‐resolved PRESS at 3 T. Magn Reson Med. 2005;53(5):1177‐1182. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0161] 161. Adalsteinsson E, Sullivan EV, Kleinhans N, Spielman DM, Pfefferbaum A. Longitudinal decline of the neuronal marker N‐acetyl aspartate in Alzheimer's disease. Lancet. 2000;355(9216):1696‐1697. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0162] 162. Adalsteinsson E, Langer‐Gould A, Homer RJ, et al. Gray matter‐N‐acetyl aspartate deficits in secondary progressive but not relapsing‐remitting multiple sclerosis. Am J Neuroradiol. 2003;24(10):1941‐1945. [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0163] 163. Spurny B, Seiger R, Moser P, et al. Hippocampal GABA levels correlate with retrieval performance in an associative learning paradigm. NeuroImage. 2019;10(204):116‐244. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0164] 164. Gu M, Kim DH, Mayer D, Sullivan EV, Pfefferbaum A, Spielman DM. Reproducibility study of whole‐brain H‐1 spectroscopic imaging with automated quantification. Magn Reson Med. 2008;60(3):542‐547. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0165] 165. Kim DH, Adalsteinsson E, Spielman DM. Simple analytic variable density spiral design. Magn Reson Med. 2003;50(1):214‐219. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0166] 166. Adalsteinsson E, Star‐Lack J, Meyer CH, Spielman DM. Reduced spatial side lobes in chemical‐shift imaging. Magn Reson Med. 1999;42(2):314‐323. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0167] 167. Bilgic B, Gagoski B, Kok T, Adalsteinsson E. Lipid suppression in CSI with spatial priors and highly undersampled peripheral k‐space. Magn Reson Med. 2013;69(6):1501‐1511. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0168] 168. Bhattacharya I, Jacob M. Compartmentalized low‐rank recovery for high‐resolution lipid unsuppressed MRSI. Magn Reson Med. 2017;78(4):1267‐1280. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0169] 169. Bhave S, Eslami R, Jacob M. Sparse spectral deconvolution algorithm for noncartesian MR spectroscopic imaging. Magn Reson Med. 2014;71(2):469‐476. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0170] 170. Sarkar S, Heberlein K, Hu XP. Truncation artifact reduction in spectroscopic imaging using a dual‐density spiral k‐space trajectory. Magn Reson Imaging. 2002;20(10):743‐757. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0171] 171. Mayer D, Yen YF, Takahashi A, et al. Dynamic and high‐resolution metabolic imaging of hyperpolarized [1‐C‐13]‐pyruvate in the rat brain using a high‐performance gradient insert. Magn Reson Med. 2011;65(5):1228‐1233. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0172] 172. Hiba B, Faure B, Lamalle L, Decorps M, Ziegler A. Out‐and‐in spiral spectroscopic imaging in rat brain at 7 T. Magn Reson Med. 2003;50(6):1127‐1133. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0173] 173. Chiew M, Jiang WW, Burns B, et al. Density‐weighted concentric rings k‐space trajectory for ¹H magnetic resonance spectroscopic imaging at 7T. NMR Biomed. 2018;31(1):1‐14:e3838. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0174] 174. Emir UE, Burns B, Chiew M, Jezzard P, Thomas MA. Non‐water‐suppressed short‐echo‐time magnetic resonance spectroscopic imaging using a concentric ring k‐space trajectory. NMR Biomed. 2017;30(7):1‐12:e3714. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0175] 175. Moser P, Hingerl L, Strasser B, et al. Whole‐slice mapping of GABA and GABA thorn at 7T via adiabatic MEGA‐editing, real‐time instability correction, and concentric circle readout. NeuroImage. 2019;184:475‐489. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0176] 176. Steel A, Chiew M, Jezzard P, et al. Metabolite‐cycled density‐weighted concentric rings k‐space trajectory (DW‐CRT) enables high‐resolution 1 H magnetic resonance spectroscopic imaging at 3‐Tesla. Sci Rep. 2018;8:1‐10. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0177] 177. Noll DC. Multishot rosette trajectories for spectrally selective MR imaging. IEEE Trans Med Imaging. 1997;16(4):372‐377. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0178] 178. Schirda CV, Zhao TJ, Yushmanov VE, et al. Fast 3D rosette spectroscopic imaging of neocortical abnormalities at 3 T: assessment of spectral quality. Magn Reson Med. 2018;79(5):2470‐2480. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0179] 179. Schirda CV, Zhao TJ, Andronesi OC, et al. In vivo brain rosette spectroscopic imaging (RSI) with LASER excitation, constant gradient strength readout, and automated LCModel quantification for all voxels. Magn Reson Med. 2016;76(2):380‐390. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0180] 180. Li Y, Yang R, Zhang CS, Zhang JX, Jia S, Zhou ZY. Analysis of generalized rosette trajectory for compressed sensing MRI. Med Phys. 2015;42(9):5530‐5544. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0181] 181. Ludwig D, Korzowski A, Ruhm L, Ladd ME, Bachert P. Three‐dimensional ³¹P radial echo‐planar spectroscopic imaging in vivo at 7T. Paper presented at: ISMRM 25th Annual Meeting and Exhibition; April 22‐27, 2017; Honolulu, HI.

[nbm4314-bib-0182] 182. Boer VO. Metabolite diffusion‐weighted imaging with golden angle radial echo planar spectroscopic imaging. Paper presented at: ISMRM Workshop on Ultrahigh Field Magnetic Resonance; March 31‐April 3, 2019; Dubrovnik, Croatia.

[nbm4314-bib-0183] 183. Kim DH, Adalsteinsson E, Spielman DM. Spiral readout gradients for the reduction of motion artifacts in chemical shift imaging. Magn Reson Med. 2004;51(3):458‐463. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0184] 184. Ebel A, Maudsley AA. Detection and correction of frequency instabilities for volumetric H‐1 echo‐planar spectroscopic imaging. Magn Reson Med. 2005;53(2):465‐469. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0185] 185. Hamilton J, Franson D, Seiberlich N. Recent advances in parallel imaging for MRI. Prog Nucl Magn Reson Spectrosc. 2017;101:71‐95. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0186] 186. Griswold MA, Breuer F, Blaimer M, et al. Autocalibrated coil sensitivity estimation for parallel imaging. NMR Biomed. 2006;19(3):316‐324. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0187] 187. Pruessmann KP. Encoding and reconstruction in parallel MRI. NMR Biomed. 2006;19(3):288‐299. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0188] 188. Dydak U, Weiger M, Pruessmann KP, Meier D, Boesiger P. Sensitivity‐encoded spectroscopic imaging. Magn Reson Med. 2001;46(4):713‐722. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0189] 189. Zhu H, Soher BJ, Ouwerkerk R, Schar M, Barker PB. Spin‐echo magnetic resonance spectroscopic imaging at 7 T with frequency‐modulated refocusing pulses. Magn Reson Med. 2013;69(5):1217‐1225. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0190] 190. Otazo R, Tsai SY, Lin FH, Posse S. Accelerated short‐TE 3D proton echo‐planar spectroscopic Imaging using 2D‐SENSE with a 32‐channel array coil. Magn Reson Med. 2007;58(6):1107‐1116. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0191] 191. Lin FH, Tsai SY, Otazo R, et al. Sensitivity‐encoded (SENSE) proton echo‐planar spectroscopic imaging (PEPSI) in the human brain. Magn Reson Med. 2007;57(2):249‐257. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0192] 192. Kirchner T, Fillmer A, Henning A. Mechanisms of SNR and line shape improvement by B ₀ correction in overdiscrete MRSI reconstruction. Magn Reson Med. 2017;77(1):44‐56. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0193] 193. Kirchner T, Fillmer A, Tsao J, Pruessmann KP, Henning A. Reduction of voxel bleeding in highly accelerated parallel H‐1 MRSI by direct control of the spatial response function. Magn Reson Med. 2015;73(2):469‐480. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0194] 194. Lustig M, Pauly JM. SPIRiT: iterative self‐consistent parallel imaging reconstruction from arbitrary k‐space. Magn Reson Med. 2010;64(2):457‐471. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0195] 195. Uecker M, Lai P, Murphy MJ, et al. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med. 2014;71(3):990‐1001. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0196] 196. Ozturk‐Isik E, Crane JC, Cha SM, Chang SM, Berger MS, Nelson SJ. Unaliasing lipid contamination for MR spectroscopic imaging of gliomas at 3T using sensitivity encoding (SENSE). Magn Reson Med. 2006;55(5):1164‐1169. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0197] 197. Sanchez‐Gonzalez J, Tsao J, Dydak U, Desco M, Boesiger P, Pruessmann KP. Minimum‐norm reconstruction for sensitivity‐encoded magnetic resonance spectroscopic imaging. Magn Reson Med. 2006;55(2):287‐295. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0198] 198. Otazo R, Lin FH, Wiggins G, Jordan R, Sodickson D, Posse S. Superresolution parallel magnetic resonance imaging: application to functional and spectroscopic imaging. NeuroImage. 2009;47(1):220‐230. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0199] 199. Ozturk‐Isik E, Chen AP, Crane JC, et al. 3D sensitivity encoded ellipsoidal MR spectroscopic imaging of gliomas at 3T. Magn Reson Imaging. 2009;27(9):1249‐1257. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0200] 200. Posse S, Otazo R, Tsai SY, Yoshimoto AE, Lin FH. Single‐shot magnetic resonance spectroscopic imaging with partial parallel imaging. Magn Reson Med. 2009;61(3):541‐547. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0201] 201. Ohliger MA, Larson PEZ, Bok RA, et al. Combined parallel and partial Fourier MR reconstruction for accelerated 8‐channel hyperpolarized carbon‐13 in vivo magnetic resonance spectroscopic imaging (MRSI). J Magn Reson Imaging. 2013;38(3):701‐713. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0202] 202. Birch R, Peet AC, Arvanitis TN, Wilson M. Sensitivity encoding for fast H‐1 MR spectroscopic imaging water reference acquisition. Magn Reson Med. 2015;73(6):2081‐2086. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0203] 203. Bonekamp D, Smith MA, Zhu H, Barker PB. Quantitative SENSE‐MRSI of the human brain. Magn Reson Imaging. 2010;28(3):305‐313. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0204] 204. Ozturk E, Banerjee S, Majumdar S, Nelson SJ. Partially parallel MR spectroscopic imaging of gliomas at 3T. In: 2006 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. New York City, New York: IEEE; 2006:493‐496. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0205] 205. Arunachalam A, Whitt D, Fish K, et al. Accelerated spectroscopic imaging of hyperpolarized C‐13 pyruvate using SENSE parallel imaging. NMR Biomed. 2009;22(8):867‐873. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0206] 206. Tropp J, Lupo JM, Chen A, et al. Multi‐channel metabolic imaging, with SENSE reconstruction, of hyperpolarized [1‐C‐13] pyruvate in a live rat at 3.0 tesla on a clinical MR scanner. J Magn Reson. 2011;208(1):171‐177. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0207] 207. Banerjee S, Ozturk‐Isik E, Nelson SJ, Majumdar S. Fast magnetic resonance spectroscopic imaging at 3 Tesla using autocalibrating parallel technique. In: 2006 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. New York City, New York: IEEE; 2006:1866‐1869. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0208] 208. Zhu XP, Ebel A, Ji JX, Schuff N. Spectral phase‐corrected GRAPPA reconstruction of three‐dimensional echo‐planar spectroscopic imaging (3D‐EPSI). Magn Reson Med. 2007;57(5):815‐820. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0209] 209. Hangel G, Strasser B, Povazan M, et al. Lipid suppression via double inversion recovery with symmetric frequency sweep for robust 2D‐GRAPPA‐accelerated MRSI of the brain at 7T. NMR Biomed. 2015;28(11):1413‐1425. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0210] 210. Banerjee S, Ozturk‐Isik E, Nelson SJ, Majumdar S. Elliptical magnetic resonance spectroscopic imaging with GRAPPA for imaging brain tumors at 3 T. Magn Reson Imaging. 2009;27(10):1319‐1325. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0211] 211. Sabati M, Zhan JP, Govind V, Arheart KL, Maudsley AA. Impact of reduced k‐space acquisition on pathologic detectability for volumetric MR spectroscopic imaging. J Magn Reson Imaging. 2014;39(1):224‐234. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0212] 212. Gu M, Liu CL, Spielman DM. Parallel spectroscopic imaging reconstruction with arbitrary trajectories using k‐space sparse matrices. Magn Reson Med. 2009;61(2):267‐272. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0213] 213. Raghavan RS, Panda A, Valette J, et al. ³¹P spectroscopic imaging with GRAPPA. Proc Int Soc Magn Reson Med. 2009;17:4317.

[nbm4314-bib-0214] 214. Shin PJ, Larson PEZ, Ohliger MA, et al. Calibrationless parallel imaging reconstruction based on structured low‐rank matrix completion. Magn Reson Med. 2014;72(4):959‐970. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0215] 215. Gordon JW, Hansen RB, Shin PJ, Feng Y, Vigneron DB, Larson PEZ. 3D hyperpolarized C‐13 EPI with calibrationless parallel imaging. J Magn Reson. 2018;289:92‐99. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0216] 216. Zierhut ML, Ozturk‐Isik E, Chen AP, Park I, Vigneron DB, Nelson SJ. H‐1 spectroscopic imaging of human brain at 3 tesla: comparison of fast three‐dimensional magnetic resonance spectroscopic imaging techniques. J Magn Reson Imaging. 2009;30(3):473‐480. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0217] 217. Feinberg DA, Setsompop K. Ultra‐fast MRI of the human brain with simultaneous multi‐slice imaging. J Magn Reson. 2013;229:90‐100. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0218] 218. Larkman DJ, Hajnal JV, Herlihy AH, Coutts GA, Young IR, Ehnholm G. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited. J Magn Reson Imaging. 2001;13(2):313‐317. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0219] 219. Breuer FA, Blaimer M, Heidemann RM, Mueller MF, Griswold MA, Jakob PM. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi‐slice imaging. Magn Reson Med. 2005;53(3):684‐691. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0220] 220. Xia P, Chiew M, Zhou X, Thomas MA, Dydak U, Emir UE. Density‐weighted concentric ring trajectory using simultaneous multi‐band acceleration: 3D metabolite‐cycled magnetic resonance spectroscopy imaging at 3T. BioRXiv. 2019. [Google Scholar]

[nbm4314-bib-0221] 221. Larson PEZ, Bok R, Kerr AB, et al. Investigation of tumor hyperpolarized [1‐C‐13]‐pyruvate dynamics using time‐resolved multiband RF excitation echo‐planar MRSI. Magn Reson Med. 2010;63(3):582‐591. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0222] 222. Larson PEZ, Kerr AB, Chen AP, et al. Multiband excitation pulses for hyperpolarized 13C dynamic chemical‐shift imaging. J Magn Reson. 2008;194(1):121‐127. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0223] 223. Lustig M, Donoho D, Pauly JM. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6):1182‐1195. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0224] 224. Dafni H, Ronen SM. Dynamic nuclear polarization in metabolic imaging of metastasis: common sense, hypersense and compressed sensing. Cancer Biomark. 2010;7(4‐5):189‐199. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0225] 225. Park I, Hu S, Bok R, et al. Evaluation of heterogeneous metabolic profile in an orthotopic human glioblastoma xenograft model using compressed sensing hyperpolarized 3D ¹³C magnetic resonance spectroscopic imaging. Magn Reson Med. 2013;70(1):33‐39. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0226] 226. von Morze C, Larson PEZ, Hu S, et al. Investigating tumor perfusion and metabolism using multiple hyperpolarized C‐13 compounds: HP001, pyruvate and urea. Magn Reson Imaging. 2012;20(3):305‐311. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0227] 227. Wiens CN, Friesen‐Waldner LJ, Wade TP, Sinclair KJ, McKenzie CA. Chemical shift encoded imaging of hyperpolarized C‐13 pyruvate. Magn Reson Med. 2015;74(6):1682‐1689. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0228] 228. Geraghty BJ, Lau JYC, Chen AP, Cunningham CH. Accelerated 3D echo‐planar imaging with compressed sensing for time‐resolved hyperpolarized C‐13 studies. Magn Reson Med. 2017;77(2):538‐546. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0229] 229. Milshteyn E, von Morze C, Reed GD, et al. Development of high resolution 3D hyperpolarized carbon‐13 MR molecular imaging techniques. Magn Reson Imaging. 2017;38:152‐162. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0230] 230. Wang JX, Merritt ME, Sherry AD, Malloy CR. Accelerated chemical shift imaging of hyperpolarized C‐13 metabolites. Magn Reson Med. 2016;76(4):1033‐1038. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0231] 231. Chen HY, Larson PEZ, Gordon JW, et al. Technique development of 3D dynamic CS‐EPSI for hyperpolarized C‐13 pyruvate MR molecular imaging of human prostate cancer. Magn Reson Med. 2018;80(5):2062‐2072. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0232] 232. Askin NC, Atis B, Ozturk‐Isik E. Accelerated phosphorus magnetic resonance spectroscopic imaging using compressed sensing. In: 2012 34th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. San Diego, California: IEEE; 2012:1106‐1109. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0233] 233. Hatay GH, Yildirim M, Ozturk‐Isik E. Considerations in applying compressed sensing to in vivo phosphorus MR spectroscopic imaging of human brain at 3T. Med Biol Eng Comput. 2017;55(8):1303‐1315. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0234] 234. Santos‐Diaz A, Noseworthy MD. Comparison of compressed sensing reconstruction algorithms for P‐31 magnetic resonance spectroscopic imaging. Magn Reson Imaging. 2019;59:88‐96. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0235] 235. Fu Y, Ijare O, Thomas G, Fazel‐Rezai R, Serrai H. Implementation of wavelet encoding spectroscopic imaging technique on a 3 tesla whole body MR scanner: in vitro results. In: 2009 31st Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Minneapolis, Minnesota: IEEE; 2009:2688‐2691. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0236] 236. Geethanath S, Baek HM, Ganji SK, et al. Compressive sensing could accelerate H‐1 MR metabolic imaging in the clinic. Radiology. 2012;262(3):985‐994. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0237] 237. Heikal AA, Wachowicz K, Fallone BG. Effect of the k‐space sampling pattern on the MTF of compressed sensing MRSI. Med Phys. 2012;39(7):4623‐4623. [Google Scholar]

[nbm4314-bib-0238] 238. Heikal AA, Wachowicz K, Fallone BG. MTF behavior of compressed sensing MR spectroscopic imaging. Med Phys. 2013;40(5):052302. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0239] 239. Heikal AA, Wachowicz K, Fallone BG. Correlation between k‐space sampling pattern and MTF in compressed sensing MRSI. Med Phys. 2016;43(10):5626‐5634. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0240] 240. Thomas MA, Nagarajan R, Huda A, et al. Multidimensional MR spectroscopic imaging of prostate cancer in vivo. NMR Biomed. 2014;27(1):53‐66. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0241] 241. Nagarajan R, Iqbal Z, Burns B, et al. Accelerated echo planar J‐resolved spectroscopic imaging in prostate cancer: a pilot validation of non‐linear reconstruction using total variation and maximum entropy. NMR Biomed. 2015;28(11):1366‐1373. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0242] 242. Breuer FA, Blaimer M, Mueller MF, et al. Controlled aliasing in volumetric parallel imaging (2D CAIPIRINHA). Magn Reson Med. 2006;55(3):549‐556. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0243] 243. Otazo R, Sodickson DK, Yoshimoto A, Posse S. Accelerated proton echo‐planar spectroscopic imaging using parallel imaging and compressed sensing. Proc Int Soc Magn Reson Med. 2009;17:331.

[nbm4314-bib-0244] 244. Iqbal Z, Wilson NE, Thomas MA. 3D spatially encoded and accelerated TE‐averaged echo planar spectroscopic imaging in healthy human brain. NMR Biomed. 2016;29(3):329‐339. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0245] 245. Burns B, Wilson NE, Furuyama JK, Thomas MA. Non‐uniformly under‐sampled multi‐dimensional spectroscopic imaging in vivo: maximum entropy versus compressed sensing reconstruction. NMR Biomed. 2014;27(2):191‐201. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0246] 246. Wright KL, Hamilton JI, Griswold MA, Gulani V, Seiberlich N. Non‐Cartesian parallel imaging reconstruction. J Magn Reson Imaging. 2014;40(5):1022‐1040. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0247] 247. Mayer D, Kim DH, Spielman DM, Bammer R. Fast parallel spiral chemical shift imaging at 3T using iterative SENSE reconstruction. Magn Reson Med. 2008;59(4):891‐897. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0248] 248. Baron CA, Dwork N, Pauly JM, Nishimura DG. Rapid compressed sensing reconstruction of 3D non‐Cartesian MRI. Magn Reson Med. 2018;79(5):2685‐2692. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0249] 249. Mayer D, Yen YF, Tropp J, Pfefferbaum A, Hurd RE, Spielman DM. Application of subsecond spiral chemical shift imaging to real‐time multislice metabolic imaging of the rat in vivo after injection of hyperpolarized C‐13(1)‐pyruvate. Magn Reson Med. 2009;62(3):557‐564. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0250] 250. Zhu B, Liu JZ, Cauley SF, Rosen BR, Rosen MS. Image reconstruction by domain‐transform manifold learning. Nature. 2018;555(7697):487‐492. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0251] 251. Hu XP, Levin DN, Lauterbur PC, Spraggins T. SLIM—spectral localization by imaging. Magn Reson Med. 1988;8(3):314‐322. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0252] 252. Kmiecik JA, Gregory CD, Liang ZP, Hrad DE, Lauterbur PC, Dawson MJ. Quantitative lactate‐specific MR imaging and H‐1 spectroscopy of skeletal muscle at macroscopic and microscopic resolutions using a zero‐quantum/double‐quantum coherence filter and SLIM/GSLIM localization. Magn Reson Med. 1997;37(6):840‐850. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0253] 253. Xu S, Yang YH, Gregory CD, Vary JC, Liang ZP, Dawson MJ. Biochemical heterogeneity in hysterectomized uterus measured by P‐31 NMR using SLIM localization. Magn Reson Med. 1997;37(5):736‐743. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0254] 254. Dong ZC, Hwang JH. Lipid signal extraction by SLIM: application to H‐1 MR spectroscopic imaging of human calf muscles. Magn Reson Med. 2006;55(6):1447‐1453. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0255] 255. von Kienlin M, Mejia R. Spectral localization with optimal pointspread function. J Magn Reson. 1991;94(2):268‐287. [Google Scholar]

[nbm4314-bib-0256] 256. Loffler R, Sauter R, Kolem H, Haase A, von Kienlin M. Localized spectroscopy from anatomically matched compartments: improved sensitivity and localization for cardiac P‐31 MRS in humans. J Magn Reson. 1998;134(2):287‐299. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0257] 257. Meininger M, Landschutz W, Beer M, et al. Concentrations of human cardiac phosphorus metabolites determined by SLOOP P‐31 NMR spectroscopy. Magn Reson Med. 1999;41(4):657‐663. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0258] 258. Pohmann R, Rommel E, von Kienlin M. Beyond k‐space: spectral localization using higher order gradients. J Magn Reson. 1999;141(2):197‐206. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0259] 259. Kostler H, Landschutz W, Koeppe S, et al. Age and gender dependence of human cardiac phosphorus metabolites determined by SLOOP P‐31 MR spectroscopy. Magn Reson Med. 2006;56(4):907‐911. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0260] 260. Landschutz W, Meininger M, Beer M, et al. Concentration of human cardiac ³¹P‐metabolites determined by SLOOP ³¹P‐MRS. Magn Reson Mater Phys Biol Med. 1998;6(2/3):155‐156. [PubMed] [Google Scholar]

[nbm4314-bib-0261] 261. Geier O, Weng AM, Toepell A, et al. Acquisition‐weighted chemical shift imaging improves SLOOP quantification of human cardiac phosphorus metabolites. Z Med Phys. 2014;24(1):49‐54. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0262] 262. Beer M, Seyfarth T, Sandstede J, et al. Absolute concentrations of high‐energy phosphate metabolites in normal, hypertrophied, and failing human myocardium measured noninvasively with P‐31‐SLOOP magnetic resonance spectroscopy. J Am Coll Cardiol. 2002;40(7):1267‐1274. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0263] 263. von Kienlin M, Beer M, Greiser A, et al. Advances in human cardiac P‐31‐MR spectroscopy: SLOOP and clinical applications. J Magn Reson Imaging. 2001;13(4):521‐527. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0264] 264. Liang ZP, Lauterbur PC. A generalized series approach to MR spectroscopic imaging. IEEE Trans Med Imaging. 1991;10(2):132‐137. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0265] 265. Kmiecik JA, Gregory CD, Liang ZP, Lauterbur PC, Dawson MJ. Lactate quantitation in a gerbil brain stroke model by GSLIM of multiple‐quantum‐filtered signals. J Magn Reson Im aging. 1999;9(4):539‐543. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0266] 266. Bashir A, Yablonskiy DA. Natural linewidth chemical shift imaging (NL‐CSI). Magn Reson Med. 2006;56(1):7‐18. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0267] 267. Khalidov I, Van de Ville D, Jacob M, Lazeyras F, Unser M. BSLIM: spectral localization by imaging with explicit B ₀ field inhomogeneity compensation. IEEE Trans Med Imaging. 2007;26(7):990‐1000. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0268] 268. Passeri A, Mazzuca S, Del Bene V. Radiofrequency field inhomogeneity compensation in high spatial resolution magnetic resonance spectroscopic imaging. Phys Med Biol. 2014;59(12):2913‐2934. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0269] 269. An L, Warach S, Shen J. Spectral localization by imaging using multielement receiver coils. Magn Reson Med. 2011;66(1):1‐10. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0270] 270. Zhang Y, Gabr RE, Zhou JY, Weiss RG, Bottomley PA. Highly‐accelerated quantitative 2D and 3D localized spectroscopy with linear algebraic modeling (SLAM) and sensitivity encoding. J Magn Reson. 2013;237:125‐138. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0271] 271. Zhang Y, Gabr RE, Schar M, Weiss RG, Bottomley PA. Magnetic resonance Spectroscopy with Linear Algebraic Modeling (SLAM) for higher speed and sensitivity. J Magn Reson. 2012;218:66‐76. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0272] 272. Farkash G, Markovic S, Novakovic M, Frydman L. Enhanced hyperpolarized chemical shift imaging based on a priori segmented information. Magn Reson Med. 2019;81(5):3080‐3093. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0273] 273. Lee P, Adany P, Choi IY. Imaging based magnetic resonance spectroscopy (MRS) localization for quantitative neurochemical analysis and cerebral metabolism studies. Anal Biochem. 2017;529:40‐47. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0274] 274. Peng X, Nguyen H, Haldar J, Hernando D, Wang XP, Liang ZP. Correction of field inhomogeneity effects on limited k‐space MRSI data using anatomical constraints. In: 2010 32nd Annual International Conference of the Ieee Engineering in Medicine and Biology Society. Buenos Aires, Argentina: IEEE; 2010:883‐886. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0275] 275. Kirchner T, Eisenring L, Pruessmann KP, Henning A. Inherent reduction of residual lipid aliasing in SENSE‐accelerated ¹H MRSI at 7T by spatially selective SRF optimization. Proc Int Soc Magn Reson Med. 2013;21:2007.

[nbm4314-bib-0276] 276. Dong Z, Peterson BS. Spectral resolution amelioration by deconvolution (SPREAD) in MR spectroscopic imaging. J Magn Reson Imaging. 2009;29(6):1395‐1405. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0277] 277. Halse ME, Callaghan PT. Imaged deconvolution: a method for extracting high‐resolution NMR spectra from inhomogeneous fields. J Magn Reson. 2007;185(1):130‐137. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0278] 278. Dong ZC, Zhang YD, Liu F, Duan YS, Kangarlu A, Peterson BS. Improving the spectral resolution and spectral fitting of H‐1 MRSI data from human calf muscle by the SPREAD technique. NMR Biomed. 2014;27(11):1325‐1332. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0279] 279. Eslami R, Jacob M. Robust reconstruction of MRSI data using a sparse spectral model and high resolution MRI priors. IEEE Trans Med Imaging. 2010;29(6):1297‐1309. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0280] 280. Eslami R, Jacob M. Spatial spectral modeling for robust MRSI. In: 2009 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. New York City, New York: IEEE; 2009:6663‐6666. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0281] 281. Eslami R, Jacob M. Correction of B ₀ inhomogeneity distortion in magnetic resonance spectroscopic imaging. In: 34th International Conference on Acoustics, Speech, and Signal Processing (ICASSP). Taipei, Taiwan: IEEE; 2009:405‐408. [Google Scholar]

[nbm4314-bib-0282] 282. Liu Y, Ma C, Clifford BA, Lam F, Johnson CL, Liang ZP. Improved low‐rank filtering of magnetic resonance spectroscopic imaging data corrupted by noise and B ₀ field inhomogeneity. IEEE Trans Biomed Eng. 2016;63(4):841‐849. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0283] 283. Liu Y, Ma C, Clifford B, Lam F, Johnson CL, Liang ZP. Field‐inhomogeneity‐corrected low‐rank filtering of magnetic resonance spectroscopic imaging data. Eng Med Biol. 2014:6422‐6425. [DOI] [PubMed]

[nbm4314-bib-0284] 284. Nguyen HM, Peng X, Do MN, Liang ZP. Spatiotemporal denoising of MR spectroscopic imaging data by low‐rank approximations. In: 2011 8th IEEE International Symposium on Biomedical Imaging: From Nano to Macro. Chicago, IL, USA: IEEE; 2011:857‐860. [Google Scholar]

[nbm4314-bib-0285] 285. DeVience SJ, Mayer D. Speeding up dynamic spiral chemical shift imaging with incoherent sampling and low‐rank matrix completion. Magn Reson Med. 2017;77(3):951‐960. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0286] 286. Milshteyn E, von Morze C, Reed GD, et al. Using a local low rank plus sparse reconstruction to accelerate dynamic hyperpolarized C‐13 imaging using the bSSFP sequence. J Magn Reson. 2018;290:46‐59. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0287] 287. Liang ZP. Spatiotemporal imaging with partially separable functions. In: 2007 Joint Meeting of the Sixth International Symposium on Noninvasive Functional Source Imaging of the Brain and Heart and the International Conference on Functional Biomedical Imaging. Hangzhou, China: IEEE; 2007:356‐357. [Google Scholar]

[nbm4314-bib-0288] 288. Lam F, Liang ZP. A subspace approach to high‐resolution spectroscopic imaging. Magn Reson Med. 2014;71(4):1349‐1357. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0289] 289. Ma C, Lam F, Ning Q, Johnson CL, Liang ZP. High‐resolution ¹H‐MRSI of the brain using short‐TE SPICE. Magn Reson Med. 2017;77(2):467‐479. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0290] 290. Lam F, Ma C, Clifford B, Johnson CL, Liang ZP. High‐resolution H‐1‐MRSI of the brain using SPICE: data acquisition and image reconstruction. Magn Reson Med. 2016;76(4):1059‐1070. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0291] 291. Peng X, Lam F, Li YD, Clifford B, Liang ZP. Simultaneous QSM and metabolic imaging of the brain using SPICE. Magn Reson Med. 2018;79(1):13‐21. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0292] 292. Guo R, Zhao YB, Li YD, Li Y, Liang ZP. Simultaneous metabolic and functional imaging of the brain using SPICE. Magn Reson Med. 2019;82(6):1993‐2002. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0293] 293. Ma C, Clifford B, Liu YC, et al. High‐resolution dynamic P‐31‐MRSI using a low‐rank tensor model. Magn Reson Med. 2017;78(2):419‐428. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0294] 294. Lee H, Song JE, Shin J, et al. High resolution hyperpolarized C‐13 MRSI using SPICE at 9.4T. Magn Reson Med. 2018;80(2):703‐710. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0295] 295. Ma C, Lam F, Liang ZP. Encoding and decoding with prior knowledge: from SLIM to SPICE. eMagRes. 2015;4(2):535‐542. [Google Scholar]

[nbm4314-bib-0296] 296. Mahmoudzadeh AP, Kashou NH. Evaluation of interpolation effects on upsampling and accuracy of cost functions‐based optimized automatic image registration. Int J Biomed Imaging. 2013;2013:395915. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0297] 297. Schmidt R, Laustsen C, Dumez JN, et al. In vivo single‐shot C‐13 spectroscopic imaging of hyperpolarized metabolites by spatiotemporal encoding. J Magn Reson. 2014;240:8‐15. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0298] 298. Schmidt R, Frydman L. In vivo 3D spatial/1D spectral imaging by spatiotemporal encoding: a new single‐shot experimental and processing approach. Magn Reson Med. 2013;70(2):382‐391. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0299] 299. Zhang ZY, Frydman L. MRSI via fully‐refocused spatiotemporal encoding with polychromatic spectral pulses. J Magn Reson. 2015;259:24‐31. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0300] 300. Iqbal Z, Nguyen D, Hangel G, et al. Super‐Resolution ¹H Magnetic Resonance Spectroscopic Imaging Utilizing Deep Learning. Front Oncol. 2019;9:1‐13:1010. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0301] 301. Larson PEZ, Kerr AB, Chen AP, et al. Multiband excitation pulses for hyperpolarized C‐13 dynamic chemical‐shift imaging. J Magn Reson. 2008;194(1):121‐127. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0302] 302. Lau AZ, Chen AP, Ghugre NR, et al. Rapid multislice imaging of hyperpolarized C‐13 pyruvate and bicarbonate in the heart. Magn Reson Med. 2010;64(5):1323‐1331. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0303] 303. Singh M, Josan S, Zhu MJ, Jhajharia A, Mayer D. Dynamic metabolic imaging of copolarized [2‐C‐13]pyruvate and [1,4‐C‐13(2)]fumarate using 3D‐spiral CSI with alternate spectral band excitation. Magn Reson Med. 2019;81(5):2869‐2877. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0304] 304. Miller JJ, Lau AZ, Tyler DJ. Susceptibility‐induced distortion correction in hyperpolarized echo planar imaging. Magn Reson Med. 2018;79(4):2135‐2141. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0305] 305. Lau JYC, Geraghty BJ, Chen AP, Cunningham CH. Improved tolerance to off‐resonance in spectral‐spatial EPI of hyperpolarized [1‐C‐13]pyruvate and metabolites. Magn Reson Med. 2018;80(3):925‐934. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0306] 306. Weiss K, Sigfridsson A, Wissmann L, et al. Accelerating hyperpolarized metabolic imaging of the heart by exploiting spatiotemporal correlations. NMR Biomed. 2013;26(11):1380‐1386. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0307] 307. Cunningham CH, Chen AP, Lustig M, et al. Pulse sequence for dynamic volumetric imaging of hyperpolarized metabolic products. J Magn Reson. 2008;193(1):139‐146. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0308] 308. Schulte RF, Sperl JI, Weidl E, et al. Saturation‐recovery metabolic‐exchange rate imaging with hyperpolarized [1‐¹³C] pyruvate using spectral‐spatial excitation. Magn Reson Med. 2013;69(5):1209‐1216. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0309] 309. von Morze C, Reed G, Shin P, et al. Multi‐band frequency encoding method for metabolic imaging with hyperpolarized [1‐C‐13]pyruvate. J Magn Reson. 2011;211(2):109‐113. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0310] 310. Schmid AI, Meyerspeer M, Robinson SD, et al. Dynamic PCr and pH imaging of human calf muscles during exercise and recovery using P‐31 gradient‐echo MRI at 7 tesla. Magn Reson Med. 2016;75(6):2324‐2331. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0311] 311. Greenman RL, Wang XE, Smithline HA. Simultaneous acquisition of phosphocreatine and inorganic phosphate images for Pi:PCr ratio mapping using a RARE sequence with chemically selective interleaving. Magn Reson Imaging. 2011;29(8):1138‐1144. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0312] 312. Ebel A, Maudsley AA, Schuff N. Correction of local B ₀ shifts in 3D EPSI of the human brain at 4 T. Magn Reson Imaging. 2007;25(3):377‐380. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0313] 313. Ebel A, Maudsley AA. Improved spectral quality for 3D MR spectroscopic imaging using a high spatial resolution acquisition strategy. Magn Reson Imaging. 2003;21(2):113‐120. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0314] 314. Motyka S, Moser P, Hingerl L, et al. The influence of spatial resolution on the spectral quality and quantification accuracy of whole‐brain MRSI at 1.5T, 3T, 7T, and 9.4T. Magn Reson Med. 2019;82(2):551‐565. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0315] 315. Wang SS, Su ZH, Ying L, et al. Accelerating magnetic resonance imaging via deep learning. In: 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI). Prague, Czech Republic: IEEE; 2016:514‐517. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0316] 316. Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated MRI data. Magn Reson Med. 2018;79(6):3055‐3071. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0317] 317. Wang G, Ye JC, Mueller K, Fessler JA. Image reconstruction is a new frontier of machine learning. IEEE Trans Med Imaging. 2018;37(6):1289‐1296. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0318] 318. Lam F, Li Y, Peng X. Constrained magnetic resonance spectroscopic imaging by learning nonlinear low‐dimensional models. Magn Reson Med. 2020;39(3):545‐555. 10.1109/TMI.2019.2930586. Epub 2019 Jul 23. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0319] 319. Ebel A, Soher BJ, Maudsley AA. Assessment of 3D proton MR echo‐planar spectroscopic imaging using automated spectral analysis. Magn Reson Med. 2001;46(6):1072‐1078. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0320] 320. Nassirpour S, Chang P, Henning A. Comparison of different acceleration methods for high‐resolution metabolite mapping using 1H FID MRSI at 9.4T. Poster presented at: 25th Annual Meeting and Exhibition of the International Society for Magnetic Resonance in Medicine (ISMRM 2017); April 22‐27, 2017; Honolulu, HI.

[nbm4314-bib-0321] 321. Strasser B, Hingerl L, Gagoski B, et al. Comparison of acceleration methods for brain MRSI at 7T. Paper presented at: ISMRM 25th Annual Meeting and Exhibition; April 22‐27, 2017; Honolulu, HI.

[nbm4314-bib-0322] 322. Durst M, Koellisch U, Frank A, et al. Comparison of acquisition schemes for hyperpolarised C‐13 imaging. NMR Biomed. 2015;28(6):715‐725. [DOI] [PubMed] [Google Scholar]

[nbm4314-bib-0323] 323. Lee BY, Zhu XH, Chen W. Quantitative analysis of spatial averaging effect on chemical shift imaging SNR and noise coherence with k‐space sampling schemes. Magn Reson Imaging. 2019;60:85‐92. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0324] 324. Maudsley AA, Andronesi OC, Barker PB, et al. Advanced magnetic resonance spectroscopic neuroimaging: experts' consensus. NMR Biomed. 2020. accepted. [DOI] [PMC free article] [PubMed] [Google Scholar]

[nbm4314-bib-0325] 325. Wilson M, Andronesi O, Barker PB, et al. Methodological consensus on clinical proton MRS of the brain: review and recommendations. Magn Reson Med. 2019;82(2):527‐550. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Accelerated MR spectroscopic imaging—a review of current and emerging techniques

Wolfgang Bogner

Ricardo Otazo

Anke Henning

Abstract

Abbreviations

1. INTRODUCTION

2. SHORT T R/T E

FIGURE 1.

FIGURE 2.

3. SPATIAL‐SPECTRAL ENCODING

FIGURE 3.

FIGURE 4.

FIGURE 5.

TABLE 1.

3.1. Cartesian SSE

3.1.1. EPSI

FIGURE 6.

3.1.2. Flyback‐EPSI and more

3.2. Non‐Cartesian SSE

3.2.1. Spirals

FIGURE 7.

3.2.2. Concentric rings

FIGURE 8.

3.2.3. Rosettes

3.2.4. Radial EPSI

4. UNDERSAMPLED MRSI

FIGURE 9.

4.1. Parallel imaging

4.1.1. SENSE

FIGURE 10.

4.1.2. GRAPPA

4.2. Multi‐band/simultaneous multi‐slice

FIGURE 11.

4.3. Compressed sensing

FIGURE 12.

5. JOINT FORCES—COMBINING SSE, UNDERSAMPLING AND SHORT T R

5.1. Cartesian

FIGURE 13.

5.2. Non‐Cartesian

FIGURE 14.

6. USING PRIOR KNOWLEDGE

6.1. Spatial prior knowledge and bias field maps: SLIM, SLOOP and SLAM

6.2. Spatial‐spectral prior knowledge and low‐rank reconstruction: toward SPICE

FIGURE 15.

6.3. Super‐resolution reconstruction

6.4. Spectral‐spatial excitation

7. SUMMARY AND OUTLOOK ON EMERGING TECHNOLOGIES

FUNDING INFORMATION

Supporting information

ACKNOWLEDGEMENTS

APPENDIX A.

Open‐source MRS/MRSI processing tools (in alphabetical order).

REFERENCES

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

2. SHORT T _R/T _E

5. JOINT FORCES—COMBINING SSE, UNDERSAMPLING AND SHORT T _R