Context-sensitive valuation and learning

Abstract

A variety of behavioral and neural phenomena suggest that organisms evaluate outcomes not on an absolute utility scale, but relative to some dynamic and context-sensitive reference or scale. Sometimes, as in foraging tasks, this results in sensible choices; in other situations, like choosing between options learned in different contexts, irrational choices can result. We argue that what unites and demystifies these various phenomena is that the brain’s goal is not assessing utility as an end in itself, but rather comparing different options to choose the better one. In the presence of uncertainty, noise, or costly computation, adjusting options to the context can produce more accurate choices.

Introduction

A standard starting point for theories of decision-making — whether in biology, psychology, economics, or computer science — is that the agent chooses options that maximize some objective function, such as expected utility or discounted future reward. However, a range of phenomena, both behavioral and neural, highlight a feature of choice that can seem paradoxical from this decision-theoretic perspective: Options appear to be evaluated not in absolute terms but instead relative to some shifting and context-dependent baseline. This can lead to inconsistent and even irrational choices in some situations. Here we review a range of such phenomena of reference-dependent evaluation, choice, and learning, which have not always been seen as connected. We argue that a common theme underlying and demystifying them is that the organism’s goal is not to compute values, as an end in itself, but instead to compare them so as to choose the action that has the highest value [1••]. The goal of ultimately producing choices motivates an emphasis on learning, storing, and computing comparative decision variables.

Foraging and marginal value

Ironically, one scenario in which the comparative nature of the decision variable is most widely recognized is when the alternatives for comparison are not known at choice time. Classic foraging theory [2], which has recently been revisited in neuroscience [3-6], considers tasks in which options are encountered serially and must be processed or rejected before discovering the next. This holds, for instance, for a predator deciding whether to chase some prey or forego it to seek another, or a foraging animal deciding when to leave a deplenished food patch to search for a replenished one. In these cases, it can be shown that optimal choice implies assessing options not in terms of their absolute value, but by their marginal value relative to the expectation over other possible options [7,2]. In particular, although specific alternatives are not known at choice time, their average value corresponds to the long-run or steady-state reward in the environment, which can then be compared to the current option to decide whether to accept it. This leads to many predictions about the context-sensitivity of choices in foraging: in essence, that organisms should be pickier in rich environments and more promiscuous when rewards are sparse [8,2] (Figure 1a). Moreover, at a computational and neural level, these considerations emphasize tracking the long-run average reward, ρ, as a key decision variable, and in turn directly learning and representing the value of foreground options not in absolute terms, r, but in the relative terms that ultimately matter for choice, for example, as r – ρ [3,4].

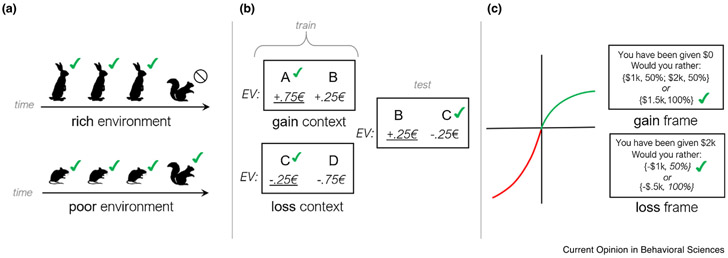
Figure 1.

Context-sensitive effects. (a) A foraging owl might reject relatively scrawny prey (squirrel) in a rich environment where rabbits are often available, but accept the same option in a poorer one. (b) People learn by trial and error to choose between options rewarded noisily with different expected value (EV, not shown to participants). People who learn that option C (a small loss in expectation) is preferred in its training context will sometimes choose it, in later probes, over an objectively better option (B, a small expected gain) which had been the worse option in its respective training context. (c) Because nominal gains have diminishing marginal utility and nominal losses have diminishing marginal dysutility, preference can shift between risk averse and risk seeking when the same outcomes are framed (relative to a different reference) as gains versus losses.

Here, the average reward ρ can also be understood as the opportunity cost of the time that would be spent processing or consuming some available option — that is, the expected potential reward that would be foregone — so that the option’s marginal value (r – ρ, net of opportunity cost) determines whether this is worthwhile [7]. Interestingly, this same logic of opportunity cost, and the same contextual average reward variable ρ for assessing it, reappears in theoretical accounts of many other situations in decision neuroscience involving speed-accuracy trade-offs or cost of time. For instance, ρ has been argued to govern action vigor [9-12], intertemporal choice [13-15], planning versus acting [16,17••], chunking of sequential actions [18], cognitive effort [19-21], and the evidence threshold for perceptual decisions [22,21].

These parallels in turn suggest a potential shared decision variable ρ and shared neural mechanism for opportunity cost tracking and contextual comparison across these different settings. One hypothesis is that ρ may be tracked by the average (e.g. tonic) level of the neuromodulator dopamine [9]. This turns out to be implied ‘for free’ by standard computational models that famously associate phasic dopamine spiking with the temporal-difference reward prediction error [23,24]. Mathematically, the long-term average of the prediction error signal equals ρ; thus if phasic dopamine signals prediction error, a slow time-average of this signal (e.g. net extracellular concentrations in striatum due to overflow and gradual reuptake) would carry ρ [25]. Because the speed of movement should be determined by the opportunity cost ρ, this observation may explain dopamine’s involvement in movement invigoration [9,11]. Recent work has also tested the suggestion that this same mechanism supports contextual evaluation and choice in patch foraging tasks; indeed, dopaminergic depletion and replacement in Parkinson’s disease [5], and dopaminergic drugs in healthy participants [26], all modulate people’s willingness to leave deplenished patches.

Relative value in simultaneous choice

Context-relative effects on valuation may seem more puzzling in more traditional decision tasks in which all options are available simultaneously, for example, selecting from a menu or trial-and-error learning about which of several options is most rewarding in ‘bandit’ problems. A standard theoretical view is that subjects should choose the action a that maximizes the expected value (over outcomes o), Q(a) = Σ₀P(o∣a)r(o). In experiential learning tasks, Q(a) can, in turn, be estimated incrementally from received outcomes, by error-driven updates as in temporal-difference learning.

A key implication of this approach is that the expected value Q(a) for each option a is independent of the other options in the choice set, so this model predicts that, following learning, it should be possible to correctly choose between novel pairs of options first encountered in separate contexts, by comparing their Q. Instead, a series of elegant studies by Palminteri and colleagues has shown that people sometimes are biased to evaluate options relative to their training context [27]. For instance, they may choose an option that was better than its alternatives during training, over one that was the worst in its own training set, even if the latter option dominates in absolute terms (Figure 1b). A similar dependence of later choices on the initial training contexts has been reported in animals such as starlings [28,29].

Results of this sort suggest that the decision variable, Q, is learned in context-relative rather than absolute units. Suggestively, Palminteri et al.’s original results can be explained by Q learning, but over relativized outcome values, for example, r – ρ, where ρ is again a context-dependent average [27]. In addition to explaining irrational choices on later probes, the dynamics by which ρ is estimated (and Q learned relative to it) over the course of initial training has further, subtler effects. For instance, small monetary losses may look disappointing at first (driving lose-shift behavior), but better than average (win-stay) later. In this way, a dynamic reference can drive changing engagement of approach and avoidance behaviors and associated neural circuits [30,31], affecting overall tendencies to perseverate or switch in choices [32], and even driving changes in response times due to Pavlovian ‘congruency’ biases between action versus inaction and reward versus punishment [33,34].

Although this baseline-relative coding leads to irrational choice on some transfer problems, it can be harmless or even advantageous in the original bandit setting, because the scale of value is underdetermined. Although AI applications and associated algorithms typically start with a well-defined objective function (e.g. points in a video game [35]), fitness for a biological organism is harder to quantify, even, presumably, for the organism itself [1••]. It is true that weighing different outcomes on a ‘common currency’ scale facilitates comparing between them, and indeed this is deeply related to core features of rational choice such as transitivity [36]. The notion of common currency or cardinal utility has also been linked to value-related signals in the brain, which scale with preference across many different types of appetitive outcomes [37]. However, preference is ordinal: it has no objective units, so any monotonic transformation of the decision variable Q (like subtracting ρ or indeed any constant) will preserve the same optimizing action. For a number of reasons, which we discuss next, dynamically adjusting this scale may facilitate efficient choice locally, at the expense of producing decision variables that are incommenserable with those learned in other contexts (Figure 1b).

First, in the foraging scenario discussed in the previous section, ρ is a proxy for the value of alternatives that have not yet been encountered. Even in a nominally simultaneous choice scenario like choice among bandits or selecting from a menu, it may also proxy for other options — for example, those whose values have not yet been computed. Subjects may covertly approach even such tasks by contemplating options serially rather than by direct comparison. In this case, a default option (e.g. sticking with the same option you chose on the previous trial) may be accepted or rejected by comparing it to a reference value, like ρ, rather than, or before, considering the actual alternatives [38]. Especially when there are many possibilities, it can save computation to stage choice in this way (as has been pointed out also in other tasks like serial hypothesis testing [39,40]). Eye-tracking data from humans [41] and unit recording data from primates [42] hint at this type of serial contemplation of options, as do correlates in fMRI of value relative to a default option [38].

Considerations about efficient learning also motivate relativized evaluation. If the goal is choosing the best option (at least within a fixed choice set/context), then learning individual action values is, strictly speaking, overkill: when there are two alternatives, for instance, it suffices to estimate the difference Q(a₁) – Q(a₂), or even just its sign [43]. Considerations like this motivate a different approach to the reinforcement learning problem in AI, known as policy gradient methods. Methods like Q-learning learn to minimize the difference between each predicted Q and the observed cardinal rs, and then compare the learned predictions in a subsequent choice step. Policy gradient methods instead take learning steps to tune unitless choice preference variables to direct choices toward options maximizing expected reward without representing their absolute values directly. This in effect combines the learning and comparison steps, and can be accomplished using sampled outcomes to estimate the gradient of obtained reward. Such algorithms include the actor-critic [23,44] and its special case for bandit tasks, called REINFORCE [45]. The stochastic gradient estimate, like the Q values, allows for an arbitrary additive constant. Here again (because each option’s outcomes are typically sampled separately but the direction of improvement depends on comparing them), the efficiency (i.e. variance) of the estimated gradient is improved by mean-correcting obtained rewards to r – ρ. A disadvantage of this approach, of course, is that the learned policies are not directly transferable to other tasks.

Efficient coding of decision variables

Another, related, reason that decision variables may be context-dependent is efficient neural coding. A standard information-theoretic analysis implies that the neural code, treated as a capacity-limited channel (quantized by spikes), should be adapted to the distribution of the variable being represented [46].

This classic idea is well-studied for perceptual variables (e.g. luminance or motion speed [47], motion aftereffects and the like), but in principle should apply equally to more abstract quantities like action values Q [48]. Here again, if the goal is to find the action a maximizing Q(a) — but using a noisy spike code — then this may be accomplished with better accuracy over an adapted transformation of Q(a) that preserves the ordering over actions while reducing error or noise from quantization [49••,50••]. Accordingly, much research on neural correlates of action value (e.g. in eye control regions such as lateral intraparietal area LIP) has shown that the response for some option a is modulated not only by Q(a) but also affected by the values of rewards concurrently offered at other options a′ [51].

Furthermore, if the neural code for some decision variable is noisy, then its readout for the purpose of guiding choice should (by standard Bayesian considerations) be adjusted toward its a priori distribution. This implies an additional reason why choices should be biased by the statistics of decision variables in the current context: these, in effect, determine the prior. A series of models and experiments shows that these corrections, when applied to predecessor quantities of Q (e.g. reward magnitudes and probabilities) lead to nonlinear subjective distortions in these quantities, which ultimately can explain a number of classic behavioral economic choice anomalies, including a further set of effects (such as ‘framing effects’; Figure 1c) involving reference sensitivity of attitudes toward risk, gain, and loss [50••,52,53].

There are some differences in emphasis between the literature on foraging and learning discussed previously, and that on efficient neural coding of decision variables. First, motivated especially by foraging, we have stressed how reference sensitivity is justified by comparison and choice. This ultimate objective is less routinely stressed in applications of efficient coding to decision variables (though see, e.g. [54,49••,50••]), since broadly similar adaptation is already justified by the more proximal objective of coding even a single action’s value accurately. Even in this simplified case, efficient coding implies adjusting the distribution of responses to the distribution of decision variables in the context. In general, this involves both shifting (e.g. mean correction, as discussed before) and also scaling (e.g. adjusting the gain of neural responses to the range of the represented variable). Research in neural coding has mostly emphasized rescaling, for example, divisive normalization and range adaptation, whereas work on foraging and learning has stressed subtractive shifts. In fact, rescaling extends to the learning case as well: parallel effects of the range (in addition to the mean) of outcomes during training have recently been shown on transfer pairings in a version of the Palminteri task, and are captured by a more general scale-shift adaptation model [55••].

Also, whereas the behavioral signatures of relativized values we discussed previously concerned effects, via learning, on subsequent transfer choices, divisive normalization models connect these phenomena to a further class of context-dependent anomalies in choices themselves [56,57]. In addition to framing, these include phenomena like decoy effects, in which preference between two options can change depending which other options are also offered. Many effects of this sort can be explained by gain control [58]. Further, as in the cases of foraging and learning, where the reference point is dynamically learned for an environment or context, neural adaptation and many of the associated behavioral anomalies can depend not just on the immediate choice set (the ‘spatial context’), but also or instead on the temporal context, for example, the recent history of options encountered [59-61].

Conclusion

We have reviewed a range of phenomena that suggest that the brain represents and learns decision variables not in absolute units, but instead relative to the context. While this can produce irrational choices in some situations, especially when switching between contexts, we have argued that it is nevertheless well motivated by a number of considerations related to efficient choice and learning within a context. Many of these considerations relate to the fact that choice ultimately depends not on an option’s absolute reward, but instead on its reward relative to other available alternatives, and this set of alternatives is context-dependent. Learning options’ values relative to one another can be seen as a computational short cut, facilitating later choice by pre-computing the comparisons. Such a strategy (and the errors it can cause) can then be seen as analogous to other phenomena of habits, which have been argued to result from storing the endpoints of decision computations, leading to context-inappropriate slips of action in later probes [62,16].

Indeed, like habits, reference-relative learning and choice is neither universal nor complete. The brain may also employ absolute values, at least some of the time. In the case of habits, but less so as yet for context-relative learning, this interpretation has led to further work on rational cost-benefit control of when to employ these approximations, versus more accurate goal-directed or model-based choice [62,16]. For neural adaptation, there has been a similar recent interest in rational control of the degree of noise in neural coding — if spikes are metabolically costly, for instance, how many should be used to code decisions in a particular context [54,52,49••]? A further question left open by this work, which would also admit of rational analysis, is what constitutes a ‘context.’ These methods can work well to the extent the brain manages to carve the space of tasks and situations up into discrete units and choose efficiently within them, while avoiding mistakes resulting from choosing between options from different contexts. Accordingly, these choice anomalies and reference dependencies are deeply tied up with a seemingly different set of theoretical and experimental issues, concerning how the brain partitions the world into distinct states or ‘latent causes’ for the purpose of learning and generalization [63-66].

Finally, while we have stressed learning a context’s value mainly so as to adjust for and ignore it when choosing within that context, the analogy with states also points to an equally important (and actually more widely appreciated) flipside to this logic. At another hierarchical level of analysis, states (i.e. contexts) are encountered sequentially, and much work in both AI and biological decisions ultimately turns on choosing over these multi-step trajectories — choosing, in part, over future states — so as to maximize long-term reward. Here, in algorithms such as the actor critic, state values also appear, but no longer as a nuisance. Instead, they play a more positive role in guiding the organism toward richer contexts [23,24,62].