Testing the length limit of loop grafting in a helical repeat protein

Abstract

Alpha-helical repeat proteins such as consensus-designed tetratricopeptide repeats (CTPRs) are exceptionally stable molecules that are able to tolerate destabilizing sequence alterations and are therefore becoming increasingly valued as a modular platform for biotechnology and biotherapeutic applications. A simple approach to functionalize the CTPR scaffold that we are pioneering is the insertion of short linear motifs (SLiMs) into the loops between adjacent repeats. Here, we test the limits of the scaffold by inserting 17 highly diverse amino acid sequences of up to 58 amino acids in length into a two-repeat protein and examine the impact on protein folding, stability and solubility. The sequences include three SLiMs that bind oncoproteins and eleven naturally occurring linker sequences all predicted to be intrinsically disordered but with conformational preferences ranging from compact globules to expanded coils. We show that the loop-grafted proteins retain the native CTPR structure and are thermally stable with melting temperatures above 60 ​°C, despite the longest loop sequence being almost the same size as the CTPR scaffold itself (68 amino acids). Although the main determinant of the effect of stability was found to be loop length and was relatively insensitive to amino acid composition, the relationship between protein solubility and the loop sequences was more complex, with the presence of negatively charged amino acids enhancing the solubility. Our findings will help us to fully realize the potential of the repeat-protein scaffold, allowing a rational design approach to create artificial modular proteins with customized functional capabilities.

Graphical abstract

Highlights

• •CTPR proteins can tolerate inter-repeat loop insertions of up to 58 amino acids.
• •There is minimal loss in thermodynamic stability.
• •Stability loss is independent of loop sequence but dependent on loop length.
• •Stability loss is entropically driven.
• •Solubility is favored by negatively charged residues in the inserted loop.

1. Introduction

Tandem-repeat proteins (subsequently referred to as repeat proteins), such as tetratricopeptide repeats (TPRs), ankyrin repeats and armadillo repeats, are a distinct structural protein class with 28% of the human proteome containing repeat elements (Pellegrini et al., 1999). Unlike globular proteins, repeat proteins form elongated, quasi-one-dimensional structures that are stabilized solely by local interactions between amino acids close in primary sequence. This characteristic allows us to both readily dissect and redesign repeat proteins as opposed to globular proteins, whose structures comprise multiple long-range contacts that generate complex topologies and are consequently much harder to manipulate (Kobe and Kajava, 2000). There are now many examples in the literature of using consensus design to generate ultra-stable proteins (Main et al., 2003a; Kajander et al., 2006; Binz et al., 2003), and consensus-designed repeat proteins represent attractive scaffolds on which to engineer new functions such as molecular recognition (Cortajarena et al., 2008; Madden et al., 2019; Boersma and Plückthun, 2011). We have shown that consensus-designed TPR proteins (CTPRs), composed of repeats of a 34-residue helix-turn-helix motif, are particularly amenable to a functionalization approach in which short binding motifs are grafted onto the loop between adjacent repeats. In a recent study, we demonstrated that extending the natural 4-residue loop of a CTPR2 protein (comprising two repeats) by up to 25 amino acids does not disrupt the overall structure of the TPR scaffold and results in only a modest loss of thermodynamic stability (Perez-Riba et al., 2018). In this study, we investigate insertions of native sequences and chose to graft intrinsically disordered regions (IDRs) from natural linkers and binding motifs.

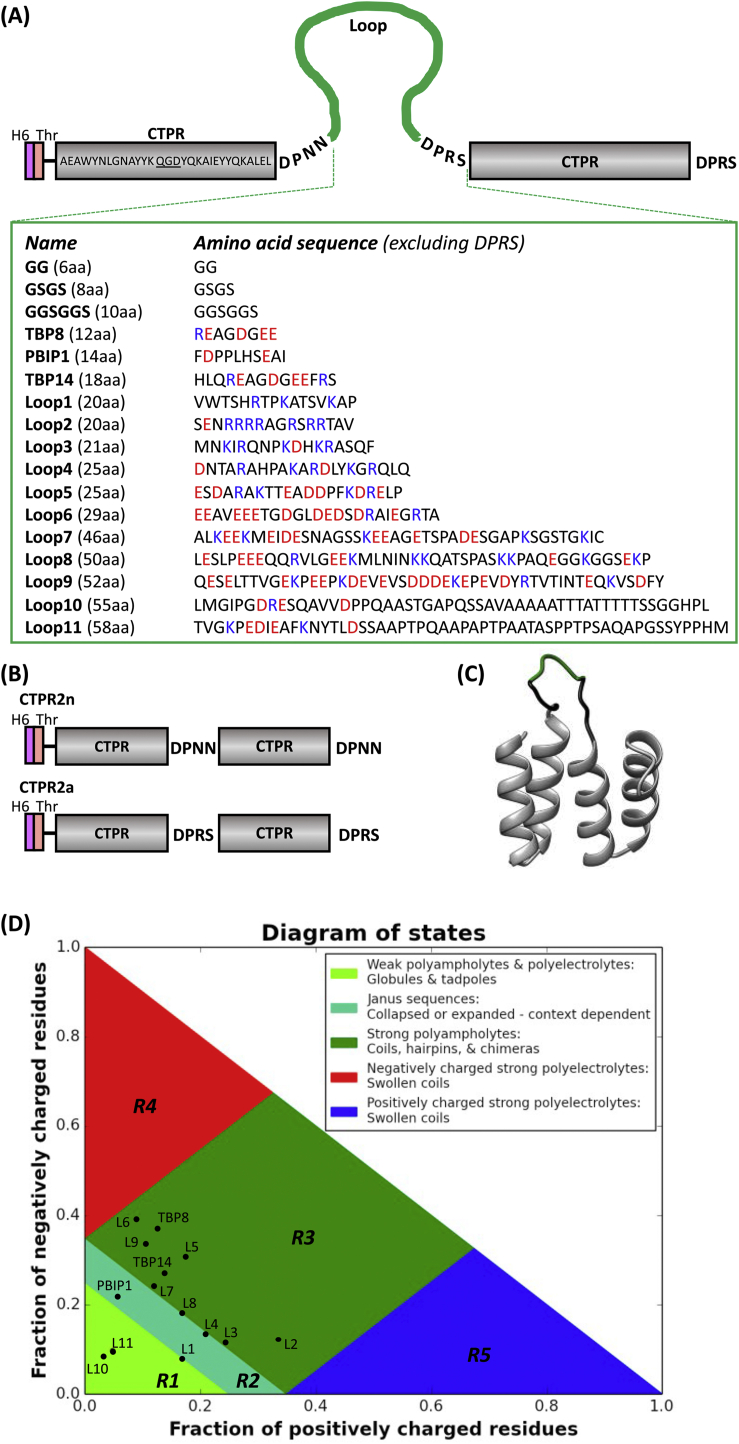
Intrinsically disordered proteins (IDPs) and IDRs are often involved in varied cellular functions (Dyson and Wright, 2005). For instance, IDRs can mediate highly specific protein-protein interactions using short sequence motifs of 3–10 residues, which may fold upon binding to promote cellular processes like transcriptional activation, signaling and cell cycle control (Dyson, 2016). These short linear motifs (SLiMs) often retain their function as short isolated peptides and when grafted onto protein scaffolds or otherwise chemically constrained (e.g. stapled peptides) (Van Roey et al., 2014). Although IDPs lack stable secondary and tertiary structures, they can adopt compact conformations (Babu, 2016; Mao et al., 2010; Das and Pappu, 2013), dependent on both amino acid composition and distribution. The main determinants of the conformational preferences of IDRs are the fraction of charged residues (FCR), the net charge per residue (NCPR), the segregation/mixing of oppositely charged residues (κ), the proline content, the pattern of proline and charged residues versus others (Ω), and the overall hydrophobicity of the sequence (Mao et al., 2010; Das and Pappu, 2013; Portz et al., 2017; Müller-Späth et al., 2010; Marsh and Forman-Kay, 2010; Das et al., 2015; Martin et al., 2016; Holehouse et al., 2017; Riback et al., 2017; Sherry et al., 2017; Gibbs et al., 2017). According to DisProt, a database of experimentally characterized IDPs, approximately 75% of IDPs are polyampholytes (i.e. sequences with both positively and negatively charged amino acids) (Sickmeier et al., 2007). Das and Pappu have proposed that the conformational tendencies are dependent on the FCR and κ in polyampholytes and on the NCPR in polyelectrolytes (Mao et al., 2010; Das and Pappu, 2013). Based on atomistic simulations they developed the CIDER program (Classification of Intrinsically Disordered Ensemble Regions), which generates a diagram of states for IDPs predicting which conformation a given primary sequence is likely to adopt (http://pappulab.wustl.edu/CIDER/analysis/) (Holehouse et al., 2017) (see Fig. 1). For the same number of charged residues, in polyampholytes (diagram of states region R3) well-mixed sequences (low κ value) show random-coil ensembles, whereas segregation of oppositely charged residues (high κ value) leads to a preference for hairpin-like conformation due to long-range electrostatic interactions. Strong polyelectrolytes (regions R4 and R5) are predicted to form swollen coils, whereas weak polyampholytes and weak polyelectrolytes (region R1) adopt globular conformations. Unstructured regions are found as linkers between folded domains, and the Pappu group has used the sequence-specific effective solvation volume (v_es) to explore the global dimension of linkers (Harmon et al., 2017). The v_es value reflects the volume occupied by the linker. A linker with a negative v_es is self-attractive and forms a compact globule, whereas a linker with a positive v_es is self-repelling, prefers to be solvated and is highly expanded. When v_es is close to zero, the attractive and repulsive interactions compensate one another and the linker forms a passive tether.

Fig. 1.

Design of two-repeat proteins with extended inter-repeat loops. (A) Names and sequences for the 17 loop inserts are shown ordered by size. Negatively charged residues are red, positively charged residues blue. The DPRS motif at the beginning and end of the second repeat is a result of DNA ligation of two digested products during cloning and is known to marginally decrease stability compared to DPNN. Note that the number of amino acids stated in brackets includes the four inserted DPRS residues. See Supplementary Table S1 for the origin of the sequences of Loop1-Loop11. (B) Two CTPR2 arrays with a DPNN (CTPR2n) or DPRS (CTPR2a) loop were used as controls (Main et al., 2003b; Kajander et al., 2005; Phillips et al., 2012a). (C) Homology model of CTPR2-GGSGGS created with Swiss Model (Waterhouse et al., 2018) based on the CTPR crystal structure PDB: 2AVP (Kajander et al., 2007). CTPRs are depicted in grey, flanking DPNN and DPRS motifs in black and the GGSGGS loop in green. (D) Location of CTPR2 arrays with extended loops in the diagram of state. Loop sequences including the flanking DPNN and DPRS were analyzed using the CIDER online software (http://pappulab.wustl.edu/CIDER/analysis/) (Das and Pappu, 2013). Data for GG, GSGS and GGSGGS loops are excluded from the plot, because sequence parameters are not meaningful for very short peptide sequences. L1-L11 indicate Loop1-Loop11. aa, amino acids; TBP, tankyrase-binding peptide; polo-box interacting protein 1; H6, polyhistidine tag; Thr, thrombin cleavage site.

The motivation for our study was two-fold. First, IDRs are frequently located between structured regions of multi-domain proteins; we sought to determine how this ‘tethering’ of IDRs affects their conformational propensities. Second, many IDRs contain SLiMs that need to be constrained in order to adopt their bioactive (binding-competent) conformations; we are exploiting the naturally modular structure of repeat proteins for applications in therapeutics and nanotechnology, and we have shown that CTPR proteins are suitable scaffolds onto which SLiMs can be readily grafted between adjacent repeats without compromising scaffold folding and with only minor loss of stability (Madden et al., 2019). Here we explore the limits of this capability by grafting IDRs with very varied amino acid compositions and up to 58 amino acids in length onto the inter-repeat loop. We chose a scaffold comprising two repeats (CTPR2), each individual repeat on either side of the loop insertion being intrinsically unstable and dependent on the highly stabilizing interface formed with the other repeat in order to fold (Aksel and Barrick, 2009). As well as seeking to understand how conformational propensities of IDRs are modulated by the context within which they are placed, we were also curious to determine how different IDR ‘guests’ might affect the folding of the repeat-protein ‘host’. For example, extended coils might have a disruptive effect by preventing the inter-repeat interface from forming, whereas compact globules might enhance the stability by providing additional stabilizing contacts. For the rational functionalization of repeat proteins, a deep understanding of how the motif's sequence and predicted conformation influences the overall structure is essential. We find that the small CTPR2 protein (two 34-residue repeats) is exceptionally tolerant of loop insertions that are almost equal in size (58 amino acids). The native structure is preserved and the loop-inserted proteins are thermostable with melting temperatures above 60 ​°C. These results will help to construct a rulebook for the functionalization of the TPR scaffold, with which we can exploit some of the estimated 100,000 SLiMs in the human proteome (Tompa et al., 2014).

2. Materials and Methods

2.1. Cloning of loop extensions in CTPR2

The pRSET A vector was used for all of the constructs. Short loop extensions (GG, GSGS, PBIP1, TBP8, TBP14, Loop1-Loop6) were added to the C-terminus of a one-repeat construct (CTPR1) by whole-plasmid round-the-horn polynucleotide chain reaction (PCR), which allows large insertion to be made into a plasmid. Primers were designed so that forward and reverse primers anneal back-to-back on the plasmid. Each primer contains a part of the sequence to be inserted on its 5′ end. Primers were phosphorylated using T4 Polynucleotide Kinase (NEB) at 37 ​°C for 45 ​min according to the manufacturer's protocol. PCR was performed with 100 ​ng DNA template using the Q5 High-Fidelity DNA Polymerase (NEB) according to the manufacturer's suggestion. The PCR product was digested with DpnI (NEB) for 30 ​min at 37 ​°C and ligation was performed with T4 Quick-Stick Ligase (Bioline) for 15 ​min ​at room temperature. A second CTPR was added by restriction enzyme digest (BamHI and HindIII) and ligation, where the vector contained the CTPR1-loop and another CTPR1 was added as insert. For long loop insertions, CTPR2-Loop7-11 were purchased as gBlocks from Integrated DNA Technologies (IDT) and inserted into the multi-cloning site of the pRSET A vector between the BamHI and HindIII restriction sites.

2.2. Protein expression

DNA was transformed into the chemically competent C41 E. coli strain by heat shock and plated on LB agar plates (Invitrogen) supplemented with ampicillin (100 ​μg/mL). Colonies were grown in 2xYT media (FORMEDIUM, #AIM2YT0210) supplemented with antibiotics overnight at 37 ​°C in 15 ​mL (small-scale) or 500 ​mL (large-scale) 2xYT media. Cultures were grown at 37 ​°C to an optical density (OD₆₀₀) of 0.6 while shaking (220 ​rpm). Expression of recombinant proteins was induced by the addition of isopropyl β-D-1-thiogalactopyranoside (IPTG) at 0.1 ​mM followed by incubation at 20 ​°C for 16 ​h. Cultures were pelleted by centrifugation (4000 ​g, 20 ​min, 4 ​°C).

2.3. Small-scale protein purification

Cell pellets from 15 ​mL cultures were resuspended in 1 ​mL BugBuster Master Mix (Millipore), lysed for 30 ​min and insoluble proteins were pelleted (20000 ​g, 1 ​min, RT). For purification of proteins in the soluble fraction (GG, GSGS, GGSGGS, TBP8, TBP14, Loop5-7, Loop9, Loop10), supernatants were added to 100 ​μL bed volume of Amintra™ Ni-NTA affinity resin (Expedeon) or Amintra™ Glutathione Resin (Expedeon). Resin was incubated for 30–60 ​min ​at RT and washed once with 1 ​mL of wash buffer 1 (50 ​mM sodium phosphate, 150 ​mM NaCl, 30 ​mM imidazole, pH 6.8 or pH 8.0 dependent on the predicted isoelectric points of the protein calculated with the ExPASy ProtParam tool (Gasteiger et al., 2005)) with 10% BugBuster, followed by two washes with wash buffer 1. Protein bound to the resin was eluted by resuspension with 1 ​mL of elution buffer 1 (50 ​mM sodium phosphate buffer, 150 ​mM NaCl, 300 ​mM imidazole). Buffer used in the purification of the cysteine-containing Loop7 was supplemented with 2 ​mM dithiothreitol (DTT). For purification of proteins in the insoluble fraction (PBIP1, Loop1-Loop4, Loop8, Loop11), insoluble cell lysate pellets were resuspended in wash buffer 2 (50 ​mM sodium phosphate buffer, 150 ​mM NaCl, 6 ​M guanidinium hydrochloride, pH 6.8 or pH 8.0 dependent on the predicted isoelectric points of the protein) and added to 100 ​μL bed volume of Amintra™ Ni-NTA affinity resin. The subsequent steps were performed as for soluble proteins, but resin was washed with wash buffer 2 three times and protein was eluted with elution buffer 2 (50 ​mM sodium phosphate buffer, 150 ​mM NaCl, 6 ​M guanidine hydrochloride, 300 ​mM imidazole).

2.4. Large-scale protein purification

CTPR2a and CTPR2n were purified from cell pellets of 500 ​mL cultures. Pellets were resuspended in lysis buffer (50 ​mM sodium phosphate pH 8.5, 150 ​mM NaCl, 30 ​mM imidazole, SIGMAFAST protease inhibitor cocktail EDTA-free (1 tablet/100 ​mL, Sigma), 400 U/mL DNase I (Sigma)) and lysed using an EmulsiFlex C5 homogenizer (Avestin) at 15000 psi. Cell debris was removed by centrifugation (40000 ​g, 30 ​min, 4 ​°C). Supernatant was filtered through a 0.22 ​μm syringe filter (Jet Biofil) and loaded onto a 5 ​mL HisTrap excel column (GE Healthcare). The column was washed with wash buffer (50 ​mM sodium phosphate pH 8.5, 150 ​mM NaCl, 30 ​mM imidazole) and protein was eluted with elution buffer (50 ​mM sodium phosphate pH 8.5, 150 ​mM NaCl, 300 ​mM imidazole). Elution fractions were analyzed on SDS-PAGE and pure fractions were pooled.

2.5. Size-exclusion chromatography

For equilibrium denaturation curves, protein was further purified by size-exclusion chromatography using either a HiLoad 16/600 Superdex 75 ​pg column or a Superdex 75 Increase 10/300 ​GL column (GE Healthcare), depending on protein amount, equilibrated with buffer (50 ​mM sodium phosphate, 150 ​mM NaCl, buffer for Loop7 additionally contains 2 ​mM DTT). Purity of pooled elution fractions was confirmed by mass spectrometry.

2.6. Equilibrium denaturation curves

Equilibrium denaturation curves were acquired in a CLARIOstar plate reader as previously described by Perez-Riba et al. (Perez-Riba and Itzhaki, 2017). Measurements were carried out in 50 ​mM sodium phosphate, 150 ​mM NaCl, pH 6.8 or pH 8.0 with increasing concentrations of guanidine hydrochloride (GdmHCl). For each protein, three plates were prepared and measured at 25 ​°C. Reads obtained from one plate were averaged, normalized, and fitted to a two-state model using equation (1), where only the native and denatured states are populated:

$$F=\frac{({\alpha }_N+{\beta }_N\left[D\right])+\left({\alpha }_D+{\beta }_D\left[D\right]\right)\exp \left(-m_{D-N}({\left[D\right]}_{50\%}-\left[D\right])/RT\right)}{1+\exp \left(m_{D-N}\left(\left[D\right]-{\left[D\right]}_{50\%}\right)/RT\right)}$$ (1)

F is the measured fluorescence intensity, α_N and α_D are the intercepts (i.e. the fluorescence at low (N) and high (D) denaturant concentrations, respectively), and β_N and β_D are the slopes of the baselines at low (N) and high (D) denaturant concentrations, describing the linear dependency of fluorescence denaturant concentration. m_D-N is the m-value, which is related to the increase in solvent exposure upon unfolding. [D]_50% is the midpoint of unfolding. R is the gas constant, and T is the temperature in Kelvin. The m-values and D_50% values were obtained from the fitting in GraphPad Prism 7, and ΔG, the free energy of unfolding in water, was calculated using equation: $\Delta G=m_{D-N}{\left[D\right]}_{50\%}$. For calculations using a fixed m-value, the obtained m-values were averaged, and a new fit was done with an m-value fixed to the averaged m-value. ΔG was recalculated with re-fitted D_50% and the average m-value. Standard errors of the mean (SEM) were calculated for m and D_50% values. The errors of ΔG were propagated from the errors of the m and D_50% values. Fraction unfolded (λ_U) was calculated for individual plates with α_N, α_D, β_N, and β_D obtained from the fixed m-value fit using equation (2):

$${\mathrm{\lambda }}_{\text{U}}=\frac{F-({\alpha }_N+{\beta }_N\left[D\right])}{\left({\alpha }_D+{\beta }_D\left[D\right]\right)-({\alpha }_N+{\beta }_N\left[D\right])}$$ (2)

λ_U from the three individual plates were averaged and plotted against [D].

2.7. Circular dichroism (CD) spectroscopy

Far-UV CD was measured on a Chirascan CD spectrometer (Applied Photophysics) in a 2 ​mm pathlength cuvette (Hellma Analytics). Protein samples were prepared in 50 ​mM sodium phosphate buffer pH 6.8 or pH 8, 50 ​mM NaCl at concentrations between 5 ​μM and 10 ​μM. Measurements were taken every 0.5 ​s between 203 ​nm and 260 ​nm wavelength using a 1 ​nm bandwidth. Thermal denaturation was monitored by ramping the temperature from 15 ​°C to 90 ​°C in 1 ​°C steps and the ellipticity at 222 ​nm recorded. Reads were repeated four times, data were averaged and presented as molar ellipticity. Melting temperatures were determined using a Boltzmann sigmoid function.

2.8. Analytical gel filtration

Analytical gel filtration was performed after affinity purification on a Superdex 75 Increase 10/300 ​GL column (GE Healthcare) in 50 ​mM sodium phosphate, 150 ​mM NaCl, pH 6.8 or pH 8.0 dependent on the predicted isoelectric point of the protein. The buffer used for the cysteine-containing Loop7 was supplemented with 2 ​mM DTT. All proteins were injected at 35 ​μM concentration except for CTPR4, which was injected at 17.5 ​μM.

2.9. Estimation of protein solubility

Soluble proteins were buffer exchanged into the respective analysis buffer (50 ​mM sodium phosphate, 150 ​mM NaCl, pH 6.8 or pH 8.0 dependent on the predicted isoelectric points of the protein, Loop7: +2 ​mM DTT) using PD MiniTrap G-25 columns (GE Healthcare, #GE28-9189-07) according to the manufacturer's protocol. Insoluble proteins purified in guanidinium hydrochloride were diluted 1:10 in native buffer without denaturant and then dialyzed in native phosphate buffer. Purified proteins were applied to Vivaspin 500 centrifugal concentrators (5000 MWCO, Sartorius, # VS0112) and concentrated up to their solubility limits (15,000 ​g, 25 ​°C) as previously described (Golovanov et al., 2004; Smialowski et al., 2007). Concentrations of the concentrated protein were measured using a NanoDrop2000 and the molar concentrations calculated. Theoretical extinction coefficients were calculated using the Expasy ProtParam Tool (https://web.expasy.org/protparam/) (Gasteiger et al., 2005). Experiments were repeated three times.

2.10. Dynamic light scattering (DLS)

The hydrodynamic diameter (D_h) was measured using the Zetasizer Nano-ZS dynamic light scattering system (Malvern Panalytical Ltd) fitted with a 633 ​nm laser. The DTS software provided by the manufacturer employs Stokes-Einstein equation to deduce D_h from the measured translational diffusion coefficients. Protein samples were prepared just before measurements and were centrifuged at 20,000 ​g for 5 ​min at 25 ​°C. Proteins were measured at the following concentrations: low (13–20 ​μM), concentrated (i.e. after protein has been concentrated to its limit; see Table 1 for concentrations) and diluted (concentrated protein diluted back to 13–20 ​μM). All measurements were carried out at 25 ​°C in 50 ​mM sodium phosphate, 150 ​mM NaCl at pH 6.8 (Loop7, Loop9) or pH 8.0 (GG, TBP8, Loop5, Loop10) depending on their predicted isoelectric point.

Table 1.

Experimentally determined stability and solubility values of the CTPR2 proteins and the sequence parameters of the loops and their conformational propensities as predicted by CIDER.

Protein	D50% (M)	m (kcal mol−1M−1)	D50% (shared m) (M)	ΔG (shared m) (kcal mol−1)	Solubility (μM)	pI	Sequence parameters and conformational propensities of the loops
							Length of loop insertion (aa)	ves	f+	f−	FCR (f+ ​+ ​f−)	NCPR (f+ ​− ​f−)	Hydropathy	Region of CIDER plot
CTPR2n	3.44 ​± ​0.01	2.06 ​± ​0.03	3.433 ​± ​0.009	−7.45 ​± ​0.09	>13,000	7.1	–	–	N.A.	N.A.	N.A.	N.A.	N.A.	N.A.
CTPR2a	3.04 ​± ​0.02	2.13 ​± ​0.07	3.04 ​± ​0.02	−6.6 ​± ​0.09	>6500	7.7	–	–	N.A.	N.A.	N.A.	N.A.	N.A.	N.A.
GG	2.784 ​± ​0.007	2.05 ​± ​0.03	2.786 ​± ​0.007	−6.04 ​± ​0.07	550 ​± ​160	7.1	6	n.d.	N.A.	N.A.	N.A.	N.A.	N.A.	N.A.
GSGS	2.77 ​± ​0.01	2.06 ​± ​0.05	2.78 ​± ​0.01	−6.02 ​± ​0.07	390 ​± ​70	7.1	8	n.d.	N.A.	N.A.	N.A.	N.A.	N.A.	N.A.
GGSGGS	2.75 ​± ​0.02	2.14 ​± ​0.03	2.75 ​± ​0.02	−5.97 ​± ​0.08	278 ​± ​16	7.1	10	n.d.	N.A.	N.A.	N.A.	N.A.	N.A.	N.A.
TBP8	2.625 ​± ​0.008	2.23 ​± ​0.03	2.623 ​± ​0.008	−5.69 ​± ​0.07	380 ​± ​80	6.3	12	n.d.	0.13	0.38	0.50	−0.25	2.00	R3
PBIP1	2.65 ​± ​0.02	2.09 ​± ​0.05	2.66 ​± ​0.01	−5.77 ​± ​0.07	50 ​± ​2	6.6	14	n.d.	0.06	0.22	0.28	−0.17	3.18	R2
TBP14	2.613 ​± ​0.008	2.19 ​± ​0.06	2.613 ​± ​0.006	−5.67 ​± ​0.06	123 ​± ​7	6.6	18	n.d.	0.14	0.27	0.41	−0.14	2.44	R3
Loop1	2.562 ​± ​0.008	2.18 ​± ​0.04	2.562 ​± ​0.007	−5.56 ​± ​0.06	16.6 ​± ​0.9	8.8	20	−0.094	0.17	0.08	0.25	0.08	3.09	R2
Loop2	2.50 ​± ​0.02	2.28 ​± ​0.06	2.50 ​± ​0.02	−5.42 ​± ​0.08	12.1 ​± ​1.0	9.5	20	0.134	0.33	0.13	0.46	0.21	2.17	R3
Loop3	2.525 ​± ​0.004	2.130 ​± ​0.009	2.526 ​± ​0.004	−5.48 ​± ​0.06	25.6 ​± ​0.8	9.0	21	−0.002	0.24	0.12	0.36	0.12	2.29	R3
Loop4	2.349 ​± ​0.008	2.16 ​± ​0.05	2.35 ​± ​0.005	−5.10 ​± ​0.06	10.4 ​± ​0.4	8.8	25	−0.097	0.21	0.14	0.35	0.07	2.65	R2
Loop5	2.405 ​± ​0.006	1.98 ​± ​0.04	2.42 ​± ​0.002	−5.25 ​± ​0.06	120 ​± ​20	6.3	25	0.027	0.17	0.31	0.48	−0.14	2.53	R3
Loop6	2.37 ​± ​0.01	2.35 ​± ​0.03	2.37 ​± ​0.01	−5.15 ​± ​0.07	360 ​± ​30	5.0	29	0.109	0.09	0.39	0.49	−0.30	2.82	R3
Loop7	2.344 ​± ​0.006	2.06 ​± ​0.06	2.349 ​± ​0.004	−5.10 ​± ​0.06	247 ​± ​12	5.7	46	0.097	0.12	0.24	0.36	−0.12	3.17	R3
Loop8	2.193 ​± ​0.004	2.22 ​± ​0.01	2.189 ​± ​0.004	−4.75 ​± ​0.05	84 ​± ​10	7.1	50	−0.014	0.17	0.19	0.35	−0.02	2.94	R3
Loop9	2.179 ​± ​0.007	2.30 ​± ​0.09	2.177 ​± ​0.007	−4.72 ​± ​0.05	550 ​± ​140	4.9	52	0.373	0.11	0.34	0.45	−0.23	2.89	R3
Loop10	2.29 ​± ​0.01	2.34 ​± ​0.02	2.29 ​± ​0.01	−4.96 ​± ​0.06	94 ​± ​3	6.6	55	−0.384	0.03	0.08	0.12	−0.05	4.06	R1
Loop11	2.18 ​± ​0.01	2.26 ​± ​0.04	2.17 ​± ​0.01	−4.71 ​± ​0.06	46 ​± ​6	6.6	58	−0.052	0.05	0.10	0.15	−0.05	3.65	R1

Free energies of unfolding were calculated by fitting the denaturation curves to a two-state model with a shared m-value. The indicated errors are the standard errors of the mean calculated from three measurements. The errors for ΔG were propagated from standard errors of the mean of D_50% and m. Solubility was analyzed by concentrating samples in spin concentrators until protein precipitation occurred; resultant protein concentration is listed (in μM). All experiments were conducted at 25 ​°C in 50 ​mM sodium phosphate, 150 ​mM NaCl at pH 6.8 or pH 8.0 dependent on the predicted isoelectric points of the proteins. Isoelectric point, pI, of the loop-grafted CTPR2 proteins (not just the loop sequence) were calculated using http://protcalc.sourceforge.net/. The loop sequences including the flanking DPNN and DPRS were analyzed using the CIDER online software. Calculations for v_es do not include the flanking DPNN and DPRS sequences. v_es, effective solvation volume; f-, fraction of negatively charged residues; f₊, fraction of positively charged residues; FCR, fraction of charged residues; NCPR, net charge per residue (positive or negative); Hydropathy was calculated according to the 0–9 Kyte-Doolittle hydrophobicity scale. Plot region indicates the location of the sequence on the diagram of states. n.d. indicates not determined. N.A., not applicable - these sequence parameters were not calculated for the shortest loop inserts.

2.11. Correlation analysis

Calculations of the properties of the inserted sequences were performed using the CIDER web-server (http://pappulab.wustl.edu/CIDER/analysis/) (Holehouse et al., 2017). Correlations between these sequence parameters and experimentally determined stabilities and solubilities were evaluated by nonparametric Spearman's rank correlation analysis. Two-tailed tests were considered significant if the p value was ≤0.05. Data were analyzed using GraphPad Prism 8.4.2.

2.12. Polymer model analysis

According to this model, the change in the free energy of unfolding (ΔΔG) upon loop insertion is assumed to be exclusively caused by a change in the entropy of the polypeptide chain, i.e. ΔΔG ​= ​-T‧ΔΔS. The values of ΔΔG were different depending on the reference protein (either CTPRa or CTPRn) used. This resulted in two data sets, -T‧ΔΔS_RS and -T‧ΔΔS_NN, (the subscript indicates the different amino acids in the loops of the two proteins). The ΔΔG values were plotted against the increment in loop length (δn) and fitted to equation (3):

$$\mathrm{\Delta }\mathrm{\Delta }G=-T\cdot \text{ΔΔ}S=T\cdot c\cdot R\cdot ln\frac{n+\delta n}{n}$$ (3)

where n is the length of the loop in the reference protein, c is a pre-exponential factor that varies dependent on the polymer model used, and R is the gas constant (Chan and Dill, 1989; Ladurner and Fersht, 1997; Viguera and Serrano, 1997). The standard deviation on the value of ΔΔG was calculated from the propagation of the standard error of the ΔG values obtained from the equilibrium denaturation curves measured in triplicate. Errors for the n and c values are expressed as standard errors of the fit.

3. Results

3.1. Design of CTPRs with loop extensions

In this study, we designed 17 proteins consisting of two consensus repeats (CTPR2) with different peptide sequences grafted onto the loop connecting the repeats (Fig. 1A, C). For the loop extensions, we selected eleven unstructured sequences, as predicted by the CIDER algorithm, that are known to connect folded domains in natural proteins (Harmon et al., 2017). The sequences were chosen to cover various lengths (from 16 to 54 residues) and different regions on the diagram of states (Fig. 1D and Table S1). Further, Loop9 and Loop10 were selected as long loops (48 and 51 residues) that, according to their highly positive and negative v_es values, respectively, are predicted to be either expanded or compact. Additionally, three SLiMs, which bind to cancer-associated targets and have been well-characterized by our group and others, were inserted. They are the tankyrase-binding peptides, TBP8 and TBP14, and a ten-residue peptide derived from the polo-box interacting protein 1 (PBIP1) that bind to tankyrase (Haikarainen et al., 2014; Guettler et al., 2011) and PLK1 (Śledź et al., 2011), respectively. Lastly, short linkers comprising between two and six amino acids (glycine and serine) were analyzed. The loops were inserted after the consensus TPR loop DPNN. After the inserted loop, a DPRS sequence was introduced for three reasons: (1) a proline residue before the second repeat assures that the whole insertion remains unstructured; (2) The RS pair is a necessary leftover from the cloning strategy, concatamerisation of BamHI and BglII DNA restriction sites; (3) some of these loops contain binding sites (Madden et al., 2019) and an equal number of spacer residues between repeat and inserted loop are recommended to avoid steric hindrance against a putative target binding. Ultimately, we aim to obtain results that are transferable to a modular platform of TPR functionalization (Fig. 1B).

3.2. Effects of loop insertion on repeat-protein stability

Small CTPR proteins show cooperative, two-state unfolding at equilibrium (Main et al., 2003a; Tang et al., 1999). To assess the impact on protein stability of extending the loop between adjacent repeats, chemical-induced equilibrium denaturation was performed by monitoring tryptophan fluorescence. All proteins showed a single unfolding transition and could be fitted to a two-state model to give the midpoints of unfolding (D_50%) and m-values (Fig. 2 and Table 1). The m-values obtained from a two-state fit were all within 10% of the median (Table 1). The m-value describes the slope of the unfolding transition and is related to the increase of surface exposure of the protein during unfolding. An m-value that is lower than expected for the size of the protein indicates that unfolding is not cooperative (i.e. not two-state). We showed previously (Perez-Riba et al., 2018) that the m-value of the CTPR2 arrays is unchanged even after loop insertions of up to 25 residues, indicating that the cooperativity is not compromised. The same behavior is observed here for loop insertions of up to 58 residues. Due to the sensitivity of the m-value to the fitting, more accurate values of the midpoints (D_50%) and free energies of unfolding (ΔG) can be calculated by fitting all of the curves to a two-state model with a fixed m-value set at the average of the m-values for all the variants (Table 1). Importantly, the values obtained for D_50% and ΔG values were similar when individual m-values or the average m-value were used. The D_50% values of the extended loop variants were lower than the values obtained for CTPR2n and CTPR2a. The longer the loop the larger the destabilizing effect, with the longest loop decreasing the stability by almost 2 ​kcal ​mol⁻¹ relative to CTPR2a. The loss in stability is not linear with increase in loop length, but rather it tends to a plateau, as discussed further below.

Fig. 2.

Effect of loop insertions on the thermodynamic stability of CTPR2 proteins. Equilibrium denaturation curves were monitored by tryptophan fluorescence at 280 ​nm. Measurements were performed at 25 ​°C in 50 ​mM sodium phosphate buffer pH 6.8 or pH 8, 50 ​mM NaCl with increasing GdmHCL concentrations. Data were fitted to a two-state model using a shared m-value.

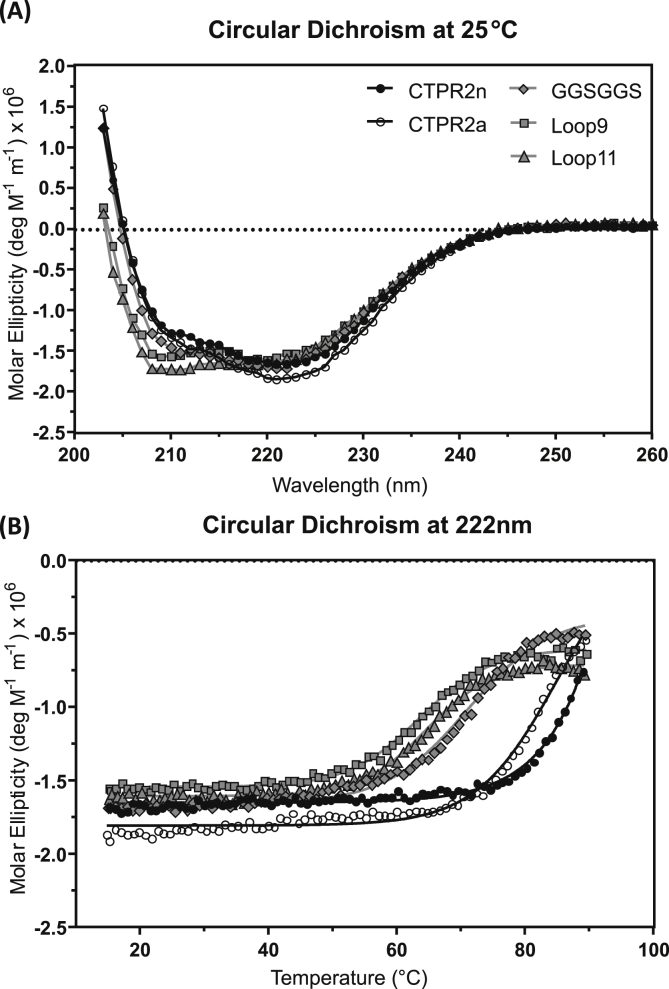
Circular dichroism spectroscopy (CD) was used to further characterize the loop-grafted proteins. The CD spectra show that the helical structure of the CTPR fold is retained (Fig. 3). Compared to the characteristic spectrum of a typical α-helical protein with a double minimum at 208 ​nm and 222 ​nm, spectra of CTPR2 proteins exhibit a less dominant 208 ​nm minimum (Phillips et al., 2012b; Millership et al., 2016). However, the CTPR2 proteins with long loop insertions have the characteristic double minimum, consistent with what we have observed previously for loop extensions of 5–25 residues (Madden et al., 2019; Perez-Riba et al., 2018, 2019). Thermal unfolding, monitored by the change in the ellipticity at 222 ​nm, shows that CTPR2 proteins are destabilized by loop insertion but that the stability remains nevertheless high, which is in line with the chemical denaturation data. Melting temperatures are in the range of 71 ​°C for a short loop extension GGSGGS to 64–65 ​°C for the longer loops Loop9 and Loop11, respectively. By comparison, the melting temperatures of the CTPR2n and CTPR2a proteins without extended loops are of the order of 85 ​°C. Thus, the largest loss of stability occurs with a short loop extension, and further loop elongation has a comparatively small effect on stability, as observed in the chemical denaturation experiments also.

Fig. 3.

Far-UV circular dichroism analysis of the CTPR2 proteins and representative loop insertions. (A) CD spectra were recorded at 25 ​°C. (B) Thermal unfolding monitored by ellipticity at 222 ​nm. Measurements were performed in 50 ​mM sodium phosphate buffer pH 6.8 or pH 8, 50 ​mM NaCl.

3.3. Effects of loop insertion on repeat-protein solubility

We next investigated whether the insertion of the sequences into the inter-repeat loops impairs the solubility of the CTPR2 protein. The elution fractions were maximally concentrated until protein precipitation occurred and concentration of the remaining soluble protein was determined by absorbance at 280 ​nm (Table 1). All of the loop insertions lowered the solubility considerably relative to the CTPR2n and CTPR2a constructs, but there were nevertheless considerable differences in the solubility of the different loops relative to each other. The solubility ranged from less than 25 ​μM (Loop1, Loop2, Loop4) to 300–550 ​μM or higher (GG, GSGS, TBP8, Loop6, Loop9). As anticipated, proteins that expressed in inclusion bodies (PBIP1, Loop1-Loop4, Loop8, Loop11) were less soluble than those that expressed in the soluble fraction. There was no correlation between solubility and loop length. For example, the loop insertion of 52 residues (Loop9) had the same solubility as the shortest loop insertion of two residues (GG).

Lastly, we confirmed that the loop-extended CTPRs are monomeric. Three-dimensional domain swapping, a process where two or more protein monomers exchange a structural element such as a beta-strand or alpha-helix to fold into an intertwined oligomer, is a well-known mechanism for oligomerization (Kundu and Jernigan, 2004; Rousseau et al., 2013; Lafita et al., 2019; Schlunegger et al., 1997; Gronenborn, 2009; Ha et al., 2015; Nandwani et al., 2019). Domain swapping is enabled by the loop connecting the swapped structural element with the rest of the structure, and the composition and length of the loop are critical factors in determining the propensity of a protein to domain swap. Certain loop features can induce domain-swapping in proteins that otherwise do not exhibit this property. To test the possibility that the loop-grafted CTPR proteins are domain-swapped, we investigated the oligomerization states of the proteins using analytical gel filtration. We found that all CTPR proteins analyzed were monomeric under the conditions tested (35 ​μM protein concentration) (Fig. S1). We also used dynamic light scattering (DLS) to characterize the size of the proteins before and after concentrating them (Fig. S2). There is a small increase in the hydrodynamic sizes of the proteins after concentrating. This is to be expected, given that we concentrated the proteins until they started to precipitate. The proteins may, at least in part, be oligomeric at the high concentrations reached or they would not be at their solubility limit. Nevertheless, upon dilution the proteins returned to sizes close to the pre-concentrating values, with the exception of some (but not all) of the variants with the largest loop insertions. For example, Loop7 (46 amino acids) returns to its original size, whereas Loop9 (52 amino acids) and Loop10 (55 amino acids) do not.

3.4. Sequence-specific effects of the loop insertions on repeat-protein stability and solubility

To further understand the effects of loop insertion on the CTPR scaffold, we compared the experimentally determined stabilities and solubilities of loop-extended CTPR2 proteins with various sequence parameters and predictions about their conformational tendencies made by the CIDER algorithm (Das and Pappu, 2013) (Fig. 4 and Fig. S3). Whereas protein stability is sensitive to loop length, it is relatively insensitive to the sequence composition. This effect is illustrated by the behavior of variants Loop1 and Loop2, which are the same length and have similar stabilities despite being in different regions of the CIDER diagram of states (Fig. 1). The stabilities strongly inversely correlate with loop length (r ​= ​−0.98), i.e. the longer the loop the less stable the protein (Fig. 4). There was no correlation between stability and either FCR or NCPR, and only a weak non-significant correlation between stability and hydropathy (r ​= ​0.47) (Fig. S3). We also looked at v_es, which reflects the volume occupied by the linker (a linker with a negative v_es being self-attractive and forming a compact globule, whereas a linker with a positive v_es being self-repelling and highly expanded). Importantly, Loop9, containing a loop of 52 residues, is destabilized similarly to other loop extensions, despite the fact that its v_es is positive (v_es ​= ​0.373) and the linker is predicted to be relatively expanded and therefore might be expected to drive the two repeats apart from each other and disrupt the inter-repeat interface (Harmon et al., 2017).

Fig. 4.

Summary of experimentally determined thermodynamic stabilities (left) and solubilities (right) of loop-extended CTPRs and relationship to sequence parameters. Protein stability (free energy of unfolding, ΔG) (A) and solubility (C) are shown, with proteins grouped according to the location of their grafted peptide sequences in the diagram of states. Relationship between protein stability and loop length (B) and protein solubility and NCPR value of the inserted loop sequence (D). Data for GG, GSGS and GGSGGS loops are excluded from the plot, because NCPR and other sequence parameters are not meaningful parameters for very short peptide sequences. The indicated errors are the standard errors of the mean calculated from three measurements. Spearman's rank correlation coefficient r is indicated, and the level of significance is shown as a two-tailed p value (statistical significance if p value ​≤ ​0.05). δn, loop extension compared to CTPR2n and CTPR2a; NCPR, net charge per residue.

Next, we plotted solubility against a number of different sequence parameters of the loop insertions (Fig. 4 and Fig. S3). There was an inverse correlation between solubility and NCPR (r ​= ​−0.86), i.e. the more negative the NCPR of the loop, the more soluble the protein (TBP8, TBP14, Loop5-Loop7, Loop9), except for PBIP1, the solubility of which might be affected by its two proline residues. In contrast, proteins with a higher fraction of positively charged residues compared to negatively charged (positive NCPR), had relatively low solubilities (Loop1-Loop4, Loop11). There was no correlation between solubility and loop length or loop hydropathy, and only a weak non-significant correlation between solubility and FCR of the loop (Fig. S3). The linker of Loop9 with a v_es ​= ​0.373 is predicted to be highly expanded and might therefore be expected to destabilize the inter-repeat interface. However, the Loop9 protein was more soluble than Loop10 (v_es ​= ​−0.384), which is of similar length but expected to be compact. The stability of Loop9 was also similar to that of Loop10 proteins, again indicating that the native inter-repeat packing is not disrupted. More data would be needed to properly test the effects of v_es on the stability and solubility of the loop-inserted CTPR proteins. Lastly, given that the CTPR2 scaffold is only 70 residues in size and therefore for some of the longer loop-inserted variants the loop constitutes almost as many residues as the CTPR scaffold, we also calculated the pI values of the proteins to have a measure of their overall charge composition. We found there was an inverse correlation between solubility and pI as well as between solubility and net charge (Fig. S4).

3.5. Entropic contributions to the destabilizing effects of loop insertion

The fact that loop length rather than loop composition is a more important determinant of the stability of the CTPR2 protein suggests that the destabilizing effect of loop insertion is related to an increase in configurational entropy of the unfolded state with increase in loop length, which translates to a larger loss of configurational entropy from circularizing the loop upon folding. Polymer theory has been used previously to characterize the relationship between the increase in loop length and the decrease of configurational entropy of the folded state, and it can be described using three parameters: the length increment (δn), a reference loop length (n) and a pre-exponential value (c) (Ladurner and Fersht, 1997; Viguera and Serrano, 1997) (see Equation (3) in Materials and Methods). c is related to the probability of circularization, i.e. the number of closed configurations compared to the total number of configurations accessible to the polymer. It was originally calculated to be 1.5 on the assumption that the polypeptide chain adopted a simple random-walk behavior (Jacobson and Stockmayer, 1950). Other models accounting for exclusion volume and for the site position of the loop within the polymer sequence have proposed values of c ranging from 1.63 to 2.4 (Chan and Dill, 1989). We assumed ΔΔG ​= ​-T‧ΔΔS and generated two data sets using either CTPR2n or CTPR2a as the reference protein, ΔΔG_exp(CTPR2n) and ΔΔG_exp(CTPR2a), respectively. Next, we set n to 4 residues, as this is the length of the loop in these two reference proteins, and we compared the fitting obtained using three different values of c, 1.5, 1.63 and 2.4, used in previous studies (ΔΔG_calc). We observed a rather poor fit of the ΔΔG_exp(CTPR2n) values to the model at low δn values, presumably as a result of the disruption of a semi-structured DPNN loop that confers a stabilization of ~1 ​kcal ​mol⁻¹ to the CTPRn interface (Perez-Riba et al., 2018; Phillips et al., 2012a; Millership et al., 2016). A better fit was observed for the ΔΔG_exp(CTPR2a) values, but with a lower c value of 1.1. This observation suggests that there is a much higher probability of loop closure than predicted by the random walk model. Fitting of ΔΔG_exp(CTPR2a) without constraining the n value gave a c value of 1.4 ​± ​0.2 and an n value of 7 ​± ​2 residues (Fig. 5).

Fig. 5.

Analysis of free energies of unfolding arising from the entropic effects of loop insertion. (A) Fit of the change of the entropy for each loop length to a simple polymer model (Equation (3), see Methods). The temperature was 25 ​°C. It was assumed that ΔΔG ​= ​-T‧ΔΔS, using CPTR2n (▲) or CTPR2a (●) as the initial stability with a reference loop length of 4 (n ​= ​4). Values of ΔΔG for a given loop length were calculated assuming theoretical c values of 1.5 (○), 1.63 (□) and 2.4 (◊). (B) Fit of ΔΔG_exp without constraining the values of n and c. Error bars represent the propagated standard error of the mean calculated from the standard error of the ΔG value (Table 1, Fig. 2). (C) Values of n and c from the fit of the experimental ΔΔG values to the polymer model (Eq. (3) of the methods section). Errors are reported as the standard error of the fit.

4. Discussion

To fully exploit the design capabilities of repeat proteins by functionalizing their inter-repeat loops, we need to understand the effects of sequence insertions on the stability and solubility of the repeat-protein scaffold and how these effects relate to the composition and length of the inserted loop. Such information would enable us to design optimized loops simply by adapting the length and composition of the functional peptide sequences. To this end, we selected 17 intrinsically disordered sequences and constrained them in a CTPR2 scaffold. Remarkably, even the introduction of very long unstructured loops of up to 58 residues (which is almost as long as the two-repeat CTPR scaffold itself) does not prevent CTPR folding. The stability is only mildly impacted by loop extensions in a length-dependent manner, whereas the solubility is affected to a greater degree and is influenced by factors other than length. We showed in our previous study that the folding cooperativity (an experimental measure of which is the m-value) of the two-repeat array is unchanged upon insertion of up to 25 residues (Perez-Riba et al., 2018). The robust cooperativity of the two-repeat array also suggests that the packing of the repeats against each other is not the rate-limiting step in their folding process, but rather it is the formation of the helices and turn within each repeat as has been suggested for other repeat proteins (Löw et al., 2008; Aksel and Barrick, 2014).

An inverse correlation between loop length and stability has been observed previously for the designed four-helix-bundle protein, Rop, upon loop insertion of up to ten glycines (Nagi and Regan, 1997) and upon loop insertion of up to ten residues in two other small proteins, chymotrypsin inhibitor 2 (CI2) and the α-spectrin SH3 domain (Ladurner and Fersht, 1997; Viguera and Serrano, 1997). The magnitude of destabilization was much greater for Rop (2.5 ​kcal ​mol⁻¹) than for CI2 and spectrin SH3 (1.7 ​kcal ​mol⁻¹ and 0.8 ​kcal ​mol⁻¹, respectively), and this difference likely reflects the structural context of the insertion sites in the three proteins: the loops at which sequences were inserted in both CI2 and spectrin are long and flexible, whereas the loop in Rop is very short. For CTPR2, although the loop is of similar length and rigidity to that of Rop, the relatively small destabilizing effect of loop insertion in CTPR2 is more similar to CI2 and spectrin. For all three proteins, the loss in stability with increasing loop length tends to a plateau. This entropic effect is as expected from polymer theory, because as further insertions are added in more flexible regions the entropic cost will be smaller (Chan and Dill, 1989), and a simple polymer model can be used to relate the loss in stability to loop length (Equation (3)). The pre-exponential value (c), a parameter related to the probability of circularization, varies depending on the polymer model used. There is also some uncertainty in how to define the loop length of the reference protein (n), as the loop may have some flexibility without any insertion and also the insertion of the first few residues may have an enthalpically destabilizing effect on the native structure by disrupting specific contacts. Lastly, the other factor related to the structural ‘context’ of the site of loop insertion is the intrinsic folding of the two halves of the structure either side of the loop, the compactness and degree of pre-order of the denatured state and the extent of interactions/interface on either side of the loop. For the CTPR proteins, we looked at using two different reference proteins, CTPR2a (DPRS loop) and CTPR2n (DPNN loop). Although their loops are the same length, CTPR2a and CTPR2n have different stabilities due to additional stabilizing interactions between the Asparagines of the DPNN loop and residues in the preceding repeat (Perez-Riba et al., 2018; Phillips et al., 2012a; Millership et al., 2016). As expected, the polymer model could not fit the relatively larger T‧ΔΔS for short loop lengths when CTPR2n was used as the reference protein. The less stable variant (CTPR2a) is not complicated by the additional enthalpic effect of loop insertion, and therefore using CTPR2n as the reference protein allows us to look exclusively at entropic effects. Assuming a reference loop length of 4, the T‧ΔΔS values are defined by a c value of 1.1, which translates to higher than expected probability of circularization and smaller than expected loss of stability. However, fitting of the data without fixing c gives an n value of 7.2 ​± ​2 and c ​= ​1.4 ​± ​0.2. In summary, it appears that the polymer model with a c value of 1.5 is sufficient to account for the loss of stability of the CTPR2 proteins as a function of loop length independent of sequence composition. This result indicates that ​the inserted sequences do not interact with the body of the protein or themselves form any significant structure - both assumptions required by the polymer model.

Previous studies have not explored loop insertions of such lengths and diverse sequence compositions. We found, perhaps somewhat surprisingly, that despite the diversity of sequences inserted, the effect on protein stability is still mainly driven by loop length; the stability is rather insensitive to the composition of the loop, with only the hydropathy of the inserted sequence showing a weak correlation. Although NCPR is predictive of conformational properties of polyelectrolyte IDRs, as are κ and FCR for polyamphylite IDRs (Mao et al., 2010; Das and Pappu, 2013), these parameters do not significantly modulate the destabilizing effect of loop insertion on the CTPR scaffold. Neither did we observe any correlation with v_es, which predicts the volume occupied by linker or tail sequences (Harmon et al., 2017). The behavior of linker IDRs has to date been studied (computationally) when located between folded domains or with a folded domain on one side (Harmon et al., 2017). Here, the single CTPR either side is only weakly folded in isolation, whereas the inter-repeat interfacial energy is very stabilizing. The large and favorable energetics of the repeat-repeat interaction might explain why the large variability in the conformational propensity of the loop sequences inserted in between does not translate into variable folding/stability of the loop-grafted protein.

High solubility is not only a prerequisite for most biophysical, structural and functional analyses of recombinant proteins but also for biotechnology and therapeutic applications. However, the formation of insoluble protein aggregates is a common limitation of the recombinant expression of rationally designed proteins. Numerous studies have demonstrated that, in general, protein solubility is affected by amino acid composition and can be predicted by properties such as content of charged (Asp, Glu, Lys and Arg) and turn-forming residues (Asn, Gly, Pro and Ser), the presence of hydrophobic stretches and length of the protein sequence (Christendat et al., 2000, Davis et al., 1999, Wilkinson et al., 1991). Here, we examined the solubilities of CTPR proteins containing loop insertions of diverse sequences. The native CTPR scaffold has a very high solubility (6.5 ​mM). All of the variants, even those with only small loop insertions, were considerably less soluble than the native scaffold. However, several of them still had reasonably high solubilities of 300–550 ​μM, including the variant with a loop insertion of 52 amino acids.

In summary, our results reveal that even large sequence insertions into inter-repeat loops of a CTPR scaffold do not disrupt its overall structure, nor do they greatly reduce its stability. Solubility rather than stability could be the limiting factor in the design of functional loop-grafted CTPR proteins, and we suggest that including negatively charged residues in the loop sequence could be beneficial for the production of highly soluble proteins. The findings presented here will facilitate the rational design of soluble and stable binding proteins and their application in synthetic biology.

CRediT authorship contribution statement

Juliane F. Ripka: Investigation, Writing - original draft, preparation, Visualization. Albert Perez-Riba: Conceptualization, Supervision, Writing - review & editing, Visualization. Piyush K. Chaturbedy: Investigation. Laura S. Itzhaki: Conceptualization, Supervision, Writing - review & editing, Funding acquisition.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary data to this article: