Abstract
Vascular grafts have long been used to replace damaged or diseased vessels with considerable success, but a new approach is emerging where native vessels are merely supported, not replaced. Although external supports have been evaluated in diverse situations – ranging from aneurysmal disease to vein grafts or the Ross operation – optimal supports and procedures remain wanting. In this paper, we present a novel application of a growth and remodeling model well suited for parametrically exploring multiple designs of external supports while accounting for mechanobiological and immunobiological responses of the supported native vessel. These results suggest that a load bearing external support can reduce vessel thickening in response to pressure elevation. Results also suggest that the final adaptive state of the vessel depends on the structural stiffness of the support via a mechano-driven adaptation, although luminal encroachment may be a complication in the presence of chronic inflammation. Finally, the supported vessel can stiffen (structurally and materially) along circumferential and axial directions, which could have implications on overall hemodynamics and thus subsequent vascular remodeling. The proposed framework can provide valuable insights into vascular adaptation in the presence of external support, accelerate rational design, and aid translation of this emerging approach.
Keywords: External support, Graft, Computational modeling, Inflammation, Growth and remodeling
1. Introduction
Many medical devices have been designed to augment vascular function in disease and injury. External support is a promising medical technology that has found applications in multiple clinical scenarios, including aortic dilatation (Cohen et al., 2007), Marfan syndrome (Treasure et al., 2014; Verbrugghe et al., 2013), the Ross procedure (Vastmans et al., 2018; Nappi et al., 2015), vein graft disease (Mehta et al., 1998; Yasuda et al., 2018; Sato et al., 2016), and tissue engineering (Zhao et al., 2016). The objective of external support in each of these applications is different — for example, it can maintain valve function and prevent over distension and rupture in Marfan syndrome, provide structural reinforcement against elevated pressure and flow in a vein graft, and reduce the potential of collapse in a tissue engineered trachea. A common underlying theme across these applications is the complex interaction between a foreign body and a soft tissue in the presence of a potentially altered mechanical environment. Multiple animal studies and human trials have reported results superior to standard care/sham controls (Treasure et al., 2014; Vastmans et al., 2018; Nappi et al., 2015; Sato et al., 2016; Jeremy et al., 2004) while other human studies have been disappointing (Murphy et al., 2007). We still lack a fundamental understanding of the effect of both the foreign body response and the altered mechanical loading on acute and chronic remodeling of the vessel. There is, therefore, a pressing need for a systematic approach to the design of these supports. To that end we propose a computational bilayered model that can simulate mechano-adaptation of a vessel in the presence of an external support that promotes inflammation. Motivated by our prior work (Latorre and Humphrey, 2018a) and availability of experimental data (Bersi et al., 2016), we use a C57BL6/J murine descending thoracic aorta as our model system.
2. Methods
2.1. Bilayered growth and remodeling theory
Mechano-adaptation in the presence of an external support is modeled using a bilayered constrained mixture theory of soft tissue growth (change in mass) and remodeling (change in structure), denoted herein as G&R (Latorre and Humphrey, 2018a,b). Global equilibrium equations for the bilayered construct, at each G&R time s, expressed in terms of layer-specific mean stresses, are given by (Latorre and Humphrey, 2018a,b),
| 1 |
| 2 |
along the circumferential (θ) and axial (z) directions, respectively; P is transmural pressure, fz axial force, a luminal radius, and hV and hS the thickness of the vessel (V ) and external support (S), respectively. Each layer is modeled as an independent constrained mixture of multiple structurally significant constituents (Humphrey and Rajagopal, 2002) with its own local variables. Layer-specific Cauchy stress, at any G&R time s, is
| 3 |
wherein both layers (Γ = V, S) are assumed to be incompressible under transient loading, enforced through a respective layer-specific Lagrange multiplier pΓ, while the mixture as a whole can change mass/volume with G&R; σ is the Cauchy stress, with α = 1, …, NΓ denoting structurally significant constituents within each layer.
The mechanical contribution of constituent α to the layer-specific Cauchy stress at the mixture level is then given by (Latorre and Humphrey, 2018a),
| 4 |
where τ ∈ [0, s] is the G&R time at which a constituent is deposited following a perturbation at G&R time 0, with the initial homeostatic state established between some distant past time −∞ and 0; governs layer-specific constituent mass production per unit current volume per time and governs constituent removal (see Eqs. (12) and (13) for particularization details) and ρ is the total mass density (Valentin et al., 2008); the symbol ^ is used to distinguish variables defined at constituent level (e.g.) from variables defined at mixture level (e.g. σ). is Cauchy stress at the constituent level,
| 5 |
where and (Baek et al., 2006). Here, FΓ maps differential position vectors from a reference configuration to the in vivo loaded mixture configurations at G&R time τ, when new material is deposited, or the current G&R time s. is the deposition stretch at which constituent α is incorporated within the mixture, and (Latorre and Humphrey, 2018). Moreover, represents the constituent and layer-specific second Piola–Kirchhoff stress determined with respect to potentially evolving natural configuration n(τ) from a stored energy function as (Latorre and Humphrey, 2018a,b),
| 6 |
Mass fractions satisfy the constraints,
| 7 |
and, consistent with Eq. (4), current mass density evolves according to
| 8 |
2.2. Particularization for a native vessel with external support
The bilayered construct consists of a native vessel (V) as the inner layer and external support (S) as the outer layer (Fig. 1). Based on prior work (Valentin et al., 2008; Wilson et al., 2012), we assume that the vessel is a mixture of structurally significant constituents: elastic fiber-dominated (e), collagen fiber-dominated (c), and smooth muscle cells (m). For illustrative purposes, we assume the external support is made of a single synthetic constituent (e.g. polymer, α = p), though the theory is general enough to accommodate multiple constituents, including co-polymer blends. The media and adventitia of the native vascular wall (Latorre and Humphrey, 2018a) have been homogenized through the thickness and are considered as a unilayered structure here (inner layer, Γ = V), not due to a limitation of the theory but rather a paucity of data on differential medial and adventitial remodeling in mice in the presence of an external polymeric support.
Fig. 1.
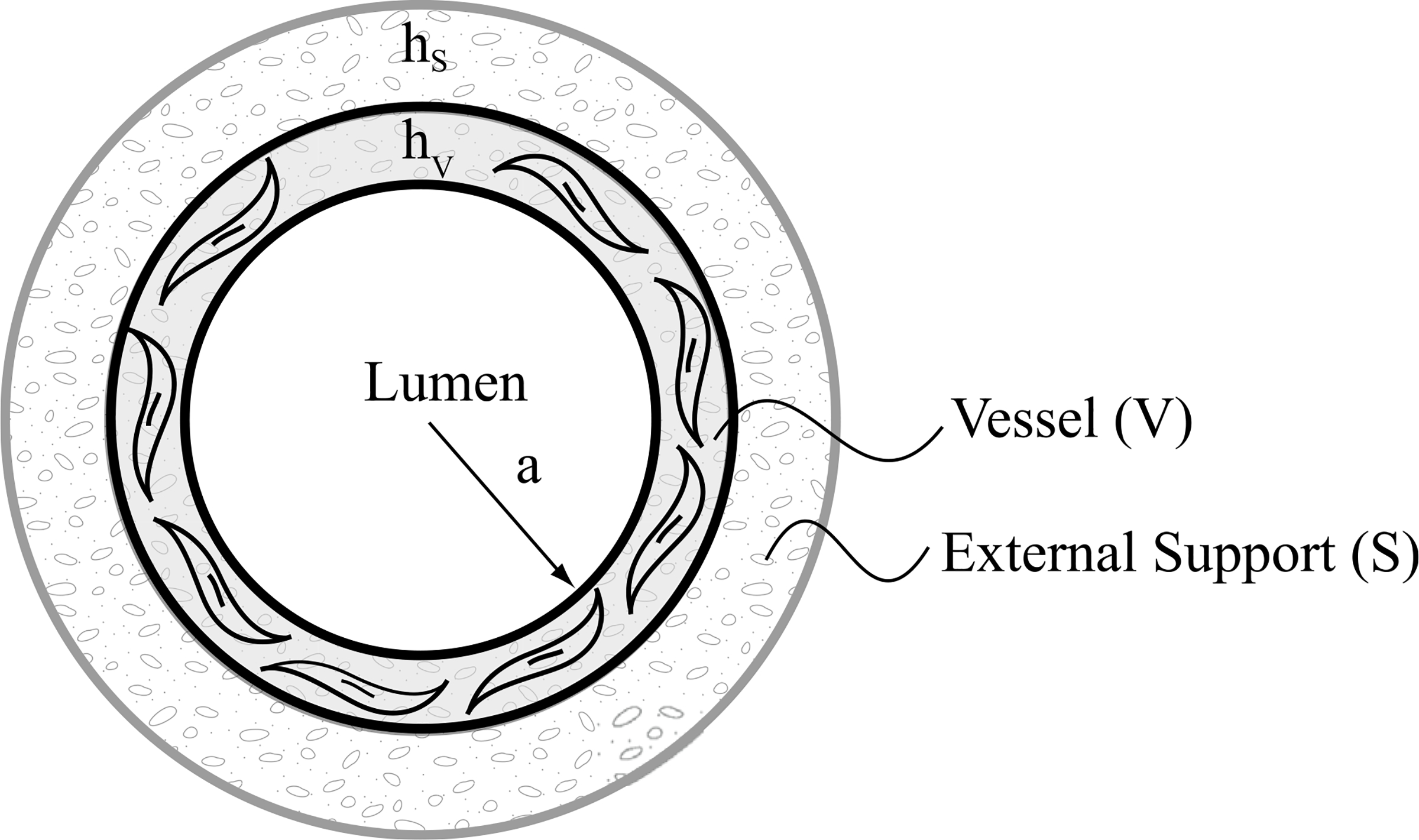
Bilayered construct with a homogenized native vessel (V) as the inner layer and a polymeric external support (S) as the outer layer. Total wall thickness h = hV+hS. It is assumed that the external support runs the length of the vessel segment of interest without affecting the in vivo axial stretch of the native vessel, which is the stretch at which the axial force does not change when the vessel is pressurized cyclically near the in vivo value.
In the inner layer, the stored energy for the elastin-dominated isotropic behavior is assumed to be of a neoHookean form,
| 9 |
where is the layer-specific first invariant of the right Cauchy–Green tensor for elastin and ce is the elastin-dominated material parameter. Smooth muscle and collagen-dominated anisotropic behaviors are assumed to be described by a ‘Fung-type’ exponential form,
| 10 |
where is the current constituent-specific stretch (Baek et al., 2006; Valentin et al., 2008), with and the corresponding constituent-specific material parameters.
For illustration, the external support is modeled using a neoHookean form,
| 11 |
where cp is the shear modulus of the synthetic material (Szafron et al., 2017), for simplicity held constant over time.
For the vessel, Γ ≡ V, in Eqs. (4) and (8), we assume a mass production function of the form (Valentin et al., 2008; Latorre and Humphrey, 2018a)
| 12 |
which is modulated by three factors: changes in pressure-induced wall stress from homeostatic values (Δσ), flow-induced wall shear stress from homeostatic values (Δτw), and a foreign body response induced inflammatory burden , assuming that the basal inflammatory state is negligible; represents a basal production rate of constituent α in vivo, written in terms of a basal rate parameter for removal and the mass density which automatically satisfies the condition of perfectly matched production and removal at the homeostatic state (Latorre and Humphrey, 2018). Note that in the absence of mechanical and inflammatory perturbations, or, more generally, for any state under mechanobiological equilibrium (Latorre and Humphrey, 2018b), the term within bracket reduces to 1, and one recovers the homeostatic values. Note, further, that dividing the mass production by its basal value yields the fold-change, as frequently reported in vascular biology studies. Constituent removal, in Eqs. (4) and (8), is assumed to follow first-order kinetics given by the decay function
| 13 |
where is a rate parameter for removal (assumed constant herein for illustrative purposes) while , and in Eq. (12) are non-dimensional gain parameters that modulate the response to deviations in wall stress (σ), shear stress (τw), and inflammation (ϱφ) from homeostatic values, respectively. The deviations from homeostatic stress values are defined as,
| 14 |
where subscript o denotes an original homeostatic value. The total mass density of the vessel remains constant for all G&R times s. Despite evidence of cellular infiltration and proliferation in some external supports (Sato et al., 2016; Jeremy et al., 2004), data are not sufficient to quantify inflammatory pathways or to build a mechanistic model of inflammation-mediated neotissue deposition in or encapsulation of an external support. One could use inflammatory cell density relative to its maximum possible density to quantify inflammatory responses (Latorre and Humphrey, 2018a) - where a homeostatic condition with no external support (i.e., no inflammation) corresponds to Δϱφ = 0 and maximum inflammation corresponds to Δϱφ =1. Since no such measurements were available for an external support application, we phenomenologically explore different inflammatory responses within the vessel (Δϱφ) which can be broadly classified into an acute response (modeled using a gamma function, Fig. 2a, (Szafron et al., 2018)), a chronic response (modeled using a sigmoid function, Fig. 2b, Valentin et al., 2011), or an acute followed by a persistent chronic response (modeled using a linear combination of the gamma and sigmoid functions, Fig. 2c). Material properties of the constituents are assumed to be unchanged in the presence of inflammation due, in part, to lack of data (unlike in Latorre and Humphrey, 2018a; Latorre et al., 2019). Since synthetic material is not produced in vivo, , with superscript p denoting polymer. The referential mass density of the synthetic material is held constant for nondegradable support simulations. For degradable support, referential density is reduced according to a sigmoidal function (Szafron et al., 2018).
Fig. 2.
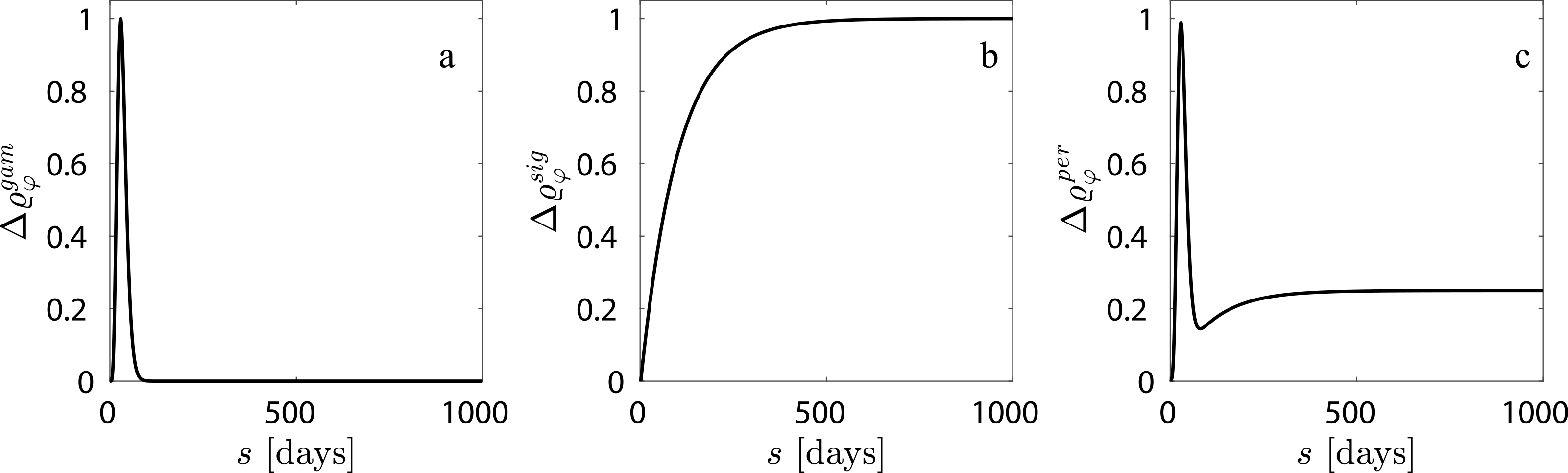
Phenomenologically modeled inflammatory responses include (a) an acute response, (b) a chronic response, and (c) an acute response followed by a persistent residual inflammation.
2.3. Simulation setup
An integro-differential system of equations that constitutes equilibrium equations (2) and (3), complemented with constitutive equations for constituent stresses (4) and mass densities (8) within a constrained mixture of constituents (3) and (7), and the layer-specific Jacobian (that relates mass densities to the cylindrical geometry through layer-specific stretches) were solved numerically. Formulations were implemented in a MATLAB (R2017a) numerical environment. At the initial time (s = 0), the native vessel is at its basal loaded state (Po ≈ 97 mmHg, consistent with parameters in Table 1) and external support is oversized with no vessel contact. At every time step we check if the outer radius of the vessel ≥ inner radius of external support. Once contact is detected we solve a bilayered equilibrium equation with external support as the outer layer. External support is load bearing only when pressure is increased above a certain threshold (set to ≈ 5% above basal) to avoid a self-compensatory regime of adaptation (Sankaran et al., 2013). To simulate preemptive treatment, we setup the simulation for the basal conditions and then subject the vessel to pressure elevation. We choose a representative 1.5 fold increase in pressure for our simulations, as the insult is severe enough to show qualitatively the utility of the framework. The thickness of the external support is 25% of the initial loaded thickness of the vessel, unless mentioned otherwise. The material and G&R parameters for the vessel have been adapted (homogenized through the thickness) from our previous work on the murine thoracic aorta (Table 1), which included validations against multiple data sets (Latorre and Humphrey, 2018a).
Table 1.
Values of model parameters used in the G&R simulations — parameters were fit to experimental data from Bersi et al. (2016) and details of the fit can be found in the appendix of Latorre and Humphrey (2018a), albeit for a bilayered vessel (media and adventitia). Here we adapt it to model a unilayered vessel. Note that contributions from collagen and smooth muscle in the circumferential direction are physically indistinguishable, hence material parameters in the circumferential direction were melded.
| Parameter | Symbol | Value |
|---|---|---|
| Arterial mass density | ρ | 1050 kg/m3 |
| Original inner vessel radius | 0.6468 mm | |
| Original outer vessel radius | 0.6870 mm | |
| Elastin material parameter | ce | 89.71 kPa |
| Collagen material parameters | , | 234.9 kPa, 4.080 |
| Smooth muscle material parameters | , | 261.4 kPa, 0.24 |
| Collagen diagonal fiber orientation | α | 29.91° |
| Elastin prestretch parameters | , , | 1.90, 1.62, 1∕ |
| Prestretch parameters | Gm, Gc | 1.20, 1.25 |
| Collagen gains | , , | 2.0, 2.5, 1 |
| Smooth muscle gains | , , | 0.8, 0.8, 0.8 |
| Mass fractions | ϕe, ϕm, , | 0.252 0.263 0.034 0.451 |
| Mass removal rates | km, kc | 1/80, 1/80 day−1 |
3. Results
3.1. Effect of support stiffness — nondegradable support, no inflammation
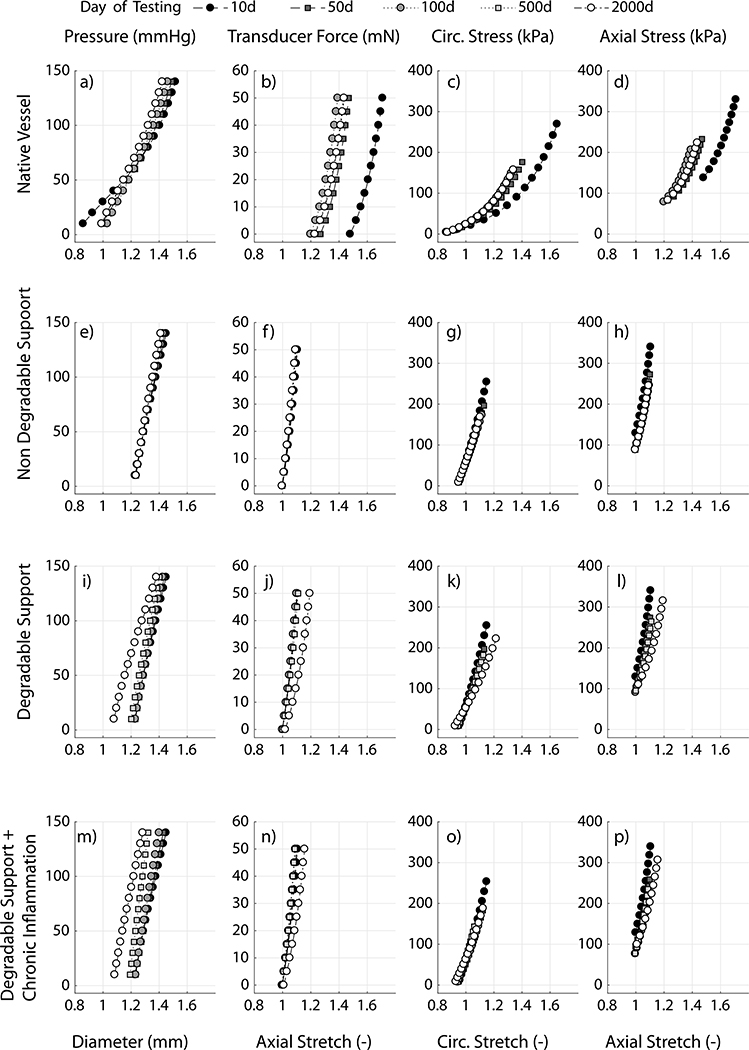
Prior applications have used materials ranging from natural tissue to synthetic polymers (Treasure et al., 2014; Vastmans et al., 2018; Sato et al., 2016; Jeremy et al., 2004; Liu et al., 1999) as external supports. We simulate mechano-adaptation of a native vessel to simulated pressure elevation in the presence of an external support with modulus cp equal to 1, 10, 100 and 1000 times the modulus of elastin (ce), to reflect the wide range of potential materials (Fig. 3). The acute pressure-distended radius of the vessel drops with increasing stiffness of the external support as it constrains overdistension of the vessel (Fig. 3b). Interestingly, long term luminal radius returns to normal values in all cases. An inverse relation is observed between final wall thickness and support modulus (Fig. 3c) as the load-bearing external support offloads the underlying vessel (Fig. 3f and h). The vessel is yet able to recover its homeostatic stress state along both axial and circumferential directions independent of the stiffness of the external support (Fig. 3e and g). Adaptation of the vascular wall in the presence of a thin-stiff support (cp = 40ce, hS = 0.25hV ) is similar to that for a thick-compliant support (cp = 10ce, hS = hV), suggesting the final configuration of the vessel in a mechano-driven adaptation is governed by the structural stiffness of the external support (Fig. 4) rather than material stiffness (Fig. 3) or thickness (Fig. A.1).
Fig. 3.
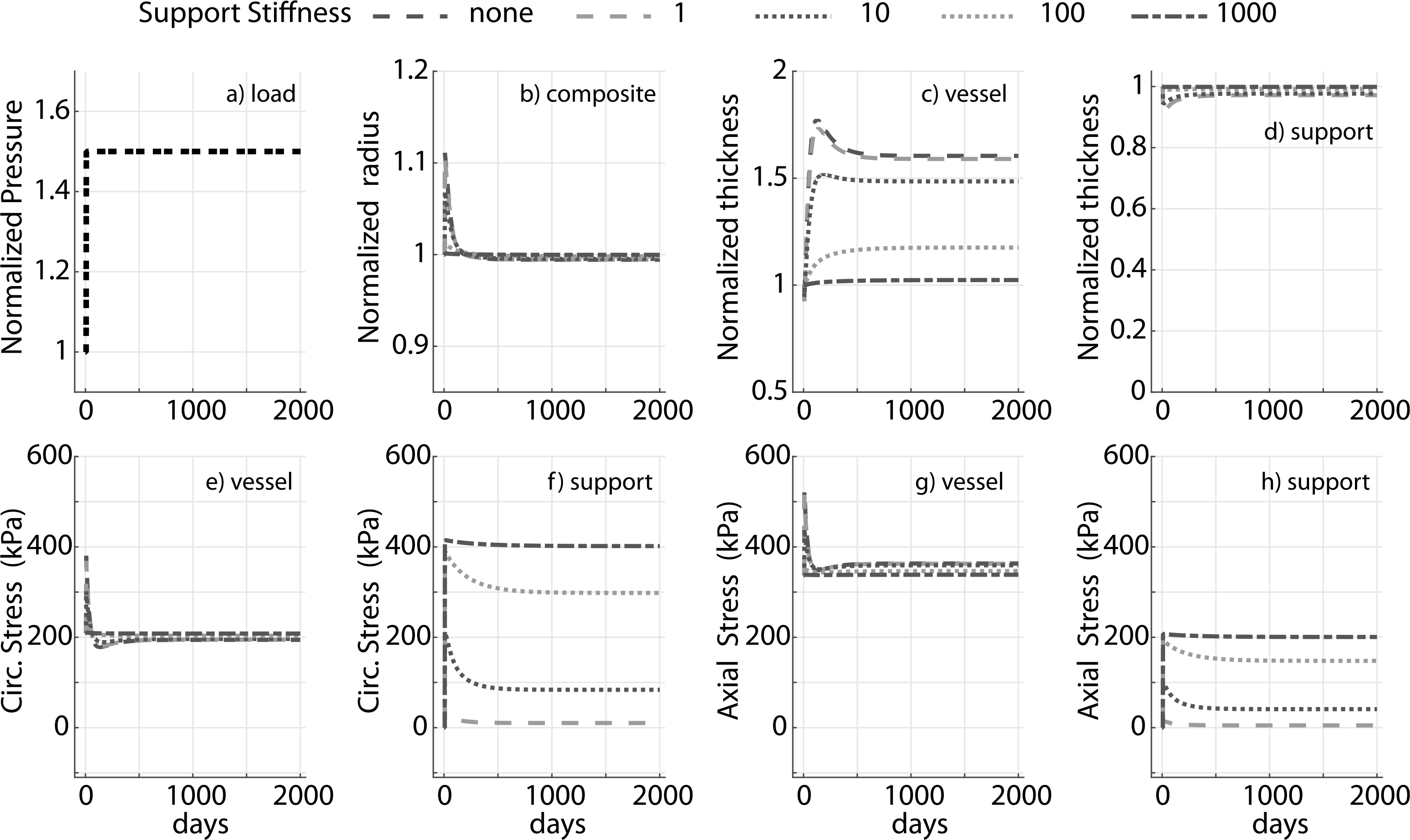
Evolution of the prescribed luminal pressure (a) and predicted responses: luminal radius (b), wall thickness (c and d), circumferential and axial stress in the native vessel (e and g) and nondegradable external support (f and h) for a 1.5 fold increase in pressure. Results compare supports with four different values of stiffness (fold change of 1, 10, 100 and 1000 with respect to ce). Adaptation without an external support (‘none’) is shown for reference. Pressure, radius, and thickness are normalized by respective initial values.
Fig. 4.
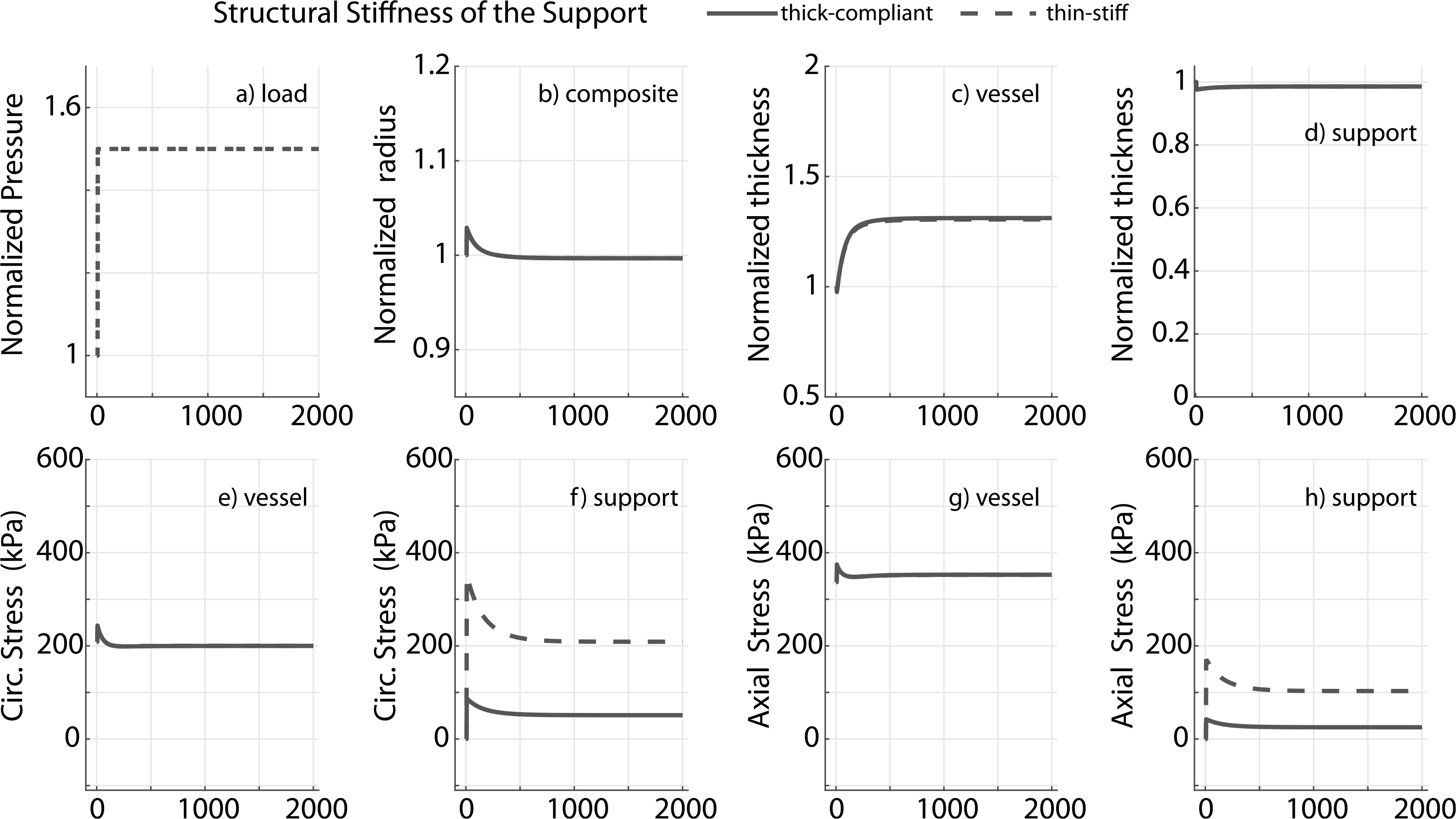
Prescribed pressure (a) and predicted evolving responses: luminal radius (b), thickness (c and d), circumferential and axial stress in the vessel (e and g) and nondegradable external support (f and h) for a 1.5 fold change in pressure. Results compare adaptation of the vessel in the presence of a thin-stiff support (cp = 40ce, hS = 0.25hV) or a thick-compliant support (cp = 10ce, hS = hV). Pressure, radius and thickness are normalized by respective initial values.
3.2. Degradation of the external support — no inflammation
Biodegradable external supports have proved promising, and in some cases superior to nondegradable ones (Sato et al., 2016). To simulate adaptation of a vessel in response to a pressure elevation in the presence of a biodegradable external support, we considered three representative degradation profiles: slow (≈ 25% degradation in 2000 days), medium (≈100% degradation in 2000 days), and fast (100% degradation in ≈100 days). We choose a support modulus 10x greater than that of elastin and a 1.5 fold increase in pressure to illustrate the results; the remaining parameters are the same as in previous simulations.
The degradation profile of the external support dictates the kinetics of adaptation (Fig. 5) but not the final resolved stress state of the vessel, which remains the same in all cases because of the overall homeostatic tendency in the absence of inflammation (Latorre and Humphrey, 2018a; Latorre et al., 2019). For example, the change in thickness is more gradual in a moderate degradation case (Fig. 5b) and could be physiologically more favorable as it allows the vessel sufficient time to produce matrix. Not surprisingly, the final vessel thickness depends on the degradation profile of the support if it is not fully degraded. For a full degradation at s = 2000 days, in the absence of inflammation, the vessel mechano-adapts to the same thickness as in a no external support case (Fig. 5c, ‘medium’ and ‘fast’). In all simulations, the homeostatic state is recovered in both the axial and circumferential directions (Fig. 5e and f). In a physiological setting, external support is accompanied by neotissue formation which we have not modeled here (Verbrugghe et al., 2013; Sato et al., 2016). Hence these simulations highlight only some contributors to the response.
Fig. 5.
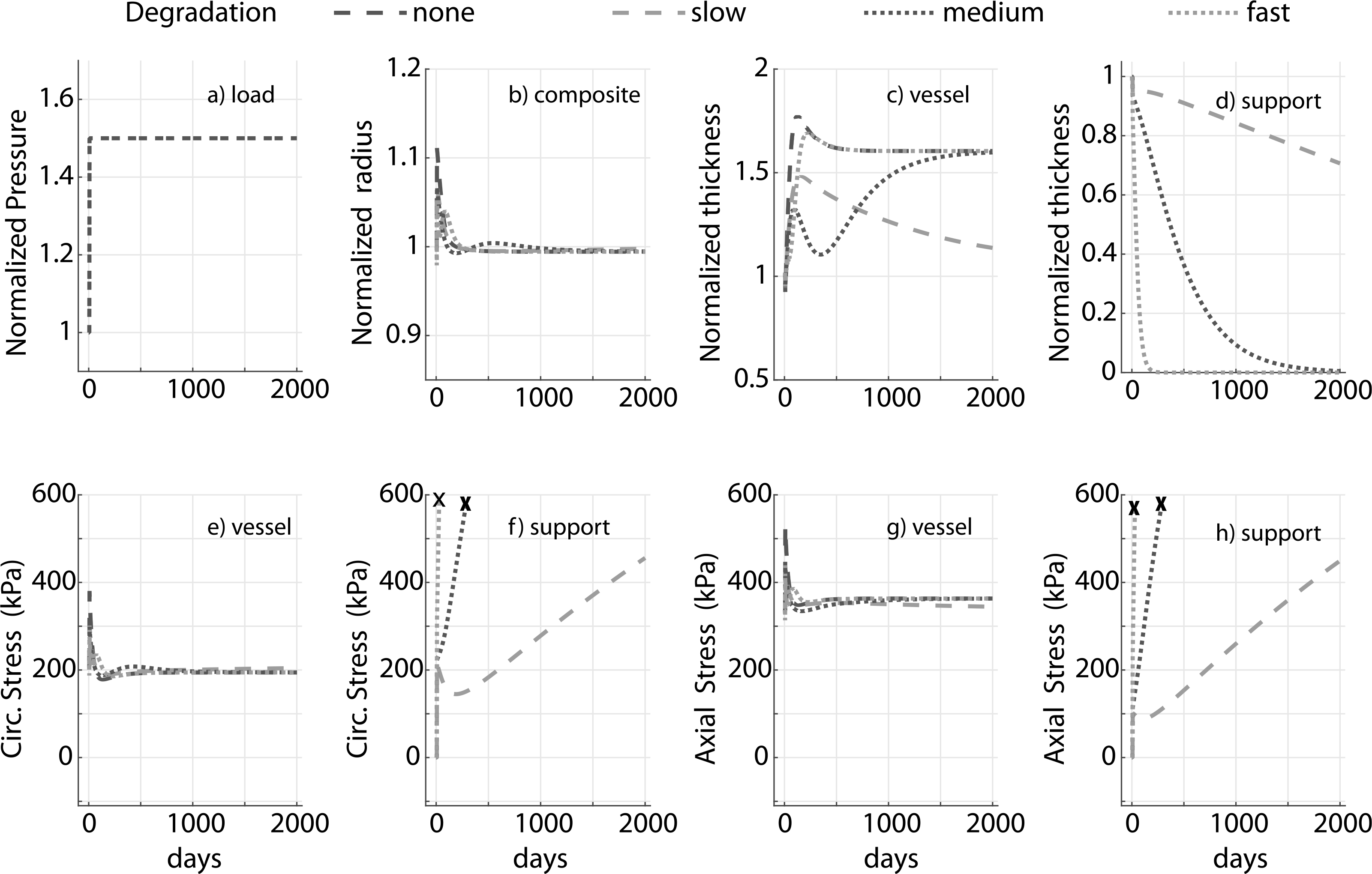
Prescribed pressure (a) and predicted evolving responses: luminal radius (b), thickness (c and d), and circumferential and axial stress in the vessel (e and g) for a 1.5 fold increase in pressure. Degradable materials lose load-bearing ability well before full degradation, so the stress curves for external support are truncated at ≈ 60% degradation (denoted by ✗). Results compare external supports with three different degradation profiles (slow, moderate, and fast). The modulus of the support cp = 10ce. Adaptation without an external support (‘none’) is shown for reference. Pressure, radius and thickness are normalized by respective initial values.
3.3. Effect of inflammation and support degradation
Adaptation for a 1.5-fold increase in pressure in the presence of inflammation for a degradable external support with cp = 10ce and a slow degradation profile for the support (≈25% degradation in 2000 days) is shown in Fig. 6. The adaptation differs drastically across different inflammatory burdens. In particular, in both the chronic (sigmoid) and persistent case, luminal radius drops below the original value (Fig. 6b).
Fig. 6.
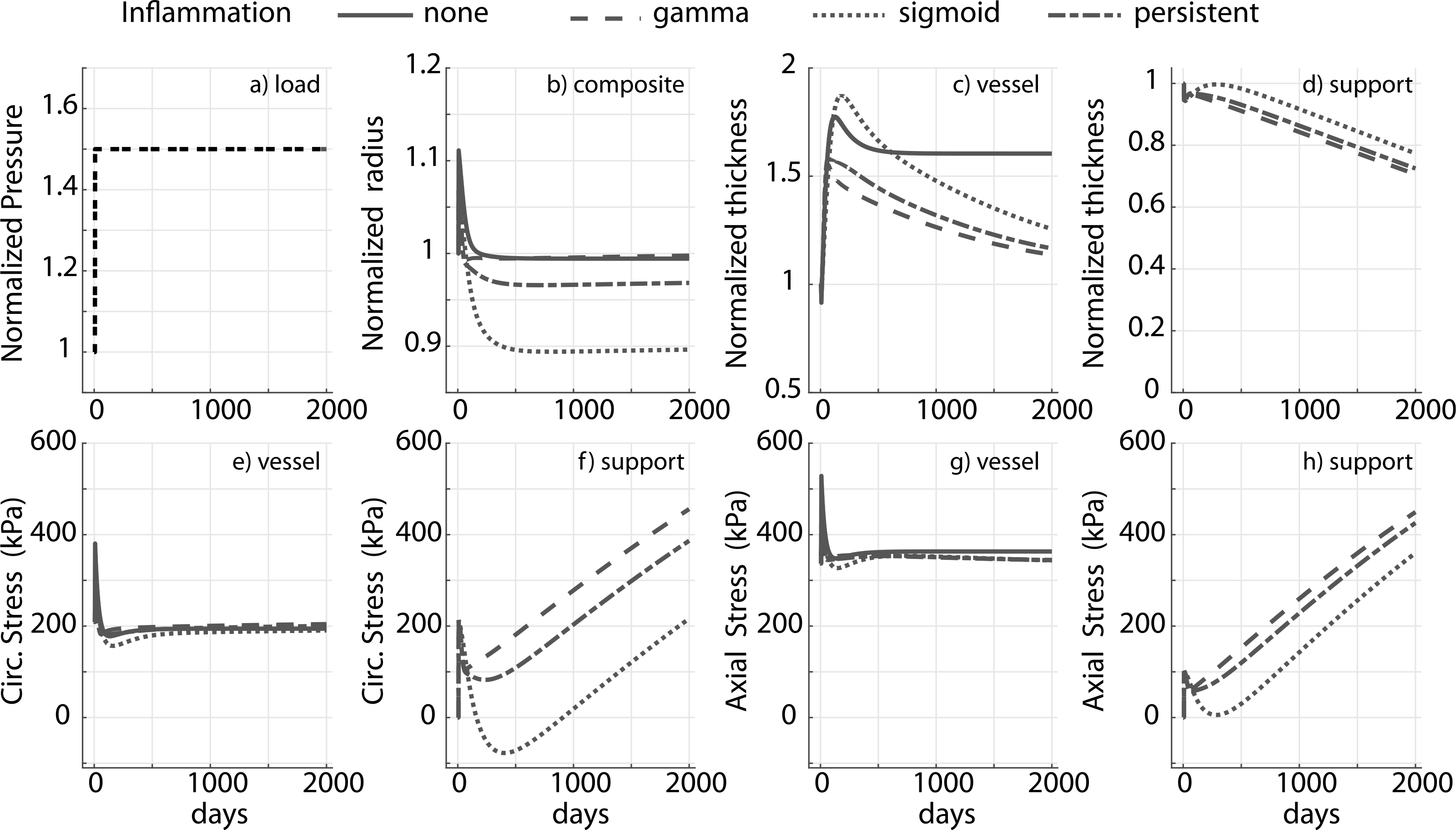
Prescribed pressure (a) and predicted evolving responses: luminal radius (b), thickness (c and d), circumferential and axial stress in the vessel (e and g) and degradable external support (f and h) with a slow degradation profile, for a 1.5-fold change in pressure. Results compare responses to different inflammatory stimuli (gamma, sigmoid and persistent). The modulus of the external support cp = 10ce. Adaptation without an external support (‘none’) is shown for reference, noting further the absence of inflammation in the absence of the foreign body. Pressure, radius and thickness are normalized by respective initial values.
In this case both an increase in transmural pressure and inflammation can lead to luminal encroachment. The axial and circumferential stresses are nevertheless restored to their homeostatic values in all of the simulated cases (Fig. 6e and g, also see Fig. A.2) though thickness is not resolved to its mechano-adaptive value at s = 2000 days, consistent with the response in Fig. 5 for a slow degradation profile. Thickness evolution for fast and moderate degradation is reported in Fig. A.3. Predicted structural and material behaviors during numerically simulated biaxial tests for the bilayered construct in the presence and absence of inflammation are summarized in Fig. 7; the corresponding prediction for a native vessel without external support, in a mechano-driven G&R adaptation, is provided for reference (Fig. 7a–d). Notice that the composite vessel-support exhibits stiffened pressure–diameter, axial force-stretch, and stress–stretch behaviors compared to the native vessel, consistent with an overall stiffening behavior (Fig. 7e–p). Noting the differences in evolving structural and material behaviors between the degradable (Fig. 7i–l) and non-degradable (Fig. 7e–h) supports, the final adaptive state is more extensible (Fig. 7j and l) and distensible (Fig. 7i and k) in the degradable case. Moreover, the structural response is more compliant with degradation of the support (Fig. 7i and j) tending towards a hypertensive mechano-driven native vessel adaptation. Improved adaptations with a degradable support are abated, however, in the presence of inflammation (Fig. 7 m–p). Additional stiffening in the chronic inflammation case can be attributed to additional mass in the construct due to inflammation.
Fig. 7.
Simulated pressure-outer diameter, axial force-stretch, and circumferential and axial stress–stretch behavior for a native vessel with no external support (a-d), with a non-degradable external support (e-h), degradable support(i-l), and degradable support with a persistent (sigmoid-type) inflammatory burden (m-p), all at 10, 50, 100, 500 and 2000 days. Simulations are reported for an external support with cp = 10ce, hS = 0.25hV and, where applicable, a slow degradation profile.
4. Discussion
Despite significant advances in both the development of new synthetic biomaterials and tissue engineering, transplant of autologous vessels remains the mainstay of vascular grafting procedures. The short-and long-term performance of these grafts is far from ideal (David et al., 2014; Oury et al., 1998; Fitzgibbon et al., 1996), however, and the community continues to explore new avenues for augmenting graft adaptation. Of these, though still under evaluation, external support has emerged as a promising strategy (Treasure et al., 2016). While the need for better designed external supports has been widely accepted, a rational approach has yet to emerge (Nappi et al., 2016 being a notable exception). The present computational model of G&R in the presence of an external support may be a step in that direction.
This model yielded several insights into vessel adaptation in the presence of an external support. For example, the model shows how a load-bearing external support can offload the vessel, thus ameliorating the compensatory increase in thickness to reach a homeostatic state in the presence of a sustained increase in pressure (Fig. 3). Further, the adaptation can be similar for thin-stiff and thick-compliant external supports, suggesting that the final state in a mechano-mediated adaptation depends on structural stiffness of the support, provided that peri-support biological responses are similar (Fig. 4). That the circumferential stress state in a ‘thin-stiff’ case (Fig. 4f) reached a value that was close to the homeostatic state suggests the stress state in the presence of an external support could be an important parameter in the design of porous scaffolds, as it might aid or abate tissue ingrowth.
Simulations suggest possible luminal encroachment in the presence of slow degradation and a long-term inflammatory burden, which could require additional intervention or pharmacological treatment (Fig. 6). Recalling previously observed adaptations in systemic hypertension with inflammation, where one observes exuberant thickening of the wall and a failure to restore homeostatic wall stress (Bersi et al., 2016; Latorre et al., 2019), the current predictions suggest possible adaptations in the presence of external support that restore both circumferential and axial stress to homeostatic values even in the presence of chronic inflammation, a surprising result. Note, therefore, that the mass production function Eq. (12) has contributions from wall stress, wall shear stress, and inflammation; these three stimuli need to balance to restore basal production. As the circumferential and axial stress are eventually restored to homeostatic values, our simulations suggest that the contribution from the shear stimulus counteracts the contribution from chronic inflammation. Although increased wall shear stresses should upregulate nitric oxide, which is anti-inflammatory, this requires a functional endothelium. Clearly, experimental studies are needed to study this model-generated hypothesis. The simulations nevertheless highlight the fact that there is a cost associated with inflammation (Kotas and Medzhitov, 2015; Wang and Medzhitov, 2019), in this case luminal encroachment. Other aspects of the model and its predictions demand experimental study. We assumed that the material properties of the matrix produced and deposited within the mixture are constant through the simulation though it is likely that the “inflammatory matrix” is stiffer. We also assumed that the preferred homeostatic stress state remains the same in the presence of external support or inflammation, yet it is possible that inflammation changes the homeostatic set-points as well as other G&R parameters (Latorre et al., 2019). Again, more data will be needed to evaluate these and other aspects of the model.
Finally, our simulations draw attention to an often overlooked, but important, biaxial coupling between axial and circumferential loading in vivo (Humphrey et al., 2009). The external support shifts the operating material and structural behavior of the construct leftwards at higher stretches for both the axial and the circumferential directions (Fig. 7). Many vascular pathologies, including elastin deficiency and damage, hypertension, and ageing, exhibit a drop in the in vivo axial stretch and a leftward shift in the structural and material behavior (Humphrey et al., 2009). Whether a leftward shift in these stress–stretch behaviors due to external support triggers a maladaptive response requires further investigation. Modeling the complex interplay amongst mechano-mediated adaptation, scaffold degradation profiles, and inflammatory burden and its influence on the long-term geometry, stress state, and composition of the vessel is nonetheless a novel application of the model and could motivate further hypothesis testing.
In treating Marfan syndrome or performing a Ross procedure, external support can be preemptive, preventing root dilatation and rupture and preserving valve function (Treasure et al., 2016). Several studies of external support have demonstrated short-term and long-term benefits of these procedures in both animal models and humans (Vijayan et al., 2002; Neufang et al., 2018; Verbrugghe et al., 2013; Treasure et al., 2014; Neri et al., 1999). Among other advantages, external support can prevent dilatation and ameliorate thickening of the wall, thus preventing stretch-induced activation of monocytes and inflammation (Liu et al., 1999) and dysfunctional mechanosensing due to thickening. Prevention of overdistension and reduced thickening are captured qualitatively in our simulations (Fig. 3). In contrast, however, there are also reports of the vessel thickening in the presence of external support due to neotissue formation and incorporation within the external support with effects on the adventitial tissue. We did not attempt to model such effects, but this would be possible given our prior simulations of in vivo neovessel development from degradable polymeric scaffolds (Szafron et al., 2018; Miller et al., 2014). As a model should, the present simulations also identified important gaps in knowledge, including a lack of data on and understanding of inflammatory profiles in the presence and absence of biodegradable supports and different levels of pressure elevation and how inflammation fundamentally affects mass turnover, that is, production and removal.
The constitutive equations for mass production and removal (Eqs. (12) and (13)) are phenomenological and based on iterative refinement and success of our earlier work on vascular adaptations under diverse situations, including ageing, aneurysm, hypertension, vein graft modeling, and tissue engineering (Valentin et al., 2011; Wilson et al., 2012; Latorre and Humphrey, 2018a; Ramachandra et al., 2017; Miller et al., 2014). Basal mass production augmented with an additive stress- or inflammation-mediated term is perhaps the simplest way to capture the physiological effects of these stimuli. This simple form has proven sufficient in many cases and was adopted here. In particular, these stimulus functions for mass production provide a simple linear form Eq. (14) that approximates a more general sigmoidal in vivo response, and is suitable for moderate perturbations. Sigmoidal or similar nonlinear functions would be needed to model more dramatic perturbations (Valentin et al., 2011). While these mass constitutive equations are generally valid and can also model atrophy (as observed in some instances of external support Neri et al., 1999), there is need for additional data (e.g. effect of external support sizing, mechanism of atrophy) and systematic parameter estimation to simulate atrophy with a bilayered theory.
We modeled the vessel as a single homogeneous layer rather than modeling separate medial and adventitial remodeling. Residual stresses (captured here using prestretches in the homeostatic state) tend to homogenize the transmural distribution of wall stress; hence, estimates of mean wall stress are comparable in uni- and bi-layered models (Bellini et al., 2014) thus allowing our mass production equations to be based on mean stress. Bilayered models of the vessel wall can better capture mechanobiological responses but there is not yet sufficient data on layer-specific stress states and responses, especially in the presence of an external support, to extend this model. Also, different materials and fabrication processes can induce nonlinearity and anisotropy in the external supports, none of which are considered in this first generation hyperelastic model. These could be potential extensions for the next generation model.
Nevertheless, we have shown how a relatively simple bilayered (vessel+support) growth and remodeling model can parametrically explore different effects of scaffold design and biological response — both mechanobiological and immunobiological. In combination with prior advances (Szafron et al., 2018; Miller et al., 2014), the present simulations suggest a way forward in the pursuit of improved external supports for diverse applications. Whereas we used material properties for a normal murine thoracic aorta for illustrative purposes, similar simulations can be specialized for diseased arteries (e.g. Marfan syndrome, Bellini et al., 2016) as well as pulmonary arteries (Vastmans et al., 2018; Ramachandra and Humphrey, 2019) or veins placed within the systemic circulation or simply supported within their native circulations (Lee et al., 2013; Ramachandra et al., 2017). Indeed, given that the research goal is different across applications, one will likely need to optimize each design according to different criteria, as, for example, radius, distensibility, structural strength, neotissue formation or reduced inflammatory response. A single, common computational framework, coupled with optimization algorithms (Szafron et al., 2019), should accelerate the design process and aid translation for a truly ‘optimal’ longterm outcome.
Acknowledgments
This work was supported by NIH grants R01 HL128602 and HL139796 to J. D. H.
Appendix
Fig. A.1.
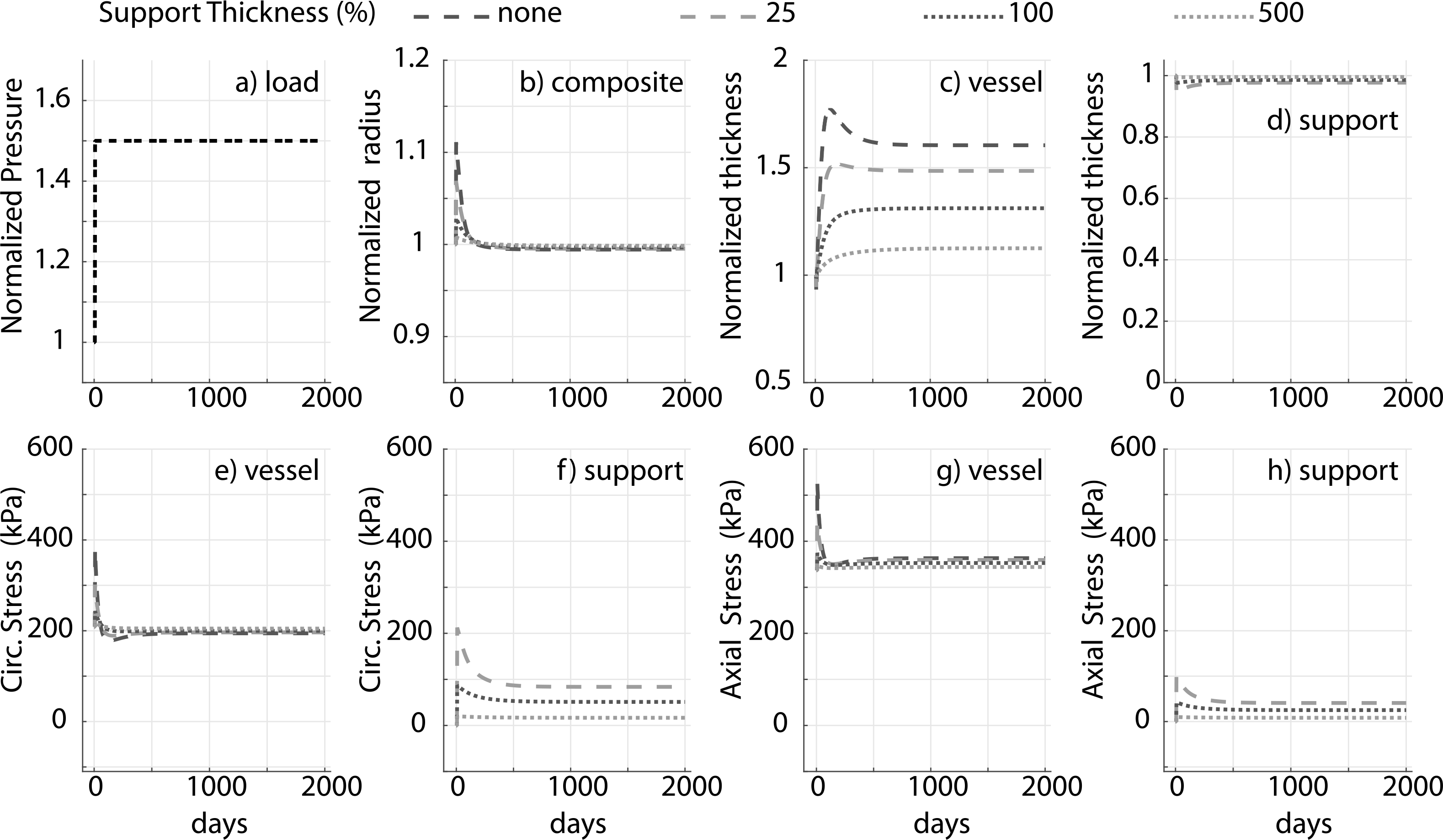
Prescribed pressure (a) and predicted evolving responses: luminal radius (b), thickness (c and d), circumferential and axial stress in the vessel (e and g) and degradable external support (f and h) for a 1.5-fold increase in pressure. Results for different initial values of the thickness (percent of vessel thickness) of the external polymeric support. Adaptation without an external support (‘none’) is shown for reference. Compare to Fig. 3 (change in material stiffness) and Fig. 4 (change in structural stiffness).
Fig. A.2.
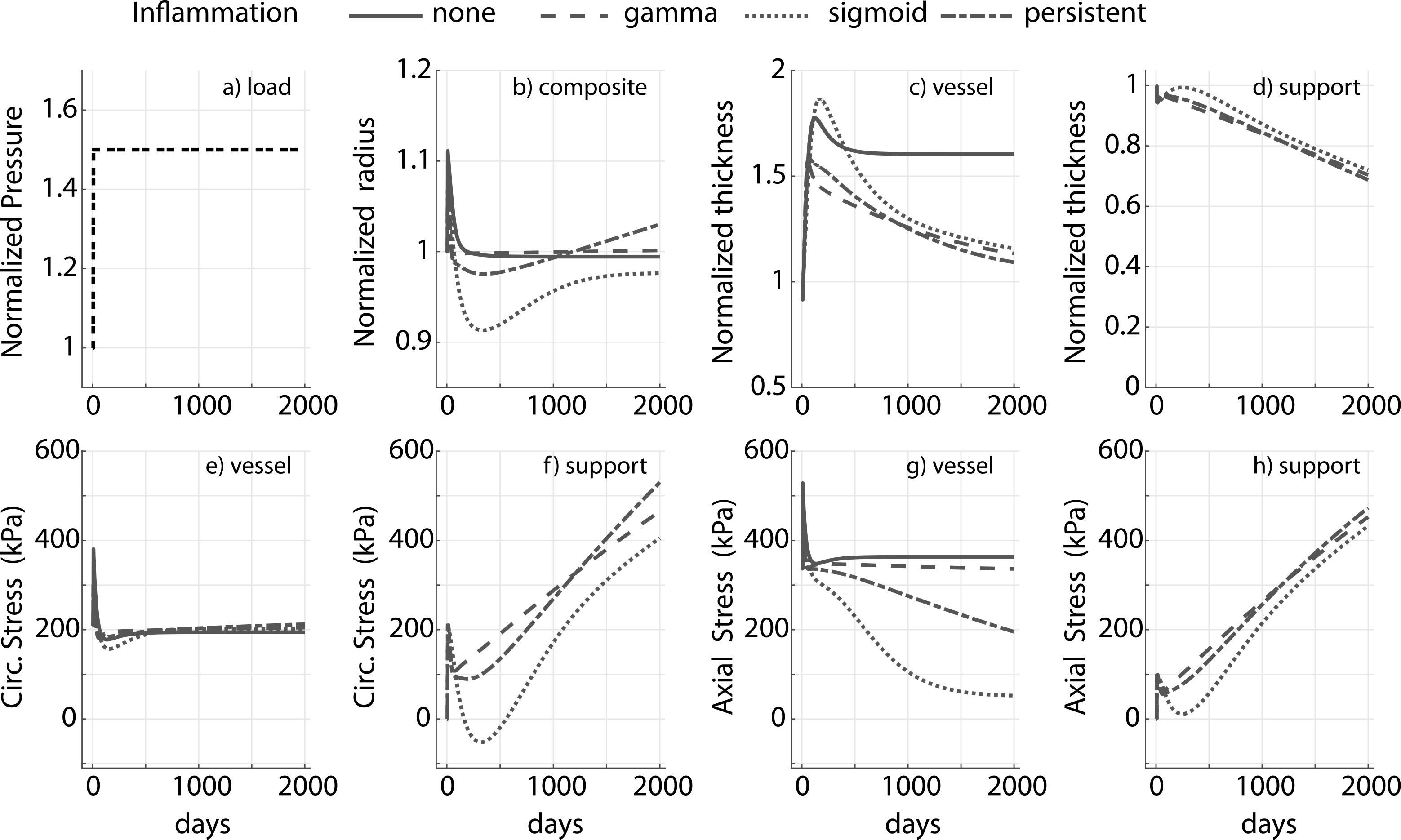
Prescribed pressure (a) and predicted evolving responses: luminal radius (b), thickness (c and d), circumferential and axial stress in native vessel (e and g) and degradable external support (f and h) with slow degradation profile, for a 1.5-fold increase in pressure. Results compare response to different inflammatory stimulus (gamma, sigmoid and persistent). In contrast to Fig. 6, in this case and notice the radius does not asymptote and axial homeostatic stress state is not restored for the sigmoid and persistent inflammation case. Modulus of external support cp = 10ce. Adaptation without an external support (‘none’) is shown for reference.
Fig. A.3.
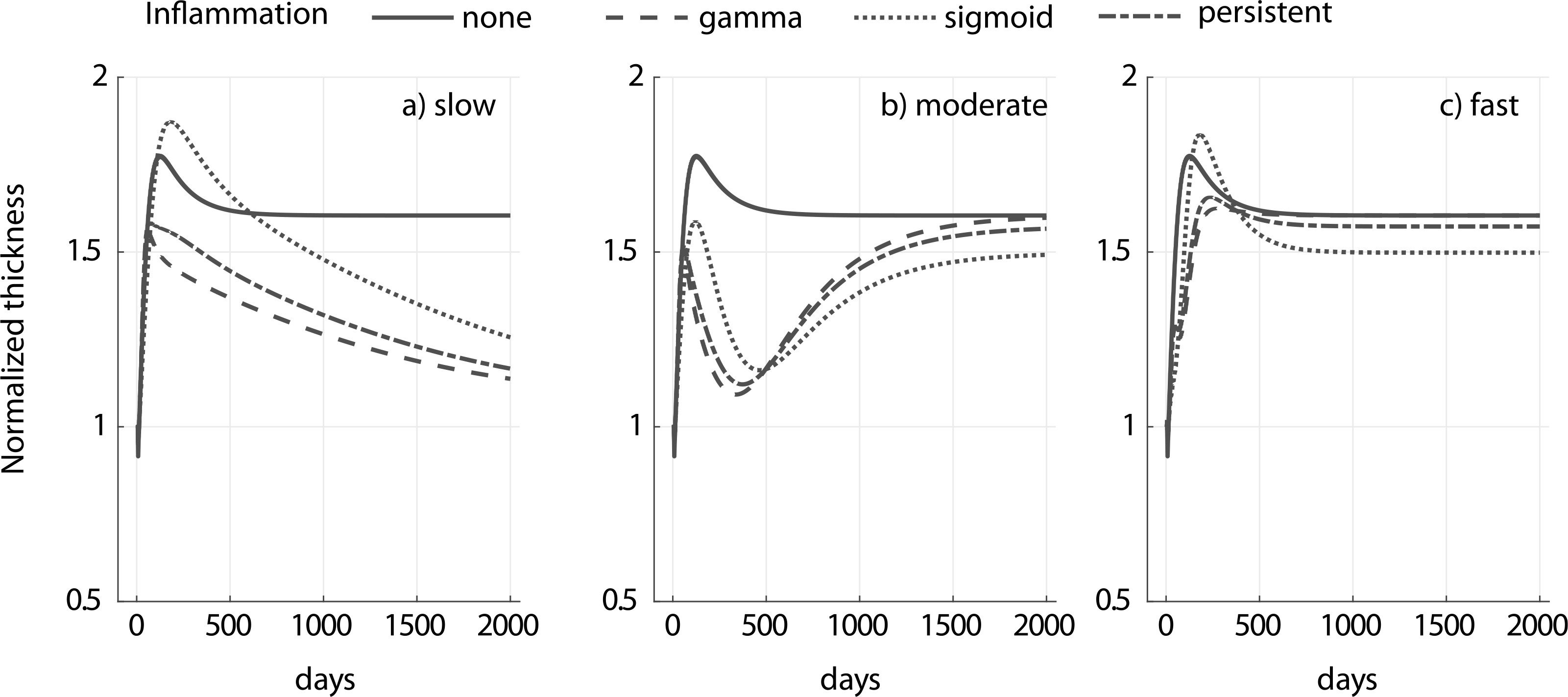
Evolution of native vessel thickness for a 1.5-fold increase in pressure and different inflammatory stimulus (gamma, sigmoid and persistent) for slow (a), moderate (b) and fast (c) degradation of an external polymeric support having a modulus cp = 10ce. Adaptation without an external support (‘none’) is shown for reference. Notice the different kinetics for the different degradation profiles. The circumferential and axial homeostatic stress states were restored in all the cases reported (similar to results in Fig. 6).
Footnotes
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Baek S, Rajagopal K, Humphrey J, 2006. A theoretical model of enlarging intracranial fusiform aneurysms. J. Biomech. Eng. 128 (1), 142–149. [DOI] [PubMed] [Google Scholar]
- Bellini C, Ferruzzi J, Roccabianca S, Di Martino E, Humphrey J, 2014. A microstructurally motivated model of arterial wall mechanics with mechanobiological implications. Ann. Biomed. Eng. 42 (3), 488–502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bellini C, Korneva A, Zilberberg L, Ramirez F, Rifkin D, Humphrey J, 2016. Differential ascending and descending aortic mechanics parallel aneurysmal propensity in a mouse model of Marfan syndrome. J. Biomech. 49 (12), 2383–2389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bersi MR, Bellini C, Wu J, Montaniel KR, Harrison DG, Humphrey JD, 2016. Excessive adventitial remodeling leads to early aortic maladaptation in angiotensin-induced hypertension. Hypertension 67 (5), 890–896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen O, Odim J, De La Zerda D, Ukatu C, Vyas R, Vyas N, Palatnik K, Laks H, 2007. Long-term experience of girdling the ascending aorta with dacron mesh as definitive treatment for aneurysmal dilation. Ann. Thorac. Surg. 83 (2), S780–S784. [DOI] [PubMed] [Google Scholar]
- David TE, David C, Woo A, Manlhiot C, 2014. The Ross procedure: outcomes at 20 years. J. Thorac. Cardiovasc. Surg. 147 (1), 85–94. [DOI] [PubMed] [Google Scholar]
- Fitzgibbon GM, Kafka HP, Leach AJ, Keon WJ, Hooper GD, Burton JR, 1996. Coronary bypass graft fate and patient outcome: angiographic follow-up of 5065 grafts related to survival and reoperation in 1388 patients during 25 years. J. Am. Coll. Cardiol. 28 (3), 616–626. [DOI] [PubMed] [Google Scholar]
- Humphrey J, Eberth J, Dye W, Gleason R, 2009. Fundamental role of axial stress in compensatory adaptations by arteries. J. Biomech. 42 (1), 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey J, Rajagopal K, 2002. A constrained mixture model for growth and remodeling of soft tissues. Math. Models Methods Appl. Sci. 12 (03), 407–430. [Google Scholar]
- Jeremy JY, Bulbulia R, Johnson JL, Gadsdon P, Vijayan V, Shukla N, Smith FC, Angelini GD, 2004. A bioabsorbable (polyglactin), nonrestrictive, external sheath inhibits porcine saphenous vein graft thickening. J. Thorac. Cardiovasc. Surg. 127 (6), 1766–1772. [DOI] [PubMed] [Google Scholar]
- Kotas ME, Medzhitov R, 2015. Homeostasis, inflammation, and disease susceptibility. Cell 160 (5), 816–827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latorre M, Bersi MR, Humphrey JD, 2019. Computational modeling predicts immuno-mechanical mechanisms of maladaptive aortic remodeling in hypertension. Internat. J. Engrg. Sci. 141, 35–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latorre M, Humphrey JD, 2018. A mechanobiologically equilibrated constrained mixture model for growth and remodeling of soft tissues. ZAMM J. Appl. Math. Mech. / Z. Angew. Math. Mech. 98 (12), 2048–2071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latorre M, Humphrey JD, 2018a. Modeling mechano-driven and immuno-mediated aortic maladaptation in hypertension. Biomech. Model. Mechanobiol. 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latorre M, Humphrey JD, 2018b. Critical roles of time-scales in soft tissue growth and remodeling. APL Bioeng. 2 (2), 026108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee Y, Naito Y, Kurobe H, Breuer C, Humphrey J, 2013. Biaxial mechanical properties of the inferior vena cava in C57BL/6 and CB-17 SCID/bg mice. J. Biomech. 46 (13), 2277–2282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu SQ, Moore M, Glucksberg MR, Mockros L, Grotberg J, Mok A, 1999. Partial prevention of monocyte and granulocyte activation in experimental vein grafts by using a biomechanical engineering approach. J. Biomech. 32 (11), 1165–1175. [DOI] [PubMed] [Google Scholar]
- Mehta D, George SJ, Jeremy JY, Izzat MB, Southgate KM, Bryan AJ, Newby AC, Angelini GD, 1998. External stenting reduces long-term medial and neointimal thickening and platelet derived growth factor expression in a pig model of arteriovenous bypass grafting. Nat. Med. 4 (2), 235. [DOI] [PubMed] [Google Scholar]
- Miller KS, Lee Y-U, Naito Y, Breuer CK, Humphrey JD, 2014. Computational model of the in vivo development of a tissue engineered vein from an implanted polymeric construct. J. Biomech. 47 (9), 2080–2087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy GJ, Newby AC, Jeremy JY, Baumbach A, Angelini GD, 2007. A randomized trial of an external Dacron sheath for the prevention of vein graft disease: The extent study. J. Thorac. Cardiovasc. Surg. 134 (2), 504–505. [DOI] [PubMed] [Google Scholar]
- Nappi F, Carotenuto AR, Di Vito D, Spadaccio C, Acar C, Fraldi M, 2016. Stress-shielding, growth and remodeling of pulmonary artery reinforced with copolymer scaffold and transposed into aortic position. Biomech. Model. Mechanobiol. 15 (5), 1141–1157. [DOI] [PubMed] [Google Scholar]
- Nappi F, Spadaccio C, Fouret P, Hammoudi N, Chachques JC, Chello M, Acar C, 2015. An experimental model of the Ross operation: Development of resorbable reinforcements for pulmonary autografts. J. Thorac. Cardiovasc. Surg. 149 (4), 1134–1142. [DOI] [PubMed] [Google Scholar]
- Neri E, Massetti M, Tanganelli P, Capannini G, Carone E, Tripodi A, Tucci E, Sassi C, 1999. Is it only a mechanical matter? Histologic modifications of the aorta underlying external banding. J. Thorac. Cardiovasc. Surg. 118 (6), 1116–1118. [DOI] [PubMed] [Google Scholar]
- Neufang A, Espinola-Klein C, Savvidis S, Schmiedt W, Poplawski A, Vahl CF, Dorweiler B, 2018. External polytetrafluoroethylene reinforcement of varicose autologous vein grafts in peripheral bypass surgery produces durable bypass function. J. Vasc. Surg. 67 (6), 1778–1787. [DOI] [PubMed] [Google Scholar]
- Oury JH, Hiro SP, Maxwell JM, Lamberti JJ, Duran CM, 1998. The Ross procedure: current registry results. Ann. Thorac. Surg. 66 (6), S162–S165. [DOI] [PubMed] [Google Scholar]
- Ramachandra AB, Humphrey JD, 2019. Biomechanical characterization of murine pulmonary arteries. J. Biomech. 84, 18–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramachandra AB, Humphrey JD, Marsden AL, 2017. Gradual loading ameliorates maladaptation in computational simulations of vein graft growth and remodelling. J. R. Soc. Interface 14 (130), 20160995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sankaran S, Humphrey JD, Marsden AL, 2013. An efficient framework for optimization and parameter sensitivity analysis in arterial growth and remodeling computations. Comput. Methods Appl. Mech. Engrg. 256, 200–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato A, Kawamoto S, Watanabe M, Suzuki Y, Takahashi G, Masaki N, Kumagai K, Saijo Y, Tabayashi K, Saiki Y, 2016. A novel biodegradable external mesh stent improved long-term patency of vein grafts by inhibiting intimal–medial hyperplasia in an experimental canine model. Gen. Thorac. Cardiovasc. Surg. 64 (1), 1–9. [DOI] [PubMed] [Google Scholar]
- Szafron JM, Ramachandra B, A., Breuer CK, Marsden AL, Humphrey JD, 2019. Optimization of tissue engineered vascular graft design using computational modeling. Tissue Eng. (ja), 1, 10.1089/ten.tec.2019.0086, 10.1089/ten.tec.2019.0086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szafron JM, Breuer CK, Wang Y, Humphrey JD, 2017. Stress analysis-driven design of bilayered scaffolds for tissue-engineered vascular grafts. J. Biomech. Eng. 139 (12), 121008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szafron J, Khosravi R, Reinhardt J, Best C, Bersi M, Yi T, Breuer C, Humphrey J, 2018. Immuno-driven and mechano-mediated neotissue formation in tissue engineered vascular grafts. Ann. Biomed. Eng. 46 (11), 1938–1950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Treasure T, Petrou M, Rosendahl U, Austin C, Rega F, Pirk J, Pepper J, 2016. Personalized external aortic root support: a review of the current status. Eur. J. Cardiothorac. Surg. 50 (3), 400–404. [DOI] [PubMed] [Google Scholar]
- Treasure T, Takkenberg JJ, Golesworthy T, Rega F, Petrou M, Rosendahl U, Mohiaddin R, Rubens M, Thornton W, Lees B, et al. , 2014. Personalised external aortic root support (PEARS) in Marfan syndrome: analysis of 1–9 year outcomes by intention-to-treat in a cohort of the first 30 consecutive patients to receive a novel tissue and valve-conserving procedure, compared with the published results of aortic root replacement. Heart 100 (12), 969–975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valentin A, Cardamone L, Baek S, Humphrey J, 2008. Complementary vasoactivity and matrix remodelling in arterial adaptations to altered flow and pressure. J. R. Soc. Interface 6 (32), 293–306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valentin A, Humphrey JD, Holzapfel GA, 2011. A multi-layered computational model of coupled elastin degradation, vasoactive dysfunction, and collagenous stiffening in aortic aging. Ann. Biomed. Eng. 39 (7), 2027–2045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vastmans J, Fehervary H, Verbrugghe P, Verbelen T, Vanderveken E, Vander Sloten J, Treasure T, Rega F, Famaey N, 2018. Biomechanical evaluation of a personalized external aortic root support applied in the Ross procedure. J. Mech. Behav. Biomed. Mater. 78, 164–174. [DOI] [PubMed] [Google Scholar]
- Verbrugghe P, Verbeken E, Pepper J, Treasure T, Meyns B, Meuris B, Herijgers P, Rega F, 2013. External aortic root support: a histological and mechanical study in sheep. Interact. Cardiovasc. Thorac. Surg. 17 (2), 334–339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vijayan V, Smith F, Angelini G, Bulbulia R, Jeremy J, 2002. External supports and the prevention of neointima formation in vein grafts. Eur. J. Vasc. Endovasc. Surg. 24 (1), 13–22. [DOI] [PubMed] [Google Scholar]
- Wang A, Medzhitov R, 2019. Counting calories: The cost of inflammation. Cell 177 (2), 223–224. [DOI] [PubMed] [Google Scholar]
- Wilson J, Baek S, Humphrey J, 2012. Importance of initial aortic properties on the evolving regional anisotropy, stiffness and wall thickness of human abdominal aortic aneurysms. J. R. Soc. Interface 9 (74), 2047–2058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yasuda S, Goda M, Shibuya T, Uchida K, Suzuki S, Noishiki Y, Yokoyama U, Ishikawa Y, Masuda M, 2018. An appropriately sized soft polyester external stent prevents enlargement and neointimal hyperplasia of a saphenous vein graft in a canine model. Artif. Organs 10.1111/aor.13399, . [DOI] [PubMed] [Google Scholar]
- Zhao L, Sundaram S, Le AV, Huang AH, Zhang J, Hatachi G, Beloiartsev A, Caty MG, Yi T, Leiby K, et al. , 2016. Engineered tissue–stent biocomposites as tracheal replacements. Tissue Eng. A 22 (17–18), 1086–1097. [DOI] [PMC free article] [PubMed] [Google Scholar]