Tumor Heterogeneity Estimation for Radiomics in Cancer

Abstract

Radiomics is an emerging field of medical image analysis research where quantitative measurements are obtained from radiological images that can be utilized to predict patient outcomes and inform treatment decisions. Cancer patients routinely undergo radiological evaluations when images of various modalities including computed tomography, positron emission tomography, and magnetic resonance images are collected for diagnosis and for evaluation of disease progression. Tumor characteristics, often referred to as measures of tumor heterogeneity, can be computed using these clinical images and used as predictors of disease progression and patient survival. Several approaches for quantifying tumor heterogeneity have been proposed, including intensity histogram-based measures, shape and volume-based features, and texture analysis. Taking into account the topology of the tumors we propose a statistical framework for estimating tumor heterogeneity using clustering based on Markov Random Field theory. We model the voxel intensities using a Gaussian mixture model using a Gibbs prior to incorporate voxel neighborhood information. We propose a novel approach to choosing the number of mixture components. Subsequently, we show that the proposed procedure outperforms the existing approaches when predicting lung cancer survival.

1. Introduction

Quantitative features of medical images are used routinely by clinicians for disease diagnosis, assessment of response to treatment, and for prediction of clinical outcomes such as survival time and disability scores. While in the past a small number of image features (such as tumor size in cancer) were obtained and recorded by radiologists by manually viewing the images, in recent years there is interest in estimating a large number of radiological image features automatically. Aerts et al. (2014) hypothesize that radiological image features obtained from medical imaging data using advanced computational techniques can describe cancerous tissues. The newly emerging field concerned with the estimation of numerous imaging features and subsequent implementation of algorithms to predict clinical outcomes and response to treatment is referred to as radiomics.

In cancer imaging, quantitative features of tumors calculated from images of various modalities such as computed tomography (CT), magnetic resonance images (MRI), and positron emission tomography (PET) are often used for diagnosis and prognosis of cancer. Cancer tumors are heterogeneous objects due to their structure, vasculature, cell types within the tumor, and functional characteristics. Herein, the term “tumor heterogeneity” refers to intratumor heterogeneity, i.e. heterogeneity of structures within a single tumor observable on a radiological image. Depending on the imaging modality used in a particular setting, various types of tumor heterogeneity can be observed on the radiological image of a patient. For example, since PET imaging is used to observe metabolic processes in the tumor, features related to tumor metabolism are used as measures of tumor heterogeneity computed from PET scans. On the other hand, since structural MRI captures the structure of the tumor, MRI scans are used to estimate tumor heterogeneity features related to tumor anatomy and shape.

Quantifying tumor heterogeneity is imperative as heterogeneity measures can be used to compare tumors with one another, develop novel targeted therapies, identify longitudinal trends in disease development, determine patient’s response to a particular treatment, and predict clinical outcomes. In addition, medical imaging is performed using noninvasive in-vivo imaging technology, which is routinely performed as part of clinical care. Hence, the analysis of tumor heterogeneity based on medical imaging can potentially be performed using routinely collected images without the need for further data collection.

One common approach to estimating tumor heterogeneity is by using the histogram, in particular the radiomic features based on the histogram of intensities of image voxels [three dimensional (3D) pixel]. A comprehensive review of the literature on histogram measures for quantifying tumor heterogeneity is given by Just (2014). In this approach, a histogram of tumor voxel intensities is calculated and features of the histogram are used as measures of heterogeneity. For example, Figure 1 presents CT scans of patients with lung cancer along with the corresponding intensity histograms. Common features in the literature include skewness, kurtosis, entropy, and percentiles of the tumor intensity histogram. For example, the histogram of tumor intensities of patient 1 in Figure 1 is more left skewed than that of patient 2 with skewness values of −2.47 and −2.13 correspondingly, while the kurtoses of intensities are 6.156 and 3.48 suggesting that the intensities of the tumor of patient 1 have a sharper peak than those of patient 2. Finally, the means (standard deviations) of the two histograms are 961.09 (sd = 201.73) and −49.12 (sd = 234.43) suggesting that the intensities of the first histogram are centered higher than those of the second histogram with similar spread. These mean, standard deviation, skewness, and kurtosis values are then used as measures of tumor heterogeneity to compare tumors. Studies evaluated the relationship of the histogram metrics with response to radiotherapy (Peng et al., 2013), as well as classification of tumor types (Gutierrez et al., 2014). A major shortcoming of these intensity histogram-based approaches is the elimination of information on spatial structure of the tumor. This is potentially a serious limitation as differences in spatial distributions of voxels with similar intensities will be missed by this approach.

Figure 1:

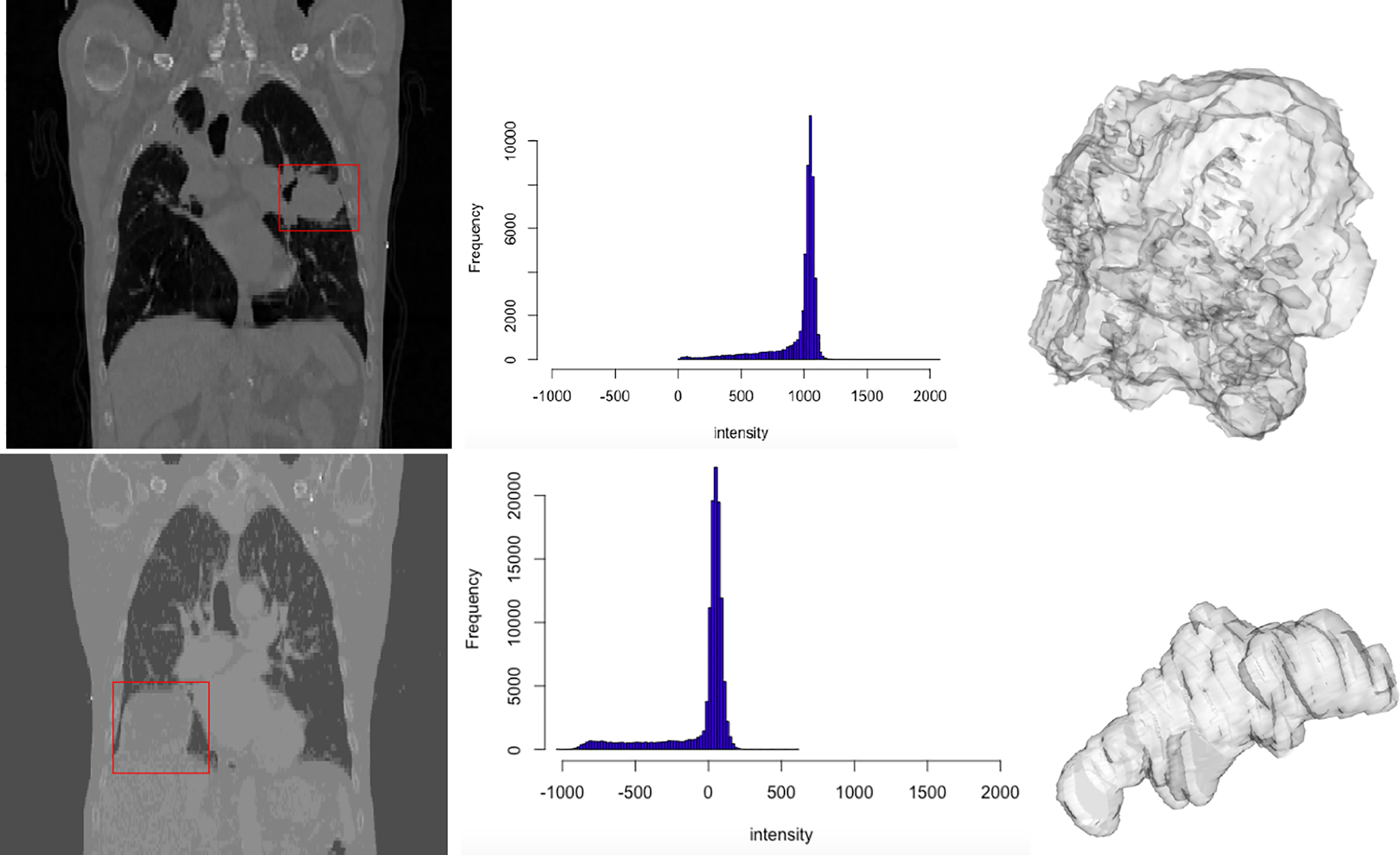
Left column: 2D slices of CT scans of two patients. The tumor is enclosed in a red box. Middle column: histograms showing the intensities of tumor voxels. Right column: 3D surface renditions of respective tumors.

We provide a brief (and by no means exhaustive) overview of a few methods for tumor heterogeneity estimation for structural images, data from other imaging modalities, and genomics in this paragraph. Brooks and Grigsby (2013) considered another intensity-based measure of heterogeneity using a pixel-level approach. The proposed measure is based on a distance-dependent mean deviation from a linear intensity gradation. Roberts et al. (2017) proposed the use of wavelet-based scaling indices for prediction of breast cancer diagnosis using mammography imaging. O’Sullivan et al. (2005) discussed the incorporation of tumor shape assessments into estimation of spatial heterogeneity of tumors using fluoro-deoxyglucose-PET data. As discussed above, there are differences in data obtained from PET imaging and mammography and those obtained using the MRI or CT technologies, hence, the methods proposed by Roberts et al. (2017) and O’Sullivan et al. (2005) may not be directly applicable to analyzing tumor heterogeneity using CT imaging as in the motivating dataset in this article. Nevo et al. (2016) discussed issues related to measurement error in biomarker data and approaches for taking into account such errors to reduce misclassification of cancer subtypes. The term “tumor heterogeneity” is widely used in statistical genomics literature to refer to variability in tumor cells. For example, Xu et al. (2015) proposed the MAD Bayes approached for inference on tumor heterogeneity using next-generation sequencing data. Ni et al. (2019) used Bayesian hierarchical varying-sparsity regression models for estimating biomarkers of tumors from proteogenomics.

Aerts et al. (2014) proposed a general approach for using descriptors of tumor heterogeneity for cancer prognosis and tumor classification by building on histogram and shape features. Four types of image features were used to quantify tumor heterogeneity: histogram summaries, shape, texture, and transformation-based features. The prognostic ability of the radiomic features was presented and validated in a large dataset of medical images from patients with lung and head-and-neck cancers. Specifically, cancer survival was considered as an outcome. Textural features were obtained using grey-level co-occurrence and grey-level run-length matrix-based approaches. Once the radiomic features were extracted Aerts et al. (2014) used the Kaplan-Meier product-limit estimator (Kaplan and Meier, 1958) to obtain associations of radiomic features with survival. One radiomic feature from each of the four types of image features was selected based on feature stability analysis to form the radiomic signature consisting of the resulting four representative features. This radiomic signature was then used in a Cox Proportional Hazards model for prediction of survival. Limitations of this approach include the choice of only four features for prediction.

The novel approach for tumor heterogeneity estimation presented in this article builds on the existing estimation methods while accounting for spatial distribution of voxels. On a high level, our proposed approach consists of 2 steps: 1) we propose a new approach for indentification of clusters of voxels with similar intensity profiles (using a methods similar to those for brain tissue segmentation Zhang et al. (2001)), 2) computation of features of the voxel intensities in these estimated clusters as measures of tumor heterogeneity. To model the voxel intensities accounting for their spatial distribution we use Markov Random Fields (MRF) (Li, 2009). We then compute within and between cluster summary measures of voxels with similar intensity profiles that describe tumor heterogeneity. We present the performance of our proposed MRF-based clustering approach in simulation studies. In addition, we show that the proposed tumor heterogeneity estimation approach performs as well as or better than other approaches in ranking images by their heterogeneity using simulated data. We then present the performance of regularized regression when predicting lung cancer patient survival using the novel estimator of tumor heterogeneity and compare the performance of this method to existing approaches using time-dependent receiver operating characteristic (ROC) curves. Specifically, we consider the Cox Proportional Hazards model (Andersen and Gill, 1982) and generalized linear models with Ridge, Lasso, and Elastic-Net penalization. We illustrate that our proposed estimation procedure outperforms other approaches when judged based on maximization of cross-validation area under the curve (AUC) as a criterion of predictive performance of the model. We show that many existing approaches to tumor heterogeneity estimation are special cases of our proposed framework.

The article is organized as follows. Section 2 presents our proposed method, where Section 2.1 provides an overview of the data, Section 2.2 describes notations used throughout the Section. Next, Section 2.3 introduces our proposed novel estimator for tumor heterogeneity, where Section 2.3.1 provides details of our proposed estimation algorithm, Section 2.3.2 shows our proposed procedure for selecting the number of Gaussian mixture components, and Section 2.3.3 presents the summary measures for evaluating tumor heterogeneity. Section 3 presents simulation results on comparison of our proposed methods with other approaches. Section 4 shows the results of the prediction of lung cancer survival using our proposed tumor heterogeneity estimation approach and existing methods. Finally, Section 5 presents concluding remarks.

2. Data and Methods

2.1. Data

In this paper, we examine cancer survival as the clinical outcome of interest. We consider data from patients with non-small cell lung cancer (NSCLC) collected at the MAASTRO Clinic (Maastricht, The Netherlands) and publicly available from The Cancer Imaging Archive (TCIA) located at http://www.cancerimagingarchive.net (Clark et al., 2013). NSCLC is the most common type of lung cancer accounting for about 85 − 90% of lung cancer diagnoses according to the American Cancer Society. The database we obtained from TCIA includes CT scans from 422 patients with inoperable, histologic, or cytologic confirmed NSCLC along with their demographic and clinical information including age, sex, histology of tumors, stage of cancer, and the clinical N and T stages for each participant. The clinical N stage corresponds to the density and spread of lymph nodes and the clinical T stage corresponds to the size and extent of the tumor. Figure 2 presents the distribution of patients in this study by their tumor histology and cancer stage. The average age of the participants in this sample is 68 years with standard deviation of 10.1. There are 290 males and 132 females. A spiral CT with a 3 mm slice thickness is performed for each participant including the complete thoracic region. Further details on data collection parameters and scanning information can be found at Aerts et al. (2015) and hence are not repeated here. Our aim is to develop a tool for prediction of cancer survival, using a novel tumor heterogeneity measure that we define herein.

Figure 2:

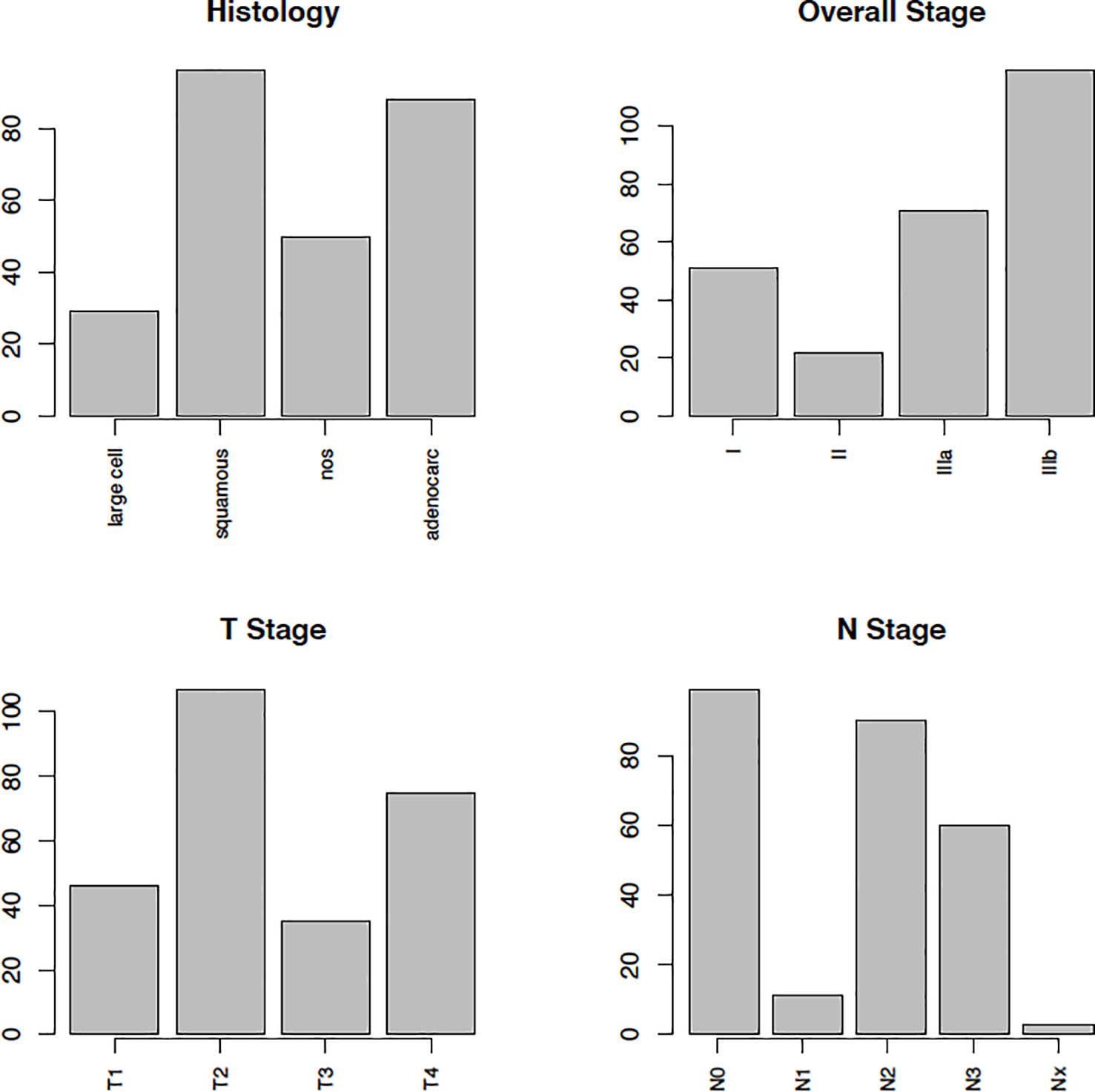
Barplots showing the distribution of clinical variables. Histology provides a description of the tumor based on the abnormality of tumor cells observed using a microscope. Overall stage of cancer indicated the size of the tumor and its spread by a number I, II, IIIa, and IIIb, where a higher number implies larger and more spread cancer. T1, T2, T3, and T4 refer to the size and extent of the tumor. The higher the number the larger or more extensive the tumor. N1, N2, and N3 refer to the number and location of lymph nodes that contain cancer (the higher the number the more lymph nodes), N0 indicates there are no nearby lymph nodes, NX implies that cancer in nearby lymph nodes is not measurable.

A few details on preprocessing of medical imaging data deserve a special note. A radiologist reviewed each CT scan and manually delineated the tumor volume by marking voxels visually identified as locations on the tumor surface. In the example illustrated in Figure 3, this delineation starts by marking four of the vertices on the tumor surface. The delineation then continues until enough surface points are obtained to delineate the full tumor surface (as shown in Figure 3 bottom left). For each participant, the coordinates of these tumor surface vertices are saved in a matrix and provided on TCIA in the RTSTRUCT format along with other scan-specific information such as the thickness of the slices, etc. Since in most cases not all vertices are marked manually, there is a need to interpolate the vertices automatically. We pre-processed these files to obtain all tumor voxels by connecting the vertices using linear interpolation in the R software (R Core Team, 2016). As a result, for each participant we obtain a V_i × 3 matrix of coordinates of all tumor voxels as presented in Figure 3 bottom right, where V_i defines the total number of tumor voxels for subject i. We can now use these coordinate matrices to extract the intensities of tumor voxels for each participant. All patients received standard of care treatments for their corresponding cancer stage, however, treatment information was not available in the database.

Figure 3:

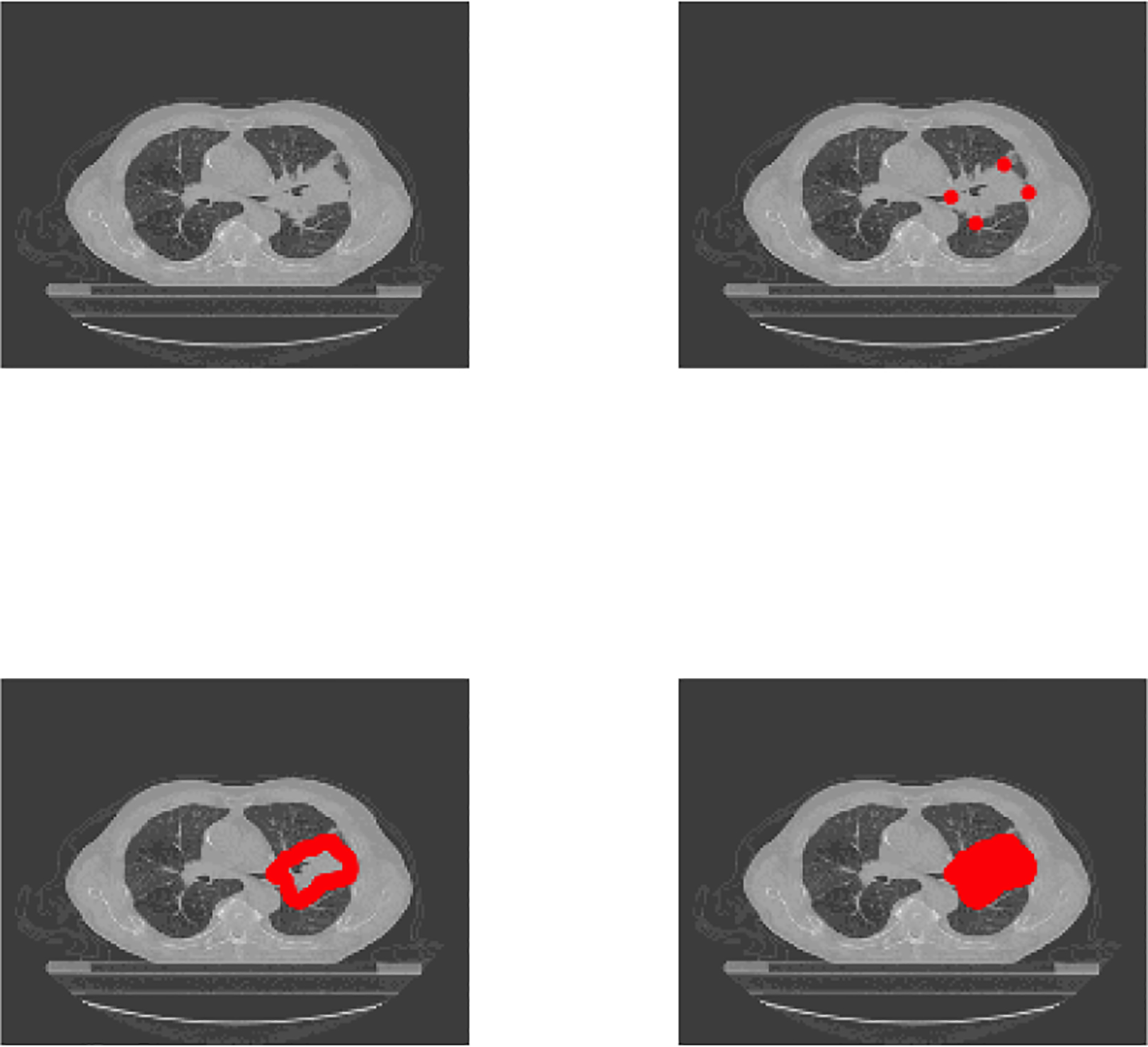
Top left: An axial slice of the CT for one patient. Top right: Four of the tumor surface vertices (in red) marked by the radiologist. Bottom left: All tumor surface points marked by the radiologist. Bottom right: The full area of the tumor identified by interpolation of surface points and identification of tumor interior points.

2.2. Notations and Existing Approaches for Tumor Heterogeneity Estimation

Let I_iv define the intensity of the CT image at voxel v = 1, …, V_i for subject i = 1, …, N, where V_i is the number of tumor voxels and N is the total number of patients. While the number of tumor voxels V_i may vary from subject to subject, for simplicity of notation we drop the subscript i and use V = V_i. Let S = {1, …, V } define the set of all tumor voxels. The coordinates of each voxel v are defined by x_v, y_v, z_v. Tumor heterogeneity for subject i is defined as a vector of functions of voxel intensities H_i = [H_i1(I_iv), …, H_in(I_iv)], where n is the total number of functions, where each function corresponds to a radiomic feature. The estimation of tumor heterogeneity can be based on intensity values at voxel level or descriptive statistics at tumor level. We first briefly review and introduce notation for some of the commonly used approaches to estimate H_i. Histogram approaches treat the vector of intensities of a tumor I_i1, …, I_iV as an independent and identically distributed set of observations from a density f_i(x). The standardized moments of f_i(x), where the jth moment is denoted by M_ij, for j = 1, …, m, are estimated and used as approximations of tumor heterogeneity. For example, if a study uses mean, variance, skewness, and kurtosis as in Figure 1 then H_i = [M_i1,M_i2,M_i3,M_i4]. As tumor shape- and volume-based features are commonly used to describe tumor heterogeneity, we define by S_i1, …, S_is, s shape- and volume-based measures. Examples of shape measures include estimates of tumor smoothness and sphericity, while the number of voxels on the tumor surface and the number of voxels within the tumor are examples of volume measures. Finally, let W_i1, …, W_iw denote the collection of features quantifying the texture of the tumor image as defined by Aerts et al. (2014). These measures estimate patterns of spatial distributions of intensities using grey level co-occurrence matrices (Haralick et al., 1973) or wavelet-based approaches (see the Supplementary Materials of Aerts et al. (2014) for more details).

2.3. Neighborhood-Based Tumor Heterogeneity

We propose a novel Neighborhood-Based Tumor Heterogeneity (NBTH) estimation method for measuring tumor heterogeneity. This approach is motivated by the intuition that: 1) a tumor is a collection of k locally homogeneous regions within the image labeled as Λ = {1, …, k}, where k may be known or estimated; 2) the descriptive characteristics of these locally homogeneous regions are related to cancer outcomes such as survival. Note, a “region” within a tumor can be thought of as a collection (or cluster) of voxels. In addition, the term “locally homogeneous region” indicates that the voxels within this region have similar intensities. After estimating locally homogeneous regions within the tumor, i.e. estimating the cluster membership label λ_v ∈ Λ for each voxel v ∈ S, we use summary characteristics of those regions to define our novel measure of tumor heterogeneity. Hence, identifying locally homogeneous clusters of voxels with similar intensity profiles and computing the characteristics of the resulting clusters is used to measure tumor heterogeneity.

In image analysis, it is common to assume that voxels in a close vicinity of each other are likely to have similar intensities. MRFs are undirected graphical models widely used in image analysis (i.e. for segmentation of different tissues in the brain Zhang et al. (2001), Wang (2012), Zhang and Ji (2009) in computer vision problems), as they provide a modeling framework for correlated entities in space such as the intensities of voxels in images. Let $\mathcal{N}=\mathcal{N}(v)$, v ∈ S define a neighborhood system, where $\mathcal{N}(v)$ is a neighborhood of a tumor voxel v such that $v\notin \mathcal{N}(v)$ and $v\in \mathcal{N}\left(v_1\right)\iff v_1\in \mathcal{N}(v)$, i.e. voxel v does not belong in its neighborhood and for any other voxel v₁, v belongs in the neighborhood of v₁ if and only if v₁ belongs in the neighborhood of v. Each voxel v ∈ S is assigned a true and unknown label λ_v ∈ Λ that determines the cluster membership of voxel v. The goal is to estimate the unknown labels λ_v. Let P(λ) denote a probability measure on the set of all possible labels Λ. We assume that the labeling field Λ is an MRF on S with respect to the neighborhood system $\mathcal{N}$, in other words

$$\forall \lambda \in \mathrm{\Lambda },P(\lambda )>0\text{and}P\left({\lambda }_v\mid {\overline{\lambda }}_{S\backslash \left\{v\right\}}\right)=P\left({\lambda }_v\mid {\overline{\lambda }}_{N(v)}\right).$$

where ${\overline{\lambda }}_{S\backslash \left\{v\right\}}$ denotes the set of cluster labels of all voxels in S excluding v and ${\overline{\lambda }}_{N(v)}$ denotes the set of cluster labels of all voxels in the neighborhood of v defined as N(v). In other words, we assume that the probability of assigning the label λ_v to voxel v depends on the labeling of the voxels in its neighborhood $\mathcal{N}$ only. A probabilistic model commonly implemented in image segmentation problems is the Finite Gaussian Mixture Model (GMM) Wang (2012), Zhu et al. (2003). FGMM models assume that the voxel intensities are independent and Gaussian mixture densities are used to model the distribution of voxel intensities. This is a convenient model to implement in our context as the voxel labels can be easily estimated, e.g. by using the expectation-maximization (EM) algorithm (Dempster et al., 1977).

In what follows, we will describe a GMM-based MRF modeling framework, and show how the cluster labels will be determined as a result. We will also introduce a method for finding an appropriate number of mixture components in GMM. The clusters emerging from this MRF-GMM modeling will be subsequently used in the definition of the novel measure of tumor heterogeneity.

2.3.1. Estimation of Mixture Component Weights in MRF

In this section, we propose a novel approach for modeling the voxel labels using the GMM framework while incorporating neighborhood voxel intensity information within the MRF framework. Without loss of generality and for clarity of notation, we drop the index for study subjects denoted herein by i. In GMM, the density function at the observation I_v at voxel v = 1, …, V is modeled using a Gaussian mixture distribution as follows.

$$f\left(I_v\mid \mathrm{\Pi },{\mu }_K,{\sigma }_K\right)=\sum _{j=1}^K{\pi }_{j,v}\frac{1}{{\sigma }_K}\varphi \left(\frac{I_v-{\mu }_{j,K}}{{\sigma }_K}\right)$$ (1)

where ϕ(·) is the probability density function of a normally distributed random variable with mean 0 and variance 1, μ_K = (μ_1,K, …, μ_K,K)^T is the vector of the mixture component means, and σ_K is the common standard deviation. In this section, we assume that the number of mixture components, defined by K, is known. Finally, π_j,v, j = 1, …, K and v = 1, …, V is the probability that voxel v has label j and Π is the V × K matrix of voxel specific probabilities π_j,v, such that ${\sum }_{j=1}^K{\pi }_{j,v}=1$, for all v ∈ 1...,V. Let Z_v denote the latent label of vth voxel, then P(Z_v = j) = π_j,v. Following the approach proposed by Eloyan and Ghosh (2011) and extended to high dimensional settings by Meng and Eloyan (2017) for estimation of Gaussian mixture based approximations of density functions, we assume the means and variance of the mixture elements defined by μ_1,K, …, μ_K,K and σ_K are fixed. Eloyan and Ghosh (2011) propose fixing the values of μ_1,K, …, μ_K,K at equidistant points on the support of the empirical distribution of the observed data points, while Meng and Eloyan (2017) propose using the k-means algorithm for selecting the means of the Gaussian mixture components using the observed data. The mixture standard deviation σ_K is set as a small value relative to the differences between the mixture element means μ_K. This approach results in a computationally efficient estimation of the mixture weights and the resulting density estimate approximates the true underlying density of the observed data in terms of minimizing the Kullback-Leibler Divergence (KLD) between the true and estimated densities. In addition, as shown by Eloyan and Ghosh (2011) and Meng and Eloyan (2017) a hypothesis testing procedure can be implemented to estimate the number of mixture components, K, within this framework. Both of these models assume that the observed voxel intensities are statistically independent. This assumption may not hold in image analysis as intensities of neighboring voxels are often close to each other due to smoothness of the image. To take into account the spatial information using the Markov random field theory, we extend the model and incorporate the spatial smoothness of the image by modeling the prior distribution of the probabilities π_j,v for individual voxels using a Gibbs function as follows.

$$p(\mathrm{\Pi })=\frac{1}{T}{e}^{-U(\mathrm{\Pi })}$$

where $U(\mathrm{\Pi })=\beta {\sum }_{v=1}^V{V}_{\mathcal{N}(v)}(\mathrm{\Pi })$ is the smoothing prior with regularization parameter β, T is the normalizing constant of the density function, $V_{\mathcal{N}(v)}(\mathrm{\Pi })$ is the clique potential function (Li, 2009). Blekas et al. (2005) and Nguyen and Wu (2012) discuss various forms of the smoothing prior U(Π) and the effect of the choice of U(Π) on parameter estimation. In this paper, we implement the smoothing prior proposed by Nguyen and Wu (2012) as it provides a computationally feasible approach for parameter estimation in our setting, where tumors are observed in 3D space and the number of voxels in some tumors observed in the NSCLC dataset analysed in this manuscript is larger than 80,000. The proposed algorithm is based on an implementation of the EM-algorithm to obtain a posteriory MAP estimates of the parameters of interest. In the kth step of the iterative EM-algorithm estimation procedure we implement the following two steps.

E-step:

We compute the expectation of the log-likelihood given the observed values and the values of the coefficients from the previous iteration. We define $f_{j,K}(x)=\varphi \left(\frac{I_v-{\mu }_{j,K}}{{\sigma }_K}\right)$ and I = (I₁, …, I_V )^T. By Bayes rule we obtain.

$$P\left(Z_v=j\mid x,{\mathrm{\Pi }}^{(k)}\right)=\frac{{\pi }_{j,v}^{(k)}{f}_{j,K}\left(I_v\right)}{{\sum }_{j=1}^K{\pi }_{j,v}^{(k)}{f}_{j,K}\left(I_v\right)}=w_{j,v}\left({\mathrm{\Pi }}^{(k)},I\right).$$

The expectation of the log-likelihood of the complete data can be derived as follows.

$$Q\left(\mathrm{\Pi }\mid {\mathrm{\Pi }}^{(k)}\right)=\sum _{v=1}^V\sum _{j=1}^K{w}_{j,v}\left({\mathrm{\Pi }}^{(k)},I\right)\left\{\log \left[f_{j,K}\left(I_v\right)\right]+\log \left({\pi }_{j,v}\right)\right\}+\log [p(\mathrm{\Pi })].$$ (2)

The smoothing prior (Nguyen and Wu, 2012) is defined as follows.

$$U(\mathrm{\Pi })=-\sum _{v=1}^V\sum _{j=1}^K{G}_{j,v}^{(k)}\log {\pi }_{j,v}\text{where}{G}_{j,v}^{(k)}=exp(\frac{\beta }{2|\mathcal{N}(v)|}\sum _{v^{\prime }\in \mathcal{N}(v)}\left(w_{j,v^{\prime }}\left({\mathrm{\Pi }}^{(k)},I\right)+{\pi }_{j,v^{\prime }}^{(k)}\right))$$

where $|\mathcal{N}(v)|$ denotes the number of elements in the neighborhood set $\mathcal{N}(v)$.

M-step:

We maximize the function Q in (2) under constraints ${\sum }_{j=1}^K{\pi }_{j,v}=1$. To obtain probabilities that satisfy these conditions Blekas et al. (2005) propose a projection of the estimated probabilities to the corresponding space. In our implementation we use the Lagrange Multiplier method to incorporate these constraints directly in the M-step of the EM-algorithm. Using the constants λ_v as coefficients for the constraints on probabilities we build the Lagrangian function to be maximized as follows.

$$Q_{\lambda }\left(\mathrm{\Pi },{\mathrm{\Pi }}^{(k)}\right)=Q\left(\mathrm{\Pi }\mid {\mathrm{\Pi }}^{(k)}\right)+\sum _{v=1}^V{\lambda }_v\left(1-\sum _{j=1}^K{\pi }_{j,v}\right).$$

By taking the derivatives with respect to π_j,v for j = 1, …, K, and λ_v we obtain the following system of equations.

$$\begin{gathered} \frac{\partial Q_{\lambda }\left(\mathrm{\Pi },{\mathrm{\Pi }}^{(k)}\right)}{\partial {\pi }_{j,v}}=\frac{w_{j,v}\left({\mathrm{\Pi }}^{(k)},I\right)}{{\pi }_{j,v}}+\frac{G_{j,v}^{(k)}}{{\pi }_{j,v}}-{\lambda }_v=0 \\ \frac{\partial Q_{\lambda }\left(\mathrm{\Pi },{\mathrm{\Pi }}^{(k)}\right)}{\partial {\lambda }_v}=1-\sum _{j=1}^K{\pi }_{j,v}=0 \end{gathered}$$ (3)

We first derive π_j,v from equation (3) and substitute the expression in the next V equations to obtain ${\widehat{\lambda }}_v=1+{\sum }_{j=1}^K{G}_{j,v}^{(k)}$. Then by substituting these values in the expression for ${\widehat{\pi }}_{j,v}^{(k+1)}$ we obtain.

$${\widehat{\pi }}_{j,v}^{(k+1)}=\frac{w_{j,v}\left({\mathrm{\Pi }}^{(k)},I\right)+G_{j,v}^{(k)}}{{\widehat{\lambda }}_v}.$$ (4)

The algorithm stops when the absolute norm difference of the updated probability matrix ${\widehat{\mathrm{\Pi }}}^{(k+1)}$ and that computed in the previous iteration ${\widehat{\mathrm{\Pi }}}^{(k)}$ is smaller than a predefined small value ϵ > 0. Finally, if the algorithm stops at iteration k + 1, cluster labels ${\widehat{\lambda }}_1,\dots ,{\widehat{\lambda }}_V$ are assigned based on the estimated probabilities as follows ${\widehat{\lambda }}_v=j$, if ${\widehat{\pi }}_{j,v}^{(k+1)}$ is highest among ${\widehat{\pi }}_{1,v}^{(k+1)},\cdots ,{\widehat{\pi }}_{K,v}^{(k+1)}$. The above determination of labels results in clusters that account for the spatial distribution of voxel intensities. Our novel measure of tumor heterogeneity is directly based on statistics of those clusters. An important question that still remains is the choice of the number of mixture components defined by K assumed to be fixed in the beginning of this Section. In the subsection that follows, we relax that assumption and propose an iterative procedure for selecting K given a starting value of K₀ based on our goal of minimizing the distance between the true density of intensities f(I) and the estimated density using our proposed approach.

2.3.2. Selection of the Number of Mixture Components

We implement a hypothesis testing procedure for estimation of the number of Gaussian mixture components in the proposed MRF-GMM procedure with the goal to minimize the distance between the true probability density function f(I_v) of the image intensities and the estimated function defined as ${\widehat{f}}_K\left(I_v\mid \widehat{\mathrm{\Pi }},{\mu }_K,{\sigma }_K\right)$. The sample estimate of KLD between true and estimated functions is $\frac{1}{V}{\sum }_{v=1}^V\log \frac{f\left(I_v\right)}{{\widehat{f}}_K\left(I_v\mid \widehat{\mathrm{\Pi }},{\mu }_K,{\sigma }_K\right)}$. The intuition for our proposed procedure is that this sample estimate cannot be directly minimized in K since the true underlying density is unknown. However, we can compute the difference of sample estimates of KLD between true and estimated density functions of two consecutive values of K, i.e. $\frac{1}{V}{\sum }_{v=1}^V\log \frac{f\left(I_v\right)}{{\widehat{f}}_K\left(I_v\mid \widehat{\mathrm{\Pi }},{\mu }_K,{\sigma }_K\right)}-\frac{1}{V}{\sum }_{v=1}^V\log \frac{f\left(I_v\right)}{{\widehat{f}}_{K+1}\left(I_v\mid \widehat{\mathrm{\Pi }},{\mu }_{K+1},{\sigma }_{K+1}\right)}=\frac{1}{V}{\sum }_{v=1}^V\log \frac{{\widehat{f}}_{K+1}\left(I_v\mid \widehat{\mathrm{\Pi }},{\mu }_{K+1},{\sigma }_{K+1}\right)}{{\widehat{f}}_K\left(I_v\mid \widehat{\mathrm{\Pi }},{\mu }_K,{\sigma }_K\right)}$. Hence, to estimate the number of components in the mixture defined by K, we consider an iterative approach where, starting from a predefined value K₀, we compute the estimated function ${\widehat{f}}_{K_0}\left(I_v\mid \widehat{\mathrm{\Pi }},{\mu }_{K_0},{\sigma }_{K_0}\right)$ using the steps of the EM-algorithm described in the previous subsection iteratively until convergence. Further, at each iteration K of the procedure we increase the number of components in the mixture by 1, estimate ${\widehat{f}}_K\left(I_v\mid \widehat{\mathrm{\Pi }},{\mu }_K,{\sigma }_K\right)$, and test whether the expected value of the difference of KLD of estimated function at iteration K and true underlying probability function and KLD of estimated function at iteration K + 1 and true probability function is equal to zero as follows.

$$H_0:E\left[\log \frac{{\widehat{f}}_{K+1}\left(I\mid \widehat{\mathrm{\Pi }},{\mu }_{K+1},{\sigma }_{K+1}\right)}{{\widehat{f}}_K\left(I\mid \widehat{\mathrm{\Pi }},{\mu }_K,{\sigma }_K\right)}\right]=0,$$ (5)

for each K ≥ K₀, where K₀ is a starting value of the number of components. As K increases by 1, we define the empirical estimate of the difference between KLD of ${\widehat{f}}_K\left(I_v\mid \widehat{\mathrm{\Pi }},{\mu }_K,{\sigma }_K\right)$ from the true function f and that of ${\widehat{f}}_{K+1}\left(I_v\mid \widehat{\mathrm{\Pi }},{\mu }_{K+1},{\sigma }_{K+1}\right)$ as follows for voxel v.

$${\widehat{\mathrm{\Delta }}}_{K,v}=\log \frac{{\widehat{f}}_{K+1}\left(I_v\mid \widehat{\mathrm{\Pi }},{\mu }_{K+1},{\sigma }_{K+1}\right)}{{\widehat{f}}_K\left(I_v\mid \widehat{\mathrm{\Pi }},{\mu }_K,{\sigma }_K\right)}$$ (6)

for v = 1, …, V. Under regularity conditions (presented by Eloyan and Ghosh (2011)) we can use the following rule for testing the hypothesis in (5) and choosing K.

$$Z_{K,v}=\sqrt{V}\frac{{\overline{\mathrm{\Delta }}}_{K,v}}{S_{\mathrm{\Delta }K,v}}$$ (7)

where ${\overline{\mathrm{\Delta }}}_{K,v}$ is the sample mean and S_ΔK,v is the sample variance of ${\widehat{\mathrm{\Delta }}}_{K,v}$. We reject the null hypothesis in (5) if z_K,v > z_α, where z_α denotes the α% upper percentile of the standard normal density for a pre-specified value of α. The procedure stops when we fail to reject the the null hypothesis or if the number of cluster labels is greater than a pre-specified maximum value of number of mixture components defined as K_m.

2.3.3. Summary Measures

After having outlined the process of voxel clustering that accounts for the spatial distribution of intensities, we are in a position to define our novel measure of tumor heterogeneity using various summary statistics emerging from those clusters. Our proposed estimator of tumor heterogeneity consists of three sets of summary measures derived from the clustering results. One set of measures relates to the mean and variability of cluster sizes, the second set relates to the summarized intensities, while the third set of features relates to cluster shapes. For example, the variability of estimated cluster sizes for a tumor with highly variable-sized clusters is expected to be large, while the variability of cluster sizes of a tumor with similarly sized intensity clusters is expected to be small. In addition to more commonly used summary measures to quantify tumor heterogeneity described below, we use the Rao’s diversity index to measure the diversity of intensities in each cluster. Rao’s Quadratic Entropy (Rao, 1982) is a statistical measure defined as the expected difference between two objects randomly selected from a given population. The difference between the objects can be quantified using any nonnegative function, including distance functions. The index will be used herein to quantify the diversity of voxel intensities within clusters of a tumor.

Let the vector [K_i1, …, K_iK]^T define the cluster sizes, the vectors ${\left[I_{i1}^{mean},\dots ,I_{iK}^{mean}\right]}^T$ and ${\left[I_{i1}^{sd},\dots ,I_{iK}^{sd}\right]}^T$ define the means and standard deviations of intensities within each cluster, the vector ${\left[I_{i1}^{Rao},\dots ,I_{iK}^{Rao}\right]}^T$ define the Rao’s index of the intensities in each cluster, and ${\left[I_{i1}^{ent},\dots ,I_{ik}^{ent}\right]}^T$ define the within cluster entropy of intensities, i.e. $K_{i1}={\sum }_{v=1}^V\text{I}\left[{\widehat{\lambda }}_{iv}=1\right],\dots ,K_{iK}={\sum }_{v=1}^V\text{I}\left[{\widehat{\lambda }}_{iv}=K\right]$, $I_{i1}^{mean}=\frac{1}{K_{i1}}{\sum }_{v=1}^V{I}_{i,v}\cdot \text{I}\left[{\widehat{\lambda }}_{iv}=1\right],\dots ,I_{iK}^{mean}=\frac{1}{K_{iK}}{\sum }_{v=1}^V{I}_{iv}\cdot \text{I}\left[{\widehat{\lambda }}_{iv}=K\right]$, $I_{i1}^{sd}=\sqrt{\frac{1}{K_{i1}-1}{\sum }_{v=1}^V{\left(I_{i,v}-I_{i1}^{mean}\right)}^2\cdot \text{I}\left[{\widehat{\lambda }}_{iv}=1\right]},\dots ,I_{iK}^{sd}=\sqrt{\frac{1}{K_{iK}-1}{\sum }_{v=1}^V{\left(I_{i,v}-I_{i1}^{mean}\right)}^2\cdot \text{I}\left[{\widehat{\lambda }}_{iv}=K\right]}$, $I_{i1}^{Rao}={\sum }_{v=1}^V{\sum }_{v^{\prime }=1}^V{P}_1\left(I_{i,v}\right)D_{i,v,v^{\prime }}{P}_1\left(I_{i,v^{\prime }}\right)\text{I}[{\widehat{\lambda }}_{iv}=\text{1}]\text{I}\left[{\widehat{\lambda }}_{i{v}^{\prime }}\text{=1}\right],\dots ,I_{iK}^{Rao}\text{=}{\sum }_{v=1}^V{\sum }_{v^{\prime }=1}^V{P}_K\left(I_{i,v}\right)D_{i,v,v^{\prime }}{\text{P}}_{\text{K}}\left(I_{I,v^{\prime }}\right)\text{I}\left[{\widehat{\lambda }}_{iv}\text{=K}\right]\text{I}\left[{\widehat{\lambda }}_{i{v}^{\prime }}\text{=}K\right]$ and $I_{i1}^{ent}={\sum }_{v=1}^V{P}_1\left(I_{i,v}\right)\log P_1\left(I_{i,v}\right)\cdot \text{I}\left[{\widehat{\lambda }}_{iv}=1\right],\dots ,I_{iK}^{ent}={\sum }_{v=1}^V{P}_K\left(I_{iv}\right)\log P_K\left(I_{i,v}\right)\cdot \text{I}[{\widehat{\lambda }}_{iv}=K]$, where P_j(·) is the empirical distribution of the observed intensities in cluster j and $D_{i,v,v^{\prime }}$ denotes the Euclidean distance between the intensities I_i,v and $D_{i,v,v^{\prime }}$. For a given total number of clusters K, to obtain the first set of summary measures related to cluster size we compute the following measures.

$$C_i^{mean}=mean\left(K_{i1},\dots ,K_{ik}\right)\text{and}{C}_i^{sd}=sd\left(K_{i1},\dots ,K_{ik}\right),$$

where $C_i^{mean}$ measures the average cluster size and $C_i^{sd}$ measures the variation among the cluster sizes. We define the second set of measures related to average intensities of the clusters as follows.

$$I_i^{mean1}=mean\left(I_{i1}^{mean},\dots ,I_{ik}^{mean}\right)\text{and}{I}_i^{mean2}=sd\left(I_{i1}^{mean},\dots ,I_{ik}^{mean}\right),$$

$$I_i^{sd1}=mean\left(I_{i1}^{sd},\dots ,I_{ik}^{sd}\right)\text{and}{I}_i^{sd2}=sd\left(I_{i1}^{sd},\dots ,I_{ik}^{sd}\right),$$

$$I_i^{Rao1}=mean\left(I_{i1}^{Rao},\dots ,I_{ik}^{Rao}\right)\text{and}{I}_i^{Rao\text{2}}=sd\left(I_{i1}^{Rao},\dots ,I_{ik}^{Rao}\right),$$

$$I_i^{ent1}=mean\left(I_{i1}^{ent},\dots ,I_{ik}^{ent}\right)\text{and}{I}_i^{ent2}=sd\left(I_{i1}^{ent},\dots ,I_{ik}^{ent}\right),$$

Finally, the third set of summary measures that will complete our definition of tumor heterogeneity is defined as S_i1, …, S_i8. These correspond to features commonly used to describe tumor shape and volume computed for each cluster and averaged across the tumor. The formulae for computing the shape features are described in (Aerts et al., 2014) and repeated here for completeness. The tumor volume is defined as S₁, and computed by counting the number of tumor voxels and multiplying by the volume of each voxel. The tumor surface area S₂ is computed by triangulation. The rest of the shape and size features are functions of S₁ and S₂. Surface to volume ratio $S_3=\frac{S_2}{S_1}$. Sphericity of the tumor $S_4=\frac{{\pi }^{1/3}{\left(6S_1\right)}^{2/3}}{S_2}$. Spherical disproportion $S_5=\frac{S_2}{4\pi R^2}$, where R is the radius of a tumor sized sphere. Maximum 3D diameter of the tumor is defined as S₆. Compactness $S_7=36\pi \frac{S_1^2}{S_2^3}$ and $S_8=\frac{S_1}{\sqrt{\pi }{S}_2^{2/3}}$.

As a result of our proposed procedure, we obtain the following vector as an estimator of tumor heterogeneity, for subject i = 1, 2, …, N.

$${\widehat{H}}_{i,NBTH}={\left(C_i^{mean},C_i^{sd},I_i^{mean1},I_i^{mean2},I_i^{sd1},I_i^{sd2},I_i^{Rao1},I_i^{Rao2},I_i^{ent1},I_i^{ent2},S_{i1}\dots ,S_{i8}\right)}^T\in R^{18\times 1}$$

When implementing the proposed algorithm, we choose the initial set of means of for the EM-algorithm described in Section 2.3.1 using the k-means algorithm Friedman et al. (2001). We select the maximum number of means defined by K_m by choosing the value of K corresponding to 80% of variance explained in the k-means procedure. Starting from a given initial value of K₀ = 2, we use our proposed selection procedure described in Section 2.3.2 to find the number of mixture components. Our proposed procedure for computing ${\widehat{H}}_{i,NBTH}$ is computationally efficient in relatively low dimensions and computationally feasible in high-dimensional settings. It took about 5 minutes to compute ${\widehat{H}}_{i,NBTH}$ for a subject with a large tumor (over 80,000 tumor voxels) in our dataset using the R software on a 1.7GHz Dual-Core Intel Core i7 processor. Next, we show simulation studies to illustrate the superior performance of the proposed method as compared with Gaussian Mixture Models and k-means clustering.

3. Simulations

We evaluate the performance of our proposed algorithm in two simulation studies: 1) we evaluate the accuracy of the proposed MRF-GMM algorithm in terms of estimation of voxel labels in an image, i.e. image segmentation, 2) we evaluate the performance of our proposed NBTH algorithm for the estimation of tumor heterogeneity in terms of ranking two images by their heterogeneity. In the first simulation study we compare the performance of our proposed MRF-GMM procedure in terms of its accuracy of labeling voxels to two existing methods - k-means and GMM (Friedman et al., 2001). K-means clustering (implemented using the kmeans function in the R software), is a distance based approach which, among numerous other applications, is used in image segmentation Dhanachandra et al. (2015) for identifying voxel labels to avoid the assumption of Gaussianity of image voxel intensities in the GMM model. Let c = (c₁, …, c_K) denote the vector of cluster centers for a given K indicating the number of clusters for the subject’s image. The k-means procedure is based on the intuition that a cluster should contain voxels with similar intensity profiles. The loss function $L(c)=\frac{1}{V}{\sum }_{v=1}^V{\min }_{1\le j\le K}{\Vert I_v-c_j\Vert }^2$ can be considered for minimization, and based on L(c) the algorithm identifies the set of cluster centers ${\widehat{c}}_1,\dots ,{\widehat{c}}_K$. The voxel labels are then assigned based on the estimated centers. We select the number of clusters in the k-means algorithm by choosing the value of K corresponding to 80% of variance explained. The GMM approach (implemented using the ClusterR package in the R software) is based on the model given in (1), while the voxel intensities are assumed to be statistically independent. We select the optimal number of clusters when implementing GMM using the Akaike information criterion (AIC), specifically, the optimal number of clusters, K, is the value of number of clusters such that an increase in K by 1 results in a change in AIC of less than 1%.

To compare the three methods in terms of clustering accuracy, we use two images used to evaluate image segmentation algorithms by Blekas et al. (2005) and Nguyen and Wu (2012) and reproduced in Figure 4. The goal of the analysis is segmentation of the three clusters in true image 1 and the four clusters in true image 2, where a cluster consists of intensities of the same color in the corresponding image. In the context of tumor imaging, the cluster would correspond to a specific tissue consisting of voxels with similar intensities. For each image, we run 100 simulations where in each simulation we add random noise to the images. To investigate the effect of the magnitude of noise on the performance of the three competitor methods we include two settings of noise for each image as follows: we add normally distributed random noise with standard deviation of σ = 1 in the first setting and standard deviation of σ = 2 in the second setting to true image 1 and normally distributed random noise with standard deviation of σ = 2 in the first setting and standard deviation of σ = 3 in the second setting to true image 2. After adding the random noise, in order to obtain relatively smooth images resembling real images, we apply a blur to the resulting noisy images where the blurring kernel is the isotropic Gaussian kernel with standard deviation of 1.

Figure 4:

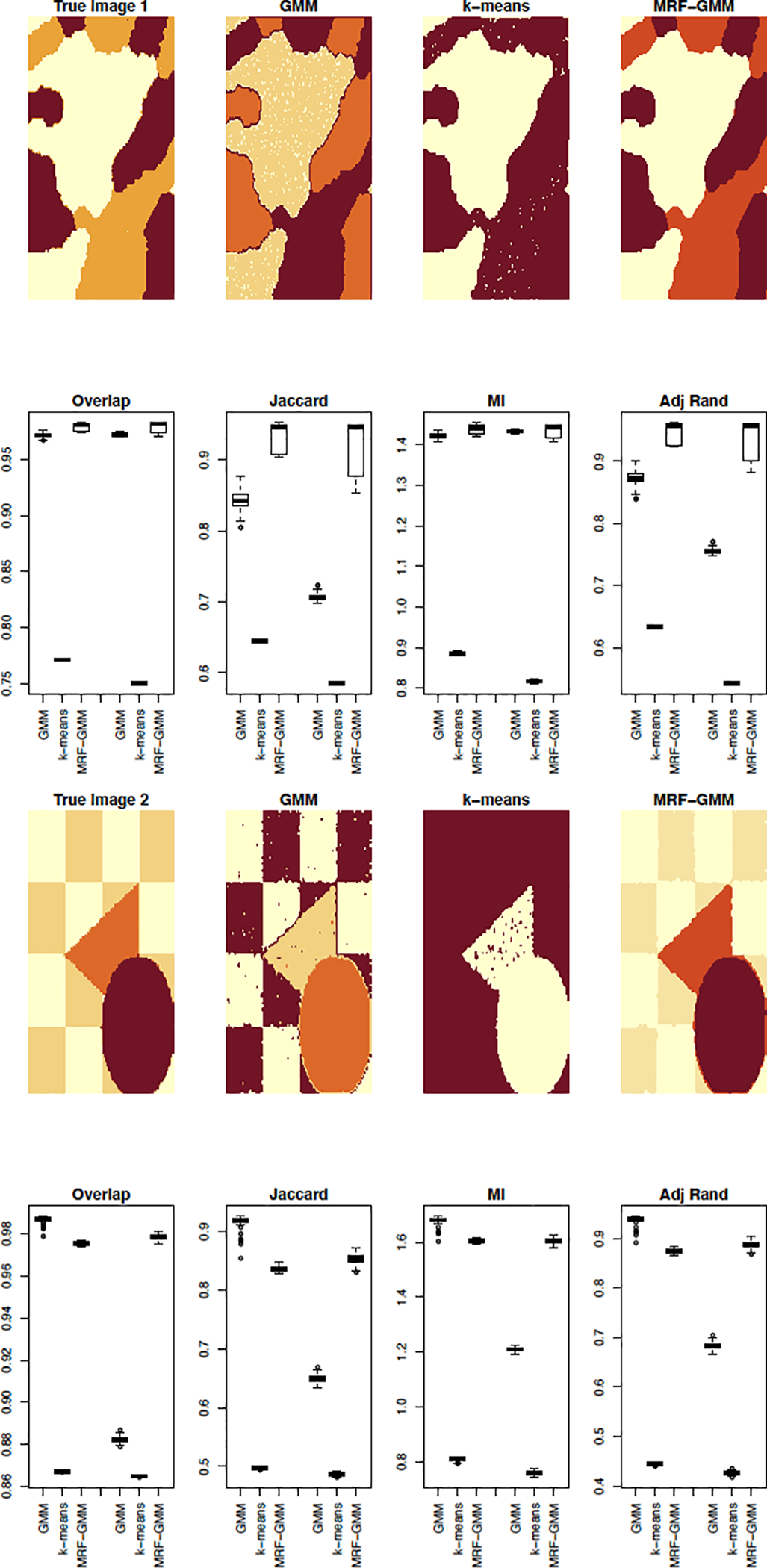
Results of clustering the voxel intensities using k-means, GMM, and our proposed MRF-GMM. The true images as well as the estimated cluster segmentations by each of the three algorithms are shown on rows 1 and 3. Each of these rows are followed by a row of boxplots showing the results of the four cluster comparison measures (overlap, Jaccard index, mutual information (MI) and adjusted Rand index) for 100 runs of the simulations. Within each boxplot figure, the first three boxplots correspond to the first added noise setting (σ = 1 and σ = 2 for true images 1 and 2 correspondingly) while the second set of three boxplots corresponds to the second added noise setting (σ = 2 and σ = 3 for true images 1 and 2 correspondingly).

For each simulation study, after estimating the cluster labels with each of the three methods, GMM, k-means, and our proposed MRF-GMM approach, we compute four measures to evaluate the accuracy of the estimated image, compared to the true image: 1) cluster overlap corresponding to the proportion of overlapping cluster voxels between the true and estimated images, 2) Jaccard Index that measures similarity between two images by computing the intersection of the voxel sets and dividing by their union, 3) Mutual Information (MI) between the clustering partitions, i.e. let ${\widehat{\mathrm{\Lambda }}}_M$ denote the set of cluster labels obtained using our proposed procedure and Λ_T denote that of the true image then the MI between the two sets is computed as ${\sum }_{j=1}^K{\sum }_{l=1}^{K}p(j,l)\log \frac{p(j,l)}{p_M(j)p_T(l)}$, where p(j, l) is the probability that the label of a point is in both the cluster labeled by j in ${\widehat{\mathrm{\Lambda }}}_M$ and the cluster labeled by l in Λ_T, p_M(j) is the probability that the label of a point belongs to the cluster indexed by j in ${\widehat{\mathrm{\Lambda }}}_M$, p_T (l) is the probably that the label of a point belongs to the cluster indexed by l in Λ_T, and 4) Adjusted Rand index (Wagner and Wagner, 2007). Higher values indicate better performance of the algorithm in terms of labeling accuracy. The mean and standard deviation of each of the clustering comparison measures are presented in Table 1 while the boxplots are shown in Figure 4. As shown by all approaches, our proposed MRF-GMM method outperforms the competitors significantly in clustering performance except for image 2 with low level added noise. Nguyen and Wu (2012) recommends setting the smoothing regularization parameter β to 12. We selected values of β at 4, 6, and 12 in our simulations and did not find a significant difference in the results in most cases.

Table 1:

Summary of cluster comparison measures given as mean (SD*100) using several measures of cluster comparisons OL - overlap, J - Jaccard Index, MI - Mutual Information, ARI - Adjusted Rand Index.

	σ = 1, image 1			σ = 2, image 1
	GMM	k-means	MRF-GMM	GMM	k-means	MRF-GMM
OL	0.97	0.77	0.98	0.97	0.75	0.98
	(0.2)	(0.04)	(0.38)	(0.09)	(0.03)	(0.43)
J	0.84	0.64	0.93	0.71	0.59	0.92
	(1.39)	(0.11)	(2.08)	(0.54)	(0.06)	(3.6)
MI	1.42	0.88	1.44	1.43	0.82	1.44
	(0.66)	(0.31)	(1.19)	(0.29)	(0.29)	(1.38)
ARI	0.87	0.63	0.95	0.76	0.54	0.94
	(1.18)	(0.13)	(1.68)	(0.49)	(0.07)	(2.94)
	σ = 2, image 2			σ = 3, image 2
	GMM	k-means	MRF-GMM	GMM	k-means	MRF-GMM
OL	0.99	0.87	0.98	0.88	0.86	0.98
	(0.13)	(0.02)	(0.07)	(0.14)	(0.03)	(0.13)
J	0.92	0.50	0.84	0.65	0.21	0.80
	(1.03)	(0.13)	(0.43)	(0.65)	(0.21)	(0.8)
MI	1.68	0.81	1.60	1.21	0.76	1.61
	(1.36)	(0.53)	(0.6)	(0.74)	(0.74)	(1.0)
ARI	0.94	0.45	0.87	0.68	0.43	0.89
	(0.08)	(0.21)	(0.36)	(0.73)	(0.36)	(0.66)

Our second simulation study evaluates the performance of our proposed NBTH method in terms of ranking images according to tumor heterogeneity. The studies based on histogram measures commonly used in the literature postulate that a lower value of uniformity of the intensities, a higher entropy, higher standard deviation of intensities, higher kurtosis values, and positive skewness all represent increased heterogeneity and are related to poorer prognosis (Davnall et al., 2012). When comparing the heterogeneity of two images using our proposed NBTH method we rank the two images by using each of the 18 ${\widehat{H}}_{i,NBTH}$ features. The final ranking of the images is assigned based on the ranking of the majority of NBTH features. Figure 5 presents the images we used for comparisons for the following two cases. We use very simplistic images in our simulations to ensure that the ranking of images by their heterogeneity is clearly visible.

Figure 5:

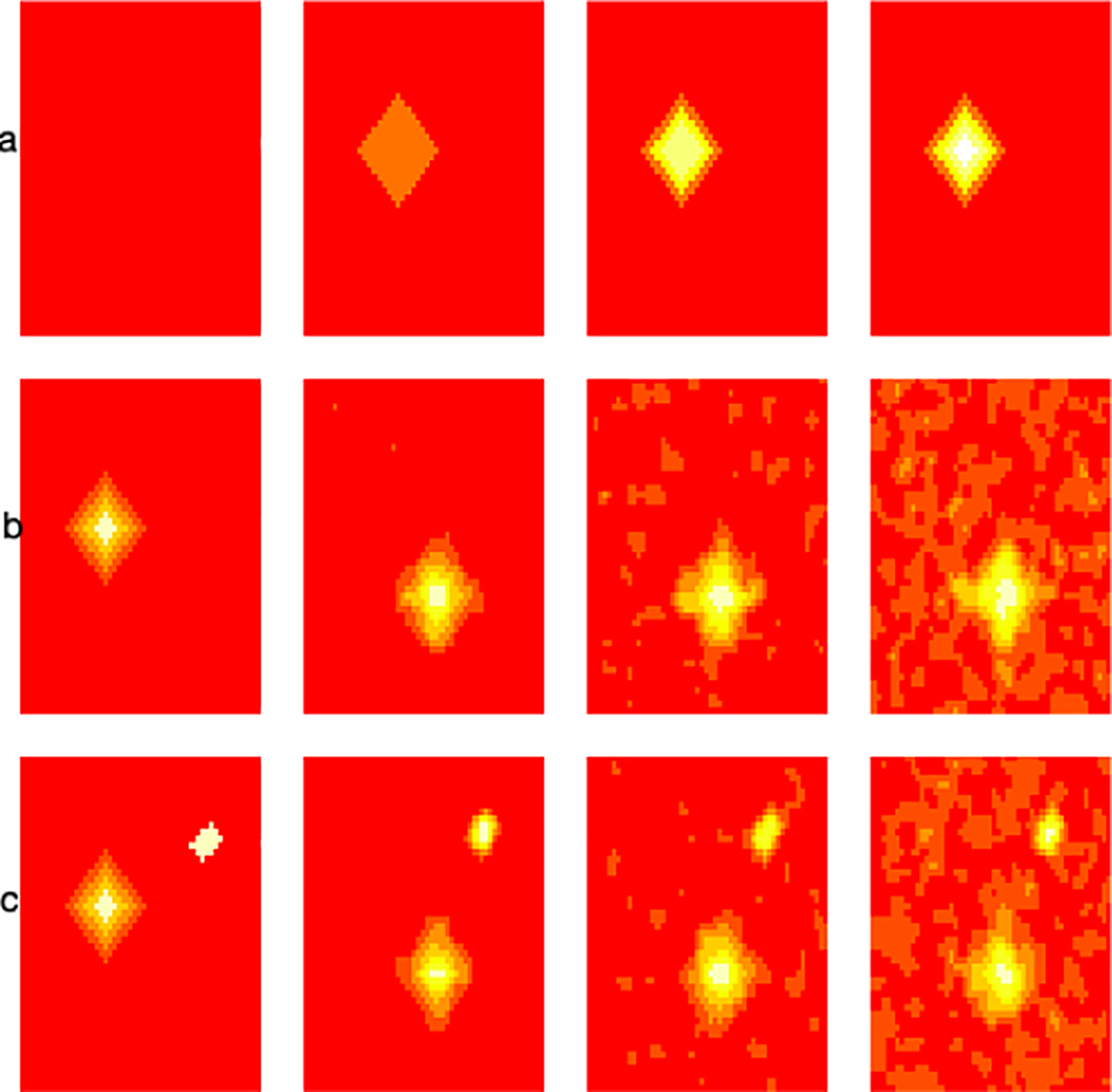
True images used in the simulations to evaluate ranking of image heterogeneity.

Case 1: we generate four 50 × 50 matrices shown in Figure 5 row (a) as follows: A₁ is a matrix of zeros (column 1), A₂ is a matrix of zeros, with a diamond of 1s containing 145 pixels (column 2), A₃ is a matrix of 0s with a diamond of 1s and additional smaller overlaid layers of 2s and 3s, A₄ is a matrix of 0s with a diamond of 1s and additional layers up to 6. In summary, the images are generated such that they are ordered in terms of their heterogeneity, i.e. A₄ is more heterogeneous than the rest, A₃ is more heterogeneous than A₂ and A₁, finally, A₂ is more heterogeneous than A₁. We run 500 simulations. In each simulation, we add random Gaussian noise with mean 0 and variance 1 to the images. We compare our proposed method to histogram measures including skewness, kurtosis, and entropy in terms of ranking these images in their heterogeneity. We found that all four methods (skewness, kurtosis, entrophy, and NBTH) correctly ranked images when comparing A₄ to A₁ and when comparing A₃ to A₁ as having higher heterogeneity than those based on A₁ in 100% of simulations. When comparing A₂ based images to those based on A₁ skewness and kurtosis ranked them correctly in terms of heterogeneity in 99% of simulations, entropy in 89%, and our proposed NBTH method in 95% simulations. In summary, our proposed method performs as well as the competitor methods in terms of ordering images in terms of heterogeneity in this simulation study.

Case 2: we use 2 images to compare the effect of higher noise on the estimation of tumor heterogeneity shown in rows (b) and (c) in Figure 5. We again run 500 simulations. The true images are shown in column 1, the images are identical except for the additional white colored collection of voxels in the image in row (c) of column 1 referred to as image 2 which implies that the image in row (c) is more heterogeneous than that in row (b) referred to as image 1. When the added random Gaussian noise has standard deviation of 1 (column 2) skewness correctly classifies image 2 as having higher heterogeneity than image 1 in 3.6% of simulations, kurtosis in 8.2%, entropy in 17% and our proposed method in 77.4%. Further, when the added noise has standard deviation 1.5 (column 3) skewness correctly ranks the images by their heterogeneity in 22% of simulations, kurtosis in 48.4%, entropy in 34.8%, and our proposed method in 89% of simulations. Finally, when the added noise has standard deviation 2 (column 4) then skewness classifies the second image as more heterogeneous than image 1 in 45.2% of the simulations, kurtosis in 68.9%, entropy in 44.2%, and our proposed NBTH method in 78% of the simulations. This simulation study shows that our proposed method performs better than the competitor methods in terms of ranking images by their heterogeneity. The R code for reproducing all results in our simulation studies is available at https://github.com/anieloyan1/NBTH.

4. Prediction of Cancer Survival

In this section we present results on the comparison of tools for prediction of cancer survival using CT scans from 422 patients with NSCLC publicly available on TCIA. We compare the performance of the proposed tumor heterogeneity estimation approach to five existing methods: two commonly used histogram based measures (skewness and kurtosis); a method for estimating texture features using grey level co-occurrence and grey level run-length features (Haralick et al., 1973); and the method described by Aerts et al. (2014) that combines many existing estimation approaches. Let T_i denote the random variable corresponding to time to the event of death for the ith participant, i.e. the survival time, and C_i denote the time to censoring, i.e. participant leaving the study, or end of study, for i = 1, …, N. Then the death status δ_i = I(T_i ≤ C_i). For participant i, we observe the outcome pair ${\tilde{T}}_i=min\left(T_i,C_i\right)$ and δ_i. In the dataset, the average observed survival time ${\tilde{T}}_i$ (including the participants where death was not observed) was 538.6 days (with sd = 417.1, and range = [10, 2165]), the censoring rate was 42%. We are interested in modeling the hazard function h_i(t) defined as the instantaneous risk of occurrence of death, based on, among other features, the novel measure of tumor heterogeneity.

$$h_i(t)=\underset{\mathrm{\Delta }t\to 0}{\lim }\left(\frac{P\left(t\le T_i\le t+\mathrm{\Delta }t\mid T_i\ge t\right)}{\mathrm{\Delta }t}\right)$$ (8)

To compare our tumor heterogeneity estimation approach to the method proposed by Aerts et al. (2014), we generated 431 radiomic features per patient following Aerts et al. (2014). We describe these procedures here briefly and refer the reader to Aerts et al. (2014) for more details. These radiomic features comprise 14 histogram features related to the first order statistics defined as M_i1, …, M_im, for m = 14 in Section 2.3. In addition, 8 features are computed related to tumor shape and size defined as S_i1, …, S_is, for s = 8. Thirty three features are related to tumor texture computed to quantify intratumor texture differences that can be observed on the CT image and defined as T_i1, …, T_it, for t = 33. The remaining 376 are based on wavelet decompositions of the CT image. We applied the Daubechies orthonormal compactly supported wavelet of length 8 least asymmetric family on the original CT images, resulting in 8 decompositions (Daubechies, 1988). For each of the decompositions, the histogram and texture features were computed (47 features in total for each decomposition), leading to a total of 376 wavelet features denoted as W_i1, …, W_iw, where w = 376. When computing radiomic features that require discretization of the voxel intensities within the CT image, we used 64 intensity levels. The corresponding vector of tumor heterogeneity features computed following the procedures proposed by Aerts et al. (2014) is denoted as ${\widehat{H}}_{i,a}=\left(M_{i1},\dots ,M_{im},S_{i1},\dots ,S_{is},T_{i1},\dots ,T_{it},W_{i1},\dots ,W_{iw}\right)$, where ${\widehat{H}}_{i,a}\in R^{431}$.

Let $X_i^1,\dots ,X_i^6$ define the clinical variables age, sex, overall cancer stage, clinical N stage, clinical T stage, and histology for patient i. We consider three sets of variables for prediction of cancer survival as follows: Set 1 - clinical variables $X_i^1,\dots ,X_i^6$; Set 2 - clinical variables $X_i^1,\dots ,X_i^6$, and the subject specific intensity histogram skewness defined by M_i3; Set 3 - clinical variables $X_i^1,\dots ,X_i^6$, and the subject specific intensity histogram kurtosis defined by M_i4; Set 4 - clinical variables $X_i^1,\dots ,X_i^6$, and the sequence of grey level feature vector that we define by ${\widehat{H}}_{i,gl}$; Set 5 - clinical variables $X_i^1,\dots ,X_i^6$, and the competitor set of radiomic features ${\widehat{H}}_{i,a}$ used to estimate tumor heterogeneity in an earlier study Aerts et al. (2014); Set 6 - clinical variables $X_i^1,\dots ,X_i^6$ and our proposed NBTH estimate of tumor heterogeneity ${\widehat{H}}_{i,NBTH}$. As our first model for association of tumor heterogeneity and hazard function we first consider the Cox Proportional Hazards model.

$$\text{Set}1:h_i(t)=h_0(t)e^{X_i^T\beta }$$

$$\mathrm{Set}2:h_i(t)=h_0(t)e^{X_i^T\beta +M_{i3}{\beta }_2}$$

$$\mathrm{Set}3:h_i(t)=h_0(t)e^{X_i^T\beta +M_{i4}{\beta }_3}$$

$$\mathrm{Set}4:h_i(t)=h_0(t)e^{X_i^T\beta +{\widehat{H}}_{i,gl}^T{\beta }_4}$$

$$\mathrm{Set}5:h_i(t)=h_0(t)e^{X_i^T\beta +{\widehat{H}}_{i,a}^T{\beta }_5}$$

$$\mathrm{Set}6:h_i(t)=h_0(t)e^{X_i^T\beta +{\widehat{H}}_{i,NBTH}^T{\beta }_6}$$

where h_i(t) is the hazard function for patient i defined in (8) and h₀(t) is the baseline hazard. We tested whether the proportional hazard assumption of a Cox Proportional Hazards model was justified in all models using a weighted residual-based method proposed by (Grambsch and Therneau, 1994) and found that the assumption was justified based on the global test in all models.

A direct application of the Cox Proportional Hazards model can be problematic when using variables in Set 5 (i.e. the model using the features estimated according to the procedure by Aerts et al. (2014) along with clinical variables) as the number of radiomic features is large compared with the number of participants. Additionally, according to the analysis of the data performed in this study we found that some of the features are highly correlated. Hence, to reduce the dimension of the radiomic features we apply principal component analysis (PCA). We compute the PCA decomposition of the radiomic feature matrix and define the first p principal components describing 95% of variability in the data by V_i1, …, V_ip. These principal components are used in addition to the clinical variables as inputs to the Cox Proportional Hazards model whenever we refer to using the features in Set 5 described above. This approach is commonly used in high dimensional data analysis and is referred to as Principal Components Regression Jolliffe (1982). This step is not necessary for the other competitor models as well as our proposed modeling approach (using features from Set 6), as the number of features is much smaller.

In addition to the Cox Proportional Hazards model, we consider several other approaches for modeling the association of tumor heterogeneity and the hazard function. In particular, we implement regularized regression approaches to relate the clinical and radiomic feature data with survival (using features from Sets 1–6) using the glmnet package in the R software. Ridge, Lasso, and Elastic-Net penalization within the Generalized linear models (GLM, Friedman et al. (2010)) are used for predictor Sets 1–6. Tuning parameter selection is performed using 10-fold cross-validation. The negative logarithm of the partial likelihood is penalized using the following penalization function.

$$\lambda \left[(1-\alpha )\Vert \beta {\Vert }_2^2/2+\alpha \Vert \beta {\Vert }_1\right]$$

where ‖ · ‖₂ describes the L₂ norm function and ‖ · ‖₁ is the L₁ norm. When α = 0 we obtain the ridge regression penalization, α = 1 gives the Lasso penalty, while other values of α result in Elastic-Net. All predictive models are trained on a subset of the data and predictions are computed on a hold out (test) set.

In addition to the Cox Proportional Hazards and regularized regression modeling, we implement machine learning algorithms for prediction of survival using each set of variables. Random survival forest (RSF), proposed by Ishwaran et al. (2008), was used to estimate cancer survival for each set of variables. RSF is an ensemble tree method that extends Breiman (2001) random forests for modeling right-censored survival data. In the first stage of the algorithm, a randomly drawn bootstrap sample of the training data is used to grow a binary tree. At the second stage, a randomly selected subset of the model variables is chosen as candidate variables for splitting each node of the tree. The tree is grown using a combination of averaging over trees and randomization. The next method we implement is the support vector machines (SVM) for survival data (Van Belle et al. (2007), Van Belle et al. (2011)). In this approach, independently right censored and observed failure time data are modeled using a health index which is a proxy between the covariates observed for the subject and their observed failure times. The risk is defined using the concordance index measuring the discriminative power of the health index. Third, we use a k-nearest neighbors survival probability prediction method (BNN) (Lowsky et al., 2013), where the survival curve prediction is constructed using a weighted Kaplan-Meier estimator based on the K most similar training observations. Finally, we apply boosting for high-dimensional time-to-event data for prediction of cancer survival (Binder et al. (2009), Binder et al. (2013)). In this approach, a boosting approach is implemented for fitting a proportional subdistribution hazards model, i.e. the instantaneous risk of having an event in the absence of competing events. This model can incorporate a large number of radiomic features (coded as optional variables), while also taking clinical covariates (coded as mandatory variables) into account.

Figure 6 presents time-dependent ROC (Heagerty et al., 2000) curves describing the results of predictive accuracy of survival based on the pairings of predictors used in the study as defined in this section. Each plot in Figure 6 corresponds to the predictive algorithm: a. Cox Proportional Hazards model with PCA, b. GLM with Lasso penalty, c. GLM with Ridge penalty, d. GLM with Elastic-Net penalty, e. Random Survival Forest, f. survival SVM, g. Boosting, h. BNN. The time-dependent ROC curves were computed for 3-year survival. The colors of the ROC curves correspond to the sets of variables used in each prediction method. Table 2 presents the area under the curve (AUC) values corresponding to each 3-year survival ROC curve in Figure 6. The implementation of survival SVM when using clinical variables and grey level features did not converge, hence the “NA” entry in Table 2. In this example, the method with the best performance in terms of maximizing the AUC is our proposed NBTH estimation procedure used in a GLM model with the Elastic-Net penalty.

Figure 6:

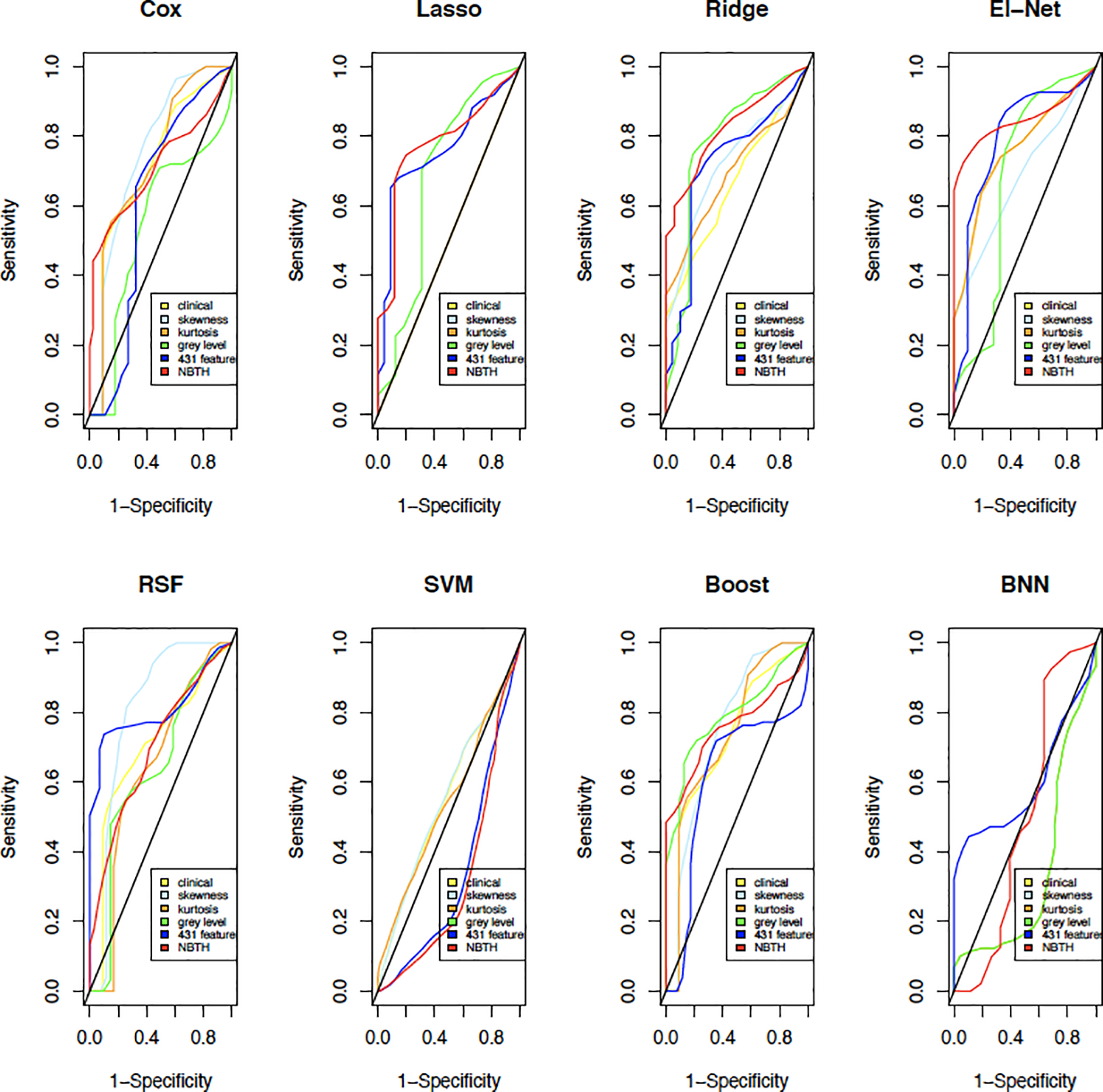
ROC curves comparing the six predictive methods using the proposed collections of tumor heterogeneity measures for 3-year survival.

Table 2:

Area under the curve for each variable set and the corresponding estimation method for 3-year survival.

	Cox	Lasso	Ridge	El-Net	RSF	SVM	Boost	BNN
Set 1	0.72	0.50	0.66	0.76	0.70	0.55	0.72	0.34
Set 2	0.76	0.50	0.72	0.68	0.80	0.55	0.75	0.34
Set 3	0.73	0.50	0.69	0.76	0.64	0.54	0.73	0.34
Set 4	0.54	0.68	0.78	0.67	0.63	NA	0.79	0.34
Set 5	0.61	0.76	0.72	0.79	0.81	0.34	0.61	0.60
Set 6	0.71	0.78	0.82	0.85	0.70	0.32	0.76	0.50

Finally, note, that the above assessment of predictive accuracy was based on a holdout method, where model accuracy was assessed for only a single testing set. Thus, to obtain a well-rounded understanding we in addition perform a more rigorous assessment of predictive accuracy using 10-fold cross-validation. Specifically, we divide the dataset into 10 subsets (folds). In each of the iterations of the cross-validation analysis we train the algorithm on 9 of the folds and apply the resulting predictive algorithm to obtain estimates of survival for the 10th fold, where each of the folds is used once as a test set. For each iteration we compute the AUCs based on time-dependent ROC curves. The average AUCs, along with their standard deviations, are presented in Table 3 and the boxplots comparing each model using cross-validation AUCs are shown in Figure 7. The results in Table 3 and Figure 7 indicate, that the incorporation of proposed NBTH features along with clinical information in a GLM model with the ridge penalty results in better predictive accuracy on average, as measured by AUC in this cross-validation analysis. In most cases, using clinical information alone results in a poor predictive performance compared with approaches incorporating texture features such as those in Set 4, 5, and 6. Similarly, when using skewness or kurtosis along with clinical variables the models perform poorly compared to the methods including texture based features. The models incorporating texture features estimated by grey level co-occurrence and grey level run-length variables in addition to clinical information perform better than using the clinical information alone, or clinical variables combined with skewness or kurtosis.

Table 3:

Average (standard deviation) AUCs from 10-fold cross-validation for each variable set and the corresponding estimation method for 3-year survival.

	Cox	Lasso	Ridge	El-Net	RSF	SVM	Boost	BNN
Set 1	0.57	0.49	0.57	0.48	0.54	0.57	0.57	0.42
	(0.12)	(0.13)	(0.15)	(0.14)	(0.15)	(0.02)	(0.12)	(0.09)
Set 2	0.57	0.51	0.57	0.50	0.58	0.57	0.57	0.42
	(0.14)	(0.14)	(0.15)	(0.15)	(0.19)	(0.02)	(0.13)	(0.09)
Set 3	0.57	0.48	0.59	0.46	0.56	0.56	0.57	0.42
	(0.11)	(0.13)	(0.13)	(0.16)	(0.13)	(0.02)	(0.12)	(0.09)
Set 4	0.55	0.63	0.62	0.61	0.66	NA	0.60	0.40
	(0.12)	(0.12)	(0.13)	(0.12)	(0.12)	NA	(0.12)	(0.09)
Set 5	0.56	0.67	0.67	0.67	0.67	0.36	0.62	0.46
	(0.15)	(0.11)	(0.11)	(0.08)	(0.09)	(0.01)	(0.09)	(0.08)
Set 6	0.65	0.66	0.71	0.68	0.66	0.32	0.68	0.32
	(0.11)	(0.11)	(0.09)	(0.10)	(0.11)	(0.02)	(0.12)	(0.07)

Figure 7:

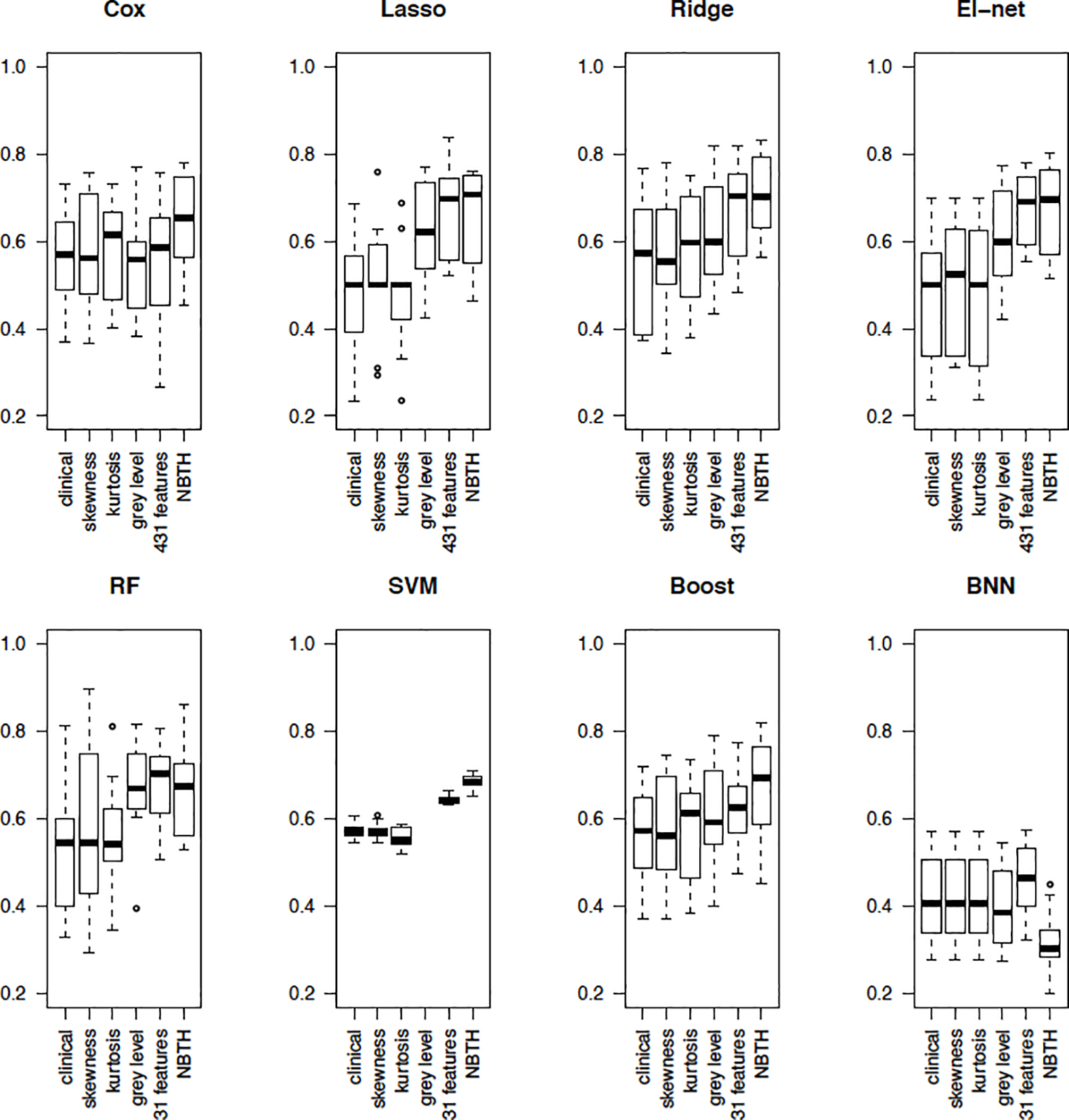
Boxplots of AUCs from 10-fold cross-validation for each model and the corresponding estimation method for 3-year survival.

5. Summary and Conclusions

As part of radiological assessment of cancer patients, images of different modalities such as CT, PET, or MRI are often collected and stored for use in disease diagnostics. The calculation of tumor heterogeneity has been based on these images and has been used for a wide spectrum of medical purposes including, but not limited to development of targeted therapies, studying disease progression, response to treatments, and in general the prediction of clinical outcomes such as survival. In this work, we investigated the estimation of tumor heterogeneity, based on medical imaging of patients with lung cancer. We discussed the existing approaches to estimation of tumor heterogeneity in radiological imaging of cancer, including histogram based approaches, and proposed a novel approach based on modeling the intensity profiles using MRFs to take into account the spatial structure of the image. Our proposed method is based on modeling the voxel intensities using a Gaussian mixture density with priors on the mixture weights to take into account the intensities of neighboring voxels. The mixture means and standard deviations are fixed, while the mixture weights are estimated using the EM-algorithm with Langrangian multipliers to model the constraints on the parameters. We compared the resulting parameter estimation to the k-means approach and GMM in simulation studies. We used the resulting MRF labeling to compute summary features describing tumor heterogeneity. Having defined the novel estimator of tumor heterogeneity, we modeled cancer survival as a function of the newly defined estimator. Further, we compared the predictive accuracy of the existing definitions to our proposed estimator when predicting cancer survival. The performance of the methods was evaluated using time-dependent ROC analysis for a cohort of lung cancer patients, followed by cross-validation. Our newly proposed estimator outperformed existing approaches in terms of predictive accuracy.

In this work, we assumed that each patient has one tumor for simplicity of notation and since the participants in the motivating NSCLC data used in this article only had one tumor. If two or more cancer tumors are present in the CT scan, then the proposed methods can be directly applied to estimate tumor-specific heterogeneity measures for each tumor of each study participant. Further investigation is necessary to find how the association of the resulting tumor specific heterogeneity measures and survival should be modeled. Another limitation of the current study is its focus on a single kind of cancer (lung). Further research needs to be conducted based on data from patients with other types of cancer (e.g. glioblastoma), to investigate the applicability of the proposed tumor heterogeneity estimation approach. In this work, our goal was to estimate a small number of image features that described tumor heterogeneity. When predicting cancer survival, future work may consider using deep learning methods to estimate survival using the full 3-dimensional image. In addition, we evaluated the stability of the proposed MRF-GMM approach for voxel labeling and the tumor heterogeneity estimator in the presence of noise in simulation studies. Future work may examine the stability of the proposed survival prediction algorithms in other similar cancer imaging data, as well as generalizability of the proposed estimator for other imaging modalities (e.g. MRI, PET) and other types of cancer.

An important advantage of our proposed definition is that it extends histogram based estimation techniques for tumor heterogeneity to include the spatial structure of the tumor. The variables entering the proposed estimator are based on an MRF labeling approach to find areas of the tumor with similar intensities. During clustering, rather than artificially fixing the number of clusters we choose the number of labels using a novel hypothesis testing-based approach and include the resulting cluster-based feature estimates along with clinical variables in machine learning for building the predictive model.

An intriguing area of future research is the use of the proposed estimator in targeted therapy development. For example, if location-specific genomic information is available from a tumor, we can identify associations of the estimated local moments and cluster features with genomic information and use these associations for targeted therapy. In particular, these associations can be used to develop predictions on what types of targeted therapies could be successfully used for treatment of a new patient based solely on their imaging. Although not considered in this article, this example shows the potential of the proposed methods in targeted therapy development.