Abstract
The reproductive number, or reproduction number, is a valuable metric in understanding infectious disease dynamics. There is a large body of literature related to its use and estimation. In the last 15 years, there has been tremendous progress in statistically estimating this number using case notification data. These approaches are appealing because they are relevant in an ongoing outbreak (e.g., for assessing the effectiveness of interventions) and do not require substantial modeling expertise to be implemented. In this article, we describe these methods and the extensions that have been developed. We provide insight into the distinct interpretations of the estimators proposed and provide real data examples to illustrate how they are implemented. Finally, we conclude with a discussion of available software and opportunities for future development.
Keywords: infectious disease outbreaks, reproduction number, reproductive number, serial interval
Abbreviations
- CI
confidence interval
- COVID-19
coronavirus disease 2019
- MERS-CoV
Middle East respiratory syndrome coronavirus
- SARS
severe acute respiratory syndrome
- SIR
susceptible-infectious-recovered
The reproductive or reproduction number, defined as the average number of secondary cases generated by an infected case, is an important quantity in infectious disease applications, with an expansive body of literature dedicated to its estimation and the public health implications of estimates for specific diseases. A notable use of this quantity is monitoring the infectiousness and transmissibility of diseases during outbreaks. For instance, in the severe acute respiratory syndrome (SARS) outbreak of 2003, estimates of the reproductive number demonstrated the impact of World Health Organization policies on reducing transmission (1). Other examples include monitoring the transmission of Ebola outbreaks (2–6), Middle East respiratory syndrome coronavirus (MERS-CoV) (7), the 2009 H1N1 influenza pandemic (8, 9), and the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) pandemic (10, 11).
Estimates of the reproductive number are also used to parameterize models to determine effective control and prevention strategies. For example, Fraser et al. (12) showed how the reproductive number, along with the amount of presymptomatic or asymptomatic transmission, can be used to determine the efficacy of control measures. Ferguson et al. (13) showed the relationship between the reproductive number and strategies for containing an influenza pandemic in Southeast Asia. Similar modeling exercises requiring accurate estimates of the reproductive number exist for many infectious diseases, including MERS-CoV, tuberculosis, and malaria (14–17). These exercises can focus on finding transmission hot spots, determining effective control policies, and examining the impact of vaccines or other pharmaceutical interventions.
Another use of the reproductive number is assessing the probability of a pathogen’s becoming established upon arrival in a new location. Such estimates were considered to predict the risk of sustained outbreaks in countries outside of China during the ongoing coronavirus disease 2019 (COVID-19) pandemic (18–20), and in West Africa during the 2014–2016 Ebola outbreak (21–24). Many other applications and examples exist. We do not aim to provide a comprehensive summary here but simply to emphasize that the reproductive number is a useful and important quantity to estimate in infectious disease outbreaks. In this article, we focus on approaches for estimating the reproductive number in real time during outbreaks using case notification data.
There are many methods of estimating the reproductive number. In general, one could group these methods into mathematical approaches, which tend to rely on the construction of a mechanistic model describing the transmission of the disease, and statistical approaches, which use existing data to derive estimators using probability theory. The mathematical approaches are arguably the methods most commonly used; however, statistical approaches are increasingly being employed. Dietz (25) and Becker (26) provide excellent summaries of many of these methods. Additionally, Wallinga and Lipsitch (27) describe the relationship between the basic reproductive number, defined as the average number of secondary cases an infectious person will generate during the initial phase of an outbreak, and exponential growth factors and generation intervals. Further, Chowell and Nishiura (28) describe methods of estimating the reproductive number for influenza, focusing on structured models, branching process theory, and counting process methods.
In the last 15 years, beginning with Wallinga and Teunis (1), there have been substantial developments in statistical approaches to estimating the reproductive number using case notification data. These methods typically require an estimate of the serial or generation interval, defined as the time between symptom onset or infection in an infector and symptom onset or infection in an infectee. This approach to estimation, using case notification data, has broad appeal, since these methods do not require specification of a disease- or outbreak-specific approximating mechanistic model and can be implemented with standard statistical software. However, because these approaches are relatively new and many extensions exist, it can be challenging to implement and interpret the different estimators. Here, we present a unifying framework for understanding and interpreting existing estimators of the reproductive number that use case notification data and describe important extensions to these methods. We draw on our collective experience to synthesize published methods that are most frequently used for this problem. We describe existing software for implementing these approaches and note instances where software does not yet exist but would be beneficial.
NOTATION AND ASSUMPTIONS
We denote the case notification data by 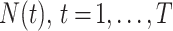 , where
, where 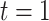 is the first observation time and
is the first observation time and 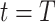 is the last time with available data. In most cases, the time unit is days; however, for settings such as tuberculosis or human immunodeficiency virus, the time unit might more appropriately be weeks or months. Data availability might also lead to the use of a coarser time scale for some outbreaks, such as the 2014–2016 Ebola outbreak, in which weekly case reports were common (21, 24). Let
is the last time with available data. In most cases, the time unit is days; however, for settings such as tuberculosis or human immunodeficiency virus, the time unit might more appropriately be weeks or months. Data availability might also lead to the use of a coarser time scale for some outbreaks, such as the 2014–2016 Ebola outbreak, in which weekly case reports were common (21, 24). Let 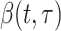 be the infectiousness of an individual at calendar time
be the infectiousness of an individual at calendar time 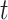 , where
, where 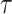 denotes the time since disease onset. We also denote the distribution of the serial interval, the time
denotes the time since disease onset. We also denote the distribution of the serial interval, the time 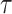 between disease onset in an infector and disease onset in an infectee, by
between disease onset in an infector and disease onset in an infectee, by 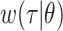 , where
, where 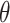 are the parameters of the probability density function used to describe the serial interval. These parameters,
are the parameters of the probability density function used to describe the serial interval. These parameters,  , might be the shape and rate parameters of a gamma distribution, for example, or probabilities of a multinomial distribution. To facilitate efficient estimation, the serial interval is often truncated to have a maximal length of
, might be the shape and rate parameters of a gamma distribution, for example, or probabilities of a multinomial distribution. To facilitate efficient estimation, the serial interval is often truncated to have a maximal length of 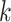 time units; that is,
time units; that is, 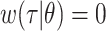 , if
, if 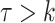 . For instance, serial intervals longer than 10 or even 7 days are unlikely in influenza (29). We note that the more biologically relevant generation interval, the time between infection in an infector-infectee pair, is more desirable, but because infection times are rarely observed, we often use the serial interval. The serial interval is an adequate surrogate for the generation interval if the times between infection and onset of symptoms are independent and identically distributed (30, 31).
. For instance, serial intervals longer than 10 or even 7 days are unlikely in influenza (29). We note that the more biologically relevant generation interval, the time between infection in an infector-infectee pair, is more desirable, but because infection times are rarely observed, we often use the serial interval. The serial interval is an adequate surrogate for the generation interval if the times between infection and onset of symptoms are independent and identically distributed (30, 31).
The methods we describe use the following assumptions in their original formulation:
The serial/generation interval and the reproductive number are statistically independent of each other.
The reproductive number follows a Poisson distribution.
All infectors appear before those they infect.
Individuals mix homogenously.
There is a closed population.
There is complete case reporting.
The first 3 assumptions are fundamental to the derivation of these methods. The last 3 have been relaxed or well-studied and their impact on estimation is understood, as we describe.
DEFINITIONS OF REPRODUCTIVE NUMBERS
We first note that there are many variants of the reproductive number that can be estimated. The basic reproductive number, 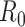 , refers to the average number of secondary cases an infectious person will generate during the initial phase of the outbreak when one might assume that everyone in the population is susceptible to disease and no control measures are in place. The effective reproductive number,
, refers to the average number of secondary cases an infectious person will generate during the initial phase of the outbreak when one might assume that everyone in the population is susceptible to disease and no control measures are in place. The effective reproductive number, 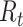 (denoted R(t) in equations below), is a time-varying version of
(denoted R(t) in equations below), is a time-varying version of 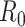 that reflects the changing levels of immunity in the population and control measures limiting transmission.
that reflects the changing levels of immunity in the population and control measures limiting transmission.
When estimating the time-varying reproductive number, we find it useful to distinguish between the case reproductive number and the instantaneous reproductive number (32). The instantaneous reproductive number describes the average number of secondary cases generated by persons who are infectious at time 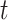 , assuming no changes to current conditions. In contrast, the case reproductive number estimates the total number of secondary cases who were infected by an individual with symptom onset at time
, assuming no changes to current conditions. In contrast, the case reproductive number estimates the total number of secondary cases who were infected by an individual with symptom onset at time 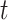 . Though similar estimates of
. Though similar estimates of 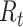 will typically be obtained if the transmission dynamics are not changing dramatically, their interpretation is fundamentally different. One way to understand the difference between these values is by examining the expected number of cases at time
will typically be obtained if the transmission dynamics are not changing dramatically, their interpretation is fundamentally different. One way to understand the difference between these values is by examining the expected number of cases at time 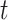 . When using the instantaneous reproductive number, one can denote the expected number of cases at time
. When using the instantaneous reproductive number, one can denote the expected number of cases at time 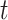 as
as
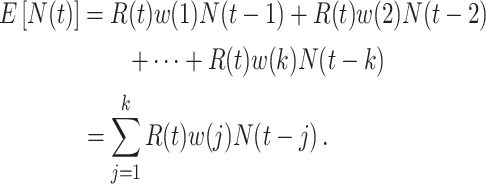 |
Here the instantaneous reproductive number is an attribute of the outbreak at time 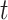 . In contrast, utilizing the case reproductive number, we have
. In contrast, utilizing the case reproductive number, we have
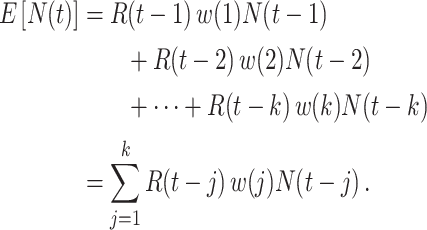 |
In this setting, the reproductive number is an attribute of cases infected at time 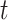 and its value is linked to the timing of disease onset for an infectious individual. The difference is subtle, but important for estimation. If a change in transmission dynamics occurs at some point (e.g., vaccine introduction), both estimators will be impacted at potentially different times (32). In our example, we show that this is not straightforward and further study through simulation is needed. Another key difference is that the case reproductive number is sensitive to right-censoring, as its estimate at time
and its value is linked to the timing of disease onset for an infectious individual. The difference is subtle, but important for estimation. If a change in transmission dynamics occurs at some point (e.g., vaccine introduction), both estimators will be impacted at potentially different times (32). In our example, we show that this is not straightforward and further study through simulation is needed. Another key difference is that the case reproductive number is sensitive to right-censoring, as its estimate at time 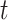 ,
, 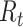 , is dependent on observing all cases infected by persons with onset time
, is dependent on observing all cases infected by persons with onset time 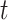 . Therefore, incomplete observation of all potential infectees of cases at time
. Therefore, incomplete observation of all potential infectees of cases at time 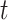 will lead to underestimation of
will lead to underestimation of 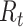 . The instantaneous reproductive number assumes there is no change to infectiousness and leverages prior cases to estimate
. The instantaneous reproductive number assumes there is no change to infectiousness and leverages prior cases to estimate 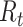 . It is particularly important that investigators understand how to correctly interpret estimates of the reproductive number to ensure that the impacts of interventions on the outbreak are appropriately modeled.
. It is particularly important that investigators understand how to correctly interpret estimates of the reproductive number to ensure that the impacts of interventions on the outbreak are appropriately modeled.
Below, we describe estimators of the basic reproductive number using case notification data. We then summarize estimators of the time-varying effective reproductive number, drawing parallels, where possible, with the basic reproductive number estimators. We illustrate these methods with 2 examples. Finally, we describe extensions to these methods.
ESTIMATORS OF THE BASIC REPRODUCTIVE NUMBER
Estimators of the basic reproductive number focus on using data during the exponential growth phase of an outbreak, assuming that all people are susceptible to infection. As we above, Wallinga and Lipsitch (27) have described how using the exponential growth rate during this period, along with an estimate of the mean generation time, can be used to derive an estimator of 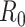 . We now describe alternative approaches to estimation during this period that leverage daily case counts.
. We now describe alternative approaches to estimation during this period that leverage daily case counts.
Sequential Bayes’ estimator of the basic reproductive number
Bettencourt et al. (33) introduced a Bayesian approach to estimating 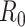 by updating the reproductive number estimate as data accumulate over time. Bayes’ theorem is used to derive the following expression.
by updating the reproductive number estimate as data accumulate over time. Bayes’ theorem is used to derive the following expression.
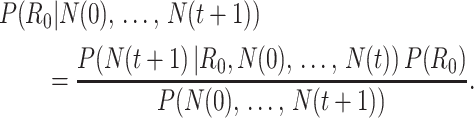 |
(1) |
Here 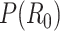 is the prior distribution of
is the prior distribution of 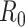 , which is parameterized with the prior information obtained from the posterior distribution of estimation through day
, which is parameterized with the prior information obtained from the posterior distribution of estimation through day 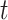 .
. 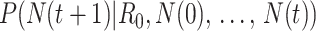 is typically parameterized using a Poisson model. The denominator is a normalizing constant that can be ignored in estimation. The posterior estimator of
is typically parameterized using a Poisson model. The denominator is a normalizing constant that can be ignored in estimation. The posterior estimator of 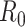 is obtained through successive application of Bayes’ theorem using the case report data. Notably, this approach does not require an explicit estimate of the serial interval but does assume that the infectious period is exponentially distributed, as it is derived from a susceptible-infectious-recovered model, which may be an oversimplification.
is obtained through successive application of Bayes’ theorem using the case report data. Notably, this approach does not require an explicit estimate of the serial interval but does assume that the infectious period is exponentially distributed, as it is derived from a susceptible-infectious-recovered model, which may be an oversimplification.
Maximum likelihood estimation
White and Pagano (34) derived a likelihood function for the stochastic process by assuming that people infect others according to a Poisson distribution with a parameter given by 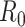 , and that those infected become symptomatic and infectious τ time units later. The joint likelihood, which involves both the serial interval and
, and that those infected become symptomatic and infectious τ time units later. The joint likelihood, which involves both the serial interval and 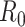 , is given by
, is given by
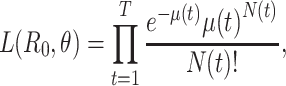 |
(2) |
where 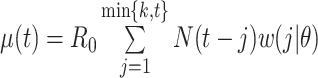 . Using case notification data, estimates for both
. Using case notification data, estimates for both 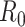 and
and 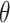 (i.e., the serial interval) can be obtained using numerical optimization routines or Bayesian approaches, where contact-trace data can be incorporated (35, 36). If numerical optimizers are used, Griffin et al. (37) have shown that joint estimation of the serial interval and
(i.e., the serial interval) can be obtained using numerical optimization routines or Bayesian approaches, where contact-trace data can be incorporated (35, 36). If numerical optimizers are used, Griffin et al. (37) have shown that joint estimation of the serial interval and 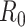 is challenging when either the reproductive number is extremely high (larger than 7) or the coefficient of variation of the serial interval is large. However, Bayesian implementations, particularly when limited contact tracing information is used, lead to more stable estimates (35, 36).
is challenging when either the reproductive number is extremely high (larger than 7) or the coefficient of variation of the serial interval is large. However, Bayesian implementations, particularly when limited contact tracing information is used, lead to more stable estimates (35, 36).
If the serial interval is known, the maximum likelihood estimator for 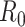 is
is
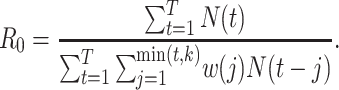 |
(3) |
This bears a strong resemblance to a branching process estimator. Nishiura (38) describes a modification of the branching process estimator where he uses the mean serial interval to group daily influenza case data and then estimates the reproductive number through time. Here the 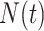 can be grouped into generational data denoted by
can be grouped into generational data denoted by 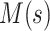 , where
, where 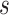 indexes generations. Then the estimator given in equation 3 does not require inclusion of the serial interval terms, and
indexes generations. Then the estimator given in equation 3 does not require inclusion of the serial interval terms, and 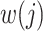 and
and 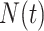 are replaced by
are replaced by 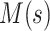 .
.
TIME-VARYING REPRODUCTIVE NUMBER
Instantaneous reproductive number, 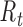
Fraser (32) developed an estimator of the time-varying instantaneous reproductive number. This estimator is derived using the so-called renewal equations. The renewal equations intuitively describe the number of cases at time 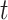 as a function of the number of prior cases multiplied by their infectiousness,
as a function of the number of prior cases multiplied by their infectiousness,
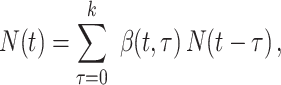 |
(4) |
where 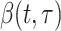 describes infectiousness as noted above. Fraser shows that if one assumes independence between calendar time and the serial interval, then
describes infectiousness as noted above. Fraser shows that if one assumes independence between calendar time and the serial interval, then 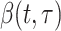 becomes
becomes
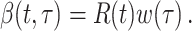 |
(5) |
Substitution of this quantity in the renewal equation (equation 4) leads to an estimator of the instantaneous reproductive number:
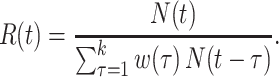 |
(6) |
This is similar to the White and Pagano estimator shown in equation 3, and it can be shown that if the renewal equation is generalized to the period where 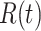 is described by
is described by 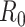 , then equation 4 becomes
, then equation 4 becomes
 |
(7) |
and the estimator for 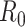 is identical to equation 3. Therefore, generalizations and results obtained for one estimator are readily translatable to the other.
is identical to equation 3. Therefore, generalizations and results obtained for one estimator are readily translatable to the other.
The time-varying estimator of 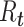 can be stabilized and smoothed by estimating
can be stabilized and smoothed by estimating 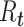 over a longer time window rather than in a 1-time step (39, 40). The basic reproductive number can be seen as a special case of this, when we assume that the instantaneous reproductive number is unchanged over the course of the initial phase of an outbreak. It is also possible to use a Bayesian approach to estimating the reproductive number that allows for the estimation of credible intervals (39). A similar formulation is derived by White and Pagano (34) using their likelihood with a gamma prior for
over a longer time window rather than in a 1-time step (39, 40). The basic reproductive number can be seen as a special case of this, when we assume that the instantaneous reproductive number is unchanged over the course of the initial phase of an outbreak. It is also possible to use a Bayesian approach to estimating the reproductive number that allows for the estimation of credible intervals (39). A similar formulation is derived by White and Pagano (34) using their likelihood with a gamma prior for 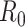 .
.
Case reproductive number, 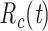
Wallinga and Teunis (1) derive an estimator of the case reproductive number by formulating the problem from a network perspective. Here the probability that case 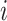 with symptom onset at time
with symptom onset at time 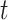 , denoted by
, denoted by  , was infected by case
, was infected by case 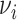 with symptom onset at time
with symptom onset at time 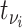 is given by the probability of a serial interval of length
is given by the probability of a serial interval of length 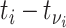 ,
, 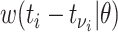 . Then assuming that cases are only infected by 1 individual, all probabilities for 1 infectee are reweighted to sum to 1 and become relative probabilities of infection,
. Then assuming that cases are only infected by 1 individual, all probabilities for 1 infectee are reweighted to sum to 1 and become relative probabilities of infection, 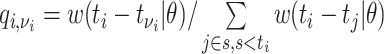 . The case reproductive number for a person developing symptoms on day
. The case reproductive number for a person developing symptoms on day 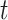 is the sum of the relative probabilities implicating that person as a potential infector,
is the sum of the relative probabilities implicating that person as a potential infector,
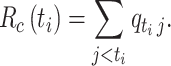 |
(8) |
This assumes that each potential infection is parameterized by the relative probability of infection. Then the expected number of infections is the expected value of each of these independent Bernoulli events. As we noted above, a drawback of this estimator is its sensitivity to right-censoring, meaning that in order to estimate 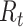 one must observe all potential secondary cases arising from infectors at time
one must observe all potential secondary cases arising from infectors at time 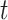 , implying that we observe all cases up to
, implying that we observe all cases up to 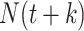 . The mathematical simplicity of the Wallinga and Teunis estimator makes this approach appealing. A Bayesian implementation of this approach allows for estimation closer to real time (9, 41), meaning that we can obtain an estimate for the reproductive number that is more relevant to the last date of data collection and minimize the impact of right-censoring.
. The mathematical simplicity of the Wallinga and Teunis estimator makes this approach appealing. A Bayesian implementation of this approach allows for estimation closer to real time (9, 41), meaning that we can obtain an estimate for the reproductive number that is more relevant to the last date of data collection and minimize the impact of right-censoring.
For estimation of 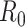 from an effective reproductive number, one can average the estimates of
from an effective reproductive number, one can average the estimates of 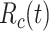 or
or 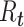 over the period of exponential growth.
over the period of exponential growth.
EXAMPLES
We illustrate these methods using data from 2 outbreaks: 1) 610 cases of influenza A/H1N1 reported in La Gloria, Mexico, over a period of 34 days in 2009 (42) and 2) 1,702 cases of SARS reported in Hong Kong, China, over a period of 96 days in 2003 (1). Figure 1 illustrates the estimation of 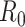 using the sequential Bayes estimator and the White and Pagano maximum likelihood estimator. We show the case notification data during the exponential growth period (the first 15 days for influenza and the first 39 days for SARS) of the outbreaks and estimates of
using the sequential Bayes estimator and the White and Pagano maximum likelihood estimator. We show the case notification data during the exponential growth period (the first 15 days for influenza and the first 39 days for SARS) of the outbreaks and estimates of 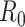 derived using the data available at each time point. For example, on day 15 of the influenza outbreak, we estimate
derived using the data available at each time point. For example, on day 15 of the influenza outbreak, we estimate 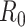 using data collected up to day 15. While the estimates are substantially different early on, by the peak of the epidemics, they begin to converge. The White and Pagano maximum likelihood estimate for influenza on day 15 of the outbreak is 1.99 (95% confidence interval (CI): 1.66, 2.33), while the sequential Bayes estimate is 1.65 (95% CI: 1.21, 2.06). Similarly, for SARS, the White and Pagano maximum likelihood estimate on the 39th day is 2.32 (95% CI: 2.08, 2.58) and the sequential Bayes estimate is 2.54 (95% CI: 1.89, 3.18).
using data collected up to day 15. While the estimates are substantially different early on, by the peak of the epidemics, they begin to converge. The White and Pagano maximum likelihood estimate for influenza on day 15 of the outbreak is 1.99 (95% confidence interval (CI): 1.66, 2.33), while the sequential Bayes estimate is 1.65 (95% CI: 1.21, 2.06). Similarly, for SARS, the White and Pagano maximum likelihood estimate on the 39th day is 2.32 (95% CI: 2.08, 2.58) and the sequential Bayes estimate is 2.54 (95% CI: 1.89, 3.18).
Figure 1.
Estimates of the basic reproductive number 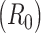 derived using data cumulatively collected during the exponential growth phase of the outbreaks for the 2009 H1N1 influenza pandemic (A) and the 2003 severe acute respiratory syndrome outbreak (B). The sequential Bayes (SB) and White and Pagano maximum likelihood (ML) estimators are shown. Estimates for each day depict the estimate of
derived using data cumulatively collected during the exponential growth phase of the outbreaks for the 2009 H1N1 influenza pandemic (A) and the 2003 severe acute respiratory syndrome outbreak (B). The sequential Bayes (SB) and White and Pagano maximum likelihood (ML) estimators are shown. Estimates for each day depict the estimate of  obtained using data available at that point. The horizontal dotted line is positioned at the critical value of 1 for
obtained using data available at that point. The horizontal dotted line is positioned at the critical value of 1 for 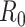 .
.
We estimate time-varying versions of the reproductive number using the case and instantaneous reproductive number estimators. In Figure 2, we include smoothed (7-day) and unsmoothed implementations of the instantaneous 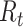 . Overall the estimates are similar, though we note that the unsmoothed instantaneous reproductive number estimates tend to reach subcritical levels more slowly than the Wallinga and Teunis estimator and smoothed estimates. Further research is needed to understand how the differences in estimates from different estimators relate to the actual disease dynamics. Software code is provided on GitHub (43) and in the Web Appendix (available at https://doi.org/10.1093/aje/kwaa211).
. Overall the estimates are similar, though we note that the unsmoothed instantaneous reproductive number estimates tend to reach subcritical levels more slowly than the Wallinga and Teunis estimator and smoothed estimates. Further research is needed to understand how the differences in estimates from different estimators relate to the actual disease dynamics. Software code is provided on GitHub (43) and in the Web Appendix (available at https://doi.org/10.1093/aje/kwaa211).
Figure 2.
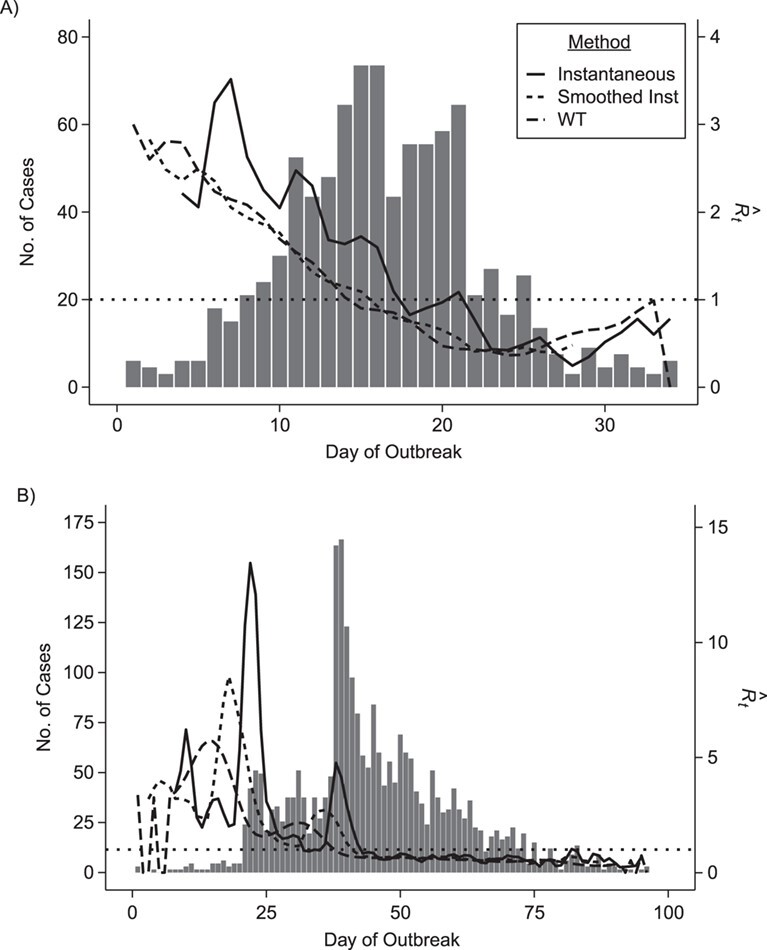
Epidemic curve data and time-varying estimated reproductive numbers (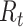 ) derived using an instantaneous estimator, a smoothed instantaneous estimator, and the Wallinga and Teunis (WT) estimator for the 2009 H1N1 influenza pandemic (A) and the 2003 severe acute respiratory syndrome outbreak (B). The horizontal dotted line is positioned at the critical value of 1 for
) derived using an instantaneous estimator, a smoothed instantaneous estimator, and the Wallinga and Teunis (WT) estimator for the 2009 H1N1 influenza pandemic (A) and the 2003 severe acute respiratory syndrome outbreak (B). The horizontal dotted line is positioned at the critical value of 1 for 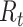 . Inst, instantaneous.
. Inst, instantaneous.
EXTENSIONS
Work has been done to relax the original model assumptions, including homogenous mixing, no imported cases, and incomplete reporting. In reality, relaxing model assumptions is of interest, as this provides increased understanding of the potentially important and realistic dynamics of an outbreak. For instance, understanding the meaningful differences in reproductive numbers between groups of individuals (defined by space, demographic factors, or pathogen strain) is helpful in mounting an appropriate targeted response to an outbreak. Accounting for movement into and out of the population is important given the interconnectedness of spatially distinct populations, leading to a more accurate sense of the relative importance of native transmission versus imported transmission.
Incomplete reporting
Two patterns of incomplete data have been described and studied: 1) undiagnosed cases, such as those missed because of reporting issues (44); and 2) the more challenging problem that we never observe outbreaks that do not take hold in a population. The latter inevitably leads to overestimation of the basic reproductive numbers (45). For the first scenario, White et al. (46) describe the implications of incomplete case report data and show that the reproductive number is unbiased if the fraction of cases reported remains constant through time. Bias in the estimate will occur if the reporting fraction changes over time—for instance, when awareness of an outbreak increases health-care-seeking behavior and testing. As an example of accounting for this, White et al. (8) use hospital data from the 2009 influenza A/H1N1 pandemic to estimate the reporting fraction.
For the second scenario, it has been documented that missingness will initially lead to overestimation of 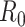 (45–47). Obadia et al. (48) propose a correction to account for this for the Wallinga and Teunis estimator, the sequential Bayes estimator, and the White and Pagano maximum likelihood estimator. For the final scenario, Rebuli et al. (47) show analytically how one can modify the estimator for the reproductive number by conditioning on observing an outbreak in the setting of a susceptible-infectious-recovered model. We are not aware of extensions of this approach to estimators based on case notification data.
(45–47). Obadia et al. (48) propose a correction to account for this for the Wallinga and Teunis estimator, the sequential Bayes estimator, and the White and Pagano maximum likelihood estimator. For the final scenario, Rebuli et al. (47) show analytically how one can modify the estimator for the reproductive number by conditioning on observing an outbreak in the setting of a susceptible-infectious-recovered model. We are not aware of extensions of this approach to estimators based on case notification data.
Inclusion of contact-trace data and genetic data
Recognizing that estimates of the serial interval or generation interval are often not reliable, nonexistent, or variable between outbreaks, there has been an effort to incorporate contact-trace data while estimating the reproductive number. At a minimum, one can estimate the serial interval from contact-trace data and then estimate the reproductive number with a 2-step process using the estimators described above (e.g., see Bettencourt and Ribeiro (33)). Using appropriate statistical approaches to estimation is important in order to account for issues in these data, including censoring and truncation (29, 49–52).
Alternatively, one can modify the above estimators, incorporating this information in estimation. For instance, contact-trace data are included either explicitly in the likelihood (35) or as prior information for the serial interval (36) using a Bayesian implementation of the White and Pagano estimator. The time-varying instantaneous reproductive number has been modified to incorporate data describing the times of symptom onset in known infector-infectee pairs (53). In that framework, interval-censored data can be included (i.e., lower and upper bounds on the timing of symptom appearance).
There has been a growing interest in methods incorporating pathogen genetic information to estimate the reproductive number. Leavitt et al. (54) and Klinkenberg et al. (55) present distinct approaches that leverage whole genome sequencing data.
Heterogeneity
The issue of heterogeneity in transmission has been discussed extensively in the modeling literature. This can take the form of identifying superspreaders (e.g., persons who have a much higher than average capacity to infect), highly transmissible pathogen strains, geographic regions with greater transmission rates, and demographic groups that are more efficient transmitters. The goal of this work is not only to improve estimators and potentially reduce standard errors but also to add meaningful insights into the underlying disease dynamics. The proposed approaches require information describing interactions between heterogeneous groups. For age groups, social contact surveys, such as those carried out by Mossong et al. (56), have been commonly used. Three main approaches exist for age-specific estimation of the reproductive number.
Glass et al. (57) modified the Wallinga and Teunis and White and Pagano methods using a next-generation matrix to accommodate 2 age groups. White et al. (58, 59) modified the probabilities of transmission in the Wallinga and Teunis estimator to accommodate a larger number of age groups. Moser et al. (60) provide a Bayesian implementation of the White and Pagano estimator of 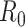 that uses contact information between heterogeneous groups as prior information. The Bayesian implementation allows increased flexibility to incorporate contact-trace data for serial interval estimation, as well. Modifying the instantaneous reproductive number to account for heterogeneity by modifying the renewal equation would be a straightforward extension.
that uses contact information between heterogeneous groups as prior information. The Bayesian implementation allows increased flexibility to incorporate contact-trace data for serial interval estimation, as well. Modifying the instantaneous reproductive number to account for heterogeneity by modifying the renewal equation would be a straightforward extension.
Imported cases
In outbreak settings, it is highly likely that infected persons will move into the population being studied, contrary to the assumptions of the methods we have presented. During the 2009 H1N1 pandemic, many infected persons arrived in the United States from Mexico, the pandemic’s suspected point of origin. All of the approaches we have presented have been modified to accommodate imported cases requiring identification of persons infected elsewhere, typically using travel history data. Estimators are modified by removing these individuals as potential infectees but retaining them as infectors.
The sequential Bayes estimator in equation 1 was modified to analyze pandemic influenza (61, 62). The Wallinga and Teunis method has also been modified by Paine et al. (61) and Cowling et al. (9). White et al. (8) modified the White and Pagano method to study pandemic influenza in the United States in 2009. More recently, Thompson (53) derived a real-time estimator of the instantaneous reproductive number and demonstrated its use on data for MERS-CoV in Saudi Arabia.
The impact of this adjustment will generally be a decrease in the estimated reproductive number. Of particular interest are scenarios in which an outbreak might be considered uncontrolled when in fact the reproductive number is below 1 (e.g., see the MERS-CoV example in Cauchemez et al. (41)).
SOFTWARE
The methods described are most commonly implemented using R software (63). We describe 2 packages for these methods (Table 1). The R0 package implements the sequential Bayes, White and Pagano, and Wallinga and Teunis estimators and provides confidence intervals. Adjustment for imported cases is also permitted (48).
Table 1.
Statistical Approaches to Estimation of the Effective Reproductive Number and the Basic Reproductive Numbera
| Approach (Reference No.) | Estimator | Extensions | R Software Package(s) |
|---|---|---|---|
Estimators of 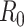
| |||
| White and Pagano (34)—serial interval known |
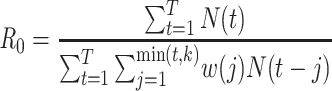
|
Imported cases (8, 47) Bayesian implementation (35, 36) Heterogeneity (58) |
R0 package (47) function: est.R0.ML, option unknown.GT = F |
| White and Pagano (34)—serial interval unknown | Maximize the likelihood w.r.t. 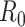 and and 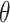 : : , ,where 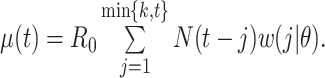
|
Imported cases (8, 47) Bayesian implementation (35, 36) Heterogeneity (58) |
R0 package (47) function: est.R0.ML, option unknown.GT = F |
| Bettencourt et al. (33) |
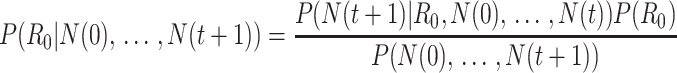
|
Imported cases (8, 60) | R0 package (47) function: est.R0.SB |
Estimators of 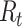
| |||
| Instantaneous reproductive number (32, 39) |
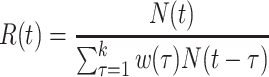
|
Importation (51) Smoothing (39) |
EpiEstim package (39, 52) |
| Case reproductive number (1) |
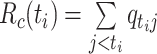 ,
,where 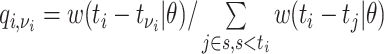
|
Heterogeneity (56, 57) Importation (47) |
R0 package (47) est.R0.TD function EpiEstim package (39, 52) |
a Notation: 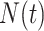 , number of new cases at time
, number of new cases at time  ;
; 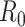 , basic reproductive number;
, basic reproductive number; 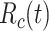 , case reproductive number at time
, case reproductive number at time 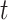 ;
; 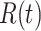 , instantaneous reproductive number;
, instantaneous reproductive number; 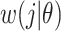 , probability of a serial interval of length j, where
, probability of a serial interval of length j, where 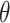 are the parameters of the serial interval density function.
are the parameters of the serial interval density function.
The EpiEstim package (53) estimates the instantaneous reproductive number, as well as the case reproductive number. Contact-trace data for informing the serial interval, imported cases, and smoothing of the reproductive numbers over a sliding window can be used to estimate the instantaneous reproductive number (39, 53). An R Shiny app (64) is also available for implementing these methods. The EpiEstim package and its accompanying software application have been used for estimating pathogen transmissibility during outbreaks of influenza (65, 66), Ebola (67, 68), Zika (69), and COVID-19 (70, 71).
Software with which to implement methods accounting for heterogeneity has not been disseminated. This would be an important addition, although of course it would require relevant data.
CONCLUSION
Accurate estimation of the reproductive number is important during infectious disease outbreaks. Timely estimates of this number are most likely obtained using case notification data and tools that are easy to implement, as is being done in the current COVID-19 pandemic. It is noteworthy that these data are not always available or of sufficient quality, meaning that data must be preprocessed in order to use these methods. We have summarized advances over more than 15 years to create statistical tools for this problem and describe important extensions to these methods. The growth of digitized health systems and increasing molecular testing present exciting opportunities to create estimators that will provide more granular understanding of transmission. As emerging infectious disease outbreaks occur, rapid dissemination of data and generation of reproductive number estimates is important for a timely and appropriate response.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Department of Biostatistics, School of Public Health, Boston University, Boston, Massachusetts, United States (Laura F. White); Center for Biostatistics in AIDS Research, Harvard T.H. Chan School of Public Health, Boston, Massachusetts, United States (Carlee B. Moser); Mathematical Institute, University of Oxford, Oxford, United Kingdom (Robin N. Thompson); and Department of Biostatistics, Harvard T.H. Chan School of Public Health, Boston, Massachusetts, United States (Marcello Pagano).
L.F.W. was supported by the US National Institute of General Medical Sciences (grant R01GM122876). R.N.T. was supported by Christ Church (Oxford University) via a Junior Research Fellowship. C.B.M. was supported by the US National Institute of Allergy and Infectious Diseases (grant UM1 AI068634).
Conflict of interest: none declared.
REFERENCES
- 1. Wallinga J, Teunis P. Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. Am J Epidemiol. 2004;160(6):509–516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Lewnard JA, Ndeffo Mbah ML, Alfaro-Murillo JA, et al. Dynamics and control of Ebola virus transmission in Montserrado, Liberia: a mathematical modelling analysis. Lancet Infect Dis. 2014;14(12):1189–1195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Althaus CL. Estimating the reproduction number of Ebola virus (EBOV) during the 2014 outbreak in West Africa. PLoS Curr. 2014;6:ecurrents.outbreaks.91afb5e0f279e7f29e7056095255b288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Majumder MS, Kluberg S, Santillana M, et al. 2014 Ebola outbreak: media events track changes in observed reproductive number. PLoS Curr. 2015;7:ecurrents.outbreaks.e6659013c1d7f11bdab6a20705d1e865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Pandey A, Atkins KE, Medlock J, et al. Strategies for containing Ebola in West Africa. Science. 2014;346(6212):991–995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Chowell G, Hengartner NW, Castillo-Chavez C, et al. The basic reproductive number of Ebola and the effects of public health measures: the cases of Congo and Uganda. J Theor Biol. 2004;229(1):119–126. [DOI] [PubMed] [Google Scholar]
- 7. Cauchemez S, Nouvellet P, Cori A, et al. Unraveling the drivers of MERS-CoV transmission. Proc Natl Acad Sci U S A. 2016;113(32):9081–9086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. White LF, Wallinga J, Finelli L, et al. Estimation of the reproductive number and the serial interval in early phase of the 2009 influenza A/H1N1 pandemic in the USA. Influenza Other Respir Viruses. 2009;3(6):267–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Cowling BJ, Lau MSY, Ho LM, et al. The effective reproduction number of pandemic influenza: prospective estimation. Epidemiology. 2010;21(6):842–846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Li Q, Guan X, Wu P, et al. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N Engl J Med. 2020;382(13):1199–1207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Wu JT, Leung K, Leung GM. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020;395(10225):689–697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Fraser C, Riley S, Anderson RM, et al. Factors that make an infectious disease outbreak controllable. Proc Natl Acad Sci U S A. 2004;101(16):6146–6151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Ferguson NM, Cummings DAT, Cauchemez S, et al. Strategies for containing an emerging influenza pandemic in Southeast Asia. Nature. 2005;437(7056):209–214. [DOI] [PubMed] [Google Scholar]
- 14. Peak CM, Childs LM, Grad YH, et al. Comparing nonpharmaceutical interventions for containing emerging epidemics. Proc Natl Acad Sci U S A. 2017;114(15):4023–4028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Metcalf C, Lessler J. Opportunities and challenges in modeling emerging infectious diseases. Science. 2017;357(6347):149–152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Dowdy DW, Golub JE, Chaisson RE, et al. Heterogeneity in tuberculosis transmission and the role of geographic hotspots in propagating epidemics. Proc Natl Acad Sci. 2012;109(24):9557–9562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Ruktanonchai NW, DeLeenheer P, Tatem AJ, et al. Identifying malaria transmission foci for elimination using human mobility data. PLoS Comput Biol. 2016;12(4):e1004846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Thompson RN. Novel coronavirus outbreak in Wuhan, China, 2020: intense surveillance is vital for preventing sustained transmission in new locations. J Clin Med. 2020;9(2):Article 498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Hellewell J, Abbott S, Gimma A, et al. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Glob Health. 2020;8(4):e488–e496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Kucharski AJ, Russell TW, Diamond C, et al. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect Dis. 2020;20(5):553–558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Althaus CL, Low N, Musa EO, et al. Ebola virus disease outbreak in Nigeria: transmission dynamics and rapid control. Epidemics. 2015;11:80–84. [DOI] [PubMed] [Google Scholar]
- 22. Thompson RN, Gilligan CA, Cunniffe NJ. Detecting presymptomatic infection is necessary to forecast major epidemics in the earliest stages of infectious disease outbreaks. PLoS Comput Biol. 2016;12(4):e1004836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Merler S, Ajelli M, Fumanelli L, et al. Containing Ebola at the source with ring vaccination. PLoS Negl Trop Dis. 2016;10(11):e0005093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Thompson RN, Jalava K, Obolski U. Sustained transmission of Ebola in new locations: more likely than previously thought. Lancet Infect Dis. 2019;19(10):1058–1059. [DOI] [PubMed] [Google Scholar]
- 25. Dietz K. The estimation of the basic reproduction number for infectious diseases. Stat Methods Med Res. 1993;2(1):23–41. [DOI] [PubMed] [Google Scholar]
- 26. Becker NG. Analysis of Infectious Disease Data. 1st ed. New York, NY: Chapman & Hall/CRC Press; 1989. [Google Scholar]
- 27. Wallinga J, Lipsitch M. How generation intervals shape the relationship between growth rates and reproductive numbers. Proc Biol Sci. 2007;274(1609):599–604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Chowell G, Nishiura H. Quantifying the transmission potential of pandemic influenza. Phys Life Rev. 2008;5(1):50–77. [Google Scholar]
- 29. Donnelly CA, Finelli L, Cauchemez S, et al. Serial intervals and the temporal distribution of secondary infections within households of 2009 pandemic influenza A (H1N1): implications for influenza control recommendations. Clin Infect Dis. 2011;52(suppl 1):S123–S130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Svensson Å. A note on generation times in epidemic models. Math Biosci. 2007;208(1):300–311. [DOI] [PubMed] [Google Scholar]
- 31. Vink MA, Bootsma MCJ, Wallinga J. Serial intervals of respiratory infectious diseases: a systematic review and analysis. Am J Epidemiol. 2014;180(9):865–875. [DOI] [PubMed] [Google Scholar]
- 32. Fraser C. Estimating individual and household reproduction numbers in an emerging epidemic. PLoS One. 2007;2(8):e758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Bettencourt LMA, Ribeiro RM. Real time Bayesian estimation of the epidemic potential of emerging infectious diseases. PLoS One. 2008;3(5):e2185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. White LF, Pagano MP. A likelihood-based method for real-time estimation of the serial interval and reproductive number of an epidemic. Stat Med. 2008;27(16):2999–3016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Becker NG, Wang D, Clements M. Type and quantity of data needed for an early estimate of transmissibility when an infectious disease emerges. Euro Surveill. 2010;15(26):19603. [PubMed] [Google Scholar]
- 36. Moser CB, Gupta M, Archer BN, et al. The impact of prior information on estimates of disease transmissibility using Bayesian tools. PLoS One. 2015;10(3):e0118762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Griffin JT, Garske T, Ghani AC, et al. Joint estimation of the basic reproduction number and generation time parameters for infectious disease outbreaks. Biostatistics. 2011;12(2):303–312. [DOI] [PubMed] [Google Scholar]
- 38. Nishiura H. Time variations in the transmissibility of pandemic influenza in Prussia, Germany, from 1918–19. Theor Biol Med Model. 2007;4:Article 20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Cori A, Ferguson NM, Fraser C, et al. A new framework and software to estimate time-varying reproduction numbers during epidemics. Am J Epidemiol. 2013;178(9):1505–1512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Parag K, Donnelly C. Using information theory to optimise epidemic models for real-time prediction and estimation. PLoS Comput Biol. 2020;17(7):e1007990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Cauchemez S, Boëlle PY, Donnelly CA, et al. Real-time estimates in early detection of SARS. Emerg Infect Dis. 2006;12(1):110–113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Fraser C, Donnelly CA, Cauchemez S, et al. Pandemic potential of a strain of influenza A (H1N1): early findings. Science. 2009;324(5934):1557–1561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. White LF. Reproductive-number-examples: code and data for estimating reproductive numbers. https://github.com/forsbee/Reproductive-number-examples. Accessed September 24, 2020.
- 44. Fefferman NH, Lofgren ET, Li N, et al. Fear, access, and the real-time estimation of etiological parameters for outbreaks of novel pathogens [preprint]. medRxiv. 2020. (doi: 10.1101/2020.03.19.20038729). Accessed May 13, 2020. [DOI] [Google Scholar]
- 45. Mercer GN, Glass K, Becker NG. Effective reproduction numbers are commonly overestimated early in a disease outbreak. Stat Med. 2011;30(9):984–994. [DOI] [PubMed] [Google Scholar]
- 46. White LF, Pagano M. Reporting errors in infectious disease outbreaks, with an application to pandemic influenza A/H1N1. Epidemiol Perspect Innov. 2010;7:Article 12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Rebuli NP, Bean NG, Ross JV. Estimating the basic reproductive number during the early stages of an emerging epidemic. Theor Popul Biol. 2018;119:26–36. [DOI] [PubMed] [Google Scholar]
- 48. Obadia T, Haneef R, Boëlle P-Y. The R0 package: a toolbox to estimate reproduction numbers for epidemic outbreaks. BMC Med Inform Decis Mak. 2012;12(1):Article 147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Lipsitch M, Cohen T, Cooper B, et al. Transmission dynamics and control of severe acute respiratory syndrome. Science. 2003;300(5627):1966–1970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Cowling BJ, Muller MP, Wong IOL, et al. Alternative methods of estimating an incubation distribution: examples from severe acute respiratory syndrome. Epidemiology. 2007;18(2):253–259. [DOI] [PubMed] [Google Scholar]
- 51. Cowling BJ, Fang VJ, Riley S, et al. Estimation of the serial interval of influenza. Epidemiology. 2009;20(3):344–347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Ma Y, Jenkins HE, Sebastiani P, et al. Using cure models to estimate the serial interval of tuberculosis with limited follow-up. Am J Epidemiol. 2020;189(11):1421–1426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Thompson RN, Stockwin JE, van Gaalen RD, et al. Improved inference of time-varying reproduction numbers during infectious disease outbreaks. Epidemics. 2019;29:100356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Leavitt SV, Lee RS, Sebastiani P, et al. Estimating the relative probability of direct transmission between infectious disease patients. Int J Epidemiol. 2020;49(3):764–775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Klinkenberg D, Backer JA, Didelot X, et al. Simultaneous inference of phylogenetic and transmission trees in infectious disease outbreaks. PLoS Comput Biol. 2017;13(5):e1005495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Mossong J, Hens N, Jit M, et al. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Med. 2008;5(3):e74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Glass K, Mercer GN, Nishiura H, et al. Estimating reproduction numbers for adults and children from case data. J R Soc Interface. 2011;8(62):1248–1259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. White LF, Archer B, Pagano M. Determining the dynamics of influenza transmission by age. Emerg Themes Epidemiol. 2014;11(1):Article 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. White LF, Archer B, Pagano M. Estimating the reproductive number in the presence of spatial heterogeneity of transmission patterns. Int J Health Geogr. 2013;12:Article 35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Moser CB, White LF. Estimating age-specific reproductive numbers—a comparison of methods. Stat Methods Med Res. 2018;27(7):2050–2059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Paine S, Mercer GN, Kelly PM, et al. Transmissibility of 2009 pandemic influenza A(H1N1) in New Zealand: effective reproduction number and influence of age, ethnicity and importations. Euro Surveill. 2010;15(24):19591. [PubMed] [Google Scholar]
- 62. Yang F, Yuan L, Tan X, et al. Bayesian estimation of the effective reproduction number for pandemic influenza A H1N1 in Guangdong Province, China. Ann Epidemiol. 2013;23(6):301–306. [DOI] [PubMed] [Google Scholar]
- 63. R Core Team . R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2019. [Google Scholar]
- 64. Cori A. EpiEstim: estimate time varying reproduction numbers from epidemic curves. (R package, version 2.2-3). https://CRAN.R-project.org/package=EpiEstim. Published May 29, 2020. Accessed December 16, 2020.
- 65. Ewing A, Lee EC, Viboud C, et al. Contact, travel, and transmission: the impact of winter holidays on influenza dynamics in the United States. J Infect Dis. 2017;215(5):732–739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Ali ST, Kadi AS, Ferguson NM. Transmission dynamics of the 2009 influenza A (H1N1) pandemic in India: the impact of holiday-related school closure. Epidemics. 2013;5(4):157–163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Agua-Agum J, Ariyarajah A, Blake IM, et al. Ebola virus disease among children in West Africa. N Engl J Med. 2015;372(13):1274–1277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Kirsch TD, Moseson H, Massaquoi M, et al. Impact of interventions and the incidence of Ebola virus disease in Liberia—implications for future epidemics. Health Policy Plan. 2017;32(2):205–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Ferguson NM, Cucunubá ZM, Dorigatti I, et al. Countering the Zika epidemic in Latin America. Science. 2016;353(6297):353–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Liu T, Hu J, Kang M, et al. Time-varying transmission dynamics of novel coronavirus pneumonia in China [preprint]. bioRxiv. 2020. (doi: 10.1101/2020.01.25.919787). Accessed March 16, 2020. [DOI] [Google Scholar]
- 71. Abbott S, Hellewell J, Thompson RN, et al. Temporal variation in transmission during the COVID-19 outbreak. https://epiforecasts.io/covid/. Published 2020. Accessed September 23, 2020.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


