Integrative structure of a complete cytokine receptor in a nanodisc opens for mechanistic decoding of disorder-based biology.
Abstract
Because of its small size (70 kilodalton) and large content of structural disorder (>50%), the human growth hormone receptor (hGHR) falls between the cracks of conventional high-resolution structural biology methods. Here, we study the structure of the full-length hGHR in nanodiscs with small-angle x-ray scattering (SAXS) as the foundation. We develop an approach that combines SAXS, x-ray diffraction, and NMR spectroscopy data obtained on individual domains and integrate these through molecular dynamics simulations to interpret SAXS data on the full-length hGHR in nanodiscs. The hGHR domains reorient freely, resulting in a broad structural ensemble, emphasizing the need to take an ensemble view on signaling of relevance to disease states. The structure provides the first experimental model of any full-length cytokine receptor in a lipid membrane and exemplifies how integrating experimental data from several techniques computationally may access structures of membrane proteins with long, disordered regions, a widespread phenomenon in biology.
INTRODUCTION
The human growth hormone receptor (hGHR) is ubiquitously expressed and is activated by human growth hormone (hGH), produced in the pituitary gland. hGHR is important for regulating growth at a cellular and systemic level (1, 2) and is involved in the regulation of hepatic metabolism, cardiac function, bone turnover, and the immune system (3). Besides direct promotion of growth, its ligand hGH can also indirectly regulate growth by initiating the synthesis of insulin-like growth factor-I, an important factor in postnatal growth (4). Excess hGH production and mutations in the hGHR gene manifest in different diseases including cancer (5) and growth deficiencies (6), with associated cardiovascular, metabolic, and respiratory difficulties, and both hGH-based agonists and antagonists of the receptor exist as approved drugs (7).
The hGHR is 1 of ~40 receptors belonging to the class 1 cytokine receptor family. The family is topologically similar with a tripartite structure consisting of a folded extracellular domain (ECD), a single-pass transmembrane domain (TMD), and a disordered intracellular domain (ICD) (8, 9). A characteristic trait of these receptors is the lack of intrinsic kinase activity, with the ICD, instead, forming a binding platform for a variety of signaling kinases and regulatory proteins (8, 10), as well as of certain membrane lipids (Fig. 1A) (9). Within the ECD, the receptors share a characteristic cytokine receptor homology domain consisting of two fibronectin type III domains (D1, N-terminal and D2, C-terminal), each with a seven-stranded β-sandwich structure. Two hallmark disulfide bonds and a conserved WSXWS motif (X is any amino acid) (11) located in D1 and D2, respectively, are suggested to be important for cell surface localization and discrimination between signaling pathways (11, 12). In hGHR, this motif is instead YGEFS (10), but the reason for this variation has remained enigmatic. Besides hGHR, group 1 of the class 1 cytokine receptors also encompasses the prolactin receptor (PRLR) and the erythropoietin (EPO) receptor. The group is considered to be the most structurally simple with one cytokine receptor homology domain and ligand binding in a homodimeric 2:1 complex (10).
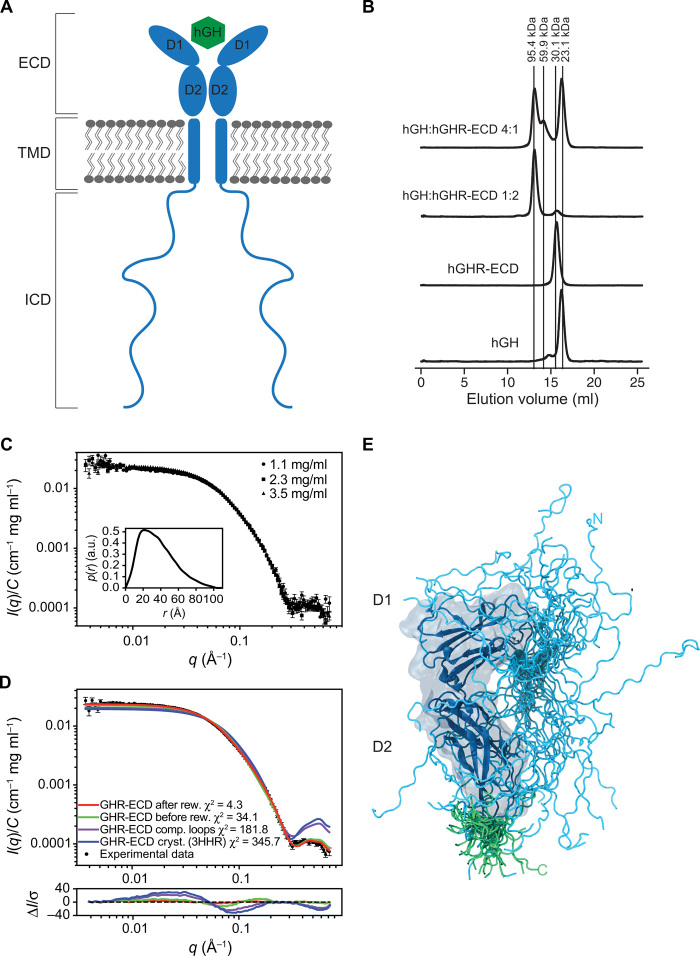
Fig. 1. The hGHR has a dynamic ECD with a broad structural ensemble.
(A) A schematic representation of homodimeric hGHR (blue) in the membrane in complex with hGH (green). ECD, Extracellular domain; TMD, transmembrane domain; and ICD, intracellular domain. (B) SEC profiles of hGHR-ECD and hGH in 20 mM Na2HPO4/NaH2PO4 (pH 7.4) and 150 mM NaCl at ratios 1:0 (hGH:hGHRECD 1:0), 0:1 (hGH:hGHR-ECD 0:1), 1:2 (hGH:hGHR-ECD 1:2), and 4:1 (hGH:hGHR-ECD 4:1). Absorption was measured at 280 nm. (C) Concentration-normalized SAXS data from hGHR-ECD (concentrations in legend) with the p(r) from the sample (3.5 mg/ml) shown as inset. a.u., absorbance units. (D) SAXS data from hGHR-ECD at 3.5 mg/ml (black dots) together with fits of the theoretical scattering curves from a crystal structure of hGRH-ECD (blue; PDB 3HHR), the same crystal structure with missing loops completed (purple), and the average (green) and reweighted average [red; reweighted against the experimental data using the Bayesian maximum entropy approach (see Materials and Methods)] of scattering curves of the 500 hGHR-ECD models with added N- and C-terminal tails. Residuals are plotted below. (E) An ensemble model of the hGHR-ECD with a representative reweighted subensemble of 100 models highlighting the N-terminal (cyan) and C-terminal (green) dynamic tails.
Receptor activation is achieved by hGH binding to hGHR via two asymmetric binding sites, leading to structural rearrangements that are propagated through the TMD to the ICD. A recent study found that when hGH binds to a preformed hGHR dimer, structural rearrangements in the ECD leads to separation of the ICDs just below the TMD (13). This leads to activation through cross-phosphorylation of the Janus kinases 2 (JAK2) bound at the proline-rich Box1 motif in the juxtamembrane region (13). Furthermore, this study demonstrated that receptor dimerization in isolation is insufficient for receptor activation (13). Nonetheless, while recent single-particle tracking studies suggested dimerization to depend on expression levels (14), it is still debated to what extent the hGHR exists as preformed dimers in vivo (15) or whether the hGHR only dimerizes upon hGH binding.
From the viewpoint of structural biology, the hGH/hGHR system has a high molecular complexity with ordered and disordered domains joined by a minimal membrane embedded part. Hence, structural characterization has, so far, been based on a divide-and-conquer approach, where the domains have been studied in isolation. This includes the crystal structures of the ECD in the monomeric state (15), in 1:1 (16) and 2:1 (17) complexes with hGH, and of hGH alone (18). Furthermore, structures of the dimeric state of the hGHR-TMD in detergent micelles have been solved by nuclear magnetic resonance (NMR) (19) spectroscopy, while the hGHR-ICD was shown by NMR to adopt a fully intrinsically disordered region (IDR) (9). A recent approach that combined experimental data with computational efforts provided a model of the similar PRLR monomer built from integration of several individual sets of experimental data recorded on isolated domains (20). This work provided the view of a full-length class 1 cytokine receptor to scale. However, no structure or model based on data collected on an intact, full-length class I cytokine receptor exists, leaving a blind spot for how the domains affect each other and are spatially organized.
Even with advances in cryo–electron microscopy (EM), the full-length hGHR remains a challenge to structural biology. With 70 kDa, the receptor is a small target for cryo-EM, but adding to this, the fact that more than 50% of the protein is intrinsically disordered leaves only ~30 kDa visible. Likewise, the disorder of the ICD also hampers crystallographic studies. On the other hand, a 70-kDa protein together with membrane mimetics make up a too large target for NMR, where the combined molecular properties would lead to slow tumbling and severe line broadening. Hence, the hGHR appears to be an orphan in structural biology, along with a large group of other membrane proteins with long, disordered regions, including most of the ~1400 human single-pass membrane proteins (21).
Integrative structural modeling is a powerful approach to combine different sources of experimental information to study the structure and dynamics of biomolecules (22). Such approaches are particularly suitable for large and dynamic molecules whose structure cannot be solved by traditional means. When experimental information comes from lower-resolution techniques, such as solution small-angle x-ray and neutron scattering (SAXS/SANS), it is often necessary to combine the experimental information with molecular simulations or other modeling techniques (22, 23). The best choice of experiments and computational models depends on the system at hand, including its size and level of flexibility. For large and highly flexible systems, coarse-grained (CG) simulations provide a suitable balance between the ability to sample many different types of conformations and capturing key aspects of protein biophysics (23, 24). Recent advances building on the use of nanodiscs (25) have further proved its applicability in membrane protein structural biology when combined with computational modeling (26, 27). However, no membrane protein with the degree of disorder seen in hGHR has previously been studied in a nanodisc or approached by small-angle scattering.
Here, we applied an integrative approach to probe the structure of the monomeric hGHR from SAXS data recorded on the full-length receptor in a nanodisc. The data were validated and interpreted by combining SAXS, NMR, and x-ray diffraction (XRD) data obtained on the individual domains of hGHR through computational modeling. This has resulted in an experimentally supported structure based on studies of an intact, full-length, single-pass cytokine receptor in a lipid membrane, a topology that represents ~40 human cytokine receptors and many other membrane proteins. Our approach exemplifies that combining SAXS and computational modeling could be the bridge required for accessing structural information on the ~1400 single-pass receptors in humans (28).
RESULTS
To arrive at the final result of this work, we took on a three-step approach. First, to aid the analysis of SAXS data on the full-length hGHR and qualify the integrity of the methodology, several different biophysical data were acquired and analyzed on isolated, individual parts of the hGHR. Second, SAXS and SANS data were acquired on the full-length hGHR in nanodiscs, expressed in yeast cells and carrying a C-terminal green fluorescent protein (GFP)–deca-histidine tag (GFP-H10). Last, all the data were interpreted and integrated using molecular dynamics (MD) simulations.
The binding-competent hGHR-ECD solution state ensemble contains disorder
While crystal structures of an N- and C-terminally truncated version of the hGHR-ECD exist (16–18), the complete hGHR-ECD has not previously been studied in solution. Therefore, to describe the ensemble of the full domain, we purified hGHR-ECD (residues 1 to 245, omitting the signal peptide) and hGH from expression in Escherichia coli. On the basis of circular dichroism (CD) data, the hGH was folded with the expected helicity (fig. S1A). The CD spectrum of hGHR-ECD had pronounced positive ellipticities around 230 nm stemming from aromatic exciton couplings, a trait of cytokine receptors, and showed additional contributions from disorder at 200 nm (fig. S1B). The functionality of the hGHR-ECD was confirmed from its ability to form complexes as determined by Kav for hGH and its 1:1 and 1:2 complexes with hGHR-ECD from analytical size exclusion chromatography (SEC) (Fig. 1B and fig. S1, C and D). By varying the ratio of hGH to hGHR-ECD, we could isolate the 1:2 complex and the 1:1 complex (GH in four times excess) and obtain the mass of hGH, hGHR-ECD, and the 1:1 and 1:2 complexes using the forward scattering from SAXS approximated through the derived pair-distance distribution functions, p(r)’s (table S1 and fig. S1, E to G). Thus, the structural and functional integrity of both renatured proteins were confirmed. Last, to understand the ensemble properties of the hGHR-ECD in solution and generate a model, we acquired SAXS data on free hGHR-ECD at varying concentrations. The concentration-normalized SAXS data fully overlaid (Fig. 1C), showing no visible interaction effects. The derived p(r) (Fig. 1C, inset) was skewed with a broad maximum around 30 Å and a maximum length (Dmax) of ~100 Å, consistent with the hGHR-ECD having a nonglobular shape. Comparison of the SAXS data to a theoretical scattering profile obtained from one of the structures of hGHR-ECD (PDB 3HHR) (17) resulted in a poor fit (Fig. 1D, blue). However, the absence of the N- (1 to 30) and C-terminal (231 to 245) tails and two disordered loops (57 to 61; 74 to 77) may account for this and highlights that these tails contribute importantly to the ensemble properties. We therefore built a model of the hGHR-ECD, where the missing loops were added. The calculated scattering profile of this model provided a slightly improved fit to the SAXS data, which further suggested that a substantial contribution to the scattering comes from the conformational heterogeneity of the N- and C-terminal tails. To address this issue, we built an ensemble of 5000 models of the full-length hGHR-ECD including the N- and C-terminal tails using the “Floppy tail” (29) protocol from Rosetta (30). An average of the theoretical scattering intensities from these models was fitted to the experimental SAXS data (Fig. 1D, green) with χ2 of 34, about five times smaller than when using the crystal structure and a single conformation with completed flexible loops. Thus, an ensemble representation including the terminal tails provided a much better fit to the SAXS data. The ensemble was further refined by reweighting against the experimental data using the Bayesian maximum entropy (BME) approach (31), which brought χ2 to 4.3 using effectively 27% of the models (Fig. 1D, red). The Rg distributions of the models before and after reweighting are shown in fig. S1H. A subensemble of 500 conformations, representative of the reweighted ensemble, was generated. Although any of these conformations would be a good representative, we selected a single structure with an Rg most similar to the experimentally determined Rg for building the model of the full-length hGHR (see below). A total of 100 conformations of this subensemble are shown in Fig. 1E, illustrating how the disordered regions contribute to the space-filling properties of the hGHR-ECD.
The monomeric hGHR-TMD is organized parallel to the membrane normal
Structures of hGHR-TMD were recently solved in dimeric states (19) in micelles of the detergent d38-dodecylphosphocholine (DPC). To describe the structure and the tilt angle of the monomeric hGHR-TMD relative to the membrane, we designed this domain of hGHR with six- and five-residue overlap with hGHR-ECD and hGHR-ICD, respectively. The resulting 36-residue hGHR-TMD (F239-R274), including an N-terminal Gly-Ser, was produced with and without isotope labeling by a fast-track production method for single-pass TMDs (32). Subsequently, the peptides were reconstituted in either lipid bilayers (see below) or 1,2-dihexanoyl-sn-glycero-3-phosphocholine (DHPC) micelles, previously used successfully for structure determination of the closely related hPRLR-TMD (20).
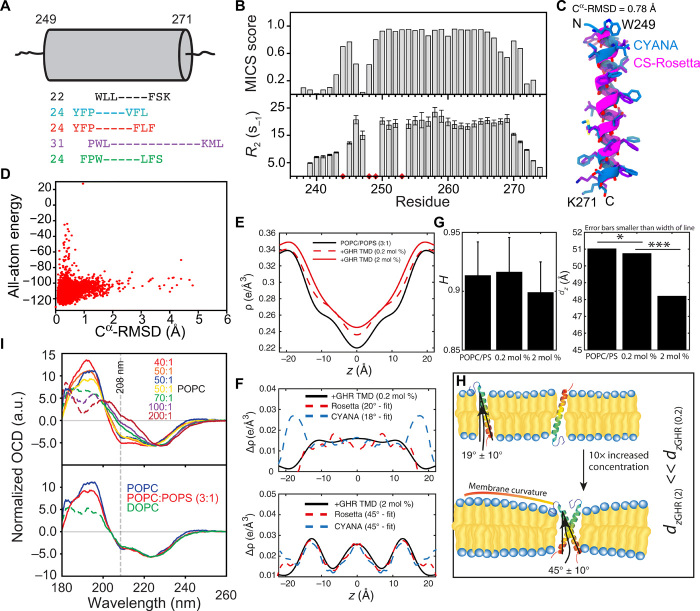
A schematic overview of the extent of the hGHR-TMD α helix determined by NMR spectroscopy or bioinformatics is shown in Fig. 2A. To compare the structural characteristics of this hGHR-TMD with the previously published structures (19), we analyzed isotope-labeled hGHR-TMD in DHPC micelles by NMR and CD spectroscopy (Fig. 2B and fig. S2, A and B). From motif identification from chemical shifts (MICS) analysis (33) of NMR backbone chemical shifts and from backbone amide R2 relaxation measurements, we observed that the hGHR-TMD populated a fully formed α helix in DHPC micelles from W249-K271 (Fig. 2B). This agrees with the findings for hGHR-TMD dimers in DPC micelles (19), suggesting the length of the TMD α helix to be maintained across different membrane mimetics. For building the full-length hGHR model (see below), we used the backbone chemical shift–derived dihedral angles (from TALOS) or the chemical shifts directly to calculate a low-resolution structure of the TMD, either by CYANA (34) or CS-Rosetta (35), respectively. The helix covered W249-K271 in both structures, which aligned with a root mean square deviation (RMSD) of the Cαs of 0.78 Å (Fig. 2, C and D).
Fig. 2. The single-pass α-helical hGHR-TMD.
(A) Extent of the hGHR-TMD α helix by NMR (black), TMHMM (blue), Phobius (red), METSAT-SVM (purple), and UniProt (green) (fig. S2). Cylinder represents length of the hGHR-TMD α helix by NMR with the first and last helical residue numbered. (Left) Predicted numbers. (B) MICS α helix probability (top) and R2 relaxation rates (bottom) of hGHR-TMD in DHPC micelles. Red diamonds, insufficient data quality or prolines. (C) Models of hGHR-TMD α helix by CYANA (blue) or CS-Rosetta (magenta). (D) Energy versus Cα-RMSD from CS-Rosetta modeling of hGHR-TMD. (E) Electron density profiles (EDPs) of lipid bilayers [POPC:POPS 3:1 mole percent (mol %)] with hGHR-TMD at 0.2 and 2 mol %, respectively. (F) Difference EDPs and best-fit profiles for the hGHR-TMD CS-Rosetta and the CYANA models, respectively. (G) Hermans orientation (left) and Lamellar spacing (right) of membranes at varying concentrations of hGHR-TMD. *, onefold change; ***, threefold change. (H) Illustration of membrane curvature. (I) Top: Oriented CD (OCD) spectra of 6 μg of hGHR-TMD in POPC, with L:P ratios varied from 1:40 to 1:200. Bottom: OCD spectra of 6 μg of hGHR-TMD in POPC, POPC:POPS (3:1), or DOPC at an L:P ratio of 50:1. The dashed lines represent nonreliable data due to too high high-tension voltage values.
To support the modeling, we reconstituted the hGHR-TMD in a more native-like membrane system of stacked bilayers. We used 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC):1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-l-serine (POPS) (3:1 molar ratio) and investigated structures and tilt angles by XRD, taking advantage of the oligomeric state of single-pass TMDs that may be manipulated through the detergent-to-protein or lipid-to-protein (L:P) ratio (19). The measured reflectivity Bragg peaks allowed us to determine the electron density profiles (EDPs), ρ(z), of the different bilayer structures (Fig. 2E) and EDP difference plots, Δρ(z) (Fig. 2F), of the membranes with and without inserted hGHR-TMD helices at varying molar ratios. The EDPs contain information about the position in the membrane and tilt angle. The EDPs of the helices were calculated for the monomer based on the CS-Rosetta and CYANA structures, respectively, and for the dimer based on a previously determined NMR structure [PDB 5OEK (19)]. This was done for different tilt angles and fitted to the experimental densities (36).
Our XRD analysis showed that at monomer conditions for the hGHR-TMD (high L:P ratio of 500:1; Fig. 2F, top), the helix remained parallel to the membrane normal (tilt angle of 19° ± 10°) without effects on membrane thickness, dz. The discrepancy between fit and experimental data at z values of ~18 Å (in the head group region of the membranes) for the CYANA model in 0.2 mole percent (mol %) results from the fact that the CYANA model includes the unstructured tail (which is not part of the Rosetta model). This tail partitions into the water phase and is not well picked up in the EDP structure. Within the membrane bilayer, the fitting to the CYANA model was, therefore, slightly better. At dimer conditions (low L:P ratio of 50:1), we found that the helix tilt angle changed to 45° ± 10° relative to the membrane normal, in accordance with the hGHR-TMD dimer structures (Fig. 2F, bottom) (19). While the membrane flatness and intactness, as measured by Hermans orientation function H, was unaffected by the presence of monomers or dimers (Fig. 2G, left), the dimer induced some membrane compression, giving rise to a slightly thinner bilayer with smaller laminar spacing, dz (Fig. 2G, right). An illustration of this behavior is shown in Fig. 2H.
To support these observations, we used oriented CD (OCD) spectroscopy with reconstitution of the hGHR-TMD in POPC, POPC:POPS (3:1), or 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) multilamellar bilayers (Fig. 2I and fig. S2C). In OCD, the ellipticity of the negative band at 208 nm, which is parallelly polarized to the helix axis, is strongly dependent on helix orientation, allowing distinction between a fully inserted state (I state, parallel to membrane normal), a tilted state (T state), and a surface-bound state (S state, perpendicular to the membrane normal). At dimer conditions (L:P ratio of 50:1), the OCD spectra showed two negative bands at 208 and 222 nm and a positive band at 190 nm in all types of membranes tested (Fig. 2I), indicating successful reconstitution with formation of helical structure. Furthermore, the negative ellipticity at 208 nm was smaller compared to that at 222 nm, demonstrating the hGHR-TMD to be either in a T state or in an equilibrium between an S state and an I state (37). Increasing the L:P ratio decreased the negative band intensity at 208 nm, which even became positive at an L:P ratio of 200:1 (Fig. 2I, top). This indicated that at monomer conditions, the hGHR-TMD populated the more parallel I state, fully supporting the results from XRD.
A C-terminal GFP has no influence on the ICD ensemble
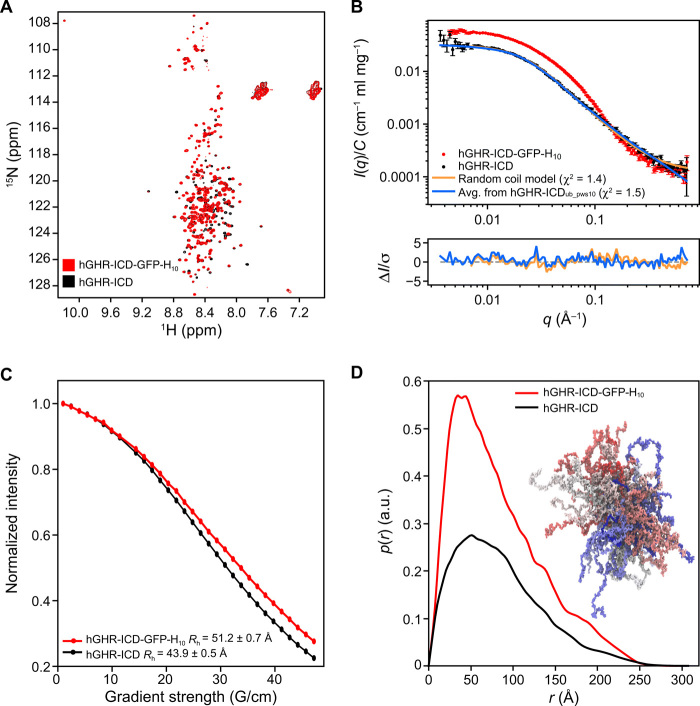
For purification of the full-length hGHR, a C-terminal GFP-H10-tag had to be included (21). To ensure that this did not introduce intra- or intermolecular interactions interfering with the hGHR-ICD ensemble, we produced the hGHR-ICD (S270-P620) without and with GFP-H10 (hGHR-ICD-GFP-H10). The 15N–heteronuclear single-quantum coherence (HSQC) spectra of these two proteins were almost identical (Fig. 3A), confirming an unperturbed ICD ensemble. We also compared SAXS data acquired on both, which revealed a large increase in the forward scattering in the presence of GFP (Fig. 3B), reflecting the increase of the molar mass from 38.6 kDa for hGHR-ICD to 68.0 kDa for hGHR-ICD-GFP-H10 (table S1). The derived p(r) functions (Fig. 3D) showed not only an increased probability of short distances because of the folded GFP but also a conserved Dmax consistent with an overall unaffected ICD coil conformation. The addition of GFP did not give rise to a significant change in Rg (65 Å for both) (Fig. 3B), whereas the hydrodynamic radius (Rh) obtained by NMR spectroscopy increased from 44 to 51 Å (Fig. 3C). We note that Rg/Rh of ~1.5 for the hGHR-ICD falls in the range typically observed for linear chains in random coil conformations, while the smaller ratio obtained for the hGHR-ICD-GFP-H10 is consistent with the hGHR-ICD-GFP-H10 containing a larger fraction of folded protein. Together, these results indicate that the C-terminal addition of GFP-H10 did not change the structural ensemble of hGHR-ICD.
Fig. 3. Properties of the hGHR-ICD ensemble.
(A) 1H-15N-HSQC spectra at 5°C of hGHR-ICD (black) and hGHR-ICD-GFP-H10 (red) at 150 and 100 μM, respectively. (B) Concentration normalized SAXS data from hGHR-ICD (black dots; 1.1 mg/ml) and hGHR-ICD-GFP-H10 (red dots; 2.2 mg/ml). Fits to the data are shown for a Gaussian random coil model (orange) and from averaged scattering profiles from 5200 conformations taken from the hGHR-ICDub_pws10 simulation (one every nanosecond) (blue). Residuals are plotted below. (C) RH of hGHR-ICD and hGHR-ICD-GFP-H10 determined from pulse-field gradient NMR. Signal decays of hGHR-ICD (black) and hGHR-ICD-GFP-H10 (red) are shown as a function of gradient strength together with the corresponding fits. (D) Concentration normalized p(r)’s derived from the above SAXS data from hGHR-ICD (black) and hGHR-ICD-GFP-H10 (red). A subensemble of 200 conformations representative of the hGHR-ICDmetaD_pws10 simulation is shown in the right side of the plot.
Scaling of the protein-water interactions is required to simulate the ensemble properties of hGHR-ICD
To aid in interpretation of the data of the full-length hGHR, the ensemble properties of the hGHR-ICD were modeled on the basis of the SAXS data following two approaches: (i) through fitting of the data by the form factor for simple (non–self-avoiding) Gaussian random coils (38) and (ii) using CG-MD simulations adapted to better represent the dynamics of intrinsically disordered proteins (IDPs), providing an ensemble that better describes the experimental data. Approach (i) provided an excellent fit to the full experimental SAXS q range, yielding an Rg of 68 ± 4 Å (Fig. 3B, orange) with a χ2 of 1.4. This showed the average conformation of the hGHR-ICD to be very well described by a simple random coil model, which implicitly assumes a scaling exponent, ν = 0.5. We also obtained similar Rg values (~65 Å) from fits using different scaling exponents (0.588 to 0.602) empirically predicted for unfolded proteins or IDPs or derived from computational analyses (table S2). Hence, the values agree closely, and the effect of assuming a simple idealized Gaussian random coil model has a negligible effect on the resulting Rg.
Protein-protein interactions may be overestimated in the Martini force field translating into unrealistic compaction of disordered regions and inability to reproduce experimentally obtained values for Rg or Rh (24). Recent reports investigating two multidomain proteins connected by flexible linkers suggested that this could be overcome by increasing the strength of protein-water interactions (24). In the case of hGHR with a long, disordered ICD, we performed unbiased and enhanced sampling metadynamics simulations using the Martini 3 force field modified by increasing the strength of the protein-water interactions in the range of 5 to 15%. Our goal was to search for a value that could provide an optimized description of the ensemble of GHR-ICD. Back-mapped atomistic conformations from these simulations were used to calculate their average Rg and to obtain theoretical scattering intensities, which were then fitted to the SAXS data of hGHR-ICD (fig. S3). Our results indicate that an increase in the protein-water interaction strength of 10% produced optimal results (Fig. 3B and fig. S3). Thus, we settled on rescaling the protein-water interaction by 10% to obtain a reliable conformational ensemble of the hGHR-ICD and to be used in the simulation of the full-length hGHR-GFP system. We note that although lowly populated (<20%) transient helices were previously observed from NMR secondary chemical shifts (9), these are not to be captured by the CG simulations or the SAXS data.
Full-length hGHR reconstituted in nanodiscs forms monomers and dimers
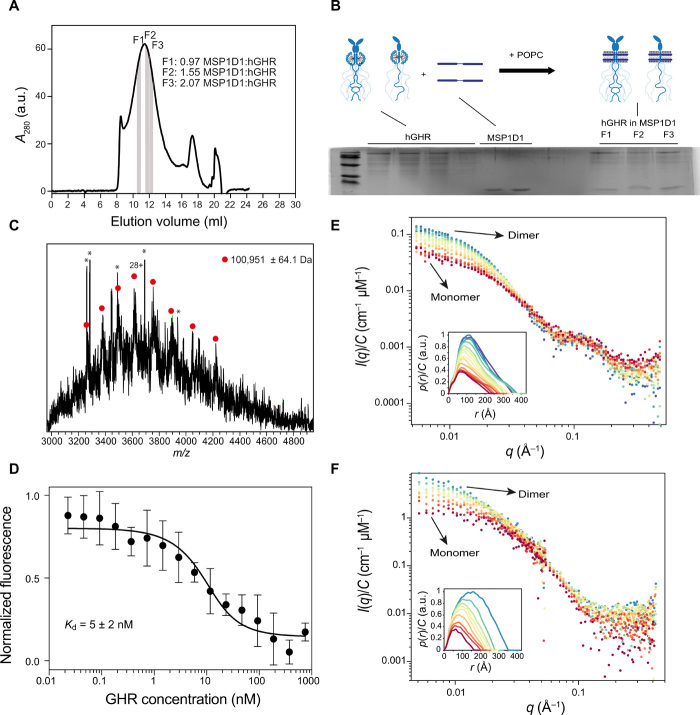
The intact hGHR tagged with GFP-His10 (hGHR-GFP) was expressed in the Saccharomyces cerevisiae strain PAP1500, purified, and reconstituted into POPC-loaded membrane scaffold protein 1D1 (MSP1D1) nanodiscs as described in Kassem et al. (21). Although an NMR solution structure of the MSP1D1ΔH5 exists based on their reconstitution with a 1,2-dimyristoyl-sn-glycero-3-phosphocholine bilayer (39), we used the MSP1D1 nanodisc and POPC, as this combination is currently the most-applied and best-characterized carrier system by SAXS and SANS (40–42), making experimental handling and subsequent computation of the nanodisc-embedded full-length structure of hGHR more reliable. In SEC, the hGHR-GFP in MSP1D1 eluted over a broad peak from 10 to 14 ml (Fig. 4A). This suggested that the hGHR-GFP was reconstituted in the discs potentially as both monomers and dimers or as higher-order oligomers. To quantify the number of hGHR-GFP per disc, we performed an SDS–polyacrylamide gel electrophoresis (PAGE) analysis of hGHR-GFP and MSP1D1 standards along with hGHR-loaded MSP1D1 discs isolated from the SEC at different elution volumes (Fig. 4B). From gel quantifications of hGHR-GFP and MSP1D1, we found the ratio over the peak to vary from ~2 hGHR-GFP per disc (F1) to ~1 hGHR-GFP per disc (F3). Since reconstitution was conducted with a 10-time excess of discs to hGHR-GFP to minimize the probability of capturing more than one hGHR-GFP per disc, we argue that the distribution across the peak likely represents the equilibrium between dimeric and monomeric hGHR-GFP. These results also suggested that the hGHR-GFP can form dimers in the absence of hGH as previously suggested (13), most likely through the TMD region (13, 15).
Fig. 4. Incorporation of hGHR-GFP into MSP1D1, functional, and structural analysis.
(A) SEC profile of hGHR-GFP-loaded MSP1D1. The areas highlighted in gray indicate fractions (F1 to F3) used for the SDS-PAGE analysis in (B). (B) SDS-PAGE analysis of hGHR-GFP and MSP1D1 standards along with hGHR-GFP-loaded MSP1D1. Fractions F1 to F3 were taken from the indicated positions of the SEC-purified hGHR-GFP-loaded MSP1D1 shown in (A). The illustration above the gel shows the stoichiometry of the hGHR-GFP-loaded MSP1D1. (C) Intact mass spectra of hGHR-GFP show a single protein population with an average mass of 100,951 ± 64 Da. Asterisks denote detergent peaks. (D) MST determination of equilibrium binding constants for hGH to hGHR-GFP-loaded MSP1D1. The mean values and SD were obtained by fitting a 1:1 binding model (full line) as described in Materials and Methods. Concentration-normalized (E) SAXS data and (F) SANS data of the nanodisc-embedded hGHR-GFP corresponding to the highlighted SEC frames in fig. S4 (C and D).
The number of lipids in the hGHR-loaded MSP1D1 nanodiscs is as expected
We used phosphorus analysis (43) performed on samples across the SEC peak (fig. S4A) to quantify the number of POPC lipids in the hGHR nanodiscs. In the fractions with dimers (F1), the ratio between MSP1D1 nanodiscs and POPC was 115 ± 19, and in the fraction with monomers (F3), it was 122 ± 17. The SD is based on two repetitive measurements each on two separate samples. This is comparable to results obtained in other studies of POPC nanodiscs with an α-helical membrane-anchored protein (27) and in good agreement with the values obtained for nanodiscs solely filled with POPC [~110 to 130 POPC per nanodisc (41)]. The number of lipids was used as input for the modeling of the SAXS data of hGHR-GFP-containing MSP1D1 nanodisc.
hGHR retains its signal peptide but is not N-glycosylated when produced in yeast
The hGHR has five confirmed N-glycosylation sites at N28, N97, N138, N143, and N282 (44), whereas it is unknown if it is O-glycosylated. To assess whether the recombinant hGHR-GFP from S. cerevisiae was N-glycosylated, the electrophoretic mobility before and after treatment with endoglycosidase H was evaluated (fig. S4B). No mobility change was observed, and the band sharpness was equally high before and after treatment, suggesting the lack of N-glycosylations. This is in line with previous observations on other human membrane proteins produced in the same yeast expression system (45). To determine whether yeast-produced hGHR-GFP was O-glycosylated, we performed Western blot with horseradish peroxidase conjugated with concanavalin A, which binds to mannose residues in O-glycosylated proteins (45). A faint band corresponding to hGHR-GFP was seen, indicating minor O-glycosylation (fig. S4B). As a negative control, MSP1D1 purified from E. coli was not detected (fig. S4B). As a final control, we recorded native mass spectrometry (MS) on the purified, full-length hGHR-GFP in detergent, before reconstitution into nanodiscs. No glycosylation was detected. Instead, as expected from the cellular localization (21), the hGHR-GFP maintained its signal peptide (SP) (expected mass of 100,850.44 Da; the small deviation in mass caused by Na+ adducts) (Fig. 4C).
Recombinant full-length hGHR-GFP reconstituted in nanodiscs is fully binding competent
To ensure that full-length hGHR-GFP embedded in the MSP1D1 nanodisc was functional, we measured equilibrium binding constants for the interaction between hGH and hGHR-GFP(MSP1D1) by microscale thermophoresis (MST). In these studies, a 20 nM solution of fluorescently labeled (NT-647-NHS) hGH was incubated with increasing concentrations of hGHR-GFP(MSP1D1) (23 pM to 750 nM) using unlabeled hGH as the control. With this approach, the dissociation constant between hGH and hGHR-GFP(MSP1D1) was determined to be Kd = 5 ± 2 nM (Fig. 4D). As another control, we previously showed that hGHR(MSP1D1) is unable to bind human prolactin (21), which cannot activate hGHR in vivo (46). The affinities of hGH for hGHR-ECD have previously been reported as 1.2 and 3.5 nM for the first and the second site of hGH, respectively (47). Taking all this into consideration, we find that our data agree well with previous findings and conclude that the nanodisc-reconstituted, yeast-produced full-length hGHR-GFP is fully binding competent.
SEC-SAXS and SEC-SANS data of the full-length hGHR-GFP in nanodiscs
We obtained structural data of the reconstituted full-length hGHR-GFP in a POPC-loaded MSP1D1 nanodisc from SEC-SAXS (Fig. 4E and fig. S4C) and SEC-SANS (Fig. 4F and fig. S4D) with p(r) functions in insets of Fig. 4 (E and F). As was the case for the initial analysis, the SEC profiles from both SEC-SAXS and SEC-SANS (fig. S4, C and D) were relatively broad and consistent with the underlying heterogeneity and systematic decrease of the particle size. Analysis of the data obtained over the SEC-SAXS and SEC-SANS elution peaks confirmed this picture, and SEC-SAXS showed Rg decreasing from 120 to ~75 Å over the frames from 10 to 14 ml (fig. S4C). The SEC-SANS–derived Rg also decreased steadily over the frames from 10 to 14 ml (fig. S4D) but were consistently ~10 Å smaller than in the SAXS experiment. The different Rg values for SAXS and SANS are a consequence of the nonhomogeneous and rather different excess scattering length density distributions of the nanodisc-embedded hGHR-GFP for x-rays and neutrons. The decrease in both the Rg, the low q scattering intensity, and the development of the p(r)’s over the SEC peaks is fully consistent with the presence of discs containing the first two and then one hGHR-GFP, respectively, as also supported by our biochemical analysis (Fig. 4, A and B). In addition to dimerization, the large Rg values obtained from the left side of the SEC peak could also arise from an overlap with the void volume (at 8 to 10 ml). We obtained a value of Dmax of ~200 to 250 Å from the SAXS data corresponding to discs with one hGHR. The low signal to noise at the right side of the SEC-SANS peak, corresponding to the monomeric fractions, did unfortunately not allow for a robust analysis of the SANS data. The dimeric fractions exhibited a significantly larger Dmax of ~350 Å in both SAXS and SANS. This larger size likely results from the larger extension of the two long uncorrelated ICDs. The shoulder around 0.1 Å−1 of the SAXS data (Fig. 4E) is a typical signature of the lipid bilayer from the embedding nanodiscs (26, 27, 48).
Below, we focus our analyses on the structure of monomeric hGHR-GFP. First, while we can build an initial model of a monomeric hGHR from the chain connectivity and structures of the ECD and TMD, building models of the hGHR dimer would require further assumptions on the dimerization interface. Second, experimental complications arise both from the potential overlap with the void volume in the SEC-SAXS/SANS experiments and from possible structural heterogeneity. This may originate not only from a dynamic monomer-dimer equilibrium but also from different dimers in the nanodisc: the biologically relevant down-down dimer conformation, a trapped up-down conformation, or higher-order structures. We therefore concentrated on the reliable SEC-SAXS data representing monomeric hGHR-GFP in a nanodisc and used these to obtain the monomeric full-length hGHR-GFP structure embedded in a nanodisc bilayer.
The structure of the monomeric full-length hGHR-GFP in a nanodisc
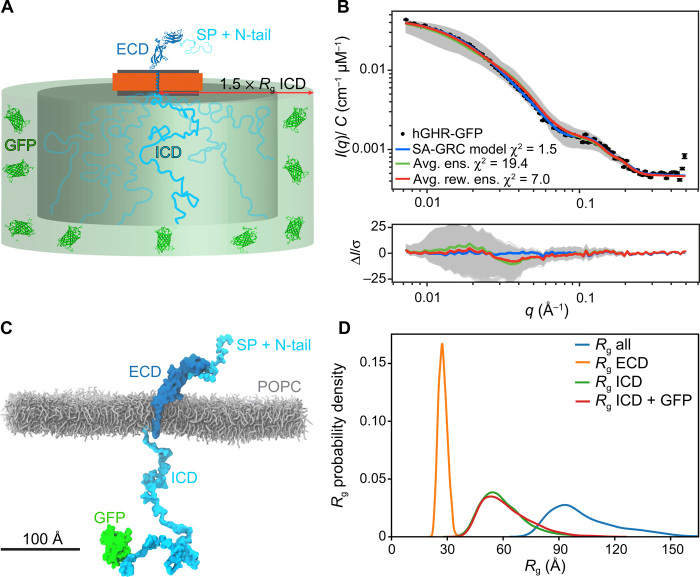
We followed a three-stage approach to derive a model of the structure of monomeric hGHR including the signal peptide and the GFP (hereafter named the hGHR-GFP) in the MSP1D1 nanodisc. First, we built a semianalytical model of the nanodisc-embedded full-length hGHR-GFP to refine the nanodisc parameters and to validate the overall structure of the complex. Second, we generated an ensemble of 6000 structures of the hGHR-GFP embedded in a POPC bilayer from 20 2-μs-long CG-MD simulations; these structures were back-mapped to all atoms and transferred to the model for the nanodisc. Last, from these models, we calculated the SAXS data of hGHR-GFP embedded in the nanodisc and compared to and refined against the SAXS data.
The semianalytical model of the SAXS scattering intensity from nanodisc-embedded hGHR-GFP (Fig. 5A) was calculated through the absolute squared sum of four scattering amplitude components arising from, respectively, the ECD-TMD, the ICD, the GFP, and the surrounding nanodisc (see Materials and Methods). The model, which implicitly includes the scattering cross-terms between the different components and take their internal phases into account, was implemented through the WillItFit platform (48). As in our previous work (26), we used a hybrid approach to the modeling, where different computational approaches were applied and combined for the four different components. Briefly, the ECD-TMD, which is connected through a flexible linker between the ECD and TMD, was represented as a single rigid body through the atomic coordinates of one of the models produced with Rosetta (see Materials and Methods). The disordered ICD and its ensemble of conformations was modeled with a Gaussian random coil model parametrized by its Rg with the center of mass displaced one Rg from the disc surface, but where the connections at the two ends, respectively, to the TMD and the GFP, were disregarded. The GFP attached to the ICD was described through its atomic coordinates (PDB 1EMA) and allowed to take a random orientation in a certain “confusion volume” in extension of the disordered ICD. For the surrounding nanodisc, we allowed, as in our previous work (26, 27, 40), the lipid bilayer disc to take a slightly elliptical shape parametrized through its axis ratio. This accounts for the combined effect of less than maximal lipid loading and shape fluctuations. As in our previous work (26, 27, 40), we further constrained and reparametrized the underlying geometrical model into physically meaningful molecular parameters such as the number of POPC per disc and the area of POPC per headgroup. The scattering intensity corresponding to the model was calculated and fitted on an absolute scale. An excellent model fit to the experimental data (χ2 = 1.5; Fig. 5B, blue) was obtained using a nanodisc containing 122 POPC lipids, each with an area per headgroup of 63 Å2 (49), an axis ratio of 1.4 of the elliptical bilayer, and an Rg of the Gaussian random coil modeling the ICD of 73 Å (see details of the model in Materials and Methods and full account of model fit parameters in table S3). The number of lipids per disc was kept fixed at the value obtained from the experimental phosphorous analysis (fig. S4A). Likewise, the axis ratio of 1.4 was fixed on the basis of previous analyses (41). We note that the resulting fitted POPC area per headgroup agrees well with previous values obtained for POPC-loaded MSP1D1 nanodiscs (27, 40) and that the Rg of the ICD accords with the value we determined for the isolated ICD. The analysis shows that the semianalytical model provides a low-resolution description of the nanodisc-embedded full-length hGHR-GFP and forms a basis for a more detailed molecular description.
Fig. 5. Model of the full-length hGHR-GFP in nanodiscs.
(A) Schematic representation of the semianalytical Gaussian random coil (SA-GRC) model. (B) Fits of the SA-GRC to the SAXS data of nanodisc-embedded hGHR-GFP (with GFP) (blue), the ensemble of 6000 conformations taken from the hGHR-GFP +POPCpws10 simulations embedded in the nanodisc model (gray), their ensemble average (green), and reweighted ensemble average (red). (C) Representative snapshot from one of the hGHR-GFP + POPCpws10 simulations (see Materials and Methods). POPC lipids are shown as gray sticks; protein is depicted in surface representation. Some lipids and all water and ions are omitted for clarity. (D) Distribution of Rg from 6000 all-atom conformations obtained from the hGHR-GFP + POPCpws10 simulation after reweighting against the SAXS data. The values are shown both for the full-length protein (blue) and for the individual structural components: ECD (orange), ICD (green), and ICD-GFP (red).
In the next stage, a CG representation was built containing the full-length hGHR-GFP receptor embedded in a POPC bilayer (Fig. 5C). The simulation included the signal peptide and, hence, residues −18 to 620 (total of 638 residues) of the hGHR plus GFP. This full-length hGHR-GFP model was simulated with Martini 3 using the 10% increase in the strength of protein-water interactions found optimal for simulation of the hGHR-ICD. We ran 20 different 2-μs-long simulations and extracted 300 conformations (one every 5 ns) from each trajectory, discarding the first 500 ns of each run to allow for equilibration, providing a total of 6000 conformations of hGHR-GFP. These were back-mapped to all-atom representations and, one by one, embedded in the analytical nanodisc model that had been optimized through the semianalytical approach and following the WillItFit-based procedure previously described (48). SAXS scattering curves were calculated from the obtained ensemble (Fig. 5B, gray) and averaged, taking the mean I(q) of the 6000 individual curves for each value of q (Fig. 5B, green). Comparison to the experimental SAXS data showed that the MD-derived model, despite not being refined against the experimental data, provided a relatively good fit to the experiments (Fig. 5B, green) with a χ2 of 19. We used the BME approach (31) to improve agreement with the data further. We tuned the hyperparameter, θ, which sets the balance between the information from the SAXS data and the force field to θ = 500 (fig. S5, A and B). This resulted in an ensemble effectively containing ≈70% of the conformations (ϕeff = 0.73) from the simulation and obtained a considerable improvement of the fit (χ2 = 7.0; Fig. 5B, red). The resulting model thus combines information about the conformational preferences of hGHR-GFP encoded in both the martini model and SAXS data.
We proceeded to analyze the structural properties of hGHR-GFP described by the reweighted ensemble. Looking at the individual domains within the full-length protein, we found (reweighted) Rg values of 60 ± 4 Å for hGHR-ICD, 62 ± 4 Å for hGHR-ICD-GFP, and 27 ± 2 Å for the hGHR-SP + ECD (Fig. 5D). Measurement of the reweighted average helix tilt angle (16° ± 1°) (see fig. S5C) shows that the TMD remains nearly parallel to the axis normal of the membrane plane as suggested by the XRD and OCD results obtained on the isolated hGHR-TMD. The ICD remained disordered and, for the most part, remained avoiding the membrane. Long-lived contacts and penetration of the bilayer were observed only for the intracellular juxtamembrane region (Q272-M277) and the Box1 motif (L278-K287) of the ICD, as well as for some residues from the ECD-TMD linker (fig. S5D, inset), in line with previous reports (9). Visual inspection of the trajectory (movie S1) showed that the ECD-TMD linker remained flexible, allowing the ECD to adopt a range of orientations while remaining mostly upright, as shown by the angle between the principal axis of the D2 domain and the z axis (reweighted average, 34° ± 3°; fig. S5E). We note that the D1 domain remained far from the lipid surface. The N-terminal tail (N-tail) of the ECD remained disordered without long-lived contacts with the folded part of the ECD or the membrane.
In summary, our integrative model of the full-length monomeric hGHR in a nanodisc, containing almost equal amounts of structural order and disorder, combines information from molecular simulations and SAXS data recorded on the complex molecular system. In this way, the model provides the first experimentally derived detailed molecular insight into the structure of an intact, full-length class 1 cytokine receptor in a lipid membrane carrier system.
DISCUSSION
Membrane proteins take on a variety of different topologies, sizes, and functions, and large portions of membrane proteins exist in tripartite structures that require different handling schemes and methodological studies. Such complexities are further amplified for membrane proteins having large fractions of structural disorder (21, 50, 51), which impose obstacles to classical structural biology. Thus, different topologies and order/disorder dispositions require different approaches, and one particular group of membrane proteins falls between the cracks by being too small and unstructured for cryo-EM, too large for NMR spectroscopy, and too dynamic for x-ray crystallography. An important subgroup of these membrane proteins, which plays key biological roles, is the cytokine receptor family.
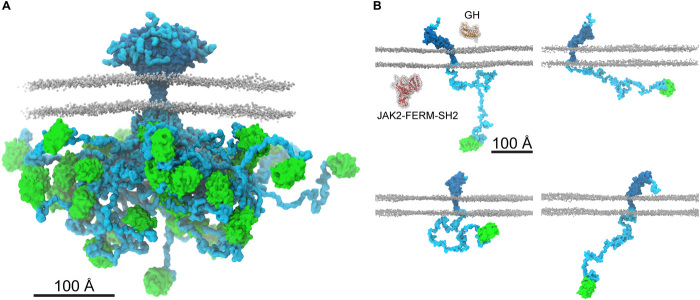
In the present work, we examined the structure of an archetypal and particularly challenging membrane protein, the cytokine receptor hGHR, for which 50% of its chain is intrinsically disordered (Fig. 6). The structure of the monomeric hGHR revealed that when inserted in a bilayer mimetic, neither the ECD nor the long, disordered ICD engage in long-lived contacts with the membrane. This is remarkable, although it should be noted that the lipids used in the current study do not fully mimic the complexity of native membranes by, e.g., lacking phosphoinositides or/and cholesterol, just as the proteoglycan layer on the extracellular side and the cytoskeleton on the inside are missing. We did, however, capture some lipid interactions by the intracellular juxtamembrane region (fig. S5D), which have been previously described (9). It is possible that the native composition of the bilayer may influence the conformation of the receptor, but, inherently, there is no affinity for the POPC bilayer. Thus, the intracellular, disordered domain protrudes from the bilayer and into the cytosol. Its average Rg of 65-70 Å corresponds to an average end-to-end distance of about twice this value. This defines its capture distance and the large search volume (Fig. 6 and fig. S5F), which allows it to scout for and engage with kinases, phosphatases, and regulatory proteins such as the signal transducer and activator of transcription (STAT), suppressors of cytokine signaling, and the cytoskeleton (52).
Fig. 6. The ensemble structure of membrane-embedded full-length hGHR-GFP.
(A) Representative ensemble of conformations obtained from the last 1.5 μs of each of the 20 runs of 2-μs hGHR-GFP + POPCpws10 simulations. Color scheme and representations as in Fig. 5C. (B) Examples of the multitude of domain orientations of hGHR-GFP in the membrane. In the first panel, the structures of hGH (PDB 3HHR_A; orange) and of JAK2-FERM-SH2 (PDB 4Z32; red) are shown. Color scheme and representation of hGHR and POPC as in Fig. 5C.
A particular noteworthy observation from the structure of hGHR is the disordered, ~30-residue N terminus of the ECD, which has been neglected in all previous structural studies. The role of this N-terminal IDR in GHR function is unknown, but N-terminal IDRs are present in other family members, including the EPOR. An isoform of the GHR with a 22-residue deletion in the disordered N-tail (d3-GHR) shows altered extracellular signal–regulated kinase 1/2 signaling but unaltered STAT5 signaling, and d3-GHR individuals show increased life spans (53). Thus, key functional relevance is coupled to the N-tail. A search in the eukaryotic linear motifs database (54) suggests the presence of a glycosaminoglycan (GAG) attachment site, 1FGFS4, in the N-tail. Of relevance to this, the WSXWS motif, which in hGHR is YGEFS, constitutes a C-mannosylation site linking the C1 atom of the α-mannose to the indole C2 atom of the tryptophan (3, 12). The WSXWS motifs has also been suggested to bind GAGs (12), so it is possible that the disordered N-tail of hGHR play similar roles as the WSXWS motif, and we notice a degenerate motif of this kind, also in the N-tail, given by the sequence 16WSLQS20. Nonetheless, the function of the disordered N-tail of hGHR remains unestablished.
The integrative nature of our approach to determine the structure of the hGHR required development and optimization of several protocols. This was particularly necessary during the modeling and fitting of the SAXS data based on the combined semianalytical and experimentally driven molecular modeling approach to account for the structure and large flexibility of the hGHR. Key to the success was a scaling of the strength of the protein-water interaction in the CG-MD simulations of the ICD and full-length hGHR. This enabled reliable fits to the disordered chain in terms of Rg. On the semianalytical modeling side, we have expanded our previous approaches to interpret scattering data from bare nanodiscs and rigid membrane proteins incorporated into these discs (26, 27, 40), to now also allow for modeling membrane proteins with significant amounts of structural disorder. We emphasize that even if the parameters of the GHR model are custom-fitted to the hGHR-GFP system, the approach is fully generalizable and may be adapted to membrane proteins of similar topology provided that high-quality scattering data are available. Thus, the use of this integrative semianalytical and MD simulation–based approach suggests that SAXS (and SANS) in combination with MD simulations is a useful way of providing structural insight into otherwise “method orphan” membrane proteins, particularly highlighting the interdomain orientations. This opens for more systematic investigations of, for example, single-pass transmembrane proteins in different environments, e.g., with respect to the lipid composition, the buffer environment, or with binding partners to understand how these very dynamic membrane proteins transduce information across the membrane. Furthermore, structures of not only other single-pass membrane proteins with similar complexity such as the cadherins and cell adhesion molecules (e.g., Down syndrome cell adhesion molecule) but also membrane proteins with long, disordered regions such as the solute carrier family 9, type II receptor serine/threonine family, and palmitoyl transferases now become accessible.
A key observation made possible from acquiring data on the full-length hGHR is the lack of restriction on the relative orientation of the domains (Fig. 6). Not only is the ICD and the N-tail disordered but also the flexible linker joining the ECD and TMD, which combined with the lack of membrane association allow them to freely reorient relative to each other, at least in the free state (Fig. 6). Thus, in addition to structure, it becomes important to consider how the flexibility of the entire chain takes on roles in signaling. From our studies, we were not able to derive whether correlated motions between the ECD and the ICD exist. However, once the hGH binds to the ECD, changes in conformation and flexibility may propagate along the chain, reaching the ICD and bound protein partners, eliciting signaling. Similar suggestions were put forward on the basis of data from solid-state NMR studies on the epidermal growth factor receptor, revealing increased dynamics in the bound state (55). Since the JAK2 binding site only constitutes ~6% of the ICD, and the STAT5 docking sites are ~200 to 300 residues away from it (56), conformational changes involving redistribution of the structural ensemble of the long, disordered region need to be achieved in a controlled manner. In addition, the ICD contains many short linear motifs (SLiMs), distributed along the chain in SLiM hotspots (8), and the space occupied by the free ICD (fig. S5, E and F) may therefore enable room for generation of larger, supramolecular signaling complexes. With the presence of two disordered chains in a dimer, the occupied space of each ICD chain may be reduced because of steric exclusion, affecting the formation and content of supramolecular complexes. With a structure of a full-length membrane protein embedded in a realistic membrane scaffold and containing a large disordered chain at hand, the understanding of regulation of signaling by disordered chains, often present in higher-order assemblies of several chains, now has a molecular platform from which new questions can be tackled.
MATERIALS AND METHODS
hGHR-ECD expression and purification
The DNA sequence coding for hGHR-ECD (1 to 245, C242S, no signal peptide) in a pET11a was bought from GenScript and transformed into competent Rosetta2 (DE3)pLysS cells. These were grown in 1 liter of LB medium with 3% (v/v) ethanol containing ampicillin and chloramphenicol (100 μg/ml) to OD600 (optical density at 600 nm) = 0.6 to 0.8, and induced by addition of 0.5 mM isopropyl-β-d-thiogalactopyranoside (IPTG) for 4 hours at 37°C and 160 revolutions per minute (RPM). The cells were harvested by centrifugation (5000g for 15 min) and resuspended in one-time phosphate-buffered saline (PBS) (140 mM NaCl, 2.7 mM KCl, 10 mM Na2H2PO4, and 1.8 mM KH2PO4) (pH 7.4) containing 25% (w/v) sucrose and 5 mM EDTA. The cells were lysed on ice by sonication using an UP400S ultrasonic processor, 6 × 30-s sonication followed by 30-s rest at 50% amplitude. Following centrifugation (20,000g, 4°C) for 25 min, the pellet was resuspended in one-time PBS (pH 7.4) containing 25% (w/v) sucrose and 5 mM EDTA, repeated three times in total. The pellet was solubilized in 500 ml of 50 mM tris-HCl (pH 8.5), 10 mM β-mercaptoethanol (bME), and 6 M urea, heated for 5 min at 55°C, and left O/N (overnight) with slow stirring at 4°C. The amount of hGHR-ECD was estimated on an SDS-PAGE by comparing to the LMW (low molecular weight and diluted to a concentration less than 0.1 mg/ml in 50 mM tris-HCl (pH 8.5), 10 mM bME, and 6 M urea. To refold, hGHR-ECD was dialyzed against 4 liters of 150 mM NaCl, 50 mM tris-HCl (pH 8.5), 10/1 mM cysteamine/cystamin at 4°C, and a molecular weight cutoff of 12 kDa until the urea concentration was below 0.1 M. Following centrifugation at 20,000g for 15 min, the sample was placed on ice and stirred slowly, while ammonium sulfate was added to a final concentration of 75% (w/v) and then left for 2 hours. The solution was centrifuged at 12,000g at 4°C for 25 min, and the pellet was dissolved in 100 ml of Milli-Q water and left for 2 hours, followed by dialysis against 30 mM NH4HCO3 (pH 8.0) overnight at 4°C. After centrifugation at 13,000g for 15 min, the supernatant was concentrated using a Millipore spin filter (10 kDa cutoff) and applied to a Superdex 75 16/85 column (GE Healthcare) at 4°C, 150 mM NaCl, and 30 mM NH4HCO3 (pH 8.5). Selected fractions were reapplied to a Superdex 200 increase 10/300 GL column in 20 mM Na2H2PO4 (pH 7.5) and 150 mM NaCl before SAXS measurements.
hGHR-ICD expression and purification
The coding region for hGHR-ICD (S270-P620) was cloned into a pGEX-4T-1 vector, containing an N-terminal glutathione S-transferase (GST)–tag followed by thrombin cleavage site and transformed into Bl21(DE3) cells. Expression was done in 1 liter of terrific broth (TB) medium containing ampicillin (100 μg/ml). At OD600 = 0.6 to 0.8, cells were induced by 1 mM IPTG for 4 hours at 37°C and 160 RPM. Cells were harvested by centrifugation and resuspended in 40 ml of one-time PBS (pH 7.4), 0.1% (v/v) Triton X-100, and a tablet complete EDTA-free protease inhibitor cocktail. The cells were lysed on ice by sonication using an UP400S ultrasonic processor, four times 30-s sonication followed by 30-s rest at 100% amplitude. Following centrifugation (20,000g, 4°C) to remove cellular debris, the lysate was applied to a glutathione Sepharose 4 fast flow column (GE Healthcare) and incubated for 2 hours at 25°C. The column was washed with 50 ml of one-time PBS (pH 7.4) and eluted 20 ml of 50 mM tris-HCl and 10 mM reduced glutathione (pH 7.4). The eluted solution was dialyzed against 1 liter of 20 mM tris-HCl and 150 mM NaCl (pH 7.4) at 4°C. The GST-tag was cleaved off by the addition of 20 U of thrombin per liter of culture, leaving residues GS in the N terminus. The sample was then concentrated; 10 mM dithiothreitol was added and heated to 72°C for 5 min, incubated on ice, and centrifuged for 20,000g at 4°C for 10 min. A final purification on a Superdex 200 increase 10/300 GL column (GE Healthcare) in 20 mM Na2H2PO4 (pH 7.5) and 150 mM NaCl was done, and selected fractions were used for SAXS measurements.
hGHR-ICD-GFP-H10 expression and purification
The coding region for hGHR-ICD (S270-P620) including an N-terminal methionine, C-terminal Tobacco Etch Virus (TEV) cleavage (ENLYFQS) site followed by a yeast enhanced GFP (EGFP) (57), and 10 histidines (hGHR-ICD-GFP-H10) in a pET-11a vector was bought from GenScript. Expression was done in 1 liter of TB medium (for SAXS) and in 15N-labeled minimal medium [22 mM KH2PO4, 62.5 mM NaH2PO4, 85.6 mM NaCl, 1 mM MgSO4, 1 ml of “trace element solution,” 4 g of glucose, and 1.5 g of NH4Cl (15N-labeled nitrogen)] (for NMR) containing ampicillin (100 μg/ml). At OD600 = 0.6 to 0.8, expression was induced by 1 mM IPTG for 3 hours at 37°C and 160 RPM. Cells were harvested by centrifugation and resuspended in 40 ml of one-time PBS (pH 7.4) and a tablet of cOmplete EDTA-free protease inhibitor cocktail. The cells were lysed on ice by sonication using an UP400S ultrasonic processor, four times 30-s sonication followed by 30-s rest at 100% amplitude. Following centrifugation (20,000g, 4°C), the pellet containing hGHR-ICD-GFP-H10 was solubilized by adding 40 ml of 20 mM NaHCO3 (pH 8.0), 150 mM NaCl, and 8 M urea. Following centrifugation (20,000g, 4°C), the supernatant was refolded by dialysis in two steps: first, by dialysis in 4 liters of 20 mM NaHCO3 (pH 8.0), 150 mM NaCl, and 4 M urea at 4°C using 3 kDa of molecular weight dialysis bag cutoff for 4 hours and then in 4 liters of 20 mM NaHCO3 (pH 8.0) and 150 mM NaCl at 4°C overnight. Following centrifugation (20,000g, 4°C), the supernatant was applied to a prepacked 5 ml of Ni resin column. The column was washed with three column volumes (CVs) of 20 mM NaCHO3 (pH 8), 150 mM NaCl, and 10 mM imidazole and eluted using 20 mM NaCHO3 (pH 8.0), 150 mM NaCl, and 250 mM imidazole. Fractions containing hGHR-ICD-GFP-H10 were concentrated and applied to a Superdex 200 16/60 increase column in 20 mM NaH2PO4/Na2H2PO4 (pH 7.5) and 150 mM NaCl. Fractions containing hGHR-ICD-GFP-H10 were analyzed by SDS-PAGE, and selected fractions were used for SAXS and NMR experiments.
hGH purification
hGH in a pJExpress414 was bought from ATUM, USA (formerly DNA2.0) and transformed into competent BL21 (DE3) cells. These were grown in 1 liter of TB containing ampicillin (100 μg/ml) to OD600 = 0.6 to 0.8 and induced by addition of 1 mM IPTG for 4 hours at 37°C and 160 RPM. Cells were harvested by centrifugation (5000g, at 4°C, 25 min) and resuspended in 50 ml of 50 mM tris, 0.5 mM EDTA (pH 8.0), and 1 mM phenylmethylsulfonyl fluoride (PMSF). Cells were lysed on ice by sonication using an UP400S ultrasonic processor, five times 30-s sonication followed by 30-s rest at 50% amplitude. Following centrifugation at 10,000g at 4°C for 15 min, the pellet was resuspended in 20 ml of 10 mM tris, 1 mM EDTA (pH 8.0), and 1 mM PMSF. The pellet was recentrifuged two times, and the supernatant was discarded and solubilized in 250 ml of 5 M guanidinium chloride (GuHCl), 200 mM Na2HPO4/NaH2PO4 (pH 7.0), and 15 mM bME. The solution was heated for 10 min at 55°C and stirred mildly for 2 hours at room temperature. The solution was diluted in denaturation buffer [5 M GuHCl, 200 mM Na2HPO4/NaH2PO4 (pH 7.0), and 15 mM bME] to reach an hGH protein concentration below 0.1 mg/ml. The solution was dialyzed in a 5-liter beaker, with a drain on the top, and filled with 5 M GuHCl, 200 mM Na2HPO4/NaH2PO4 (pH 7.0), and 15 mM bME. A peristaltic pump was used to add refolding buffer [20 mM NH4HCO3 (pH 8.0) and 200 mM NaCl] at the bottom of the beaker with a flow rate of 1.5 ml/min. After 3 days, when the GuHCl concentration was below 1.5 M, the dialysis bags were transferred to a new 5-liter beaker with 20 mM NH4HCO3 (pH 8.0) and 200 mM NaCl and dialyzed three times until the concentration of GuHCl was below 0.1 M. Following centrifugation for 18,000g for 10 min, the supernatant was concentrated using a Millipore Pellicon module to approximately 30 ml. The solution was applied to a Superdex 75 26/600 column in 20 mM NH4HCO3 and 100 mM NaCl (pH 8.0). Selected fractions were dialyzed against 5 liters of 20 mM tris (pH 8.0) twice and applied to a HiTrap QFF of 5 ml. The sample was eluted in 20 mM tris (pH 8.0) by a salt gradient from 0 to 1 M NaCl at a flow rate of 5 ml/min over 20 CV. Selected fractions were flash-frozen in liquid nitrogen and left at −20°C before use.
Analytical SEC
Analytical SEC experiments of a set of samples with various ratios of hGH:hGHR-ECD were run on Superdex 200 increase 10/300 GL column in 20 mM Na2HPO4/NaH2PO4 (pH 7.4) and 100 mM NaCl at room temperature with a flow rate of 0.5 ml/min. Protein sample concentration was in the micromolar range but varied. The column was calibrated using conalbumin (75 kDa), ovalbumin (44 kDa), carbonic anhydrase (29 kDa), ribonuclease A (13.7 kDa), acetone, and blue dextran, and apparent partition coefficient, Kav, was determined for all peaks.
Circular dichroism spectroscopy
Far-ultraviolet CD spectra were recorded on 10 μM hGHR-TMD in 2 mM DHPC, 5 μM hGH, and 5 μM hGHR-ECD in 10 mM Na2HPO4/NaH2PO4 (pH 7.4). The spectra were recorded on a Jasco J-810 spectropolarimeter in a 1-mm quartz glass Suprasil cuvette (Hellma) at 20°C. A total of 10 scans were accumulated from 260 to 190 nm for each sample, and buffer background was recorded at identical setting and subtracted. For hGHR-TMD, the background included 2 mM DHPC. The scan mode was continuous with a speed of 10 nm/min and a data pitch of 0.1 nm. The spectra were processed and smoothened (means-movement method, convolution width of 25) and converted into mean residue ellipticity values.
hGHR-TMD purification
hGHR-TMD was expressed in E. coli and purified as previously described (32).
Oriented circular dichroism
hGHR-TMD was dried under a flow of N2 and subsequently dissolved in MeOH:CHCl3 (5:1) to reach a final stock solution of hGHR-TMD (0.4 mg/ml). To validate the concentration, 100 μl of the stock solution was dried under N2 flow and resuspended in 100 μl of 50 mM SDS in phosphate buffer (pH 7.0), and the absorbance at 280 nm was measured. Lipid stock solutions of POPC, DOPC, and POPC/POPS (3:1) were prepared in MeOH:CHCl3 (1:1) at 0.25 and 5 mg/ml. The protein and lipid stock solutions were mixed in the following L:P ratios: 40:1, 50:1, 70:1, 100:1, 150:1, and 200:1. Six micrograms of protein was applied to a quartz glass with a Hamilton pipette for each experiment. The sample was spread over a fixed circular area on the glass and subsequently dried under vacuum for 3 hours to remove the MeOH:CHCl3. The dried sample was mounted in a sample holder and was hydrated overnight in a chamber with a saturated K2SO4 solution at 20°C. Last, the samples were loaded into a rotor in a Jasco J-810 spectropolarimeter, and the spectra were recorded from eight different angles: 0°, 45°, 90°, 135°, 180°, 225°, 270°, and 315°. Each spectrum was measured twice from 260 to 180 nm with a scanning speed of 20 nm/min, a data pitch of 0.1, and a response time of 8 s. The spectra were averaged, and the reference OCD spectra from samples with the same amount of lipid were subtracted. The OCD spectra were recorded from eight different angles to even out linear dichroism (fig. S2C) (37). The spectra from different angles were averaged, background subtracted, and normalized to the intensity at 222 nm. High-voltage effects prevented the measurement of higher L:P ratios.
X-ray diffraction
Highly oriented multilamellar membranes were prepared on single-side polished silicon wafers. POPC (Avanti), POPS (Avanti), and 1,2-dimyristoyl-sn-glycero-3-phospho-l-serine (Sigma-Aldrich) were mixed with hGHR-TMD at 2 and 20 mol % concentrations in 2,2,2-trifluoroethanol:chloroform [1:1 (v/v)] at a solution concentration of 18 mg/ml. The wafers were sonicated in 1,2-dichloromethane for 30 min and then rinsed with alternating methanol and water (18.2 megaOhm·cm). The wafers were dried, and 75 μl of the solution was deposited. After drying, the samples were placed in a vacuum for 24 hours at 37°C to allow for trace solvent evaporation and annealing. Samples were then hydrated in a closed chamber at 97% relative humidity with a separate K2SO4-saturated solution for 48 hours before scanning.
XRD data were obtained using the Biological Large Angle Diffraction Experiment (BLADE) at McMaster University. BLADE uses a 9-kW (45 kV, 200 mA) CuKα rotating anode at a wavelength of 1.5418 Å using a Rigaku HyPix-3000 two-dimensional semiconductor detector with an area of 3000 mm2 and 100 μm2 of pixel size (58). All samples were prepared and measured in replicates to check for consistency. EDPs were determined from specular reflectivity, as previously described (36). The lamellar spacing, dz, was determined from the spacing of the reflectivity Bragg peaks. Hermans orientation function was determined by integrating the intensity of the third Bragg peak as function of the meridonal angle ϕ (the angle relative to the qz axis), as described in (59). The CYANA and CS-Rosetta models of the monomer and the Protein Data Bank (PDB) structure of the dimer (PDB 5OEK) were used and fitted to the difference electron density. The calculation uses the electronic distribution of each atom of the molecule. To account for thermal motions, a Gaussian distribution, with a half width of 3.5 Å, is placed at the correct position, and all the atomic contributions are added. The linear electron density is then calculated by projecting the calculated electronic distribution on a linear axis and fitting to the experimental data. Position and tilt angle were determined from the fit by shifting the molecule along the z axis and varying the z projection (60).
NMR spectroscopy and structure of the TMD
NMR spectra were recorded on a 750-MHz (1H) Bruker AVANCE spectrometer equipped with a cryogenic probe. Unless otherwise specified, all NMR samples contained 10% (v/v) D2O and 1 mM 4,4-dimethyl-4-silapentane-1-sulfonic acid (DSS). Proton chemical shifts were referenced internally to DSS at 0.00 parts per million (ppm), with heteronuclei referenced by relative gyromagnetic ratios. Free induction decays were transformed and visualized in NMRPipe or TopSpin (Bruker Biospin) and analyzed using CcpNmr Analysis software. For hGHR-TMD, all NMR spectra were recorded at 37°C in 2 mM tris(2-carboxyethyl)phosphine (TCEP), 0.05% (v/v) NaN3, 50 mM NaCl, and 20 mM Na2HPO4/NaH2PO4 (pH 7.4). The spectra for backbone assignments of hGHR-TMD [HNCO, HNCAHC, HNCA, HNCACB, CBCA(CO)NH, 1H, and 15N-HSQC] were measured on 1 mM 13C,15N-hGHR-TMD solubilized in 210 mM DHPC. Secondary structure content was evaluated from backbone chemical shifts using the MICS program (33). R2 transverse relaxation rates of 0.5 mM 15N-hGHR-TMD in 110 mM DHPC were determined from a series of 1H,15N-HSQC spectra with varying relaxation delays between 10 and 250 ms and triple replica at 130 ms. The relaxation decays were fitted to single exponentials and relaxation times determined using CcpNmr Analysis software. A low-resolution model of hGHR-TMD was calculated using CYANA (34) including only dihedral angle restraints derived from the backbone chemical shifts using TALOS (61). Standard settings were used calculating 50 conformers with 4000 torsion angle dynamics steps. The 10 best conformers, with the lowest CYANA target function score, was used for further modeling. In addition, a model of hGHR-TMD was calculated using CS-Rosetta (35). The chemical shifts obtained for the hGHR-TMD were used as an input for the CS-Rosetta server (https://spin.niddk.nih.gov/bax/nmrserver/csrosetta/) from which 3- and 9-nucleotide oligomer fragments were obtained and used for de novo modeling. We adapted previously described protocols (62) to the relevant parts of the calculation: (i) ab initio modeling using the NMR-derived chemical shifts, (ii) definition of the membrane-spanning region, and (iii) rescoring of the Rosetta energy considering the chemical shifts. A total of 1000 models were generated. Clustering of the 10 lowest-energy models around the lowest one, with Cα-RMSD < 2 Å for the W249 – K271 region, indicated successful prediction (see Fig. 2D).
All NMR data of hGHR-ICD and hGHR-ICD-GFP-H10 were acquired at 5°C to minimize amide exchange in 1 mM TCEP, 150 mM NaCl, and 20 mM Na2HPO4/NaH2PO4 (pH 7.4). 1H,15N-HSQC spectra were acquired at concentrations of 150 μM for 15N-hGHR-ICD and 100 μM for 15N-hGHR-ICD-GFP-H10. The hydrodynamic radii (Rh) of hGHR-ICD and hGHR-ICD-GFP-H10 were determined from a series of 1H,15N-HSQC spectra with preceding pulse-field gradient stimulated-echo longitudinal encode-decode diffusion filter and with the gradient strength increasing linearly from 0.963 to 47.2 G cm−1. To determine the diffusion coefficients (D), the decay curves of the amide peaks were plotted against the gradient strength and fitted in Dynamics Center (Bruker) using
in which I is the intensity of the NMR signal at the respective gradient strength, I0 the intensity without applied gradient, x the gradient strength in G cm−1, γ = 26,752 rad G s−1, δ = 3 ms, and Δ = 250 ms. RH was calculated from the diffusion coefficient using the Stokes-Einstein relation, RH = kBT/(6πηD), with η being the viscosity of water at 5°C.
Production of full-length hGHR
See Kassem et al. (21) for expression, purification, and reconstitution of hGHR-GFP in POPC-containing MSP1D1 nanodiscs. pMSP1D1 was a gift from S. Sligar (Addgene plasmid no. 20061; http://n2t.net/addgene:20061; RRID:Addgene_20061) (63).
Native mass spectrometry
Purified hGHR-GFP in detergent was desalted and concentrated using C4 ZipTips (Merck Millipore), eluted into 50% acetonitrile/0.1% formic acid, and directly infused into an Orbitrap Fusion Tribrid mass spectrometer equipped with an offline nanospray source using borosilicate capillaries (Thermo Scientific). The capillary voltage was 1.5 kV in positive ionization mode, and the pressure in the ion-routing multipole was maintained at 0.11 torr. Ten percent of HCD activation energy in the ion trap was used to dissociate any residual detergents from the protein. Spectra were acquired in the Orbitrap mass analyzer operated in high mass mode between 1500 to 6000 mass/charge ratio (m/z) with an injection time of 10 ms and a resolution of 60,000 full width at half maximum at 200 m/z. Data were analyzed using Excalibur (Thermo Scientific) and UniDec (unidec.chem.ox.ac.uk) software packages.
Phosphorus analysis
The POPC-hGHR-GFP ratio of the formed nanodiscs with POPC-hGHR-GFP inserted was determined by phosphorus analysis (43). This was done by hydrolyzing POPC in H2SO4 to release free phosphate (PO4−3), which reacted with molybdate to produce a blue chromophore, absorbing at 812 nm. A series of phosphate standards from 0 to 80 nM Na2HPO4 and hGHR-GFP in MSP1D1 at approximately 1 μM were prepared. Aliquots of 175 μl of each sample were transferred to glass tubes. HClO4 was added [400 μl, 72% (v/v)] to each sample, and the glass tubes were loosely closed using glass pearls. The samples were heated to 180°C in a heating block in a fume hood for 1 hour and then left at room temperature to cool for 30 min. Four milliliters of 125 mM (NH4)6Mo7O24 × four H2O was added to each sample and vortexed, followed by addition of 500 μl of 10% (w/w) ascorbic acid and vortexed again. Samples were then heated to 80°C for 10 min in a water bath and subsequently cooled in ice water. Absorption was measured at 812 nm. A phosphate standard curve was generated, using the Na2HPO4 standards, by linear regression and was used to determine the content of phosphate in the hGHR-GFP in MSP1D1 samples.
Gel quantification of hGHR-GFP-loaded nanodiscs
Standards of hGHR-GFP and MSP1D1 with a known absorption at 280 nM were prepared and loaded in different amounts of the same gel and three aliquots of hGHR-GFP-loaded nanodiscs taken from three different positions of the SEC elution profile (fractions 1, 2, and 3). The gels were stained with Coomassie brilliant blue G-250 (Bio-Rad) and subsequently destained in 15% (v/v) ethanol, 5% (v/v) acetic acid, and 5% glycerol (v/v). Gel images were obtained on a LAS 4000 imager (GE Healthcare, USA), and the images were quantified in ImageJ. The intensities of the standards were fitted by linear regression, and the amount of hGHR-GFP relative to MSP1D1 was quantified accordingly.
Microscale thermophoresis
hGH was labeled with NT-647-NHS (64) using the Monolith NT Protein Labeling Kit RED-NHS (NanoTemper Technologies) for 1 hour at room temperature with NT-647-NHS at a molar ratio of 1:3 in labeling buffer following the protocol. These conditions favor the modification of the N-terminal amino group. Free dye was separated from reacted dye using the provided desalting column. The ratio between fluorophore and protein was 0.2. The equilibrium binding between 20 nM NT-647-NHS–labeled hGH and hGHR (MSP1D1) was calculated from the change in thermophoresis ΔFnorm = ΔFhot/ΔFcold measured on a Monolith NT.115 (NanoTemper Technologies). For hGHG120R, the raw fluorescence change was used to determine the binding affinity. A twofold dilution series of monomeric hGHR-GFP from 750 nM to 23 pM was prepared in 20 mM Na2HPO4/NaH2PO4 (pH 7.4) and 100 mM NaCl and measured in triplicates. Samples were loaded into the Monolith NT.115 Premium Capillaries (NanoTemper Technologies), and the thermophoresis and raw fluorescence signals were measured at 25°C with a light-emitting diode power of 80% and an infrared laser power of 100%. The dissociated constant Kd was obtained by fitting the data by
where Y is the measured fluorescence/MST, X is the ligand concentration, [P]total is the total concentration of the protein, Yf is the estimated end point of the titration, and Y0 is the start point.
N-glycosylation removal by endoglycosidase H
One microgram of purified full-length hGHR-GFP was incubated with 500 U of Endo-H (New England Biolabs, USA) at 4°C in 20 mM NaH2PO4/Na2HPO4 (pH 7.4), 150 mM NaCl, and 5% (v/v) glycerol. The sample was separated and analyzed on a 15% SDS-PAGE gel and visualized by in-gel fluorescence on a LAS 4000 imager (GE Healthcare, USA).
Western blotting
hGHR-GFP was separated on a 15% SDS-PAGE gel and blotted to a polyvinylidene difluoride. Horseradish peroxidase–conjugated concanavalin A (Sigma-Aldrich, L6397) was used to identify O-glycosylations after Western blotting. Chemiluminescence was detected by using the Immobilon Western Chemiluminescent HRP Substrate from Millipore and the LAS 4000 imager (GE Healthcare, USA).
Small-angle x-ray and neutron scattering
SAXS data on hGH, hGHR-ECD, and the hGH:hGHR-hECD 1:1 and 1:2 complexes were collected at the PETRA III, P12 beamline (DESY Synchrotron, Hamburg), following standard procedures at 8°C. All samples were concentrated and run on a Superdex 200 increase 10/300 GL in 20 mM Na2HPO4/NaH2PO4 (pH 7.4) and 150 mM NaCl before measuring. The most concentrated top fractions were taken, except for 1:1 complex, where the fraction was taken to the right of the peak, to make sure the hGH:hGHR-ECD 1:2 complex was absent in the sample. hGH was measured at 1.8 mg/ml, ECD at 3.5 mg/ml, hGH:hGHR-ECD 1:1 complex at 0.3 mg/ml, and the hGH:hGHR-ECD 1:2 complex at 1.3 mg/ml. The scattering curves, each of which has an average of 40 frames, were recorded, and the buffer was measured before and after each sample. The processing and preliminary data analysis was done using the ATSAS package (65). As a part of the process, buffer scattering curves before and after the sample were averaged and subtracted from the scattering curve of the sample. The scattering curves were scaled into units of 1/cm using a measurement of water as secondary standard and subsequently logarithmically rebinned. For the full-length hGHR in MSP1D1, in-line SEC-SAXS of the sample in 20 mM Na2HPO4/NaH2PO4 (pH 7.4) and 150 mM NaCl was performed at BM29 (European Synchrotron Radiation Facility, Grenoble) equipped with a Superose 6 increase 10/300 GL (GE Healthcare) running at a flow rate of 0.75 ml/min. In-line SEC-SANS data on the full-length hGHR in MSP1D1 were recorded on the D22 small-angle scattering diffractometer at Institute Laue-Langevin, Grenoble, France. The in-line SEC was performed using a the recently commissioned and described modular HPLC system (Serlabo) in 20 mM Na2HPO4/NaH2PO4 (pH 7.4) and 150 mM NaCl on a Superose 6 increase 10/300 GL (GE Healthcare) (42, 66). The flow rate was lowered from the 0.75 ml/min used in the SEC-SAXS measurements to 0.05 ml/min when the peak was reached in the lower-intensity SANS to get as good counting statistics on the individual frames as possible. Two settings were used, 11.2 and 2.0 m (with collimation lengths of 11.2 and 2.8 m, respectively), giving a q range between 0.0044 and 0.46 Å−1. The intensities were binned into 30-s frames.
Modeling of the hGHR-ECD
To build a model of the full-length hGHR-ECD that covers the same sequence of the construct used in the experimental procedures, the following steps were performed: (i) We selected a previously determined crystal structure of the GHR-ECD (chain C of PDB entry 3HHR, residues 32 to 236) (17). (ii) We built models for the missing loops (residues 57 to 61 and 74 to 77) using the MODELLER interface of Chimera (67). (iii) The missing N-terminal (residues 1 to 31) and C-terminal (residues 237 to 245) tails were modeled as ensembles to capture their flexibility in the fitting of SAXS data. The Rosetta (30) routine Floppy tail (29) was used to generate 5000 conformations of both tails.
Modeling of the hGHR ECD-TMD linker
The linker between the hGHR-ECD and hGHR-TMD (S237-W249) is not present in the available structures of hGHR-ECD, and its structure may play a relevant role in determining the proper ECD-TMD orientation. Thus, this linker was modeled to provide a starting conformation of the hECD-TMD region of hGHR for further use in the modeling of the full-length hGHR structure. To do this, the recently developed mp_domain_assembly protocol (68) in Rosetta_MP was used. We used the model described above of the ECD with missing loops completed (residues 32 to 236, i.e., without the SP and N- and C-terminal tails) and the TMD structure corresponding to an NMR-derived CYANA model (residues 250 to 272). A total of 5000 models were built with the best 10 (according to their Rosetta score) selected for further analysis, and the best-ranked model was used as a rigid body in the semianalytical models of hGHR-GFP in a nanodisc and as starting conformation in the building of the full-length hGHR-GFP CG model (see below).
Modeling of the hGHR-ICD
We built a model of the hGHR-ICD (residues 288 to 638) as a random coil from its sequence using PyMOL. This all-atom model was used to build a CG system using the martinize.py and insane.py scripts to obtain a system of protein, water, and 150 mM NaCl with the martini 3 (m3.b3.2) (69) topology. The system contained a total of 455,457 beads and size of 383 Å by 383 Å by 383 Å. This system was used as the initial structure to perform all the GHR-ICD CG simulations (see below).
Structural model for the full length hGHR-GFP
A full-length model of intact hGHR-GFP with the signal peptide on its N terminus and a GFP on its C terminus was built using the different parts modeled separately. A representative conformation from the reweighted subensemble of the full-length ECD (residues 1 to 237) was aligned to the best model of the ECD-TMD to obtain a complete ECD-TMD structure (residues 1 to 272). A representative structure of the ICD (residues 273 to 620) was taken from the back-mapped conformation from the CG-MetaD-Rg simulation with 10% increase in the protein-water interaction strength (see below). Rotations of the peptide bond between residues 273 and 274 had to be adjusted to allow the correct orientation of the ICD with respect to the TMD and the membrane plane. EGFP (PDB 1EMA) was added at residue 620. The signal peptide (residues −18 to −1) was added to the N terminus of this model as a coil using MODELLER. This all-atom model was used to build a CG system using the martini Maker module (70) of CHARMM-GUI to obtain a system of protein (hGHR-GFP) + POPC + water + 150 mM NaCl for the martini 2 force field. The topology was later adapted to open the beta version of martini 3 (m3.b3.2) (69). The final system contains 453,662 beads and has a size of 361 Å by 361 Å by 406 Å.
CG-MD simulations
MD simulations were performed with Gromacs 2016, 2018, or 2019 (71) using the open beta version of the martini 3 (3.b3.2) force field (69). In some simulations, we increased the strength of interactions between protein and water to avoid excessive compaction of the disordered regions. To find the optimal factor to change these protein-water interactions, we performed two sets of simulations of the GHR-ICD system with different values of the protein-water interaction strengths (increased between 5 and 15%). Unbiased simulations were performed with a 5% (5.6 μs), 6% (3.1 μs), 8% (3.3 μs), and 10% (5.2 μs) increase, while metadynamics simulations (see below) were performed with a 10% (10.1 μs), 11% (10.1 μs), 12% (10.1 μs), 13% (10.1 μs), 14% (9.9 μs), and 15% (9.4 μs) increase. On the basis of the best reproduction of Rg and best fit to the hGHR-ICD SAXS data (see fig. S3), we chose a 10% increase in interaction strength and used this also for the simulation of the hGHR-GFP + POPC system.
We performed 20 independent unbiased MD simulations (2 μs each) of the hGHR-GFP + POPC system with a time step of 5 fs. Other simulation parameters, common to all the CG simulations performed, were chosen following the recommendations in (72). Briefly, the Verlet cutoff scheme was used considering a buffer tolerance of 0.005 kJ/(mol ps atom). The reaction field method was used for Coulomb interactions with a cutoff of 11 Å and a dielectric constant of εr = 15 for water. For van der Waals interactions, the cutoff scheme with a cutoff of 11 Å was used. The velocity rescaling thermostat was used with a reference temperature of T = 300 and 310 K for the hGHR-ICD and hGHR-GFP + POPC simulations, respectively, with a coupling constant of τT = 1 ps. For the equilibrations, the Berendsen barostat was used (p = 1 bar, τp = 3 ps), whereas the production runs were performed with a Parrinello-Rahman barostat (p = 1 bar, τp = 12 ps) (73). A semi-isotropic pressure coupling was used for the hGHR-GFP system embedded on a lipid bilayer. For all systems, an initial round of equilibrations with decreasing constraints applied to the protein beads (hGHR-ICD) and protein beads and lipid beads (hGHR-GFP) was performed.
Sampling of the hGHR-ICD simulations with an increase in the protein-water interactions of 10, 11, 12, 13, 14, and 15% was enhanced using a well-tempered metadynamics (74) protocol applied with PLUMED 2.5 (75). The Rg of the protein was used as collective variable within the boundaries of 30 to 110 Å. The metadynamics parameters used were a bias factor of 50, Gaussian height of 4.2 kJ/mol, and collective variable space Gaussian widths equal to 0.3.
Analysis of the MD trajectories was performed using plugins and analysis tools implemented in VMD, GROMACS, and PLUMED together with in-house-prepared tcl and python scripts. All molecular renderings were done with VMD.
Fitting of the SAXS data of the hGHR-ECD and hGHR-ICD
Similar protocols were used to fit the SAXS data of the hGHR-ECD and hGHR-ICD with the conformations obtained from the modeling of hGHR-ECD and MD simulations of hGHR-ICD, respectively: (i) For the hGHR-ECD, the SAXS profile of each model was directly calculated and fitted to the SAXS data using Pepsi-SAXS (76), with all parameters free. For the conformations obtained from different hGHR-ICD simulations, an initial round of back-mapping was performed to go from CG to all atoms as described in (58), before calculating and fitting its SAXS profile with Pepsi-SAXS. (ii) From the fits, the average value of the hydration shell contrast was calculated (hGHR-ECD = 7.4%; hGHR-ICD = 4%) and used as a fixed parameter in a second round of fitting. (iii) The average scattering profile of the ensemble was calculated directly from the Pepsi-SAXS intensity files and compared to the data. (iv) In the case of hGHR-ECD, the BME (31) procedure was used to reweight the ensemble against the experimental data. From the reweighted ensemble, a representative subensemble of 500 conformations was obtained.
Semianalytical model for the ND-embedded hGHR-GFP
To generate the semianalytical model for the full-length hGHR-GFP, a hybrid approach, which combines analytical approaches to describe the nanodisc and the hGHR-ICD with rigid body modeling for the ECD-TMD and the GFP, was implemented in the WillItFit (48) framework. The mathematical model for hGHR-GFP in nanodiscs, illustrated in Fig. 5A, is composed of four distinct amplitude components arising from the ECD-TMD, the ICD, the attached GFP, and the surrounding nanodisc. The final expression for the total scattering intensity was calculated on the absolute scale as the orientationally averaged scattering amplitude squared according to standard theory of small-angle scattering
where ⟨…⟩Ω denotes the orientational average, ∣…∣ denotes the complex norm, n is the number density of particles, and is the scattering amplitude of each component for a single particle, each of which is equipped with a phase factor accounting for its relative position in the complex. Subscript ECD-TMD refers to the ECD with the TMD, ICD refers to the intrinsically disordered ICD, and GFP refers to the green fluorescent protein, which is fused to the ICD. ND refers to the surrounding POPC-loaded nanodisc. For each amplitude term, , we furthermore have ensured correct normalization through , where Δρ is the average excess scattering length density, V is the molecular volume, and is the normalized form factor amplitude for the relevant component. The model for the surrounding nanodisc, , is the same as we have described previously (40): A stack of five elliptical cylinders representing the phospholipid bilayer is surrounded by a hollow elliptical cylinder representing the two stacked MSPs. As done previously (40), molecular constraints were systematically implemented to constrain the nanodisc solution space. As a part of this, the height of the MSP was fixed to a value of 25.8 Å, as derived from a high-resolution structure of nanodiscs (39), and values for the molecular volume (ν) for the POPC lipids were taken from the literature (49). The scattering amplitudes of the ECD-TMD and the GFP of the hGHR were calculated from their atomic coordinates as a part of our WillItFit (48) framework as outlined in previous work (26) and incorporated into the ND as rigid bodies. PDB 1EMA was used for the GFP atomic coordinates, while those of the flexible ECD-TMD were obtained from one of the back-mapped structures from one of the (full-length) GHR-GFP + POPCpws10 simulations, but considering only the residues that comprise the SP, ECD, ECD-TMD linker, and TMD (residues −18 to 270). We used our previously developed formalism (26) to ensure that the TMD displace lipids in the ND and for adjusting the excess scattering lengths of the lipid-embedded residues by considering their lipid environment rather than the solvent (26). To gain computational speed, we described the scattering from the ICD as a Gaussian random coil where the form factor for the average scattering intensity is readily described through the analytical Debye function (38) parameterized through the average Rg of the coil. The center of mass of the Gaussian random coil was placed one Rg below the center of the lower interface between nanodisc lipid headgroups and solvent. The averaged form factor amplitude for a Gaussian random coil required for the off-diagonal cross-terms in the calculation of I(q) in the above equation is given by the so-called Hammouda function (77), which is also a function of the Rg of the coil. Hence, we used the same modeling principle as previously applied for polymer-modified micelles (78) to take into account the scattering contribution from a flexible ICD, which is connected to a nanodisc-embedded TMD in the model. Following a similar philosophy, the scattering from the GFP was randomly oriented and located within a certain allocated confusion volume. This way, the model captures the dynamically evolving position of the GFP with respect to the rest of the system. For the modeling of the shape of the confusion volume, we attempted to mimic the bowl-like distribution of GFP below the bilayer as observed in the CG-MD simulation of hGHR in a lipid bilayer (see Fig. 6F) by placing the GFP randomly in a thick cylindrical shell below the nanodisc (see Fig. 6A, inner and outer shell radii equal to, respectively, 1 and 1.5 times the Rg of hGHR-ICD). However, we found that the actual shape of the confusion volume, whether it was bowl shaped or simply spherical and centered under the disc, only had a minor effect. The WillItFit implementation of the model can be downloaded free for use (see Code availability section in Acknowledgments).
Acknowledgments
We thank S. A. Sjørup and J. H. Martinsen for skilled technical assistance and N. T. Johansen for guidance with nanodisc preparations, SAXS and SANS measurements, and data reduction. We also thank the D22 technicians M. Jacques, A. Martel, and L. Porcar; the beamline scientists M. Brennich and P. Pernot at BM29; and beamline scientist H. Mertens at P12 for technical support during beamtimes, including pilot beamtimes. Funding: This work has been supported by the Novo Nordisk Foundation Synergy program (#NNF15OC0016670; to B.B.K. and L.A.) and Challenge Program (REPIN, #NNF18OC0033926; to B.B.K.), the Lundbeck Foundation (to B.B.K.), and the Lundbeck Foundation Initiative BRAINSTRUC (R155-2015-2666; to K.L.-L., B.B.K., and L.A.). We authors acknowledge the ILL, France for the allocated SEC-SANS beamtime as well as the European Synchrotron Radiation Facility (ESRF) and PETRAIII at the Deutsches Elektronen-Synchrotron (DESY), Germany for the allocated SAXS beamtime. We acknowledge access to computational resources from the Danish National Supercomputer for Life Sciences (Computerome) and the ROBUST Resource for Biomolecular Simulations (supported by the Novo Nordisk Foundation, NNF18OC0032608). Author contributions: N.K., R.A.-S., K.B., M.C.R., P.A.P., K.L.-L., L.A., and B.B.K. designed the research. N.K., R.A.-S., K.B., A.B., H.S., A.K., Y.W., C.S., A.J.L., J.B., M.L., and A.S.U. performed research and/or contributed new reagents. N.K., R.A.-S., K.B., A.B., H.S., A.K., C.S., J.B., M.L., M.C.P., Y.W., M.C.R., P.A.P., K.L.-L., L.A., and B.B.K. analyzed data. N.K., R.A.-S, K.B., L.A., and B.B.K. wrote the paper with input from all the authors. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. All SAS data and MD data and models are available on Github at https://github.com/Niels-Bohr-Institute-XNS-StructBiophys/GHRSASData and https://github.com/Niels-Bohr-Institute-XNS-StructBiophys/GHRModel, respectively, and the chemical shifts of the GHR-TMD are deposited in BioMagResBank under the accession number 50798. Additional data related to this paper may be requested from the authors. Code availability: All codes used in this study are available on Github (https://github.com/Niels-Bohr-Institute-XNS-StructBiophys/GHRModel). The implemented WillItFit routines have been updated on the WillItFit repository at SourceForge: https://sourceforge.net/projects/willitfit/.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/27/eabh3805/DC1
REFERENCES AND NOTES
- 1.Liongue C., Ward A. C., Evolution of Class I cytokine receptors. BMC Evol. Biol. 7, 120 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Madsen K., Friberg U., Roos P., Edén S., Isaksson O., Growth hormone stimulates the proliferation of cultured chondrocytes from rabbit ear and rat rib growth cartilage. Nature 304, 545–547 (2005). [DOI] [PubMed] [Google Scholar]
- 3.Waters M. J., Brooks A. J., Growth hormone receptor: Structure function relationships. Horm. Res. Paediatr. 76, 12–16 (2011). [DOI] [PubMed] [Google Scholar]
- 4.Yakar S., Rosen C. J., Beamer W. G., Ackert-Bicknell C. L., Wu Y., Liu J.-L., Ooi G. T., Setser J., Frystyk J., Boisclair Y. R., LeRoith D., Circulating levels of IGF-1 directly regulate bone growth and density. J. Clin. Invest. 110, 771–781 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chhabra Y., Wong H. Y., Nikolajsen L. F., Steinocher H., Papadopulos A., Tunny K. A., Meunier F. A., Smith A. G., Kragelund B. B., Brooks A. J., Waters M. J., A growth hormone receptor SNP promotes lung cancer by impairment of SOCS2-mediated degradation. Oncogene 37, 489–501 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mullis P. E., Genetics of isolated growth hormone deficiency. J. Clin. Res. Pediatr. Endocrinol. 2, 52–62 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Shimatsu A., Nagashima M., Hashigaki S., Ohki N., Chihara K., Efficacy and safety of monotherapy by pegvisomant, a growth hormone receptor antagonist, in Japanese patients with acromegaly. Endocr. J. 63, 337–347 (2016). [DOI] [PubMed] [Google Scholar]
- 8.Seiffert P., Bugge K., Nygaard M., Haxholm G. W., Martinsen J. H., Pedersen M. N., Arleth L., Boomsma W., Kragelund B. B., Orchestration of signaling by structural disorder in class 1 cytokine receptors. Cell Commun. Signal 18, 132 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Haxholm G. W., Nikolajsen L. F., Olsen J. G., Fredsted J., Larsen F. H., Goffin V., Pedersen S. F., Brooks A. J., Waters M. J., Kragelund B. B., Intrinsically disordered cytoplasmic domains of two cytokine receptors mediate conserved interactions with membranes. Biochem. J. 468, 495–506 (2015). [DOI] [PubMed] [Google Scholar]
- 10.Waters M. J., The growth hormone receptor. Growth Hormon. IGF Res. 28, 6–10 (2016). [DOI] [PubMed] [Google Scholar]
- 11.Baumgartner J. W., Wells C. A., Chen C. M., Waters M. J., The role of the WSXWS equivalent motif in growth hormone receptor function. J. Biol. Chem. 269, 29094–29101 (1994). [PubMed] [Google Scholar]
- 12.Olsen J. G., Kragelund B. B., Who climbs the tryptophan ladder? On the structure and function of the WSXWS motif in cytokine receptors and thrombospondin repeats. Cytokine Growth Factor Rev. 25, 337–341 (2014). [DOI] [PubMed] [Google Scholar]
- 13.Brooks A. J., Dai W., O’Mara M. L., Abankwa D., Chhabra Y., Pelekanos R. A., Gardon O., Tunny K. A., Blucher K. M., Morton C. J., Parker M. W., Sierecki E., Gambin Y., Gomez G. A., Alexandrov K., Wilson I. A., Doxastakis M., Mark A. E., Waters M. J., Mechanism of activation of protein kinase JAK2 by the growth hormone receptor. Science 344, 1249783 (2014). [DOI] [PubMed] [Google Scholar]
- 14.Wilmes S., Hafer M., Vuorio J., Tucker J. A., Winkelmann H., Löchte S., Stanly T. A., Pulgar Prieto K. D., Poojari C., Sharma V., Richter C. P., Kurre R., Hubbard S. R., Christopher Garcia K., Moraga I., Vattulainen I., Hitchcock I. S., Piehler J., Mechanism of homodimeric cytokine receptor activation and dysregulation by oncogenic mutations. Science 367, 643–652 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Brown R. J., Adams J. J., Pelekanos R. A., Wan Y., McKinstry W. J., Palethorpe K., Seeber R. M., Monks T. A., Eidne K. A., Parke M. W., Waters M. J., Model for growth hormone receptor activation based on subunit rotation within a receptor dimer. Nat. Struct. Mol. Biol. 12, 814–821 (2005). [DOI] [PubMed] [Google Scholar]
- 16.Sundström M., Lundqvist T., Rödin J., Giebel L. B., Milligan D., Norstedt G., Crystal structure of an antagonist mutant of human growth hormone, G120R, in complex with its receptor at 2.9 Å resolution. J. Biol. Chem. 271, 32197–32203 (1996). [DOI] [PubMed] [Google Scholar]
- 17.de Vos A. M., Ultsch M., Kossiakoff A. A., Human growth hormone and extracellular domain of its receptor: Crystal structure of the complex. Science 255, 306–312 (1992). [DOI] [PubMed] [Google Scholar]
- 18.Chantalat L., Jones N. D., Korber F., Navaza J., Pavlovsky A. G., The crystal-structure of wild-type growth-hormone at 2.5 Angstrom resolution. Protein Pept. Lett. 2, 333–340 (1995). [Google Scholar]
- 19.Bocharov E. V., Lesovoy D. M., Bocharova O. V., Urban A. S., Pavlov K. V., Volynsky P. E., Efremov R. G., Arseniev A. S., Structural basis of the signal transduction via transmembrane domain of the human growth hormone receptor. Biochim. Biophys. Acta Gen. Subj. 1862, 1410–1420 (2018). [DOI] [PubMed] [Google Scholar]
- 20.Bugge K., Papaleo E., Haxholm G. W., Hopper J. T. S., Robinson C. V., Olsen J. G., Lindorff-Larsen K., Kragelund B. B., A combined computational and structural model of the full-length human prolactin receptor. Nat. Commun. 7, 11578 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kassem N., Kassem M. M., Pedersen S. F., Pedersen P. A., Kragelund B. B., Yeast recombinant production of intact human membrane proteins with long intrinsically disordered intracellular regions for structural studies. Biochim. Biophys. Acta Biomembr. 1862, 183272 (2020). [DOI] [PubMed] [Google Scholar]
- 22.Ward A. B., Sali A., Wilson I. A., Biochemistry. Integrative structural biology. Science 339, 913–915 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cárdenas R., Martínez-Seoane J., Amero C., Combining experimental data and computational methods for the non-computer specialist. Molecules 25, 4783 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Larsen A. H., Wang Y., Bottaro S., Grudinin S., Arleth L., Lindorff-Larsen K., Combining molecular dynamics simulations with small-angle X-ray and neutron scattering data to study multi-domain proteins in solution. PLoS Comput. Biol. 16, e1007870 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bayburt T. H., Grinkova Y. V., Sligar S. G., Self-assembly of discoidal phospholipid bilayer nanoparticles with membrane scaffold proteins. Nano Lett. 2, 853–856 (2002). [Google Scholar]
- 26.Kynde S. A. R., Skar-Gislinge N., Pedersen M. C., Midtgaard S. R., Simonsen J. B., Schweins R., Mortensen K., Arleth L., Small-angle scattering gives direct structural information about a membrane protein inside a lipid environment. Acta Crystallogr. Sect. D Biol. Crystallogr. 70, 371–383 (2014). [DOI] [PubMed] [Google Scholar]
- 27.Skar-Gislinge N., Kynde S. A. R., Denisov I. G., Ye X., Lenov I., Sligar S. G., Arleth L., Small-angle scattering determination of the shape and localization of human cytochrome P450 embedded in a phospholipid nanodisc environment. Acta Crystallogr. D Biol. Crystallogr. 71, 2412–2421 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bugge K., Lindorff-Larsen K., Kragelund B. B., Understanding single-pass transmembrane receptor signaling from a structural viewpoint-what are we missing? FEBS J. 283, 4424–4451 (2016). [DOI] [PubMed] [Google Scholar]
- 29.Kleiger G., Saha A., Lewis S., Kuhlman B., Deshaies R. J., Rapid E2-E3 assembly and disassembly enable processive ubiquitylation of cullin-RING ubiquitin ligase substrates. Cell 139, 957–968 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Leaver-Fay A., Tyka M., Lewis S. M., Lange O. F., Thompson J., Jacak R., Kaufman K., Renfrew P. D., Smith C. A., Sheffler W., Davis I. W., Cooper S., Treuille A., Mandell D. J., Richter F., Ban Y.-E. A., Fleishman S. J., Corn J. E., Kim D. E., Lyskov S., Berrondo M., Mentzer S., Popović Z., Havranek J. J., Karanicolas J., Das R., Meiler J., Kortemme T., Gray J. J., Kuhlman B., Baker D., Bradley P., ROSETTA3: An object-oriented software suite for the simulation and design of macromolecules. Methods Enzymol. 487, 545–574 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bottaro S., Bengtsen T., Lindorff-Larsen K., Integrating molecular simulation and experimental data: A bayesian/maximum entropy reweighting approach. Methods Mol. Biol. 2112, 219–240 (2020). [DOI] [PubMed] [Google Scholar]
- 32.Bugge K., Steinocher H., Brooks A. J., Lindorff-Larsen K., Kragelund B. B., Exploiting hydrophobicity for efficient production of transmembrane helices for structure determination by NMR spectroscopy. Anal. Chem. 87, 9126–9131 (2015). [DOI] [PubMed] [Google Scholar]
- 33.Shen Y., Bax A., Identification of helix capping and b-turn motifs from NMR chemical shifts. J. Biomol. NMR 52, 211–232 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Güntert P., Automated NMR structure calculation with CYANA. Methods Mol. Biol. 278, 353–378 (2004). [DOI] [PubMed] [Google Scholar]
- 35.Shen Y., Lange O., Delaglio F., Rossi P., Aramini J. M., Liu G., Eletsky A., Wu Y., Singarapu K. K., Lemak A., Ignatchenko A., Arrowsmith C. H., Szyperski T., Montelione G. T., Baker D., Bax A., Consistent blind protein structure generation from NMR chemical shift data. Proc. Natl. Acad. Sci. U.S.A. 105, 4685–4690 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Khondker A., Dhaliwal A. K., Saem S., Mahmood A., Fradin C., Moran-Mirabal J., Rheinstädter M. C., Membrane charge and lipid packing determine polymyxin-induced membrane damage. Commun. Biol. 2, 67 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bürck J., Wadhwani P., Fanghänel S., Ulrich A. S., Oriented circular dichroism: A method to characterize membrane-active peptides in oriented lipid bilayers. Acc. Chem. Res. 49, 184–192 (2016). [DOI] [PubMed] [Google Scholar]
- 38.Debye P., Molecular-weight determination by light scattering. J. Phys. Colloid Chem. 51, 18–32 (1947). [DOI] [PubMed] [Google Scholar]
- 39.Bibow S., Polyhach Y., Eichmann C., Chi C. N., Kowal J., Albiez S., McLeod R. A., Stahlberg H., Jeschke G., Güntert P., Riek R., Solution structure of discoidal high-density lipoprotein particles with a shortened apolipoprotein A-I. Nat. Struct. Mol. Biol. 24, 187–193 (2017). [DOI] [PubMed] [Google Scholar]
- 40.Skar-Gislinge N., Simonsen J. B., Mortensen K., Feidenhans’l R., Sligar S. G., Lindberg Møller B., Bjørnholm T., Arleth L., Elliptical structure of phospholipid bilayer nanodiscs encapsulated by scaffold proteins: Casting the roles of the lipids and the protein. J. Am. Chem. Soc. 132, 13713–13722 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Skar-Gislinge N., Johansen N. T., Høiberg-Nielsen R., Arleth L., Comprehensive study of the self-assembly of phospholipid nanodiscs: What determines their shape and stoichiometry? Langmuir 34, 12569–12582 (2018). [DOI] [PubMed] [Google Scholar]
- 42.Johansen N. T., Pedersen M. C., Porcar L., Martel A., Arleth L., Introducing SEC-SANS for studies of complex self-organized biological systems. Acta Crystallogr. Sect. D Struct. Biol. 74, 1178–1191 (2018). [DOI] [PubMed] [Google Scholar]
- 43.Rouser G., Siakotos A. N., Fleischer S., Quantitative analysis of phospholipids by thin-layer chromatography and phosphorus analysis of spots. Lipids 1, 85–86 (1966). [DOI] [PubMed] [Google Scholar]
- 44.Harding P. A., Wang X. Z., Kelder B., Souza S., Okada S., Kopchick J. J., In vitro mutagenesis of growth hormone receptor Asn-linked glycosylation sites. Mol. Cell. Endocrinol. 106, 171–180 (1994). [DOI] [PubMed] [Google Scholar]
- 45.Bjørkskov F. B., Krabbe S. L., Nurup C. N., Missel J. W., Spulber M., Bomholt J., Molbaek K., Helix-Nielsen C., Gotfryd K., Gourdon P., Pedersen P. A., Purification and functional comparison of nine human Aquaporins produced in Saccharomyces cerevisiae for the purpose of biophysical characterization. Sci. Rep. 7, 16899 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wennbo H., Gebre-Medhin M., Gritli-Linde A., Ohlsson C., Isaksson O. G. P., Törnell J., Activation of the prolactin receptor but not the growth hormone receptor is important for induction of mammary tumors in transgenic mice. J. Clin. Invest. 100, 2744–2751 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kouadio J.-L. K., Horn J. R., Pal G., Kossiakoff A. A., Shotgun alanine scanning shows that growth hormone can bind productively to its receptor through a drastically minimized interface. J. Biol. Chem. 280, 25524–25532 (2005). [DOI] [PubMed] [Google Scholar]
- 48.Pedersen M. C., Arleth L., Mortensen K., WillItFit : A framework for fitting of constrained models to small-angle scattering data. J. Appl. Crystallogr. 46, 1894–1898 (2013). [Google Scholar]
- 49.Kucerka N., Tristram-Nagle S., Nagle J. F., Structure of fully hydrated fluid phase lipid bilayers with monounsaturated chains. J. Membr. Biol. 208, 193–202 (2005). [DOI] [PubMed] [Google Scholar]
- 50.Minezaki Y., Homma K., Nishikawa K., Intrinsically disordered regions of human plasma membrane proteins preferentially occur in the cytoplasmic segment. J. Mol. Biol. 368, 902–913 (2007). [DOI] [PubMed] [Google Scholar]
- 51.Kjaergaard M., Kragelund B. B., Functions of intrinsic disorder in transmembrane proteins. Cell. Mol. Life Sci. 74, 3205–3224 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.A. J. Brooks, F. Dehkhoda, B. B. Kragelund, in Principles of Endocrinology and Hormone Action, A. Belfiore, D. LeRoith, Eds. (Springer International Publishing, Cham, 2018), pp. 157–185; 10.1007/978-3-319-44675-2_8. [DOI]
- 53.Ben-Avraham D., Govindaraju D. R., Budagov T., Fradin D., Durda P., Liu B., Ott S., Gutman D., Sharvit L., Kaplan R., Bougnères P., Reiner A., Shuldiner A. R., Cohen P., Barzilai N., Atzmon G., The GH receptor exon 3 deletion is a marker of male-specific exceptional longevity associated with increased GH sensitivity and taller stature. Sci. Adv. 3, e1602025 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Gouw M., Michael S., Sámano-Sánchez H., Kumar M., Zeke A., Lang B., Bely B., Chemes L. B., Davey N. E., Deng Z., Diella F., Gürth C. M., Huber A. K., Kleinsorg S., Schlegel L. S., Palopoli N., Roey K. V., Altenberg B., Reményi A., Dinkel H., Gibson T. J., The eukaryotic linear motif resource - 2018 update. Nucleic Acids Res. 46, D428–D434 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Kaplan M., Narasimhan S., de Heus C., Mance D., van Doorn S., Houben K., Popov-Čeleketić D., Damman R., Katrukha E. A., Jain P., Geerts W. J. C., Heck A. J. R., Folkers G. E., Kapitein L. C., Lemeer S., van Bergen En Henegouwen P. M. P., Baldus M., EGFR dynamics change during activation in native membranes as revealed by NMR. Cell 167, 1241–1251.e11 (2016). [DOI] [PubMed] [Google Scholar]
- 56.Wang X., Darus C. J., Xu B. C., Kopchick J. J., Identification of growth hormone receptor (GHR) tyrosine residues required for GHR phosphorylation and JAK2 and STAT5 activation. Mol. Endocrinol. 10, 1249–1260 (1996). [DOI] [PubMed] [Google Scholar]
- 57.Cormack B. P., Bertram G., Egerton M., Gow N. A. R., Falkow S., Brown A. J. P., Yeast-enhanced green fluorescent protein (yEGFP): A reporter of gene expression in Candida albicans. Microbiology 143, 303–311 (1997). [DOI] [PubMed] [Google Scholar]
- 58.Khondker A., Malenfant D. J., Dhaliwal A. K., Rheinstädter M. C., Carbapenems and lipid bilayers: Localization, partitioning, and energetics. ACS Infect. Dis. 4, 926–935 (2018). [DOI] [PubMed] [Google Scholar]
- 59.Himbert S., Blacker M. J., Kihm A., Pauli Q., Khondker A., Yang K., Sinjari S., Johnson M., Juhasz J., Wagner C., Stöver H. D. H., Rheinstädter M. C., Hybrid erythrocyte liposomes: Functionalized red blood cell membranes for molecule encapsulation. Adv. Biosyst. 4, 1900185 (2020). [DOI] [PubMed] [Google Scholar]
- 60.Bider R.-C., Lluka T., Himbert S., Khondker A., Qadri S. M., Sheffield W. P., Rheinstädter M. C., Stabilization of lipid membranes through partitioning of the blood bag plasticizer di-2-ethylhexyl phthalate (DEHP). Langmuir 36, 11899–11907 (2020). [DOI] [PubMed] [Google Scholar]
- 61.Shen Y., Delaglio F., Cornilescu G., Bax A., TALOS+: A hybrid method for predicting protein backbone torsion angles from NMR chemical shifts. J. Biomol. NMR 44, 213–223 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Reichel K., Fisette O., Braun T., Lange O. F., Hummer G., Schäfer L. V., Systematic evaluation of CS-Rosetta for membrane protein structure prediction with sparse NOE restraints. Proteins 85, 812–826 (2017). [DOI] [PubMed] [Google Scholar]
- 63.Denisov I. G., Grinkova Y. V., Lazarides A. A., Sligar S. G., Directed self-assembly of monodisperse phospholipid bilayer Nanodiscs with controlled size. J. Am. Chem. Soc. 126, 3477–3487 (2004). [DOI] [PubMed] [Google Scholar]
- 64.Jerabek-Willemsen M., André T., Wanner R., Roth H. M., Duhr S., Baaske P., Breitsprecher D., MicroScale Thermophoresis: Interaction analysis and beyond. J. Mol. Struct. 1077, 101–113 (2014). [Google Scholar]
- 65.Petoukhov M. V., Franke D., Shkumatov A. V., Tria G., Kikhney A. G., Gajda M., Gorba C., Mertens H. D. T., Konarev P. V., Svergun D. I., New developments in the ATSAS program package for small-angle scattering data analysis. J. Appl. Crystallogr. 45, 342–350 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Jordan A., Jacques M., Merrick C., Devos J., Forsyth V. T., Porcar L., Martel A., SEC-SANS: Size exclusion chromatography combined in situ with small-angle neutron scattering. J. Appl. Crystallogr. 49, 2015–2020 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Pettersen E. F., Goddard T. D., Huang C. C., Couch G. S., Greenblatt D. M., Meng E. C., Ferrin T. E., UCSF Chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 25, 1605–1612 (2004). [DOI] [PubMed] [Google Scholar]
- 68.Koehler Leman J., Bonneau R., A novel domain assembly routine for creating full-length models of membrane proteins from known domain structures. Biochemistry 57, 1939–1944 (2018). [DOI] [PubMed] [Google Scholar]
- 69.P. C. T. Souza, S. J. S. Marrink, Martini 3 - Open Beta-Release (2020); http://cgmartini.nl.
- 70.Qi Y., Ingólfsson H. I., Cheng X., Lee J., Marrink S. J., Im W., CHARMM-GUI martini maker for coarse-grained simulations with the martini force field. J. Chem. Theory Comput. 11, 4486–4494 (2015). [DOI] [PubMed] [Google Scholar]
- 71.Abraham M. J., Murtola T., Schulz R., Páll S., Smith J. C., Hess B., Lindahl E., GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 1–2, 19–25 (2015). [Google Scholar]
- 72.de Jong D. H., Baoukina S., Ingólfsson H. I., Marrink S. J., Martini straight: Boosting performance using a shorter cutoff and GPUs. Comput. Phys. Commun. 199, 1–7 (2016). [Google Scholar]
- 73.Parrinello M., Rahman A., Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 52, 7182–7190 (1981). [Google Scholar]
- 74.Barducci A., Bussi G., Parrinello M., Well-tempered metadynamics: A smoothly converging and tunable free-energy method. Phys. Rev. Lett. 100, 020603 (2008). [DOI] [PubMed] [Google Scholar]
- 75.PLUMED consortium , Promoting transparency and reproducibility in enhanced molecular simulations. Nat. Methods 16, 670–673 (2019). [DOI] [PubMed] [Google Scholar]
- 76.Grudinin S., Garkavenko M., Kazennov A., Pepsi-SAXS: An adaptive method for rapid and accurate computation of small-angle X-ray scattering profiles. Acta Crystallogr. Sect. D Struct. Biol. 73, 449–464 (2017). [DOI] [PubMed] [Google Scholar]
- 77.Hammouda B., Structure factor for starburst dendrimers. J. Polym. Sci. Part B Polym. Phys. 30, 1387–1390 (1992). [Google Scholar]
- 78.Pedersen J. S., Gerstenberg M. C., Scattering form factor of block copolymer micelles. Macromolecules 29, 1363–1365 (1996). [Google Scholar]
- 79.Wei Y., Thyparambil A. A., Latour R. A., Protein helical structure determination using CD spectroscopy for solutions with strong background absorbance from 190 to 230nm. Biochim. Biophys. Acta Proteins Proteomics 1844, 2331–2337 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Sommese R. F., Sivaramakrishnan S., Baldwin R. L., Spudich J. A., Helicity of short E-R/K peptides. Protein Sci. 19, 2001–2005 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Hansen S., BayesApp: A web site for indirect transformation of small-angle scattering data. J. Appl. Crystallogr. 45, 566–567 (2012). [Google Scholar]
- 82.Sonnhammer E. L., von Heijne G., Krogh A., A hidden Markov model for predicting transmembrane helices in protein sequences. Proc. Int. Conf. Intell. Syst. Mol. Biol. 6, 175–182 (1998). [PubMed] [Google Scholar]
- 83.Käll L., Krogh A., Sonnhammer E. L. L., A combined transmembrane topology and signal peptide prediction method. J. Mol. Biol. 338, 1027–1036 (2004). [DOI] [PubMed] [Google Scholar]
- 84.Käll L., Krogh A., Sonnhammer E. L. L., Advantages of combined transmembrane topology and signal peptide prediction—The Phobius web server. Nucleic Acids Res. 35, W429–W432 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Jones D. T., Improving the accuracy of transmembrane protein topology prediction using evolutionary information. Bioinformatics 23, 538–544 (2007). [DOI] [PubMed] [Google Scholar]
- 86.UniProt Consortium , UniProt: A hub for protein information. Nucleic Acids Res. 43, D204–D212 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Zheng W., Best R. B., An extended guinier analysis for intrinsically disordered proteins. J. Mol. Biol. 430, 2540–2553 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Riback J. A., Bowman M. A., Zmyslowski A. M., Knoverek C. R., Jumper J. M., Hinshaw J. R., Kaye E. B., Freed K. F., Clark P. L., Sosnick T. R., Innovative scattering analysis shows that hydrophobic disordered proteins are expanded in water. Science 358, 238–241 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Kohn J. E., Millett I. S., Jacob J., Zagrovic B., Dillon T. M., Cingel N., Dothager R. S., Seifert S., Thiyagarajan P., Sosnick T. R., Hasan M. Z., Pande V. S., Ruczinski I., Doniach S., Plaxco K. W., Random-coil behavior and the dimensions of chemically unfolded proteins. Proc. Natl. Acad. Sci. U.S.A. 101, 12491–12496 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Marsh J. A., Forman-kay J. D., Sequence determinants of compaction in intrinsically disordered proteins. Biophys. J. 98, 2383–2390 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Johansen N. T., Tidemand F. G., Nguyen T. T. T. N., Rand K. D., Pedersen M. C., Arleth L., Circularized and solubility-enhanced MSPs facilitate simple and high-yield production of stable nanodiscs for studies of membrane proteins in solution. FEBS J. 286, 1734–1751 (2019). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/27/eabh3805/DC1