Initiator Types and the Causal Question of the Prevalent New-User Design: A Simulation Study

Abstract

New-user designs restricting to treatment initiators have become the preferred design for studying drug comparative safety and effectiveness using nonexperimental data. This design reduces confounding by indication and healthy-adherer bias at the cost of smaller study sizes and reduced external validity, particularly when assessing a newly approved treatment compared with standard treatment. The prevalent new-user design includes adopters of a new treatment who switched from or previously used standard treatment (i.e., the comparator), expanding study sample size and potentially broadening the study population for inference. Previous work has suggested the use of time-conditional propensity-score matching to mitigate prevalent user bias. In this study, we describe 3 “types” of initiators of a treatment: new users, direct switchers, and delayed switchers. Using these initiator types, we articulate the causal questions answered by the prevalent new-user design and compare them with those answered by the new-user design. We then show, using simulation, how conditioning on time since initiating the comparator (rather than full treatment history) can still result in a biased estimate of the treatment effect. When implemented properly, the prevalent new-user design estimates new and important causal effects distinct from the new-user design.

Abbreviations

ACNU

active comparator, new user

SMR

standardized morbidity ratio

Editor’s note: An invited commentary on this article appears on page 1349.

Estimating unbiased treatment effects with nonexperimental data is challenging. Over the past two decades, new-user study designs have become the standard in evaluating drug safety and effectiveness using nonexperimental data (1). If referent groups of these new-user studies are treated with a similarly indicated drug of interest, the design is sometimes referred to as an active comparator, new-user (ACNU) study (2). This design starts follow-up at the time of initiation and excludes those who have used either the treatment of interest or the active comparator. This exclusion protects against potential bias from confounding by indication (3), induced by including nonusers, and potential healthy adherer bias (i.e., selection bias) (4) induced by including prevalent users, as well as depletion of susceptible persons (5, 6). These studies estimate the treatment effect of initiating one treatment (the treatment of interest) compared with initiating another treatment alternative (the active comparator) (4).

While the ACNU study design effectively protects against these biases, it has some limitations. Because ACNU studies exclude patients with recent exposure to the comparator, sample size is reduced, and inference is limited to new users naive to both treatments. In some situations, there are a limited number of new users of a treatment of interest without recent exposure to the comparator (e.g., half of those starting dabigatran have been previously exposed to warfarin) (7). In particular, when a standard treatment already exists for a condition, many of the people starting a newly approved treatment alternative have previously used the standard treatment. Similar exposure patterns occur when a payer requires prior use of the standard treatment before covering a new and more expensive alternative.

The prevalent new-user design has been proposed to overcome these limitations by including initiators of the treatment of interest with past use of the comparator (8). To reduce bias from confounding by indication and healthy-user bias, initiators of the treatment of interest are matched to users of the comparator on time or number of prescriptions since initiating the comparator. Further matching is then performed based on a time-conditional propensity score that controls for confounding by measured variables. Thus, the study design essentially treats the duration or extent of prior comparator use as a confounder.

In this work, we enumerate and compare the causal parameters estimated by the ACNU and prevalent new-user designs in the context of 3 different types of initiators of the treatment of interest. Next, we use simulation to examine when conditioning on time since comparator initiation, but not full exposure history, can lead to biased treatment effect estimates.

METHODS

Types of initiators

Suppose we have data on lifetime use of a treatment of interest (treatment A) and an active comparator (treatment B) in a population of patients, and we are interested in estimating the effect of initiating treatment A on all-cause mortality. Use of these treatments is exclusive: If a patient is taking treatment A, they are not taking treatment B, and vice versa.

If we define the time of initiation of treatment A as T₀, we may characterize initiators as type 1A, 2A, or 3A as shown in Figure 1A and various users of treatment B as type 1B, 2B, or 3B as shown in Figure 1B. Type 1A initiators are new users—patients with no historical use of treatment B. These individuals contribute to an ACNU analysis. All new users have an identical and interchangeable exposure history: They have used neither A nor B.

Figure 1.

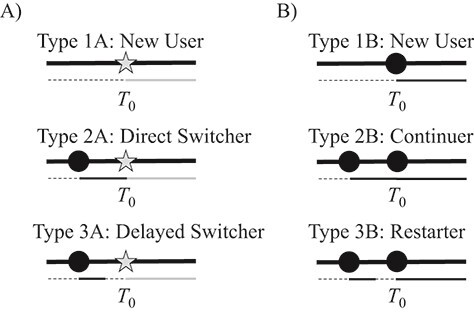
Infographic showing treatment histories of various types of initiators of treatment A and users of B. Panel A includes the initiators of treatment A (types 1A–3A) and panel B includes the 3 corresponding individuals taking treatment B that would be “ideal” counterfactual contrasts for types 1A–3A. Gray stars represent prescriptions for A, while black circles represent prescriptions for B. Below each set of prescriptions is a secondary timeline showing time with no treatment (dashed black), time treated with A (gray), and time treated with B (solid black).

Two other types of initiators with past use of B are presented in Figure 1A. Type 2A initiators—direct switchers—initiate treatment A immediately after a period of use of treatment B. Type 3A initiators—delayed switchers—initiate treatment A after a period of no treatment following a period of use of treatment B. In both cases, the switching followed, either directly or indirectly, a new-use period of treatment B.

Unlike new users, not all direct switchers have the same exposure history, nor do all delayed switchers. For example, one direct switcher might have received 1 previous prescription for treatment B that lasted 30 days while another might have been continuously on treatment B for 5 years with dozens of prescriptions. Similarly, some delayed switchers will have been off treatment B for months; others will have been off it for a few days.

Notably, type 1A, type 2A, and type 3A are only the simplest types. For the purposes of describing the causal effect estimated by the prevalent new-user design and identifying scenarios where matching on time since comparator initiation could lead to bias, we have limited our analysis to these types for simplicity. In real data, some initiators of treatment A will have had multiple past use periods of treatment B before switching, giving them more complicated treatment histories. The fact that we rarely have the ability to look at treatment use across an individual’s lifespan adds another layer of complexity.

Causal parameters of interest

The ACNU and prevalent new-user designs answer different causal questions. Assuming we are estimating the treatment effect in the initiators of treatment A (i.e., average treatment effect in the treated), the ACNU design answers the question “what if new users of treatment A naive to treatment B had instead, counter to fact, started using treatment B?” (9) In the context of the types in Figure 1, this means we are contrasting one set of new users (type 1A) with another set (type 1B). Conversely, the prevalent new-user design answers the question “what if initiators of treatment A had instead initiated, continued, or restarted treatment B at the time of their treatment-A initiation?” Using the types, we are contrasting type 1A initiators (new users of A) with type 1B initiators (new users of B), type 2A initiators (direct switchers) with type 2B initiators (continuers), and type 3A initiators (delayed switchers) with type 3B initiators (restarters). If treatment effects are homogeneous (i.e., the effect of initiating treatment A is not modified by prior treatment with B on the scale of interest), these two questions might have the same answer, but when treatment effects vary by treatment history, the answers might diverge.

By explicitly stating the causal question, we can see that matching on time since starting treatment B or the number of past prescriptions for treatment B might not be sufficient to identify a population of continuers and restarters that is exchangeable with the population of treatment A initiators. The direct and delayed switchers in Figure 1 might both have been on treatment B for the same length of time and the same number of prescriptions but could have different exposure histories. If we match only on time since starting treatment B or the number of past prescriptions for treatment B, we might match a type 2A with a type 3B or a type 3A with a type 2B despite them having differing risks for the outcome. We sought to illustrate, via simulation, the impact of implementing a prevalent new-user analysis using propensity scores conditional on time since starting the comparator alone (rather than on full treatment history) on bias of the estimated treatment effect.

Simulated data

We simulated 40,000 patients who were new users of treatment B at time 0 (i.e., there were no new users of treatment A) and followed these individuals for an additional 4 time periods (e.g., years) or until death. At years 1, 2, 3, and 4, patients on treatment B could: 1) switch to treatment A or 2) stop taking treatment B. Those who stopped taking treatment B could either: 1) initiate treatment A or 2) restart treatment B at each subsequent time point. Once treatment A was initiated, patients remained on A for the rest of the study duration (i.e., A was not switched or stopped). There were 3 confounders (2 binary, 1 continuous) modeled with logit-linear effects on stopping or restarting treatment B and initiating treatment A. Treatments A and B were modeled to be equally protective for the outcome under study versus a referent of no treatment (risk ratio for all-cause mortality comparing treatment A vs. no treatment and treatment B vs. no treatment were both 0.80). The simulation was replicated 500 times.

We examined 7 scenarios. The first 5 scenarios used identical coefficients for the relationship between the confounders and exposure that resulted in approximately 26% of the population initiating treatment A. Approximately 50% of these individuals were direct switchers and 50% were delayed switchers at the time of starting treatment A.

In the first scenario, the risk of all-cause mortality was a log-linear function of the 3 confounders and time since new use of treatment B (i.e., study start). An association between time since new use of a treatment and the outcome can be expected when an event becomes more likely over time, such as with worsening heart failure (10).

In the next 6 scenarios, the log-linear function of mortality included additional treatment history–based characteristics. In the second scenario, cumulative continuous exposure to B decreased outcome risk (e.g., B is a treatment that becomes progressively more effective over time with continued use until discontinued, like some cancer therapies (11) or antibiotic treatments (12)); in the third scenario, outcome risk was increased by time without any therapy (e.g., being on either treatment helps slow progression, akin to angiotensin-converting-enzyme inhibitors slowing microvascular complications of diabetes) (13); and in the fourth scenario, outcome risk increased in the year individuals restarted treatment B (e.g., treatment B has a period of high initial risk of an outcome or a safety event that fades over time, like bleeding outcomes with warfarin) (14). In the fifth scenario, direct switchers to treatment A, but not delayed switchers to treatment A, experienced an increased risk of the outcome (e.g., lingering amounts of treatment B in the system interact poorly with treatment A).

To examine the effect of the distribution of types of switchers (direct vs. delayed), in the sixth scenario, the associations between the confounders and stopping were changed so that approximately 90% of initiators of A were direct switchers. In this scenario, the outcome was associated with the 3 confounders, time since new use of treatment B, and cumulative continuous exposure to B (equivalent log-linear model to the one in the second scenario). Finally, in the seventh scenario, there was a low prevalence of both delayed switching to A and restarting of B. The specific models used to generate all 5 simulated populations are listed in Table 1.

Table 1.

Key Parameters Used to Generated Simulated Populations in Each Scenario

Simulation Component	Scenario 1	Scenario 2	Scenario 3	Scenario 4	Scenario 5	Scenario 6	Scenario 7
Description of scenario	Time since new use of B impacts outcome	Continuous exposure to B affects outcome	Time off treatment A and B affects outcome	Recently restarting B affects outcome	Recently switching to A affects outcome	Scenario 2, delayed switchers are rare	Scenario 2, delayed switchers and restarters are rare
Confounder distributions	Prevalence of C1: 50%	See scenario 1	See scenario 1	See scenario 1	See scenario 1	See scenario 1	See scenario 1
	Prevalence of C2: 50% Mean of C3: 1.0; standard deviation of C3: 0.5
Direct switching	Logit (P(switch)) = log(0.1) + log(1.5) × C1 + log(1.5) × C2 + log(0.8) × C3	See scenario 1	See scenario 1	See scenario 1	See scenario 1	See scenario 1	See scenario 1
Outcome risk model	Log (P(risk)) = log(0.10) + log(0.8) × (current treatment with A) + log(0.8) × (current treatment with B) + log(2.0) × C1 + log(1.5) × C2 + log(0.9) × C3 + log(1.1) × (time since initiating B)	See scenario 1	See scenario 1	See scenario 1	See scenario 1	See scenario 1	See scenario 1
Stopping B	Logit (P(stop)) = log(0.6) + log(2.0) × C1 + log(2.0) × C2 + log(1.2) × C3	See scenario 1	See scenario 1	See scenario 1	See scenario 1	Intercept = log(0.03)	Intercept = log(0.03)
Restarting with B	Logit (P(restartB)) = log(0.2) + log(2/3) × C1 + log(2/3) × C2 + log(0.8) × C3	See scenario 1	See scenario 1	See scenario 1	See scenario 1	See scenario 1	Intercept = log(0.06)
Delayed switching to B	Logit (P(restartA)) = log(0.2) + log(1.5) × C1 + log(1.5) × C2 + log(0.8) × C3	See scenario 1	See scenario 1	See scenario 1	See scenario 1	See scenario 1	Intercept = log(0.06)
Additions to outcome risk model	None	Log(0.75) × continuous exposure to B in the treatment episode	Log(1.4) × recent time spent without A or B	Log(2.0) × recently restarting B	Log(2.0) × directly switching to A	See scenario 2	See scenario 2

Abbreviations: C, confounder; P, probability.

Estimating the risk ratio

After generating the data sets, we identified the population that had started treatment A and described their treatment histories. We then identified those who had continued (or restarted) treatment B with an identical treatment history to the initiators of treatment A. An individual who stayed on treatment B throughout the study and did not experience an outcome could thus act as a comparator with direct switchers who switched during the second, third, or fourth study periods and be represented multiple times in the final data set. We obtained 4 different risk ratios for 1-year (or 1-time-unit) all-cause mortality. First, to obtain the true risk ratio, we simulated counterfactual outcomes for each initiator of A under the counterfactual treatment that they had instead continued or restarted B. The true effect was estimated using all 500 replicates (sample size: 20 million).

Second, to estimate the crude risk ratio, we estimated the risk ratio within each replicate without adjusting for confounding by any covariates. This risk ratio gives a sense of the direction and magnitude of confounding.

Third, we estimated each individual’s probability of initiating treatment A using multivariable regression including the 3 confounders, stratified by time since new use of treatment B. For example, patients who initiated treatment A in the third time period were combined with patients who continued on or restarted B in the third time period and a propensity score model was fitted in this population. This was done separately for each stratum of time since initiation of treatment B. We then used standardized morbidity ratio (SMR) weighting (such that each initiator of treatment A received a weight of 1 and each continuer or restarter of treatment B received a weight of 1 divided by 1 minus their estimated probability of initiating treatment A) (15) so that the distribution of confounding variables in continuers and restarters of treatment B matched the distribution of confounding variables in those initiating treatment A in each time-based stratum. Asymptotically, this approach is a more conservative version of the time-conditional matching methods proposed by Suissa et al. (8) Rather than ignoring the intercept and pooling information across multiple strata via conditional logistic regression (which can lead to model misspecification in some strata when the correct model depends on calendar period), it makes sure to balance covariates within each stratum at the cost of precision.

Finally, in the fourth analysis, we again estimated each individual’s probability of initiating treatment A using stratified multivariable regression including the 3 confounders. Rather than stratify by time since initiation of treatment B, however, we instead stratified by full treatment history. After applying SMR weights based on these probabilities, the distribution of confounding variables in continuers and restarters of treatment B matched the distribution of confounding variables in those initiating treatment A in each treatment history stratum.

To summarize results, we calculated the average risk ratio with 95% confidence intervals for each analytical approach under each scenario. Confidence intervals were calculated from the standard deviation of the risk ratio across the 500 replicates. We also calculated relative bias as the difference between the average estimated risk ratio and the true risk ratio divided by the true risk ratio on the log scale. Confidence intervals of the relative error were calculated using the Monte Carlo standard error estimate (16). For full simulation and analytical code, see Web Appendix 1 (available at https://doi.org/10.1093/aje/kwaa283).

RESULTS

Table 2 contains the distribution of confounders and key variables in the cohort of treatment A initiators as well as the treatment B comparator population in scenario 1 before and after applying time- and treatment history–stratified SMR weights. On average, direct switchers started treatment A after 1.36 years, while delayed switchers started treatment A after 2.46 years. Distributions for the other scenarios were typically similar, except for scenarios 6 and 7. In scenario 6, just 9% of the treatment-A initiator population were delayed switchers, and in scenario 7, just 3% of the treatment-A initiator population were delayed switchers and 0.2% of the treatment B time periods were restarters (for full tables for those 2 scenarios, see Web Tables 1 and 2). The time-stratified SMR weights were effective at balancing the distribution of the confounders and the mean amount of time since initiating treatment B. The time-stratified weights did not balance the distribution of direct switchers or continuers (51% in the treatment-A initiator population, 77% in the weighted treatment-B initiator population) or exposure to treatment B during the most recent treatment episode (mean of 0.70 years vs. 1.31 years). Conversely, the treatment history–stratified SMR weights balanced all distributions.

Table 2.

Average Distributions^a of Key Variables in Initiators of Treatment A, the Comparator Population Treated With Treatment B at Each Time Point, and the Standardized Morbidity Ratio–Weighted Comparator Populations in the Baseline Scenario

Variable	Initiators of A (n = 10,275)		Crude Comparators (n = 22,216)		SMR time  Comparators (n = 10,272)		SMR treat  Comparators (n = 10,271)
	Mean	%	Mean	%	Mean	%	Mean	%
Confounder 1		52		33		52		52
Confounder 2		55		35		55		55
Confounder 3	0.97		0.98		0.97		0.97
Time since initiating B	1.89		1.55		1.89		1.89
Continuous years of treatment with B at baselineb	0.70		1.27		1.31		0.70
Direct switchers to A or continuers of B		52		89		77		51
Delayed switchers to A or restarters of B		49		11		23		49

Abbreviations: SMR, standardized morbidity ratio; SMR_time, with SMR weights based on time-stratified propensity scores; SMR_treat, with SMR weights based on treatment history–stratified propensity scores.

^a Across all 500 replicates.

^b This quantity resets when individuals are not treated with B, meaning that for restarters it will be 0 while for delayed switchers it can be anywhere from 1 to 3 depending on their previous exposure history.

Table 3 shows the true risk ratio, crude risk ratio, weighted risk ratio, and relative bias of each weighted risk ratio in all 7 scenarios, while Table 4 presents the standard errors and the mean squared error of the log risk ratio for all 7 scenarios. Standard errors were higher for the treatment history–stratified analyses than the time-stratified analyses, as expected given the smaller treatment history strata. While both methods yielded similar results in scenario 1, the time-stratified estimates were biased in scenarios 2, 3, and 4, although the amount of bias varied considerably depending on the ways treatment history was associated with the outcome. Interestingly, the time-stratified approach was unbiased in scenario 5, likely for the same reason that there is no need to adjust for confounders that are associated only with the outcome in the treated when estimating the average treatment effect in the treated (17). Even in scenario 6, when 90% of the initiators of treatment A were direct switchers, the time-stratified estimates were still slightly biased—this bias reduced further in scenario 7 when restarting treatment B was also made less common.

Table 3.

True and Estimated Risk Ratios, as Well as Relative Bias, for Each Analytical Method When Comparing Treatment A With Treatment B in Each Scenario

Result	Scenario 1 a		Scenario 2 b		Scenario 3 c		Scenario 4 d		Scenario 5 e		Scenario 6 f		Scenario 7 g
	RR	95% CI	RR	95% CI	RR	95% CI	RR	95% CI	RR	95% CI	RR	95% CI	RR	95% CI
True risk ratioh	1.00		1.33		1.00		0.66		1.48		1.33		1.33
Crude	1.29	1.22, 1.36	2.06	1.93, 2.19	1.49	1.54, 1.74	1.14	1.08, 1.21	1.91	1.82, 2.00	1.64	1.54, 1.74	1.57	1.47, 1.67
SMRtime	1.00	0.94, 1.07	1.57	1.45, 1.69	1.12	1.36, 1.54	0.79	0.74, 0.84	1.48	1.40, 1.57	1.44	1.36, 1.54	1.38	1.30, 1.47
SMRtreat	1.00	0.93, 1.07	1.33	1.22, 1.45	1.00	1.24, 1.44	0.66	0.62, 0.70	1.48	1.39, 1.58	1.33	1.24, 1.44	1.33	1.24, 1.43
	Bias	95% CI	Bias	95% CI	Bias	95% CI	Bias	95% CI	Bias	95% CI	Bias	95% CI	Bias	95% CI
Crude	1.29	1.22, 1.46	1.54	1.45, 1.65	1.49	1.16, 1.31	1.74	1.64, 1.84	1.29	1.23, 1.35	1.23	1.16, 1.31	1.18	1.11, 1.25
SMRtime	1.00	0.94, 1.07	1.18	1.09, 1.27	1.12	1.02, 1.16	1.20	1.13, 1.28	1.00	0.94, 1.06	1.09	1.02, 1.16	1.04	0.97, 1.10
SMRtreat	1.00	0.93, 1.07	1.00	0.92, 1.09	1.00	0.93, 1.08	1.00	0.94, 1.06	1.00	0.93, 1.07	1.00	0.93, 1.08	1.00	0.93, 1.07

Abbreviations: CI, confidence interval; RR, risk ratio; SMR, standardized morbidity ratio; SMR_time, with SMR weights based on time-stratified propensity scores; SMR_treat, with SMR weights based on treatment history–stratified propensity scores.

^a Time since new use of B associated with the outcome.

^b Cumulative exposure to B also associated with the outcome.

^c Time off treatment associated with the outcome.

^d Recently restarting treatment B associated with the outcome.

^e Recently directly switching to treatment A associated with the outcome.

^f Delayed switching is rare.

^g Delayed switching and restarting are both rare.

^h From counterfactuals across all 500 replicates.

Table 4.

Standard Error and Mean Squared Error of Each Analytical Method When Comparing Treatment A to Treatment B in Each Scenario

Result	Standard Error
	Scenario 1 a	Scenario 2 b	Scenario 3 c	Scenario 4 d	Scenario 5 e	Scenario 6 f	Scenario 7 g
Crude	0.028	0.032	0.029	0.028	0.025	0.031	0.031
SMRtime	0.032	0.039	0.031	0.032	0.029	0.032	0.031
SMRtreat	0.036	0.043	0.034	0.033	0.034	0.038	0.036
	Mean Squared Error
	Scenario 1 a	Scenario 2 b	Scenario 3 c	Scenario 4 d	Scenario 5 e	Scenario 6 f	Scenario 7 g
Crude	0.0649	0.1921	0.1590	0.3057	0.0648	0.0441	0.0271
SMRtime	0.0010	0.0283	0.0131	0.0338	0.0009	0.0079	0.0023
SMRtreat	0.0013	0.0019	0.0011	0.0011	0.0012	0.0015	0.0013

Abbreviations: SMR, standardized morbidity ratio; SMR_time, with SMR weights based on time-stratified propensity scores; SMR_treat, with SMR weights based on treatment history–stratified propensity scores.

^a Time since new use of B associated with the outcome.

^b Cumulative exposure to B also associated with the outcome.

^c Time off treatment associated with the outcome.

^d Recently restarting treatment B associated with the outcome.

^e Recently directly switching to treatment A associated with the outcome.

^f Delayed switching is rare.

^g Delayed switching and restarting are both rare.

DISCUSSION

With the ACNU design, epidemiologists estimate the difference between initiating treatment A and initiating treatment B in new users naive to both treatments A and B. The prevalent new-user design is a useful approach to asking other causal questions, like “what is the effect of switching in those that directly switch from treatment B to treatment A?” and “what would have happened to those who had a delayed switch to treatment A from treatment B had they instead restarted treatment B?” These questions are important for public health.

Because of potential heterogeneity in treatment history among switchers, matching on or stratifying by time since initiation alone might not always be sufficient to remove confounding bias. In our simulations, when cumulative exposure to treatment B (within a treatment episode or overall), recently restarting treatment B, or time spent off treatment A or B was associated with the outcome, stratifying on time alone resulted in bias. In such cases, matching, stratification, or confounder adjustment techniques that incorporate additional aspects of treatment history are needed. These analyses are less necessary when delayed switching to A and restarting B are rare, and when the only treatment history–related characteristic related to the outcome is recently switching to treatment A, analyses conditioning on time can be unbiased and more precise.

Because we were predominantly interested in demonstrating how and when time-stratified propensity scores might generate biased effect estimates, we have examined simplified scenarios. First, our presented results are limited to estimating risk ratios with limited follow-up. We have chosen to present risk ratios because the causal interpretation of a hazard ratio in these scenarios might be complicated due to administrative censoring (e.g., delayed switchers cannot exist until the third time period) and the lack of proportional hazards. Additionally, we used SMR weighting to ensure a constant target population across simulations and increase simulation speed. It is possible that propensity score matching might behave slightly differently, particularly in small data sets when there are several design choices that must be made (e.g., to match with or without replacement). We hope to see future research specifically exploring the impact of these design decisions on the bias of effect estimates, and hope that our code can be used to explore impacts of other factors like the magnitude of the effect of treatment A and treatment B on the outcome.

Second, we conducted an “intention to treat” analysis where individuals were not censored at the time of treatment switch. Choice of analytical approach between “intention to treat” versus “per protocol” in comparative effectiveness research has important implications on the intended causal parameter (18). In a “per-protocol” analysis, the estimated treatment effect is the joint effect of initiating treatment A and remaining on treatment A compared with continuing/restarting treatment B and remaining on treatment B. When we are interested in the “per-protocol” effect, individuals are censored at treatment stopping or switching, and analyses should account for potential selection bias (19).

Additionally, we had large data sets with a simple treatment history value and only 3 confounders, making the stratification and fit of the SMR-weighted models straightforward. Just as time-conditional propensity-score methods have to coarsen data to enable model estimation (either by combining days into months or switching to number of prescriptions used), any realistic implementation of treatment history–based methods will have to do the same, particularly when there is a large number of covariates. Future methodological work examining when these obstacles indicate use of a time-conditional propensity score and conducting sensitivity analyses for unmeasured confounding by treatment history would be informative.

Our primary simulations also used static (i.e., non–time-varying) and independent confounders. To evaluate whether our results were robust to the presence of a confounder that changed over time and was affected by the treatment and other confounders, we created a second set of simulations with such a covariate (for code, see Web Appendix 2). Given the intention-to-treat nature of our analysis and the comparatively small number of confounders, the results were very similar (see Web Table 3).

Finally, our simulations were designed to demonstrate potential biases rather than give plausible magnitudes of potential bias and precision; given the number of variables involved (sample size, overall trend of switching, delayed switching, restarting in the population, how confounders impact continuing treatment, overall prevalence of use, etc.), these quantities are likely to be very specific to the outcomes and treatments under study. Future plasmode simulations (20) leveraging observed real-world relationships between covariates, switching, exposure, and the outcome would give a better sense of the magnitude of the bias and precision trade-off between the time-stratified and exposure history–stratified designs. This might be especially important when some observed confounders are, themselves, proxies for treatment history, and can at least partially close those confounding paths.

There are some other points worth considering with respect to the causal questions that can be examined by the prevalent new-user design. Consider patients who have taken the comparator in the past but have discontinued it either temporarily or permanently because of emergent contraindications. The actual periods of time when these individuals are taking neither treatment A nor treatment B were not included as potential comparators for the treatment A initiators in our analysis—only the periods when they had once again started using treatment B. This approach aligns the causal question more with the ACNU design, but there might be instances in which including these periods of time produces estimates for a treatment effect that are more useful for public health.

For example, patients who discontinue the comparator might have done so for reasons related to onerous side effects or hypersensitivity reactions. If these patients initiate the treatment of interest, restarting the comparator might not be a realistic counterfactual, and finding matches or weighted equivalents of these individuals would be very difficult. In such circumstances, a more relevant question could be “What if those who initiated the treatment of interest had instead not initiated it?” Such a question is not addressable using a conventional ACNU approach but is still potentially critical for public health. Analytically, this might be achievable by allowing patients who are not on any treatment into the data set of potential comparators, but combining or contrasting these results with the results from an ACNU analysis would be highly inappropriate.

The prevalent new-user design can answer other important public health questions that cannot be addressed with an ACNU design, for example, questions related to the safety and effectiveness of drug discontinuation and deprescribing. Rather than looking at treatment A and treatment B, one can instead focus on matching those discontinuing treatment B to those who stay on treatment B based on their overall treatment history and time since initiating treatment B. Provided that key confounders are measured and included in the propensity score model, the focus can shift from questions like “what if everyone in the population taking treatment B discontinued it?” to “what would have happened to those that discontinued treatment B had they instead remained on treatment?” A similar argument can be made for using the prevalent new-user design to study the effect of augmenting therapy.

CONCLUSIONS

The prevalent new-user design is a tool to answer new and important epidemiologic and public health questions. When conducting these studies, it is important that researchers clearly articulate the effect being studied and acknowledge how it differs from an ACNU study of the same treatments, especially when directly comparing study results. Overall, the prevalent new-user design can provide useful estimates of treatment effects that are not restricted to new users. However, researchers should consider matching, stratifying, or adjusting for additional treatment-related characteristics beyond time since starting the comparator when the outcome might be a complex function of disease progression and prior treatment.