Skip to main content
PMC home page
Royal Society of Chemistry logoLink to Royal Society of Chemistry
. 2021 Feb 19;23(10):5984–5991. doi: 10.1039/d0cp06452a

Molecular insights on poly(N-isopropylacrylamide) coil-to-globule transition induced by pressure†

Letizia Tavagnacco 1, Ester Chiessi 2,✉, Emanuela Zaccarelli 1,✉
PMCID: PMC8247264  PMID: 33666621

Abstract

By using extensive all-atom molecular dynamics simulations of an atactic linear polymer chain, we provide microscopic insights into poly(N-isopropylacrylamide) (PNIPAM) coil-to-globule transition addressing the roles played by both temperature and pressure. We detect a coil-to-globule transition up to large pressures, showing a reentrant behavior of the critical temperature with increasing pressure in agreement with experimental observations. Furthermore, again confirming the experimental findings, we report the existence at high pressures of a new kind of globular state. It is characterized by a more structured hydration shell that is closer to PNIPAM hydrophobic domains, as compared to the globular state observed at atmospheric pressure. Our results highlight that temperature and pressure induce a PNIPAM coil-to-globule transition through different molecular mechanisms, opening the way for a systematic use of both thermodynamic variables to tune the location of the transition and the properties of the associated swollen/collapsed states.

By using extensive all-atom molecular dynamics simulations of an atactic linear polymer chain, we unveil the role of pressure in the coil-to-globule transition of poly(N-isopropylacrylamide) (PNIPAM).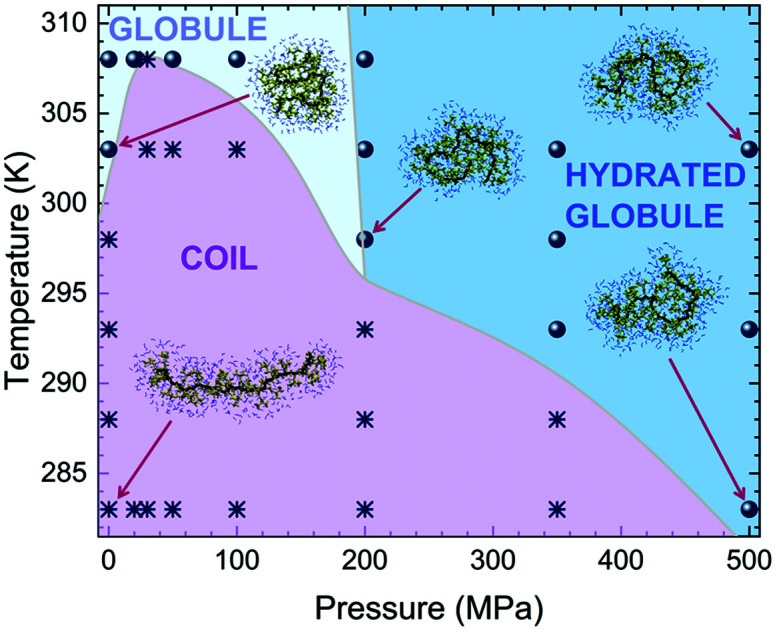graphic file with name d0cp06452a-ga.jpg

Introduction

The rational design of materials that can fulfill targeted functions is at the frontier of research, notwithstanding the considerable progress made in macromolecular science in the last few years.1 Thermosensitivity of polymers in solution, whose thermodynamic foundations were laid by Flory in the middle of the last century,2 is still one of the most investigated properties, being exploited in various nano and bio-technological applications.3–7 Among synthetic polymers, poly(N-isopropylacrylamide) (PNIPAM) is of particular interest because its lower critical solution temperature (LCST) in water at atmospheric pressure is about 305 K,8 close to body temperature. The temperature-induced phase separation of the PNIPAM aqueous solution was shown to occur with a coil-to-globule transition followed by the aggregation of polymer chains. In PNIPAM-based network systems, the change from a coiled to a collapsed (globule) chain conformation at the LCST originates a volume phase transition (VPT),4 at a VPT temperature (VPTT) similar to the LCST value. Hence, at atmospheric pressure, chemically cross-linked hydrogels and microgels of this polymer are found in a water-rich swollen state at ambient temperature, while, for temperatures above the VPTT, water is partially expelled from the polymer network and the systems collapse.9 Moreover, at low temperatures, PNIPAM microgels were found to efficiently retain and confine water,10 the polymer–water interactions being a key ingredient for the PNIPAM solution behavior.11–14 Several studies using different experimental techniques have addressed the changes induced by temperature across the VPT, from both the structural15–17 and the dynamical18,19 points of view, and more recently the aid of numerical simulations turned out to be crucial in deeply understanding microgels’ phase behavior.20 Although studying equilibria of polymers in solution is computationally challenging,21–24 atomistic simulations have provided useful insights on the effects of the stereochemistry and the nature of the functional groups on the lower critical solution temperature of the polymers.25–27 Furthermore, they allowed understanding the role of the structure of the surrounding solvent28,29 and the key factors that cause the phenomenon.11,12,30

Pressure (P), like temperature (T), also induces a macroscopic phase separation of PNIPAM in aqueous solution,31 but its role has been rather less investigated so far and the molecular mechanisms occurring upon pressure changes have yet to be fully unveiled. By relying on the analogy of temperature-induced coil-to-globule transition of PNIPAM to the globular protein cold renaturation, the increase of pressure is expected to induce an increase of the transition temperature, namely a stabilization of coil states.32–34 This is indeed observed also in PNIPAM for P ≲ 100 MPa.35,36 However, an opposite effect is detected at higher pressures where the temperature solubility range of PNIPAM chains is reduced.35–37 Such a reentrant phase behavior is also found in hydrogels:38 while up to pressures of about 150 MPa swollen states are stabilized up to temperatures about 10 K larger than the VPTT at atmospheric pressure, a further increase of pressure causes gradual shrinking. Moreover, hydrogels display a transition between a low pressure shrunken state and a high pressure shrunken state.38 This feature is confirmed in PNIPAM microgels using small angle X-ray scattering and Fourier transform infrared spectroscopy (FTIR) experiments where the collapsed states at high pressure are significantly more hydrated than those occurring at atmospheric pressure.39,40 The effect of size re-increasing by applying pressure is found to be independent of the polymer architecture.41 Since pressure seems to always favor the formation of more hydrated states,40 the presence of a genuine coil-to-globule transition has been questioned at high pressures.42

Altogether these findings show that pressure increases the water affinity of PNIPAM and plays an antagonistic effect with respect to temperature,39 with a balance that depends on the specific (P,T) conditions. It is thus important to carry out an extensive study covering a wide range of T and P, in order to understand the concerted effects of these two state variables. Surprisingly, up-to-date, there have been no numerical studies on pressure effects on the PNIPAM coil-to-globule transition in water. Here, we fill this gap by exploring the PNIPAM phase diagram using extensive all-atom molecular dynamics (MD) simulations of an atactic polymer chain at infinite dilution. Our results reveal that temperature and pressure both induce a conformational transition of PNIPAM, but through different molecular mechanisms. This leads to a reentrant behavior of the coil-to-globule transition with increasing pressure and to the emergence of a ‘hydrated’ globular state at high pressures, in qualitative agreement with experiments.

Computational procedure

The PNIPAM phase diagram is investigated by performing all-atom MD simulations on a linear polymer chain, made of 30 repeating units, at infinite dilution. To reproduce the experimental conditions, we model the polymer chain with an atactic stereochemistry.12,25 PNIPAM is described with a modified version of the OPLS-AA force field,43 which includes the implementation by Siu et al.44 Indeed, the original OPLS-AA force field was shown to fail in reproducing the aqueous solubility of NIPAM.21,22 In addition, a similar modified version of the OPLS-AA force field was found to properly describe the behaviour of N-isopropylpropionamide in aqueous solution at high pressures.45 The Tip4p/ICE model46 is employed for water, in order to adopt a simulation setup that was found to well reproduce PNIPAM coil-to-globule transition induced by temperature,12 and the dynamics of PNIPAM at low temperatures in quantitative agreement with neutron scattering experiments.10,47 Simulations are performed in a range of pressure between 0.1 and 500 MPa for temperatures between 283 and 308 K, with a temperature step of 5 K. Trajectory data are collected for ∼0.3 μs at each point in the P–T phase diagram. To take into account both a proper sampling of the phase space23,24 and the demanding computational cost required when infinite dilution conditions are employed, we have validated the reproducibility of single trajectories by performing two replicas of the state points at atmospheric pressure as well as of those in the lower P domain (from atmospheric pressure up to 200 MPa) starting from different initial configurations. As shown in Fig. S1–S4 of the ESI,† a good reproducibility of the data is observed, even when different initial configurations (either extended or collapsed chain) are employed. Further details on the simulation protocol are reported in Sections I–III of the ESI.†

Results and discussion

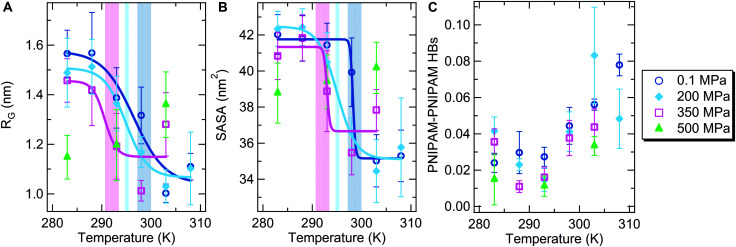
We start by probing the high pressure regime (P ≥ 200 MPa) and examine the T-dependence of the average radius of gyration RG of the polymer chain. This observable signals the occurrence of the coil-to-globule transition, that is the infinite dilution manifestation of the phase separation taking place at the critical point.48Fig. 1A reports RG as a function of temperature in the range between 283 and 308 K for P = 0.1, 200, 350 and 500 MPa, while the corresponding time evolution for each studied state point is shown in Figs. S1 (replica 1) and S5 of the ESI.† For all pressure conditions except P = 500 MPa, we distinguish a temperature region where extended conformations are populated, attributable to coil states, and, at higher temperatures, the transition to the globule state. We further characterize the coil-to-globule transition of the polymer by calculating its average solvent accessible surface area (SASA), shown in Fig. 1B, that fully reflects the behavior of RG. At each pressure, the transition temperature (Tc) is defined as the inflection point of the sigmoidal fitting curve to the data in Fig. 1A and B. At atmospheric pressure, Tc is estimated to be 298.5(±1.5) K, in qualitative agreement with a coil-to-globule transition temperature of ∼305 K measured for PNIPAM single chains with a high degree of polymerization in water.49

Fig. 1. Temperature dependence of (A) the PNIPAM radius of gyration; (B) the solvent accessible surface area. Data represent time averaged values over the last 100 ns and standard deviation. Solid lines are the sigmoidal fit. The transition temperature values, equal to 298.5 ± 1.5 K, 295.0 ± 0.5 K, and 292.0 ± 1.5 K at 0.1 MPa, 200 MPa, and 350 MPa, respectively, are identified by vertical bands including error bars. (C) Temperature dependence of the total number of PNIPAM–PNIPAM hydrogen bonds normalized to the number of repeating units. Data calculated at pressure values of 0.1, 200, 350 and 500 MPa are shown with blue circles, light blue diamonds, pink squares and green triangles, respectively.

Fig. 1

Open in a new tab

Analyzing the behavior of Tc and RG, we notice three main features: (i) by increasing pressure, Tc decreases until no transition is observed for 500 MPa within the investigated T-range; (ii) for T < Tc, the isothermal increase of pressure gradually reduces RG up to a collapse of the polymer chain at 500 MPa; (iii) for T > Tc, the isothermal increase of pressure induces an increase of RG. Notably, we observe in Fig. 1A that at 500 MPa, the polymer chain adopts in the whole investigated T-range a collapsed conformational state, which actually swells rather than deswells with increasing temperature. If we compare the high-P collapsed states with low-P ones at high T, we find larger values of RG and SASA at high pressure, suggesting a higher degree of hydration of the polymer chain. These results are consistent with the results of experimental studies on PNIPAM hydrogels, microgels and linear chains,38–40,50 validating our in silico model, which can thus be further exploited to gain important insights into the effects of pressure and temperature on the PNIPAM solution behavior.

To this aim, we analyze the intramolecular interactions of the polymer chain. In Fig. 1C, the average number of the total intrachain hydrogen bonds per polymer residue is reported as a function of temperature for different values of pressure. For T ≤ 293 K, a small number of intramolecular hydrogen bonds are found, being weakly affected by changes in T and P. In contrast, for T > 293 K temperature and pressure act differently: while the number of PNIPAM–PNIPAM hydrogen bonds is increased by temperature, it is reduced by pressure. To account for the effect of neighboring hydrogen bonding groups, we have also monitored the formation of hydrogen bonds as a function of the topological distance between the PNIPAM repeating units in the polymer chain. As reported in Fig. S6 of the ESI,† the number of hydrogen bonds between distant residues increases across the transition temperature. The detected P-dependence is in agreement with evidence based on FTIR experiments.39 In addition, we directly compare the low and high pressure collapsed states and observe that the number of PNIPAM–PNIPAM hydrogen bonds at 500 MPa and 283 K is considerably lower than that at 0.1 MPa and 308 K, again indicating a higher exposition of amide groups to water at high pressure. However, we notice that the importance of these effects on the phase behavior is limited since the enthalpic contribution related to the formation of PNIPAM–PNIPAM hydrogen bonds, which favours globule conformational states, plays only a minor role in the coil-to-globule transition.51

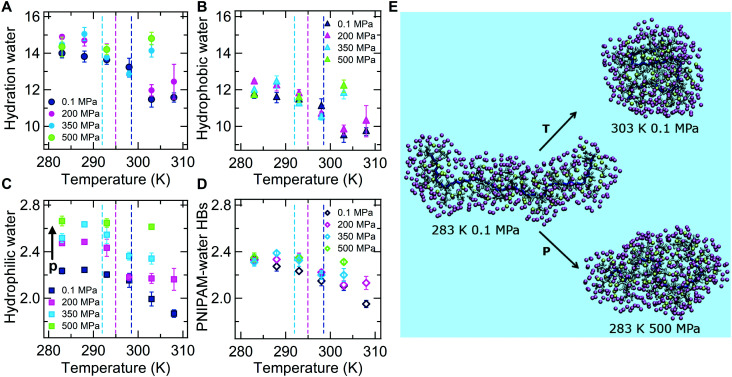
We now turn our attention to the hydration properties of PNIPAM. In Fig. 2A, we report the average number of hydration water molecules as a function of temperature and pressure, finding that at low pressures the coil-to globule transition occurs with a drop of hydration water molecules, although the polymer chain remains largely hydrated.52 Importantly, such a drop is strongly reduced with increasing pressure. Actually, at 200 and 350 MPa and at a temperature sufficiently higher than the corresponding Tc, we detect a rehydration of the chain, not associated with a concomitant increase of the SASA (Fig. 1B). Furthermore, the number of hydration water molecules remains roughly constant with temperature at 500 MPa and the associated collapsed state at 283 K is characterized by a similar hydration degree to coil states occurring at the same temperature, but at lower pressures.

Fig. 2. Temperature dependence of (A) the number of hydration water molecules; (B) the number of hydrophobic water molecules; (C) the number of hydrophilic water molecules and (D) PNIPAM–water hydrogen bonds. Data calculated at pressure values of 0.1, 200, 350 and 500 MPa are shown in blue, pink, light blue and green, respectively. Numerical results are averaged over the last 100 ns of simulation and normalized to the number of repeating units. Vertical dashed lines mark the Tc values at 0.1 MPa (blue), 200 MPa (pink), and 350 MPa (light blue). (E) Snapshots of a coil state at low T and atmospheric pressure, a globule state at high T and atmospheric pressure, a hydrated globule-like state at low T and high pressure. PNIPAM atoms are shown in grey, with backbone carbons highlighted in blue. Oxygen atoms of hydration water are also displayed in pink and yellow when surrounding the hydrophobic and hydrophilic groups, respectively.

Fig. 2

Open in a new tab

In order to evaluate how the local environment affects PNIPAM hydration, we compare the individual contributions of hydrophobic and hydrophilic hydration water, defined as water molecules whose oxygen atoms are found at a distance from PNIPAM nitrogen/oxygen atoms lower than 0.35 nm or at a distance from methyl carbon atoms of PNIPAM lower than 0.55 nm, displayed in Fig. 2B and C. A loss of both kinds of water is detected across the coil-to-globule transition, while an increase of coordination is observed by applying pressure at high temperature. Qualitatively, hydrophobic water, which represents the major contribution, exhibits the same temperature/pressure behavior of the total hydration water. Instead, we find that temperature and pressure have an opposite effect on hydrophilic water: an isobaric temperature increase reduces its number while an isothermal increase of pressure increases it. We also notice that the collapsed states at high P have a larger number of hydrophilic water molecules as compared to the swollen state at atmospheric pressure. We further investigate the structuring of hydrophilic water molecules by calculating the average number of PNIPAM-water hydrogen bonds, reported in Fig. 2D. We observe that at ambient pressure, the number of PNIPAM–water hydrogen bonds is similar to the number of hydrophilic water molecules and thus all these molecules directly interact with the polymer. Differently, at high pressure, there is a significant amount of water molecules that surround amide groups, but do not form hydrogen bonds with PNIPAM, although the number of these bonds is large. Moreover, the associated clustering of hydration water molecules shows a reduction of the average size upon isobaric temperature increase, whereas no net variation is detected upon isothermal pressure increase, even in the presence of globule states (see Fig. S7 in the ESI†). Further characterization of the structuring of water molecules in the first solvation shell was carried out by calculating the tetrahedrality order parameter which varies between 0 in an ideal gas and 1 in a perfect tetrahedral network.53 As shown in Fig. S8 of the ESI,† water in the first solvation shell is less structured than in the bulk, as detected for poly(N-vinylcaprolactam) in a diluted aqueous solution.54 In addition, while temperature monotonically decreases the structuring of bulk and hydration water, pressure acts differently by reducing the water order in the bulk and by increasing it in the first solvation shell. This increase of tetrahedral coordination by applying pressure is similar to that observed for the number of hydration water molecules in the surrounding of hydrophilic PNIPAM groups (Fig. 2C). The increase of the hydrophilic component in the ensemble of the hydration water molecules could contribute to the higher tetrahedrality, by considering that the coordination to nitrogen and oxygen atoms of PNIPAM is accounted for. However, the characteristic lifetime of PNIPAM–water hydrogen bond interactions decreases with pressure (see Table S1 in the ESI†).

Combining these results with those obtained for the behavior of RG (Fig. 1A), we observe that collapsed states at high and low P with comparable RG (e.g. 350 MPa at 298 K and 0.1 MPa at 303 K) clearly show different hydration properties. We thus provide direct evidence that pressure-induced globular conformations do not imply dehydration and that, despite an increased hydration, the coil-to-globule transition still occurs at high pressure, differently from the interpretation of ref. 42. This is illustrated in the snapshots of Fig. 2E, which compares the coil state at low T and atmospheric pressure with the two different shrunken states: the standard globule and the so-called hydrated globule.

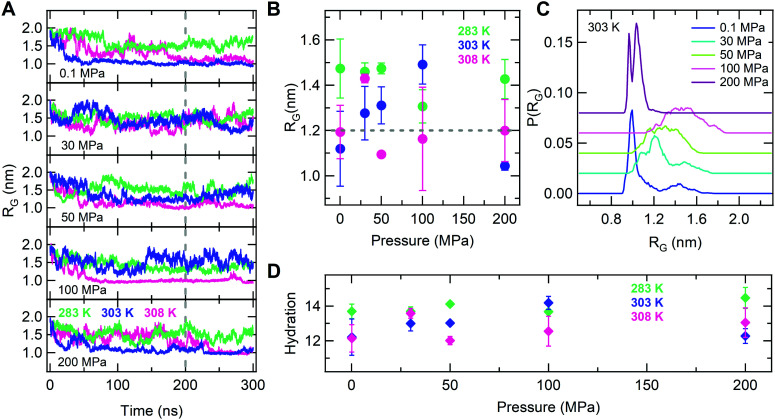
Having established the PNIPAM behavior at high pressures, we now turn to examine the lower P domain (from atmospheric pressure up to 200 MPa) and the possibility to observe a reentrant deswelling transition. It is important to note that the experimental evidence of this phenomenon is robust and independent of the macromolecular architecture, though the range of pressures and temperatures where it is observed is very narrow. Hence, it is a big challenge to detect this feature using simulations, because of the need to scan a wide region of the phase diagram with enough resolution and the consequent very high computing cost. Nonetheless, we report in Fig. 3A the selected results for the chain RG at different pressures in the range 0.1–200 MPa for representative temperatures across the boundaries of the critical point. While we observe the transition to a collapsed state for 0.1 and 200 MPa at T = 303 and 308 K, we clearly detect the persistence of swollen states at 30, 50 and 100 MPa at 303 K. In addition, the chain also remains swollen at T = 308 K and P = 30 MPa, whereas it undergoes a coil-to-globule transition for 50 and 100 MPa at the same temperature. We can thus genuinely discriminate the occurrence of a non-monotonic variation of the Tc within the investigated time window. To test the reproducibility of this feature, we have performed two independent simulations of the state points reported in Fig. 3A using initial configurations with different conformation and we have calculated the corresponding average radius of gyration, while the corresponding time evolution for each studied state point is shown in Fig. S9 of the ESI.† The results reported in Fig. 3B clearly highlight the non-monotonic change of the chain RG by increasing pressure, proving the reentrant behavior, which is particularly evident at T = 303 K. This feature is also reflected in the corresponding behavior of the radius of gyration distribution P(RG), that is reported in Fig. 3C. This figure also shows, in analogy to its corresponding one at ambient pressure (Fig. S3, ESI†), the presence of more than one peak for Rg, signaling that several chain conformations are populated within the examined 100 ns, with numerous transitions between such conformations (Fig. S9, ESI†). The latter interval thus appears to be sufficient, for the present model, to probe the occurrence of the coil-to-globule transition under equilibrium conditions. Fig. 3D reports the number of hydration water molecules across the reentrance for the three studied temperatures. While this number is found to be roughly constant in the investigated P-interval for T = 283 K, a non-monotonic behavior in pressure is observed at the two highest temperatures: hydration has a maximum at P ∼ 100 MPa and at P ∼ 30 MPa for T = 303 K and T = 308 K, respectively. In both cases, hydration at first increases, then decreases and finally re-increases again for large pressures, as already shown in Fig. 2A. A favourable comparison between the results obtained from different replicas is also reported in Fig. S10 of the ESI.† Of course, these results refer to the study of only two replicas and we are aware that advanced sampling will be needed in the future to verify these findings, but we stress that the non-monotonic behavior was observed individually for both replicas, as well as being in full agreement with experiments.

Fig. 3. Reentrant behavior at low pressures: (A) the radius of gyration as a function of time at P = 0.1, 30, 50, 100 and 200 MPa; (B) the average radius of gyration as a function of pressure calculated over the last 100 ns trajectory interval for two independent replicas at T = 283, 303 and 308 K. The dashed horizontal lines mark the critical value used to define collapsed conformations; (C) distribution of the radius of gyration P(RG) as a function of pressure at 303 K; (D) the number of hydration water molecules per PNIPAM residue as a function of pressure. Data refer to T = 283, 303 and 308 K. The analysis in C and D is also performed over the last 100 ns and averaged over two independent replicas.

Fig. 3

Open in a new tab

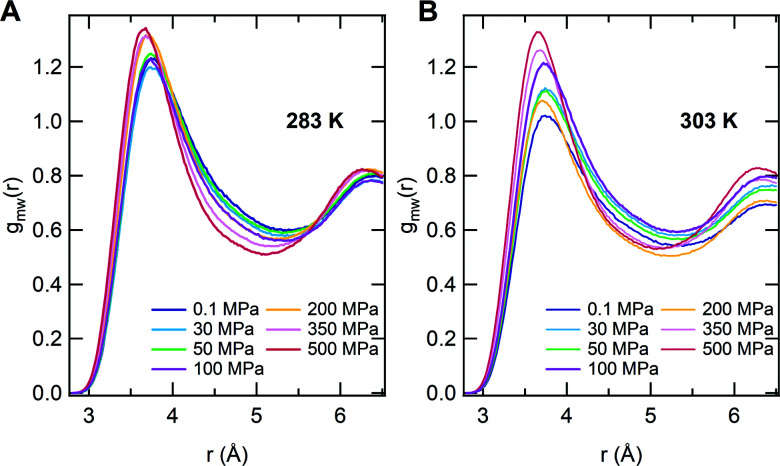
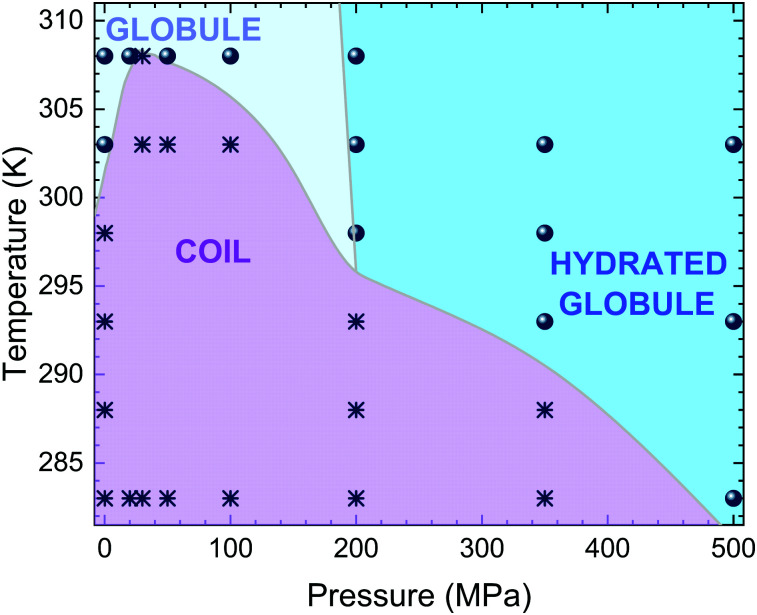
In order to obtain spatial information on the hydration properties, we finally report the radial distribution functions between C atoms of side chain methyl groups and water oxygen gmw(r) in Fig. 4. At T = 283 K, we find that the position of the main peak of gmw(r) is roughly constant up to P ∼ 100 MPa, moving toward smaller distances with a further increase of P. At the same time the peak height at first decreases, showing a minimum for P = 30 MPa, and then continuously increases. Non-monotonic effects are even more evident for T = 303 K, where the peak height increases up to 100 MPa and shows a marked decrease for 200 MPa, also revealing a change in the structuring of hydration water. A final increase of the peak height is detected in the high pressure regime. Notably, the features of gmw(r) for globular conformations at high pressures indicate a stronger coordination of water to hydrophobic domains of PNIPAM, as experimentally detected.42 These findings demonstrate the non-trivial interplay between temperature and pressure, which taken on their own would have antagonistic effects on the chain behavior: while a T-increase induces the chain to shrink reducing water contact, a P-increase promotes polymer hydration due to the more restricted volume of the tightly hydrated chain. However, when combined together, these two effects give rise to unexpected behaviors. At pressures up to about 50 MPa, the gain of hydration water upon increasing pressure pushes the coil-to-globule transition at higher T. Then, at intermediate pressures maximum hydration is reached and an overall reduction of the chain size with a concomitant decrease of Tc is detected. This implies that the two mechanisms driven by pressure and temperature are almost balanced for 100 MPa ≲ P ≲ 200 MPa, where the coil-to-globule transition occurs at the same temperature as for atmospheric pressure. For higher pressures, the decrease of Tc persists, but with a change in the hydration mechanism, that is signalled by the decrease of the gmw(r) peak position, so that collapsed states for P ≳ 200 MPa manifest as hydrated globules. The resulting phase diagram, with all studied state points, is reported in Fig. 5. While this is to be intended as a schematic illustration due to the limited number of state points that were scanned in such an extended region of the phase diagram, particularly concerning the globule to hydrated globule transition, we note that it looks remarkably similar to that determined by turbidimetry measurements in ref. 55. We plan to further investigate this aspect in more detail in the near future.

Fig. 4. Radial distribution functions for water oxygen atoms around PNIPAM methyl groups gmw for different pressures at T = 283 K (A) and T = 303 K (B). The analysis is performed over the last 100 ns trajectory interval.

Fig. 4

Open in a new tab

Fig. 5. Summary of the PNIPAM phase diagram. State points related to coil and globule conformations are assigned on the basis of the average radius of gyration of the polymer chain, if above or below 1.2 nm, and are shown with asterisks and circles, respectively. To distinguish between globular and hydrated globular states we use the tentative criterion of the number of hydration water molecules being ≳12.5 for the latter. The slope of the boundary line is determined from the fact that hydration tends to increase with increasing temperature at high pressures, but should only be used as a guess, awaiting for experimental confirmation, due to the few state points examined in this region. Coloured areas and phase boundaries are a guide to the eye.

Fig. 5

Open in a new tab

Conclusions

In conclusion, this work provides a comprehensive description of the molecular changes occurring in the PNIPAM solution behavior when both temperature and pressure are varied. We have highlighted the complex pressure-dependence of the coil-to-globule transition, encompassing a non-monotonic dependence of Tc with increasing pressure as well as the presence of two different shrunken states at low and high pressures, respectively, in full qualitative agreement with experimental observations.36,38,39

Overall these findings point out both the great potentiality of atomistic simulations to unveil the microscopic behavior of polymers in solution and the high computational cost required to adequately sample the phase space. Hence, they call for future studies addressing the search of advanced sampling methods that would work within a reasonable simulation time scale. In this respect, the use of accurate coarse-grained models which allow extended simulation times appears to be particularly promising, as recently shown for the PNIPAM coil-to-globule transition at ambient pressure.56

Finally, it is important to stress that the behavior of RG with increasing pressure along the T = 303 K isotherm, corresponding to a pressure-induced rehydration of the globular conformation (Fig. 1A and 2A), is analogous to the P-induced denaturation of globular proteins.57 As detected for pressure-denaturated proteins, at 303 K and high pressure PNIPAM retains a compact structure with water molecules penetrating the core.58 Although the molecular mechanism of the pressure induced denaturation is still debated,59–64 one of the main working hypotheses is the attenuation of the hydrophobic interactions between nonpolar side chains with increasing pressure,65,66 similar to what detected in the present work for PNIPAM. Indeed, the increased hydration of the hydrophobic regions of the polymer (Fig. 4) witnesses the decrease of intrachain hydrophobic contacts. These findings thus also reinforce the role of PNIPAM as a useful model system to study the hydration properties of proteins.

Conflicts of interest

There are no conflicts to declare.

Supplementary Material

CP-023-D0CP06452A-s001

Acknowledgments

We acknowledge support from the European Research Council (ERC-CoG-2015, Grant No. 681597 MIMIC) and from MIUR (FARE Project SOFTART No. R16XLE2X3L), and CINECA-ISCRA for HPC resources.

†

Electronic supplementary information (ESI) available: Model and simulation procedure, trajectory analysis, comparison between two replicas at atmospheric pressure, structural characterization of PNIPAM coil-to-globule transition, PNIPAM–PNIPAM hydrogen bonding, water molecule structuring, comparison between two replicas at pressures below 200 MPa. See DOI: 10.1039/d0cp06452a

Notes and references

  1. Lutz J.-F. Lehn J.-M. Meijer E. Matyjaszewski K. Nat. Rev. Mater. 2016;1:1–14. doi: 10.1038/natrevmats.2016.24. [DOI] [Google Scholar]
  2. Flory P. J., Principles of polymer chemistry, Cornell University Press, 1953 [Google Scholar]
  3. Stuart M. A. C. Huck W. T. Genzer J. Müller M. Ober C. Stamm M. Sukhorukov G. B. Szleifer I. Tsukruk V. V. Urban M. et al. . Nat. Mater. 2010;9:101–113. doi: 10.1038/nmat2614. [DOI] [PubMed] [Google Scholar]
  4. Fernandez-Nieves A., Wyss H., Mattsson J. and Weitz D. A., Microgel suspensions, Wiley Online Library, 2011 [Google Scholar]
  5. Agrawal G. Agrawal R. Small. 2018;14:1801724. doi: 10.1002/smll.201801724. [DOI] [PubMed] [Google Scholar]
  6. Karg M. Pich A. Hellweg T. Hoare T. Lyon L. A. Crassous J. J. Suzuki D. Gumerov R. A. Schneider S. Potemkin I. I. et al. . Langmuir. 2019;35:6231–6255. doi: 10.1021/acs.langmuir.8b04304. [DOI] [PubMed] [Google Scholar]
  7. Di Napoli B. Franco S. Severini L. Tumiati M. Buratti E. Titubante M. Nigro V. Gnan N. Micheli L. Ruzicka B. et al. . ACS Appl. Polym. Mater. 2020;2(7):2791–2801. doi: 10.1021/acsapm.0c00342. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Halperin A. Kröger M. Winnik F. M. Angew. Chem., Int. Ed. 2015;54:15342–15367. doi: 10.1002/anie.201506663. [DOI] [PubMed] [Google Scholar]
  9. Lopez C. G. Richtering W. Soft Matter. 2017;13:8271–8280. doi: 10.1039/C7SM01274H. [DOI] [PubMed] [Google Scholar]
  10. Zanatta M. Tavagnacco L. Buratti E. Bertoldo M. Natali F. Chiessi E. Orecchini A. Zaccarelli E. Sci. Adv. 2018;4:eaat5895. doi: 10.1126/sciadv.aat5895. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Deshmukh S. A. Sankaranarayanan S. K. Suthar K. Mancini D. C. J. Phys. Chem. B. 2012;116:2651–2663. doi: 10.1021/jp210788u. [DOI] [PubMed] [Google Scholar]
  12. Tavagnacco L. Zaccarelli E. Chiessi E. Phys. Chem. Chem. Phys. 2018;20:9997–10010. doi: 10.1039/C8CP00537K. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Niebuur B.-J. Lohstroh W. Appavou M.-S. Schulte A. Papadakis C. M. Macromolecules. 2019;52:1942–1954. doi: 10.1021/acs.macromol.8b02708. [DOI] [Google Scholar]
  14. Tavagnacco L. Chiessi E. Zanatta M. Orecchini A. Zaccarelli E. J. Phys. Chem. Lett. 2019;10:870–876. doi: 10.1021/acs.jpclett.9b00190. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Saunders B. R. Langmuir. 2004;20:3925–3932. doi: 10.1021/la036390v. [DOI] [PubMed] [Google Scholar]
  16. Stieger M. Richtering W. Pedersen J. S. Lindner P. J. Chem. Phys. 2004;120:6197–6206. doi: 10.1063/1.1665752. [DOI] [PubMed] [Google Scholar]
  17. Conley G. M. Aebischer P. Nöjd S. Schurtenberger P. Scheffold F. Sci. Adv. 2017;3:e1700969. doi: 10.1126/sciadv.1700969. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Sierra-Martin B. Retama J. R. Laurenti M. Barbero A. F. Cabarcos E. L. Adv. Colloid Interface Sci. 2014;205:113–123. doi: 10.1016/j.cis.2013.11.001. [DOI] [PubMed] [Google Scholar]
  19. Zanatta M. Tavagnacco L. Buratti E. Chiessi E. Natali F. Bertoldo M. Orecchini A. Zaccarelli E. J. Chem. Phys. 2020;152:204904. doi: 10.1063/5.0007112. [DOI] [PubMed] [Google Scholar]
  20. Rovigatti L. Gnan N. Tavagnacco L. Moreno A. J. Zaccarelli E. Soft Matter. 2019;15:1108–1119. doi: 10.1039/C8SM02089B. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Botan V. Ustach V. Faller R. Leonhard K. J. Phys. Chem. B. 2016;120:3434–3440. doi: 10.1021/acs.jpcb.6b00228. [DOI] [PubMed] [Google Scholar]
  22. Mochizuki K. Sumi T. Koga K. Sci. Rep. 2016;6:24657. doi: 10.1038/srep24657. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Garca E. J. Hasse H. Eur. Phys. J. Spec. Top. 2019;227:1547–1558. doi: 10.1140/epjst/e2018-800171-y. [DOI] [Google Scholar]
  24. Dalgicdir C. van der Vegt N. F. J. Phys. Chem. B. 2019;123:3875–3883. doi: 10.1021/acs.jpcb.9b01644. [DOI] [PubMed] [Google Scholar]
  25. Chiessi E. Paradossi G. J. Phys. Chem. B. 2016;120:3765–3776. doi: 10.1021/acs.jpcb.6b01339. [DOI] [PubMed] [Google Scholar]
  26. de Oliveira T. E. Mukherji D. Kremer K. Netz P. A. J. Chem. Phys. 2017;146:034904. doi: 10.1063/1.4974165. [DOI] [PubMed] [Google Scholar]
  27. de Solorzano I. O. Bejagam K. K. An Y. Singh S. K. Deshmukh S. A. Soft Matter. 2020;16:1582–1593. doi: 10.1039/C9SM01798D. [DOI] [PubMed] [Google Scholar]
  28. Deshmukh S. A. Kamath G. Suthar K. J. Mancini D. C. Sankaranarayanan S. K. Soft Matter. 2014;10:1462–1480. doi: 10.1039/C3SM51750K. [DOI] [PubMed] [Google Scholar]
  29. Tavagnacco L. Zaccarelli E. Chiessi E. J. Mol. Liq. 2020;297:111928. doi: 10.1016/j.molliq.2019.111928. [DOI] [Google Scholar]
  30. Podewitz M. Wang Y. Quoika P. K. Loeffler J. R. Schauperl M. Liedl K. R. J. Phys. Chem. B. 2019;123:8838–8847. doi: 10.1021/acs.jpcb.9b06125. [DOI] [PubMed] [Google Scholar]
  31. Osaka N. Shibayama M. Kikuchi T. Yamamuro O. J. Phys. Chem. B. 2009;113:12870–12876. doi: 10.1021/jp902960b. [DOI] [PubMed] [Google Scholar]
  32. Taniguchi Y. Suzuki K. J. Phys. Chem. 1983;87:5185–5193. doi: 10.1021/j150643a025. [DOI] [Google Scholar]
  33. Weingand-Ziadé A. Renault F. Masson P. Biochim. Biophys. Acta, Protein Struct. Mol. Enzymol. 1997;1340:245–252. doi: 10.1016/S0167-4838(97)00051-4. [DOI] [PubMed] [Google Scholar]
  34. Heinisch O. Kowalski E. Goossens K. Frank J. Heremans K. Ludwig H. Tauscher B. Z. Lebensm.-Unters. Forsch. 1995;201:562–565. doi: 10.1007/BF01201586. [DOI] [PubMed] [Google Scholar]
  35. Kunugi S. Takano K. Tanaka N. Suwa K. Akashi M. Macromolecules. 1997;30:4499–4501. doi: 10.1021/ma961770r. [DOI] [Google Scholar]
  36. Niebuur B.-J. Chiappisi L. Zhang X. Jung F. Schulte A. Papadakis C. M. ACS Macro Lett. 2018;7:1155–1160. doi: 10.1021/acsmacrolett.8b00605. [DOI] [PubMed] [Google Scholar]
  37. Otake K. Karaki R. Ebina T. Yokoyama C. Takahashi S. Macromolecules. 1993;26:2194–2197. doi: 10.1021/ma00061a008. [DOI] [Google Scholar]
  38. Kato E. J. Appl. Polym. Sci. 2005;97:405–412. doi: 10.1002/app.21764. [DOI] [Google Scholar]
  39. Grobelny S. Hofmann C. H. Erlkamp M. Plamper F. A. Richtering W. Winter R. Soft Matter. 2013;9:5862–5866. doi: 10.1039/C3SM27653H. [DOI] [Google Scholar]
  40. Pühse M. Keerl M. Scherzinger C. Richtering W. Winter R. Polymer. 2010;51:3653–3659. doi: 10.1016/j.polymer.2010.06.011. [DOI] [Google Scholar]
  41. Kunugi S. Kameyama K. Tada T. Tanaka N. Shibayama M. Akashi M. Braz. J. Med. Biol. Res. 2005;38:1233–1238. doi: 10.1590/S0100-879X2005000800011. [DOI] [PubMed] [Google Scholar]
  42. Meersman F. Wang J. Wu Y. Heremans K. Macromolecules. 2005;38:8923–8928. doi: 10.1021/ma051582d. [DOI] [Google Scholar]
  43. Jorgensen W. L. Maxwell D. S. Tirado-Rives J. J. Am. Chem. Soc. 1996;118:11225–11236. doi: 10.1021/ja9621760. [DOI] [Google Scholar]
  44. Siu S. W. I. Pluhackova K. Böckmann R. A. J. Chem. Theory Comput. 2012;8:1459–1470. doi: 10.1021/ct200908r. [DOI] [PubMed] [Google Scholar]
  45. Mochizuki K. Sumi T. Koga K. Phys. Chem. Chem. Phys. 2016;18:4697–4703. doi: 10.1039/C5CP07674A. [DOI] [PubMed] [Google Scholar]
  46. Abascal J. L. F. Sanz E. Fernández R. G. Vega C. J. Chem. Phys. 2005;122:234511. doi: 10.1063/1.1931662. [DOI] [PubMed] [Google Scholar]
  47. Tavagnacco L. Zanatta M. Buratti E. Rosi B. Frick B. Natali F. Ollivier J. Chiessi E. Bertoldo M. Zaccarelli E. Orecchini A. Phys. Rev. Res. 2021;3(1):013191. doi: 10.1103/PhysRevResearch.3.013191. [DOI] [Google Scholar]
  48. Wu C. Wang X. Phys. Rev. Lett. 1998;80:4092–4094. doi: 10.1103/PhysRevLett.80.4092. [DOI] [Google Scholar]
  49. Wu C. Zhou S. Macromolecules. 1995;28:8381–8387. doi: 10.1021/ma00128a056. [DOI] [Google Scholar]
  50. Lietor-Santos J. J. Sierra-Martin B. Gasser U. Fernández-Nieves A. Soft Matter. 2011;7:6370–6374. doi: 10.1039/C1SM05328K. [DOI] [Google Scholar]
  51. Pica A. Graziano G. J. Mol. Liq. 2019;285:204–212. doi: 10.1016/j.molliq.2019.04.071. [DOI] [Google Scholar]
  52. Pelton R. J. Colloid Interface Sci. 2010;348:673–674. doi: 10.1016/j.jcis.2010.05.034. [DOI] [PubMed] [Google Scholar]
  53. Errington J. R. Debenedetti P. G. Nature. 2001;409:318–321. doi: 10.1038/35053024. [DOI] [PubMed] [Google Scholar]
  54. Mochizuki K. Phys. Chem. Chem. Phys. 2020;22:1053–1060. doi: 10.1039/C9CP05491J. [DOI] [PubMed] [Google Scholar]
  55. Niebuur B.-J. Chiappisi L. Jung F. Zhang X. Schulte A. Papadakis C. M. Macromolecules. 2019;52:6416–6427. doi: 10.1021/acs.macromol.9b00937. [DOI] [Google Scholar]
  56. Pérez-Ramrez H. Odriozola G. Phys. Chem. Chem. Phys. 2020;22:17913–17921. doi: 10.1039/D0CP03101A. [DOI] [PubMed] [Google Scholar]
  57. Mozhaev V. V. Heremans K. Frank J. Masson P. Balny C. Proteins: Struct., Funct., Bioinf. 1996;24:81–91. doi: 10.1002/(SICI)1097-0134(199601)24:1&#x0003c;81::AID-PROT6&#x0003e;3.0.CO;2-R. [DOI] [PubMed] [Google Scholar]
  58. Hummer G. Garde S. Garcia A. E. Paulaitis M. E. Pratt L. R. Proc. Natl. Acad. Sci. U. S. A. 1998;95:1552–1555. doi: 10.1073/pnas.95.4.1552. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Kauzmann W. Nature. 1987;325:763–764. doi: 10.1038/325763a0. [DOI] [Google Scholar]
  60. Royer C. A. Biochim. Biophys. Acta, Protein Struct. Mol. Enzymol. 2002;1595:201–209. doi: 10.1016/S0167-4838(01)00344-2. [DOI] [PubMed] [Google Scholar]
  61. Imamura H. Kato M. Proteins: Struct., Funct., Bioinf. 2009;75:911–918. doi: 10.1002/prot.22302. [DOI] [PubMed] [Google Scholar]
  62. Rouget J.-B. Aksel T. Roche J. Saldana J.-L. Garcia A. E. Barrick D. Royer C. A. J. Am. Chem. Soc. 2011;133:6020–6027. doi: 10.1021/ja200228w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Roche J. Caro J. A. Norberto D. R. Barthe P. Roumestand C. Schlessman J. L. Garcia A. E. Royer C. A. et al. . Proc. Natl. Acad. Sci. U. S. A. 2012;109:6945–6950. doi: 10.1073/pnas.1200915109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Mori Y. Okumura H. J. Phys. Chem. Lett. 2013;4:2079–2083. doi: 10.1021/jz400769w. [DOI] [PubMed] [Google Scholar]
  65. Paliwal A. Asthagiri D. Bossev D. P. Paulaitis M. E. Biophys. J. 2004;87:3479–3492. doi: 10.1529/biophysj.104.050526. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Paschek D. Garca A. E. Phys. Rev. Lett. 2004;93:238105. doi: 10.1103/PhysRevLett.93.238105. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

CP-023-D0CP06452A-s001
CP-023-D0CP06452A-s001.pdf (3MB, pdf)

Articles from Physical Chemistry Chemical Physics are provided here courtesy of Royal Society of Chemistry

RESOURCES