Image-domain Material Decomposition for Spectral CT using a Generalized Dictionary Learning

Abstract

The spectral computed tomography (CT) has huge advantages by providing accurate material information. Unfortunately, due to the instability or overdetermination of material decomposition model, the accuracy of material decomposition can be compromised in practice. Very recently, the dictionary learning based image-domain material decomposition (DLIMD) can obtain high accuracy for material decompositions from reconstructed spectral CT images. This method can explore the correlation of material components to some extent by training a unified dictionary from all material images. In addition, the dictionary learning based prior as a penalty is applied on material components independently, and many parameters would be carefully elaborated in practice. Because the concentration of contrast agent in clinical applications is low, it can result in data inconsistency for dictionary based representation during the iteration process. To avoid the aforementioned limitations and further improve the accuracy of materials, we first construct a generalized dictionary learning based image-domain material decomposition (GDLIMD) model. Then, the material tensor image is unfolded along the mode-1 to enhance the correlation of different materials. Finally, to avoid the data inconsistency of low iodine contrast, a normalization strategy is employed. Both physical phantom and tissue-synthetic phantom experiments demonstrate the proposed GDLIMD method outperforms the DLIMD and direct inversion (DI) methods.

I. Introduction

The spectral CT system usually employs a photon counting detector (PCD) to collect projections of several (greater than two) energy bins/channels and then reconstructs the channel-wise spectral CT images by utilizing image reconstruction techniques [1]. The huge merits of spectral CT is that it can provide quantitative analysis and distribution of materials for some specific applications, such as differentiating small (≤30mm) hepatic hemangioma (HH) from small hepatocellular carcinoma (HCC) [2], focal liver lesions characterization[3] and left ventricular thrombus diagnosis [4]. Indeed, spectral CT equipped with the PCD can improve the signal-to-noise ratio (SNR) of measurements by counting the number and energy of received photons in theory. However, in fact, due to spectral distortions (e.g. fluorescence x-ray effects, charge sharing, K-escape, pulse pileups), the spectral CT projection datasets are corrupted by complicated noises [5] which compromise the final accuracy of material decomposition. How to achieve high precision of material information is one challenge for spectral CT in clinical applications.

To improve the decomposed material accuracy, it is of great significance to develop advanced material decomposition methods. Regarding the material decomposition methods, they can be divided into two classes: direct and indirect methods [6]. Although the direct-type algorithms can directly achieve material images from multi-energy projections [7, 8] by employing a known x-ray source spectrum, the used x-ray spectrum depends on many factors, such as scatter radiation, detector response, and so on [9]. Furthermore, it is a challenge to model and estimate x-ray spectrum in practice [10, 11]. Although the regularization priors (i.e., total variation (TV) [12, 13]) have been employed to suppress noise to some extent by penalizing material maps independently, the material decomposition results are still not satisfactory and they need further improvement.

The indirect decomposition techniques can further be divided into projection-based and image-based methods [14]. For the former, the raw measurements can be separated into several specific material projections and then image reconstruction algorithms are applied on single material projections [15, 16]. In this model, the noise can be magnified by decomposing measurements into several single material projections, and the accuracy of decomposed materials can be compromised. The image-based methods can be summarized as two procedures: image reconstruction and material decomposition. To obtain high quality spectral CT images from noise-corrupted projections, numerous iterative-based image reconstruction models were proposed. For examples, total variation (TV) constraint was imposed on each energy channel [17]. The Local HighlY constrained backPRojection Reconstruction (HYPR‐LR) [18] was proposed to exploit data redundancies in the energy domain. The tight frame sparsity was extended to low-dose spectral breast computed tomography (CT) [19]. The patch-based low-rank reconstruction model was established for sparse-view projections [20]. The prior rank, intensity and sparsity model (PRISM) was proposed to characterize the low-rank and sparsity of spectral CT [21]. In 2016, the prior image constraint compressed sensing was employed to realize spectral CT reconstruction (SPICCS)[22]. Similar to hyperspectral image [23, 24], the images from different energy bins share similar structures . Thus, the tensor dictionary learning (TDL) [25] –based reconstruction model was also proposed. To improve the performance of TDL in low-dose case, the image gradient L₀-norm was incorporated into TDL and generated the L₀TDL method [26]. Incorporating the high quality averaged image, the average-image-incorporated block-matching and 3D (aiiBM3D) filtering method was proposed [27]. Furthermore, with nonlocal similarities of spectral CT images, the sparse matrix decomposition [28], spatial-spectral cube matching frame (SSCMF) [29], non-local spectral similarity (MECT-NSS) [30] and non-local low-rank cube-based tensor factorization (NLCTF) were also proposed [31] Recently, the total image constrained diffusion tensor (TICDT) was developed for multi-energy reconstruction [32] and so on [33, 34].

The aforementioned images reconstruction techniques are mainly focusing on improving image reconstruction quality. Although the high reconstruction quality can benefit material decomposition accuracy to some extent for X-ray imaging [8, 25], the final accuracy may be limited by image quality improvement. Aiming at the 2^nd step of image-domain material decomposition, numerous iterative image-domain material decomposition (IID-MD) methods were proposed [35-38]. However, the conventional IID-MD methods are mainly focusing on the dual-energy CT (DECT, a simple spectral CT prototype). For examples, Niu et al. proposed an iterative material decomposition method using full variance-covariance matrix of material components for DECT, and the quadratic smoothness penalty function was later introduced to improve the accuracy of decomposed materials [39]. Then, the models of edge-preserving with non-local mean [37], spectral diffusion[40], nonlinear decomposition [41], penalized weighted least-square with similarity-based regularization (PWLS-SBR)[42], entropy minimization[43], average image-induced non-local mean [44], data-driven sparsity [8], multiscale penalized weighted least-squares [45], fully convolutional network [46], PWLS-TNV-ℓ₀ [47] and so on were proposed. However, the aforementioned methods are mainly designed to implement material decomposition for DECT rather than spectral CT. As for material decomposition methods for spectral CT, Tao et al. [48] proposed a prior knowledge aware iterative denoising material decomposition (MD-PKAD) model to decompose basis materials from reconstructed images[49]. In addition, a multiple constraint image-domain material decomposition (MCIMD) method was also proposed and validated by numerical simulations [50].

Very recently, we proposed a dictionary learning-based image-domain material decomposition (DLIMD) method [51]. In the DLIMD model, the regularized prior is penalized on each material component independently, and there are many parameters to be determined for practical applications. Besides, each material is considered independently in the process of material decomposition, the correlation of different components is also relaxed. Finally, because the concentration of contrast agent(s) is low in clinical applications, it can result in data inconsistency for dictionary based representation during the iteration process. In this study, we develop a generalized DLIMD (GDLIMD) to avoid these limitations. The contributions of GDLIMD are as follows. First, we construct a generalized DLIMD (GDLIMD) model for material decomposition of spectral CT. Second, the material tensor image is unfolded along mode-1 to enhance the correlation of different materials. Third, a normalization strategy is employed to avoid the data inconsistency of low contrast agents.

The remainder of this paper is organized as follows. In section II, the spectral CT image reconstruction and image-domain material decomposition models for spectral CT will be presented. In section III, both physical phantom and tissue-synthetic phantom experiments are performed to evaluate the performance of GDLIMD. In section IV, we will discuss some related issues and conclude this paper.

II. Material and method

A. Spectral CT image reconstruction

X-ray image reconstruction is a typical inverse problem, and it is usually unstable and irreversible. Considering the noise in projections, the forward model of the typical fan-beam X-ray CT can be modelled as a discrete linear system,

$$\mathit{y}=\mathit{P}\mathit{x}+ϵ,$$ (1)

where $\mathit{x}\in {\mathbb{R}}^l(I=I_W\times I_H)$ is the vectorization of 2D CT image, $\mathit{y}\in {\mathbb{R}}^M(M=M_1\times M_2)$ is the sinogram, I_W and I_H are the width and height of image, M₁ and M₂ represent the numbers of views and detector units, $\mathit{P}\in {\mathbb{R}}^{M\times 1}$ represents the CT system matrix depending on specific scanning geometry, and $ϵ\in {\mathcal{R}}^M$ is noise which comes from the instability of scanning architecture, x-ray source, detector response and so on. To obtain high-quality images, the detector unit number, projection view number and image size are usually large. This makes it impossible to save the matrix P in memory. Therefore, it is impossible to solve Eq. (1) directly by employing a matrix inversion transform. To avoid this limitation, image x usually can be reconstructed from projections y by an iterative strategy by minimizing the following optimization problem

$$\underset{\mathit{x}}{\text{argmin}}\frac{1}{2}\Vert \mathit{y}-\mathit{P}\mathit{x}{\Vert }_2^2,$$ (2)

where ∥.∥₂ is the L₂-norm for a vector. Eq. (2) is a least square convex optimization problem, and it can be solved by searching the minimization point. It can be furtherly expressed as

$${\mathit{P}}^T(\mathit{P}\mathit{x}-\mathit{y})=0.$$ (3)

Eq. (3) can is equivalent to

$${\mathit{P}}^T\mathit{P}\mathit{x}={\mathit{P}}^T\mathit{y}+{\mathit{P}}^T\mathit{P}{\mathit{x}}^{(k)}-{\mathit{P}}^T\mathit{P}{\mathit{x}}^{(k)},$$ (4)

where k is the current iteration. Here, the reconstructed image can be achieved by the following expression

$${\mathit{x}}^{(k+1)}={\mathit{x}}^{(k)}-{\lambda }^{(k)}{\mathit{P}}^T(\mathit{P}{\mathit{x}}^{(k)}-\mathit{y}).$$ (5)

where λ^(k) is a relaxation factor. Since the projections contain noise, it is difficult to find appropriate solution using Eq. (5). The regularization prior usually is used to find the satisfied solution. To further optimize Eq. (5), a regularization prior can be introduced. Then, the image reconstruction model can be modeled as

$$\underset{\mathit{x}}{\text{argmin}}\frac{1}{2}\Vert \mathit{y}-\mathit{P}\mathit{x}{\Vert }_2^2+\tau \mathit{R}(\mathit{x}),$$ (6)

where τ > 0 is a regularization factor, which can be carefully selected by a specific case in practice. From Eq. (6), one can see that it contains two terms, i.e., data fidelity term $\frac{1}{2}\Vert \mathit{y}-\mathit{Px}{\Vert }_2^2$ and regularization prior R(x). Considering different features of CT images, R(x) corresponds to different expressions and further result in different image techniques. To improve the reconstructed image quality, TV [52, 53] is a typical regularizer to characterize piece-wise constant of image reconstruction. Besides, wavelet frame [54], image gradient L₀-norm [55], low-rank [56] , and so on, are also treated as R(x) for different reconstruction applications.

Regarding the spectral CT, the x-ray spectrum is divided into several energy bins/channels, and the multiple projection datasets can be obtained from one scan. For each energy bin, we can obtain a single-energy image. Again, we can reconstruct multiple spectral CT images for the same the object using spectral CT projections. Similar to Eq. (6), spectral CT reconstruction model can be formulated as follow

$$\underset{\mathit{x}}{\text{argmin}}\left(\sum _{c=1}^C\frac{1}{2}\Vert {\mathit{y}}_c-\mathit{P}{\mathit{x}}_c{\Vert }_2^2\right)+\mu {\mathit{R}}_1(\mathit{x}),$$ (7)

where c (c = 1,2, ⋯ , C) is the index of energy channels and C represents the number of energy channels. ${\mathit{x}}_c\in {\mathbb{R}}^l(\mathrm{c}=1,2,\cdots ,C)$ is a vectorization image from c^th energy channel. x_c is c^th row of the mode-3 unfolding of the reconstructed image in terms of 3^rd order tensor $\mathit{x}\in {\mathbb{R}}^{l_1\times l_2\times C}$. y_c represents c^th row of the mode-3 unfolding of the measurement in terms of 3^rd order tensor $\mathit{y}\in {\mathbb{R}}^{M_1\times M_2\times C}$. Similar to the conventional CT reconstruction model, the first term in Eq. (7) (i.e., ${\sum }_{c=1}^C\frac{1}{2}\Vert {\mathit{y}}_c-{\mathit{Px}}_c{\Vert }_2^2$ ) represents spectral CT data fidelity and its errors come from the summation error of all energy channels. μ > 0 is designed to balance the data fidelity term and regularization prior for spectral CT.

To obtain the optimized solution of Eq. (7), ${\mathit{R}}_1(\mathcal{X})$ can be considered as regularization prior. Here, the model of Eq. (7) can be solved by introducing $\mathcal{F}$ to replace $\mathcal{X}$. Then, Eq. (7) can be rewritten as the following two sub-problems:

$$\underset{\mathit{x}}{\text{argmin}}\left(\sum _{c=1}^C\frac{1}{2}\Vert {\mathit{y}}_c-\mathit{P}{\mathit{x}}_c{\Vert }_2^2\right)+\frac{h}{2}\Vert \mathit{x}-{\mathcal{F}}^{(k)}{\Vert }_F^2,$$ (8a)

$$\underset{\mathcal{F}}{\text{argmin}}\frac{1}{2}\Vert \mathcal{F}-{\mathit{x}}^{(k+1)}{\Vert }_2^2+\mu {\mathit{R}}_1(\mathcal{F}).$$ (8b)

As for Eq. (8a), it is equal to the following problem

$$\underset{\{{\mathit{x}}_c{\}}_{c=1}^C}{\text{argmin}}\sum _{c=1}^C\frac{1}{2}\Vert {\mathit{y}}_c-\mathit{P}{\mathit{x}}_c{\Vert }_2^2+\frac{h}{2}\sum _{c=1}^C\Vert {\mathit{x}}_c-{\mathit{f}}_c^{(k)}{\Vert }_F^2.$$ (9)

Here, $\{{\mathit{x}}_c{\}}_{c=1}^C$ can be separately updating by the following expression

$$\begin{gathered} {\mathit{x}}_c^{(k+1)}={\mathit{x}}_c^{(k)}-{\lambda }^{(k)}\times \\ \left({\mathit{P}}^T\mathit{P}{\mathit{x}}_c^{(k)}-{\mathit{y}}_c)+h({\mathit{x}}_c^{(k)}-{\mathit{f}}_c^{(k)})\right),c=1,\dots ,C, \end{gathered}$$ (10)

where I is the equality transform. Almost all optimized iteration-type regularized image reconstruction models are to choose an appropriate prior, i.e., the specific regularization forms of R₁ (∙) in Eq. (7). As far as we know, all regularization forms about R₁ (∙) can fall into two classes: channel-dependent and channel-independent. Regarding the channel-dependent priors, the correlation of different channel images $\{{\mathit{f}}_c{\}}_{c=1}^C$ are considered in the formulated reconstruction models, such as TDL[25], SSCMF[29] and NLCTF. In such cases, Eq. (8b) is not equal to a set of single energy bin model and then optimize them one by one. As for channel-independent regularizers (e.g., TV-based model [17], aiiBM3D[27], (SPICCS)[22]), Eq. (8b) can is equal to the following optimization model

$$\underset{\{{\mathit{F}}_c{\}}_{c=1}^C}{\text{argmin}}\sum _{c=1}^C\frac{1}{2}{\Vert {\mathit{F}}_c-{\mathit{X}}_c^{(k+1)}\Vert }_2^2+\sum _{c=1}^C{\mu }_c{\mathit{R}}_1({\mathit{F}}_c),$$ (11)

where μ_c represents the regularization parameter of c^th energy channel. F_c and X_c represent the matrix forms of f_c and x_c.

B. Material decomposition

To decompose the material images $\{{\mathit{u}}_n{\}}_{n=1}^N$ (N is the number of basis materials) from reconstructed channel-wise spectral CT images x_c(1 ≤ c ≤ C), the basis material decomposition process can be characterized as

$$\left[\begin{array}{ccc}\hfill {\omega }_{11}\hfill & \hfill \cdots \hfill & \hfill {\omega }_{1N}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\omega }_{C1}\hfill & \hfill \cdots \hfill & \hfill {\omega }_{CN}\hfill \end{array}\right]\left[\begin{array}{c}\hfill ({\mathit{u}}_1{)}^T\hfill \\ \hfill ⋮\hfill \\ \hfill ({\mathit{u}}_N{)}^T\hfill \end{array}\right]=\left[\begin{array}{c}\hfill {\mathit{x}}_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathit{x}}_C\hfill \end{array}\right],$$ (12)

where ω_cn is the attenuation coefficients of n^th material in c^th energy bin and it can be calculated by averaging a uniform region in the n^th material [57]. To simplify Eq. (12), it can be further expressed as

$$\mathbf{w}{\mathit{u}}_{(3)}={\mathit{x}}_{(3)},$$ (13)

where = $\left[\begin{array}{ccc}\hfill {\omega }_{11}\hfill & \hfill \cdots \hfill & \hfill {\omega }_{1N}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\omega }_{C1}\hfill & \hfill \cdots \hfill & \hfill {\omega }_{CN}\hfill \end{array}\right]\in {\mathbb{R}}^{C\times N}$ , $\mathcal{U}\in {\mathcal{R}}^{l_W\times I_H\times N}$ is a 3^rd order tensor representing the material images, and. ${\mathcal{U}}_{(3)}\in {\mathcal{R}}^{N\times M}$ and ${\mathcal{X}}_{(3)}\in {\mathcal{R}}^{C\times M}$ are the mode-3 unfolding of $\mathcal{U}$ and $\mathcal{X}$. From Eq. (13), it can be seen that the direct inversion (DI) method [35] can be adopted to obtain the material components. Again, $\mathcal{U}$ can be obtained by the following expression

$${\mathcal{U}}_{(3)}=({\mathbf{w}}^{\mathrm{T}}\mathbf{w}{)}^{-1}{\mathbf{w}}^{\mathrm{T}}{\mathit{x}}_{(3)}$$ (14)

However, the process of material decomposition usually is instable. To further improve the accuracy of material decomposition, the disturbance within spectral CT images should be considered in the material decomposition model. Thus, considering the disturbance, Eq. (13) can be rewritten as

$$\mathbf{w}{\mathcal{U}}_{(3)}={\mathit{x}}_{(3)}+\sigma ,$$ (15)

where $\sigma \in {\mathcal{R}}^{C\times M}$ represents the disturbance. To decrease the error of decomposition results as much as possible, it is appropriate to adopt the least square linear programming problem to formulate the optimization problem with Eq. (15),

$$\underset{\mathit{u}}{min}\frac{1}{2}\Vert {\mathit{x}}_{(3)}-\mathbf{w}{\mathcal{U}}_{(3)}{\Vert }_F^2,$$ (16)

where ∥∙∥_F is Frobenius norm. Noting that Eq. (16) is a convex quadratic optimization, it can be easily solved. As the aforementioned, the regularization prior can be introduced into Eq. (16) to constrain the feasible domain so that to search an appropriate solution for material images, i.e., Eq. (16) can be further reformulated as

$$\underset{\mathit{u}}{min}\left(\frac{1}{2}\Vert {\mathit{x}}_{(3)}-\mathbf{w}{\mathcal{U}}_{(3)}{\Vert }_F^2+\frac{\theta }{2}{\mathit{R}}_2(\mathcal{U})\right),$$ (17)

where θ is a regularization parameters to balance decomposition model. $\frac{1}{2}\Vert {\mathcal{X}}_{(3)}-\mathbf{w}{\mathcal{U}}_{(3)}{\Vert }_F^2$ is the data fidelity of material decomposition and ${\mathit{R}}_2(\mathcal{U})$ is a regularization term of the material images.

To further shrink the feasible domain of material decomposition, the volume conservation can be employed as a constraint for multi-material components. The summation of pixel value from multiple materials at the same position should be one [58]. Considering the air, we have,

$$\left(\sum _{n=1}^N{\mathcal{U}}_{i_w{i}_{h}n}\right)+{\mathit{A}}_{i_w{i}_h}=1(1\le i_w\le I_W,1\le i_h\le I_H),$$ (18)

where ${\mathcal{U}}_{i_w{i}_{h}n}$ represents the (j₁, j₂, m)^th pixel value of $\mathcal{U}$. A_iwih represents the (j₁, j₂)^th pixel value of A. Besides, the pixel value of A_iwih is assumed binary (0 or 1), and pixel value of $\mathcal{U}$ should be ranged from zero to 1, i,e.,

$$0\le \mathcal{U}\le 1.$$ (19)

Introducing the above two constraints, the dictionary learning based image-domain material decomposition (DLIMD) model [51] can be formulated as Eq. (20).

$$\begin{gathered} \underset{\mathcal{U},\{{\beta }_n{\}}_{n=1}^N}{min}(\sum _{n=1}^N\frac{{\theta }_n}{2}\sum _{i=1}^I\left(\Vert {\mathbf{E}}_i({\mathbf{U}}_n)-\widehat{\mathbf{D}}{\beta }_{ni}{\Vert }_F^2+v_{ni}\Vert {\beta }_{ni}{\Vert }_0\right)\phantom{)} \\ \phantom{(}+\frac{1}{2}\Vert {\mathit{x}}_3-\mathbf{w}{\mathcal{U}}_{(3)}{\Vert }_F^2),s.t.0\le \mathcal{U} \\ \le 1,\left(\sum _{n=1}^N{\mathcal{U}}_{i_w{i}_{h}n}\right)+{\mathit{A}}_{i_w{i}_h}=1, \end{gathered}$$ (20)

where U_n is the matrix form of n^th material images, β_ni is sparse representation coefficients of i^th image patch within n^th material image, ${\beta }_m=\{{\beta }_m{\}}_{i=1}^I$, E_i(U_n) is the i^th image patch extraction operator from U_n, and $\widehat{\mathbf{D}}$ is the trained dictionary.

In Eq. (20), the dictionary $\widehat{\mathbf{D}}$ is achieved from all material components to characterize image similarity. However, each material component is individually considered in the decomposing process, it can overlook the correlation of different materials. Besides, each material map has itself regularization parameters θ_n(n = 1, … , N) , sparse representation error ε_n(n = 1, … , N) and atom number L_n (n = 1, … , N). It becomes a big challenge for choosing a series of appropriate parameters in practice. Therefore, to overcome these limitations of DLIMD method, a generalized dictionary learning based image-domain material decomposition (GDLIMD) method is proposed as follow:

$$\begin{gathered} \underset{\mathcal{U},\beta }{min}(\frac{\theta }{2}\sum _{i=1}^I\left(\Vert {\mathbf{E}}_i({\mathcal{U}}_{(1)})-\widehat{\mathbf{D}}{\beta }_i{\Vert }_F^2+v_i\Vert {\beta }_i{\Vert }_0\right)\phantom{)} \\ \phantom{(}+\frac{1}{2}\Vert {\mathit{x}}_3-\mathbf{w}{\mathcal{U}}_{(3)}{\Vert }_F^2)s.t.0\le \mathcal{U} \\ \le 1,\left(\sum _{n=1}^N{\mathcal{U}}_{i_w{i}_{h}n}\right)+{\mathit{A}}_{i_w{i}_h}=1, \end{gathered}$$ (21)

where ${\mathcal{U}}_{(1)}$ represents the mode-1 unfolding of tensor $\mathcal{U}$, θ is the regularized parameter, and v_i is the Lagrange multiplier. Because the material component distribution depends on the imaging object, it can be significantly different among material channels. Generally speaking, the maximum value with respect to materials is significantly different. To address the issue, a weighting vector $\mathbf{z}\in {\mathcal{R}}^N$ is introduced into Eq. (21) for normalizing material fraction across material channels:

$${\mathbf{z}}_n=\frac{1}{\max ({\mathbf{U}}_n)},$$ (22)

where max(U_n) represents the maximum positive value of U_n. The weighting vector z can be calculated from the material components during each iteration. Therefore, the normalized material component maps can be expressed as

$$\widehat{\mathcal{U}}=\mathcal{K}(\mathcal{U},\mathbf{z}),$$ (23)

where $\mathcal{K}$ represents the weight operation for $\mathcal{U}$, i.e., ${\widehat{\mathbf{U}}}_n={\mathbf{z}}_n\times {\mathbf{U}}_n$. Similarly, $\mathcal{U}$ can be recovered from Eq. (23). Again,

$$\mathcal{U}={\mathcal{K}}^{-1}(\widehat{\mathcal{U}},\mathbf{z}),$$ (24)

where ${\mathcal{K}}^{-1}$ represents the inverse weight operation. To avoid the aforementioned inconsistency of fraction with different materials, the normalized material maps $\widehat{\mathcal{U}}$ rather than the raw material tensor $\mathcal{U}$ is considered in Eq. (21), and it can be modified as Eq. (25).

$$\begin{gathered} \underset{\mathcal{U},\beta }{min}(\frac{\theta }{2}\sum _{i=1}^I\left(\Vert {\mathbf{E}}_i({\mathcal{U}}_{(1)})-\widehat{\mathbf{D}}{\beta }_i{\Vert }_F^2+v_i\Vert {\beta }_i{\Vert }_0\right)\phantom{)} \\ \phantom{(}+\frac{1}{2}\Vert {\mathit{x}}_3-\mathbf{w}{\mathcal{U}}_{(3)}{\Vert }_F^2)s.t.0\le \mathcal{U} \\ \le 1,\left(\sum _{n=1}^N{\mathcal{U}}_{i_w{i}_{h}n}\right)+{\mathit{A}}_{i_w{i}_h}=1. \end{gathered}$$ (25)

According to the APPENDIX, Eq. (25). can be updated by following three sub-problem

$$\underset{\widehat{\mathcal{U}}}{min}\left(\frac{1}{2}{\Vert ({\mathbf{w}}^{\mathbf{T}}\mathbf{w}+\gamma ){\mathcal{U}}_{i_w{i}_h\#}-\left({\mathbf{w}}^{\mathbf{T}}{\mathit{x}}_{\#i_w{i}_h}+\gamma {\mathit{d}}_{i_w{i}_h\#}^{(k)}\right)\Vert }_F^2\right)\forall i_w,i_h,s.t.(\sum \begin{array}{c}N\hfill \\ n=1\hfill \end{array}{\mathcal{U}}_{i_w{i}_{h}n})+{\mathit{AA}}_{i_w{i}_h}=1,0\le \mathcal{U}\le 1,$$ (26a)

$$\underset{\mathit{d},\beta }{min}\left(\begin{array}{c}\hfill \frac{\gamma }{2}{\Vert {\mathit{d}}_{(3)}-{\left(\mathcal{K}({\mathcal{U}}^{(k+1)},{\mathbf{z}}^{(k)})\right)}_{(3)}\Vert }_F^2\hfill \\ \hfill +\frac{\theta }{2}\sum _{i=1}^I\left(\begin{array}{c}\hfill {\Vert {\mathbf{E}}_i\left(\mathcal{K}(\mathit{d},{\mathbf{z}}^{(k)}{)}_{(1)}\right)-\widehat{\mathbf{D}}{\beta }_i\Vert }_F^2\hfill \\ \hfill +v_i\Vert {\beta }_i{\Vert }_0\hfill \end{array}\right)\hfill \end{array}\right),$$ (26b)

$${\mathbf{z}}_n^{(k+1)}=\frac{1}{\max ({\mathbf{U}}_n^{(k+1)})}.$$ (26c)

Eq. (26b) is a dictionary learning based image denoising model [59], and we can obtain d^(k+1) by normalizing the iteration results of Eq. (26a) and then denormalizing the iteration results of Eq. (26b). During the process of dictionary learning based image denoising, the parameters of sparsity level L and tolerance of representation error ε play important roles in controlling the dictionary quality and material decomposition accuracy. In this study, the proposed GDLIMD method mainly contains three parameters of ε, L and θ. The main steps of GDLIMD are summarized in Algorithm I.

Since there is no regularizer prior for the DI model (i.e., Eq. (16)), its ability is weak to suppress noise and reduce artifacts. Compared with the DI method, the previous DLIMD has a good capability to suppress noise and reduce artifacts. However, according to the DLIMD mathematical model (i.e., Eq. (20)), each material corresponds to a series of parameters. This means there are lots of parameters that should be chosen in practice for implementing material decomposition. In contrast, the GDLIMD model (i.e., Eq. (21)) can not only reduce the number of parameters but also fully explore the correlation among different materials by updating the z_n during each iteration.

Algorithm I: GDLIMD

$$\begin{array}{cc}\hfill & \mathrm{Input}:\eta ,\epsilon ,L,T,K\text{and}\text{other parameters};\text{Initialization of}{\mathcal{U}}^{(0)}=0,{\mathit{d}}^{(0)}=\hfill \\ \hfill & 0,{\mathbf{z}}^{(0)}=\mathit{I},k=0.\hfill \\ \hfill & \mathrm{Output}:\text{Material decomposition tensor}\mathcal{U}.\hfill \\ \hfill & \mathrm{Part}I:\mathrm{Dictionary}\mathrm{training}\hfill \\ \hfill & 1:\text{Recontructing channel-wise spectal CT images};\hfill \\ \hfill & 2:\text{Formulating the material attenuation matrix using reconstruction results};\hfill \\ \hfill & 3:\text{Decomposing the reconstructed images using DI method};\hfill \\ \hfill & 4:\text{Normalizing the DI results};\hfill \\ \hfill & 5:\text{Extracting image patches to form a dictionary trining dataset};\hfill \\ \hfill & 6:\text{Training a dictionary using K-SVD technique}.\hfill \\ \hfill & \mathrm{Part}\mathrm{II}:\mathrm{Material}\mathrm{decomposition}\hfill \\ \hfill & 7:\mathbf{While}\text{not convergence}\mathbf{do}\hfill \\ \hfill & 8:\text{Updating}{\mathcal{U}}^{(k+1)}\text{using Eq.(26a)};\hfill \\ \hfill & 9:\text{Finding and processing the air pixels in}{\mathcal{U}}^{(k+1)}\text{using DI technique};\hfill \\ \hfill & 10:\text{Normalizing}\mathcal{U}\text{using}\mathbf{z};\hfill \\ \hfill & 11:\text{Updating}\mathit{d}\text{and}\beta \text{using Eq.(26b)};\hfill \\ \hfill & 12:\text{Denormalizing}{\mathit{d}}^{(k+1)}\text{using}\mathbf{z};\hfill \\ \hfill & 13:\text{Updating}\mathbf{z}\text{using Eq.(26c)};\hfill \\ \hfill & 14:k=k+1;\hfill \\ \hfill & 15:\text{End}\mathbf{While}\hfill \end{array}$$

III. Experiments and Results

To evaluate the advantages of the developed GDLIMD method for decomposition of multiple materials, the physical phantom and tissue-synthetic phantom are employed in this study. Since the dictionary learning based material decomposition method outperforms the TV-based method, only DI and DLIMD are selected as comparisons. To quantitatively analyze the decomposition results with different methods, the root means square error (RMSE), peak-signal-to-noise ratio (PSNR) and structural similarity (SSIM) are employed as metrics. As the aforementioned, while the DLIMD has different parameters for different materials, the developed GDLIMD mainly contains three parameters, i.e., regularization parameter θ , atom number L and error parameter ε. As for the dictionary learning, the number of image patches is set as 10⁴ in both physical phantom and tissue-synthetic phantom experiments. The size of image patch is 9×9 and 8×8 for physical phantom and tissue-synthetic phantom cases. The optimized parameters used in material decomposition process are listed in Table I.

Table I.

The parameter setting for the developed GDLIMD technique.

Parameters	θ	L	ε
Physical Phantom	0.00168	14	0.080
Tissue-synthetic phantom (FBP case)	0.0030	12	0.010
Tissue-synthetic phantom (NLCTF case)	0.0030	16	0.00015

A. Physical Phantom

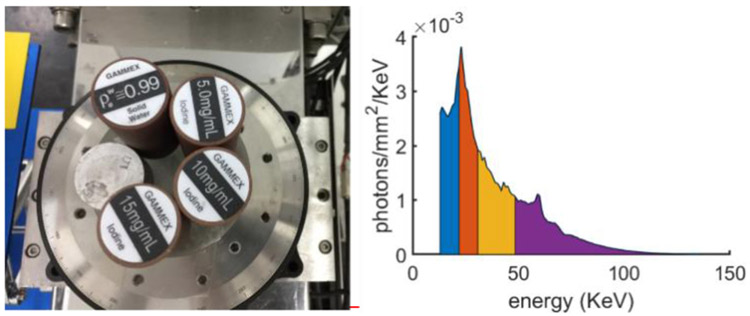
Fig. 1 demonstrates the physical phantom which consists of three different basic materials (aluminum, water and iodine). The phantom contains five cylinders and their details can also refer to Fig. 1 (a). The spectral CT system has a 225Kv micro-focus x-ray source from YXLON and PCD (XC-Hydra FX20) from Xcounter with 2 energy bins. Here, the PCD contains 2048 detector units with 0.1 mm length, and every 4 cells are combined to improve SNR. The projection size is 512×1080×4, where 1080 is the number of projection views. The process of scanning consumes 36 minutes. The x-ray spectrum is divided into 4 energy bins (i.e., [13.0, 22.0], (22.0, 30.8], (30.8, 48.5] and (48.5, 137], unit: KeV) by scanning 2 times (see Fig. 1 (b)). The distances starting from x-ray source to rotation axis and PCD are 182.68 mm and 440.50 mm, respectively, resulting in an FOV with radius of 41.3 mm. The reconstructed material image includes 256×256 pixels each of which covers an area of 0.324×0.324 mm².

Fig. 1.

Physical phantom and the used x-ray spectrum in experiments. Left is physical phantom and right represents the x-ray emitted spectrum.

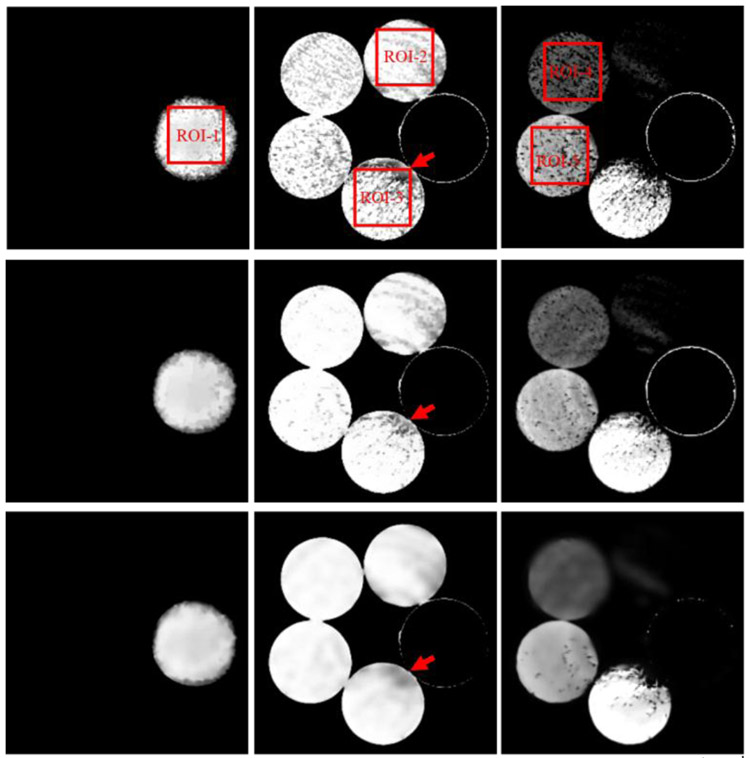
The reconstructed images of physical phantom by FBP are in Fig. 2. To evaluate the performance of GDLIMD for material decomposition, the FBP results are decomposed into three basic materials (i.e., aluminum, water and iodine) using the DI method for comparison as shown in Fig. 3. From Fig. 3, one can see the decomposed images for the iodine material appear some non-uniform pattern. In fact, from Fig. 2, we can observe that the reconstructed channel-wise images contain beam hardening artifacts, and this can affect the material decomposition accuracy. Besides, the material decomposition is performed on the reconstructed image pixel-by-pixel, and each pixel is considered independently. This is another source of the non-uniform pattern. To further improve the material accuracy, we assume the iodine component and aluminum cannot exist in the same pixel. From Fig. 3, it can be seen that both DLIMD and GDLIMD can obtain higher accuracy than the DI method in all material images. Compared with the previous DLIMD method, the GDLIMD method can obtain higher material image quality than the DLIMD method. To fully understand this point, it is necessary to clarify the generation of dictionary. First, the normalization is performed on the DI material decomposition results. It can help to minimize the bias of different material decomposition. Then, all stacked material decomposition results are unfold along mode-1 to enhance the level of sparse representation. Finally, the SVD is employed to train the unified dictionary. In this study, because the accuracy of low concentration iodine is normalized to the same range of water and aluminum, the ability of dictionary representation is enhanced and the accuracy of iodine contrast is improved. Once the accuracy of iodine contrast is improved, the accuracy of water and aluminum will be increased simultaneously with the constraint of volume conservation. Particularly, in terms of water component, the GDLIMD results contain less artifacts, which is confirmed by the region indicated by the red arrow. As for the iodine contrast component, the GDLIMD can obtain remarkably accuracy than the DLIMD, i.e., the GDLIMD can remove the outlier artifacts in the DLIMD and DI methods.

Fig. 2.

Image reconstruction results of the physical phantom from FBP. The 1^st- 4^th columns represent 1^st -4^th energy bins and their display window is [0 1.3]cm⁻¹.

Fig. 3.

Three basis material decomposition results of FBP images. The 1^st- 3^rd columns represent aluminum, water and iodine, and their display windows are [0.5 1], [0.8 1] and [0 0.003]. The 1^st- 3^rd rows represent DI, DLIMD and GDLIMD methods, respectively.

It is important to perform quantitative analysis for the decomposed materials in practical applications. Five regions of interest (ROIs) are extracted from Fig. 3 and then they are evaluated in this study. Besides, three referred indexes including RMSE, SSIM and FSIM are employed and the quantitative results are summarized in Table II. Here, the ground truth of five extracted ROIs can be obtained from Fig. 1. Particularly, the ground truth of ROIs 1–3 are three uniform rectangles with values of 1.0, 1.0, 0.997. The iodine contrast agent concentration of ROIs 4–5 are 5mg/mL and 10mg/mL, respectively. Table II demonstrates the DI always obtains the highest RMSE with smallest PSNR and SSIM values. Again, the difference between material decomposed images using DI and ground truth is the biggest than those obtained by the DLIMD and GDLIMD methods. Compared with the previous DLIMD method, the proposed GDLIMD can obtain smaller RMSEs and higher SSIM and FSIM values of all decomposed materials.

Table II.

Quantitative evaluation results of ROIs 1-5.

		DI	DLIMD	GDLIMD
ROI-1	RMSE(10−4)	889.0	828.4	808.1
	PSNR	21.026	21.635	21.851
	SSIM	0.9560	0.9925	0.9930
ROI-2	RMSE(10−4)	324.0	271.4	267.1
	PSNR	29.793	31.329	31.467
	SSIM	0.9732	0.9977	0.9979
ROI-3	RMSE(10−4)	594.16	269.82	255.58
	PSNR	24.522	31.379	31.850
	SSIM	0.6689	0.9515	0.9577
ROI-4	RMSE(10−4)	5.2525	1.8115	1.7582
	PSNR	65.593	74.839	75.100
	SSIM	0.4118	0.8483	0.9333
ROI-5	RMSE(10−4)	6.8538	2.3989	2.3163
	PSNR	63.281	72.400	72.704
	SSIM	0.6200	0.9165	0.9474

As for the computational cost, similar to our previous DLIMD method, the proposed GDLIMD algorithm can also be divided into two parts: dictionary training and material decomposition. All material decomposition techniques are implemented on a PC (i7–6700, 8.0 GB memory) with Matlab (version 2014b). Since the DI contains no regularization constraint, it has the smallest computational costs than DLIMD and GDLIMD methods. Compared with the DLIMD method performing dictionary representation on material images one by one, the GDLIMD perform the dictionary representation on the mode-1 unfolding of material tensor at one time. In fact, the DI, DLIMD and GDLIMD consume 22.79, 44.17 and 44.30 seconds, respectively. Obviously, compared with the DI method, the DLIMD and GDLIMD algorithms can consume comparable computational costs.

B. Tissue-synthetic phantom experiment

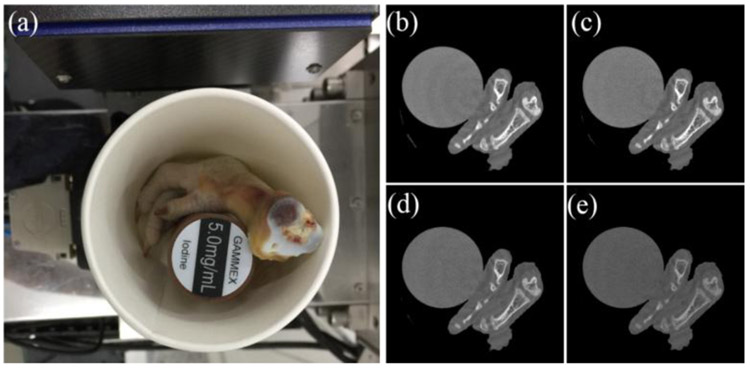
The specimen consists of chicken feet and 5 mg/mL iodine solution cylinder to imitate the clinical application, as shown in Fig. 4(a). In this study, the PILATUS3 PCD from DECTRIS has 4 energy-channels (i.e., [13.0, 22.0], (22.0, 30.8], (30.8, 48.5] and (48.5, 137], unit:KeV) to obtain multi-energy projections. The PCD has 515 cells and each of which covers a length of 0.15 mm. The projections are acquired from 720 views within one full scan. As for fan-beam scanning geometry, the distances between X-ray source and rotational center is 35.27 cm, and the distance between X-ray source and detector is 43.58 cm. The reconstructed spectral CT image by FBP contains 512 × 512 × 4 pixels and each of them is 0.122 × 0.122mm² as shown in Fig. 4(b)-(e).

Fig. 4.

Tissue-synthetic specimen and the corresponding reconstructed images by FBP. (a) is the specimen photo and (b)-(e) are FBP results from 1^st-4^th energy channels with a display window [0 0.5] cm⁻¹.

To evaluate the performance of the proposed GDLIMD method, three basis material decomposition (i.e., bone, soft tissue and 5mg/mL iodine contrast agent) results by the DI, DLIMD and GDLIMD methods are given in Fig. 5. From Fig. 5, one can see the iodine images from all methods contain some non-uniform regions. This is because the reconstructed channel-wise images contain ring artifacts because the detector responses of this new PCD are not consistent, which can be observed in Fig. 4. In fact, the ring artifacts in the reconstructed images already have been significantly suppressed.

Fig. 5.

Material decomposition results of the FBP images with preclinical datasets. 1^st-3^rd columns represent the DI, DLIMD and GDLIMD methods, and 1^st-3^rd rows represent the bone, soft tissue and iodine with the display windows [0.25 0.5], [0.85 0.95] and [0.0004 0.001], respectively.

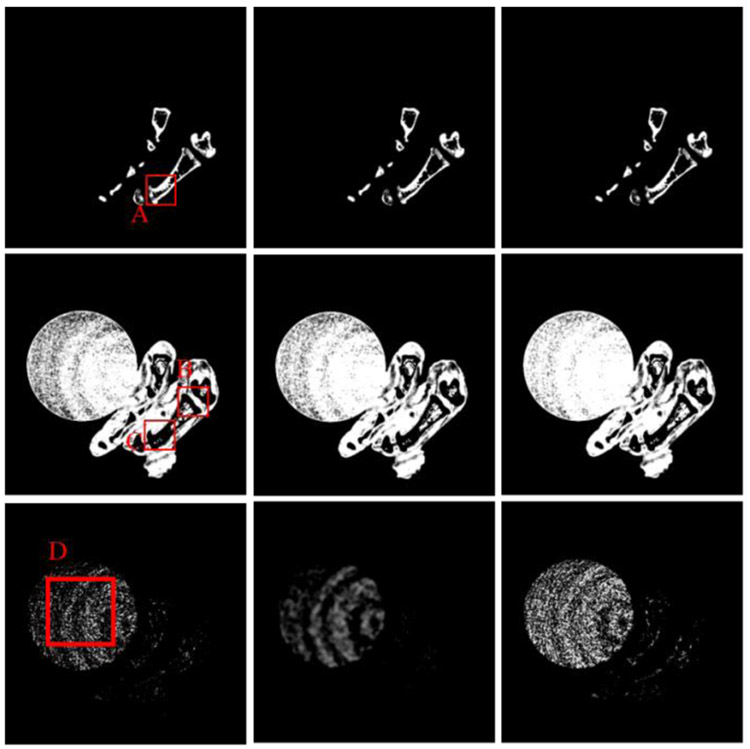
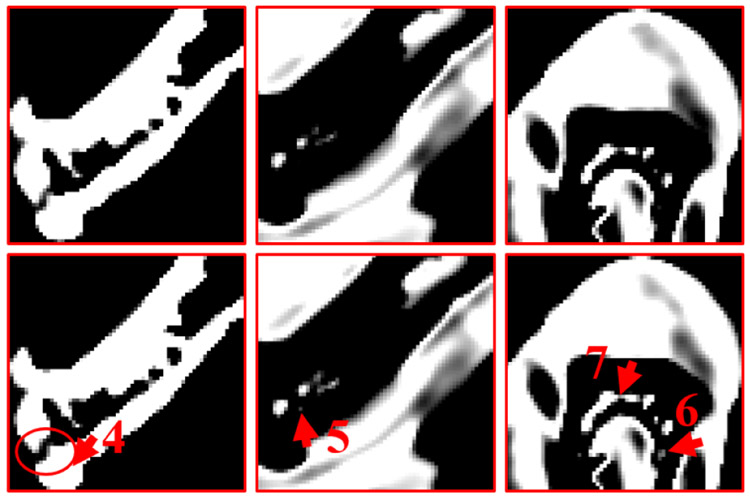
Regarding the bone, the image edge of bony structure is obviously blurred in the DI results. Compared with the DI method, the DLIMD and GDLIMD methods can provide clear image edges. Furthermore, to make a comparison between the DLIMD and GDLIMD, the ROI “A” is extracted and magnified in Fig. 6. From the structure marked with arrow “1”, it can be seen that the gap of two small bones can be clearly observed in the GDLIMD. However, it is difficult to discriminate the gap in the DLIMD and DI results. For decomposition results of soft tissue, compared with the DLIMD method, the developed GDLIMD can provide more image features and complete image structures. Two soft tissue ROIs “B” and “C” are extracted and magnified in Fig. 6. It can be observed that the accuracy of soft tissue by DLIMD and GDLIMD is much better than that obtained by the DI method. Besides, the image features indicated by arrows “2” and “3” recovered by GDLIMD method are more clear than those by the DLIMD method. In terms of the iodine contrast agent, compared with the DLIMD results, many pixels are wrongly classified as iodine contrast agent. This issue can be avoided in the following NLCTF case, which will be discussed in next section. The iodine concentration is 5.0mg/mL, which can be treated as the ground truth. Here, the RMSEs and mean value of extracted ROI “D” are calculated in Table III. Table III demonstrates the GDLIMD can obtain the largest mean value of iodine and the smallest RMSE in FBP reconstruction case.

Fig. 6.

The magnified ROIs of “A”, “B” and “C”. The 1^st-3^rd columns are the DI, TVMD and DLIMD methods. The 1^st-3rd rows represent the ROIs “A”, “B” and “C”, where the display windows are [0.29 0.33], [0.70 0.72] and [0.68 0.72], respectively.

Table III.

Quantitative evaluation of ROI “D” (unit: mg/mL).

		DI	DLIMD	GDLIMD
FBP	Mean	1.908	2.3551	2.8938
	RMSE	3.372	2.6889	2.4217

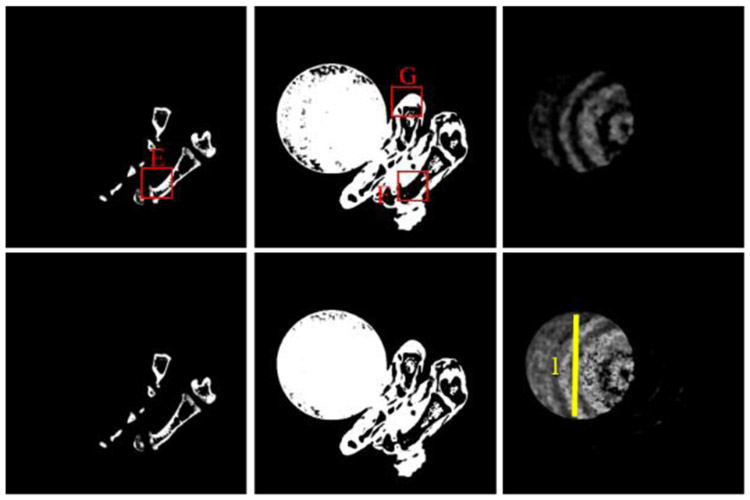
To validate the outperformance of GDLIMD method using advanced reconstruction results, the NLCTF [31] results are also decomposed into three basis materials and their decomposition results are further shown in Fig. 7. Four ROIs marked with “E” ,“F” and “G” are extracted and also magnified in 2^nd-3^rd rows of Fig. 8. It can be seen from Figs. 7-8 that the GDLIMD results have much more image features, especially for image features marked with arrows “4”, “5”, “6” and “7”.

Fig. 7.

Material decomposition of the NLCTF reconstruction results. 1^st -3^rd columns represent the bone, soft tissue and iodine contrast, where the display windows [0.25 0.5], [0.90 0.92] and [0.0004 0.001], respectively. The 1^st-2^nd rows represent DLIMD and GDLIMD methods.

Fig. 8.

The magnified ROIs marked with “E”, “F” and “G” and the corresponding display windows are [0.29 0.33], [0.85 0.95] and [0.89 0.94], respectively.

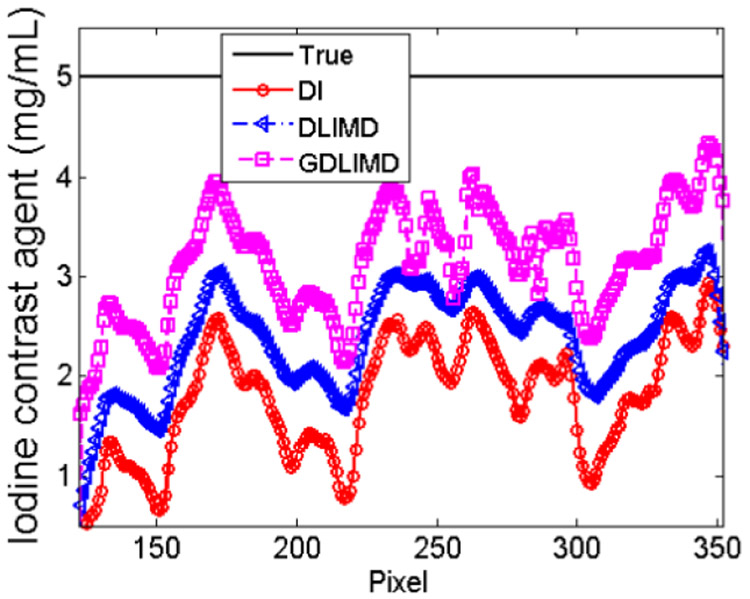
To further evaluate the accuracy of iodine contrast agent, the representative profile of the yellow line indicated by “1” in Fig. 7 from NLCTF cases are shown in Fig. 9. It can be seen that the profile from GDLIMD is approach to the theoretical truth of iodine contrast concentration by comparing with the DI and DLIMD methods. It can further be confirmed the outperformance of GDLIMD method.

Fig. 9.

The representative profile of yellow line 1 in Fig.7.

IV. Discussions and Conclusions

To further optimize material decomposition results and avoid the parameters selection dilemma of the DLIMD method, the generalized version of DLIMD, i.e., GDLIMD, is developed in this study. Compared with the DLIMD method [51], the contribution of GDLIMD are threefold. First, to overcome the data inconsistency from contrast component, the range of all material components are normalized to [0, 1], which is beneficial to parameters selection. Second, in the GDLIMD model, the decomposed materials are unfolded as mode-1 format to enhance the capability of dictionary representation by exploring the correlation of materials. Because the unified dictionary is trained from the normalized material maps rather than single material by unfolding the decomposed materials, one material can borrow the dictionary atoms from other materials to enhance the sparse representation in some cases. Third, except that the constraints of volume conservation [58] and the bound of each material pixel value are introduced into GDLIMD, the constraint on the basis of preclinical applications (i.e., the concentration of contrast is no more than 5%) is also considered in the model to further improve the decomposition accuracy. Two real datasets, including the physical phantom and tissue-synthetic datasets, are utilized to assess and evaluate the proposed GDLIMD method, and the results demonstrate the advantages of GDLIMD.

Although the GDLIMD method can obtain higher accuracy of material decomposition in image-domain than the DLIMD method, there are still some rooms for improvement. First, different from many parameters in previous DLIMD method, the GDLIMD mainly contains three parameters to be selected. Here, these parameters are only empirically optimized by comparing three indexes in physical phantom and visual evaluation in tissue-synthetic phantom experiments. However, how to select a series of parameters in practical application is still open. Fortunately, the channel-wise spectral CT images can be reconstructed in advance. From these reconstructed channel-wise images, we can observe some details of the imaging object, which could be good for parameters estimation and selection for the followup material decomposition. Of course, if there exists strong noise, it would be a good strategy to perform denoising operation material decomposition. Second, both physical phantom and tissue-synthetic phantom datasets consist of three different basis materials, which reduce the complexity of normalization strategy. Again, a simple normalization method is employed in this study. To further improve the performance of GDLIMD method in multiple material decomposition (greater than 3), we will optimize the design of normalization method in our further plan.

In conclusion, based on the idea of previous DLIMD model, we develop a generalized DLIMD (GDLIMD) method for image-domain material decomposition with spectral CT. Both physical phantom and tissue-synthetic phantom experiments highlight the advantages of GDLIMD technique. This will be of significance to improve accuracy of material decomposition for spectral CT.

APPENDIX

Substituting the Eq. (23) into Eq. (25), we can obtain Eq. (A.1).

$$\begin{gathered} \underset{\mathcal{U},\beta ,\mathbf{z}}{min}(\frac{\theta }{2}\sum _{i=1}^I\left(\Vert {\mathbf{E}}_i(\mathcal{K}(\mathcal{U},\mathbf{z}{)}_{(1)})-\widehat{\mathbf{D}}{\beta }_i{\Vert }_F^2+v_i\Vert {\beta }_i{\Vert }_0\right)\phantom{)} \\ \phantom{(}+\frac{1}{2}\Vert {\mathcal{X}}_{(3)}-\mathbf{w}{\mathcal{U}}_{(3)}{\Vert }_F^2),st0\le \mathcal{U} \\ \le 1,\left(\sum _{n=1}^N{\mathcal{U}}_{i_w{i}_{h}n}\right)+{\mathit{A}}_{i_w{i}_h}=1, \end{gathered}$$ (A.1)

Similar to the DLIMD model, Eq. (A.1) equals to the following constrained problem of Eq. (A.2) by introducing d

$$\begin{gathered} \underset{\mathcal{U},\beta ,\mathbf{z},\mathbf{d}}{min}\left(\begin{array}{c}\hfill \frac{\theta }{2}\sum _{i=1}^I\left(\Vert {\mathbf{E}}_i(\mathcal{K}(\mathit{d},\mathbf{z}{)}_{(1)})-\widehat{\mathbf{D}}{\beta }_i{\Vert }_F^2+v_i\Vert {\beta }_i{\Vert }_0\right)\hfill \\ \hfill +\frac{1}{2}\Vert {\mathcal{X}}_{(3)}-\mathbf{w}{\mathcal{U}}_{(3)}{\Vert }_F^2\hfill \end{array}\right) \\ s.t.\left(\sum _{n=1}^N{\mathcal{U}}_{i_w{i}_{h}n}\right)+{\mathit{A}}_{i_w{i}_h}=1,\mathit{d}=\mathcal{U}, \end{gathered}$$ (A.2)

Eq. (A.2) can be further divided into three sub-problems Eqs. (A.3)-(A.5).

$$\begin{gathered} \underset{\mathcal{U}}{min}\left(\frac{1}{2}\Vert {\mathcal{X}}_{(3)}-\mathbf{w}{\mathcal{U}}_{(3)}{\Vert }_F^2+\frac{\gamma }{2}\Vert \mathcal{U}-{\mathit{d}}^{(k)}{\Vert }_F^2\right), \\ s.t.\left(\sum _{n=1}^N{\mathcal{U}}_{i_w{i}_{h}n}\right)+{\mathit{A}}_{i_w{i}_h}=1,0\le \mathcal{U}\le 1, \end{gathered}$$ (A.3)

$$\underset{\mathit{d},\beta }{min}\left(\begin{array}{c}\hfill \frac{\gamma }{2}{\Vert {\mathit{d}}_{(3)}-{\left(\mathcal{K}({\mathcal{U}}^{(k+1)},{\mathbf{z}}^{(k)})\right)}_{(3)}\Vert }_F^2\hfill \\ \hfill +\frac{\theta }{2}\sum _{i=1}^I\left(\begin{array}{c}\hfill {\Vert {\mathbf{E}}_i\left(\mathcal{K}(\mathit{d},{\mathbf{z}}^{(k)}{)}_{(1)}\right)-\widehat{\mathbf{D}}{\beta }_i\Vert }_F^2\hfill \\ \hfill +v_i\Vert {\beta }_i{\Vert }_0\hfill \end{array}\right)\hfill \end{array}\right),$$ (A.4)

$$\underset{\mathbf{z}}{min}\left(\begin{array}{c}\hfill \frac{\gamma }{2}{\Vert {\mathit{d}}_{(3)}^{(k+1)}-{\left(\mathcal{K}({\mathcal{U}}^{(k+1)},{\mathbf{z}}^{(k)})\right)}_{(3)}\Vert }_F^2\hfill \\ \hfill +\frac{\theta }{2}\sum _{i=1}^I\left({\Vert {\mathbf{E}}_i\left(\mathcal{K}(\mathit{d},{\mathbf{z}}^{(k)}{)}_{(1)}\right)-\widehat{\mathbf{D}}{\beta }_i\Vert }_F^2\right)\hfill \end{array}\right).$$ (A.5)

Eq. (A.3) is a constrained convex programmable optimization problem. Following the same procedures of DLIMD method, it can be simplified as the following expression

$$\begin{gathered} \underset{{\mathcal{U}}_{i_w{i}_h\#}}{min}\left(\frac{1}{2}{\Vert {\mathcal{X}}_{\#i_w{i}_h}-\mathbf{w}{\mathcal{U}}_{i_w{i}_h\#}\Vert }_F^2+\frac{\gamma }{2}{\Vert {\mathit{d}}_{i_w{i}_h\#}^{(k)}-{\mathcal{U}}_{i_w{i}_h\#}\Vert }_F^2\right), \\ \forall i_w,i_h,s.t.\left(\sum _{n=1}^N{\mathcal{U}}_{i_w{i}_{h}n}\right)+{\mathit{A}}_{i_w{i}_h}=1,0\le \mathcal{U}\le 1. \end{gathered}$$ (A.6)

Eq. (A.6) can be furtherly rewritten as

$$\begin{gathered} \underset{{\mathcal{U}}_{i_w{i}_h\#}}{min}\left(\frac{1}{2}{\Vert {\mathcal{X}}_{\#i_w{i}_h}-\mathbf{w}{\mathcal{U}}_{i_w{i}_h\#}\Vert }_F^2+\frac{\gamma }{2}{\Vert {\mathit{d}}_{i_w{i}_h\#}^{(k)}-{\mathcal{U}}_{i_w{i}_h\#}\Vert }_F^2\right), \\ \forall i_w,i_h,s.t.\left(\sum _{n=1}^N{\mathcal{U}}_{i_w{i}_{h}n}\right)+{\mathit{A}}_{i_w{i}_h}=1,0\le \mathcal{U}\le 1. \end{gathered}$$ (A.7)

Furtherly, Eq. (A.7) equals to

$$\begin{gathered} \underset{\widehat{\mathcal{U}}}{min}\left(\frac{1}{2}{\Vert ({\mathbf{w}}^{\mathbf{T}}\mathbf{w}+\gamma ){\mathcal{U}}_{i_w{i}_h\#}-\left({\mathbf{w}}^{\mathbf{T}}{\mathit{x}}_{\#i_w{i}_h}+\gamma {\mathit{d}}_{i_w{i}_h\#}^{(k)}\right)\Vert }_F^2\right), \\ \forall i_w,i_h,s.t.\left(\sum _{n=1}^N{\mathcal{U}}_{i_w{i}_{h}n}\right)+{\mathit{A}}_{i_w{i}_h}=1,0\le \mathcal{U}\le 1, \end{gathered}$$ (A.8)

where ${\mathcal{X}}_{\#i_w{i}_h}={\left[{\mathit{x}}_{1i_w{i}_h},\dots ,{\mathit{x}}_{C{i}_w{i}_h}\right]}^T$, ${\mathcal{U}}_{i_w{i}_h\#}={\left[{\mathcal{U}}_{i_w{i}_{h}1},\dots ,{\mathcal{U}}_{i_w{i}_{h}N}\right]}^T$ and ${\mathit{d}}_{i_w{i}_h\#}^{(k)}={\left[{\mathit{d}}_{i_w{i}_{h}1}^{(k)},\dots ,{\mathit{d}}_{i_w{i}_{h}N}^{(k)}\right]}^T$. diag(z) is the diagonalization of weight vector z. Considering Eq. (22), the problem of Eq. (A.5) can be updated as

$${\mathbf{z}}_n^{(k+1)}=\frac{1}{\max ({\mathbf{U}}_n^{(k+1)})}.$$ (A.9)