Abstract
The P2 purinergic receptor family implicated in many physiological processes, including neurotransmission, mechanical adaptation and inflammation, consists of ATP-gated non-specific cation channels P2XRs and G-protein coupled receptors P2YRs. Different cells, including bone forming osteoblasts, express multiple P2 receptors; however, how P2X and P2Y receptors interact in generating cellular responses to various doses of [ATP] remains poorly understood. Using primary bone marrow and compact bone derived osteoblasts and BMP2-expressing C2C12 osteoblastic cells, we demonstrated conserved features in the P2-mediated Ca2+ responses to ATP, including a transition of Ca2+ response signatures from transient at low [ATP] to oscillatory at moderate [ATP], and back to transient at high [ATP], and a non-monotonic changes in the response magnitudes which exhibited two troughs at 10−4 and 10−2 M [ATP]. We identified P2Y2 and P2X7 receptors as predominantly contributing to these responses and constructed a mathematical model of P2Y2R-induced inositol trisphosphate (IP3) mediated Ca2+ release coupled to a Markov model of P2X7R dynamics to study this system. Model predictions were validated using parental and CRISPR/Cas9-generated P2Y2 and P2Y7 knockouts in osteoblastic C2C12-BMP cells. Activation of P2Y2 by progressively increasing [ATP] induced a transition from transient to oscillatory to transient Ca2+ responses due to the biphasic nature of IP3Rs and the interaction of SERCA pumps with IP3Rs. At high [ATP], activation of P2X7R modulated the response magnitudes through an interplay between the biphasic nature of IP3Rs and the desensitization kinetics of P2X7Rs. Moreover, we found that P2Y2 activity may alter the kinetics of P2X7 towards favouring naïve state activation. Finally, we demonstrated the functional consequences of lacking P2Y2 or P2X7 in osteoblast mechanotransduction. This study thus provides important insights into the biophysical mechanisms underlying ATP-dependent Ca2+ response signatures, which are important in mediating bone mechanoadaptation.
Author summary
ATP-sensitive purinergic receptors comprise a network of cell-surface receptors that activate upon ATP binding, allowing them to transmit information in a tissue- and context-dependent manner. In bone, mechanically stimulated osteoblasts release ATP that stimulates low- and high-affinity P2 receptors in neighboring cellular populations, inducing appropriate physiological responses. P2 receptor signaling is characterized by elevations in intracellular calcium levels. When simultaneously stimulated by their common ligand, ATP, the contribution of each P2 receptor subtype gives rise to a complex calcium response, exhibiting oscillatory characteristics and biphasic dose-dependent behaviours. Here we used experimental and computational modeling approaches to determine the underlying dynamics of ATP-mediated calcium signaling in osteoblasts. The latter was done by developing a mathematical model that was comprised of a subset of low- (P2X7) and high- (P2Y2) affinity P2 receptors, reflecting the conserved P2 expression observed across different osteoblast models. We demonstrated that this model recapitulates experimental recordings of ATP-induced calcium signaling in osteoblasts and describes the dynamic interplay between P2Y2 and P2X7 receptors in the P2 receptor network.
Introduction
Extracellular ATP has long been implicated in diverse physiological functions [1], including neurotransmission [2], mechanical adaptation [3] and the regulation of inflammation [4]. Extracellular purines signal through 7 ionotropic receptors, i.e., the P2X ligand-gated nonspecific cation channels, and 8 metabotropic receptors, i.e., the P2Y G-protein coupled receptors [5].
ATP is the physiological agonist for all P2X receptors (P2XRs) as well as the P2Y2 and P2Y11 receptors (P2Y2R and P2Y11R, respectively) [6]. Together they cover a range of extracellular ATP concentrations ([ATP]) spanning six orders of magnitude (10−8 M to 10−2 M) [7]. P2XRs are fast acting (~10 ms activation), allowing the permeation of Na+, K+ and Ca2+ through the channel [8] whereas P2YRs activate various types of secondary messengers, and thus act on a slower timescale than P2XRs [9]. Elevations in cytosolic free Ca2+ concentration ([Ca2+]i) is one of the hallmarks of ATP-induced signaling in many cell types, including bone-forming osteoblasts [7,10–13]. The mechanism by which P2XRs and P2YRs alter [Ca2+]i differs: P2XR activation increases Ca2+ influx across the plasma membrane [14] while P2YR activation enhances Ca2+ release from the endoplasmic reticulum (ER) by stimulating the Gq protein signaling pathway, ultimately leading to the production of inositol triphosphate (IP3) and the activation of IP3 receptors (IP3Rs) [15]. The ATP dose dependence of osteoblast responses to [ATP] was shown to be complex and does not have a clear plateau component, an outcome not explainable by the addition of individual receptor responses [7]. While it was proposed that specific interactions between the high-affinity, mid-range and low-affinity P2Rs may explain the [ATP]-dependence, no mechanistic studies at the level of cellular signaling has yet been performed.
Markov models of P2X2/4/7R were previously developed to decipher the kinetics of ATP binding to these receptors and illustrate the interplay between receptor activation, priming, desensitization, internalization and deactivation [16–21]. Mathematical modeling has similarly been used to provide insights into the P2Y receptor signaling, particularly in the regulation of IP3R-mediated Ca2+ release [22,23]. However, how P2X and P2Y receptors interact and what are their respective roles in generating cellular responses to various doses of [ATP] remains poorly understood.
In this study, we combined detailed experimental and computational studies of ATP-induced Ca2+ signals in primary mouse osteoblasts and BMP2-transfected C2C12 osteoblastic cells. We demonstrated the specific contributions of P2Y2 and P2X7 receptors to global Ca2+ responses using CRISPR/Cas9 -generated P2Y2 and P2Y7 knockouts in osteoblastic C2C12-BMP cell lines, and dissected the mechanisms of P2Y2 and P2X7 contributions to generating different patterns of oscillatory and sustained Ca2+ signals using mathematical modeling.
Results
ATP-mediated P2R Ca2+ responses in murine osteoblasts
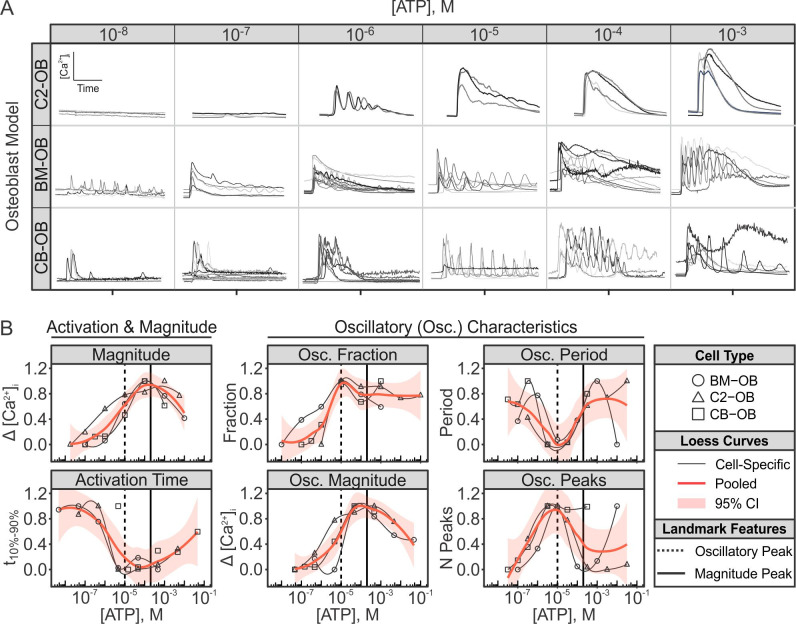
ATP-stimulated P2R Ca2+ responses were assessed in three independent murine osteoblasts models: BMP2-transfected C2C12 osteoblastic cells (C2-OB), bone-marrow-derived osteoblasts (BM-OB), and compact-bone-derived osteoblasts (CB-OB). Osteoblasts were loaded with Ca2+-indicator dye Fura2, stimulated with varying doses of ATP, and changes in [Ca2+]i were recorded using live cell fluorescent microscopy (Fig 1). Qualitatively, the recorded Ca2+ response time-series signatures demonstrated a general trend of exhibiting transient single-peaked responses at low [ATP], multi-peaked oscillatory responses at mid-range [ATP], and relatively sustained single/multi-peaked response at high [ATP] (Fig 1A). The Ca2+ responses at each [ATP] were analysed by quantifying several parameters, including overall response magnitudes and activation times, as well as oscillatory fractions, magnitudes, periods and peaks (see S1 Table for definitions) [13]. Similar to previous study [7], we harmonized dose-response profiles across osteoblast models by first aligning the responses along the dose-axis to match troughs/peaks, followed by rescaling the responses to a [0,1] interval (S1 Fig). Such alignment allowed us to account for (i) inconsistencies in ATP solution preparations between experiments and (ii) varied dose-sensitivities across cell lines. Calcium responses induced by low [ATP] (<10−7 M) were consistently associated with low response magnitudes and slow activation kinetics (Fig 1A, left two columns), with little to no oscillatory component (Fig 1B). Increasing [ATP] further induced responses with faster activation kinetics and higher magnitudes (Fig 1A, middle two columns). This also coincided with the emergence of high frequency oscillations (~10–20 s periods; Figs 1B and S1B and S1C) which peaked at ~10−5 M ATP stimulation. Notably, the oscillatory peak did not coincide with the peak magnitude. Instead, as cells were stimulated with higher [ATP], the oscillatory component began to diminish, exhibiting lower frequency oscillations and fewer oscillatory peaks, while response magnitude continued to increase, peaking at ~2×10−4 M [ATP] (Fig 1A, right two columns, and 1B). For [ATP] >2×10−4 M, the response magnitude decreased with increasing [ATP] in all osteoblast lines. Thus, in all osteoblast models, the intracellular Ca2+ response to ATP shifts with increase in [ATP] from a transient with a single narrow peak, to oscillatory and back to transient with a pronounced wide peak.
Fig 1. ATP-induced Ca2+ response characteristics are conserved across murine osteoblast lines.
Fura2-loaded BMP2-transfected C2C12 osteoblastic cells (C2-OB), bone-marrow-derived osteoblasts (BM-OB), or compact-bone-derived osteoblasts (CB-OB) were stimulated with ATP (10−8 to 10−3 M), changes in [Ca2+]i were recorded, and characteristic parameters of individual cell-level Ca2+ responses were quantified. (A) Representative ATP-induced Ca2+ signature responses for different osteoblastic lines. Recording duration: 120 s. (B) Activation time, magnitude and oscillatory characteristics of Ca2+ responses in different osteoblastic cells were aligned to obtain consensus on dose-dependency behaviours (see S1 Fig for intermediary alignment steps). Data are response means, normalized to peak dose-response. Solid curves: Loess curves fit to normalized response means. Vertical solid lines: peak magnitude; Vertical dashed lines: peak oscillatory activity; CI: confidence interval, M: molar concentration.
P2Y2 and P2X7 receptors orchestrate the ATP-mediated Ca2+ responses
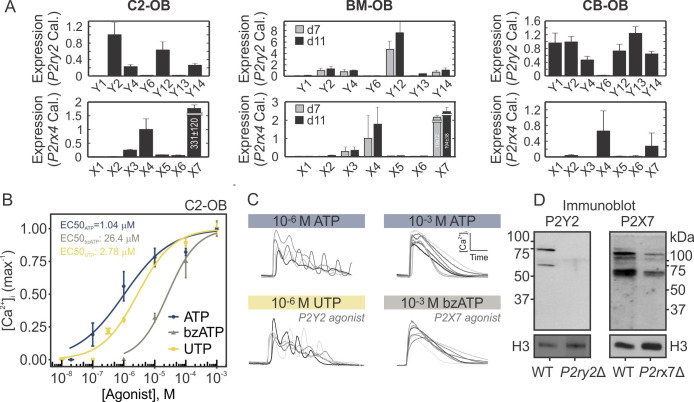
To examine which P2 receptors contribute to the ATP-induced Ca2+ responses, we first examined their expression in osteoblastic cells of different origin. Among the P2Y family, P2ry2, P2ry4, P2ry12, and P2ry14 transcripts were detected in all osteoblastic cells by RT-qPCR (Fig 2A top). Among the P2X family, P2rx4 and P2rx7 transcripts were the most abundantly expressed in all osteoblastic cells (Fig 2A bottom). These expression profiles suggest that P2Y2, 4, 12, 14 and P2X4, 7 are the predominant P2 receptor subtypes expressed in osteoblastic cells, among which P2Y2 and P2X7 were the most abundant transcripts. To confirm that P2Y2 and P2X7 receptors are functional, we stimulated Fura2-loaded C2-OB cells with ATP and receptor-specific agonists: the P2Y2-agonist UTP and P2X7-agonist bzATP (Fig 2B). Consistent with previously characterized P2 receptor sensitivities [7], we found that the estimated EC50s were 1.0 μM for ATP, 2.8 μM for UTP and 26.4 μM for bzATP in C2-OB cells. Importantly, the oscillatory Ca2+ responses evoked by 10−6 M ATP were recapitulated following stimulation with 10−6 M UTP, and similarly, the sustained responses evoked by 1 mM ATP were observed following 1 mM bzATP stimulation, suggesting that P2Y2 and P2X7 receptors dominate the responses to lower and higher [ATP], respectively (Fig 2C). Using CRISPR-Cas9 double-nickase constructs, we generated clonal C2-OB cells harboring mutations in P2ry2 (P2ry2Δ) or P2rx7 (P2rx7Δ) (Fig 2D) to further investigate the independent contribution of P2Y2 and P2X7 to the P2-mediated Ca2+ responses (presented in subsequent sections).
Fig 2. Functional P2Y2 and P2X7 are expressed in osteoblastic cells.
(A) P2 expression determined by RT-qPCR in C2-OB, BM-OB, and CB-OB. Relative transcript expression was calculated by ΔΔCT method, and P2ry2 and P2rx4 were used as calibrators for P2Y and P2X receptors, respectively. Data are means ± SEM, n = 3 independent cultures per cell line. (B) Fura2-loaded C2-OB cells were stimulated by ATP, UTP, or BzATP and [Ca2+]i response magnitudes were measured. Data are normalized means ± SEM (markers) fitted with hill functions (curves) for their dose-response curves. (C) Representative Ca2+ responses observed in C2-OB stimulated by 10−6 M ATP or UTP, and 10−3 M ATP or BzATP. (D) P2Y2 and P2X7 protein expression assessed by immunoblot in WT, P2ry2Δ and P2rx7Δ C2-OB whole cell lysates. Histone H3 was used as a loading control.
A flux-balance-based model of P2Y2R and P2X7R driven Ca2+ responses
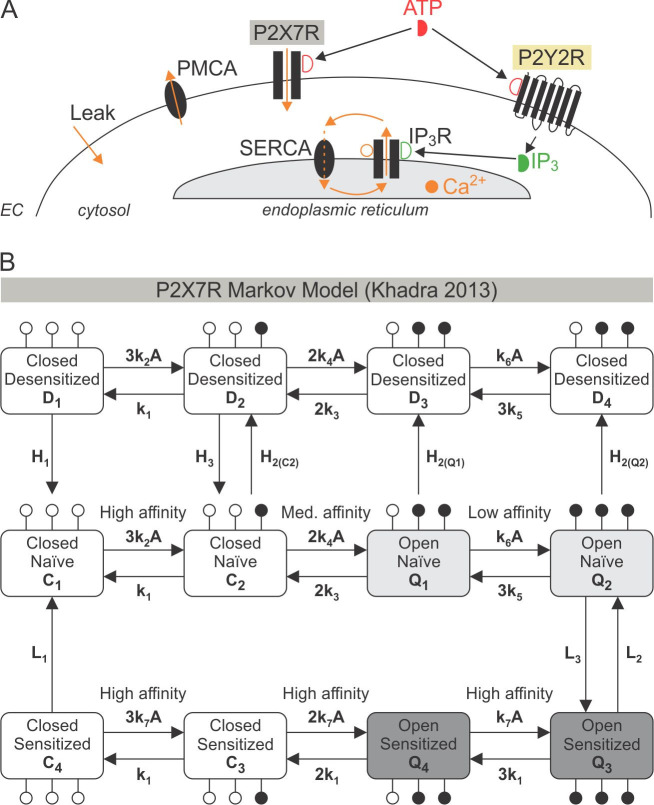
To decipher the underlying biophysical mechanisms governing the ATP-stimulated Ca2+ responses in osteoblasts, we developed a mathematical model that integrates P2Y2R-mediated Ca2+ release, as described by the Li-Rinzel model of the IP3R [24], with a Markov model of P2X7R kinetics adapted from [18] (Fig 3). The cell was divided into two compartments (Fig 3A), the endoplasmic reticulum (ER) and the cytosol, with Ca2+ concentrations in each compartment denoted by [Ca2+]ER and [Ca2+]i, respectively. The detailed description of the model is given in Methods. Briefly, the model describes (i) Ca2+ mobilization across cell membrane, including Ca2+ influx through P2X7R receptor channels (JP2X7) and the constant inward leak (JINleak), as well as Ca2+ efflux through the plasma-membrane-Ca2+-ATPase (PMCA) pumps (JPMCA); and (ii) Ca2+ mobilization across ER membrane, including P2Y2R-mediated Ca2+-induced Ca2+-release (CICR) through IP3R (JIP3R), Ca2+ leak across the ER membrane (JERleak), and Ca2+ uptake through the sarco/endoplasmic Ca2+ ATPase (SERCA) pumps (JSERCA). The reduced two-dimensional Li-Rinzel model for IP3R-mediated CICR was chosen for its simplicity and ability to produce transitions between the desired modes of activity; it follows the Hodgkin-Huxley gating formalism (see Methods), with two fast activation variables and one slow inactivation variable that depend on [IP3] and [Ca2+]i, producing an open probability profile for CICR that is biphasic with respect to [Ca2+]i. Given that P2Ys modulate intracellular Ca2+ responses indirectly by stimulating IP3 production, an equation describing [ATP]-dependent IP3 production was added to the P2Y2R submodel.
Fig 3. Schematic of the mathematical model describing P2 receptor-mediated Ca2+ responses.
(A) ATP activates P2X7 and P2Y2 receptors on the plasma membrane, stimulating Ca2+ entry and IP3 production, respectively. IP3 production leads to Ca2+ release from the endoplasmic reticulum (ER) through IP3Rs. Sarco/endoplasmic Ca2+ ATPase (SERCA) activity replenishes the ER and allows for Ca2+ oscillations when combined with the biphasic response of IP3Rs to Ca2+ due to Ca2+-induced Ca2+-release (CICR). Ca2+ is removed from the cell by plasma membrane Ca2+ ATPases (PMCA). A constant inward Ca2+ leak ensures positive [Ca2+]i in the absence of ATP. EC: extracellular space. (B) Schematic of the P2X7R Markov Model. Middle, lower and upper rows: Fraction of P2X7Rs in naïve, sensitized and desensitized states, respectively. Open and solid circles: Sites unoccupied and occupied by ATP, respectively. Receptors in the closed (Ci) and desensitized (Di) states have closed channel pores, whereas receptors in the open (Qi) states, have open channel pores with identical conductance, i = 1−4. Model parameter values are listed in Table 1.
Ca2+ flux through P2X7R, JP2X7, on the other hand, was determined by the Ca2+ current (IP2X7) through the receptor channels generated by a 12-state Markov P2X7R sub-model (Fig 3B) [18]. The P2X7R submodel assumes that each receptor has three ATP binding sites, two of which must be occupied for the receptor to be open, and that each state represents the fraction of receptors with a given number of occupied ATP-binding sites (Fig 3B, solid circles). The closed, Ci, and desensitized, Di, states are non-conducting, whereas the open states Qi (i = 1−4) possess the same conductance gX7. The states were divided into three rows corresponding to desensitized (Fig 3B, top row), naïve (Fig 3B, middle row) and sensitized or primed (Fig 3B, bottom row) states, respectively. The naïve row is comprised of the states C1, C2, Q1, Q2 that have not been exposed to ATP for a prolonged period of time, whereas the sensitized and desensitized rows are comprised of the states C3, C4, Q3, Q4 (D1, D2, D3, D4) that have been previously exposed to ATP. The forward and backward transitions along each row describe ATP binding and unbinding, respectively, whereas downward and upward transitions between the rows represent receptor sensitization (middle to bottom row), desensitization (middle to top row) or recovery (bottom/top to middle row). The rate of desensitization increases as more ATP molecules bind to P2X7R and the open probability along the sensitized row is larger than that for the naïve row.
Combining the two submodels together produced the following model:
| (1) |
| (2) |
| (3) |
where fc and fER represent the fraction of free Ca2+ in the cytosol and ER, respectively, as a result of buffering with 0 < fc < fER << 1, γ is the ratio between cytosolic and ER volume, αATP is the maximum rate of IP3 production by P2Y2 in response to ATP, kATP is the half-maximum production of IP3 through P2Y2R and δATP is the rate of IP3 degradation.
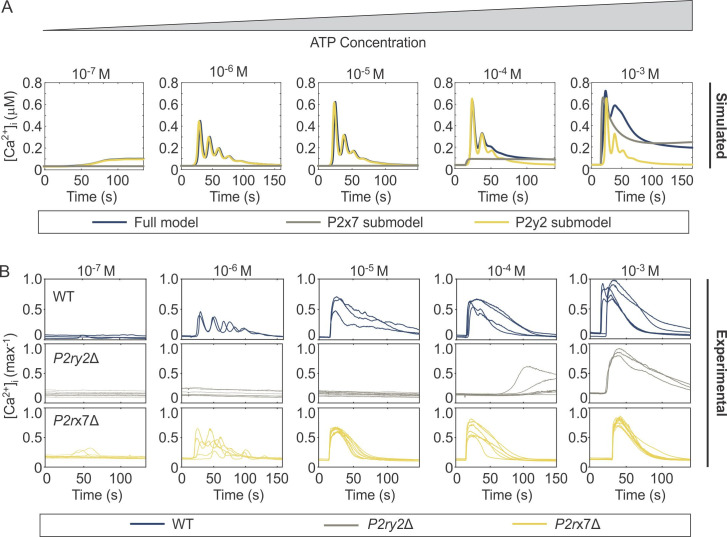
Using the model parameters provided in Table 1, we simulated Ca2+ responses to different [ATP] in three specific cases: (i) in naïve cells expressing both P2Y2R and P2X7R using the full model (Fig 4A, blue curves), (ii) in cells that do not express P2Y2R, using the submodel for P2X7 component only (Fig 4A, grey curves), and (iii) in cells that do not express P2X7R using the submodel for P2Y2 component only (Fig 4A, yellow curves). The simulated Ca2+ responses were compared with those obtained experimentally in WT (Fig 4B, blue curves), P2ry2Δ (Fig 4B, grey curves) and P2rx7Δ (Fig 4B, yellow curves) C2-OB cells. As shown, the responses to low [ATP] were predominantly P2Y2-mediated, while the response to high [ATP] were jointly mediated by P2Y2 and P2X7. Notably, the characteristic two-peaked response to 10−3 M observed in experimental recordings (Figs 1A and 4B) was predicted by the full model (Fig 4A) of WT cells, but was abolished in P2ry2Δ and P2rx7Δ recordings and in simulations of P2X7 and P2Y2 submodels. These data strongly support the interaction between P2Y2 and P2X7 receptors in generating this unique signaling feature.
Table 1. Mathematical Model Parameters.
| Buffering & Scaling | |||
| Symbol | Value | Description | Reference |
| fc | 0.01 | Cytosolic Ca2+ buffering | [38] |
| fER | 0.025 | ER Ca2+ buffering | [38] |
| γ | 9 | cytosol/ ER volume ratio | [39] |
| Plasma Membrane Fluxes | |||
| JINleak | 0.15 μMs-1 | Inward leak across plasma membrane | Fitted† |
| vPMCA | 30 μMs-1 | Maximum PMCA activation | Fitted† |
| kPMCA | 0.45 μM | PMCA Ca2+ affinity | [32] |
| ER Fluxes | |||
| vSERCA | 22.5 μMs-1 | Maximum SERCA activation | Fitted† |
| kSERCA | 0.105 μM | SERCA Ca2+ affinity | [32] |
| vERleak | 0.03 s-1 | Rate of Ca2+ leak across ER membrane | Fitted† |
| Li Rinzel IP3R Models | |||
| d1 | 0.13 μM | IP3 dissociation constant (Ca2+ unbound from inactivation site) | [24] |
| d2 | 1.049 μM | Ca2+ dissociation constant from the inactivation site (IP3 bound) | [24] |
| d3 | 0.9434 μM | IP3 dissociation constant (Ca2+ bound to inactivation site) | [24] |
| d5 | 0.08234 μM | Ca2+ dissociation constant from activation site | [24] |
| a2 | 0.2 μMs-1 | Ca2+ binding rate to the inactivation site | [24] |
| vIP3R | 15 μMs-1 | Maximum flux through IP3Rs | Fitted† |
| P2X7R Model | |||
| gX7 | 2.5x10-8 Ms-1 | P2X7R conductance of both naïve and sensitized open states | Adjusted*** |
| E | 0 mV | Reversal potential | [18] |
| k1 | 0.3 s-1 | Transition rates between states (Fig 3B, along the same row) | [18] |
| k2 | 1265 M-1s-1 | [18]* | |
| k3 | 2.4 s-1 | [18] | |
| k4 | 1581 M-1s-1 | [18]* | |
| k5 | 1.58 s-1 | [18] | |
| k6 | 221 M-1s-1 | [18]* | |
| k7 | 316 M-1s-1 | [18]* | |
| L1 | 0.0001 | Transition rates between naïve (Fig 3B, middle row) and sensitized (Fig 3B, bottom row) | [18] |
| L2 | 0.004 | [18] | |
| L3 | 0.3 | [18] | |
| H1 | 0.001 | Transition rates between naïve (Fig 3B, middle row) and desensitized (Fig 3B, upper row) | [18] |
| H2(C2) | 0.01 | [18] | |
| H2(Q1) | 0.05 | Adjusted*** | |
| H2(Q2) | 0.8 | Adjusted*** | |
| V | -0.06 V | Membrane Potential | [18] |
| fCa | 0.046 | Fraction of P2X7R flux that is Ca2+ | [36] |
| Vosteo | 6.5 pL | Osteoblast volume | [35,40] |
| IP3 Dynamics | |||
| αATP | 0.03 μMs-1 | Maximum rate of IP3 production driven by ATP | [30,41]** |
| kATP | 1 μM | Sensitivity of IP3 production to [ATP] | Fitted† |
| δ | 0.01 s-1 | Degradation rate of IP3 | [30,41]** |
*Parameter values in [18] were fitted to BzATP. To capture the lower binding affinity of ATP to P2X7R, these parameter values were rescaled here (by dividing them by the factor 31.625).
**Parameter values from [30] were used as an upper bound for the parameters in this work, based on the significantly slower IP3 dynamics reported in living cells in [41].
*** As stated in the text, these values were adjusted due to the evidence that P2X7R do not dilate and that P2X7R desensitization increases with more ATP binding.
†These parameter values were determined by fitting the model to data of dose-responses of ATP-induced [Ca2+]i elevations shown in Fig 7.
Fig 4. Comparison of simulated and experimental dynamics of ATP-induced [Ca2+]i responses.
(A) Time series simulations of [Ca2+]i responses generated by the complete model of P2Y2 and P2X7 (full model, blue), P2X7 submodel (grey) and P2Y2 submodel (yellow). Parameter values are provided in Table 1. (B) Experimental recordings of [Ca2+]i responses in WT (blue), P2ry2Δ (grey) and P2rx7Δ (yellow) C2-OB cells in response to varying [ATP].
One interesting aspect of the recordings and simulations displayed in Fig 4 was the observation of oscillatory Ca2+ responses at intermediate [ATP], with transient responses at low and high [ATP], indicating that the mathematical model developed in this study recapitulates the characteristic Ca2+ signatures observed in C2-OB cells over a physiological range of [ATP].
P2Y2 drives the transition from transient to oscillatory Ca2+ responses
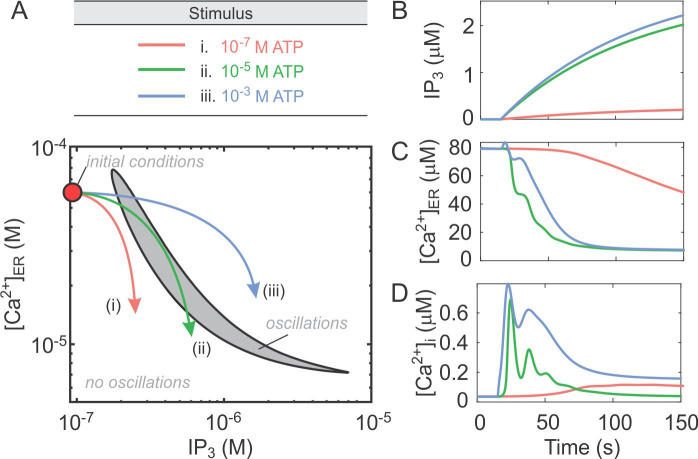
Since the oscillatory component required P2Y2 activity in both experimental and simulated responses to ATP, we next investigated how the transition between transient and oscillatory responses is achieved by the P2Y2 receptor. Given that [IP3] and [Ca2+]ER are slow variables in the model defined by Eqs (1)–(3), we set JP2X7R = 0 and applied slow-fast analysis on the resulting P2Y2 receptor model by assuming that these two variables change slowly relative to other “fast” variables in the model. We set the two variables ([IP3] and [Ca2+]ER) as independent adjustable parameters in the P2Y2 model and investigated how the steady state dynamics of fast variables change when [IP3] and [Ca2+]ER are altered. The two-parameter bifurcation diagram (Fig 5) exhibited an oscillatory region in the “parameter” space formed by [IP3] and [Ca2+]ER within which [Ca2+]i is periodic (Fig 5, grey region). Outside this region, [Ca2+]i attained steady state values that are [IP3] and [Ca2+]ER-dependent. The boundary of this oscillatory region (generated by two supercritical Hopf bifurcations) defined the threshold for [Ca2+]i to transition between these two main patterns of activity: quiescence and oscillatory. Thus the application of increasing [ATP] in this model would induce an increase in IP3 (since [IP3]∝[ATP]) and a decrease in [Ca2+]ER, generating three possible scenarios for the time courses of [Ca2+]i. When low [ATP] is applied the trajectory stays to the left of the oscillatory region (Fig 5A, red arrow) because the ATP-induced IP3 increase is low (Fig 5B, red curve) and [Ca2+]ER remains high (Fig 5C, red curve), resulting in a low magnitude persistent transient response (Fig 5D, red curve). Intermediate [ATP] results in a hybrid response that becomes periodic when the trajectory crosses the left boundary of the oscillatory regime (Fig 5A, green curve), due to a higher increase in IP3 and a faster decrease in [Ca2+]ER (Fig 5B and 5C, green curves), leading to a response characterized by damped oscillations (Fig 5D, green curve). When high [ATP] is applied, the trajectory crosses the oscillatory region very briefly (Fig 5A, blue curve) because even though the ATP-induced IP3 increase is higher (Fig 5B, blue curve), the [Ca2+]ER does not decrease as fast (Fig 5C, blue curve) due to the biphasic nature of IP3Rs incorporated in the P2Y2 sub-model and the interaction of SERCA pumps with IP3Rs [24]; this results in a high magnitude semi-persistent response (Fig 5D, blue curve). The aforementioned mechanism suggests that the heterogeneity in Ca2+ response profiles at a given [ATP] observed experimentally (Fig 1A) may be due to variations in the initial conditions, such as the expression levels of PMCA/SERCA pumps and IP3R, potentially leading to differences in the initial [IP3] and [Ca2+]ER. These simulations demonstrate that the oscillatory response strongly depends on the initial [IP3] and [Ca2+]ER, and that when increasing doses of [ATP] are applied, P2Y2-mediated changes in [IP3] and [Ca2+]ER result in different patterns of Ca2+ responses.
Fig 5. Ca2+ oscillatory response dynamics defined by the P2Y2-induced changes in [Ca2+]ER and [IP3].
The model defined by Eqs (1)–(3), was examined with JP2X7R = 0. (A) The slow variables representing [IP3] and [Ca2+]ER were set to be independent parameters and the continuation method in XPPATU was applied to track two supercritical Hopf bifurcation points that enclose the oscillatory region (grey region). Arrows indicate the three possible scenarios that describe the changes in [IP3] and [Ca2+]ER during Ca2+ responses: 10−7 M ATP response trajectory remains outside the oscillatory region (red), 10−5 M ATP response trajectory spends an extended period of time inside the oscillatory region (green) and 10−3 M ATP response trajectory briefly crosses through the oscillatory region (blue). (B-D) Simulated changes in IP3 (B), [Ca2+]ER (C) and [Ca2+]i (D) following the application of 10−7 M ATP (red) 10−5 M ATP (green) or 10−3 M ATP (blue).
P2X7 modulates the magnitude of Ca2+ response to ATP
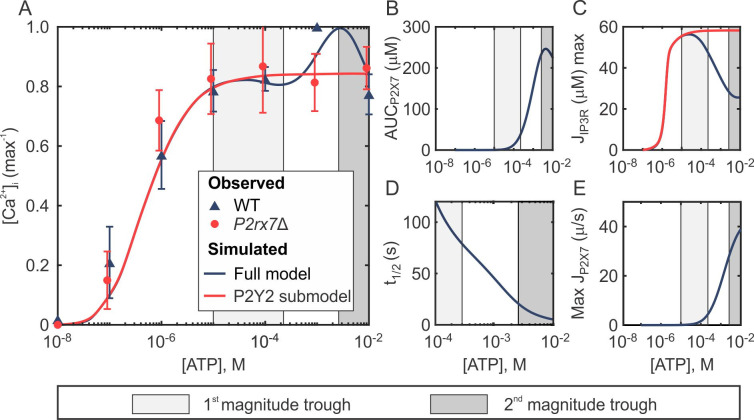
We next investigated the non-monotonic [ATP]-dependent dose-response profile for the magnitude of Ca2+ response observed across all osteoblastic lines (Fig 1B). Using the model defined by Eqs (1)–(3), we generated Ca2+ responses to [ATP] ranging between 10−8 to 10−2 M ATP (in 10−8 M [ATP] increments), and computed the maximum [Ca2+]i reached within 120 s (Fig 6A). The full model (Fig 6A, blue curve) recapitulated the experimental magnitude dose-response profile (Fig 6A blue triangles), including the troughs at moderate (Fig 6A, light grey region) and elevated (Fig 6A, dark grey region) [ATP] within the plateau component of the response. This dose-dependency became monotonic in experimental recordings of Fura2-loaded P2rx7Δ C2-OB cells stimulated with ATP (Fig 6A, red circles) and in the model lacking P2X7Rs (Fig 6A, red curve), strongly implicating P2X7 in this phenomenon. Therefore, we next plotted the total Ca2+ flux through P2X7Rs, estimated as the area under the P2X7R flux curve, as well as the maximal Ca2+ fluxes through P2X7Rs and IP3Rs predicted by the model (Fig 6B–6E). When P2X7R-mediated Ca2+ entry became evident at 10−5 M ATP (Fig 6B, light grey region), the maximum flux through IP3Rs in the full model (Fig 6C, black curve) dropped below that of the P2X7R-lacking submodel (Fig 6C, red curve) due to the biphasic dependence of IP3Rs on [Ca2+]i, resulting in the first trough in the dose-response (Fig 6A, light grey region). At high 10−2 M [ATP], on the other hand, the time required for the P2X7R flux to decay to half of its maximum (t1/2) decreased (Fig 6D). As a result, despite the maximum P2X7R flux continually increasing (Fig 6E), the Ca2+ entering through P2X7R began to decrease at elevated [ATP] (Fig 6B, dark grey), resulting in the second trough in the dose-response (Fig 6A, dark grey). Taken together, these simulations indicate that the non-monotonic Ca2+ dose-response to ATP is driven by an interplay between the biphasic nature of IP3Rs and the desensitization kinetics of P2X7Rs.
Fig 6. Interaction between P2Y2R and P2X7R underlies the non-monotonic magnitude dose-dependency.
(A) The magnitude dose-responses of ATP-induced [Ca2+]i elevations. Markers indicate experimental means ± SEM in wild-type (WT; blue) and P2rx7Δ (red) C2-OB cells. Curves indicate simulated data generated by the full model (blue) and P2Y2 submodel (red). (B) P2X7R-mediated Ca2+ entry estimated from simulated area under the P2X7R flux curve (0–10 s). (C) Simulated maximal flux through IP3Rs in the full model (blue) and P2Y2 only submodel (red). (D) Rate of P2X7R desensitization estimated from simulated time required for P2X7R flux to decay to half of its maximum. (E) Simulated maximum flux through P2X7Rs. Shaded regions in all panels: characteristic first (light grey) and second (dark grey) magnitude troughs observed in WT cells that disappear in P2rx7Δ cells.
Contribution of P2Y2 to Ca2+ responses at high [ATP]
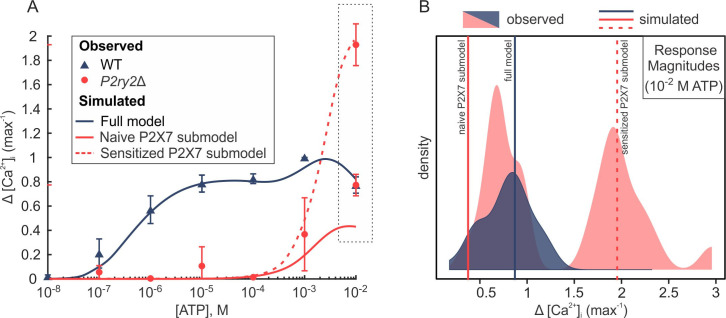
Next, we examined why the Ca2+ response to high [ATP] is dramatically affected in P2ry2Δ cells (Figs 4B and 7A). We examined the magnitudes of Ca2+ responses to 10−2 M [ATP] in WT P2ry2Δ cells, and found that in the absence of P2Y2R, response magnitudes exhibited a distinct bimodal distribution with one cluster of responses similar to those in WT, and another one with much higher response magnitudes (Fig 7B). We hypothesized that the bimodality in the P2X7R-mediated responses is due to P2X7Rs being in the naïve or sensitized initial state [20]. To verify this, we used the P2X7 submodel to simulate the Ca2+ response in two different scenarios: initiating the P2X7-simulations from the naïve closed state C1 (i.e., C1(0) = 1, Ci(0) = 0, for i = 2−4, and Qi(0) = Di(0) = 0, for i = 1−4), or from the sensitized closed state C4 (i.e., C4(0) = 1, Ci(0) = 0, for i = 1−3, and Qi(0) = Di(0) = 0, for i = 1−4). These two scenarios reflect the heterogeneity in the distribution of unstimulated P2X7R as being predominantly in the naïve or sensitized states. Plotting the [ATP]-dependent dose-response curve for [Ca2+]i generated from these time series simulations revealed that P2X7R responses initiated from C1 produced a dose-response curve that plateaued at a depressed level of [Ca2+]i (~ 40% of max WT response; Fig 7A, solid red curve), close to the mean of the left mode of the distribution (Fig 7B). In contrast, P2X7R responses initiated from C4 state produced a dose-response curve that plateaued at an elevated [Ca2+]i (~ 200% of max WT response; Fig 7A, dashed red curve), closely matching the mean of the right mode of the distribution (Fig 7B). These data suggest that P2Y2 activation may alter the kinetics of P2X7 towards favouring naïve state activation.
Fig 7. P2Y2 alters P2X7-mediated [Ca2+]i response to high [ATP].
(A) The magnitude dose-responses of ATP-induced [Ca2+]i elevations. Markers indicate experimental means ± SEM in wild-type (WT; blue) and P2ry2Δ (red) C2-OB cells. Curves indicate simulated data generated by the full model (blue), a P2X7 submodel initiated from the naïve closed state C1 (solid red curve), or a P2X7 submodel initiated from the sensitized closed state C4 (dashed red curve). (B) Density distributions of experimental Ca2+ response magnitudes to 10−2 M [ATP] in WT cells (blue density; unimodal) and P2ry2Δ cells (red density; bimodal). Vertical lines show simulated response magnitudes (10−2 M [ATP]) obtained by the full model (solid blue line), naïve P2X7 submodel (solid red line) and sensitized P2X7 submodel (dashed red line).
Functional contributions of P2Y2 and P2X7 to mechanotransductive signaling
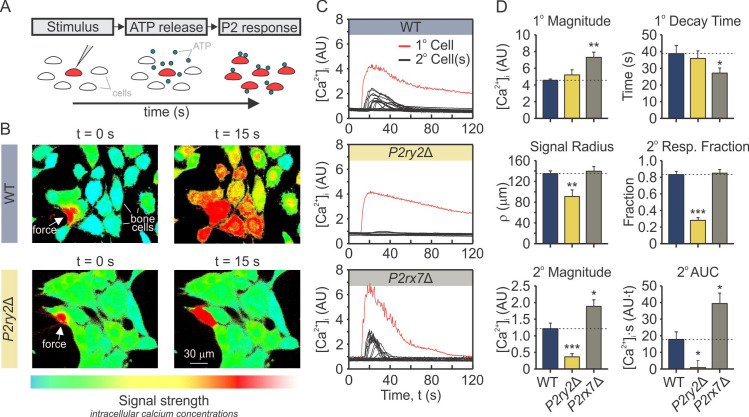
To investigate the potential functional consequences of the complex interactions between P2Y2 and P2X7, we examined how the absence of each of these receptors affects ATP-mediated mechanotransduction. We have previously shown that mechanical stimulation of a single “primary” osteoblast with a glass micropipette leads to the release of 10−5 to 10−4 M ATP into the pericellular space, which then diffuses to stimulate neighbouring non-mechanically perturbed “secondary” cells [11,12]. Here, we mechanically stimulated a single fura2-loaded osteoblast from parental C2-OB, or clones deficient in P2Y2, P2ry2Δ, or P2X7, P2rx7Δ and recorded [Ca2+]i responses in the primary and secondary cells (Fig 8A). We found that while in P2rx7Δ cells the response was qualitatively similar to WT, in P2ry2Δ cells secondary responses were abolished (Fig 8B and 8C). Quantitatively, the primary response was unaffected in P2ry2Δ cells, but exhibited higher magnitude and faster decay in P2rx7Δ cells (Fig 8C and 8D). The suppression of the secondary response in P2ry2Δ cells was evident by the reduced signaling radius (p = 9×10−3), fractions of responding cells (p = 5×10−11), response magnitudes (p = 2×10−4) and areas under the curves (AUC; p = 0.02) (Fig 8B–8D, yellow). In contrast, in P2rx7Δ cells, the signaling radius and fraction of responding secondary cells was unaffected; however, the response magnitudes and areas under the curves of secondary cells were significantly higher in P2rx7Δ cells compared to parental C2-OB cells (Fig 8C and 8D, grey). These data demonstrate that P2Y2 receptor is critical for the secondary responses, consistent with its high sensitivity to ATP. In addition, the contribution of P2X7 to Ca2+ responses is evident even though extracellular ATP in these experiments remained below [ATP] required to stimulate P2X7. Taken together, these data strongly support the importance of an interplay between P2Y2R and P2X7R.
Fig 8. P2Y2R and P2X7R contribution to mechanically stimulated signals in bone cells.
(A) Fura2-loaded C2-OB cells were plated on a glass-bottom dish and individual cell (primary; 1°) was mechanically stimulated with a glass-micropipette inducing ATP release into the extracellular space, which subsequently stimulated P2 responses in neighbouring cells (secondary; 2°). (B) Representative images of [Ca2+]i (pseudocolor of 340/380 ratio) in C2-OB parental (top) and P2ry2Δ (bottom) cultures, in which a single cell was mechanically stimulated at t = 0 s (white arrows). The snapshot at 15 s demonstrate secondary responses in neighboring cells. Red traces: primary responses; Black traces: secondary responses. (C) Time-series recordings in WT (top panel), P2ry2Δ (middle panel), and P2rx7Δ (lower panel) cells. (D) Quantification of primary and secondary [Ca2+]i response parameters, including signaling radius, fractions of responding cells, response magnitudes and areas under the curves in WT (blue), P2ry2Δ (yellow), and P2rx7Δ (grey) cells. Data are means ± SEM, *p<0.05, **p<0.01 and ***p<0.001 indicate comparisons between WT and P2ry2Δ or P2rx7Δ cells assessed by ANOVA and Bonferroni-corrected t-test. AU: arbitrary units.
Discussion
In this study, we demonstrated that the patterns of P2R-mediated Ca2+ responses to ATP are conserved across three independent murine osteoblast models and identified the P2Y2 and P2X7 receptors as the dominant P2 receptors contributing to these responses. Based on previous experimental evidence highlighting the role of IP3 in regulating calcium responses [11], we constructed a flux-balance based mathematical model of Ca2+ signals induced by the activation of high affinity P2Y2R and low affinity P2X7R. Model predictions were validated by comparing the results of simulations to experimental data of ATP-generated Ca2+ signaling in parental and CRISPR/Cas9 -generated P2Y2 and P2Y7 knockouts in osteoblastic C2C12-BMP cells. We demonstrated that activation of P2Y2R by progressively increasing [ATP] induces a transition from transient to oscillatory to transient Ca2+ responses due to the biphasic nature of IP3R activation/inactivation kinetics and the interaction of SERCA pumps with IP3Rs. At high [ATP], activation of P2X7R was found to modulate the peak response magnitudes through an interplay between the biphasic nature of IP3Rs and the desensitization kinetics of P2X7Rs. Moreover, our study suggests that P2Y2 activity may also alter the kinetics of P2X7 towards favouring naïve state activation. Finally, we demonstrated that functional consequences of lacking P2Y2 or P2X7 are evident beyond the absence of a signal at the expected range of ATP concentrations. Taken together, these findings support a model in which the response to ATP is not a simple superposition of individual P2 receptors, but a complex context-specific functional response build through interactions of multiple P2 receptors.
Our experimental studies focused on characterizing ATP-mediated calcium responses in osteoblasts. In investigating these calcium responses, we chose to stimulate cells with a range of physiologically-relevant ATP concentrations (10 nM to 10 mM), such that 10–100 nM ATP represented small fluxes above baseline extracellular ATP concentrations, 1–100 μM ATP represented concentrations achieved following mechanical stimulation, and 1–10 mM ATP represented intracellular [ATP] that has the capacity to spill into the extracellular space and stimulate P2 receptor signalling following traumatic tissue injury [3,7,11]. We have found that murine osteoblastic cells from different sources exhibit similar patterns in their ATP concentration-dependence of Ca2+ responses, including non-trivial features such as the transition of response from transient to oscillatory and back to transient when increasing [ATP], and the presence of two troughs in the plateau phase of the magnitude dose-response curve at high [ATP]. These finding suggest that P2 receptors contributing to these responses are also conserved. P2 receptors are ubiquitously expressed in every mammalian cell, with cell- and tissue-type specific patterns of expression [5] Consistent with previous reports [25,26], we demonstrated that the pattern of P2 receptors expressed across different murine osteoblast models is consistent at the mRNA level, and identified ATP-sensitive P2X7 and P2Y2 receptors as the dominant P2 receptor subtypes in osteoblasts. In keeping with their important roles in bone, P2rx7-/- and P2ry2-/- mice have been shown to exhibit severe bone phenotypes, with P2rx7-/- mice demonstrating significant deficiency in bone mineral density and truncated response to mechano-adaptive loading [27,28], and P2ry2-/- mice similarly experiencing osteopenia and altered mechanotransducive responses [29]. In our study, CRISPR-Cas9 double-nickase generated clonal C2-OB cells lacking P2ry2 or P2rx7 showed altered responses to sustained ATP stimulation, which translated into significant changes in mechanotransductive [Ca2+]i signaling. Thus, P2Y2 and P2X7 receptors play critical roles in mediating the osteoblast response to ATP, particularly in the context of mechanotransducive signaling in bone.
In every osteoblast model, we found that there was a finite range of [ATP] over which oscillatory [Ca2+]i response is prevalent. The oscillatory behaviour was abolished in P2ry2Δ cells, but preserved in P2rx7Δ cells, strongly implicating P2Y2 as a mediator of oscillations. Using the mathematical model of P2Y2-induced changes in [IP3] and [Ca2+]ER allowed us to examine the mechanism of transition between oscillatory and non-oscillatory (transient) responses. We found that moderate IP3 production evokes an oscillatory response because of two factors: i) CICR by the IP3Rs that exerts negative feedback on the receptors and inhibits them, and ii) the interaction of IP3Rs with SERCA that pumps Ca2+ back into the ER. In contrast, at low [ATP], the Ca2+ released by IP3Rs is insufficient to feedback and inhibit the receptors, whereas at high [ATP], IP3Rs become constitutively activated, making CICR larger than that in the moderate case but no longer able to inactivate the receptors; this produces, as a result, transient Ca2+ responses in both cases. While this model prediction is interesting, its validation is limited by difficulties in experimentally measuring osteoblastic IP3 dynamics. Specifically, little is known about the basal [IP3] (assumed to be 0 μM in our model), which plays a significant role in whether solutions will pass through the oscillatory region obtained in the [IP3] and [Ca2+]ER space. Furthermore, the ability of the model to predict some of the experimental response profiles observed at elevated [ATP] is limited by the chosen P2Y2R-IP3R sub-model, which is unable to slowly decay after a rapid increase in [Ca2+]i [24]. Given the large heterogeneity of responses at these concentrations, choosing a simplified P2Y2R-IP3R sub-model was prioritized over the ability to reproduce some response patterns. In spite of these limitations, experimental and modeling data agree on the critical role of P2Y2-induced IP3-mediated Ca2+ release from ER in generating oscillatory Ca2+ responses to ATP.
Another conserved feature in ATP dose dependence in osteoblasts is the non-monotonic changes in the response magnitude. A similar dose-response curve, with troughs at 10−4 M and 10−2 M ATP and a peak at 10-3M ATP was reported in MC3T3-E1 osteoblasts [7]. While we have previously suggested that the decrease in the response magnitude may be mediated by negative effects of one of the receptors that are active at mid-range [ATP] [7], current study demonstrates that similar regulation is achieved through interactions between P2Y2 and P2X7. In particular, we have found that these characteristic throughs disappear in P2rx7Δ cells. Using the mathematical model, we showed that at 10−4 M ATP, the additional Ca2+ influx through now activated P2X7 inhibits P2Y2-induced IP3R activity due to the biphasic dependence of IP3Rs on [Ca2+]i. As a result, the peak [Ca2+]i response, which is predominantly mediated by IP3R activity, decreases, creating the first trough in the dose-response curve at 10−4 M [ATP]. With further increase in [ATP], the activation of P2X7Rs, known to monotonically increase with [ATP], starts to outweigh the reduced IP3R activity, causing the peak [Ca2+]i response to rise, reaching a global maximum around 10−3 M ATP. After that, the rate of P2X7R desensitization (that increases with [ATP]) becomes large enough to impede Ca2+ influx through the receptors, resulting in a decrease in the peak [Ca2+]i response (now predominantly mediated by P2X7Rs) which creates the second trough in the dose-response curve at 10−2 M ATP. These data demonstrate how activation of low affinity P2X7 may affect the responses mediated by the high affinity P2Y2. Our study also suggests the reciprocal effect of P2Y2 on the function of P2X7 through facilitating the naïve state activation of P2X7. Indeed, previous studies have documented such an effect through the allosteric regulation of P2XR (including P2X7R) by Ca2+ [17,19], suggesting that Ca2+ release from the ER through the P2Y2 pathways may underly the altered kinetics of P2X7. Taken together, our study demonstrates multiple points of interactions between P2Y2 and P2X7 receptors, which are not only activated at very different ranges of ATP concentration, but also belong to different classes of receptors.
Finally, our study demonstrates that the absence of either P2Y2 or P2X7 has significant implications on ATP-mediated mechanotransduction. We used an experimental setup in which the mechanical stimulation of a single osteoblasts generates a micro-injury in its cell membrane, leading to a release of ATP that signals to neighboring (secondary) cells [11]. First, we showed that in the absence of P2Y2, the transmission of ATP signal to neighboring cells is effectively interrupted. These findings are consistent with previous reports that osteoblasts from P2Y2-/- mice exhibited dramatic reduction in fluid flow-induced Ca2+ responses even though the ATP release was similar to WT osteoblasts [29]. Second, we have found that in the absence of P2X7, both primary and secondary responses are significantly altered. While local ATP concentrations at the site of micro-injury may support the involvement of P2X7 in generating the Ca2+ response of the primary cell [11,12], the observed changes in the secondary responses are surprising, since we have previously shown that the amount of ATP released in these experiments is below the concentrations required for P2X7 activation [11]. Nevertheless, this observation is consistent with previously suggested alterations in mechanotransductive signaling in P2X7 deficient mice [27,28]. Thus, our study supports the important role of P2 receptor network in generating a mechanotransductive signal that conveys complex information to neighbouring cells.
In conclusion, this study provided a complex mechanism of interdependency between the action of high affinity G-protein coupled receptor P2Y2 and a low affinity ligand gated ion channel P2X7. Using a combination of experimental studies in osteoblastic cells with the full compliment of P2 receptors, as well as osteoblasts deficient in P2Y2 or P2X7, and mathematical modeling of P2Y2R-mediated Ca2+ release coupled to a Markov model of P2X7R dynamics, allowed us to explore the intricate details of the subcellular signaling induced by ATP in bone forming osteoblasts. The conclusions drawn demonstrated causative links between the exposure to mechanical force, early ATP-mediated signaling, and mechanoadaptive response of bone tissue.
Materials and methods
Software
Figure preparation: CorelDRAWX8 (Corel); Mathematical Modeling: MATLAB R2018a (MathWorks), XPPAUT 8.0. Statistical Analysis: R version 4.0.0 (R Foundation for Statistical Computing).
Solutions and reagents
Refer to S1 Text for a complete list of materials used in this study.
Cell culture
The C2C12 cell line (ATCC CRL-1772) stably transfected with BMP-2 (C2-Ob cells) was plated at 104 cells/cm2 in DMEM (supplemented with 10% FBS, 1% sodium pyruvate, 1% penicillin streptomycin) and cultured for 2–3 days prior to experiments. Absence of mycoplasma contamination was verified in cryo-preserved stocks of C2-OB cells using PCR-based detection kit.
Generation of P2R knockout cell lines
C2-Ob cells were plated in 6-well plates at 100,000 cell/well density 2 days prior to transfection. On the day of transfection, 7.5 μL lipofectamine was diluted in 125 μL Opti-MEM medium (Solution A) and 5 μg P2ry2 or P2rx7 CRISPR/Cas9 plasmid and 10 μL P3000 reagent were diluted in a separate 125 μL aliquot of Opti-MEM (Solution B). Solutions A and B were then pooled in a 1:1 ratio and incubated at room temperature for 15 min. Cell media was aspirated and 250 μL of the pooled DNA-lipid complex solution was added to cells and left to incubate at 37°C for 3 days. 3 days post-transfection, cells were visualized using fluorescent microscope to verify successful transfection through the presence of GFP-positive cells. Transfected cultures were transferred to fresh DMEM media and treated with 5 μM puromycin for 7 days to select for puromycin-resistant clones. After selection, cells were transferred into puromycin-free media, allowed 3 days for recovery, and re-plated in 96 well plates at a ~1 cell per well density. After 3 weeks of expansion, half of each single-cell colony was re-plated in 96-well plates and the other half was collected for genomic DNA extraction using DNeasy kit. Genomic DNA for each single-cell colony was amplified by touchdown PCR using primer sets designed to flank the genomic region targeted by Cas9 (S2 Table), and amplicons were separated on a gel to screen for clones with evident band shifts. Selected clones were subsequently validated by immunoblot analysis, and termed P2ry2Δ and P2rx7Δ cells, for P2ry2 and P2rx7, respectively.
Quantitative real-time polymerase chain reaction (qRT-PCR)
Total RNA was isolated using RNeasy kit and QIAshredder columns and reverse transcribed using cDNA reverse transcription kit. Real time qPCR was performed using QuantStudio 7 Flex PCR System, with SYBR Green or TaqMan Master Mix. Primer sequences are provided in S2 Table and cycling conditions in S3 Table.
Intracellular Ca2+ recordings and analysis
Cells were plated on glass-bottom 35 mm dishes or 48-well plates (MatTek Corporation), for single-cell mechanical stimulation and agonist application experiments, respectively. Cell were loaded with Fura2-AM for 30 min, acclimatized in physiological solution (PS) for 10 min on the stage of an inverted fluorescence microscope (Nikon T2000), and imaged as described previously [11]. For each recording, all cells within the field-of-view at 40x magnification were imaged (~15–30 cell per imaging experiment). The Ca2+ response parameters were analyzed using a previously developed MATLAB algorithm (https://github.com/NMikolajewicz/Calcium-Signal-Analyzer) [13]. To assess ATP dose-dependencies, Fura2-loaded C2-Ob or CB-Ob cells were bathed in 270 μL PS and 30 μL of UDPG, ATP or ADP solutions at 10× final concentration were added (e.g., 30 μL of 10−5 M ATP solution was added to cells to achieve 10−6 M ATP stimulation).
Immunoblotting
Cell lysates were extracted in RIPA lysis buffer and samples were prepared and subject to SDS-PAGE on a 10% (w/v) acrylamide gel as previously described [11]. Blotted nitrocellulose membranes were incubated with primary antibodies overnight (1:1000 dilution, 5% BSA in TBST, 4°C) and secondary antibodies were applied for 1 h (1,1000 dilution, 5% BSA in TBST, rt) prior to visualization with chemiluminescence system.
Mechanical-stimulation
Single osteoblastic cells were stimulated by local membrane indentation with a glass micropipette using a FemtoJet microinjector NI2 (Eppendorf Inc.), as previously described [11].
Statistical analysis
Data are presented as representative images, means ± standard error (SE) or means ± 95% confidence intervals (CI), as specified in each figure panel along with sample sizes N (number of independent experiments) and n (number of technical replicates). Curve fitting and [Ca2+]i transient characterization were performed in R. Statistical significance was assessed by one- or two-way ANOVA (as specified) and post-hoc two-way unpaired Students t-tests were adjusted using the Bonferroni correction. Significance levels were reported as single symbol (*p<0.05), double symbol (**p<0.01) or triple symbol (***p<0.001).
Mathematical model
The mathematical model consisted mainly of Eqs (1)–(3). The individual terms JINleak, JIPR, JERleak, JPMCA, JSERCA and JP2X7, listed in Eqs (1) and (2), were the key Ca2+ fluxes considered in this model, as described below.
(1) Plasma Membrane Ca2+ Leak (JINleak). A constant inward leak across cell membrane to ensure that total [Ca2+] within the cell remained positive. It was assumed to be constant (see Table 1).
(2) IP3R Ca2+ Flux (JIP3R): The Ca2+ flux through IP3Rs, given by
| (4) |
where vIP3R is the maximum rate of Ca2+ release by the IP3R and OIP3R is the IP3R open probability, defined by
| (5) |
which follows a Hodgkin-Huxley gating formalism adopted by De Young and Keizer [30] and later simplified by Li and Rinzel [24]. In this simplification, the activation by IP3 (defined by m∞) and [Ca2+]i (defined by n∞) through binding to the receptor were assumed to be instantaneous, given by
| (6) |
whereas the inactivation by [Ca2+]i (defined by the gating variable h), also through binding, was assumed to occur at a much slower time scale governed dynamically by
| (7) |
where
| (8) |
In the study by De Young and Keizer [30] the values of di (i = 1, 2, 3, 5) were fit to experimental data [31]. Note that the dependence of activation and inactivation of OIP3R on [Ca2+]i in Eq (5) due to CICR makes the profile of IP3R open probability biphasic with respect to [Ca2+]i.
(3) ER Ca2+ Leak (JERleak). A small leak across the ER membrane [24], given by
| (9) |
where vERleak is the maximal rate of Ca2+ leak from the ER.
(4) Ca2+ ATPase Activity (JPMCA and JSERCA). Ca2+ removal by PMCA and Ca2+ re-uptake into the ER by SERCA described by Hill functions [32,33], given by
| (10) |
where x = PMCA, SERCA, vx is the maximal pumping rate and kx is the affinity of the pump to bind to Ca2+.
(5) P2X7R Ca2+ Flux (JP2X7). Ca2+ flux through P2X7Rs. A 12-state Markov model [18] was initially used to compute the current, given by
| (11) |
where gX7 is the conductance of the P2X7R open states Qi, i = 1−4 [18]. With emerging evidence suggesting that P2XRs do not dilate [16,34], the maximum conductance of open (Q1 and Q2) and sensitized/primed (Q3 and Q4) states in this P2X7R sub-model were assumed to be equal. We also assumed that the rate of desensitization increased with ATP binding (H2(C2)<H2(Q1)<H2(Q2)) and that the open probability is higher in the desensitized row (i.e., k7>kj, j = 2, 4, 6). These modifications kept the time series simulations of the P2X7R model generally unchanged. To obtain the overall Ca2+ flux through these channels, we then used the formalism from Zeng et al. [35] to convert ionic current to flux, scaled by a fraction that represents the average Ca2+ flux [36] relative to that for Na+ and K+. The latter was necessary as P2X7Rs are non-selective cation channels. Using the above description, the following expression was used to describe this flux
| (12) |
where z is the valence of Ca2+ (z = +2), F is Faraday’s constant, Vosteo is the volume of the osteoblast in liters and fCa is the fraction of Ca2+ flux through P2X7R.
Slow-fast analysis
“Slow-fast” analysis is a mathematical technique that divides a dynamics model, such as the one described by Eqs (1)–(12), into two subsystems: a fast and slow one, followed by setting the slow variables to be independent parameters. The goal in doing so is to analyze the dynamics of the fast subsystem with respect to those newly defined parameters. This well-known technique that was also applied in [24] allows you to define the distinct regions of behaviour with respect to the slow variables and determine how trajectories of the original model could evolve in time when passing between these regions.
Software and numerical methods
All time-series simulations were performed in MATLAB (Mathworks, Natick, MA). Initially, all simulations were run for a period of 2000 s in the absence of ATP to obtain the resting state of the cell. The basal [IP3] (the [IP3] in the absence of extracellular ATP) was assumed to be zero. P2Y2R and P2X7R knockout recordings were simulated by setting JP2X7 and JIP3R (Eqs (5) and (12)) to zero, respectively. These simulations were then used to compute [ATP]-dependent dose-response curves of [Ca2+]i by evaluating the maximum Ca2+ response at each ATP dose in MATLAB. The bifurcation analysis (Fig 5) was performed using XPPAUT (a freeware available online at http://www.math.pitt.edu/~bard/xpp/xpp.html). To facilitate reproduction of results, the codes used to perform simulations of the model can be obtained online [37]. These simulations can be run by solving the function “fullmodel.m” using the ordinary differential equation solver ode15s. Figs 4A, 6 and 7 can be obtained by running the files titled “Fig 4A.m”, “Fig 6.m” and “Fig 7.m”, respectively.
Supporting information
(A-C) Schematic illustrating processing of ATP-dose-dependent response curves (A). ATP dose-dependent responses from three independent murine cell lines (A, left panel; B) were aligned using a linear transformation to match peaks/troughs (A, middle panel; C) and responses were rescaled to [0,1] interval (A, right panel; Fig 1C). Curves: Loess curves; Markers: Response means (circle: BM-OB; triangle: C2-OB; square: CB-OB).
(TIF)
(PDF)
(PDF)
(PDF)
(PDF)
Acknowledgments
Special thanks to Dr. M. Murshed (McGill, Montreal) for C2-OB cells and Dr. P. Grutter and his graduate students M. Anthonisen and M. Rigby (McGill, Montreal) for glass capillary puller.
Data Availability
All relevant data are within the manuscript and its Supporting Information files. The codes used to generate the computational results are available here: www.medicine.mcgill.ca/physio/khadralab/Codes/code_ploscomp2.html.
Funding Statement
This work was supported by the Natural Sciences and Engineering Research Council of Canada (https://www.nserc-crsng.gc.ca/index_eng.asp) discovery grants to AK and SVK, the Fonds Nature et technologies (http://www.frqnt.gouv.qc.ca/en/accueil) team grant to AK and the Canadian Institutes for Health Research (https://cihr-irsc.gc.ca/e/193.html) grant to SVK (CIHR MOP-77643). NM was supported by the Faculty of Dentistry McGill University (https://www.mcgill.ca/dentistry/) and le Réseau de Recherche en Santé Buccodentaire et Osseuse (http://www.rsbo.ca/). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Verkhratsky A, Burnstock G. Biology of purinergic signalling: its ancient evolutionary roots, its omnipresence and its multiple functional significance. Bioessays. 2014;36(7):697–705. doi: 10.1002/bies.201400024 [DOI] [PubMed] [Google Scholar]
- 2.Burnstock G, Ralevic V. Purinergic signaling and blood vessels in health and disease. Pharmacological reviews. 2014;66(1):102–92. doi: 10.1124/pr.113.008029 [DOI] [PubMed] [Google Scholar]
- 3.Mikolajewicz N, Mohammed A, Morris M, Komarova SV. Mechanically stimulated ATP release from mammalian cells: systematic review and meta-analysis. Journal of Cell Science. 2018;131(22). doi: 10.1242/jcs.223354 [DOI] [PubMed] [Google Scholar]
- 4.Bours M, Dagnelie PC, Giuliani AL, Wesselius A, Di Virgilio F. P2 receptors and extracellular ATP: a novel homeostatic pathway in inflammation. Front Biosci (Schol Ed). 2011;3:1443–56. doi: 10.2741/235 [DOI] [PubMed] [Google Scholar]
- 5.Burnstock G. Physiology and pathophysiology of purinergic neurotransmission. Physiological reviews. 2007. doi: 10.1152/physrev.00043.2006 [DOI] [PubMed] [Google Scholar]
- 6.Jacobson KA, Costanzi S, Joshi BV, Besada P, Shin DH, Ko H, et al., editors. Agonists and antagonists for P2 receptors. Novartis Foundation symposium; 2006: Wiley Online Library. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Xing S, Grol MW, Grutter PH, Dixon SJ, Komarova SV. Modeling interactions among individual P2 receptors to explain complex response patterns over a wide range of ATP concentrations. Frontiers in physiology. 2016;7:294. doi: 10.3389/fphys.2016.00294 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Coddou C, Yan Z, Obsil T, Huidobro-Toro JP, Stojilkovic SS. Activation and regulation of purinergic P2X receptor channels. Pharmacological reviews. 2011;63(3):641–83. doi: 10.1124/pr.110.003129 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Erb L, Weisman GA. Coupling of P2Y receptors to G proteins and other signaling pathways. Wiley Interdisciplinary Reviews: Membrane Transport and Signaling. 2012;1(6):789–803. doi: 10.1002/wmts.62 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Grol MW, Pereverzev A, Sims SM, Dixon SJ. P2 receptor networks regulate signaling duration over a wide dynamic range of ATP concentrations. J Cell Sci. 2013;126(Pt 16):3615–26. doi: 10.1242/jcs.122705 [DOI] [PubMed] [Google Scholar]
- 11.Mikolajewicz N, Zimmermann EA, Willie BM, Komarova SV. Mechanically stimulated ATP release from murine bone cells is regulated by a balance of injury and repair. ELife. 2018;7:e37812. doi: 10.7554/eLife.37812 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mikolajewicz N, Sehayek S, Wiseman PW, Komarova SV. Transmission of mechanical information by purinergic signaling. Biophysical journal. 2019;116(10):2009–22. doi: 10.1016/j.bpj.2019.04.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mackay L, Mikolajewicz N, Komarova SV, Khadra A. Systematic characterization of dynamic parameters of intracellular calcium signals. Frontiers in physiology. 2016;7:525. doi: 10.3389/fphys.2016.00525 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.North RA. Molecular physiology of P2X receptors. Physiological reviews. 2002. doi: 10.1152/physrev.00015.2002 [DOI] [PubMed] [Google Scholar]
- 15.Burnstock G. Purine and purinergic receptors. Brain and Neuroscience Advances. 2018;2:2398212818817494. doi: 10.1177/2398212818817494 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mackay L, Zemkova H, Stojilkovic SS, Sherman A, Khadra A. Deciphering the regulation of P2X4 receptor channel gating by ivermectin using Markov models. PLoS computational biology. 2017;13(7):e1005643. doi: 10.1371/journal.pcbi.1005643 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Khadra A, Yan Z, Coddou C, Tomić M, Sherman A, Stojilkovic SS. Gating properties of the P2X2a and P2X2b receptor channels: experiments and mathematical modeling. J Gen Physiol. 2012;139(5):333–48. doi: 10.1085/jgp.201110716 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Khadra A, Tomić M, Yan Z, Zemkova H, Sherman A, Stojilkovic SS. Dual gating mechanism and function of P2X7 receptor channels. Biophys J. 2013;104(12):2612–21. doi: 10.1016/j.bpj.2013.05.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yan Z, Khadra A, Sherman A, Stojilkovic SS. Calcium-dependent block of P2X7 receptor channel function is allosteric. J Gen Physiol. 2011;138(4):437–52. doi: 10.1085/jgp.201110647 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Yan Z, Khadra A, Li S, Tomic M, Sherman A, Stojilkovic SS. Experimental characterization and mathematical modeling of P2X7 receptor channel gating. J Neurosci. 2010;30(42):14213–24. doi: 10.1523/JNEUROSCI.2390-10.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zemkova H, Khadra A, Rokic MB, Tvrdonova V, Sherman A, Stojilkovic SS. Allosteric regulation of the P2X4 receptor channel pore dilation. Pflugers Arch. 2015;467(4):713–26. doi: 10.1007/s00424-014-1546-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lemon G, Brockhausen J, Li GH, Gibson WG, Bennett MR. Calcium mobilization and spontaneous transient outward current characteristics upon agonist activation of P2Y2 receptors in smooth muscle cells. Biophys J. 2005;88(3):1507–23. doi: 10.1529/biophysj.104.043976 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fedorov IV, Rogachevskaja OA, Kolesnikov SS. Modeling P2Y receptor-Ca2+ response coupling in taste cells. Biochim Biophys Acta. 2007;1768(7):1727–40. doi: 10.1016/j.bbamem.2007.04.002 [DOI] [PubMed] [Google Scholar]
- 24.Li Y, Rinzel J. Equations for InsP3 receptor-mediated [Ca2+] i oscillations derived from a detailed kinetic model: a Hodgkin-Huxley like formalism. Journal of theoretical Biology. 1994;166(4):461–73. doi: 10.1006/jtbi.1994.1041 [DOI] [PubMed] [Google Scholar]
- 25.Hoebertz A, Townsend-Nicholson A, Glass R, Burnstock G, Arnett T. Expression of P2 receptors in bone and cultured bone cells. Bone. 2000;27(4):503–10. doi: 10.1016/s8756-3282(00)00351-3 [DOI] [PubMed] [Google Scholar]
- 26.Orriss IR, Key ML, Brandao-Burch A, Patel JJ, Burnstock G, Arnett TR. The regulation of osteoblast function and bone mineralisation by extracellular nucleotides: The role of p2x receptors. Bone. 2012;51(3):389–400. doi: 10.1016/j.bone.2012.06.013 [DOI] [PubMed] [Google Scholar]
- 27.Ke HZ, Qi H, Weidema AF, Zhang Q, Panupinthu N, Crawford DT, et al. Deletion of the P2X7 nucleotide receptor reveals its regulatory roles in bone formation and resorption. Molecular Endocrinology. 2003;17(7):1356–67. doi: 10.1210/me.2003-0021 [DOI] [PubMed] [Google Scholar]
- 28.Zeng D, Yao P, Zhao H. P2X7, a critical regulator and potential target for bone and joint diseases. Journal of cellular physiology. 2019;234(3):2095–103. doi: 10.1002/jcp.27544 [DOI] [PubMed] [Google Scholar]
- 29.Xing Y, Gu Y, Bresnahan JJ, Paul EM, Donahue HJ, You J. The roles of P2Y 2 purinergic receptors in osteoblasts and mechanotransduction. PLoS One. 2014;9(9):e108417. doi: 10.1371/journal.pone.0108417 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.De Young GW, Keizer J. A single-pool inositol 1, 4, 5-trisphosphate-receptor-based model for agonist-stimulated oscillations in Ca2+ concentration. Proceedings of the National Academy of Sciences. 1992;89(20):9895–9. doi: 10.1073/pnas.89.20.9895 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Watras J, Ehrlich BE. Bell-shaped calcium-response curves of lns (l, 4, 5) P 3-and calcium-gated channels from endoplasmic reticulum of cerebellum. Nature. 1991;351(6329):751–4. doi: 10.1038/351751a0 [DOI] [PubMed] [Google Scholar]
- 32.Croisier H, Tan X, Perez-Zoghbi JF, Sanderson MJ, Sneyd J, Brook BS. Activation of store-operated calcium entry in airway smooth muscle cells: insight from a mathematical model. PloS one. 2013;8(7):e69598. doi: 10.1371/journal.pone.0069598 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Chen Y-f, Cao J, Zhong J-n, Chen X, Cheng M, Yang J, et al. Plasma membrane Ca2+-ATPase regulates Ca2+ signaling and the proliferation of airway smooth muscle cells. European Journal of Pharmacology. 2014;740:733–41. doi: 10.1016/j.ejphar.2014.05.055 [DOI] [PubMed] [Google Scholar]
- 34.Li M, Toombes GE, Silberberg SD, Swartz KJ. Physical basis of apparent pore dilation of ATP-activated P2X receptor channels. Nature neuroscience. 2015;18(11):1577–83. doi: 10.1038/nn.4120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zeng S, Li B, Zeng S, Chen S. Simulation of spontaneous Ca2+ oscillations in astrocytes mediated by voltage-gated calcium channels. Biophysical journal. 2009;97(9):2429–37. doi: 10.1016/j.bpj.2009.08.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Egan TM, Khakh BS. Contribution of calcium ions to P2X channel responses. Journal of Neuroscience. 2004;24(13):3413–20. doi: 10.1523/JNEUROSCI.5429-03.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mikolajewicz N, Smith D, Komarova SV, Khadra A. High-affinity P2Y2 and low-affinity P2X7 receptor interaction modulates ATP-mediated calcium signalling in murine osteoblasts. Anmar Khadra Repository 2020 2021:Available from: www.medicine.mcgill.ca/physio/khadralab/Codes/code_ploscomp2.html. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tsai J-C, Zhang W, Kirk V, Sneyd J. Traveling waves in a simplified model of calcium dynamics. SIAM Journal on Applied Dynamical Systems. 2012;11(4):1149–99. [Google Scholar]
- 39.Alberts B, Johnson A, Lewis J, Raff M, Roberts K, Walter P. The endoplasmic reticulum. Molecular Biology of the Cell 4th edition: Garland Science; 2002. [Google Scholar]
- 40.Zouani OF, Rami L, Lei Y, Durrieu M-C. Insights into the osteoblast precursor differentiation towards mature osteoblasts induced by continuous BMP-2 signaling. Biology open. 2013;2(9):872–81. doi: 10.1242/bio.20134986 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Matsu-ura T, Michikawa T, Inoue T, Miyawaki A, Yoshida M, Mikoshiba K. Cytosolic inositol 1, 4, 5-trisphosphate dynamics during intracellular calcium oscillations in living cells. Journal of Cell Biology. 2006;173(5):755–65. doi: 10.1083/jcb.200512141 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(A-C) Schematic illustrating processing of ATP-dose-dependent response curves (A). ATP dose-dependent responses from three independent murine cell lines (A, left panel; B) were aligned using a linear transformation to match peaks/troughs (A, middle panel; C) and responses were rescaled to [0,1] interval (A, right panel; Fig 1C). Curves: Loess curves; Markers: Response means (circle: BM-OB; triangle: C2-OB; square: CB-OB).
(TIF)
(PDF)
(PDF)
(PDF)
(PDF)
Data Availability Statement
All relevant data are within the manuscript and its Supporting Information files. The codes used to generate the computational results are available here: www.medicine.mcgill.ca/physio/khadralab/Codes/code_ploscomp2.html.