PAIREF: paired refinement also for Phenix users

Support for the refinement engine phenix.refine has been implemented into PAIREF, a tool providing automatic paired refinement.

Abstract

In macromolecular crystallography, paired refinement is generally accepted to be the optimal approach for the determination of the high-resolution cutoff. The software tool PAIREF provides automation of the protocol and associated analysis. Support for phenix.refine as a refinement engine has recently been implemented in the program. This feature is presented here using previously published data for thermolysin. The results demonstrate the importance of the complete cross-validation procedure to obtain a thorough and unbiased insight into the quality of high-resolution data.

1. Introduction  

During diffraction data processing, a cutoff is usually applied to reject high-resolution data that do not improve the model during structure refinement. In recent decades, a number of criteria have been used to decide on this cutoff (Karplus & Diederichs, 2015 ▸). Nowadays, paired refinement is considered to be the optimal approach for the determination of this parameter (Karplus & Diederichs, 2012 ▸; Diederichs & Karplus, 2013 ▸). In brief, a conservative cutoff has to be chosen first to secure reliable data. Data from higher resolution shells are added in a stepwise process to the model refinement and their impact on the model quality is verified. Such an approach is time-consuming and prone to errors when no automation is available. Paired refinement is particularly sensible in the later stages of structure refinement when the decision on the refinement program has already been made.

Recently, we developed an automatic tool (Malý et al., 2020 ▸) for paired refinement that uses REFMAC5 (Murshudov et al., 2011 ▸) for structure refinement. PAIREF provides comprehensive data analysis together with merging statistics, correlation coefficients (for example CC_work and CC*) and indicators of the stability of structure refinement. Here, we present a new feature of PAIREF: a module that performs structure refinement with phenix.refine (Afonine et al., 2012 ▸). The algorithm does not differ from that relying on REFMAC5. Structure-refinement parameters for phenix.refine can be specified in detail through a definition file (option --def setting.def). Besides the current implementation of paired refinement in the Phenix package (Liebschner et al., 2019 ▸), our tool provides additional features, for example a complete cross-validation procedure (Brünger, 1993 ▸; Jiang & Brünger, 1994 ▸). For each set of test reflections, the paired refinement protocol is run in parallel, and averaged data-quality indicators are reported. Both the standard and the complete cross-validation procedure are shown for test data. Moreover, a graphical user interface (Fig. 1 ▸) has recently been developed to simplify job execution.

Figure 1.

PAIREF graphical user interface set for the execution of run 1.

2. Materials and methods  

One of the previously reported cases where paired refinement using REFMAC5 proved to be helpful was the crystal structure of thermolysin. In the previous report (Winter et al., 2018 ▸), the initial high-resolution cutoff was set to 1.8 Å and reflections were added in thin shells with a width of 0.01 Å. A decrease in R _gap (R _gap = R _free − R _work) was observed up to a resolution of 1.56 Å. Similarly, we carried out paired refinement while adding shells with a width of 0.10 Å, referred to as run 0 in this manuscript (Malý et al., 2020 ▸). The R _free values systematically decreased up to a resolution of 1.5 Å, which indicates model improvement. Thus, we suggested cutting the data at this resolution level. Here, we show the results from paired refinement carried out with PAIREF using phenix.refine (Phenix version 1.16-3546) instead of REFMAC5.

We performed three distinct runs of PAIREF using the previously reported diffraction data for thermolysin. The diffraction images were processed with xia2 (Winter, 2010 ▸) employing DIALS (Winter et al., 2018 ▸) and AIMLESS (Evans & Murshudov, 2013 ▸) at 1.5 Å resolution in space group P6₁22. The input model for all runs originated from the structure of thermolysin (PDB entry 3n21; Behnen et al., 2012 ▸) with water molecules. To remove model bias, the atomic coordinates were perturbed by an average of 0.25 Å and all ADPs were set to their average value with phenix.pdbtools (Liebschner et al., 2019 ▸). Subsequently, restrained refinement was performed with phenix.refine at a resolution of 1.8 Å, converging sufficiently in 12 cycles. We performed three PAIREF runs: run 1, a standard run with the addition of high-resolution shells with a width of 0.10 Å; run 2, a fine-sliced standard run with a width of 0.01 Å; and run 3, the complete cross-validation procedure using all 20 sets of test reflections with a shell width of 0.10 Å. As an example, the command to launch run 1 (in the Unix shell or Phenix Command Prompt) is cctbx.python -m pairef --XYZIN 3n21_edit05_shaken.pdb --HKLIN thermc_merged.mtz -u thermc_unmerged.mtz --phenix --project thermc_step0-10A_phenix --prerefinement-ncyc 12 -i 1.8 -r 1.7,1.6,1.5,1.4; the execution of this run using the graphical interface is also shown in Fig. 1 ▸.

The results are shown in Fig. 2 ▸. The related merging statistics and details of run 0 have previously been published (Malý et al., 2020 ▸).

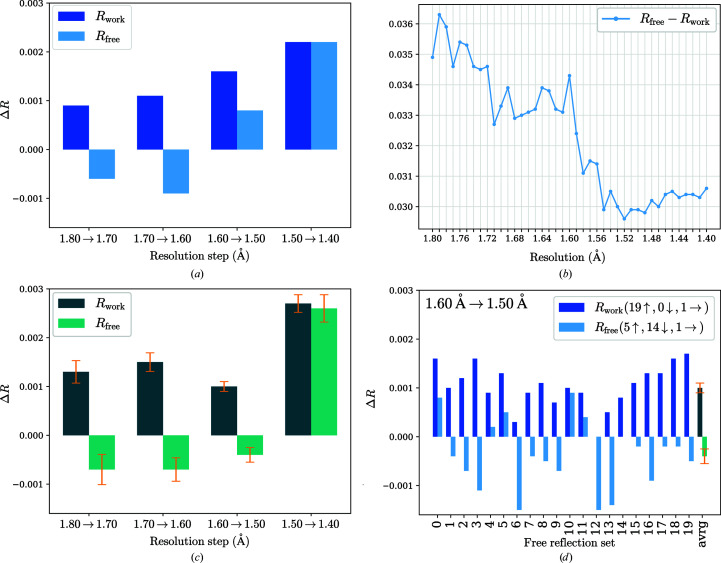
Figure 2.

Report plots given by PAIREF from three different runs of paired refinement using phenix.refine with the thermolysin data. The differences in the overall R values were obtained as follows: for each incremental step of resolution increase X→Y, the R values were calculated at the lower resolution X. (a) Run 1: differences in the overall R values; resolution shells with a width of 0.10 Å were added stepwise. R _free decreases up to 1.60 Å resolution, indicating model improvement. (b) Run 2: graph of R _gap calculated using data up to 1.8 Å resolution depending on the high-resolution cutoff; resolution shells with a width of 0.01 Å were added stepwise. Minimal R _gap is observed at 1.52 Å resolution. (c) Run 3: differences in the overall R values averaged over all 20 sets of test reflections. The standard error of the mean is shown in orange. (d) Run 3: differences in the overall R values relating to all 20 sets of test reflections for the incremental step of resolution from 1.6 to 1.5 Å. Despite the increasing R _free value while using the original set (test flag equals 0) and four other sets, R _free decreases for 14 sets. After averaging over all 20 sets, a decreasing trend is observed for this resolution shell.

3. Results and discussion  

Paired refinements using the thermolysin data demonstrate the differences that may appear using various refinement engines together with the importance of the complete cross-validation procedure (Fig. 2 ▸). Results from the individual runs, run 0 (REFMAC5, 0.10 Å step), run 1 (phenix.refine, 0.10 Å step), run 2 (phenix.refine, 0.01 Å step) and run 3 (phenix.refine, 0.10 Å step, complete cross-validation), vary in the suggestion of cutoff choice: 1.5, 1.6, 1.52  and 1.5 Å, respectively. For instance, we obtain different suggestions with phenix.refine and REFMAC5 (runs 0 and 1) while using the standard scenario, i.e. a 0.10 Å step and exclusion of the original set of test reflections (test flag equals 0). Moreover, the complete cross-validation procedure (run 3) suggests a higher cutoff, at 1.5 Å, than the standard run 1. As the former provides more general and meaningful insight into the quality of high-resolution data (Figs. 2 ▸ c and 2 ▸ d), it leads us to a final decision on the high-resolution cutoff at 1.5 Å resolution. This choice is in agreement with the fine-sliced run 2, where the R _gap value is minimal at 1.52 Å (Fig. 2 ▸ b). The last resolution shell (1.6–1.5 Å) merging statistics are as follows: I/σ(I) = 0.8, R _p.i.m. = 0.598, CC_1/2 = 0.445, completeness 91.8% (Malý et al., 2020 ▸).

PAIREF now supports both of the most frequently used refinement programs. The refinement approach of phenix.refine differs from that of REFMAC5 in several aspects (Shabalin et al., 2018 ▸), such as bulk-solvent modeling (Weichenberger et al., 2015 ▸), second-derivatives approximation and separate refinement of coordinates and ADPs. Thus, certain variations in the paired refinement results could be expected. The use of PAIREF is not intended as a tool to decide on the choice of the refinement program, but rather as a step in structure refinement. Both refinement engines specifically treat special cases such as twinning (Campeotto et al., 2018 ▸), extremes of resolution (Headd et al., 2012 ▸; Kovalevskiy et al., 2018 ▸), complex NCS and mixed anistropic/isotropic ADP refinement etc. Hence, the support for multiple refinement programs in PAIREF can be useful when particular data qualities need to be addressed differently (Švecová et al., 2021 ▸).

The complete cross-validation procedure is recommended for thorough determination of the proper resolution cutoff. The information value of the PAIREF analysis could be further increased by the implementation of a statistic which is independent of the selection of test reflections: R _complete (Luebben & Gruene, 2015 ▸). A detailed description of the PAIREF program and its algorithm, output and possibilities is provided in the primary reference (Malý et al., 2020 ▸) and at the web page https://pairef.fjfi.cvut.cz.

Funding Statement

This work was funded by Ministerstvo Školství, Mládeže a Tělovýchovy grants CZ.02.1.01/0.0/0.0/16_019/0000778 , CZ.02.1.01/0.0/0.0/15_003/0000447, and CZ.1.05/1.1.00/02.0109; Grantová Agentura České Republiky grant 18-10687S ; Akademie Věd České Republiky grant 86652036; České Vysoké Učení Technické v Praze grant SGS19/189/OHK4/3T/14.