Characterizing Intra-soma Diffusion with Spherical Mean Spectrum Imaging

Abstract

Most brain microstructure models are dedicated to the quantification of white matter microstructure, using for example sticks, cylinders, and zeppelins to model intra- and extra-axonal environments. Gray matter presents unique micro-architecture with cell bodies (somas) exhibiting diffusion characteristics that differ from axons in white matter. In this paper, we introduce a method to quantify soma microstructure, giving measures such as volume fraction, diffusivity, and kurtosis. Our method captures a spectrum of diffusion patterns and scales and does not rely on restrictive model assumptions. We show that our method yields unique and meaningful contrasts that are in agreement with histological data. We demonstrate its application in the mapping of the distinct spatial patterns of soma density in the cortex.

1. Introduction

Biophysical models utilizing diffusion magnetic resonance imaging (dMRI) are powerful tools for mapping brain microstructure, affording insights into tissue architecture [1–5] and revealing pathological and developmental patterns [6]. The focus of most microstructure models is white matter, where water molecules diffuse directionally. In gray matter, the microstructure is more heterogeneous, involving somas (cell bodies), dendrites, glial cells, unmyelinated axons, etc. Models dichotomizing gray matter signal as either extra-neurite or intra-neurite suffer from model simplification and are bound to bias microstructure estimates.

It has been shown for the first time in [7] that intra-soma diffusion can be modeled as a separate compartment distinct from intra-neurite and extra-neurite compartments. The soma and neurite density imaging (SANDI) [7] model relies on the assumptions that extra-neurite diffusion is isotropic and that intra-soma diffusivity is similar to that of free water. These assumptions do not hold in practice as extra-neurite diffusion are shown to be anisotropic [2,4,5] and intra-soma diffusion is isotropic and restricted [8]. In this paper, we demonstrate that spherical mean spectrum imaging (SMSI) [1,2] can be extended to quantify intra-soma diffusion. SMSI captures a spectrum of diffusion patterns from coarse to fine scales. We extended SMSI for quantification of soma microstructure, giving measures such as volume fraction, diffusivity, and kurtosis. Our method captures a spectrum of diffusion patterns and scales and does not rely on restrictive assumptions, such as fixed compartment number and diffusivity. We show that our method yields unique and meaningful contrasts that are in agreement with histological data. We demonstrate its application in mapping the distinct spatial patterns of soma density in the cortex.

2. Method

2.1. Soma Compartment Model

As observed in the spherical mean technique (SMT) [3], the spherical mean of the dMRI signal ${\overline{S}}_b$ only depends on b-value and diffusivity but not the fiber orientation distribution. For a micro-environment with diffusion that can be represented using a tensor model, the spherical mean is defined as

$$\frac{{\overline{S}}_b}{S_0}={\int }_0^1\text{exp}\left(-b{\lambda }_{\perp }\right)\text{exp}\left(-b\left({\lambda }_{\parallel }-{\lambda }_{\perp }\right)x^2\right)dx$$ (1)

$$={\int }_0^1{h}_b\left({\lambda }_{\parallel },{\lambda }_{\perp },x\right)dx={\overline{h}}_b\left({\lambda }_{\parallel },{\lambda }_{\perp }\right),$$ (2)

where λ_∥ is the parallel diffusivity and λ_⊥ is the perpendicular diffusivity [3]. SMSI [1] views the spherical mean as a linear combination of contributions from multiple micro-environments, i.e.,

$${\overline{S}}_b=S_0\sum _i\nu \left[i\right]{\overline{h}}_b\left({\lambda }_{\parallel }\left[i\right],{\lambda }_{\perp }\left[i\right]\right).$$ (3)

The i-th micro-environment is associated with parallel diffusivity λ_∥[i], perpendicular diffusivity λ_⊥[i], and volume fraction ν[i]. Different sub-spectra can be derived from the spherical mean spectrum as follows:

• The intra-neurite (neu) diffusion sub-spectrum with high parallel and low to no perpendicular diffusion, typical in neurites (axons and dendrites) and commonly represented as “sticks” or cylinders with τ⁻²λ_∥[i] ≥ λ_⊥[i] ≥ 0 where τ is the geometric tortuosity [9].

• The extra-cellular (ec) diffusion sub-spectrum with high parallel and mod-erate perpendicular diffusion, typical in extra-cellular space and commonly represented as zeppelins with λ_∥[i] > λ_⊥[i] > τ⁻²λ_∥[i]. Unlike SANDI [7], this condition allows the extra-cellular compartment to be anisotropic, as widely shown in [1,4,5].

• The intra-soma (is) diffusion sub-spectrum with slow isotropic diffusion, represented as spheres with diffusion that is more restricted than free water [7], i.e., λ_∥[i] > λ_⊥[i] ≤ 1 μm²/ms. This range covers typical diffusivity within cell bodies [8].

• The fast-isotropic (fi) diffusion sub-spectrum including free-water diffusion, represented by spheres with 2 μm²/ms ≤ λ_∥[i] > λ_⊥[i] ≤ 3 μm²/ms.

Figure 1 illustrates the model.

Fig. 1. Model.

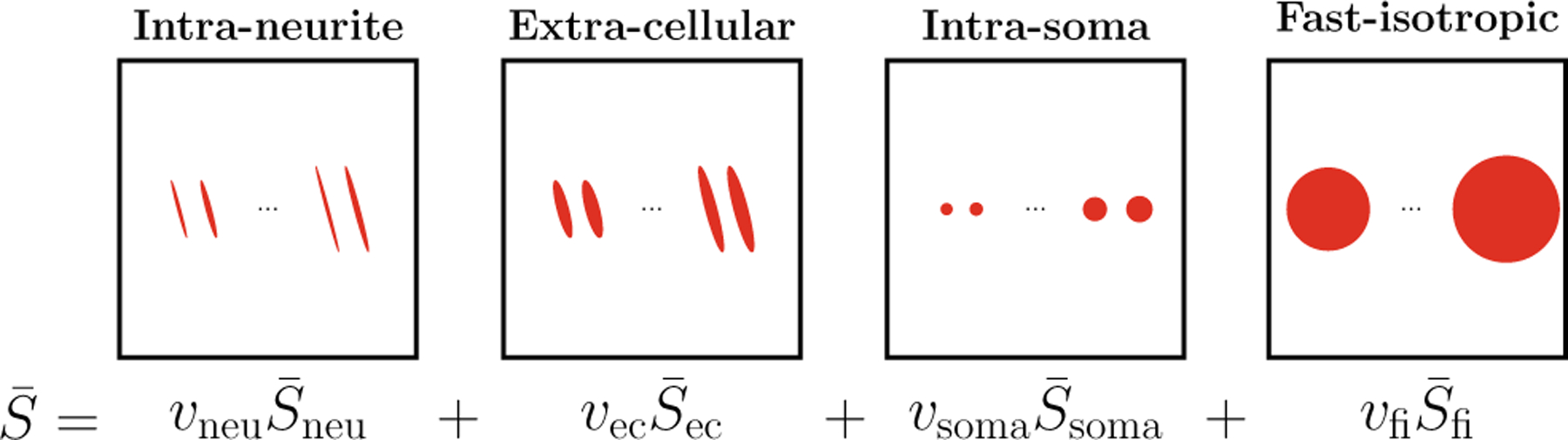
The spherical mean signal is contributed by the intra-neurite (neu), extra-cellular (ec), intra-soma (soma), and fast-isotropic (fi) diffusion compartments. SMSI represents each compartment with atoms of multiple diffusivity values.

2.2. Implementation Details

SMSI solves for the volume fraction ν[i] via elastic net

$$\nu =\underset{\nu ⪰0}{argmin}{\Vert \left(\begin{array}{c}A\\ \sqrt{{\gamma }_2}I\end{array}\right)\nu -\left(\begin{array}{c}\overline{S}\\ 0\end{array}\right)\Vert }_2^2+{\gamma }_1{\Vert \text{diag}\left(w\right)\nu \Vert }_1,$$ (4)

where $A=\left[{\overline{h}}_b\left({\lambda }_{\parallel }\left[1\right],{\lambda }_{\perp }\left[1\right]\right),{\overline{h}}_b\left({\lambda }_{\parallel }\left[2\right],{\lambda }_{\perp }\left[2\right]\right),\dots \right]\in {ℝ}^{n\times p}$ is a dictionary with atoms representing spherical mean signals of micro-environments covering the different sub-spectra as described above. n is the number of b-shells and p is the number of atoms. w is a weight vector and γ₁ and γ₂ are tuning parameters that control the contributions of the ℓ1 and ℓ2 regularization terms, respectively.

It has been reported that the spherical mean signal from linear encoding dMRI can be ambiguous [10]. That is, within the typical range of b-values (b ≤ 3000 s/mm²), the spherical mean signal of an anisotropic tensor can be indistinguishable from the spherical mean signal of a combination of multiple isotropic tensors with different diffusivity values. We address this problem by using the full direction-sensitized diffusion signal to disambiguate between anisotropic and isotropic diffusion.

Weighting with Full Signal Spectrum (FSS):

The full diffusion signal S can be represented as the spherical convolution between the fiber orientation distribution function (fODF) and the kernel h. Using spherical harmonics (SHs), S can be expressed as the product of rotational SHs, H, the SH of even order up to order L, ${\mathcal{Y}}_L$, and the SH coefficients of the fODF, φ. In line with [9] and the spirit of SMSI, let $\mathcal{H}\left({\lambda }_{\parallel }\left[i\right],{\lambda }_{\perp }\left[i\right]\right)$ be the matrix of rotational SHs of h(g|ω, λ_∥[i], λ_⊥[i]), and φ_i be the SH coefficients of the fODF corresponding to h(g|ω, λ_∥[i], λ_⊥[i]), the full signal can be discretized as [11]

$$S\approx \sum _i\mathcal{H}\left({\lambda }_{\parallel }\left[i\right],{\lambda }_{\perp }\left[i\right]\right){\mathcal{Y}}_L{\phi }_i=\mathcal{B}\Phi .$$ (5)

$\mathcal{B}$ can be seen as a dictionary matrix and Φ, a matrix containing φ_i, ∀i, can be solved with Tikhonov regularization [9]

$$\underset{\Phi }{\mathit{\text{min}}}{\Vert \left(\begin{array}{c}\mathcal{B}\\ \sqrt{{\gamma }_3}\text{diag}\left(w^{\prime }\right)\end{array}\right)\Phi -\left(\begin{array}{l}S\hfill \\ 0\hfill \end{array}\right)\Vert }_2^2.$$ (6)

To ensure that the fODF of anisotropic atoms does not degenerate to become isotropic, we first solve (6) with weight vector w′ set to one for all atoms and reapply (6) with w′ set to a higher value for any atom with GFA < 0.3. This approach penalizes low GFA anisotropic fODF and disambiguates anisotropic and isotropic diffusion in case of degeneracy [1]. From the final solution, a set of weights, ν_FSS, is calculated as the 0-th order SH coefficient from Φ.

Weighting with Spherical Mean Spectrum (SMS):

Similar to [1], we first use the spherical mean signals of shells with b ≤ 1000 s/mm² in solving (4) with w set to one for all atoms. This will help improve the estimates of the volume fractions of fast isotropic diffusion atoms as the associated signals decay rapidly and become trivial at higher b value. The solution to this step results in a set of weights, ν_SMS.

Iterative Estimation:

We then solve for the volume fractions using all b-shells via iterative re-weighted elastic net, where in the j-th iteration we have

$${\nu }_j=\underset{{\nu }_j⪰0}{argmin}{\Vert \left(\begin{array}{c}A\\ \sqrt{{\gamma }_2}I\end{array}\right){\nu }_j-\left(\begin{array}{c}\overline{S}\\ 0\end{array}\right)\Vert }_2^2+{\gamma }_1{\Vert \text{diag}\left(w_j\right){\nu }_j\Vert }_1,$$ (7)

where $w_j\left[i\right]=\frac{1}{\xi +{\nu }_{j-1}\left[i\right]}$ with ξ being a constant and ν₀ is computed as the element-wise geometric mean of ν_FSS and ν_SMS. Regularization parameters γs are determined via grid search as in [1].

2.3. Intra-soma Diffusion Properties

From ν, the volume fraction of the intra-soma compartment can be determined. Note that intra-soma diffusion can be characterized by multiple slow isotropic diffusion atoms with different diffusivity values and hence deviates from Gaussianity. To characterize diffusional non-Gaussianity, we derive a soma kurtosis model from [12]

$$\text{ln\hspace{0.17em}}{\overline{S}}_{\text{soma }}\left(b\right)=-b{\lambda }_{\text{soma }}+\frac{b^2}{6}{K}_{\text{soma }}{\lambda }_{\text{soma}}^2,$$ (8)

where ${\overline{S}}_{\text{soma}}$ is the normalized spherical mean signal contribution from the soma compartment, λ_soma is the soma diffusivity, and K_soma is the soma kurtosis.

3. Experiments

For evaluation, we used the dMRI data of 4 healthy adults, each with 12, 24, and 48 diffusion-weighted images respectively for b = 1000, 2000, 3000 s/mm² and 6 B0 images. Each diffusion-weighted image has an isotropic resolution of 1.5mm. The images were corrected for motion and off-resonance artifacts [13]. SMSI parameters were set according to [1].

3.1. Microstructure

Figure 2 presents the parametric maps for a representative subject. In white matter, the intra-neurite volume fraction (v_neu) is high, in line with previous observations that these regions contain mostly myelinated axons [2,4,14], giving a clear contrast for major fiber bundles such as forceps major, forceps minor, cortical spinal tract. The extra-cellular volume fraction (v_ec) is higher in superficial white matter and some gray matter regions. The fast-isotropic diffusion volume fraction (v_fi) is high in the ventricles and peripheral regions where there is little to no microscopic barriers to water diffusion.

Fig. 2. Tissue Microstructure.

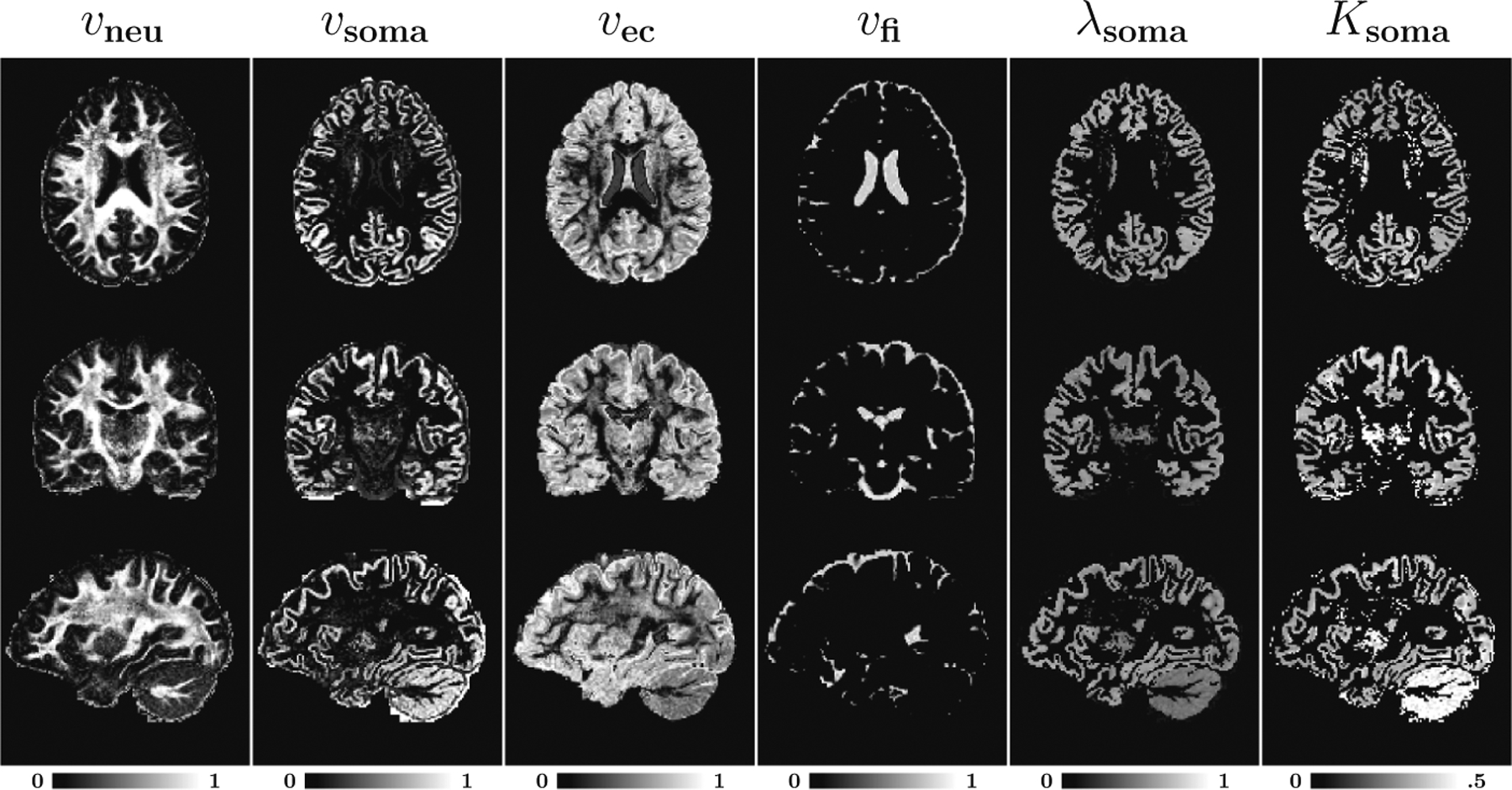
Microstructural properties of a representative subject: Intra-neurite volume fraction (v_neu), intra-soma volume fraction (v_soma), extra-cellular volume fraction (v_ec), fast-isotropic diffusion volume fraction (v_fi), soma diffusivity (λ_soma), and soma kurtosis (K_soma).

The intra-soma volume fraction (v_soma) is higher in the cortical ribbon. The typical value is between 0.1–0.2, which are in line with observations in [7,15]. The soma diffusivity (λ_soma) is mostly around 0.6 μm²/ms in the cortex and is slightly lower in the cerebellum. The soma kurtosis (K_soma), although small, is non-zero and is highest in the cerebellar gray matter. This could be due to the unique structure of the cerebellar cortex with a dense layer of granule cells and Purkinje cells with complex dendritic spines [8].

3.2. Histology

Figure 3 illustrates the similarity between our results and ex-vivo histological images. The intra-neurite volume fraction map is strikingly similar to myelin stain. The intra-soma volume fraction map is similar to cell nuclei stain, with higher values in the cerebral and cerebellar gray matter. These results demonstrate that our method provides biologically meaningful contrasts resembling ex-vivo stains. This also underscores the importance of dMRI as an in vivo histology tool that can avoid the limitations of ex-vivo staining, such as distortions caused by the slicing and staining processes.

Fig. 3. Resemblance to Stained Sections.

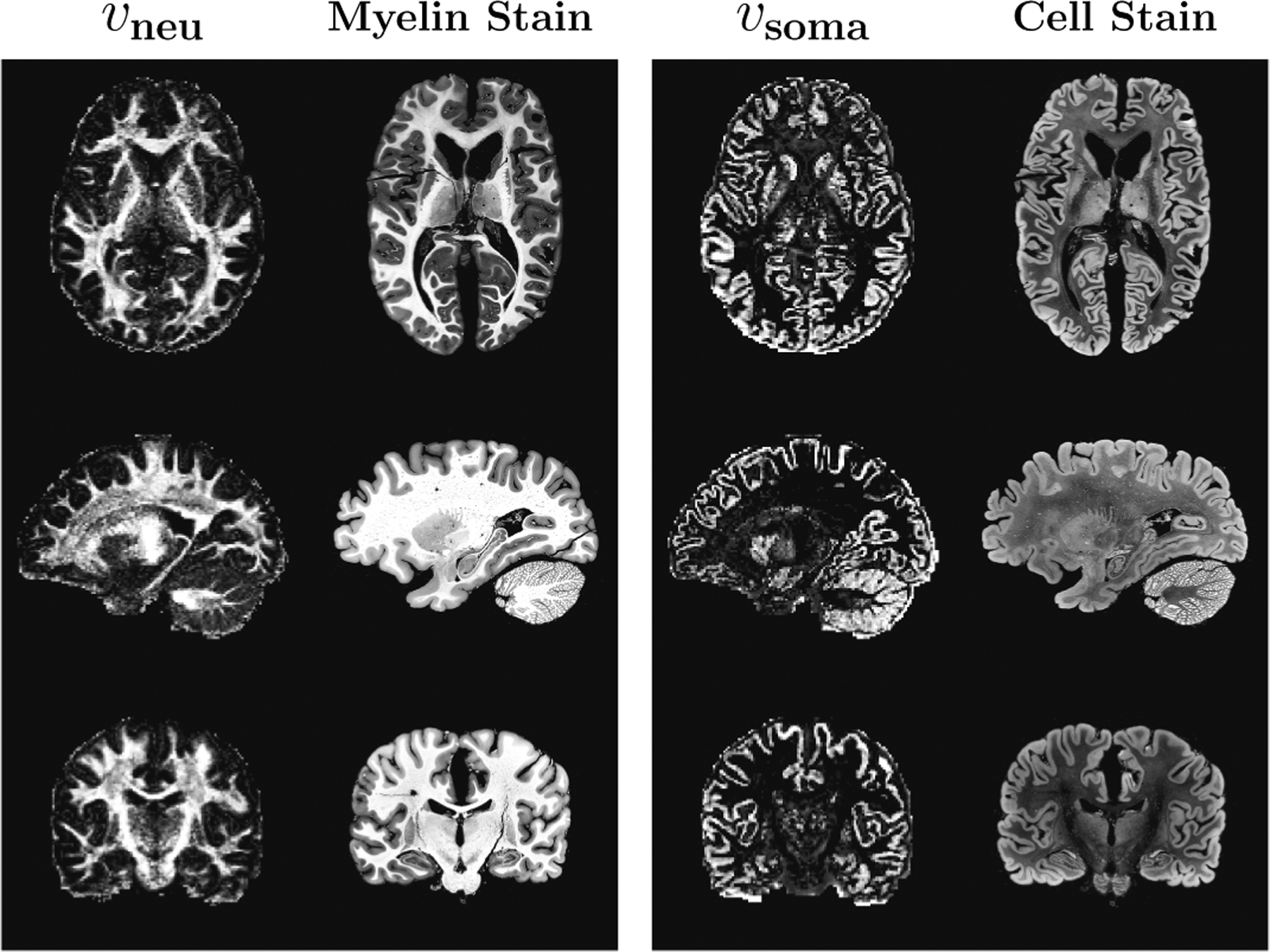
Intra-neurite volume fraction (v_neu), which provides contrast related to neurite density, poses striking similarity with myelin stain. Intra-soma volume fraction (v_soma), which provides information related to soma density, shows remarkable resemblance with cell stain. Stained sections were obtained from https://msu.edu/~brains/brains/human/index.html.

3.3. Cortical Patterns

We constructed the cortical surfaces from the T1- and T2-weighted images as described in [16,17] and mapped the parametric maps onto the cortical surface as described in [18]. Figure 4 shows the average maps of 4 healthy adults. The intra-neurite volume fraction is higher in the motor and somatosensory areas, confirming the pattern observed in [19]. On the other hand, the soma maps reveal distinct patterns, with relatively low values in the motor area, but higher values in the occipital and temporal lobes.

Fig. 4. Cortical Patterns.

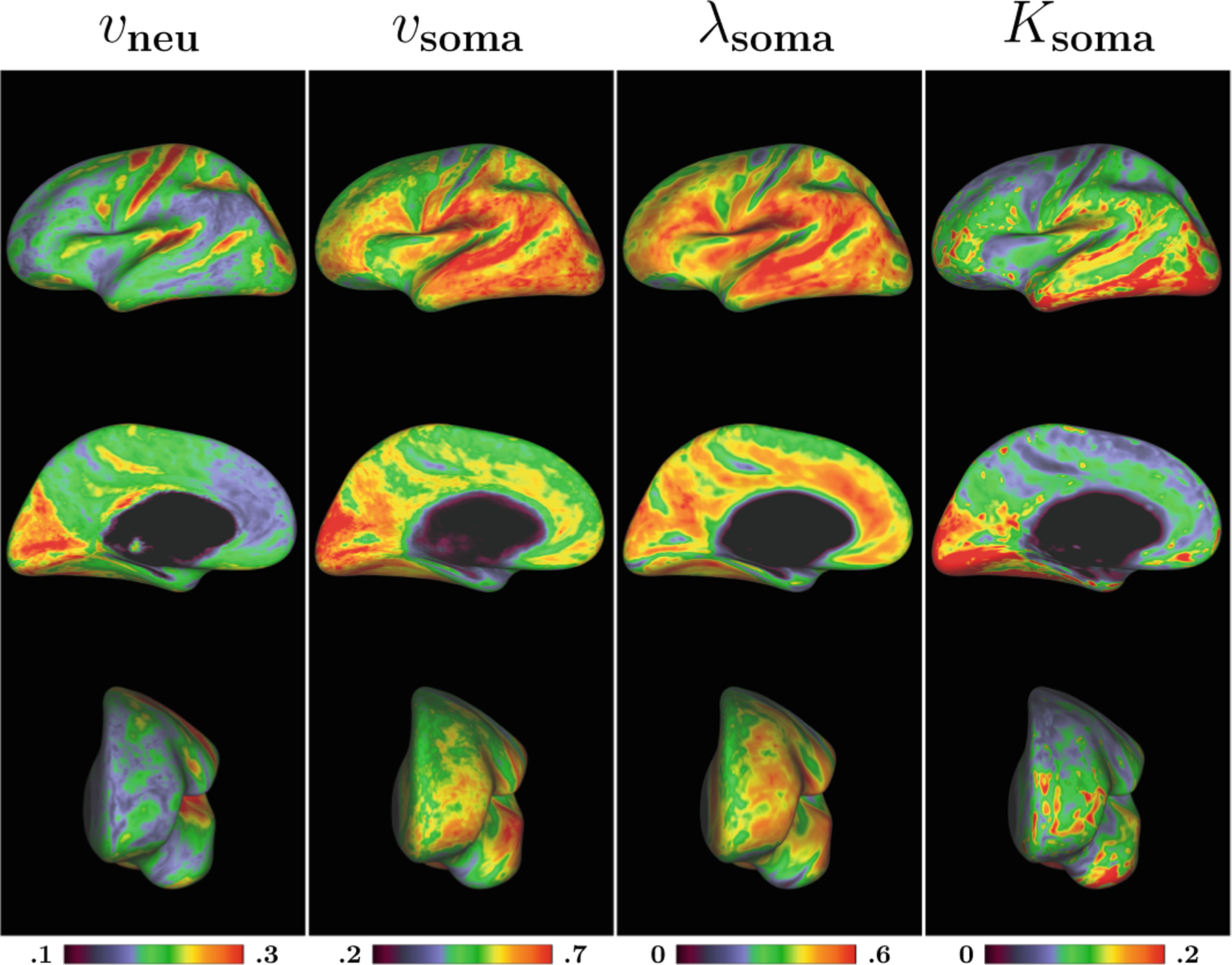
Average cortical maps of intra-neurite volume fraction (v_neu), intra-soma volume fraction (v_soma), soma diffusivity (λ_soma), and soma kurtosis (K_soma) of 4 healthy adults.

3.4. Number of Shells

To evaluate the effect of the number of b-shells on microstructure estimation using our model, we acquired a 21-shell data of a healthy adult with b-values ranging from 500 s/mm² to 3000 s/mm² with step size 125 s/mm². There are 4 to 24 diffusion-weighted (DW) images in each shell, and 13 non-DW images, resulting in a total of 307 volumes. We fitted our model to 4 different sampling schemes:

1. The 21-shell dataset consisting of all volumes;

2. The 11-shell dataset with b-values from 500 s/mm² to 3000 s/mm² with step size 250 s/mm²;

3. The 6-shell dataset with b-values from 500 s/mm² to 3000 s/mm² with step size 500 s/mm²;

4. The 3-shell-1000 with b-values from 1000 s/mm² to 3000 s/mm² with step size 1000 s/mm²; and

5. The 3-shell-500 dataset with b-values from 500 s/mm² to 2500 s/mm² with step size 1000 s/mm².

In Fig. 5, indices from different schemes were compared with those from the reference (21-shell). The higher number of shells, the closer the results to the reference. However, even at only 3 b-shells, almost all indices are comparable to the reference with correlation coefficient (R) greater than 0.95. The only exception is v_fi from the 3-shell-1000 scheme, showing slightly lower R due to the lack of a lower b-shell for effective estimation of the fast isotropic diffusion compartment. Nevertheless, the correlation coefficient R > 0.89 is still sufficiently high for most practical situations. The results demonstrate that our method is suitable for datasets with at least 3 b-shell, such as the Human Connectome Project (HCP) [20] and the Baby Connectome Project (BCP) [21].

Fig. 5. Number of b-Shells.

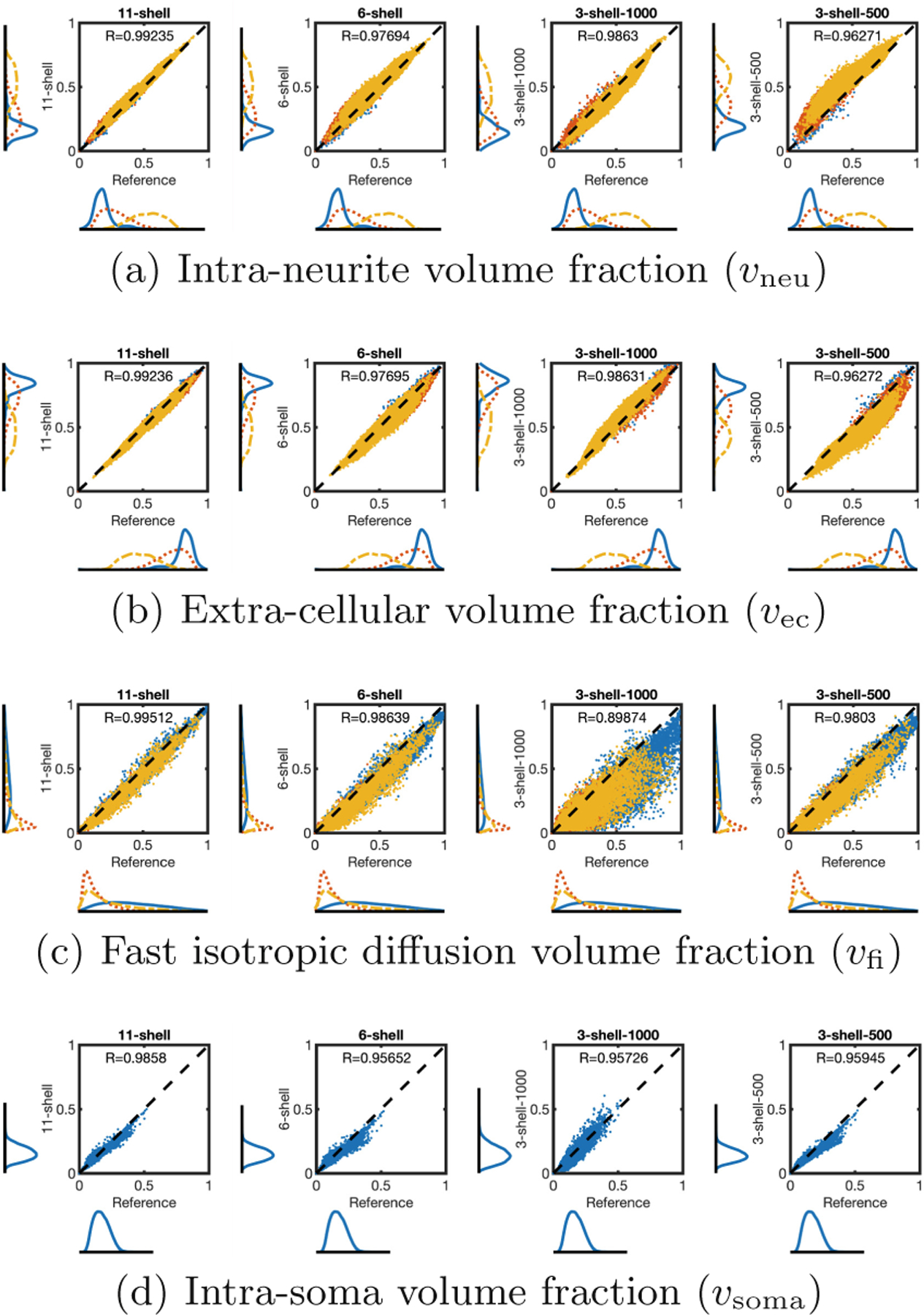
Scatter plots and histograms of representative indices given by sampling schemes 11-shell, 6-shell, 3-shell-1000, and 3-shell-500 with 21-shell as the reference. Voxels are classified as CSF (red), gray matter (blue), or white matter (yellow). For better visibility, only one in every six voxels is shown. Since intra-soma volume fraction is negligible in white matter and CSF, only gray matter voxels are shown in (d).

4. Conclusions

We have presented a method to characterize soma diffusion properties and have shown that biologically meaningful contrasts resembling histological data can be produced. Future work entails applying our method to investigating changes in the cerebral cortex in relation to development, aging, and diseases.