Few-shot learning creates predictive models of drug response that translate from high-throughput screens to individual patients

Abstract

Cell-line screens create expansive datasets for learning predictive markers of drug response, but these models do not readily translate to the clinic with its diverse contexts and limited data. In the present study, we apply a recently developed technique, few-shot machine learning, to train a versatile neural network model in cell lines that can be tuned to new contexts using few additional samples. The model quickly adapts when switching among different tissue types and in moving from cell-line models to clinical contexts, including patient-derived tumor cells and patient-derived xenografts. It can also be interpreted to identify the molecular features most important to a drug response, highlighting critical roles for RB1 and SMAD4 in the response to CDK inhibition and RNF8 and CHD4 in the response to ATM inhibition. The few-shot learning framework provides a bridge from the many samples surveyed in high-throughput screens (n-of-many) to the distinctive contexts of individual patients (n-of-one).

Translating biomarkers from basic research to clinical utility involves transfer of information across a series of contexts in which data are progressively harder to obtain. In vitro platforms such as human cell culture are amenable to high-throughput screening, yielding large datasets characterizing the molecular profiles of thousands of cell lines and their responses to millions of chemical compounds, genetic interventions or environments^1,2. Promising indications may progress to advanced culture systems and animal models^3,4, few of which are further evaluated in human cohorts and, ultimately, used in diagnosis and treatment of individual patients.

It is well known that drug-response predictions learned in cell-line or animal models do not always transfer to clinical contexts in a straightforward manner^5–7. For example, dual inhibition of epidermal growth factor receptor (EGFR) and vascular epidermal growth factor receptor (VEGFR) had been found to induce sustained tumor regression in a mouse model of EGFR-mutant, nonsmall-cell lung cancer⁸, whereas follow-up clinical studies failed to replicate such an effect⁹. Similarly, upregulation of the insulin-like growth factor 1 receptor gene (IGF1R) had been noted as a prominent marker of tamoxifen resistance in breast cancer cell lines¹⁰, whereas the seemingly opposite behavior—reduced IGF-1R protein levels—was observed in tamoxifen-resistant patients¹¹. It remains unclear whether such failures are caused by fundamental irreconcilable differences between biological contexts or missed opportunities to identify the correct markers that are likely to translate. A key challenge in marker selection is that the common signal is easily overwhelmed by context-specific patterns, especially given the very limited amounts of data available in patients relative to cell lines.

To improve biomarker transfer across contexts, we formulated a neural network model, translation of cellular response prediction (TCRP), using the technique of few-shot learning^12,13. Few-shot learning is an emerging method of transfer learning, a field that postulates that prior knowledge acquired in one problem domain can be reused and applied to solve different but related problems^14–16. Transfer learning has proven instrumental in fields such as linguistics, where people (and machines) can learn to speak a new language much more quickly if they have extensive prior knowledge of a related tongue, which can be transferred efficiently to the new one¹⁷. Recent applications in biomedicine include an improved ability to identify chemical compounds with biological activity¹⁸ or to classify tissue type and tumor grade in histopathological images¹⁹.

Few-shot learning aims to identify widely applicable input features by optimizing their transferability rather than their overall prediction accuracy as in conventional learning approaches (Methods). In an initial ‘pretraining’ phase (Fig. 1, top), the model is exposed to a variety of different predefined contexts, each of which is represented by numerous training samples. In a second ‘few-shot learning’ phase (Fig. 1, bottom), the model is presented with a new context not seen previously, and further learning is performed on a small number of new samples. Neural networks trained by this two-phase design have been shown to learn surprisingly rapidly in the new context relative to models trained by conventional means^20–23.

Fig. 1 |. Study design.

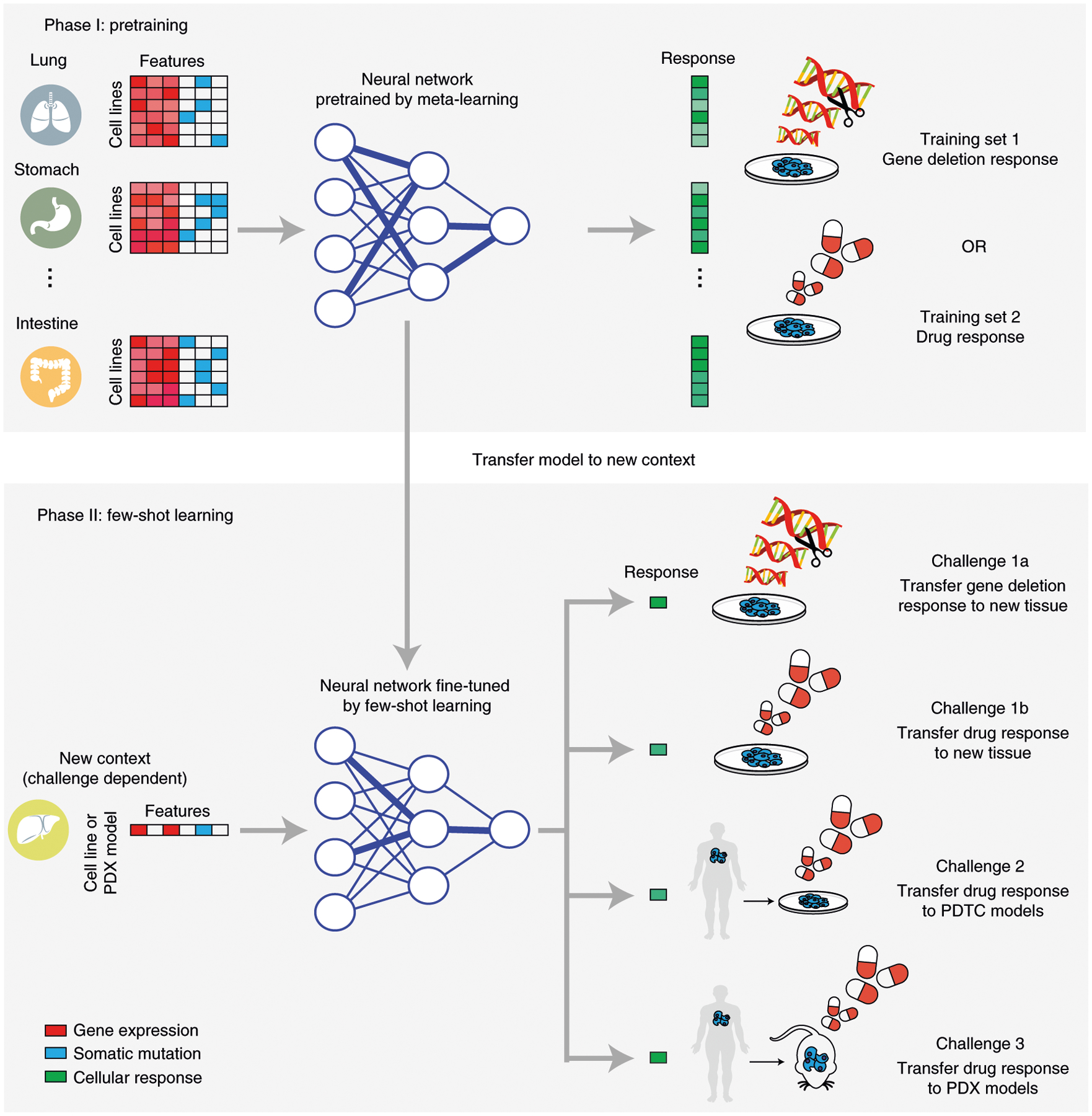
Three distinct translation challenges are considered. Each challenge involves a pretraining phase (top) based on cell-line response data across tissues, followed by a few-shot learning phase (bottom) in which data in the new context are presented for additional learning, one sample at a time. Challenge 1: transfer of CRISPR (challenge 1a) or drug (challenge 1b) response model for prediction in the context of a new tissue. Challenge 2: transfer of model to PDTCs in vitro. Challenge 3: transfer of model to PDXs in vivo.

In the present study, we applied the few-shot learning paradigm to three context-transfer challenges of high interest in predictive medicine: (1) transfer of a predictive model learned in one tissue type to the distinct contexts of other tissues; (2) transfer of a predictive model learned in tumor cell lines to patient-derived tumor cell (PDTC) cultures in vitro; and (3) transfer of a predictive model learned in tumor cell lines to the context of patient-derived tumor xenografts (PDXs) in mice in vivo (Fig. 1 and Table 1).

Table 1 |.

Summary of datasets used for challenges

	Pretraining phase				Few-shot learning phase
	Agent	Platform	Tissue	Source	Agent	Platform	Tissue	Source
1a	CRISPR	Cell line	19 types	DepMap	CRISPR	Cell line	1 of 9 typesa	DepMap
1b	Drug	Cell line	30 types	GDSC1000	Drug	Cell line	1 of 19 typesa	GDSC1000
2	Drug	Cell line	30 types	GDSC1000	Drug	PDX-derived cell lines	Breast	PDTC BioBank
3	Drug	Cell line	30 types	GDSC1000	Drug	Xenograft	4 of 6 types	PDX Encyclopedia

^aAll available tissue types used for pretraining; only types with >14 samples used for few-shot learning.

Results

Challenge 1: transfer across tissue types.

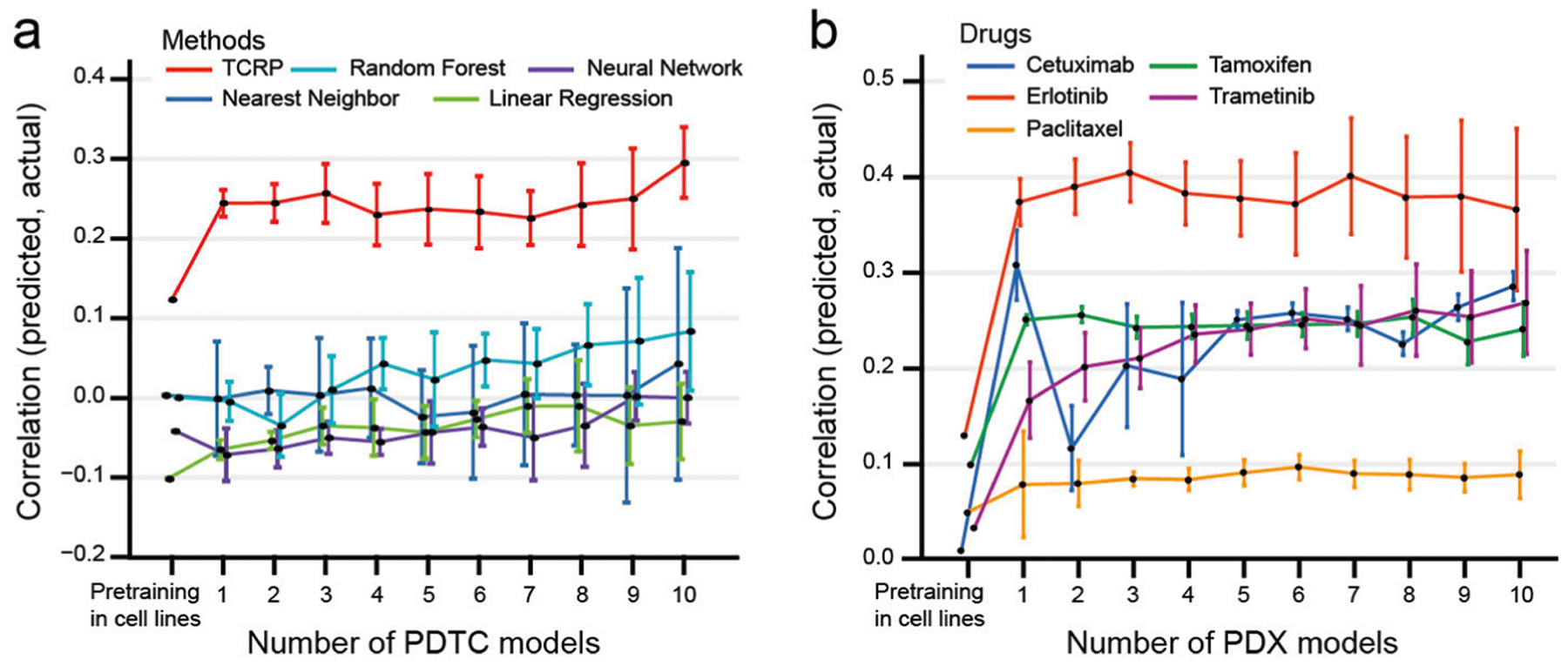
For the first challenge, we evaluated the ability of our TCRP model to predict the growth rates of tumor cell lines from a target tissue for which very few samples were available for learning. Data were taken from a recent survey of 335 human cell lines from 19 tissues, in which cell growth rates had been measured across a genome-wide panel of gene disruptions using clustered, regularly interspaced, short palindromic repeats (CRISPR). This resource has been called the Dependency Map, or DepMap (ref.¹; Methods and Table 1). For each cell line, this same survey had summarized the binary genotype status of genes (0 = unmutated or synonymous mutation; 1 = nonsynonymous mutation) and their quantitative messenger RNA abundance levels during nominal growth. For each CRISPR gene disruption (focusing on 469 genes with demonstrated tumor growth dependencies; Extended Data Fig. 1), we trained TCRP alongside a collection of conventional learning models to predict the growth responses of all cell lines. During this process, 1 of the 19 tissues was designated as the target. A training set was then created that included all cell lines from the other 18 tissues but only a small number of cell lines from the target tissue; the remaining target cell lines constituted the test set. TCRP was trained in two phases, first on the large number of cell lines from the 18 tissues (pretraining phase), and then on the small number of cell lines available from the target tissue (few-shot learning phase; Fig. 1 and Methods). Conventional models were trained using a standard one-phase training procedure, by pooling all samples designated as training, after which the model was evaluated on all samples designated a test. Key questions were how quickly a predictive model transfers to the new tissue, having been trained mainly on others, and to which tissues the model transfers worst/best.

Models displayed a range of prediction accuracies during pretraining, as assessed by fivefold cross-validation, with conventional random forests performing best (Extended Data Fig. 2a and Methods). However, when testing on the target tissue, no model performed better than random, demonstrating the difficulty posed by new contexts (Fig. 2a). We then entered into the few-shot learning phase. For conventional models, accuracy improved very slowly as samples from the new tissue were added to the training set. In contrast, TCRP improved rapidly, with an average gain of 829% in performance after examining only 5 additional samples (Fig. 2a). Tissues with the most improvement were the kidney, urinary tract and pancreas (Fig. 2b). For example, we observed a very high accuracy when predicting the response to CRISPR knockout of the gene encoding hepatocyte nuclear factor 1β (HNF1B), for which TCRP achieved a performance of 0.60 (Pearson’s correlation) in contrast to the second best approach (random forests, 0.19). The importance of HNF1B to tumor growth has been verified in multiple cancer types, including hepatocellular carcinoma, pancreatic carcinoma, renal cancer, ovarian cancer, endometrial cancer and prostate cancer²⁴.

Fig. 2 |. Transfer of predictive models across tissue types.

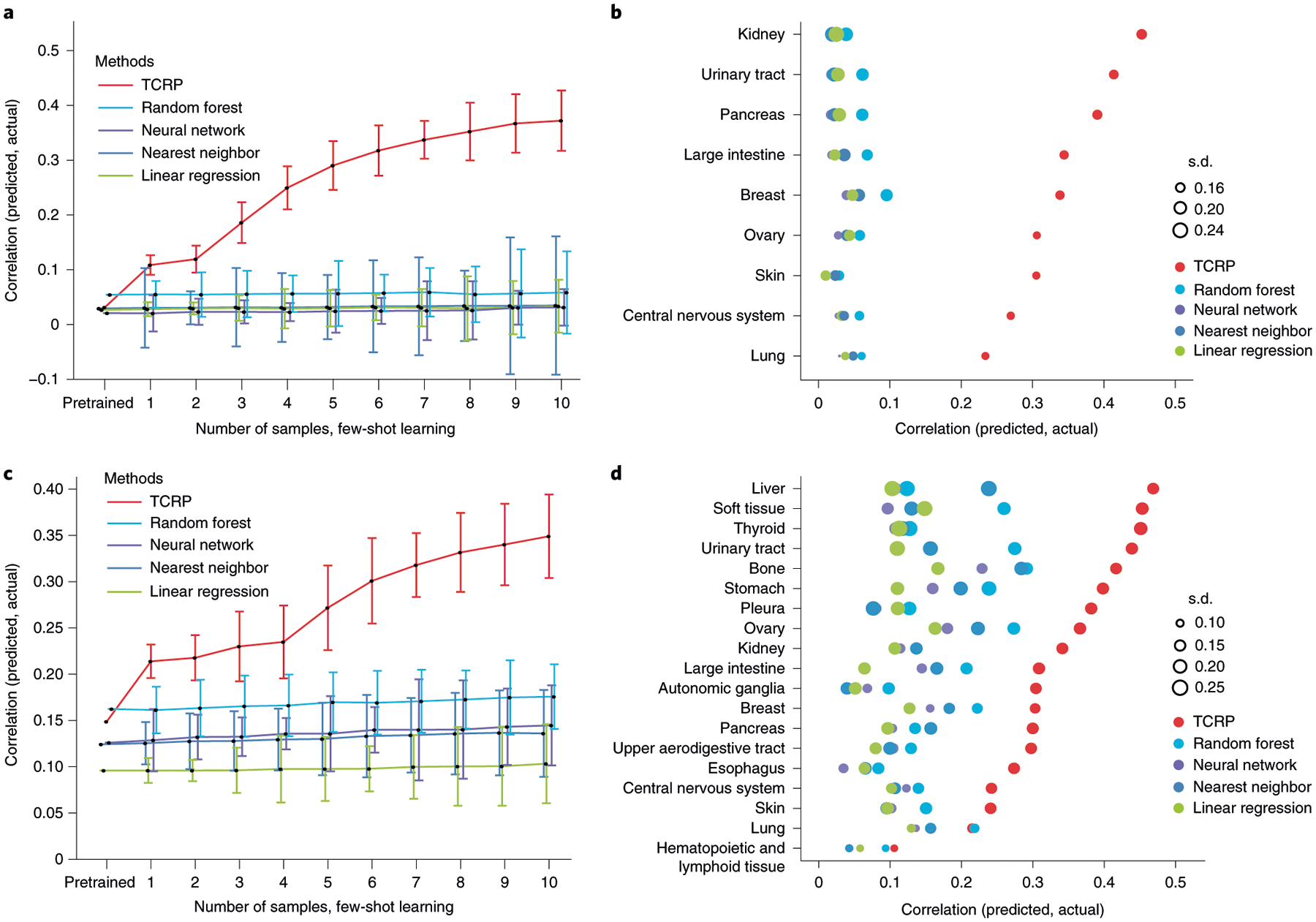
a, Challenge 1a. For each CRISPR gene knockout and target tissue, model accuracy is measured by Pearson’s correlation between predicted and actual drug responses, considering only the test samples from the target. The plot shows the average model accuracy across CRISPR knockouts (y axis, mean ± 95% confidence interval (CI)) as a function of the number of cell lines (from n = 0 cell lines to n = 10 cell lines) from the target tissue provided to the model during training (x axis), considering in total n = 335 cell lines with n = 469 gene disruptions. b, Model accuracy (x axis) is displayed separately for each tissue in challenge 1a (y axis). Accuracy is the average achieved when training includes five to ten samples of the target tissue. The accuracy s.d. is shown over all CRISPR gene knockouts (point size). c, As for a for models trained on perturbations with n = 199 targeted drugs and n = 1,001 cell lines. d, As for b for models trained on perturbations with targeted drugs.

We also conducted a related challenge 1b, in which cell growth response data were drawn from a high-throughput pharmacogenomic screen of 255 anti-cancer drugs (including both US Food and Drug Administration–approved and experimental compounds; Methods and Table 1) administered to each of 990 cancer cell lines encompassing 30 tissues. This dataset has been called the Genomics of Drug Sensitivity in Cancer (GDSC1000) resource². Similar to challenge 1a, but for each drug, TCRP was trained alongside conventional learning models to predict the growth sensitivity of cell lines using their molecular markers. As before, TCRP learned rapidly when switching to the target tissue, with the largest improvements seen when learning from the first few cell-line samples (Fig. 2c,d and Extended Data Fig. 2b). We found that the accuracy of drug predictions was correlated with the accuracy of CRISPR predictions across the tissues examined (Spearman’s ρ = 0.73, P = 0.01), with tissues such as the urinary tract generating highly accurate predictions in both settings, and tissues such as the central nervous system, skin and lung generating poor predictions.

Challenge 2: transfer to PDTCs.

Next, we studied whether models of drug response trained on cell lines could be transferred to preclinical contexts (challenge 2; Fig. 3a). For this challenge we used data on breast cancer PDTCs made available by Project Biobank⁴ (Methods and Table 1). In this previous study, tumors (n = 83) were biopsied, subjected to whole-exome and mRNA sequencing to generate molecular profiles, and implanted in immunodeficient mice. PDTCs were then isolated from the host mice and tested for drug responses in vitro. From these data we selected 50 drugs for which the protein targets were well characterized, with drugs administered to 15–19 PDTCs each. For each drug, TCRP was pretrained using the cell-line drug-response data from challenge 1b before switching context to PDTCs.

Fig. 3 |. Transfer of cell-line models to PDTC lines.

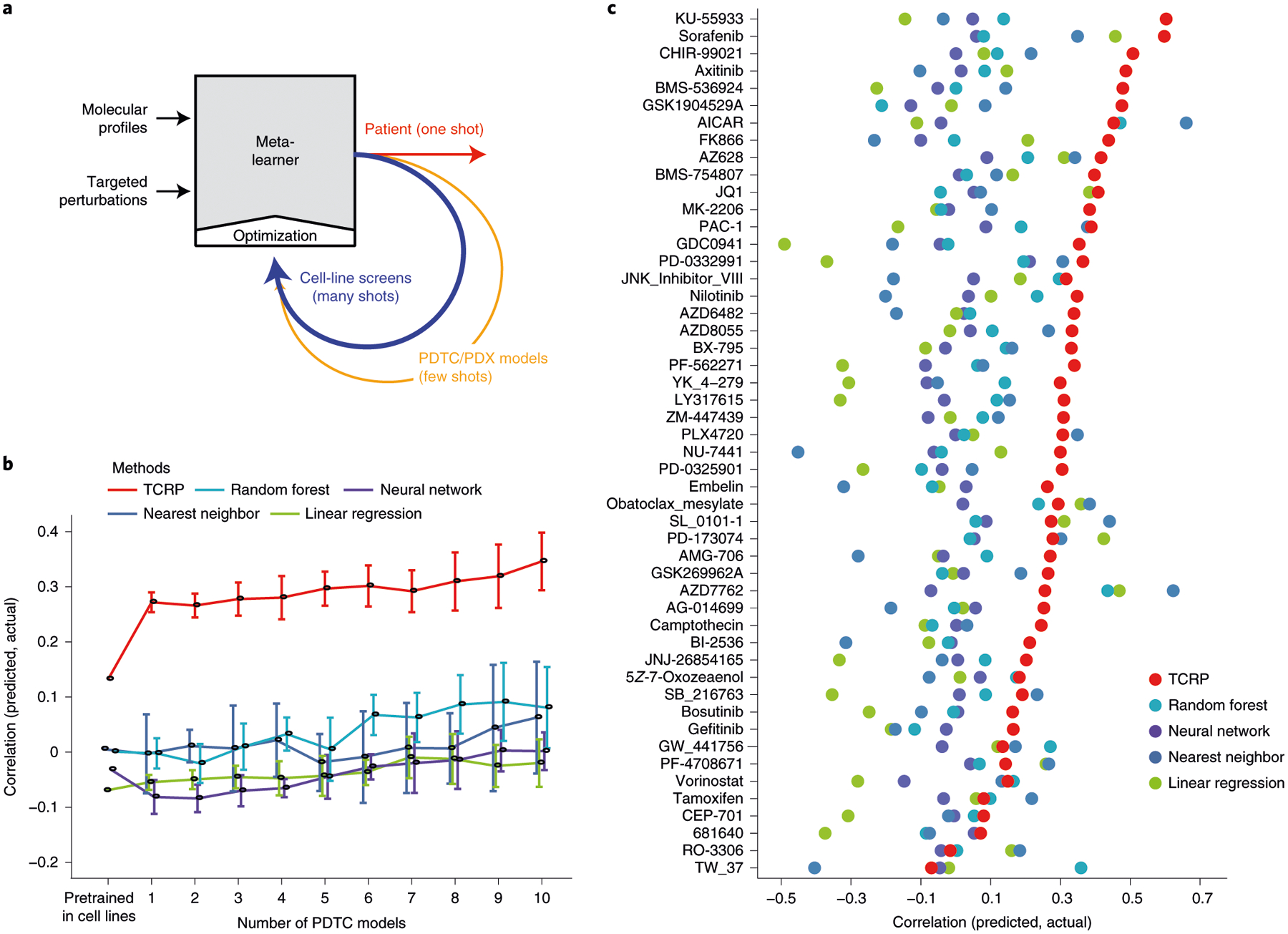
a, Schema for translating a predictive model from cell lines to patients using few-shot learning. The model is trained over successive rounds of data, each with fewer samples but closer to the desired clinical context. b, Challenge 2. Predictive models were pretrained using responses of breast cancer cell lines to targeted perturbations with a particular drug (Table 1). Few-shot learning was then performed on 0–10 PDTC breast tumor samples exposed to that drug (x axis), and model accuracy (Pearson’s correlation, y axis, mean ± 95% CI) validated using the remaining held-out PDTC samples. Results averaged across 48 drugs on n = 83 PDTC models. c, Predictive accuracy (x axis) is displayed separately for each drug model (y axis, mean ± 95% CI) on n = 83 PDTC models. Colors as in previous figures.

As observed with earlier challenges, all models performed poorly when switching contexts, achieving accuracies near or below zero (Extended Data Fig. 2c). However, once again we observed that TCRP improved substantially after exposure to each new patient sample: the average performance was r = 0.30 at 5 samples, reaching r = 0.35 at 10 samples versus r < 0.10 for the runner-up (Fig. 3b,c and Extended Data Fig. 3a). Nearly all drug predictions were improved by the few-shot paradigm. For example, the ATM inhibitor KU-55933 had the top performing drug-response predictions, with Pearson’s correlation of 0.56 between predicted and actual growth response measurements (top row of Fig. 3c, average performance over 5–10 samples). KU-55933 also represented the largest improvement over conventional approaches, where the best performing conventional model, the random forest, obtained correlations of approximately 0.12.

Challenge 3: transfer to PDXs in mice.

Finally, in challenge 3 we went a step further, moving from PDTCs tested against drugs in vitro to PDXs tested against drugs in live mice (Fig. 4a, and Extended Data Figs. 3b and 4). For this purpose we obtained data for 228 PDX mouse models from the PDX Encyclopedia²⁵, where each model was exposed to 1 of the 5 drugs on which TCRP had been trained in cell lines (cetuximab, erlotinib, paclitaxel, tamoxifen and trametinib; Table 1). Genotype and mRNA transcriptomes of each PDX were also provided, from which we obtained the molecular features used by TCRP to make drug-response predictions. In cell lines, the predicted output from TCRP was the area under the dose–response curve (AUC); for PDXs, the analogous measurement was the percentage change in tumor volume resulting from drug treatment in vivo (Δvol). Therefore, these predicted and measured values were each normalized to a standard normal distribution to translate between the two (z-score; Methods).

Fig. 4 |. Transfer of cell-line models to PDXs.

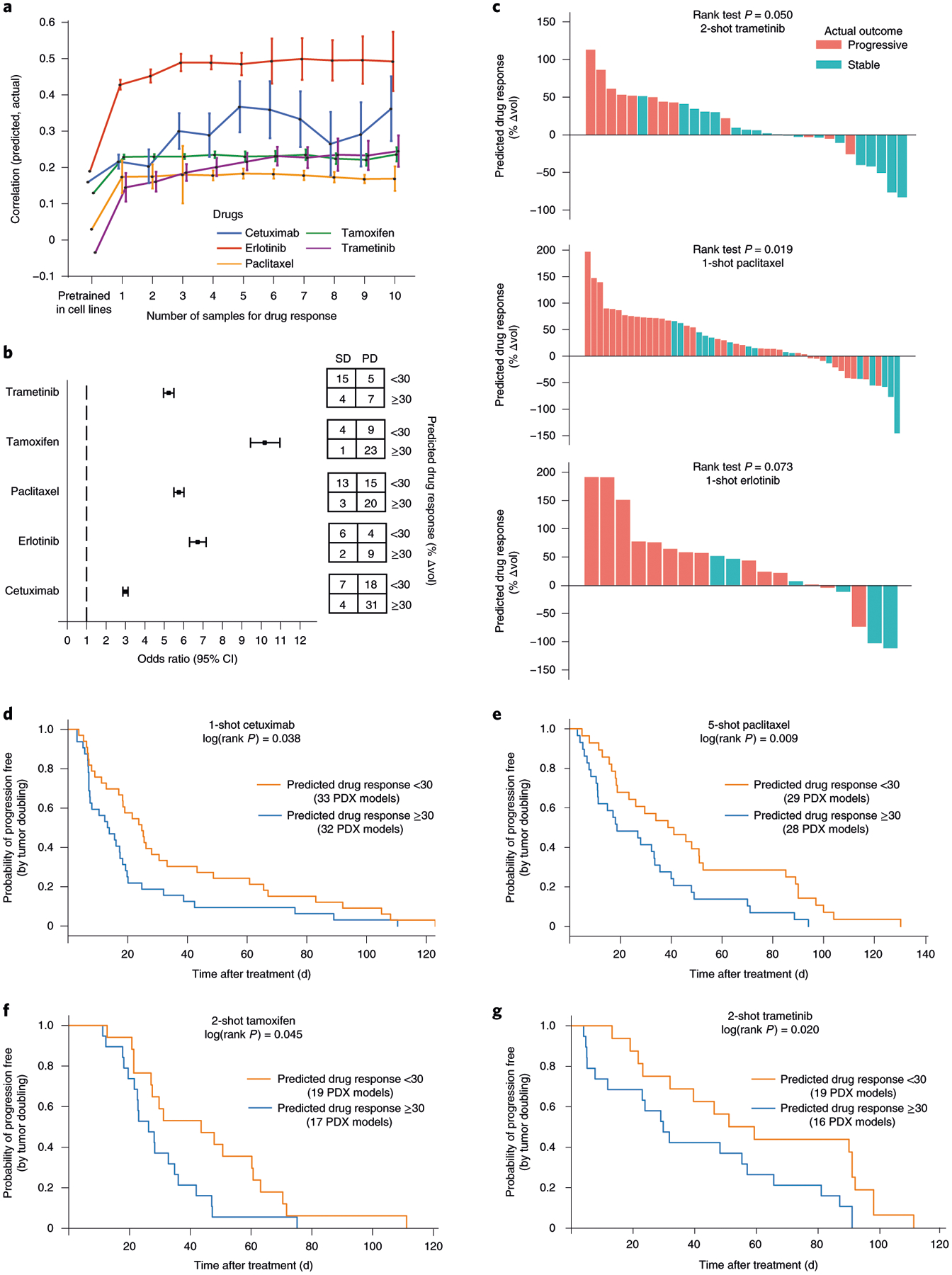
a, Challenge 3. Predictive models were pretrained using responses of cancer cell lines to targeted perturbations with drugs, one model per drug. Few-shot learning (x axis, number of few-shot samples used) was performed using PDX samples exposed to one of five drugs (line colors), and the improved model used to predict the change in tumor volume (Δvol; Methods). Accuracy of this prediction was validated using the actual changes in volume of the remaining held-out PDXs (Pearson’s correlation, y axis, mean ± 95% CI). This experiment included in total n = 228 PDX models. b, Odds ratio. We evaluated the odds of obtaining SD:PD outcomes when stratifying tumors into predicted responsive versus unresponsive subtypes (predicted Δvol < or ≥30%, respectively). Odds ratio (left) and corresponding contingency table (right), are shown for each drug (n = 31 samples for trametinib, n = 37 for tamoxifen, n = 51 for paclitaxel, n = 21 for erlotinib and n = 60 for cetuximab). Error bar represents mean ± 95% CI. c, Ranking of all PDX samples (x axis) by the predicted Δvol (y axis) for trametinib, paclitaxel and erlotinib. Color indicates actual clinical outcome. The rank P value is calculated by using a one-sided Wilcoxon’s Mann–Whitney U-test (n = 31 samples for trametinib, n = 51 for paclitaxel and n = 20 for erlotinib). d–g, Kaplan–Meier survival plots when stratifying tumors into responsive versus unresponsive subtypes for cetuximab (d) on n = 65 PDX models, paclitaxel (e) on n = 57 PDX samples, tamoxifen (f) on n = 36 PDX samples and trametinib (g) on n = 35 PDX samples. The log(rank P value) is calculated using a two-sided χ² test.

Although TCRP models pretrained on cell-line data initially performed poorly in predicting PDX responses, we observed significant improvements during training on the first few PDX samples (Fig. 4a). Such improvements were seen for all five drugs and led to a range of final prediction accuracies from r = 0.50 for erlotinib to r = 0.18 for paclitaxel (Spearman’s correlation between predicted and actual drug response after training on ten PDX samples; Fig. 4a and Extended Data Fig. 3b). We also explored the effect of translating the continuously valued drug-response predictions to discrete treatment outcomes, as are typically assigned in a clinical setting, by designating each response as progressive disease (PD, Δvol ≥ 30%) or stable disease (SD) or better (Δvol < 30%). We found that these predicted binary classifications were strongly associated with the observed PD/SD outcomes, with a range of odds ratios from 3.0 (cetuximab) to 10.5 (tamoxifen) (Fig. 4b,c). For cetuximab, paclitaxel, tamoxifen and trametinib, but not erlotinib, we found that the predicted PD/SD designations also showed significant differences in progression-free survival, depending on how many PDX samples had been used for few-shot learning (Fig. 4d–g).

Interpreting the predictive models.

A common critique of machine-learning systems is that they produce ‘black boxes’, the predictions of which are difficult to interpret^26,27. In the present study, as we had focused on drugs with known specific targets, we found that model predictions typically could be explained by molecular markers within that target’s pathway (using models constrained to these features; Methods and Extended Data Fig. 5). For example, a top feature in predicting the response of PDTCs to PD-0332991 (palbociclib; Fig. 5a,b) was the expression of the gene encoding RB-like factor (RBL2), a cell-cycle transcriptional repressor inactivated by CDK4/6. RBL2 expression was associated with palbociclib resistance (third from top in Fig. 5c; r = 0.47), suggesting that high RBL2 protein activity masks upstream inhibition of CDK4/6 by the drug. Another important feature was somatic mutation of SMAD4, encoding a transcriptional modulator repressing CDK4 transcription²⁸ (Fig. 5d). SMAD4 inactivation may release CDK4 to drive the cell cycle²⁹, with CDK4 repression counteracting this effect (Fig. 5b). Although SMAD4 mutation was rare in PDTCs (1/19 samples), it was much more common in cell lines (43/811 samples). The model had learned to strongly rely on the SMAD4 mutation during pretraining, where the large number of SMAD4 mutant samples is strongly associated with drug response. When switching to the PDTC dataset, this prior information was combined with the effect of SMAD4 mutation in the new dataset to jointly estimate its importance to the drug response.

Fig. 5 |. Model interpretation to identify predictive markers.

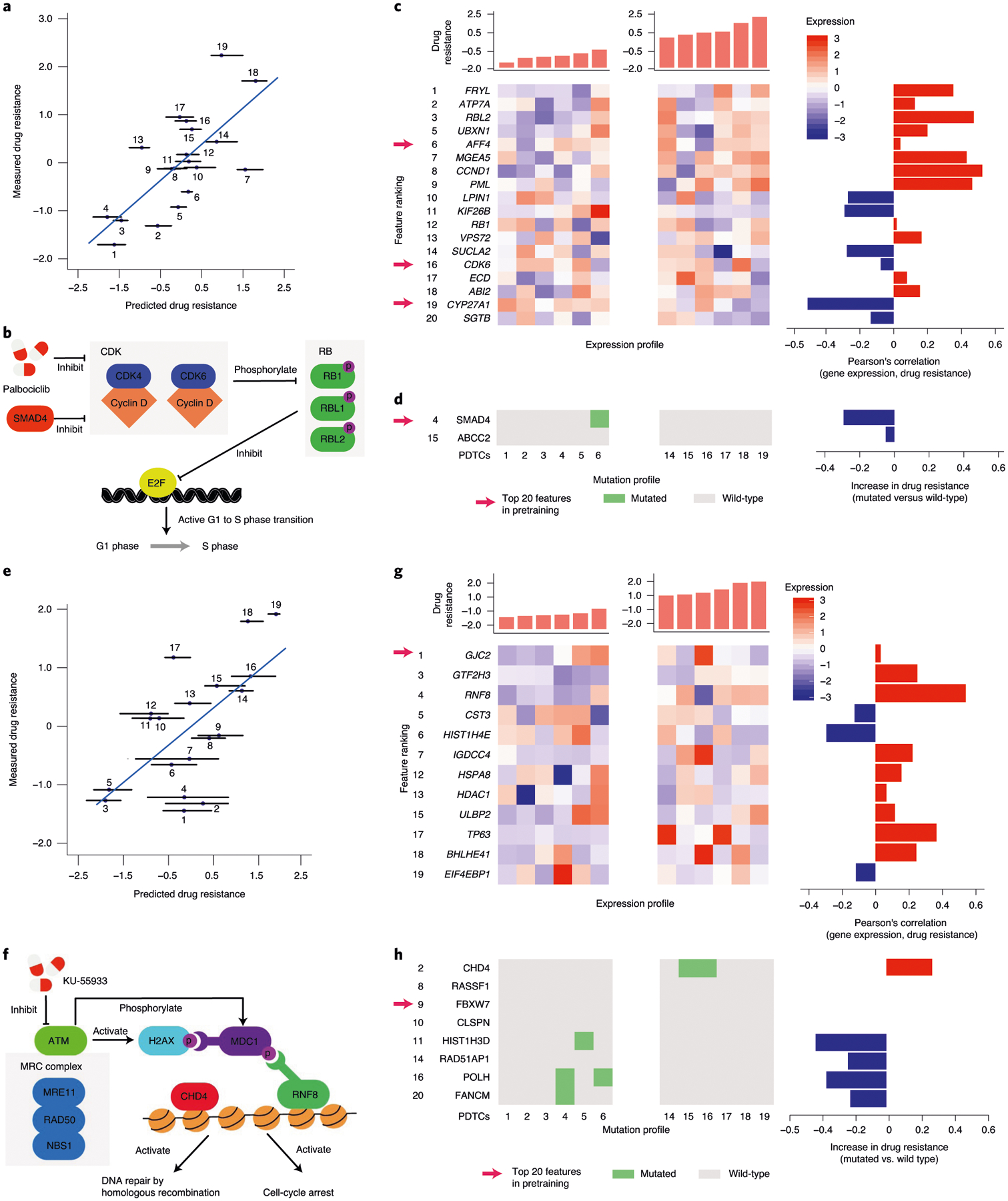
a, Measured versus predicted resistance to the CDK4/6 inhibitor palbociclib after few-shot learning on five PDTC samples treated with this drug on n = 19 test PDTC models. The error bars indicate the minimum/maximum value of the predictions across ten randomizations. b, Schematic of CDK pathway with palbociclib targets and selected molecular markers. c, Left: mRNA expression profiles for the top expression-based features of palbociclib. Right: Pearson’s correlation of palbociclib resistance and mRNA expression for the top expression-based features. d, Left: somatic mutation profiles for the top mutation-based features of palbociclib. Right: increase of palbociclib resistance when comparing mutated and wild-type samples for each top feature. e, Same as a for the response to ATM inhibitor KU-55933 on n = 19 PDTC models. f, Schematic of ATM pathway with selected predictive markers. g,h, Same as c and d for the response to ATM inhibitor KU-55933. Numbered sample labels in a and e correspond to PDTC sample numbers in c,d,g and h, in which molecular profiles for the six most sensitive and six most resistant samples are shown (PDTC1-6 and PDTC14-19, respectively) within n = 19 PDTC models.

As a second example, a top feature in the response to ATM inhibition (KU-55933; Fig. 5e,f) was the expression of RNF8, for which the protein is recruited to DNA double-stranded breaks (DSBs) after activation of ATM by DNA damage^30–32. RNF8 expression was correlated with KU-55933 resistance (third from top in Fig. 5g; r = 0.54), suggesting that, when RNF8 activity is high, ATM is not limiting for DSB repair. Also correlated with drug resistance was mutation of CHD4 (Fig. 5h), encoding the chromodomain–helicase–DNA-binding subunit of NuRD, a complex essential for chromatin relaxation at DSBs³³. Disabled NuRD may interfere with DNA repair, masking the effects of ATM inhibition. Alternatively, it may dampen the impact of ATM on CHD4-dependent cell-cycle progression³⁴.

A notable third example involved BRAF inhibition, to which tumors tend to be sensitive in the context of a BRAF-activating mutation. It is well established that some tissue types respond to BRAF inhibition more strongly than others; for instance, BRAF-mutant melanomas are generally responsive whereas BRAF-mutant colorectal tumors are not, for reasons that are not fully understood but are partially explained by expression of EGFR³⁵. As expected from these previous observations, the TCRP model predicted significant sensitivity to the BRAF inhibitor dabrafenib in BRAF-mutant cells, but not in wild-type cells, with a much more pronounced effect in melanoma than in colorectal cancer (CRC) (Fig. 6a). Of note, the drug response predicted by TCRP was significantly more accurate than the response predicted solely based on BRAF mutation and EGFR expression status (Fig. 6b), raising the question of which features TCRP had used to achieve higher accuracy. Further examination indicated that the model drew from a combination of novel features (Fig. 6c–f). These included expression of MRAS, which has been shown to function as a RAF phosphatase³⁶, expression of 14-3-3 genes YWHAE and YWHAH, which interact with RAF proteins in signal transduction³⁷, and mutation of RAPGEF1 (Rap guanine nucleotide exchange factor 1), a gene central to activation of the Ras/Raf/MEK/ERK signal transduction pathway.

Fig. 6 |. Model predictions and interpretation for the BRAF inhibitor dabrafenib.

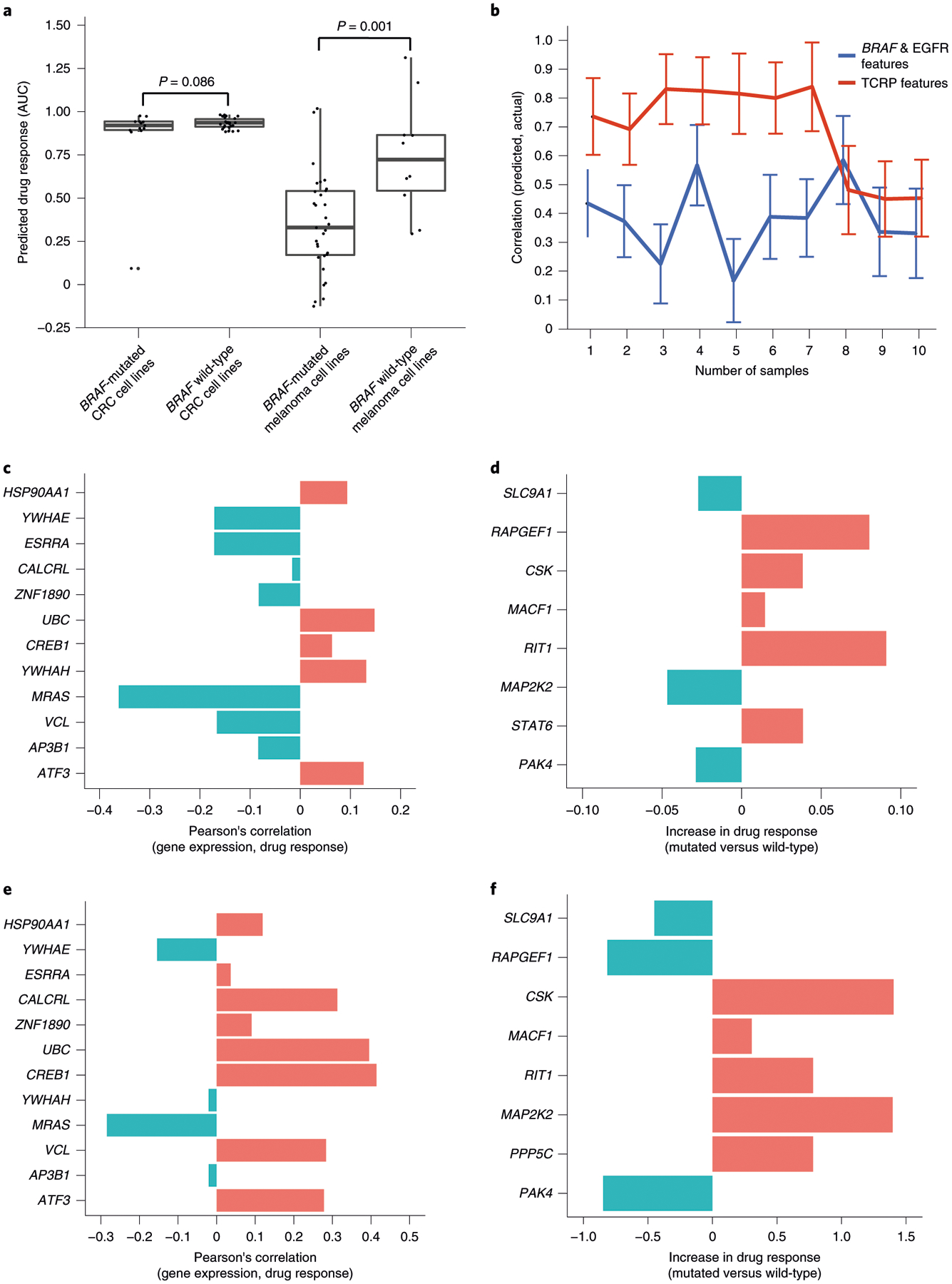
a, Box plots of predicted dabrafenib response for n = 39 CRC and n = 42 melanoma cell lines with respect to BRAF mutation status. The rank P value is calculated by using a one-sided Wilcoxon’s Mann–Whitney U-test on a total of n = 81 cell lines. The error bar represents mean ± 95% CI. b, Prediction accuracy of the TCRP model for CRC and melanoma cell lines used for a. Accuracy (y axis) is shown as a function of additional training samples used for few-shot learning (x axis). Accuracy mean and s.d. calculated over ten random samples of cell lines selected from n = 39 CRC and n = 42 melanoma cell lines used for training. c, Pearson’s correlation of dabrafenib response (AUC) and mRNA expression for the top expression-based features for CRC (ranked in decreasing importance from top to bottom; Methods). d, Relative change in dabrafenib response (AUC) on somatic mutation of each of the top mutation-based features for CRC (ranked in decreasing importance from top to bottom; Methods). e, Similar to c for melanoma. f, Similar to d for melanoma.

Discussion

Recently an abundance of tumor response data has been generated for targeted perturbations in numerous contexts. The usual way of analyzing these data is to pool all samples, under the assumption that accruing the maximal amount of data will result in a predictive model with the greatest statistical power. In the present study, we have identified a more efficient means of building predictive models, using the technique of few-shot learning. The two-phase learning procedure overlays naturally on the process of translating observations from basic research in vitro to predictive markers in tumors (Fig. 3a). First, in a basic research phase, a general predictive model is pretrained from extensive data generated in high-throughput, cell-based screens. Second, in a preclinical or clinical phase, few-shot learning is used to tune the general model to make predictions for a specific type of human tumors, by testing drugs with high predicted sensitivity in settings such as PDTCs and PDXs and, ultimately, patients. Thus far, few-shot learning shows encouraging performance in multiple datasets and translation scenarios where conventional learning fails. In all three challenges we examined, the initial pretraining phase was the same: optimizing the model for transfer across cell lines of different tissue types. Notably, this particular transfer task was sufficiently general to enable predictive models to transfer from cell lines to the settings of PDTCs and PDXs.

Models such as TCRP may have compelling applications in clinical contexts seeking to implement precision medicine, in which the task is to match a patient’s specific molecular profile to an optimal course of therapy. For this purpose, molecular tumor boards have been established in many cancer centers, where clinical experts must often make treatment decisions for a patient based on just a few precious cases with matching histopathology and molecular profiles. A second compelling application is in the pharmaceutical industry, in which a key goal is to select patients who are most likely to respond to a targeted agent. In both cases, classic predictive models have been hampered by lack of access to large numbers of well-characterized clinical samples, that is, samples for which molecular profiles have been coupled to precise information on treatment outcomes.

In this regard, an important question for future exploration concerns the degree to which an approach such as TCRP is ready for use in clinical or pharmaceutical settings. There are many uncertainties when deciding on treatment, and how the predictive value of the models built here compare with other molecular and clinical markers, and their predictive values, will need to be determined for each disease setting. In terms of absolute predictive performance, we observed a range of accuracies across the drugs examined, with some drugs yielding promising results. For example, in the PDX analysis of paclitaxel (Fig. 4b,c,e), a drug nonresponse was predicted for 23 tumors, of which 20 were in agreement with the actual observations of tumor growth in mice, a very high success rate by any standard (20/23 = 87% correct predictions of PD). As another example, nonresponse of PDX tumors to tamoxifen was correctly predicted in 23/24 of cases (96%). In these analyses, a nonresponse (PD) was called if the change in tumor volume was ≥30%, the standard threshold implemented by the PDX Encyclopedia^25,38. Given more data and a focused clinical study, one could probably tune the prediction threshold to drive performance higher. For example, at a threshold value >60%, TCRP predicts paclitaxel nonresponse with 100% accuracy given the current PDX dataset (14/14 patients). Future investigations with larger cohorts of PDX models or patients will be able to shed further light on the best clinical uses of few-shot learning.

In our analysis of both the PDTC (Fig. 3b) and the PDX (Fig. 4a) datasets, we noted that the performance of few-shot learning improves quickly and then appears to saturate. Further inspection reveals that the reason for this phenomenon relates to the balance of training versus test samples during evaluation. Given a fixed number of tumor samples, as the number of few-shot training samples increases, the number of testing samples decreases proportionally. In turn, a fewer number of testing samples means that the statistical power used to evaluate the prediction performance gets weaker, with a concomitant increase in variance. For most drugs in the PDTC dataset, a total of 19 tumor samples was available to be split between training and validation. To evaluate performance for 1-shot learning, 18 of these samples were therefore available as a test set, whereas, for 10-shot learning, only 9 samples were available for testing.

We also observed that drug responses were better predicted in some tissues than in others (Fig. 2b,d). Although the poor predictive power in some tissues is in need of further investigation, a potential factor relates to the substantial molecular heterogeneity observed within some cancer tissue types. For example, cell lines of lung tumors have been organized into as many as nine subtypes based on their transcriptomic profiles, in contrast to pancreatic tumor cell lines which appear far more homogeneous³⁹. These findings are superficially in agreement with those of our study, in that drug-response predictions in lung cancer lines are less predictive than those of the pancreas (Fig. 2b,d).

Although the results demonstrated in the present study were obtained with gene mutation and mRNA expression features, the TCRP framework is general with potential relevance to many other data types, such as copy-number variants, features extracted from histopathological images or data transferred from disease models in other species. Furthermore, although each perturbation by CRISPR (challenge 1a) or drugs (all other challenges) was considered a separate machine-learning task, a worthy future direction would be to explore the extent to which information can be transferred from one perturbation to another. If important information is shared, one might pursue a single unified model with predictive capacity across many or all drugs rather than training models separately.

A final future direction is to better understand the relationship between the predictability of a drug and its pharmacological properties, including its number of recognized targets and off-target effects (that is, polypharmacology). This relationship is difficult to study with the present TCRP, for which features are selected from the pathway of each known target, yielding a tendency to include more features for drugs that have more known targets (Methods). On the other hand, our understanding of drug-target genes and pathways is far from complete, and the protein network we used for feature selection is not cancer specific. Future model configurations using the same numbers of biomarkers across drugs will potentially shed light on the complex interactions between drug response and polypharmacology.

Methods

Challenge 1a.

Overview.

The first challenge was based on the Cancer Dependency Map (DepMap), which used CRISPR/Cas9 gene editing to disrupt nearly all (~17,700) human genes in each of 335 cancer cell lines (19 tissues), in each case measuring the relative cellular growth response¹. The machine-learning task was to use molecular features of each cell line to predict its growth response to the gene disruptions. Each gene disruption was considered as a separate learning task, in which cell lines represent learning samples. We studied 469 gene disruptions that had been reported by DepMap to have demonstrated the ability to influence cellular growth, as evidenced by the presence of at least one cell line for which the response was at least 6 s.d.s away from the mean across cell lines¹. Even though there is a modest difference between the distribution of fitness values for all genes versus the selected genes (Extended Data Fig. 1a), we did not observe a strong relationship between the overall fitness effect of a gene knockout and model predictive performance (Extended Data Fig. 1b).

Task-specific features.

Features for learning were based on gene somatic mutations and expression levels for each cell line, as reported in the Cancer Cell Line Encyclopedia (CCLE) project⁴⁰ and downloaded from the DepMap website (https://depmap.org/portal/download). For each learning task (CRISPR gene disruption, see above) we selected genes reported as having either a protein– protein interaction (PPI) or an mRNA co-expression relationship (|r| > 0.4) with the disrupted gene. The PPI data were taken as the union of the InBioMap⁴¹, PathwayCommons⁴² and CORUM⁴³ databases. The co-expression relationship is calculated over all the cell lines from the feature mRNA expression data. Such a feature-selection strategy, based on the molecular network neighborhood of the disrupted gene, was similar to that adopted earlier by the DepMap project. We further removed gene expression features for which the s.d.s fell into the lowest 10% over all genes and excluded genes with fewer than 10 somatic mutations across cell lines. The somatic mutations and mRNA expression levels of the remaining genes were applied to construct the input feature vector for each cell line.

Labels.

Sample labels were taken as the growth response of a cell line to the CRISPR disruption of interest (see above) using the CERES-corrected single-gene disruption scores downloaded from DepMap (https://depmap.org/portal). These scores are calculated by comparing the abundances of guide RNAs for the disrupted gene between the starting plasmid pool and the end of the CRISPR disruption experiment. The CERES method⁴⁴ then processes these scores by removing effects due to copy-number variation.

Few-shot design.

For each gene disruption learning problem, the 19 tissues represented by DepMap cell lines were split such that 18 tissues were used in the pretraining phase and the remaining tissue was held for the few-shot phase. To ensure sufficient samples for performance evaluation, this held-out tissue was selected from among the 9 tissues having ≥15 cell lines. In the few-shot phase, we randomly selected k cell lines as the few-shot samples to fine tune the model (k = [0 … 10], plotted along the x axis of Fig. 2a) and used the remaining cell lines as testing data. For each k, the selection of few-shot samples was random, so we repeated this selection 20 times and reported the average and s.d. of the prediction performance over these replicates (y axis of Fig. 2a).

Challenge 1b.

Overview.

This challenge was based on the dataset collected by the GDSC1000 project², which systematically tested the cellular growth responses elicited by a panel of 265 drugs applied to each of 1,001 tumor cell lines (representing 30 tissues). The machine-learning task was to use molecular features of each cell line to predict its growth response to a drug. Each drug was considered as a separate learning task, in which cell lines represent learning samples. We focused on 199 drugs for which the mechanism of action was at least partially characterized, that is, with a documented protein target or pathway. Drug target and pathway information was obtained from Table S1G of the original GDSC1000 paper².

Task-specific features.

Task-specific features were constructed for each drug by selecting genes having PPI or mRNA co-expression relationships (|r| > 0.4) with the documented drug targets, with the PPI and mRNA co-expression networks defined as per challenge 1a above. For drugs with multiple targets, we included all PPI/co-expressed neighbors of these targets. As above, we further removed gene expression features for which the s.d.s fell into the lowest 10% over all genes and excluded genes with <10 somatic mutations across cell lines. Somatic mutations and mRNA expression levels of the remaining selected genes were applied to construct the input feature vector for each cell line.

Labels.

Sample labels were taken as the growth response of a cell line to the drug of interest, using the AUC as the measure of drug response. All drug response data were downloaded from the GDSC1000 website: https://www.cancerrxgene.org/gdsc1000/GDSC1000_WebResources.

Few-shot design.

For each drug, the tissues were split such that one tissue was held out for the few-shot phase, and the remaining tissues were used in the pretraining phase. We required the held-out tissue to have data for ≥15 cell lines to provide sufficient samples for the few-shot learning phase. A consequence of this requirement was that the number of held-out tissues differed from drug to drug, because drugs had a variable number of cell lines for which drug responses had been measured². Similar to challenge 1a, in the few-shot phase we randomly selected k cell lines from the held tissue as few-shot samples to fine tune the model (k = [0 … 10], plotted along the x axis of Fig. 2c) and used the remaining cell lines as testing data. For each k, the selection of few-shot samples was random, so we repeated this selection 20 times and reported average and s.d. of prediction performance over all of these replicates (y axis of Fig. 2c).

Challenge 2.

Overview.

In this second challenge, we pretrained TCRP to predict drug responses in the GDSC1000 dataset (see Challenge 1b) and then subjected this model to few-shot learning using a study of PDTCs⁴. This previous study obtained 83 human breast tumor biopsies and, using mice as an intermediary, established distinct human cell cultures from these tumors. Each of these human cell cultures was exposed to a panel of drugs, from which we considered the 50 drugs with known protein targets and for which cell-line responses had also been measured in the GDSC1000 dataset. The machine-learning task was to use the pretrained model to predict the growth response of these PDTCs to each drug. Each drug was considered as a separate learning task, in which PDTCs represent learning samples.

Features.

We considered gene expression and mutation features that had been characterized in both the PDTC and the GDSC1000 datasets. Both drug-specific features and mini-cancer genome features were evaluated. Expression and somatic mutation data of the PDTC dataset were downloaded from https://figshare.com/articles/Bruna_et_al_A_biobank_of_breast_cancer_explants_with_preserved_intra-tumor_heterogeneity_to_screen_anticancer_compounds_Cell_2016/2069274.

Labels.

For the PDTC responses, we used the AUC as the measure of drug response, similar to the GDSC1000 dataset in challenge 1b. These data were downloaded from the same site as above: https://figshare.com/articles/Bruna_et_al_A_biobank_of_breast_cancer_explants_with_preserved_intra-tumor_heterogeneity_to_screen_anticancer_compounds_Cell_2016/2069274.

Few-shot design.

In the few-shot learning phase, we randomly selected k PDTCs as the few-shot samples to fine tune the model (k = [0 … 10], plotted along the x axis of Fig. 3b), and used the remaining cell lines as testing data. For each k, the selection of few-shot samples was random, so we repeated this selection 20 times and reported the average and s.d. of prediction performance over all of these replicates (y axis of Fig. 3b).

Challenge 3.

In this third challenge, we pretrained TCRP to predict drug responses in the GDSC1000 dataset (see Challenge 1b) and then used few-shot learning to transfer it to make drug-response predictions in a study of PDXs²⁵. This previous study created a large collection of mouse xenografts of human tumor biopsies, all characterized for tumor somatic mutations and mRNA expression levels. PDXs were exposed to a panel of drug treatments (one PDX per animal per treatment) during which in vivo tumor growth was measured. Here the machine-learning task was to use the pretrained TCRP to predict tumor growth in vivo. In particular, we used data for 228 PDX mouse models, where each model was exposed to one of the five drugs on which TCRP had been trained in cell lines (cetuximab, erlotinib, paclitaxel, tamoxifen and trametinib).

Mini-cancer genome features.

Expression and somatic mutation data for all PDX samples were downloaded from Supplementary Table 1 of the original paper²⁵. Most drugs in the PDX dataset do not have known drug targets, a requirement for feature selection in previous challenges (see above). Therefore, we adopted an alternative means of selecting features that does not require knowledge of drug mechanism of action, as introduced in recent work⁴⁵. These features were based on the ‘mini-cancer genome panel’, a set of known cancer-related genes collected by the Center for Personalized Cancer Treatment (CPCT, The Netherlands)⁴⁶. From this panel, we first removed gene expression and mutation features that had not been characterized in both the PDX and the GDSC1000 datasets. Second, we removed gene expression features for which the s.d.s fell into the lowest 10% over all genes in GDSC1000, and we removed gene mutation features with <10 somatic mutations across GDSC1000 cell lines. The somatic mutations and mRNA expression levels of the remaining selected genes were applied to construct the input feature vector for each cell line. In this scenario, all learning tasks (drugs) shared the same feature set.

Labels.

PDX drug response was measured by the minimum change in tumor volume in comparison to baseline, over the period from 10 d post-treatment until completion of the study (Δvol in the main text). This measure captures the speed, strength and durability of the in vivo response; all values were downloaded from Supplementary Table 1 of the original paper²⁵. When comparing TCRP predictions to Δvol measurements, both were normalized to a standard normal distribution to translate between the two (that is, z-score).

Few-shot design.

In the few-shot learning phase, we randomly selected k PDXs as the few-shot samples to fine tune the model (k = [0 … 10], plotted along the x axis of Fig. 4a) and used the remaining PDX samples as testing data. For each k, the selection of few-shot samples was random, so we repeated this selection 20 times and reported average and s.d. of prediction performance over all of these replicates (y axis of Fig. 4a).

TCRP neural network model.

We trained a multilayer neural network model to predict the phenotype of a tumor sample using its molecular features. For each sample i, the output of the j + 1th layer $h_i^{(j+1)}$ is defined as a nonlinear function of the output of the jth layer $h_i^{(j)}$ as follows:

$$h_i^{(j+1)}=\text{Relu}\left(\text{Linear}\left(h_i^{(j)}\right)\right)$$ (1)

where Linear $\left(h_i^{(j)}\right)$ is a linear function of $h_i^{(j)}$ defined as $W^{(j)}\times h_i^{(j)}+b^{(j)}$.W^(j) is the weight matrix and b^(j) is the bias vector. Relu is the rectified linear activation function⁴⁷ which thresholds values <0 to exactly 0. The first layer $h_i^{(1)}$ is the input molecular feature of sample i and the last layer $h_i^{(N)}$ acts as its final prediction ${\widehat{p}}_i(\theta )$,where θ is a parameter containing W^(j) and b^(j) from all the linear layers. For each machine-learning task, we scan all combinations of layers = {1,2} and hidden neurons = {5,10,15,20}, and determine the architecture of the neural network by crossvalidation. All parameters are trained by minimizing the mean square error function, L, which is a function of sample set, C, and parameters, θ:

$$L(C,\theta )=\frac{1}{M}{\Sigma }_{c_i\in C}{\left(p_i-{\widehat{p}}_i(\theta )\right)}^2$$ (2)

where _pi is the measured label for sample i and M is the number of samples in C.

Model pretraining phase.

In the pretraining phase, the aim is to train a neural network model that can quickly adapt to a new learning task with only a few additional training samples. The rationale is to acquire prior knowledge from a set of related tasks where training samples are abundant. In the present study, we adopted an established computational framework called the Model Agnostic Meta-Learning (MAML) algorithm¹⁹. Meta-learning approaches such as MAML seek to identify universal knowledge across multiple conditions and then to transfer this knowledge to make robust predictions in a new condition. In recent studies, the MAML technique has shown superior performance in comparison to other meta-learning frameworks¹⁹, and it is a flexible and model agnostic such that it can be applied to any gradient-based learning algorithm.

For each training iteration, we first sample a subset S_i of 12 tissue types from the pool S of all types available. S_i is then randomly partitioned into two nonoverlapping sets of six cell lines T and six cell lines V. A loss function adapted from equation (2) is defined as follows with respect to S:

$$E_{S_i\in S}\left[E_{<T,V>\in S_i}\left[L\left(V,\theta -\alpha \frac{\partial L(T,\theta )}{\partial \theta }\right)\right]\right]$$ (3)

Here L is a mean square error function with respect to V. The second argument of the loss function is a one-step gradient descent that seeks a better regression loss for cell-line set T. We then optimize equation (3) using the gradient descent algorithm Adam⁴⁸. Note that using the gradient descent requires calculation of a second-order gradient-of-loss function L. The intuition is that, for each training iteration of minimizing equation (3), we seek parameters θ that can achieve a smaller regression loss on cell-line set V after performing one iteration of the gradient descent on a distinct cell-line set T. A total of 200 training iterations were performed, sampling different S_i values, with each S_i including 20 partitions.

Few-shot learning phase.

In the second training phase, we observe a task Q with only a few training samples (for example, cell lines, PDTCs or PDX models). We perform only one iteration of gradient descent to achieve θ_few–shot suitable for the new task (for example, new tissue or mouse models):

$${\theta }_{\text{few-shot }}={\theta }_{\text{pretraining }}-{\alpha \frac{\partial L(Q,\theta )}{\partial \theta }|}_{\theta ={\theta }_{\text{pretraining }}}$$ (4)

Here θ_pretraining is the TCRP model trained in the pretraining phase. In theory, one can perform multiple iterations of gradient descent using equation (4) until convergence. However, one of the unsolved problems in the field of meta-learning is that the few-shot model can be easily overfit on a new task, given its very few samples. Therefore, we chose to update parameters only once. Note that α in equations (3) and (4) refers to the same hyperparameter. The structure of the neural network was defined as in equation (1).

Nested crossvalidation.

The appropriate architecture of a neural network is dependent on the particular problem and datasets. For drug-prediction problems (challenges 1b, 2 and 3), all hyperparameters, including mini-batch size and the size of T and V, were determined by the technique of nested crossvalidation as previously described⁴⁹. For challenge 1a, we used regular crossvalidation due to the greater number of prediction tasks.

Interpreting TCRP model predictions.

We used the framework of local interpretable model-agnostic explanations (LIME)⁵⁰ to generate locally faithful explanations for the TCRP neural network model. LIME works by taking the feature vector of a query sample of interest and perturbing it randomly, resulting in many perturbed samples around this query. Subsequently, it trains a much simpler interpretable model on this perturbed neighborhood (Extended Data Fig. 5). In this way, LIME can select important features specific for sample i, which is the major difference from conventional feature selection methods that act globally over all samples, not locally to a sample of interest. More formally, for the molecular feature vector f_i of each sample i, we generated N (=10,000) perturbed samples. Each of these perturbed samples j was created by adding to the original features of independent Gaussian noise with mean 0 and s.d. 1. For each perturbed sample, we made a prediction g_ij using the TCRP neural network. A second, simpler model, regularized linear regression, was then trained to fit the perturbed samples to their corresponding neural network predictions {g_ij}. Empirically, we applied both Elastic Net⁵¹ and Lasso⁵² regularization methods with different sparsity parameters (={0.1,0.01,0.001,0.0001}). The final ranking of features was averaged from the rankings produced by Elastic Net and Lasso over all sparsity parameters and over all tested samples. LIME was chosen over alternative model interpretation techniques, such as layer-wise relevance propagation⁵³, because these other techniques do not generate sample-specific explanations. LIME is an approximation of gradient-based methods⁵⁴ and could be used interchangeably with those methods in our work.

Implementation details of competing methods.

We used the Python package ‘scikit-learn’ (http://scikit-learn.org/stable/index.html) to implement four conventional machine learning methods: random forests, conventional neural networks, K nearest neighbors (KNN) and linear regression, as follows.

Random forests.

For random forests, we chose the maximum depth for each of the learning tasks based on fivefold crossvalidation.

Conventional neural networks.

Conventional neural network models were implemented using the PyTorch library (https://pytorch.org), selecting the number of hidden neurons (={5, 10, 20, 30, 40, 50, 100}), layers (={1, 2}) and learning rates (={0.1, 0.01, 0.001}) based on fivefold nested crossvalidation. For each machine-learning task (for example, drugs and gene perturbations), there are approximately (or fewer than) 1,000 cell-line examples (+ <20 PDTC/PDX models in some cases); thus, the data do not support a very deep neural network architecture with many parameters. Therefore, we focused on exploration of small neural network architectures in the present study. The number of hidden layers (={1, 2}) and the number of hidden neurons (={5, 10, 15, 20}) of the neural network were also determined by crossvalidation. We implemented the algorithm using the PyTorch library (https://pytorch.org) running on Tesla K20 graphics processing units. The nonlinear transformation was the same as equation (1) and optimized using Adam⁴⁸. Notice that both TCRP and this baseline method rely on a neural network model; however, the two models are trained in different ways and with potentially different network architectures (no. of hiddens, layers) due to separate crossvalidation processes.

K nearest neighbors.

For the KNN algorithm, to evaluate the accuracy of a sample i in the training data, we ruled out sample i when making its prediction. Otherwise, KNN will achieve a zero prediction error on the training set. The best ‘K’ for KNN was selected using fivefold crossvalidation.

Linear regression.

For the final conventional method, we implemented linear regression with the regular least squares loss of function and without regularization.

Statistics and reproducibility.

Sample size, data exclusion criteria and randomization on the test data are extensively explained in Methods. The investigators were not blinded to allocation during experiments or outcome assessment.

Reporting Summary.

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Extended Data

Extended Data Fig. 1 |. Analysis of fitness versus predictive performance for the panel of gene knockouts in our study.

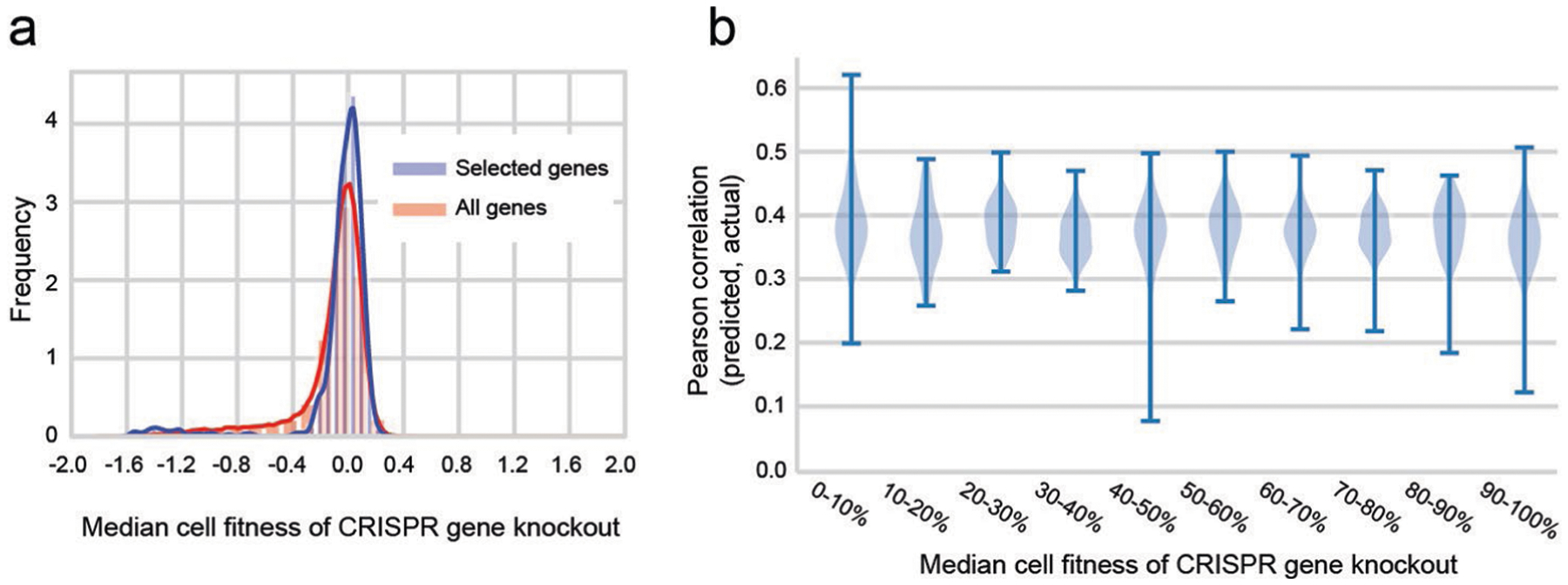
a, Distribution of relative growth values after CRISPR gene knockout, median for all n = 341 cell lines. Blue: pooling knockouts of all n = 17670 genes; Pink: pooling n = 469 knockouts of genes selected in our study. Fitness is corrected by the Copy Number Variation by the CERES algorithm. b, For each knockout of a selected gene, predictive performance (y axis) is computed as the Pearson correlation between predicted and actual growth measurements over all n = 341 cell lines. This performance is displayed as a function of the median growth fitness of that knockout (x axis). Growth fitness is binned according to percentiles, for example the first bin (0–10%) represents the top 10% of selected genes with the strongest median effects on growth. The distribution of predictive performance for each bin is shown with a violin plot. Error bars represent 95% confidence interval.

Extended Data Fig. 2 |.

Training accuracy of TCRP and other baseline models for all challenges.

Extended Data Fig. 3 |. Alternative calculation of model performance using Spearman correlation.

While Pearson correlation is used to calculate model performance in the main text, this supplemental figure provides equivalent performance calculations using the non-parametric rank-based Spearman correlation. a, Related to Fig. 3b on n = 83 PDTC models. b, Related to Fig. 4a on n = 228 PDX models.

Extended Data Fig. 4 |. Comparison of transferability of different machine learning models to patient-derived xenografts.

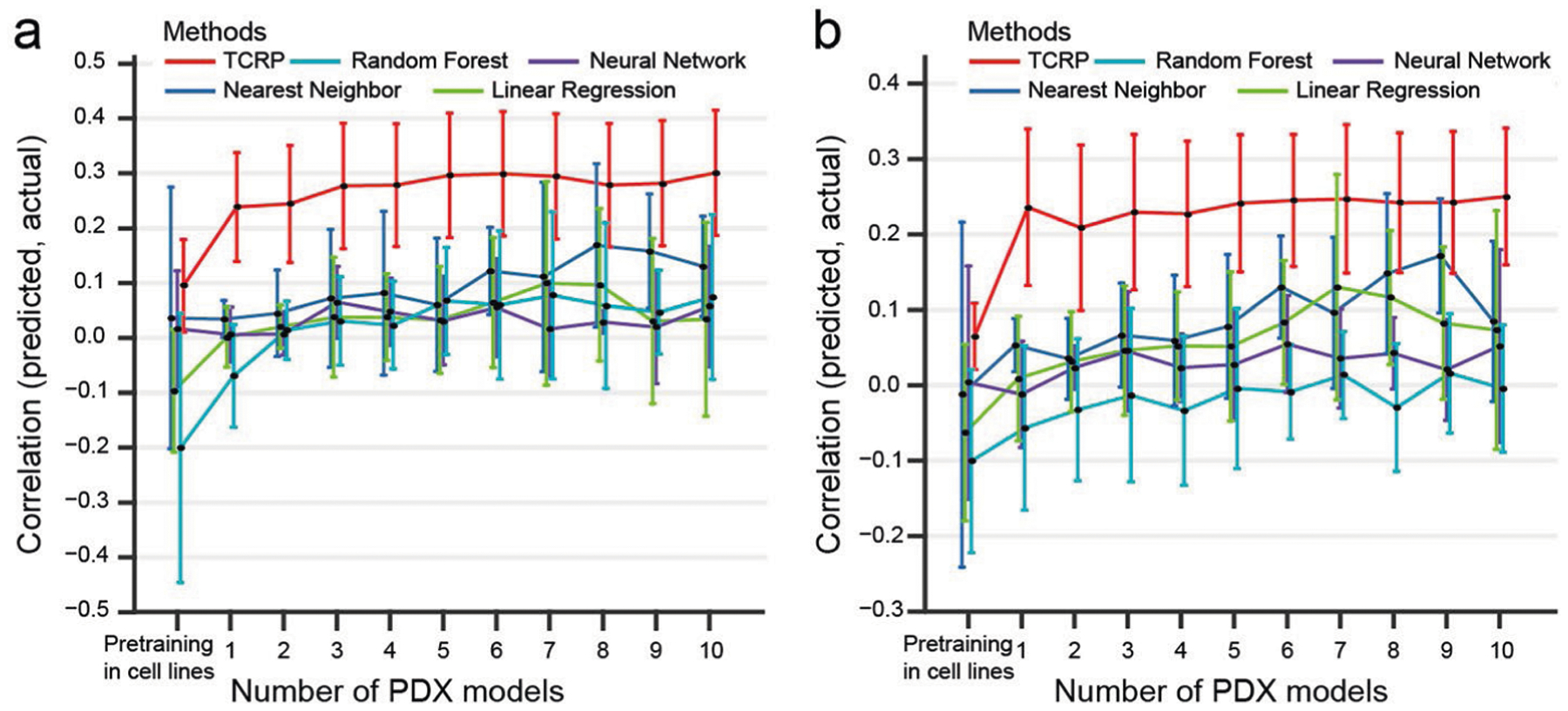
Predictive models were pre-trained using responses of cancer cell lines to perturbations with drugs, one model per drug. Few-shot learning was then performed on 0–10 PDX breast tumor samples exposed to that drug (x-axis), and model accuracy (y-axis) was measured by a, Pearson correlation or b, Spearman correlation on the remaining held-out PDX samples. Results averaged across five drugs (see main text). This experiment considers n = 228 PDX models.

Extended Data Fig. 5 |. Interpreting the TCRP model with the framework of Local Interpretable Model-Agnostic explanations (LIMe).

See Methods.