Abstract
Persistent homology is a powerful tool for characterizing the topology of a data set at various geometric scales. When applied to the description of molecular structures, persistent homology can capture the multiscale geometric features and reveal certain interaction patterns in terms of topological invariants. However, in addition to the geometric information, there is a wide variety of nongeometric information of molecular structures, such as element types, atomic partial charges, atomic pairwise interactions, and electrostatic potential functions, that is not described by persistent homology. Although element-specific homology and electrostatic persistent homology can encode some nongeometric information into geometry based topological invariants, it is desirable to have a mathematical paradigm to systematically embed both geometric and nongeometric information, i.e., multicomponent heterogeneous information, into unified topological representations. To this end, we propose a persistent cohomology based framework for the enriched representation of data. In our framework, nongeometric information can either be distributed globally or reside locally on the datasets in the geometric sense and can be properly defined on topological spaces, i.e., simplicial complexes. Using the proposed persistent cohomology based framework, enriched barcodes are extracted from datasets to represent heterogeneous information. We consider a variety of datasets to validate the present formulation and illustrate the usefulness of the proposed method based on persistent cohomology. It is found that the proposed framework outperforms or at least matches the state-of-the-art methods in the protein-ligand binding affinity prediction from massive biomolecular datasets without resorting to any deep learning formulation.
Keywords: topological data analysis, machine learning, biophysics, drug design
AMS subject classifications. 55U30, 55U10, 92C40
1. Introduction.
With the advancements in sensor hardware, data collection software, data organization, and storage frameworks, various databases are expanding at an unprecedented speed where a large part of the newly accumulated data is high-dimensional, highly complex, diverse, and often noisy. The rapid growth of databases demands robust and automatic data analysis tools. Currently, many widely used data analysis methods make assumptions of data complexity and the underlying dimensionality. Other methods require knowledge from domain experts. An emerging family of data analysis methods, topological data analysis (TDA), answers these demands by combining ideas from algebraic topology with multiscale analysis [13]. Making minimal assumptions of data, TDA characterizes the shapes of data in various dimensions, scans over a wide range of scales, and is often robust against noise.
Computational homology represents the topological structures of various dimensions by algebraic structures, usually based on a fixed discrete topological space of interest. A discrete topological representation can be derived by building a simplicial complex upon a point cloud with a chosen scale parameter determining the topology or by building a cubical complex upon volumetric data with a chosen isovalue. Continuous topological spaces can also be approximated by discrete representations, e.g., a tessellation of a manifold. Homology groups contain generators associated with the holes of certain dimensions in the topological space. While computational homology captures the shape characteristics of a fixed structure, such characteristics are insufficient to cover a wide range of scales. A great variety of other structures might share the same characteristics. In mathematics, it is common to eliminate degeneracy by introducing an extra dimension. Therefore, instead of examining the data at a fixed scale, persistent homology scans a sequence of topological spaces associated with a varying parameter that determines the topologies built upon the data.
Persistence describes the shapes and the corresponding scales of data by representing the data as a continuum of topological spaces, which is called a filtration, and tracking homology features along this course of varying spaces. Via filtration, a collection of topological spaces is built on the data associated with different values of a scale parameter. Persistent homology tracks at what stage of the filtration homology generators appear and how they persist along the subsequent course of the filtration. The persistent homology theory was formulated along with practical algorithms by Edelsbrunner, Letscher, and Zomorodian [25]. A formal mathematical foundation was later established by Zomorodian and Carlsson [57]. An earlier work, size function [26], examines the connected components of topological spaces and can be regarded as a version of 0th dimensional persistent homology. Persistent homology has found applications in many fields–for example, image processing [7], biology [19, 16, 53, 55, 54, 47, 28, 10], and fields in mathematics such as dynamical systems [37]. Theoretical development has flourished since persistent homology was proposed; examples are zigzag persistence [14] and multidimensional persistence [15]. There has been continuous advancement in algorithm development such as Perseus [39], PHAT [5], and Ripser [4], paving the way for the analysis of complex and large datasets.
A point cloud dataset in the Euclidean space allows the usage of radius filtration associated with alpha complex [24]. A more general distance filtration associated with a Vietoris–Rips complex [31] or a Čech complex can be used to allow a predefined distance function suitable for specific applications [53, 55]. It is also possible to use a more flexible construction by directly assigning filtration values to simplices in a complex which is considered as the final structure at the end of the filtration. In many applications, persistent homology is used to analyze the topological structures of datasets with generalized but homogeneous information. For example, once the genetic distance between genes is defined by the number of mutations, persistent homology can be used to analyze the topological properties of a gene evolution dataset. When the information of a dataset is heterogeneous, i.e., multicomponent information is involved, special treatments are needed. For example, vineyards [18, 41] are used to study spatiotemporal data.
In dealing with chemical and biological datasets, persistent homology was found to neglect crucial chemical and biological information during the topological simplification of the geometric complexity. Element-specific persistent homology was introduced to retain some chemical and biological information of the molecular datasets in the topological invariants [9, 11, 10, 8]. In fact, retaining some information of element types while using persistent homology to characterize the geometric point cloud representing the molecules can already deliver top predictions in worldwide drug design competitions [42]. However, in addition to the point cloud in the Euclidean space representing the coordinates of atoms, there is a lot of other valuable physical and chemical information such as atomic partial charges, Coulomb and van der Waals interactions between atoms, and hydrophobic interactions among carbon atoms. A pressing need is to encode the physical and chemical information into the topological representations. This need is common in practical data analysis, where the data has multiple dimensions with heterogeneous meanings. It is questionable to consider such a dataset as one single high-dimensional point cloud and directly apply persistent homology analysis. Consequently, there is a broad need to integrate the multicomponent nongeometric information into topological representations of the geometric information. To this end, we utilize the cohomology theory to assign functions on the persistence barcodes that depict the nongeometric information.
Cohomology provides a richer algebraic structure for a topological space. Cohomology theory has been applied in both mathematics and the field of data analysis. One well-known cohomology theory is de Rham cohomology, which studies the topological features of smooth manifolds using differential forms. The de Rham cohomology has led to further theoretical developments such as Hodge theory. Recently, a discrete exterior calculus framework has been established [32] where manifolds are approximated by mesh-like simplicial complexes and the discrete counterparts of the continuous concepts such as differential forms are defined thereafter. This framework has many applications. For example, the harmonic component of the discrete Hodge decomposition has been used in sensor network coverage problems to localize holes in a sensor network [6]. Cohomology theory has also been applied to topological data analysis. A 1-dimensional cohomology was used to assign circular values to the input data associated with a homology generator [21], which further led to applications in several fields including the analysis of neural data [48] and the study of periodic motion [50]. Persistent cohomology in higher dimensions has been used to produce coordinate representations that reduce dimensionality while retaining the topological property of data [46]. Generalized weighted (co)homology and the weighted Laplacian were introduced with applications to graphs [52]. Computationally, the duality between homology and cohomology [20] has set the basis for constructing more efficient algorithms that utilize cohomology to compute persistent homology barcodes. Several code implementations, such as Dionysus [40] and Ripser [4], drastically speed up the persistent homology computation by utilizing this property.
In this work, we introduce an enriched representation of data. We seek a formulation that organizes geometric information into a simplicial complex while encoding chemical, physical, and biological properties into functions fully or partially defined on simplicial complexes locally associated with the cohomology generators. To this end, we need a representation that can locate homology generators. When manifold-like simplicial complexes are available, we can look for harmonic (in the sense of the Laplace–de Rham operator) cohomologous cocycles under the framework of discrete exterior calculus [33]. A discrete version of the Hodge–de Rham theorem guarantees the uniqueness of the harmonic cocycle if certain conditions are satisfied [33]. However, this method requires the proper construction of the Hodge star operator, which usually relies on a well-defined dual complex, while in general applications this is not always feasible. For example, when a user-defined dissimilarity matrix is used with the Rips complex, the dissimilarity measurement may not satisfy to be a distance. Therefore, we relax our requirement on geometric accuracy and use a combinatorial Laplacian on simplicial complexes. Then, the smoothness of a cocycle can be measured by the Laplacian. Specifically, given a representative cocycle of a homology generator, we look for a cohomologous cocycle that minimizes the norm of the output under the Laplacian. We can then consider such smoothed cocycles which distribute smoothly around the holes of certain dimensions as measures on simplicial complexes and describe the input functions defined on the simplicial complexes by integrating with respect to these measures. The present formulation also utilizes a filtration process to assign a function over the filtration interval associated with each bar in the barcode representation to deliver an enriched barcode representation of persistent homology. A weighted Wasserstein distance is defined and implemented subsequently to facilitate the comparison of these enriched barcodes generated from datasets.
In the rest of this paper, the background of persistent homology and cohomology is given in section 3, and persistent cohomology enriched barcodes with the accompanying data analysis tools are developed in section 4. In section 5, we illustrate the proposed method by simple examples, example datasets, and the characterization of molecules. Finally, we also demonstrate the utility of the proposed persistent cohomology by the prediction of protein-ligand binding affinities from large datasets.
2. Motivation.
The development of the method in this work is for a scenario in topological data analysis, specifically persistent homology where the data has multiple heterogeneous dimensions while it is not appropriate to compute geometry/topology with all the dimensions together. However, the dimensions that are not considered for topological characterization may carry useful information. This work reacquires this additional information by building maps upon the persistent homology results using cohomology.
More precisely, consider a dataset containing N data points each having a description vector of size . An example can be a set of N atoms from a molecule with recording the Cartesian coordinates of the atoms, where persistent homology computation can be directly applied by considering the dataset as a point cloud in . However, there can be more information in the dataset. For example, in addition to the coordinates, there can be partial charges on the atoms in a dataset. In this case, it is not appropriate to directly compute persistent homology by considering the dataset as a point cloud in . A more general situation is that the elements in the description vector contain both geometric information and nongeometric information. For simplicity, we assume the elements are already sorted such that the first m are for geometry and the following n elements are for nongeometric features. We can compute a certain dimensional persistent homology for the submatrix X(1, … , N; 1, … , m) and obtain a barcode PH(X) = {[bi, di)}i∈I which is basically a collection of half-open intervals. Then, the method in this work derives a function on the intervals reflecting the information given in . For a bar [bi, di) in the barcode and a filtration value (which is a parameter in persistent homology related to scale) ϵ ∈ [bi, di), f*([bi, di), ϵ) describes the information carried by associating with this particular bar at the specific filtration value. In the earlier example with 1-dimensional persistent homology, this reflects the average charge of atoms distributing on the loop or the tunnel associated with the bar.
3. Theoretical background.
3.1. Simplex and simplicial complex.
For point clouds, their topological analysis and characterization can be carried out via simplices and simplicial complexes. The convex hull of a set of k + 1 affinely independent points in is a (geometric) k-simplex denoted σ which can be represented by [v0, … , vk], and each vi is called a vertex of the simplex. A simplex τ is a face of σ if the vertices of τ are a subset of the vertices of σ and this relationship is denoted τ ≤ σ. A simplicial complex is a finite collection of simplices X = {σi}i satisfying that the intersection of any two simplices in X is either an empty set or a common face of the two and all the faces of a simplex in X are also in X. The collection of all k-simplices in X is denoted Xk. The dimension of a simplicial complex is the highest dimension of its simplices.
3.2. Homology and cohomology.
Given a simplicial complex X, a k-chain on it is a finite formal sum of all simplices in Xk, c = Σiaiσi where ai are coefficients. The set of all k-chains in X with the addition given by the addition of coefficients forms a group called the kth chain group denoted Ck(X). The orientation of a simplex is given by the ordering of its vertices, and two orderings give the same orientation if and only if they differ by an even number of permutations. For example, [v0, v1] = −[v0, v1] and [v0, v1, v2] = [v1, v2, v0]. The boundary operator ∂k : Ck(X) → Ck−1(X) is a linear mapping that maps a k-simplex to the alternating sum of its codimension-1 faces,
where denotes the absence of vi. When there is no ambiguity, we simply denote ∂k by ∂. We say that a k-chain is a boundary if it is in the image of ∂k+1. A k-chain is a k-cycle if its image under ∂k is 0, the chain with all coefficients equal to 0. The kth homology group is the quotient group Hk(X) = Ker(∂k)/Im(∂k+1) containing equivalence classes of k-cycles. Im(∂k+1) is a subgroup of Ker(∂k) following that ∂k ∘ ∂k+1 = 0. Two k-cycles are in the same equivalence class in Hk(X) if they differ by the boundary of a (k+1)-chain and they are called homologous.
Cohomology is also a sequence of abelian groups associated to the topological space X and is defined from cochain groups. Specifically, a k-cochain is a function α : Xk → R where R is a commutative ring. The set of all k-cochains following the addition in R is called the kth cochain group denoted Ck(X, R). The coboundary operator dk: Ck−1(X, R) → Ck(X, R) maps a cochain to a cochain of one dimension higher and is the counterpart of boundary operators for chains, namely
for a (k − 1)-cochain α. It should be noted that in the matrix representation of the two operators, dk and ∂k are transposes of each other provided we take the natural basis for the chain group and the natural corresponding basis for the cochain group. When there is no ambiguity, we simply refer to dk using d. A k-cochain is called a coboundary if it is in the image of dk. A k-cochain is called a cocycle if its image under dk+1 is 0. The coboundary operators have the property that dk+1 ∘ dk = 0 following that . The kth cohomology group is defined to be the quotient group Hk(X, R) = Ker(dk+1)/Im(dk). Two cocycles are called cohomologous if they differ by a coboundary.
In practice, some finite field is usually used for the efficient computation of persistent (co)homology. From now on, we consider finite fields with some prime p.
3.3. Persistence.
We are interested in the evolution of a simplicial complex and hope to track how the topological feature changes as the simplicial complex changes. Given a simplicial complex X and a function , for any , a sublevel set of X is defined as
The function g is required to satisfy that g(τ) ≤ g(σ) for any σ and any τ ≤ σ. Since X is a finite collection of simplices, we can have a finite sorted range of g as where xi < xj if i < j. The filtration of X associated with g is an ordered sequence of subcomplexes of X,
| (3.1) |
Let be the coefficient field for the chain groups. Persistent homology keeps track of the appearance and disappearance of homology classes along the filtration, which also includes the information of the homology of each fixed simplicial complex in filtration {X(xi)}i. Since we are working over a field, the homology groups Hk(X(xi)) can be represented as vector spaces. The inclusion map connecting the groups induces a sequence of linear transformations on the vector spaces as
| (3.2) |
A persistence module {Vi, ϕi} is a collection of a sequence of vector spaces Vi and linear transformations connecting them ϕi : Vi → Vi+1. An interval module is a persistence module where and 0 otherwise; and fi is the identify when possible and 0 otherwise. A special case of a theorem of Gabriel [27] implies that a nice enough persistence module can be decomposed uniquely as a direct sum of interval modules, . The collection of half-open intervals B can be visualized as barcodes, which represent topological invariants as horizontal line segments, or persistence diagrams, which use points in a 2-dimensional plot to describe topological events.
Similarly, persistent cohomology can be derived with the following relationship:
The universal coefficient theorem for cohomology [30, Theorem 3.2] implies that there is a natural isomorphism so that the cohomology group can be considered as the dual space of the homology group. This property further implies that and thus persistent homology and persistent cohomology have identical barcodes [20]. For the computation of persistent (co)homology, we refer the reader to [44, 20]. Though we are not aware of any general guidance for the choice of the coefficient set, that is, the choice of p in , a recent study suggests that in practice a persistence diagram rarely changes when p changes if we consider a filtration in [43].
4. Method.
4.1. Smoothed cocycle.
Some representative cocycles in persistent cohomology may not reflect the overall location and structure associated with their cohomology generators. To better embed the additional information in the data into cohomology generators, we look for a smoothed representative cocycle in each cohomology class. The smoothness of functions can be measured by using a Laplacian. We then construct smoothed representative cocycles with this Laplacian. There can be many choices for the Laplacian operator such as the discrete Hodge Laplacian [22] for manifold-like complexes and the graph Laplacian [17] or its higher-order generalizations [22] for graphs. In this work, our object of study is typically a simplicial complex with simplices of different dimensions glued together. Moreover, we may work with abstract simplicial complexes in certain applications. Therefore, we choose the combinatorial Laplacian [29, 34] in this work for its general applicability.
A Laplacian for cochains can be defined by first defining an inner product and using the induced adjoint operator. Here, we consider the case of real coefficients. The adjoint of the operator dk with respect to this inner product can be defined by
| (4.1) |
Then, a Laplacian on can be defined by
| (4.2) |
For a cochain group, α1, , the inner product can be defined as
| (4.3) |
or with some weights,
| (4.4) |
where ω(σ) is the weight of σ.
Under the inner product defined in (4.3), the boundary operator ∂k is the adjoint of the coboundary operator dk leading to the combinatorial Laplacian . The matrix representation of this operator can be constructed as
| (4.5) |
where Bk is the kth boundary matrix. The two terms respectively capture upper adjacency (two k-simplices being faces of a common (k + 1)-simplex) and lower adjacency (two simplices sharing a common nonempty codimension-1 face) among the k-simplices.
Consider a real weight function on the simplices in (4.4); the weighted boundary operator can be defined as
| (4.6) |
where is a face of σ omitting vertex i [34, 52]. Based on this, the weighted combinatorial Laplacian can be constructed as
| (4.7) |
where Ak is the matrix representation of the weighted boundary operator .
4.2. Persistent cohomology enriched barcode.
We describe the workflow in this section. Given a simplicial complex X of dimension n, and a function with 0 ≤ k ≤ n, we seek a method to embed the information of f on the persistence barcodes obtained with a chosen filtration of X. In other words, we seek a representation of f on cohomology generators. To this end, smoothed representations are first computed for cohomology generators. One such smoothed representation induces a measure on the simplicial complex which allows us to integrate f on X. We describe the protocol of our approach below.
Dimension greater than 0.
Consider a filtration of X, ∅ = X(x0) ⊆ X(x1) ⊆ … ⊆ X(xl) = X, and an associated persistent cohomology with a prime p other than 2. We follow de Silva, Morozov, and Vejdemo-Johansson [21] for the construction of an initial representative integer cocycle. Let ω be a representative cocycle for a persistence interval [xi, xj) of dimension k > 0. A lifting of ω with integer coefficients ω′ is first constructed satisfying that ω(σ) ≠ ω′(σ) (mod p) and for all σ ∈ Xk. It is possible that ω′ is not an integer (i.e., dω′ ≠ 0), and if this is the case, by writing dω′ = pη with , we can solve for η = dγ with . Then a valid integer cocycle ω′ − pγ can be obtained. This lifting fails when there is p-torsion in which is very rare in real data [21]. In case it fails, another prime number is chosen, and the procedure is repeated. Now we assume that we have obtained an integer cocycle which is also a real cocycle.
Given a Laplacian on cochains to measure smoothness, a smooth cocycle can be obtained by solving a minimization problem,
| (4.8) |
letting . This smoothed cocycle induces a measure μ on Xk by setting and
| (4.9) |
To obtain a sequence of such smoothed real k-cocycles for the cohomology generator along a persistence interval, we restrict the representative integer cocycle to subcomplexes of X and repeat the smoothing computation. Consider the integer k-cocycle at filtration value x. The corresponding smoothed real k-cocycle can be obtained by running the optimization problem for as (4.8) on , and it induces a measure μx on Xk(x) as described in (4.9). It suffices to compute for all different filtration values in [xi, xj) because we have a finite filtration which gives .
A function can be defined for each persistence interval [xi, xj) as
| (4.10) |
for t Ƞ [0, 1). We call each of the collection of persistence intervals being associated with one such function f* an enriched persistent barcode.
Dimension 0.
In the case of dimension 0, persistent homology tracks the appearance and merging of connected components. It is convenient to assign a smooth 0-cocycle to a persistence interval by assigning 1 to the nodes in the connected component associated with the interval right before the generator is killed due to merging with another connected component. This is implemented with a union-find algorithm.
4.3. Preprocessing of the input function.
When given the original input function associated with the input data, we first need to generate a cochain of the dimension of interest based on this input function. The procedures in several situations are discussed in the rest of this section.
Case 1.
When given a function , and we are interested in its behavior associated with a k-dimensional homology where k0 ≠ k, we need to interpolate or extrapolate f0 to a function . We assume that f0 is unoriented, i.e., f0(σ) = f0(−σ). A simple way is to take unweighted averages,
| (4.11) |
where each is a k0-simplex satisfying that if k > k0 and if k < k0 and nσ is the total number of such k0-simplices. A weighted version based on geometry can be defined as
| (4.12) |
where wi is the reciprocal of the distance between the barycenters of σ and .
An example of this situation is the pairwise interaction strengths between atoms of a molecule which are naturally defined on edges connecting the vertices representing the atoms. Another example is the atomic partial charges defined on the vertices representing the atoms in a molecule or a molecular complex.
Case 2.
When given a function with n ≥ k and a geometric simplicial complex, we can integrate it on every k-simplex in X to obtain a function . For simplicity, we require f0 to be bounded. Then, fi is defined as
| (4.13) |
for a k-simplex σ and ∫σ dσ computes the k-dimensional volume of σ. In many cases, f0 is given as results of numerical simulations which are often defined on grid points. Then, the integrals can be computed by some chosen quadrature formula and by interpolating f0 to the collocation points.
4.4. Weighted Wasserstein distance for persistent cohomology enriched barcodes.
An enriched bar can be represented by three elements: birth value b, death value d, and function f* constructed by (4.10). Given two enriched barcodes of the same dimension represented by and , we would like to quantify their difference. We first define two pairwise distances, i.e., Δb, which measures the distance between two persistence intervals
| (4.14) |
and Δf, which measures the difference between f* and f′*,
| (4.15) |
In the numerical examples, we use p = 1. In practice, it is sometimes is too costly to compute the output values of f* for all possible filtration values, and only a subset of possible filtration values is selected, such as only the middle value of a bar. In this case, we use the middle Riemann sum to approximate the integration in (4.15). For a bijection where and are subsets of I and J, the associated penalties are defined as
| (4.16) |
and
| (4.17) |
The qth weighted Wasserstein distance is defined as
| (4.18) |
where γ is a weight parameter, Θ is the set of all valid mappings, and we denote the minimizer by θq,γ. Note that both and are metrics, and thus the weighted Wasserstein distance also satisfies to be a metric.
Similar to the receiver operating characteristic curve, instead of fixing γ, we let it change from 0 to 1, which results in a function defined as
| (4.19) |
and we call it a Wasserstein characteristic curve.
4.5. Implementation.
We use the computational topology software Dionysus [40] to compute the persistent cohomology. Persistent cohomology not only provides useful representative cocycles but also speeds up the computation of persistence barcodes. Interested readers are referred to the literature [21, 20]. The (weighted) Laplacian is obtained from boundary matrices. Big (weighted) boundary matrices for the last frame in the filtration are first constructed with the simplices ordered by the filtration value. Then we can simply take the submatrices to obtain the (weighted) Laplacian defined in (4.6) and (4.7). The matrices are implemented using sparse matrix data structures to facilitate efficient computation in the subsequent least square problem in (4.8). The least square problem, i.e., min ‖Ax – b‖2 with , , is solved by using the sparse.linalg.lsqr module in the SciPy package (version 0.18.1) [36] for solving least square problems with sparse matrices.
To compute the weighted Wasserstein distance in (4.18), we consider the optimization problem as an assignment problem and solve it by the Hungarian algorithm. Given two enriched barcodes and , we first construct a pseudobarcode for each of them to account for the situation where a bar is not paired with another. The pseudobarcodes are and . Then the assignment problem between B ⋃ BB′ and B′ ⋃ B′B is solved with the cost . The linear_sum_assignment tool under the optimize module of the SciPy package [36] is used.
The method in this work is implemented as a Python package, and it is available at github.com/GWWEI/EnrichedBarcode together with a notebook reproducing the examples in this paper.
5. Numerical results.
5.1. Simple examples.
Consider a simplicial complex X with four vertices and four edges (01, 02, 13, 23) with unit length that forms a square as shown on the left in Figure 1. The 1-cochain is a real cocycle. The notation means that and . The combinatorial Laplacian matrix is
when a uniform weight of 1 is assigned to all edges. Then, we obtain a smoothed cocycle with a 0-cochain which minimizes to 0.
Figure 1.
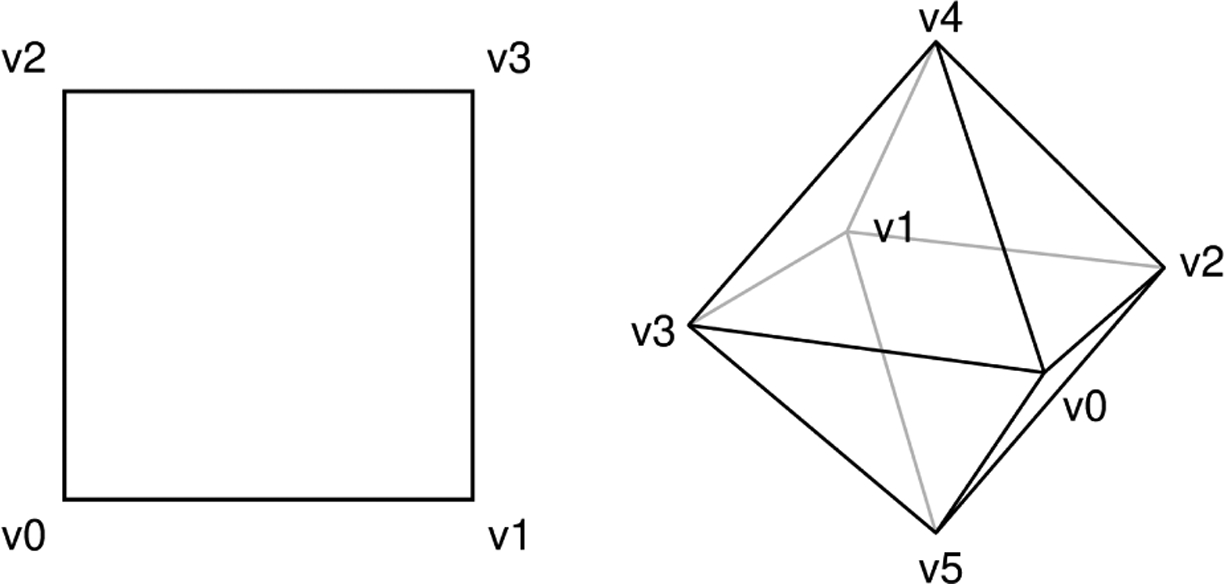
Left: A (geometric) simplicial complex with four vertices and four equal-length edges. Right: A simplicial complex with six vertices, twelve edges, and eight triangles.
On the right of Figure 1, we consider a simplicial complex (an octahedron) with six vertices, twelve edges, and eight triangles (024, 025, 034, 035, 124, 125, 134, 135). The 2-cochain is a real cocycle. The associated smoothed cocycle . We observe that in both cases, the absolute value of each smoothed cocycle annotates a weight function that depicts the loop and the cavity.
5.2. Persistent cohomology analysis of synthetic datasets.
In this section, we show the smoothed representative 1- and 2-cocycles and the enriched barcodes using synthetic datasets. We create some example input functions defined on the nodes and aim to reflect the information about these functions on the enriched barcodes.
Annuluses.
We first consider a point cloud sampled from two adjacent annuluses with radii 1 and centered at (0, 0) and (2, 2) as shown in Figure 2. The persistent cohomology computation was carried out using a Vietoris–Rips complex based filtration with the Euclidean distance. There are two persistent H1 bars associated to the two significant circles whose smoothed cocycles show the contribution of simplices to the bars (see Figure 2).
Figure 2.
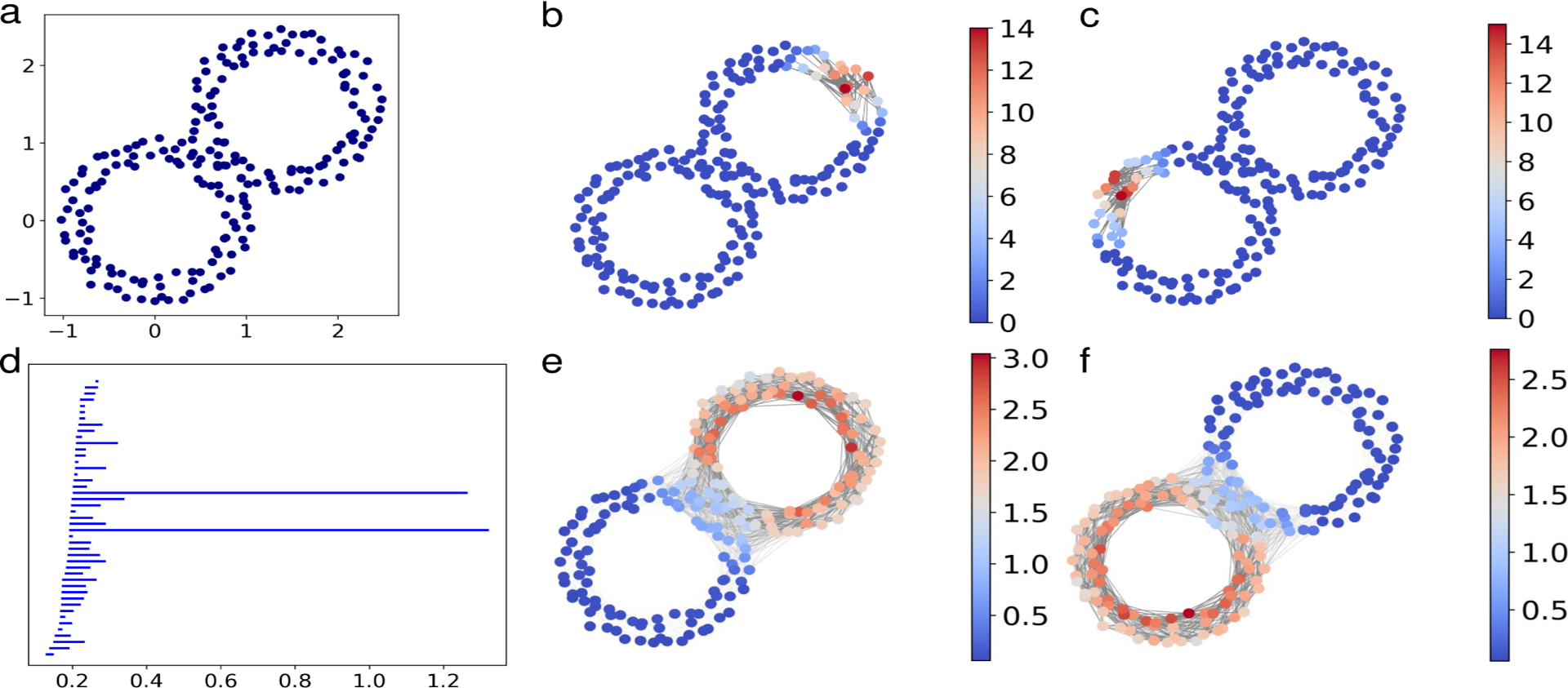
a: A point cloud sampled from two adjacent annulus. b,c: Two representative cocycles corresponding to the two long bars in the H1 barcode. d: The H1 persistence barcode of the point cloud with Vietoris-Rips filtration. e,f: The smoothed cocycles. In b, c, e, and f, the node color shows the weight induced by the smoothed cocycle projected to the nodes and the opaqueness of edges shows the weight induced by the smoothed cocycle.
Given datasets with similar geometry but different nongeometric information, values on the nodes in this case, we can use enriched barcodes to distinguish between them as shown in Figure 3. The Wasserstein characteristics curve defined in (4.19) for datasets in Figure 3, i.e., D1, D2, and D3, are generated. Here, D1 and D2 have the same geometry, and thus their curve is more on the left side, which means there is a smaller distance between their persistent homology barcodes. On the other hand, D3 has a similar value assignment on the points as that of D2, so their curve is on the bottom, which means there is a smaller distance in the nongeometric information.
Figure 3.
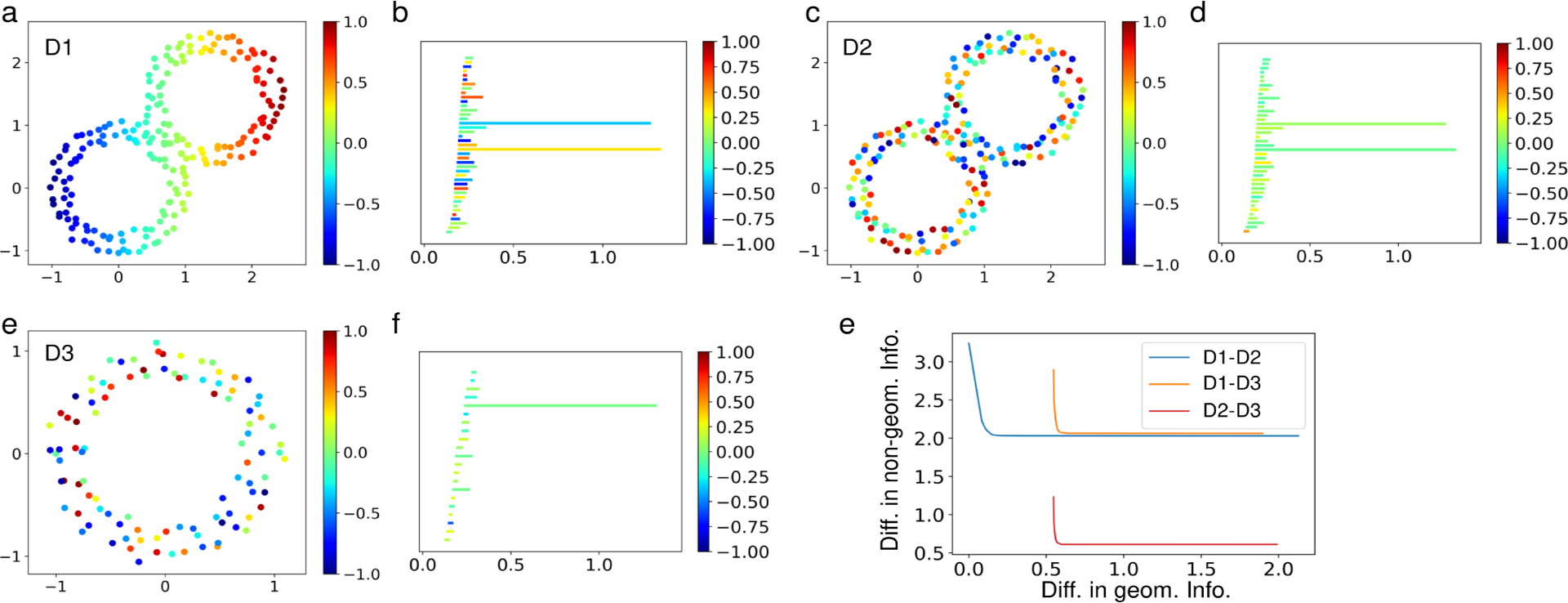
a–f: Three datasets with nongeometric information on the nodes and their H1 enriched barcodes. e: The Wasserstein characteristics curves among these three datasets. The computation is done on a finite set of γ values, from 0 to 1 with a step size of 0.005.
Cuboid with cavities.
In this example, we consider a rectangular cuboid ([0, 4] × [0, 2] × [0, 2]) containing two spherical cavities with radius of 0.5 centered at (1, 1, 1) and (3, 1, 1). Two thousand points are first sampled from a uniform distribution over the cuboid, and those inside the balls are deleted. The dataset with values on the points, the two smoothed cocycles corresponding to the two voids, and the enriched barcodes are shown in Figure 4.
Figure 4.

a: The points sampled from an object which is a with two spherical cavities. b and c: Two representative cocycles corresponding to the two long bars in the H2 barcode. d: The persistent cohomology enriched H2 barcode showing the two voids in the blue and red regions of the original dataset. e and f: The two smoothed 2-cocycles. The faces where the cocycles take absolute values greater than or equal to 0.005 are plotted as grey triangles and the point size shows the weight projected to the points from the 2-simplices. The smoothing is done on the subcomplexes associated to the filtration values at the middle of the corresponding bars.
5.3. Persistent cohomology analysis of molecules.
Cyclic and cage-like structures often exist in complicated macromolecules in various scales. They can be as small as a benzene (a ring) containing 6 heavy atoms or an adamantane (a cage) containing 10 heavy atoms. Some macromolecules have a global configuration of cyclic or cage-like structures such as buckminsterfullerene and carbon nanotubes which consist of tens or hundreds of atoms. Persistent cohomology is good at detecting these structures in multiple scales, and when we label the atoms by their element types, we can also reveal the element composition of the detected structures. Specifically, if oxygen is of interest, we construct an input function f0 (see section 4.3) that is defined on the nodes representing the atoms and outputs 1 on oxygen atoms and 0 elsewhere. We illustrate this application using a cyclic structure cucurbit[8]uril and a cage-like structure B24N24 cage in this section. The traditional persistent homology barcodes will only show the structure of the molecule without the element type information. If we take subsets of atoms of selected element types, the resulting barcode does not faithfully represent the original structure. By using the enriched barcodes, we can quantify the element type composition of each bar while retaining the original structure. For example, the enriched barcode shows that there are eight medium-sized H1 bars that mainly consist of carbon and nitrogen atoms, which can be confirmed by observing the molecular structure (Figure 5).
Figure 5.
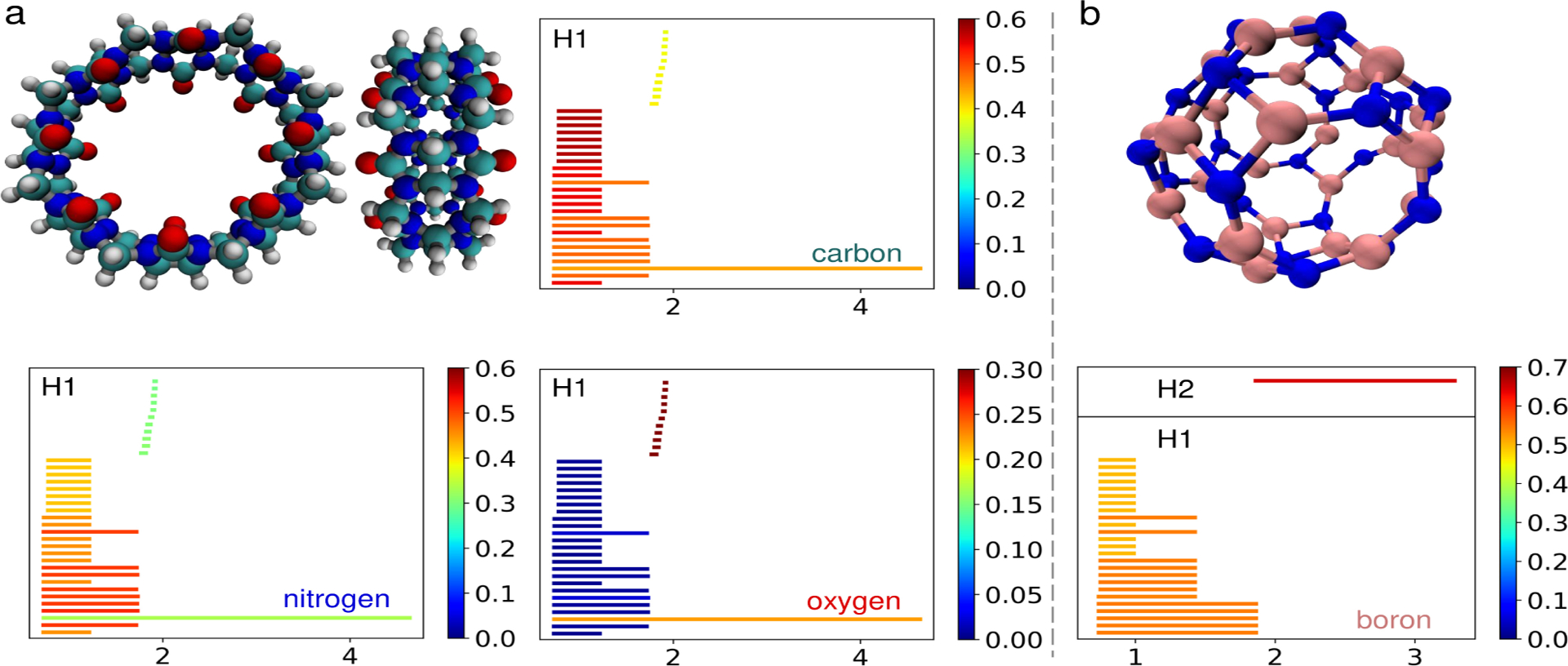
a: The cucurbit[8]uril molecule viewed from two different angles. The hydrogen, carbon, nitrogen, and oxygen atoms are colored in white, cyan, blue, and red, respectively. b: A boron nitride cage structure (B24N24 with nitrogen and boron atoms colored in blue and pink). The enriched barcodes are obtained by assigning 1 to the nodes of the corresponding atom type and 0 elsewhere.
Cucurbituril.
In this example, we consider a macrocyclic molecule cucurbit[8]uril from the cucurbituril family. The molecule contains eight 6-membered rings and sixteen 5-membered rings consisting of carbon and nitrogen atoms. The rings form a big cyclic structure with a relatively tighter opening surrounded by oxygen atoms. The structure is taken from the provided structure in the SAMPL6 challenge [1], and the resulting H1 barcodes are shown in Figure 5a.
Boron nitride cage.
The fullerene-like boron nitride cages exhibit spherical structures similar to fullerenes but consist of boron and nitrogen atoms. The global spherical structure is composed of a collection of local rings containing several atoms. A possible structure of B24N24 cage given in the supporting information of [56] is used in this example. The molecule and the enriched barcode are shown in Figure 5b.
In this application, the element type could be substituted by other information that the user is interested in, such as partial charge, van der Waals potential, and electrostatic solvation free energy.
5.4. Prediction of protein-ligand binding affinities.
In this example, we show the usefulness of the enriched barcode in an important real application. An important component of computer-aided drug design is the prediction of protein-ligand binding affinities based on given protein-ligand complex structures. Persistent homology is good at identifying rings, tunnels, and cavities in various scales which are crucial to the protein-ligand complex stability and instability. In addition to geometry and topology, chemical and biological complexities also need to be addressed toward a practically useful method for this application. The important chemical and biological information includes atom properties such as atom types, atomic charges, and interaction strengths. Information from bioinformatics study such as the conservation scores of protein residues can also play an essential role. To this end, for example, the behavior of atoms of different element types can be described by computing persistent homology for subsets of atoms of the molecule of certain element types [11]. The interaction between protein and ligand can be emphasized by prohibiting an edge to form between two atoms either both in the protein or both in the ligand. The electrostatic interactions can be revealed by tweaking the distance matrix used for filtration to be the interaction strength computed with a chosen physical model such as Coulomb’s law [8]. However, the approaches described above disturb the original geometry and topology of the protein-ligand complexes. With the method proposed in this work, we are able to naturally embed the information such as atom type, atomic partial charges, and electrostatic interactions to the barcodes without disturbing the original geometric and topological setup of the molecular systems. An example of enriched barcodes is shown in Figure 6. In this example, the H1 and H2 barcodes identified many cycles in the whole molecule, the carbon network, and the nitrogen-oxygen network. We constructed the enriched barcodes with the input nongeometric information (the absolute value of Coulomb potential between two atoms) defined on the edges. As expected, the electrostatic interaction is the most inferior in the hydrophobic network (set of carbon atoms) and is the most active in the hydrophilic network (set of nitrogen and oxygen atoms). Interestingly, the electrostaic interaction is more active in H1 and H2 bars with smaller birth values in the all heavy atom characterization as shown in Figure 6. This may indicate that the local active sites may be involved in stronger electrostatic interactions.
Figure 6.
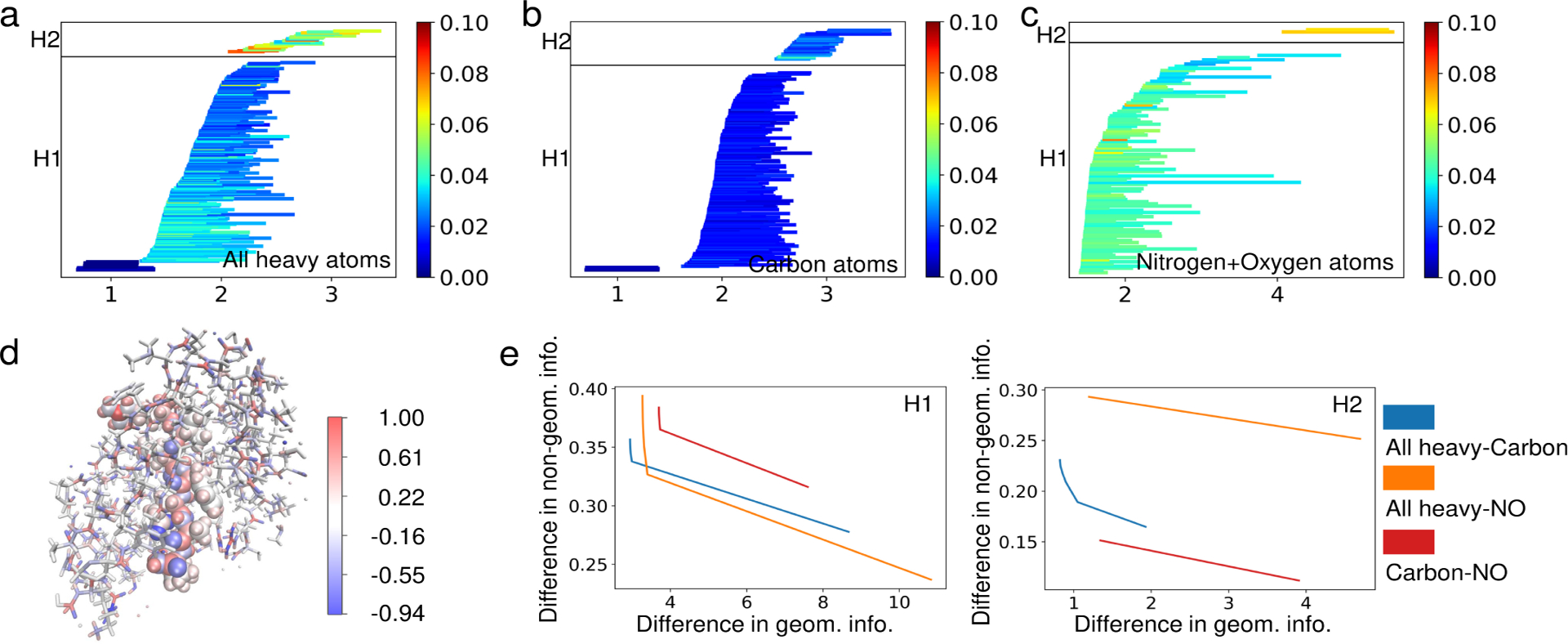
Enriched barcodes focusing on electrostatic interactions. a, b, and c: Enriched barcodes for electrostatic interaction strengths (quantified using absolute values of Coulomb potentials) generated by computing persistent cohomology with alpha complex filtration on all heavy atoms, all carbon atoms, and nitrogen and oxygen atoms, respectively. d: The ligand (as van der Waals spheres) and the surrounding protein atoms (within 12 Å of ligand as thick sticks) of PDB entry 1a94. The color reflects the strength of electrostatic interactions. e: The Wasserstein distance curves for the comparison of the enriched barcodes. We computed for a grid of γ values from 0 to 1 with a step size of 0.02.
We compute the persistent cohomology enriched barcodes for protein-ligand complexes, turn them into structured features, and feed these features to machine learning methods for the prediction of binding affinities. The procedure is validated on datasets from the PDBbind database [38], which includes experimentally derived protein-ligand complex structures and the associated binding affinities.
Enriched barcodes generation.
In addition to the traditional barcode obtained from persistent homology computation, we would also like to add descriptions of the electrostatic properties of the system. An efficient characterization of this property is the Coulomb potential where the interaction between two point charges is relatively described by qiqj/rij, where qi and qj are the point charges with a distance of rij. The atomic partial charges of proteins are assigned by using PDB2PQR software [23] with CHARMM22 force field. Two types of constructions of the physical information are used to characterize the systems.
For dimension 0, a collection of subsets of atoms is first identified according to atom types. Specifically, 10 element types (C, N, O, S, P, F, Cl, Br, I, H) are considered for ligands, 5 element types are considered for proteins (C, N, O, S, H), and a total of 50 subsets of atoms are selected by choosing one element type from each component (protein or ligand). The pairwise distance matrix based on Euclidean distance is tweaked by setting distances between atoms either both from protein or both from ligand to infinity which emphasizes the interactions between protein and ligand. Based on the tweaked distance matrix, persistent (co)homology computation with the Rips complex is performed. The electric potential is computed for each atom with its nearest neighbor in the different part of the protein-ligand complex and is put on this atom as the additional information. We define the input function to take 0 on protein atoms and to take the value discussed above on ligand atoms. The average potential over ligand atoms in each 0-cocycle representative is used to generate features. In this way, the favorability of the protein ligand electrostatic interactions is explicitly described.
For dimensions 1 and 2, the input function is defined to output the absolute value of electric potential on edges connecting two atoms to characterize the interaction strengths. The Coulomb potential is modeled as
where ke is Coulomb’s constant, qi and qj are the partial charges of atoms i and j, and rij is the distance between the two atoms. Persistent (co)homology with alpha complex is computed on three subsets of the protein-ligand complexes, all heavy atoms, all carbon atoms, and all oxygen/nitrogen atoms. For simplicity, all enriched barcodes are computed only at the middle points of the bars.
Featurization of barcodes.
Given an enriched barcode, obtained by applying the proposed method to a dataset with an input function f0 (see section 4.3), we turn it into a fixed shape array required by the machine learning algorithms we choose. Here, the input function is or described in the previous section when computing 0th dimensional persistent (co)homology or in higher dimensions.
For dimension 0, we first identify a range of scales to focus on, and in this application we are interested in the interval [0, 12)Å. The interval is then divided into 6 subintervals to address different types of interactions. For dimension 0, we are interested in the death values of the bars. Therefore, a collection of index sets marking the death values of the bars that fall into each subinterval is calculated as
For dimensions 1 and 2, we are interested in the interval [0, 6)Å with Alpha complex filtration. The interval is then divided into 6 equal-length subintervals . We then define a collection of index sets marking the bars that overlap with each subinterval,
Given a collection of index sets {Ij}j, a feature vector vh(B) is defined as
Basically, given m subintervals, we turn the barcode into a feature vector of length m counting the number of persistence bars intersecting with each subinterval. When is used, it characterizes the number of component merging events in each filtration parameter interval. When is used, it reflects the ranks of homology groups at a certain stage along the course of filtration.
A feature vector vf(B, f0) can be generated subsequently to address the information of the predefined function on the homology generators,
where , which is simply in this application. This jth entry of this feature vector is simply the average value of for bars [bi, di) that intersect with the jth subinterval.
While the featurization procedure is effective in this application given that we have some prior understanding of molecular interactions, the readers may also find other featurization methods useful for general applications such as persistence images [2] and a template function based method [49].
Machine learning algorithm.
The application of predicting protein-ligand binding affinity based on structures can be regarded as a supervised learning problem. Generally speaking, we are given a collection of pairs of input and output {(xi, yi)} and there chosen which is a model is a function M(x; θ) with tunable parameters θ. The training process is to find a specific setting for the function M that globally or locally minimizes a penalty function which depends on the given data {(xi, yi)} and the parameter set θ. Once trained, the model can be used to predict the output for a newly given input.
In general, the proposed persistent cohomology can be combined with any advanced machine learning algorithm, such as deep neural networks [10]. However, the goal of the present work is to illustrate the utility of the proposed persistent cohomology. Therefore, we choose a relatively robust and efficient algorithm, the gradient booting trees (GBT) method, for testing the accuracy of our method. GBT is an ensemble of trees methods with single decision trees as building blocks. The training of a GBT model is done by adding one tree at a time according to the reduction of loss in the current model. In practice, different randomly selected subsets of the training data and features are used for each update of the model to reduce overfitting. For every result reported in Table 2, a parameter search is done by 5-fold cross-validation within the training set where the model performance is assessed by Pearson’s correlation coefficient. The candidate values for hyper-parameters tried are summarized in Table 1. Another hyper-parameter max feature is set to sqrt because of the relatively large number of features. The GradientBoostingRegressor module in the scikit-learn (version 0.17.1) [45] software is used.
Table 2.
The predictor performance is evaluated by training on PDBbind refined set excluding the core set and testing on the core set of a certain year’s version. The median Pearson’s correlation coefficient (root mean squared error in pKd/pKi unit) among 10 repeated experiments is reported for persistent homology (PH) and persistent cohomology (PC). In the PC, electrostatic information is utilized.
| PDBbind | v2007 | v2013 | v2015 | v2016 |
|---|---|---|---|---|
| Dim 0 PH | 0.802 (1.47)) | 0.754 (1.56) | 0.745 (1.56) | 0.824 (1.32) |
| Dim 0 PC | 0.796 (1.50) | 0.768 (1.53) | 0.763 (1.53) | 0.833 (1.31) |
| Dim 1&2 PH | 0.726 (1.65) | 0.706 (1.67) | 0.718 (1.62) | 0.767 (1.46) |
| Dim 1&2 PC | 0.738 (1.65) | 0.784 (1.46) | 0.780 (1.47) | 0.781 (1.41) |
Table 1.
Candidate values for hyper-parameters of the gradient boosting trees model.
| Hyper-parameters | Candidate values |
|---|---|
| n_estimators | 5000, 10000, 20000 |
| max_depth | 4, 8, 16 |
| min_samples_split | 5, 10, 20 |
| learning_rate | 0.0025, 0.005, 0.01 |
| subsample | 0.25, 0.5, 0.75 |
| min_samples_leaf | 1, 3 |
Binding affinity predictions.
We test the improvement of the enriched barcodes with electrostatic information in the cases of 0th dimension and higher dimensions using the PDBbind database. The predictor performance is improved by using the enriched barcode embedding the electrostatics information. The results are listed in Table 2. This study indicates that the electrostatic information incorporated in the persistent cohomology generally improves the binding affinity predictions. There is an exception in the v2007 dataset where adding in electrostatic information causes reduced accuracy. We believe that this is due to the small size and low diversity of the v2007 dataset compared to other datasets. The disadvantage of the overfitting due to the introduction of more features outweighs the benefit brought about by the extra information. The approach proposed in this work can be generalized to other physical properties, such as van der Waals interactions.
We also compare our method to some well-known methods of different kinds using the PDBbind v2016 dataset: KDEEP [35] using the advanced deep learning technique; RF-Score [3] using random forest, which has a similar level of complexity compared to GBT; X-Score [51], a consensus empirical scoring function; and cyScore [12], an empirical scoring function combining geometric descriptions (e.g., curvature and surface area) and physical terms (e.g., electrostatics and hydrogen bonds). In the test, the PDBbind 2016 core set is used as the testing set, and the PDBbind 2016 refined set excluding the core set is used as the training set. We report the performance of our model using all features, i.e., conventional persistence barcode features and enriched barcode features about Coulomb interactions of dimensions 0 (Rips filtration), 1, and 2 (alpha filtration). With only Coulomb interactions as the additional feature, our cohomology method achieves a performance comparable to the state-of-the-art methods as shown in Figure 7.
Figure 7.

Performance comparison of our method to some other methods on PDBbind v2016 dataset (the core set as the test set and the rest of the refined set as the training set). The metrics used are Pearson’s correlation coefficient (Rp) and root-mean-squared-error (RMSE). The results of other methods are taken from [35].
6. Conclusion.
Algebraic topology, particularly persistent homology, has been devised to simplify high-dimensional complex geometric information in terms of topological invariants. However, during the topological abstraction of biomolecular datasets, some physical, chemical, and biological information is neglected. Therefore, there is a pressing need to embed physical, chemical, and biological information, such as atom types, partial charges, and pairwise interaction strengths in a dataset, into the topological invariants generated from the geometric (i.e., structural) information of the dataset. In general, when analyzing datasets with persistent homology, the geometric information is built into topological invariants while nongeometric information is usually neglected. In duality to homology, cohomology allows us to retain crucial nongeometric information in topological modeling. Utilizing the richer information carried by cohomology, we introduce an enriched topological data representation by encoding in the topological invariants the additional physical information from the dimensions that are not used for persistent homology computation. The nongeometric information is attached to the topological invariants in regular persistent homology computation. This is achieved by finding a smoothed representative cocycle with respect to a Laplacian for simplicial complexes. The smoothed cocycles then serve as measures on the simplicial complexes and allow us to integrate the additional information. As a result, in addition to the original persistence barcodes, functions of filtration values associated with each persistence pair are constructed, which enriches the information carried by the original barcodes. A similarity score based on Wasserstein distance is introduced to analyze these enriched barcodes. The properties of the proposed methods are illustrated with various numerical experiments including synthetic datasets, small molecules, and protein-ligand complexes. We show that the enriched barcode can depict the element compositions and electrostatic interactions corresponding to the detected topological features. For the protein-ligand binding affinity prediction that motivated the current development, we show that by adding electrostatics information to the barcodes, the present persistent cohomology enriched barcode improves the performance in the practical prediction of protein-ligand binding affinities from massive datasets. The results obtained from the proposed method are comparable to the other state-of-the-art methods on commonly used benchmarks. The proposed method is potentially useful for a wide range of applications that contain nongeometric information in data which does not warrant direct application of traditional persistent homology.
Funding:
This work was funded by NSF grants DMS-1721024, DMS-1761320, and IIS1900473, NIH grant R01GM126189, Pfizer, and Bristol-Myers Squibb.
REFERENCES
- [1].SAMPL6 Challenge, https://drugdesigndata.org/about/sampl6; accessed 2018-04-10.
- [2].Adams H, Emerson T, Kirby M, Neville R, Peterson C, Shipman P, Chepushtanova S, Hanson E, Motta F, and Ziegelmeier L, Persistence images: A stable vector representation of persistent homology, J. Mach. Learn. Res, 18 (2017), pp. 218–252. [Google Scholar]
- [3].Ballester PJ and Mitchell JBO, A machine learning approach to predicting protein-ligand binding affinity with applications to molecular docking, Bioinformatics, 26 (2010), pp. 1169–1175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Bauer U, Ripser: Efficient Computation of Vietoris-Rips Persistence Barcodes, preprint, https://arxiv.org/abs/1908.02518, 2019.
- [5].Bauer U, Kerber M, Reininghaus J , and Wagner H, PHAT–persistent homology algorithms toolbox, J. Symbolic Comput, 78 (2017), pp. 76–90. [Google Scholar]
- [6].Bell N and Hirani AN, PyDEC: Software and algorithms for discretization of exterior calculus, ACM Trans. Math. Software, 39 (2012), 3. [Google Scholar]
- [7].Bendich P, Edelsbrunner H, and Kerber M, Computing robustness and persistence for images, IEEE Trans. Vis. Comput. Graphics, 16 (2010), pp. 1251–1260. [DOI] [PubMed] [Google Scholar]
- [8].Cang Z, Mu L, and Wei GW, Representability of algebraic topology for biomolecules in machine learning based scoring and virtual screening, PLOS Comput. Biol, 14 (2018), e1005929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Cang Z and Wei GW, Analysis and prediction of protein folding energy changes upon mutation by element specific persistent homology, Bioinformatics, 33 (2017), pp. 3549–3557. [DOI] [PubMed] [Google Scholar]
- [10].Cang Z and Wei GW, TopologyNet: Topology based deep convolutional and multi-task neural networks for biomolecular property predictions, PLOS Comput. Biol, 13 (2017), e1005690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Cang Z and Wei GW, Integration of element specific persistent homology and machine learning for protein-ligand binding affinity prediction, Int. J. Numer. Methods Biomed. Engrg, 34 (2018), e2914. [DOI] [PubMed] [Google Scholar]
- [12].Cao Y and Li L, Improved protein–ligand binding affinity prediction by using a curvature-dependent surface-area model, Bioinformatics, 30 (2014), pp. 1674–1680. [DOI] [PubMed] [Google Scholar]
- [13].Carlsson G, Topology and data, Bull. Amer. Math. Soc, 46 (2009), pp. 255–308. [Google Scholar]
- [14].Carlsson G and De Silva V, Zigzag persistence, Found. Comput. Math, 10 (2010), pp. 367–405. [Google Scholar]
- [15].Carlsson G and Zomorodian A, The theory of multidimensional persistence, Discrete Comput. Geom, 42 (2009), pp. 71–93. [Google Scholar]
- [16].Chan JM, Carlsson G, and Rabadan R, Topology of viral evolution, Proc. Natl. Acad. Sci. USA, 110 (2013), pp. 18566–18571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Chung FRK, Spectral Graph Theory, CBMS Reg. Conf. Ser. Math 92, AMS, Providence, RI, 1997. [Google Scholar]
- [18].Cohen-Steiner D, Edelsbrunner H, and Morozov D, Vines and vineyards by updating persistence in linear time, in Proceedings of the 22nd Annual Symposium on Computational Geometry, ACM, New York, 2006, pp. 119–126. [Google Scholar]
- [19].Dabaghian Y, Mémoli F, Frank L, and Carlsson G, A topological paradigm for hippocampal spatial map formation using persistent homology, PLOS Comput. Biol, 8 (2012), e1002581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].De Silva V, Morozov D, and Vejdemo-Johansson M, Dualities in persistent (co)homology, Inverse Problems, 27 (2011), 124003. [Google Scholar]
- [21].De Silva V, Morozov D, and Vejdemo-Johansson M, Persistent cohomology and circular coordinates, Discrete Comput. Geom, 45 (2011), pp. 737–759. [Google Scholar]
- [22].Desbrun M, Hirani AN, Leok M, and Marsden JE, Discrete Exterior Calculus, preprint, https://arxiv.org/abs/math/0508341, 2005.
- [23].Dolinsky TJ, Nielsen JE, McCammon JA, and Baker NA, PDB2PQR: An automated pipeline for the setup, execution, and analysis of Poisson-Boltzmann electrostatics calculations, Nucleic Acids Res, 32 (2004), pp. W665–W667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Edelsbrunner H, Weighted Alpha Shapes, Technical report UIUCDCS-R-92–1760, Department of Computer Science, University of Illinois at Urbana-Champaign, Urbana, IL, 1992. [Google Scholar]
- [25].Edelsbrunner H, Letscher D, and Zomorodian A, Topological persistence and simplification, Discrete Comput. Geom, 28 (2001), pp. 511–533. [Google Scholar]
- [26].Frosini P and Landi C, Size theory as a topological tool for computer vision, Pattern Recognition Image Anal., 9 (1999), pp. 596–603. [Google Scholar]
- [27].Gabriel P, Unzerlegbare Darstellungen. I, Manuscripta Math, 6 (1972), pp. 71–103. [Google Scholar]
- [28].Gameiro M, Hiraoka Y, Izumi S, Kramar M, Mischaikow K, and Nanda V, A topological measurement of protein compressibility, Jpn. J. Ind. Appl. Math, 32 (2015), pp. 1–17. [Google Scholar]
- [29].Goldberg T, Combinatorial Laplacians of Simplicial Complexes, Senior thesis, Bard College, Addandale-on-Hudson, NY, 2002. [Google Scholar]
- [30].Hatcher A, Algebraic Topology, Cambridge University Press, Cambridge, UK, 2001. [Google Scholar]
- [31].Hausmann J-C, On the Vietoris-Rips complexes and a cohomology theory for metric spaces, in Prospects in Topology, Ann. of Math. Stud 138, Princeton University Press, Princeton, NJ, 1995, pp. 175–188. [Google Scholar]
- [32].Hirani AN, Discrete Exterior Calculus, Ph.D. thesis, California Institute of Technology, Pasadena, CA, 2003. [Google Scholar]
- [33].Hirani AN, Kalyanaraman K, Wang H, and Watts S, Cohomologous Harmonic Cochains, preprint, https://arxiv.org/abs/1012.2835, 2010.
- [34].Horak D and Jost J, Spectra of combinatorial Laplace operators on simplicial complexes, Adv. Math, 244 (2013), pp. 303–336. [Google Scholar]
- [35].Jiménez J, Skalic M, Martinez-Rosell G, and De Fabritiis G, KDEEP: Protein–ligand absolute binding affinity prediction via 3D-convolutional neural networks, J. Chem. Inform. Model, 58 (2018), pp. 287–296. [DOI] [PubMed] [Google Scholar]
- [36].Jones E, Oliphant T, Peterson P, et al. , SciPy: Open Source Scientific Tools for Python, 2001, http://www.scipy.org/.
- [37].Kramar M, Levanger R, Tithof J, Suri B, Xu M, Paul M, Schatz MF, and Mischaikow K, Analysis of Kolmogorov flow and Rayleigh-B\’enard convection using persistent homology, Phys. D, 334 (2016), pp. 82–98. [Google Scholar]
- [38].Liu Z, Li Y, Han L, Liu J, Zhao Z, Nie W, Liu Y, and Wang R, PDB-wide collection of binding data: Current status of the PDBbind database, Bioinformatics, 31 (2015), pp. 405–412. [DOI] [PubMed] [Google Scholar]
- [39].Mischaikow K and Nanda V, Morse theory for filtrations and efficient computation of persistent homology, Discrete Comput. Geom, 50 (2013), pp. 330–353. [Google Scholar]
- [40].Morozov D, Dionysus: Library for Computing Persistent Homology, 2012, https://mrzv.org/software/dionysus2/, https://github.com/mrzv/dionysus.
- [41].Munch E, Applications of Persistent Homology to Time Varying Ssystems, Dissertation, Duke University, Durham, NC, 2013. [Google Scholar]
- [42].Nguyen DD, Cang Z, Wu K, Wang M, Cao Y, and Wei G-W, Mathematical deep learning for pose and binding affinity prediction and ranking in D3R grand challenges, J. Computer-Aided Molecular Des, 33 (2019), pp. 71–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Obayashi I and Yoshiwaki M, Field Choice Problem in Persistent Homology, preprint, https://arxiv.org/abs/1911.11350, 2019.
- [44].Otter N, Porter MA, Tillmann U, Grindrod P, and Harrington HA, A roadmap for the computation of persistent homology, EPJ Data Sci, 6 (2017), 17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, Vanderplas J, Passos A, Cournapeau D, Brucher M, Perrot M, and Duchesnay E, Scikit-learn: Machine learning in Python, J. Mach. Learn. Res, 12 (2011), pp. 2825–2830. [Google Scholar]
- [46].Perea JA, Multiscale projective coordinates via persistent cohomology of sparse filtrations, Discrete Comput. Geom, 59 (2018), pp. 175–225. [Google Scholar]
- [47].Perea JA, Deckard A, Haase SB, and Harer J, Sw1pers: Sliding windows and 1-persistence scoring; discovering periodicity in gene expression time series data, BMC Bioinformatics, 16 (2015), p. 257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Rybakken E, Baas N, and Dunn B, Decoding of neural data using cohomological feature extraction, Neural Comput., 31 (2019), pp. 68–93. [DOI] [PubMed] [Google Scholar]
- [49].Tymochko S, Munch E, and Khasawneh FA, Adaptive Partitioning for Template Functions on Persistence Diagrams, preprint, https://arxiv.org/abs/1910.08506, 2019.
- [50].Vejdemo-Johansson M, Pokorny FT, Skraba P, and Kragic D, Cohomological learning of periodic motion, Appl. Algebra Engrg. Comm. Comput, 26 (2015), pp. 5–26. [Google Scholar]
- [51].Wang R, Lai L, and Wang S, Further development and validation of empirical scoring functions for structure-based binding affinity prediction, J. Computer-Aided Molecular Des, 16 (2002), pp. 11–26. [DOI] [PubMed] [Google Scholar]
- [52].Wu C, Ren S, Wu J, and Xia K, Weighted (Co)homology and Weighted Laplacian, preprint, https://arxiv.org/abs/1804.06990, 2018.
- [53].Xia KL and Wei GW, Persistent homology analysis of protein structure, flexibility and folding, Int. J. Numer. Methods Biomed. Engrg, 30 (2014), pp. 814–844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Xia KL and Wei GW, Multidimensional persistence in biomolecular data, J. Comput. Chem, 36 (2015), pp. 1502–1520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Xia KL and Wei GW, Persistent topology for cryo-EM data analysis, Int. J. Numer. Methods Biomedical Engrg, 31 (2015), e02719. [DOI] [PubMed] [Google Scholar]
- [56].Zhang S, Wang Q, Kawazoe Y, and Jena P, Three-dimensional metallic boron nitride, J. Amer. Chem. Soc, 135 (2013), pp. 18216–18221. [DOI] [PubMed] [Google Scholar]
- [57].Zomorodian A and Carlsson G, Computing persistent homology, Discrete Comput. Geom, 33 (2005), pp. 249–274. [Google Scholar]


