A Model-Informed Method for the Purpose of Precision Dosing of Isoniazid in Pulmonary Tuberculosis

Abstract

Background and Objective

This study aimed to develop and evaluate a population pharmacokinetic model and limited sampling strategy for isoniazid to be used in model-based therapeutic drug monitoring.

Methods

A population pharmacokinetic model was developed based on isoniazid and acetyl-isoniazid pharmacokinetic data from seven studies with in total 466 patients from three continents. Three limited sampling strategies were tested based on the available sampling times in the dataset and practical considerations. The tested limited sampling strategies sampled at 2, 4, and 6 h, 2 and 4 h, and 2 h after dosing. The model-predicted area under the concentration–time curve from 0 to 24 h (AUC₂₄) and the peak concentration from the limited sampling strategies were compared to predictions using the full pharmacokinetic curve. Bias and precision were assessed using the mean error (ME) and the root mean square error (RMSE), both expressed as a percentage of the mean model-predicted AUC₂₄ or peak concentration on the full pharmacokinetic curve.

Results

Performance of the developed model was acceptable and the uncertainty in parameter estimations was generally low (the highest relative standard error was 39% coefficient of variation). The limited sampling strategy with sampling at 2 and 4 h was determined as most suitable with an ME of 1.1% and RMSE of 23.4% for AUC₂₄ prediction, and ME of 2.7% and RMSE of 23.8% for peak concentration prediction. For the performance of this strategy, it is important that data on both isoniazid and acetyl-isoniazid are used. If only data on isoniazid are available, a limited sampling strategy using 2, 4, and 6 h can be employed with an ME of 1.7% and RMSE of 20.9% for AUC₂₄ prediction, and ME of 1.2% and RMSE of 23.8% for peak concentration prediction.

Conclusions

A model-based therapeutic drug monitoring strategy for personalized dosing of isoniazid using sampling at 2 and 4 h after dosing was successfully developed. Prospective evaluation of this strategy will show how it performs in a clinical therapeutic drug monitoring setting.

Supplementary Information

The online version contains supplementary material available at 10.1007/s40262-020-00971-2.

Key Points

Model-informed precision dosing may aid in optimizing tuberculosis treatment

We developed a population pharmacokinetic model for isoniazid and its metabolite based on the largest and most diverse dataset thus far and thoroughly validated its suitability for purposes of dose individualization

We found that sampling at 2 and 4 h with data on both isoniazid and acetyl-isoniazid, or sampling at 2, 4, and 6 h without the metabolite could be used to predict exposure (area under the concentration–time curve)

Background

Although the disease burden of tuberculosis (TB) is falling, it remains one of the top ten causes of death globally and is the leading cause of death from a single infectious agent [1]. The average global treatment success rate for drug-susceptible TB was estimated at 85% in 2017 [1]. Despite this high success rate, it still means that one out of every seven patients treated for TB has an unfavorable treatment outcome. This shows that a significant part of the patients does not respond adequately to treatment. A possible reason for not responding to treatment is suboptimal anti-TB drug exposure [2].

Isoniazid (INH) is one of the pillars on which treatment of drug-susceptible TB is based and is listed as an essential medicine by the World Health Organization [3]. Low INH concentrations compared to the median in a population have been reported to be common and are often a result of high inter-individual variability (IIV) in the pharmacokinetics of this drug [4–7]. A large part of this variability can be attributed to the polymorphic N-acetyltransferase 2 (NAT2) enzyme that catalyzes the acetylation of INH into its acetyl-INH metabolite [8].

Large inter-individual variability in pharmacokinetics is one of the motives and prerequisites for therapeutic drug monitoring (TDM) [2]. Therapeutic drug monitoring is an approach to personalize drug dosing by measuring a patient’s drug exposure and comparing it to a drug-specific target level and adjusting the dose if needed. The exposure is approximated by sampling at drug-specific planned times. This strategy is called a limited sampling strategy (LSS). The area under the concentration–time curve over a dosing interval (0–24 h, AUC₂₄) in relation to a minimal inhibitory concentration has been proposed to be the most important predictor of treatment outcome for the first-line TB drugs [9–12]. However, many different pharmacokinetic (PK) target suggestions exist [2, 9, 13–16]. Some of these have a peak concentration (C_max) target while others use AUC₂₄. Lacking anything more precise, a population median AUC₂₄ value of INH corrected for acetylator status could serve as a PK target as it is known that the standard dose is generally effective [2].

We propose the use of a model-based TDM method using individual predictions from a population PK model for INH. Using a model-based method for TDM has several advantages: it can use flexible sampling times, it allows exposure predictions following dose adjustments, and it can use data from previous sampling occasions for the same patient in the prediction. Available models for INH are often based on data from a single-center study with a limited sample size limiting the generalizability of their use for dose individualization [4, 5, 17–22]. The aim of this study was to develop and evaluate a model-based TDM approach for INH in adult patients with pulmonary TB using a population-PK model suitable for dose individualization in programmatic treatment.

Methods

Data

The data originated from seven previously conducted studies, including data from both clinical trials and TDM [14, 23–28]. All studies included patients with pulmonary TB. The study data are presented in Table 1. In total, data of 466 patients from three continents were used to develop the PK model. These PK data consisted of 2546 INH and 2236 acetyl-INH concentrations collected during an interval range of 0–24 h. Of these concentrations, 6.0% of the INH and 10.9% of the acetyl-INH observations were measured as ‘below the limit of quantification’ (BLQ), which ranged from 0 to 27.3% depending on the study.

Table 1.

Overview of the included study data

	Semvua [23]	Tostmann [24]	Burhan [25]	Aarnoutse [26]	Magis-Escurra [14]	Boeree [27]	Van Beek [28]	Total
Included patients	23	40	180	62	14	97	52	466
Observed data points
Total	92	619	534	1189	154	1804	390	4782
INH	92	309	263	619	154	898	211	2546
Acetyl-INH	0	310	271	570	0	906	179	2236
Data points BLQ, n (%)
Total	2 (2.2)	54 (8.7)	1 (0.2)	40 (3.4)	42 (27.3)	249 (13.8)	7 (1.8)	395 (8.3)
INH	2 (2.2)	27 (8.7)	0 (0)	5 (0.8)	42 (27.3)	72 (8.0)	4 (1.9)	152 (6.0)
Acetyl-INH	–	27 (8.7)	1 (0.4)	35 (6.1)	–	177 (19.5)	3 (1.7)	243 (10.9)
Typical sampling hours	2 and 6 h	Full PK, 9 samples 0–24 h	2 h, full PK for 9 patients	Full PK, 11 samples 0–24 h	Full PK, 11 samples 0–24 h	Full PK, 9 samples 0–24 h	2, 4, and 6 h	–
Samples, median (range)	4 (4–4)	8 (4–9)	1 (1–13)	10 (7–11)	11 (10–11)	9 (5–10)	4 (1–8)	–
Number of occasions	2	1	1	1	1	1	1 (2 for 14 patients)	–
Bioanalysis method	UPLC-UV	UPLC-UV	UPLC-UV	UPLC-UV	LC-MS/MS	UPLC-UV	LC-MS/MS	–
Country of origin	Tanzania	Tanzania	Indonesia	Tanzania	The Netherlandsa	Tanzania and South Africa	The Netherlandsa	–
Setting	Clinical trial	Clinical trial	Clinical trial	Clinical trial	TDM	Clinical trial	TDM	–

BLQ below limit of quantification, h hour, INH isoniazid, LC-MS or liquid chromatography-mass spectrometry, PK pharmacokinetics, TDM therapeutic drug monitoring, UPLC ultra-performance liquid chromatography

^aWhile the patients from these studies were treated in The Netherlands, the TB population in The Netherlands is very heterogenous with many different ethnical backgrounds

Four studies involved intensive PK sampling with at least nine samples taken after a dose of INH [14, 24, 26, 27], two studies involved limited sampling with two to three samples taken [23, 28], and one study involved limited sampling with one sample taken for all except nine individuals who were sampled intensively [25]. Five studies only included measurements of a single occasion [14, 24–27], one study included some measurements of second occasions [28], and one included measurements for second occasions for all individuals [23]. One study included data that were collected during TDM practice [28]. Five studies included PK data on both INH and acetyl-INH [24–28], while the other two studies included PK data on INH [14, 23].

The analysis of INH and acetyl-INH concentrations was performed in The Netherlands for all studies, using either ultra-performance liquid chromatography with ultraviolet detection or liquid chromatography–tandem mass spectrometry [29]. Both methods were extensively validated in accordance with European Medicines Agency and US Food and Drug Administration guidelines. Accuracy was between 99.4 and 108.8% and between 95.6 and 111.3% and the intra- and inter-assay coefficients of variation (CVs) were less than 12.6% and 10.5% for the ultra-performance liquid chromatography with ultraviolet detection and liquid chromatography–tandem mass spectrometry methods, respectively, dependent on the concentration. The lower limits of quantification for INH and acetyl-INH for the ultra-performance liquid chromatography method were 0.0253 mg/L and 0.162 mg/L, and these were 0.0452 mg/L and 0.0450 mg/L for the liquid chromatography-tandem mass spectrometry method. Performance of the assays was externally evaluated by participation in an international proficiency testing program [30].

Software

R version 3.4.3 was used for data management, statistics, and plotting [31]. Model development was performed using the nonlinear mixed-effects modeling program, NONMEM version 7.4 with Pirana as an interface [32, 33]. The first-order conditional estimation method with interaction was used for estimation. PsN version 4.7 was used as an aid for advanced functionalities [33]. The Xpose4 R package version 4.6.1 was used for graphical visualization of the visual predictive checks (VPCs) [33].

Pharmacokinetic Model Development

The PK model was developed with a stepwise approach [34]. The INH concentration data were included one study at a time, starting with the studies that had the most informative and dense sampling. After finishing the base INH model, the acetyl-INH data were added to the model. One- and two-compartment disposition models were explored to describe the pharmacokinetics of INH and acetyl-INH. A well-stirred liver model was tested instead of first-order elimination to describe the first-pass effect of INH. The molecular weight of INH and acetyl-INH was used to transform drug concentrations to molar concentrations to model the formation of acetyl-INH from INH. The bioavailability of INH was assumed to be 100% and all estimated PK parameters should be interpreted as apparent oral PK parameters. All volume and clearance parameters were allometrically scaled with total body weight using an exponent of 1 or 0.75, respectively [35]. Allometric scaling based on fat-free mass was not considered because height is not always readily available in TDM practice. NAT2 genotypic data were not determined in the included studies. A mixture model to distinguish between different groups of NAT2 metabolizers in the absence of genotypic data was applied [36]. It is known that the distribution of NAT2 metabolic function is trimodal [8]. The mixture model was tested with two as well as three metabolizer groups as it can be difficult to distinguish the three mixture groups as is seen in other models [4, 17]. In case two, metabolizer groups were used, the fast and intermediate metabolizers were grouped, as metabolization rates of these groups are closer together than those of the slow metabolizers, which have more deviant metabolization rates.

Inter-individual variability in the pharmacokinetics of INH was assumed to be log-normally distributed. Inter-occasion variability was not assessed because the number of individuals who were sampled on multiple occasions was limited. For residual variability, additive, proportional, and combined models were tested for both INH and acetyl-INH. Below the limit of quantification data were handled using the M6 method as described by Beal [37]. The M3 method was tested but did not perform better than the M6 method and increased numerical instability. Using this method, in the elimination phase, the first datapoint BLQ is replaced by the lower limit of quantification/2, and subsequent BLQ points are ignored. In the absorption phase, it is the last datapoint BLQ that is replaced and all previous BLQ points that are ignored. The minimum additive error for data BLQ was fixed to 50% of the lower limit of quantification values.

The number of potential covariates tested was kept low because of the purpose of our model; the covariates available in TDM practice are generally quite limited. It was opted to include only the allometric scaling with total body weight to not hamper a general implementation of the model in routine TDM. Although we did test the impact of formulation differences, but no effect could be identified.

Pharmacokinetic parameter uncertainty was assessed using sampling importance resampling [38, 39]. Sampling importance resampling is a fast method to determine parameter uncertainty which is free of distributional assumptions, a good alternative to the bootstrap. The initial estimates for the SIR were based on a successful covariance step and inflated by factor 1.5. The samples per iteration were 1000, 1000, 1000, 2000, and 2000, the re-samples per iteration were 200, 400, 500, 1000, and 1000. Parameter precision was presented using the calculated 95% confidence intervals (CIs). The predictive performance of the final model was assessed using VPCs and goodness-of-fit plots. The VPCs were prediction corrected and the PsN mixture option was used [40, 41].

Comparison of Limited Sampling Strategies

The performance of three LSSs was tested. These LSSs had sampling times at 2 h, 2 and 4 h, and 2, 4, and 6 h after dosing. These LSSs were chosen considering that sampling at 2 and 6 h, introduced by Peloquin et al., is common for TB drugs, and we have added a 4-h sampling point in our TDM service [2, 42]. In addition, samples with these sampling times were available within most of the datasets. Sampling at 2 and 6 h was not included as it does not offer any benefit over sampling at 2 and 4 h, which is more feasible to perform in clinical practice. For each LSS, the performance of AUC₂₄ and C_max prediction was determined using the patients who had a full PK curve including samples at 2, 4, and 6 h after dosing (169 patients from five studies) [14, 24–27]. The performance of the LSSs was also compared to the performance of the model without any sampling to assess the added value of sampling in TDM. The most suitable LSS was selected based on predictive performance and clinical practicality. The performance of predicting the AUC₂₄ was regarded as more important than that of the C_max. In these assessments, the mean error (ME) and root mean square error (RMSE) and their 95% CIs of the prediction of AUC₂₄ and C_max were calculated as measures of bias and precision [43, 44]. The ME and RMSE were expressed as a percentage of the mean of the corresponding model-estimated parameter using the full PK curve.

The most suitable LSS was used to perform a fit-for-purpose analysis, meaning that it was investigated how well the pharmacokinetics of INH could be predicted from a previous measurement [45]. The patients including data of a second occasion and the sampling times for the selected LSS were used for this. Apart from the most suitable LSS, ‘no sampling’ was tested as well to evaluate the amount of variability explained by the most suitable LSS. Suitable data for this analysis were available from 13 patients from only one study [28]. The performance of predicting the AUC₂₄ for the second occasion was determined using the ME and RMSE.

Importance of Acetyl-INH Data and Mixture Component for the Predictive Performance

The added value of both the acetyl-INH metabolite data and inclusion of a mixture model accounting for the polymorphic NAT2 clearance was assessed for the most suitable LSS. The selected LSS was used to provide AUC₂₄ predictions using only the INH data. These predictions were compared to model predictions using the full dataset, including the acetyl-INH data. To determine the added benefit of a mixture model to the performance of predicting the AUC₂₄, the mixture component was removed, and model parameters were re-estimated. The performance was again compared using the ME and RMSE.

Results

Pharmacokinetic Model

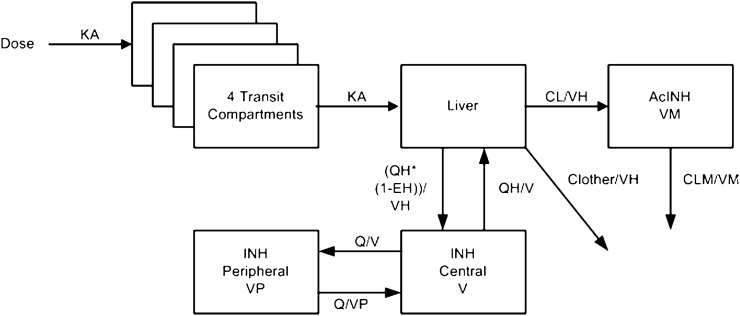
The final model is depicted in Fig. 1. It included four transit absorption compartments going into a well-stirred liver model [46]. The pharmacokinetics of INH was best described by a two-compartment disposition model. Acetyl-INH pharmacokinetics was characterized using a single compartment and first-order elimination. Metabolization in the liver compartment could either clear INH or transform it into acetyl-INH. It was not possible to estimate INH clearance as a trimodal distribution using a mixture model and thus a bimodal mixture model was included. The volume of the liver compartment and hepatic plasma flow were fixed to 1 L and 49.5 L/h, respectively, and allometrically scaled on total body weight like other volume and clearance parameters.

Fig. 1.

Schematic overview of the final isoniazid (INH) population pharmacokinetic model. The dose enters the well-stirred liver compartment via a four-compartmental transit model. Absorption constant (KA) is defined as the number of transit compartments plus 1, divided by the mean transit time (MTT). From the liver compartment, the drug can be distributed to the central INH compartment or be metabolized into acetyl-isoniazid (AcINH) or other metabolites. From the central AcINH compartment, the drug is cleared through first-order elimination. Isoniazid pharmacokinetics are described using a two-compartment disposition model and AcINH pharmacokinetic by a one-compartment disposition model. CL clearance into acetyl-isoniazid, CL other clearance into other metabolites than acetyl-isoniazid, CLM clearance of the acetyl-isoniazid metabolite, EH hepatic extraction ratio, Q inter-compartmental clearance, QH hepatic plasma flow, V central volume of isoniazid, VH hepatic volume, VM central volume of the acetyl-isoniazid metabolite, VP peripheral volume of isoniazid

The final model parameter estimates and their uncertainty are shown in Table 2. Uncertainty in the parameter estimates was generally low (relative standard error, RSE < 12%CV), except for the IIV of the central volume of acetyl-INH (RSE = 40%CV) and the correlation between the IIV of the clearances (RSE = 71%CV). The absorption processes were variable between individuals with an IIV estimated at 83.2%CV (95% CI 78.1–91.7). The proportion of fast NAT2 acetylators in the studies was estimated at 43.4% (95% CI 38.4–48.9). Slow acetylators typically had 13% of the intrinsic NAT2 clearance of fast acetylators. The second clearance pathway, not through NAT2, typically made up 74% of the total clearance for slow acetylators and 27% of the clearance for fast acetylators. A correlation was found between the clearance through acetylation and through other pathways, but the uncertainty of this correlation was quite high (0.143, 95% CI − 0.0620, 0.325). Additionally, a correlation between the proportional residual errors of INH and acetyl-INH was found.

Table 2.

Final model parameter estimates

Parameter	Estimate	95% CI	RSE (%CV)
Isoniazid
Central volume, V (L)	57.5	54.9–59.4	2.2
Absorption constant, KA (/h)	5.42	5.40–5.44	0.1
Proportion fast acetylators	0.434	0.384–0.489	6.6
Clearance (L/h)
Fast acetylators, CLF	32.7	28.6–37.6	7.7
Slow acetylators, CLS	4.31	3.85–4.75	7.4
Other clearance pathways, CLO	12.1	11.2–13.1	4.3
Peripheral volume, VP (L)	18.7	16.8–20.5	4.2
Inter-compartmental clearance, Q (L/h)	2.48	2.10–2.87	8.2
IIV V (%CV)	26.4	23.4–29.3	6.5
IIV KA (%CV)	83.2	78.1–91.7	4.9
IIV CLF/CLS (%CV)a	57.5	51.9–63.3	5.0
IIV CLO (%CV)	37.9	34.4–41.0	5.1
Proportional error (%)	37.5	36.4–38.7	3.0
Acetyl-isoniazid
Central volume, VM (L)	39.2	36.1–42.2	4.3
Clearance, CLM (L/h)	6.65	6.10–7.22	4.5
IIV VM (%CV)	10.3	5.98–14.2	37
IIV CLM (%CV)	36.7	34.2–40.4	5.3
Proportional error (%)	23.3	22.8–24.0	2.8
Correlations
Acetylation-other clearance pathways	0.143	−0.0620; 0.325	39
Parent error-metabolite error	0.601	0.556-0.656	2.9

CI confidence interval, CV coefficient of variation, h hour, IIV inter-individual variability, L liter, RSE relative standard error

^aThe clearances for fast and slow acetylators shared one estimated IIV

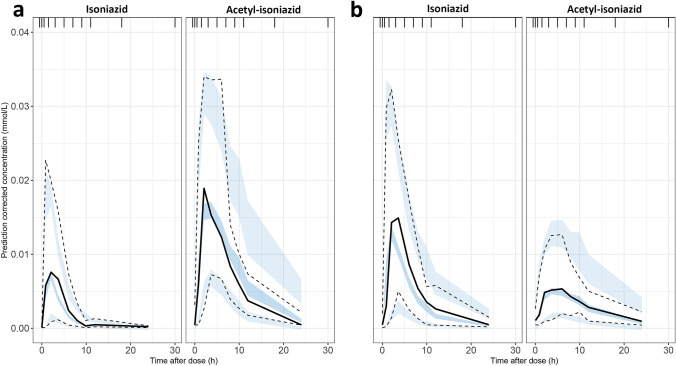
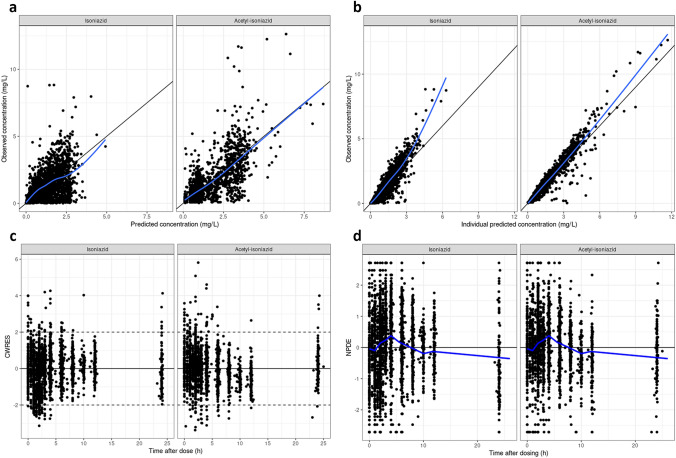
The VPCs, shown in Fig. 2, generally describe the model well. Some limitations of the model can be discerned from this figure. The model does not describe the median observed peak perfectly. Furthermore, the model simulates concentrations that are slightly too high on the upper end of the concentration range for acetyl-INH at timepoints after 8 h. The VPCs of the model were deemed satisfactory for TDM using the AUC₂₄. The performance of the model for TDM using the C_max should be explored further. Other goodness-of-fit plots are shown in Fig. 3 and do not show any obvious misspecifications. The full code of the final model is included in the Electronic Supplementary Material (ESM).

Fig. 2.

Basic goodness-of-fit plots for the final isoniazid population pharmacokinetic model. a, b The observed concentrations plotted against the model-predicted concentrations or the individual model-predicted concentrations. The black lines represent the line of unity, and the blue lines represent the local polynomial regression fit. c The conditionally weighted residuals plotted against the time after dose. The solid lines are the y = 0 lines, and the dashed lines define the range between which you want the majority of the observations to lie. d The normalised prediction distribution errors plotted against the time after dose. The solid lines are the y = 0 lines and the blue lines are the means per time bin

Fig. 3.

Visual predictive checks of the final isoniazid population pharmacokinetic model for a slow metabolizers and b fast metabolizers. The visual predictive checks are based on 1000 simulations and prediction corrected. The PsN mixture option was used and the plots are based on the individual probability for belonging to a subpopulation [36]. The solid lines represent the mean of the observed concentrations and the dashed lines represent the 2.5th and 97.5th percentiles. The shaded areas represent the 95% confidence interval of the 2.5th, 50th, and 97.5th percentiles of the simulated concentrations

Comparison of Limited Sampling Strategies

The AUC₂₄ and C_max predicted by the LSSs were compared to the AUC₂₄ and C_max predicted by the model based on full PK curves. Scatterplots of this are shown in ESM 1. The bias and precision of these strategies are shown in Table 3. The LSS using only one sample performed substantially worse in both bias and precision than the strategies with two or three sampling points. The strategies employing sampling at 2 and 4, and 2, 4, and 6 hours after dosing have a similar performance. Based on bias, precision, clinical practicality, and conformity with a previously developed strategy for rifampicin [28], the strategy using sampling at 2 and 4 hours after dosing was selected as the most suitable.

Table 3.

Predictive performance comparison of the limited sampling strategies

Data used for prediction	Sampling strategy	AUC0–24		Cmax
		RMSE, % (SD)	ME, % (95% CI)	RMSE, % (SD)	ME, % (95% CI)
No data	No sampling	73.7 (4.0)	55.8 (48.5, 63.1)	44.1 (2.4)	25.3 (19.9, 30.8)
INH + AcINH	2, 4, and 6 h	21.8 (1.2)	1.6 (−1.7, 4.8)	24.2 (1.3)	4.2 (0.6, 7.8)
	2 and 4 h	23.4 (1.3)	−1.1 (−4.6, 2.4)	23.8 (1.3)	2.7 (−0.9, 6.3)
	2 h	34.0 (1.8)	10.0 (5.1, 14.9)	26.5 (1.4)	6.0 (2.1, 9.9)
INH	2, 4, and 6 h	20.9 (1.1)	1.7 (−1.5, 4.8)	23.8 (1.3)	1.2 (−2.4, 4.8)
	2 and 4 h	28.9 (1.6)	−1.8 (−6.2, 2.6)	23.5 (1.3)	0.1 (−3.5, 3.7)
	2 h	59.1 (3.2)	36.1 (29.1, 43.2)	27.0 (1.5)	11.7 (8.0, 15.4)

Both the ME and RMSE are depicted as a percentage of the mean of the corresponding model-estimated parameter using the full pharmacokinetic curve

AcINH acetyl-isoniazid, AUC_0–24 area under the concentration–time curve from 0 to 24 h, CI confidence interval, C_max peak concentration, INH isoniazid, ME mean error, RMSE root mean square error, SD standard deviation

To assess if the model and LSS is fit for purpose, the AUC₂₄ of a second sampling occasion was predicted using data from a first sampling occasion. The fit-for-purpose analysis of the model using the 2- and 4-h sampling strategy resulted in an ME of 25.7% and an RMSE of 37.2%. Without sampling in the first occasion, the ME was 82.7% and the RMSE 117.9%.

Importance of Acetyl-INH Data and Mixture Component for the Predictive Performance

The final model using the 2- and 4-h LSS without the acetyl-INH data had an ME of − 1.8% and an RMSE of 28.9% for estimating the AUC₂₄. For estimation of the C_max, the ME was 0.1% and the RMSE 23.5%. Comparison to data in Table 3 shows that the prediction of the model without acetyl-INH data is less precise compared to the predictions including acetyl-INH for the 2- and 4-h sampling strategy. For the 2-, 4-, and 6-h strategy without acetyl-INH data, the estimation of the AUC₂₄ had an ME of 1.7% and an RMSE of 20.9%. For estimation of the C_max, the ME was 1.2% and the RMSE 23.8%. This is comparable to the performances of the 2-, 4-, and 6-h and 2- and 4-h strategies including acetyl-INH data. ESM 2a shows the effect of removing the acetyl-INH data on the performance of predicting the AUC₂₄ for the 2- and 4-h sampling strategy.

The re-estimated model without a mixture component using the 2- and 4-hour LSS had an ME of − 1.1% and RMSE of 24.6% for AUC₂₄ estimation, and an ME of 7.7% and RMSE of 23.3% for estimation of the C_max, meaning that the mixture component was not essential for the predictive performance of the model. The estimated PK parameters for the model without a mixture component were similar to those of the final model, except for the clearance representing both metabolization groups and their IIV. The new clearance has a value of 9.12 L/h and lies in between the clearances of the slow and fast metabolizers as estimated by the final model. The estimated IIV of this clearance has increased drastically by more than two-fold to 115.8%CV. ESM 2b shows the effect of removing the mixture model on the performance of predicting the AUC₂₄.

Discussion

In this project, we have developed a model describing the pharmacokinetics of INH based on a large and diverse dataset. The model should have a wider applicability and be better suited for TDM in various populations compared to previously published models, which were all based on studies from a single country [4, 5, 17–22]. We also introduced and evaluated a model-based TDM approach for personalized dosing of INH using sampling at 2 and 4 h or 2, 4, and 6 h after dosing. These approaches will allow for dose adjustments of INH in programmatic TB treatment.

The structure of the final PK model is comparable to those previously described [5, 17, 21]. The estimated clearances and proportion of fast NAT2 acetylators described in this model are very similar to those previously described [17]. As in other published INH models, our model could only separate two of the three acetylator subgroups [17, 18]. We did not differentiate between acetylator proportions for different ethnicities, which are known to vary [47]. The other model parameters are also mostly similar to those described previously [5, 17]. The estimates for the peripheral volume and intercompartmental clearance for INH vary between the different models. During the model building process, we encountered instability problems, making it difficult to estimate some of the model parameters. Explanations for this could be the large number of different data sources included in the model building dataset and the model complexity. The VPCs of the model are acceptable and it has been shown that the model performs well for the purpose of TDM. As such, we do not see the instability as a sign of an underlying problem. We opted to have a limited inclusion of covariates in view of the purpose of this model. For other purposes, the model could probably be improved by the inclusion of additional covariates. While inter-occasion variability is known to be present for INH, we were unable to identify it in our model [4, 17]. It has been described that inter-occasion variability may impact the predictive performance of model-based dosing algorithms [48]. Despite this, we showed in the fit-for-purpose evaluation using multiple occasions that the model performed well.

The LSS with sampling at 2 and 4 h after dosing was selected as the most suitable strategy. Previously, we introduced a model-based TDM approach for rifampicin, just like INH a pillar within the TB treatment [28]. This approach also uses a LSS with sampling at 2 and 4 h after dosing, which means that the method described here and for rifampicin are compatible in clinical practice. In this study, we decided to develop a new PK model rather than evaluate existing models like we did for the model-based approach for rifampicin. This decision was based on the added value of a model built on a large and diverse dataset. A better LSS could potentially have been found using an optimal design experiment. However, by sticking to predefined sampling times, we were able to evaluate the proposed strategy using the existing time points in the dataset.

For unbiased predictions using the 2- and 4-h LSS, acetyl-INH concentration data were needed. If using this LSS without acetyl-INH PK data input, the performance of predicting the AUC₂₄ will be lower. However, if acetyl-INH data are not available, it can be compensated for by adding a 6-h sampling time. Removing the mixture component and re-estimating the model parameters shows that not accounting for the polymorphic clearance of INH does not have a major impact on performance of the exposure prediction. After removing the mixture component, the variability caused by the polymorphic NAT2 clearance is described by an IIV more than two times the size before removing the mixture component. This increase in variability probably compensates for the lack of mixture model and prevents a significant drop in performance of the LSS.

While we present a sampling strategy using 2- and 4-h sampling times, deviation from these sampling times does not mean exposure prediction is not trustworthy anymore. The presented strategy should be seen as a flexible sampling strategy. Using sampling times that deviate from the LSS is one of the benefits of using a model-based approach. However, we did not evaluate the impact of deviating from the proposed sampling times as such sampling time deviations were not sufficiently present in the data because of the regulated nature of the included studies. It would have been possible to simulate deviating sampling times as input for the sampling strategies, but this was beyond the purpose of this study.

We tested if the LSS was fit for purpose by assessing the performance of predicting the exposure of a future sampling occasion. We showed that the strategy is able to explain most of the variability in the pharmacokinetics by comparing its performance to that without sampling. The explained variability is determined by IIV as inter-occasion variability was not included in the model. By incorporating inter-occasion variability in the model, the performance of predicting a future occasion could be further improved [48]. Prospective evaluation of this method is needed to show how well it will perform in a real TDM setting.

The model-based TDM approach has advantages, but is also a complex methodology in terms of software usage and underlying theory [49]. For this reason, implementation of a model-based TDM approach in clinical practice should be combined with a user-friendly interface to improve the ease of use. Furthermore, the translation from the model-based results to clinical advice is crucial for successful implementation.

Conclusions

We developed a model-based LSS using INH and acetyl-INH data from sampling at 2 and 4 h after dosing to be used for individualized dosing in TDM practice. Alternatively, a 2-, 4-, and 6-h LSS can be used if only collecting PK data on INH and not on acetyl-INH. Prospective evaluation of this strategy will show how it performs in a clinical TDM setting.

Supplementary Information

Below is the link to the electronic supplementary material.

Declarations

Funding

No funding was received specifically for this study or for the preparation of this article. Elin M. Svensson is supported by PanACEA, which is part of the European and Developing Countries Clinical Trials Partnership (EDCTP) 2 programme supported by the European Union (Grant number TRIA2015-1102-PanACEA).

Conflict of interest

All authors declare no conflicts of interest that could have influenced the submitted work.

Ethical approval

The data used in this study was collected in line with the principles of the Declaration of Helsinki. Approval was granted by institutional review boards and independent ethics committees for each study of which data was used in this work.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Availability of data and material

Not applicable.

Code availability

The model code is available within the supplemental materials.

Author contributions

SvB, RtH and ES performed the analysis, data interpretation and writing of the manuscript. JA, CME and RE were involved in data collection, data interpretation and writing of the manuscript. MB, EB, RD, AD, SG, CM, NN, NH, WH, MH, GK, KR, IS, HS and AT were involved in data collection and contributed to the writing of the manuscript.