Principles and open questions in functional brain network reconstruction

Abstract

Graph theory is now becoming a standard tool in system‐level neuroscience. However, endowing observed brain anatomy and dynamics with a complex network representation involves often covert theoretical assumptions and methodological choices which affect the way networks are reconstructed from experimental data, and ultimately the resulting network properties and their interpretation. Here, we review some fundamental conceptual underpinnings and technical issues associated with brain network reconstruction, and discuss how their mutual influence concurs in clarifying the organization of brain function.

Graph theory is now becoming a standard tool in system‐level neuroscience. However, endowing observed brain anatomy and dynamics with a complex network representation involves often covert theoretical assumptions and methodological choices which affect the way networks are reconstructed from experimental data, and ultimately the resulting network properties and their interpretation. Here, we review some fundamental conceptual underpinnings and technical issues associated with brain network reconstruction, and discuss how their mutual influence concurs in clarifying the organization of brain function.

​

1. INTRODUCTION

The introduction of complex network theory in neuroscience has represented a profound methodological but also in many ways conceptual revolution, promoting new research avenues (Bullmore & Sporns, 2009). A network is a collection of nodes and pairwise relations between them, called edges or links (Newman, 2003). Endowing a system with a network structure means identifying some of its parts with the former, and physical or more abstract relations between them with the latter. In spite of its apparent straightforwardness, such an operation is highly non‐trivial from both a conceptual and a practical viewpoint and comes with a set of often implicit assumptions.

Representing a system with a network structure does not necessarily entail that the system's properties are those of the associated network and that the system actually works as a network. Thus, at a fundamental level, network neuroscience must address the question of whether network structure reflects genuine aspects of brain phenomenology or is an epiphenomenon of coordinated dynamical activity in the same way as spatio‐temporal electrical field fluctuations are sometimes thought of. But even supposing that brain function emerges from some network property of anatomy and the dynamics taking place on it, a no less fundamental question for neuroscientists is how to extract this structure from data. Before even addressing the ontological question, it is therefore necessary to ascertain that the reconstruction is carried out properly. What “properly” means is of course highly non‐trivial, context‐specific, and crucially depends on the way the data on brain activity are collected, analysed and interpreted.

Network reconstruction from empirical data involves discretionary choices at all steps, to which graph theory per se provides no direction (Papo, Zanin, & Buldú, 2014; Zanin et al., 2012). For instance, there are no criteria for the choice of the space to be represented with a network structure, and for the definition of its boundaries, nodes and edges (Papo, Zanin, & Buldú, 2014). The reconstruction process in general and these choices in particular are somehow associated with assumptions on the characteristics of the studied system. For instance, endowing brain anatomy and dynamics with a network structure may seem prima facie rather similar processes, but differ in some fundamental (not merely technical) ways. An obvious difference lies in the definition of edges, which is far more straightforward in the former case than in the latter, but the most fundamental difference is to do with the definition of functional brain imaging's object, namely, functional brain activity.

In the remainder, we review the conceptual bases of functional network reconstruction from standard system‐level neuroimaging recordings (Section 2). In particular, we show that defining functional brain activity, extracting it from neuroimaging data and representing it with bona fide functional networks involve essentially similar conceptual steps. This theoretical introduction analyses issues seldom examined in other neuroscience reviews, but which turn out to be essential to understanding the technical aspects of the reconstruction process (Section 3). The interaction between functional brain activity characterization and network representation, and the extent to which the definition of what is functional in brain activity depends on the particular way in which brain networks are reconstructed is discussed throughout.

2. PROLEGOMENA TO NETWORK RECONSTRUCTION

System‐level functional neuroimaging techniques afford discrete time‐varying images of some aspect of neural physiology, typically associated with some physiological or cognitive function. Neuroimaging data therefore constitute a coarse‐grained version of “true” brain activity, implicitly meaning that there exists some map between the former and the latter.

The first important issue is determining the conditions under which and extent to which neuroimaging data and, more specifically the variables used to quantify them, allow recovering the system and make the system observable, that is, the internal states of the whole system can be reconstructed from the system's outputs (Kalman, 1961). Thus, neuroimaging data analysis can be thought of as a reconstruction or inverse problem (Nguyen, Zecchina, & Berg, 2017) (cf. Section 2.2.2). Supposing brain activity in fact has a structure of some kind, for example, a symmetry, the aim of neuroimaging data analysis should be to preserve at least some context‐specific properties of the underlying structure. The presence of structure induces specific equivalence classes, that is, sets whose elements are equivalent in terms of some relation, and allows measuring quantities over the considered spaces. These should ideally be preserved in the mapping.

A second important issue is that what needs to be quantified is in general not brain dynamics, but functional brain activity. However, the activity recorded with neuroimaging techniques such as functional magnetic resonance imaging (fMRI), electro‐ (EEG) or magneto‐encephalography (MEG), which is generally called functional, is not genuinely functional per se. Functional brain activity can be thought of as a particular structure of brain dynamics, that is, a particular set of relations among the elements composing dynamics which reflect a specific function. Extracting function from bare dynamics represents a non‐trivial though often implicit process (Papo, 2019). As a consequence, functional brain imaging should provide a map between true and coarse‐grained space's respective structure.

Finally, network neuroscience aims at characterizing brain anatomy, dynamics and ultimately function by endowing them with a network representation, and describing them in terms of properties of this representation. A network can be thought of as a discrete version of a continuous space, equipped with a particular structure. Thus, in network reconstruction, the codomain of the map from true brain structure is a coarse‐grained and discrete image of (some aspect of) brain anatomy and dynamics. Both its objects (i.e., the nodes) and the relations among them (i.e., the edges) are endowed with basic properties. Altogether, network analysis of system‐level neuroimaging data involves a complex characterization of the system's functional space, via neuroimaging and network coarse‐graining. Crucially, these properties depend on the way functional brain activity is defined. Defining functional brain activity, extracting it from neuroimaging data and representing it with bona fide functional networks correspond to as many coarse‐graining processes, which though implying a reduction in information, in the temporal and spatial domains, involve essentially similar conceptual steps.

2.1. From brain dynamics to functional brain activity

Perhaps the most common way of representing system‐level brain activity and therefore the time‐varying data produced by standard neuroimaging techniques is as the output of an underlying spatially‐extended dynamical system embedded in the 3D anatomical space. The space Φ associated with the dynamics is typically treated as scalar, vector, or tensor field, ¹ either in the time domain, ranging from experimental to developmental or evolutionary time scales or, in somehow equivalently ways, in the frequency domain or in phase space.

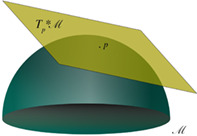
Whatever the domain in which it is defined, the space has in general some additional structure, that is, some relationship among its elements. The space Φ is often identified with the anatomical space itself and treated as a smooth Euclidean space. This means that on such a space a distance is defined, that is, a rule to calculate the length of curves connecting points of the space, and that the tools of standard calculus can be used to carry out operations within the space, and comparing or evaluating differences across conditions. However, when considered at the whole brain spatial scale, neither anatomy nor global dynamics can in general be thought of as a simple Euclidean space. The folded structure resulting from brain gyrification produces an object with non‐trivial geometry. Perhaps more importantly, anatomically contiguous brain areas may radically differ in terms of dynamics and function. Φ can nonetheless be equipped with some geometry providing a way of defining distances. This can be done by assuming the anatomically‐embedded dynamical space to be locally Euclidean, an approximation typically adopted in anatomical data analysis. The resulting space is a manifold M, that is, a geometric object consisting of a collection of Euclidean patches, which are local descriptions of Φ covering the space. Such a construct is akin to a standard geographical atlas, which is nothing else but a collection of local charts projected on the plane. Overall, the resulting geometry is Euclidean within patches, but of a different nature at longer spatial scales (cf. Section 3.3.1). The main problems with such a space are understanding the conditions under which its parts are distinguishable, how the charts are related to each other, how to treat overlaps between two separate charts and changes in the description of the same set in different coordinates (Robinson, 2013a) (see Figure 1).

FIGURE 1.

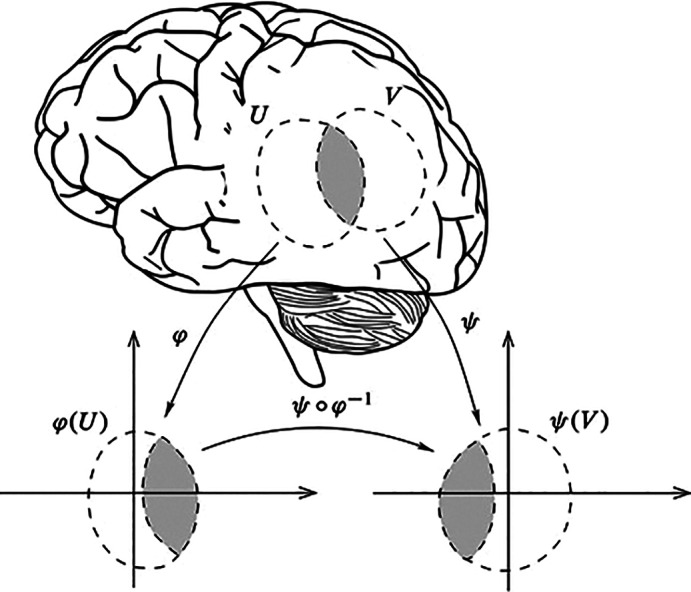
An n‐dimensional manifold M can be described locally by the n‐dimensional real space ℝ ⁿ. A local chart (φ, U) is an open subset of the manifold U ⊆ M together with a one to one map φ: U→ℝ ⁿ from this subset to an open set of the Euclidean space. The piecewise one‐to‐one mapping to the Euclidean space allows generalizing Euclidean space properties onto manifolds. A transition map between two open subsets of ℝ ⁿ provides a way to compare two charts of an atlas

While representing brain activity in a metric space equipped with a distance may seem to facilitate neuroscientists' life, it may not capture essential non‐metric aspects of functional brain organization (Petri et al., 2014; Reimann et al., 2017). It may then be useful to represent Φ as a space the elements of which do not derive internal relations from a metric (Petri et al., 2014). The space Φ may for instance be endowed with a topological structure (Lee, 2010). A topological space is a set of elements together with a topology, that is, a collection of open sets satisfying some basic properties. Intuitively, a set is open if, starting from any of its points and going in any direction, it is possible to move a little and still lie inside the set. The notion of open set provides a fundamental way to define nearness, and hence properties such as continuity, connectedness, and closeness, without explicitly resorting to distances. Nearness is maintained as the space is stretched without tearing. This naturally allows comparing systems of different metric size and differing local properties, a desirable characteristic given the intrinsic variability of individual brains. Thus, altogether, a topological representation affords two important advantages over a usual metric space: a more flexible notion of distance, and a robust way to compare conditions (Ghrist, 2014).

Treating brain activity as the output of a dynamical system, it can be modelled as a topological dynamical system where in addition to rules prescribing the matching conditions between overlapping charts, one defines some function accounting for the temporal evolution of such a structure. Considering the dynamics of such systems complexifies the picture. This is because brain activity has non‐random structure not just in the anatomical space but also in its dynamics (Papo, 2013). For instance, at long time scales, brain fluctuations are characterized by non‐trivial properties such as scale invariance (Fraiman & Chialvo, 2012; Novikov, Novikov, Shannahoff‐Khalsa, Schwartz, & Wright, 1997). The presence of such properties induces for instance a particular geometry (fractal geometry) in the time domain. This structure interacts with the spatial structure (Papo, 2014), potentially giving rise to arbitrarily complex topological properties (Zaslavsky, 2002).

2.1.1. Notion of functional space

Neuroimaging can help pursuing cognitive neuroscience's dual goal: understanding on the one hand how brain anatomical structure and the dynamics unfolding on it control function, and on the other hand, how the demands of cognitive or physiological tasks act on brain anatomy and dynamics, producing functional subdivisions in the brain. This can be accomplished by mapping a space Ψ of cognitive functions {ψ ₁, ψ ₂, …, ψ _J}, non‐observable when using a given system‐level neuroimaging technique, onto a finite set of functions {ϕ ₁, ϕ ₂, …, ϕ _K} ∈ Φ of aspects of brain anatomy or physiology associated with observable fitness or performance measures {γ ₁, γ ₂, …, γ _L} ∈ Γ from subjects carrying out given tasks or just resting. When using Φ to make sense of Ψ, one ultimately aims at defining the space of equivalence classes under some relation defined on Φ, for example, the space of points for which brain activity has the same amplitude. In the opposite case, Φ is partitioned into functionally meaningful units using cognitive tasks as probes. In general, one seeks the best way to project one space onto the other, inducing partitions as accurate and fine as possible. Thus, defining functional brain activity using neuroimaging techniques involves partitioning two complex spaces, respectively made observable by behaviour and brain recording techniques, putting a structure on the set of equivalence classes, and mapping the corresponding structures, thereby parameterizing one space by another space. How to construct these partitions, what form the corresponding space may take, and therefore what may be regarded as functional, depends on the way $\left(\mathrm{\Psi },{\mathcal{S}}_{\mathrm{\Psi }}\right)$ and $\left(\Phi ,{\mathcal{S}}_{\Phi }\right),$ where $\mathcal{S}$ denotes a generic structure, are defined and mapped onto each other through π (or π ^′). Within such a space, coordinates and transitions between charts in one space are defined by corresponding charts in the other space used to parameterize it.

Structure of the functional space

Subdivisions of the functional space depend on the way Φ and Ψ are defined, on their respective structure, and on the way they are mapped onto each other through some function π (or π ^′) (see Figure 2). π can be thought of as a map preserving structure, as ideally one would like subdivisions in one space to be mapped onto subdivisions in the other, though its nature, properties (e.g., invertibility, continuity) and the ones it preserves may be context‐specific. Carving functional equivalence classes from brain activity ultimately involves moving from dynamical equivalence classes, with identical dynamical properties and specific phase and parameter space symmetries, to functional ones comprising patterns of neural activity that can achieve given functional properties (Lizier & Rubinov, 2012; Ma, Trusina, El‐Samad, Lim, & Tang, 2009). This in turn requires considering the structure induced by the time evolution of the space produced by the map π (or π ^′). Functional structure results from the combination of two aspects: on the one hand, the accessibility structure in the neurophysiological space, that is, which observable variations are realizable in the neighbourhood of underlying neuronal configurations at scales below the observed ones; on the other hand, the neurophysiological neutrality structure of observable variations in the space in which these are evaluated, that is, those changes in one space which have no consequence on the space onto which they are projected. The combination of these two factors may give rise to a rather non‐trivial structure. Notably, various important properties, for example, nearness and neighbourhood, may qualitatively change when considering function rather than bare dynamics, the former possibly turning out not to be a metric or even a topological space (Stadler, Stadler, Wagner, & Fontana, 2001). The very definition of other properties, such as path dependence and robustness, may also vary in the dynamics‐to‐function transition.

FIGURE 2.

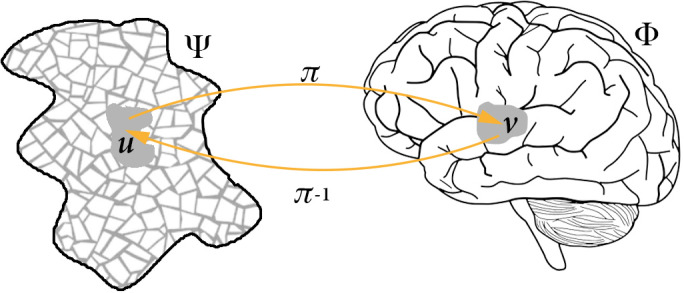
Genuinely functional activity results from a complex relation between the structure ${\mathcal{S}}_{\mathrm{\Phi }}$ of the neurophysiological space Φ and the structure ${\mathcal{S}}_{\mathrm{\Psi }}$ of the abstract space Ψ of cognitive functions made observable by performance measures Γ (see text above). Thus subdivisions in one space are used to define subdivisions in the other

2.2. From functional activity to functional networks

2.2.1. Network structure

An increasingly popular way to equip neuroimaging data with structure consists in endowing them with a network structure (Bullmore & Sporns, 2009). A network is a pair G = (V, E), where V is a finite set of nodes and E ⊆ V ⊗ V a set of ordered pairs of V called edges (or links). E is a symmetric and antireflexive relation on V for simple networks, and an anti‐symmetric one for directed ones (Estrada, 2011).

In a sense, network analysis operates in the same way as neuroimaging itself. Neuroimaging data can prima facie be thought of as kinetic models with a noise term averaging over brain activity at scales that are not detectable by a given recording device (Zaslavsky, 2002). This means that there exists a map $\tilde{\pi }:{\mathrm{\Phi }}_{\mathit{\text{NObs}}}\to {\mathrm{\Phi }}_{\mathit{Obs}}$between non‐observable and observable activity. Recovering the hidden structure at microscopic scales would require finding a generating partition, an arduous task often impossible in experimental contexts (Kantz & Schreiber, 2004; Schulman & Gaveau, 2001). Associating the brain space with a network structure constitutes a particular coarse‐graining wherein each portion of Φ_Obs, an essentially continuous space (though empirical data are of course discrete), is identified with a discrete point. This process bears similarities with the way the centre of mass summarizes a whole mechanical system, an operation made possible by the system's symmetries. Furthermore, insofar as in a discrete space all points are isolated, ² a network structure, however, defined, induces a separation property in Φ_Obs, even when the spaces summarized by each node are not separated ³ ones. In analogy with the general way of defining brain function, such networks, which are associated with the structure of bare dynamics, should be called dynamical, while functional networks should be reserved for structures inducing partitions of Φ_Obs through behavioural measures Γ. In this sense, defining network nodes, the starting point of functional network analysis, already incorporates a specification of functional brain activity.

Φ_Obs can loosely be thought to emerge from the renormalization of neural activity at scales not observable with a given neuroimaging technique (Allefeld, Atmanspacher, & Wackermann, 2009). The way microscopic scales renormalize into macroscopic ones and the properties the $\tilde{\pi }$ map induces are poorly understood but could help determining the scale at which Φ is locally isomorphic to ℝ ⁿ and can effectively be treated as a topological manifold. Likewise, the level of neural operation at which connectivity becomes functionally relevant determines the scales at which a system can effectively be considered a network. At this scale, which may be induced by permutation symmetry with respect to a given property at microscopic scales, connectivity and collectivity are equivalent. Macroscopic parcellations in the anatomical space may then consist of topographical regions for which such symmetry holds.

Important functional elements are also incorporated in the relations between network nodes. In network neuroscience, the relation E is predicated upon connectedness and correlation lato sensu is usually used as a proxy for neighbourhood in the relevant space. Connectedness is one of the most important properties of topological spaces expressing the intuitive idea that an entity cannot be represented as the sum of two parts separated from each other, or, more precisely, as the sum of two non‐empty disjoint open‐closed subsets. Connectedness is preserved under mappings preserving the topological properties of a given space. The choice of connectedness is consistent with the proposed role of dynamical connectivity in healthy brain function (Varela, Lachaux, Rodriguez, & Martinerie, 2001) and in several neurological and psychiatric conditions (Alderson‐Day, McCarthy‐Jones, & Fernyhough, 2015; Friston, 1998; Hahamy, Behrmann, & Malach, 2015; Hilary & Grafman, 2017; Hohenfeld, Werner, & Reetz, 2018; Schmidt et al., 2013; Stephan, Friston, & Frith, 2009). The relations among the component nodes induce both metric (though not Euclidean) and topological properties.

Altogether, while a network representation should in principle clarify key aspects of functional brain activity, in turn, the assumptions on what should be regarded as functional have a profound impact on the associated networks, introducing circularity between definition and quantification of functional brain activity.

2.2.2. Reconstruction‐related principles

The network neuroscience endeavour is a particular inverse problem (Nguyen et al., 2017), involving the reconstruction of connectivity kernels given a prescribed dynamics of the activity field (Coombes, beim Graben, Potthast, & Wright, 2014) (Cf. Section 3.5). Insofar as the activity field is discretized, and that the key aspect is not dynamics per se but function, characterizing functional brain activity using network reconstruction involves determining the set of all networks that generate a given function. Inverse problems are by definition ill‐posed in the absence of boundary conditions. Specifying these conditions involves choices of varying degrees of arbitrariness. Reconstruction should ideally fulfil some partially inter‐related criteria:

1. Reducibility. A fundamental question relates to whether brain activity can indeed be reduced to a network representation. The brain is a disordered spatially extended system with complex dynamics and incompletely understood functional organization. While complex networks' properties are well‐equipped to reflect many aspects of such a system, for instance its strong disorder (Dorogovtsev, Goltsev, & Mendes, 2008), how much information is lost as a result of discretization, and the extent to which information loss depends on the particular way a network is reconstructed and the scale at which this happens are still poorly understood issues.

2. Observability. An issue related to reducibility and which is still poorly understood, is to what extent and under what conditions a network representation enables good observability, that is, allows recovering the states (Letellier & Aguirre, 2002) of the underlying high‐dimensional system (Aguirre, Portes, & Letellier, 2018).

3. Structural similarity. Ideally, the network structure should reflect that of the underlying functional space, that is, there should be a map between them that preserves structure.

4. Property preservation. An adequate structure should therefore preserve fundamental dynamical and structural properties of the underlying space. These properties include (a) the ability to obtain a dynamical rule for the system (Allefeld et al., 2009), and (b) symmetries (Cross & Gilmore, 2010). At least in its classical formulation, a network representation introduces symmetries, which may not be intrinsic to the system. For instance, nodes are typically taken to be essentially equal, implying a global symmetry of the space on which the network is defined.

5. Intrinsicality. Network properties should be intrinsic, that is, they should show some invariance with respect to the way the network structure through which they are identified is reconstructed.

Which properties of brain dynamics and function networks can, actually do, or should document, and what this implies in terms of network properties, constitute fundamental issues that need to be addressed in network reconstruction.

3. BRAIN NETWORK RECONSTRUCTION

Endowing brain dynamics with a network representation is consistent with models representing global brain activity as emerging from the coupling of oscillating neuronal ensembles (Ashwin, Coombes, & Nicks, 2016; Hoppensteadt & Izhikevich, 1997; Sreenivasan, Menon, & Sinha, 2017). In this sense, network neuroscience can be seen as a particular neural field theory (Coombes & Byrne, 2019), wherein a finite number of neural masses interact according to a given context‐dependent topology (Cabral, Hugues, Sporns, & Deco, 2011).

However, not only is writing equations for brain dynamics based on empirical data an arduous task (Brückner, Ronceray, & Broedersz, 2020; Crutchfield & McNamara, 1987; Friedrich, Peinke, Sahimi, & Tabar, 2011), but at the scales typical of standard system‐level non‐invasive neuroimaging techniques, it is not trivial to define oscillators. At these scales, the definition of node is far less intuitive than for example, at the single neuron ones, where units are clearly defined. Nodes then ought to be identified in a different way. This often involves some form of functional projection on the anatomical space, whereby nodes map spatially local characteristics of the system's microscopic scales. However, the anatomy‐to‐function map is complex and poorly understood, as dynamical patterns of brain activity emerge in a spatially and temporally non‐local way from brain connectivity at all scales (Kozma & Freeman, 2016). Furthermore, no clear recipe exists to define relationships among nodes or to choose among the many available alternatives (Pereda, Quiroga, & Bhattacharya, 2005).

Functional network reconstruction is typically presented as a process involving node and edge definition and comprising a sequence of discrete steps. This division is in large part both heuristic, as discretional decisions at each step crucially depend on choices made at the others, and incomplete, as node and edge characterization is for instance logically preceded by the choice of the space on which the network structure is defined. In the remainder of this section, we provide an account of the various aspects in the reconstruction process, their reciprocal relationships, their dependence on often covert assumptions on functional brain activity as well as their brain recording technique specificity.

3.1. Space identification

Typically the space to be endowed with a network structure is isomorphic to the anatomical space on which the recorded dynamics takes place. Often the anatomical space would constitute both the embedding and the configuration space ⁴ for the dynamics. This characterization presents features that may simplify the analysis. For instance, the space can be endowed with the usual Euclidean metric. In addition, it makes interpretations in physiological terms and comparisons between anatomical and dynamical networks straightforward.

In fMRI studies, the anatomical space is not only the space where the brain dynamics take place but also the space where the imaging data are collected. The case of MEG and EEG is more complicated: while the data origins from electric dynamics of source points located on the brain surface, or in the source space, signals are recorded by magnetometers, gradiometers, and electrodes outside of the skull, in the sensor space. Functional networks can be constructed in both spaces. Sensor space analysis directly investigates the temporal similarity between signals from different sensors. For source‐space analysis, on the other hand, the dynamics of sources on the brain surface are first reconstructed via electromagnetic inverse modelling, also known as source reconstruction (for a review on source reconstruction approaches, cf. Hämäläinen, Hari, Ilmoniemi, Knuutila, & Lounasmaa, 1993; Grech et al., 2008; Schoffelen & Gross, 2009, He, Sohrabpoir, Brown, & Liu, 2018). While sensor‐space analysis is often selected for its relative simplicity and reduced computational cost, source‐space analysis offers higher spatial resolution, facilitating interpretation of results in neurophysiological context (Palva & Palva, 2012; Schoffelen & Gross, 2009). Source‐space analysis is also less prone to errors originating from signal mixing (cf. Section 3.5.2).

The anatomical space is not the same for all brains. In particular, fMRI data are collected in the so‐called native space of each subject, and also MEG and EEG data may be source‐modelled to native space. However, the brain regions used as functional network nodes (cf. Section 3.2.1) are defined in some standard space, the most commonly used being the Montreal Neurological Institute space (Collins, 1994; Collins, Neelin, Peters, & Evans, 1994; Evans, Collins, & Milner, 1992; Evans, Marrett, et al., 1992). Therefore, neuroimaging data are typically transformed to a standard space prior to network construction. The transformation aims to map homologous areas of different subjects into a single area in the standard space (Brett, Johnsrude, & Owen, 2002). Depending on the assumed connection between function and anatomy, this can be done by matching brain size and outline or more detailed anatomical structures such as sulci (Brett et al., 2002). Another, although more rare, option is to map the ROI definitions to each subject's native space and construct networks there. Some studies report no difference in network metrics between spaces (van den Heuvel, Stam, Boersma, & Hulshoff Pol, 2008); according to others, however, native‐space networks have more local structure and clearer local hubs than standard‐space ones (Magalhães, Marques, Soares, Alves, & Sousa, 2015). Furthermore, network metrics calculated in the native space and normalized by metrics obtained from random networks of corresponding size are better predictors for IQ of children suffering from epilepsy than their standard‐space counterparts, although the standard‐space metrics outperform the non‐normalized native space ones (Paldino, Golriz, Zhang, & Chu, 2019). However, effects of the standard‐space transformation on network structure and metrics are not fully known, and the selection of optimal space probably depends on multiple factors, including the definition of network nodes (Magalhães et al., 2015).

The anatomical space is only one of the many classes of spaces that can in principle be endowed with a network structure. For instance, network theory may be used to describe the phase space in which brain activity lives (Baiesi, Bongini, Casetti, & Tattini, 2009; Thurner, 2005). Such a representation seems particularly appropriate in regard to the phase space characteristics of complex systems such as the brain, where not all possible states are homogeneously populated, and microscopic dynamics is restricted to some states and the paths uniting them (Bianco et al., 2007; Sherrington, 2010). In a multilayer network approach (Boccaletti et al., 2014; Kivelä et al., 2014) to brain activity (Buldú & Papo, 2018), the relevant space may be the frequency domain (Brookes et al., 2016; Buldú & Porter, 2018; Guillon et al., 2017). In this approach, network nodes are identified with signal frequency bands, and edges with their particular relationship, reflecting the frequency‐specific aspect of long‐range interactions associated with cognitive function (Siegel, Donner, & Engel, 2012). Finally, the network structure need not be isomorphic to the anatomical structure (Papo, Zanin, & Buldú, 2014; Papo, Zanin, Pineda, et al., 2014). The space may for instance be of a more abstract nature, for example, the space of pathological features of a given disease or of the relationships between different diseases (Borsboom & Cramer, 2013; Zanin et al., 2014). This would reflect the fact that the relevant space may qualitatively differ, depending on the goals of a given research, which could range from simply finding differences between conditions to modelling brain activity.

3.2. Space partitioning

Nodes are the basic objects of a network structure and constitute the microscopic scale of network analysis. Network theory prescribes nothing as to their properties other than their pointwise nature.

Defining nodes from dynamical brain imaging data implies partitioning the space, quotienting it by a given property and identifying the open sets of the topology thus induced with discrete points. This is achieved through a complex renormalization process which involves a number of discretionary choices to define the following partially interrelated properties:

1. General construction criteria/principles. These may include anatomy‐based rules, resorting for instance to available atlases, or dynamics‐based ones. The various methods differ in the stage at which function enters the picture.

   One class of methods, referred to as data‐driven in the remainder of this article, tries to commit as little as possible to prior theory, to let function emerge from the dynamics. The maximally non‐committal possibility would involve a one‐to‐one map to the microscopic scales induced by the brain recording device's precision. For non‐invasive system‐level electrophysiological techniques, this ground partition could prima facie coincide with the sensor space and the main issue is how well sensors sample the underlying dynamical system. Working on a source reconstructed space would allow far more reliable interpretations in terms of activity in anatomically defined brain regions, however both the accuracy of the inverse model and the partition of the source points affects analysis outcomes (Palva et al., 2018), and tend to limit the size of the reconstructable network. In fMRI, voxels induce a partition of the anatomical space and the main issue is finding a functionally meaningful covering of this ground partition.

   Another class of methods, a priori atlases, uses prior knowledge, for example, anatomical or histological landmarks, to define partitions of the anatomical space, taking into account the disordered nature of the functional space, the general idea being to directly carve functionally meaningful parcellations. Here, the problem lies in the complex anatomy‐dynamics‐function relationship.

2. Membership rules, for example, topographical localization in the anatomical space or statistical criteria, as in clustering methods (Jain, Murty, & Flynn, 1999) directly reflect the chosen reconstruction principles.

3. Space partition rules, for example, partitioning stricto sensu, fuzzy (Simas & Rocha, 2015) or overlapping (Palla, Derényi, Farkas, & Vicsek, 2005) parcellations, or size rules, enforcing in different ways separation on the relevant space. Furthermore, space partitions need not be time‐invariant and nodes may be time‐varying entities in the space in which they are defined; for instance, nodes could be spatially non‐stationary in the anatomical space (cf. Section 3.4.3).

4. Geometric or topological metarules. Typically, parcellating the anatomical space involves forming macronodes, called regions of interest (ROIs). In this case, other important properties such as locality, compactness and connectedness in the anatomical space are often required. These properties are motivated by a classical anatomy‐to‐function projection, but also by the need to perform operations in the relevant space, such as comparing different parts of the space (cf. Section 3.3.1). A well‐behaved space would for instance permit using the powerful tools of calculus and differential geometry, and handling scalar or vector fields allowing operations such as transport within the underlying manifold. Relaxing these properties may imply allowing the emergence of non‐trivial properties of the underlying space, and would require tools for example, from computational topology (Robinson, 2013a) capable of handling such systems. This would also help conceiving of observed brain dynamics in terms of a function space (Papo, 2019) and therefore a more flexible and intuitive way of representing brain function.

Independent of the exact criteria applied to reduce the number of nodes in the transition from voxel or source‐point level to the level of ROIs, the process involves delineating functionally separate brain units, a task that goes under the name of parcellation (Stanley et al., 2013). As a basic requirement, a parcellation should minimize the amount of information lost in the transition from voxels or source points to ROIs. To this end, ROIs must be functionally homogeneous, or in other words, comprise voxels or source points similar enough to be presented with a single ROI time series (Stanley et al., 2013). Functional homogeneity can be measured as the similarity of, for example, voxel or source point time series (Göttlich et al., 2013; Korhonen, Saarimäki, Glerean, Sams, & Saramäki, 2017; Ryyppö, Glerean, Brattico, Saramäki, & Korhonen, 2018; Stanley et al., 2013), voxel or source point connectivity profiles (Craddock, James, Holzheimer, Hu, & Mayberg, 2012; Gordon et al., 2016), general linear model parameters describing voxel activation (Thirion et al., 2006), or the observed activity z scores (Schaefer et al., 2017). The selection of the appropriate measure of functional homogeneity depends on how ROI time series are observed (cf. “Renormalization of ROIs' internal properties” section below).

In addition to functional homogeneity, the goodness of a parcellation can be evaluated in terms of agreement with brain microstructure (cytoarchitecture and myelination), performance in simple network‐based classification tasks (e.g., gender classification), and in the case of data‐driven parcellations (cf. “A priori atlases or data‐driven parcellations?” section below) also reproducibility, that is, the ability to produce similar ROIs from different datasets of the same subject (Arslan et al., 2018).

Creating a parcellation optimal in all these measures is challenging (Arslan et al., 2018). Therefore, what parcellation scheme to adopt hinges on the studies' general purpose. For instance, if the purpose is characterizing brain function or modelling brain activity, then nodes should closely reflect the properties that one intends to model. However, network analysis may simply be used as a convenient tool to achieve less ambitious goals though often of primary importance, such as discriminating between populations or conditions along some feature.

3.2.1. Defining ROIs

Motivation for using ROIs

A typical whole‐brain fMRI protocol is associated with ~10⁶ voxels, while in MEG/EEG, when source reconstruction is applied, the data collected by some hundreds of sensors are typically inverse modelled as time series of ~10⁶ source points. As described above (cf. Section 3.2), these voxels or source points may appear as natural node candidates for functional brain network analysis. However, often network nodes depict larger spatially continuous clusters of voxels or source points, referred to as ROIs. The appropriate definition of ROIs is equally important for analysis of fMRI and source‐modelled MEG and EEG data. Often, the same ROI definition approaches can be used for analysing both imaging modalities, in particular if the MEG or EEG source reconstruction is based on anatomical information from MRI (Cottereau, Ales, & Norcia, 2015). Instead, the problem of ROI definition is not relevant for sensor‐space MEG and EEG analysis, where network nodes naturally depict the measurement sensors.

There are several reasons for using ROIs as network nodes. The most important is dimensionality reduction: the large amount of nodes may lead to a noisy adjacency matrix, in particular since the signal‐to‐noise ratio (SNR) of voxel and source point time series is often not particularly high (de Reus & van den Heuvel, 2013; Zalesky, Fornito, Hardling, et al., 2010). In general, interpreting relations or even providing a graphical representation may prove arduous for the voxel and source‐point‐level networks (Papo, Buldú, Boccaletti, & Bullmore, 2014). Besides, the large number of nodes in the voxel and source‐point‐level networks increases the computational cost of obtaining higher‐order topological properties. Furthermore, cognitive functions are known to cover cortical areas larger than single voxels or source points (Shen, Tokoglu, Papademetris, & Constable, 2013; Wig et al., 2011). Therefore, outcomes of ROI‐level analysis may be easier to interpret in the neurophysiological context than those of voxel or source‐point level ones.

Unlike nodes of many other networks, ROIs are not spatially pointwise. Consequently, their reconstruction involves defining both boundaries (cf. “Renormalization of ROI boundaries” section below) and internal properties, which determine the way each of these regions interacts with other ones (cf. “Renormalization of ROI's internal properties” section below). The latter introduces an intrinsic relationship between node and edge definition.

A priori atlases or data‐driven parcellations?

The lack of a standard method for brain parcellation into regions (Eickhoff, Thirion, Varoquaux, & Bzdok, 2015) has led to a wide variety of definitions of functional brain network nodes (Zalesky, Fornito, Hardling, et al., 2010).

From a methodological viewpoint, the various ROI definition methods can be divided into two categories. Most parcellation techniques are based on mapping a priori atlases (e.g., Desikan et al., 2006; Fan et al., 2016; Fischl et al., 2004; Power et al., 2011), defined in terms of, for example, anatomy or function, onto the subject's brain. On the other hand, data‐driven techniques parcellate the brain using the features of the present data (Honnorat et al., 2015; Parisot, Arslan, Passerat‐Palmbach, Wells, & Rueckert, 2016).

Brain functions range from highly localized to highly extended (Robinson, 2013b). The atlas approaches are based on the assumption that a relatively small number of localized ROIs, representing the underlying dominant modes, can accurately capture distributed brain dynamics (Robinson, 2013b). However, this assumption is not guaranteed to hold, and checking its validity with experimental data is hard. Indeed, data‐driven parcellations outperform a priori atlases in terms of functional homogeneity (Craddock et al., 2012; Gordon et al., 2016) and amount of information maintained in the transition from voxels to ROIs (Thirion, Varoquaux, Dohmatob, & Poline, 2014). Besides, data‐driven parcellations yield higher prediction accuracy in the classification of fMRI data collected during different tasks (Sala‐Lloch, Smith, Woolrich, & Duff, 2019; Shirer, Ryali, Rykhlevskaia, Menon, & Greicius, 2012) or from different subject cohorts, for example, patients and healthy control subjects (Dadi et al., 2019). Despite the evidence supporting data‐driven parcellations, a priori atlases are still commonly used, since they are easy to apply and may allow more straightforward interpretation of results than the data‐driven approaches.

From a conceptual viewpoint, it is interesting to compare how these methods differ in the way they allow function to emerge (cf. Section 2.1.1). These two methods, which belong to two qualitatively different approaches, respectively theory‐ and data‐driven, differ in the space used to parameterize brain activity. Atlas‐based approaches use a local projection of function on anatomy, whereas data‐driven approaches typically use bare dynamics. Thus, the former approach already contains a parcellation of the space onto which the dynamics is defined. What is studied is an ensemble of oscillators interacting according to the coupling scheme imposed by the anatomical network (Cabral et al., 2011; Deco, Jirsa, & McIntosh, 2011). Interestingly, function features both as an a priori ingredient of the space in which dynamics takes place and as a subset of the associated space which emerges from network dynamics at appropriate coupling values (Pillai & Jirsa, 2017). In data‐driven approaches, parcellations, and therefore ultimately function both emerge from dynamics. However, data‐driven approaches may in fact contain geometrical and topological constraints on how brain function is projected onto brain anatomy (cf. Sections 3.2 and “Renormalization of ROI boundaries”). Ultimately this may contribute to reducing differences in the parcellations produced by the two methods.

Furthermore, while in the former method the parameterizing space is static by construction, in the latter it can potentially by time‐varying. However, as the time axis is collapsed, the two approaches lose one of the dimensions in which they differ. These factors help explaining why, although the difference between atlases and data‐driven approaches may look fundamental, the two methods may yield overlapping results, under some conditions. Many parcellation strategies first introduced as data‐driven ones have led to static sets of ROIs that are used as a priori atlases (e.g., Craddock et al., 2012; Schaefer et al., 2017; Shen et al., 2013). Such an approach obviously saves time and computational power. On the other hand, there is no reason to assume that the accuracy of a parcellation strategy would remain intact if it is used as an atlas instead of a data‐driven approach.

Renormalization of ROI boundaries

In the following sections, we review parcellation strategies grouped by the brain features they make use of and the ROI properties they aim to optimize. Some of these strategies produce by definition a priori atlases while others can be both used to define atlases and applied as data‐driven techniques. Most of the techniques can be applied to both functional neuroimaging and electrophysiological recordings.

Microstructural parcellations

Parcellating the brain based on cell‐level microstructure has a long tradition, tracing back to the seminal work of Brodmann on brain cytoarchitecture (Brodmann, 1909) and Vogt and Vogt (1919) on myeloarchitecture. These parcellation strategies are based on the diversity of cell types in the brain: different cells are assumed to specialize on different tasks, and boundaries of functionally homogeneous ROIs should therefore follow the boundaries between different cell types. The first microstructural atlases were defined in 2D and excluding the intrasulcular surface, which means that before using these areas as network nodes, they need to be translated to a 3D space (Zilles & Amunts, 2010). The best‐known example of such translation is the Talairach–Tournoux atlas, a 3D generalization of the Brodmann areas (Talairach & Tournoux, 1988). Some Brodmann areas are still commonly used as ROIs in both fMRI and MEG and EEG analysis, and they are also used as a naming reference for creating new parcellations.

The early microstructural parcellations were based on light microscopy studies and carried no reference to anatomical landmarks of the brain, while the modern approaches combine cell‐level staining methods with large‐scale structural neuroimaging (Amunts & Zilles, 2015). For example, Ding et al. (2016) applied Nissl staining and NFP and PV immunolabelling, together with MRI and diffusion weighted imaging, to label 862 grey and white matter structures in the brain of a 34‐year‐old female. The JuBrain atlas (Amunts, Schleicher, & Zilles, 2007; Caspers, Eickhoff, Zilles, & Amunts, 2013) combines cell staining with macroanatomical landmarks to create a probabilistic parcellation or, in other words, a set of maps telling for each voxel the probability to belong to each of the 106 regions of the atlas. The Julich–Brain project (Amunts, Mohlberg, Bluday, & Zilles, 2020) combines probabilistic cytoarchitectural maps from different sub‐studies; these maps are obtained with modified Merker staining and anatomical information from MRI using post‐mortem data of 10 subjects selected from a 23‐subject pool. The Julich–Brain atlas is available as maximum probability maps, where each voxel is assigned to the ROI it has the highest probability to belong to (Eickhoff et al., 2005; Eickhoff, Heim, Zilles, & Amunts, 2006), as well as in probabilistic maps of individual ROIs that allow more detailed, distribution‐based localization of brain activation (Eickhoff et al., 2007). At the moment, the Julich–Brain atlas contains 120 areas per hemisphere, covering around 80% of the cortical volume; however, the atlas is continuously updated with new areas as new sub‐studies are published (Amunts et al., 2020).

Microstructure‐based parcellation strategies rely on post mortem data, which obviously limits their use to construction of a priori defined atlases only. Furthermore, the availability of such data limits the number of brains used for the microstructure‐based parcellation strategies; the atlases may even be based on a single brain, and their generalizability to other subject populations is rarely addressed.

Anatomical parcellations

In many commonly‐used parcellation strategies, the criteria for defining a cortical area are based on structure–function associations at the level of cortical areas in the anatomical space (Amunts & Zilles, 2015). Anatomical parcellation strategies use data collected with non‐invasive imaging methods, typically structural MRI. Therefore, these parcellations may use a larger number of subjects than the microstructural ones, yielding improved generalizability. However, the anatomical parcellation processes are typically time‐consuming and require significant amounts of manual work, which means that these parcellation strategies are rarely used in a data‐driven way.

Anatomical ROIs are commonly used as nodes of functional brain networks constructed from both fMRI and source‐modelled MEG and EEG data. The probably most commonly used one is the automated anatomical labeling (AAL) atlas (Rolls, Huang, Lin, Feng, & Joliot, 2020; Rolls, Joliot, & Tzourio‐Mazoyer, 2015; Tzourio‐Mazoyer et al., 2002), whose ROIs are obtained by manually labelling a high‐resolution single‐subject MR image based on the main sulci. The latest version of AAL, AAL3 (Rolls et al., 2020) contains 166 ROIs. Another commonly used anatomical parcellation, the Desikan–Killiany atlas (Desikan et al., 2006) was constructed by manually labelling the cortex of 40 subjects of varying age and healthy status into 34 areas per hemisphere and turning these areas into a cortical atlas using a probabilistic algorithm. Besides being used as an atlas of its own, the Desikan–Killiany atlas forms a part of the probabilistic Harvard–Oxford (HO) parcellation that combines multiple atlases (Desikan et al., 2006; Frazier et al., 2005; Goldstein et al., 2007; Makris et al., 2006). In HO, each voxel is given, separately, the probability to belong to each of the 48 cortical and 21 subcortical ROIs.

HO, Desikan–Killiany, and AAL all offer an atlas for assigning ROI labels to voxels after transforming the data from subjects' native space to some standard space. An opposite approach is used by, for example, the Automated Nonlinear Image Matching and Anatomical Labelling (ANIMAL) parcellation (Collins, Holmes, Peters, & Evans, 1995) and the Destrieux parcellation (Destrieux, Fischl, Dale, & Halgren, 2010; Fischl et al., 2004), also known as the FreeSurfer parcellation after the commonly used FreeSurfer analysis software (Fischl, 2012). In these parcellations, the a priori atlas of ROI labels is first transformed to the native space and voxels are assigned with ROI labels before transformation to the standard space. ANIMAL comprises an a priori atlas observed from the averaged MR images of 305 subjects, an iterative, hierarchical multiscale algorithm for mapping the atlas to native space, and a linear transformation from the native space back to a standard space for group‐level analysis. In the Destrieux parcellation, the atlas consists of voxels' probabilities of belonging to certain ROIs (74 per hemisphere), given the anatomical location and ROI labels of neighbouring voxels, and the transformation from standard to native space is done using anisotropic non‐stationary Markov random fields (MRFs).

The size of ROIs created by anatomical parcellations tends to vary widely. While this variation may be a genuine property of the brain (Wig et al., 2011), it may also bias the outcome of network analysis, depending on how the network edges are defined. To eliminate this bias, some studies have further fine‐tuned anatomical ROIs by splitting them to sub‐areas along the axis with the largest variance in voxel or source point location (Palva, Kulashekhar, Hämäläinen, & Palva, 2011; Palva, Monto, Kulashekhar, & Palva, 2010).

In microstructural and anatomical parcellation methods, Ψ is mapped onto the anatomical Euclidean space, inheriting the functional partition defined on this space based on average anatomical structure, physiology, or cytoarchitecture (Brodmann, 1909). Both Ψ and Φ are then assumed to have modular structure (Fodor, 1983), the underlying assumption being that information is (locally) compact in the anatomical support. However, higher‐level cognitive function, for example, executive functions, reasoning or thinking, are associated with complex spatio‐temporal organization and correspondingly complex phenomenology (Papo, 2015), and emerging function is spatially and temporally non‐local (Kozma & Freeman, 2016). These functions are typically supported by redundant and degenerate ⁵ systems wherein a number of brain structures can generate functionally equivalent behaviour (Price & Friston, 2002). Φ may therefore turn out to be too low‐dimensional to capture the complexity of both Φ and Ψ, and this severely limits the ability to account for the complex phenomenology of executive function and its disruption in pathology (cf. Section 2.1.1). Degeneracy may reflect a higher dimensional input–output space and combinatorial complexity (Brezina, 2010; Brezina & Weiss, 1997) but may also be a purely dynamical effect of a system with non‐linear and history‐dependent interactions (cf. “Structure of the functional space” section above).

Functional parcellations

In functional parcellation approaches, ROIs are defined as functional equivalence classes, that is, as groups of voxels or source points with similar functional profile. The definition of these parcellations depends on recording techniques and the temporal scales of brain activity. For fast sensory processes, which typically have a characteristic duration and a topographically more stereotyped identity, functional ROIs can be defined by stimulus properties and response functions, for example, the dynamical range, that is, the range of stimulus intensities resulting in distinguishable neural responses, or the dynamical repertoire, that is, the number of distinguishable responses. On the other hand, for processes lacking a characteristic duration and stereotypical topography such as thinking or reasoning (Papo, 2015), defining functional parcellations is conceptually and technically arduous. This approach suffers from some of the issues encountered by anatomy‐based methods (cf. “Anatomical parcellations” section above), namely a spatially local and time‐invariant vision of brain function, an approximation which may be useful in some cases but untenable in others, and further illustrates a degree of circularity in the definition of function in network neuroscience (cf. Section 2.2.1).

Historically, the term ROI has referred to a part of the brain, typically a set of fMRI voxels, subject to a specific interest because of its observed activation during a certain task. This is still the standard way to define functional ROIs: ROI centroids are defined as the peak coordinates of activation maps related to a task or a set of tasks and the ROI is formed by setting a relatively small sphere or cube around the centroid (Power et al., 2011; Stanley et al., 2013; Wang et al., 2011). This approach produces ROIs of at least approximately uniform size.

Typically, the spherical functional ROIs cover only a part, even as little as 1%, of grey matter (Stanley et al., 2013), which obviously leads to losing information from the excluded voxels. Furthermore, activation‐based parcellations are limited by the fact that the tasks used in the activation mapping scans obviously cover only a minor part of the brain's functional repertoire (Eickhoff et al., 2018).

Using the parcellations based on activation maps in a data‐driven way requires additional activation mapping scans. Therefore, these parcellations are typically used as a priori atlases and cannot account for individual variation between subjects. The parcellation of Blumensath et al. (2013) addresses this problem by maximizing the similarity of voxel time series inside ROIs instead of localizing activity peaks. The approach is twofold: first, small parcels are grown around numerous (up to several thousands) seed voxels. Next, hierarchical clustering is used to combine these parcels into final ROIs; cutting the clustering tree at different stages produces different numbers of ROIs.

Another commonly used functional parcellation approach, especially in fMRI analysis, is the independent component analysis (ICA) (Calhoun, Liu, & Adali, 2009). The numerous ICA approaches can be divided into two domains: the temporal ICA (tICA) (Biswal & Ulmer, 1999; Smith et al., 2012) and the spatial ICA (sICA) (Calhoun, Liu, & Adali, 2009; McKeown et al., 1998). tICA identifies temporally independent signal components, possibly originating from spatially overlapping areas. These components are, by definition, not correlated, which precludes their use as network nodes (Pervaiz, Vidaurre, Woolrich, & Smith, 2020). sICA, on the other hand, divides the data into a set of spatially independent components, that is, components originating from non‐overlapping voxels. For group‐level analysis, there are several approaches that first perform group sICA and then register the detected components back to each subject's native space (Calhoun, Liu, & Adali, 2009). Despite the spatial independence requirement of sICA, temporal dependencies between the components are possible, allowing definition of network edges as temporal similarity between the sICA components. The spatial independence requirement ensures that the sICA‐based nodes do not overlap; however, depending on the selected number of components, the nodes may be spatially discontinuous.

The ICA‐based parcellation approaches search for components of brain activity that are independent either in time or in space. However, the brain activity components are unlikely to be fully independent in either domain, which questions the accuracy of ICA‐based ROIs (Harrison et al., 2015; Pervaiz et al., 2020). The PROFUMO approach (Harrison et al., 2015) addresses this problem by dividing the brain activity into probabilistic functional modes (PFMs) using a Bayesian inference model. While PROFUMO maximizes the joint independence of PFMs in space and time, there is no strict condition for independence in either domain alone. Therefore, PFMs may overlap spatially and be correlated, allowing to investigate the functional connectivity between them. Similar approaches, the Abraham, Dohmatob, Thirion, Samaras, and Varoquaux's (2013) and the DiFuMo parcellation (Dadi et al., 2020), use dictionary learning to obtain soft, mostly non‐overlapping functional modes of brain activity.

Unlike many other functional and connectivity‐based parcellation approaches (see below), sICA and functional mode approaches are rarely used for obtaining ROI atlases. Instead, they are typically applied to construct ROIs from the present data in a truly data‐driven manner.

Functional parcellation approaches are more common in fMRI studies than in analysis of MEG and EEG data. However, both ROIs around activity peaks (Cottereau et al., 2015) and ICA approaches (Chen, Ros, & Gruzelier, 2013) have been successfully applied on source‐modelled MEG and EEG.

Connectivity‐based parcellations

Connectivity‐based parcellations aim to produce ROIs that contain voxels or source points with maximally similar connectivity profiles. This approach resorts to a combination of topological (connectivity, contiguity, compacity) and geometrical (local continuity) criteria as a proxy for function (Varela et al., 2001), and as means to define ROIs (cf. Sections 2.2.1 and 3.2). Note that, while in principle allowing a certain degree of non‐locality, such a principle is mitigated by these a priori assumptions.

These parcellations can operate either at the level of single subjects, producing individual ROIs, or at the group level, combining connectivity observed in multiple subjects (Arslan et al., 2018). Connectivity‐based parcellation approaches may be roughly divided into two classes: local gradient approaches and global similarity approaches (Eickhoff et al., 2018; Schaefer et al., 2017).

The local gradient approaches detect ROI boundaries as sudden changes in the connectivity landscape between two neighbouring voxels (Schaefer et al., 2017). For example, the approach introduced by Cohen et al. (2008) and further developed by Nelson et al. (2010) creates for each of the seed points in a 3‐mm grid a connectivity profile similarity map compared to the rest of the seeds. An edge detection algorithm then detects the potential ROI boundaries in each of these similarity maps. The group‐level average of these boundaries gives the probability of each voxel to be part of a ROI boundary, and ROIs can be detected by applying a watershed algorithm on this probability map. Later, Power et al. (2011) complemented this parcellation approach with a bunch of functionally defined ROIs to create the Power atlas. Wig, Laumann, and Petersen (2014) and Gordon et al. (2016) have suggested similar approaches.

The gradient approaches do not directly address the similarity of voxel connectivity profiles, although they in practice often produce ROIs with relatively high connectional homogeneity (Gordon et al., 2016; Schaefer et al., 2017). Parcellation approaches based on global connectivity similarity, on the other hand, cluster together voxels with maximally similar connectivity profiles, independent on their spatial location (Schaefer et al., 2017). For example, Craddock et al. (2012) obtained ROIs using normalized cut (NCUT) spectral clustering that maximizes similarity inside clusters and dissimilarity between clusters; the optimization target may be either the temporal similarity of voxel time series or the spatial similarity of their connectivity maps. Group‐level ROI atlases for a priori use, obtained from 41 subjects either by averaging connectivity matrices before NCUT or by a second clustering round on cluster membership matrices, are available at several resolutions (Craddock et al., 2012). The approach of Shen et al. (Shen, Papademetris, and Constable, 2010; Shen, Tokoglu, Papademetris, and Constable, 2013) uses the same clustering method but addresses the problem of group‐level parcellation by a multigraph extension that finds the optimal set of ROIs for multiple subjects at once. Also the Shen ROIs, obtained from 79 subjects, are available as an a priori atlas at multiple resolutions (Shen et al., 2013).

Since the parcellation approaches based on global similarity explicitly optimize connectional homogeneity, they may produce ROIs better suited for network nodes than those produced by the local gradient approaches (Schaefer et al., 2017). However, the maximization of global similarity does not necessarily lead to spatially continuous ROIs (Schaefer et al., 2017). Craddock et al. (2012) solved this by adding a continuity term to the clustering target function, while in the Shen parcellation, the continuity requirement is implicitly included in the multigraph approach (Shen et al., 2013).

The latest generation of connectivity‐based parcellations combines the local and global approaches and different features of the data, possibly even multiple imaging modalities. The Brainnetome atlas (Fan et al., 2016) of 210 cortical and 36 subcortical ROIs is constructed from the data of 40 subjects based on anatomical information from MRI, structural connectivity from diffusion tensor imaging, and functional activation and connectivity from fMRI during rest and task. Glasser et al. (2016) applied a local gradient approach to detect 360 cortical and subcortical ROIs from the data of 210 subjects; the multimodal data used in this approach included MRI to address myelination and cortical thickness from MRI, task‐fMRI to address activation, rest‐fMRI to address functional connectivity, and the topography of some areas, in particular the visual cortex. Schaefer et al. (2017) combine global similarity of function (in terms of voxel time series), local gradients of functional connectivity, and the spatial continuity requirement into a gradient‐weighted MRF model; the ROIs obtained with this approach from the data of 1,489 subjects are available as a priori atlases at several resolutions.

Similarly to functional parcellations, connectivity‐based parcellation approaches are not particularly popular in MEG and EEG studies. Due to differences in the temporal scale of imaging modalities, connectivity‐based a priori atlases constructed from fMRI data may not be optimal for analysing MEG and EEG data. However, many of the data‐driven approaches are essentially network clustering methods and can be applied on the source‐point‐level connectivity matrix of MEG and EEG data to obtain connectivity‐based ROIs.

Random parcellations

In addition to parcellations based on different features of neuroimaging data, functional brain network nodes can be defined at random. Typically, the random parcellations are used as a reference, against which the other parcellation approaches are compared (see, e.g., Craddock et al., 2012; Gordon et al., 2016). However, Fornito, Zalesky, and Bullmore (2010) used ROIs grown around random seeds only guided by spatial proximity to show that the size and number of nodes affects the properties of functional brain networks. Although random ROIs lack neurophysiological interpretation, they have shown surprisingly high functional homogeneity (Craddock et al., 2012; Gordon et al., 2016) and also yielded network properties comparable to those observed with optimized parcellation approaches (Craddock et al., 2012).

Renormalization of ROIs' internal properties

In classic graph‐theoretical analysis, nodes are considered as point‐like entities. However, unlike the nodes of theoretical graphs and many real‐life networks, ROIs are spatially extended and comprise several lower‐level units with individual dynamics. A network‐based treatment of the anatomical space partitioned into ROIs could take a community structure or network‐of‐networks approach (Gao, Li, & Havlin, 2014; Schaub, Delvenne, Rosvall, & Lambiotte, 2017), wherein each ROI is treated as a sub‐network or as a network in its own right. The results about non‐trivial connectivity structure inside ROIs of anatomical and connectivity‐based parcellations (Ryyppö et al., 2018; Stanley et al., 2013) would support such an approach.

However, addressing the dimension reduction goal often requires collapsing ROIs into equivalent point‐wise nodes. The connectivity between ROIs depends on the way the voxel or source point dynamics inside ROIs are summarized or, in other words, how well ROIs' internal structure is accounted for. However, while the importance of properly defined ROI boundaries is already widely acknowledged, less attention is paid on how the time series of individual voxels or source points are combined to obtain a single ROI time series.

The by far most common approach is to obtain ROI time series as an unweighted average of the time series of voxels or source points. In the ideal case of functionally perfectly homogeneous ROIs, these time series would differ from each other only in terms of independent noise, and averaging would increase the SNR by eliminating this noise (Stanley et al., 2013). In reality, however, in particular ROIs of a priori atlases often show low to mediocre functional homogeneity (Göttlich et al., 2013; Korhonen et al., 2017; Stanley et al., 2013). Therefore, unweighted averaging often leads to losing information (Stanley et al., 2013) and in the worst case to spuriosities in observed connectivity (Korhonen et al., 2017).

An obvious way to decrease the loss of information in unweighted averaging is to assign the voxel or source point time series with weights before averaging. For example, the approach of S. Palva et al. (2011) addresses the possible phase inhomogeneity inside ROIs in source‐reconstructed MEG/EEG data: source points on different walls of a sulcus tend to have a phase difference of π, leading to signal cancelation if their time series are averaged without further consideration (Ahlfors et al., 2010; Cottereau et al., 2015). To avoid this, S. Palva et al. (2011) first calculated the phase distribution inside ROIs, identified the two groups of source points with different phases, and before averaging shifted the phase of one of these groups by π while keeping the amplitude intact. Another, also MEG/EEG‐oriented approach (Korhonen, Palva, & Palva, 2014) weighted source point time series by their ability to retain their original dynamics in a simulated MEG/EEG measurement (forward modelling) and source reconstruction. The approach increases functional homogeneity, measured in terms of phase synchrony, of ROIs and decreases spurious connectivity between ROIs. However, because of the weight thresholding of this approach, many source point time series get weight 0 and get excluded from further analysis (Korhonen et al., 2014).

In studies of fMRI data, the weighted average approach has been applied by defining the ROI time series in terms of the strongest intra‐ROI principal component analysis (PCA) components (Sato et al., 2010; Zhou et al., 2009). In this approach, the number of components to use remains as a free parameter; in the work of Zhou et al. and Sato et al., the number was relatively low, typically less than 10.

As an extreme case of weighted averaging, the time series of a single source point can be selected to represent the whole ROI. In this approach, all but the chosen source point time series are assigned with weight 0. For example, Hillebrand, Barnes, Bosboom, Berendse, and Stam (2012) used as ROI time series the source point time series with the highest signal power within the ROI, while O'Neill et al. (2017) used the time series of ROIs' centres of mass. While this approach avoids the possibly corrupting effects of averaging, it voluntarily discards the information from a vast majority of source points. Furthermore, it does not account for the risk of the highest‐power source point being an outlier or having particularly low SNR.

In parcellation approaches based on spatially overlapping functional modes (see section “Functional parcellations” above), averaging voxel or source point time series is less straightforward. These parcellations often require more sophisticated ways for renormalizing ROI time series. For example, Dadi et al. (2020) obtained the time series of their functional modes in terms of linear regression.

A separate time series renormalization step is not included in all parcellation approaches. The sICA approaches as well as some functional mode approaches define ROIs as the spatial origins of certain signal components, and these components are obviously used as ROI time series. In MEG/EEG analysis, time series renormalization can be overcome also by the beamformer source reconstruction approach (van Veen, van Drongelen, Yuchtman, & Suzuki, 1997). This approach filters the signals of measurement sensors to detect the independent activity originating on a set of source points on the brain surface; if the number of these source points is small enough and their location is motivated by, for example, anatomy or function observed in previous studies, the source‐reconstructed signals can be directly used as ROI time series.

3.3. Edge identification

In addition to space parcellation, another key step in brain network reconstruction requires identifying edges. Edges play a double role in the network structure: on the one hand, they incorporate the structure's relational information; on the other hand, in the statistical mechanics approach, the system's degrees of freedom are represented by the interactions, so that edges, rather than nodes constitute the system's genuine particles, their maximum number playing the role of the system's volume (Gabrielli, Mastrandrea, Caldarelli, & Cimini, 2019).

Edges are usually designed to reflect essential aspects of brain dynamics and function. Thus, in principle, edges should incorporate as much neurophysiological detail as required by the study's purpose. However, the neurophysiological plausibility of edge metrics is subjected to a number of other constraints. Any metric operationalizing the functional elements that edges are supposed to handle necessarily reflects a specific angle under which brain activity is envisioned (e.g., dynamical or information‐theoretic) and is predicated upon basic assumptions on brain dynamics and function. For instance, how information is transported, that is, whether via modulations of mean firing rates (Litvak, Sompolinsky, Segev, & Abeles, 2003; Shadlen & Newsome, 1998), through temporally precise spike‐timing patterns (Abeles, 1991; Buzsaki, Llinas, Singer, Berthoz, & Christen, 1994), or otherwise, and how it is processed at various spatial and temporal scales of neural activity, are still poorly understood though seemingly context‐specific phenomena. To provide a mathematical characterization of known properties, edge reconstruction has mainly drawn its conceptual framework from nonlinear dynamics and synchronization theory (Arenas, Díaz‐Guilera, Kurths, Moreno, & Zhou, 2008; Boccaletti, Kurths, Osipov, Valladares, & Zhou, 2002), and information theory (Rieke, Warland, van Steveninck, & Bialek, 1999), to produce a variety of edge metrics with various characteristics (Pereda et al., 2005; Rubinov & Sporns, 2010). This conceptual background allows addressing dynamics, but only somehow indirectly function. For instance, information‐based metrics would at first sight seem to directly quantify a crucial ingredient of brain function. However, only part of the information effectively transferred can be thought to have a genuine functional meaning, due to both thermodynamic and informational inefficiency of neural circuitry (Sterling & Laughlin, 2015; Still, Sivak, Bell, & Crooks, 2012). Moreover, understanding the functional meaning of information transfer in heavily coarse‐grained signals is not straightforward.

Finding an adequate mathematical representation constitutes a further set of constraints to the physiological plausibility of connectivity metrics. Each metric comes with its own set of characteristics and shortcomings. For instance, metrics may quantify statistical dependency (often referred to as functional connectivity ⁶ ) or causal interactions (effective connectivity) (Friston, 1994; Horwitz, 2003); may be linear or nonlinear (Paluš, Albrecht, & Dvořák, 1993). Some connectivity metrics may be symmetric, while others, for example, Granger causality (Ding, Chen, & Bressler, 2006; Granger, 1969; Hlaváčková‐Schindler, Paluš, Vejmelka, & Bhattacharya, 2007), connectivity estimates from graph learning algorithms (e.g., Sun et al., 2012), or transfer entropy (Schreiber, 2000; Vicente, Wibral, Lindner, & Pipa, 2011) are directed and asymmetric. Measures may or may not distinguish between direct and indirect connectivity (Smith et al., 2011; Vejmelka & Paluš, 2008). Carefully selected matrix regularizators may embed assumptions about network structure, for example, sparsity or modularity, into estimation of coherence‐based connectivity metrics (Qiao et al., 2016). Finally, given the role of oscillations in brain activity (Başar, 2012; Fries, 2005; Schnitzler & Gross, 2005; Varela et al., 2001), connectivity is sometimes evaluated in a frequency‐specific way both in EEG and fMRI data analysis (Brookes et al., 2011; Hipp & Siegel, 2015), and corresponding frequency‐specific networks at rest (Boersma et al., 2011; Hipp, Hawellek, Corbetta, Siegel, & Engel, 2012; Qian et al., 2015) and associated with the execution of cognitive tasks (Wu, Zhang, Ding, Li, & Zhou, 2013), can be reconstructed from electrophysiological data, which are inherently broadband, but also from relatively narrow‐band BOLD fMRI recordings (Thompson & Fransson, 2015).

Statistical limitations reducing a given metrics' ability to track dynamics and function may also be specific to each connectivity metric. For instance, the minimum time‐interval required to estimate a simple linear correlation is much shorter than the corresponding one for Granger causality. More generally, complex mutual relationships are grossly simplified and most metrics do not allow accounting for functionally meaningful neurophysiological properties such as feedback loops, or inhibition.

Other limitations may stem from the edge reconstruction process itself, which may not take into account key available aspects of brain dynamics. For instance, synaptic pathways' finite conduction velocity and paths' varying length, give rise to dynamical phenomena such as partial synchrony (Hoppensteadt & Izhikevich, 1997), and polysynchrony (Stewart, Golubitsky, & Pivato, 2003), wherein some neurons oscillate synchronously while others do not, but also asynchronous behaviour, including polychrony, that is, time‐locked but asynchronous firing patterns (Izhikevich, 2006), and traveling waves (Muller, Chavane, Reynolds, & Sejnowski, 2018). To account for these phenomena, time lags should be incorporated into the dynamics at any scale of the analysis. In practice, though, reconstruction often turns out to be independent of system's characteristic time scales and at zero‐lag, producing dynamically spurious edges and ultimately distorting the temporal complexity of function. Moreover, if connectivity metrics reflect interregional communication and information transport modes, they should be stationary neither in time nor in the anatomical space. The indication would then be to reconstruct with region‐specific, possibly time‐varying connectivity metrics (Malagarriga, Villa, García‐Ojalvo, & Pons, 2017; Zanin, Pereda, et al., 2021) and time‐lags (Novelli, Wollstadt, Mediano, Wibral, & Lizier, 2019).

Brain recording devices' characteristics, for example, the sources of noise and artefacts of the device (cf. Section 3.5.2) or the physiological signal's characteristic used by each technique to characterize brain activity, may constitute further constraints to the physiological meaningfulness of reconstructed edges. For instance, fMRI's poor temporal resolution severely constrains the range of possible metrics, so that functional connectivity is typically estimated through the Pearson correlation between brain regions. It also forces evaluating metrics over a time‐window which may span the whole available epoch (Bastos & Schoffelen, 2016), spuriously compressing dynamics (cf. Section 3.5).

On the other hand, sophisticated edge identification can help to compensate for noise in network structure. In MEG and EEG analyses, a common source of such noise is signal mixing, that is, false edges caused by the fact that the dynamics of each source are captured by multiple measurement sensors (for details, cf. Section  3.5.2). A significant part of the false edges created by signal mixing are zero phase lag connections (Palva et al., 2018) and can therefore be eliminated by using connectivity metrics insensitive to zero phase lag connectivity, such as the imaginary part of coherence (Nolte et al., 2004), phase lag index (Stam et al., 2007), imaginary phase locking value (Palva & Palva, 2012), weighted phase lag index (Vinck et al., 2011), or orthogonalized correlation coefficient (Hipp et al., 2012; Brookes et al., 2012). As a downside, using these metrics means losing information about the true zero phase lag connections as well.

Overall, the particular metric that is being used results from a combination of functional assumptions, available mathematical tools, and constraints associated with the recording technique, and the specific goals of a given study. An important illustration of this statement is represented by the prominence of bivariate connectivity measures both in functional brain imaging (Bastos & Schoffelen, 2016) and electrophysiology (Lehnertz, 2011; Pereda et al., 2005), though multivariate ones have also been proposed (Lizier, Heinzle, Horstmann, Haynes, & Prokopenko, 2011). Whether pairwise connectivity reflects a true brain operating mode is all but a well‐established fact. The rationale for this choice can at least partially be traced to extra‐physiological factors, ranging from a long‐established conceptual framework dating back to the very onset of neuropsychological modelling, to early studies suggesting the preponderance of pairwise connectivity in neural activity (Schneidman, Berry, Segev, & Bialek, 2006), but also availability of analytical tools. However, even at short time scales, peaks in pairwise correlations may well be non‐local network effects involving other neuronal populations and feeling the influence of external fields (Roudi, Dunn, & Hertz, 2015).

3.3.1. Effects of edge metrics on network properties

The choice of a particular metric or class of metrics may potentially induce a corresponding change in properties of the associated network structure. For instance, the relation used to identify edges may affect the reconstructed network's topological and metric properties (Zanin, Pereda, et al., 2021) (cf. Section 3.6.1). Furthermore, while the choice of the embedding space is essentially a discretionary choice unrelated to network analysis (cf. Section 3.3), the edge metric determines the nature of the attractor space ⁷ and the set of operations allowed on it ⁸ by inducing a specific matrix, hence a particular space with its geometrical properties (Amari & Nagaoka, 2007). For example, normalized covariance matrices are associated with positive definite matrices, while the Pearson's correlation is associated with positive semi‐definite matrices. The space induced by these matrices may not be a vector space, so that some operations (e.g., subtractions) may not be well‐defined, and equipping it with a distance may be arduous (Bonnabel & Sepulchre, 2010; Lenglet, Rousson, Deriche, & Faugeras, 2006; Pennec, Fillard, & Ayache, 2006). For instance, when directly applied to covariance matrices, classical matrix computations may yield inaccurate results and numerical artefacts (Arsigny, Fillard, Pennec, & Ayache, 2007). While Whitney's embedding theorem (Whitney, 1936) ensures that an n‐dimensional manifold can at least be embedded into a 2n‐dimensional Euclidean space, affording an extrinsic view of the true space, an intrinsic view independent of the embedding space requires a different geometry (Pennec, 2006). One possibility consists in representing the underlying space as a Riemannian manifold, that is, a manifold M equipped with metrics on the tangent spaces which vary smoothly from point to point (Amari & Nagaoka, 2007). The structure of a Riemannian manifold can be specified by a Riemannian metric, that is, a continuous collection of scalar products on the tangent bundle T*M at each point of M, which is invariant under affine transformations (cf. Figure 3). This allows extending Euclidean properties to the manifold. Importantly, this also allows using classification or prediction algorithms, which cannot act in a Riemannian manifold (Krajsek, Menzel, & Scharr, 2016; Pervaiz et al., 2020).

FIGURE 3.

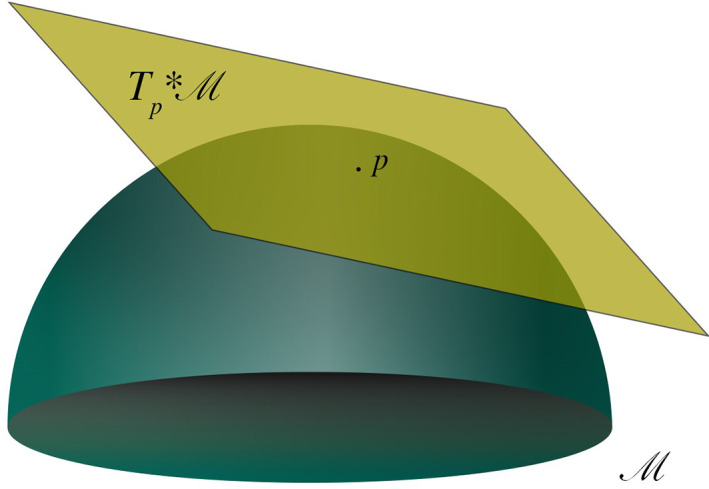
Manifold M and the corresponding tangent space T _p*M at point p. At each point p of M, there is one and only one tangent vector, and a scalar product can be defined in the associated tangent space T*M. If M is the space of positive definite matrices, T*M is identified with the Euclidean space of symmetric matrices. The M ↦ T*M homomorphism allows replacing the Riemannian metric in M with the Euclidean metric in T*M, and treating the projected connectivity matrices in the tangent space as Euclidean objects

A similar structure arises naturally when considering diffusion tensor images, in which each voxel is associated with the symmetric positive definite matrix induced by the covariance tensor image (Lenglet et al., 2006; Pennec et al., 2006), or when aggregating data from different subjects of a given experiment, which induce a manifold where each point is the dynamic covariance matrix (Ng, Varoquaux, Poline, Greicius, & Thirion, 2015; Varoquaux, Baronnet, Kleinschmidt, Fillard, & Thirion, 2010), as well as in genuine functional methods such as Hidden Markov models (HMMs; cf. Sections 2.1.1 and 3.4.1).

Equipped with a Riemannian geometry, the space has in principle additional structure with respect to a topological manifold. On the one hand, Riemannian tangent space parameterization allows preserving the geometry of functional connectivity. This has a clear meaning when analysing the brain's anatomical structure, as the tangent space parameterization preserves the geometry of anatomy‐embedded functional connectivity, but its meaning is less straightforward in the functional space, which is not guaranteed to be a smooth manifold even when the dynamical space is (cf. Section 2.1.1). On the other hand, for a given Riemannian space, a further discretionary element is given by the choice of a distance among the many available ones that can be defined on the space of covariance matrices. Each of these distances has specific properties (Arsigny et al., 2007; Yger, Berar, & Lotte, 2016), and relative task‐specific performance level, some performing better in terms of classification accuracy, while others are better in terms of computational efficiency (Chevallier, Kalunga, Barthélemy, & Monacelli, 2021).

Finally, different edge metrics may also induce different physics associated with the system's network structure. For instance symmetric connectivity readily accounts for equilibrium systems, whereas, asymmetric coupling matrices can be thought of as out‐of‐equilibrium systems with breakdown of detailed balance. In this perspective, choices associated with edges and the way these are constructed, for example, hybrid reconstruction with space‐ and time‐varying properties, represent not only a technical but also a theoretical challenge, in that they induce spaces with non‐trivial geometries and corresponding physics.

3.3.2. Classical versus Bayesian reconstruction

The standard way of identifying edges in functional networks is a frequentist one, in that a single value (e.g., the correlation coefficient or any other synchronization metric) is extracted from each pair of nodes and encoded as the weight of the corresponding edge. This approach, besides creating problems related with the pruning of the network, as we will see below, further has another disadvantage: the uncertainty about the edge is lost. In other words, any metric can only yield an estimation of the real connectivity strength, due to factors like the finiteness of the time series, or the presence of observational noise. The solution to this can be found in Bayesian statistics (Bolstad & Curran, 2016). Specifically, Bayesian inference considers data to be fixed, and the model parameters to be random, as opposed to what frequentist inference does. Furthermore, Bayesian inference—unlike frequentist—estimates a full probability model, including hypothesis testing. Disregarding such uncertainty may lead to the detection of wrong topological structures, and specifically to an overestimation of the presence of regularities and non‐trivial (i.e., non‐random) structures (Zanin, Belkoura, Gomez, Alfaro, & Cano, 2018).

3.3.3. Pruning and binarization

The natural result of the previous edge identification step is, in many cases, a weighted clique: when the metric used to estimate functional connectivity yields a value and not a statistical test, a weight is assigned to each edge, corresponding to the detected functional strength. Afterwards, such cliques are usually binarized, that is, the fully connected graphs are pruned according to some rule applied to edge weights, and unitary weights are assigned to surviving edges. The direct analysis of the weighted cliques would in principle represent the best solution, as they codify all the available information about the dynamics of the brain; on the other hand, any pruning procedure inevitably deletes some information. Still, network binarization entails some important advantages.

Brain networks are expected to be naturally sparse, as increasing the connectivity implies a higher physiological cost, although the true anatomical and, as a consequence, dynamic connectivity density might be grossly underestimated (Wang & Kennedy, 2016). Secondly, most of the topological metrics available in network theory have originally been developed for unweighted graphs, to only subsequently be adapted to weighted ones; therefore, a larger set of (better validated) tools is available to the researcher. Furthermore, edges with small connectivity values may just be the result of statistical fluctuations or of noise, such that deleting them can improve the understanding of the system, and in some cases even avoid biases (van Wijk, Stam, & Daffertshofer, 2010). A pruning can also help deleting indirect, second order correlations, which do not represent direct dynamical relationships (Vakorin, Krakovska, & McIntosh, 2009). Lastly, network analysis benefits from their graphical representation, which is meaningful only in the case of sparse structures.

Two main alternatives for network binarization are available, respectively called absolute and proportional thresholding. In the former case, all edges whose strength exceeds an absolute threshold τ are retained, while all the others are deleted (Váša, Bullmore, & Patel, 2018). This usually yields networks with a different number of edges across subjects, and most importantly, across groups (e.g., between control subjects and patients). This may lead to statistically significant differences in network metrics, even when these are not due to underlying disease‐related topological differences. As such, this approach has been suggested to be less appropriate for case–control studies (Nichols et al., 2017). The second approach partly overcomes this issue, by including in each network a fixed number of the strongest edges, hence the name of proportional (van den Heuvel et al., 2017); note that this approach is often referred to in literature as an analysis in which the density (Jalili, 2016) or network cost (Achard & Bullmore, 2007) is kept constant.

Thresholds are important tools for revealing a system's structure. For instance, if the underlying space can be thought of as a differential manifold, its topology can be defined by analysing the level sets of a function defined on this manifold (Milnor, 1963). Changes in the manifold topology can be related to the critical points of a sufficiently general function; for instance, under certain hypotheses, phase transitions can be related to changes in the topology of the level sets of the system's Hamiltonian (Caiani, Casetti, Clementi, & Pettini, 1997; Casetti, Pettini, & Cohen, 2000).

The dynamical and functional structure of the attractor underlying a given network representation should ideally be robust with respect to the way the network is built. However, each threshold type can be thought of as a particular cut into the relevant space, highlighting a specific set of properties of the underlying system, and is associated with its own renormalization flow, percolation threshold and, as a consequence, phenomenological properties. Suppose a given condition, for example, a pathology, only involves a change in dynamical coupling strength, but no change in overall network topology. Then, an absolute threshold may spuriously indicate that a given condition modifies topology when it actually does not. Conversely, a proportional threshold highlights the structure of networks of strongest edges, independent of the magnitude of the coupling strength. However, if genuine function is a non‐linear function of coupling strength, proportional thresholding may incorrectly consider functionally inequivalent networks as indistinguishable. Another aspect that is worth considering when using thresholds is that the optimum fraction of actual edges needed to characterize the system may be condition‐specific and this may correspond to a significantly higher percentage of edges then the one typically retained in the analysis (Zanin et al., 2012). Finally, in the presence of nonlinearities, the importance of edges is not necessarily proportional to their strength. Moreover, weak edges have been shown to have a strong impact on network topology; their inclusion can induce transitions from fractal to small‐world universality classes (Gallos, Makse, & Sigman, 2012; Rozenfeld, Song, & Makse, 2010), and affect network dynamics and the processes taking place on it (Csermely, 2004; Karsai, Perra, & Vespignani, 2014).

3.4. Network dynamics

In practice, network reconstruction of brain function often turns out to be independent of the underlying dynamics, in particular of the system's characteristic time scales. This means that more often than not, functional brain networks are constructed as static networks: connectivity estimates are calculated over the whole measurement time series, so that the obtained network structure represents the average connectivity over the whole measurement. This approach may help to increase sensitivity of connectivity estimates and therefore produce less noisy networks (Smith et al., 2011; Van Dijk et al., 2010). However, since the brain needs to respond to varying stimuli in a continuously changing environment, it is natural to assume that also functional connectivity changes in time (Hutchison et al., 2013). Therefore, the static approach probably does not reveal the full picture of functional connectivity. An important step towards deeper understanding on the dynamics of functional networks is the concept of chronnectome (Calhoun, Miller, Pearlson, & Adalı, 2014; Iraji, DeRamus, et al., 2019). While the connectome (Sporns, Tononi, & Kötter, 2005) represents static connectivity between brain areas, the chronnectome involves also a temporal dimension, describing the brain function as a set of reoccurring, temporal connectivity patterns (Calhoun et al., 2014).

Dynamics of functional brain networks can be addressed from multiple different viewpoints. In what follows, we adopt the threefold division of Iraji, Miller, Adali, and Calhoun (2020): changes in network edges, changes in boundaries of ROIs used as network nodes, and changes in both edges and nodes, that is, time‐varying networks with time‐dependent nodes. ⁹

3.4.1. Edge dynamics

Changes in edge weight and related network structure have been widely reported in functional brain networks extracted from both fMRI and MEG/EEG data. These changes take place both at longer time scales, that is, across the human lifespan (fMRI: Meunier, Achard, Morcom, & Bullmore, 2009; Hwang, Hallquist, & Luna, 2013; Cao et al., 2014; Geerligs, Renken, Saliasi, Maurits, & Lorist, 2015; Gu et al., 2015; Marek, Hwang, Foran, Hallquist, & Luna, 2015; MEG/EEG: Micheloyannis et al., 2009; Smit et al., 2012; Boersma et al., 2013; Vecchio, Miraglia, Bramanti, & Rossini, 2014; Hou et al., 2018; Moezzi et al., 2019) or between health and disease (fMRI: Calhoun, Eichele, & Pearlson, 2009; MEG/EEG: Stam et al., 2009; Buldú et al., 2011; de Haan et al., 2012), and at shorter scales, between different cognitive tasks (fMRI: Sakoğlu et al., 2010; Richiardi, Eryilmaz, Schwartz, Vuilleumier, & van de Ville, 2011; Shirer et al., 2012; Leonardi, Shirer, Greicius, & van de Ville, 2014; MEG/EEG: Bassett, Meyer‐Lindenberg, Achard, Duke, & Bullmore, 2006; Palva, Monto, Kulashekhar, & Palva, 2010; Hipp, Engel, & Siegel, 2011; O'Neill et al., 2015, 2017) and also spontaneously over time in rest (fMRI: Honey, Kötter, Breakspear, & Sporns, 2007; Shehzad et al., 2009; Allen et al., 2014; Liao et al., 2015; MEG/EEG: Chu et al., 2012; de Pasquale et al., 2012; de Pasquale, Della Penna, Sporns, Romani, & Corbetta, 2016). Even spontaneous changes in functional connectivity are not random: functional brain networks fluctuate between states of different metastable connectivity profiles (Calhoun et al., 2014; Ma, Calhoun, Phlypo, & Adalı, 2014; Núñez et al., 2021) and increased and decreased global efficiency (Cocchi et al., 2017; Zalesky, Fornito, Cocchi, Gollo, & Breakspear, 2014). In particular, the community structure of functional brain networks tends to reorganize over time and between different tasks (Bassett et al., 2011; Jones et al., 2012). The time‐dependent connectivity of single ROIs is assumed to reflect their function: flexible or transient nodes with frequently changing connectivity play different roles during different tasks, while more stable nodes form the long‐term backbone of functional connectivity (Allen et al., 2014; Ryyppö et al., 2018; Salehi, Karbasi, Barron, Scheinost, & Constable, 2020; Zalesky et al., 2014).

Methods used to estimate functional connectivity (cf. Section 3.3) measure similarity of node signals over time. Therefore, they do not allow estimation of temporally point‐like edges that would be characteristic to temporal networks (Holme & Saramäki, 2012). Instead, most studies on the short‐scale dynamics of functional brain networks use time windows. In this approach, the neuroimaging time series are divided into a set of consequent or overlapping time windows and a network is constructed inside each window (Hutchison et al., 2013; Yu et al., 2018). The windows should be short enough to catch the changes in functional connectivity, while too short a window length easily results in noisy connectivity estimates (Hutchison et al., 2013; O'Neill et al., 2018; Sakoğlu et al., 2010). The optimal window overlap depends on the research question at hand, and varies from zero in the case of consequent time windows (e.g., Bassett et al., 2011) to the maximal overlap between one‐sample size sliding windows used to obtain time‐resolved connectivity (Cocchi et al., 2017; Zalesky et al., 2014). Typically, networks constructed in different time windows share a common set of nodes, which allows investigating evolution of both single edges and more global network properties over time. Separated time windows can be combined into a single network with multilayer approaches using time windows as layers (Bassett et al., 2011) or with hypergraph approaches where the nodes of the hypergraph represent the edges of networks calculated in time windows (Bassett, Wymbs, Porter, Mucha, & Grafton, 2014; Davison et al., 2015; Gu et al., 2017).

Despite the popularity of the time window approach, the interpretation of its outcomes is not fully straightforward. In particular, statistical significance of the observed changes in functional connectivity needs to be evaluated carefully, and probability to detect significant connectivity fluctuations can be surprisingly low (Hindriks et al., 2016; O'Neill et al., 2018). This limitation can be partially overcome by HMMs that use Bayesian inference to divide the data into states with characteristic activity and connectivity patterns and previously unknown lifetimes (Baker et al., 2014; Vidaurre et al., 2016; Vidaurre et al., 2018; Vidaurre, Smith, & Woolrich, 2017; Woolrich et al., 2013) (cf. Section 3.5) or by time‐frequency analysis where wavelet transfer coherence is used to quantify the similarity of two signals as a function of time and frequency (Chang & Glover, 2010). However, although these approaches detect areas showing similar dynamics at a certain time point, they do not construct networks and do not therefore allow further network‐oriented analysis.

3.4.2. Changes in ROI boundaries

So far, most studies of functional brain network dynamics have concentrated on connectivity between static ROIs. However, both internal connectivity structure and functional homogeneity of ROIs change over time (Ryyppö et al., 2018). Therefore, if the aim is to minimize information losses in node renormalization, ROIs should change in a time‐varying fashion. For example, Salehi et al. (2020) used exemplar‐based clustering (Salehi, Karbasi, Shen, Scheinost, & Constable, 2018) to define time‐dependent functional ROIs from fMRI data. Boundaries of these ROIs varied between cognitive tasks, and the ROI configuration allowed predicting which task the subject was facing and how well they performed in it.

The spatial chronnectome approach (Iraji, DeRamus, et al., 2019) divides the brain into sources or temporally synchronized neural assemblies. These sources can be, for example, ROIs or larger functional systems (sometimes referred to as brain networks); nodes of functional brain networks represent the sources (Iraji et al., 2020). Sources do not need to be static objects; instead, they can manifest themselves as a set of spatial states of voxels strongly synchronized with the source time series (Iraji, DeRamus, et al., 2019). Since the spatial location of sources may change in time, their connectivity cannot be modelled by static nodes (Calhoun et al., 2014).

As an example of the changing spatial states of sources, Iraji, DeRamus, et al. (2019) reported four different states present in fMRI data, each consisting of a partly different set of voxels, for the well‐known default mode network (Fox et al., 2005). In another fMRI study, Iraji, Fu, et al. (2019) detected the spatial states for nine brain systems and further clustered them into functional modules of those spatial states of different systems that co‐occurred more often than others. Similar time‐varying spatial states of the so‐called resting‐state networks have been reported also in MEG data (de Pasquale et al., 2010; O'Neill et al., 2015), although, to the best of our knowledge, these states have not been considered as candidates for network nodes.

3.4.3. Time‐varying networks with time‐dependent nodes

Very few studies have so far applied network tools to investigate functional brain networks with time‐dependent nodes. The approach introduced by Nurmi, Korhonen, and Kivelä (2019) is based on multilayer networks. Layers of this network represent time windows and nodes are defined independently on each layer by clustering fMRI voxels into ROIs with maximal functional homogeneity. Edges inside layers quantify functional connectivity in terms of Pearson correlation or some other similarity measure (cf. Section 3.3), while inter‐layer edges represent spatial overlap of ROIs. After constructing the network, the approach allows more sophisticated analysis in terms of, for example, multilayer motifs (Battiston, Nicosia, Chavez, & Latora, 2017) or multilayer clustering analysis (Mucha, Richardson, Macon, Porter, & Onnela, 2010).

Using time‐dependent nodes requires particular methodological rigor: renormalizing ROI boundaries over time may lead to fluctuating number of nodes, and care should be taken when comparing the associated topologies. However, given the growing evidence for the dynamic nature of brain networks, the benefits of brain network analysis with time‐dependent nodes are obvious (Iraji et al., 2020; Nurmi et al., 2019; Ryyppö et al., 2018). Indeed, the study of spatiotemporal dynamics of brain networks is one of the most important future directions for network neuroscience, and the appearance of new network approaches with time‐dependent nodes is merely a question of time.

3.5. Missing data, sub‐sampling and errors

The general assumption in experimental science is that available data accurately sample the underlying dynamical system. However, while the last decades have gifted neuroscience with considerably expanded access to finer spatio‐temporal scales of brain anatomy and dynamics, empirical neuroimaging data should always be treated as incomplete observations of a system with vastly heterogeneous pieces of hardware, with various aspects of the reconstruction process potentially inducing missing edges or nodes and, more generally, biased sampling of the relevant space.

On the one hand, instrumental techniques such as EEG or MEG do not necessarily ensure a correct sampling of the underlying dynamical system. Confounding variables may arise at various preprocessing stages, both in EEG/MEG and fMRI analysis (Pereda et al., 2005). Furthermore, the aspect of neural activity captured by other techniques may afford an insufficient representation of relevant variables responsible for the dynamics. For instance, poor definition of connectivity dynamics may cause fMRI‐based networks to miss information that may be crucial to the discrimination between conditions, for example, pathology‐specific brain dynamics, in spite of its good spatial definition (Zanin, Ivanoska, et al., 2021). On the other hand, discretionary choices throughout the reconstruction process may create or annihilate edges even for a given resolution level (cf. Section 3.3.2). At a more conceptual level, the effective scales at which the reconstruction is carried out have important consequences on the resulting network structure. This is not just because topological network properties of an inherently multiscale system such as the brain are scale‐dependent (Gallos et al., 2012), but is also to do with the effective sparseness of neural networks. On the one hand, even at the scales typical of standard system‐level neuroimaging techniques, neural circuitry is probably far more connected than often acknowledged (Wang & Kennedy, 2016). On the other hand, discretizing connections between a limited number of nodes entails that these are average connectivities, and the active units they approximate actually travel indirectly through a multitude of polysynaptic paths unaccounted for by the connection matrices between macroscopic ROIs (cf. “A priori atlases or data‐driven parcellations?” section above) or of typical EEG‐based analyses (Gramfort et al., 2013), whether sensor‐ or source‐based (cf. Section 3.5.1) (Galán, 2008; Robinson, 2013b; Robinson et al., 2016). All these factors concur in inducing a recording technique‐ and variable‐specific (Angulo, Moreno, Lippner, Barabási, & Liu, 2017) observability of brain dynamics, and as a consequence, of the underlying functional space, the extent of which is still incompletely understood.

Partial information on the structure could in principle be dealt with by resorting to maximum entropy models (Squartini, Caldarelli, Cimini, Gabrielli, & Garlaschelli, 2018) (cf. Section 2.2.2). These models yield ensembles of graphs whose topology is maximally random, given a chosen set of structural properties used as constraints, naturally providing a null distribution for quantities that are not directly constrained (Jaynes, 1957), which can be used to approximate an unknown under‐sampled probability distributions.

Thinking of observed data as the output of a process obeying detailed balance and with pairwise couplings, the model parameters can be inferred using equilibrium statistics, and likelihood maximization. In general, though, the generating process is unknown, and what is sought is a statistical description of the data in terms of a simpler model matching some property of the observed data, from the mean activity of individual populations and the correlations between them (Meshulam et al., 2017; Roudi, Tyrcha, & Hertz, 2009; Schneidman et al., 2006; Tang et al., 2008; Tkačik, Schneidman, Berry II, & Bialek, 2009; Tkačik et al., 2013), to specific combinations of activity and silence (Ganmor, Segev, & Schneidman, 2011) or higher‐order correlations (see Yeh et al., 2010, Savin & Tkačik, 2017, and Nguyen et al., 2017 for critical reviews of maximum entropy methods in neuroscience). Time‐dependent variants could provide tractable null models for the time‐varying dynamics of neural activity as an alternative to latent linear dynamical systems models. These methods prove unwieldy for very high‐dimensional spaces (Roudi et al., 2015), but can in principle be used at sufficiently coarse‐grained scales.

The partial information issue can also be dealt with through functional and effective network inference methods. These methods, which are designed to infer minimal models of the parent sets for each target node in the network (Runge, 2018; Sun, Taylor, & Bollt, 2015) or at least to identify features of its structure and dynamics, and to reflect the properties of groups of nodes in the structure (Novelli & Lizier, 2020), can be used to minimize spurious edges (Novelli et al., 2019). Model‐based edge‐prediction methods (Clauset, Moore, & Newman, 2008; Guimerà & Sales‐Pardo, 2009) yield relative probabilities for the probability of edge existence, given a generative model fitted to the observed data, which can then be used to reconstruct the network given the number of missing or spurious edges. However, information on missing edges is in general not available in neuroimaging studies. Recently, a Bayesian network‐reconstruction method has been proposed which allows optimal estimates of network structure from complex data in arbitrary formats (Newman, 2018). However, this method assumes uniform error rates and the existence of each edge is estimated via repeated measurements. Peixoto (2018) developed a similar approach, applying nonparametric Bayesian inference to a model coupling generative models of network structure, incorporating given topological properties, and models of the noisy measurement process. This method yields a reconstructed network together with its associated uncertainty estimate, based on the posterior distribution over all possible reconstructions and allows handling single edge measurements without direct error estimates.

3.5.1. Subsampling in electrophysiological studies

Electrophysiological techniques generally suffer from severe space under‐sampling. This problem is particularly acute when identifying nodes with recording sensors. Identifying nodes with sensors drastically under‐sample electrical activity at scales not observable by system‐level electrophysiological techniques leading to a coarse graining of the dynamics. This introduces a spatial scale irrespective of the actual system organization, resulting in spatial correlations in the topology of reconstructed networks, and ultimately affects topological network properties (Lee, Kim, & Jeong, 2006; Stumpf, Wiuf, & May, 2005).

Limitations in the amount of data and in the reliability of edge estimation (due to the presence of noise, of common sources or the inability of most estimators to distinguish between direct and indirect interactions) likely lead to the spurious addition, deletion or changes in the nature of edges. Spurious edges between nodes of similar degree may for instance decrease the average shortest path length and increase the clustering coefficient (Lee et al., 2006), leading to erroneously classify them as assortative, even when their true structure is disassortative (Bialonski, 2012). On the other hand, randomly sub‐sampled scale‐free networks generally turn out not to be scale‐free (Stumpf et al., 2005). Finally, in multiple electrode recordings, each sensor picks up many sources at small scales, but their number constrains the sampling on large ones, and this can lead to distortions in global topological properties of the reconstructed network (Gerhard, Pipa, Lima, Neuenschwander, & Gerstner, 2011).

3.5.2. Noise and noise reduction

Functional neuroimaging measurements, like every physiological recording, are a mixture of real signal and noise. For example, subject motion (Power et al., 2014; Power, Barness, Snyder, Schlaggar, & Petersen, 2012; van Dijk, Sabuncu, & Buckner, 2012), physiological noise from breathing and heartbeat (Birn, Smith, Jones, & Bandettini, 2008; Chang, Cunningham, & Glover, 2009; Chen et al., 2020; Dagli, Ingeholm, & Haxby, 1999; Shmueli et al., 2007), fMRI scanner drift (Hutchison et al., 2013), and noise from electric devices in MEG and EEG (Hämäläinen et al., 1993; Michel & Brunet, 2019) increase the noise level of measurement signals, leading to undesired increase in functional connectivity variance both inside and between subjects (Pervaiz et al., 2020). There are several ways to reduce the noisy component of the neuroimaging time series, including finite impulse response filters (Vorobyov & Cichocki, 2002), Kalman filters (Bartoli & Cerutti, 1983), spectral interpolation (Leske & Dalal, 2019), and wavelet transformation (Olkkonen, Pesola, Olkkonen, Valjakka, & Tuomisto, 2002; Yu, 2009). Unfortunately, many preprocessing steps applied to increase the SNR, for instance global signal regression (Fox, Zhang, Snyder, & Raichle, 2009; Gotts et al., 2013) or spatial smoothing (Alakörkkö, Saarimäki, Glerean, Saramäki, & Korhonen, 2017; Fornito, Zalesky, & Breakspear, 2013; Stanley et al., 2013; Triana, Glerean, Saramäki, & Korhonen, 2020; Wu et al., 2011), may have unexpected and undesired effects on the observed network structure.

The importance of well‐reasoned measurement and preprocessing pipelines has been widely covered in the literature (e.g., Andellini, Cannatà, Gazzellini, Bernardi, & Napolitano, 2015; Aurich, Alves Filho, Marques da Silva, & Franco, 2015; Michel & Brunet, 2019; Shirer, Jiang, Price, Ng, & Greicius, 2015). Therefore, in what follows, we will concentrate on methods proposed for handling the noise remaining in the network structure after network construction. These methods are particularly important when working on large, public datasets that, while opening insights on brain function at population level (Van Essen et al., 2013; Vidaurre et al., 2018), deny the end user the control on data collection and sometimes even on data preprocessing.

Noise in network structure is particularly problematic in studies including comparison of networks, for example, between different tasks or subject groups. Low SNR, together with the rigorous significance threshold required by the high number of comparisons, makes it hard to detect the often subtle differences between groups (Zalesky, Fornito, & Bullmore, 2010). The statistical power may be increased already at the network construction stage by reducing the number of nodes, using larger ROIs instead of measurement voxels or source points. However, an inaccurate definition of ROIs can easily lead to spurious network structure (cf. section 3.2.1).

Coarse‐graining approaches avoid this problem by reducing network dimensionality after connectivity estimation. For example, network‐based statistic (Zalesky, Fornito, & Bullmore, 2010) improves statistical power by searching for network components, that is, clusters of edges, that differ significantly between subject groups instead of testing for single edges. In the approach of Kujala et al. (2016), the nodes of the coarse‐grained network are modules of voxel‐level network, while edge weights between the modules represent the number of significant voxel‐level edges. The small number of nodes in the coarse‐grained network allows intuitive comparisons between rest and task states or healthy and diseased populations (Kujala et al., 2016). In the analysis of network dynamics, applying PCA on the connectivity patterns before clustering them into connectivity states may help to reduce the dimensionality and therefore to control the noise (Kafashan, Palanca, & Ching, 2018; Laumann et al., 2010).

In addition to the issues raised by high dimensionality, networks constructed from MEG and EEG data suffer from noise characteristic for these imaging modalities: artificial and spurious connectivity due to signal mixing (Palva & Palva, 2012; Schoffelen & Gross, 2009). In electrophysiological measurements, each measurement sensor collects signals from several neighbouring brain sources. Therefore, artificial connectivity is observed between each pair of neighbouring sources. Furthermore, when the signals of two sources are connected by a true functional edge, the neighbours of these two sources appear to be connected to each other by spurious edges. Signal mixing is most prominent in sensor‐space analysis, while source reconstruction separates the signals of different sources to some extent (Kujala et al., 2006; Palva & Palva, 2012; Schoffelen & Gross, 2009), particularly if the source reconstruction approach is optimized for detecting independent signal components. Examples of such approaches include the combination of ICA and sLORETA algorithm used by Chen et al. (2013), the minimum overlap component analysis approach by Marzetti, del Gratta, and Nolte (2008), and the multivariate autoregressive (MVAR)‐EfICA approach (Gómez‐Herrero, Atienza, Egiazarian, & Cantero, 2008) that combines PCA and ICA to remove zero‐time lag similarities, MVAR modelling to quantify time‐delayed similarities, and swLORETA to localize the cortical sources.

Clever definition of network edges can significantly reduce artificial connectivity (cf. Section 3.3), albeit at the cost of losing also true connections with zero phase lag. The hyperedge bundling approach (Wang et al., 2018) handles spurious connectivity by turning the network into a hypergraph (Battiston et al., 2020) with hyperedges connecting groups of nodes. The hyperedges are defined so that each of them should contain a true functional connection and all of its spurious reflections (Wang et al., 2018). Although edge bundling slightly reduces the spatial resolution of connection mapping, the approach detects true connections with high accuracy and notably reduces the number of false positive connections (Wang et al., 2018).

When using machine‐learning based classifier algorithms for detecting connectivity differences between tasks or subject groups, noise together with small sample sizes may increase variance in classifier weights and therefore reduce classification accuracy (Ng et al., 2015). Moreover, the connectivity estimates used as classification features are often interrelated, which violates the assumptions of most classification algorithms (Ng et al., 2015). These issues can be partly alleviated with tools from Riemannian geometry (Ng et al., 2015; Pervaiz et al., 2020) (cf. Section 3.1). Effects of noise can be further reduced by applying conventional matrix regularization techniques in the ambient space where the data have been collected (Pervaiz et al., 2020) or covariance shrinkage estimators (Chen, Wiesel, Eldar, & Hero, 2010; Ledoit & Wolf, 2004; Rahim, Thirion, & Varoquaux, 2019) either in the ambient space or in the tangential space of the Riemannian manifold.

3.6. Assessing and improving network reconstruction

In the absence of a set of principled criteria for the choice of network reconstruction parameters, a fundamental question in network neuroscience is understanding the extent to which the topological properties of the reconstructed networks are intrinsic of the system under description or, at least, are robust with respect to the way networks are reconstructed from experimental recordings (Papo, Zanin, & Buldú, 2014; Stanley et al., 2013; Zalesky, Fornito, Hardling, et al., 2010; Zanin et al., 2012). Reconstruction methods in general and renormalization procedures in particular have been shown to potentially qualitatively affect topological properties (Gallos et al., 2012; Stumpf et al., 2005). Specifically, a study on node renormalization found that global topological properties such as small‐worldness may be robust to the parcellation technique and overall number of nodes, although the quantitative aspect of these properties may be grossly affected (Zalesky, Fornito, Hardling, et al., 2010).

3.6.1. Looking backward, looking forward: From statistics to data mining

When the functional brain networks of two or more groups, for example, of patients suffering from given pathologies, are extracted and characterized, it is only natural to hope to see a difference between them, or, in other words, that the pathology under study translates itself into a different network structure. The next logical step is thus to assess the significance of such difference, and specifically of the difference between some topological metrics calculated on the networks.

Traditionally this has been performed by resorting to statistics. Given the two probability distributions yielded by the considered metric for the two sets of subjects, the equality of their average can be assessed through a Welch's t test; alternatively, the hypothesis that both distributions are equivalent (i.e., not just the average) can be tested through a Kolmogorov–Smirnov test. In both cases, the result will be a p‐value, which has to be compared against a desired significance level, and eventually corrected for multiple comparisons. Leaving aside the important discussion about the fallacies associated with only relying on the p‐value in science (Dixon, 2003; Goodman, 1999; Goodman, 2008), it is important to highlight that such tests only provide an assessment of the equality of the two distributions (or of their mean values), but yield little information about the usefulness of the result.

To clarify this point, suppose that the result consists in two probability distributions, of the same shape and only slightly shifted (i.e., almost perfectly overlapping). Provided enough samples (i.e., subjects and networks) are available, the resulting test will detect a statistical significant difference, independently on the magnitude of the shift. Nevertheless, it would be virtually impossible to create a diagnostic test from this result: the minimal difference between both distributions implies that any applied criteria would have an almost random output (Lin, Lucas Jr, & Shmueli, 2013).

The previous example illustrates an important point: statistical significance of results does not equate to usefulness. How can then this latter aspect be assessed? The solution can be found in data mining (Han, Pei, & Kamber, 2011; Vapnik, 2013), and specifically in the score yielded by a classification algorithm trained to discriminate between the two subject classes using the metrics extracted from the complex functional networks. High classification scores (thus, low errors) imply that the differences between the two groups are not just significant, but also useful for the creation of discrimination rules. In a more abstract way, the difference between statistics and data mining can be interpreted as a temporal one: the former looks backward, at what the differences were in the past data, while the latter looks forward, that is, at what these data tell us about future patients.

The interplay between p‐value and classification score is a complex one, being a function not just on the difference between the two groups, but also on the number of available instances—see figure 6 in Zanin et al. (2016). As already seen, a large number of instances may yield significant p‐values even in the absence of a useful difference; on the other hand, having only few instances may cause unreliable classification results (due to an overfitted learning), which needs to be confirmed through a p‐value examination. As such, it is convenient to take both into account when evaluating the relevance of a functional network analysis.

3.6.2. Effects on brain network characteristics

One fundamental issue is to appraise the extent to which the properties of the reconstructed system are invariant with respect to the discretionary steps in the network reconstruction process.

In more general terms, this issue is to be framed within the concept of generalizability, that is, how universal are the results obtained with a specific analysis. Generalizability has traditionally been tackled from two different points of view. On the one hand, one can perform test–retest analyses, that is, record the same subjects two or more times and compare the resulting networks, for then checking if the resulting networks kept the same properties over time. Several studies have addressed this issue (Deuker et al., 2009; Hardmeier et al., 2014; Höller et al., 2017), and observed that generalizability depends on factors such as frequency band or length of time series. On the other hand, one may check how the resulting topological metrics depend on methodological decisions such as the used software package (Mahjoory et al., 2017), the chosen frequency band (Pashkov & Dakhtin, 2019), scalp versus source data (Antiqueira, Rodrigues, van Wijk, da Costa, & Daffertshofer, 2010; Lai, Demuru, Hillebrand, & Fraschini, 2018; Palva, Monto, & Palva, 2010), anatomical versus dynamical networks (Ponten, Daffertshofer, Hillebrand, & Stam, 2010), or in general the combination of different steps (Pervaiz et al., 2020). Possibly, the most complete example of such analysis has been proposed in (Botvinik‐Nezer et al., 2020), where 70 independent teams were asked to process the same data with the aim of testing a same set of hypotheses.

While it has theoretically been shown that some connectivity patterns are more stable, and hence appear more frequently in any analysis (Malagarriga et al., 2017), the previous studies also highlight that the topological metrics of the reconstructed networks strongly depend on the methodological choices made by the researcher. This is clearly a problem, as it undermines the generalizability of results; but also represents an advantage. Specifically, this variability of results suggests that different choices help focusing on different aspects of brain dynamics, and hence some may be more suitable for different tasks, for example, for the identification of a specific pathology. This condition‐specific character has been exploited in various studies (Bosch, Herrera, López, & Maldonado, 2018; Yu, Lei, Song, Liu, & Wang, 2019; Zanin et al., 2012), in which the idea is to use the score of a classification task to guide the generation of the network (see Figure 4). In spite of promising results, it is not clear how this strategy affects generalizability, that is, if the best reconstruction process is universal for a given condition, or whether this depends on the characteristics of the studied data.

FIGURE 4.

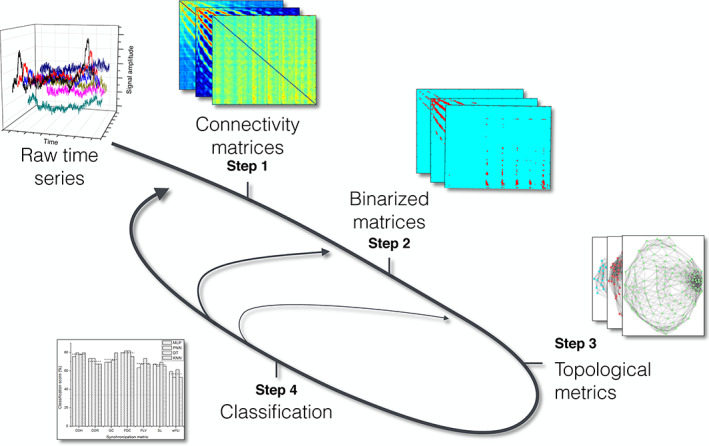
A general recipe for post hoc iterative network reconstruction parameter update. Instead of fixing parameters (e.g., edge density, which topological metric to extract) a priori, the proposed methodology involves reconstructing networks using a large set of different parameters; the corresponding discrimination power is then evaluated using a classification problem, and the combination yielding the clearest difference between two groups of patients is chosen as the most informative one. See Zanin et al. (2012) for details

4. CONCLUDING REMARKS

Defining what is functional in brain activity is an arduous task. Functional network reconstruction should ultimately lead to the characterization of functional brain activity and could therefore assist in addressing this question. However, as we illustrated, the image of function that it provides is at least partially dependent on prior assumptions on function. Thus, the answers to fundamental questions such as “How much of brain phenomenology does a network representation help in revealing?,” “How do network properties emerge?,” “Do they have a functional meaning?,” “What network‐related aspect of brain activity can we expect to be able to reconstruct from standard neuroimaging technique recordings?” depend to some extent on the way these networks are reconstructed and, more specifically, on the (often covert) assumptions underlying the reconstruction process. The extent to which methodology matters is poorly understood, and various questions are still unanswered. For instance, are all network properties equally sensitive to methodological choices? The existing literature suggests that some properties may be more robust than others. For example, very similar scale‐free and small‐world features of brain networks are observed using different node definition strategies (Arslan et al., 2018), even with randomly selected nodes that most probably do not match the true functional organization of the brain (Fornito et al., 2010). However, although the selected brain parcellation may matter relatively little in simple network analysis in healthy subjects, the role of node definition is probably more crucial when aiming to detect the subtle changes in network structure due to, for example, diseases or aging (Arslan et al., 2018).

To evaluate the extent to which a network representation genuinely documents the way the brain carries out the functions it is supposed to fulfil is ultimately tantamount to determining whether the topological properties are intrinsic or extrinsic, leading to a better understanding of emergence of functional dynamics (Atmanspacher, 2012). To do so, implies steps at various levels.

At a network representation level, this involves constructing a structure which is able to document, and ideally, to generate, these properties. On the one hand, although several aspects of edge (and node) definition are largely independent of the space in which the network is constructed, and much of what has been said here equally applies to structures such as multi‐layer graphs, hypergraphs, or simplices (Battiston et al., 2020), constructs alternative to the standard network structure may modify microscopic network scale properties and introduce new ones. For instance, in a simplex, not only nodes but also edges have non‐trivial degree. Thus, these structures may affect topology, geometry and underlying physics of the reconstructed network. On the other hand, revisiting the basics of functional network reconstruction and its main goal leads to reconsidering the very identity and role of the structure to be used in pursuit of that goal. Can a structure of time dependent, possibly spatially overlapping nodes still be called a network and analysed as such? In the same vein, network neuroscience will likely undergo a trajectory wherein nodes and connections will be thought of in a different way, possibly integrating different known properties of neural activity such as inhibition or complex feedback loops. Their specification will as a consequence change from its current one. While network features have historically been predicated upon dynamical system and information theory, to render representations more context‐independent, network neuroscience will possibly increasingly summon constructs from disciplines such as computational topology (Carlsson, 2009; Edelsbrunner & Harer, 2010; Petri et al., 2014; Reimann et al., 2017; Stolz, 2014; Zomorodian, 2005) or statistical physics (Bianconi & Rahmede, 2016), and explanations at various levels (Marr, 1982) and of different types (Illari & Williamson, 2012; Tozzi & Papo, 2020). New constructs may include neurophysiological properties, such as inherent disorder and lack of translational invariance, and may result in representations with non‐trivial emergent geometry (Bianconi & Rahmede, 2017) accounting for phenomenology as yet poorly documented, at least in network terms, for example, topological phase transitions (Santos et al., 2019) or frustration (Gollo & Breakspear, 2014). Ultimately, this may help changing representations of brain function not just by producing constructs more robust to the specification of the space in which they are embedded as well as inter‐subject variability and noise, but also by changing the underlying vision of brain function in the first place.

At the assessment level, this will involve checking the statistical but, more importantly, also the functional significance (Demirel, 2014; Ma et al., 2009) of the network properties emerging from brain imaging data analysis. Overall, the series of relevant questions should then be: is the mapping from data to networks reliable? Is it statistically significant? Is it functionally significant? Ultimately, though, genuine breakthroughs will also require parallel conceptual advances in the way bona fide brain function is understood at various levels, which would allow incorporating “stylized facts” within the network construction process. Such descriptions may help determining when the functional space can be endowed with a network representation, how reproducible it is, and when this representation ceases to be appropriate, at least as a modelling tool (Papo, 2019).

Finally, an aspect that silently underpins most functional network reconstruction efforts, but that is seldom made explicit is that a complex network representation is a very simplified representation of brain activity, usually focused on some specific aspects, for example, how information is propagated in different brain regions; and seeking answers to specific questions, for example, how a pathology modifies this propagation. A representation may be useful without being a model of brain functioning, and its worth context‐specific rather than general. As in simplified underground maps, where the way stations and lines and their spatial location are tailored towards a specific aim without representing the system as a whole with all its characteristics, network neuroscientists should choose those elements that yield the representation that best serves their specific goals.

CONFLICT OF INTEREST

The authors declare no conflict of interest.

Korhonen, O. , Zanin, M. , & Papo, D. (2021). Principles and open questions in functional brain network reconstruction. Human Brain Mapping, 42(11), 3680–3711. 10.1002/hbm.25462

DATA AVAILABILITY STATEMENT

This is a Review article—to which no data are associated.