Determining the location of isolation hospitals for COVID‐19 via Delphi‐based MCDM method

Abstract

The existing contagious epidemic disease, [SARS]‐CoV‐2, has been one of the biggest public health problems that humankind combatting against since December 2019. Answering the increase in the number of infected patients during the pandemic is one of the biggest challenges for healthcare systems, where resources have already been employed by a significant number of patients. While assigning most of the resources to infected people is an effective way in a short‐term planning, its bitter effects on regular healthcare cannot be undervalued. Moreover, within this plan the risk of spreading the disease to other patients and healthcare providers is another risk that should not be underestimated. Therefore, in this study, we proposed the Delphi‐based multicriteria decision‐making (MCDM) framework for selecting the most appropriate location for an isolation hospital serving only epidemic‐based patients with mild to moderate symptoms. The integrated framework consists of Delphi, Best–Worst Method, and interval type‐2 fuzzy Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) methodologies. Nine most effecting criteria are considered in the evaluation of five alternative locations in a real case study conducted at the European side of Istanbul. Ataturk Airport is determined as the best location to set up an isolation hospital based on determined nine evaluation criteria. The effectiveness and robustness of the framework are analyzed through comparative and sensitivity analyses.

1. INTRODUCTION

Pandemics are generally categorized as one of the natural disasters, ¹ which directly threat the human beings' lives and their well‐being. In the last century, three deadly outbreaks were occurred, and the last one was H1N1 outbreak, which caused the death of approximately between 151,700 and 575,400 individuals all over the world in the first year of the disease. ² At the end of 2019 a new version of coronavirus raised and caused a pandemic, which is named as COVID‐19, all over the world. ³ Its main cause is the SARS‐CoV‐2 virus. ⁴ Comparing the number of deaths that these outbreaks caused, COVID‐19 has already exceeded the number recorded for H1N1 pandemic, and only in about 9 months almost one million people lost their lives. Thus, it can be concluded that the overspread rate of COVID‐19 is extremely fast, and almost all states are impacted by COVID‐19. The intensity of an epidemic usually changes based on the immune states of people, person‐to‐person contacts, transmission rate, transportation modes, weather conditions, ⁵ and most importantly health service availabilities within the region. Thus, efficient safety techniques as well as the reactive healthcare systems are very important to flat the fast growth of the COVID‐19 and handle the caseload on healthcare institutions.

Owing to the fast transmission rate of COVID‐19, authorities encountered a very high demand of caseload in hospitals with limited resource availability. Furthermore, treating both COVID‐19‐related patients and other patients, which are diagnosed with different illnesses in the same hospital, increases the risk of outbreak of the pandemic even more. Moreover, since the demand is uncertain, unless rapid and effective precautions are taken the deficiency in the capacity of hospitals is unavoidable. Thus, creating extra resources or managing the healthcare institutions became more essential to take the pandemic under control, and in return more lives will be saved. Although canceling or postponing the routine healthcare services is reflected as a useful decision, its severe influences should not be undervalued. Therefore, the postponement cannot be prolonged more because it may cause extreme demand on the capacity of hospitals when they retrieve their preoutbreak functionality back. Consequently, the hospitals should continue their routine operations while they answer the demand causes from the pandemic. Although this attitude is adopted by some decision makers (DMs), determining designated hospitals ⁶ , ⁷ and allocating COVID‐19‐related patients to these designated hospitals are more useful in terms of reducing the risk of contamination to other patient types and healthcare professionals. Besides allocating patients with heavy symptoms of COVID‐19 who need Intensive Care Units (ICUs) or ventilators to designated hospitals, setting up isolation hospitals (a.k.a. Fangcang) is another important precaution that was taken by some countries. Isolation hospitals function as shelter hospitals to isolate, aid, and monitor the patients who have minor or mild symptoms. Fang et al. ⁸ defined this strategy as one of the most effective ways to take the spread of a pandemic under control. Basically, these types of hospitals are constructed by converting wide public areas or buildings into temporary shelter hospitals. They also indicated that the USA, UK, and some other governments have already established these kinds of hospitals, like, the ones established in China, which are called Fangcang hospitals. Furthermore, healthcare DMs adopt or develop different alternatives to cope with pandemic. For instance, applying only home isolation is one of them or treating all infected patients at hospitals is another option, and so on so forth. However, none of them has been seen as an effective alternate except a combination of them as suggested by World Health Organization (WHO). ² WHO ² suggestions can be seen in Figure 1.

Figure 1.

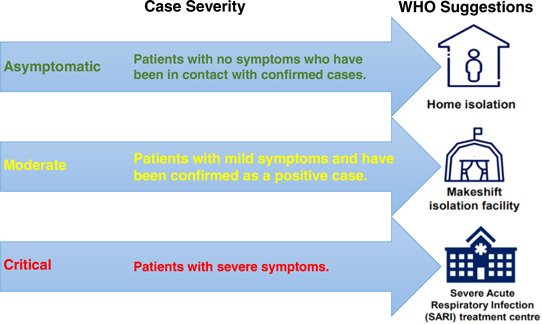
WHO recommendations based on case severity ⁹ [Color figure can be viewed at wileyonlinelibrary.com]

Considering the recommendations provided by WHO, DMs should optimize their hospital resources. However, it is clear that because of excessive demand load none of the governments is able to host and treat their patients in fully equipped hospitals. Thus, isolation hospitals need to be constructed and patients with mild or moderate symptoms should be taken under control until they heal in order not to contaminate other people or their families. The issue that arises here is the location selection of isolation hospitals, which is affected by several criteria, such as technical, social, environmental, medical conditions, and so forth. Since multiple alternate locations need to be assessed considering multiple conflicting criteria, an accurate decision‐making technique is needed to make the finest decision.

Here, the most effective option is to apply the multicriteria decision‐making (MCDM) approach to make a compromise decision among the possible conflicting criteria and determine the most appropriate location among multiple alternative locations. MCDM techniques are extensively applied to such problems and provided robust and qualified solutions. ¹⁰ , ¹¹ In addition, MCDM methods give the ability of considering DMs' ambiguities and vagueness thoughts in assessing isolation hospitals locations by embedding Interval Type‐2 Fuzzy numbers in the evaluation process.

Therefore, in this study, we proposed a decision‐making framework, which consists of three main steps, to determine the location of isolation hospital under a fuzzy environment. A real application is applied for the European side of Istanbul, which is one of the most crowded cities in the world and that struggles with the high number of infected people by COVID‐19. Determining the criteria that need to be considered to select the most appropriate location is one of the critical steps of the decision‐making process. Within this concept, a Delphi method is used because it is widely preferred to create a consensus among group members' opinions. ¹² On the basis of the survey conducted to group members several criteria were reduced to nine, which are the construction cost and time, land space, including green areas, accessibility in terms of distance and time, geographical barriers for vehicles' accesses, population density at candidate locations, distance to hospitals, expandability, social convenience, and availability of parking lots. Once the criteria were highlighted, their weights needed to be determined as the second step. The criteria weights were determined by applying the Best–Worst Method (BWM). ¹³ BWM functions by comparing the best and the worst criteria, which are predetermined by the group members, with other criteria. Then a maxi–min formulation is developed and optimized to obtain the importance of weights of all criteria. ¹³ Since it is easier and time saving than matrix‐based MCDM methods, such as Analytic Hierarchy Process (AHP), which requires more comparisons, BWM is chosen in determining the weights of the criteria. Several successful implications have been conducted in the literature as in References [14, 15, 16]. As the third step, five alternative locations, which were Ataturk Airport, Atatürk Olympic Stadium, Beylikduzu/Gurpinar Seafood Market Hall, Yenikapi rally area, and Fatih Sultan Mehmet student dormitory, were evaluated via Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), which is introduced by Hwang and Yoon, ¹⁷ using Interval Type‐2 Fuzzy Sets. Uncertainty in the DMs' opinions was handled by embedding Interval Type‐2 Fuzzy numbers to address the vague and incomplete information better in the real‐world applications. The primary advantage of the proposed approach for the location selection of isolation hospitals is that it has simplified calculations and provided reasonable and practical solutions due to good computational efficiency comparing to other methods.

The rest of the study is designed as follows: a literature review of the applications that applied MCDM methodologies in the location selection field is exhibited in Section 2. The problem statement and stages of the integrated framework are provided in Section 3. In Section 4, a real case application is functioned to show the applicability of the suggested framework for the isolation hospital location selection at the European side of Istanbul. Results and discussions, and comparative and sensitivity analyses are also presented in Section 4. Lastly, we provided conclusions and future directions of the study in Section 5.

2. LITERATURE REVIEW

DMs often face with the location selection problems during their business processes under different conditions. Since location selection is a part of a decision‐making discipline, MCDM approaches are widely preferred in this science and several studies were published in this sense. Four main topics were reviewed in this section: recently published TOPSIS‐based location selection applications, general applications of the Delphi method, BWM, and the literature on isolation (Fangcang) hospitals and medical support.

Ashrafzadeh et al. ¹⁸ applied fuzzy TOPSIS to select the most suitable location for the warehouse locating problem under partial or incomplete information for a company that operates in Iran. It can be seen that any type of criteria may be considered in the TOPSIS method. Guo and Zhao ¹⁹ applied fuzzy TOPSIS to evaluate and rank the alternative locations to set up charging stations of electrical vehicles. Deveci et al. ²⁰ applied fuzzy TOPSIS along with Weighted Aggregated Sum Product Assessment (WASPAS) method to select most effective location for a car‐sharing station in Istanbul. Chang et al. ²¹ integrated the fuzzy Delphi, analytic network process (ANP) and TOPSIS methods to determine locations for Taiwanese service apartments. Via their real case study they showed the effectiveness of the proposed integrated approach. Considering the above‐mentioned literature, TOPSIS provides easiness in creating combined methods. Furthermore, the application areas of TOPSIS are vast, such as charging station selection for electrical vehicles, ¹⁹ warehouse, ¹⁸ car sharing, ²⁰ service apartments, ²¹ and so forth.

Delphi method is used to obtain the most effectual factors and a good set of candidate locations, because Delphi can lead to better criteria selection ²¹ by applying a consensus decision. Hsu and Yang ²² used a fuzzy Delphi method because of its straightforwardness in selecting an effective criterion set. Wu et al. ²³ applied the modified Delphi method and AHP for the selection of a hospital in Taiwan. Chang et al. ²⁴ applied the fuzzy Delphi approach along with binary goal programming and ANP to the Alishan forest railway for the selection of renewal strategies. Also, Chang et al. ²¹ integrated the fuzzy Delphi with ANP and TOPSIS approaches to select the locations for service apartments. On the basis of the literature, the Delphi method is one of the bests to determine criteria and alternatives for a topic.

Furthermore, BWM was first proposed by Rezaei ¹³ as a solution approach to MCDM problems. As in many other MCDM methods, this approach also considers several criteria to select the best alternative amongst multiple. The process of BWM starts with selecting the most and the least important criteria (the best and the worst, respectively). These criteria are selected by the DMs, in our case they are the experts. Even it is a new method it has already been applied to several MCDM problems owing to its simple and clear procedure. Rezaei ¹³ used BWM to obtain the importance weights of criteria to segment the suppliers of a medium‐sized high‐tech company. Some other applications of BWM method may be summarized as follows: selection of supplier(s), ²⁵ identification of the best configuration of key performance indicators for the surface transportation of air freight. ²⁶ Further, the fuzzy extension of the BWM is proposed by Guo and Zhao, ²⁷ and then Wang et al. ²⁸ applied the fuzzy extension of BWM with IVIF and MULTIMOORA to evaluate science and technology projects.

MCDM methods have been extensively used in emergency decision‐making problems and recently applied in taking decisions against COVID‐19 pandemics. ²⁹ , ³⁰ , ³¹ , ³² , ³³ Furthermore, locating regular and field hospitals has been extensively studied in the literature. However, the location selection of isolation hospitals has not been considered so far. The isolation hospitals are very important for governments to take the pandemics under control and latterly to terminate. Isolation hospitals serve as field or shelter hospitals to separate, aid, and monitor the pandemic‐related patients. Fang et al. ⁸ specified that the isolation hospitals are one of the most effective ways to control epidemic diseases' spread and lessen the deaths. They are usually constructed by converting wide public places/buildings into temporary hospitals. By following this strategy the capacity of hospitals can be increased easily because isolation hospitals do not need much effort to construct. Fang et al. ⁸ also stated that some other countries, such as the USA and UK, have already established such hospitals as the ones in China. The effects of isolation hospitals on the spread of pandemic is analyzed extensively lately in the literature. Fang et al. ⁸ determined some important criteria on the location selection of Fangcang hospitals, while Chen et al. ³⁴ highlighted the advantages of these types of hospitals as easy to be built, providing isolation of infected people from the public and increasing the healthcare system capability by providing extra capacity without much burden. As an effect of isolation hospitals, Dickens et al. ³⁵ showed that the institutional‐based isolation strategy decreases the contamination by approximately 57%, while home‐based isolation decreases around 20%. They suggested to select stadiums, hotels, or dormitories as alternative places. A supportive study is conducted by Pan et al., ³⁶ who proposed a differential equation‐based model to explain the spread of COVID‐19 and to evaluate the effects of isolation on the process. Their results also support the results provided by Dickens et al. ³⁵ Moreover, Cai et al. ³⁷ examined the impacts of isolation hospitals on the number of COVID‐19‐based deaths. They concluded that the isolation hospitals have a great support on reducing the number of mortalities as highlighted by Zeng et al. ³⁸ Lastly, the process of setting up isolation hospitals is studied by Shen et al. ³⁹ Albeit, many studies were conducted on the importance and impacts of setting up isolation hospitals, and the section selection criteria, none of them proposed an approach to determine the best location for isolation hospitals. The most related study is done by Hashemkhani Zolfani et al., ⁴⁰ which determines the most appropriate location for a temporary hospital. Therefore, we proposed a Delphi‐based BWM and interval type‐2 fuzzy TOPSIS as an integrated MCDM framework for the location selection of an isolation hospital. For the validation, a case study is accompanied at the European side of Istanbul.

3. RESEARCH METHODOLOGY

This section is devoted to explain the integrated MCDM framework and is divided into two subsections, which are interval type‐2 fuzzy sets, and integrated Delphi‐based BWM and interval type‐2 fuzzy TOPSIS.

3.1. Interval type‐2 fuzzy sets

As an extension of the theory of the fuzzy sets introduced by Zadeh, ⁴¹ type‐2 fuzzy sets are presented in 1975 by Zadeh. ⁴² Type‐2 fuzzy sets are introduced to handle more uncertainty with two membership values and it produces more precise and robust results. ⁴³ , ⁴⁴

Definition 1

((Mendel et al. ⁴⁵ )) $\stackrel{\approx }{A}$ is a type‐2 fuzzy set, which is identified in X universal set, and ${\mu }_{\widetilde{\stackrel{~}{A}}}$ is shown as type‐2 fuzzy membership function. $\widetilde{\stackrel{~}{A}}$ is stated as in the following formula:

$$\widetilde{\stackrel{~}{A}}=\left\{\right((x,u),{\mu }_{\widetilde{\stackrel{~}{A}}}(x,u))\mathrm{|}\forall x\in X,\forall u\in J_x\subseteq [0,1],0\le {\mu }_{\widetilde{\stackrel{~}{A}}}(x,u)\le 1\left)\right\},$$

where $J_x$ shows an interval between 0 and 1. Furthermore, $\widetilde{\stackrel{~}{A}}$ type‐2 fuzzy set is also stated in a different way as follows:

$$\widetilde{\stackrel{~}{A}}=\underset{x\in X}{\overset{.}{\int }}\underset{u\in J_x}{\overset{.}{\int }}{\mu }_{\widetilde{\stackrel{~}{A}}}(x,u)/(x,u),$$ (1)

where $J_x\subseteq [0,1]$, ∫∫ shows all satisfactory combinations of $x$ and $u$ values.

Definition 2

((Mendel et al. ⁴⁵ )) However, interval type‐2 fuzzy sets are appropriate for real‐world applications since the calculations are easier to apply.

Let $\widetilde{\stackrel{~}{A}}$ be a type‐2 fuzzy set in the universe of statement X and ${\mu }_{\widetilde{\stackrel{~}{A}}}$ denotes a type‐2 membership function. If all ${\mu }_{\widetilde{\stackrel{~}{A}}}(x,u)=1$, the set $\widetilde{\stackrel{~}{A}}$ is expressed as the interval type‐2 fuzzy set. An interval type‐2 fuzzy set is denoted as a distinct condition of $\widetilde{\stackrel{~}{A}}$ type‐2 fuzzy set and presented as follows:

$$\widetilde{\stackrel{~}{A}}=\underset{x\in X}{\overset{.}{\int }}\underset{u\in J_x}{\overset{.}{\int }}1/(x,u),$$ (2)

where $J_x\subseteq [0,1]$.

Definition 3

((Lee and Chen ⁴⁶ )) Let trapezoidal interval type‐2 fuzzy set be

$${\widetilde{\stackrel{~}{A}}}_i=\left({\tilde{A}}_i^{\mathrm{U}},{\tilde{A}}_i^{\mathrm{L}},)\right)=\left(a_{i1}^{\mathrm{U}},a_{i2}^{\mathrm{U}},a_{i3}^{\mathrm{U}},a_{i4}^{\mathrm{U}}\mathrm{;}{H}_1\left({\tilde{A}}_i^{\mathrm{U}},)\right),H_2\left({\tilde{A}}_i^{\mathrm{U}},)\right),)\right),\left(a_{i1}^{\mathrm{L}},a_{i2}^{\mathrm{L}},a_{i3}^{\mathrm{L}},a_{i4}^{\mathrm{L}}\mathrm{;}{H}_1\left({\tilde{A}}_i^{\mathrm{L}},)\right),H_2\left({\tilde{A}}_i^{\mathrm{L}},)\right),)\right),$$ (3)

where ${\tilde{A}}_i^{\mathrm{U}}$ and ${\tilde{A}}_i^{\mathrm{L}}$ are type‐1 fuzzy sets, $a_{i1}^{\mathrm{U}},a_{i2}^{\mathrm{U}},a_{i3}^{\mathrm{U}},a_{i4}^{\mathrm{U}}\mathrm{;}{a}_{i1}^{\mathrm{L}},a_{i2}^{\mathrm{L}},a_{i3}^{\mathrm{L}}$, $a_{i4}^{\mathrm{L}}$ are the points of reference of trapezoidal interval type‐2 fuzzy set, $H_j\left({\tilde{A}}_i^{\mathrm{U}},)\right)$, as $1\le j\le 2$ $a_{i(j+1)}^U$ shows the membership level of ${\widetilde{\stackrel{~}{A}}}_i$, upper trapezoidal membership function, $H_j\left({\tilde{A}}_i^{\mathrm{L}},)\right),$ as $1\le j\le 2 a_{i(j+1)}^{\mathrm{L}}$ shows the membership level of ${\widetilde{\stackrel{~}{A}}}_i$, lower trapezoidal membership function and $1\le j\le 2$, $H_j\left({\tilde{A}}_i^{\mathrm{L}},)\right)$.

$${\tilde{A}}_i^{\mathrm{L}},1\le j\le 2,H_1\left({\tilde{A}}_i^{\mathrm{U}},)\right)\in \left[0,1,]\right],H_2\left({\tilde{A}}_i^{\mathrm{U}},)\right)\in \left[0,1,]\right],H_1\left({\tilde{A}}_i^{\mathrm{L}},)\right)\in \left[0,1,]\right],H_2\left({\tilde{A}}_i^{\mathrm{L}},)\right)\in \left[0,1,]\right],\mathrm{and} 1\le i\le n.$$

Definition 4

((Lee and Chen ⁴⁶ )) Let two trapezoidal interval type‐2 fuzzy sets be

$$\begin{array}{ccl}{\widetilde{\stackrel{~}{A}}}_1& =& \left({\tilde{A}}_1^{\mathrm{U}},{\tilde{A}}_1^{\mathrm{L}},)\right)\\ & =& \left(\left(a_{11}^{\mathrm{U}},a_{12}^{\mathrm{U}},a_{13}^{\mathrm{U}},a_{14}^{\mathrm{U}}\mathrm{;}{H}_1\left({\tilde{A}}_1^{\mathrm{U}},)\right),H_2\left({\tilde{A}}_1^{\mathrm{U}},)\right),)\right),\left(a_{11}^{\mathrm{L}},a_{12}^{\mathrm{L}},a_{13}^{\mathrm{L}},a_{14}^{\mathrm{L}}\mathrm{;}{H}_1\left({\tilde{A}}_1^{\mathrm{L}},)\right),H_2\left({\tilde{A}}_1^{\mathrm{L}},)\right),)\right),)\right) \mathrm{and}\\ {\widetilde{\stackrel{~}{A}}}_2& =& \left({\tilde{A}}_2^{\mathrm{U}},{\tilde{A}}_2^{\mathrm{L}},)\right)\\ & & \left(\left(a_{21}^{\mathrm{U}},a_{22}^{\mathrm{U}},a_{23}^{\mathrm{U}},a_{24}^{\mathrm{U}}\mathrm{;}{H}_1\left({\tilde{A}}_2^{\mathrm{U}},)\right),H_2\left({\tilde{A}}_2^{\mathrm{U}},)\right),)\right),\left(a_{21}^{\mathrm{L}},a_{22}^{\mathrm{L}},a_{23}^{\mathrm{L}},a_{24}^{\mathrm{L}}\mathrm{;}{H}_1\left({\tilde{A}}_2^{\mathrm{L}},)\right),H_2\left({\tilde{A}}_2^{\mathrm{L}},)\right),)\right),)\right).\end{array}$$

Some arithmetical operations are as follows:

The addition of trapezoidal interval type‐2 fuzzy sets:

$${\widetilde{\stackrel{~}{A}}}_1⨁{\widetilde{\stackrel{~}{A}}}_2=\left({\tilde{A}}_1^{\mathrm{U}},{\tilde{A}}_1^{\mathrm{L}},)\right)⨁\left({\tilde{A}}_2^{\mathrm{U}},{\tilde{A}}_2^{\mathrm{L}},)\right)=\left(\left(a_{11}^{\mathrm{U}}+a_{21}^{\mathrm{U}},a_{12}^{\mathrm{U}}+a_{22}^{\mathrm{U}},a_{13}^{\mathrm{U}}+a_{23}^{\mathrm{U}},a_{14}^{\mathrm{U}}+a_{24}^{\mathrm{U}}\mathrm{;}\min \left(H_1\left({\tilde{A}}_1^{\mathrm{U}},)\right),H_1\left({\tilde{A}}_2^{\mathrm{U}},)\right),)\right),\min \left(H_2\left({\tilde{A}}_1^{\mathrm{U}},)\right),H_2\left({\tilde{A}}_2^{\mathrm{U}},)\right),)\right),)\right),\left(a_{11}^{\mathrm{L}}+a_{21}^{\mathrm{L}},a_{12}^{\mathrm{L}}+a_{22}^{\mathrm{L}},a_{13}^{\mathrm{L}}+a_{23}^{\mathrm{L}},a_{14}^{\mathrm{L}}+a_{24}^{\mathrm{L}}\mathrm{;}\min \left(H_1\left({\tilde{A}}_1^{\mathrm{L}},)\right),H_1\left({\tilde{A}}_2^{\mathrm{L}},)\right),)\right),\min \left(H_2\left({\tilde{A}}_1^{\mathrm{L}},)\right),H_2\left({\tilde{A}}_2^{\mathrm{L}},)\right),)\right),)\right),)\right).$$ (4)

The subtraction of trapezoidal interval type‐2 fuzzy sets:

$${\widetilde{\stackrel{~}{A}}}_1\ominus {\widetilde{\stackrel{~}{A}}}_2=\left({\tilde{A}}_1^{\mathrm{U}},{\tilde{A}}_1^{\mathrm{L}},)\right)\ominus \left({\tilde{A}}_2^{\mathrm{U}},{\tilde{A}}_2^{\mathrm{L}},)\right)=\left(\left(a_{11}^{\mathrm{U}}-a_{24}^{\mathrm{U}},a_{12}^{\mathrm{U}}-a_{23}^{\mathrm{U}},a_{13}^{\mathrm{U}}-a_{22}^{\mathrm{U}},a_{14}^{\mathrm{U}}-a_{21}^{\mathrm{U}}\mathrm{;}\min \left(H_1\left({\tilde{A}}_1^{\mathrm{U}},)\right),H_1\left({\tilde{A}}_2^{\mathrm{U}},)\right),)\right),\min \left(H_2\left({\tilde{A}}_1^{\mathrm{U}},)\right),H_2\left({\tilde{A}}_2^{\mathrm{U}},)\right),)\right),)\right),\left(a_{11}^{\mathrm{L}}-a_{24}^{\mathrm{L}},a_{12}^{\mathrm{L}}-a_{23}^{\mathrm{L}},a_{13}^{\mathrm{L}}-a_{22}^{\mathrm{L}},a_{14}^{\mathrm{L}}-a_{21}^{\mathrm{L}}\mathrm{;}\min \left(H_1\left({\tilde{A}}_1^{\mathrm{L}},)\right),H_1\left({\tilde{A}}_2^{\mathrm{L}},)\right),)\right),\min \left(H_2\left({\tilde{A}}_1^{\mathrm{L}},)\right),H_2\left({\tilde{A}}_2^{\mathrm{L}},)\right),)\right),)\right),)\right).$$ (5)

The multiplication of trapezoidal interval type‐2 fuzzy sets:

$${\widetilde{\stackrel{~}{A}}}_1\otimes {\widetilde{\stackrel{~}{A}}}_2=\left({\tilde{A}}_1^{\mathrm{U}},{\tilde{A}}_1^{\mathrm{L}},)\right)\otimes \left({\tilde{A}}_2^{\mathrm{U}},{\tilde{A}}_2^{\mathrm{L}},)\right)=\left(\begin{array}{c}\left(a_{11}^{\mathrm{U}}\mathsf{x}{a}_{21}^{\mathrm{U}},a_{12}^{\mathrm{U}}\mathsf{x}{a}_{22}^{\mathrm{U}},a_{13}^{\mathrm{U}}\mathsf{x}{a}_{23}^{\mathrm{U}},a_{14}^{\mathrm{U}}\mathsf{x}{a}_{24}^U\mathrm{;}\min \left(H_1\left({\tilde{A}}_1^{\mathrm{U}},)\right),H_1\left({\tilde{A}}_2^{\mathrm{U}},)\right),)\right),\min \left(H_2\left({\tilde{A}}_1^{\mathrm{U}},)\right),H_2\left({\tilde{A}}_2^{\mathrm{U}},)\right),)\right),)\right),\\ \left(a_{11}^{\mathrm{L}}\mathsf{x}{a}_{21}^{\mathrm{L}},a_{12}^{\mathrm{L}}\mathsf{x}{a}_{22}^{\mathrm{L}},a_{13}^{\mathrm{L}}\mathsf{x}{a}_{23}^{\mathrm{L}},a_{14}^{\mathrm{L}}\mathsf{x}{a}_{24}^{\mathrm{L}}\mathrm{;}\min \left(H_1\left({\tilde{A}}_1^{\mathrm{L}},)\right),H_1\left({\tilde{A}}_2^{\mathrm{L}},)\right),)\right),\min \left(H_2\left({\tilde{A}}_1^{\mathrm{L}},)\right),H_2\left({\tilde{A}}_2^{\mathrm{L}},)\right),)\right),)\right)\end{array},)\right).$$ (6)

Trapezoidal interval type‐2 fuzzy sets and the arithmetic operations between scalar k:

$${\widetilde{\stackrel{~}{A}}}_1=\left({\tilde{A}}_1^{\mathrm{U}},{\tilde{A}}_1^{\mathrm{L}},)\right)=\left(\left(a_{11}^{\mathrm{U}},a_{12}^{\mathrm{U}},a_{13}^{\mathrm{U}},a_{14}^{\mathrm{U}}\mathrm{;}{H}_1\left({\tilde{A}}_1^{\mathrm{U}},)\right),H_2\left({\tilde{A}}_1^{\mathrm{U}},)\right),)\right),\left(a_{11}^{\mathrm{L}},a_{12}^{\mathrm{L}},a_{13}^{\mathrm{L}},a_{14}^{\mathrm{L}}\mathrm{;}{H}_1\left({\tilde{A}}_1^{\mathrm{L}},)\right),H_2\left({\tilde{A}}_1^{\mathrm{L}},)\right),)\right),)\right)$$

and the exact value of k is defined as

$$k{\widetilde{\stackrel{~}{A}}}_1=\left(\begin{array}{c}\left(k\mathsf{x}{a}_{11}^{\mathrm{U}},k\mathsf{x}{a}_{12}^{\mathrm{U}},k\mathsf{x}{a}_{13}^{\mathrm{U}},k\mathsf{x}{a}_{14}^{\mathrm{U}}\mathrm{;}{H}_1\left({\tilde{A}}_1^{\mathrm{U}},)\right),H_2\left({\tilde{A}}_1^{\mathrm{U}},)\right),)\right),\\ \left(k\mathsf{x}{a}_{11}^{\mathrm{L}},k\mathsf{x}{a}_{12}^{\mathrm{L}},k\mathsf{x}{a}_{13}^{\mathrm{L}},k\mathsf{x}{a}_{14}^{\mathrm{L}}\mathrm{;}{H}_1\left({\tilde{A}}_1^{\mathrm{L}},)\right),H_2\left({\tilde{A}}_1^{\mathrm{L}},)\right),)\right)\end{array},)\right),$$ (7)

$$\frac{{\widetilde{\stackrel{~}{A}}}_1}{k}=\left(\begin{array}{c}\left(\frac{1}{k}\mathsf{x}{a}_{11}^{\mathrm{U}},\frac{1}{k}\mathsf{x}{a}_{12}^{\mathrm{U}},\frac{1}{k}\mathsf{x}{a}_{13}^{\mathrm{U}},\frac{1}{k}\mathsf{x}{a}_{14}^{\mathrm{U}}\mathrm{;}{H}_1\left({\tilde{A}}_1^{\mathrm{U}},)\right),H_2\left({\tilde{A}}_1^{\mathrm{U}},)\right),)\right),\\ \left(\frac{1}{k}\mathsf{x}{a}_{11}^{\mathrm{L}},\frac{1}{k}\mathsf{x}{a}_{12}^{\mathrm{L}},\frac{1}{k}\mathsf{x}{a}_{13}^{\mathrm{L}},\frac{1}{k}\mathsf{x}{a}_{14}^{\mathrm{L}}\mathrm{;}{H}_1\left({\tilde{A}}_1^{\mathrm{L}},)\right),H_2\left({\tilde{A}}_1^{\mathrm{L}},)\right),)\right)\end{array},)\right),$$ (8)

where k > 0 (Figure 2).

Figure 2.

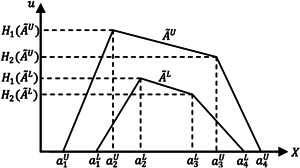
The upper and lower trapezoidal membership functions ${\tilde{A}}_i^{\mathrm{U}}$and ${\tilde{A}}_i^{\mathrm{L}}$, respectively, of the interval type‐2 fuzzy set ${\widetilde{\stackrel{~}{A}}}_i$ ⁴⁷ ​​​​​​

3.2. The proposed method: Delphi‐based BWM and interval type‐2 fuzzy TOPSIS

In this study, we have developed an MCDM methodology consisting of BWM and TOPSIS method based on type‐2 fuzzy sets to select the best location for an isolation hospital. In both stages expert opinions are constituted by applying the modified Delphi method. ⁴⁸ , ⁴⁹ These evaluations are used as inputs to the proposed integrated MCDM framework. First, experts determined the important criteria (factors) to evaluate the alternative locations. Once the criteria weights are calculated using the BWM, all alternative locations are ranked by applying the interval type‐2 fuzzy TOPSIS method. The use of the TOPSIS method extended with interval type‐2 fuzzy sets to handle the unavoidable fuzziness and uncertainty of real‐world problems better.

This integrated MCDM framework is applied to select the most appropriate location for an isolation hospital during COVID‐19 in Istanbul. The steps of the integrated method are detailed as follows:

• Step 1. Create a group of experts comprising DMs. The set of k DMs is E = DM ₁, DM ₂, …, DM _k.

• Step 2. Determine alternative locations and evaluation criteria. Using the Delphi method, alternative locations, $A\mathit{=}\{A_1\mathit{,}{A}_2,\text{…},A_n\}$, and evaluation criteria, $C=\{c_1,c_2,\text{…},c_m\}$, are determined.

• Step 3. Determine the criteria weights. Once the DMs evaluated criteria using the values 1–9, the BWM is applied to determine the criteria weights, $w_m$.

  $$W=\{w_1,w_2,\text{…},w_m\}.$$ (9)
• Step 4. Construct decision matrix. An MCDM problem is made of some alternatives $\left(A_{\mathit{1}}\mathit{,}{A}_{\mathit{2}}\mathit{,}\mathit{\dots }\mathit{,}{A}_n,)\right)$ and multiple criteria $(c_1,c_2,\text{…},c_m)$, in where each alternative has a score with respect to each criterion $({\widetilde{\stackrel{~}{p}}}_{11},{\widetilde{\stackrel{~}{p}}}_{12},\text{…},{\widetilde{\stackrel{~}{p}}}_{nm})$. Then, the decision matrix can be expressed as

  $$P=\left({\widetilde{\stackrel{~}{p}}}_{\mathit{ij}},)\right)=\begin{array}{c}\begin{array}{ccc}{c}_1& c_2& \text{…}\end{array}{c}_m\\ \begin{array}{c}\begin{array}{c}{A}_1\\ A_2\\ \text{…}\end{array}\\ A_n\end{array}\left[\begin{array}{c}\begin{array}{ccc}{\widetilde{\stackrel{~}{p}}}_{11}& {\widetilde{\stackrel{~}{p}}}_{12}\text{…}& {\widetilde{\stackrel{~}{p}}}_{1m}\\ {\widetilde{\stackrel{~}{p}}}_{21}& {\widetilde{\stackrel{~}{p}}}_{21}\text{…}& {\widetilde{\stackrel{~}{p}}}_{2m}\\ \text{⋮}& \ddots & \text{⋮}\end{array}\\ \begin{array}{ccc}{\widetilde{\stackrel{~}{p}}}_{n1}& {\widetilde{\stackrel{~}{p}}}_{n2}\text{…}& {\widetilde{\stackrel{~}{p}}}_{\mathit{nm}}\end{array}\end{array}\right],\end{array}$$ (10)

  where

  $${\widetilde{\stackrel{~}{p}}}_{\mathit{ij}}=\left(\left(a_{11}^{\mathrm{U}},a_{12}^{\mathrm{U}},a_{13}^{\mathrm{U}},a_{14}^{\mathrm{U}}\mathrm{;}{H}_1\left({\tilde{A}}_1^{\mathrm{U}},)\right),H_2\left({\tilde{A}}_1^{\mathrm{U}},)\right),)\right),\left(a_{11}^{\mathrm{L}},a_{12}^{\mathrm{L}},a_{13}^{\mathrm{L}},a_{14}^{\mathrm{L}}\mathrm{;}{H}_1\left({\tilde{A}}_1^{\mathrm{L}},)\right),H_2\left({\tilde{A}}_1^{\mathrm{L}},)\right),)\right),)\right).$$

• Step 5. The following linguistic terms (Table 1) are used in DMs evaluations of the alternatives considering the determined criteria.

• Step 6. Construct the normalized fuzzy decision matrix. To abstain the complication of scientific calculations in a decision‐making course of the type of criteria, in particular larger of benefits and smaller cost, the normalization process is performed to convert several criteria measures into similar measures. The normalization process is applied as in the following equations:

  $$\widetilde{\stackrel{~}{R}}={\left[{\tilde{r}}_{\mathit{ij}}\right]}_{\mathit{nxm}}, i=1,2,\text{…},n, j=1,2,\text{…},m,$$ (11)

  $${\widetilde{\stackrel{~}{r}}}_{\mathit{ij}}=\left(\left(\frac{a_{i1}^{\mathrm{U}}}{a_{i^{⁎}}^{\mathrm{U}}},\frac{a_{i2}^{\mathrm{U}}}{a_{i^{⁎}}^{\mathrm{U}}},\frac{a_{i3}^{\mathrm{U}}}{a_{i^{⁎}}^{\mathrm{U}}},\frac{a_{i4}^{\mathrm{U}}}{a_{i^{⁎}}^{\mathrm{U}}}\mathrm{;}{H}_1\left({\tilde{A}}_j^{\mathrm{U}},)\right),H_2\left({\tilde{A}}_j^{\mathrm{U}},)\right),)\right),\left(\frac{a_{i1}^{\mathrm{L}}}{a_{i^{⁎}}^{\mathrm{U}}},\frac{a_{i2}^{\mathrm{L}}}{a_{i^{⁎}}^{\mathrm{U}}},\frac{a_{i3}^{\mathrm{L}}}{a_{i^{⁎}}^{\mathrm{U}}},\frac{a_{i4}^{\mathrm{L}}}{a_{i^{⁎}}^{\mathrm{U}}}\mathrm{;}{H}_1\left({\tilde{A}}_i^{\mathrm{L}},)\right),H_2\left({\tilde{A}}_i^{\mathrm{L}},)\right),)\right),)\right),$$ (12)

  $${\widetilde{\stackrel{~}{r}}}_{\mathit{ij}}=\left(\left(\frac{a_{i^{-}}^{\mathrm{U}}}{a_{i4}^{\mathrm{U}}},\frac{a_{i^{-}}^{\mathrm{U}}}{a_{i3}^{\mathrm{U}}},\frac{a_{i^{-}}^{\mathrm{U}}}{a_{i2}^{\mathrm{U}}},\frac{a_{i^{-}}^{\mathrm{U}}}{a_{i1}^{\mathrm{U}}}\mathrm{;}{H}_1\left({\tilde{A}}_i^{\mathrm{U}},)\right),H_2\left({\tilde{\mathrm{A}}}_i^{\mathrm{U}},)\right),)\right),\left(\frac{a_{i^{-}}^{\mathrm{U}}}{a_{i4}^{\mathrm{L}}},\frac{a_{i^{-}}^{\mathrm{U}}}{a_{i3}^{\mathrm{L}}},\frac{a_{i^{-}}^{\mathrm{U}}}{a_{i2}^{\mathrm{L}}},\frac{a_{i^{-}}^{\mathrm{U}}}{a_{i1}^{\mathrm{L}}}\mathrm{;}{H}_1\left({\tilde{A}}_i^{\mathrm{L}},)\right),H_2\left({\tilde{A}}_i^{\mathrm{L}},)\right),)\right),)\right),$$ (13)

  where B and C are the sets of benefit and cost criteria, and $a_{i^{⁎}}^{\mathrm{U}}=\underset{i}{\max }{a}_{\mathit{ij}}^{\mathrm{U}},j\in B \text{and }{a}_{i^{-}}^{\mathrm{U}}=\underset{i}{\min }{a}_{\mathit{ij}}^{\mathrm{U}},j\in C.$
• Step 7. Compute the weighted normalized decision matrix. It is obtained by multiplying the importance weights of criteria and the values of normalized decision matrix as

  $${\widetilde{\stackrel{~}{v}}}_{\mathit{ij}}=w_j·{\widetilde{\stackrel{~}{r}}}_{\mathit{ij}},$$ (14)

  where ${\widetilde{\stackrel{~}{v}}}_{\mathit{ij}}$ is the weighted interval type‐2 fuzzy numbers.
• Step 8. The ranking values of interval type 2 fuzzy numbers are calculated by Equation (15), which is introduced by Kahraman et al. ⁵⁰

  $$Rank\left({\widetilde{\stackrel{~}{v}}}_{ij}\right)={\displaystyle \frac{\frac{\left(a_{j4-}{a}_{j1},)\right)+\left(H_1\left({\tilde{A}}_j^{\mathrm{U}},)\right)\ast a_{j2}^{\mathrm{U}}-a_{j1}^{\mathrm{U}},)\right)+\left(H_2\left({\tilde{A}}_j^{\mathrm{U}},)\right)\ast a_{j3}^{\mathrm{U}}-a_{j1}^{\mathrm{U}},)\right)}{4}+a_{j1}^{\mathrm{U}}+\frac{\left(a_{j4}^{\mathrm{L}}-a_{j1}^{\mathrm{L}},)\right)+\left(H_1\left({\tilde{A}}_j^{\mathrm{L}},)\right)\ast a_{j2}^{\mathrm{L}}-a_{j1}^{\mathrm{L}},)\right)+\left(H_2{({\tilde{A}}_j^{\mathrm{L}})\ast a}_{j3}^{\mathrm{L}}-a_{j1}^{\mathrm{L}},)\right)}{4}+a_{j1}^{\mathrm{L}}}{2}}.$$ (15)
• Step 9. Determine the Positive Ideal Solution (PIS) and Negative Ideal Solution (NIS). In this step $\left(x^{\mathit{⁎}},)\right)$ and $\mathrm{NIS}\left(x^{-}\right)$ are determined as

  $$x^{⁎}=\left(\left(,v_1^{⁎},v_2^{⁎},\text{…},v_m^{⁎},\right)\right)=\underset{i}{\max }\left.\left\{\mathrm{Rank}\left({\widetilde{\stackrel{~}{v}}}_{\mathit{ij}},)\right)\right\}\right|j\in B,\underset{i}{\min }\left.\left\{\mathrm{Rank}\left({\widetilde{\stackrel{~}{v}}}_{\mathit{ij}},)\right)\right\}\right|j\in C,$$ (16)

  $$x^{-}=\left(\left(,v_1^{-},v_2^{-},\text{…},v_m^{-},\right)\right)=\underset{i}{\min }\left.\left\{\mathrm{Rank}\left({\widetilde{\stackrel{~}{v}}}_{\mathit{ij}},)\right)\right\}\right|j\in B,\underset{i}{\max }\left.\left\{\mathrm{Rank}\left({\widetilde{\stackrel{~}{v}}}_{\mathit{ij}},)\right)\right\}\right|j\in C,$$ (17)

  where B and C are related to benefit and cost criteria, correspondingly.
• Step 10. The distances to $\mathrm{PIS}\left(d_i^{⁎}\right)$ and $\mathrm{NIS}\left(d_i^{\mathit{‐}}\right)$ are calculated as follows:

  $$d_i^{⁎}=\sum _{j=1}^m\sqrt{{\left(\mathrm{Rank}\left({\widetilde{\stackrel{~}{v}}}_{\mathit{ij}},)\right)-v_j^{⁎},)\right)}^2}, i=1,2,\text{…},n,$$ (18)

  $$d_i^{-}=\sum _{j=1}^m\sqrt{{\left(\mathrm{Rank}\left({\widetilde{\stackrel{~}{v}}}_{\mathit{ij}},)\right)-v_j^{-},)\right)}^2}, i=1,2,\text{…},n.$$ (19)

• Step 11. The calculation of closeness coefficients (${\mathrm{CC}}_i$) of each alternative is done via Equation (20). Then, the alternatives are ranked considering the descending order of $\mathrm{CC}$.

$$\mathrm{CC}\left(i,)\right)=\frac{d_i^{-}}{d_i^{-}+d_i^{⁎}}.$$ (20)

Table 1.

Linguistic terms to evaluate the alternatives ⁵¹

Linguistic terms	Interval type‐2 fuzzy sets
Very poor (VP)	((0, 1, 1, 3; 1, 1), (0.5, 1, 1, 2; 0.9, 0.9))
Poor (P)	((1, 3, 3, 5; 1, 1), (2, 3, 3, 4; 0.9, 0.9))
Fair (F)	((3, 5, 5, 7; 1, 1), (4, 5, 5, 6; 0.9, 0.9))
Medium good (MG)	((5, 7, 7, 9; 1, 1), (6, 7, 7, 8; 0.9, 0.9))
Good (G)	((7, 9, 9, 10; 1, 1), (8, 9, 9, 9.5; 0.9, 0.9))
Very good (VG)	((9, 10, 10, 10; 1, 1), (9.5, 10, 10, 10; 0.9, 0.9))

This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.

4. APPLICATION

The application of the proposed approach is applied to the location selection of isolation hospitals for serving patients who are infected with COVID‐19 in Istanbul.

4.1. Problem description

The presence of patients infected with COVID‐19 in hospitals increases the risk of epidemics in the hospitals in terms of spreading the pandemic to other patients and healthcare professionals. Therefore, the government has decided to create temporary pandemic designated hospitals to treat patients infected with COVID‐19 only. Turkey, in the early days of the epidemic of COVID‐19 continued to be one of the safest countries. However, after a few months, COVID‐19 increased its spread rate with an incremental trend in almost all cities of Turkey, specifically in Istanbul. ⁵²

Istanbul, as an international metropolitan, has more than 15 million residents living at the Asian and European continentals. Moreover, Istanbul is one of the largest business centers in the world, where hundreds of flights around the world transport individuals every day via Istanbul. ⁵³ Therefore, Istanbulers are under the risk of being infected with COVID‐19 because human circulation is very high. With the highest number of residents in Turkey, Istanbul has the highest number of infected individuals as well. Further, the European side of Istanbul has a higher number of infected patients comparing to Asian side.

To treat patients with mild symptoms and who do not need ICU or ventilators are need to be isolated from public and their families. However, since the capacity of regular or designated hospitals is limited a temporary isolation hospital is needed to be constructed. For this, large‐scale public areas can be used to develop isolation hospitals, which provide essential social and medical environments for the quarantined patients with mild symptoms. Transforming these public spaces into isolation hospitals is an effective way to quickly advance the functionality of the healthcare systems throughout the pandemics. To reduce the number of new infections and minimize the density of patients at regular hospitals, isolation hospitals are suggested to Istanbul for preventing the contamination within the household and society. Thus, in the isolation hospitals established, the patients will be taken under control and a standard and effective treatment will be provided to prevent the disease from getting worse.

To construct isolation hospitals in different regions of the city, five community members were selected to apply their experiences and opinions: two members were from healthcare institutions, two were from municipality, and the last one was from academy. All members have at least 10 years of experience. Once we conducted the first, second, and third rounds of a survey related to selection of appropriate site and the evaluation criteria for isolation hospitals, respectively, with feedbacks, we integrated expert opinions to reach a consensus. As a result, five different large‐scale public areas were selected at the European side of Istanbul, and nine criteria were determined to select the most appropriate location. The locations of alternative venues are shown in Figure 3, and the explanations of the selected criteria and venues are as follows:

• Land space including green areas (C1):

  The selected isolation hospitals should be large scale as stadiums or exhibition centers. Since these hospitals separate patients from their relatives and society, while supplying medical care, monitoring, nutrition, accommodation, and social activities, enough space should be available to socialize and receive all types of services.

• Accessibility in terms of distance and time (C2):

  Large‐scale public spaces are generally at the center of metro areas. Thus, patients should reach these hospitals very comfortably and easily, and they should be close to many main arteries.

• Geographical barriers for vehicles' (car, ambulance, and helicopter) access (C3):

  Constructed isolation hospitals should have wide open spaces with unobstructed large space that can easily handle the rapid arrival of ambulances and helicopters in emergence situations.

• Population density of candidate location (C4):

  Patients with COVID‐19 epidemic disease should be isolated from areas where the population has density without hindering the social activities of the community.

• Expandability (availability of land for long term expansion) (C5):

  In case of emergency, these isolation hospitals should be established in a place with sufficient space that can be expanded with additional bed capacity in a short time.

• Social convenience (public nuisance) (C6):

  The selected sites for isolation hospitals must be far from the public due to a lack of social acceptability or negative public perceptions.

• Distance to regular hospitals (C7):

  Large‐scale areas being evaluated should not be far from the regular hospitals so that the patients whose illness worsen from mild to severe can be rapidly transferred for further treatment.

• Availability of parking lots (C8):

  In the area of isolation hospitals there should be enough parking lots to serve ambulances, helicopters, healthcare institution‐related vehicles, police vehicles, catering service vehicles, waste management vehicles, and the vehicles of patients who come to isolation hospital by their cars for the treatment.

• Construction cost and time (C9):

  Selected sites for the isolation hospitals should be rapidly built in a short time period with lower cost.

• Yenikapi rally area (A1):

  Yenikapi Rally Area has about 250 km² space area with a wide transport network. Transportation to Yenikapı from different points of Istanbul is easily provided via both rail and public transportation modes. It is also possible to reach Yenikapı by minibuses and buses departing from Bakırköy, Eminönü, and Taksim as the center points of Istanbul. ⁵⁴

• Ataturk Olympic Stadium (A2):

  Ataturk Olympic Stadium is a stadium located in Başakşehir district on a 584‐ha area. Within the stadium, there are 100 toilets for men, 90 toilets for women, and 60 toilets and sinks for disabled people. The total area of the stadium, which is built on a 52,000‐m² floor area, together with the plaza is 120,000 m². ⁵⁵

• Atatürk Airport (A3):

  Atatürk Airport is located within the borders of Bakırköy district, which is one of the largest districts of Istanbul, and Yeşilköy district, whose center is by the sea. The airport land is bordered by the Marmara Sea in the south and the D‐100 highway in the north. It has a total area of 11 million and 650 km². Further, it has a wide transportation network, which includes buses, minibuses, railway, and taxis. ⁵⁶

• Gürpınar Seafood Market Hall (A4):

  Gürpınar Seafood Market Hall is located in Gürpınar/Beylikdüzü, between Büyükçekmece district and Küçükçekmece lakes in Istanbul, on the Marmara Sea coast, and 6.5 km far from the D‐100 Highway. It has a closed area of approximately 60,000 m² built on the sea by approximately 220,000 m² of filled area. ⁵⁷

• Fatih Sultan Mehmet (FSM) Student Dormitory (A5):

Figure 3.

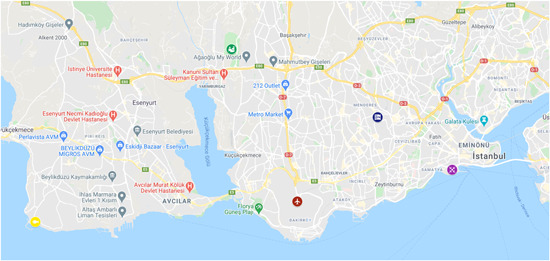
Locations of alternative public venues [Color figure can be viewed at wileyonlinelibrary.com]

• FSM Student Dormitory is a state dormitory affiliated to dormitories institution, and located within the borders of Davutpaşa Campus. FSM Student Dormitory consists of six blocks with the capacity of over 3000 people. ⁵⁸

4.2. Application procedure of the case study

In this section, the problem of the location selection of isolation hospitals within the European side of Istanbul is solved by the above‐mentioned framework. The methodology construction and results are examined in detail by applying comparative and sensitivity analyses.

The application procedure is constructed as in Figure 4:

• Modified Delphi method: To construct isolation hospitals at the European side of Istanbul, which has the higher density of COVID‐19 patients in the city, five community members were selected to specify their experiences and opinions. Accordingly, two members were from healthcare institutions, two were from municipality, and one was from academy, who have at least 10 years of experience. To incorporate expert opinions and to come up with a consensus decision, three rounds of a questionnaire were directed. At the end, nine criteria and five alternative locations were determined as the most suitable and available locations at the European side of Istanbul by applying the modified Delphi method.

• BWM: Once we defined the set of evaluation criteria and alternative locations by applying modified Delphi method, DMs determined the best and worst criteria according to their opinions and preferences. Then, they provided their preferences of the best criterion over other criteria, and all criteria over the worst criterion. By following the steps of BWM the weights of criteria and their ranks are obtained as in Table 2.

Figure 4.

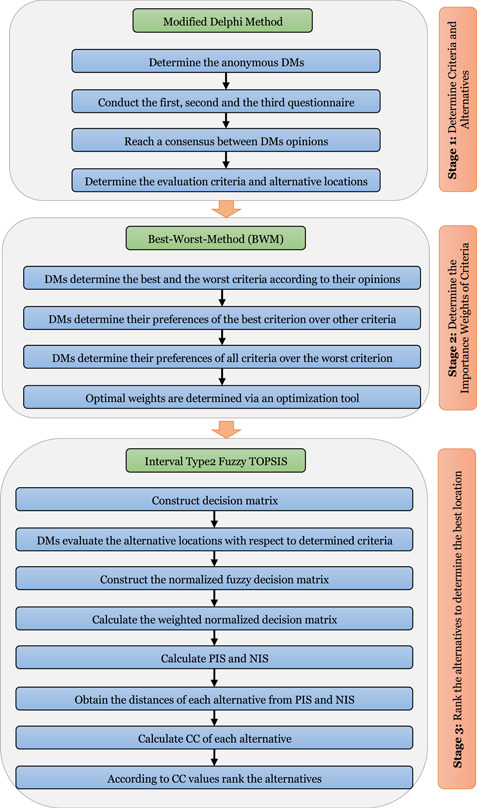
Stages of the proposed framework. BWM, Best–Worst Method; CC, closeness coefficient; DM, decision maker; NIS, Negative Ideal Solution; PIS, Positive Ideal Solution; TOPSIS, Technique for Order of Preference by Similarity to Ideal Solution [Color figure can be viewed at wileyonlinelibrary.com]

Table 2.

Importance weights of the evaluation criteria

	Criteria
	C1	C2	C3	C4	C5	C6	C7	C8	C9
Weight	0.104	0.292	0.148	0.033	0.086	0.073	0.093	0.112	0.059
Rank	4	1	2	9	6	7	5	3	8

This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.

The significance of these nine criteria are calculated by BMW, and these weight values are used as inputs to the interval type‐2 fuzzy TOPSIS.

• Interval Type‐2 Fuzzy TOPSIS: Interval Type‐2 Fuzzy TOPSIS calculations were employed for obtaining the ranking of alternative locations for the isolation hospital. Accordingly, these alternative locations were assessed based on nine criteria by DMs using linguistic statements employed in Table 1. By converting linguistic variables to corresponding interval Type‐2 fuzzy numbers, the decision matrix is obtained as shown in Table 3. Later, the fuzzy normalized decision matrix was calculated by using Equations (11)–(13). The interval Type‐2 fuzzy normalized decision matrix was presented in Table 4. The weighted fuzzy normalized decision matrix was calculated by multiplying criteria weights obtained by BWM. Next, the defuzzified values of the interval type‐2 fuzzy sets were determined for obtaining the defuzzified weighted decision matrix via Equations (14) and (15). Afterwards, PIS and NIS were calculated by Equations (16) and (17) for each alternative location considering all criteria. The ranking values of the interval type‐2 fuzzy set and PIS and NIS for alternatives are given in Table 5. Further, the distances from the PIS and NIS are calculated by Equations (18) and (19), respectively. The distance values of alternatives from PIS and NIS are shown in Table 6. Lastly, the closeness coefficient was calculated by Equation (20) to rank the isolation hospital locations (see Table 6).

Table 3.

Decision matrix

Criteria	Yenikapi	Olympic Stadium	Atatürk Airport	Beylikduzu	FSM
C1	((3, 5, 5, 7; 1, 1), (4, 5, 5, 6; 0.9, 0.9))	((5, 7, 7, 9; 1, 1), (6, 7, 7, 8; 0.9, 0.9))	((7, 9, 9, 10; 1, 1), (8, 9, 9, 9.5; 0.9, 0.9))	((5, 7, 7, 9; 1, 1), (6, 7, 7, 8; 0.9, 0.9))	((3, 5, 5, 7; 1, 1), (4, 5, 5, 6; 0.9, 0.9))
C2	((5, 7, 7, 9; 1, 1), (6, 7, 7, 8; 0.9, 0.9))	((7, 9, 9, 10; 1, 1), (8, 9, 9, 9.5; 0.9, 0.9))	((9, 10, 10, 10; 1, 1), (9.5, 10, 10, 10; 0.9, 0.9))	((7, 9, 9, 10; 1, 1), (8, 9, 9, 9.5; 0.9, 0.9))	((7, 9, 9, 10; 1, 1), (8, 9, 9, 9.5; 0.9, 0.9))
C3	((7, 9, 9, 10; 1, 1), (8, 9, 9, 9.5; 0.9, 0.9))	((3, 5, 5, 7; 1, 1), (4, 5, 5, 6; 0.9, 0.9))	((1, 3, 3, 5; 1, 1), (2, 3, 3, 4; 0.9, 0.9))	((3, 5, 5, 7; 1, 1), (4, 5, 5, 6; 0.9, 0.9))	((5, 7, 7, 9; 1, 1), (6, 7, 7, 8; 0.9, 0.9))
C4	((7, 9, 9, 10; 1, 1), (8, 9, 9, 9.5; 0.9, 0.9))	((5, 7, 7, 9; 1, 1), (6, 7, 7, 8; 0.9, 0.9))	((7, 9, 9, 10; 1, 1), (8, 9, 9, 9.5; 0.9, 0.9))	((5, 7, 7, 9; 1, 1), (6, 7, 7, 8; 0.9, 0.9))	((7, 9, 9, 10; 1, 1), (8, 9, 9, 9.5; 0.9, 0.9))
C5	((3, 5, 5, 7; 1, 1), (4, 5, 5, 6; 0.9, 0.9))	((5, 7, 7, 9; 1, 1), (6, 7, 7, 8; 0.9, 0.9))	((7, 9, 9, 10; 1, 1), (8, 9, 9, 9.5; 0.9, 0.9))	((5, 7, 7, 9; 1, 1), (6, 7, 7, 8; 0.9, 0.9))	((3, 5, 5, 7; 1, 1), (4, 5, 5, 6; 0.9, 0.9))
C6	((1, 3, 3, 5; 1, 1), (2, 3, 3, 4; 0.9, 0.9))	((5, 7, 7, 9; 1, 1), (6, 7, 7, 8; 0.9, 0.9))	((7, 9, 9, 10; 1, 1), (8, 9, 9, 9.5; 0.9, 0.9))	((3, 5, 5, 7; 1, 1), (4, 5, 5, 6; 0.9, 0.9))	((3, 5, 5, 7; 1, 1), (4, 5, 5, 6; 0.9, 0.9))
C7	((3, 5, 5, 7; 1, 1), (4, 5, 5, 6; 0.9, 0.9))	((5, 7, 7, 9; 1, 1), (6, 7, 7, 8; 0.9, 0.9))	((5, 7, 7, 9; 1, 1), (6, 7, 7, 8; 0.9, 0.9))	((5, 7, 7, 9; 1, 1), (6, 7, 7, 8; 0.9, 0.9))	((5, 7, 7, 9; 1, 1), (6, 7, 7, 8; 0.9, 0.9))
C8	((3, 5, 5, 7; 1, 1), (4, 5, 5, 6; 0.9, 0.9))	((7, 9, 9, 10; 1, 1), (8, 9, 9, 9.5; 0.9, 0.9))	((9, 10, 10, 10; 1, 1), (9.5, 10, 10, 10; 0.9, 0.9))	((5, 7, 7, 9; 1, 1), (6, 7, 7, 8; 0.9, 0.9))	((3, 5, 5, 7; 1, 1), (4, 5, 5, 6; 0.9, 0.9))
C9	((5, 7, 7, 9; 1, 1), (6, 7, 7, 8; 0.9, 0.9))	((7, 9, 9, 10; 1, 1), (8, 9, 9, 9.5; 0.9, 0.9))	((7, 9, 9, 10; 1, 1), (8, 9, 9, 9.5; 0.9, 0.9))	((5, 7, 7, 9; 1, 1), (6, 7, 7, 8; 0.9, 0.9))	((1, 3, 3, 5; 1, 1), (2, 3, 3, 4; 0.9, 0.9))

Abbreviation: FSM, Fatih Sultan Mehmet.

This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.

Table 4.

Interval type‐2 fuzzy normalized decision matrix

Criteria	Yenikapi	Olympic Stadium	Atatürk Airport	Beylikduzu	FSM
C1	((0.3, 0.5, 0.5, 0.7; 1, 1), (0.4, 0.5, 0.5, 0.6; 0.9, 0.9))	((0.5, 0.7, 0.7, 0.9; 1, 1), (0.6, 0.7, 0.7, 0.8; 0.9, 0.9))	((0.7, 0.9, 0.9, 1; 1, 1), (0.8, 0.9, 0.9, 0.95; 0.9, 0.9))	((0.5, 0.7, 0.7, 0.9; 1, 1), (0.6, 0.7, 0.7, 0.8; 0.9, 0.9))	((0.3, 0.5, 0.5, 0.7; 1, 1), (0.4, 0.5, 0.5, 0.6; 0.9, 0.9))
C2	((0.5, 0.7, 0.7, 0.9; 1, 1), (0.6, 0.7, 0.7, 0.8; 0.9, 0.9))	((0.7, 0.9, 0.9, 1; 1, 1), (0.8, 0.9, 0.9, 0.95; 0.9, 0.9))	((0.9, 1, 1, 1; 1, 1), (0.95, 1, 1, 1; 0.9, 0.9))	((0.7, 0.9, 0.9, 1; 1, 1), (0.8, 0.9, 0.9, 0.95; 0.9, 0.9))	((0.7, 0.9, 0.9, 1; 1, 1), (0.8, 0.9, 0.9, 0.95; 0.9, 0.9))
C3	((0.10, 0.11, 0.11, 0.14; 1, 1), (0.11, 0.11, 0.11, 0.13; 0.9, 0.9))	((0.14, 0.20, 0.20, 0.33; 1, 1), (0.17, 0.20, 0.20, 0.25; 0.9, 0.9))	((0.20, 0.33, 0.33, 1; 1, 1), (0.25, 0.33, 0.33, 0.5; 0.9, 0.9))	((0.14, 0.20, 0.20, 0.33; 1, 1), (0.17, 0.20, 0.20, 0.25; 0.9, 0.9))	((0.11, 0.14, 0.14, 0.20; 1, 1), (0.13, 0.14, 0.14, 0.17; 0.9, 0.9))
C4	((0.10, 0.11, 0.11, 0.14; 1, 1), (0.11, 0.11, 0.11, 0.13; 0.9, 0.9))	((0.11, 0.14, 0.14, 0.20; 1, 1), (0.13, 0.14, 0.14, 0.17; 0.9, 0.9))	((0.1, 0.11, 0.11, 0.14; 1, 1), (0.11, 0.11, 0.11, 0.13; 0.9, 0.9))	((0.11, 0.14, 0.14, 0.20; 1, 1), (0.13, 0.14, 0.14, 0.17; 0.9, 0.9))	((0.1, 0.11, 0.11, 0.14; 1, 1), (0.11, 0.11, 0.11, 0.13; 0.9, 0.9))
C5	((0.3, 0.5, 0.5, 0.7; 1, 1), (0.4, 0.5, 0.5, 0.6; 0.9, 0.9))	((5, 7, 7, 9; 1, 1), (6, 7, 7, 8; 0.9, 0.9))	((0.7, 0.9, 0.9, 1; 1, 1), (0.8, 0.9, 0.9, 0.95; 0.9, 0.9))	((0.5, 0.7, 0.7, 0.9; 1, 1), (0.6, 0.7, 0.7, 0.8; 0.9, 0.9))	((0.3, 0.5, 0.5, 0.7; 1, 1), (0.4, 0.5, 0.5, 0.6; 0.9, 0.9))
C6	((0.1, 0.3, 0.3, 0.5; 1, 1), (0.2, 0.3, 0.3, 0.4; 0.9, 0.9))	((0.5, 0.7, 0.7, 0.9; 1, 1), (0.6, 0.7, 0.7, 0.8; 0.9, 0.9))	((0.7, 0.9, 0.9, 1; 1, 1), (0.8, 0.9, 0.9, 0.95; 0.9, 0.9))	((0.3, 0.5, 0.5, 0.7; 1, 1), (0.4, 0.5, 0.5, 0.6; 0.9, 0.9))	((0.3, 0.5, 0.5, 0.7; 1, 1), (0.4, 0.5, 0.5, 0.6; 0.9, 0.9))
C7	((0.14, 0.20, 0.20, 0.33; 1, 1), (0.17, 0.20, 0.20, 0.25; 0.9, 0.9))	((0.5, 0.7, 0.7, 0.9; 1, 1), (0.6, 0.7, 0.7, 0.8; 0.9, 0.9))	((0.11, 0.14, 0.14, 0.20; 1, 1), (0.13, 0.14, 0.14, 0.17; 0.9, 0.9))	((0.11, 0.14, 0.14, 0.20; 1, 1), (0.13, 0.14, 0.14, 0.17; 0.9, 0.9))	((0.11, 0.14, 0.14, 0.20; 1, 1), (0.13, 0.14, 0.14, 0.17; 0.9, 0.9))
C8	((0.3, 0.5, 0.5, 0.7; 1, 1), (0.4, 0.5, 0.5, 0.6; 0.9, 0.9))	((0.7, 0.9, 0.9, 1; 1, 1), (0.8, 0.9, 0.9, 0.95; 0.9, 0.9))	((0.9, 1, 1, 1; 1, 1), (0.95, 1, 1, 1; 0.9, 0.9))	((0.5, 0.7, 0.7, 0.9; 1, 1), (0.6, 0.7, 0.7, 0.8; 0.9, 0.9))	((0.3, 0.5, 0.5, 0.7; 1, 1), (0.4, 0.5, 0.5, 0.6; 0.9, 0.9))
C9	((0.11, 0.14, 0.14, 0.20; 1, 1), (0.13, 0.14, 0.14, 0.17; 0.9, 0.9))	((0.10, 0.11, 0.11, 0.14; 1, 1), (0.11, 0.11, 0.11, 0.13; 0.9, 0.9))	((0.1, 0.11, 0.11, 0.14; 1, 1), (0.11, 0.11, 0.11, 0.13; 0.9, 0.9))	((0.11, 0.14, 0.14, 0.20; 1, 1), (0.13, 0.14, 0.14, 0.17; 0.9, 0.9))	((0.20, 0.33, 0.33, 1; 1, 1), (0.25, 0.33, 0.33, 0.5; 0.9, 0.9))

Abbreviation: FSM, Fatih Sultan Mehmet.

This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.

Table 5.

Ranking values of the trapezoidal interval type‐2 fuzzy set and fuzzy PIS and NIS for alternatives

	Yenikapi	Olympic Stadium	Atatürk Airport	Beylikduzu	FSM	PIS	NIS
C1	0.051	0.071	0.089	0.071	0.051	0.089	0.051
C2	0.199	0.250	0.279	0.250	0.250	0.279	0.199
C3	0.017	0.030	0.059	0.030	0.021	0.059	0.017
C4	0.004	0.005	0.004	0.005	0.004	0.005	0.004
C5	0.042	0.059	0.074	0.059	0.042	0.074	0.042
C6	0.021	0.050	0.063	0.035	0.035	0.063	0.021
C7	0.019	0.013	0.013	0.013	0.013	0.019	0.013
C8	0.055	0.096	0.107	0.077	0.055	0.107	0.055
C9	0.008	0.007	0.007	0.008	0.024	0.024	0.007

Abbreviations: FSM, Fatih Sultan Mehmet; NIS, Negative Ideal Solution; PIS, Positive Ideal Solution.

This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.

Table 6.

Closeness coefficients (CC) and rankings of the five alternatives

Alternatives	d*	d −	CC	Ranking
A 1 (Yenikapi)	0.124	0.006	0.047	5
A 2 (Olympic Stadium)	0.053	0.078	0.595	2
A 3 (Atatürk Airport)	0.018	0.123	0.872	1
A 4 (Beylikduzu)	0.064	0.065	0.502	3
A5 (FSM)	0.091	0.056	0.381	4

This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.

4.3. Results and discussions

Against an increment in the spread rate of the epidemic, the results showed that the best location to set up an isolation hospital among alternatives is the Atatürk Airport, which is located at a central point where it can be reached by air, roadways, and railways, and has many indoor empty areas, is far from residential districts, and has extensive infrastructure facilities. Thus, transforming the Ataturk Airport into an isolation hospital by equipping with the necessary tools and health professionals to fight against the spread of COVID‐19 also meets the expectations of government administrators and DMs.

Following Atatürk airport, Atatürk Olympic Stadium has emerged as the most appropriate location for an isolation hospital. Therefore, it may also be considered as a second isolation hospital location due to its large area, which can be extended if the number of patients increases, easy transportation, and being away from the crowded districts of the city.

On the other hand, although Yenikapı rally area is close to the hospitals it is ranked as the last option, because it is in the middle of the crowd of the city and its accessibility is not easy due to the heavy traffic within the region.

4.4. Comparative and sensitivity analyses

In this subsection, to validate the effectiveness and feasibility of the proposed method for the evaluation of alternative locations to set up isolation hospitals, we performed a comparative analysis with other two methods, including Interval Type‐2 Fuzzy‐based AHP and TOPSIS method, which is introduced by Gorener et al. ⁵⁹ and Interval Type‐2 Fuzzy‐based WASPAS method, which is proposed by Ghorabaee et al. ⁶⁰ The results reveal that the integrated Delphi‐based BWM and interval type‐2 fuzzy TOPSIS framework generate consistent and reasonable results with the other existing methods (see Table 7). This proposed Delphi‐based BWM and Interval Type‐2 Fuzzy TOPSIS framework are reasonable and practical for evaluating the location of isolation hospitals against COVID‐19 outbreak. As a vector‐based method, BWM is employed for weighting the criteria since it is more efficient and easier for pairwise comparisons. BWM requires fewer pairwise comparisons compared with matrix‐based MCDM methods. The use of TOPSIS method extended with interval type‐2 fuzzy sets handles the unavoidable fuzziness and uncertainty of real‐world problems better.

Table 7.

Comparative analysis with the existing methods

Alternative locations	Gorener's hybrid type‐2 fuzzy MCDM method		Ghorabaee's interval type‐2 fuzzy WASPAS method		Proposed approach
	CC score	Rankings	WASPAS score	Rankings	CC score	Rankings
A 1 (Yenikapi)	0.032	5	0.664	5	0.047	5
A 2 (Olympic Stadium)	0.577	2	0.789	2	0.595	2
A 3 (Atatürk Airport)	0.948	1	0.853	1	0.872	1
A 4 (Beylikduzu)	0.488	3	0.776	3	0.502	3
A 5 (FSM)	0.346	4	0.727	4	0.381	4

Abbreviations: CC, closeness coefficient; MCDM, multicriteria decision making; WASPAS, Weighted Aggregated Sum Product Assessment.

This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.

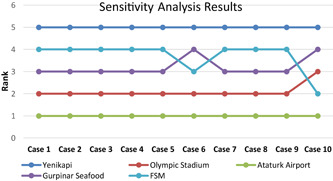
Sensitivity analysis was directed to check the robustness of the results. To execute the sensitivity analysis, the weights of criteria are manipulated and 10 different cases were created consisting of extreme cases, such as selecting only the most important criterion and consider the weights of other criteria the same and vice versa. All cases are solved using the GAMS optimization tool. The results of the optimization are provided in Table 8. Further, the impacts of changing the weights of criteria on the ranking of alternative location rankings are presented in Figure 5.

Table 8.

Weights of criteria determined for sensitivity analysis

	Cases
Criteria	1	2	3	4	5	6	7	8	9	10
C1	0.086	0.059	0.059	0.059	0.121	0.065	0.097	0.114	0.122	0.029
C2	0.357	0.529	0.059	0.059	0.030	0.095	0.150	0.147	0.122	0.167
C3	0.086	0.059	0.059	0.059	0.095	0.146	0.057	0.065	0.122	0.050
C4	0.040	0.059	0.059	0.529	0.101	0.056	0.097	0.046	0.122	0.154
C5	0.086	0.059	0.059	0.059	0.181	0.146	0.276	0.133	0.122	0.103
C6	0.086	0.059	0.059	0.059	0.060	0.065	0.128	0.302	0.122	0.079
C7	0.086	0.059	0.059	0.059	0.302	0.270	0.097	0.071	0.122	0.075
C8	0.086	0.059	0.059	0.059	0.050	0.126	0.067	0.092	0.122	0.269
C9	0.086	0.059	0.529	0.059	0.060	0.030	0.031	0.031	0.020	0.075

This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.

Figure 5.

Rank of alternative locations with respect to different criteria weights [Color figure can be viewed at wileyonlinelibrary.com]

Once the cases in sensitivity analysis were analyzed it was seen that Ataturk Airport ranked as the first while Yenikapi was ranked as the last in all 10 cases. Ranking of other alternative locations did not fluctuate a lot, which showed the robustness of the framework. On the other hand, the changes in rankings showed the sensitivity of ranking procedure of the framework considering the criteria weights. In particular, when the weight of Availability of Parking Lots (C8) was the highest, the ranking was changed significantly, which meant the results were sensitive to Availability of Parking Lots. Moreover, as seen in case 6, when the weight of Distance to Hospitals (C7) was increased the change in ranking was slightly changed. Overall, results of sensitivity analysis showed that the framework produced robust and valid results.

Consequently, the comparative analysis results showed that the integrated Delphi, BWM, and interval type‐2 fuzzy TOPSIS method are efficient and consistent with the other methods' results, and the sensitivity analysis demonstrated the stability of the results of the proposed framework.

5. CONCLUSIONS

With its emergence in Wuhan/China, the COVID‐19 pandemic rapidly spread all over the world. Since its appearance, countries have developed various policies to deal with the pandemic. Within this scope, in Turkey, to fight against the COVID‐19 starting from March 2020 all hospitals (private or public) were declared as pandemic hospitals and the burden of the pandemic is shared among all hospitals. On the other hand, due to the limited resources at healthcare institutions all infected people cannot be monitored in hospitals. Thus, as in all countries, Turkey is searching for alternate solutions, such as monitoring infected people considering the limited capacity of the hospitals.

In this context, a framework to determine the best locations for isolation hospitals was proposed for the treatment of patients who show mild to moderate symptoms and do not need special treatment. Setting isolation hospitals was inspired by Fangcang/makeshift/shelter hospital applications, which have successful applications in many countries around the world, especially as in China. In this study, the locations of isolation hospitals were investigated to get the maximum benefit from them. Thus, Istanbul, which includes approximately 60% of total number of cases in Turkey, is selected.

On the basis of the Modified Delphi method, five alternative locations and nine evaluation criteria were determined by consulting the experiences and opinions of experts in the field. Criteria were evaluated by BWM and it was revealed that the most three important criteria were accessibility, geographical barriers for vehicles, and availability of parking lots. Considering the significance of the evaluation criteria and the degree of satisfying these criteria five alternative locations were assessed by applying type‐2 fuzzy TOPSIS method. Atatürk Airport, which is located in Bakırköy and is currently not operating, was obtained as the most suitable isolation hospital location. The result is satisfactory to establish a temporary isolation hospital at Atatürk Airport because it is located at the most central point where it can be reached by air, roadways, and railways, has many indoor vacancies, is far from residential area, and has extensive infrastructure facilities.

The validation of the effectiveness, feasibility, and robustness of the proposed method is proved by performing comparative analyses with other two existing methods and sensitivity analyses. Consequently, the comparative analysis showed that the Delphi‐based BWM and interval type‐2 fuzzy TOPSIS framework is efficient and consistent with other methods, and the sensitivity analysis validated the robustness of the method. For further research, the framework can be easily applied in other cities of Turkey and in the world provided that the region‐specific characteristics are updated. It is predicted that the number of COVID‐19 cases can be kept under control with the application of the proposed framework.

Aydin N, Seker S. Determining location of isolation hospitals for COVID‐19 via Delphi‐based MCDM method. Int J Intell Syst. 2021;36:3011–3034. 10.1002/int.22410