Abstract
The world is reeling in the midst of the novel coronavirus pandemic with fear of rising toll due to the deadly virus. Decision making during a pandemic outbreak has numerous challenges. Covid19 has become a challenging problem for organizations, countries and the world at large. It is even more complicated when governments and medical care communities are changing their priorities based on the growing challenges and level of effectiveness of measures taken in other countries. In this study, a potential application of a well-known MCDM method called the Group Best–Worst Method is presented to overcome such challenges and draw the strategies to handle COVID19 outbreak. The methodology is applied to rank the 10 identified strategies based on their relative importance provided by multiple groups of stakeholder. These strategies focus on social distancing, medical care, essential commodities, financial support to poor people, public awareness, overall impact of COVID19, digital surveillance of infected or doubtful people, maintaining the economy of the country, and an effect on industries. Furthermore, the local and global weights along with ranking order of strategies are obtained. A sensitivity analysis has also been done to show the change in global weights and ranking order of strategies.
Keywords: MCDM, BWM, COVID-19, Corona virus, Challenges, Strategy
1. Introduction
Coronaviruses are among the largest viruses that cause different diseases in animals such as pigs, dogs, cats, snakes, bats, etc. The consumption of these animals may cause the disease in humans [1], [2]. In December-2019, a novel coronavirus appeared in the form of pneumonia cases in Wuhan, a city in the Hubei Province of China [3]. It is identified as an infectious disease, which became pandemic and spread rapidly throughout China. Afterward, an increasing number of infected cases were also found in other countries throughout the world. In February 2020, this disease was labeled as COVID-19, and its virus is referred to as Severe Acute Respiratory Syndrome CoronaVirus 2 (SARS-CoV-2) by the World Health Organization (WHO) [4]. Many countries are at the point of coronavirus outbreaks, with many instances of community transmission. Governments from many countries have imposed complete lockdown throughout their countries and urged citizens to maintain social distancing or self-quarantine. Handling the rapid spread of the disease is very crucial since the number of infected people is increasing, and it is alarming, particularly in countries such as the USA, Italy, Spain, Germany, and Iran, where the situations threaten to go out of control. Now the spread is practically universal; most of the world is in a lockdown mode. It is being considered to be the largest crisis since World War-II [5].
The identification of adequate response to an emergency situation is essential, be it Nipah virus (NIV), Hemagglutinin Type 1, and Neuraminidase Type 1 (H1N1) or COVID-19. All evidence is now pointing to the fact that as the pandemic reaches the community spread stage, the death count will increase. The increase in the number of patients can collapse the healthcare system of any country, as was already observed in the case of Italy and the USA. No country can afford community transmission. Delay in planning to face the challenges and threats posed by the growing pandemic of COVID-19 will worsen the situation [6]. Countries that have designed the strategies in a stepwise manner in the early days of the pandemic performed better in restricting the spread of disease. The strategies adopted so far includes lockdown, widespread testing, digital surveillance of peoples (i.e., identifying and monitoring people who have been in close contact with someone infected), and isolation of infected patients, see [7], [8], [9].
Digital surveillance raises ethical and privacy issues since it involves monitoring someone’s movement. It is therefore challenging for Governments to adopt tracking and monitoring mechanisms. According to the news in [10], [11], the Israeli government also announced plans to use digital technologies to track the infected/doubtful citizens of COVID-19. Usually, such a surveillance system is used to track terrorist groups. Prime Minister Benjamin Netanyahu quoted that “in all my years as prime minister, I have avoided using these means among the civilian public, but there is no choice”.
The government of India initially worked on a plan drawn in consultation with 14 key ministries [12]. It was decided to see the pattern of the virus spread by conducting preemptive and early tests of people with suspected symptoms and controlling the direction of the economy. Following that idea, their focus was on identifying and setting up quarantine and isolation centers. At that stage, the government imposed a complete lockdown of the country. Initially, the lockdown was from 24 March 2020 to 14 April 2020, but it was again extended up to 3 May 2020 [13]. The Health Ministry claims that the stringent lockdown measure for such a long period helped contain the exponential growth of COVID-19 in India. However, this continuous lockdown has created a considerable challenge of ensuring food security for poor people. In this regard, it has been advised that government should put more money in the hands of daily-wages people, farmers, and laborers.
It is evident that better planning is always required to deal with a pandemic of such scale that has happened first time in our lifetime. Such planning would also help in controlling future pandemics and crises arising out of them affecting businesses and commercial establishments, availability, and price controlling of foods, etc. However, the strategies adopted so far are not enough to tackle this condition of COVID-19, as there are many reports of people facing grave difficulties of various nature. We need a more detailed and robust plan of action considering multiple criteria that get affected during a pandemic. Recently, authors in [14] have reviewed the challenges of decision making in influenza outbreaks. They concluded that “The relationship between science and public health decision making is relatively understudied but is deserving of greater attention”. The prioritization of strategies for overcoming the challenges to effective decision making in the outbreak response needs a transparent decision-making process.
So, there is a need to study COVID-19 strategies to tackle the COVID-19 outbreak. This study explores and evaluates a criteria framework for intervention strategies in the Indian context using a Multi-criteria decision-making approach known as Group best–worst method [15]. We have applied the extended BWM, i.e., Group Best–Worst Method (GBWM) [15], where four groups of stakeholders, namely health workers, social workers, academicians, and common citizens, are considered.
The aims of this study are: (1) to identify the intervention strategies to handle COVID-19 outbreak using an extensive review of reports and articles; and (2) to develop prioritization and ranking of the identified factors using Group Best–Worst Method.
Considering all of these points, we did a study on the potential application of the scientific method on intervention strategies for the COVID-19 outbreak. At present, we have not seen any work in literature that focuses on the evaluation and ranking of intervention strategies for COVID-19 outbreak in general or using the Multi-Criteria Decision-Making method. Multi-Criteria Decision Making (MCDM) methods have found their application in multiple real-life domains. An application of the MCDM method, i.e., the Best–Worst Method (BWM) [16] which has never been used in the evaluation of intervention strategies for a pandemic, is applied in this work.
In the next section, the literature review of MCDM and BWM is discussed. Section 3 is about the methodology applied to determine the weights and rank of strategies. In Section 4, the case study is explained, and results are obtained. Section 5 is about discussion of results and finally, Section 6 is the conclusion of present work.
2. Literature review
This section is about the literature review of tools and techniques of multi-criteria decision-making and best–worst method. The wide application of MCDM and BWM is explained in the following subsections.
2.1. Multi criteria decision making
Decision-making in the public health system is a complex task because of conflicting trade-offs between criteria. The variability of perceptions of different stakeholders often varies greatly both within and across societies. The existence of differences in perceptions is normal in a pluralist society. Tools and techniques, which can handle such complexity to take decisions are needed. MCDM methods help the individual or group of decision-makers to take appropriate and transparent decisions in complex situations. It helps to determine the ranking of alternatives and choosing the superior one using an appropriate method based on some criteria. It has been applied in wide range of applications such as social sciences, engineering, economics, health care, and management [17], [18], [19], [20], [21], [22], [23]. A wide variety of MCDM methods exists in literature such as Elimination and Choice Expressing Reality (ELECTRE) [24], Data Envelopment Analysis (DEA) [25], Analytic Hierarchy Process (AHP) [26], [27], Analytic Network Process (ANP) [28], Measuring Attractiveness by a Categorical-Based Evaluation Technique (MACBETH) [29], Multi-Attribute Utility Theory (MAUT) [30], Best–Worst Method (BWM) [16], Preference Ranking Organization Method for Enrichment Evaluations (PROMETHEE) [23], and Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) [22]. MCDM methods are divided into two-step procedures. In the first step, information related to the values and weights of criteria should be obtained, and then in the second step, the ranking of alternatives is determined.
A limited number of studies illustrated the application of MCDM methods in the context of evaluation of infectious disease outbreaks and intervention strategies. Recently, the TOPSIS approach has been applied by Majumder et al. [31] to select significant risk factors and continuous monitoring of death due to COVID-19. Ozgur maraz [32] applied AHP methodology to help public health policymakers to prioritize and evaluate effective pandemic mitigation strategies. The decision on various strategies to control contagious animal quarantine diseases are also evaluated [33], [34]. Two MCDM methods, namely fuzzy-AHP and fuzzy-VIKOR, are utilized [35] to help multiple stakeholders to prioritize intervention strategies for influenza. An application of the AHP method for the Korean immunization program was also presented [36]. Aenishaenslin et al. [37] implemented PROMETHEE to assess various prevention and control strategies for Lyme disease in Quebec city of Canada. Lopez and Gunasekaran [38] have applied the fuzzy logic-based VIKOR method for evaluating H1N1 Influenza vaccination strategies in Vellore city of India. Pooripussarakul et al. [39] implemented the best–worst scaling method for vaccine immunization program in Thailand. AHP has been used for risk assessment of infectious diseases in china [40], [41]. Also, there are studies on risk assessment strategies of zoonotic diseases in Japan [42], and India [43] involving multiple stakeholders. Lopez et al. [44] have proposed a fuzzy VIKOR based approach, which presents a selection of alternatives based on people, space, and time for the prevention and safety of dengue fever in India. Another study [45] applied the AHP approach along with geospatial technique to map vector-borne diseases in Kolkata, India.
2.2. Best–worst method
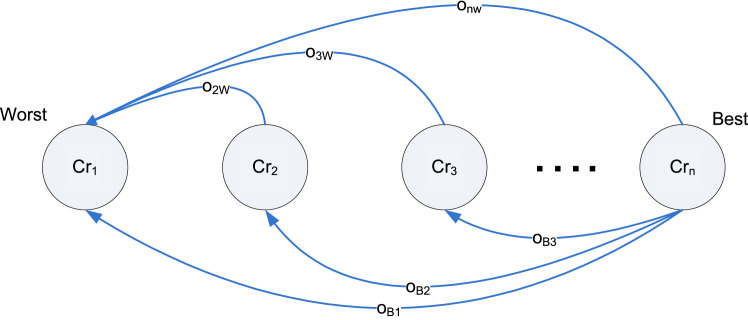
As explained in the previous section, there are many MCDM methods for solving decision-making problems. For different types of decision-making problems, different types of MCDM methods are employed. The task of selecting an appropriate method is difficult. There are different ways of selecting a particular MCDM method. It may be based on information required to input, i.e., data and parameters of the method, based on modeling effort, and outcomes [46], [47]. For our problem, we want a complete ranking and scores of identified factors. Methods such as MACBETH, MAUT, ANP, AHP, and BWM are used for obtaining such outcomes. The required input information for MAUT is in the form of a utility function; for ANP, it is a pairwise comparison on a ratio scale and inter-dependencies; for AHP, it is a pairwise comparison on a ratio scale, for MACBETH, pairwise comparison on an interval scale is required, whereas, for BWM, it is a pairwise comparison on an integer scale from 1–9. The strength of effort input is in decreasing order for MAUT, ANP, MACBETH, AHP, and BWM. AHP is the most famous MCDM approach for determining complete ranking and scores of factors with an average effort input. BWM came in 2015 only, [16]. As compared to AHP, the best–worst method has less effort input due to less number of pairwise comparisons. Also, these pairwise comparisons are based on a 1–9 integer scale, which reduces the complexity of pairwise comparisons. A two-tier approach is adopted for pairwise comparisons. In the first step, the pairwise comparison is made between the best available criterion to other criteria. In the second step, other criteria are compared with the worst available criterion. This comparison is shown in Fig. 1. Compared to AHP, BWM uses less number of comparisons that further reduces efforts in collecting data [16]. Moreover, this method uses only integer numbers for comparisons, which makes it more applicable than other methods like AHP [48].
Fig. 1.
Pairwise comparisons in BWM.
There are many advantages of BWM over AHP. Following are the reasons of preferring BWM over AHP [16], [48], [49], [50], [51].
-
1.
The BWM provides results with better reliability than the AHP method. Both methods use pairwise comparisons to determine weights and ranking of criteria. BWM has only two vectors for Best to others and Others to worst criteria comparisons. This leads to fewer comparisons with respect to matrix-based methods, such as AHP. It contributes to lesser data collection, calculation, and analysis time.
-
2.
In BWM, their are comparisons which is much lesser than comparisons in AHP i.e. .
-
3.
The BWM provides higher reliable results as the comparisons are more consistent than AHP due to the elimination of redundant comparisons.
-
4.
In BWM, the pairwise comparisons are made by integer values on a 1–9 scale. In contrast, AHP uses a scale of fractional numbers, i.e., 1/9–9 scales. This gives an advantage to BWM on AHP by easy analytical evaluation, understanding, and interpretation of comparisons with respect to human perception and cognition.
-
5.
BWM is more data-efficient than the AHP method. In AHP, the solution becomes inconsistent if CR is greater than 0.1. This leads to the need to revise the comparisons to improve CR. Revisiting comparisons in two vectors of BWM is much easier than the comparison matrix of AHP.
Keeping all the advantages of the best–worst method, we have applied this method to solve the problem of prioritization of COVID-19 strategies.
This method has a wide variety of applications such as service selection on the cloud, delivery services, manpower planning, airline operations, etc. [51]. Related contributions are discussed in this section. BWM was proposed by Rezaei in [16] to solve MCDM problems, which is then extended using neutrosophic sets, Markov chain, and fuzzy sets by other authors in multiple domains. In the oil and gas industry, BWM is used to rank various forces working in the supply chain management process. Manufacturing companies applied BWM to evaluate the social sustainability of supply chains [52]. BWM is extended using fuzzy triangular numbers, in which weights of criteria are computed using the Graded Mean Integration Representation (GMIR) method [53]. Gupta and Barua in [54] utilized BWM to investigate the most important driving factor of technological innovation in the context of Micro, Small, and Medium Enterprises (MSME) in India. Gupta et al. in [55] assess the most promising barrier of energy-efficiency in India. In different literature, authors have proposed the hybrid approach of BWM and VIKOR. Here authors aim to assess the best airline based on the attributes of service quality. These attributes are prioritized using BWM, and assessment is done with VIKOR [54]. There are different biomass technologies available, and selecting the best one is always a difficult task. This is determined based on important relative factors using BWM [56]. In other literature, You et al. [57] extends BWM to ELECTRE-III for decision-making problems. With this hybrid approach, the authors attempt to use fewer comparisons with consistent results and elimination and choice translation reality within the intuitionistic environment. Salimi and Rezaei in [58] use BWM to investigate the outcomes of the academic-industry research projects and the objective of the industry behind projects. The procedure is referred to as a measure of efficiency.
Shojaei et al. [59] proposed BWM, VIKOR, and Taguchi loss function integration model to evaluate the airport facilities. Nawaz et al. [60] proposed a cloud broker architecture framework, which helps in selecting cloud services based on the performance of computing resources. First, they applied the Markov chain to determine the pattern of users’ preferences. Then they linked this pattern to the cloud services that are ranked using BWM. With the help of this framework, they compared the consistencies of BWM and AHP methods. Mou et al. [61] applied the BWM method in the intuitionistic fuzzy multiplicative environment to solve the multi-criteria group decision-making problems. BWM is also applied to select the supplier according to the importance of food supply chain content [50]. In other literature, authors investigate the vendors’ capabilities, and interest towards a particular item [49]. Following the above approaches, some improved versions of BWM have been proposed and employed in offering optimal and unique solutions using interval analysis [48], and ranking attributes of MCDM problem with fuzzy information [62].
Some other applications of BWM have been encountered in suggesting the best location for bioethanol plants, finding the best business strategy for a profit of a company, evaluating the performance of a hospital, and determining consumers’ preferences for consumable items [63], [64], [65], [66]. Recently, [67] have applied fuzzy best–worst method in wireless ad-hoc networks problem. To the best of our knowledge, this work is the first effort to analyze challenges while drawing strategies in the event of COVID-19 outbreak using GBWM.
3. Methodology
This section illustrates the methodology to rank the strategies using a multi-criteria decision-making method for a group of experts known as Group Best–Worst Method [15]. This method is applied when we have multiple decision-makers (DMs), and responses are collected from each decision-maker. The advantage of GBWM over BWM is that it considers combined decisions for all DMs.
In BWM [16], initially, the DM determines the best and worst criterion out of the set of criteria. After that, the pairwise comparisons between best criterion and other criteria, between other criteria and worst criterion are required from the DM. These comparisons are based on the linguistic scale given in Table 1. The scale varies from equally important to extremely important, with numeric values from 1 to 9. Based on these comparisons, a mathematical model has been formulated and applied to the collected responses. After that, results in terms of optimal weights of criteria are evaluated.
Table 1.
Linguistic terms and their numeric scale values for pairwise comparisons.
| Scale | Linguistic term | Scale | Linguistic term |
|---|---|---|---|
| 1 | Equally Important (EI) | 6 | Intermediate (IVI) |
| 2 | Intermediate (IEM) | 7 | Very Important (VI) |
| 3 | Moderately Important (MI) | 8 | Intermediate (IVE) |
| 4 | Intermediate (IMI) | 9 | Extremely Important (EI) |
| 5 | Important (I) |
In GBWM, we assume decision-makers and criteria regarding the decision problem. The step by step procedure of the GBWM algorithm are presented as follows:
Step 1. The set of decision criteria i.e. which are needed to be prioritized are identified.
Step 2. Each decision-maker should select the most important (the best) criterion and the least important (the worst) criterion from the set of criteria at step 1.
Step 3. The pairwise comparison of preferences between the best criterion and all other criteria, and a pairwise comparison of all criteria with the worst criterion are performed using the comparison scale given in Table 1. The comparisons are collected from each DM on a scale of 1 to 9, i.e., equally to extremely important.
The Best to Others () and Others to Worst () preferences are shown in Eqs. (1), (2).
| (1) |
| (2) |
Here, and represents the pairwise preference value between best to other criterion and to worst criterion, , respectively.
Step 4. The pairwise comparisons obtained in the linguistic form are converted to numeric form using Table 1. To find the optimal weights () for ranking of criteria, we will utilize the following mathematical programming model of GBWM.
Model 1:
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
Here, and are the weights of best or most important and worst or least important criteria, respectively. Also, is the set of the decision-maker, is the index for criteria, and is the weight of decision-maker . The weight of criterion is represented by . The inconsistency in pairwise comparisons provided by th DM is denoted by . The above model is non-linear in nature, which is difficult to solve. So the linear programming model of model 1 is formulated as model 2. Solving model 2 will provide optimal weight values and inconsistency values for each decision-maker.
Model 2:
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
Step 5. After solving model 2, the optimal values of are utilized to determine the consistency ratio () for each decision-maker and further to calculate group consistency ratio () for group decision making. A comparison is said to be fully consistent when . where is the preference of best criterion over criterion , is the preference of criterion over the worst criterion, and is the preference of best criterion over worst criterion. The reliability of pairwise comparisons has been checked using the Consistency ratio . The formulation for CR of th decision-maker and the group is given by
| (19) |
| (20) |
Where, for th DM, is the optimal value of inconsistency obtained by solving model 2. is the weight given to th decision-maker based on the expertise level. The Consistency Index (CI) is a fixed value given in Table 2 for the value of given by each DM. If is zero, it implies that the solution is fully consistent, and as increases, the consistency decreases.
Table 2.
Consistency index table.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Consistency index (max ) | 0.00 | 0.44 | 1 | 1.63 | 2.30 | 3 | 3.73 | 4.47 | 5.23 |
4. Case study
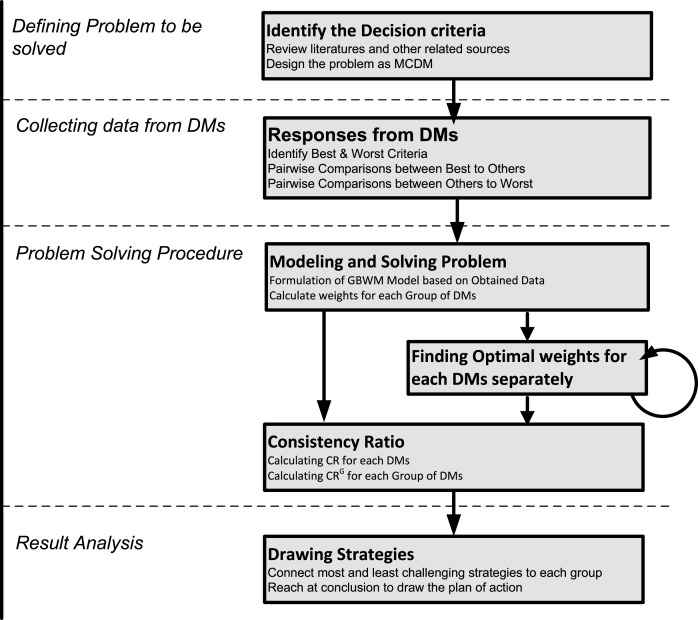
As mentioned before, this paper presents the first study on the prioritization of strategies for the COVID-19 outbreak. The present research work is based on the prioritization of intervention strategies to tackle the COVID-19 outbreak. Decision-making during a pandemic outbreak has numerous challenges. These challenges create pressure on authorities due to high public attention and expectation for speedy and effective actions, uncertain & potential economic impact of a pandemic, and decision complexity due to the involvement of a multitude of criteria and interests of stakeholders. In this regard, the authors discussed the step-by-step procedure of calculating weights and ranking of strategies using the MCDM method, i.e., GBWM, as depicted in Fig. 2. The procedural steps are divided into four parts. It starts from defining the problem, then collecting data from the DMs, mathematical modeling of the problem and solving the models, and finally, result analysis. The explanation of these steps for our case study is presented in this section.
Fig. 2.
Flow chart of Research methodology.
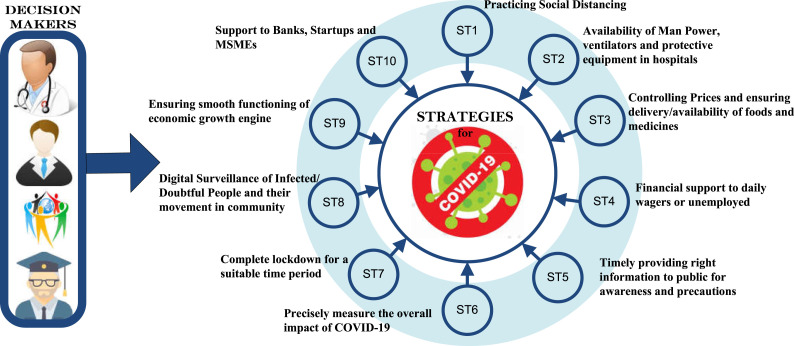
Initially, an in-depth study of the present condition of COVID-19 is done on identifying the criteria, i.e., possible challenges and strategies to handle outbreaks globally. These are selected based on a thorough study of literature [7], [8], [9], [68], [69], [70], [71]. We have identified ten strategies that motivate us to draw a suitable plan for such crises. A brief description and notations of criteria, i.e., intervention strategies, are presented in Fig. 3. The explanation is listed below:
Fig. 3.
Criteria to tackle COVID-19 outbreak.
Identified strategies
According to WHO, as of 3 March 2020, the COVID-19 pandemic has infected about 3.43 million people, and almost 2,44,000 people have lost their lives. The rapid spread of the virus has stressed global health systems and prompted widespread social and economic disruption. Almost all the countries affected by COVID-19 have started some stringent measures nationwide to fight against the spread of COVID-19. These include stopping/limiting international air travel, closing industries, offices along with educational institutions, prohibiting large gatherings at public places, including at religious places. However, it is not easy to replicate the strategies of the United States and Europe into developing countries as these countries cannot provide social security for the poor, unemployed, or the daily wagers who form the majority of the population. Similarly, it is not possible to have large-scale testing due to the limited availability of testing equipment. In such circumstances, the following list includes the major measures being taken by the majority of the countries that constitute the key list of strategies in this study.
1. Practicing Social Distancing (ST1):
The WHO has been recommending social distancing as the most effective measure against the deadly virus for which there is no known vaccination so far. Physical distancing measures and movement restrictions often referred to as “shutdowns” or “lockdowns” can slow COVID-19 transmission by limiting contact between people. Many countries have reported social distancing as the most effective measure to contain further spread of the Corona Virus [72], [73], [74].
2. Availability of manpower, ventilators, and personal protective equipment in hospitals (ST2):
Given the large number of infected people in many developed countries, it is assumed that there may be a large number of infections in India also. In such a scenario, the availability of testing kits and ventilators in a very large number is an important concern. Further, the availability of trained manpower besides doctors is going to be a challenge. Private companies are continuously working on innovative ways to develop vaccines. They should scale up the production and distribution of testing kits, personal protective equipment (PPE), ventilators, medical oxygen and other essential medical equipments [75], [76], [77], [78].
3. Controlling prices and ensuring delivery/availability of foods, medicines, and other essential items (ST3):
Controlling prices of medicines and other essential commodities is an urgent necessity as poor and daily wagers are going to suffer the most if these are not controlled. The Government of India has already applied the Drug Price Control Regulation for all 24 classes of medical devices. Similar measures need to be in place against hoarding or overpricing of groceries and other food items. Further, regular availability of essential items to be ensured so that people do not panic for buying or hoarding daily needed items [79], [80], [81].
4. Financial support to poor, daily wagers, and unemployed (ST4):
The continuous country-wide lockdown has hit the poor and daily wagers the most. Although Central and State governments have announced financial packages, including direct benefit transfer to the bank accounts of such people, there are many challenges to deliver these benefits in a large country like China, India, USA, etc.. Further, these measures need to be enhanced significantly as the uncertainty over job and employment can persist months even after the COVID-19 gets over [82], [83], [84].
5. Timely providing the right information to the public for awareness and precautions (ST5):
There is panic among common people in this time of lockdown. Large volumes of fake news spreading like wildfires through social media are blamed largely for this. While the Hon’ble Prime Minister of India and other State functionaries have repeatedly assured the public about the availability of essential goods in the country, there are still many reports of people hoarding food items in much larger quantities than usual. Further, it is extremely important to inform public about the COVID-19 symptoms and the available challenges for them to approach or report in the event of such symptoms [85], [86], [87], [88].
6. Precisely measuring the overall impact of COVID-19 (ST6):
It is very challenging to measure or make an estimation of the likely health, financial and economic impacts of COVID-19. However, it is very important for Governments to have an idea about the impact in order to set allocation of financial resources and plan to check against unprecedented recessions or devaluation of the currency. A good estimation of virus growth trajectory is vital to come up with sufficient numbers of hospital beds, quarantine facilities, financial packages, etc [89], [90], [91].
7. Complete lockdown for a suitable time period (ST7):
So far, complete lockdown is believed to be the best strategy to enforce social distancing and thus contain the outbreak of COVID-19. However, it is very tricky to decide the required duration of lockdown, as it has got financial and many other implications. Having a large duration may be safer, but it can increase suffering for citizens, particularly the vulnerable sections. Besides, continuous lockdown for a very longer period will severely hit business and industries [92], [93], [94].
8. Digital Surveillance of infected/doubtful People and their movement in the community (ST8):
There is always a danger of the community spread of COVID-19. In such a scenario, it requires contact tracing, that is, identifying and monitoring people who have been in close contact with someone infected. But, in densely populated urban areas, it is a tall order. Digital surveillance may be the best alternative. Tracing past mobile locations through GPS and, if required, tracing the quarantined persons through GPS or surveillance mechanism can be done as a strong measure. However, there are ethical and legal aspects of privacy involved in monitoring movements [95], [96], [97], [98].
9. Ensuring smooth functioning of economy (ST9):
Continuation of economic activities is must to meet the challenges of providing basic amenities to a country having around 1.5 billion population. The financial institutions were already in severe stress due to Non-Performing Assets (NPAs) even before the Corona outbreak. Complete lockdown of industries may significantly hit the GDP rate and can ultimately lead to severe recession [99], [100], [101].
10. Support to banks, startups, and MSMEs (ST10):
Banks and other Non-Banking Financial Company (NBFCs) have landed to industries. The complete lockdown will eventually make it difficult for industries to pay back to banks. Similarly, Medium, Small, and Micro Industries will suffer, and that may result in further NPAs. Besides, MSMEs generate a large number of jobs in the organized and unorganized sectors. The Government should immediately consider to infuse liquidity in to these financial institutions to avoid a 2008 like situation that happened due to failure of multiple financial institutions [102], [103], [104], [105].
Data collection
These ten identified strategies are considered as criteria that are to be prioritized. With these criteria, we prepared a questionnaire to conduct a survey that included simple questions asking the importance of each challenge over the others, based on the requirement of GBWM. Data has been collected from four different groups of decision-makers — health-workers, academicians, social workers, and common citizens. It was an online survey using Google Forms. The questionnaire comprised of ten questions. Some questions were related to the impact of the COVID-19 to create interest in respondents. The remaining questions are based on the pairwise comparisons of strategies, in which decision-makers were asked to choose the most and least challenging area followed by the reasons for their selections. The questions were asked to find the relative importance of each strategy in comparison to other strategies.
Apparently, stakeholders from different groups will have different viewpoints on the importance and usefulness of different strategies. For example, health workers, academicians, social workers, and ordinary citizens will have different opinions on the importance of complete lockdown in the whole country. Their responses to different strategies will vary depending on their understanding, knowledge, and roles in society. The responses of ordinary citizens may differ in the way information is conveyed and treatment or prevention mechanisms are available to them. On the societal aspects of diseases, a group of experts does not include the common citizens. However, in the case of pandemics, all types of stakeholders are affected when measures like lockdown, social distancing, etc., are enforced. Based on this, the four groups of stakeholders (or decision-makers) have been taken into consideration for the relative importance of the strategies. The survey was executed during 1 April-2020 to 15 April-2020. A complete lockdown was imposed in this period, which gives us an opportunity to have a quick response from the stakeholders. A total of 31 responses were received during the data collection period. All the responses were manually checked to identify incomplete entries. For the case study, we have chosen 20 responses (5 for each group) out of the 31 responses. The remaining 11 responses have been dropped from this analysis because of meaningless answers such as most challenging and least challenging areas are the same, assignment of more importance to least challenging area than other challenging areas, which is not possible.
The most challenging area can be found by asking simple questions such as “As an expert, please select the most/least challenging area for authorities to control the outbreak of COVID-19.” When we have ten choices of criteria, as mentioned, user’s choices may differ in terms of context, understanding, and knowledge. Therefore case study leads to group decision making. Once the best and the worst challenging areas are selected, the connections between the two challenges can be determined by asking questions like “rate importance of the th challenging area in comparison with th challenging areas”. While the overall goal of each respondent while selecting challenges is to defeat the COVID-19 outbreak, the following question was asked: “rate importance of Practicing Social Distancing in comparison to Digital Surveillance”. With respect to each group, each challenging area, is compared with all the other challenging areas, and responses were collected in different tables. The importance obtained is used to compute the weights by applying the MCDM models. In this study, BWM is used to determine the relative weights of each criterion. The process to compute weights of the challenging criteria is described in the following subsection.
In Appendix A, pairwise comparisons of strategies by the decision-makers from all the four groups are presented in tabular form. The data has been collected in linguistic form and then transformed in numeric form using the scale of Table 1. As already mentioned, initially, the DM has to select the most and least important criterion. Based on this selection further, the DM has to compare pairwise between the best criterion with other criteria and other criteria with the worst criterion.
Mathematical modeling and solution
The quantitative form of data is used for the mathematical formulation of model 1 and then of model 2, as explained in the methodology section. A total of four models for each group has been formulated. While formulating the problem model for each group of decision-makers, the weight , was considered equal within each group. Here, , and each represent a set of five decision-makers from categories health workers, social workers, academicians, and common citizens, respectively. The mathematical models for all four groups are formulated in Appendix B.
After formulation, the mathematical programming models are solved for the collected data using optimization solver [106], [107] and the optimal weights of all ten strategies for each group of DMs has been obtained. The results are presented in Table 3. For each group of decision-makers, i.e., health workers, social workers, academicians, and others (common citizens), the strategies are ordered with respect to their rank based on their weights. After obtaining the results, the consistency ratio has been determined to check the reliability of the results. CR value for each decision-maker in each group is determined, and then the maximum CR value is considered for . The obtained values of , CR for each DM and for the group () are presented in Table 4. Among groups, the least value of consistency is for Health workers, i.e., 0.1252, and the most consistent value is for the Others group, i.e., 0.04. The value for all groups of decision-makers has been found consistent and acceptable.
Table 3.
Ranking of strategies with respect to the group of stakeholders.
| Health-workers |
Social workers |
Academicians |
Others |
||||
|---|---|---|---|---|---|---|---|
| Criteria | Weight | Criteria | Weight | Criteria | Weight | Criteria | Weight |
| ST2 | 0.1956 | ST7 | 0.1902 | ST1 | 0.1936 | ST1 | 0.3287 |
| ST1 | 0.1325 | ST1 | 0.1605 | ST2 | 0.1291 | ST2 | 0.1077 |
| ST3 | 0.1325 | ST2 | 0.1501 | ST7 | 0.1291 | ST3 | 0.1077 |
| ST7 | 0.1199 | ST3 | 0.1141 | ST3 | 0.1162 | ST7 | 0.1077 |
| ST4 | 0.0736 | ST4 | 0.0667 | ST6 | 0.0807 | ST8 | 0.0769 |
| ST5 | 0.0736 | ST5 | 0.0667 | ST4 | 0.0717 | ST4 | 0.0769 |
| ST6 | 0.0736 | ST6 | 0.0713 | ST5 | 0.0717 | ST5 | 0.0598 |
| ST8 | 0.0666 | ST8 | 0.0634 | ST8 | 0.0717 | ST6 | 0.0598 |
| ST10 | 0.0666 | ST10 | 0.0634 | ST9 | 0.0717 | ST9 | 0.0397 |
| ST9 | 0.0652 | ST9 | 0.0535 | ST10 | 0.0645 | ST10 | 0.0353 |
Table 4.
Group consistency ratio ()
| Group | CR = /CI | |
|---|---|---|
| Health-workers () | (0.4670/5.23, 0.4670/5.23, 0.4670/4.47, 0.4670/5.23, 0.4670/3.73) | 0.1252 |
| Academicians () | (0.4517/5.23, 0.4517/5.23, 0.4517/4.47, 0.4517/5.23, 0.4517/5.23) | 0.1010 |
| Social Workers () | (0.4101/5.23, 0.4101/5.23, 0.4101/4.47, 0.4101/5.23, 0.4101/5.23) | 0.0917 |
| Others () | (0.2096/5.23, 0.2096/5.23, 0.2096/5.23, 0.2096/5.23, 0.2096/5.23) | 0.0400 |
5. Results and discussion
MCDM is used to prioritize strategies while making complex decisions. It helps to evaluate different choices based on priorities of criteria determined by different groups of decision-makers. This work identified and prioritized multiple strategies for Governments to apply in order to contain the COVID-19 outbreak. As mentioned earlier, it is very difficult to take an appropriate decision during such pandemics because any such decision will directly or indirectly impact the whole population of a country. In India, the outbreak of the COVID-19 can be more destructive because of high population density. The nature of the disease being able to spread in close contact may easily affect a larger population. Recently, the WHO has recommended “Test, Test, and Test”. But, timely diagnosis of a large sample of the population is not possible since the medical resources are less in comparison to the requirement. In order to provide enough isolation wards for the increasing number of COVID-19 patients, several buildings, including hotels, schools, banquet halls, and train compartments, are being readied as temporary quarantine and treatment facilities.
For the case study presented in this paper, we identified four different groups of respondents and determined their priorities among different decision choices based on pairwise comparisons. Their responses show that the preferences of different DM groups are different. For each group, the top four criteria are Availability, Distancing, Controlling, and lockdown. The health-workers, social-workers, academicians, and other groups have combinedly given 56%, 61%, 54%, and 62% of weights to these four criteria, respectively.
From Table 3, it can be concluded that according to the group health-workers, “availability of medical professionals, ventilators and PPE”should be the most important measure against the COVID-19 outbreak. They believe that the readiness of hospitals and health centers is of utmost importance to deal with infected patients. From this, it is clear that the breakdown of the health system during such a pandemic will surely put an unimaginable loss to human lives. The second and third important strategies prioritized by this group are the “social distancing”, and “controlling prices and availability of daily needs”. The second and third strategies have equal weights. Ignoring social distancing will raise the number of infected cases and may collapse the whole system. However, if daily needed essential items are not sufficiently available, people may throng markets and shops, violating social distancing. Therefore, these two criteria are very much related to each other. Without social distancing or non-availability of basic commodities, the situation may worsen.
For Social workers, complete lockdown is the topmost strategy, and social distancing is the second important one. This may be because they believe without a lockdown, social distancing is not possible to implement. The lack of awareness of a large section of the population about this pandemic, its relation with sanitation and hygiene, as well as its symptoms, precautions, and cure, may directly impact the effectiveness of distancing. Therefore, a forcefully imposed total lockdown can help to keep people within their homes and may stop the rapid spread of the virus. For them, “availability of medical professionals, ventilators, and PPE” is the third important criteria.
For academicians and others, social distancing and availability are the top two priorities. They, too, believe that social distancing is key to break the chain of virus spread. For the group academicians, complete lockdown is the third important criterion, while for the other group, controlling prices is the third important criterion.
Business and economy are the two least important criteria chosen by all the four groups. That means people are least concerned about the functioning of business and economic activities in this pandemic time. But once the spread of disease comes under control, there would be a strong requirement of kick-starting the functioning of businesses and the economy. Partial or graded opening of lockdown will help the economy to sustain to some extent.
Global weights of strategies and sensitivity analysis
In Table 3, the weights obtained are local weights with respect to pairwise comparisons of each group of decision makers. However, in order to suggest an effective strategy, we need to determine the combined or global weights of all the strategies. That means, we need to consider the preferences of all groups together. Also, each group may have different weightage in combined decision making. This will effect the global weights of strategies. For this, a new mathematical model based on GBWM is formulated as follows:
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
| (28) |
| (29) |
Here, and are the corresponding weights assigned to each group of decision-makers i.e. health workers (), social workers (), academicians (), and others (), respectively. The sum of all weights, . The complete set of DMs is denoted by D. A sensitivity analysis for ten sets of and has been done to determine global weight () and ranking of strategies. The groups of DMs have different weightage because of their understanding and knowledge of the COVID-19 outbreak. The global weight of strategies are determined based on multiple weight set (WS) i.e. (, , , ). An analysis has been done to see the variation in global weights of strategies due to change in WS values. A total of ten WS values are considered and presented in Table 5 with their respective notations.
Table 5.
Weight set (WS) values of (, , , )
| WS | (, , , ) | WS | (, , , ) |
|---|---|---|---|
| WS1 | (0.1, 0.5, 0.2, 0.2) | WS6 | (0.5, 0.3, 0.1, 0.1) |
| WS2 | (0.2, 0.4, 0.2, 0.2) | WS7 | (0.5, 0.3, 0.15, 0.05) |
| WS3 | (0.3, 0.2, 0.3, 0.2) | WS8 | (0.6, 0.2, 0.1, 0.1) |
| WS4 | (0.3, 0.3, 0.2, 0.2) | WS9 | (0.7, 0.2, 0.05, 0.05) |
| WS5 | (0.4, 0.3, 0.2, 0.1) | WS10 | (0.8, 0.1, 0.05, 0.05) |
The global weights of all the ten strategies, along with their order of ranking, are presented in Table 6. The global weight of strategies for weight sets WS6, WS7, WS8, WS9, and WS10 was found to be the same. In these weight sets, more than 50% weightage, i.e., , is given to the health workers. After health workers, the second-highest weight, i.e., , is given to the social workers. For these WS values, we have seen that the global weights of strategies are equal to the local weights of strategies that are obtained for the group of health workers. The four most important strategies are ST2 followed by ST1, ST3, and ST7, respectively. The least important strategy is ST9.
Table 6.
Global ranking of strategies for weight set (, , , ).
| WS1 |
WS2 |
WS3 |
WS4 |
WS5 |
|||||
|---|---|---|---|---|---|---|---|---|---|
| Criteria | Weight | Criteria | Weight | Criteria | Weight | Criteria | Weight | Criteria | Weight |
| ST7 | 0.1902 | ST7 | 0.1902 | ST1 | 0.1363 | ST2 | 0.1640 | ST2 | 0.1890 |
| ST1 | 0.1604 | ST1 | 0.1604 | ST2 | 0.1363 | ST1 | 0.1375 | ST1 | 0.1329 |
| ST2 | 0.1500 | ST2 | 0.1500 | ST3 | 0.1363 | ST7 | 0.1323 | ST3 | 0.1329 |
| ST3 | 0.1141 | ST3 | 0.1141 | ST7 | 0.1363 | ST3 | 0.1312 | ST7 | 0.1217 |
| ST6 | 0.0713 | ST6 | 0.0713 | ST4 | 0.0757 | ST6 | 0.0764 | ST4 | 0.0738 |
| ST4 | 0.0667 | ST4 | 0.0667 | ST5 | 0.0757 | ST4 | 0.0729 | ST5 | 0.0738 |
| ST5 | 0.0667 | ST5 | 0.0667 | ST6 | 0.0757 | ST5 | 0.0729 | ST6 | 0.0738 |
| ST8 | 0.0634 | ST8 | 0.0634 | ST8 | 0.0757 | ST8 | 0.0729 | ST8 | 0.0676 |
| ST10 | 0.0634 | ST10 | 0.0634 | ST9 | 0.0757 | ST10 | 0.0729 | ST10 | 0.0676 |
| ST9 | 0.0534 | ST9 | 0.0534 | ST10 | 0.0757 | ST9 | 0.0667 | ST9 | 0.0663 |
| WS6 |
WS7 |
WS8 |
WS9 |
WS10 |
|||||
|---|---|---|---|---|---|---|---|---|---|
| Criteria | Weight | Criteria | Weight | Criteria | Weight | Criteria | Weight | Criteria | Weight |
| ST2 | 0.1956 | ST2 | 0.1956 | ST2 | 0.1956 | ST2 | 0.1956 | ST2 | 0.1956 |
| ST1 | 0.1325 | ST1 | 0.1325 | ST1 | 0.1325 | ST1 | 0.1325 | ST1 | 0.1325 |
| ST3 | 0.1325 | ST3 | 0.1325 | ST3 | 0.1325 | ST3 | 0.1325 | ST3 | 0.1325 |
| ST7 | 0.1199 | ST7 | 0.1199 | ST7 | 0.1199 | ST7 | 0.1199 | ST7 | 0.1199 |
| ST4 | 0.0736 | ST4 | 0.0736 | ST4 | 0.0736 | ST4 | 0.0736 | ST4 | 0.0736 |
| ST5 | 0.0736 | ST5 | 0.0736 | ST5 | 0.0736 | ST5 | 0.0736 | ST5 | 0.0736 |
| ST6 | 0.0736 | ST6 | 0.0736 | ST6 | 0.0736 | ST6 | 0.0736 | ST6 | 0.0736 |
| ST8 | 0.0666 | ST8 | 0.0666 | ST8 | 0.0666 | ST8 | 0.0666 | ST8 | 0.0666 |
| ST10 | 0.0666 | ST10 | 0.0666 | ST10 | 0.0666 | ST10 | 0.0666 | ST10 | 0.0666 |
| ST9 | 0.0652 | ST9 | 0.0652 | ST9 | 0.0652 | ST9 | 0.0652 | ST9 | 0.0652 |
The global weights of strategies obtained for WS1 and WS2 are also the same and equal. In these two, the highest weightage is given to social workers, i.e., . The weightage to academicians () and others () is considered to have an equals weightage of 0.2. Their global weights are similar but not exactly the same as local weights. We noticed that there is a change of ranking for strategies 4, 5, and 6. ST6 is the fifth important strategy followed by ST4 and ST5, whereas, in local weights, ST4 is the fifth important strategy followed by ST5 and ST6. The last three least important strategies and the first four most important strategies obtained are the same as the local ranking of strategies.
For WS3 i.e. (0.3, 0.2, 0.3, 0.2), we got equal weight of 0.1353 for top four strategies i.e. ST1, ST2, ST3 and ST7. Similarly, we got an equal weight of 0.0757 for the remaining six strategies. The most important global strategy is ST1, and the least important global strategy is ST10. For WS4 and WS5, ST2 is the most important strategy followed by ST1. The least important strategy is ST9.
For all WS values, It has been found that ST1, ST2, ST3, and ST4 are the first four important strategies for the COVID-19 outbreak. The last three important strategies are ST8, ST10, and ST9. The variation in weights among the groups, i.e. (, , , ) impacts the change in global weights and ranking of criteria. The global weights have shown a variation when less weightage is given to health workers. However, there is no change in global weights for WS values, where more than 0.5 weightage is given to health workers.
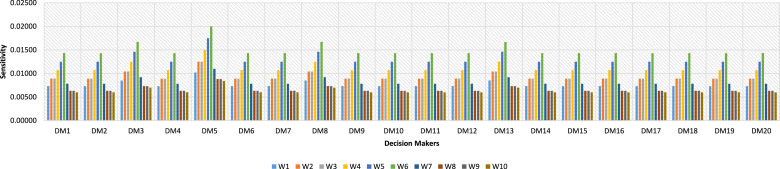
To check the reliability of global weights, the consistency ratio for each decision-maker using Eq. (19) is determined for all WS values and presented in Table 7. It has been found that these ratios are highly consistent and acceptable. This indicates good reliability of global weights. The sensitivity of CR values with respect to each DM is presented in Fig. 4. It can be seen that for all DMs, the CR value is highest for WS6, whereas it is least for WS10. The global CR values obtained by Eq. (20) is also presented in Table 8. The for all WS values are highly consistent and better than the of Health workers, social workers, academicians, and common citizens presented in Table 4. It shows that the consistency is higher in the case of combined decisions of all groups. The is maximum for WS10 and minimum for WS2, WS3 & WS4.
Table 7.
CR values for weight set (, , , ).
| DMs | (, , , ) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| WS1 | WS2 | WS3 | WS4 | WS5 | WS6 | WS7 | WS8 | WS9 | WS10 | |
| 1 | 0.0078 | 0.0063 | 0.0063 | 0.006 | 0.00730 | 0.0089 | 0.0089 | 0.0107 | 0.0125 | 0.0143 |
| 2 | 0.0078 | 0.0063 | 0.0063 | 0.006 | 0.00730 | 0.0089 | 0.0089 | 0.0107 | 0.0125 | 0.0143 |
| 3 | 0.0092 | 0.0073 | 0.0073 | 0.007 | 0.00850 | 0.0104 | 0.0104 | 0.0125 | 0.0146 | 0.0167 |
| 4 | 0.0078 | 0.0063 | 0.0063 | 0.006 | 0.00730 | 0.0089 | 0.0089 | 0.0107 | 0.0125 | 0.0143 |
| 5 | 0.011 | 0.0088 | 0.0088 | 0.0084 | 0.01020 | 0.0125 | 0.0125 | 0.015 | 0.0175 | 0.02 |
| 6 | 0.0078 | 0.0063 | 0.0063 | 0.006 | 0.00730 | 0.0089 | 0.0089 | 0.0107 | 0.0125 | 0.0143 |
| 7 | 0.0078 | 0.0063 | 0.0063 | 0.006 | 0.00730 | 0.0089 | 0.0089 | 0.0107 | 0.0125 | 0.0143 |
| 8 | 0.0092 | 0.0073 | 0.0073 | 0.007 | 0.00850 | 0.0104 | 0.0104 | 0.0125 | 0.0146 | 0.0167 |
| 9 | 0.0078 | 0.0063 | 0.0063 | 0.006 | 0.00730 | 0.0089 | 0.0089 | 0.0107 | 0.0125 | 0.0143 |
| 10 | 0.0078 | 0.0063 | 0.0063 | 0.006 | 0.00730 | 0.0089 | 0.0089 | 0.0107 | 0.0125 | 0.0143 |
| 11 | 0.0078 | 0.0063 | 0.0063 | 0.006 | 0.00730 | 0.0089 | 0.0089 | 0.0107 | 0.0125 | 0.0143 |
| 12 | 0.0078 | 0.0063 | 0.0063 | 0.006 | 0.00730 | 0.0089 | 0.0089 | 0.0107 | 0.0125 | 0.0143 |
| 13 | 0.0092 | 0.0073 | 0.0073 | 0.007 | 0.00850 | 0.0104 | 0.0104 | 0.0125 | 0.0146 | 0.0167 |
| 14 | 0.0078 | 0.0063 | 0.0063 | 0.006 | 0.00730 | 0.0089 | 0.0089 | 0.0107 | 0.0125 | 0.0143 |
| 15 | 0.0078 | 0.0063 | 0.0063 | 0.006 | 0.00730 | 0.0089 | 0.0089 | 0.0107 | 0.0125 | 0.0143 |
| 16 | 0.0078 | 0.0063 | 0.0063 | 0.006 | 0.00730 | 0.0089 | 0.0089 | 0.0107 | 0.0125 | 0.0143 |
| 17 | 0.0078 | 0.0063 | 0.0063 | 0.006 | 0.00730 | 0.0089 | 0.0089 | 0.0107 | 0.0125 | 0.0143 |
| 18 | 0.0078 | 0.0063 | 0.0063 | 0.006 | 0.00730 | 0.0089 | 0.0089 | 0.0107 | 0.0125 | 0.0143 |
| 19 | 0.0078 | 0.0063 | 0.0063 | 0.006 | 0.00730 | 0.0089 | 0.0089 | 0.0107 | 0.0125 | 0.0143 |
| 20 | 0.0078 | 0.0063 | 0.0063 | 0.006 | 0.00730 | 0.0089 | 0.0089 | 0.0107 | 0.0125 | 0.0143 |
Fig. 4.
Sensitivity of each decision maker with respect to tuned weights.
Table 8.
Group CR values for weight set (, , , ).
| (, , , ) |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| WS1 | WS2 | WS3 | WS4 | WS5 | WS6 | WS7 | WS8 | WS9 | WS10 | |
| 0.011 | 0.0088 | 0.0088 | 0.0088 | 0.01020 | 0.0125 | 0.0125 | 0.015 | 0.0175 | 0.02 | |
6. Conclusion, limitation and future direction
The aim of this study is to identify and prioritize the most important criteria, i.e., intervention strategy for handling the COVID-19 outbreak. We have identified those criteria which are logical and followed worldwide to tackle the COVID-19 outbreak. To prioritize the criteria, we created an online questionnaire based on the methodology to collect the preferences of DMs. We have evaluated a set of ten criteria, ranked by twenty DMs belonging to four different groups. Due to conflicting criteria, selecting the best criteria is a complex MCDM problem.
This paper shows a potential application of an MCDM method known as the GBWM to prioritize criteria while dealing with the novel coronavirus (COVID-19) outbreak in consultation with different stakeholders. GBWM approach can accurately handle the qualitative opinions of stakeholders and help to make an informative decision. The method focuses on the ranking of criteria to control the COVID-19 outbreak according to the preferences of health workers, social workers, academicians, and ordinary citizens. The criteria are scored and ranked based on their relative importance. GBWM method considers less pairwise comparisons and provides more reliable results. It gives freedom to analyze results based on the expertise level of each decision-maker.
The process followed in this work supports transparent decision-making and consists of elicitation and evaluation. Elicitation comprises of identification of criteria, i.e., intervention strategies and choosing the MCDM method based on which the criteria are to be evaluated. In the evaluation process, the local and global weights of criteria are evaluated. A sensitivity analysis for ten different WS values of groups has been done. Results in terms of global weights and rank of criteria are evaluated and analyzed for each set of WS, i.e. (, , , ).
The local weights show that “Availability of manpower, ventilators & personal protective equipments in hospitals” and “Complete lockdown for a suitable time period” are the most important criteria for the group of health workers and social workers, respectively. Whereas “Ensuring smooth functioning of economy” is the least important criteria for these groups. For academicians and common citizens, “practicing social distancing” is the most important criteria, while “supports banks, startups, and MSMEs” is the least important criteria. It has been seen that the ranking of global weights keeps changing as per WS values. It shows that the global weights of criteria will be similar to local weights of health workers if is greater or equal to 0.5. The reason may be because health workers are the front-line force to tackle COVID-19 patients. Their safety and availability is the foremost thing. The result obtained could help the decision-makers while drawing intervention strategies against the COVID-19 outbreak. The present study could support complex decision-making with conflicting interests of stakeholders. It could help to choose the strategy considering individual and combined interests of stakeholders.
The present study, however, has some limitations and points to some future directions as well. We have considered a sample of only twenty decision-makers from four different groups, considering five DM from each group. Also, we have not considered decision-makers from categories such as administrators, ministers, or government representatives, who play various key roles in decision making and effective implementations of those decisions in any country. In the future, the sample size and expertise level of decision-makers can be increased for further study. In this study, we have prioritized a set of ten strategies. As of now, the COVID-19 disease and its impact are less known to the world, and everyone is struggling to devise effective strategies. So the number of strategies can be further added or removed in the future with respect to the development and understanding of the COVID-19 disease. In future, this work can be further extended by applying other MCDM methods. Further extension can be done by incorporating uncertainty in the form of fuzzy, hesitant fuzzy, intuitionistic fuzzy, neutrosophic fuzzy, or probabilistic information. A comparison with this work may provide more insight.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The author of this paper would like to thank all the experts whose responses in the survey made the results of this paper possible. The authors are thankful to the editor and reviewers for their suggestions to improve the manuscript.
Compliance with ethical standards
Informed consent
Informed consent has been obtained from all individual participants included in the study.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Footnotes
Supplementary material related to this article can be found online at https://doi.org/10.1016/j.asoc.2021.107642.
Appendix A. Supplementary data
The following is the Supplementary material related to this article.
Appendix A provides the tables of responses collected from the experts. Appendix B provides the mathematical models of BWM formulated for all four stakeholders. Appendix C provides the Questionnaire for data collection.
References
- 1.van der Hoek L., Pyrc K., Jebbink M.F., Vermeulen-Oost W., Berkhout R.J., Wolthers K.C., Wertheim-van Dillen P.M., Kaandorp J., Spaargaren J., Berkhout B. Identification of a new human coronavirus. Nature Med. 2004;10(4):368–373. doi: 10.1038/nm1024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Zhu N., Zhang D., Wang W., Li X., Yang B., Song J., Zhao X., Huang B., Shi W., Lu R., et al. A novel coronavirus from patients with pneumonia in China, 2019. N. Engl. J. Med. 2020 doi: 10.1056/NEJMoa2001017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chen N., Zhou M., Dong X., Qu J., Gong F., Han Y., Qiu Y., Wang J., Liu Y., Wei Y., et al. Epidemiological and clinical characteristics of 99 cases of 2019 novel coronavirus pneumonia in Wuhan, China: A descriptive study. Lancet. 2020;395(10223):507–513. doi: 10.1016/S0140-6736(20)30211-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.2020. Director-general’s remarks at the media briefing on 2019-nCoV on 11 February 2020. https://www.who.int/dg/speeches/detail/who-director-general-s-remarks-at-the-media-briefing-on-2019-ncov-on-11-february-2020. (Accessed 12 February 2020) [Google Scholar]
- 5.Tech. rep., BBC News, 2020. https://www.bbc.com/news/world-52114829. (Accessed 01 April 2020).
- 6.Darko A., Chan A.P.C., Ameyaw E.E., Owusu E.K., Pärn E., Edwards D.J. Review of application of analytic hierarchy process (AHP) in construction. Int. J. Comput. Math. 2019;19(5):436–452. [Google Scholar]
- 7.Tech. rep., The Economic times, 2020. https://economictimes.indiatimes.com/news/international/world-news/best-strategies-against-virus-track-isolate-communicate/articleshow/74687696.cms?from=mdr. Retrieved on 23-04-2020.
- 8.Tech. rep., The Guardian, 2020. https://www.theguardian.com/world/2020/feb/03/more-surveillance-tighter-controls-chinas-coronavirus-crackdown. Retrieved on 23-04-2020.
- 9.Tech. rep., The Guardian, 2020. https://www.theguardian.com/commentisfree/2020/mar/15/uk-covid-19-strategy-questions-unanswered-coronavirus-outbreak. Retrieved on 23-04-2020.
- 10.Tech. rep., Reuters, 2020. https://www.reuters.com/article/us-health-coronavirus-israel/israel-to-use-anti-terror-tech-to-counter-coronavirus-invisible-enemy-iduskbn21113v. (Accessed 01 April 2020).
- 11.Tech. rep., Economic Times, 2020. https://economictimes.indiatimes.com/news/defence/invisible-enemy-israel-to-use-anti-terror-tech-to-track-coronavirus-suspects/articleshow/74635005.cms. (Accessed 01 April 2020).
- 12.Tech. rep., Economic Times, 2020. https://economictimes.indiatimes.com/news/politics-and-nation/india-works-on-3-month-plan-to-stagger-dole/articleshow/74819187.cms. (Accessed 01 April 2020).
- 13.Tech. rep., The Economic times, 2020. https://economictimes.indiatimes.com/news/india-lockdown. Retrieved on 23-04-2020.
- 14.Salajan A., Tsolova S., Ciotti M., Suk J.E. To what extent does evidence support decision making during infectious disease outbreaks? A scoping literature review. Evid. Policy. 2020 [Google Scholar]
- 15.Safarzadeh S., Khansefid S., Rasti-Barzoki M. A group multi-criteria decision-making based on best-worst method. Comput. Ind. Eng. 2018;126:111–121. [Google Scholar]
- 16.Rezaei J. Best-worst multi-criteria decision-making method. Omega. 2015;53:49–57. [Google Scholar]
- 17.Velasquez M., Hester P.T. An analysis of multi-criteria decision making methods. Int. J. Oper. Res. 2013;10(2):56–66. [Google Scholar]
- 18.Zavadskas E.K., Turskis Z. Multiple criteria decision making (MCDM) methods in economics: An overview. Technol. Econ. Dev. Econ. 2011;17(2):397–427. [Google Scholar]
- 19.Kazimieras Zavadskas E., Antucheviciene J., Adeli H., Turskis Z. Hybrid multiple criteria decision making methods: A review of applications in engineering. Sci. Iran. 2016;23(1):1–20. [Google Scholar]
- 20.Kabir G., Sadiq R., Tesfamariam S. A review of multi-criteria decision-making methods for infrastructure management. Struct. Infrastructure Eng. 2014;10(9):1176–1210. [Google Scholar]
- 21.Nobre F.F., Trotta L.T.F., Gomes L.F.A.M. Multi-criteria decision making–an approach to setting priorities in health care. Stat. Med. 1999;18(23):3345–3354. doi: 10.1002/(sici)1097-0258(19991215)18:23<3345::aid-sim321>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
- 22.Behzadian M., Otaghsara S.K., Yazdani M., Ignatius J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012;39(17):13051–13069. [Google Scholar]
- 23.Behzadian M., Kazemzadeh R.B., Albadvi A., Aghdasi M. PROMETHEE: A comprehensive literature review on methodologies and applications. European J. Oper. Res. 2010;200(1):198–215. [Google Scholar]
- 24.Roy B. Readings in Multiple Criteria Decision Aid. Springer; 1990. The outranking approach and the foundations of electre methods; pp. 155–183. [Google Scholar]
- 25.Charnes A., Cooper W.W., Rhodes E. Measuring the efficiency of decision making units. European J. Oper. Res. 1978;2(6):429–444. [Google Scholar]
- 26.Saaty T.L. The Analytic Hierarchy Process. Springer; 1989. Group decision making and the AHP; pp. 59–67. [Google Scholar]
- 27.Shameem M., Khan A.A., Hasan M.G., Akbar M.A. Analytic hierarchy process based prioritisation and taxonomy of success factors for scaling agile methods in global software development. IET Software. 2020;14(4):389–401. [Google Scholar]
- 28.Sipahi S., Timor M. The analytic hierarchy process and analytic network process: An overview of applications. Manage. Decis. 2010 [Google Scholar]
- 29.Costa C.A.B.E., Vansnick J.-C. Advances in Decision Analysis. Springer; 1999. The MACBETH approach: Basic ideas, software, and an application; pp. 131–157. [Google Scholar]
- 30.Dyer J.S. Multiple Criteria Decision Analysis: state of the Art Surveys. Springer; 2005. MAUT—Multiattribute utility theory; pp. 265–292. [Google Scholar]
- 31.Majumder P., Biswas P., Majumder S. Application of new TOPSIS approach to identify the most significant risk factor and continuous monitoring of death of COVID-19. Electron. J. Gen. Med. 2020;17 em234. [Google Scholar]
- 32.Araz O.M. Integrating complex system dynamics of pandemic influenza with a multi-criteria decision making model for evaluating public health strategies. J. Syst. Sci. Syst. Eng. 2013;22(3):319–339. [Google Scholar]
- 33.Mourits M., Oude Lansink A. New Approaches to the Economics of Plant Health. Springer; Heidelberg, Germany: 2007. Multi-criteria decision making to evaluate quarantine disease control strategies; pp. 131–144. [Google Scholar]
- 34.Mourits M., Van Asseldonk M., Huirne R. Multi criteria decision making to evaluate control strategies of contagious animal diseases. Prev. Vet. Med. 2010;96(3–4):201–210. doi: 10.1016/j.prevetmed.2010.06.010. [DOI] [PubMed] [Google Scholar]
- 35.Samanlioglu F. Evaluation of influenza intervention strategies in Turkey with fuzzy AHP-VIKOR. J. Healthc. Eng. 2019;2019 doi: 10.1155/2019/9486070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Shin T., Kim C.-B., Ahn Y.-H., Kim H.-Y., Cha B.H., Uh Y., Lee J.-H., Hyun S.-J., Lee D.-H., Go U.-Y. The comparative evaluation of expanded national immunization policies in Korea using an analytic hierarchy process. Vaccine. 2009;27(5):792–802. doi: 10.1016/j.vaccine.2008.10.075. [DOI] [PubMed] [Google Scholar]
- 37.Aenishaenslin C., Hongoh V., Cissé H.D., Hoen A.G., Samoura K., Michel P., Waaub J.-P., Bélanger D. Multi-criteria decision analysis as an innovative approach to managing zoonoses: Results from a study on lyme disease in Canada. BMC Public Health. 2013;13(1):897. doi: 10.1186/1471-2458-13-897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lopez D., Gunasekaran M. Proceedings of the Fifth International Conference on Fuzzy and Neuro Computing, FANCCO-2015. Springer; 2015. Assessment of vaccination strategies using fuzzy multi-criteria decision making; pp. 195–208. [Google Scholar]
- 39.Pooripussarakul S., Riewpaiboon A., Bishai D., Muangchana C., Tantivess S. What criteria do decision makers in Thailand use to set priorities for vaccine introduction? BMC Public Health. 2016;16(1):684. doi: 10.1186/s12889-016-3382-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tu C., Fang Y., Huang Z., Tan R. Application of the analytic hierarchy process to a risk assessment of emerging infectious diseases in shaoxing city in southern China. Jpn. J. Infect. Dis. 2014;67(6):417–422. doi: 10.7883/yoken.67.417. [DOI] [PubMed] [Google Scholar]
- 41.Li X., Liu T., Lin L., Song T., Du X., Lin H., Xiao J., He J., Liu L., Zhu G., et al. Application of the analytic hierarchy approach to the risk assessment of Zika virus disease transmission in Guangdong province, China. BMC Infect. Dis. 2017;17(1):65. doi: 10.1186/s12879-016-2170-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kadohira M., Hill G., Yoshizaki R., Ota S., Yoshikawa Y. Stakeholder prioritization of zoonoses in Japan with analytic hierarchy process method. Epidemiol. Infect. 2015;143(7):1477–1485. doi: 10.1017/S0950268814002246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Yasobant S., Saxena D., Bruchhausen W., Memon F.Z., Falkenberg T. Multi-sectoral prioritization of zoonotic diseases: One health perspective from ahmedabad, India. PLoS One. 2019;14(7) doi: 10.1371/journal.pone.0220152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lopez D., Manogaran G., Varatharajan R., Abbas K.M. An intelligent decision support system to prevent and control of dengue. J. Ambient Intell. Humaniz. Comput. 2018:1–17. [Google Scholar]
- 45.Ali S.A., Ahmad A. Spatial susceptibility analysis of vector-borne diseases in KMC using geospatial technique and MCDM approach. Model. Earth Syst. Environ. 2019;5(3):1135–1159. [Google Scholar]
- 46.Guitouni A., Martel J.-M., Vincke P., North P. A framework to choose a discrete multicriterion aggregation procedure. Def. Res. Establ. Valcatier. 1998 [Google Scholar]
- 47.Ishizaka A., Nemery P. John Wiley & Sons; 2013. Multi-Criteria Decision Analysis: methods and Software. [Google Scholar]
- 48.Rezaei J. Best-worst multi-criteria decision-making method: Some properties and a linear model. Omega. 2016;64:126–130. [Google Scholar]
- 49.Rezaei J., Wang J., Tavasszy L. Linking supplier development to supplier segmentation using best worst method. Expert Syst. Appl. 2015;42(23):9152–9164. [Google Scholar]
- 50.Rezaei J., Nispeling T., Sarkis J., Tavasszy L. A supplier selection life cycle approach integrating traditional and environmental criteria using the best worst method. J. Cleaner Prod. 2016;135:577–588. [Google Scholar]
- 51.Mi X., Tang M., Liao H., Shen W., Lev B. The state-of-the-art survey on integrations and applications of the best worst method in decision making: Why, what, what for and what’s next? Omega. 2019;87:205–225. [Google Scholar]
- 52.Ahmad W.N.K.W., Rezaei J., Sadaghiani S., Tavasszy L.A. Evaluation of the external forces affecting the sustainability of oil and gas supply chain using best worst method. J. Clean. Prod. 2017;153:242–252. [Google Scholar]
- 53.Guo S., Zhao H. Fuzzy best-worst multi-criteria decision-making method and its applications. Knowl.-Based Syst. 2017;121:23–31. [Google Scholar]
- 54.Gupta H., Barua M.K. Identifying enablers of technological innovation for Indian MSMEs using best–worst multi criteria decision making method. Technol. Forecast. Soc. Change. 2016;107:69–79. [Google Scholar]
- 55.Gupta P., Anand S., Gupta H. Developing a roadmap to overcome barriers to energy efficiency in buildings using best worst method. Sustainable Cities Soc. 2017;31:244–259. [Google Scholar]
- 56.van de Kaa G., Kamp L., Rezaei J. Selection of biomass thermochemical conversion technology in the netherlands: A best worst method approach. J. Cleaner Prod. 2017;166:32–39. [Google Scholar]
- 57.You X., Chen T., Yang Q. Approach to multi-criteria group decision-making problems based on the best-worst-method and electre method. Symmetry. 2016;8(9):95. [Google Scholar]
- 58.Salimi N., Rezaei J. Measuring efficiency of university-industry Ph. D. projects using best worst method. Scientometrics. 2016;109(3):1911–1938. doi: 10.1007/s11192-016-2121-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Shojaei P., Haeri S.A.S., Mohammadi S. Airports evaluation and ranking model using taguchi loss function, best-worst method and VIKOR technique. J. Air Transp. Manag. 2018;68:4–13. [Google Scholar]
- 60.Nawaz F., Asadabadi M.R., Janjua N.K., Hussain O.K., Chang E., Saberi M. An MCDM method for cloud service selection using a Markov chain and the best-worst method. Knowl.-Based Syst. 2018;159:120–131. [Google Scholar]
- 61.Mou Q., Xu Z., Liao H. An intuitionistic fuzzy multiplicative best-worst method for multi-criteria group decision making. Inform. Sci. 2016;374:224–239. [Google Scholar]
- 62.Hafezalkotob A., Hafezalkotob A. A novel approach for combination of individual and group decisions based on fuzzy best-worst method. Appl. Soft Comput. 2017;59:316–325. [Google Scholar]
- 63.Kheybari S., Kazemi M., Rezaei J. Bioethanol facility location selection using best-worst method. Appl. Energy. 2019;242:612–623. [Google Scholar]
- 64.Khanmohammadi E., Zandieh M., Tayebi T. Drawing a strategy canvas using the fuzzy best–worst method. Global J. Flex. Syst. Manage. 2019;20(1):57–75. [Google Scholar]
- 65.Liao H., Mi X., Yu Q., Luo L. Hospital performance evaluation by a hesitant fuzzy linguistic best worst method with inconsistency repairing. J. Cleaner Prod. 2019;232:657–671. [Google Scholar]
- 66.Massaglia S., Borra D., Peano C., Sottile F., Merlino V.M. Consumer preference heterogeneity evaluation in fruit and vegetable purchasing decisions using the best–worst approach. Foods. 2019;8(7):266. doi: 10.3390/foods8070266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Ahmad N., Hasan M.G. Self-adaptive query-broadcast in wireless ad-hoc networks using fuzzy best worst method. Wirel. Netw. 2020:1–16. [Google Scholar]
- 68.Tech. rep., Bloomberg Quint, 2020. https://www.bloombergquint.com/coronavirus-outbreak/coronavirus-managing-covid-19-lessons-from-keralas-nipah-outbreak. Retrieved on 23-04-2020.
- 69.Tech. rep., GatesNotes, 2020. https://www.gatesnotes.com/health/how-to-respond-to-covid-19. Retrieved on 23-04-2020.
- 70.Tech. rep., The Caravan, 2020. https://caravanmagazine.in/health/covid-19-coronavirus-kerala-vijayan-shailaja-healthcare-system. Retrieved on 23-04-2020.
- 71.Anderson R.M., Heesterbeek H., Klinkenberg D., Hollingsworth T.D. How will country-based mitigation measures influence the course of the COVID-19 epidemic? Lancet. 2020;395(10228):931–934. doi: 10.1016/S0140-6736(20)30567-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Thunström L., Newbold S.C., Finnoff D., Ashworth M., Shogren J.F. The benefits and costs of using social distancing to flatten the curve for COVID-19. J. Benefit-Cost Anal. 2020;11(2):179–195. [Google Scholar]
- 73.Venkatesh A., Edirappuli S. Social distancing in covid-19: What are the mental health implications? BMJ. 2020;369 doi: 10.1136/bmj.m1379. [DOI] [PubMed] [Google Scholar]
- 74.Qian M., Jiang J. COVID-19 and social distancing. J. Public Health. 2020:1–3. doi: 10.1007/s10389-020-01321-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Ranney M.L., Griffeth V., Jha A.K. Critical supply shortages—the need for ventilators and personal protective equipment during the covid-19 pandemic. N. Engl. J. Med. 2020;382(18) doi: 10.1056/NEJMp2006141. [DOI] [PubMed] [Google Scholar]
- 76.Stewart C.L., Thornblade L.W., Diamond D.J., Fong Y., Melstrom L.G. Personal protective equipment and COVID-19: A review for surgeons. Ann. Surg. 2020;272(2) doi: 10.1097/SLA.0000000000003991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Cohen J., van der Meulen Rodgers Y. Contributing factors to personal protective equipment shortages during the COVID-19 pandemic. Prev. Med. 2020 doi: 10.1016/j.ypmed.2020.106263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Pecchia L., Piaggio D., Maccaro A., Formisano C., Iadanza E. The inadequacy of regulatory frameworks in time of crisis and in low-resource settings: Personal protective equipment and COVID-19. Health Technol. 2020;10(6):1375–1383. doi: 10.1007/s12553-020-00429-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Arafat S.Y., Kar S.K., Kabir R. Possible controlling measures of panic buying during COVID-19. Int. J. Mental Health Addict. 2020:1–3. doi: 10.1007/s11469-020-00320-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Prentice C., Chen J., Stantic B. Timed intervention in COVID-19 and panic buying. J. Retail. Cons. Serv. 2020;57 [Google Scholar]
- 81.Singh S., Kumar R., Panchal R., Tiwari M.K. Impact of COVID-19 on logistics systems and disruptions in food supply chain. Int. J. Prod. Res. 2020:1–16. [Google Scholar]
- 82.Buheji M., da Costa Cunha K., Beka G., Mavric B., De Souza Y., da Costa Silva S.S., Hanafi M., Yein T.C. The extent of covid-19 pandemic socio-economic impact on global poverty. A global integrative multidisciplinary review. Am. J. Econ. 2020;10(4):213–224. [Google Scholar]
- 83.Ozili P.K. Covid-19 pandemic and economic crisis: The Nigerian experience and structural causes. J. Econ. Adm. Sci. 2020 [Google Scholar]
- 84.Blustein D.L., Duffy R., Ferreira J.A., Cohen-Scali V., Cinamon R.G., Allan B.A. Elsevier; 2020. Unemployment in the time of COVID-19: A research agenda. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Ros M., Neuwirth L.S. Increasing global awareness of timely COVID-19 healthcare guidelines through FPV training tutorials: Portable public health crises teaching method. Nurse Educ. Today. 2020;91 doi: 10.1016/j.nedt.2020.104479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Que J., Yuan K., Gong Y., Meng S., Bao Y., Lu L. Raising awareness of suicide prevention during the COVID-19 pandemic. Neuropsychopharmacol. Rep. 2020;40(4):392–395. doi: 10.1002/npr2.12141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Organization W.H., et al. World Health Organization; 2020. Coronavirus disease 2019 (COVID-19):: Situation report, 86. [Google Scholar]
- 88.Wolf M.S., Serper M., Opsasnick L., O’Conor R.M., Curtis L., Benavente J.Y., Wismer G., Batio S., Eifler M., Zheng P., et al. Awareness, attitudes, and actions related to COVID-19 among adults with chronic conditions at the onset of the US outbreak: A cross-sectional survey. Ann. Intern. Med. 2020;173(2):100–109. doi: 10.7326/M20-1239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Loomba S., de Figueiredo A., Piatek S.J., de Graaf K., Larson H.J. Measuring the impact of COVID-19 vaccine misinformation on vaccination intent in the UK and USA. Nature Hum. Behaviour. 2021:1–12. doi: 10.1038/s41562-021-01056-1. [DOI] [PubMed] [Google Scholar]
- 90.Jarvis C.I., Van Zandvoort K., Gimma A., Prem K., Klepac P., Rubin G.J., Edmunds W.J. Quantifying the impact of physical distance measures on the transmission of COVID-19 in the UK. BMC Med. 2020;18:1–10. doi: 10.1186/s12916-020-01597-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Herrero C., Villar A. A synthetic indicator on the impact of COVID-19 on the community’s health. PLoS One. 2020;15(9) doi: 10.1371/journal.pone.0238970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Nilima N., Kaushik S., Tiwary B., Pandey P.K. Psycho-social factors associated with the nationwide lockdown in India during COVID-19 pandemic. Clin. Epidemiol. Global Health. 2020;9:47–52. doi: 10.1016/j.cegh.2020.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Dwivedi L.K., Rai B., Shukla A., Dey T., Ram U., Shekhar C., Dhillon P., Yadav S., Unisa S. IIPS; Mumbai: 2020. Assessing the impact of complete lockdown on COVID-19 infections in India and its burden on public health facilities. [Google Scholar]
- 94.Massarotti C., Adriano M., Cagnacci A., Gorlero F., Gustavino C., Vallerino G., Paolucci R., Di Luca M., Anserini P., Ferraiolo A. Asymptomatic SARS-CoV-2 infections in pregnant patients in an Italian city during the complete lockdown. J. Med. Virol. 2021;93(3):1758–1760. doi: 10.1002/jmv.26458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Kumar A., Sharma K., Singh H., Naugriya S.G., Gill S.S., Buyya R. A drone-based networked system and methods for combating coronavirus disease (COVID-19) pandemic. Future Gener. Comput. Syst. 2020;115:1–19. doi: 10.1016/j.future.2020.08.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Kitchin R. Vol. 44. 2020. Using digital technologies to tackle the spread of the coronavirus: Panacea or folly; pp. 1–24. (The Programmable City Working Paper). [Google Scholar]
- 97.Sönmez G., Celik E. ORSAM; 2020. Digital Fight Against Covid-19 and the “New Normal” for Security Institutions. [Google Scholar]
- 98.Chivers W. Resisting digital surveillance reform: The arguments and tactics of communications service providers. Surveill. Soc. 2019;17(3/4):517–532. [Google Scholar]
- 99.Debata B., Patnaik P., Mishra A. COVID-19 pandemic! it’s impact on people, economy, and environment. J. Public Aff. 2020;20(4) [Google Scholar]
- 100.Laborde D., Martin W., Swinnen J., Vos R. COVID-19 risks to global food security. Science. 2020;369(6503):500–502. doi: 10.1126/science.abc4765. [DOI] [PubMed] [Google Scholar]
- 101.Dell’Ariccia G., Mauro P., Spilimbergo A., Zettelmeyer J. Vol. 1. 2020. Economic policies for the COVID-19 war. (IMF Blog). [Google Scholar]
- 102.Utz R., Feyen E., Vazquez Ahued F., Nie O., Moon J. World Bank; 2020. Macro-Financial Implications of the COVID-19 Pandemic. [Google Scholar]
- 103.Arunachalam R.S., Crentsil G. An Online Participative Conference for Central Bankers, Ministries of Finance, Financial Sector Development & Financial Inclusion Professionals, Commercial & Microfinance Bankers, NBFIs, DFIs, MFIs, Consultants, FINTECH & RegTech Companies, Investors, Ins. The Financial Inclusion Advocacy Centre; 2020. Financial inclusion in the era of COVID-19. [Google Scholar]
- 104.Ncube C.N. 2020. The impact of COVID-19 on MSMEs in Developing Countries. [Google Scholar]
- 105.Jones E. Covid-19 and the EU economy: Try again, fail better. Survival. 2020;62(4):81–100. [Google Scholar]
- 106.Server N. 2016. State-of-the-Art Solvers for Numerical Optimization. [Google Scholar]
- 107.Czyzyk J., Mesnier M.P., More J.J. NEOS server. IEEE Comput. Sci. Eng. 1998;5(3):68–75. doi: 10.1109/99.714603. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix A provides the tables of responses collected from the experts. Appendix B provides the mathematical models of BWM formulated for all four stakeholders. Appendix C provides the Questionnaire for data collection.