Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2021 Mar 16;27(23):6936–6944. doi: 10.1002/chem.202004041

Chemical Bonding in Homoleptic Carbonyl Cations [M{Fe(CO)5}2]+ (M=Cu, Ag, Au)

Sudip Pan 1,2, Sai Manoj N V T Gorantla 2, Devaborniny Parasar 3, H V Rasika Dias 3,✉, Gernot Frenking 1,2,✉
PMCID: PMC8252735  PMID: 33534147

Abstract

Syntheses of the copper and gold complexes [Cu{Fe(CO)5}2][SbF6] and [Au{Fe(CO)5}2][HOB{3,5‐(CF3)2C6H3}3] containing the homoleptic carbonyl cations [M{Fe(CO)5}2]+ (M=Cu, Au) are reported. Structural data of the rare, trimetallic Cu2Fe, Ag2Fe and Au2Fe complexes [Cu{Fe(CO)5}2][SbF6], [Ag{Fe(CO)5}2][SbF6] and [Au{Fe(CO)5}2][HOB{3,5‐(CF3)2C6H3}3] are also given. The silver and gold cations [M{Fe(CO)5}2]+ (M=Ag, Au) possess a nearly linear Fe‐M‐Fe’ moiety but the Fe‐Cu‐Fe’ in [Cu{Fe(CO)5}2][SbF6] exhibits a significant bending angle of 147° due to the strong interaction with the [SbF6]− anion. The Fe(CO)5 ligands adopt a distorted square‐pyramidal geometry in the cations [M{Fe(CO)5}2]+, with the basal CO groups inclined towards M. The geometry optimization with DFT methods of the cations [M{Fe(CO)5}2]+ (M=Cu, Ag, Au) gives equilibrium structures with linear Fe‐M‐Fe’ fragments and D 2 symmetry for the copper and silver cations and D 4d symmetry for the gold cation. There is nearly free rotation of the Fe(CO)5 ligands around the Fe‐M‐Fe’ axis. The calculated bond dissociation energies for the loss of both Fe(CO)5 ligands from the cations [M{Fe(CO)5}2]+ show the order M=Au (D e=137.2 kcal mol−1)>Cu (D e=109.0 kcal mol−1)>Ag (D e=92.4 kcal mol−1). The QTAIM analysis shows bond paths and bond critical points for the M−Fe linkage but not between M and the CO ligands. The EDA‐NOCV calculations suggest that the [Fe(CO)5]→M+←[Fe(CO)5] donation is significantly stronger than the [Fe(CO)5]←M+→[Fe(CO)5] backdonation. Inspection of the pairwise orbital interactions identifies four contributions for the charge donation of the Fe(CO)5 ligands into the vacant (n)s and (n)p AOs of M+ and five components for the backdonation from the occupied (n‐1)d AOs of M+ into vacant ligand orbitals.

Keywords: bonding analysis, carbonyl complexes, Dewar–Chatt–Duncanson model, metal–metal bonding

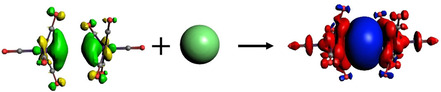
Donation of an electron pair from the HOMO of [Fe(CO)5]2 to the 4s LUMO of Cu+ giving the (+,+) component of the Fe‐Cu‐Fe σ bond in [Cu{Fe(CO)5}2]+. The associated charge flow with the direction red→blue is given by the deformation density.

graphic file with name CHEM-27-6936-g005.jpg

Introduction

Carbonyl complexes may be considered as parent system of transition metal compounds and as prototypical model for the Dewar–Chatt–Duncanson (DCD) [1] description of the chemical bond in metal carbonyls. The DCD model was introduced in 1952 by Dewar [1a] for explaining the platinum–ethylene bond in Zeise's salt [2] [Cl3Pt(C2H4)]− in terms of σ donation [Cl3Pt]−←C2H4 and π backdonation [Cl3Pt]−→C2H4. It was then generalized to other metals M and ligands L by Chatt and Duncanson,[ 1b , 1d ] who showed that the model of dative bonding in combination with the 18‐electron rule suggested by Langmuir in 1921 [3] is a powerful tool to explain the structure and reactivity of transition metal compounds, which carry a variety of ligands that have main‐group atoms bonded to the metal. The general bonding scheme of the DCD model for such complexes is shown in Figure 1. The metal atom M has a vacant σ acceptor orbital and an occupied π donor orbital, which interact with an occupied σ orbital and a vacant π orbital of the ligand L. [4] There are variations of the DCD model with a reversed situation where the metal atom M has an occupied σ orbital and a vacant π orbital whereas the ligand L has vacant σ acceptor orbital and an occupied π donor orbital. [5] Another variant are complexes in which the ligand L is a double donor with occupied σ and π orbitals, which represent a double Lewis base requiring a metal with vacant σ and π orbitals for appropriate orbital interactions. Examples for such ligands are carbones CL2 [6] and the heavier group‐14 tetrylones EL2 (E=Si–Sn), [7] where the ligands L are bonded to a divalent atom C or E in the electronic 1D state with the four valence electrons occupying two lone‐pair orbitals with σ and π symmetry. [8] Complexes with tetrylone ligands are experimentally known [9] and their bonding situation was studied with theoretical methods. [10]

Figure 1.

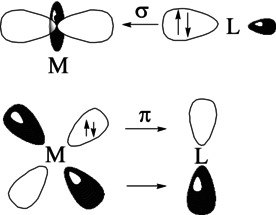
Figure 1

Open in a new tab

Schematic presentation of the orbital interactions between a transition metal M and a ligand L following the DCD model.

However, there is a binding situation that is not directly covered by the standard DCD model. This concerns complexes where the ligand L itself is an electronically saturated transition metal complex, which possess dative bonds between two transition metals. Heterometallic complexes featuring metal–metal bonds including those involving group 8 species have been a key topic for many decades,[ 11 , 12 , 13 ] and have been investigated for their structures, bonding, properties and reactivity (e.g., catalysis, luminescence), [14] as well as due to their relevance in biology. [15] The structures and bonding of heterometallic complexes involving coinage metal (Cu, Ag, Au) ions and Fe(CO)5 have been of particular interest to us for some time. [16] Although Fe(CO)5 was first reported in 1891 [17] and its chemistry with Lewis bases is well‐known, [18] the metal complexes in which this organometallic, 18‐electron complex acting as a Lewis basic ligand L are very rare.[ 12 , 19 ] For example, during late 1920s, Hock and Stuhlmann investigated the chemistry of Fe(CO)5 with several mercury(II) salts and managed to isolate products with mixed metallic compositions. [12] Structurally well‐characterized molecules involving the Fe(CO)5 ligand appeared only recently.[ 14a , 16a , 16b , 19b ] They include a homoleptic [20] silver(I) complex synthesized by Krossing et al. in 2014 as the adduct [Ag{Fe(CO)5}2][Al{OC(CF3)3}4] [19b] and the more recently isolated [Ag{Fe(CO)5}2][B{3,5‐(CF3)2C6H3}4] [16a] with a different counter ion by one of us. These complexes contain a silver cation [Ag{Fe(CO)5}2]+ which features two Fe(CO)5 moieties bonded to a bare Ag+. They are particularly well suited for studying the orbital interactions in molecules where the ligand L (i.e., Fe(CO)5) itself is an electronically saturated complex. The X‐ray structure analysis shows a nearly linear Fe‐Ag‐Fe’ moiety and somewhat bent basal CO ligands of the Fe(CO)5 moieties with eclipsed conformation, which have a distorted square‐pyramidal geometry. Figure 2 shows schematically the structure of the [Ag{Fe(CO)5}2]+ cation. The inspection of the molecular orbitals suggested a multi‐center Ag‐Fe−C bonding scenario, but the extent of the contribution of the individual MOs of the Fe(CO)5 ligands and Ag+ was not addressed.

Figure 2.

Figure 2

Open in a new tab

Schematic view of the structure of [Ag{Fe(CO)5}2]+.

The pairwise orbital interactions of a chemical bond can be identified, and their strength can be estimated with the energy decomposition analysis (EDA) in conjunction with the natural orbitals for chemical valence (NOCV) scheme. The EDA‐NOCV method has been proven to provide detailed insight into the nature of the chemical bond for different classes of molecules, which possess electron‐sharing bonds A–B or dative bonds A→B. It is particularly suited to answer the question about the relevance of the individual orbital interactions of metal‐ligand bonds of complexes of transition metals but also for main‐group adducts. In this work, we report a thorough analysis of the bonding between Ag+ and the Fe(CO)5 ligands in the [Ag{Fe(CO)5}2]+ cation. We also analyze the bonds in copper and gold homologous [M{Fe(CO)5}2]+ (M=Cu, Au). The latter cations have been synthesized for the first time as salt compounds with different anions and structurally characterized by X‐ray analysis. The present work is a theoretical study with supporting experimental data where we report (a) the syntheses and X‐ray structures of [Cu{Fe(CO)5}2]SbF6, [Ag{Fe(CO)5}2][SbF6] and [Au{Fe(CO)5}2][HOB{3,5‐(CF3)2C6H3}3] and (b) a bonding analysis of the cations [M{Fe(CO)5}2]+ (M=Cu, Ag, Au) using a variety of charge‐ and energy decomposition methods.

Results and Discussion

Experimental studies

We have isolated three, highly reactive, and thermally sensitive, hetero‐trimetallic adducts involving Fe(CO)5 and CuI, AgI, and AuI. The silver adduct, [Ag{Fe(CO)5}2][SbF6] is relatively easier to manipulate compared to the copper and gold complexes noted below, but it is still rather reactive and decomposes rapidly at room temperature. The copper complex, [Cu{Fe(CO)5}2][SbF6] was obtained from a reaction between, in situ generated [Cu(C2H4)3][SbF6] [21] with Fe(CO)5 in dichloromethane at −70 °C. The solutions of [Cu{Fe(CO)5}2][SbF6] compound decompose easily upon warming to room temperature. The X‐ray quality crystal of [Cu{Fe(CO)5}2][SbF6] obtained at −20 °C. Solid sample of [Cu{Fe(CO)5}2][SbF6] displays IR bands at 2131, 2084, 2031, 1997 cm−1. For comparison, free Fe(CO)5 displays its IR bands at 2024 and 2000 cm−1 in liquid Xe, [22] while the dicationic, non‐classical [23] [Fe(CO)6][SbF6]2 displays its νCO bands at much higher frequency (2242, 2219, 2205 cm−1). [24]

The X‐ray crystal structure of [Cu{Fe(CO)5}2][SbF6] is depicted in Figure 3. It crystallizes in the P21/c space group with two chemically similar, but crystallographically different molecules of [Cu{Fe(CO)5}2][SbF6] in the asymmetric unit. Notably, despite the smaller size, copper center in [Cu{Fe(CO)5}2][SbF6] adopts a three‐coordinate, distorted trigonal planar geometry. The copper atom is bonded to two Fe(CO)5 moieties and one of the fluorine atoms of the [SbF6]− ion. The Cu−Fe distances of [Cu{Fe(CO)5}2][SbF6] (average 2.465 Å) are smaller than the Ag−Fe distances of [Ag{Fe(CO)5}2][SbF6] (see below) despite having a higher coordination number at Cu (3 vs. 2 in the silver complex). The Fe‐Cu‐Fe angle is significantly larger (≈147°) than the ideal 120° angle of trigonal planar sites. Two cis‐carbonyl groups on each molecule show significant leaning toward copper as evident from Cu‐Fe‐C angles, with smallest values at 68.7(4)° and 69.2(3)° for these molecules in the asymmetric unit. They may be described as semi‐bridging carbonyls, [25] but the related Fe‐C‐O bond angles do not deviate much from linearity. The [Cu{Fe(CO)5}2][SbF6] is the first copper(I)‐Fe(CO)5 complex to our knowledge, and shows that copper(I) can also form adducts with Fe(CO)5. We have observed an analogy between Fe(CO)5 and CO in their interaction with gold or coinage metal ions. [16b] In that regards, it is noteworthy that although three and four‐coordinate copper‐carbonyls are known, [26] there are no structurally characterized, two‐coordinate [Cu(CO)2]+ complexes to our knowledge. In contrast, well‐authenticated, two‐coordinate [Ag(CO)2]+ and [Au(CO)2]+ systems have been reported in the literature. [27]

Figure 3.

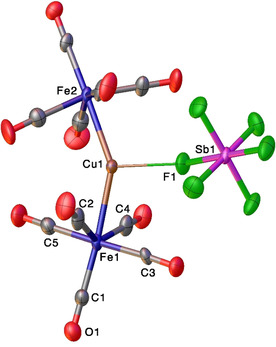
Figure 3

Open in a new tab

Molecular structure of Cu{Fe(CO)5}2FSbF5. Only one of the two chemically similar, but crystallographically different molecules in the asymmetric unit is shown here. Selected bond lengths (Å) and angles (°): Cu1−Fe1 2.4681(17), Cu1−Fe2 2.4577(17), Cu1−F1 2.325(6), Fe1‐Cu1‐Fe2 147.46(7), F1‐Cu1‐Fe1 103.59(17), F1‐Cu1‐Fe2 108.46(17); For the second molecule: Cu2−Fe3 2.4773(17), Cu2−Fe4 2.4581(17), Cu2−F7 2.231(7), Fe3‐Cu2‐Fe4 149.03(7), F7‐Cu2‐Fe3 100.0(2), F7‐Cu2‐Fe4 110.9(2).

The [Ag{Fe(CO)5}2][SbF6] was obtained directly from a reaction between Fe(CO)5 and AgSbF6. It is also challenging to isolate as traces of moisture will afford [(μ‐H2O)Ag‐Fe(CO)5]2[SbF6]2. [16a] The related [Ag{Fe(CO)5}2][B{3,5‐(CF3)2C6H3}4] and [Ag{Fe(CO)5}2][Al{OC(CF3)3}4] are the only other related species in the literature,[ 14a , 19b ] but they involve much larger counter ions. X‐ray crystal structure of [Ag{Fe(CO)5}2][SbF6] is presented considering that such compounds are rare and provide useful information. The X‐ray crystal structure of [Ag{Fe(CO)5}2][SbF6] is illustrated in Figure 4, and it contains discrete [Ag{Fe(CO)5}2]+ cations with a linear and trinuclear Fe‐Ag‐Fe core. The iron centers adopt a distorted octahedral geometry. The silver atom of the Ag{Fe(CO)5}2 moiety sits on an inversion center, with two equal Fe−Ag distances at 2.5893(2) Å. This Ag−Fe distance is similar to that observed in [Ag{Fe(CO)5}2][B{3,5‐(CF3)2C6H3}4] (2.5925(2) Å) and [Ag{Fe(CO)5}2][Al{OC(CF3)3}4] (2.5965(6), 2.5998(7) Å). The carbonyl groups perpendicular to the Fe‐Ag‐Fe axis adopt the familiar eclipsed configuration, as seen in [Ag{Fe(CO)5}2][B{3,5‐(CF3)2C6H3}4] and [Ag{Fe(CO)5}2][Al{OC(CF3)3}4]. They also lean slightly towards the central silver atom, with the largest deviation from ideal 90° at 78.51(8)°.

Figure 4.

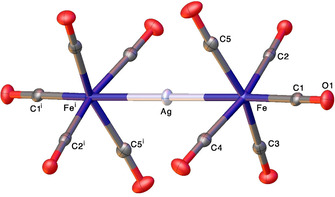
Figure 4

Open in a new tab

Molecular structure of [Ag{Fe(CO)5}2][SbF6]. The [SbF6]− anion has been omitted for clarity. Selected bond lengths (Å) and angles (°): Ag−Fe 2.5893(4), Ag−Fei 2.5893(4), Fe‐Ag‐Fei 180.0. Fe−C1 1.848(3), Fe−C3 1.840(3), Fe−C5 1.830(3), Fe−C4 1.835(3), Fe−C2 1.819(3), C3‐Fe‐Ag 78.51(8), C1‐Fe‐Ag 176.29(8) C5‐Fe‐Ag 80.12(9), C4‐Fe‐Ag 80.70(8), C2‐Fe‐Ag 83.79(8).

The gold analog [Au{Fe(CO)5}2][SbF6] containing the [Au{Fe(CO)5}2]+ cation was very challenging to synthesize due to the instability. Direct synthesis using AuCl, AgSbF6 and Fe(CO)5 in dichloromethane at −70 °C was not successful due to extensive decomposition as evident from the formation of black materials. Decomposition during the synthesis is less severe when in situ generated [Au(C2H4)3][SbF6] [21] was treated with Fe(CO)5. The resulting solid shows IR bands at 2128, 2060 and 2037 cm−1 indicating the possible formation of [Au{Fe(CO)5}2][SbF6]. Despite numerous attempts, this molecule did not produce crystals suitable for X‐ray crystallographic study. We have then explored the use of a larger anion such as [B{3,5‐(CF3)2C6H3}4]−, although there was a risk of “naked” gold cleaving the B−C bond as noted earlier. [28] The reaction of AuCl with Na[B{3,5‐(CF3)2C6H3}4] in the presence of ethylene to generate [Au(C2H4)3]+, followed by the addition of Fe(CO)5 produced a mixture that shows relatively less decomposition, but still not very stable above −20 °C. Again, despite several attempts, we could not obtain crystalline [Au{Fe(CO)5}2][B{3,5‐(CF3)2C6H3}4], although the resulting white solid indicated the presence of product that contains metal carbonyl bands as in [Mes3PAu‐Fe(CO)5][SbF6] [16b] and [(NHC)Au‐Fe(CO)5][SbF6][ 14c , 16b ] systems. After several days at −20 °C, we obtained a crystalline product in low yield from this solution, which upon analysis by X‐ray diffraction indicated to be [Au{Fe(CO)5}2][HOB{3,5‐(CF3)2C6H3}3]. The anion is a likely result of gold(I) cleaving the B−C bond of [B{3,5‐(CF3)2C6H3}4]− and adventitious moisture trapping the boron containing product. These crystals of [Au{Fe(CO)5}2][HOB{3,5‐(CF3)2C6H3}3] survive a few minutes at room temperature and displays its IR bands at 2131 and 2069 cm−1.

The X‐ray structure of [Au{Fe(CO)5}2][HOB{3,5‐(CF3)2C6H3}3] is illustrated in Figure 5. Although the anionic moiety is quite large as a result of [HOB{3,5‐(CF3)2C6H3}3]− anion H‐bonding to a H2O‐B{3,5‐(CF3)2C6H3}3, the more important cation [Au{Fe(CO)5}2]+ is well‐behaved and shows the presence of a two‐coordinate gold atom. The gold center shows essentially linear geometry with the Fe‐Au‐Fe angle of 174.80(4)°. The Fe−Au bond distances of 2.5423(13) and 2.5455(12) Å are marginally shorter than the Fe−Au bond lengths observed for [Mes3PAu‐Fe(CO)5][SbF6] [16b] and [(NHC)Au‐Fe(CO)5][SbF6][ 14c , 16b ] with P‐Au‐Fe or C‐Au‐Fe coordination spheres at the gold, which range from 2.5535(3)‐2.5696(5) Å. The carbonyl groups perpendicular to the Fe‐Au‐Fe show eclipsed configuration. The cis‐CO groups lean slightly towards the central gold atom, with the largest deviation from ideal 90° at 76.3(3)°.

Figure 5.

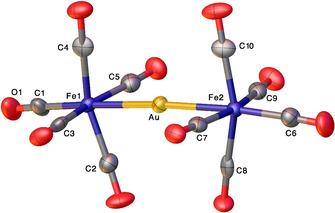
Figure 5

Open in a new tab

Molecular structure of [Au{Fe(CO)5}2][HOB{3,5‐(CF3)2C6H3}3]. Only the cationic [Au{Fe(CO)5}2]+ moiety is shown here. Selected bond lengths (Å) and angles (°): Au−Fe1 2.5423(13), Au−Fe2 2.5455(12), Fe1‐Au‐Fe2 174.80(4), Fe1−C1 1.851(10), Fe1−C2 1.829(10), Fe1−C3 1.838(10), Fe1−C4 1.820(10), Fe1−C5 1.828(10), Fe2−C6 1.841(10), Fe2−C7 1.837(9), Fe2−C8 1.819(10), Fe2−C9 1.844(9), Fe2−C10 1.844(9), C1‐Fe1‐Au 173.9(3), C6‐Fe2‐Au 174.1(3), C2‐Fe1‐Au 78.6(3), C3‐Fe1‐Au 85.1(3), C4‐Fe1‐Au 82.7(3), C5‐Fe1‐Au 78.8(3), C7‐Fe2‐Au 84.0(3), C8‐Fe2‐Au 76.3(3), C9‐Fe2‐Au 81.3(3), C10‐Fe2‐Au 83.3(3).

Theoretical studies

We optimized the geometries of the cations [M{Fe(CO)5}2]+ (M=Cu, Ag, Au) at the BP86‐D3(BJ)/def2‐TZVPP level of theory. Figure 6 shows the calculated structures and the most important bond lengths and angles in comparison with the experimental data. The computed geometries exhibit a linear Fe‐M‐Fe’ moiety where the basal carbonyl ligands are somewhat inclined toward the coinage metal M. The copper and silver cations have D 2 symmetry with two different tilting angles whereas the gold cation has D 4d symmetry where all basal carbonyl ligands have the same bending angle. There is nearly free rotation of the Fe(CO)5 ligands about the Fe‐M‐Fe’ axis. A geometry optimization of [M{Fe(CO)5}2]+ (M=Cu, Ag) with enforced D 4 or D 4d symmetry gives structures that are less than 2 kcal mol−1 (Cu) or ≤0.1 kcal mol−1 (Ag) higher in energy than the D 2 equilibrium structure. The D 4 form of [Au{Fe(CO)5}2]+ is only 0.1 kcal mol−1 above the D 4d structure (Table S1, Supporting Information).

Figure 6.

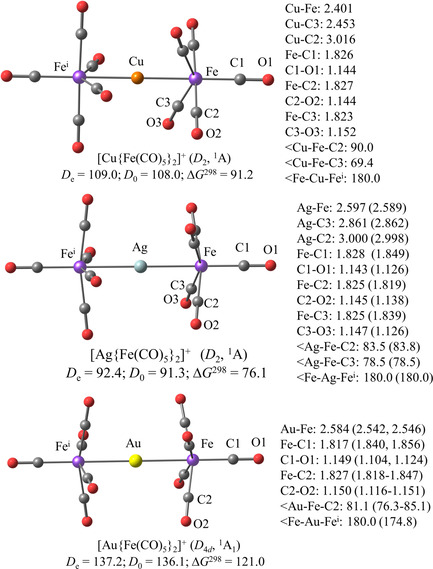
Figure 6

Open in a new tab

Calculated geometries and relevant bond lengths and bond angles of [M{Fe(CO)5}2]+ (M=Cu, Ag, Au). Experimental values are given in parentheses. Calculated bond dissociation energies D e, zero‐point energy corrected bond dissociation energies D 0 and free energy change ΔG[298] at 298 K for the dissociation reaction [M{Fe(CO)5}2]+→M++2 Fe(CO)5. All calculated values are obtained at the BP86‐D3(BJ)/def2‐TZVPP level of theory. Bond distances are given in Å, angles in degree and energies in kcal mol−1.

The calculated bond lengths and angles of the silver and gold complexes are in reasonably good agreement with the X‐ray data, where the slight bending angle Fe‐M‐Fe’ (M=Ag, Au) is likely due to the weak interactions with the anion. A much stronger bending of Fe‐Cu‐Fe’=148° is experimentally observed for the copper cation in the complex [Cu{Fe(CO)5}2][SbF6], which exhibits a rather short Cu−F distance (Figure 3). We think that the distortion from a linear structure is due to the interactions of the cation with the SbF6 − anion, which also causes a lengthening of the Cu−Fe bonds. The calculated M−Fe bond lengths of the silver and gold cations are a bit longer than the experimental values, but the theoretical Cu−Fe distance is shorter than the X‐ray values (Figure 6). Figure 6 shows also the calculated bond dissociation energies (BDE) for the loss of the Fe(CO)5 ligands from M+. The values suggest that the thermodynamic stabilities of the cations [M{Fe(CO)5}2]+ has the order M=Au (D e=137.2 kcal mol−1) >Cu (D e=109.0 kcal mol−1) >Ag (D e=92.4 kcal mol−1), which follows the well‐known trend of transition metals.4a

We analyzed the electronic structures of the cations [M{Fe(CO)5}2]+ with the QTAIM (quantum theory of Atoms In Molecules) method. [29] Figure 7 shows the Laplacian distribution of the electron density, ∇2ρ(r) at the M‐Fe‐C plane and the bond paths and bond critical points (BCPs). There are spherical areas of relative charge depletion (∇2ρ(r)>0, blue solid lines) around the metal atoms and areas of charge accumulation (∇2ρ(r)<0, red dashed lines) at the CO groups, which are typical for carbonyl complexes.[ 29 , 30 ] Noteworthy is the absence of BCPs between the coinage metal M and the CO groups. A recent QTAIM analysis of the hexacarbonyl cations [Ag{M(CO)6}2]+ (M=Cr, Mo, W) and the isoelectronic anions [Ag{M(CO)6}2]− (M=V, Nb, Ta) showed for all complexes BCPs between the silver atom and the carbon atoms of the tilting CO ligands of M(CO)6. [31] There were also BCPs in the hexacarbonyls for the Ag–M interactions of the group‐4 and group‐5 atoms M but not for the group‐3 metals Cr, V. This indicates that the interactions between the coinage metals M and the CO ligands of the pentacarbonyls in [M{Fe(CO)5}2]+ are less pronounced than the interactions between Ag and CO in the hexacarbonyls in [Ag{M(CO)6}2]+ (M=Cr, Mo, W) and [Ag{M(CO)6}2]− (M=V, Nb, Ta). However, the absence or occurrence of BCPs should not be regarded as proof of the presence or absence of a chemical bond, but rather as an indication of the relative strength of the interatomic interactions. [32]

Figure 7.

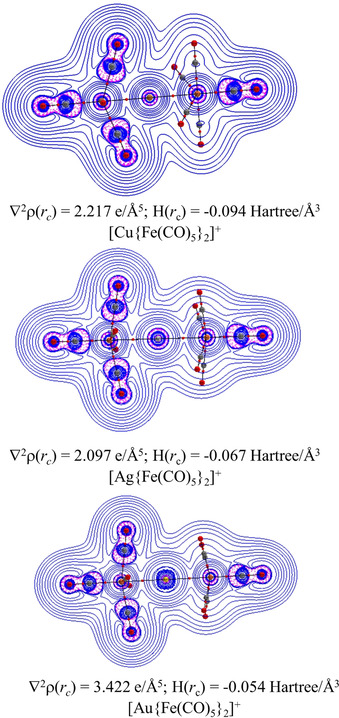
Figure 7

Open in a new tab

The plot of the Laplacian of the electron density, ∇2ρ(r) at the M‐Fe‐C plane of [M{Fe(CO)5}2]+ (M=Cu, Ag, Au) complexes at the BP86‐D3(BJ)/def2‐TZVPP/x2C‐TZVPall//BP86‐D3(BJ)/def2‐TZVPP level. The values for ∇2ρ(rc) and H(r c) are given at the BCP of M−Fe.

Detailed information about the nature of the chemical bonding in the cations and particularly about the strength of the pairwise orbital interactions is available from the EDA (Energy Decomposition Analysis) [33] in conjunction with the NOCV (Natural Orbitals for Chemical Valence) [34] method. The EDA‐NOCV [35] method has been proven to give deep insight into the nature of the chemical bond.[ 8 , 36 ] Unlike most other approaches such as QTAIM,[29] ]NBO (natural bond orbitals), [37] IQA (interacting quantum atoms)[ 38 , 39 ] or conceptual DFT (density functional theory), [40] which analyze the final electronic structure of the molecules, the EDA‐NOCV method first identifies the interacting fragments before bond formation and then analyzes the interactions between the moieties that make up the molecule. The search for the best choice of the interacting moieties is not always trivial but comparing the calculated values of the EDA components has proven to be a reliable indicator for finding the best fragments. It has been shown that those fragments that give the least change in electronic energy during bond formation provide the best description of the components that make up the final bond.[ 10c , 41 ] The EDA‐NOCV method thus complements the results of the above‐mentioned approaches, but provides additional information about the interactions that are not directly apparent from them. One must be aware, however, that the EDA‐NOCV results represent a model that can be interpreted in a physically meaningful way, which should not be confused with the physical mechanism of forming a chemical bond.

Table 1 shows the numerical results of the EDA‐NOCV calculations of [M{Fe(CO)5}2]+ (M=Cu, Ag, Au) using M+ and {Fe(CO)5}2 as interacting fragments. The intrinsic interaction energy ΔE int between the frozen fragments has the same order for M=Au > Cu > Ag as the BDEs. This is because the BDE and the ΔE int differ only by the geometric relaxation energy of the Fe(CO)5 ligands, which are not very large. The most interesting result comes from the breakdown of the orbital term ΔE orb into the pairwise orbital interactions ΔE orb(1)−ΔE orb(9), which come from the covalent bonding between M+ and the Fe(CO)5 ligands. The remaining orbital stabilization ΔE orb(rest) is due to relaxation of the fragment orbitals.

Table 1.

EDA‐NOCV results for [M{Fe(CO)5}2]+ (M=Cu, Ag, Au) complex at the BP86‐D3(BJ)/TZ2P‐ZORA//BP86‐D3(BJ)/def2‐TZVPP level. Energy values are in kcal mol−1.

Energy terms

Orbital interaction

Cu+ (3d) [10] +[Fe(CO)5]2

Ag+ (4d) [10] +[Fe(CO)5]2]

Au+ (5d) [10] +[Fe(CO)5]2

ΔE int

 

−118.4

−97.6

−146.6

ΔE Pauli

 

128.5

116.0

160.0

ΔE disp [a]

 

−7.6 (3.1 %)

−10.5 (4.9 %)

−11.7 (3.8 %)

ΔE elstat [a]

 

−120.3 (48.7 %)

−108.8 (51.0 %)

−153.3 (50.0 %)

ΔE orb [a]

 

−119.0 (48.2 %)

−94.2 (44.1 %)

−141.5 (46.2 %)

ΔE orb(1) [b]

[Fe(CO)5]→M+(s)←[Fe(CO)5]

(+,+) σ donation

−46.8 (39.3 %)

−46.0 (48.8 %)

−85.6 (60.5 %)

ΔE orb(2) [b]

[Fe(CO)5]→M+(pσ)←[Fe(CO)5]

(+,‐) σ donation

−16.6 (13.9 %)

−12.8 (13.6 %)

−14.5 (10.2 %)

ΔE orb(3) [b]

[Fe(CO)5]→M+(pπ)←[Fe(CO)5]

π donation

−4.3 (3.6 %)

−3.0 (3.2 %)

−3.2 (2.3 %)

ΔE orb(4) [b]

[Fe(CO)5]→M+(pπ)←[Fe(CO)5]

π donation

−4.2 (3.5 %)

−2.9 (3.1 %)

−3.2 (2.3 %)

ΔE orb(5) [b]

[Fe(CO)5]←M+(dσ)→[Fe(CO)5]

σ backdonation + M+ polarization

−6.9 (5.8 %)

−4.8 (5.1 %)

−6.7 (4.7 %)

ΔE orb(6) [b]

[Fe(CO)5]←M+(dπ)→[Fe(CO)5]

π backdonation

−8.4 (7.1 %)

−3.1 (3.3 %)

−3.6 (2.5 %)

ΔE orb(7) [b]

[Fe(CO)5]←M+(dπ)→[Fe(CO)5]

π backdonation

−6.1 (5.1 %)

−2.5 (2.7 %)

−3.6 (2.5 %)

ΔE orb(8) [b]

[Fe(CO)5]←M+(dδ)→[Fe(CO)5]

δ backdonation

−4.2 (3.5 %)

−1.8 (1.9 %)

−2.4 (1.7 %)

ΔE orb(9) [b]

[Fe(CO)5]←M+(dδ)→[Fe(CO)5]

δ backdonation

−2.5 (2.1 %)

−1.8 (1.9 %)

−2.4 (1.7 %)

ΔE orb(rest) [b]

 

−19.0 (16.0 %)

−15.5 (16.5 %)

−16.3 (11.5 %)
Open in a new tab

[a] The values in parentheses show the contribution to the total attractive interaction ΔE elstat+ΔE orb+ΔE disp. [b] The values in parentheses show the contribution to the total orbital interaction ΔE orb.

There are four orbital terms ΔE orb(1)−ΔE orb(4), which come from charge donation of the occupied ligand orbitals into the vacant (n)s and (n)p AOs of M+ denoted as [Fe(CO)5]→M+←[Fe(CO)5]. The remaining five contributions are due to backdonation from the occupied (n−1)d AOs of M+ into vacant ligand orbitals [Fe(CO)5]←M+→[Fe(CO)5]. The nature of the orbital interactions and the involved orbitals comes to the fore by inspecting the associated deformation densities Δρ (1)−Δρ (9) and the connected fragment orbitals. The plots of the copper complex [Cu{Fe(CO)5}2]+ are shown in Figure 8. The deformation densities Δρ (1)−Δρ (9) and the connected fragment orbitals of the silver and gold complex look very similar, they are shown in Figures S1 and S2 of the Supporting Information.

Figure 8.

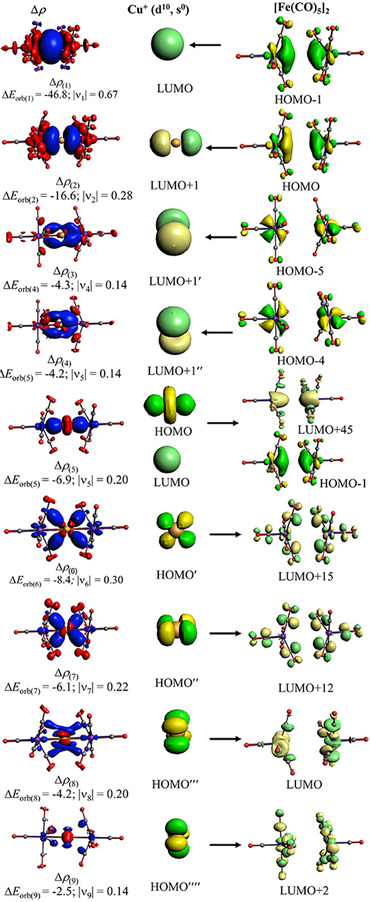
Figure 8

Open in a new tab

The shape of the deformation densities, Δρ (1)‐(9) which are associated with ΔE orb(1)‐(9), and the most important associated fragment orbitals for [Cu{Fe(CO)5}2]+ at the BP86‐D3(BJ)/TZ2P‐ZORA//BP86‐D3(BJ)/def2‐TZVPP level. The isovalue is 0.0004 au. The eigenvalues υ give the size of the charge migration. The direction of the charge flow of the deformation densities is red→blue.

The values in Table 1 show that the donation [Fe(CO)5]→M+←[Fe(CO)5] is, as expected, significantly stronger than the [Fe(CO)5]←M+→[Fe(CO)5] backdonation. The largest contribution to the orbital interactions comes from the donation into the (n)s AO of M+ followed by the donation into the (n)pσ AO. The significant role of the (n)p AOs of M+ is remarkable, because the NBO method considers only the (n)s and (n−1)d AOs of the transition metals as genuine valence orbitals whereas the (n)p AOs are treated as Rydberg orbitals with less priority. [37] This has already been criticized in the literature. [42] A visual inspection of the [Fe(CO)5] ligand orbitals shows (Figures 8, S1 and S2) that the donation [Fe(CO)5]→M+←[Fe(CO)5] comes mainly from occupied orbitals in which the AOs of Fe are dominant. In contrast, the backdonation [Fe(CO)5]←M+→[Fe(CO)5] takes place into π* orbitals of CO. The orbital interaction ΔE orb(5) comprises the backdonation from the (n−1)dz2 AO of M+ which mixes with the (n)s AO and donates electronic charge into a hybrid MO of the ligands, which is a mixture of the LUMO+45 with the HOMO‐1. The orbital term ΔE orb(5) is thus a combination of σ backdonation and polarization. The calculated partial charges in [M{Fe(CO)5}2]+ give positive charges for the coinage metal atoms M of +0.58 e (Cu), +0.44 e (Ag) and +0.23 e (Au) by the NBO 6.0 method. [43]

Conclusions

In this work, we report the syntheses of the copper, silver, and gold complexes [Cu{Fe(CO)5}2][SbF6], [Ag{Fe(CO)5}2][SbF6] and [Au{Fe(CO)5}2][HOB{3,5‐(CF3)2C6H3}3], which contain the homoleptic carbonyl cations [M{Fe(CO)5}2]+ (M=Cu, Ag, Au) involving organometallic Fe(CO)5 ligands. This completes the coinage metal cations, for which the silver homologue [Ag{Fe(CO)5}2]+ stabilized by different anions had been reported before. Structural data of the rare, trimetallic Cu2Fe, Ag2Fe, and Au2Fe complexes [Cu{Fe(CO)5}2][SbF6], [Ag{Fe(CO)5}2][SbF6] and [Au{Fe(CO)5}2][HOB{3,5‐(CF3)2C6H3}3] are also reported. The silver and gold cations [M{Fe(CO)5}2]+ (M=Ag, Au) possess a nearly linear Fe‐M‐Fe’ moiety but the copper cation in [Cu{Fe(CO)5}2][SbF6] exhibits a significant bending angle of 148° due to the strong interaction with the [SbF6]− anion. The Fe(CO)5 ligands adopt a distorted square‐pyramidal geometry in the cations [M{Fe(CO)5}2]+, with the basal CO groups inclined towards M. The geometry optimization with DFT methods of the cations [M{Fe(CO)5}2]+ (M=Cu, Ag, Au) gives equilibrium structures with linear Fe‐M‐Fe’ fragments and D 2 symmetry for the copper and silver cation and D 4d symmetry for the gold cation. There is nearly free rotation of the Fe(CO)5 ligands around the Fe‐M‐Fe’ axis. The calculated bond dissociation energies for the loss of both Fe(CO)5 ligands from the cations [M{Fe(CO)5}2]+ show the order M=Au (D e=137.2 kcal mol−1) > Cu (D e=109.0 kcal mol−1) > Ag (D e=92.4 kcal mol−1). The QTAIM analysis shows bond paths and bond critical points for the M–Fe linkage but not between M and the CO ligands. The EDA‐NOCV calculations suggest that the [Fe(CO)5]→M+←[Fe(CO)5] donation is significantly stronger than the [Fe(CO)5]←M+→[Fe(CO)5] backdonation. Inspection of the pairwise orbital interactions identifies four contributions for the charge donation of the Fe(CO)5 ligands into the vacant (n)s and (n)p AOs of M+ and five components for the backdonation from the occupied (n−1)d AOs of M+ into vacant ligand orbitals.

Experimental Section

Crystallographic data

Deposition numbers 1999550, 1999551, and 2027017 contain the supplementary crystallographic data for this paper. These data are provided free of charge by the joint Cambridge Crystallographic Data Centre and Fachinformationszentrum Karlsruhe Access Structures service.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

Click here for additional data file. (2.4MB, pdf)

Acknowledgements

This work was supported by the Robert A. Welch Foundation (Grant Y‐1289 to H.V.R.D.) and by the Deutsche Forschungsgemeinschaft (Grant FR 641/34‐1 to GF). Open access funding enabled and organized by Projekt DEAL.

S. Pan, S. M. N. V. T. Gorantla, D. Parasar, H. V. R. Dias, G. Frenking, Chem. Eur. J. 2021, 27, 6936.

Contributor Information

Prof. Dr. H. V. Rasika Dias, Email: dias@uta.edu.

Prof. Dr. Gernot Frenking, Email: frenking@chemie.uni-marburg.de.

References

  • 1. 
  • 1a. Dewar M. J. S., Bull. Soc. Chim. Fr. 1951, 18, C79; [Google Scholar]
  • 1b. Chatt J., Duncanson L. A., J. Chem. Soc. 1953, 2939–2947; [Google Scholar]
  • 1c. Frenking G., J. Organomet. Chem. 2001, 635, 9–23; [Google Scholar]
  • 1d. Modern Coordination Chemistry: The Legacy of Joseph Chatt (Eds.: Leigh G. J., Winterton N.), The Royal Society of Chemistry, London, 2002. [Google Scholar]
  • 2. Zeise W. C., J. Chem. Phys. 1831, 62, 393–441. [Google Scholar]
  • 3. Langmuir I., Science 1921, 54, 59–67. [DOI] [PubMed] [Google Scholar]
  • 4. 
  • 4a. Frenking G., Fröhlich N., Chem. Rev. 2000, 100, 717–774; [DOI] [PubMed] [Google Scholar]
  • 4b. Elschenbroich C., Organometallics , 3rd ed., Wiley-VCH, Weinheim, 2006. [Google Scholar]
  • 5. Goedecke C., Hillebrecht P., Uhlemann T., Haunschild R., Frenking G., Can. J. Chem. 2009, 87, 1470. [Google Scholar]
  • 6. 
  • 6a. Tonner R., Öxler F., Neumüller B., Petz W., Frenking G., Angew. Chem. Int. Ed. 2006, 45, 8038–8042; [DOI] [PubMed] [Google Scholar]; Angew. Chem. 2006, 118, 8206–8211; [Google Scholar]
  • 6b. Tonner R., Frenking G., Angew. Chem. Int. Ed. 2007, 46, 8695–8698; [DOI] [PubMed] [Google Scholar]; Angew. Chem. 2007, 119, 8850–8853; [Google Scholar]
  • 6c. Tonner R., Frenking G., Chem. Eur. J. 2008, 14, 3260–3272; [DOI] [PubMed] [Google Scholar]
  • 6d. Tonner R., Frenking G., Chem. Eur. J. 2008, 14, 3273–3289; [DOI] [PubMed] [Google Scholar]
  • 6e. Frenking G., Tonner R., Pure Appl. Chem. 2009, 81, 597–614. [Google Scholar]
  • 7. 
  • 7a. Takagi N., Shimizu T., Frenking G., Chem. Eur. J. 2009, 15, 3448–3456; [DOI] [PubMed] [Google Scholar]
  • 7b. Takagi N., Shimizu T., Frenking G., Chem. Eur. J. 2009, 15, 8593–8604. [DOI] [PubMed] [Google Scholar]
  • 8. 
  • 8a. Frenking G., Tonner R., Klein S., Takagi N., Shimizu T., Krapp A., Pandey K. K., Parameswaran P., Chem. Soc. Rev. 2014, 43, 5106–5139; [DOI] [PubMed] [Google Scholar]
  • 8b. Frenking G., Hermann M., Andrada D. M., Holzmann N., Chem. Soc. Rev. 2016, 45, 1129–1144. [DOI] [PubMed] [Google Scholar]
  • 9. Zhao L., Chai C., Petz W., Frenking G., Molecules 2020, 25, 4943. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10. 
  • 10a. Nguyen T. A. N., Frenking G., Chem. Eur. J. 2012, 18, 12733–12748; [DOI] [PubMed] [Google Scholar]
  • 10b. Nguyen T. A. N., Frenking G., Mol. Phys. 2013, 111, 2640–2646; [Google Scholar]
  • 10c. Petz T. W., Andrada D. M., Hermann M., Frenking G., Neumüller B., Z. Anorg. Allg. Chem. 2017, 643, 1096–1099. [Google Scholar]
  • 11. 
  • 11a. Coffey C. E., Lewis J., Nyholm R. S., J. Chem. Soc. 1964, 1741–1749; [Google Scholar]
  • 11b. Nowell I. N., Russell D. R., Chem. Commun. (London) 1967, 817. [Google Scholar]
  • 12. 
  • 12a. Hock H., Stuhlmann H., Chem. Ber. 1928, 61B, 2097–2101; [Google Scholar]
  • 12b. Hock H., Stuhlmann H., Chem. Ber. 1929, 62B, 2690–2693; [Google Scholar]
  • 12c. Hock H., Stuhlmann H., Chem. Ber. 1929, 62B, 431–437. [Google Scholar]
  • 13. 
  • 13a. Davis H. B., Einstein F. W. B., Glavina P. G., Jones T., Pomeroy R. K., Rushman P., Organometallics 1989, 8, 1030–1039; [Google Scholar]
  • 13b. Batchelor R. J., Einstein F. W. B., Pomeroy R. K., Shipley J. A., Inorg. Chem. 1992, 31, 3155–3157; [Google Scholar]
  • 13c. Shipley J. A., Batchelor R. J., Einstein F. W. B., Pomeroy R. K., Organometallics 1991, 10, 3620–3629. [Google Scholar]
  • 14. 
  • 14a. Bauer J., Braunschweig H., Dewhurst R. D., Chem. Rev. 2012, 112, 4329–4346; [DOI] [PubMed] [Google Scholar]
  • 14b. Berry J. F., Lu C. C., Inorg. Chem. 2017, 56, 7577–7581; [DOI] [PubMed] [Google Scholar]
  • 14c. Powers I. G., Uyeda C., ACS Catal. 2017, 7, 936–958; [Google Scholar]
  • 14d. Pyykkö P., Chem. Rev. 1997, 97, 597–636; [DOI] [PubMed] [Google Scholar]
  • 14e. Gade L. H., Angew. Chem. Int. Ed. 2000, 39, 2658–2678; [DOI] [PubMed] [Google Scholar]; Angew. Chem. 2000, 112, 2768–2789; [Google Scholar]
  • 14f. Gray T. G., Sadighi J. P. in Molecular Metal-Metal Bonds (Ed.: Liddle S. T.), Wiley-VCH, Weinheim, 2015, pp. 397–428; [Google Scholar]
  • 14g. Buchwalter P., Rosé J., Braunstein P., Chem. Rev. 2015, 115, 28–126. [DOI] [PubMed] [Google Scholar]
  • 15. 
  • 15a. Lindahl P. A., J. Inorg. Biochem. 2012, 106, 172–178; [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15b. Kampa M., Pandelia M. E., Lubitz W., van Gastel M., Neese F., J. Am. Chem. Soc. 2013, 135, 3915–3925. [DOI] [PubMed] [Google Scholar]
  • 16. 
  • 16a. Wang G., Ceylan Y. S., Cundari T. R., Dias H. V. R., J. Am. Chem. Soc. 2017, 139, 14292–14301; [DOI] [PubMed] [Google Scholar]
  • 16b. Wang G., Ponduru T. T., Wang Q., Zhao L., Frenking G., Dias H. V. R., Chem. Eur. J. 2017, 23, 17222–17226; [DOI] [PubMed] [Google Scholar]
  • 16c. Ponduru T. T., Wang G., Manoj S., Pan S., Zhao L., Frenking G., Dias H. V. R., Dalton Trans. 2020, 49, 8566–8581. [DOI] [PubMed] [Google Scholar]
  • 17. Mond L., Langer C., J. Chem. Soc. Trans. 1891, 59, 1090–1093. [Google Scholar]
  • 18. 
  • 18a. Albers M. O., Singleton E., Coville N. J., Inorganic Syntheses: Reagents Transition Metal Complex and Organometallic Syntheses, Vol. 28 (Ed.: Angelici R. J.), Wiley, New York, 1990, pp. 179–186; [Google Scholar]
  • 18b. Therien M. J., Trogler W. C., Inorganic Syntheses: Reagents Transition Metal Complex and Organometallic Syntheses, Vol. 28 (Ed.: Angelici R. J.), Wiley, New York, 1990, pp. 173–179; [Google Scholar]
  • 18c. Whitmire K. H., Kelly A. T., Hofmann C., Comprehensive Organometallic Chemistry III, Elsevier, 2007, pp. 1–75; [Google Scholar]
  • 18d. Pettit R., Emerson G. F., Adv. Organomet. Chem. 1964, 1, 1–46; [Google Scholar]
  • 18e. Knölker H.-J., Chem. Rev. 2000, 100, 2941–2962. [DOI] [PubMed] [Google Scholar]
  • 19. 
  • 19a. Braunschweig H., Dewhurst R. D., Hupp F., Kaufmann C., Phukan A. K., Schneider C., Ye Q., Chem. Sci. 2014, 5, 4099–4104; [Google Scholar]
  • 19b. Malinowski P. J., Krossing I., Angew. Chem. Int. Ed. 2014, 53, 13460–13462; [DOI] [PubMed] [Google Scholar]; Angew. Chem. 2014, 126, 13678–13680; [Google Scholar]
  • 19c. Dean P. A. W., Ibbott D. G., Bancroft G. M., J. Chem. Soc. Chem. Commun. 1976, 901–902. [Google Scholar]
  • 20.The hetero-metallic iron complexes [M{Fe(CO)5}2]+ (M=Cu, Ag, Au) are homoleptic with regard to the coinage metal M, which carries two Fe(CO)5 ligands.
  • 21. Dias H. V. R., Fianchini M., Cundari T. R., Campana C. F., Angew. Chem. Int. Ed. 2008, 47, 556–559; [DOI] [PubMed] [Google Scholar]; Angew. Chem. 2008, 120, 566–569. [Google Scholar]
  • 22. Portius P., Bühl M., George M. W., Grevels F.-W., Turner J. J., Organometallics 2019, 38, 4288–4297. [Google Scholar]
  • 23. 
  • 23a. Lupinetti A. J., Frenking G., Strauss S. H., Angew. Chem. Int. Ed. 1998, 37, 2113–2116; [DOI] [PubMed] [Google Scholar]; Angew. Chem. 1998, 110, 2229–2232; [Google Scholar]
  • 23b.A. J. Lupinetti, S. H. Strauss, G. Frenking, Prog. Inorg. Chem. 2001, 49, 1–112.
  • 24. Bernhardt E., Bach C., Bley B., Wartchow R., Westphal U., Sham I. H. T., von Ahsen B., Wang C., Willner H., Thompson R. C., Aubke F., Inorg. Chem. 2005, 44, 4189–4205. [DOI] [PubMed] [Google Scholar]
  • 25. Curtis M. D., Han K. R., Butler W. M., Inorg. Chem. 1980, 19, 2096–2101. [Google Scholar]
  • 26. Groom C. R., Bruno I. J., Lightfoot M. P., Ward S. C., Acta Crystallogr. Sect. B 2016, 72, 171–179. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27. 
  • 27a. Hurlburt P. K., Rack J. J., Dec S. F., Anderson O. P., Strauss S. H., Inorg. Chem. 1993, 32, 373–374; [Google Scholar]
  • 27b. Willner H., Schaebs J., Hwang G., Mistry F., Jones R., Trotter J., Aubke F., J. Am. Chem. Soc. 1992, 114, 8972–8980. [Google Scholar]
  • 28. Weber S. G., Zahner D., Rominger F., Straub B. F., Chem. Commun. 2012, 48, 11325–11327. [DOI] [PubMed] [Google Scholar]
  • 29. Bader R. F. W., Atoms in Molecules, A Quantum Theory, Oxford University Press, Oxford, 1990. [Google Scholar]
  • 30. 
  • 30a. Pan S., Zhao L., Dias H. V. R., Frenking G., Inorg. Chem. 2018, 57, 7780–7791; [DOI] [PubMed] [Google Scholar]
  • 30b. Chi C., Pan S., Meng L., Luo M., Zhao L., Zhou M., Frenking G., Angew. Chem. Int. Ed. 2019, 58, 1732–1738; [DOI] [PubMed] [Google Scholar]; Angew. Chem. 2019, 131, 1746–1752. [Google Scholar]
  • 31. Bohnenberger J., Kratzert D., Gorantl S. M. N. V. T., Pan S., Frenking G., Krossing I., Chem. Eur. J. 2020, 26, 17203–17211. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32. 
  • 32a. Foroutan-Nejad C., Shahbazian S., Marek R., Chem. Eur. J. 2014, 20, 10140–10152; [DOI] [PubMed] [Google Scholar]
  • 32b. Bader R. F. W., J. Phys. Chem. A 2009, 113, 10391–10396. [DOI] [PubMed] [Google Scholar]
  • 33. 
  • 33a. Ziegler T., Rauk A., Inorg. Chem. 1979, 18, 1755–1759; [Google Scholar]
  • 33b. Bickelhaupt F. M., Baerends E. J., in Reviews in Computational Chemistry, Vol. 15 (Eds.: Lipkowitz K. B., Boyd D. B.), Wiley-VCH, Weinheim, 2000, pp. 1–86; [Google Scholar]
  • 33c. Te Velde G., Bickelhaupt F. M., Baerends E. J., Fonseca Guerra C., Van Gisbergen S. J. A., Snijders J. G., Ziegler T., J. Comput. Chem. 2001, 22, 931–967. [Google Scholar]
  • 34. 
  • 34a. Mitoraj M., Michalak A., J. Mol. Model. 2007, 13, 347–355; [DOI] [PubMed] [Google Scholar]
  • 34b. Mitoraj M., Michalak A., Organometallics 2007, 26, 6576–6580. [Google Scholar]
  • 35. 
  • 35a. Mitoraj M., Michalak A., Ziegler T., J. Chem. Theory Comput. 2009, 5, 962–975; [DOI] [PubMed] [Google Scholar]
  • 35b. Michalak A., Mitoraj M., Ziegler T., J. Phys. Chem. A 2008, 112, 1933–1939. [DOI] [PubMed] [Google Scholar]
  • 36. 
  • 36a. Zhao L., von Hopffgarten M., Andrada D. M., Frenking G., WIREs Comput. Mol. Sci. 2018, 8, e1345; [Google Scholar]
  • 36b. Zhao L., Schwarz W. H. E., Frenking G., Nat. Rev. Chem. 2019, 3, 48–63; [Google Scholar]
  • 36c. Frenking G., Bickelhaupt F. M., The Chemical Bond. Fundamental Aspects of Chemical Bonding, (Eds.: Frenking G., Shaik S.), Wiley-VCH, Weinheim, 2014, p. 121–158; [Google Scholar]
  • 36d. Zhao L., Hermann M., Holzmann N., Frenking G., Coord. Chem. Rev. 2017, 344, 163–204. [Google Scholar]
  • 37. Weinhold F., Landis C., Valency and Bonding, A Natural Bond Orbital Donor–Acceptor Perspective, Cambridge University Press, Cambridge, 2005. [Google Scholar]
  • 38. 
  • 38a. Martin Pendas A., Blanco M. A., Francisco E., J. Chem. Phys. 2004, 120, 4581–4592; [DOI] [PubMed] [Google Scholar]
  • 38b. Martin Pendas A., Francisco E., Blanco M. A., J. Comput. Chem. 2005, 26, 344–351; [DOI] [PubMed] [Google Scholar]
  • 38c. Blanco M. A., Martin Pendas A., Francisco E., J. Chem. Theory Comput. 2005, 1, 1096–1109; [DOI] [PubMed] [Google Scholar]
  • 38d. Francisco E., Martin Pendas A., Blanco M. A., J. Chem. Theory Comput. 2006, 2, 90–102; [DOI] [PubMed] [Google Scholar]
  • 38e. Martin Pendas A., Blanco M. A., Francisco E., J. Comput. Chem. 2007, 28, 161–184. [DOI] [PubMed] [Google Scholar]
  • 39.The IQA approach analyzes the interactions between atomic fragments, which are taking from the QTAIM partitioning of the electronic structure. It provides information about the interactions between fragments that built after bond formation, whereas the EDA-NOCV approach uses fragments prior to bond formation. For further details see ref. [38].
  • 40. 
  • 40a. Chermette H., J. Comput. Chem. 1999, 20, 129–154; [Google Scholar]
  • 40b. Geerlings P., De Proft F., Langenaeker W., Chem. Rev. 2003, 103, 1793–1873. [DOI] [PubMed] [Google Scholar]
  • 41. 
  • 41a. Zhang Q., Li W.-L., Xu C., Chen M., Zhou M., Li J., Andrada D. M., Frenking G., Angew. Chem. Int. Ed. 2015, 54, 11078–11083; [DOI] [PubMed] [Google Scholar]; Angew. Chem. 2015, 127, 11230–11235; [Google Scholar]
  • 41b. Andrada D. M., Frenking G., Angew. Chem. Int. Ed. 2015, 54, 12319–12324; [DOI] [PubMed] [Google Scholar]; Angew. Chem. 2015, 127, 12494–12500; [Google Scholar]
  • 41c. Mohapatra C., Kundu S., Paesch A. N., Herbst-Irmer R., Stalke D., Andrada D. M., Frenking G., Roesky H. W., J. Am. Chem. Soc. 2016, 138, 10429–10432; [DOI] [PubMed] [Google Scholar]
  • 41d. Scharf L. T., Andrada M., Frenking G., Gessner V. H., Chem. Eur. J. 2017, 23, 4422–4434; [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41e. Hermann M., Frenking G., Chem. Eur. J. 2017, 23, 3347–3356; [DOI] [PubMed] [Google Scholar]
  • 41f. Georgiou D. C., Zhao L., Wilson D. J. D., Frenking G., Dutton J. L., Chem. Eur. J. 2017, 23, 2926–2934; [DOI] [PubMed] [Google Scholar]
  • 41g. Wu Z., Xu J., Sokolenko L., Yagupolskii Y. L., Feng R., Liu Q., Lu Y., Zhao L., Fernández I., Frenking G., Trabelsi T., Francisco J. S., Zeng X., Chem. Eur. J. 2017, 23, 16566–16573; [DOI] [PubMed] [Google Scholar]
  • 41h. Andrada D. M., Casalz-Sainz J. L., Pendas A. M., Frenking G., Chem. Eur. J. 2018, 24, 9083–9089; [DOI] [PubMed] [Google Scholar]
  • 41i. Jerabek P., Schwerdtfeger P., Frenking G., J. Comput. Chem. 2019, 40, 247–264; [DOI] [PubMed] [Google Scholar]
  • 41j. Saha R., Pan S., Merino G., Chattaraj P. K., Angew. Chem. Int. Ed. 2019, 58, 8372–8377; [DOI] [PubMed] [Google Scholar]; Angew. Chem. 2019, 131, 8460–8465. [Google Scholar]
  • 42. 
  • 42a. Maseras F., Morokuma K., Chem. Phys. Lett. 1992, 195, 500–504; [Google Scholar]
  • 42b. Bayse C. A., Hall M. B., J. Am. Chem. Soc. 1999, 121, 1348–1358; [Google Scholar]
  • 42c. Diefenbach A., Bickelhaupt F. M., Frenking G., J. Am. Chem. Soc. 2000, 122, 6449–6458. [Google Scholar]
  • 43. Glendening E. D., Landis C. R., Weinhold F., J. Comput. Chem. 2013, 34, 1429–1437. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

Click here for additional data file. (2.4MB, pdf)

Articles from Chemistry (Weinheim an Der Bergstrasse, Germany) are provided here courtesy of Wiley

RESOURCES