Abstract
The increasing availability of extensive and accurate clinical data is rapidly shaping cardiovascular care by improving the understanding of physiological and pathological mechanisms of the cardiovascular system and opening new frontiers in designing therapies and interventions. In this direction, mathematical and numerical models provide a complementary relevant tool, able not only to reproduce patient‐specific clinical indicators but also to predict and explore unseen scenarios. With this goal, clinical data are processed and provided as inputs to the mathematical model, which quantitatively describes the physical processes that occur in the cardiac tissue. In this paper, the process of integration of clinical data and mathematical models is discussed. Some challenges and contributions in the field of cardiac electrophysiology are reported.
Keywords: arrhythmia, artificial intelligence, cardiac electrophysiology, digital twin, mathematical models, numerical simulation
1. INTRODUCTION
In the last decades, mathematical and numerical modeling of the cardiovascular system is a research topic that has attracted remarkable interest because of the increasing impact of cardiovascular diseases worldwide. The aim is, on one hand, to better understand the physical and quantitative processes governing the cardiovascular system, and, on the other hand, the opening of new frontiers in therapeutic planning and the design of implantable devices.
Mathematical models of cardiac electrophysiology are dynamical systems that quantitatively describe the electrical processes occurring in the cardiac tissue, at different scales, that is, from the cellular to the tissue level. In each cardiac cell, the variation of the electric potential across the membrane is due to the imbalance of ionic species’ concentration between the extracellular and the intracellular media. Ion channels enable the exchange of those species, causing the depolarization and successive repolarization of the cells. At the macroscopic level, the propagation of the electric signal, in the form of a transmembrane potential, is described by means of partial differential equations (PDEs), suitably coupled with ordinary differential equations (ODEs) modeling the ionic currents in the cells. Differential equations describe a suitable balance between relevant variables (e.g., the transmembrane potential, the concentration of ionic species) and their rate of variation. If the latter only concerns variation in time, we will obtain an ODE, whereas a PDE is generated when rates of variations are expressed with respect to the time coordinate as well as to the spatial coordinates. Thanks to a transmission process between different scales, the action potential generated at the cellular level results in a travelling depolarization front, followed by a second polarization front, restoring the initial condition. While the tissue is still depolarized, an extra stimulus is unable to initiate another action potential for a given amount of time. This time window, during which the tissue is not re‐excitable, is defined as refractory period and plays a key role in the induction and sustainment of arrhythmias. 1
These mathematical models provide a flexible platform that can be used to integrate clinical data, to create a virtual model able to reproduce patient‐specific outputs, or to augment experimental data, by predicting and exploring unseen scenarios through changes in model parameters. 2 Patient‐specific data, such as the specific heart geometrical shape, the electrical conduction properties, and other material properties, could be provided as input to the mathematical model and the latter would produce outcomes, that is, the electric potential, electrograms (EGMs), and activation maps, which represent the solutions to the mathematical model. The accurate simulation of a physiological process requires complete and accurate data and the ability of translating clinical information into model inputs. This is an extremely active research field, spanning a broad range of applications from molecular medicine to heart diseases (see, e g., 3, 4, 5, 6 and reference therein).
Large‐scale clinical data are widely used to improve clinical decisions and therapy planning, providing detailed information about heart function and dysfunctions. In addition, the availability of accurate—and easy to acquire—clinical data has allowed the rapid development of mathematical models for a better understanding of the complex mechanisms driving cardiac electrophysiology. Here are a few highlights:
The study of arrhythmogenic and arrhythmic properties to identify specific indicators (biomarkers) of a pathological condition that might support clinical decisions. 7 , 8 , 9
Computational pharmacologic safety tests, aiming at evaluating whether dangerous drug side‐effects, such as arrhythmias, might occur. 10
Protocols for suggesting targets of ablation for ischemic and fibrotic patients. 11 , 12
Implantable devices optimization, aiming at improving cardiac resynchronization therapy treatments for heart failure 13 and defibrillation mechanisms. 14
Non‐invasive reconstruction of activation maps from body surface potential mapping and electrocardiograms (ECGs). 15
More substantial progresses are expected in the next few years: enhanced clinical data will enable more accurate mathematical models that will allow to capture phenomena occurring at the fine scales and finally to provide patient‐specific simulations. In this paper, we review the main steps of this process in the context of cardiac electrophysiology, starting from the description of the mathematical models and clinical data. We will then describe how to develop a possible data‐model integration pipeline for the construction of in silico subject‐specific models.
2. MATHEMATICAL MODELS
The electric potential propagation is a complex process linking together the micro scale of the single cell ion channel to the macro‐scale represented by the whole heart tissue. A mathematical model consists therefore of two parts: a cellular model given by a system of ODEs, and a macroscopic model at the tissue level given by a system of PDEs. The variables of cellular models are the ionic species concentrations, whose evolution in time is regulated by several detailed membrane models involving an increasing number of ionic currents. 16 Cells are typically aligned with their neighbors, forming an organized structure of fibers and sheets, allowing the heart tissue to behave as a continuum. For this reason, macroscopic models relying on PDEs are derived using homogenization (a special form of differential averaging) procedures; the resulting bidomain equations 17 characterize the behavior of the intra‐ and extra‐cellular potentials, that is, their values at every spatial point of the heart muscles and at any time during a heartbeat. Under simplifying assumptions, the bidomain system can be replaced by the monodomain equation, 18 a reaction‐diffusion model expressing the evolution of the transmembrane potential (the difference between extra‐ and intra‐cellular potentials). In this equation, the reaction term is defined by the cellular model, forming a two‐ways coupling between the cellular and the tissue model. Further simplifications, like, for example, the eikonal model, 19 , 20 can be introduced if one is interested in simulating the depolarization time at every spatial point of the heart tissue. The complexity of mathematical models is directly related to its ability to reproduce complex phenomena: for example, reentry arrhythmias require the use of the bidomain or the monodomain model coupled with an ionic model for cellular dynamics, and cannot be captured by the eikonal model. The choice of a model over another also depends on the available data and the clinical questions to be answered.
2.1. Inputs
To maintain a flexible framework, able to represent different physiological and pathological scenarios, mathematical models are often expressed in terms of parameters, defining, for example, the conductivity tensor, the fiber orientation, the ionic channel coefficient, and the applied current. This latter can encode the complex activation heart mechanism (from the sinoatrial node to the Purkinje system) or a pacing sequence. Other input parameters can locally influence activation, recovery, and action potential duration, but their knowledge is considerably limited, due to the intrinsic difficulty in carrying out in vivo and in vitro experiments for their estimation 21 and because of the multiple sources of error in the measurements. Moreover, parameters exhibit a spatial heterogeneity over different regions of the heart, and depend on the choice of the cell model.
Further information is needed to identify a (unique) solution to the mathematical models, depending on initial and boundary conditions. A simplifying choice usually made at the boundary of the domain is to neglect the ability of the rest of the body to conduct the electrical signal, which is mathematically expressed by homogeneous Neumann boundary conditions. However, different types of boundary conditions can be imposed to take into account the electric transmission between the heart domain and the rest of the body, by assuming this latter to act as a passive conductor. This adds an additional PDE (Laplace equation) with the torso potential as a further unknown.
Instead, initial conditions allow to represent the initial state of the variables in both physiological (sinus rhythm) and pathological regimes. The nonlinearity of the problem makes the model extremely sensitive to these initial data: for instance in a fibrillation regime, perturbation of initial conditions can influence the localized reentry patterns.
2.2. Outputs of interest
For a given choice of the input parameters, the geometry, and the initial and boundary conditions, the mathematical models provide several outputs of interest, such as:
The space‐time evolution of the electric potential, that is, changes in propagation speed and refractory period depending on heart rate and physiological/pathological conditions at both the cellular and the tissue level.
The space‐time evolution of ionic species, which can take into account drug actions and metabolic imbalances.
EGMs at any given point of the domain, and consequently activation and voltage maps with an arbitrary resolution.
The time window over which these quantities are evaluated might correspond to a single heartbeat or be longer, enabling to represent also spontaneous ectopic activation, arrhythmias induction, and sustainment, that is, the formation of localized or macro‐reentry circuits and their stability.
2.3. Forward and inverse problems
The map going from the input parameters to the outputs is usually defined as the forward problem, which consists of two steps: the determination of the problem solution and the evaluation of the outputs, which are specific observations of the solution itself. In this framework, the main goals are either (a) to evaluate the effects knowing the causes, such as computing an activation sequence for a given pacing protocol or (b) to quantify the propagation of input uncertainties to the outputs (forward uncertainty quantification). An inverse problem consists, instead, of estimating the input parameters from noisy observations of the output, which is the problem of finding the causes that generate the available noisy diagnostic measurements. This task can be expressed through either a PDE‐constrained optimization problem, yielding a deterministic estimate of the unknown inputs, or a statistical inverse problem, whose solution is a probabilistic distribution describing the range of most likely inputs.
2.4. Numerical discretization
The computation of forward problems solution is obtained through numerical discretization algorithms, which allow to approximate the solution on a computational grid, that is, a finite set of points discretizing the domain over which the mathematical model is defined (the heart tissue). These algorithms encode the original mathematical problem into a discrete system of (nonlinear, differential) equations, which is then solved on (super)‐computers providing the values of the solution at each vertex of the computational grid (typically, few hundred thousand or even million of points). The most common methods used in this context are the finite element method, the finite difference method, the finite volume method, or the isogeometric analysis (see 22, 23, 24 and references therein). The numerical approximation of the solution is usually a time‐expensive task, due to time and space constraints required by the numerical method to accurately reproduce the electrical activity of the heart. Together with the technological developments leading to a constant increase of computing power during the recent years, there is a continuous development of new methods and algorithms aimed at improving the performance of numerical cardiac solvers, such as reduced‐order model techniques 25 among others.
The solution of an inverse problem requires even more sophisticated sampling or optimization algorithms, depending upon several computations of the forward map for different values of the input parameters. The ability to efficiently solve such a problem in a clinical context is still challenging, as it requires accurate and extremely efficient computational models, possibly relying on reduced order models, 25 , 26 machine learning emulators, 27 , 28 or artificial intelligence algorithms. 29
3. CLINICAL DATA
The acquisition of clinical data may take place through three different modalities: electrical recordings, imaging, and patient records.
Electrical signals can be recordered either non‐invasively or invasively using a mapping catheter. The conventional 12‐leads ECG is a set of bipolar and unipolar signals, characterized by the superposition of three waves: P‐wave, generated by atrial depolarization, QRS complex, generated by ventricular depolarization, and T‐wave, generated by ventricular polarization. Pattern modifications of those three waves are used to identify electrical dysfunctions at the organ scale, with a consequent low‐resolution.
A higher resolution alternative is represented by EGMs, acquired by a multipolar catheter close to the endocardium (and/or the epicardium). EGMs are invasive, but they enable the local identification of the electrical properties measured by the small electrodes. For clinical procedures, such as ablations, those detailed invasive data are acquired to identify damaged portions of tissue leading to arrhythmias.
Cardiac imaging is another possible approach to characterize tissue properties. Starting from magnetic resonance and late gadolinium enhancement (LGE) images, it is possible to reconstruct heart geometry and to identify structural defects in the myocardium.
4. DATA‐MODEL INTEGRATION
The integration of available multiple clinical measurements and data within mathematical models may be crucial to develop tools to support clinical practice and procedures, and ultimately enabling personalized therapies. This process of model personalization consists of selecting/identifying those input parameters able to reproduce the electrical behavior observed in a specific patient. Once this calibration process is complete, the personalized model can give insights on the pathological mechanism of the patient and evaluate different treatment scenarios (e.g., testing potential ablation strategies). To trust its predictive capabilities, a personalized model has to be assessed through its validation, verification, and uncertainty quantification. 30
The data‐model integration framework faces however several challenges:
The limits imposed by the spatial resolution of imaging and catheter mapping, and the possible absence or paucity of patient‐specific data (ionic properties). Thanks to technological innovation, spatial resolution has been continuously improved in recent years, leading to catheter equipped with 2.5/3 mm spaced electrodes and high‐resolution LGE images with a voxel size of 1.25 × 1.25 × 2.5 mm. 31 However, these procedures are performed only on patients who have received a diagnosis of a certain pathology. For this reason, the data‐model integration aims also to improve the diagnosis capability using routine non‐invasive exams, such as ECGs, aided by subject‐specific numerical simulations.
The high intra‐ and inter‐patient variability in the geometry, physical coefficients, boundary conditions, and initial conditions. Considering all these sources of uncertainty might entail high computational costs given the numerical simulations and consequently compromise model personalization.
The time required to process data and perform the numerical simulation has to be compatible with the clinical timeline.
In recent years, several groups have faced these challenges. An example of an integrated pipeline for the prediction of activation maps resulting from different pacing conditions can be found in ref. 32 , where mathematical models with different levels of complexity are adopted for estimating parameters, such as conductivities, with reduced computational costs. The role of uncertainty has been taken into account for the first time in ref. 33. Since then, the approach of combining models of different complexity has been used to make the solution of inverse problems and uncertainty quantification feasible. 34 , 35 , 36
5. GENERATION OF A PATIENT‐SPECIFIC MODEL
The construction of a virtual patient‐specific model can be obtained by setting up a complex pipeline, whose schematic representation is reported in Figure 1. We can identify four main steps:
Heart geometry reconstruction, through the segmentation of the domain by either automatic or manual tools based on mathematical and geometric methods.
Generation of a computational mesh, which consists of a fine partition of the heart volume in simple geometrical elements (tetrahedra or hexahedra). Numerical solution would then be approximated on each vertex of this computational mesh using discretization techniques.
Definition of model input parameters using clinical data: this task could be performed in a basic way, encoding simple mathematical relationships between clinical data and model parameters—for example, by adjusting electrical conductivities to reproduce conduction velocities or activation patterns, as shown in ref. 37, and adopting rule‐based fiber distributions. 38 , 39 This approach is not always successful, especially when considering detailed models with highly nonlinear input‐output relationships and limited experimental observations. In a more rigorous way, this identification of model parameters could be formulated as an optimization problem, or as an inverse problem, whose solution is a probabilistic distribution describing the range of most likely inputs.
Numerical approximation of the problem solution (in terms of electric potential onto the computational mesh), post‐processing of the results for determining clinically relevant outputs, such as activation maps, surface ECG, and intracardiac EGMs.
FIGURE 1.
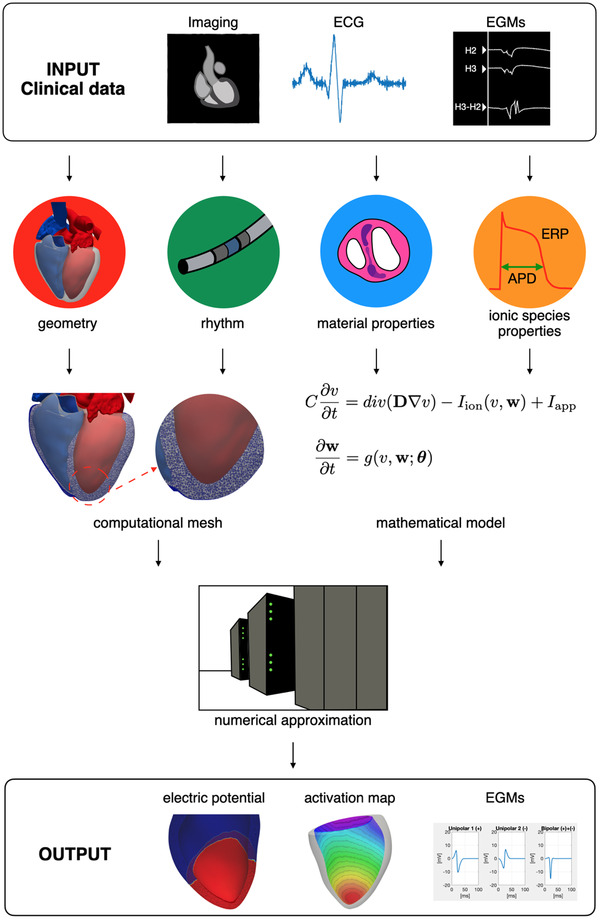
Data‐model integration pipeline. Heart shape is obtained from the Zygote Solid 3D Heart Model 60 [Color figure can be viewed at wileyonlinelibrary.com]
These steps allow the construction of a pipeline for the evaluation of the forward map. As an example, we report below the construction of a sinus‐rhythm simulation on a patient‐specific geometry segmented from MRI images (Numerical simulations were executed on the iHeart cluster [Lenovo SR950 8x24‐Core Intel Xeon Platinum 8160, 2100 MHz and 1.7 TB RAM] at MOX‐Department of Mathematics, Politecnico di Milano. Numerical models and methods have been implemented within lifex [https://lifex.gitlab.io/lifex], a new in‐house high‐performance C++ FE library mainly focused on cardiac applications based on deal.II FE core [https://www.dealii.org].). Figure 2 displays an example of left ventricle geometry in the end‐diastolic configuration reconstructed in ref. 40 with manual segmentation based on the combination of thresholding and smoothing algorithms. The thresholding process locates regions of interest by distinguishing MRI images voxels of the object from the rest (background), whether the voxel brightness is greater or smaller than a global threshold value. Then, smoothing filters are usually applied in order to remove artifacts or regions, such as the papillary muscles or the valves area.
FIGURE 2.
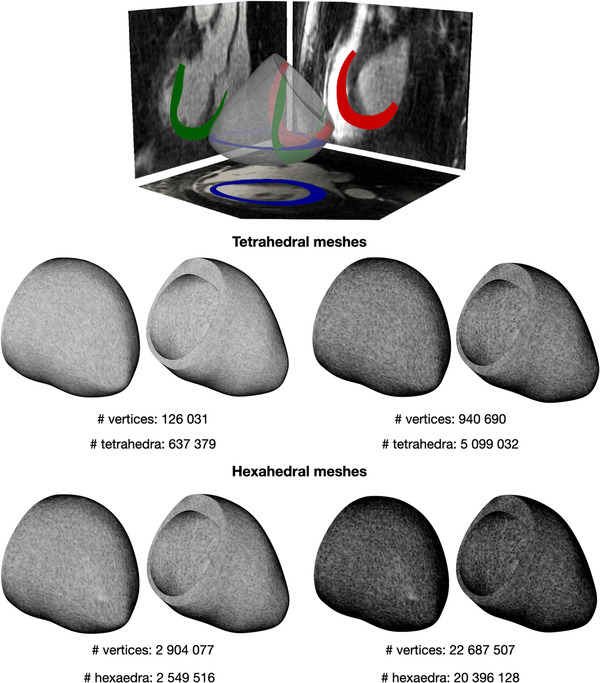
Two tetrahedral (center) and two hexahedral (bottom) meshes with different levels of refinement. Geometry was obtained from segmentation of patient specific MRI images (top image from ref. 40) [Color figure can be viewed at wileyonlinelibrary.com]
Once the geometry is reconstructed, it is possible to generate a mesh by partitioning the input domain in tetrahedral or hexahedral cells with an arbitrary edge length (Figure 2, bottom). Tiny cells, with an average diameter smaller than the characteristic width of the electric potential wavefront (range 0.2−0.7 mm 41 ), are required to ensure that the numerical approximation can correctly capture the conduction velocities of the electric potential propagation, but they inevitably increase the number of total vertices on which the solution must be approximated. The left ventricle geometry was divided into three consecutive regions: the endocardium (15% of LV wall), the mid‐layer of the myocardium (70% of LV wall) and the epicardium (15% of LV wall).
To describe the model parameters, it is necessary to characterize the material properties of the tissue, such as the electrical conductivity properties, the applied current and the refractory properties of the tissue. Those ingredients fully characterize the ventricular activation sequence. Conduction properties are significantly anisotropic since the heart is made of fibers, that is, groups of cells with the same orientation. Fibers constitute a privileged direction of propagation, characterized by faster conduction with respect to the cross‐fiber direction. Furthermore, the muscle cells are also organized in sheets, going from the endocardium to the epicardium and characterized by different fiber orientations. Fiber and sheets distributions are hardly identifiable from standard medical images, therefore mathematical rule‐based models are usually adopted. 38 , 39 Figure 3 shows fiber reconstruction using the rule‐based algorithm proposed in ref. 42 for different choices of the epicardial and endocardial angles.
FIGURE 3.
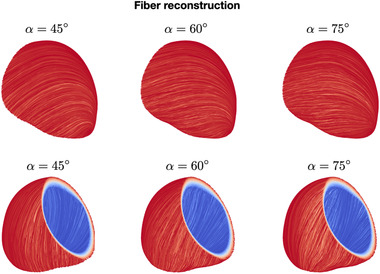
Fiber reconstructions obtained with different choices of rule‐based model parameters (epicardial and endocardial angles) [Color figure can be viewed at wileyonlinelibrary.com]
To mimic a physiological activation sequence (Figure 4), we follow the approach proposed in ref. 43, which has been validated on ECG measurements. We choose three sites of earliest activation, representing the approximate locations on the endocardium of the septal, anterior and posterior fascicles. Moreover, to surrogate the Purkinje fiber structure, we consider a maximum velocity of 1.2 m/s in the endocardium, which is coherent with the conduction velocity measurements in healthy tissue recorded in ref. 9.
FIGURE 4.
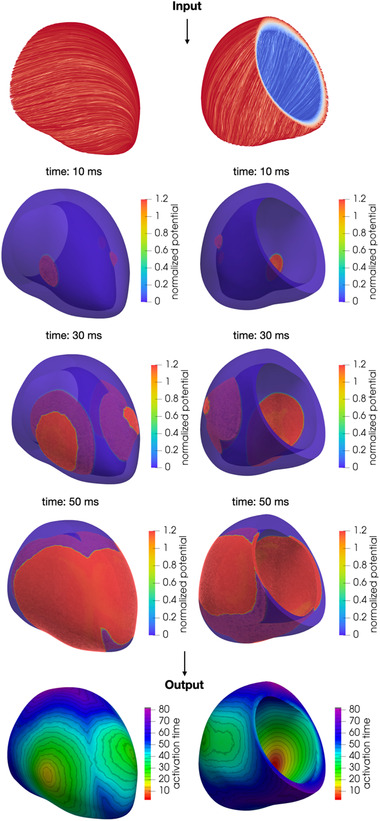
Numerical simulation of the transmembrane potential in sinus rhythm and activation map obtained as a post‐processing of the numerical simulation [Color figure can be viewed at wileyonlinelibrary.com]
Conductivity along fiber enables the approximation of conduction velocity of 0.6 m/s in the myocardium and the epicardium. While conductivities in the transverse to the fiber orientation and along the sheet normal direction lead to a conduction velocity that is, respectively, 2/3 and 1/3 of the conduction velocity longitudinal to the fiber direction.
We adopt the monodomain model coupled with the Ten Tusscher–Panfilov model of the human ventricle myocyte. 44 Output (unipolar) activation map is finally computed by post‐processing the numerical approximation of the transmembrane potential solution: in each point of the computational mesh, the activation time is approximated as the time at which the absolute value of the time derivative of the transmembrane potential attains its maximum value.
6. PATHOLOGICAL CONDITIONS
Electrical disorder phenomena, such as post‐ischemic ventricular tachycardia (VT), atrial tachycardia (AT), ventricular fibrillation (VF), or atrial fibrillation (AF), are the result of the concurrence of a series of structural and functional factors that lead to the formation (induction) of re‐entry circuits and subsequently to their sustainment. These circuits (Figure 5) are divided into:
Macro‐reentry, typical of VT and AT, if in their path, the signal rotates around physical obstacles (pulmonary veins or valves) or lines of block, due to the presence of scarring tissue, forming the so‐called isthmus.
Localized reentry, typical of VF and AF, if the signal rotates around fixed anchoring points (lines of blocks or patchy fibrotic tissue) or if the signal has a center of rotation (rotor) that dynamically changes its position in the tissue.
FIGURE 5.
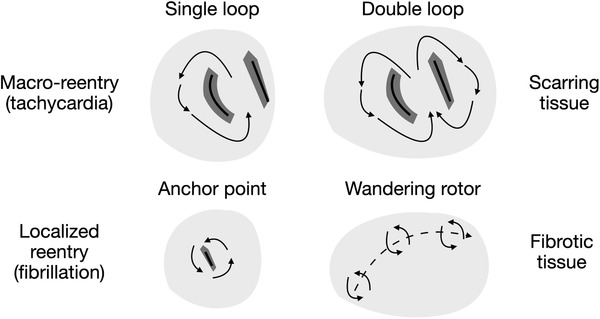
Localized and macro‐reentries
Electrophysiological studies, through the acquisition of endocavitary signals, aim at recognizing those arrhythmogenic regions, which can form localized or macro‐reentry circuits. Activation maps and EGMs morphology reveal the presence of areas of slowing (fibrotic tissue) and conduction blocking (scar tissue). 45 , 46 The mathematical analysis of these data, in the form of biomarkers calculation, provides a first quantitative tool in support of the electrophysiologist. 9 Mathematical operators, such as the spatial gradient of activation time and the conduction velocity field divergence and rotor, provide a quantitative description of the conduction speed, wavefront collision and pivot point, respectively. Those biomarkers enable substrate characterization and might enhance our understanding of the mechanism behind arrhythmias. 47
To simulate electrical dysfunctions, model parameterization must be appropriately adjusted to include ectopic beats or pacing protocols, encoded in the parametrization of the applied current, as well as modified conduction and refractory properties. These latter are encoded by the heterogeneous diffusion tensor and the coefficients of the cell model governing the ion channels properties, respectively. 48 , 49 , 50
Figure 6 shows an example of localized reentry induction caused by an ectopic impulse, such as the ones coming from the pulmonary veins described in ref. 51. In this numerical simulation, conduction and refractory properties are randomly modified to mimic the presence of tissue fibrosis. 12 , 52 , 53 These heterogeneous properties form the substrate for the induction of a localized reentry and its sustainment. In this setting, we observe the formation of an anchor point, around which the wavefront continuously re‐excite the tissue due to the reduced head–tail interaction caused by the modified refractory properties. 47
FIGURE 6.
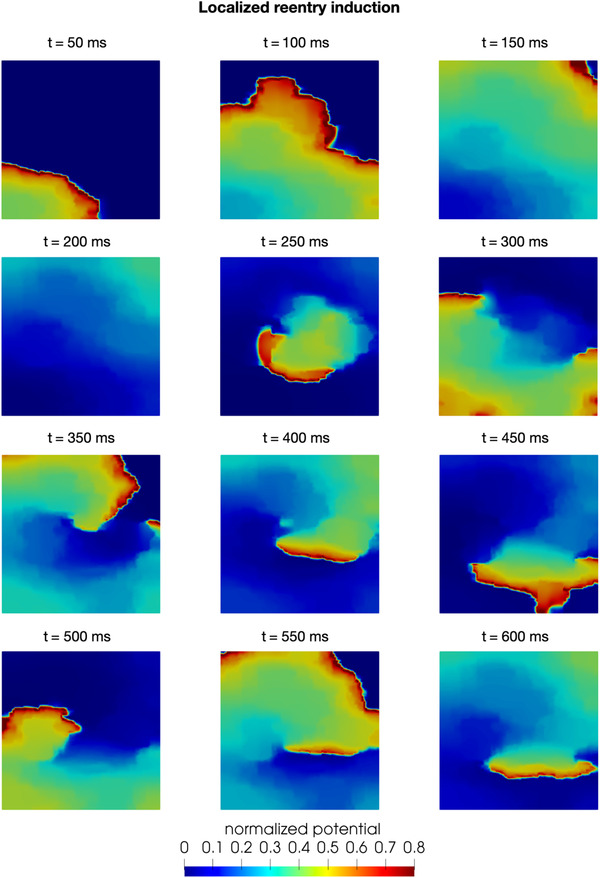
Numerical simulation of a pathological condition: localized reentry induction and sustainment on a tissue slab [Color figure can be viewed at wileyonlinelibrary.com]
7. PERSPECTIVES
The construction of customized cardiac models with the integration of clinical data will increase the ability to respond to the challenges posed by the clinicians.
In this direction, algorithms and methodologies borrowed from artificial intelligence are becoming more and more tools for the analysis of clinical data and data‐model integration. In this context, the most adopted tool are artificial neural networks (ANNs), which consist of an interconnected groups of nodes (neurons) able to “learn” to perform either classification or regression tasks, after they have been trained on a (usually, extremely large) sample of labeled clinical data. For instance, ANNs have been already applied to arrhythmia classification from single‐lead ECG data of 53,877 patients in ref. 54, showing a performance comparable to human experts.
ANNs might be also used as a tool for data‐model integration: physical constraints (encoded by parametrized mathematical model) can be enforced during the training process of the network, leading to the so‐called physics‐informed neural networks, 55 a new generation of computational models able to solve both the forward problem, starting from observed data, and the inverse problem, identifying unknown model parameters or incomplete data. A proof‐of‐concept about their capability in reconstructing activation maps has been performed in ref. 56. Finally, ANNs might also accelerate parametrized model evaluation, by creating extremely cheap, yet accurate, reduced‐order models. 57 , 58 , 59
These tools stand nowadays at the basis of the construction of “digital twins,” which are virtual tools purposely built to continuously integrate patient‐specific clinical data acquired over time, into physics‐based or artificial intelligence models. 3
8. CONCLUSIONS
The final objective of data‐model integration is to support clinical decisions and interventions. As we have discussed and shown through examples in this paper, this process is at the beginning of its development, but it has already proved to be effective in some relevant clinical applications in cardiac electrophysiology, paving the way to tackle more complex pathological conditions.
ACKNOWLEDGEMENTS
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 740132, iHEART ‐ An Integrated Heart Model for the simulation of the cardiac function, P.I. Prof. A. Quarteroni).

Pagani S, Dede’ L, Manzoni A, Quarteroni A. Data integration for the numerical simulation of cardiac electrophysiology. Pacing Clin Electrophysiol. 2021;44:726–736. 10.1111/pace.14198
DATA AVAILABILITY STATEMENT
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
REFERENCES
- 1. Nattel S. New ideas about atrial fibrillation 50 years on. Nature. 2002;415:219‐226. [DOI] [PubMed] [Google Scholar]
- 2. Quarteroni A, Dede’ L, Manzoni A, Vergara C. Mathematical Modelling of the Human Cardiovascular System: Data, Numerical Approximation, Clinical Applications. Cambridge Monographs on Applied and Computational Mathematics Cambridge: Cambridge University Press; 2019. [Google Scholar]
- 3. Corral‐Acero J, Margara F, Marciniak M, et al. The ‘Digital Twin’ to enable the vision of precision cardiology. Eur Heart J. 2020;41:4556‐4564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Winslow RL, Trayanova N, Geman D, Miller MI. Computational medicine: translating models to clinical care. Sci Transl Med. 2012;4:158rv11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Chabiniok R, Wang VY, Hadjicharalambous M, et al. Multiphysics and multiscale modelling, data‐model fusion and integration of organ physiology in the clinic: ventricular cardiac mechanics. Interface Focus. 2016;6:20150083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Whittaker DG, Clerx M, Lok Lei C, Christini DJ, Mirams GR. Calibration of ionic and cellular cardiac electrophysiology models. WIREs Syst Biol Med. 2020;12:e1482. 10.1002/wsbm.1482 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Karma A. Physics of cardiac arrhythmogenesis. Annu Rev Condens Matter Phys. 2013;4:313‐337. [Google Scholar]
- 8. Ciaccio EJ, Coromilas J, Wan EY, et al. Slow uniform electrical activation during sinus rhythm is an indicator of reentrant VT isthmus location and orientation in an experimental model of myocardial infarction. Comput Methods Programs Biomed. 2020;196:105666. [DOI] [PubMed] [Google Scholar]
- 9. Frontera A, Pagani S, Limite LR, et al. Outer loop and isthmus in ventricular tachycardia circuits: characteristics and implications. Hearth Rhythm. 2020;17:1719‐1728. [DOI] [PubMed] [Google Scholar]
- 10. Mirams GR, Davies MR, Cui Y, Kohl P, Noble D. Application of cardiac electrophysiology simulations to pro‐arrhythmic safety testing. Br J Pharmacol. 2012;167(5):932‐945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Prakosa A, Arevalo HJ, Deng D, et al. Personalized virtual‐heart technology for guiding the ablation of infarct related ventricular tachycardia. Nat Biomed Eng. 2018;2:732‐740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Boyle PM, Zghaib T, Zahid S, et al. Computationally guided personalized targeted ablation of persistent atrial fibrillation. Nat Biomed Eng. 2019;3:870‐879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Lee A, Costa CM, Strocchi M, Rinaldi CA, Niederer SA. Computational modeling for cardiac resynchronization therapy. J Cardiovasc Transl Res. 2018;11:92‐108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Trayanova NA, Costantino J, Ashihara T, Plank G. Modeling defibrillation of the heart: approaches and insights. IEEE Rev Biomed Eng. 2011;4:89‐102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Cluitmans M, Brooks DH, MacLeod R, et al. Validation and opportunities of electrocardiographic imaging: from technical achievements to clinical applications. Front Physiol. 2018;9:1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Elshrif MM, Cherry EM. A quantitative comparison of the behavior of human ventricular cardiac electrophysiology models in tissue. PLoS One. 2014;9:e84401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Henriquez CS. Simulating the electrical behavior of cardiac tissue using the bidomain model. Crit Rev Biomed Eng. 1993;21:1‐77. [PubMed] [Google Scholar]
- 18. Potse M, Dubé B, Richer J, Vinet A, Gulrajani R M. A comparison of monodomain and bidomain reaction‐diffusion models for action potential propagation in the human heart. IEEE Trans Biomed Eng. 2006;53:2425‐2435. [DOI] [PubMed] [Google Scholar]
- 19. Jacquemet V. An eikonal approach for the initiation of reentrant cardiac propagation in reaction–diffusion models. IEEE Trans Biomed Eng. 2010;57:2090‐2098. [DOI] [PubMed] [Google Scholar]
- 20. Pezzuto S, Kal'avsky P, Potse M, Prinzen FW, Auricchio A, Krause R. Evaluation of a rapid anisotropic model for ECG simulation. Front Physiol. 2017;8:256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Fink M, Niederer SA, Cherry EM, et al. Cardiac cell modelling: observations from the heart of the cardiac physiome project. Prog Biophys Mol Bio. 2011;104:2‐21. [DOI] [PubMed] [Google Scholar]
- 22. Vigmond J, Weber dos Santos R, Prassl AJ, et al. Solvers for the cardiac bidomain equations. Prog Biophys Mol Bio. 2008;96:3‐18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Niederer, SA , Kerfoot, E , Benson, AP , Bernabeu, MO , Bernus, O , Bradley, C , … & Smith, NP . Verification of cardiac tissue electrophysiology simulators using an N‐version benchmark. Phil Trans R Soc A. 2011;369:4331‐4351. 10.1098/rsta.2011.0139 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Pegolotti L, Dede’ L, Quarteroni A. Isogeometric analysis of the electrophysiology in the human heart: numerical simulation of the bidomain equations on the atria. CMAME. 2019;343:52‐73. [Google Scholar]
- 25. Pagani S, Manzoni A, Quarteroni A. Numerical approximation of parametrized problems in cardiac electrophysiology by a local reduced basis method. CMAME. 2018;340:530‐558. [Google Scholar]
- 26. Gerbeau JF, Lombardi D, Schenone E. Reduced order model in cardiac electrophysiology with approximated Lax pairs. Adv Comput Math. 2015;41:1103‐1130. [Google Scholar]
- 27. Coveney S, Corrado C, Roney CH, et al. Gaussian process manifold interpolation for probabilistic atrial activation maps and uncertain conduction velocity. Phil Trans R Soc A. 2020;378:20190345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Coveney S, Clayton RH. Sensitivity and uncertainty analysis of two human atrial cardiac cell models using Gaussian process emulators. Front Physiol. 2020;11:364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Feeny AK, Chung MK, Madabhushi A, et al. Artificial intelligence and machine learning in arrhythmias and cardiac electrophysiology. Circ Arrhythm Electrophysiol. 2020;13:e007952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Clayton RH, Aboelkassem Y, Cantwell CD, et al. An audit of uncertainty in multi‐scale cardiac electrophysiology models. Phil Trans R Soc A. 2020;378:20190335. 10.1098/rsta.2019.0335 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Lintingre P‐F, Nivet H, Clément‐Guinaudeau S, et al. High‐resolution late gadolinium enhancement magnetic resonance for the diagnosis of myocardial infarction with nonobstructed coronary arteries. JACC Cardiovasc Imaging. 2020;13:1135‐1148. [DOI] [PubMed] [Google Scholar]
- 32. Camara O, Sermesant M, Lamata P, et al. Inter‐model consistency and complementarity: learning from ex‐vivo imaging and electrophysiological data towards an integrated understanding of cardiac physiology. Prog Biophys Mol Bio. 2011;107:122‐133. [DOI] [PubMed] [Google Scholar]
- 33. Konukoglu E, Relan J, Cilingir U, et al. Efficient probabilistic model personalization integrating uncertainty on data and parameters: application to Eikonal‐diffusion models in cardiac electrophysiology. Prog Biophys Mol Bio. 2011;107:134‐146. [DOI] [PubMed] [Google Scholar]
- 34. Quaglino A, Pezzuto S, Koutsourelakis P, Auricchio A, Krause R. Fast uncertainty quantification of activation sequences in patient‐specific cardiac electrophysiology meeting clinical time constraints. Int J Numer Methods Biomed Eng. 2018;34:e2985. [DOI] [PubMed] [Google Scholar]
- 35. Pagani S. Reduced‐order models for inverse problems and uncertainty quantification in cardiac electrophysiology. (2017) PhD thesis, Mathematical Models and Methods in Engineering, Department of Mathematics, Politecnico di Milano.
- 36. Costabal FS, Matsuno K, Yao J, Perdikaris P, Kuhl E. Machine learning in drug development: characterizing the effect of 30 drugs on the QT interval using Gaussian process regression, sensitivity analysis, and uncertainty quantification. CMAME. 2019;348:313‐333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Mendonca Costa C, Hoetzl E, Rocha BM, Prassl AJ, Plank G. Automatic parameterization strategy for cardiac electrophysiology simulations. Comput Cardiol. 2013:373‐376. [PMC free article] [PubMed] [Google Scholar]
- 38. Bayer JD, Blake RC, Plank G, Trayanova NA. A novel rule‐based algorithm for assigning myocardial fiber orientation to computational heart models. Ann Biomed Eng. 2012;40:2243‐2254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Piersanti R, Africa PC, Fedele M, et al. Modeling cardiac muscle fibers in ventricular and atrial electrophysiology simulation. CMAME. 2021; 373:113468. [Google Scholar]
- 40. Gerbi A, Dede’ L, Quarteroni A. A monolithic algorithm for the simulation of cardiac electromechanics in the human left ventricle. Math Eng. 2019; 1:1‐37. [Google Scholar]
- 41. Plank G, Zhou L, Greenstein JL, et al. From mitochondrial ion channels to arrhythmias in the heart: computational techniques to bridge the spatio‐temporal scales. Philos Trans A Math Phys Eng Sci. 2008; 366:3381‐3409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Rossi S, Lassila T, Ruiz‐Baier R, Sequeira A, Quarteroni A. Thermodynamically consistent orthotropic activation model capturing ventricular systolic wall thickening in cardiac electromechanics. Eur J Mech A Solids. 2014;48:129‐142. [Google Scholar]
- 43. Augustin CM, Crozier, A , Neic, A , et al. Patient‐specific modeling of left ventricular electromechanics as a driver for haemodynamic analysis. Europace. 18, 2016: iv121‐iv129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. ten Tusscher KHWJ, Panfilov AV, Alternans and spiral breakup in a human ventricular tissue model. Am J Physiol. 2006;291:1088‐1100. [DOI] [PubMed] [Google Scholar]
- 45. Frontera A, Melillo F, Baldetti L, et al. High‐density characterization of the ventricular electrical substrate during sinus rhythm in post‐myocardial infarction patients. JACC Clin Electrophysiol. 2020;6:799‐811. [DOI] [PubMed] [Google Scholar]
- 46. Hadjis A, Frontera A, Rosario Limite L, et al. Complete electroanatomic imaging of the diastolic pathway is associated with improved freedom from ventricular tachycardia recurrence. Circ Arrhythm Electrophysiol. 2020;13:e008651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Jalife J. Rotors and spiral waves in atrial fibrillation. J Cardiovasc Electrophysiol. 2003;14:776‐780. [DOI] [PubMed] [Google Scholar]
- 48. Fenton FH, Cherry EM, Hastings HM, Evans SJ. Multiple mechanisms of spiral wave breakup in a model of cardiac electrical activity. Chaos. 2002;12:852‐892. [DOI] [PubMed] [Google Scholar]
- 49. Dierckx H, Fenton FH, Filippi S, Pumir A, Sridhar S. Simulating normal and arrhythmic dynamics: from sub‐cellular to tissue and organ level. Front Phys. 2019;7:89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Campos FO, Whitaker J, Neji R, et al. Factors promoting conduction slowing as substrates for block and reentry in infarcted hearts. Biophys J. 2019;117:2361‐2374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Haïssaguerre M, Jaïs P, Shah DC, et al. Spontaneous initiation of atrial fibrillation by ectopic beats originating in the pulmonary veins. N Engl J Med. 1998;339:659‐666. [DOI] [PubMed] [Google Scholar]
- 52. Jacquemet V, Henriquez CS. Genesis of complex fractionated atrial electrograms in zones of slow conduction: a computer model of microfibrosis. Hearth Rhythm. 2009. 6:803‐810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. McDowell KS, Vadakkumpadan F, Blake R, et al. Methodology for patient‐specific modeling of atrial fibrosis as a substrate for atrial fibrillation. J Electrocardiol. 2012; 45 640‐645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Hannun AY, Rajpurkar P, Haghpanahi M, et al. Cardiologist‐level arrhythmia detection and classification in ambulatory electrocardiograms using a deep neural network. Nat Med. 2019;25:65‐69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Raissi M, Perdikaris P, Karniadakis GE. Physics‐informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput Phys. 2019;378:686‐707. [Google Scholar]
- 56. Sahli Costabal F, Yang Y, Perdikaris P, Hurtado DE, Kuhl E. Physics‐informed neural networks for cardiac activation mapping. Front Phys. 2020;8: 42 10.3389/fphy.2020.00042 [DOI] [Google Scholar]
- 57. Fresca S, Manzoni A, Dede’ L, Quarteroni A. Deep learning‐based reduced order models in cardiac electrophysiology. PLoS One. 2020;15:e0239416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Regazzoni F, Dede’ L, Quarteroni A. Machine learning for fast and reliable solution of time‐dependent differential equations. J Comput Phys. 2019;397:108852. [Google Scholar]
- 59. Regazzoni F, Dede’ L, Quarteroni A. Machine learning of multiscale active force generation models for the efficient simulation of cardiac electromechanics. CMAME. 2020;370:113268. [Google Scholar]
- 60. Zygote Media Group Inc. Zygote solid 3D heart generation II development report. Technical report, 2014.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.


