Evaluating Morphological Features of Electrocardiogram Signals for Diagnosing of Myocardial Infarction Using Classification-Based Feature Selection

Abstract

Background:

Cardiovascular disease (CVD) is the first cause of world death, and myocardial infarction (MI) is one of the five primary disorders of CVDs which the patient electrocardiogram (ECG) analysis plays a dominant role in MI diagnosis. This research aims to evaluate some extracted features of ECG data to diagnose MI.

Methods:

In this paper, we used the Physikalisch-Technische Bundesanstalt database and extracted some morphological features, such as total integral of ECG, integral of the T-wave section, integral of the QRS complex, and J-point elevation from a cycle of normal and abnormal ECG waveforms. Since the morphology of healthy and abnormal ECG signals is different, we applied integral to different ECG cycles and intervals. We executed 100 of iterations on a 10-fold and 5-fold cross-validation method and calculated the average of statistical parameters to show the performance and stability of four classifiers, namely logistic regression (LR), simple decision tree, weighted K-nearest neighbor, and linear support vector machine. Furthermore, different combinations of proposed features were employed as a feature selection procedure based on classifier's performance using the aforementioned trained classifiers.

Results:

The results of our proposed method to diagnose MI utilizing all the proposed features with an LR classifier include 90.37%, 94.87%, and 86.44% for accuracy, sensitivity, specificity, respectively. Also, we calculated the standard deviation value for the accuracy of 0.006.

Conclusion:

Our proposed classification-based method successfully classified and diagnosed MI using different combinations of presented features. Consequently, all proposed features are valuable in MI diagnosis and are praiseworthy for future works.

Introduction

Myocardial infarction

The first cause of world death is cardiovascular disease (CVD), which causes more death than other diseases annually. In 2015, about 17.7 million people died from CVD, accounting for 31% of the world's total deaths, of which about 7.4 million people died from the stroke and 7.6 million deaths were because of coronary heart disease. Myocardial infarction (MI) is one of the five main complications of CVDs, which include persistent angina, unstable angina, heart failure, MI, and sudden death.[1,2] Consequently, early diagnosis of MI has critical importance in medical applications for the effective treatment of patients.

MI or “heart attack” occurs when one of the coronary arteries is completely blocked. A region of the myocardium fed by the coronary artery dies, and loses its blood and deprives of oxygen and other nutrients. The sudden and total occlusion of the artery, which precipitates the infarction, is usually due to coronary artery spasm or superimposed thrombosis.[3] As the ST-segment is the most widely used feature for MI detection, the onset of MI can be distinguished into two kinds of MI, namely an ST-segment elevation MI, which is caused by the blockage of an artery from the heart, and a non-ST-segment elevation MI, which depends on T-inversion or ST depression.[4,5,6,7]

Usually, in most cases of infarction, electrocardiogram (ECG) signal processing based on the investigation of the morphology of multi-lead ECG results in precise diagnosis.[8] Early ECG variations and specific electrocardiographic changes associated with MI occurred with the onset of myocardial dysfunctions.[3,7]

During acute MI, the ECG evolves through three stages:

1. T-wave peaking followed by T-wave inversion

2. ST-segment elevation

3. Emergence of a new Q-wave.

However, during an acute infarction, commonly, all three states can appear in the ECG, but it is possible to have any of these conditions without another one. For example, it is not unusual at all that the ST-segment elevation occurs without T-wave inversion. Considering all the three states, we can predict MI with the least error.[3,9] Some of these methods introduced are as follows:

1. If the T-wave peaks and then reverses, it represents myocardial ischemia. In addition, if an acute MI occurs, then T-wave can remain reverse about more than a few months to several years

2. If the ST-segment raises and joins with the T-wave, then it indicates a myocardial injury. Furthermore, the ST-segment usually recovers to baseline within a few hours when infarction happens

3. If a new Q-wave appears within hours to days, then it signifies MI. In most cases, the Q-wave persists for the rest of the patient life.[3]

The localization of infarction is essential since its prognostic and therapeutic effects are in the heart regions, which are already dead. Infarctions categorized into several general anatomic categories. These are inferior infarctions, lateral infarctions, anterior infarctions, and posterior infarctions. Combinations can also be realized, such as anterolateral infarctions, which are very common.[3]

1. Inferior infarction: The structural electrocardiographic changes of infarction reveal in the inferior leads such as II, III, and AVF

2. Lateral infarction: In this infarction, the occlusion of the left circumflex artery leading to changes in the left lateral leads AVL, I, V5, and V6

3. Anterior infarction: This infarction marked by specific changes in the precordial leads (V1–V6)

4. Posterior infarction: In this infarction, since there are no leads overlying the posterior wall of the heart, therefore, the anterior leads, especially V1, are needed to investigate for reciprocal changes, which are indeed essential to diagnose posterior MI.

Research background

According to all studies, MI diagnosing generally constitutes four major phases, including signal preprocessing step, ECG wave segmentation, feature extraction, and classification. In general, signal features extracted from the time-domain, the frequency-domain, and the transform-domain.[5,10] The importance of an efficient feature selection method is undeniable and affects the overall performance of classification methods.

There are several automated, semi-automated, or manual signal segmentation approaches for signal feature extraction. For example, Al Touma et al. proposed a system which utilized two algorithms, and the first algorithm could detect the critical points on the ECG waveforms and the second algorithm could detect possible MI based on the analysis of the aforementioned critical points.[4] Further, Gupta and Kundu applied a statistical index, namely dissimilarity factor “D” to classify normal and inferior MI data, without the need for any direct clinical feature extraction. Accordingly, the T-wave and the QRS sections of inferior MI datasets were automatically extracted from the leads II, III, and aVF and then compared with corresponding segments of healthy patients using the Physikalisch-Technische Bundesanstalt (PTB) database.[11]

Some research analyzes and investigates the effects and arrangements of each MI feature. Carley presented that the location of leads V1–V6 depends on historical convention, and there is clear evidence that ST-elevation, indicative of acute MI, exists outside of the standard 12-lead ECG.[12] Accordingly, we consider it as an essential factor to detect and localize MI in the current study. Besides, Muhammad Arif et al. employed time-domain features of each beat in the ECG signal, including T-wave amplitude, Q-wave, and ST-elevation using K-nearest neighbor (KNN) classifier in an automated scheme for diagnosis and localization of MI.[13] Similarly, Safdarian et al. applied two new time-domain features including total integral and T-wave integral as morphological signal features to detect and localize the MI in the left ventricle of the heart.[14]

On the other hand, some researches focused on the features in the frequency domain or the transform domain of the ECG signal. As an example, Nidhyananthan et al. proposed a wavelet-based method, which applied for detecting MI along with user-identity using a support vector machine (SVM) classifier to classify the normal and abnormal cases in these signals. In addition, the RR interval utilized to authenticate the ECG signal.[15] In addition, Sharma et al. represented a novel technique on multiscale energy and Eigen space approach to detect and localize MI from multi-lead ECG. Moreover, the nearest neighbor (KNN), and the SVM, along with both linear and radial basis function kernels applied as classifiers.[16]

Moreover, Noorian et al. proposed the radial basis function neural networks classifier with wavelet coefficient as features extracted from frank lead to diagnose and localize MI.[17] Moreover, Tripathy et al. proposed the multiscale convolutional neural network for automatic MI localization using the Fourier-Bessel (FB) series expansion-based empirical wavelet transform (EWT) for signal segmentation and feature extraction.[8] Concerning the use of neural networks, similarly, Zhang et al. proposed a multi-lead bidirectional-gated recurrent unit neural network, and their results show that the algorithm has higher sensitivity, positive predictivity, accuracy, and universality.[7]

In this study, we focused on the feature selection section as an essential part of a successful MI diagnosing and classification. We presented a classification-based feature selection method to analyze the worthiness of the extracted ECG morphological features and to tackle the problem of feature selection.

Objectives

The main objective of our study is to evaluate the efficiency of the proposed extracted morphological features from ECG data in MI diagnosis and not necessarily diagnosing MI only. The higher the quality of ECG extracted features, the better the results in the early diagnosis of MI.

Materials and Methods

Signal acquisition

In this study, we proposed a classification-based feature selection procedure to evaluate the ECG morphological features for diagnosing MI. At this point, we collect our ECG data from PhysioNet. In the PTB database, the ECGs were derived from patients with various heart diseases and healthy volunteers.[18]

In our research, we have assigned two diagnostic classes, including 148 MI subjects and 52 standard control subjects, since we investigated MI types. Consequently, the sum of 59 healthy ECG records alongside 156 MI records forms the complete database of 215 signal records.

Signal preprocessing and feature extraction from electrocardiogram signals

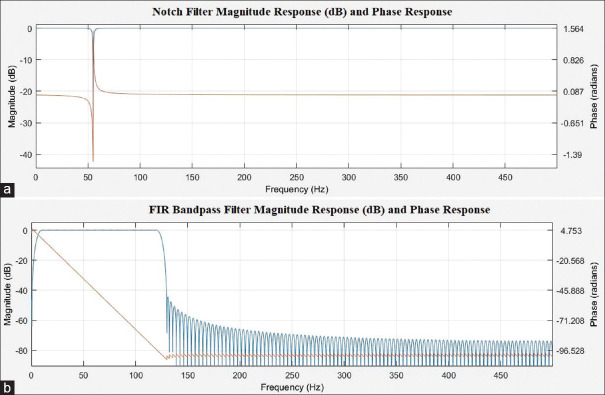
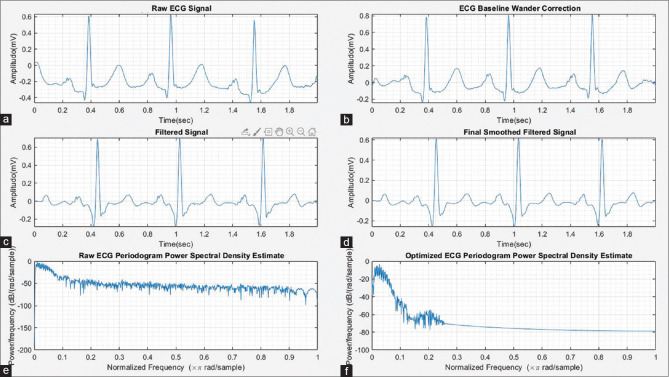
The raw ECG records contain various artifacts such as muscle noise, power line interference noise, and baseline wander.[4,10] In this article, we implemented two filters, namely the band-pass FIR filter (ECG band 0.5–150 Hz) and IIR notch filter (55 Hz) to remove noise from ECG signals. The notch filter removes the power line interference noise of 50–60 Hz. Moreover, the band-pass FIR filter is designed using a minimum order Kaiser window for the removal of ECG baseline wander. We utilized MATLAB filter design application and the design configuration summary of each filter presented and also, the Bode plot for the filters and also, signal optimization are shown in Figures 1 and 2.

Figure 1.

(a) Notch filter magnitude response (dB) and phase response; (b) FIR band-pass Filter magnitude response (dB) and phase response

Figure 2.

(a) Raw electrocardiogram signal, (b) electrocardiogram baseline wander correction, (c) filtered electrocardiogram signal, (d) final smoothed filtered electrocardiogram signal, (e) raw electrocardiogram periodogram power spectral density estimate, and (f) optimized electrocardiogram periodogram power spectral density estimate

IIR notch filter

• Filter order: 2

• Sampling frequency: 1000

• Notch Bandwidth: 10 Hza

• Passband ripple (Apass): 0.1 dB

FIR band-pass filter

• Filter order: 124

• Sampling frequency: 1000

• Window: Kaiser

• End of the first stopband (Fstop1): 0.5 Hz

• Beginning of the passband (Fpass1): 10 Hz

• End of the passband (Fpass2): 100 Hz

• Beginning of the second stopband (Fstop2): 150 Hz

• Passband ripple (Apass): 0.1 dB

• Stopband attenuation for both stopbands (Astop1, Astop2): 40 dB.

In this review, we focused on ECG features and identified fundamental characteristics to extract, classify, and eventually determine exact MI types, which are presented below:

1. Peaking of the T-wave (hyperacute T-wave) followed by inversion of the T-wave

2. Elevation of the ST segment.

The idea is to integrate the ECG signal and extract the above features. Accordingly, we compute definite integrals of “ECG cycle,” “QRS complex,” and “T-wave” using “trapz” function in MATLAB (R2016b) software. As a result, we can extract morphology variations and hyperacute T-wave features of ECG signal in MI as well. Furthermore, we use ECG J-point elevation value to estimate ST-elevation and also extract it as a feature from three ECG leads, namely lead I, lead II, and lead V2.

According to the MATLAB software, the “trapz” operates numerical integration via the trapezoidal method, which can divide the area down into trapezoidal segments to approximate the integration over an interval. Therefore, the approximation is as follows:

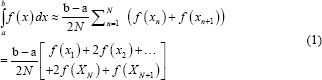
Where the spacing between each point is equal to the scalar value .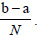

Thus, we obtain a general “features matrix” with 215 rows and 11 columns, which include features and labels. Consequently, the features extraction process of ECG signals accomplishes. The final features matrix arrays contain {F1, F2, F3, F4, F5, F6, F7}; features accompany with two class and four class labels.

• F1: Integral of a complete ECG cycle

• F2: Integral of ORS complex

• F3: Integral of T-wave

• F4: ST elevation in lead I

• F5: ST elevation in lead II

• F6: ST elevation in lead V2

• F7: T-wave inversion (0 for no inversion and 1 for inversion).

The laptop we used had Windows 8.1 as the operating system, a Core i7 CPU, and 12 GB of RAM.

In this study, initially, we create a database from ECG-extracted features. Subsequently, we can classify MI and obtain the results using a 5-fold cross-validation technique to detect MI from ECG data. The 5-fold cross-validation divides the ECG data into four training datasets and a validation dataset as the inputs of four classifiers, namely the fine decision tree, the linear SVM (L-SVM), the weighted KNN, and the logistic regression (LR). We suggest the diagnosis of MI by evaluating ECG data using two procedures, including the two-class and the four-class classification. The dataset in the two-class classification method contains healthful records and MI records, however; in the four-class classification procedure, we have healthful records, inferior, anterior, and posterior MI records.

Statistical analysis

Statistical analyses to investigate the relationship between the features

To test the normality of the data (features extracted from the ECG signals), the test of the normality of the following features was performed in SPSS software (Version 20, IBM Corp. Released 2011. IBM SPSS Statistics for Windows, Version 20.0. Armonk, NY: IBM Corp.).

Features include F1, F2, F3, F4, F5, F6, and F7; Table 1 shows the test results for the above features.

Table 1.

Tests of normality of the features

Features	Kolmogorov-Smirnova			Shapiro-Wilk
	Statistic	df	P	Statistic	df	P
F1	0.094	215	0.000	0.879	215	0.000
F2	0.056	215	0.093	0.981	215	0.006
F3	0.051	215	0.200*	0.975	215	0.001
F4	0.513	215	0.000	0.424	215	0.000
F5	0.435	215	0.000	0.585	215	0.000
F6	0.402	215	0.000	0.616	215	0.000
F7	0.442	215	0.000	0.577	215	0.000

*This is a lower bound of the true significance, ^aLilliefors significance correction

As shown in Table 1, and according to P value and the skewness results for all seven sets of extracted features, it indicates that the features are abnormal. Furthermore, Table 1 represents the comparison of variance status and skewness values of all three groups of the above characteristics.

Since the data of all seven groups of features do not have a normal distribution, parametric tests (such as t-test or ANOVA test) cannot be used to analyze these features. Therefore, we must use nonparametric analyses to investigate the independence of features. We then examine whether there is a significant difference between the seven sets of extracted features using the Friedman nonparametric test.

The results of Friedman nonparametric test show that there is a significant difference between the seven groups of different features due to the P < 0.01. In other words, the Chi-square value of Friedman's test is confirmed with an error of <1% and a confidence level of 99%. According to Tables 2 and 3, because of the significant difference between the different groups of extracted features, we can use them to enter classification algorithms. Finally, let us look at the accuracy, sensitivity, and specificity values used by classifying algorithms on these data.

Table 2.

Statistical analysis for the features

Statistics	F1	F2	F3	F4	F5	F6	F7
Valid (n)	215	215	215	215	215	215	215
Missing (n)	0	0	0	0	0	0	0
Mean	0.0001	0.0056	0.0063	0.1488	0.3163	0.3814	0.3023
SD	0.00050	0.01447	0.01238	0.35676	0.46611	0.48686	0.46034
Variance	0.000	0.000	0.000	0.127	0.217	0.237	0.212
Skewness	0.816	0.186	−.428	1.987	0.796	0.492	0.867
SE of skewness	0.166	0.166	0.166	0.166	0.166	0.166	0.166
Kurtosis	10.122	1.281	2.195	1.967	−1.380	−1.775	−1.260
SE of kurtosis	0.330	0.330	0.330	0.330	0.330	0.330	0.330

SE – Standard error; SD – Standard deviation

Table 3.

Friedman test

Ranks	Mean rank
F1	3.47
F2	4.09
F3	4.42
F4	3.52
F5	4.17
F6	4.47
F7	3.87
Test statisticsa
n	215
χ2	49.306
df	6
Asymptotic P	0.000

^aFriedman test

Statistical analysis to examine the relationship between data sets of extracted features from healthy and myocardial infarction classes

To test the normality of the data (extracted features from ECG signals of healthy and patient data), the following test of the normality of the following features was performed in SPSS software (Version 20). Review classes are given below.

• Healthy

• Patients with MI.

Moreover, the features examined in the above have seven independent classes including F1, F2, F3, F4, F5, F6, and F7.

In the previous section, the normality test was examined. At this stage, since the two healthy and MI classes represent two completely independent nonparametric groups, we use Mann–Whitney and Kolmogorov–Smirnov tests.

First, the tests above are performed on all seven features for two class labels (only healthy and only MI). Table 4 shows the results of the above two tests and reveals that all the features extracted from healthy ECG and MI samples (except for feature 4) in both groups (with label 1 for healthy and label 2 for MI, respectively) have a P < 0.05 value for both tests, which means that there is a significant difference between the data of healthy individuals and MI for these extracted features (except for the feature number 4, of course).

Table 4.

Mann-Whitney and Kolmogorov-Smirnov test

Mann-Whitney test	F1	F2	F3	F4	F5	F6	F7
Mann-Whitney test statisticsa
Mann-Whitney U	3066.000	3102.000	1058.000	4303.000	3563.500	3365.500	2792.000
Wilcoxon W	15312.000	15348.000	13304.000	6073.000	5333.500	5135.500	4562.000
Z	−3.774	−3.685	−8.707	−1.192	−3.168	−3.611	−5.590
Asymptotic P (two-tailed)	0.000	0.000	0.000	0.233	0.002	0.000	0.000
Two-sample Kolmogorov-Smirnov test statisticsa
Most extreme differences, absolute	0.330	0.294	0.655	0.065	0.226	0.269	0.393
Positive	0.330	0.294	0.655	0.000	0.000	0.000	0.000
Negative	−0.024	−0.013	0.000	−0.065	−0.226	−0.269	−0.393
Kolmogorov-Smirnov Z	2.156	1.923	4.284	0.425	1.476	1.758	2.573
Asymptotic P (two-tailed)	0.000	0.001	0.000	0.994	0.026	0.004	0.000

^aGrouping variable: Label_2_class

Then, analyses are performed on all seven features for four class labels (healthy samples and three types of MI patient samples). At this stage, since one healthy class and three patient classes represent four completely independent groups, we use Kruskal–Wallis and median tests because these tests can be performed on more than two independent nonparametric groups.

In Table 5, the results of the above two tests indicate that all the extracted features from the ECG signals of healthy and patient samples (except for F4 in the Kruskal–Wallis test, and F2 and F4 in the median test for all four healthy and patient classes, label 1, label 2, label 3, and label 4, respectively) have valued P < 0.05 for both tests. It means that there is a significant difference between the data of healthy people and MI patients for all the extracted features, except for the two features mentioned above. Therefore, choosing these features to distinguish between healthy data and three MI patient groups is rational and performs acceptable discrimination between the classes as well.

Table 5.

Kruskal-Wallis and median tests

	F1	F2	F3	F4	F5	F6	F7
Kruskal-Wallis test statisticsa
χ2	45.620	13.594	82.702	2.374	11.126	59.767	36.221
df	3	3	3	3	3	3	3
Asymptotic P	0.000	0.004	0.000	0.499	0.011	0.000	0.000
Median test statisticsa
n	215	215	215	215	215	215	215
Median	0.0001	0.0049	0.0057	0.0000	0.0000	0.0000	0.0000
χ2	35.824b	4.324b	70.553b	2.385c	11.178d	60.047e	36.390f
df	3	3	3	3	3	3	3
Asymptotic P	0.000	0.229	0.000	0.496	0.011	0.000	0.000

^aGrouping variable: Label_4_Class, ^b2 cells (25.0%) have expected frequencies <5. The minimum expected cell frequency is 2.5, ^c2 cells (25.0%) have expected frequencies <5. The minimum expected cell frequency is 0.7, ^d2 cells (25.0%) have expected frequencies <5. The minimum expected cell frequency is 1.6, ^e2 cells (25.0%) have expected frequencies <5. The minimum expected cell frequency is 1.9., ^f2 cells (25.0%) have expected frequencies <5. The minimum expected cell frequency is 1.5

According to Table 5, the significant difference between the different classes of extracted features is noticeable, and we can use them to enter classification algorithms.

Classification

In this section, we compute integral of filtered ECG signal to extract aforementioned features, and next, we choose J-point elevation value in mv unit manually for 215 data samples and use these characteristics to create feature matrix. Furthermore, we apply 5-fold and 10-fold cross-validation for each of the classifiers and calculate the sensitivity and specificity using these two formulas below.[7,10,19,20]

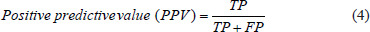
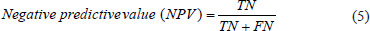
Moreover, we executed 100 iterations for 5-fold and 10-fold cross-validation on the 2-class and 4-class classification to show the stability of the proposed models.

K-fold cross-validation

The cross-validation estimate of accuracy equals the overall number of correct classifications divided by the number of samples in the dataset. Accordingly, assume that the inducer J maps a given dataset into a classifier and D(_i) is the test set that includes sample x_i = (v_i, y_i). Note that δ is the mean square error function, then the cross-validation estimate of accuracy is:[21]

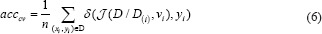
Logistic regression

LR is used to describe the data and explain the relationship between a dependent binary variable and one or more independent variables.[22,23] The regression analysis uses the log odds to compute output Y. Further, it tackles the problem of probabilities limitation and uses a cost function to compute the individual cost of each observation Yp. The LR equation is:

β = A0+A1(x) (7)

Further,

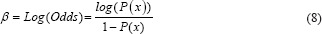
We define a cost function threshold of 0.5 for decision-making, so we have:

if Y ≥ 0.5: cost = -Log(Y_p)     (9)

if Y ≤ 0.5: cost = -Log(1-Y_p)     (10)

Where β is the log odds and A0 and A1 are logistic coefficients with initial values determined by optimization, which must minimize the cost function. Hence, the probability Y using a sigmoid function is:

Linear support vector machine

In machine learning, the SVMs include supervised learning models, which are a set of points in the n-dimensional data that specify the boundaries of the classes to classify the data. Consider a collection of training samples that each sample belongs to one or the other of two classes, the SVM finds the optimal hyperplane, which splits all data points of one class from those of the other class.[10,24]

This discussion follows Hastie et al.[24] and Cristianini and Shawe-Taylor.[25] The training data define as a set of points (vectors) x_i along with their groups y_i. For some dimension d, the x_i ∊ R^d, and the y_i = ±1. The equation of a hyperplane is:

f(x) = βx' + b(12)

Where β ∊ R^d and b is a real number.

The following problem defines the optimal separating hyperplane (i.e., the decision boundary). Find β and b, which minimize ||β|| such that for all data points (x_i,y_i), y_jf (x_j) ≥ 1–ξ_i. Hence, for i ∊ {1,…, n}, we define ξ_i = max (0, 1–y_jf (x_j)). The support vectors are the x_i on the boundary for those which y_jf (x_j) = 1. For mathematical ease, the problem is usually assumed as the equivalent problem of minimizing ||β||.[24,26] In our work and according to MATLAB, the length of beta is equal to the number of predictors used to train the model so for more information check MATLAB help. Finally, we have:

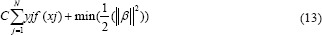
Where if C grows too large, the algorithm will reduce ||β||, leading to a hyperplane that classifies each training sample correctly. Conversely, if C becomes too small, then the algorithm increases ||β|| causing large training error.[26]

Decision tree

The decision tree learning is one of the predictive modeling methods applied in statistics, which maps observations about an item (presented in the branches) to conclude on the target value of the item (shown in the leaf). In tree classification, the target variable can accept a limited set of values; in these tree structures, leaves and branches, respectively, represent class labels and a combination of features, which leads to those class labels.[10,27]

K-nearest neighbors' algorithm

One of the nonparametric methods in pattern recognition is the KNN algorithm utilized for classification, which the term nearest is the foundation of the KNN so that each new instance compares to all prior cases and then assigns to the group with closer samples to each other. Since the KNN output is a class membership, therefore, the KNN assigns the sample to the class most common among its k nearest neighbors (k is a positive integer, typically small). The sample assigns to a class of that single nearest neighbor if k = 1.[10,22]

In the weighted KNN classifier, we assign a weight 1/k to the k nearest neighbors and all others a weight zero. That is, where the i^th nearest neighbor assigns a weight ω_ni with 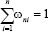.[23]

Let 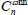denotes the weighted nearest classifier with weights 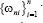. With regard to regularity conditions on class distributions, the excess risk has the following asymptotic expansions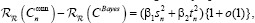

for constants β₁ and β₂, where 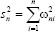and .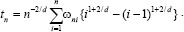

The optimal weighting scheme 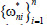, which moderates the two terms in the aforementioned above, is given as follows:

set 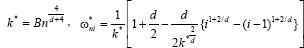for i = 1,2 …,k^* and 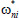for i = k^* + 1,…,n.[19]

Results

According to Table 6, in two-class classification, the LR represents optimal accuracy, sensitivity, and specificity considering the standard deviation (SD) value and is more reliable caparisoning the other classifiers to diagnose MI. The comprehensive analysis of two-class classification reveals that the LR with 90.37% of precision has a better performance in comparison with the others. In the four-class classification, we should estimate sensitivity and specificity for each class individually. Therefore, in Table 7, we only report accuracy and related SD values for the models. The true-positive rate (TPR) (sensitivity), the false-negative rate (FNR), the positive predictive value (PPV), and the false predictive rate (FPR) for each classifier are determined in Figures 3-6.

Table 6.

5-fold and 10-fold cross-validation for two-class classification using different classifiers

Method	Classifier	Mean accuracy	SD	Sensitivity	Specificity	FPR	NPV	PPV
5-fold cross validation for two-class classification	Logistic regression	90.344	0.00793	94.872	86.441	13.55	86.44	94.87
	Linear SVM	88.809	0.00980	95.59	78.407	21.59	87.05	92.13
	Weighted KNN	85.772	0.01041	94.231	69.492	30.50	82	89.09
	Simple tree	82.772	0.02041	98.718	83.051	16.94	96.07	93.90
10-fold cross validation for two-class classification	Logistic regression	90.372	0.00618	94.872	86.441	13.559	86.441	94.872
	Linear SVM	89.06	0.00769	95.622	78.407	21.593	87.142	92.133
	Weighted KNN	86.181	0.00823	94.231	69.492	30.508	82	89.091
	Simple tree	83.823	0.01455	98.718	83.051	16.949	96.078	93.902

SD – Standard deviation; PPV – Positive predictive value; NPV – Negative predictive value; FPR – False predictive rate; SVM – Support vector machine; KNN – K-nearest neighbor

Table 7.

5-fold and 10-fold cross-validation for four-class classification using different classifiers

Method	Classifier	Mean accuracy	SD
5-fold cross validation for four-class classification	Simple tree	63.96	0.0243
	Linear SVM	73.09	0.0115
	Weighted KNN	68.07	0.0172
10-fold cross validation for four-class classification	Simple tree	63.93	0.0210
	Linear SVM	73.44	0.0072
	Weighted KNN	68.32	0.0116

SD – Standard deviation; SVM – Support vector machine; KNN – K-nearest neighbor

Figure 3.

Two-class classification confusion matrices using 10-fold cross-validation for (a) logistic regression, (b) linear support vector machine, (c) weighted K-nearest neighbor, and (d) simple tree classifiers

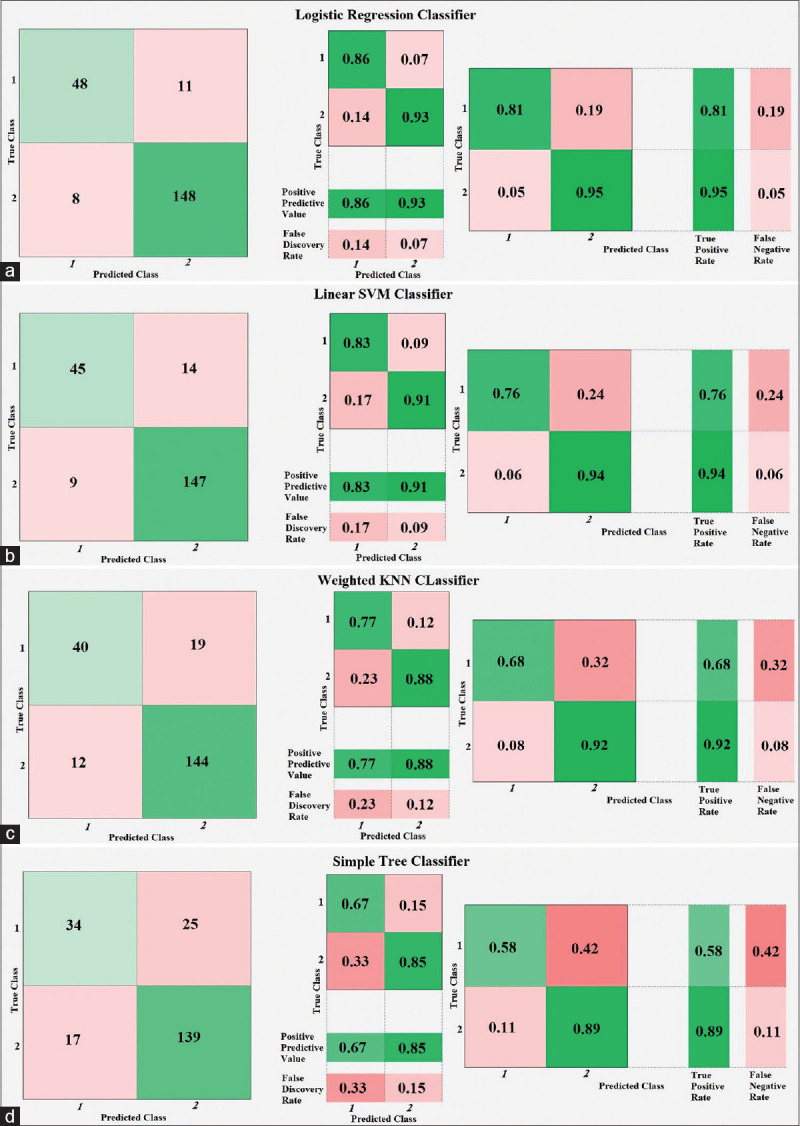
Figure 6.

Four-class classification confusion matrices using 10-fold cross-validation for simple tree classifier

Figure 5.

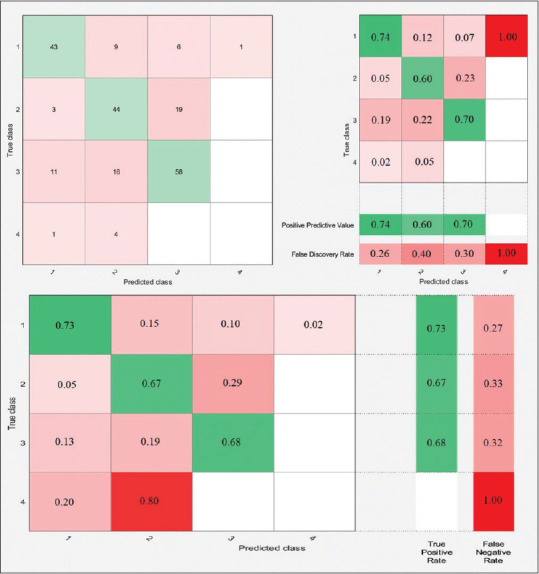
Four-class classification confusion matrices using 10-fold cross-validation for weighted K-nearest neighbor classifier

Discussion

There are representative performance schematics of all classifiers and their confusion matrices, as shown in Figures 3-6. Let us define each class to analyze the two-class and four-class classifications.

• Two-class classification

  Class 1: healthy records, Class 2: MI records.

• Four-class classification

  Class 1: healthy records, Class 2: anterior MI records, Class 3: inferior MI records, and Class 4: posterior MI records.

For example, in Figure 3a, the left-sided image represents the number of observations for the LR classifier. Moreover, the middle schematic indicates PPV and FPR. Furthermore, the right-sided schematic shows the TPR and FNR for each class in the two-class classification using 10-fold cross-validation. According to the aforementioned right-sided image, TPR for the first class is 81%, declaring that 81% of normal records correctly classified as healthy ECG, and FNR for the first class is 19%, demonstrating that 19% of healthy ECG records misclassified and predicted as MI records. Accordingly, the same comprehension analytic procedure can be applied for the four-class classification in, Figures 4-6 for different classifiers.

Figure 4.

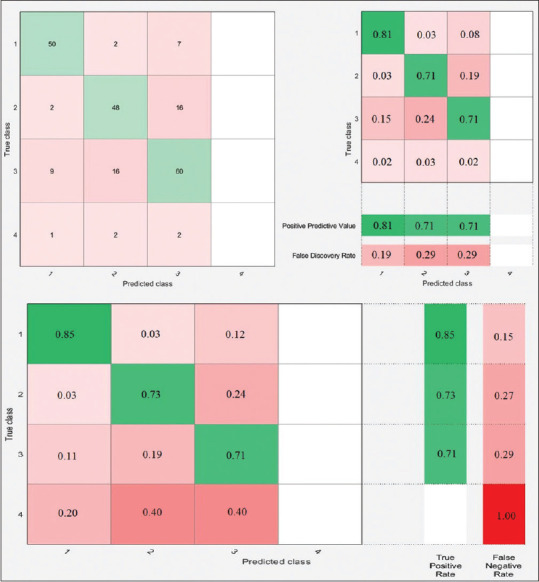
Four-class classification confusion matrices using 10-fold cross-validation for linear support vector machine classifier

According to Tables and Figures, the performance of L-SVM with 73.44% of accuracy is considerable in four-class classification. Note that all classifiers failed to predict the fourth class successfully just because of minimal sample volume.

As our main objective is to show how valuable is the strength of extracted features in the successful diagnosis of the MI, it is more satisfying to choose a different combination of signal features as an efficient method to observe how the accuracy of each classifier changes. According to the feature matrix, it consists of seven key features, namely F1, F2, F3, F4, F5, F6, and F7. In the proposed method, three signal features remain as default. Since F1, F2, and F3 extracted from lead II, we consider them as homogenous features and should always persist.

Based on Table 8, the precision of all classifiers with the set of {F1, F2, F3, F5, F6, F7} is more reliable in comparison with other sets of selected features in two-class classification. Furthermore, the F4, which is the set of J-point elevation values of ECG signals of lead I in mv, decreases the accuracy of classifiers. On the other hand, it seems that ignoring F4 from all features leads to a significant increase in the precision of classifiers.

Table 8.

10-fold cross-validation for two-class and four-class classification with different classifiers and also various combinations of selected features

Method			10-fold cross-validation
Four-class classification	Feature selection	F1	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
		F2	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
		F3	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
		F4	✓	✓	✓	✓	-	-	✓	✓	-	✓	-	-	✓
		F5	✓	✓	✓	-	✓	-	-	✓	-	-	✓	✓	-
		F6	✓	✓	-	✓	✓	✓	-	-	-	-	✓	-	✓
		F7	✓	-	✓	✓	✓	✓	✓	-	✓	-	-	✓	-
	Classifier accuracy	Simple tree (%)	64.7	64.7	63.7	64.7	64.7	64.7	63.7	63.7	63.7	63.7	64.7	63.7	64.7
		Linear SVM (%)	73.0	72.6	59.1	70.2	74.0	70.7	64.2	60.5	61.4	63.7	73.5	61.9	70.7
		Weighted KNN (%)	67.9	66.0	54.9	69.8	69.8	70.7	58.1	53.0	57.2	58.1	69.8	59.5	68.8
Two-class classification	Feature selection	F1	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
		F2	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
		F3	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓	✓
		F4	✓	✓	✓	✓	-	-	✓	✓	-	✓	-	-	✓
		F5	✓	✓	✓	-	✓	-	-	✓	-	-	✓	✓	-
		F6	✓	✓	-	✓	✓	✓	-	-	-	-	✓	-	✓
		F7	✓	-	✓	✓	✓	✓	✓	-	✓	-	-	✓	-
	Classifier accuracy	Simple tree (%)	83.7	83.7	82.8	83.7	83.7	83.7	82.8	82.8	82.8	82.8	83.7	84.7	83.7
		Linear SVM (%)	89.8	89.8	84.7	89.3	89.8	89.3	81.9	84.2	82.3	81.9	89.3	80.9	88.8
		Weighted KNN (%)	87.9	87.0	86.0	87.0	88.8	88.8	84.2	87.0	83.7	84.7	86.5	85.1	87.4
		Logistic regression (%)	90.7	90.2	84.2	89.3	91.2	89.3	83.3	85.1	81.9	82.3	91.2	82.8	90.2

SD – Standard deviation; SVM – Support vector machine; KNN – K-nearest neighbor

As noted in the Statistical Analysis section, in the two-class analysis, the F4 feature did not differ significantly between healthy and MI samples. According to Tables 4 and 5, in four-class analysis, the same F4 feature did not make a significant difference between healthy and three MI samples, which confirms the best results of all the classifiers in distinguishing between extracted features. Note that other extracted features ({F1, F2, F3, F5, F6, F7}), following statistical analysis, and the results of the accuracy of all the classifiers presented in this article, have a significant difference, both in two-class labeling and in four-class labeling.

In MI diagnosis studies, various approaches applied including using wavelet, applying a similarity factor between normal, MI record-keeping, employing eigenvalue, and the energy of ECG signal as extracted features. Since our method applied mentioned classifiers, a similar approach should be compared to our work to achieve a reasonable assessment. Accordingly, Table 9 presents a comparison of our results to other research works. In the proposed method, it is clear that in 10-fold cross-validation with the LR classifier, the accuracy, sensitivity, and specificity achieved an acceptable result in comparison with the others. According to Tables 6-9, we executed 100 iterations for 5-fold and 10-fold cross-validation and calculating the statistical average and SD on the two-class and four-class classification to show that the proposed method along with the “Statistical Analysis” section has acceptable and reliable results and the compatibility of both results is not accidental.

Table 9.

The comparative analysis of the proposed method with other methods for two-class classification

Two-class classification of MI
Methods	Extracted features	Classifier	Accuracy (%)	Sensitivity (%)	Specificity (%)
Proposed method	Integral of ECG and J-point value	Weighted KNN	87.9	94	73
		Linear SVM	89.8	95	76
		Logistic regression	90.37	94	83
L. N. Sharma et al.[16]	Multiscale wavelet energies and eigenvalues of multiscale covariance matrices	KNN	82.28	81.98	82.32
		Linear SVM	88.02	87.23	88.53
S. Selva Nidhyananthan et al.[15]	Multiscale wavelet energies and eigenvalues of multiscale covariance matrices	Linear SVM	90.42	89	87
Naser Safdarian et al.[14]	Integral of ECG and T-wave	KNN	89.47	NA	NA

SVM – Support vector machine; KNN – K-nearest neighbor; MI – Myocardial infarction

Conclusion

In this study, we examined different extracted features from ECG data in a classification-based feature selection method, and the results show that they are more efficient in the two-class classification in comparison with the four-class. The ECG J-point belonging to all leads is a valuable feature, but in case of better accuracy, it is recommended to extract it by precise automatic algorithms. In addition, the results show that eliminating the F4 feature, which consists of the values of J-point in lead I, approximately increases the precision of all classifiers in the proposed combination of features space. It is essential to point out the more accurate extraction algorithms, the better classification, and results. Finally, the proposed features are valuable for the diagnosis and localization of MI and are recommended for future works.

Suggestions and future studies

There are several suggestions for future studies. To improve the performance of classifiers, the accuracy of the feature extraction technique should increase. As a whole, these are our suggestions for future research:

1. A robust and precise algorithm to detect all parts of ECG correctly

2. Detect pathologic Q wave and extract it as a feature

3. Using other classifiers and especially the nonlinear classifiers.

Compliance with ethical standards

Disclosure of potential conflicts of interest

Since data have obtained from PhysioNet Database free of charge, this study has not funded by any real person or legal institution.

Informed consent and research involving human participants and/or animals

This article does not contain any studies with human participants and/or animals performed by any of the authors but as we have obtained human participant's data from PhysioNet Database so, there have been no practical experiments on human by any of the present authors.

Financial support and sponsorship

None.

Conflicts of interest

There are no conflicts of interest.

BIOGRAPHIES

Seyed Ataddin Mahmoudinejad received the B.Eng. Degree in biomedical engineering from the Islamic Azad University of Dezful, Dezful, Iran, in 2013. In 2015, he graduated from the M.Sc. Eng. in biomedical engineering from Islamic Azad University of Kazeroon, Kazeroon, Iran. Since then, he has been with the Technology Development Centre, Dezful University of Medical Sciences, Dezful, Iran. Also, he is currently a member of the Intellectual Property Committee of the Medical University of Dezful. In 2019, he became a PhD student at the medical university of Tehran, Tehran, Iran. His researches interests are biomedical signal processing artificial intelligence and medical robotic. He studies biomedical engineering in the field of medical robotic until now.

Email: a-mahmoudinejad@razi.tums.ac.ir

Naser Safdarian received M.Sc in Biomedical Engineering from Science and Research Branch, Islamic Azad University, Tehran, Iran, in 2011. His researches interests are Biomedical Signal Processing, especially ECG and EMG Signal Processing, Intelligence Algorithms, Optimization, and Medical Image Processing. He is currently a PhD student in Biomedical Engineering.

Email: naser.safdarian@yahoo.com