Abstract
Water, being the universal solvent, acts as a competing agent in fundamental processes, such as folding, aggregation or biomolecular recognition. A molecular understanding of hydrophobic hydration is of central importance to understanding the subtle free energy differences, which dictate function. Ab initio and classical molecular dynamics simulations yield two distinct hydration water populations in the hydration shell of solvated tert-butanol noted as “HB-wrap” and “HB-hydration2bulk”. The experimentally observed hydration water spectrum can be dissected into two modes, centered at 164 and 195 cm–1. By comparison to the simulations, these two bands are attributed to the “HB-wrap” and “HB-hydration2bulk” populations, respectively. We derive a quantitative correlation between the population in each of these two local water coordination motifs and the temperature dependence of the solvation entropy. The crossover from entropy to enthalpy dominated solvation at elevated temperatures, as predicted by theory and observed experimentally, can be rationalized in terms of the distinct temperature stability and thermodynamic signatures of “HB-wrap” and “HB-hydration2bulk”.
Hydrophobic hydration has been the subject of controversial debates about whether hydration water can be described as ice-like (iceberg model)1 or as clathrate cages,2 i.e., formed by hydrogen bond structures with enhanced tetrahedral order. The free energy cost of solvating hydrophobic solutes in water depends on the solute size as described in Lum–Chandler–Weeks (LCW) theory.3 For small solutes (e.g., radii of <0.4 nm), the water hydrogen bond (HB) network responds elastically to accommodate the solute cavity, but a reduced number of intact network configurations results in an entropy decrease that is proportional to the excluded volume of the solute.4 On the other hand, interfacial thermodynamics applies for larger solutes, i.e., beyond nanometer size. This involves breaking water–water HBs and a corresponding change in enthalpy.4 More specifically, according to LCW theory, an interfacial hydration water layer is formed that minimizes the number of broken HBs compared to bulk water, nevertheless resulting in an enthalpic cost that scales with the surface area of the hydrophobic solute.
On the basis of this model, additional studies proposed that water molecules form a tetrahedral HB cage around small, spherical solutes (<1 nm in diameter), while for solutes beyond 1 nm, a structural “crossover” is predicted yielding a vapor–liquid-like interface with a dewetted zone close to larger hydrophobic solutes and extended hydrophobic surfaces.4−6 Raman and infrared (IR) experiments proposed the existence of tetrahedral hydration water structures around small hydrophobic solutes,7,8 while nuclear magnetic resonance,9 pump–probe two-dimensional (2D) IR,10 and femtosecond mid-IR11 spectroscopic studies revealed an increase in the relaxation and reorientation times of water around hydrophobes compared to bulk water. This could be explained by an excluded volume effect without invoking a specific (“ice-like/clathrate-like”) water structure.12
The theoretical predictions of LCW theory were confirmed by a series of precise temperature- and chain length-dependent Raman spectroscopy studies of hydrated alcohol chains,3,7,8,13 observing an overall crossover from more red-shifted (more tetrahedral) to blue-shifted (more disordered) water OH stretch vibrations for higher temperatures and larger alcohol chains. Because any increase in temperature increases the number of broken HBs in water, a crossover between the two hydrophobic hydration mechanisms could be observed even for small solutes at high temperatures.4,6 Enhanced ordering of water was also observed in the case of hydrophobic interfaces.14 Notably, an enhanced strength of water–water HBs and an increased tetrahedral network structure in the vicinity of small hydrophobic solutes go beyond predictions from LCW theory, which instead describes an elastic response of the HB network structure to the solute cavity.4 Accordingly, molecular dynamics (MD) simulations15 indicate that on average the local water structure is similar to the bulk, with the coexistence of strong water–water pair correlations and less ordered water configurations.
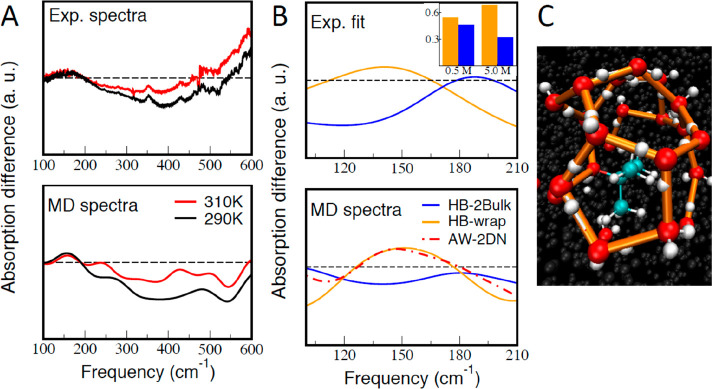
Here, we investigate the properties of the water HB network in the vicinity of the tert-butanol solute via THz spectroscopy and MD simulations. We present in Figure 1A the absorption difference spectrum αdifference. αdifference describes the THz spectrum of water in the hydration layer and is obtained by subtracting the volume-scaled absorption spectrum of bulk water αbulk from the absorption spectrum of the solution αsolution (see ref (16) for details). The measurements were carried out for a 0.5 M alcohol concentration at two temperatures (290 and 310 K) between 100 and 600 cm–1, thereby extending the frequency range of earlier measurements.16 The absorption of aqueous solutions in the 100–210 cm–1 region can be attributed to contributions from the translational and intermolecular hydrogen bond stretch modes of water, while the intramolecular solute modes are restricted to higher frequencies (see Figure S7 and ref (17)). Previously, we could show that the absorption spectrum of hydration water can be dissected into a sum of two hydration water intermolecular stretching modes centered at 164 and 195 cm–1, both of which differ from those of bulk water, which has a broader absorption band centered around 200 cm–1.16,17 While the amplitude of each of these two hydration water bands, called ν164 and ν195, is temperature-, concentration-, and solute-dependent, the center frequency and the line width are almost constant (see ref (16) and Table S1). The ν195 component displays the most pronounced temperature dependence with a rapid decrease in intensity for an increase in temperature, while the ν164 component is less sensitive to an increase in temperature. This distinct temperature dependence also allows the separation of both. The hydration water band at 164 ± 2 cm–1 is considerably red-shifted compared to bulk water (at ∼200 cm–1), indicating a weaker hydrogen bond, whereas the hydration water band at 195 ± 2 cm–1 has an almost bulk-like center frequency. However, the line widths of each of these hydration water bands are considerably reduced compared to that of bulk water (see Figure 1B), making them easily distinguishable from bulk water.
Figure 1.
THz fingerprints of the hydration water around tert-butanol. (A) Comparison of experimental (top) and theoretical (bottom) difference spectra, obtained by subtracting the bulk water spectrum from the spectrum of a 0.5 M aqueous solution of tert-butanol, for two temperatures (310 and 290 K), over the range of 100–600 cm–1. (B) In the top panel, each concentration- and temperature-dependent difference spectrum can be dissected into two hydration water components. Here, we show these in orange and blue with their respective amplitudes for a 0.5 M aqueous solution of tert-butanol at 290 K. In the inset, the concentration-dependent amplitudes of each of the two hydration water components are shown for concentrations of 0.5 M and 5.0 M at 290 K. The bottom panel shows theoretical difference spectra calculated for each of the two interfacial H-bond populations, HB-wrap (orange) and HB-hydration2bulk (blue), at 0.5 M and 290 K. For comparison, the difference spectrum calculated for the HB population forming the 2D HB network at the air–water interface (AW-2DN) is also reported (red). (C) Snapshot from DFT-MD simulations highlighting in orange the HB-wrap population, forming the 2D polygonal HB network wrapped around the alcohol.
In the following, we present the results of ab initio MD (AIMD) simulations (50 ps). The first hydration layer of water around tert-butanol consists of all water molecules within 5.5 Å of the central carbon atom of the molecule (C-tert), which corresponds to the first minimum of the radial distribution function of water oxygen atoms around C-tert. The H-bonds formed between water molecules, as well as the H-bonds formed between water molecules and the alcohol function of tert-butanol, are defined using the geometrical criterion proposed by White et al.,32 with an O–O distance of ≤3.5 Å and an O–H–O angle of ≥140°. The simulations show that the hydration shell of tert-butanol can be divided into two parts, i.e., an innermost part (60% of hydration water molecules) within 2 Å of the van der Waals surface of the hydrophobic moiety (see Figure S1), where water is undercoordinated and “dynamically slow” with respect to bulk, and an outer part (40%) for distances of >2 Å (≤3.5 Å), where water is slightly overcoordinated with respect to bulk but shows “bulk-like” dynamics.
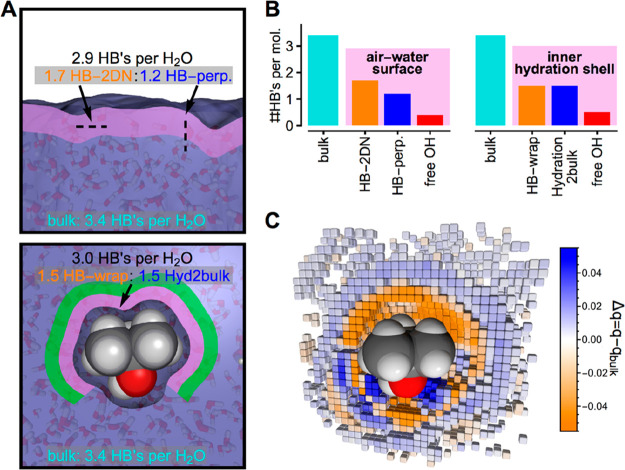
The separation into two populations holds with respect to multiple criteria (Table 1). Note that two distinct water populations have also been reported for the solvated NALMA peptide,18 with an inner hydration layer interacting with the surface on a longer time scale and an outer (“bulk-like”) hydration layer interacting mostly with other water molecules. Water molecules in the inner hydration shell of tert-butanol are found to form a HB network wrapped around the alcohol [290 and 310 K (see Figure 1C for an illustration)]. The inner layer contains two distinct populations of water–water HBs, each involved on average in 1.5 H-bonds per molecule: one HB population links all water molecules in an extended network of H-bonded 2D polygons hosting the solute [called HB-wrap (orange in Figure 1C)], and the other HB population connects the network of 2D polygons to the outer hydration layer or directly to bulk water (HB-hydration2bulk).
Table 1. Comparison of the Average Numbers of Water Molecules within the First Hydration Layer (#water) as Obtained from DFT-MD and Classical MD Simulations and Their Average Coordination Numbers (#HB-total, number of HBs formed per hydration water molecule) and Average Numbers of HB-wrap (#HB-wrap) and HB-hydration2bulk (#HB-int2bulk) (top) and Structural and Dynamical Properties of the Inner and Outer Hydration Layers as Deduced from MD Simulations (bottom).
| MD | #water (first shell) | #HB-total (HBs/molecule) | #HB-wrap (HBs/molecule) | #HB-int2bulk (HBs/molecule) |
|---|---|---|---|---|
| DFT-MD | 18.2 | 3.0 | 1.5 | 1.5 |
| classical MD | 18.5 | 3.0 | 1.5 | 1.5 |
| property of hydration water | inner layer | outer layer |
|---|---|---|
| distance from the solute | <2 Å from the vdW surface | 2–3.5 Å from the vdW surface |
| water coordination | 3.0 water–water HBs/molecule | 3.5 water–water HBs/molecule |
| nature of HBs formed | HB-wrap, HB-hydration2bulk | HB-hydration2bulk |
| HB O–O distance | 2.85 Å | 2.75 Å |
| tetrahedrality | q – qbulk = −0.03 | q – qbulk = 0.01 |
| HB dynamics | τHB = 1.36 ps | τHB = 1.04 ps |
| orientation dynamics | τμ = 2.92 ps | τμ = 1.88 ps |
| residence time | τresid = 8.9 ps | τresid = 2.1 ps |
In a further step, we also used classical MD to compute the time-averaged local orientational order parameter q on a three-dimensional (3D) grid around the solute. Water and alcohol oxygens are treated as coordination sites in the definition of q, which equals 0 for an ideal gas and 1 for a perfectly tetrahedral arrangement.19 Classical MD simulations (100 ns) are used to ensure sufficient sampling within each grid point (details in the Supporting Information). The employed TIP4P/2005 model for water20 was specifically chosen for its realistic description of the structural properties of water over a wide range of temperatures. We note that the characteristics of the hydration water HB network observed in the AIMD are maintained in the classical MD on the 100 ns time scale (see Table 1). The spatial decomposition of Δq confirms the existence of the two distinct hydration water populations. The coordination of water molecules close to tert-butanol is homogeneous and less tetrahedral than in bulk water (orange voxels in Figure 2C). This undercoordinated region corresponds to the inner hydration shell in which water molecules contribute on average 1.5 HBs to HB-wrap and 1.5 HBs to HB-hydration2bulk. The tetrahedral order increases relative to that of the bulk liquid for favorable H-bonding sites in the vicinity of the alcohol OH group, where water molecules form one supplementary H-bond with the tert-butanol (blue voxels in Figure 2C). In the outer hydration shell (>2 Å from the van der Waals surface of the hydrophobic moiety), water hydrating the hydrophobic moiety also exhibits an increased tetrahedral order relative to that of the bulk. HBs in this region contribute to the HB-hydration2bulk population. The average of this outer layer and the inner layer with undercoordinated water is consistent with an overall small increase in tetrahedral order in the hydration shell, which reproduces on average previous theoretical predictions and observations in which the local heterogeneity of the hydration water structure has not been explicitly considered.7,8,15,21 Our findings are in line with those of a previous simulation study, which also observed a nonhomogeneous water–water HB distribution in the hydration shell of hydrophobic groups.15 Thus, a locally resolved treatment is crucial for answering the question of whether a tetrahedral or a disordered water structure dominates.
Figure 2.
Solvation environment of tert-butanol. (A) Illustration of the comparison between HB connectivity patterns at the air–water surface and in the inner hydration shell of tert-butanol in a bulk solution. (B) Corresponding numerical values in addition to occurrences of free OH bonds. (C) Spatial distribution of the tetrahedral order parameter for water molecules in the solvation environment of tert-butanol at 293 K (Δq = q – qbulk). Shown are 0.5 Å3 voxels for which the local average tetrahedral order differs significantly from that of the bulk. Orange (blue) colors indicate a decrease (an increase) in q for the local coordination environment of a water molecule with respect to the bulk.
In addition, we investigated the hydrogen bond, orientation, and translation dynamics of the two populations. Whereas an average lifetime of the hydrogen bond (τHB) of 1.08 ps was found for HB-hydration2bulk, which is almost bulk-like (τHB = 1.04 ps), a deceleration of the HB dynamics was observed for HB-wrap (τHB = 1.36 ps). Changes in the orientation relaxation dynamics are quantified on the basis of MD simulations by calculation of the water dipole reorientation time τμ (Figure S11). We deduced τμ values of 2.92 ps for the water molecules forming the HB-wrap in the inner layer and 4.36 ps for the three water molecules close to the OH group of tert-butanol. A much faster and “bulk-like” water orientation dynamics was observed in the outer layer, where τμ = 1.88 ps. This is in line with previous studies reporting a slower orientation dynamics in the vicinity of hydrophobic solutes.9−12 See Table 1 for a summary. Surprisingly, and in contradiction with an “ice-like” picture, our work shows that this “slow” water population close to the hydrophobic solute (inner layer) is undercoordinated rather than tetrahedrally coordinated. Also, the water residence time is increased in the inner layer (8.9 ps) compared to that in the outer layer (2.1 ps).
A temperature-dependent analysis of Δq similar to Figure 2C demonstrates that the HB-wrap population in the inner hydration layer persists longer with an increase in temperature than the more tetrahedrally ordered HB-hydration2bulk in the outer layer. Thus, we attribute the previously reported onset of the experimentally observed transition from an overall increased tetrahedral order to more disordered water with increasing temperature9−12,16 rather than to an overall homogeneous change to a more local decrease in tetrahedrality in the outer hydration shell, while the inner shell (contributing to the HB-wrap population as probed in the 164 cm–1 band) persists up to higher temperatures. The eventual collapse of the inner shell at high temperatures [here predicted at ∼330 K (see the Supporting Information)] explains the significant increase in the number of undercoordinated water molecules and dangling OH bonds with an increase in temperature as observed in the previous Raman spectroscopic studies of small alcohol chains.13 Thus, both pictures can be reconciled when going from a local to a global perspective.
AIMD Simulations of the THz Fingerprints. To link the two HB-wrap and HB-hydration2bulk populations to the experimentally observed THz spectrum, we compare in Figure 1A the experimental (top) and simulated (bottom) absorption difference spectra αdifference. The theoretical difference spectrum is obtained from AIMD in the same way as in the experiments. We have simulated the spectrum of water molecules in a simulation box including one tert-butanol solute and subtracted the simulated bulk water spectrum obtained from a simulation box of liquid water at the same temperature. As shown in Figure 1A, we find a remarkable quantitative agreement between experiment and simulation for both temperatures (290 and 310 K) up to 210 cm–1. Only qualitative agreement is obtained beyond and up to 600 cm–1, because in this region we find significant spectroscopic signatures from tert-butanol modes, which are not included in the water spectral calculations (see Figure S7). In Figure 1B, we display the difference spectrum (in the frequency range of 90–210 cm–1) dissected into individual contributions from the two identified HB populations. This is achieved by restricting the theoretical spectroscopic calculation to hydration water contributions from either HB-wrap (orange) or HB-hydration2bulk (blue). Notably, we obtain two broad bands centered at 164 and 195 cm–1, which nicely match the ν195 and ν164 components extracted from the experiments (see Figure S6 for the same decomposition at 310 K).
Upon further investigation, the HB-hydration2bulk population is found to be most similar to HBs in bulk water in terms of intermolecular distance [same average 2.75 Å O–O distance as in bulk water]. Therefore, the center frequency is almost unshifted compared to the bulk (195 vs 200 cm–1). For the 164 cm–1 hydration water mode, the simulations show that the substantial red-shift by ∼30 cm–1 relative to the bulk water (200 cm–1) is caused by longer and therefore weaker HBs within the HB-wrap population compared to bulk water (2.85 Å vs 2.75 Å). We point out that the same 164 cm–1 fingerprint is also observed upon formation of a tetrakaidecahedron 51262 clathrate cage around the small solute tetrahydrofuran (THF),22 as well as at the air–water interface (Figure 1B), where an extended 2D H-bond network of 2D polygons is formed,23−25 reminiscent of the HB-wrap population.
To further validate our assignment of the ν195 and ν164 bands, we report additional concentration-dependent measurements ranging from 0.2 to 5 M. Our measurements reveal that the partial contribution of ν195 is decreasing relative to that of ν164, as the concentration is increased from 0.5 to 5.0 M (inset of Figure 1B). With an increase in the concentration beyond 1–3 M, tert-butanol molecules are expected to start sharing their hydration shells or to partially desolve upon either an increase in solute concentration in a random mixture26 or aggregation.27−29 In both cases, the THz hydration water spectrum at 5 M will feature increased contributions from the inner versus outer hydration shell compared to a 0.5 M solution due to the initial depletion of the outer hydration layer. Experimentally, we observe initially a decrease in the intensity of the 195 cm–1 band followed by a decrease in the intensity of the 164 cm–1 band only at higher concentrations, which is in agreement with our assignments of these two bands to the outer shell HB-hydration2bulk population and the inner shell HB-wrap population. In more detail, between 0.2 and 3 M, we observe a linear decrease in the outer shell HB-hydration2bulk population but no significant change in the HB-wrap population (see the Supporting Information). Thus, we observe no conclusive indication for an onset of aggregation. By contrast, beyond 3 M, we observe a decrease in the inner hydration shell HB-wrap population as well as a systematic blue-shift of the center frequencies of the 195 cm–1 and (to a lesser extent) 164 cm–1 bands. This is in line with both the formation of solvent-shared dimers and the onset of desolvation upon aggregation.
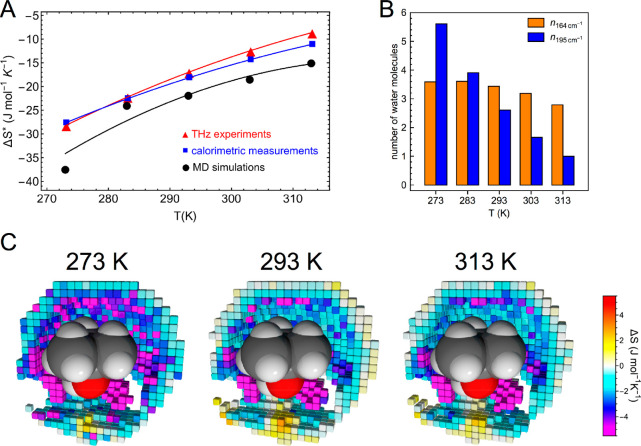
THz Calorimetry. The spectroscopic detection of the THz fingerprint spectra of the separate HB populations is the working principle of “THz calorimetry”.16 We show that these give rise to not only distinct vibrational frequencies but also distinct thermodynamic properties. In the following, we compare the experimental data with an MD-based analysis (3D-2PT)30 that spatially resolves the local entropy per water molecule in the hydration shell of tert-butanol, S(r), and its change relative to the bulk [ΔS(r) = S(r) – Sbulk]. The analysis is performed on the same 3D grid used to quantify the spatially resolved tetrahedral order parameter and utilizes the same 100 ns trajectories (Figure 3A,C). At low temperatures, the local entropy of water molecules directly hydrating tert-butanol is reduced relative to that of bulk water, resulting in a negative contribution to the solvation entropy (Figure 3C). This effect is largest for water molecules in hydrogen-bonding sites around the solute hydroxyl group. Close to the OH group, we also find water with increased entropy in unfavorable H-bonding sites (yellow). In the inner hydration shell around hydrophobic methyl groups, the negative contributions to the solvation entropy are less pronounced but significant and diminish only slightly within the range of 273–313 K, in agreement with our observations for variations of the local tetrahedral order parameter Δq and the spectroscopic signals for HB-wrap at 164 cm–1. Changes with temperature are most pronounced in the outer hydration shell, which contribute to the negative solvation entropy only at temperatures lower than 283 K (white voxels in Figure 3C and Figure S2). In contrast to the initial expectation, undercoordinated hydration water in the inner shell contributes most to the negative solvation entropy.
Figure 3.
Temperature-dependent changes in hydration
water structure affect
solvation entropy. (A) THz-active contributions to the solvation entropy, 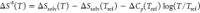 with Tref =
400 K (see the Supporting Information and
refs (16) and (29)), of tert-butanol in the investigated temperature range as deduced from MD
simulations (black circles), changes in the THz spectra (red triangles),
and conventional calorimetry (blue squares). (B) Effective number
of hydration waters contributing to each THz band (ν164 and ν195) obtained from the experimental spectra.
(C) Illustration of the tert-butanol molecule and
its first hydration shell at 273, 293, and 313 K. Voxels indicate
regions with a >30% increase in the water number density relative
to the bulk liquid (the 3D analogue of the first peak in a radial
distribution function), and the color illustrates local variations
in the absolute entropy per water molecule relative to bulk water
at the corresponding temperature [ΔS(r) = S(r) – Sbulk].
with Tref =
400 K (see the Supporting Information and
refs (16) and (29)), of tert-butanol in the investigated temperature range as deduced from MD
simulations (black circles), changes in the THz spectra (red triangles),
and conventional calorimetry (blue squares). (B) Effective number
of hydration waters contributing to each THz band (ν164 and ν195) obtained from the experimental spectra.
(C) Illustration of the tert-butanol molecule and
its first hydration shell at 273, 293, and 313 K. Voxels indicate
regions with a >30% increase in the water number density relative
to the bulk liquid (the 3D analogue of the first peak in a radial
distribution function), and the color illustrates local variations
in the absolute entropy per water molecule relative to bulk water
at the corresponding temperature [ΔS(r) = S(r) – Sbulk].
In Figure 3A, we compare the temperature dependence of the THz-active changes in the solvation entropy ΔS*(T) = ΔSsolv(T) − ΔSsolv(Tref) − ΔCp(Tref)log(T/Tref) obtained independently from the MD simulations, THz calorimetry, and conventional calorimetry. ΔS*(T) describes changes in the solvation entropy of the solute that go beyond expected effects resulting from a constant heat capacity difference ΔCp between the hydration shell and bulk water and therefore reports on the thermodynamic impact of structural changes. A constant value of ΔCp was determined at a high reference temperature (Tref = 400 K), for which the structural differences between hydration and bulk water are considered negligible due to the breakdown of the HB network (see the Supporting Information and ref (16) for details). The simulations yield the solvation entropy as an integral over local contributions. We point out that the largest contribution to ΔS is due to cavity formation. However, this contribution follows a strict linear temperature dependence, TΔScavity, with ΔScavity being constant. Most notably, the next largest contribution to ΔS* from hydration water is due to the HB-wrap in the inner shell (164 cm–1 band), while the finer details of the temperature dependence of ΔS* in the range of 273–313 K can almost exclusively be attributed to decreasing contributions from the HB-hydration2bulk population in the outer shell (195 cm–1 band).
Final Picture of the Hydrophobic Hydration Layer. Our combined findings from THz absorption and simulations provide a refined picture for the hydrogen bond network surrounding hydrophobic solutes and concentration- and temperature-induced changes thereof. We describe the local coexistence of two components of the HB network, with distinct structural, dynamical, and thermodynamic properties. This includes undercoordinated (HB-wrap) and tetrahedral (HB-hydration2bulk) H-bonding environments. On the basis of the novel simulations results, we assign the two previously experimentally observed THz hydration water bands to these two water HB populations. The well-known concentration- and temperature-dependent structural crossover of the hydration shell can be rationalized in the context of the distinct local extension and temperature stability of these two HB populations. Here, we propose that the concept of two HB populations coexisting in the hydration shell of hydrophobic solutes at low temperatures is more general. In line with previous studies,9−11,18,31 we restore a molecular view with a slower translational and reorientational dynamics of water near hydrophobic groups. The innermost part of the first hydration layer was characterized as having at least one O–H bond tangential to the solute31 and a smaller number of water–water H-bonds, corresponding to our HB-wrap population. The slow hydration water dynamics experimentally observed by NMR,9 2D IR,10 and femtosecond mid-IR11 spectroscopies can now be explained, because these probe mostly water molecules in the inner layer (dominated by the HB-wrap). This inner layer is undercoordinated, thus not “ice-like” but showing motifs of a 2D network and a decreased HB stretching frequency compared to that of bulk water. The undercoordination in the inner layer along with the only slightly enhanced coordination in the outer layer is in line with neutron diffraction results for a solution of methane in water at 18 °C and 180 bar, which suggested that, if anything, the overall averaged structure of water is marginally less tetrahedral than that of pure water at the same temperature and pressure.32 The molecular picture provided here for hydrophobic hydration explains the finer details of the experimentally observed temperature dependence of the solvation entropy as well as the previous experimental studies in a comprehensive way. One of the future challenges will be to extend THz calorimetry to probe hydration water properties around hydrophobic and hydrophilic sites of proteins to understand and optimize the role of the local solvation in biomolecular recognition processes. The combination of advanced THz spectroscopic technologies and simulations opens the way to tackling these challenges.
Materials and Methods
DFT-Based Molecular Dynamics Simulations. Born–Oppenheimer DFT-based molecular dynamics simulations (DFT-MD) were carried out on a 0.2 M aqueous solution of tert-butanol (2-methyl-2-propanol) at temperatures of 290 and 310 K. The electronic representation consists of the BLYP33,34 functional, including Grimme D2 correction for dispersion.35,36 Simulations were performed for a cubic box (19.734 Å)3 composed of a liquid phase of 256 water molecules solvating one tert-butanol molecule. Trajectories were recorded for 50 ps in the NVE ensemble after a proper equilibration. The theoretical IR spectra were calculated using our previously developed strategy37 based on the Fourier transform of the correlation function of velocities modulated by atomic polar tensors (APT) (see the Supporting Information).
Classical Molecular Dynamics Simulations. Classical molecular dynamics simulations of tert-butanol solvated in water were carried out with the Gromacs 4.6.1 software package.38 The OPLS all-atom39 and TIP4P/200520 force fields were used to describe the solute and water. The systems were equilibrated for 1 ns in the isobaric–isothermal (NPT) ensemble at target pressures of 1 bar and temperatures of 273, 283, 293, 303, and 313 K, followed by 100 ns production simulations in the NVT ensemble. The analyses were performed on a three-dimensional cubic grid centered on the immobilized solute molecule to spatially resolve the local tetrahedral order and the local molecular entropies of water in the hydration shell of the solute. The local tetrahedral order is quantified using the orientational order parameter introduced by Errington and Debenedetti.26 The local molecular entropies are calculated by means of the 3D-2PT approach of Persson et al.29 (see also the Supporting Information).
THz-FTIR Absorption Spectroscopy. Spectra of 0.5 M tert-butanol aqueous solutions were recorded in the frequency range of 50–600 cm–1 by FTIR absorption spectroscopy at 290 and 310 K. In addition, we carried out concentration-dependent measurements from 0.2 to 5 M at room temperature in the frequency range of 50–450 cm–1. THz-FTIR measurements were performed using a Bruker Vertex 80v spectrometer equipped with a liquid helium-cooled bolometer from Infrared Laboratories as a detector. The sample solutions were placed in a temperature-controlled liquid transmission cell from Harrick with polycrystalline diamond windows and a 15–25 μm thick Kapton spacer; 128 scans with a resolution of 2 cm–1 were averaged for each spectrum. The spectra were smoothed with a 2 cm–1 wide (five points) moving average. The effective molar extinction of the hydrated solute was deduced as described in refs (16). The temperature-dependent spectral changes in the low-frequency range were directly correlated with the changes in heat capacity, enthalpy, and entropy, following the analysis in ref (16). See also the Supporting Information.
The data sets generated and analyzed during this study are available from the corresponding authors on reasonable request. For data processing and visualization, VMD, Xmgrace, Mathematica, and POV-ray 3.6 were used. All further information about data processing is contained in the text and Supporting Information.
Acknowledgments
M. Havenith acknowledges financial support by ERC Advanced Grant 695437 THz-Calorimetry. This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germanýs Excellence Strategy (EXC 2033-390677874-RESOLV). S.P., D.R.G., and M.-P.G. received financial support from bilateral France-Germany ANR-DFG DYNAWIN Grant 14-CE35-0011-01, and HPC resources from GENCI-France Grant 072484 (CINES/IDRIS/TGCC) are acknowledged.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.0c00846.
Spatially resolved water q parameter and hydration entropy around tert-butanol in the explored temperature range (Figures S1 and S2), THz spectra of tert-butanol at different concentrations and temperatures (Figures S3 and S4), supplementary theoretical THz spectra (Figures S5–S7), correlation functions for orientational and translational hydration water dynamics (Figure S8), supplementary THz calorimetric data (Figure S9), and experimental fit results and parameters (Tables S1 and S2) (PDF)
Author Contributions
V.C.N., S.P., and F.S. contributed equally to this work. All authors designed and performed research. F.S., G.S., and M. Havenith collected and analyzed experimental data. S.P., D.R.G., and M.-P. Gaigeot performed and analyzed ab initio molecular dynamics simulations. V.C.N. and M. Heyden performed and analyzed classical molecular dynamics simulations. All authors wrote the paper.
The authors declare no competing financial interest.
Supplementary Material
References
- Frank F. S.; Evans M. W. Free volume and entropy in condensed systems III. Entropy in binary liquid mixtures; Partial molar entropy in dilute solutions; Structure and thermodynamics in aqueous electrolytes. J. Chem. Phys. 1945, 13, 507–532. 10.1063/1.1723985. [DOI] [Google Scholar]
- Pratt L. R. Theory of hydrophobic effects. Annu. Rev. Phys. Chem. 1985, 36, 433–449. 10.1146/annurev.pc.36.100185.002245. [DOI] [PubMed] [Google Scholar]
- Lum K.; Chandler D.; Weeks J. D. Hydrophobicity at small and large length scales. J. Phys. Chem. B 1999, 103, 4570–4577. 10.1021/jp984327m. [DOI] [Google Scholar]
- Chandler D. Interfaces and the driving force of hydrophobic assembly. Nature 2005, 437, 640–647. 10.1038/nature04162. [DOI] [PubMed] [Google Scholar]
- Matysiak S.; Debenedetti P. G.; Rossky P. J. Dissecting the energetics of hydrophobic hydration of polypeptides. J. Phys. Chem. B 2011, 115, 14859–14865. 10.1021/jp2079633. [DOI] [PubMed] [Google Scholar]
- Huang D. M.; Chandler D. Temperature and length scale dependence of hydrophobic effects and their possible implications for protein folding. Proc. Natl. Acad. Sci. U. S. A. 2000, 97, 8324–8327. 10.1073/pnas.120176397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis J. G.; Gierszal K. P.; Wang P.; Ben-Amotz D. Water structural transformation at molecular hydrophobic interfaces. Nature 2012, 491, 582–585. 10.1038/nature11570. [DOI] [PubMed] [Google Scholar]
- Grdadolnik J.; Merzel F.; Avbelj F. Origin of hydrophobicity and enhanced water hydrogen bond strength near purely hydrophobic solutes. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 322–327. 10.1073/pnas.1612480114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishihara Y.; Okouchi S.; Uedaira H. Dynamics of hydration of alcohols and diols in aqueous solutions. J. Chem. Soc., Faraday Trans. 1997, 93, 3337–3342. 10.1039/a701969f. [DOI] [Google Scholar]
- Bakulin A. A.; Pshenichnikov M. S.; Bakker H. J.; Petersen C. Hydrophobic molecules slow down the hydrogen-bond dynamics of water. J. Phys. Chem. A 2011, 115, 1821–1829. 10.1021/jp107881j. [DOI] [PubMed] [Google Scholar]
- Petersen C.; Tielrooij K. J.; Bakker H. J. Strong temperature dependence of water reorientation in hydrophobic hydration shells. J. Chem. Phys. 2009, 130, 214511. 10.1063/1.3142861. [DOI] [PubMed] [Google Scholar]
- Laage D.; Stirnemann G.; Hynes J. T. Why water reorientation slows without iceberg formation around hydrophobic solutes. J. Phys. Chem. B 2009, 113, 2428–2435. 10.1021/jp809521t. [DOI] [PubMed] [Google Scholar]
- Wu X.; Lu W.; Streacker L. M.; Ashbaugh H. S.; Ben-Amotz D. Temperature-dependent hydrophobic crossover length scale and water tetrahedral order. J. Phys. Chem. Lett. 2018, 9, 1012–1017. 10.1021/acs.jpclett.7b03431. [DOI] [PubMed] [Google Scholar]
- Strazdaite S.; Versluis J.; Backus E. H. G.; Bakker H. J. Enhanced ordering of water at hydrophobic surfaces. J. Chem. Phys. 2014, 140, 054711. 10.1063/1.4863558. [DOI] [PubMed] [Google Scholar]
- Duboué-Dijon E.; Laage D. Characterization of the local structure in liquid water by various order parameters. J. Phys. Chem. B 2015, 119, 8406–8418. 10.1021/acs.jpcb.5b02936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Böhm F.; Schwaab G.; Havenith M. Mapping hydration water around alcohol chains by THz calorimetry. Angew. Chem., Int. Ed. 2017, 56, 9981–9985. 10.1002/anie.201612162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heyden M.; Sun J.; Funkner S.; Mathias G.; Forbert H.; Havenith M.; Marx D. Dissecting the THz spectrum of liquid water from first principles via correlations in time and space. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 12068–73. 10.1073/pnas.0914885107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson M. E.; Malardier-Jugroot C.; Head-Gordon T. Effects of co-solvents on peptide hydration water structure and dynamics. Phys. Chem. Chem. Phys. 2010, 12, 393–405. 10.1039/B915888J. [DOI] [PubMed] [Google Scholar]
- Errington J. R.; Debenedetti P. G. Relationship between structural order and the anomalies of liquid water. Nature 2001, 409, 318–321. 10.1038/35053024. [DOI] [PubMed] [Google Scholar]
- Abascal J. L. F.; Vega C. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. 10.1063/1.2121687. [DOI] [PubMed] [Google Scholar]
- Stiopkin I. V.; Weeraman C.; Pieniazek P. A.; Shalhout F. Y.; Skinner J. L.; Benderskii A. V. Hydrogen bonding at the water surface revealed by isotopic dilution spectroscopy. Nature 2011, 474, 192–195. 10.1038/nature10173. [DOI] [PubMed] [Google Scholar]
- Funke S.; Sebastiani F.; Schwaab G.; Havenith M. Spectroscopic fingerprints in the low frequency spectrum of ice (Ih), clathrate hydrates, supercooled water and hydrophobic hydration reveal similarities in the hydrogen bond network motifs. J. Chem. Phys. 2019, 150, 224505. 10.1063/1.5097218. [DOI] [PubMed] [Google Scholar]
- Pezzotti S.; Galimberti D. R.; Gaigeot M.-P. 2D H bond network as the topmost skin to the air–water interface. J. Phys. Chem. Lett. 2017, 8, 3133–3141. 10.1021/acs.jpclett.7b01257. [DOI] [PubMed] [Google Scholar]
- Pezzotti S.; Serva A.; Gaigeot M.-P. 2D-HB-network at the air-water interface: a structural and dynamical characterization by means of ab-initio and classical molecular dynamics simulations. J. Chem. Phys. 2018, 148, 174701. 10.1063/1.5018096. [DOI] [PubMed] [Google Scholar]
- Serva A.; Pezzotti S.; Bougueroua S.; Galimberti D. R.; Gaigeot M.-P. Combining ab-initio and classical molecular dynamics simulations to unravel the structure of the 2D-HB-network at the air-water interface. J. Mol. Struct. 2018, 1165, 71–78. 10.1016/j.molstruc.2018.03.074. [DOI] [Google Scholar]
- Rankin B. M.; Ben-Amotz D.; van der Post S. T.; Bakker H. J. Contacts between alcohols in water are random rather than hydrophobic. J. Phys. Chem. Lett. 2015, 6, 688–692. 10.1021/jz5027129. [DOI] [PubMed] [Google Scholar]
- Bowron D. T.; Finney J. L.; Soper A. K. Structural investigation of solute-solute interactions in aqueous solutions of tertiary butanol. J. Phys. Chem. B 1998, 102, 3551–3563. 10.1021/jp972780c. [DOI] [Google Scholar]
- Nishikawa K.; Kodera Y.; Iijima T. Fluctuations in the particle number and concentration and the Kirkwood-Buff parameters of tert-Butyl alcohol and water mixtures studied by Small-Angle X-ray Scattering. J. Phys. Chem. 1987, 91, 3694–3699. 10.1021/j100297a047. [DOI] [Google Scholar]
- Overduin D.; Patey G. N. Comparison of simulation and experimental results for a model aqueous tert-butanol solution. J. Chem. Phys. 2017, 147, 024503. 10.1063/1.4990505. [DOI] [PubMed] [Google Scholar]
- Persson R. A. X.; Pattni V.; Singh A.; Kast M.; Heyden M. Signatures of solvation thermodynamics in spectra of intermolecular vibrations. J. Chem. Theory Comput. 2017, 13, 4467–4481. 10.1021/acs.jctc.7b00184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galamba N. Water’s structure around hydrophobic solutes and the iceberg model (2013). J. Phys. Chem. B 2013, 117, 2153. 10.1021/jp310649n. [DOI] [PubMed] [Google Scholar]
- Buchanan P.; Aldiwan N.; Soper A. K.; Creek J. L.; Koh C. A. Decreased structure on dissolving methane in water. Chem. Phys. Lett. 2005, 415, 89. 10.1016/j.cplett.2005.08.064. [DOI] [Google Scholar]
- Becke A. D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A: At., Mol., Opt. Phys. 1988, 38, 3098–3100. 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
- Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- Grimme S. Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Comput. Chem. 2004, 25, 1463–1473. 10.1002/jcc.20078. [DOI] [PubMed] [Google Scholar]
- Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
- Galimberti D. R.; Milani A.; Tommasini M.; Castiglioni C.; Gaigeot M. P. Combining static and dynamical approaches for infrared spectra calculations of gas phase molecules and clusters. J. Chem. Theory Comput. 2017, 13, 3802–3813. 10.1021/acs.jctc.7b00471. [DOI] [PubMed] [Google Scholar]
- Hess B.; Kutzner C.; van der Spoel D.; Lindahl E. GROMACS 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L.; Maxwell D. S.; Tirado-Rives J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. 10.1021/ja9621760. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.