Quantum Machine Learning Algorithms for Drug Discovery Applications

Abstract

The growing quantity of public and private datasets focused on small molecules screened against biological targets or whole organisms provides a wealth of drug discovery relevant data. This is matched by the availability of machine learning algorithms such as Support Vector Machines (SVM) and Deep Neural Networks (DNN) that are computationally expensive to perform on very large datasets with thousands of molecular descriptors. Quantum computer (QC) algorithms have been proposed to offer an approach to accelerate quantum machine learning over classical computer (CC) algorithms, however with significant limitations. In the case of cheminformatics, which is widely used in drug discovery, one of the challenges to overcome is the need for compression of large numbers of molecular descriptors for use on a QC. Here we show how to achieve compression with datasets using hundreds of molecules (SARS-CoV-2) to hundreds of thousands of molecules (whole cell screening datasets for plague and M. tuberculosis) with SVM and the data re-uploading classifier (a DNN equivalent algorithm) on a QC benchmarked against CC and hybrid approaches. This study illustrates the steps needed in order to be “quantum computer ready” in order to apply quantum computing to drug discovery and to provide the foundation for this field to build on.

INTRODUCTION

The rapidly growing public and private datasets that are focused on small molecules screened against known biological targets or whole organisms ¹ provides a wealth of data to facilitate drug discovery. Increasingly, this is used to create machine learning models ² which can be used for enabling target-based design ^3-5, predict on- or off-target effects and create scoring functions ^{6, 7}. The pharmaceutical industry and academic laboratories are increasingly using and exploring machine learning applications in drug discovery to mine and model their data generated from years of high throughput screening ⁸. This is allowing rapid identification of molecules for neglected diseases such as Ebola ⁹ and Chagas disease ¹⁰, presenting lead compounds which can then be moved rapidly into in vivo models ^11-13 and this approach can be more widely applied in cheminformatics. Recent examples have illustrated the speed with which the machine learning combined with in vitro testing continuum can generate new leads compared to traditional efforts ¹⁴. The availability of thousands of structure-activity datasets, (some of which in turn contain data for hundreds of thousands of molecules screened against a single target or organism ^{2, 15}), presents a computational challenge with machine learning methods such as classifiers like support vector machines (SVM) on a classical computer (CC) ¹⁶.

Recently the potential of quantum machine learning has been illustrated using two methods such as a variational quantum circuit and a quantum kernel estimator ¹⁷. In addition, new machine learning methods for quantum computing continue to be developed ^{18, 19} which creates opportunities to expand the possible applications of machine learning to drug discovery and toxicology. Like many emerging technologies, the quantum computer (QC) has been proposed as likely to transform early-stage pharmaceutical research and development as well as providing a potential solution for datasets that would be intractable if performed on a CC ^{20, 21}. One area of interest in early drug discovery is in cheminformatics for virtual screening and optimization, where small molecules are frequently described by fingerprint descriptors which can lead to tens of thousands of vectors called multiple fingerprint features (MFF) ²². While this may be important for many aspects of applying machine learning to chemistry ²³, it also creates significant challenges when using these massive numbers of descriptors on a QC. This is mainly because we do not have enough resources and techniques to represent compounds with such large descriptors on QCs as the system will collapse.

Herein we describe how we have applied multiple approaches to compress the descriptors for QC while also demonstrating applications to drug discovery datasets on a range of scales that would be broadly applicable for drug discovery. We also describe hybrid approaches that merge QC with CC for machine learning applied to these datasets curated from public sources. These include 132 small molecule inhibitors of SARS-CoV-2 in Vero cells ²⁴, 18,886 inhibitors of Mycobacterium tuberculosis ²⁵ as well as several larger datasets for inhibitors of Krabbe disease (β-Galactocerebrosidase, Pubchem Assay 1159614, 44,809 compounds), Cathepsin B (Pubchem Assay 453, 63,331 compounds), Plague (Yersinia pestis, Pubchem Assay 898, 139,861 compounds), a second much larger dataset for M. tuberculosis (293,937 compounds) ²⁶ and hERG (306,587 compounds) ¹⁵. All these datasets were curated and prepared using Assay Central ²⁵ (See Methods) and the models can be applied for predicting new molecules for these targets or diseases.

METHODS

Experimental Procedures

Data curation

Our proprietary Assay Central software ^{27, 28} is a framework for curating high-quality datasets and building Bayesian machine learning models. Each dataset was subjected to the same standardization processes (i.e. removing salts, metal complexes and mixtures) prior to building models. Duplicate parent compounds with finite concentration activities are merged into a single entry. Classification models such as these require a defined threshold of bioactivity. The SARS-CoV-2 model used a threshold of 6.65 μM; Cathepsin B used >20% inhibition; the three M. tuberculosis models used the thresholds as described; the Krabbe model used actives defined by the authors; plague used a threshold at ≥50% inhibition; the hERGcentral dataset was >50% inhibition; The large M. tuberculosis model used a cut off where MIC₉₀ or IC₉₀ < 10 mg/ml or 10mM and a selectivity index (SI) greater than 10 was used (where SI = MIC₉₀ or IC₉₀/CC₅₀) ²⁶. The curated files that were output from Assay Central were then employed for quantum machine learning.

Running our algorithms on QC

We used IBM’s ibmq_rochester for executing our algorithms. Figure S1 shows the architecture of ibmq_rochester. Colors represent error probabilities for controlled-NOTs and readout on qubits ²⁹. This architecture has 53 qubits linked in the network. These 53 qubits are assembled and connected following the property of hexagonal lattices which is advantageous when it comes to minimizing unwanted interactions (Figure S1) ²⁹. The error in reporting the accuracies can be ±3% depending on the time of day the code is run due to their recalibration. The QC is recalibrated once a day at unknown times. The algorithm was run with shots=2048.

Descriptor Compression for Quantum Machine Learning of SARS-CoV-2 data

As the extended connectivity fingerprint diameter 6 (ECFP6) has been widely applied in cheminformatics ²⁷ we used the Morgan Fingerprint (with radius 3), which is equivalent to the ECFP6 fingerprint in RDkit ³⁰. The Morgan Fingerprint generates binary numbers whose default size is 2048 bits. While this is acceptable for use on a CC, it is not acceptable for use on a QC as 2048 bits exceeds the maximum capacity of current state-of-technology gate-based QCs. Apart from this, having a relatively big descriptor size, around 1000, can also be a challenge. This is because with the increase in size/usage of qubits on the QC the network, to represent descriptors, accuracy fails because of decoherence noise introduced in the qubit system ³¹. Depending on the architecture of QC being used, it can happen that not all qubits are linked with each other. Having no linkage or communication between every qubit adds further noise to this system. We attempted two approaches to solve this utilizing QC alone or a hybrid where part of the code is run on the QC.

We propose four methods (utilizing QC alone or a hybrid where part of the code is run on the QC) to encode the 2048 descriptor features. Method 1 used Principal Component Analysis (PCA) that is widely applied in data compression ³². Method 2 used a common dimension reduction technique of Linear Discriminant Analysis (LDA) which also considers the target class along with the predictors ³³. In this we simply take a projection of points into some other hyperplane. In Method 3, we designed an algorithm where first we divide the 2048 molecule fingerprint bits into ‘x’ groups, such that, each group has ‘k’ bits. This means that k should divide 2048 completely leaving out with 0 as the remainder. These ‘k’ bits are then converted into base 10 or decimal value. This process is repeated until all the groups are converted to decimal. Method 4 uses an algorithm where we keep track of positions of 1 in the whole array.

Another approach we have applied is a hybrid approach in which the QC is used to perform part of the calculation while performing the remainder on a CC. This removes the storage limitation on QC as this is provided by the CC, hence leaving the processing to the QC. A data re-uploading classifier was used as described further below ³⁴. Here, unlike SVM where we were reducing to 2-3 dimensions, we can reduce to 3-10 dimensions to consider the qubit architecture. For our purpose, we reduced to 6 dimensions using the Method 1 and Method 3 for SVM. In this approach, we load data into a single qubit by performing a simple unitary operation U (x1, x2, x3) where x1, x2, x3 are the coordinates of the point. When dimensions are greater than three, we can have U (x1, x2, x3, x4, x5, x6) to (U (x1, x2, x3) U (x4, x5, x6)). Using this approach, we can therefore store a datapoint which has 6 dimensions. We can have a similar unitary U (θ₁, θ₂, θ₃) for rotation of datapoint in bloch sphere (Figure 1). Here we make a two-qubit connected layer to introduce non-linearity in our network.

Figure 1.

A high-level abstraction of how data is stored in the bloch sphere. The two layers - A and B, with U(x_A) denoting unitary applied on input vector, U(θ_A) representing the unitary applied to rotate the vector in the bloch sphere.

The hybrid algorithm helps in introducing non-linearity to the model which makes use of the Adam stochastic gradient optimizer ³⁵. We tuned different parameters using an iterative process for the following: Optimizer (Adagrad and Adam), Epochs, batch-size and the number of hidden layers.

The CC details on which the algorithms were executed:

The computational server used was a Supermicro EATX DDR4 LGA 2011, Intel Computer CPU 2.1 8 BX80660E52620V4, Crucial 64GB Kit (16GBx4) DDR4 2133 (PC42133) DR x4 288 Pin Server Memory CT4K16G4RFD4213 / CT4C16G4RFD4213, 1-5 x EVGA GeForce GTX 1080 Ti FOUNDERS EDITION GAMING, 11GB GDDR5X, Intel 730 SERIES 2.5Inch Solid State Drive SSDSC2BP480G410, WD Gold 4TB Datacenter Hard Disk Drive 7200 RPM Class SATA 6 Gb/s 128MB Cache 3.5 Inch WD4002FYYZ, Supermicro 920 Watt 4U Server.

Quantum SVM:

The initial algorithm we have compared is an SVM implemented using the Qiskit library ³⁶ which uses Least-Square SVM (LS-SVM) ³⁷. Qiskit chooses M_ij =x_i x_j as the ansatz where M_ij is the kernel matrix and x_i x_j are the datapoints in the dataset ³⁸. When working with QC we first formulate the ansatz and try to minimize it. This ansatz formulates the SVM hyperplane which divides the datasets. We have chosen the ansatz such that we get a line as an output. The main reason we selected linear fit and not polynomial fit because we wanted to avoid the scenario of non-convergence kernels. This ansatz equation determines the shape the hyperplane will take. We made use of already available QSVM (Quantum SVM) code available in the Qiskit library. For the dataset, the SVM’s depth was set to 2. Entanglement was set to ‘full’ and the skip_qobj_validation parameter for quantum instance was set to False.

Data re-uploading classifier:

The MFF molecular descriptor ²² was also used with the four methods to achieve better accuracy rates. The data re-uploading classifier is very similar to a deep neural network (DNN) ³⁴ ,implemented using the existing library in the Pennylane tool ³⁹, where a single qubit represents a neural network layer. A DNN consists of 2 or more hidden layers. So, to replicate the DNN properties and introduce non-linearity, we make use of 2 qubits as an analogy to 2-layer Neural networks. With the above MFF descriptor we get 71,375 vectors. Sandfort et al. ²² postulated that this leads to overfitting and the same results were observed with MFF followed by our data reduction algorithm. For all datasets in this study, the data re-uploading classifier had hyperparameters set to – Training set size: (70% of dataset), Test set size: (30% of dataset), train accuracy rate: 61.2%, test accuracy rate: 61%, number of layers: 4, batch-size: 32, epochs: 10, optimizer: Adam, learning rate: 0.6, cross fold validation: 5.

RESULTS

Descriptor Compression for Quantum Machine Learning of SARS-CoV-2 data

Within the QC, a quantum algorithm is used to solve the direct product ³⁷ to solve for matrix operations and using it to then calculate the M(the kernel matrix)/. Then a quantum algorithm can be used to transform into waveforms to solve the system of linear equations ³⁸. This approach solves the complete SVM on a QC. While SVM generally provides promising results, it takes considerable time to solve linear equations to solve for Kernel Matrix using feature maps (1.24 minute for each datapoint) and hence, any time advantage for QC is likely not achievable. It should be noted that the connection to the qubit architecture also plays an instrumental role in driving the accuracy rates which may vary slightly for the best accuracy value. The accuracy rates reported are therefore a best value achieved on the QC or QC simulator.

In order to reduce the molecular descriptor features such that they can be represented and stored in our limited number of qubits (53 qubits for the ibmq-rochester, Fig. S1). We have initially demonstrated the application of QC with a SARS-CoV-2 Vero cell inhibition dataset consisting of 132 compounds of which 66 were found to be active with the IC₅₀ activity threshold of 6.65 μM which was selected using our Assay Central software ²⁴. We reduced the molecular descriptor dimensions from 2048 descriptor features to 2-3 using multiple techniques. Method 1 (i.e., PCA) resulted in accuracy rates on a CC with 1GPU of 37% using the kernel algorithm = RBF (Radial Basis Function) whereas on a QC accuracy was 33% (N= 3). Method 2 (i.e., LDA) resulted in accuracy rates of 40% using a kernel algorithm on a CC while on QC this was 39% (N = 3). An example of a molecule compressed using Method 3 is shown in Figure 2. Method 3 resulted in a greatly improved accuracy rate of 61% on a CC using kernel algorithm=‘poly’ and 59.6% on a QC (n=3).

Figure 2.

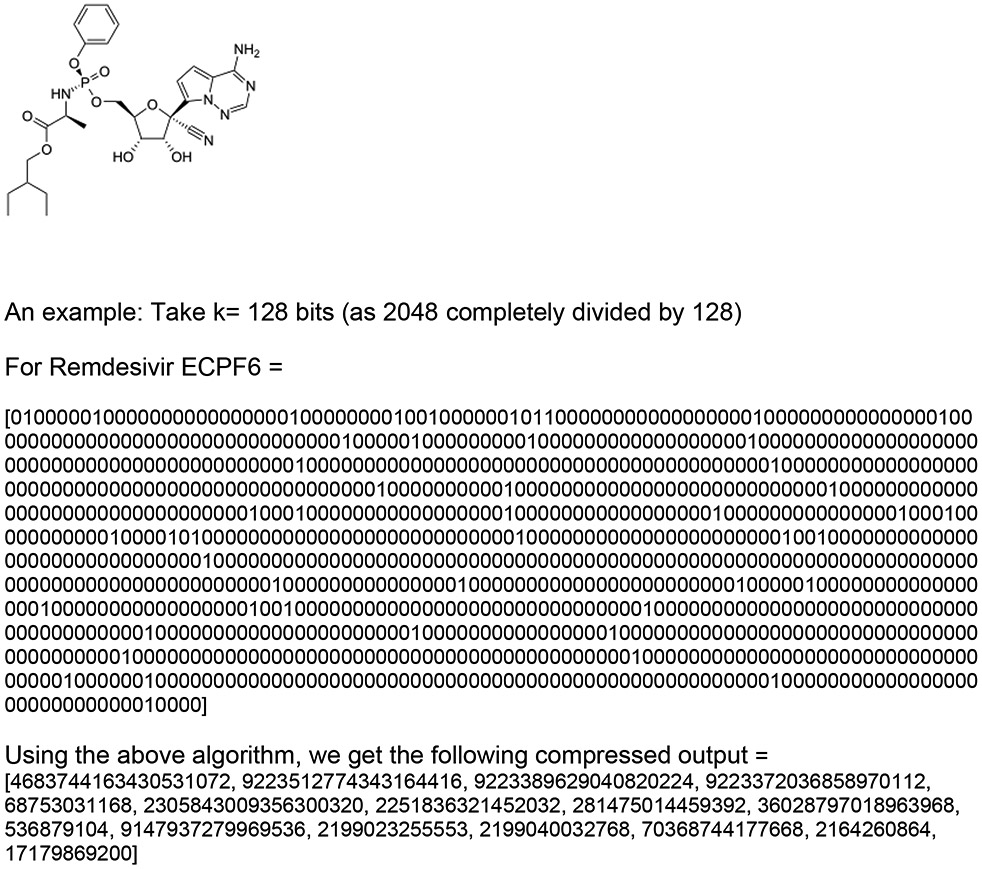
An example of a molecule and its compression using Method 3. 2D representation of the antiviral Remdesivir, and an illustration of the ECFP6 descriptor for Remdesivir and the compressed output.

Applying Method 4 using the same example of Remdesivir, we get two values [−21086,−502690]- where −21086 is storing the positions of 1’s and −502690 is storing the positions of 0’s. Using this approach, we get two dimensions that can be easily fed into the model. All the algorithms discussed above try to retain most of the information from the molecular descriptors as much as possible. This resulted in accuracy rates on the CC of 59% using kernel algorithm=‘sigmoid’ and on the QC of 59.25% (with n=2).

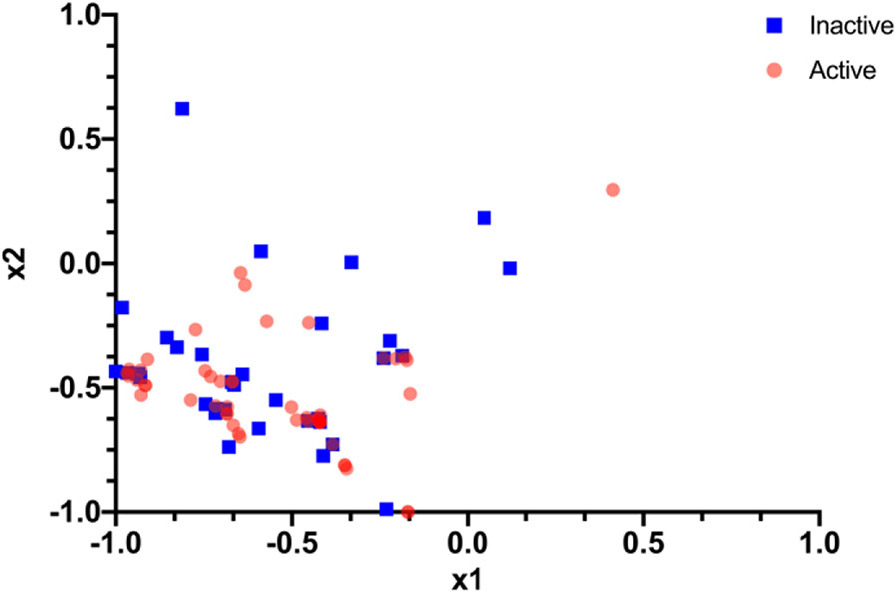
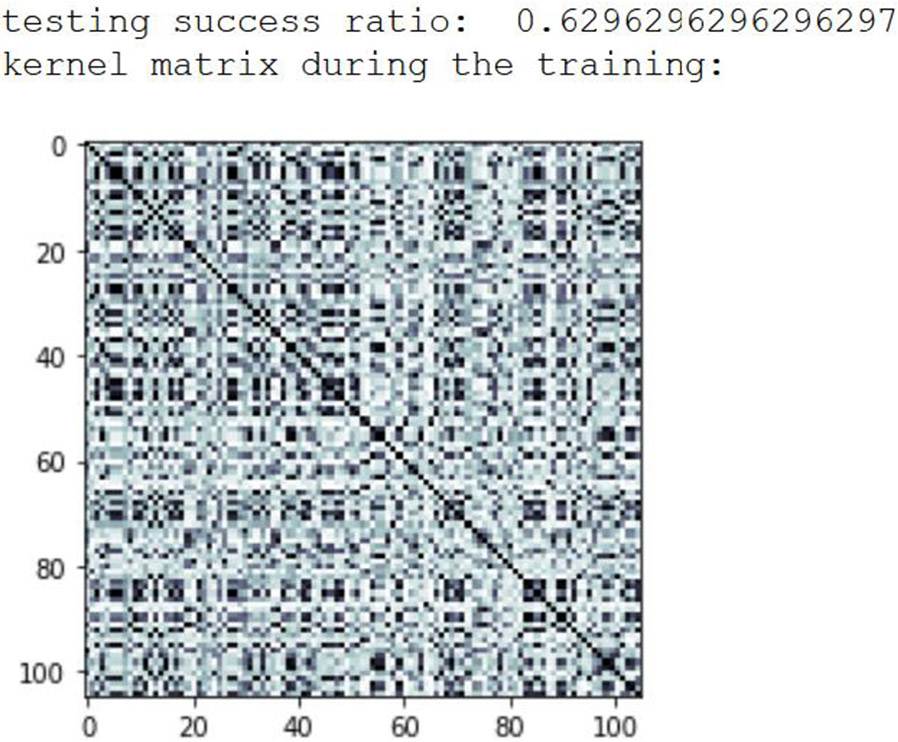
These four methods were implemented on the QC and then tried as combinations and the accuracy was compared with the CC (Table 1). The most promising results were obtained when combining Method 1 and Method 3 (k=128). The improved results for k=128 are due to the increased spread (more variance) as compared to other k values when combined with PCA (Figure 3). This makes it easier to obtain a hyperplane separating the two classes (active or not active). The Kernel matrix obtained from running the SVM model on a QC is shown in Figure 4.

Table 1.

The accuracy rates achieved with different combinations of methods. Method 1 (PCA), Method 2 (LDA), Method 3 and Method 4 using SVM on the classical and the quantum computer.

Combination	Accuracy on QC (%)	Accuracy on CC (%)
PCA + Method 3(k=64)	<30	47
PCA + Method 3(k=128)	62.9	65
PCA + Method 3(k=256)	59.25	60
PCA + Method 3(k=512)	41	44
LDA + Method 3(k=64)	31	36
LDA + Method 3(k=128)	<30	35
LDA + Method 3(k=256)	<30	31
LDA + Method 3(k=512)	32	59
PCA + Method 4(2)	59.25	60
LDA + Method 4(2)	57	57

Figure 3.

The spread of the data for the SARS-CoV-2 dataset after applying Method 1 and Method 3. “x1” and “x2” are the top two features respectively (for all the compounds) obtained after applying these two methods.

Figure 4.

Kernel Matrix obtained using PCA and Method 3 for the SARS-CoV-2 dataset.

Another approach we have applied is that of the hybrid approach (i.e., QC performs part of the calculation and CC the remainder) to remove the storage limitation on QC. We reduced the datapoint to 6 dimensions using the Method 1 and Method 3 for SVM. We loaded data into a single qubit by performing a simple unitary operation U (x1, x2, x3) where x1, x2, x3 are the coordinates of the point. When dimensions are greater than three, we can have U (x1, x2, x3, x4, x5, x6) to (U (x1, x2, x3) U (x4, x5, x6)). We have a similar unitary U (θ₁, θ₂, θ₃) for rotation of datapoint in bloch sphere (Figure 4) to make a two-qubit connected layer. For the same SARS-CoV-2 dataset, we obtained accuracy rates of 61%.

Applications of Quantum Machine Learning to M. tuberculosis datasets

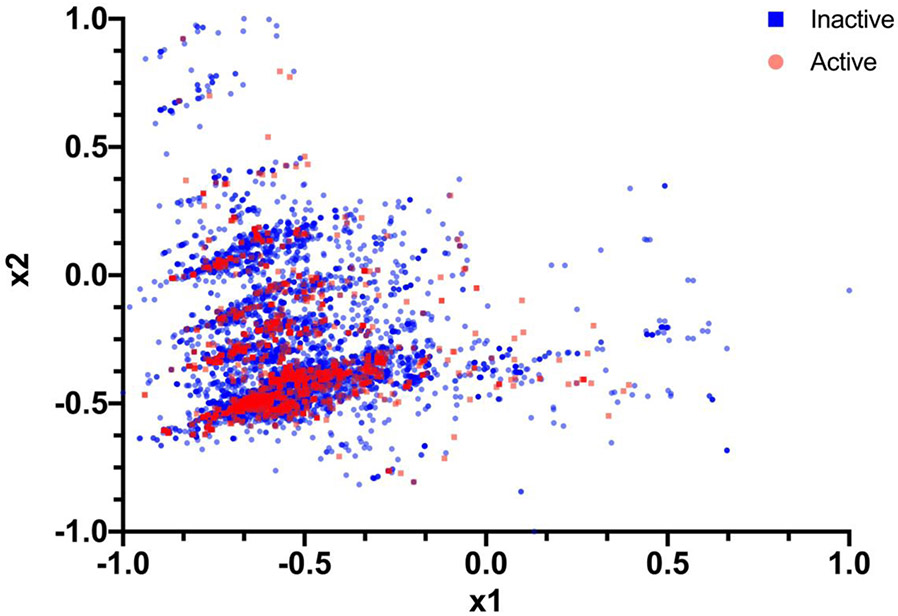
The same hybrid algorithm was then implemented on M. tuberculosis datasets, which were representative of high throughput screening data (i.e., tens of thousands of compounds). For all these datasets, we applied Method 1 and Method 3 for reducing the dimension and feeding it into our data re-uploading classifier as well as for plotting and visualization purposes. We also worked with the MFF descriptors ²² which generated a 71,375-descriptor vector. Datasets for in vitro inhibitors of M. tuberculosis had three variants, namely with a cutoff at of 100nM, 1μM and 10 μM ²⁵. Figure 5 shows a plot for the 100nM cutoff M. tuberculosis dataset when we reduced it into 2 dimensions. For these three datasets the data re-uploading classifier was run and then compared with the results obtained with CC (Table 2, Table S1). In Table 2 we see that the accuracy obtained on a QC is closer to that obtained on a CC with a slight time advantage over CC, such that there is a trade-off of accuracy and speed with these datasets. All of the above reported data are implemented on a QC (ibmq_rochester).

Figure 5.

A 2D plot representing the spread of data for the M. tuberculosis (100nM) dataset. This takes the important features using dimension = 2 instead of 6. “x1” and “x2” are the top two features respectively (for all the compounds) that have been calculated using Method 1 and Method 3.

Table 2.

Comparing accuracy and run time results for M. tuberculosis inhibition datasets (18,886 compounds) ²⁵ using data re-uploading classifier on CC with 3 GPU’s versus QC with 5-fold cross-validation using SVM.

Dataset threshold (number of actives)	Time on CC (min)	CC Accuracy (%)	Time on QC (min)	QC Accuracy (%)
100 nM (645)	125	97.1	104	90.5
1 mM (2351)	144	90.4	101	81.4
10 mM (7762)	229	75.6	153	54.9

Applications of Quantum Machine Learning to Large in vitro Datasets

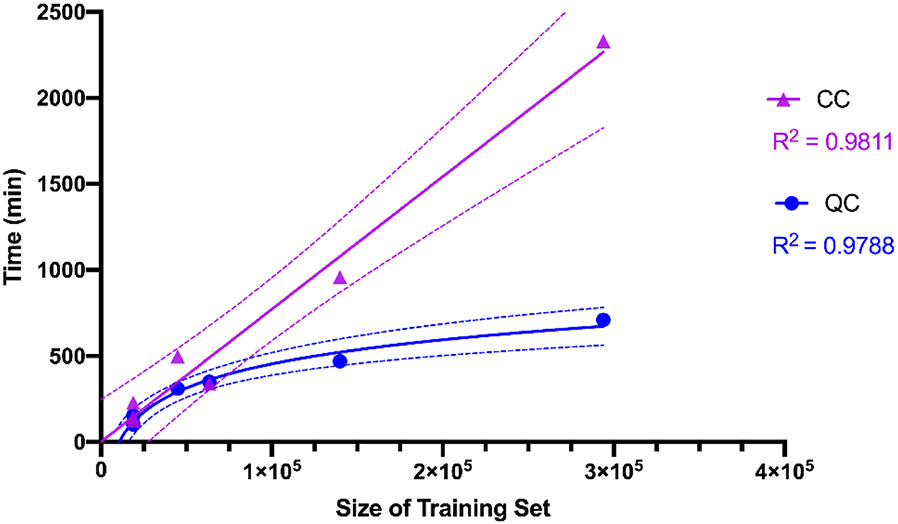
The data re-uploading classifier algorithm ³⁴ was implemented with the ECFP6 molecular descriptor, and tested with five considerably larger drug discovery datasets ranging from 44,000 – 293,000 molecules on a QC simulator (Table 3). Running them on a QC with the transfers of data was the major overhead here for such large datasets. We find that the results obtained are very comparable with a slight time advantage for the QC simulator over CC. The linearity of calculation time on a CC with dataset size was apparent and this plateaued for the QC simulator (Figure 6).

Table 3.

Comparing large scale drug discovery datasets on a Quantum Computer Simulator and CC with 5 GPU’s for data re-uploading classifier using the ECFP6 descriptor obtained from Method 1 and Method 2. Algorithms on QC Simulator were run for 10 epochs with 5 fold cross validation unless noted. ND = not determined.

		QC			CC
Dataset target	Total compounds (active)	Training accuracy (%)	Testing accuracy (%)	Time on QC (min/epoch)	Training accuracy (%)	Time on CC (min)
Cathepsin B	63,331 (75)	99.4	99.1	35 (10 epochs)	99.8	341.25
Krabbe disease	44,809 (63)	91.2	92.4	31 (10 epochs)	99.9	497.91
Plague	139,861 (223)	92.9	93.1	47 (10 epochs)	99.8	958.59
M. tuberculosis	293,937 (6104)	90.4	91.3	71 (10 epochs)	97.9	2329.4
hERG	306,587 (233)	82.7	82.5	313 (ran for 5 epochs)	ND	ND

Figure 6.

Comparing dataset size with run time for Quantum Computer (QC) simulator and Classical Computer (CC). Linear or non-linear (semi-log) fit lines for the data generated. These show the likely relationship of CC and QM model size versus calculation time is on a linear and semi-log scale, respectively. The dotted lines represent the 99% confidence bands of these lines to highlight the likelihood of this relationship.

DISCUSSION

We have discussed four approaches and their combination for compression of the molecular descriptors, followed by calculation of the machine learning model on a QC. We found that the results were optimal when combining Method 3 and Method 1, most likely due to the increased spread of data after employing these techniques. Further, we applied both the QC and hybrid approach to train our model. With the current QC hardware available, the option of choosing the hybrid approach for drug discovery is likely optimal. When dealing with bigger in vitro structure-activity datasets on the order of tens of thousands of molecules, we found that the data communication overhead between computer and cloud-based QC was much larger than the actual time taken for a circuit to execute on QC. Plotting the time versus size of a dataset for CC vs QC simulator also suggests the likely potential speed of model building on a QC with larger datasets if we are able to replicate the same settings on a QC (Figure 6). Now that we have optimized these steps for machine learning we have demonstrated that QC can handle ‘very large’ drug discovery datasets on the order of hundreds of thousands of molecules. At the time of this work data for SARS-CoV-2 available for machine learning was in the hundreds of molecules and now it is likely in the low thousands of molecules ²⁴ and yet such datasets clearly do not require the performance of QC. However, the larger high-throughput screening datasets for other targets and diseases that have been amassing in public databases like PubChem ⁴⁰ and ChEMBL ¹ present significant challenges for SVM and deep neural network as well as other computationally intensive tools. QC is therefore a viable approach to overcoming some of these limitations and allowing practical computing times. With thousands of such datasets now readily available, being able to curate and update them quickly will be important as new screening data are added. Obviously, as we start to see DNA encoded libraries with sizes in the millions to possibly billions of molecules being used for generating high throughput screening data, then we will likely need QC for machine learning with algorithms that are compute intensive in order to see results in a reasonable time. This study demonstrates the non-linear scaling of compute time on a QC with multiple independent datasets of different sizes, compared with the linearity observed on a CC. As quantum machine learning develops, the accessibility of QC will increase for drug discovery cheminformatics applications as we have demonstrated here. Future studies to evaluate these and other quantum machine learning models will also need to involve prospective prediction and experimental validation in order to provide convincing evidence of their value for drug discovery.

Abbreviations

CC

Classical computer

DNN

Deep Neural Networks

ECFP6

Extended connectivity fingerprint radius 6

LDA

Linear Discriminant Analysis

MFF

multiple fingerprint features

PCA

Principal Component Analysis

QC

Quantum computer

SVM

Support Vector Machines