Estimation of the lower limits for feasible Ra-223 SPECT imaging: a Monte Carlo simulation study

Abstract

Objective(s):

Ra-223 is a promising radionuclide for the treatment of skeletal metastases in castration-resistant prostate cancer patients. This study aims to estimate the lower limits for feasible Ra-223 single-photon emission computerized tomography (SPECT) imaging using a Monte Carlo simulation study.

Methods:

The SPECT images were produced on a homemade code: the Monte Carlo simulation of electrons and photons for SPECT (MCEP-SPECT). The National Electrical Manufacturers Association (NEMA) phantom with six hot spheres of diameters of 37, 28, 22, 17, 13, and 10 mm installed inside, was used. The background activity concentration was 0.6 kBq/mL, and the ratios of hot concentrations to the background (R_HB) were 25, 20, 15, 10, and 5. When R_HB was 15, the background concentrations of 1.5, 0.9, 0.3, and 0.15 kBq/mL were also tested. The energy window was 84 keV±10%. The number of projections was 60/360°, and the acquisition time was 60 s per projection. Two kinds of collimators: middle-energy general-purpose (MEGP) and high-energy general-purpose (HEGP), were examined. The SPECT images were evaluated based on two quantitative indexes: contrast-to-noise ratio (CNR) for detectability and contrast recovery coefficient (CRC) for quantitative accuracy.

Results:

The CRC for the HEGP collimator was 35–40%, while the CRC for the MEGP collimator was 25–30%. The CNRs for the MEGP collimator were larger than those for the HEGP collimator. The CNRs of the hot spheres with diameters less than 22 mm were lower than 5.0 for both collimators, when R_HB and the background concentration were 15 and 0.6 kBq/mL, respectively. Based on the obtained results, it was estimated that the lower limit of R_HB for the detection of the hot sphere with a diameter of 37 mm would be approximately 20 if the background concentration is 0.05 kBq/mL.

Conclusions:

The MEGP collimator is superior in terms of detectability, while the HEGP collimator is superior in terms of quantitative accuracy. When the lesion size is small, the MEGP collimator may be favorable. Based on these results, the estimated lower limit of the activity concentration would be approximately 1 kBq/mL if the background concentration is 0.05 kBq/mL for a large lesion.

Introduction

Ra-223 is a promising α-targeted emitter utilized for the remediation of skeletal metastases in castration-resistant prostate cancer patients (1-9). Ra-223 emits several X-rays (70–90 keV) and γ-rays (150–300 keV) after the α-decay (10), and these photons have been used in the imaging of lesions. The planar images of Ra-223 are useful and have been used to depict the uptake in lesion sites. However, the detection and quantification of the activity are difficult because of the overlap of several structures. Single-photon emission computerized tomo-graphy (SPECT) imaging technique is a powerful alternative for avoiding these problems. However, the SPECT imaging of Ra-223 is challenging, because the administered dose is not sufficient (55 kBq/kg) and the radiation energy

spectra are wide. The largest decay rate is of 84 keV, followed by those of 154 keV and 270 keV (10). In general, the energy window is set around 84 keV. However, the photons scattered from the higher-energy level and characteristic X-rays from the lead septa of the collimator contaminate the energy window and decrease image quality (11).

Despite the difficulties, some researchers have reported the feasibility of Ra-223 SPECT imaging (12-15) for the last several years. Owaki et al. have investigated on the feasibility and clinical usefulness of Ra-223 SPECT (12). They performed image acquisition of Ra-223 in phantom and patients with prostate cancer. Benabdallah et al. have studied the optimization of imaging parameters for Ra-223 SPECT using NEMA and TORSO phantoms (13). Recently, Gustafsson et al. have reported a study in which they used Monte Carlo simulation and phantom measurements, and discussed the limitation of quantitative SPECT for Ra-223 (14).

The SPECT imaging is based on the principle of planar imaging, where the performance of the collimator is important. We had reported the simulation studies of Ra-223 planar imaging, which were focused on the impact of the collimator on the quality of the planar images. In the earlier study, we simulated the Ra-223 planar images for 84, 154, and 270 keV photo peaks using medium-energy general-purpose (MEGP) and low-energy general-purpose (LEGP) collimators (11). The results suggested that the MEGP collimator is more suitable for Ra-223 imaging than the LEGP collimator. In the next study, we attempted to quantitatively evaluate the Ra-223 images produced by five collimators: two MEGPs, two LEGPs, and one high-energy general-purpose (HEGP) collimator, using machine learning, i.e., the channelized Hotelling observer (CHO) method (16). The results revealed that the MEGP collimators exhibited better performance for Ra-223 imaging than the LEGP and HEGP collimators in terms of the detectability of lesions.

In this study, we expanded these studies to SPECT imaging and estimated the lower limits for feasible Ra-223 SPECT imaging. In the above mentioned studies (12-15), the setting of background activity concentration surrounding the hot area was limited; the ratio of background concentration to hot area was 0, 1/20 (12-14) or 1/30 (15). The settings seem to be too mild to investigate the lower limit of detectable concentration for Ra-223 SPECT, because the artifacts owing to the fluctuation of signal counting in the background disturbs the detectability. We simulated the Ra-223 SPECT images under various conditions using the Monte Carlo simulation code to investigate the lower limits for feasible SPECT imaging. Based on the results of our previous study, two collimators were examined to produce the SPECT images to assess the impact on the image quality: the MEGP collimator, which exhibited the best performance in our previous study (16), and the HEGP collimator, which was used in the experimental study of Ra-223 SPECT imaging by Qwaki. The simulated images were evaluated based on two quantitative indexes: the contrast-to-noise ratio (CNR) for detectability and the contrast recovery coefficient (CRC) for quantitative accuracy. Using these indexes, we estimated the lower limit conditions for obtaining feasible Ra-223 SPECT images.

Methods

The Monte Carlo simulation in this study is the MCEP-SPECT model, which is based on the gamma camera simulation codes: HEXAGON and NAI, developed by Tanaka et al (17). The HEXAGON code simulates the transport of photons and electrons in the medium and in the collimator. The NAI code treats the NaI crystal and the back compartments. In regard to I-123, the simulated sensitivity spectra in the range between 50 and 600 keV agreed well with experimental results (17). In our previous study (16), we commented on the difference between the simulated energy spectrum and the experimental spectrum measured by Owaki et al. (12). The simulated spectrum approximately agreed with the experimental one.

Figure 1 shows the gamma camera setup for the simulation studies. The size of the collimator and the NaI crystal was 40 cm × 40 cm. To simulate the effects of the backscatter photons from the backward components (photomultiplier tubes), a glass and an aluminum plate were placed behind the NaI crystal. The distance between the center of the phantom and the gamma camera was 26 cm.

Figure 1.

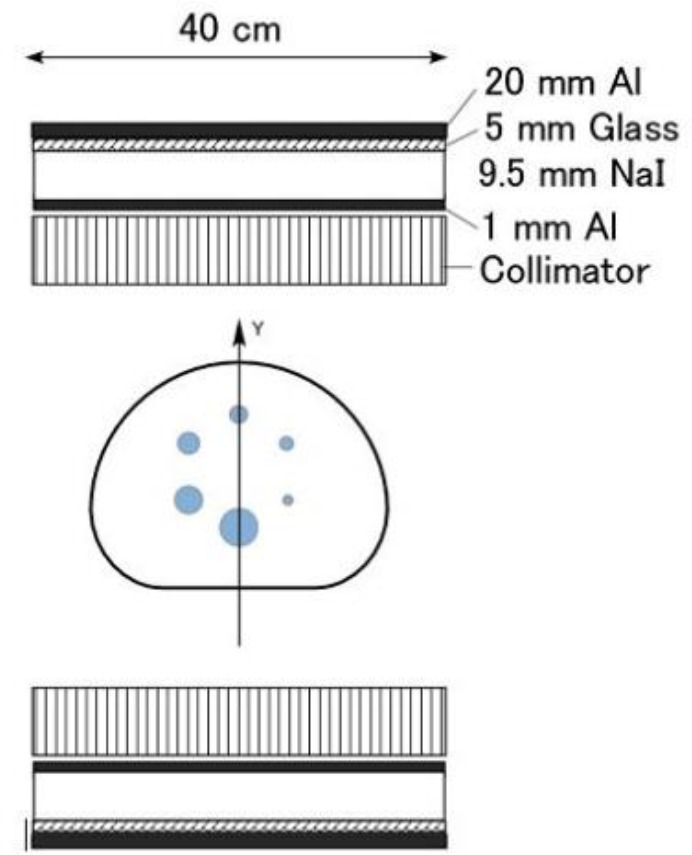
Setup of the gamma camera for the simulation and cross-sectional view of the phantom. The gamma cameras were fixed at a distance of 26 cm from the center of the phantom

The National Electrical Manufacturers Association phantom was used for all the simulations. The diameters of the spheres were 37, 28, 22, 17, 13, and 10 mm. The background activity concentration of Ra-223 was 0.6 kBq/mL, and the ratios of the hot concentrations to the background (R_HB) were 25, 20, 15, 10, and 5. When R_HB was 15, the background concentrations of 1.5, 0.9, 0.3, and 0.15 kBq/mL were also tested.

The major photo peaks of Ra-223 appear at 84, 154, and 270 keV. In this study, the energy window was set to 84 keV±10%. The number of projections was 60/360°, and the acquisition time was 60 s per projection. The image reconstruction algorithm used was the subset expectation maximization (OSEM) with attenuation correction using the Prominence Processor (version 3.1, distributed by the Prominence Conference; not for sale), a software package for imaging in nuclear medicine. The projection data were preprocessed by the Butterworth filter (order: 8, cutoff frequency: 0.5 cycle/cm). Using the Chang attenuation correction method, the attenuation coefficient was 0.2 cm⁻¹ (20). Scattering correction was not attempted in this study. The number of subsets and iterations was set to 6 and 10, respectively, by referring to the previous study by Owaki

et al. (12).

Table 1 shows the dimensions of the collimators tested in this study. The MEGP collimator used here was the same as the one used in our previous study (16), and the HEGP collimator was the one used in the study of Owaki et al. (12). To indicate the fundamental characteristics of the collimator, we investigated the full width at half maximum (FWHM) of the point spread function (PSF), which represents the response of an imaging system to a point source. The relationship between the FWHM of PSF and the source-to-collimator distance is simplified as follows:

FWHM = Ax + B (mm)          (1)

Where x is the source-to-collimator distance, and A and B are the specific constants for each collimator. Coefficient A indicates the spread per unit distance or the degree of point spread, and B indicates a fundamental resolution. To obtain the data, we simulated image blurring through planar images of the point source on each collimator using HEXAGON and NAI. The geometric arrangement of point source imaging is illustrated in Figure 3. The size of the point source was 1 mm × 1 mm × 1 mm, and the distances between the source and collimator were 100, 200, and 300 mm.

Table 1.

Dimensions of six collimators. The HEGP collimator is the same one used in the study of Owaki et al

	Septal thickness (cm)	Hole diameter (cm)	Hole length (cm)
HEGP	0.18	0.4	6.6
MEGP	0.108	0.337	4

The simulated SPECT images were evaluated based on two quantitative indexes: CRC and CNR. The CNR is expressed as

$\mathit{CNR}=\frac{C_H-C_B}{{\mathit{SD}}_B}$           (2),

Where C_H is the mean count inside the region-of-interest (ROI) of the hot area, C_B is the mean count inside the ten ROIs of the background areas, and SD_B is the standard deviation of the counts inside the background ROIs. The CNR is a ratio of the net magnitude of the signal in the hot area to the fluctuation of the background, and it indicates the detectability of the hot area.

The CRC is expressed as

$\mathit{CRC}=\frac{\frac{C_H}{C_B-1}}{R_{\mathit{HB}}-1}\times 100\left(\%\right)$          (3),

$R_{\mathit{HB}}=\frac{A_H}{A_B^{\text{'}}}$

Where A_H and A_B are the activity concentrations of the hot sphere and the background, respectively; R_HB is the ratio of the hot concentra-

tion to the background. The CRC indicates the measurement accuracy and the quantitative accuracy of the activity. Ten background ROIs were set, as shown in Figure 2.

Figure 2.

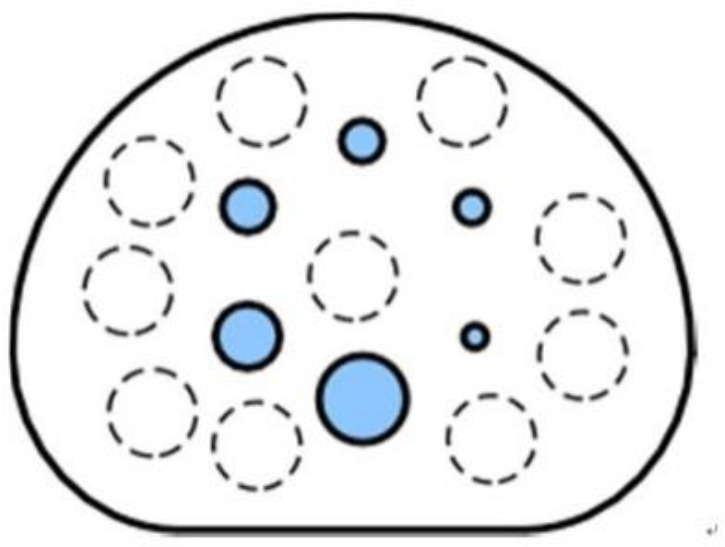
ROIs in the calculation of the CNR and the CRC. The solid circles represent the hot areas, and the dashed circles represent the background areas

Results

Table 2 shows the coefficients A and B which are presented in Equation (7) for two collimators. These coefficients of the HEGP collimator were smaller than those of MEGP. This result implies that the images obtained with the HEGP collimator have smaller blurring and better image resolution.

Table 2.

Coefficients A and B in Equation (1)

	A	B (mm)
HEGP	0.050	3.8
MEGP	0.070	4.9

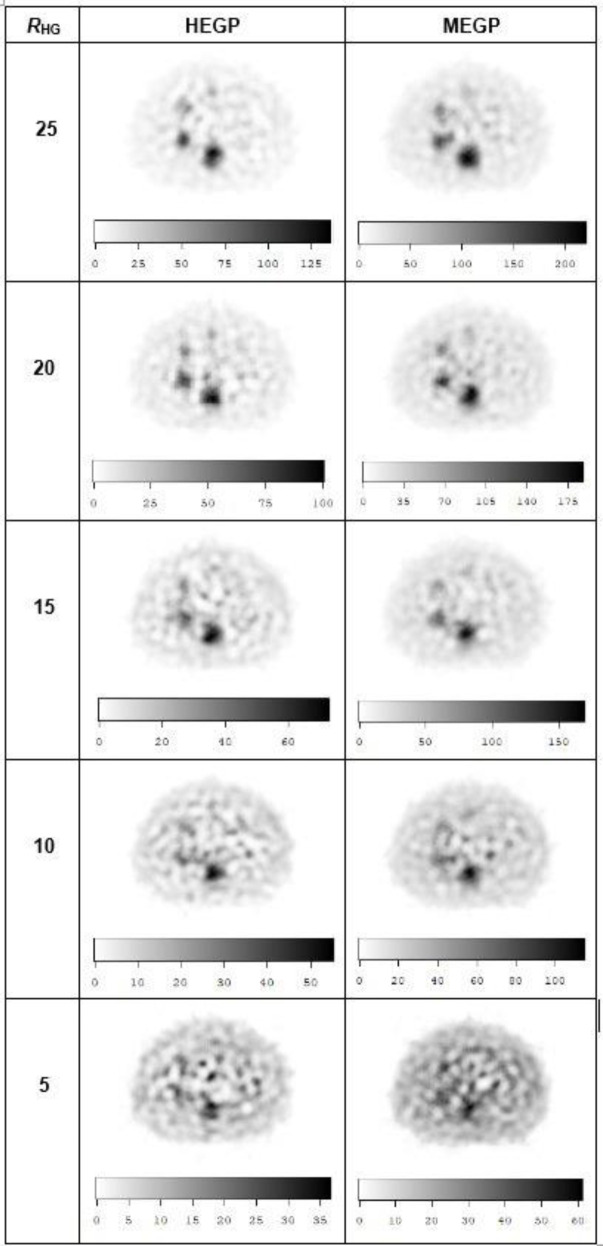
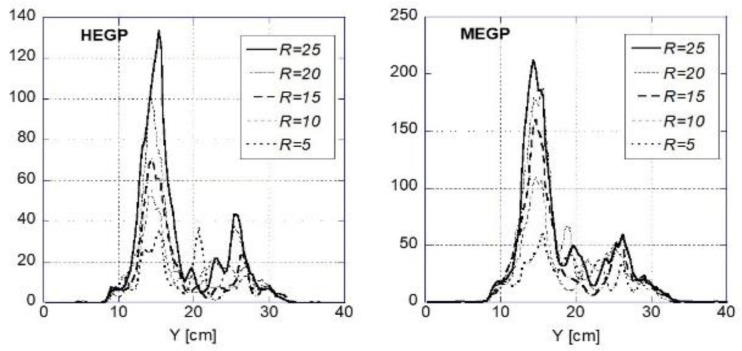
Figure 3 shows the simulated SPECT images for the background concentration of 0.6 kBq/mL. Hot spheres with diameters larger than 22 mm were visible for both collimators. Figure 4 shows the profiles of images shown in Figure 3 along the vertical axis on the phantom, which is shown in Figure 1 (Y-axis). Some small artifacts appeared near the center of the phantom. These artifacts are caused by scattered photons owing to hot spheres around the central ROI. The ROI values of background in the central region were larger than those of other background ROIs by the factor of 1.5–2. This overestimation might be caused by the artifacts and the overcorrection of the Chang method.

Figure 3.

Simulated SPECT images for the background concentration of 0.6 kBq/mL

Figure 4.

Profiles of images shown in Fig. 3 along the central vertical axis on the phantom

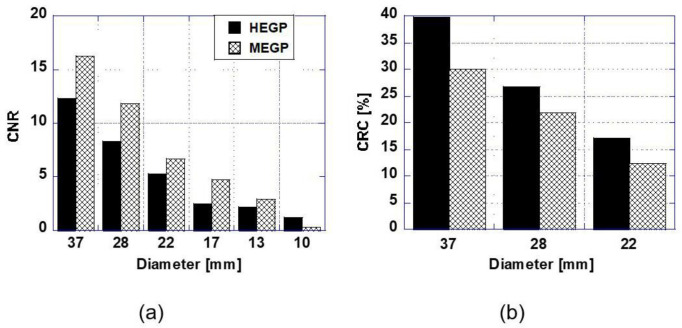
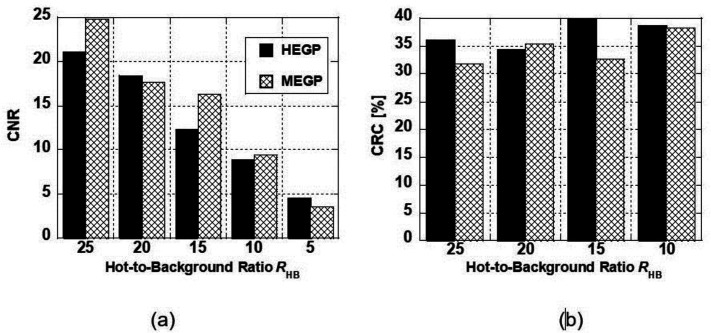
Figure 5(a) shows the CNRs of the hot spheres in the images of Figure 3. The CNR for the MEGP collimator was larger than that for the HEGP collimator. The MEGP collimator showed the largest CNR at 37 mm; however, the CNR decreased rapidly as the sphere diameter decreased. Provided that the criterion of CNR to obtain an effective image is 5.0 (18), the spheres with diameters larger than 22 mm would remain detectable for both collimators, which agrees with the visual impression of the images in Figure 3.

Figure 5 (b) shows the CRCs in the case where the CNR is more than 5.0. The CRCs rapidly decreased as the sphere diameter decreased due to partial volume effects. In contrast to CNR, the CRCs for the HEGP collimator were larger than those for the MEGP collimator.

Figure 5.

(a) CNRs and (b) the CRCs of the hot spheres in the images of Figure 3. RHB is 15, and the background concentration is 0.6 kBq/mL. The CRCs in the case where the CNR is larger than 5 are shown

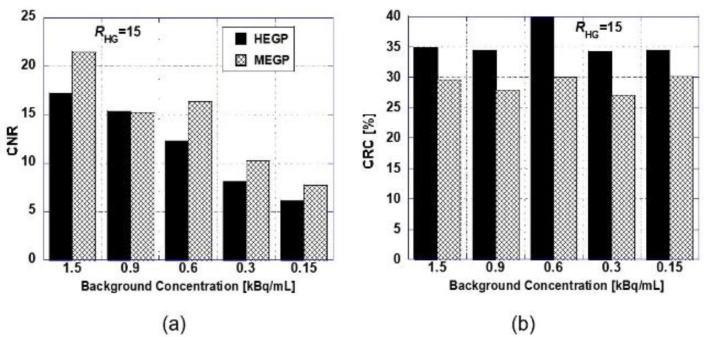
Figure 6 shows the CNR and CRC values of the sphere with a 37-mm diameter when the background concentration changed from 1.5 to 0.15 kBq/mL and R_HB was 15. Under these conditions, the CNRs exceeded 5, i.e., the hot sphere was detectable. However, the case of 0.15 kBq/mL was critical for detection. Figure 7shows

the CNR and CRC values of the sphere with a 37-mm diameter when R_HB changed. When R_HB was less than 10, the CNRs were less than 5.0 (undetectable) for both collimators. Figures 6(b) and 7(b) confirm that the CRC does not depend on the background concentration and R_HB, although they somewhat fluctuated.

Figure 6.

(a) CNRs and (b) the CRCs of the hot sphere with a 37-mm diameter when RHB is 15

Figure 7.

(a) CNRs and (b) the CRCs of the hot sphere with a 37-mm diameter when the background concentration is 0.6 kBq/mL. The CRCs in the case where the CNR is larger than 5 are shown

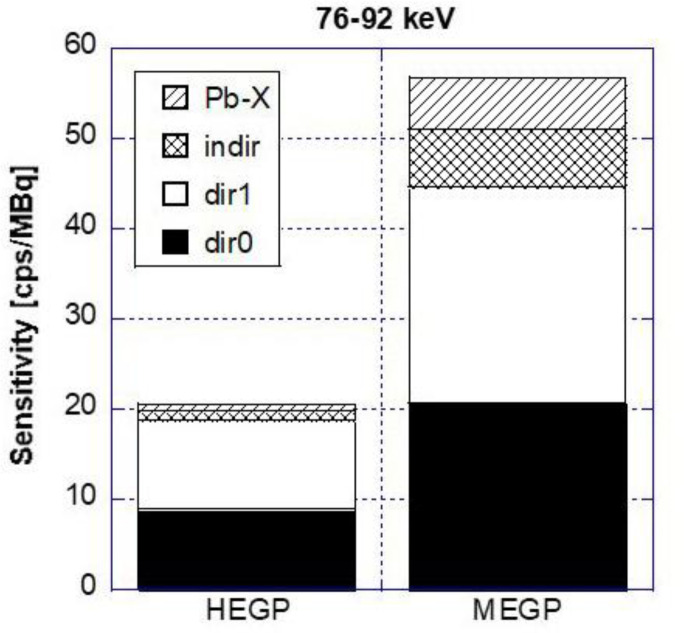
Figure 8 shows the simulated partial sensitivity of gamma camera in the 84 keV ±10 % window. The direction of projection was the posterior of the phantom. Partial sensitivity means the sensitivity of each photon detection process; “dir0,” ”dir1,” ”indir,” and “Pb-X.” The “dir0” denotes detected photons that pass through the collimator hole without any interaction with a phantom and collimator. Photons that interact with the phantom but travel through the collimator hole are indicated as “dir1;” photons that collide with, penetrate, or interact with the collimator wall regardless of whether they interact with the phantom or not are shown as “indir”; photons of characteristic X-rays from lead are shown as “Pb-X.” The total sensitivity of the MEGP collimator in this study was more than twice that of the HEGP collimator; however, the fraction of partial sensitivity of “dir0” for HEGP was larger than that for MEGP. Additionally, the partial sensitivity of “indir” and “Pb-X” for HEGP was much smaller than that for MEGP.

Figure 8.

Simulated partial sensitivity (cps/MBq) in the window of 84 keV ± 10%. The direction of projection was the phantom posterior

Discussion

This study aims to estimate the lower limits for feasible Ra-223 SPECT imaging. In our previous study, we investigated the impact of collimators on Ra-223 planar images using the CHO method. The CHO method evaluates the detectability using the signal-to-noise ratio, which corresponds to the CNR in SPECT imaging. In this study, we added CRC to evaluate the quantitative accuracy of the Ra-223 SPECT images. The setting of the activity concentration was the most difficult challenge in this study because the real concentration in the human body was unknown. Thus, we set the background concentration and the hot-to-background ratio to a wide range (0.15–1.5 kBq/mL and 5–25, respectively).

The results showed that the images produced by the MEGP collimators were superior to those by other collimators in terms of the CNR, i.e., the detectability. This agrees with the results of our previous study using the CHO method (16). In contrast, the CRCs for the HEGP collimators were larger than those for the MEGP collimators. This result agrees with the result reported by Owaki et al. They showed that the lesion-to-background ratio (LBR) of the Ra-223 SPECT image of a patient’s body, obtained using the HEGP collimator, was larger than that obtained using the MEGP collimator (12). The LBR in their study corresponds to C_H/C_B in Equation (3); this implies that the CRC for the HEGP collimator was larger than that for the MEGP collimator.

This is caused by the high aspect ratio and relatively thick septa of the HEGP collimator. The aspect ratio is the ratio of the whole length to the whole diameter. The collimator with a relatively high aspect ratio efficiently blocks oblique incidence photons, and thicker septa block the scattered photons scattered and characteristic X-ray caused by high-energy photons. These characteristics are verified by the results shown in Table 2 and Figure 8. Table 2 shows that the images with the HEGP collimator have smaller blurring and better resolution, and Figure 8 shows that the scatter components (“indir” and “Pb-X”) in the HEGP collimator are much smaller than those in MEGP. The smaller scattering photons reduce the partial volume effect and result in larger CRC.

Conversely, the HEGP collimators decrease the photon count because of their relatively high aspect ratio and thick septa, as shown in Figure 8; thus, the fluctuation of the background concentration increases, which results in smaller CNRs for the HEGP collimators.

The lower limits of detection for the lesions are important in considering the feasibility of SPECT imaging. The parameters to consider are the lesion size, hot-to-background ratio (R_HB), and background concentration (A_B). For the lesion size, it was difficult to detect spheres with diameters smaller than 22 mm when A_B and R_HB were 0.6 kBq/mL and 15, respectively. The lower limit of R_HB was approximately 5 when A_B was 0.6 kBq/mL and the lesion size was 37 mm. The lower limit of A_B was assumed to be less than 0.15 kBq/mL when R_HB was 15 and the lesion size was 37 mm. These results were obtained under limited conditions. The lower limit is derived using the criterion that the CNR should exceed 5; therefore, the CNR should be estimated under arbitrary conditions.

It is possible to approximate the CNR for the arbitrary values of A_B and R_HB. Equation (2) can be rewritten using Equation (3) as follows:

$\mathit{CNR}=\frac{C_B(\frac{C_H}{C_B}-1)}{{\mathit{SD}}_B}=\frac{C_B\left(\frac{\mathit{CRC}\left[\%\right]}{100}\right)(R_{\mathit{HB}}-1)}{{\mathit{SD}}_B}$ ,           (4)

The standard deviation (SD_B) is proportional to $\sqrt[2]{C_B}$ , and the count (C_B) is proportional to the background activity (A_B). Since the CRC does not depend on A_B or R_HB when the sphere size is constant, as is shown in Figs. 6 and 7, the CNR would be proportional to . If the CNR is CNR₀ when the background activity and the hot-to-background ratio are A_B0 and R_HB0, respectively, the CNR for A_B and R_HB would be

$\mathit{CNR}={\mathit{CNR}}_0\times \sqrt[2]{\frac{A_B}{A_{B_0}}}\frac{R_{\mathit{HB}}-1}{{\mathit{RHB}}_0-1}$,           (5)

This is a rough guess; however, it helps to estimate an approximate CNR. For example, for the HEGP collimator, when the diameter was 37 mm, the CNR₀, R_HB0, and A_B0 values were 12, 15, and 0.6 kBq/mL, respectively, as shown in Fig. 5(a). Therefore, if A_B and R_HB are 0.1 kBq/mL and 20, respectively, the CNR would be 6.6.

What is required is the minimum R_HB (or A_B) for which the CNR exceeds a criterion (5 in this study). The minimum value is the lower limit.

$\sqrt[2]{A_B}\left(R_{\mathit{HB}}-1\right)=\frac{5}{{\mathit{CNR}}_0}\sqrt[2]{A_{\mathit{BO}}}(R_{\mathit{HBO}}-1)$       (6)

For example, if A_B is 0.1 kBq/mL, the lower limit of R_HB would be 15. If A_B is 0.05 kBq/mL, the lower limit would increase to 21 (namely, the activity concentration in the sphere is approximately 1 kBq/mL) for the lesion size of 37 mm. The concentration of 0.05 kBq/mL is close to the dose used in the standard protocol: 55 kBq per kg of body weight. This is important information to consider in determining the feasibility of SPECT imaging in a few hours after the Ra-223 injection. In regard to the lower concentration several days after injection, the lower limit can be estimated using Eq. (6). For example, when the background concentration is 0.01 kBq/mL (20 % of 0.05 kBq/mL), the lower limit of R_HG is 46. Gustafsson et al., in their previous study, concluded that the activity concentration estimation using Ra-223 SPECT imaging is feasible for reasonably large structures (approximately 30 mL or larger) at concentrations of approximately 1 kBq/mL (14). Our estimation above supports their suggestion.

These estimations were based on the sphere with a diameter of 37 mm. The lower limit increases with the diameter because of the small CNR. For the sphere with a 22-mm diameter, CNR₀ was 6, as shown in Figure 5(a); therefore, if A_B is 0.1 kBq/mL, the lower limit of R_HB would be 30. If A_B is 0.05 kBq/mL, the lower limit would be 41, which is twice of that for 37-mm diameter. For the MEGP collimator, the lower limits are smaller than those for the HEGP collimator because of its larger CNR₀ value. In the case where the lesion is small, MEGP collimators may be more suitable.

Several important factors were not considered in this study. First, the investigation of other energy windows centered at 154 and 270 keV. These additional energy windows might increase the CNRs by increasing the photon count. The second factor is the scattering correction. The effect of this factor depends on various conditions; for activity concentration, lesion size, main/sub-window setting, and collimator. The scattering correction may be positive in the case of large lesion and high activity concentration; however, it should be negative for small lesion and low concentration owing to a decrease in the photon count as a result of subtraction. The third factor is the phantom: the phantom and the radioactivity distribution were simple here; however, in a more complicated model, the detection criterion for the CNR might be different from that in this study (5). The criterion affects the estimation of the lower limits; therefore, further investigation using a more realistic setting would be required. To solve this problem, employing an anthropomorphic phantom, such as the extended cardiac torso phantom (XCAT), for the simulation would be useful (14, 19).

Conclusions

In this study, we investigated the impact of collimators and the conditions for obtaining valid SPECT images using a Monte Carlo simulation. The simulation results showed that the MEGP collimator is superior to the HEGP collimator in terms of detectability, while the HEGP collimator is superior in terms of quantitative accuracy. Overall, the HEGP collimator is suitable for Ra-223 SPECT imaging; however, in the case where the lesion is small, the MEGP collimator may be more suitable. The results also suggested that it was difficult to detect hot spheres with diameters below about 20 mm, under the conditions in this study. Based on these results, the estimated lower limit of the activity concentration was approximately 1 kBq/mL for the background concentration of 0.05 kBq/mL (i.e. R_HB = 20) and lesion size of 37 mm.