Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Jun 23;11(13):8370–8381. doi: 10.1021/acscatal.1c01851

Kinetics and Mechanism of Plasmon-Driven Dehalogenation Reaction of Brominated Purine Nucleobases on Ag and Au

Anushree Dutta †, Robin Schürmann †, Sergio Kogikoski Jr †, Niclas S Mueller ‡, Stephanie Reich ‡, Ilko Bald †,*
PMCID: PMC8256422  PMID: 34239772

Abstract

graphic file with name cs1c01851_0008.jpg

Plasmon-driven photocatalysis is an emerging and promising application of noble metal nanoparticles (NPs). An understanding of the fundamental aspects of plasmon interaction with molecules and factors controlling their reaction rate in a heterogeneous system is of high importance. Therefore, the dehalogenation kinetics of 8-bromoguanine (BrGua) and 8-bromoadenine (BrAde) on aggregated surfaces of silver (Ag) and gold (Au) NPs have been studied to understand the reaction kinetics and the underlying reaction mechanism prevalent in heterogeneous reaction systems induced by plasmons monitored by surface enhanced Raman scattering (SERS). We conclude that the time-average constant concentration of hot electrons and the time scale of dissociation of transient negative ions (TNI) are crucial in defining the reaction rate law based on a proposed kinetic model. An overall higher reaction rate of dehalogenation is observed on Ag compared with Au, which is explained by the favorable hot-hole scavenging by the reaction product and the byproduct. We therefore arrive at the conclusion that insufficient hole deactivation could retard the reaction rate significantly, marking itself as rate-determining step for the overall reaction. The wavelength dependency of the reaction rate normalized to absorbed optical power indicates the nonthermal nature of the plasmon-driven reaction. The study therefore lays a general approach toward understanding the kinetics and reaction mechanism of a plasmon-driven reaction in a heterogeneous system, and furthermore, it leads to a better understanding of the reactivity of brominated purine derivatives on Ag and Au, which could in the future be exploited, for example, in plasmon-assisted cancer therapy.

Keywords: hot-electrons, plasmon-driven catalysis, fractal kinetics, brominated purines, SERS, hole scavengers

Introduction

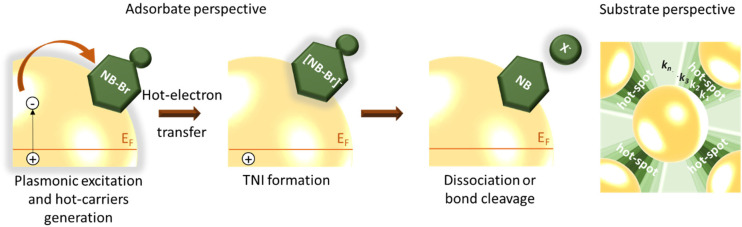
Visible-light-driven chemical reactions on the surface of plasmonic nanostructures form the basis of plasmon chemistry. That is to say, an incident photon of certain energy when impinged on the surface of a nanoparticle (NP) can trigger the collective oscillation of the free electron cloud which results in the generation of a localized surface plasmon (LSP).1−3 When the oscillating electron cloud dephases, electron–electron scattering on the NP surface results in the generation of nonequilibrium high-energy electrons for a short time scale that are referred to as “hot electrons”.4,5 The hot electrons (charge carriers) can easily get transferred to an unoccupied orbital of a nearby chemisorbed or physisorbed reactant molecule to induce a chemical reaction within the system via transient electronic exchange. This is termed as a surface plasmon (SP)-induced reaction and is often studied by SERS.6,7

Several mechanistic models described by dissociative electron attachment (DEA),8 desorption induced by electronic transition (DIET), and desorption induced by multiple electronic transitions (DIMET),9,10 among others, have been put forward to study and understand the nature of some exemplary plasmon-induced reactions. For example, the mechanism of plasmon-induced dissociation reactions of O2 and H2 has been explained on the basis of the formation and relaxation of transient negative ions (TNIs) resulting in vibrational excitation of the neutral molecules.9,11,12 On a similar ground, an initial report from our group demonstrates the C–Br bond cleavage in 8-bromoadenine (BrAde) adsorbed on aggregates of Au and Ag via hot electron transfer based on the DEA model.8 Along this line, an understanding over controlling and increasing the efficiency of the same plasmon-induced reaction was laid forward by Liu et al.13 using different applied potentials and laser light. In principle, a three-step mechanism based on DEA has been proposed which is generalized as follows:3,8,13

  • (i)
    The first step involves the generation of hot electrons upon laser illumination at a selected wavelength described by eq 1.
    graphic file with name cs1c01851_m001.jpg 1
  • (ii)
    The next step involves the transfer of generated primary hot electrons to the lowest unoccupied molecular orbital (LUMO) of adsorbed bromonucleobases (BrNBs) resulting in the formation of TNI (BrNB*–) described by eq 2.
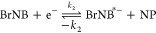
    graphic file with name cs1c01851_m002.jpg 2

    Alternatively, a direct electron transfer (chemical interface damping, CID) could also be possible via a coherent tunnelling process before it interacts with the electron cloud resulting in the formation of the TNI.14,15

  • (iii)

    Further, the metastable BrNB*– so formed undergoes cleavage of the C–Br bond generating a bromide anion and a nucleobase radical.

graphic file with name cs1c01851_m003.jpg 3

The overall dehalogenation reaction was understood considering a pseudo-first-order reaction rate law.8 However, the factors that influence the kinetic rate law, the reaction rate and possible product generation still need to be understood to develop a complete idea of the reaction mechanism. Another important aspect that would affect the reaction rate of plasmon-induced reactions in a heterogeneous medium would be the spatial inhomogeneous distribution of electrons on the surface and hotspots of nanostructures.16 It is important to account for these when deriving the kinetic rate equation for all heterogeneous surface reactions induced by plasmons.8,9

The probability and mechanism of such surface plasmon-induced reactions depends on several factors namely–feasibility of hot electron transfer and availability of low lying molecular orbitals of the adsorbate toward TNI formation,3,8,9,17 nature and structure of plasmonic substrate,18−22 incident photon intensity and excitation energy,8,20,23−27 nature of the adsorbates,14,28 temperature of metallic nanostructures,25,29,30 and so on. Importantly, the availability of hot electrons and their transfer highly depends upon the recovery of metallic atoms from their hot hole counterpart generated by plasmon excitation which determines the success of a plasmon-induced reaction to a great extent.23,31 The knowledge of the same would allow one to develop an understanding of different reaction rates observed on different plasmonic substrates based on the adsorbate of interest.8

Bromoderivatives of purine nucleobases are potential radiosensitizers in cancer therapy and exhibit a pronounced susceptibility to free and plasmonically generated low energy electrons.32,33 We chose them as a model system to understand the reaction rate law and mechanism of plasmon-induced dehalogenation. The excitation of surface plasmons in aggregates of Ag and Au drives the C–Br bond cleavage of brominated purines on the metal surface. The reaction rate law will be discussed on the basis of the DEA model described in our previous work8 along with addressing the following questions: (i) What parameters determine the reaction rate law? (ii) How is the reaction rate influenced by hot hole deactivation? (iii) What could be the possible dehalogenation products and the plausible role of reaction products and byproducts in the hole-scavenging mechanism? (iv) How does the hot-hole-scavenging mechanism affect the reactivity of purine derivatives on different plasmonic substrates? Next, the plausible mechanism of plasmon-induced dehalogenation reaction will be discussed by elucidating the reaction rate dependence on illumination energy and irradiance. Finally, on the basis of the kinetic data, the reactivity of the two different purine derivatives on Ag and Au substrate will be compared. The overall reaction kinetics is monitored in real time using SERS, which allows one to trigger and simultaneously track the reaction with a confocal Raman microscope.

Results and Discussion

Plasmon-Induced Dehalogenation Reaction in 8-BrGua and 8-BrAde by SERS

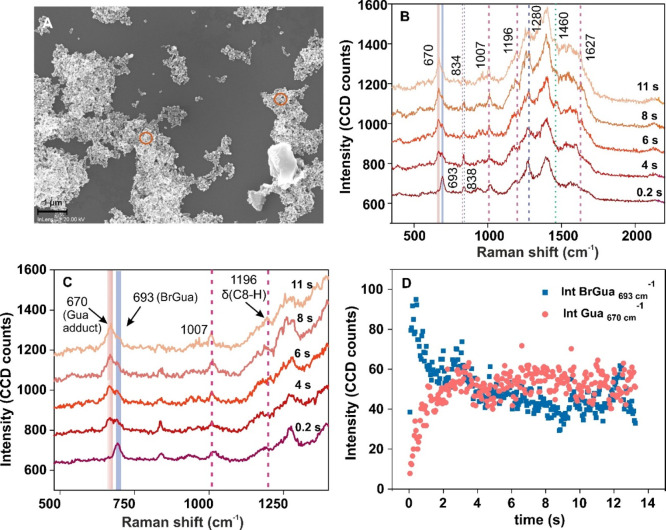
The dehalogenation reaction of BrGua adsorbed on AgNPs and AuNPs was carried out under continuous-wave (CW) illumination in ambient condition using a selected laser excitation source. Details of the synthesis of AgNPs and the preparation of the SERS substrate can be found in the Supporting Information (SI). UV–vis absorption spectra of citrate stabilized AgNPs and AuNPs dispersion is shown in Figure S1 (Supporting Information, SI). Field emission scanning electron microscopy (FESEM) of BrGua-coated AgNPs (Figure 1A and Figure S2A,B; SI) and AuNPs (Figure S2C–E; SI) surfaces reveals the aggregated nature of nanostructures. SERS measurements were carried out approximately on the regions shown in the FESEM images (Figure 1A, orange circles, and Figure S2C; SI) to ensure reproducible SERS.

Figure 1.

Figure 1

Open in a new tab

(A) Representative FESEM image of BrGua-coated aggregated AgNPs. (B) SERS spectra recorded during BrGua dissociation on aggregated AgNPs under CW illumination at different time intervals using a 532 nm laser source (laser power: 0.2 mW; data acquisition time: 0.05 s; accumulation: 300) and marked bands in blue and pink correspond to the ring breathing mode of BrGua and Gua adduct, respectively, shown as (C) zoom-in view of the SERS spectra (500–1300 cm–1) recorded in panel A. (D) Plot showing change in SERS intensity of the ring-breathing mode of BrGua at 670 cm–1 against that of the Gua adduct at 693 cm–1 as a function of laser illumination time.

Figure 1B shows the SERS spectra recorded at different time intervals during dissociation of BrGua on AgNPs under CW illumination with a 532 nm laser. The SERS spectra reveal characteristic sharp peaks at 693 cm–1 (due to a ring breathing mode, solid blue line) along with other peaks at 838 and 1280 cm–1 extracted at t = 0.2 s (dotted blue line). The cleavage of the C–Br bond in BrNBs was ascertained by a decrease in the SERS peak intensity at 693 cm–1 in due course of the reaction time with the concomitant rise of a peak at 670 cm–1, characteristic of the ring breathing mode of Gua (Figure 1B). The peak rising at 1196 cm–1 (dotted lines in pink; Figure 1C) is assigned to a C8–H bending mode (δ), affirming the Gua formation (via Gua radical intermediate)34 supported by additional peaks rising at 834, 1007, and 1627 cm–1. In all cases, the reaction was monitored until saturation of the peak intensity was observed.

Additionally, the SERS spectrum recorded for Gua under the same illumination condition as of BrGua (Figure S3) showed no change in ring breathing mode intensity at 670 cm–1, indicating the stable nature of Gua. All peak assignments have been done with respect to reference SERS frequencies tabulated in ref (34). In general, slight deviations in the wavenumber position of the vibrational modes of BrGua and Gua from the reference SERS values and fluctuations in peak intensity were occasionally observed. This could be attributed to inhomogeneous interparticle gaps resulting in varying structural orientation of the molecules in the aggregates or to local lattice heating.35,36 Further details of the experimental results on the dehalogenation reaction of BrAde studied on Ag aggregates can be found in Figure S4, SI.

Proposed Dehalogenation Reaction Pathway and Kinetic Analysis of BrNBs (BrGua and BrAde) on Ag and Reaction Rate Law

The dehalogenation pathway has been proposed taking into account eqs 1–3 based on the DEA model8 and has been summarized in Scheme 1. Equation 1 involves the generation of hot electrons marked by <100 fs lifetime.3 The plasmon decay (e– – e– scattering) takes place on the fs time scale, and the fraction of effective hot electrons that are generated and transferred remains low with numbers on the order of 10–4–10–8.29,37 This allows us to consider the formation of TNI in eq 2 to be slow and possibly the rate limiting step. Next, the metastable BrNB*– so formed undergoes cleavage of the C–Br bond generating a bromide anion and a nucleobase radical (eq 2). The dissociation proceeds on a repulsive potential presumably within a single vibrational period (i.e., within tens of fs). Hence, this is considered to be the fast step of the dehalogenation reaction.9,11

Scheme 1. Schematic Showing the Plasmon-Excitation-Induced Dehalogenation Pathway of Brominated Purines on an Ag Nanostructure and the Varying Observed Rate Constants of the Reaction on the Aggregated Nanostructure (across the Hot-Spots and the Residual Surface).

Scheme 1

Open in a new tab

Considering the three elementary steps, the general rate of the dehalogenation of brominated purines can be written as below:

graphic file with name cs1c01851_m004.jpg 4

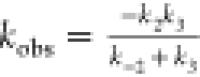where Inline graphic is the observed rate constant of the reaction. We refer to the SI for a detailed derivation and discussion. Equation 4 reflects that the rate of dehalogenation depends on the concentration of adsorbed BrNBs and effective hot charge carriers directing the dehalogenation kinetics to follow a second order rate law. This could be possible as the illumination area encompasses both hot-spots and remaining surface of the nanostructure, which creates a hot electron concentration gradient in due course of the reaction8,9

However, considering a rapid excitation-relaxation process during hot-electron generation under CW illumination,3 the time averaged local concentration of the hot-electrons e– can be considered constant in the initial time. Alternatively, considering the dissociation of the TNI (BrNB*–) to be the fast step (as described above), we can write k3 ≫ k–2. These assumptions lead to a simplified pseudo first order eq 5 which can be expressed as below:

graphic file with name cs1c01851_m006.jpg 5

where k′obs = −k1k2[NP] and refers to a pseudo-first-order reaction constant. Detailed considerations can be found in the SI, equations S1–12.

Therefore, we fit the experimental SERS kinetic data (Figure 1D) with the first-order integrated rate equation (equation S15, SI) obtained from the rate law described in eq 5. The reaction kinetics was tracked by monitoring the relative decrease in SERS intensity at 693 cm–1 (IBrGua) and corresponding rise in peak at 670 cm–1 (IGua) due to product over time t as shown in Figure 1D. Interestingly, a time dependence of k′obs was found (Figure S5, SI) unlike that observed in classical first-order kinetics. This is indicative of the heterogeneous surface reaction that occurs in confined spaces with a limited mobility of the reactants—characteristic of fractal-like reaction kinetics.38 It should be mentioned that other factors, such as local temperature and inhomogeneous reaction sites, might affect the reaction rate constant of a heterogeneous reaction taking place in a confined space as well as plasmonic field enhancement in the case of plasmon-mediated reactions, as might be the case herein.8,9,38

We report on the aggregated nature of the nanostructures (Figure 1A) which results in the generation of inhomogeneous reaction sites. Consequently, the hot spots created in the junction between the NP aggregates serves as confined reaction sites, which exhibit the highest electric field enhancement than on the residual surface.39 The presence of such hot spots and the electric field gradient generated across the hot-spot and the residual surface is also confirmed by FDTD simulations, where the geometry was chosen to reproduce an exemplary region (shown in Figure S6A) of BrGua-coated Ag aggregates. The electric field enhancement was simulated for the four different excitation wavelengths, including 488, 532, 633, and 785 nm, as shown in Figure S6B–E. The inhomogeneity of the system due to the electric field gradient and hence the time dependence of the reaction rate constant can be explained as follows: in general, a higher reaction rate is expected at the local hot spots than on the rest of the surface due to a higher local concentration of hot electrons. Therefore, within the reaction zone, the gradual change in the local environment in terms of temperature and field enhancement would generate a reaction trajectory, leading to a gradient of reaction constants represented in Scheme 1 on the right-hand side.8 The region with higher reaction rate (hot-spot) dominates the reaction trajectory in the initial time which is gradually replaced by reaction on the remaining surface that would exhibit lower reaction constant. Therefore, inhomogeneous distribution of the reaction site (substrate perspective) within the illumination zone dominates over the kinetic process (adsorbate perspective), inducing time dependence of the electron transfer step designated by rate constant k2.

Therefore, we use the term time-dependent reaction-coefficient (k′obs) typically used in fractal-like reaction kinetics,38 instead of a reaction constant in, for example, (pseudo-) first-order kinetics, which is typically used for a well-stirred mixture of reactants. The time-dependent k′obs is therefore replaced by relation (6) in the electron transfer step (eq 2) designated by the rate coefficient k2 taking into account the inhomogeneity of the system.38,40

graphic file with name cs1c01851_m007.jpg 6

where h refers to fractal dimension, t refers to time, and kf refers to the fractal reaction constant which is a time-independent parameter. Introducing the fractal relation (6) into the pseudo-first-order rate law in eq 5 allows us to obtain the following relation:

graphic file with name cs1c01851_m008.jpg 7

where eq 7 represents the general expression for the pseudo-first-order fractal kinetic equation and kf1 refers to the reaction constant of the reaction. Detailed derivation of eq 7 is provided in the SI. Herein, we consider [BrGua] and [Gua]to be proportional to the decay and rise in SERS intensity at 693 and 670 cm–1, respectively. Importantly, to exclude the contribution from background noise arising in heterogeneous systems and to achieve improved goodness of the curve fit we consider taking the ratio of SERS signal intensity of IGua and IBrGua obtained in Figure 1D to extract reaction constant kf1, which led to eq 8. It is to be mentioned that kf1 will be used as key parameter to discuss all kinetics results and comparison.

graphic file with name cs1c01851_m009.jpg 8

The fitted kinetic data in Figure 2 corresponds to the SERS time trace from BrGua on AgNPs. The pseudo-first-order fractal constant kf1 extracted from the fit with eq 8 is 0.03 ± (1.3 × 10–4) s–1 with R2 = 0.952. A similar trend was observed for time trace data obtained from the dehalogenation reaction observed on BrAde on AgNPs with 633 nm laser (data not shown).

Figure 2.

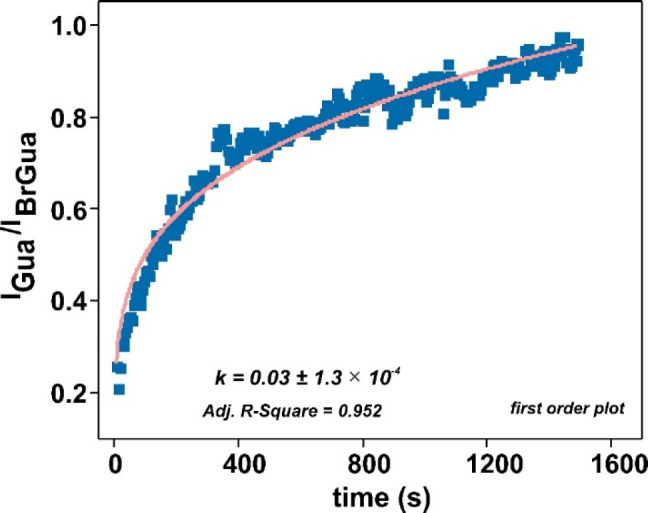
Figure 2

Open in a new tab

IGua/IBrGua versus time plot when fitted to pseudo-first-order (eq 8) integrated fractal rate expression with the pink curve showing the corresponding fit (laser: 633 nm; 1 mW, 5 s).

Next, to comment on the possible dehalogenation products and the role of reaction products and byproducts in the hole deactivation mechanism, we discuss eqs 9 and 10 in further continuation to eqs 1–3, which has been detailed in the SI and depicted in Scheme 2.

graphic file with name cs1c01851_m010.jpg 9
graphic file with name cs1c01851_m011.jpg 10

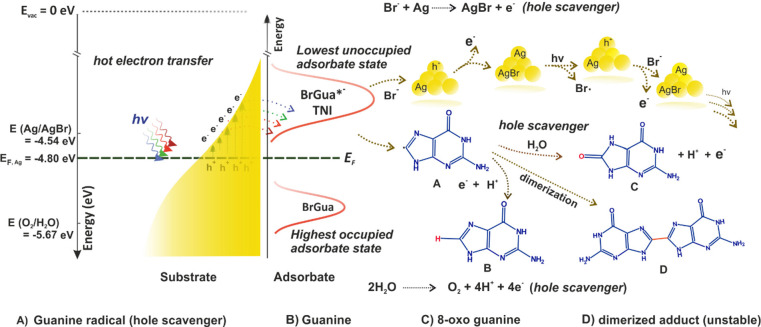
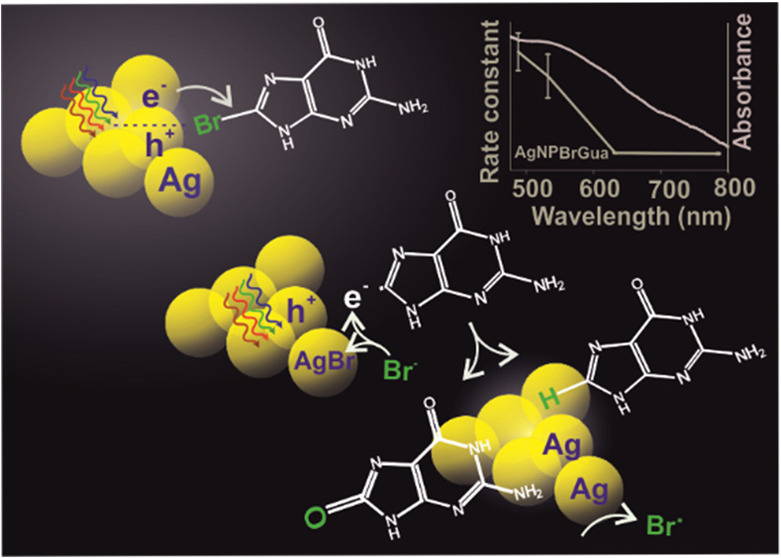
Scheme 2. Schematic Representation of the Overall Plasmon-Induced Dehalogenation Process and Plausible Pathway of Hot Hole Reaction and Fate of Nucleobase Radical (Taking the Example of BrGua) on Ag Surface.

Scheme 2

Open in a new tab

Energy levels shows absolute electrochemical energies, E (eV) with respect to the vacuum level.

The nucleobase radical generated after dehalogenation could translate to form a neutral nucleobase (Gua or Ade) product consuming a H+ ion and an additional electron.8 Additionally, owing to its high tendency toward oxidation compared to its stable hydrogenated counterpart, it may preferentially follow a one-electron oxidation (eq 11) to generate the oxo-product of guanine and adenine, or it may undergo dimerization to form the dimerized adduct.41,42 (refer to equations S20–26, SI)

graphic file with name cs1c01851_m012.jpg 11

For example, the peak arising at around 1460 cm–1 at 6 s (Figure 1B) can be assigned to vibrational bands characteristic of oxidation of Gua.42 A very similar feature characteristic of guanine oxidation at around 1610–1620 cm–1 could be seen which can be assigned to the oxo product of Gua, namely, 8-oxoguanine or 8-hydroxoguanine.42,43 It should be mentioned that although the vibrational band corresponding to oxidized reaction products can be assigned, a direct quantitative analysis of the oxidized product in the spectral range 1600–1630 and 1400 cm–1 could not be carried out because of their close overlap with the band features of their nonoxidized counterpart. Further, observations made in SERS spectra recorded for the dehalogenation reaction of BrAde (Figure S4A) are included in SI. Importantly, time series normal Raman measurements of BrGua and BrAde were carried out under CW illumination using 532 nm laser source as a control study (Figure S7A,C). No decay in the intensity of ring breathing mode (or cleavage of the C–Br bond) of BrGua and BrAde reflected from Figure S7B and D, respectively, was noted, indicating that the bromonucleobases do not undergo decomposition in the absence of plasmonic nanoparticles. That is to say, brominated purines do not show any photoreactivity in the visible range, which is also clear from the absorption spectra recorded for BrGua and BrAde solution (Figure S8A and B), respectively. Additionally, in a recent study, we irradiated 5-bromouracil in the absence of nanoparticles, with focused ns-laser pulses (532 nm, 4 × 109 W/cm2) and observed neither a cleavage of the C–Br bond nor any other decomposition of the bromonucleobase.44

Like we discussed before, the hole deactivation is an important step, therefore we propose two plausible pathways that can lead to hole deactivation during the dehalogenation reaction (as shown below and refer to equations S22–33, SI). A first plausible hole reduction pathway proposed is the oxidation of the product nucleobase radical (eq 11). The oxidation of the free nucleobases is very well studied in solid electrodes by electrochemical techniques.45,46 On a silver electrode, the values for the oxidation of deoxyguanosine 5′-triphosphate (dGTP) start around 0.49 V vs SHE (Standard hydrogen electrode).47 Typically, the triphosphate backbone shifts the oxidation potential of nucleotides toward a more positive potential by almost 0.250 V compared with the bases.46 Therefore, it is likely that the oxidation of Gua takes place around 0.3 V vs SHE, which indicates toward the consumption of an unstable Gua radical product in the hole reduction, which can undergo oxidation even at a lower potential than 0.3 V vs SHE. This appears just above the Fermi energy of the AgNP centered around 0.36 V vs SHE (or, E (eV) = −4.80 eV, absolute electrochemical energy with respect to vacuum given by the relation: E (eV)= −(4.44 + ESHE) eV13 such that the electrons generated by the oxidation of the base or base radical would be consumed by the hot-holes without any energetic loss. The same can be expected in the case of Ade dehalogenation, considering very small shifts in terms of potential values, since the oxidation of the Ade base also occurs around 0.3 V vs SHE.47 A schematic description of the plasmon-induced dehalogenation process and plausible pathways of hot hole reaction and fate of nucleobase radical product are summarized in Scheme 2.

Second, we propose that the Br– byproduct from the reaction can act as hole scavenger. This involves a favorable one-electron transfer reaction to the hole that occurs at a potential of 0.10 V vs SHE (−4.54 eV)48 with respect to the Fermi energy of 0.36 V vs SHE (−4.80 eV).13 This would result in the formation of photosensitive AgBr on the Ag surface (eq 12) which has also been reported by Xie et al. in one of their seminal works.31

graphic file with name cs1c01851_m013.jpg 12

However, because of high photosensitivity (AgI > AgBr > AgCl),31 photodissociation of AgBr could easily regenerate an Ag atom and a bromide radical (equation S29, SI) that further engages in stepwise redox processes (refer to SI, equation S30–32 and Scheme 2) to continue the reaction cycle. A third possible pathway for the hole reduction reaction involves water oxidation (equation S23). However, the hole consumption via oxidation of the nucleobase radical and Br– anion proposed to occur on the interface of Ag NPs are more likely to supersede the four-hole oxidation of H2O23 (1.23 V vs SHE (−5.67 eV)) due to their favorable oxidation potential with respect to Fermi energy.

As assumed in a first approximation in the derivation of the rate equation, the electron transfer to the adsorbate is the rate-determining step. Nevertheless, in the case of insufficient and slow hole reaction, k5 would likely overrule the kinetics of the initial steps marking itself to be the rate-determining step without affecting the kinetic rate laws defined. Having said that, favorable hot hole reaction as discussed above still allows consideration of time-average concentration of hot electrons to be constant under CW illumination. Therefore, we consider a pseudo-first-rate law and rely on the integrated first-order fractal kinetic, eq 8, to derive further kinetic parameters in the rest of the discussion.

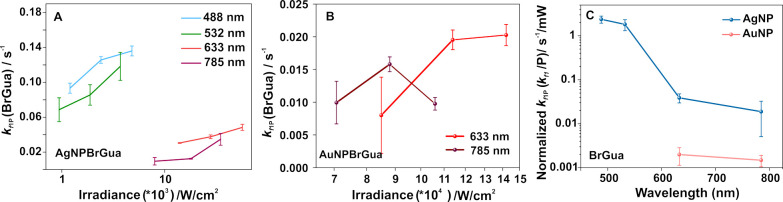
Indeed, that the hole deactivation mechanism is prevalent and places an important role in deciding the reaction rate is further supported by carrying out a dehalogenation reaction of brominated nucleobases on AuNPs. For this, the dehalogenation reaction kinetics were monitored on aggregates of Ag and Au at different laser power (irradiance; W/cm2) under different incident photon energy, viz., 488, 532, 633, and 785 nm. Figure 3A shows the semilog plot of kf1 versus irradiance obtained at four different illumination wavelengths (for the reaction monitored in case of BrGua). Reaction rate constant compared at different irradiance (Figure 3A and Figure S9 for BrGua and BrAde on Ag, respectively) showed an increase in value with irradiance at all the wavelengths.

Figure 3.

Figure 3

Open in a new tab

(A) Semilog plot of reaction rate constant plotted as a function of irradiance at different laser wavelength (X-axis is in log scale) determined for dehalogenation reaction of BrGua on (A) AgNPs and (B) AuNPs. Error bar represents the standard deviation of kf1 values from three different independent measurements carried on different reaction spots. (C) Semilog plot of rate constant kf1 normalized with respect to lowest incident laser power (P, mW) expressed by kf1P = kf1/P plotted at different laser wavelength for dehalogenation of BrGua on AgNPs (blue) and AuNPs (pink), respectively. (Y-axis is in log scale).

In contrast to the case of Ag, the dehalogenation reaction on Au could only be followed with 633 and 785 nm laser illumination. SERS spectra recorded for brominated purines on Au surfaces under laser illumination at 488 and 532 nm were dominated by a visible emission background (Figure S10A,B and Figure S11A) which made the traceability of the reaction difficult. This can be explained by radiative recombination attributed to interband transitions in Au that occur in the range of 2.6–2.8 eV close to 488 and 532 nm laser excitation resulting in plasmon damping (obscuring SERS signal) in addition to off resonance excitation.49 The weak Raman scattering signal (ring stretching vibration) from BrAde adsorbed on Au aggregates when illuminated with the 532 nm laser is shown in Figure S11A. Further description of kinetics and SERS spectra of brominated purines adsorbed on Au aggregates can be found in SI.

The SERS time traces were fit with eq 8 to obtain the pseudo-first-order kinetic constant for the case of both BrGua and BrAde on the Au substrate (Figure 3B and Figure S12, respectively) under 633 and 785 nm laser illumination. However, the reaction kinetics observed at laser powers above 6 mW did not show significant differences in the reaction rate constant (for both BrGua and BrAde when studied with 633 and 785 nm laser excitation). This is supported by the kf1 vs irradiance in Figure 3B and Figure S12 unlike that observed in Figure 3A and Figure S9. This could possibly be attributed to the small range of laser power selection, which did not allow seeing discernible gradients in the respective reaction coefficients. Nevertheless, the reaction rate observed at 633 nm was higher than at 785 nm for both BrGua and BrAde on Au albeit less pronounced than for the Ag substrate (summarized in Figure 3C and Figure S13). The rate constant (kf1) extracted for making the above comparison was normalized with respect to lowest incident laser power (P, mW) expressed by kf1P = kf1/P plotted at different laser wavelengths.

This can be explained by the hole deactivation pathway prevalent on AuNPs surface. In case of Au also, we consider the one-hole oxidation of Br– (via AuBr2–, eq 13) and oxidation of nucleobases (and their corresponding nucleobase radicals; eq 11), which could serve as a potent hole scavenger along with water oxidation.

graphic file with name cs1c01851_m014.jpg 13

However, unlike Ag, the oxidation potential of Br–/Br2 (centered around 1.24 V vs SHE)50 and that of nucleobase or nucleobase radical oxidation (centered around 1.20 V vs SHE)51,52 is quite large. This lies close to water oxidation at 1.23 V vs SHE which might limit the efficiency of hot hole reduction on an Au surface, thereby diminishing the dehalogenation reaction rate on the Au surface contrary to what was observed in the case of AgNPs. That is, an inefficient hole deactivation will induce a time delay in the relaxation of the NP system before any subsequent new photoexcitation (e–-h+ formation) can take place limiting the kinetic rate of dehalogenation on Au as observed.23 In such a situation, any increase in laser power (photon density) will still result in generation of hot carriers which would be available for hot-electron transfer. However, further increase in photon density under such slow hole deactivation rate will lead to a regime which would allow the relaxation of the photo excited carrier via nonradiative e–-h+ recombination (that occurs in ps time scale)53 to compete over the hot-electron transfer process. This will limit the number of effective hot-charge carrier available to participate in the dehalogenation reaction resulting in either saturated or diminished value of reaction rate coefficients as reflected in Figure 3B or Figure S12. This explains the overall lower reaction rate observed experimentally on the Au surface at 633 and 785 nm when compared to Ag. A schematic describing the plasmon-induced dehalogenation process and plausible pathways of hot hole reaction and fate of nucleobase radical product on Au surface is presented in Scheme S1. Hence, this draws our attention to the fact that the overall plasmon mediated reaction rate might be limited by the feasibility of hole deactivation.23

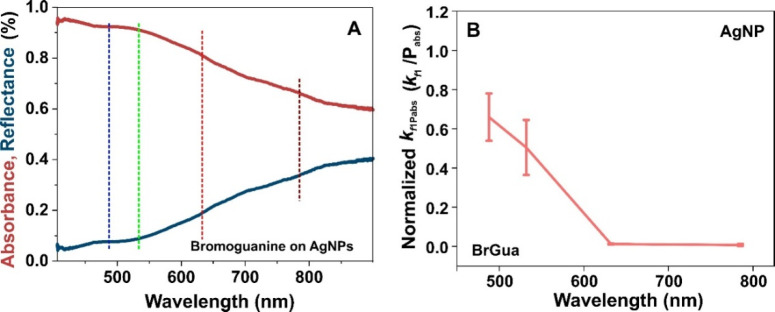
Importantly, the success of a plasmon-induced reaction (initiated by hot electron transfer) is often questioned either by the existence of a thermally driven reaction pathway or rate acceleration by simple plasmon heating. For an electron-driven photochemical reaction, a linear increase in reaction rate with the laser intensity is expected—that is, rate ∝ intensityn with n = 1, which however deviates to show a super linear dependence with n > 1 for very high laser intensity or under fs-pulsed laser illumination.26 However, a photothermal process shows deviation from such linearity and exhibits an Arrhenius type dependence between the reaction rate and laser intensity for a linear dependence of temperature on the laser power.37 The reaction rate coefficient compared at different irradiance (Figure 3A and Figure S9 for BrGua and BrAde on Ag, respectively) shows almost a linear trend although a deviation from linearity is observed at higher irradiance. The steep rise in rate constant observed at the highest irradiance (for some wavelength, viz., 532 and 785 nm) could still be the signature of electron-driven photochemical reaction that is mainly observed in extended metallic nanostructures as described in detail by Linic and co-worker in one of their seminal work.26 The presence of multiple active hot-spot sites which supports higher rate of hot electron formation at higher photon density results in efficient resonance transfer of electrons to the LUMO of the adsorbate which might be one of the reason for steep rise in reaction rate. Furthermore, a steep rise at the highest irradiance (at different wavelength) could also be due to the dominance of thermal process or plasmon heating. As no clear trend is reflected for both the cases studied, we do not solely depend on reaction rate vs irradiance comparison to analyze the nature of the plasmon mechanism (thermal versus nonthermal). This is because a plasmon-induced reaction which is necessarily initiated via hot electrons might still be influenced photothermally when monitored at high laser power due to localized plasmon heating.25,27 Additionally, the microabsorbance spectrum shown in Figure 4A, red band (and Figure S14, yellow band) recorded on the region shown in Figure S15A for BrGua-coated AgNPs (and Figure S15B for BrAde) shows pronounced absorbance at 488 nm. This could also lead to a temperature increase aiding the reaction thermally.

Figure 4.

Figure 4

Open in a new tab

(A) Absorbance and corresponding reflectance spectra recorded on the region shown in Figure S15A for BrGua coated AgNPs. (B) Rate constant (kf1) normalized with respect to absorbed laser power (Pabs in mW) expressed by kf1Pabs(kf1Pabs = kf1/Pabs) plotted at different laser wavelength for BrGua coated AgNPs. Pabs = incident power × absorbance. The absorbance of the substrate used for the normalization has been determined from microabsorbance spectra recorded in panel A. The error bar represents the standard deviation of kf1 values from three different independent measurements.

Further, we compare the reaction rate constant normalized to the absorbed power under different laser excitation wavelengths to comment on the role of hot electrons in plasmon-induced dehalogenation. The rate constant (kf1) normalized with respect to the absorbed power Pabs given by the expression kf1Pabs(kf1Pabs = kf1/Pabs, where Pabs = Incident Power × Absorbance (λ)) plotted at different wavelengths showed an increasing trend with increase in laser excitation energy following the order BrGuak488 > BrGuak532 > BrGuak633 > BrGuak785 (Figure 4B). The microabsorbance spectrum in Figure 4A showed a decrease in absorbance with an increase in wavelength; and, the field enhancement calculated according to the FDTD simulations (determined on an exemplary regions of BrGua coated Ag aggregates) follows the order: E488 > E532 > E633 > E785 (Figure S6, refer to SI for details). The experimental reflectance spectrum (Figure 4A, blue curve) also closely resembles the simulated reflectance spectrum shown in Figure S16. Typically, plasmon-induced reactions observed on regions that correspond to higher absorbance and high field enhancement should exhibit higher reactivity because of the higher rate of hot electron generation under resonant illumination.20,27 Therefore, highly pronounced absorption (indicated by dotted colored lines - blue and green, Figure 4A) and comparatively high field enhancement at 488 and 532 nm (Figure S6B and C, SI) would result in buildup of population of hot carriers in this regime explaining the observed trend in reactivity. On the other hand, off resonance and lower optical absorption at 633 and 785 nm under low photon energy on Ag substrate and lower plasmonic field enhancement (Figure S6D and E, SI) explains the corresponding lower reaction rate observed. A very similar argument holds true in case of dehalogenation kinetics for BrAde on AgNPs (refer to Figure S14).

Next, in the case of nonthermal or hot electron-driven processes, the energy distribution of the hot carriers depends upon the excitation wavelength as high energy photons can excite electrons far from the Fermi level compared with lower-energy photons.17,27 Based on the decreasing energy of hot carriers with increasing wavelength, a significant drop in reaction rate should be observed in the case of a hot electron-driven process. Furthermore, temperature rise of a system depends upon the amount of absorbed optical energy.2 Therefore, in case of a nonthermal process, the reaction rate normalized to the absorbed number of photons should show a wavelength dependence with maxima in the spectral range where hot electron generation is efficient.27 A clear dependence of reaction coefficient normalized to absorbed power versus wavelength can be observed in Figure 4B and Figure S17 with maxima at the SPR region of Ag nanoparticles in the case of both BrGua and BrAde, respectively. This allowed us to conclude that the dehalogenation reaction is driven by hot-electron indicating toward the nonthermal nature of the reaction. However, we do not completely eliminate the thermal activation of reactants and hot charge carriers with increase in irradiance and laser energy.

Additionally, we considered analyzing the relative SERS response of the brominated purines on the surface of Ag and Au. Therefore, a histogram plot showing relative normalized SERS intensity of BrAde and BrGua on the aggregated surface of AgNPs and AuNPs under 633 and 785 nm laser excitation is shown in Figure S18. We arrive at a conclusion that the SERS sensitivity of BrAde is higher compared with BrGua on both Ag and Au substrate. Also, Ag appears to be a better SERS substrate for both BrAde and BrGua than Au, which was apparently clear from Figure 3C and Figure S13.

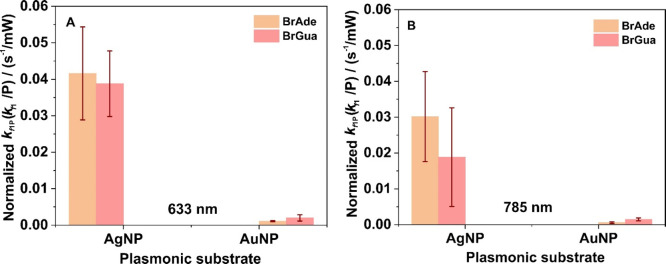
Lastly, we took interest to know whether the observed kinetics is dependent upon the nature of brominated purines involved. Overall, our findings showed comparatively higher reactivity of BrAde on AgNPs than BrGua, which reverses its reactivity on the AuNP surface under both the laser illumination at 632 and 785 nm independent of their relative SERS sensitivity response. This is shown by the bar diagrams in Figure 5A,B of the rate constant (kf1) normalized with respect to incident laser power (P) expressed by kf1P, although an explanation for the reactivity of brominated purines on the respective plasmonic substrates demands a separate study as a whole. However, a preliminary idea of the higher reactivity of BrGua over BrAde on the AuNPs surface could be drawn taking into account the binding affinity of the respective unsubstituted nucleobases on Au and AgNPs and shift in density of states upon surface adsorption.54−58 A plausible reasoning for the observation has been discussed in SI.

Figure 5.

Figure 5

Open in a new tab

Bar graph showing the comparison of normalized rate constant (kf1P, normalization done with respect to lowest laser power) for dehalogenation of both BrAde and BrGua on AgNPs and AuNPs under (A) 633 nm and (B) 785 nm laser excitation. The normalized rate constant of dehalogenation of BrAde is relatively higher than BrGua on AgNPs surface, whereas dehalogenation of BrGua is relatively higher than the rate of dehalogenation of BrAde on AuNPs surface.

Conclusions

In summary, hot-electron-induced cleavage of C–Br bonds, release of Br–, and formation of a reactive radical intermediate are proposed to be the essential steps that form the basis of the kinetic rate equation. Based on a proposed kinetic model, the time-average constant concentration of hot electrons and time scale of the dissociation of transient negative ions (TNI) is considered to play a critical role in defining the rate law. Therefore, a pseudo-first-order dehalogenation kinetics has been implemented considering the time-averaged concentration of hot electrons to be constant. Importantly, Br– and product nucleobase radical play an important role in hole deactivation which ultimately guides the dehalogenation rate. Although the reaction rate is initially suggested to be limited by electron transfer to the LUMO of adsorbed BrNBs, we arrive at the conclusion that insufficient hole deactivation could impede the reaction rate significantly marking itself as rate-determining step for the overall reaction. The favorable oxidation potential of Br– and the nucleobases radicals toward hole reaction explains the overall higher reactivity of dehalogenation kinetics observed on Ag, which is compromised on Au surfaces because of the large oxidation potential of both Br– and the nucleobase radical.

Higher reaction rate observed at the higher laser energy has been explained by pronounced surface plasmon resonance (SPR) absorption accompanied by high plasmonic enhancement in the case of Ag compared with Au, which results in the generation of higher concentration of hot carriers. We further conclude on the hot-electron-driven nature of the dehalogenation reaction over the thermal nature by showing the wavelength dependency of the reaction rate normalized to absorbed optical power. The dehalogenation reaction rate law is independent of the nature of brominated nucleobases and the plasmonic substrate, although the feasibility of the reaction and their corresponding reaction rate is guided by nature of the brominated purines and the plasmonic substrate involved. Based on the present findings, future implications lie in further monitoring of hot-electron-induced reactions in brominated purines when incorporated in long ss and ds DNA by the SERS method.59 The success of which would direct one to employ the bromo-derivative of the purines and other potent electrophilic radiosensitizers for real time study in cellular environment for upgraded cancer therapy.

Materials and Methods

Chemicals

Guanine (Gua), 8-bromoguanine (BrGua), silver nitrate (AgNO3), and trisodium citrate were purchased from Sigma-Aldrich (Germany). 8-Bromoadenine (BrAde) was purchased from Carbosynth (U.K.). Sodium hydroxide (NaOH) was purchased from Merck. AuNPs (diameter 40 nm) were purchased from BBI solutions. Si-wafers were purchased from CrysTec GmbH (100 mm, p-Typ). All chemicals were used as received without further purification. Milli-Q grade water was used for synthesis and experimental work.

Synthesis of AgNPs

AgNPs were synthesized following Lee and Meisel protocol60 with some modifications. Briefly, 1 mM AgNO3 dissolved in 500 mL of Milli-Q water were heated up to boil under reflux condition at 125 °C with constant stirring (600 rpm). This was followed by addition of 10 mL of 155 mM sodium citrate to the same solution using a syringe and the boiling was continued for another 1 h. The formation of AgNPs was ensured by the appearance of final brown-yellow color of the dispersion. Detailed characterization of as synthesized AgNP dispersion has already been presented in ref (34).

SERS Study

Sample Preparation

Citrate (cit) stabilized Ag and Au NPs were first functionalized with brominated analogue of purine derivative, viz., BrAde and BrGua.34

AgNPs

In the first step, 1 mL of as-synthesized AgNP dispersion was purified by centrifugation at 2000 rcf for 10 min at 20 °C, and the precipitate was redispersed in 1 mL of Milli-Q water. Next, 20 μL of 0.5 mM solution of Gua and their brominated analogue of Gua and Ade were mixed with 80 uL of centrifuged AgNPs dispersion and allowed to incubate for 1 h at room temperature. Because of poor water solubility, 0.5 mM of Gua and BrGua were made in NaOH solution such that the final concentration of NaOH is 13 mM and 0.8 mM respectively. Upon 1 h of incubation, the resulting mixture was centrifuged at 1000 rcf for 10 min at 20 °C (×2), and the precipitate was redispersed in 20 μL Milli-Q water. Immediately, 10 μL of the sample dispersion was drop cast on a cleaned Si-substrate and was left for overnight drying at ambient condition.

AuNPs

The AuNP samples for SERS measurements were prepared by similar method except for few changes as stated. Then 1 mL of AuNP dispersion was purified by centrifugation at 2000 rcf for 10 min at 20 °C, and the precipitate was redispersed in 1 mL of Milli-Q water. Next, 20 μL of 0.5 mM solution of brominated analogue of Ade and Gua were mixed with 80 μL of centrifuged AuNPs dispersion and allowed to incubate for 1 h at room temperature. Due to poor water solubility, 0.5 mM of BrGua were made in NaOH solution such that the final concentration of NaOH is 2 and 4.4 mM respectively. Upon 1 h of incubation, the resulting mixture was centrifuged at 1000 rcf for 10 min at 10 °C (×2), and the precipitate was redispersed in 20 μL Milli-Q water. Immediately, 10 μL of the sample dispersion was drop cast on a cleaned Si-substrate and was left for overnight drying in ambient condition.

Upon treatment, the brominated derivatives of purines preferentially get adsorbed on the surface of NPs, replacing the citrate as surface stabilizers meanwhile inducing aggregation in the dispersion.54 This is further facilitated during the two-step centrifugation process, which helped remove the citrate layer from Ag and AuNPs and simultaneously inducing aggregation of NPs via intermolecular H-bonds or by π–π* stacking interaction between the brominated analogues.34,55,61 The extent of induced aggregation depends upon the type of brominated nucleobases and their respective binding energies toward NPs.

SERS Kinetic Measurements

Kinetic measurements of brominated purines treated AgNPs and AuNPs were carried out using WITec alpha300 Raman–microscope equipped with four different excitation laser sources (488, 532, 632, and 785 nm) under a 10× objective (NA = 0.25). The laser power, integration, and accumulation time for each measurement employed can be found as stated where necessary. All measurements were carried out in triplicate in different sample areas. All SERS spectra obtained were processed using WITec Project 5 and Origin 9.1 software.

Microabsorbance Measurements

The measurements were performed with a microabsorbance spectrometer, which is described elsewhere in detail.62 Briefly, light from a supercontinuum laser (Fianium, SC-400–4) was guided through a beamsplitter toward a modified microscope and focused on the sample with an Olympus SLMPlan FLN 20× objective with an NA of 0.25. The reflected light was collected by the same objective and guided by an optical fiber (Oceans optics QP600–2-UV-BX) to the spectrometer (Avantes, Avaspec 3648). The microabsorbance spectra were measured at characteristic places that were similar to the SERS measurement spots. The reflectance of the Si substrate close to the measurement position was used as a reference IReference for reflection. The reflectance was calculated as

graphic file with name cs1c01851_m015.jpg

The absorbance was determined as A = 1 – R, since transmission was prevented by the Si substrate.

Finite-Difference Time-Domain Method (FDTD)

FDTD simulations of AgNP on a Si substrate have been carried out using the software Lumerical FDTD Solutions 8.6.3 with a mesh size of 1 nm. The Si substrate was covered with a 2 nm SiO2 layer and decorated with cylindrical 40 nm AgNPs imported from SEM images of the sample. A linear polarized plane wave source (400 to 900 nm) irradiated the sample from the top and a power monitor above the light source recorded the reflectance of the sample. The E-field was monitored in the xy-plane in the center of the AgNPs.

Acknowledgments

We thank Dr. Frank Jaiser for recording the FESEM images. This research was supported by the European Research Council (ERC; consolidator grant no. 772752). S.R and N.S.M were supported by the European Research Council (ERC) within the project DarkSERS (772108) and the Focus Area NanoScale of Freie Universitaet Berlin.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acscatal.1c01851.

  • Detailed derivation of reaction rate law; integrated rate equation; stepwise redox reaction involved in hot-hole reaction; UV–vis spectra of BrGa and BrAde solution and Ag and AuNP dispersion; FESEM images of BrGua coated aggregates of AgNPs and AuNPs; normal Raman time-series spectra of BrGua and BrAde; time-series SERS spectra of BrAde on AgNPs and SERS spectra of bromoderivatives of purines on AuNPs; corresponding kinetics rate constant versus time plot; kinetic rate constant plot at different wavelength and power; plot of normalized rate constant with respect to power and absorbed power at different wavelength of BrAde on Ag and AuNPs; normalized SERS intensity plot of BrGua and BrAde on Ag and Au; microabsorbance-reflectance plot of BrAde coated AgNPs; FDTD simulation of field enhancement values at different wavelength and 3D-FDTD simulated reflectance spectra (PDF)

The authors declare no competing financial interest.

Supplementary Material

cs1c01851_si_001.pdf (2.5MB, pdf)

References

  1. Zhang Y.; He S.; Guo W.; Hu Y.; Huang J.; Mulcahy J. R.; Wei W. D. Surface-Plasmon-Driven Hot Electron Photochemistry. Chem. Rev. 2018, 118, 2927–2954. 10.1021/acs.chemrev.7b00430. [DOI] [PubMed] [Google Scholar]
  2. Brooks J. L.; Warkentin C. L.; Saha D.; Keller E. L.; Frontiera R. R. Toward a Mechanistic Understanding of Plasmon-Mediated Photocatalysis. Nanophotonics 2018, 7, 1697–1724. 10.1515/nanoph-2018-0073. [DOI] [Google Scholar]
  3. Zhang Z.; Zhang C.; Zheng H.; Xu H. Plasmon-Driven Catalysis on Molecules and Nanomaterials. Acc. Chem. Res. 2019, 52, 2506–2515. 10.1021/acs.accounts.9b00224. [DOI] [PubMed] [Google Scholar]
  4. Manjavacas A.; Liu J. G.; Kulkarni V.; Nordlander P. Plasmon-Induced Hot Carriers in Metallic Nanoparticles. ACS Nano 2014, 8, 7630–7638. 10.1021/nn502445f. [DOI] [PubMed] [Google Scholar]
  5. Chang L.; Besteiro L. V.; Sun J.; Santiago E. Y.; Gray S. K.; Wang Z.; Govorov A. O. Electronic Structure of the Plasmons in Metal Nanocrystals: Fundamental Limitations for the Energy Efficiency of Hot Electron Generation. ACS Energy Lett. 2019, 4, 2552–2568. 10.1021/acsenergylett.9b01617. [DOI] [Google Scholar]
  6. Zhan C.; Chen X. J.; Huang Y. F.; Wu D. Y.; Tian Z. Q. Plasmon-Mediated Chemical Reactions on Nanostructures Unveiled by Surface-Enhanced Raman Spectroscopy. Acc. Chem. Res. 2019, 52, 2784–2792. 10.1021/acs.accounts.9b00280. [DOI] [PubMed] [Google Scholar]
  7. Feng H. S.; Dong F.; Su H. S.; Sartin M. M.; Ren B. In Situ Investigation of Hot-Electron-Induced Suzuki-Miyaura Reaction by Surface-Enhanced Raman Spectroscopy. J. Appl. Phys. 2020, 128, 173105. 10.1063/5.0023623. [DOI] [Google Scholar]
  8. Schürmann R.; Bald I. Real-Time Monitoring of Plasmon Induced Dissociative Electron Transfer to the Potential DNA Radiosensitizer 8-Bromoadenine. Nanoscale 2017, 9, 1951–1955. 10.1039/C6NR08695K. [DOI] [PubMed] [Google Scholar]
  9. Linic S.; Christopher P.; Ingram D. B. Plasmonic-Metal Nanostructures for Efficient Conversion of Solar to Chemical Energy. Nat. Mater. 2011, 10, 911–921. 10.1038/nmat3151. [DOI] [PubMed] [Google Scholar]
  10. Ho W. Reactions at Metal Surfaces Induced by Femtosecond Lasers, Tunneling Electrons, and Heating. J. Phys. Chem. 1996, 100, 13050–13060. 10.1021/jp9535497. [DOI] [Google Scholar]
  11. Christopher P.; Xin H.; Linic S. Visible-Light-Enhanced Catalytic Oxidation Reactions on Plasmonic Silver Nanostructures. Nat. Chem. 2011, 3, 467–472. 10.1038/nchem.1032. [DOI] [PubMed] [Google Scholar]
  12. Mukherjee S.; Libisch F.; Large N.; Neumann O.; Brown L. V.; Cheng J.; Lassiter B.; Carter E. A.; Nordlander P.; Halas N. J. Hot Electrons Do the Impossible: Plasmon-Induced Dissociation of H2 on Au. Nano Lett. 2013, 13, 240–247. 10.1021/nl303940z. [DOI] [PubMed] [Google Scholar]
  13. Liu J.; Cai Z. Y.; Sun W. X.; Wang J. Z.; Shen X. R.; Zhan C.; Devasenathipathy R.; Zhou J. Z.; Wu D. Y.; Mao B. W.; Tian Z. Q. Plasmonic Hot Electron-Mediated Hydrodehalogenation Kinetics on Nanostructured Ag Electrodes. J. Am. Chem. Soc. 2020, 142, 17489–17498. 10.1021/jacs.0c07027. [DOI] [PubMed] [Google Scholar]
  14. Boerigter C.; Aslam U.; Linic S. Mechanism of Charge Transfer from Plasmonic Nanostructures to Chemically Attached Materials. ACS Nano 2016, 10, 6108–6115. 10.1021/acsnano.6b01846. [DOI] [PubMed] [Google Scholar]
  15. Kazuma E.; Jung J.; Ueba H.; Trenary M.; Kim Y. Real-space and real-time observation of a plasmon-induced chemical reaction of a single molecule. Science 2018, 360, 521–526. 10.1126/science.aao0872. [DOI] [PubMed] [Google Scholar]
  16. Linic S.; Chavez S.; Elias R. Flow and Extraction of Energy and Charge Carriers in Hybrid Plasmonic Nanostructures. Nat. Mater. 2021, 10.1038/s41563-020-00858-4. [DOI] [PubMed] [Google Scholar]
  17. Yu Y.; Wijesekara K. D.; Xi X.; Willets K. A. Quantifying Wavelength-Dependent Plasmonic Hot Carrier Energy Distributions at Metal/Semiconductor Interfaces. ACS Nano 2019, 13, 3629–3637. 10.1021/acsnano.9b00219. [DOI] [PubMed] [Google Scholar]
  18. Mueller N. S.; Vieira B. G. M.; Hoing D.; Schulz F.; Barros E. B.; Lange H.; Reich S. Direct optical excitation of dark plasmons for hot electron generation. Faraday Discuss. 2019, 214, 159–173. 10.1039/C8FD00149A. [DOI] [PubMed] [Google Scholar]
  19. Mukherjee S.; Zhou L.; Goodman A. M.; Large N.; Ayala-Orozco C.; Zhang Y.; Nordlander P.; Halas N. J. Hot-Electron-Induced Dissociation of H2 on Gold Nanoparticles Supported on SiO2. J. Am. Chem. Soc. 2014, 136, 64–67. 10.1021/ja411017b. [DOI] [PubMed] [Google Scholar]
  20. Schürmann R.; Ebel K.; Nicolas C.; Milosavljević A. R.; Bald I. Role of Valence Band States and Plasmonic Enhancement in Electron-Transfer-Induced Transformation of Nitrothiophenol. J. Phys. Chem. Lett. 2019, 10, 3153–3158. 10.1021/acs.jpclett.9b00848. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Cortés E.; Xie W.; Cambiasso J.; Jermyn A. S.; Sundararaman R.; Narang P.; Schlücker S.; Maier S. A. Plasmonic Hot Electron Transport Drives Nano-Localized Chemistry. Nat. Commun. 2017, 8, 1–10. 10.1038/ncomms14880. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Pal S.; Dutta A.; Paul M.; Chattopadhyay A. Plasmon-Enhanced Chemical Reaction at the Hot Spots of End-to-End Assembled Gold Nanorods. J. Phys. Chem. C 2020, 124, 3204–3210. 10.1021/acs.jpcc.9b08523. [DOI] [Google Scholar]
  23. Kim Y.; Smith J. G.; Jain P. K. Harvesting Multiple Electron-Hole Pairs Generated through Plasmonic Excitation of Au Nanoparticles. Nat. Chem. 2018, 10, 763–769. 10.1038/s41557-018-0054-3. [DOI] [PubMed] [Google Scholar]
  24. Zhou L.; Swearer D. F.; Zhang C.; Robatjazi H.; Zhao H.; Henderson L.; Dong L.; Christopher P.; Carter E. A.; Nordlander P.; Halas N. J. Quantifying Hot Carrier and Thermal Contributions in Plasmonic Photocatalysis. Science 2018, 362, 69–72. 10.1126/science.aat6967. [DOI] [PubMed] [Google Scholar]
  25. Koopman W.; Sarhan R. M.; Stete F.; Schmitt C. N. Z.; Bargheer M. Decoding the Kinetic Limitations of Plasmon Catalysis: The Case of 4-Nitrothiophenol Dimerization. Nanoscale 2020, 12, 24411–24418. 10.1039/D0NR06039A. [DOI] [PubMed] [Google Scholar]
  26. Christopher P.; Xin H.; Marimuthu A.; Linic S. Singular Characteristics and Unique Chemical Bond Activation Mechanisms of Photocatalytic Reactions on Plasmonic Nanostructures. Nat. Mater. 2012, 11, 1044–1050. 10.1038/nmat3454. [DOI] [PubMed] [Google Scholar]
  27. Rodio M.; Graf M.; Schulz F.; Mueller N. S.; Eich M.; Lange H. Experimental Evidence for Nonthermal Contributions to Plasmon-Enhanced Electrochemical Oxidation Reactions. ACS Catal. 2020, 10, 2345–2353. 10.1021/acscatal.9b05401. [DOI] [Google Scholar]
  28. Foerster B.; Spata V. A.; Carter E. A.; Sönnichsen C.; Link S. Plasmon Damping Depends on the Chemical Nature of the Nanoparticle Interface. Sci. Adv. 2019, 5, eaav0704. 10.1126/sciadv.aav0704. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Dubi Y.; Un I. W.; Sivan Y. Thermal Effects - an Alternative Mechanism for Plasmon-Assisted Photocatalysis. Chem. Sci. 2020, 11, 5017–5027. 10.1039/C9SC06480J. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Jain P. K. Taking the Heat off of Plasmonic Chemistry. J. Phys. Chem. C 2019, 123, 24347–24351. 10.1021/acs.jpcc.9b08143. [DOI] [Google Scholar]
  31. Xie W.; Schlücker S. Hot Electron-Induced Reduction of Small Molecules on Photorecycling Metal Surfaces. Nat. Commun. 2015, 6, 7570. 10.1038/ncomms8570. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Schürmann R.; Tsering T.; Tanzer K.; Denifl S.; Kumar S. V. K.; Bald I. Resonant Formation of Strand Breaks in Sensitized Oligonucleotides Induced by Low-Energy Electrons (0.5–9 eV). Angew. Chem., Int. Ed. 2017, 56, 10952. 10.1002/anie.201705504. [DOI] [PubMed] [Google Scholar]
  33. Schürmann R.; Vogel S.; Ebel K.; Bald I. The physico-chemical basis of DNA radiosensitization – Implications for cancer radiation Therapy. Chem. - Eur. J. 2018, 24, 10271–10279. 10.1002/chem.201800804. [DOI] [PubMed] [Google Scholar]
  34. Dutta A.; Schürmann R.; Bald I. Plasmon Mediated Decomposition of Brominated Nucleobases on Silver Nanoparticles – A Surface Enhanced Raman Scattering (SERS) Study. Eur. Phys. J. D 2020, 74, 1–9. 10.1140/epjd/e2019-100115-1. [DOI] [Google Scholar]
  35. King M. D.; Khadka S.; Craig G. A.; Mason M. D. Effect of Local Heating on the SERS Efficiency of Optically Trapped Prismatic Nanoparticles. J. Phys. Chem. C 2008, 112, 11751–11757. 10.1021/jp803219x. [DOI] [Google Scholar]
  36. Micic M.; Klymyshyn N.; Lu H. P. Finite Element Method Simulations of the Near-Field Enhancement at the Vicinity of Fractal Rough Metallic Surfaces. J. Phys. Chem. B 2004, 108, 2939–2947. 10.1021/jp030773k. [DOI] [Google Scholar]
  37. Baffou G.; Bordacchini I.; Baldi A.; Quidant R. Simple Experimental Procedures to Distinguish Photothermal from Hot-Carrier Processes in Plasmonics. Light: Sci. Appl. 2020, 9, 108. 10.1038/s41377-020-00345-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Kopelman R. Fractal Reaction Kinetics. Science 1988, 241, 1620–1626. 10.1126/science.241.4873.1620. [DOI] [PubMed] [Google Scholar]
  39. Le Ru E. C.; Etchegoin P. G.; Meyer M. Enhancement Factor Distribution around A single Surface-Enhanced Raman Scattering Hot Spot and Its Relation to Single Molecule detection. J. Chem. Phys. 2006, 125, 204701. 10.1063/1.2390694. [DOI] [PubMed] [Google Scholar]
  40. Sieland F.; Schneider J.; Bahnemann D. W. Fractal Charge Carrier Kinetics in TiO2. J. Phys. Chem. C 2017, 121, 24282–24291. 10.1021/acs.jpcc.7b07087. [DOI] [Google Scholar]
  41. Li Q.; Batchelor-Mcauley C.; Compton R. G. Electrochemical Oxidation of Guanine: Electrode Reaction Mechanism and Tailoring Carbon Electrode Surfaces to Switch between Adsorptive and Diffusional Responses. J. Phys. Chem. B 2010, 114, 7423–7428. 10.1021/jp1021196. [DOI] [PubMed] [Google Scholar]
  42. Ibañez D.; Santidrian A.; Heras A.; Kalbáč M.; Colina A. Study of Adenine and Guanine Oxidation Mechanism by Surface-Enhanced Raman Spectroelectrochemistry. J. Phys. Chem. C 2015, 119, 8191–8198. 10.1021/acs.jpcc.5b00938. [DOI] [Google Scholar]
  43. D’Amico F.; Cammisuli F.; Addobbati R.; Rizzardi C.; Gessini A.; Masciovecchio C.; Rossi B.; Pascolo L. Oxidative Damage in DNA Bases Revealed by UV Resonant Raman Spectroscopy. Analyst 2015, 140, 1477–1485. 10.1039/C4AN02364A. [DOI] [PubMed] [Google Scholar]
  44. Marques T. S.; Schürmann R.; Ebel K.; Heck C.; Smiałek M. A.; Eden S.; Mason N.; Bald I. Kinetics of molecular decomposition under irradiation of gold nanoparticles with nanosecond laser pulses—A 5-Bromouracil case study. J. Chem. Phys. 2020, 152, 124712. 10.1063/1.5137898. [DOI] [PubMed] [Google Scholar]
  45. Chiorcea-Paquim A. M.; Oliveira-Brett A. M. Nanostructured Material–Based Electrochemical Sensing of Oxidative DNA Damage Biomarkers 8-Oxoguanine and 8-Oxodeoxyguanosine: A Comprehensive Review. Microchim. Acta 2021, 188, 1–13. 10.1007/s00604-020-04689-7. [DOI] [PubMed] [Google Scholar]
  46. Chiorcea-Paquim A.-M.; Oliveira-Brett A. M. DNA Electrochemical Biosensors for In Situ Probing of Pharmaceutical Drug Oxidative DNA Damage. Sensors 2021, 21, 1125. 10.3390/s21041125. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Fan C.; Song H.; Hu X.; Li G.; Zhu J.; Xu X.; Zhu D. Voltammetric Response and Determination of DNA with a Silver Electrode. Anal. Biochem. 1999, 271, 1–7. 10.1006/abio.1999.4102. [DOI] [PubMed] [Google Scholar]
  48. Rezaei-Zarchi S.; Saboury A. A.; Norouzi P.; Hong J.; Barzegar A.; Ganjali M. R.; Ghourchian H.; Moosavi-Movahedi A. A.; Javed A.; Rostami A. A. Electrochemical Recognition of Metalloproteins by Bromide-Modified Silver Electrode - A New Method. Int. J. Mol. Sci. 2007, 8, 723–735. 10.3390/i8070723. [DOI] [Google Scholar]
  49. Zhang X.; Huang C.; Wang M.; Huang P.; He X.; Wei Z. Transient Localized Surface Plasmon Induced by Femtosecond Interband Excitation in Gold Nanoparticles. Sci. Rep. 2018, 8, 1–7. 10.1038/s41598-018-28909-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Tariq M. Electrochemistry of Br–/Br2 Redox Couple in Acetonitrile, Methanol and Mix Media of Acetonitrile–Methanol: An Insight into Redox Behavior of Bromide on Platinum (Pt) and Gold (Au) Electrode. Z. Phys. Chem. 2020, 234, 295–312. 10.1515/zpch-2018-1321. [DOI] [Google Scholar]
  51. Zari N.; Mohammedi H.; Amine A.; Ennaji M. M. DNA Hydrolysis and Voltammetric Determination of Guanine and Adenine Using Different Electrodes. Anal. Lett. 2007, 40, 1698–1713. 10.1080/00032710701298479. [DOI] [Google Scholar]
  52. Ferapontova E. E. Electrochemistry of Guanine and 8-Oxoguanine at Gold Electrodes. Electrochim. Acta 2004, 49, 1751–1759. 10.1016/j.electacta.2003.12.006. [DOI] [Google Scholar]
  53. Link S.; El-Sayed M. A. Spectral Properties and Relaxation Dynamics of Surface Plasmon Electronic Oscillations in Gold and Silver Nanodots and Nanorods. J. Phys. Chem. B 1999, 103, 8410–8426. 10.1021/jp9917648. [DOI] [Google Scholar]
  54. Schürmann R.; Bald I. Effect of Adsorption Kinetics on Dissociation of DNA-Nucleobases on Gold Nanoparticles under Pulsed Laser Illumination. Phys. Chem. Chem. Phys. 2017, 19, 10796–10803. 10.1039/C6CP08433H. [DOI] [PubMed] [Google Scholar]
  55. Yu L.; Li N. Binding Strength of Nucleobases and Nucleosides on Silver Nanoparticles Probed by a Colorimetric Method. Langmuir 2016, 32, 5510–5518. 10.1021/acs.langmuir.6b01192. [DOI] [PubMed] [Google Scholar]
  56. Demers L. M.; Östblom M.; Zhang H.; Jang N. H.; Liedberg B.; Mirkin C. A. Thermal Desorption Behavior and Binding Properties of DNA Bases and Nucleosides on Gold. J. Am. Chem. Soc. 2002, 124, 11248–11249. 10.1021/ja0265355. [DOI] [PubMed] [Google Scholar]
  57. Andrews K. M.; Pearl T. P. Modification of Ag(111) Surface Electronic Structure via Weak Molecular Adsorption of Adenine Measured with Low Temperature Scanning Tunneling Microscopy and Spectroscopy. J. Chem. Phys. 2010, 132, 214701. 10.1063/1.3427248. [DOI] [PubMed] [Google Scholar]
  58. Zhang X.; Sun C. Q.; Hirao H. Guanine Binding to Gold Nanoparticles through Nonbonding Interactions. Phys. Chem. Chem. Phys. 2013, 15, 19284–19292. 10.1039/C3CP52149D. [DOI] [PubMed] [Google Scholar]
  59. Kogikoski J. S.; Dutta A.; Bald I.. Spatial Separation of Plasmonic Hot Electron Generation and a Hydrodehalogenation Reaction Center Using a DNA Wire. ChemRxiv, Mar. 1, 2021. 10.26434/chemrxiv.14114306.v2 [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Lee P. C.; Meisel D. Adsorption and Surface-Enhanced Raman of Dyes on Silver and Gold Sols. J. Phys. Chem. 1982, 86, 3391–3395. 10.1021/j100214a025. [DOI] [Google Scholar]
  61. Carnerero J. M.; Sánchez-Coronilla A.; Martín E. I.; Jimenez-Ruiz A.; Prado-Gotor R. Quantification of Nucleobases/Gold Nanoparticles Interactions: Energetics of the Interactions through Apparent Binding Constants Determination. Phys. Chem. Chem. Phys. 2017, 19, 22121–22128. 10.1039/C7CP03692B. [DOI] [PubMed] [Google Scholar]
  62. Green M. A. Self-consistent optical parameters of intrinsic silicon at 300 K including temperature coefficients. Sol. Energy Mater. Sol. Cells 2008, 92, 1305–1310. 10.1016/j.solmat.2008.06.009. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

cs1c01851_si_001.pdf (2.5MB, pdf)

Articles from ACS Catalysis are provided here courtesy of American Chemical Society

RESOURCES