High Channel Count Microphone Array Accurately and Precisely Localizes Ultrasonic Signals from Freely-Moving Mice

Abstract

Background:

An integral component in the assessment of vocal behavior in groups of freely interacting animals is the ability to determine which animal is producing each vocal signal. This process is facilitated by using microphone arrays with multiple channels.

New Method and Comparison with Existing Methods:

Here, we made important refinements to a state-of-the-art microphone array based system used to localize vocal signals produced by freely interacting laboratory mice. Key changes to the system included increasing the number of microphones as well as refining the methodology for localizing and assigning vocal signals to individual mice.

Results:

We systematically demonstrate that the improvements in the methodology for localizing mouse vocal signals led to an increase in the number of signals detected as well as the number of signals accurately assigned to an animal.

Conclusions:

These changes facilitated the acquisition of larger and more comprehensive data sets that better represent the vocal activity within an experiment. Furthermore, this system will allow more thorough analyses of the role that vocal signals play in social communication. We expect that such advances will broaden our understanding of social communication deficits in mouse models of neurological disorders.

INTRODUCTION

Communication is vital for dynamic, flexible group behavior (Bradbury and Vehrencamp, 1998). As animals interact in groups, they communicate using a variety of signals. For instance, male peacock spiders wave their ornate abdomens at nearby females (Girard and Endler, 2014; Girard et al., 2011), queen bees signal their reproductive interests to drones with secretions from the mandibular gland (Trhlin and Rajchard, 2011), elephant fish discharge electrical signals while attacking other animals (Scheffel and Kramer, 2000), and tree frogs indicate reproductive interest with mating calls (Gerhardt, 1974). The production and detection of auditory cues has been particularly well studied (e.g., (Briefer, 2012; Greenfield, 2015; Parsons et al., 2008; Seyfarth and Cheney, 2003; Soltis, 2010; Watts and Stookey, 2000)). These types of signals are used by various species in a myriad of different contexts, including the courtship behaviors of hammer-headed bats (Bradbury, 1977) and the aggressive encounters of Siberian hamsters (Keesom et al., 2015). The direct role auditory signals play in shaping complex social behavior, however, is less clear. Understanding the context in which vocalizations are emitted as well as the function of vocalizations during social behavior requires the ability to discern which animal is vocalizing during group interaction. To study vocal emission in large, natural environments, multi-channel microphone arrays have been implemented.

Microphone arrays collect auditory cues arriving at each of the microphones at different times. This information is then used to triangulate the origin of the sound in order to identify which animal produced it. In aquatic environments, arrays have facilitated the ability to examine the vocal activity of animals over long periods of time and large regions of space (e.g., (Clark and Ellison, 2000; Mellinger and Clark, 2000)). Baleen whale recordings, for example, have been used to assess species distribution (Heimlich et al., 2005), abundance (George et al., 2004), and behavior (Stimpert et al., 2007). In terrestrial environments, these methods have also been implemented. With a microphone array, Payne and colleagues showed that the calling patterns of African elephants provide information about the size of a pack (Payne et al., 2003; Thompson et al., 2010). Moreover, Celis-Murillo et al. (2009) were able to survey the abundance, richness, and composition of wild birds with the aid of a microphone array. Taken together, these examples demonstrate that microphone arrays provide a powerful, non-invasive tool for observing the vocal activity of individual animals in their natural habitat during group interactions.

Although microphone arrays are instrumental in assessing the vocal activity of animals in the wild, their capacity has been relatively untapped in the laboratory. A number of animal models of communication are being assessed in the laboratory. For instance, mice emit ultrasonic vocalizations, which are high-pitched vocal signals, during pup-retrieval (D’Amato and Populin, 1987; Hahn and Lavooy, 2005; Smith, 1976), courtship behaviors (Maggio et al., 1983; Whitney and Nyby, 1979), and same-sex interactions (Moles and D’Amato, 2000). Given the fact that genes associated with vocal and behavioral disorders can be selectively manipulated (e.g., (Jiang et al., 2010; Picker et al., 2006; Shu et al., 2005; Yang et al., 2012)), mice provide a powerful system for investigating communication. However, an essential component of understanding the role these vocal signals play in shaping social behavior requires identifying which animal produced which vocalization. This task was quite challenging before Neunuebel et al. (2015) first implemented a 4-channel microphone array in the laboratory. The 4-channel system probabilistically assigned signals to freely interacting animals, revealing that female mice were vocally active during courtship. One of the drawbacks to this approach was that a large percentage of the signals were not attributed to a single mouse, limiting the number of directly addressable questions. In another study, Heckman et al. (2017) utilized a two-microphone system to assess vocal communication during snout-to-snout interaction between two mice on adjacent platforms. The system was used to show sex differences in acoustic communication, but the scope of social interactions was restricted. Although both of these studies presented important technical advances towards the ability to study social communication in mice, the application of sound source localization techniques in a controlled laboratory setting has not yet reached its full potential.

The objective of the present study was to build upon the system developed by Neunuebel et al. (2015), as this system allows assessment of communication during naturalistic social behaviors. Here we provide key advances for each of the three fundamental steps required for attributing vocal signals to individual animals: detection, localization, and assignment. Step one, signal detection, refers to extracting signals from the audio data recorded on the microphone array. Step two, signal localization, provides an estimate of where the signal originated in the arena. The final step, signal assignment, is the attribution of the signal to a particular animal. An enhanced capacity to assign vocal signals will facilitate the ability to determine a more comprehensive vocal repertoire for individual animals and assess how vocal signals are used as a means of communication during innate behavior.

RESULTS

Signal detection

According to Peterson (1954), a major impediment to signal detection is discriminating relevant patterns of information (signal) from distracting patterns of information (noise). When detecting auditory cues, this process is improved by increasing the number of microphones present which thereby enhances the strength of the signal in relation to background noise (Kokkinakis and Loizou, 2010). To improve the ratio of signal to noise in our microphone array, we doubled the number of channels used by Neunuebel et al. (2015), increasing from four channels to eight. A total of 29 recording sessions, each with more than 25 female-urine-elicited ultrasonic vocal signals, were recorded from 19 individual male mice using an 8-channel microphone array (Figure 1A). The 29 data sets were subsequently processed in three different ways to directly compare signal detection with 8 channels and 4 channels. First, data from all eight channels was processed together as a single unit (8 microphone configuration). Next, data from a subset of four microphones was processed together. There were two configurations with four microphones. One configuration was the four even-numbered microphones (Even configuration), and the second configuration was the four odd-numbered microphones (Odd configuration). These arrangements ensured that, in every configuration, at least one microphone on each wall of the arena was represented. Our objective was to use these three configurations to evaluate the impact that the number of microphones had on signal detection.

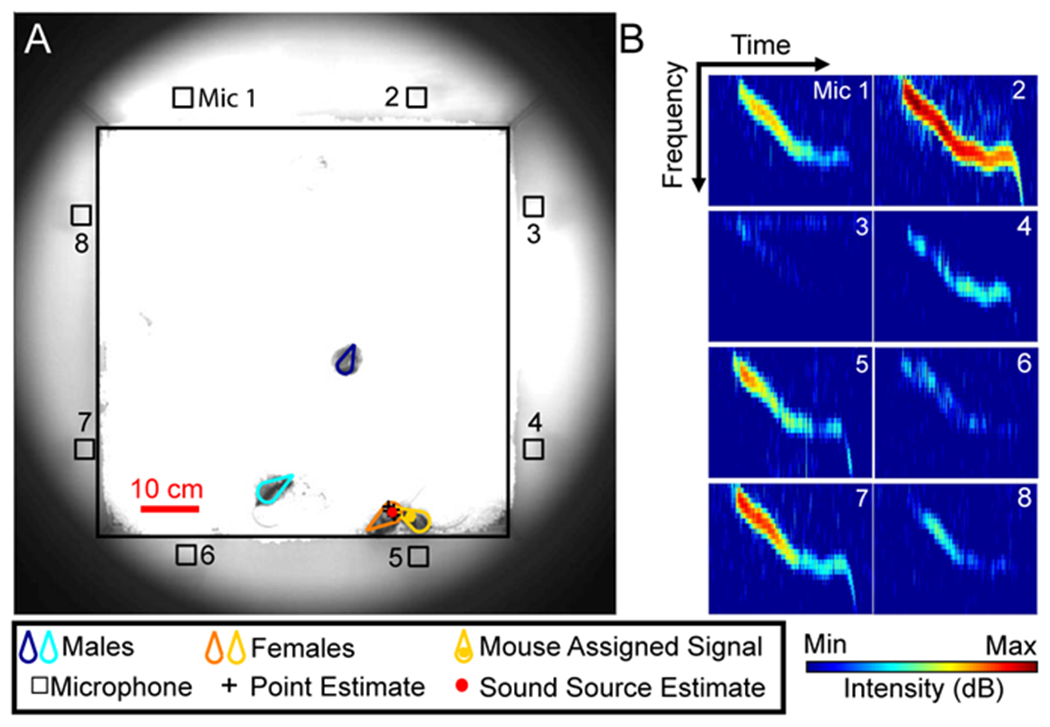
Figure 1. Signal detection.

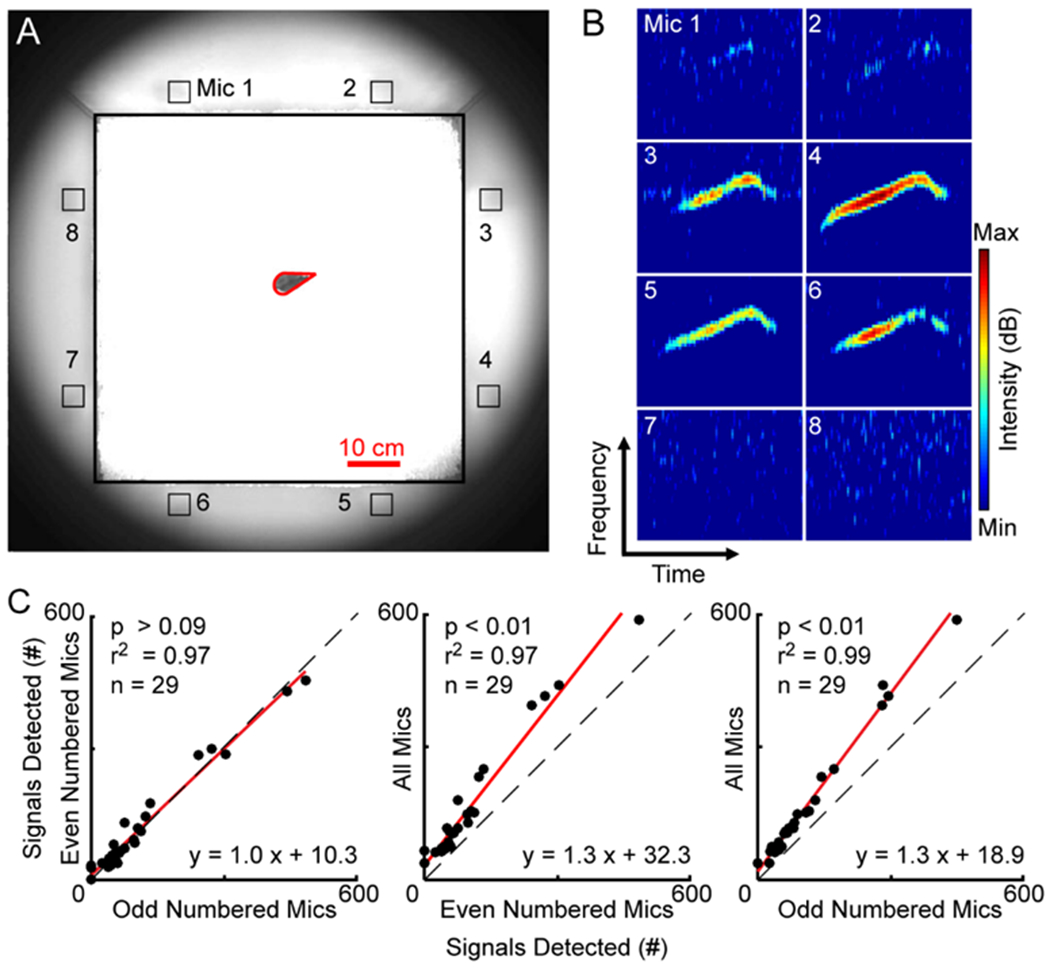
A, Image shows the location of the mouse (outlined in red) in the recording arena as well as the position of the microphones (Mic 1 – 8) along the periphery of the cage. B, Spectrograms showing a vocal signal detected on 4 of the 8 channels in the microphone array when the mouse was at the location shown in panel A. Numbers on the spectrograms correspond to the microphones shown in A. C, General linear mixed-effects models were used to calculate the regressions (red lines) comparing the number of vocal signals detected using different system configurations. Identity lines shown with dashed black lines. Each point is the number of signals detected in a recording session (n = 29). The equations are that of the regression lines through the data, with the fit of the lines indicated by the r² values, and the p-values denoting the comparisons between the slopes of the regression and identity lines.

Vocal signals were detected automatically using multitaper spectral analysis (Seagraves et al., 2016), and confirmed by manual inspection (Figure 1B). Signals were detected in 29, 26, and 28 sessions for the 8-channel, even-channel, and odd-channel configurations, respectively. For all three configurations, the number of signals detected per data set was non-Gaussian; therefore, the central tendency and variability were reported as median and IQR values (IQR_25-75). For the even numbered microphone configuration, the number of vocal signals detected in each recording session ranged from 19 to 482 (median = 71, IQR = 48-122). The odd numbered microphone configuration detected 10 to 448 (median = 68, IQR = 40-136), and the 8-channel configuration detected 37 to 603 (median = 110, IQR = 70-193). To directly compare the capacity of the different system configurations, we employed a method similar to Seagraves et al. (2016) and used a generalized-linear mixed-effects regression model (GLME) to calculate the regression between each pair of configurations (Figure 1C). The regression line for the even and odd configurations had a slope similar to the identity line (slope = 1.0, t score = 1.7, p > 0.09), indicating that there was no difference between the two configurations. In contrast, the slopes representing the regression for the 8-channel configuration compared to both even and odd configurations were significantly different than the identity line. Both regressions were shifted above the identity line (slope eight-even = 1.3, t score = 7.2, p < 10⁻⁷; eight-odd slope = 1.3, t score = 17.2, p < 10⁻²⁰), indicating that the 8-channel configuration detected more signals than either of the 4-channel configurations. This difference was also apparent when comparing the total number of signals extracted across all data sets. Over the 29 data sets, the even and odd numbered microphone systems detected 3295 and 3342 signals, respectively. In contrast, the 8-channel system detected 5011 signals, an increase of nearly 50% relative to either of the 4-channel configurations. Thus, increasing the number of microphones enhanced the system’s ability to detect vocal signals in a large arena.

Signal localization

Neunuebel et al. (2015) used a Snippets approach to estimate the location at which each vocal signal originated. In this approach, each signal was partitioned into smaller pieces, called snippets, spanning 5 ms in duration and 2 kHz in bandwidth (i.e., change in frequency). For each snippet, a single location, referred to as a point estimate, was found that best explained when the signal arrived at each microphone in the array. The coordinates of all point estimates were then averaged to estimate the location from which the entirety of the signal originated, termed the sound source. Supplemental Figure 1 shows localization examples using this method with four microphones (Snippets 4) as well as eight microphones (Snippets 8). For the 8-channel system, 3671 out of 5011 signals were localized (Table 1), while 1737 out of 3295 signals were localized with the Even configuration, and 1743 out of 3342 signals were localized with the Odd configuration. Comparing the Even and Odd Snippets configurations with a GLME showed a significant difference in the number of signals localized (slope = 0.9, t score = 3.4, p < 0.01), such that the Even configuration localized more signals per data set (Supplemental Figure 2). Based upon these results, the Even configuration was used to represent the 4-channel data, as it was a more conservative comparison with the 8-channel data.

Table 1:

Number of vocal signals available for use at each step underlying assignment. The last column, Assigned-No Density, is the total number of signals assigned to an animal following all processing steps

	Detected	Localized	Assigned	Assigned-No Density
Snippets 4	3183	1737	1162	1344
Snippets 8	5011	3671	2543	2939
Jackknife 4	3183	3177	1646	2437
Jackknife 8	5011	4939	3089	4590

The 8-channel configuration localized 73% of the detected signals, whereas the even and odd configurations localized 55% and 52%, respectively. Despite the improvement, 27% of the signals remained unlocalized with the eight-microphone approach. When further examining the unlocalized signals, every signal had three or fewer snippets (Figure 2A). In contrast, the majority of localized signals had four or more snippets (3546 out of 3671). A significant difference in number of snippets was observed between groups (Mann-Whitney U-Test, z = 54.04, p<10⁻¹⁵⁰). Because the number of snippets is determined by a signal’s duration and bandwidth, longer signals with a larger bandwidth should have more snippets compared to shorter signals with smaller bandwidths. If this were the case, the Snippets approach would be biasing the results towards signals of a longer duration and a larger bandwidth. Therefore, we compared the duration and bandwidth of signals that were localized and unlocalized. The majority of unlocalized signals were shorter than 13 ms (870 out of 1355), whereas the majority of localized signals were longer than 16 ms (1894 out of 3671) (Figure 2B). A statistical comparison indicated a significant difference between groups (Mann-Whitney U-Test, z = 30.19, p < 10⁻¹⁰⁰). Bandwidth also differed between the two groups, as the majority of unlocalized signals had a bandwidth smaller than 9 kHz (753 out of 1355), whereas the majority of localized signals had a bandwidth larger than 12 kHz (2030 out of 3671) (Figure 2C). The bandwidths of unlocalized and localized signals were significantly different (Mann-Whitney U-Test, z=25.42, p<10⁻¹⁰⁰).

Figure 2: Signal localization is impeded by number of snippets.

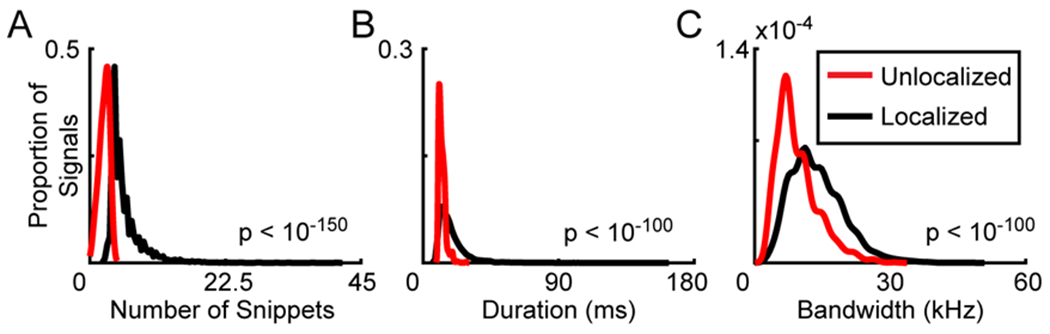
Histograms showing the features of signals detected with the 8-microphone configuration. Using the Snippets method to determine the source location of each sound (Neunuebel et al., 2015), signals were either localized (black) or unlocalized (red). Data smoothed using a kernel density function that applied Scott’s rule to determine bin size (Scott, 2010). A Mann-Whitney U-Test was used to compare localized and unlocalized signals. A. Number of snippets comprising signals. B. Duration of signals. C. Bandwidth of signals.

Taken together, these results suggest that the Snippets approach biases the results towards signals of longer duration and to a lesser extent larger bandwidth. To overcome these biases, we implemented a novel approach for signal localization. This new approach, Jackknife, used the same algorithm as Snippets to estimate the location of the sound source, but instead of partitioning the signal into discrete, small pieces, it localized the entire signal as a single unit (Figure 3A). This circumvented the bias that the previous system had toward longer signals and larger bandwidths. For each vocal signal, the Jackknife method systematically excluded one microphone and used the remaining microphones to calculate a single point estimate. This process was repeated such that each microphone was excluded once. Thus, the number of point estimates was determined by the number of microphones. Figure 3B shows a schematic for the first point estimate. During the first step of the process, information about the vocal signal recorded on channel one of the array is excluded and the estimate is derived only using data from channels 2 through 8. As shown in Figure 3C–E, three additional point estimates are calculated by excluding channels 2, 3, and 8. In our 8-channel system, this is repeated four additional times where each of the four remaining microphones is left out of the calculation once, producing a total of eight point estimates (Figure 3F). These eight estimates are then used to estimate the location of the sound source.

Figure 3. Jackknife schematic.

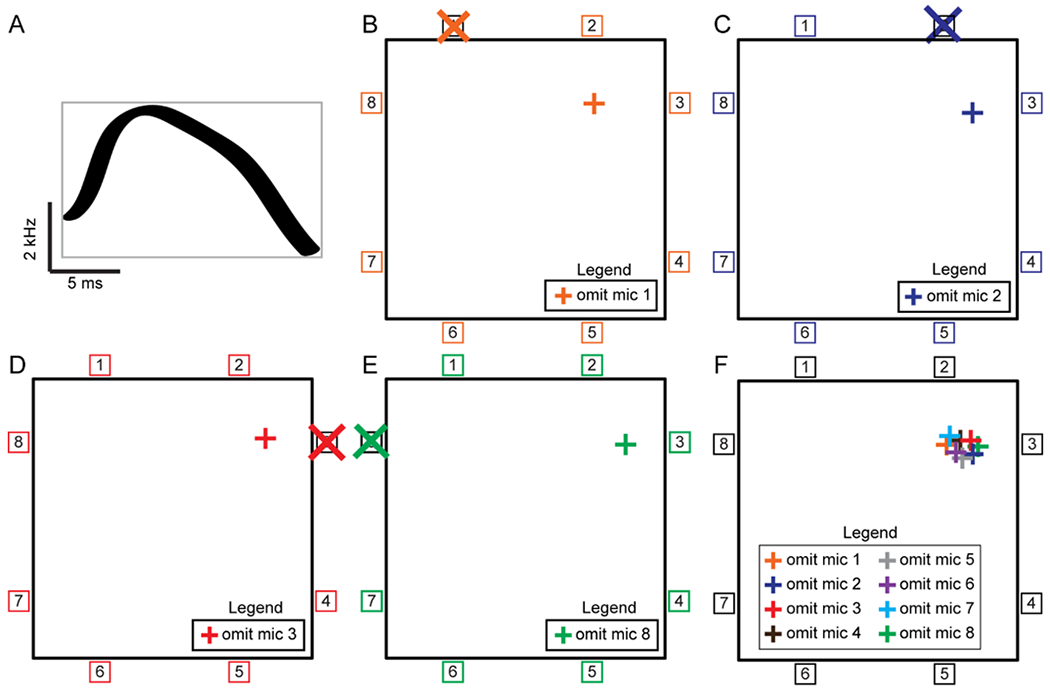
A-F, The Jackknife approach of sound source localization implemented a statistical resampling strategy that systematically excluded one of the microphones and used all remaining microphones to estimate the sound source. Each microphone was omitted once, leaving as many point estimates as there were microphones. All further steps were identical to the Snippets approach described in Neunuebel et al. (2015) and METHODS. The schematic shows the Jackknife approach applied to audio data collected with an 8-channel microphone array. A, The entire duration and full frequency range of the hypothetical vocal signal was used to estimate the location (gray box). B, Point estimate calculated by excluding microphone 1. C, Point estimate calculated by excluding microphone 2. D, Point estimate calculated by excluding microphone 3. E, Point estimate calculated by excluding microphone 8. F, Combination of 8 point estimates. Cartoons showing point estimates calculated by omitting microphones 4-7 are not shown.

To gauge the capacity of the Jackknife method of sound source localization, we compared the Jackknife approach to the Snippets approach. When applying the Jackknife approach to audio data collected on 8 channels (Jackknife 8), 99% of the detected signals were localized (Table 1; 4939 of 5011). Examples of sound source localization using the Jackknife 8 approach are shown in Supplemental Figure 1. The number of signals localized by Jackknife 8 was 35% higher than the Snippets 8 approach, which only localized 3671 signals. When applying the Jackknife approach to data collected on four channels (Jackknife 4; examples in Supplemental Figure 1), 3177 of the 3183 detected vocal signals were localized (99.8%). For each individual data set (Figure 4A), the Jackknife 8 configuration localized 36 to 597 signals (median = 110, IQR = 69- 190) and the even numbered configuration localized 25 to 480 (median = 71, IQR = 48-122). The Snippets method localized fewer signals, with Snippets 8 localizing 25 to 488 vocal signals in each recording session (median = 76, IQR = 49-131), and Snippets 4 localizing 7 to 324 (median = 39, IQR = 20-67).

Figure 4. Signal localization.

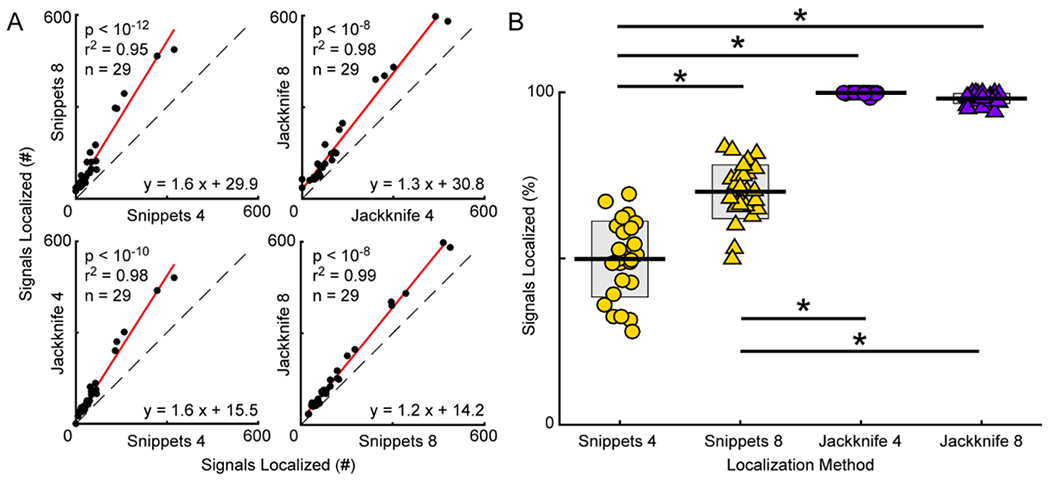
A, General linear mixed-effects models were used to calculate the regressions (red lines) comparing the number of vocal signals localized using different system configurations. Identity lines shown with dashed black lines. Each point is the number of signals localized in a recording session (n = 29). The equations are that of the regression lines through the data, with the fit of the lines indicated by the r² values, and the p-values denoting the comparisons between the slopes of the regression and identity lines. B, Percentage of signals localized in each data set for the different system configurations. Each point represents data from one recording session. The central line is the mean. Gray boxes indicate standard deviation. * p < 0.05.

To directly compare the number of signals localized in each of the different configurations, GLMEs were calculated for the following: 1) Snippets 4 and Snippets 8, 2) Jackknife 4 and Jackknife 8, 3) Snippets 4 and Jackknife 4, and 4) Snippets 8 and Jackknife 8. In every recording session, Snippets 8 localized more vocal signals than Snippets 4, as indicated by the regression line with a slope that significantly differed from the slope of the identity line (regression slope = 1.6, t score = 3.4, p < 10⁻¹²). Similar to the Snippets approach, the Jackknife 8 method localized more vocal signals in each recording session than Jackknife 4 (regression slope = 1.3, t score = 16.1, p < 10⁻⁸). Interestingly, when comparing the Jackknife and Snippets approaches, the Jackknife method localized significantly more signals than the Snippets method regardless of the number of microphones used (slope Jackknife 4 and Snippets 4 = 1.6, t score = 16.1, p < 10⁻¹⁰; slope Jackknife 8 and Snippets 8 = 1.2, t score = 13.6, p < 10⁻⁸).

To account for the variability in the number of signals detected in each experiment, we determined the percentage of signals localized in each data set and used this information to compare the different configurations (Figure 4B). For each recording session, the percentage was calculated by dividing the total number of localized signals by the total number of detected signals. Snippets 4 localized 28 to 69 percent of signals in each recording session (mean = 49.9%, std = 11.4%). The percentages increased with more microphones, as Snippets 8 localized 50 to 83 percent of the signals (mean = 70.1%, std = 8.1%). In contrast, the Jackknife method localized 98 to 100 percent of signals with four microphones (mean = 99.9%, std = 0.004%), and 94 to 100 percent of signals with eight microphones (mean = 98.2%, std = 1.5%). A 2-way ANOVA with localization method and number of microphones as factors was conducted, which showed a main effect of localization method (F_(1,106) = 859.8, p < 10⁻⁵¹; Snippets: mean = 60.5%, std = 14.1%; Jackknife: mean = 99.0%, std = 1.4%) and number of microphones (F_(1,106) = 48.3, p < 10⁻⁹; four microphones: mean = 74.9%, std = 26.5%; eight microphones: mean = 84.1%, std = 15.3%), as well as a significant interaction (F_(1,106) = 68.1, p<10⁻¹²). This ANOVA was followed by a Tukey’s test to calculate pairwise differences. Post-hoc corrections for multiple comparisons were made with the Benjamini-Hochberg procedure, as this procedure is a powerful correction that controls for the rate of false discovery (McDonald, 2014). After applying this method of post-hoc correction, there were significant differences in the number of signals localized between all pairs (all p < 10⁻⁷) excluding Jackknife 4 vs Jackknife 8 (p > 0.8). Thus, increasing the number of microphones as well as applying the Jackknife method led to significant improvement in the ability to localize signals.

Signal assignment

To determine how vocalizations impact behavior, it is critical that localized signals are assigned to specific mice. Assigning vocal signals to freely socializing mice requires a logical, statistics-based approach, such as that used by Neunuebel et al. (2015). Therefore, we used the same approach. Briefly, the likelihood that a signal was emitted from every point in the cage, called the probability density, was calculated for each localized signal. Each mouse in the arena was assigned the density value corresponding to the location of the mouse’s nose, with a higher density value indicating a higher likelihood that the signal originated from that animal. A mouse probability index (MPI) was subsequently calculated for each signal using the formula:

$$MP{I}_n=\frac{D_n}{{\sum }_{i=1}^M{D}_i}$$

where n = mouse index, M = total number of mice, and D = density value assigned to the mouse. This index was calculated for each mouse in the arena, and if the MPI for a single mouse exceeded 0.95, indicating a 95% likelihood that the signal was emitted by that particular animal, the signal was assigned to that mouse. If no mouse had an MPI exceeding 0.95, that signal was classified as unassigned. The MPI threshold of 0.95 was taken from Neunuebel et al. (2015) because the study showed that a threshold of 0.95 offered the best trade-off between the number of signals assigned and the accuracy of assignment.

To confirm that the MPI threshold of 0.95 was equally applicable to the 8-channel system, we also varied the threshold value and assessed the accuracy of our new system (Supplemental Figure 3). To assess the accuracy of each configuration with this MPI threshold, we modeled a mouse social environment by randomly generating three virtual mice within the cage boundaries at the time of each vocal signal. This approach, which was identical to Neunuebel et al. (2015), permitted us to directly quantify the accuracy and precision of the system during group interaction, since it ensured, with absolute certainty, that the origin of each vocal signal was known. As previously reported, we evaluated the systems using MPI thresholds of 0.50 to 1.00. Varying the MPI threshold had less of an effect on the Jackknife method than the Snippets method. With the Jackknife 8 method, at an MPI value of 0.50, meaning an approximately 50 percent likelihood that a particular animal emitted a signal, 95.7 percent of signals were assigned. For the assigned signals, 97.3 percent were assigned correctly. Snippets 8, on the other hand, assigned 95.6 percent of signals with an MPI value of 0.50, but only 94.2 percent of those signals were assigned accurately. However, at the 0.95 MPI level, Snippets 8, while only assigning 80.0 percent of total signals, accurately assigned 97.3 percent of those signals. Jackknife 8 was not strongly affected by increasing the MPI threshold, still assigning 92.2 percent of signals, with 98.2 percent of those being assigned accurately. Because altering the MPI threshold did not have a large effect on either of the 8-channel systems, we opted for a more conservative approach and kept the 0.95 MPI threshold.

Next, we used an MPI threshold of 0.95 to compare the number of signals assigned with each configuration. The even-numbered microphones outperformed the odd-numbered using the Snippets method of sound source localization (Supplemental Figure 4); thus, the Even configuration was used to represent the 4-channel data. As seen in Table 1, there were a total of 1162, 2543, 1646, and 3089 signals assigned to one of the four mice (one real and three fake mice) with over 95% certainty using Snippets 4, Snippets 8, Jackknife 4, and Jackknife 8, respectively. Jackknife 8 assigned the largest number of signals, assigning 121%, 188%, and 216% as many as Snippets 8, Jackknife 4, and Snippets 4.

Examining the number of signals assigned in each recording session showed the same pattern, with Jackknife 8 assigning more signals per experiment than any other system (Figure 5A). Jackknife 4 assigned a median of 37 signals per experiment (IQR = 21-64) compared to a median of 24 for Snippets 4 (IQR = 15-48). With 8 channels, the Jackknife approach also assigned more signals per experiment than the Snippets approach (Jackknife 8: median = 67, IQR = 42-120; Snippets 8: median = 49, IQR = 32-88). A GLME indicated a significant difference in number of signals assigned by configuration, with Jackknife assigning more vocal signals in each experiment than Snippets (Jackknife 4 vs. Snippets 4: slope = 1.4, t score = 7.8, p < 10⁻⁸; Jackknife 8 vs. Snippets 8: slope = 1.1, t score = 6.5, p < 10⁻⁶). The regressions also indicated that increasing from four to eight microphones increased the number of signals assigned in each experiment (Jackknife 4 vs. Jackknife 8: slope = 1.5, t score = 11.8, p < 10⁻⁸; Snippets 4 vs. Snippets 8: slope = 1.8, t score = 12.0, p < 10⁻⁶).

Figure 5. Signal assignment.

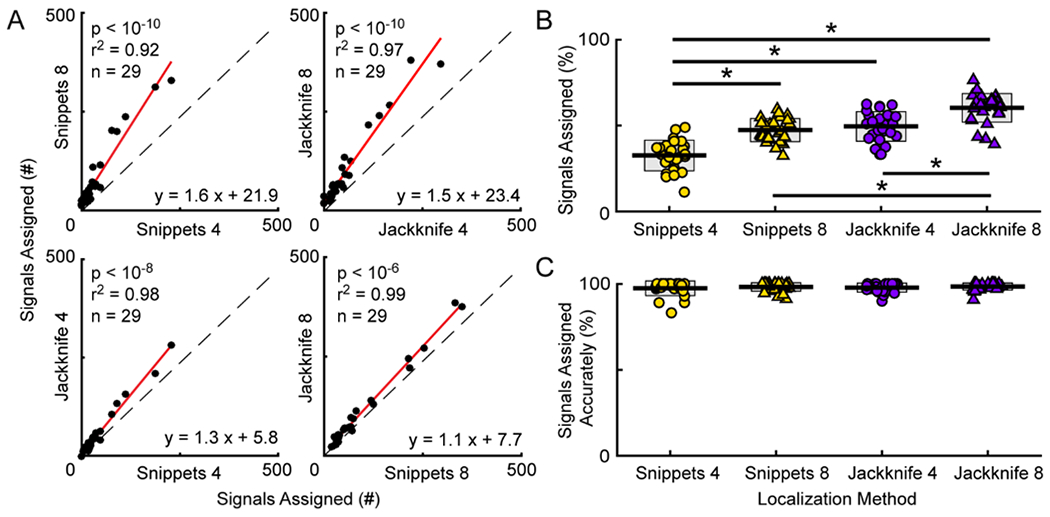
A, General linear mixed-effects models were used to calculate the regressions (red lines) comparing the number of vocal signals assigned using different system configurations. Identity lines shown with dashed black lines. Each point is the number of signals assigned in a recording session (n = 29). The equations are that of the regression lines through the data, with the fit of the lines indicated by the r² values, and the p-values denoting the comparisons between the slopes of the regression and identity lines. B, Percentage of signals assigned in each data set for the different system configurations. * p < 0.05. C, Percentage of assigned signals attributed to the correct mouse in each data set for the different approaches. There were no significant differences across groups. B, C, Each point is the percentage from a single data set. Central line is the mean. Gray boxes indicate standard deviation.

Figure 5B shows the percentage of signals from each data set that were assigned to an animal. For the Snippets method, 11 to 49 percent of signals were assigned when applying the approach to four-channels (mean = 32.5%, std = 8.9%), as compared to 32 to 59 percent when applying the method to eight-channels (mean = 47.3%, std = 6.7%). The Jackknife approach dramatically increased the percentage of signals assigned, with Jackknife 4 assigning 33 to 63 percent of signals (mean = 49.5%, std = 8.6%) and Jackknife 8 assigning 39 to 76 percent of signals (mean = 60.3%, std = 8.3%). Jackknife 8, which assigned the highest percentage of signals, assigned 28 percent more signals than the Snippets 4 configuration. A 2-way ANOVA (localization method X number of microphones) revealed a main effect of localization method (F_(1,106) = 92.3, p < 10⁻¹⁰; Snippets: mean = 40.3%, std = 10.8%; Jackknife: mean = 55.2%, std = 10.0%), as well as number of microphones (F_(1,106) = 67.7, p < 10⁻¹⁰; four microphones: mean = 41.0%, std = 12.2%; eight microphones: mean = 53.8%, std = 9.9%), with no significant interaction (p = 0.20). After correcting for multiple comparisons, post-hoc statistical tests revealed significant differences for all possible pairs (all p < 0.001) except for Jackknife 4 vs Snippets 8 (p > 0.7), with Jackknife 8 assigning a significantly larger proportion of signals than any other configuration.

Although Jackknife 8 increased the number of signals assigned, a possibility exists that the additional signals may have been assigned to the incorrect animal. Therefore, to confirm that the increase in assignment occurred without compromising accuracy, we calculated the percentage of signals that were assigned to the real mouse. The percentage was determined by dividing the total number of signals assigned to the real mouse by the total number of signals assigned. Figure 5C shows that Jackknife 8 correctly assigned an average of 98 percent of signals (range = 90.7 to 100.0, std = 2.1). Similar to Jackknife 8, the other configurations were highly accurate (Jackknife 4, mean = 97.8, range = 89.9 to 100.0, std = 2.6; Snippets 4: mean = 97.4, range = 83.3 to 100.0, std = 4.3; Snippets 8: mean = 98.2, range = 91.2 to 100.0, std = 2.5). A 2-way ANOVA was conducted to compare the percentage of correctly assigned signals. The analysis showed no significant differences, with no main effect of localization method (F_(1,106) = 0.3, p = 0.6; Snippets: mean = 97.8%, std = 3.4%; Jackknife: mean = 98.1%, std = 2.3%) or number of microphones (F_(1,106) = 1.6, p = 0.2; four microphones: mean = 97.6%, std = 3.5%; eight microphones: mean = 98.3%, std = 2.3%), and no interaction term (F_(1,106) = 0.02, p > 0.8); these analyses validated that signal assignment was accurate regardless of system configuration.

After evaluating assignment accuracy, we quantified how close the estimated source location was to the true source. To calculate this, we measured distance error, or the distance between the nose of the mouse (where the signal actually originated) and the estimated source location (estimate of where the signal originated) for all assigned signals. Conducting an adjusted Fisher-Pearson coefficient of skewness test for each configuration confirmed that the distributions of distance error were non-Gaussian and positively skewed (Supplemental Figure 5A-D; Jackknife 4, D₍₁₆₂₅₎ = 0.7, p < 10⁻⁵; Jackknife 8, D₍₃₀₂₈₎ = 0.7, p < 10⁻⁵; Snippets 4, D₍₁₁₄₀₎ = 0.7, p < 10⁻⁵; Snippets 8, D₍₂₄₉₂₎ = 0.7, p < 10⁻⁵). The median distance error for Jackknife 8 was 1.8 cm with an IQR of 1.1-2.9 cm. The median distance error was greater for the other three configurations (Jackknife 4, median = 2.9, IQR = 1.6-5.4 Snippets 4, median = 2.9, IQR = 2.0-4.8; Snippets 8, median = 2.5, IQR = 1.5-4.1). To convert the positively skewed error distributions into data sets that more closely represented a normal distribution, we used a log-transformation (Zar, 2010). A 2-way ANOVA was conducted on the transformed data to compare the effects of localization approach and number of microphones on distance error. Means and standard deviations were then back transformed and reported in centimeters. There were significant main effects of number of microphones (F_(1,8285) = 269.6, p < 10⁻⁵⁸; four microphones: mean = 11.0 cm, std = 7.9 cm; eight microphones: mean = 5.0 cm, std = 6.3 cm) and localization method (F_(1,8285) = 50.2, p < 10⁻¹²; Jackknife: mean = 5.4 cm, std = 7.2 cm; Snippets: mean = 8.3 cm, std = 6.6 cm), as well as a significant interaction (F_{(1, 1,8285)} = 82.9, p < 10⁻¹⁸). After conducting Benjamini-Hochberg post-hoc statistical analyses to correct for multiple comparisons, significant differences were found between all pairs (all p < 10⁻⁵) excluding Jackknife 4 vs Snippets 4 (p > 0.60), with Jackknife 8 having significantly smaller error distances for assigned signals than all other system configurations. These results provide additional support that Jackknife 8 is the most accurate and precise of the four configurations.

Next, the spatial distribution of where the assigned signals were being localized relative to the position of the mouse was examined. This was achieved by translating the sound source estimates and mouse positions to a reference frame centered on the mouse (Supplemental Figure 5E). The area surrounding the mouse (225 cm²) was partitioned into a 9-binned grid (3 x 3) and this area was centered on the mouse’s nose. Based on this configuration, the nose of the mouse was always located in bin 5. All sound source estimates falling outside the bins were classified as “Out.” For each configuration, the majority of sound source estimates were clustered around the head of the mouse (Supplemental Figure 5E–H). When using the Jackknife approach with 8-channels, there were 2148 estimates located in bin 5 (Supplemental Figure 5L). This was 60.78% more than the second highest total (Supplemental Figure 5K; Snippets 8 = 1336). Supplemental Figure 5I–J shows that Jackknife 4 had 732 estimates located in bin five and Snippets 4 had 532 estimates. For Jackknife 8, the number of sound source estimates was significantly different between bins (Χ²_0.05,8 = 11171.4, p < 10⁻¹⁰). This was similar for all other configurations (Jackknife 4, Χ²_0.05,8 = 2305.7, p < 10⁻¹⁰; Snippets 4, Χ²_0.05,8 = 1760.2, p < 10⁻¹⁰; Snippets 8, Χ²_0.05,8 = 4959.7, p < 10⁻¹⁰). For each configuration, more sounds were estimated to have originated in bin five than expected based on a uniform distribution between the bins (Supplemental Figure 5I–L). These results indicate that all four configurations are capable of localizing and assigning vocal signals, and these signals are clustered around the nose of the animal; however, Jackknife 8 is the most accurate configuration.

Density Quantification

Despite the fact that Jackknife 8 increased the number of accurately assigned vocal signals, 38% of the detected signals remained unassigned. To identify the reason why signals were not assigned, we plotted the relative distance between the estimated sound source location and the location of the source’s nose for all unassigned signals (Supplemental Figure 6). The majority of these signals (1153 out of 1835) fell within 4 cm of the nose of the mouse, indicating that the constraints for assigning signals may not be optimized for the Jackknife configuration. The assignment process has two requirements for a localized signal to be assigned to an individual animal: 1) the MPI value for that mouse must exceed 0.95, and 2) the density value at the nose must exceed 1 m⁻². An MPI value of 0.95 indicates a 95% certainty that the signal was produced by that particular animal. Density is a measure of the probability that the signal originated from every point in the arena, and thus density decreases with distance from the sound source estimate. Therefore, the density threshold of 1 m⁻² was implemented by Neunuebel et al. (2015) to prevent poorly localized signals from being assigned to an animal that was not close to the estimated source location. Inspection of the unassigned signals showed that 85% exceeded the 0.95 MPI threshold, whereas only 8% exceeded the 1 m⁻² density threshold. Therefore, the density threshold appeared to play a major role in preventing localized signals from being assigned to an individual mouse. To examine signals that were unassigned solely because they failed to reach the density threshold, we selected unassigned signals with an MPI value above 0.95 and a density value below 1 m⁻². When looking at the distance error for these signals, the results were striking. The majority of the signals were still precisely localized by each of the four configurations (Supplemental Figure 7), as shown by the rightward-skewed error distributions with peaks located approximately 4 cm from the nose of the mouse (Snippets 4, skewness = 2.6 Jackknife 4, skewness = 2.0; Snippets 8, skewness = 2.9; Jackknife 8, skewness = 2.8). This evidence suggests that a density threshold may be adversely impacting the ability to assign signals to an individual animal, especially when using the Jackknife 8 approach.

The sensitivity of Jackknife 8 to the density threshold may have been caused by the number of estimates used to calculate the probability density function. For the Snippets approach, the number of point estimates for localized signals ranged from 3 to 41 (Figure 2). In contrast, the number of point estimates was the same for every signal when using the Jackknife approach. To quantify the impact that the number of point estimates played in determining density, we created a simulation that calculated the probability density function for 1000 fake signals. Each fake signal consisted of a specified number of randomly generated point estimates located within the cage boundaries. The spread of the point estimates was unconstrained in this version of the simulation. The first run of the simulation calculated the probability density function for 1000 fake signals, each with four point estimates. During the second run, the simulation calculated the probability density function for 1000 fake signals, each with six point estimates. The number of point estimates for each run ranged from 4 to 22. Four was used as the starting point for the simulation because all unlocalized signals had fewer than four points, and thus a minimum value of four ensured that all generated point estimates would be equivalent to those of a localized signal. Figure 6A shows that more point estimates led to a decrease in the maximum density value, indicating that the number of point estimates used to calculate the probability density function does not explain the sensitivity of Jackknife 8 to the density threshold.

Figure 6. Density Quantification.

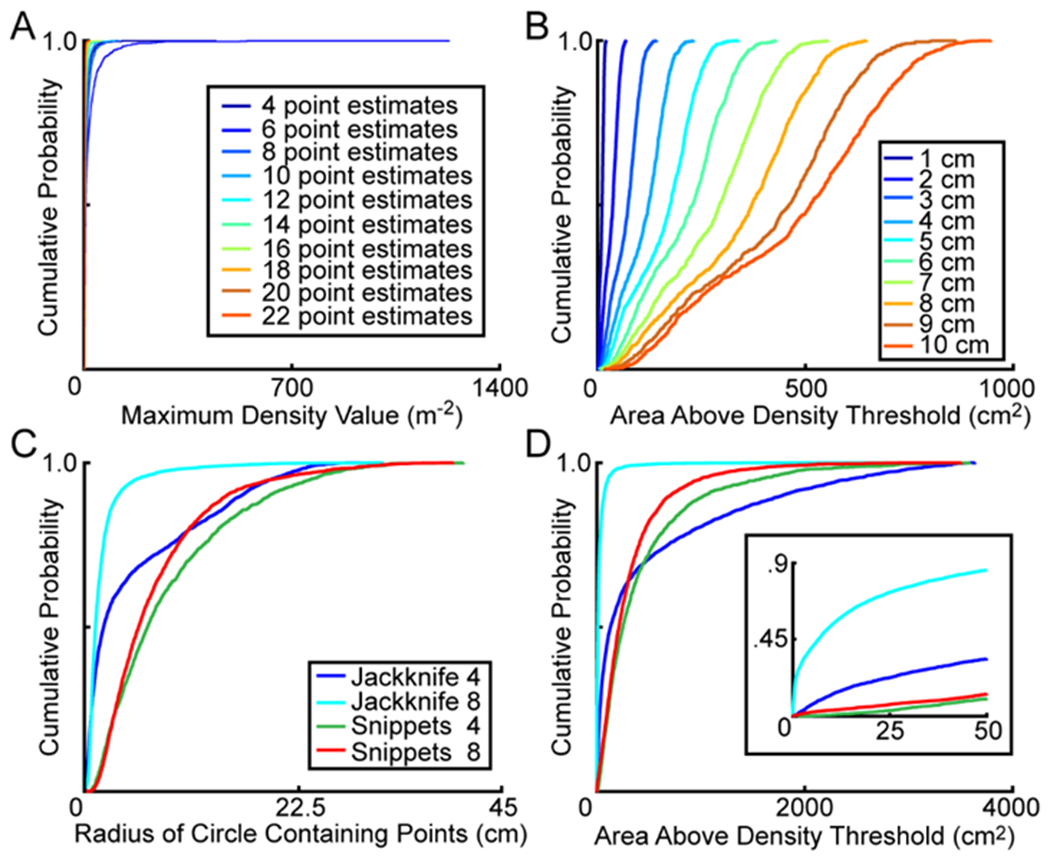
A, Results from 10 simulations assessing the impact that the number of point estimates had on the maximum density in the arena. For every simulation, 1000 fake signals were generated, each with a specified number of point estimates (indicated by color) located at random positions within the boundaries of the arena. For each fake signal, the point estimates were used to calculate the probability density function across the cage and then the maximum density was determined. B, Results from 10 simulations assessing the impact that the spread between point estimates had on density. For every simulation, 1000 fake signals were generated, each with eight point estimates enclosed by a circle with a radius of a specific length (ranging from 1 to 10 cm). For each fake signal, the eight point estimates were used to calculate the probability density function across the cage and then the area of the cage exceeding the density threshold of 1 m⁻² was determined. The size of the circle used in each simulation is differentiated by color. C, Cumulative probability plots showing variability in point estimate spread for each of the four configurations. For each localized vocal signal, the smallest possible circle enclosing the point estimates was determined. D, Cumulative probability plots showing the total area of the cage exceeding the density threshold of 1 m⁻². Line colors match those in panel C and indicate each of the four configurations. The inset shows the area above the density threshold in the range of 0 to 50 cm² and emphasizes the differences between the four configurations.

Another variable that might underlie the sensitivity of Jackknife 8 to the density threshold is the distance between each of the individual point estimates (i.e., point estimate spread). To examine the effect that point estimate spread had on the probability density function, we ran a second simulation. For this simulation, we calculated the probability density function for 1000 fake signals, each consisting of eight point estimates. The spread of the point estimates was constrained in this version of the simulation, with all eight randomly generated points confined within a circle of a specified radius. To increase the area of point spread, we systematically varied the length of the circle’s radius from 1 to 10 cm, with areas ranging from 3.1 to 314.2 cm². The first run of the simulation calculated the probability density function for 1000 fake signals that were all enclosed by a circle with a radius of 1 cm (the total area of each circle was 3.1 cm²). The second run of the simulation calculated the probability density function for 1000 fake signals that were all contained within a circle with a radius of 2 cm (area = 12.6 cm²). For each fake signal, we used the calculated probability density function to compute the area in the cage that exceeded the density threshold of 1 m⁻². The results of this simulation showed that as the point spread increased, the area of space exceeding the density threshold also increased (Figure 6B). A larger area of space exceeding the density threshold would increase the distance an animal could be from the estimated sound source location while still exceeding the threshold. This means that if two signals were localized to a point falling the same distance from the nose of an animal, but the point estimates from the first signal were more spread out than those from the second signal, the first signal would more likely be assigned to a mouse. Therefore, a system that more precisely calculated point estimates would be at a disadvantage in signal assignment.

To determine whether the point spread simulation accurately represented our data, we quantified the point estimate spread across the four configurations. For every configuration, the size of the point spread for each assigned signal was calculated by finding the smallest circle that enclosed all of the point estimates. The radius of the circle was determined by finding the largest distance between the overall sound source estimate and an individual point estimate, and this was assessed for all vocal signals. The distributions of the radii for each of the configurations were non-Gaussian (Figure 6C). For Jackknife 8, the median radius was 1.17 cm with an IQR of 0.7-2.0 cm. For the other configurations, the radii of the circles containing the point spreads were larger (Jackknife 4, median = 2.1 cm, IQR = 0.7-9.3 cm; Snippets 4, median = 6.8, IQR = 3.4-12.8 cm; Snippets 8, median = 5.8 cm, IQR = 3.3-10.1). After log-transforming each of the data sets to more closely approximate a normal distribution, a 2-way ANOVA was conducted with number of microphones and localization approach as factors. There were significant main effects of both localization method (F_(1,13504) = 4535.8, p < 10⁻²⁰; Snippets: mean = 8.1 cm, std = 6.6 cm; Jackknife: mean = 1.3 cm, std = 5.0 cm), and number of microphones (F_(1,13504) = 394.7, p < 10⁻²⁰; four microphones: mean = 6.8 cm, std = 7.1 cm; eight microphones: mean = 4.4 cm, std = 5.3 cm), as well as a significant interaction (F_(1,13504) = 195.1, p < 10⁻¹⁰). Following Benjamini-Hochberg post-hoc corrections for multiple comparisons, all pairwise comparisons remained significant (all p < 0.002), with Jackknife 8 having the smallest point spread and Snippets 4 having the largest.

After determining that Jackknife 8 had the smallest point estimate spread, we next quantified the spread of the density function. To do this, we computed the probability density function across the floor of the arena for each vocal signal in our data sets, and determined the total area of space where the function exceeded the threshold value of 1 m⁻². Based on the results of our simulation, we would expect the density spread for Jackknife 8 to be less than that of the other configurations. This would indicate that, even though this system had the highest resolution, signals falling close to the nose of the animal would be less likely to exceed the density threshold, and these signals would therefore be less likely to be assigned. The results matched our prediction (Figure 6D), with the area of space exceeding the density threshold in the Jackknife 8 condition being less than that of the other three configurations (Jackknife 8: median = 8.5 cm², IQR = 1.1-27.8 cm²; Snippets 8: median = 211.2 cm², IQR = 97.7-396.6 cm²; Jackknife 4: median = 127.4 cm², IQR = 29.0-277.2 cm²; Snippets 4: median = 242.3 cm², IQR = 110.3-532.5 cm²). The data were nonparametric, and thus we normalized with a log transformation to conduct a 2-way ANOVA. The ANOVA showed significant main effects of both localization method (F_(1,13088) = 2705.8, p < 10⁻²⁰; Jackknife: mean = 233.7 cm², std = 568.4 cm²; Snippets: mean = 349.6 cm², std = 412.7 cm²) and number of microphones (F_(1,13088) = 1876.1, p < 10⁻²⁰; four microphones: mean = 487.6 cm², std = 707.0 cm²; eight microphones: mean = 155.4 cm², std = 279.1 cm²), as well as a significant interaction (F_(1,13088) = 1320.3, p < 10⁻²⁰). Following post-hoc corrections for multiple comparisons, all pairwise comparisons remained significant (all p < 10⁻⁴), with Jackknife 8 having the smallest density spread and Snippets 4 having the largest. These results verify the predictions of the point spread simulations and suggest that the reduced point spread in the Jackknife 8 method is the reason for the disproportionate number of unassigned signals falling in close proximity to the nose of the animal.

Removing Density

Subsequently, we removed the density threshold from our analyses and assessed the assignment capabilities of each configuration. For these analyses, each system had a without-density condition (No Density) where the density threshold was not implemented, and a with-density condition (Density) where the density threshold was implemented. As observed in signal assignment with a density threshold, the Even configuration outperformed the Odd configuration (Supplemental Figure 8), and therefore all reported four-microphone data comes from the even configuration. After removing the density threshold, the number of signals assigned in all four configurations increased (Figure 7). For Jackknife 8, the number of signals assigned per experiment increased from a median of 67 with the threshold (IQR = 42-120) to a median of 101 without the threshold (IQR = 63-180). The slope of the regression line fitting the number of signals assigned per experiment with or without a density threshold for Jackknife 8 was also significantly different than the slope of the identity line (slope = 1.4, t score = 15.2, p < 10⁻¹⁹), indicating that this increase in assignment was consistent across data sets. There was a median of 37 signals assigned per experiment using Jackknife 4 Density (IQR = 21-64), and 53 signals per experiment using Jackknife 4 No Density (IQR = 35-85). The slope of the regression between these two conditions was significantly larger than that of the identity line (slope = 1.4, t score = 16.1, p < 10⁻³⁰). For the Snippets approach, using either 4 or 8 channels, the number of signals assigned increased after removing the density threshold (Snippets 4 Density, median = 24, IQR = 15-48; Snippets 4 No Density, median = 28, IQR = 17-53; Snippets 8 Density, median = 49, IQR = 32-88; Snippets 8 No Density, median = 57, IQR = 38-98). This effect was replicated when comparing the with-density vs without-density regression lines, as both the Snippets 4 and Snippets 8 regressions had slopes that were significantly different than the identity line (Snippets 4, slope = 1.2, t score = 3.4, p < 10⁻⁵; Snippets 8, slope = 1.1, t score = 15.9, p < 10⁻¹⁹).

Figure 7. Removing density threshold increases the number of signals assigned to mice.

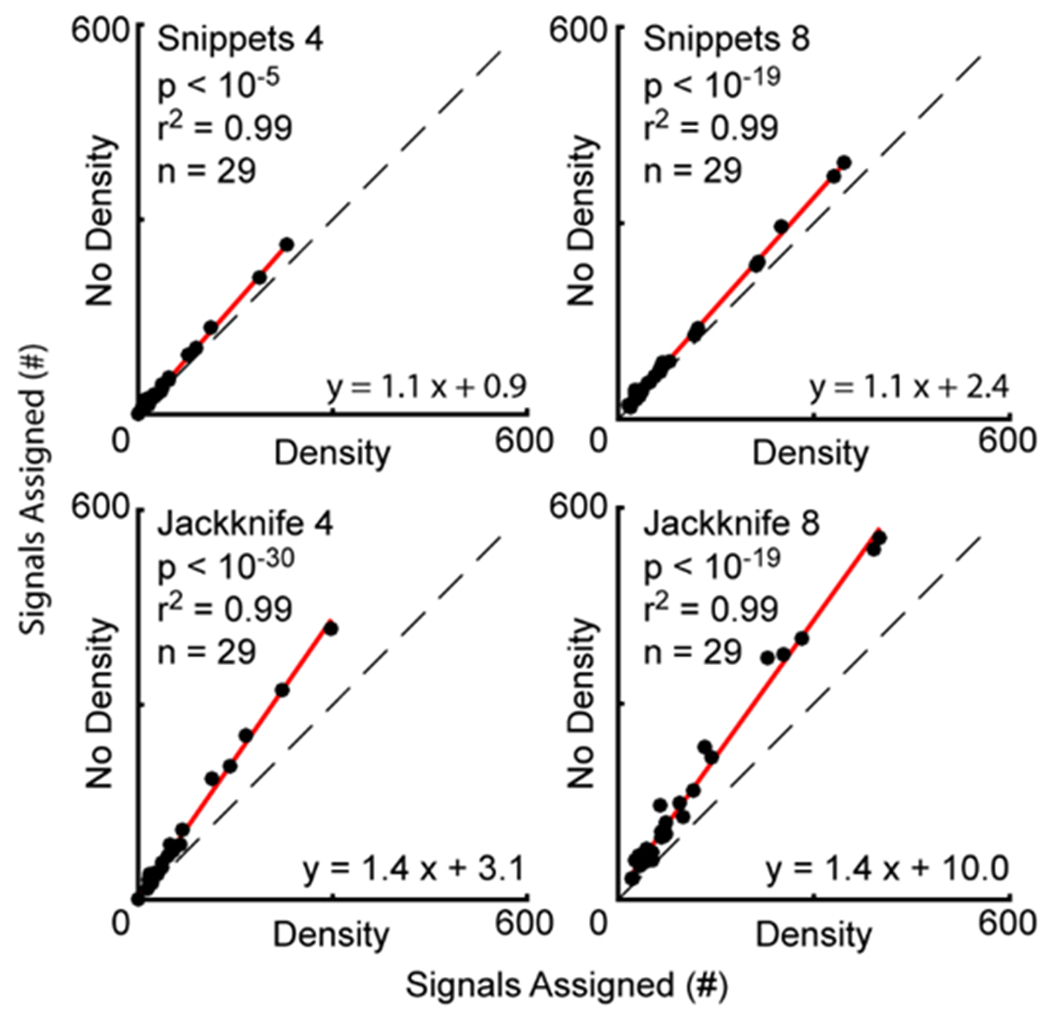
General linear mixed-effects models were used to calculate the regressions (red lines) comparing the number of vocal signals assigned using different system configurations. Identity lines shown with dashed black lines. Each point is the number of signals assigned in a recording session (n = 29). The equations are that of the regression lines through the data, with the fit of the lines indicated by the r² values, and the p-values denoting the comparisons between the slopes of the regression and identity lines.

To directly compare the ability of the systems to assign signals with- versus without-density cutoffs, we ran a 3-way ANOVA with the number of microphones, localization method, and presence of density threshold as factors (Figure 8A). There were main effects of number of microphones (F_(1,213) = 209.6, p < 10⁻¹⁰; four microphones; mean = 48.4%, std = 18.0%; eight microphones; mean = 63.6%, std = 17.7%), localization method (F_(1,213) = 561.1, p<10⁻¹⁰; Snippets: mean = 43.9%, std = 11.9%; Jackknife: mean = 68.8%, std = 17.3%), and density (F_(1,213) = 265.8, p<10⁻¹⁰; Density: mean = 47.7%, std = 12.8%; No Density: mean = 65.0%, std = 21.0%). There were also two significant interaction effects, number of microphones by density (F_(1,213) = 5.3, p = 0.02), and analysis type by density (F_(1,213) = 91.1, p<10⁻¹⁰). Post-hoc corrections for multiple comparisons showed significant differences between all pairwise comparisons (all p < 0.002) excluding Snippets 4 Density vs Snippets 4 No Density, Snippets 8 No density vs Jackknife 8 Density, and Snippets 8 Density vs Jackknife 4 Density (all p values > 0.046; significance determined by Benjamini-Hochberg post-hoc correction). Jackknife 8 No Density had a significantly higher proportion of assigned signals than all other configurations (mean = 90.8%, std = 3.3%), followed by Jackknife 4 No Density (mean = 73.2%, std = 9.3%). Notably, removal of the density threshold from either Jackknife configuration led to a significant increase in the proportion of signals assigned (Jackknife 8 with density: mean = 60.3%, std = 8.3%; Jackknife 4 with density: mean = 49.5%, std = 8.6%). Taken together, these results indicate that removal of the density threshold leads to a significant increase in the proportion of signals assigned in both Jackknife configurations, as well as the Snippets 8 configuration, providing further evidence that the density threshold is an unnecessary component with these novel system configurations.

Figure 8. Jackknife approach with 8 microphones and no density threshold accurately assigns more vocal signals to mice compared to other approaches.

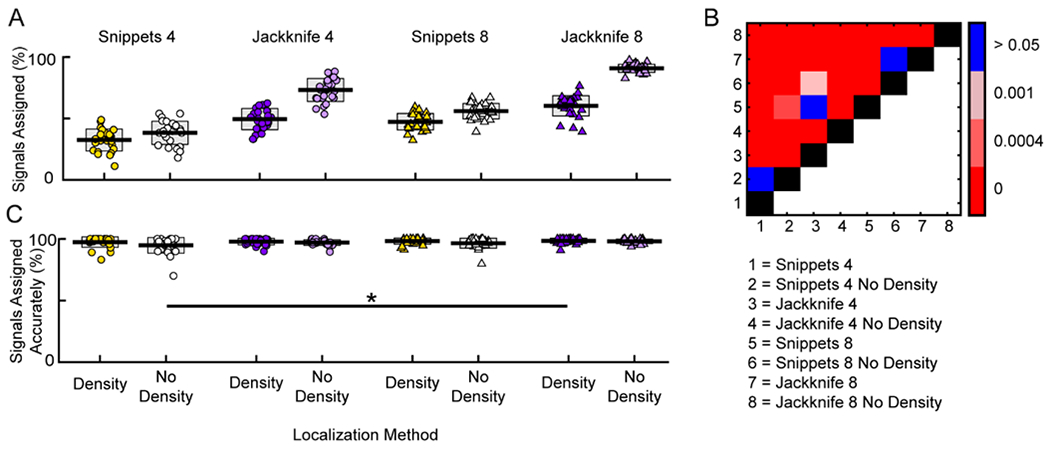
A, Percentage of signals assigned in each data set for the different system configurations. Localization method and number of microphones is indicated above the graph. Presence of a density threshold is indicated beneath C. B, Heat map of significance for all pairwise comparisons in A. Red hues indicate significant pairwise differences, while blue indicates a non-significant difference. Black represents the identity line and white indicates that no comparisons were made. Numbers corresponding to configuration are indicated below the plot. C, Percentage of assigned signals attributed to the correct mouse in each data set for the different approaches. One significant difference was detected (Snippets 4 No Density vs Jackknife 8 with density). A,C, Each point is the percentage from a single data set. Central line is the mean. Gray boxes indicate standard deviation. * p < 0.05

Because the density threshold was originally implemented to prevent poorly localized signals from being assigned to incorrect mice, we examined the accuracy of assignment across configurations following the removal of the threshold. This was achieved by analyzing the percentage of assigned signals attributed to the correct animal. A 3-way ANOVA was conducted with the number of microphones, localization method, and presence of a density threshold as factors (Figure 8C). There were main effects of number of microphones (F_(1,213) = 4.9, p < 0.05; four microphones: mean = 96.7%, std = 4.3%; eight microphones: mean = 97.8%, std = 2.8%), localization method (F_(1,213) = 5.5, p < 0.05; Snippets: mean = 96.7%, std = 4.6%; Jackknife: mean = 97.8%, std = 2.2%), and density (F_(1,213) = 8.2, p < 0.01; Density: mean = 98.0%, std = 2.9%; No Density: mean = 96.6%, std = 4.1%). No significant interactions were observed (all p-values > 0.1). Post-hoc corrections for multiple comparisons showed that the percentage of correctly assigned signals for Snippets 4 No Density and Jackknife 8 Density were significantly different (p < 10⁻³), but there were no significant differences between with-density versus without-density when looking at a single localization method. In conjunction with the previous analysis, these results indicate that removal of the density clause significantly increased the proportion of signals that were assigned without significantly altering the accuracy of assignment.

Although mice emit ultrasonic vocalizations when animals are far apart (Mun et al., 2015; Portfors and Perkel, 2014; Sales, 1972) the majority of social communication occurs when mice are in close proximity. To control for this, we ran a more stringent simulation to generate virtual mice. This simulation randomly generated a single virtual mouse at the time of each vocal signal, with the nose of the virtual mouse confined to within 10 cm of the real mouse’s nose. This allowed us to assess the ability of our system to assign signals with another mouse in close proximity. More importantly, this control analysis overestimated the error rate and provided a lower bound for the accuracy. All four configurations without the density threshold were examined using the more stringent simulation. Jackknife 8 assigned 3898 vocal signals to the correct mouse, with an average of 83 percent of signals assigned per experiment (range = 73.0 to 89.6%, std = 3.6%) (Supplemental Figure 9A). Jackknife 4 assigned a total of 1919 vocalizations with an average of 59 percent of signals per experiment (range = 39.5 to 73.7%, std = 9.3%). Snippets 8 assigned a total of 1675 signals (mean per experiment = 32.6%, std = 6.2%), and Snippets 4 assigned a total of 773 signals (mean per experiment = 22.7%, std = 5.4%). A 2-way ANOVA comparing the proportion of signals assigned with this method showed significant effects of both number of microphones (F_(1,105) = 186.1, p < 10⁻²⁰), and analysis method (F_(1,105) = 1257.1, p<10⁻⁵⁰), as well as a significant interaction (F_(1,105) = 30.1, p<10⁻⁵). As with all previous analyses, Jackknife 8 continued to assign a larger proportion of signals than the other three configurations, even in this more restricted condition. The possibility exists that our new system configuration is less accurate than the other configurations when mice are in close proximity. Thus, a 2-way ANOVA (localization method by number of microphones) was conducted to assess assignment accuracy (Supplemental Figure 9B). The analysis showed that there were no differences between configurations, with no main effect of localization method (F_(1,108) = 2.5, p > 0.1; Snippets: mean = 90.6, std = 6.7, Jackknife: mean = 92.4, std = 4.4), or number of microphones (F_(1,108) = 0.83, p > 0.3; 8 mics: mean = 91.9%, std = 4.9%; 4 mics: mean = 90.9%, std = 6.6%), and no interaction (F_(1,108) = 0.61, p = 0.44). This finding, in conjunction with the finding that Jackknife 8 assigned a larger proportion of signals in all conditions, indicates that the Jackknife method of sound source localization, regardless of the number of microphones and the distance between mice, outperforms the Snippets method.

The previous control analysis accounted for the distance between two mice when vocal signals are typically emitted; however, it assumes that the other mouse’s behavior is unrelated to the behavior of the real mouse. To account for any correlated behavior between two mice, the position of the random mouse relative to the real mouse was determined using actual mouse social interaction data. The distance between mice was obtained from a recording when four mice were interacting. During this experiment, two males and two females interacted within the behavioral arena for 5 hours. As with the single mouse data, we continually recorded audio and video data. After recording, the positions of the mice were tracked and the x- and y-coordinates of each of the four mice were obtained for every video frame. We used this information to compute the relative distance between male 1 (who is akin to the single mouse in the 29 data sets used to test the configurations) and the next closest animal for every frame of video. To determine the locations of the random mouse that more accurately simulated the actual social behavior of mice, we randomly selected a distance from the distribution of distances between male 1 and the closest mouse. This information was then used to evaluate the ability of the Jackknife 8 No Density configuration to correctly assign vocal signals (Supplemental Figure 10). Jackknife 8 No Density accurately assigned 98.5 percent of the total assigned signals (IQR = 97.06-99.29%). Therefore, this analysis confirmed that the system was incredibly accurate in assigning signals even in conditions that mirror the social behavior of freely interacting mice.

Although the virtual mouse simulations provide a good estimate to assess how well the system works because each vocal signal can be attributed to a single animal, the simulations fail to account for how sound propagation may be impacted by the presence of another mouse. For example, if a second mouse is present, then the fur of the mouse receiving the signal may absorb or reflect vocal signals emitted by the vocalizing animal. To account for this possibility, we recorded vocal signals emitted by a male mouse in the presence of an anesthetized female mouse. Two recordings were conducted and each recording lasted for 5 minutes. Similar to the virtual mouse simulation, all vocal signals can be attributed to a single mouse (Whitney et al., 1973). The results of this analysis revealed that a total of 141 signals were detected and 128 of these signals were assigned (90.78%). Of the signals that were assigned, 125 were accurately assigned to the male mouse (97.67%). This control experiment indicates that our system is able to accurately determine the source of vocal signals when two animals are present.

Assigning Vocal Signals as Mice Freely Interact

Here, we demonstrate the capacities of the Jackknife 8 No Density configuration in a representative experiment. As described previously, four mice were allowed to freely interact for five hours. A total of 12335 vocal signals were detected, of which 12274 were localized (99.51%). There were 8042 signals assigned to the mice (65.20%). Figure 9 shows an example of a vocal signal that was assigned to one of the females when she was in close proximity to the other female. During the 5-hour experiment, female 1 emitted 9.96% of the assigned vocalizations, whereas female 2 emitted 6.38% of the vocalizations. Male 1 produced 17.02% and male 2 emitted 66.64%. There were significant differences in the number of signals emitted by each of the mice (x² = 10594, p < 10⁻¹⁰). These results provide a proof of concept that the system is capable of assigning vocal signals to individual mice as they socially interact.

Figure 9. Example showing a vocal signal assigned to a female mouse as multiple mice freely interacted.

A, Image shows the location of four mice in the recording arena as well as the position of the microphones (Mic 1 – 8). Female mice are indicated with orange and gold. Male mice are shown with blue and cyan. B, Spectrograms show a vocal signal detected on multiple channels in the microphone array when the mice were at the location shown in panel A. Numbers on the spectrograms correspond to the microphones shown in A. Using Jackknife 8 No Density, we determined that the vocal signal was produced by the female outline in gold.

CONCLUDING COMMENTS

The majority of studies examining the vocal behavior of mice utilize a single microphone. This approach has been beneficial for understanding general contexts needed to elicit vocalizations (Chabout et al., 2015; Chabout et al., 2012; D’Amato and Moles, 2001; Ehret, 2005; Hanson and Hurley, 2012; Moles et al., 2007; Mun et al., 2015; Panksepp et al., 2007; Williams et al., 2008) and has generated excitement for using mice as a system to study neurological disorders associated with communication deficits (Bader et al., 2011; Peca et al., 2011; Penagarikano et al., 2011; Penagarikano et al., 2015). However, in most cases, mice emit ultrasonic vocalizations during social interactions (Sales, 1972), although it has been reported that mice also vocalize when they are alone (Mun et al., 2015). Because mice lack prominent visual features to help identify potential vocalizers (Chabout et al., 2012), one of the main experimental challenges is to identify which animal produced a particular vocalization when interacting in groups. Previous studies have used devocalized males as a control to show that female mice are not vocally active when interacting with a male (Sugimoto et al., 2011; Warburton et al., 1989). However, female mice possess the biological machinery necessary for producing vocalizations (Mahrt et al., 2016; Moles et al., 2007; Moles and D’Amato, 2000). Recently, two studies have shown that female mice vocalize during interactions with males and both findings used multiple microphones to attribute vocalizations to specific mice (Heckman et al., 2017; Neunuebel et al., 2015). This technological advance has allowed experimenters to triangulate where the sound was emitted and assign the vocalization to a specific mouse, thereby opening up the possibility of tracking the vocal behavior of individual mice as they socially interact.

In the present study, we further advance this technology by increasing the number of microphones as well as refining the approach for localizing and assigning vocal signals to individual mice. The improvements we have incorporated into the new approach allow localization of mouse vocalizations with unprecedented precision. We anticipate that this optimized system will enable efficient and reliable assessment of the function of vocal communication in murine models of social behavior.

METHODS

Subjects

Male mice (n = 19; age: 2-5 months) of varying genetic strains (C57BL6/J [n=2], B6.Cast-Cdh23^Ahl+/Kjn Homo [n = 7], Cacna1c^tm2ltl/J WT [n=8], Cacna1c^tm2ltl/J Het [n = 1], B6.129S7-Shank3^tm1Yhj/J Het [n=1]), were used to test the precision and accuracy of the microphone array system. C57BL/6J mice are the most widely used inbred strain from Jackson Laboratory. B6.Cast-Cdh23^Ahl+/Kjn homozygous mice are a congenic strain that carries the wild type allele of Cdh23 (formerly Ahl) producing C57BL/6 mice that are not susceptible to age related hearing loss (Johnson et al., 1997). Cacna1c^tm2ltl/J heterozygous mice have a TS2-neo mutation that is associated with severe Timothy Syndrome (TS2) and an inverted neomycin resistance cassette, all inserted at the end of exon 8 of the CaV1.2 L-type calcium channel locus (Bader et al., 2011). Cacna1c^tm2ltl/J wild-type are the wild-type littermates of Cacna1c^tm2ltl/J Het mice. B6.129S7-Shank3^tm1Yhj/J heterozygous mice have a neo cassette replacing the PDZ domain (exons 13-16) of the Shank3 gene, resulting altered expression of the Shank3b isoform (Peca et al., 2011). Mice were bred and raised in a vivarium housed in the Life Science Research Facility at the University of Delaware. Founding members of all breeding colonies were purchased from Jackson Laboratory (Jackson Laboratory; Bar Harbor, ME; stock numbers: 000664, 019547, 002756, 017688). Test subjects were weaned at three weeks and tagged with a light-activated, microtransponder (PharmaSeq, Inc.; Monmouth Jct, NJ; p-Chip injector) that was implanted into their tail. Breeding status at the time of experiment was variable; some males were members of a breeding pair (n = 3), while others were either isolate housed (n = 2) or housed with multiple other males (max four males per cage; n = 14). Ten of the mice had prior experience with females, while nine were inexperienced. Mice were maintained on a 12/12 dark-light cycle with ad libitum access to food and water. Mice were housed in individually ventilated cages containing ALPHA -dri bedding (Animal Specialties and Provisions, LLC; Watertown, TN; ALPHA-dri).

For the four mouse data used to account for actual distances between animals and used as a proof of concept, all four animals (two males and two females) were homozygous B6.Cast-Cdh23^Ahl+/Kjn mice. These animals were 15-16 weeks of age. All four mice were isolate housed for the two weeks preceding their behavioral recordings. At least two days before the recording, the fur of the animals was painted with a harmless hair bleach such that our tracking program could distinguish the animals from each other based upon back pattern (Ohayon et al., 2013). The following day, these animals were exposed to a single animal of the opposite sex for a maximum of 10 minutes (the interaction was observed, and terminated if copulation was attempted). Otherwise, these animals were cared for in the same manner as outlined in the previous paragraph.

For recordings involving an anesthetized female, the female was C57BL6/J WT (n = 1; age = 11 weeks), and the males were homozygous B6.Cast-Cdh23^Ahl+/Kjn mice (n = 2; age = 12 weeks). Two weeks prior to recording, both males were painted with harmless hair bleach and exposed to the female prior to her being anesthetized. Care for these animals was otherwise identical to all other animals.

Behavioral Experiments

A total of 89 experiments were conducted by placing a single male mouse into the behavioral arena for 10 minutes. For an experiment to be included in our analyses, a minimum of 25 vocal signals needed to be detected over the 10-minute recording session. If fewer than 25 vocal signals were detected, the program for determining the sound source was not run. Of the 89 recording sessions, only 29 sessions had over 25 detected vocal signals, and thus only these 29 recordings were used to evaluate the different system configurations.

Data used to evaluate the different system configurations was collected in conjunction with multiple experiments. Therefore, single mouse recordings were preceded by different events. For one of the data sets, the 10-minute recording was preceded by a 1-hour pairing between a male and a female. For three of the data sets, the 10-minute recording followed a 5-hour session in which four animals, two males and two females, were allowed to freely interact. In all other cases, in an attempt to elicit vocal activity, female scent cues were added to the cage prior to the introduction of the male. This was done by either allowing a female to explore the environment for 3-5 minutes directly preceding the recording session, introducing freshly soiled bedding from the cage of a female, or combining female exploration and freshly soiled bedding. The number of recordings in a single day varied (4-10), but males were tested only once within a span of 24 hours.

A single experiment was run in which four animals were free to socially interact (see Removing Density). The animals (two males and two females) were age-matched, placed into our behavioral arena, and allowed to freely interact for a total of 5 hours.

To test the system when two mice were present, an anesthetized female was paired with an awake male. This was repeated with two different males. The female selected for the experiment was in estrus as determined using non-invasive vaginal lavage (Cora et al., 2015). Prior to anesthetizing the female, she interacted with each male for three minutes. Anesthesia was induced with 2.5% isoflurane in oxygen and maintained with a cocktail of ketamine (100 mg/kg) and xylazine (5 mg/kg). Once it was confirmed that the female was deeply anesthetized and unresponsive, she was placed into the center of the recording arena. Next, a single male was placed into the arena. Audio and video data were recorded for five minutes. After removing the first male, the second male was placed into the arena and an additional five-minute recording session was conducted. After the second male was removed, the female was placed beneath a heat lamp and allowed to recover from anesthesia. Motr was unable to track the anesthetized, stationary female, therefore, the position of the female was manually tracked.

The University of Delaware Animal Care and Use Committee approved all experimental protocols.

Recordings

For each experiment, audio and video data were simultaneously recorded in an anechoic chamber. Audio data were recorded via an 8-channel microphone array. Each microphone detected audio data (Avisoft-Bioacoustics; Glienicke, Germany; CM16/CMPA40-5V) that was sampled at 250,000 Hz (National Instruments; Austin, TX; PXIe-1073, PXIe-6356, BNC-2110), and low-pass filtered (200 kHz; Krohn-Hite, Brockton, MA; Model 3384). Video data was captured with a camera (FLIR; Richmond, BC, Canada; GS3-U3-41C6M-C) externally triggered at 30 Hz using a trigger pulse sent from the PXIe-6356 card. The trigger pulse was simultaneously sent to the National Instruments equipment and the camera through a BNC splitter; thus, the pulse was time stamped at the sampling rate of the audio recording. BIAS software was used to record each video and the program was developed by Kristin Branson, Alice Robie, Michael Reiser, and Will Dickson (https://bitbucket.org/iorodeo/bias/downloads/). Software, custom-written in Matlab (Mathworks; Natick, MA; version 2014b), was used to synchronize and control all recording devices. Audio and video data were concurrently stored on a PC (Hewlett-Packard; Palo Alto, CA; Z620).

Because the position of each of the mice in each frame of the video is used to assign vocal signals to an animal, the resolution of the system is constrained by the frame rate. Here, video images were capture at 30 frames per second (i.e., 1 frame every 33.3 ms). If mice were to move rapidly, then errors in assignment may increase. To overcome any errors caused by a slower video sampling rate, one could increase the sampling rate. While a greater frame rate would decrease the distance an animal could move within a single frame of video, higher sampling rates would lead to larger video files, and therefore require more time to process the data. Fortunately, when examining the speed each mouse traveled in each of the described experiments, no mouse exceeded 0.8 m/s, which translates to a maximum of 2.67 centimeters traveled between frames (Supplemental Figure 11A). We found that there was not a strong correlation between speed and distance error (Supplemental Figure 11B). Similar results were observed when multiple mice were interacting (Supplemental Figure 11C,D). Consequently, sampling at 30 frames per second allotted an acceptable trade-off between processing time and accuracy of position.

Recordings were conducted in a mesh-walled (McMaster-Carr; Robbinsville, NJ; 9318T25) cage. Originally, the recording cage was a cylinder (height of 91.4 cm and a diameter of 68.6 cm). The mesh walls of the cylinder were affixed to the top and bottom of a metal frame by securing the mesh between pairs of plastic rings surrounding the arena, one pair at both the top and the bottom. The plastic rings were screwed into a metal frame. We found that, with longer interactions (five hours or greater), the mice were able to escape from the enclosure. Thus, after 3 recordings, we changed the shape of the recording cage to a cuboid with a frame (width = 76.2 cm, length = 76.2 cm, height = 60.96 cm) made of extruded aluminum (8020, Inc.; Columbia City, IN). Both the cylindrical and cuboid cages were surrounded by Sonex foam (Pinta Acoustic, Inc.; Minneapolis, MN; VLW-35). With the Jackknife 8 method, there were no significant differences between the two shapes in terms of the proportion of signal assigned (mean cuboid rig = 90.75%, std = 3.23%; mean cylindrical rig = 91.49%, std = 5.03%; t(27) = −0.36; p = 0.72), or in the proportion of assigned signals that were assigned correctly (mean cuboid rig = 98.11%, std = 1.79%, mean cylindrical rig = 97.33%, std = 1. 71%; t(27) = −0.86, p = 0.40). Therefore, analyses were conducted by combining the data collected in the cylindrical and cuboid cages.

Because all recordings were performed in the dark, infrared lights (GANZ; Cary, NC; IR-LT30) positioned above the cage were used to illuminate the mice instead of incandescent light. Each microphone was surrounded by a ring of LEDs that, when active, was visible through the cage walls. Microphone centroids were 10.8 cm above the floor of the arena. For the cylindrical cage, microphones were evenly spaced along the periphery of the wall of the arena. For the cuboid cage, microphones were evenly spaced on each wall of the arena such that their centers were separated by 38.1 cm and were 19.05 cm from the closest corner. To determine microphone positions within each recording session, LEDs were turned on during a 15-second recording session prior to the start of any experiments and turned off for all subsequent recordings. During the pre-experimental recording session, a ruler was placed in the cage to convert camera pixels to meters. To increase the color contrast between the floor of the cage and the mice, the arena was filled to a depth of approximately 0.5 inches with ALPHA-dri bedding.

All recordings were preprocessed on a computer cluster housed at the University of Delaware. The data analysis pipeline consisted of tracking the animals, extracting vocal signals, and assigning vocal signals to mice. These processes are described below. For any researchers that are interested in adopting these methods for videos of long duration, we would strongly recommend looking into similar resources.

Tracking

Automatic tracking of the mice was conducted using the Motr tracking program (Motr; Ohayon et al. (2013); http://motr.janelia.org). For each video frame, Motr fit an ellipse around the recorded mouse, and output the x and y positions of the centroid, as well as the major axis, minor axis, and heading direction. For every 5000 frames of video, it took approximately 2 hours to processes using a single computer processor. Tracking output was visually confirmed by viewing the tracking video in Matlab.

Generating Virtual Mice

When assessing the capacitates of the different system configurations, all recordings were completed with a single male mouse vocalizing in response to either female pheromonal cues or an anesthetized female. In both conditions, vocal signals could be produced by only one animal. To assess the ability of the system when recording from multiple animals, a group environment was simulated using three methods and applied to data collected when a single male was present. The first method, which is the method used for all primary analyses, created three virtual mice in each frame associated with when a vocal signal was emitted. To do this, three randomly selected pairs of x- and y-coordinates, each confined within the cage boundaries, were chosen for each frame. Each of these points represented the nose of a virtual mouse. This gave the system four possible sources to which to attribute the vocal signal; the real source and the three randomized sources. This method allowed us to assess the accuracy of signal assignment. The second method, which is referenced in Supplemental Figure 9, included only a single virtual mouse, but the nose of this mouse was within 10 cm of the nose of the real animal. This method mimicked the capabilities of the system with another mouse in close proximity. The third method, which is referenced in Supplemental Figure 10, used a single virtual mouse, but the position of the virtual mouse was determined based on actual mouse social interactions. Four mice, 2 males and 2 females, were allowed to interact for 5 hours. For every video frame, the distance between the mouse identified as male 1 and the closest mouse to male 1 was calculated. This conditional distribution was used to determine the position of the fake mouse. The third approach tested the capabilities of the system in a condition that more closely resembles the natural behavior of groups of freely interacting mice. Despite the more conservative nature of the second and third approach for generating a virtual mouse, all approaches led to the same conclusions.

Audio Segmentation

Automatic extraction of vocal signals from multiple channels of audio recordings was conducted via multi-taper spectral analysis (Seagraves et al., 2016). When analyses focused on quantifying an 8-channel system, 8 channels were used to extract vocal signals. If an analysis was run to quantify a 4-channel system, four of the total eight channels were used to extract vocal signals. Regardless of the number of channels, the following steps were automatically applied: audio data were bandpass filtered between 30 and 110 kHz (thus removing all audible or low frequency sounds), and then segments overlapping in time were Fourier transformed using multiple discrete prolate spheroidal sequences as windowing functions (K = 5, NW = 3). An F-test (Percival and Walden, 1993) was used to gauge whether each time-frequency point exceeded the noise threshold (p < 0.05). This procedure was run on multiple segment lengths for each microphone channel to capture a range of spectral and temporal scales (NFFTs = 64, 128, 256). Data were combined into a single spectrogram and convolved with a square box (11 pixels in frequency by 15 in time) to fill in small gaps before the location of continuous regions, with a minimum of 1500 pixels, were assessed. Due to the fact that discontinuous signals could be produced by different animals, each non-continuous signal was extracted separately as long as there were no harmonics present. Harmonic signals were defined as overlapping signals in which the duration of overlap exceeded 90 percent of the duration of the shortest signal, and the frequencies between individual signals that overlapped in time were integer multiples of each other (Neunuebel et al., 2015). When harmonics were present, information pertaining to the lowest fundamental frequency was used to localize the sound. For a 10-minute recording session, the total processing time for the audio data on all eight channels was less than 20 minutes. After automatically extracting vocal signals, data was subsequently viewed with a custom written Matlab program to manually confirm that the signals were consistent with the features of vocal signals.

Sound Source Localization

The first method of sound source localization (Snippets) was detailed in Neunuebel et al. (2015). Briefly, signals were broken into discrete pieces, called snippets, defined by 5 ms in duration and a 2-kHz change in frequency. The source location of each individual snippet was computed (termed point estimate). Once the source location of all snippets had been estimated, outliers were removed. The x- and y-coordinates of all remaining point estimates were averaged to determine an overall estimate of the source position. The probability that the signal came from each individual location on the cage floor was calculated based upon a grid-sampling technique outlined in Neunuebel et al. (2015). If any more than one point fell within a single square of the grid covering the floor (measuring 0.25 mm x 0.25 mm), those points were quantified as a single unique point. The system required three unique point estimates to localize the signal. If there was too much overlap in the point estimates, the system was unable to localize the signal. The inability to assign signals due to point estimates being too close together was not a common issue.

Assuming the signal had at least three unique points, their locations were used to calculate a probability density function over the cage. Each animal in the arena was assigned a density based upon the value of this function at their nose. Nose positions were determined with Motr. Densities were used to calculate a mouse probability index MPI for every mouse (formula shown in RESULTS). Signals were only assigned to an individual if the MPI exceeded 0.95, indicating a 95% certainty that the signal originated from no other animal in the arena.

The second method (Jackknife) instead relied upon a jackknife resampling method to estimate sound source (Figure 3). This technique sequentially ignored the signal from a single microphone in the array, leading to a position estimate based upon the remaining microphones. Each microphone in the array was excluded a single time, causing the number of point estimates to equal the number of microphones. Once all estimates were determined, an overall estimate of source position was calculated in the same manner as outlined previously, except without removing outliers. The original system developed by Neunuebel et al. (2015) utilized a density threshold before assigning a signal to an individual animal. Density is the probability density at that position on the cage floor. The cutoff for this measure was set at 1 m⁻² to prevent poorly localized signals from being assigned to mice that were not near the estimated source location.

The software used to determine the sound source localization and assign vocal signals to mice is setup to process data in parallel, which means that multiple jobs are run simultaneously. The number of vocal signals processed within a single job is customizable. We optimized the program to run on a computer cluster such that each job contained 30 vocal signals. With this configuration, it required approximately 3 hours to run a job on a single processor. For experiments of longer duration, we strongly advise processing the data using a high-performance computer cluster. However, a desktop computer can be used to process the data.

To check the localization, the output of the sound source localization programs was loaded into a custom written Matlab program, which individually plotted the arena at the frame of emission of a single vocal signal, the location of the mice, each point estimate, and the overall estimate of the source position.

All Matlab code is available upon request.

Analyses

To directly compare the capacity of the system with each of the different configurations, the same data sets were processed with both the Jackknife and Snippets sound source localization approaches (Table 2). Therefore, each of the 29 data points per analysis type represents a single recording session, but the 29 sessions in, for example, the Snippets 4 analysis are the same data sets as those in Jackknife 8, just analyzed with a different system configuration.

Table 2:

System configurations. Chart of the features of each of the different configurations discussed in the main text. Alterations were made to the localization method (Snippets or Jackknife), the number of microphones (4 or 8), and whether or not the density threshold was implemented.

Analysis Name	Localization Method	Number of Microphones	Density Threshold
Snippets 4	Snippets	4	Yes
Snippets 8	Snippets	8	Yes
Jackknife 4	Jackknife	4	Yes
Jackknife 8	Jackknife	8	Yes
Snippets 4 No Density	Snippets	4	No
Snippets 8 No Density	Snippets	8	No
Jackknife 4 No Density	Jackknife	4	No
Jackknife 8 No Density	Jackknife	8	No

Statistics

For all regressions, a general linear mixed-effects model (GLME) was fitted to the data, with the input variable being the x-axis, and the output variable being the y-axis. The slope of the regression was compared to the identity line at y=x (GLME; response variable modeled with Normal distribution, identity link function; performed with the fitglme function in MATLAB 2016a, MathWorks, Natick, MA, USA).

For all group wise comparisons, an ANOVA was conducted, followed by a Tukey’s HSD for pairwise comparisons. If indicated, data were log transformed to more closely represent a normal distribution. To correct for multiple comparisons, all results were subsequently run through Benjamini-Hochberg post-hoc corrections.

To compare localized and unlocalized signals, a Mann-Whitney U-Test was conducted.

A chi-square was conducted to compare the number of signals localized in each bin around the nose of the mouse.

Skewness calculations were conducted in Matlab. This function contained a built-in correction for the data being a sample and not the entirety of the population.

To compare the proportion of signal assigned correctly with the cylindrical and cuboid configurations, a t-test was conducted.

Models

Maximum density (model):

To model the maximum density value within the arena as a function of number of point estimates, the number of points was systematically increased from 4 to 22 by increments of 2. Each individual point estimate was assigned a random x- and y-coordinate within the arena. Using the locations of these points, the probability density over the arena was calculated, using the same procedure as used with actual data, and the maximum density value was recorded. For each number of point estimates (4-22), this was repeated 1000 times.

Area above density threshold (model):

This simulation was created to assess the effect of point spread on the total area exceeding the density threshold. To do this, a circle of radius X (ranging from 1 cm to 10 cm) was drawn around the center of the behavioral arena, and eight point estimates were randomly chosen that fell within this circle. Using these eight points, the probability density over the cage was calculated, and the total area exceeding the density cutoff of 1 m⁻² was computed. This was repeated 1000 times per radius.

Radius of circle containing points (real data):

To determine the smallest circle that could contain all point estimates, the distance between each point estimate and the overall source estimate was calculated. The largest distance between a single point estimate and the overall source estimate was determined and used as the radius, since all other points were closer to the source estimate and would be enclosed by the circle. This was done with all localized signals in all four configurations.

Area above density threshold (real data):

Given the location of the actual point estimates, the total area of space exceeding the density threshold for each vocalization was calculated via the Matlab function convhull. This function finds the smallest polygon that can contain all points, in this case all point estimates, and outputs the area of that shape. This was applied to every localized signal for each of the four configurations.

HIGHLIGHTS.

• Novel approach for localizing vocal signals from freely moving mice robustly and repeatedly worked on an array with 8 microphones, but is applicable to arrays with 4 channels.

• Automated vocal signal detection algorithm facilitated the sound source localization process.

• Automated tracking software determined mouse position at the time of vocal signal emission and enabled probabilistic determination of which mouse vocalized.

• For assigned signals, the system correctly identified the vocalizing mouse over 98% of the time.