Recent Force Field Strategies for Intrinsically Disordered Proteins

Abstract

Intrinsically disordered proteins (IDPs) are widely distributed across eukaryotic cells, playing important roles in molecular recognition, molecular assembly, post-translational modification, and other biological processes. IDPs are also associated with many diseases such as cancers, cardiovascular diseases, and neurodegenerative diseases. Due to their structural flexibility, conventional experimental methods cannot reliably capture their heterogeneous structures. Molecular dynamics simulation becomes an important complementary tool to quantify IDP structures. This review covers recent force field strategies proposed for more accurate molecular dynamics simulations of IDPs. The strategies include adjusting dihedral parameters, adding grid-based energy correction map (CMAP) parameters, refining protein–water interactions, and others. Different force fields were found to perform well on specific observables of specific IDPs but also are limited in reproducing all available experimental observables consistently for all tested IDPs. We conclude the review with perspective areas for improvements for future force fields for IDPs.

Graphical Abstract

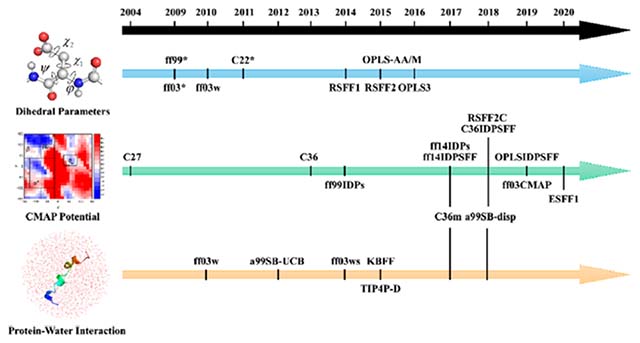
INTRODUCTION

Intrinsically disordered proteins (IDPs) are widely distributed across eukaryotic cells, comprising more than 40% of eukaryotic proteins.¹ Even if IDPs lack physiologically stable three-dimensional structures,² they are found to be integral parts of biological processes such as molecular recognition, molecular assembly, post-translational modification, and others.^3–5 IDPs are also mostly associated with many diseases such as cancers, cardiovascular diseases, and neurodegeneration diseases.^6–9 For example, disordered structures are found in the p53 tumor suppressor,⁹ the abnormally phosphorylated Tau protein,⁷ and the prion protein.¹⁰ The disease associated IDPs have a highly disordered central core region that often serves as a drug target site. The structural studies of these core disordered region are desirable for the discovery of tissue-specific drugs.¹¹

Due to the dynamical nature of IDPs, their structures cannot be determined easily as structured proteins by conventional experimental methods (i.e., X-ray,¹² nuclear magnetic resonance (NMR),¹³ small-angle X-ray scattering (SAXS),¹⁴ Forster resonance energy transfer (FRET),¹⁵ circular dichroism (CD), or single molecular spectroscopy¹⁶). These methodologies can only provide mean attributes and global structural signatures of IDPs for the entire assemblies. Furthermore, these methodologies cannot capture the diversified conformers of IDPs, a rather significant feature for IDPs. Therefore, additional methodologies are required to further quantify the IDP structures, so that further structural and dynamical properties can be carried out.

With recent advancements in hardware (i.e., graphic processing units) and software (i.e., replica exchange methods,¹⁷ high-performance molecular simulations have become routinely available to investigate the IDPs. These simulation methods can be used to calculate average observables in the same way as experimental methods. However, simulations methods do have limitations, with the most significant being the inconsistency in empirically developed physical models used for IDP simulations. The inconsistency can be attributed broadly into the issues in the force fields and the water models, which are both crucial for the accuracy of molecular simulations. For decades, researchers have tried hard to develop better force fields and water models to improve simulation results in folded proteins,^18–20 such as AMBER force fields,²¹ CHARMM force fields,²² OPLS-AA force fields,²³ and GROMOS force fields.²⁴ However, it is more difficult to simulate IDPs, due to their extreme flexibility leading to more broadly distributed conformational states and also more potential local energy traps.

Many force fields have also been tailored for simulation studies of IDPs, with two major rationales for improving their quality. The first is to adjust force field parameters that may lead to global optimization, which means that the performance of both folded and nonfolded protein (IDPs) simulations can be improved. The second is to adjust the propensities of secondary structures to make it possible to observe unfolded secondary structures widely seen in IDPs. In certain cases, these reparametrization efforts amount to retraining an existing base force field. Training data are primarily derived from experimental and/or quantum mechanical data. Different training sets certainly lead to force fields of different applicability. For example, if we are interested in rebalancing the propensities of IDP secondary structures, we may use short peptides as training models, such as (AAQAA)3 for α-helix,²⁵ GB1 hairpin,²⁶ and chigolin for β-hairpin.²⁷ In this article, we review some of the IDP force fields that have recently been developed and the strategies adopted for their reparametrization.

Adjusting Dihedral Parameters.

Dihedral angles can be divided into backbone dihedrals (i.e., ϕ and ψ) and side-chain dihedrals (i.e., χ₁ and χ₂). Currently, refinement of the backbone dihedral parameters is more common among recent IDP force fields. For several protein force fields, the most common issue in simulations of IDPs is overestimating populations of secondary structures, such as α-helix and β-sheet, which are often disordered in IDPs. Many protein force fields uniformly lead to overestimation.^28–31 One way to resolve the limitation is to incorporate dihedral data of coil fragments into the training sets used to train force fields. Indeed, reparameterization of dihedral parameters is often the first choice to improve a protein force field.

In general, the dihedral potential energy function will be described as eq 1.

$$E_{\text{dihedral}}=\sum _{\text{dihedrals}}{K}_{\chi }[1+\cos (n\chi -\sigma )]$$ (1)

The K_χ means the energetic parameter that determines barrier heights, χ is the value of the dihedral, n is the periodicity or multiplicity, and σ is the phase.

The backbone parameter is part of the whole dihedral parameter, which in current force fields, often described as eq 2.

$$E_{\text{dihedral}}=\sum _{\text{dihedrals}}\left[\frac{V_1}{2}(1+\cos \phi )+\frac{V_2}{2}(1-\cos 2\phi )+\frac{V_3}{2}(1+\cos 3\phi )+\frac{V_4}{2}(1-\cos 4\phi )\right]$$ (2)

V₁–V₄ have similar meanings as K_χ, and φ represents the backbone dihedral (i.e., ϕ and ψ).

For IDP force fields, this approach has been used in ff03* and ff99SB*,³² based on the ff03¹⁸ and ff99SB,¹⁹ respectively. Both of the force fields use Lifson–Roig helix–coil theory³³ to calculate the helix–coil parameters. These two force fields can somehow fit in with NMR experiments for folded proteins and short peptides. However, the helical contents are overestimated by ff03* with respect to that of ff03, while the helical contents of ff99SB* are underestimated with respect to that of ff99SB. Note that both ff03* and ff99SB* were developed in the context of the TIP3P water.³⁴ Another ff03 series force field, ff03w, was found to improve over ff03* in the context of the TIP4P/2005 water.³⁵ Two recent OPLS protein force fields (i.e., OPLS-AA/M³⁶ and OPLS3³⁷) were also developed with this strategy, and both involve reparameterization of the backbone dihedral and side-chain dihedral with respect to training set of ab initio torsional energy scanning data of blocked dipeptides. The OPLS-AA/M made progress in simulating proline dipeptides and glycine tripeptides, showing its ability to simulate IDPs. The OPLS3 force field was found to perform well in protein–ligand binding simulations.³⁷ In the CHARMM force fields, CHARMM22*³⁸ is also a result of refitting effort of CHARMM22³⁹ following a similar strategy. This force field mainly focuses on the folding and unfolding transitions. During a 100 μs simulation of the villin headpiece (PDB ID: 2F4K), CHARMM22* gave the best agreement with both the kinetic and thermodynamic properties of experimental data.

In addition to direct refitting of universal dihedral parameters, it is also possible to use residue-specific dihedral parameters to further improve agreement with experimental observables. Using this strategy, the RSFF1⁴⁰ and RSFF2⁴¹ force fields were developed by Wu and co-workers. Both efforts were based on rotamer distributions from a protein coil library as the training set. It is worth pointing out that the RSFF1 is derived from OPLS/AA⁴² while the RSFF2 is derived from ff99SB,¹⁹ but both followed similar workflows. Both RSFF1 and RSFF2 successfully fold the α-helix part in Trp-cage and Homeodomain and the β-sheet part in Trpzip-2 and GB1 hairpin. Moreover, the RSFF2 solves the problem that RSFF1 overestimates the stability of both α-helix and β-sheet.

Adding CMAP Parameters.

CMAP is the shorthand notation for grid-based energy correction map,^43,44 based on a two-dimensional distribution of backbone dihedrals. Both backbone dihedrals are evenly divided by a sampling bin size, typically 15°. This would result in a total of 576 bins covering the two-dimensional dihedral space per residue. The conformational free energy of each bin can then be calculated as eq 3.

$$\mathrm{\Delta }{G}_i=-RT\text{ln}\left(\frac{N_i}{N_{\max }}\right)$$ (3)

where N_i, refers to the number of dihedral data falling in bin i, (the value is to set to 1, if there is no dihedral data to prevent singularity) and N_max refers to the total number of dihedral data in the sampling.

The conformational free energy of each residue can therefore be derived from both a database ($\mathrm{\Delta }{G}_i^{\mathrm{DB}}$) and a force field simulation ($\mathrm{\Delta }{G}_i^{\mathrm{MM}}$), and the correction value of CMAP can be represented as eq 4.

$$E_i^{\mathrm{CMAP}}=\mathrm{\Delta }{G}_i^{\mathrm{DB}}-\mathrm{\Delta }{G}_i^{\mathrm{MM}}$$ (4)

Apparently, only a discrete set of 576 energy correction values can be obtained if the bin size is 15°. The bicubic interpolation method⁴⁵ can then be used to generate a continuous and smooth energy correction surface in order to compute the energy correction value for any conformation, as in eq 5.

$$f(\varphi ,\psi )=\sum _{i=1}^4\sum _{j=1}^{4}cij{\left(\frac{\varphi -{\varphi }_{\mathrm{L}}}{\mathrm{\Delta }\varphi }\right)}^{i-1}{\left(\frac{\psi -{\psi }_{\mathrm{L}}}{\mathrm{\Delta }\psi }\right)}^{i-1}$$ (5)

where ϕ_L and ψ_L refer to the backbone dihedrals of the conformation of interest, while Δϕ and Δψ refer to the bin size (15°).

Initially, the CMAP method was used in CHARMM22/CMAP (also termed as CHARMM27) based on CHARMM22.^39,44 Although CHARMM27 has balanced between the helix and coil, it cannot generate a stable hairpin structure and overestimating the helical conformation when simulating the α-synuclein.⁴⁶ Thus, a subsequent force field CHARMM36 improves the potential of CMAP, based on experimental NMR data.⁴⁷ The newer force field was found to enhance cooperativity of helix and hairpin formation, while retaining comparatively high accuracy when simulating folded proteins. However, left-handed helices could be overpopulated when simulating some IDPs with CHARMM36. CHARMM36m was later developed and solved this limitation.⁴⁸ In CHARMM36m, C_α atoms are divided into three groups according to residue type: CT2 for glycine, CP1 for proline, and CT1 for the remaining 18 amino acids. This amounts to adopting a minimal residue-specific CMAP strategy. CHARMM36m is also a balanced force field for both IDPs and folded proteins, since its training set includes not just IDPs. Another force field a99SB-disp,⁴⁹ using similar strategy to CHARMM36m⁴⁸ and based on the ff99SBildn and TIP4P-D water model, is mildly refined the torsional parameters and nonbond parameters.^49,50 This force field tends to balance between the IDPs and folded proteins. However, the problems occur upon simulating the aggregation of Aβ_16–22⁵¹ and Aβ₄₀,⁵² with inaccuracy of the β-hairpin conformations.

Previous studies indicate that the amino acid composition of IDPs differs considerably from that of folded proteins.^53,54 Thus, in early residue-specific CMAP force fields for IDPs, i.e., ff99IDPs^28,55 (developed from ff99SBildn⁵⁰) and ff14IDPs²⁹ (developed from ff14SB), the CMAP potential is only modified for eight disorder-promoting amino acids (G, A, S, P, R, Q, E, and K), compiled from NMR data of IDPs.⁵⁶ In subsequent development of CMAP-based force fields, ff14IDPSFF⁵⁷ and CHARMM36IDPSFF,^58,59 the use of CMAP potential is expanded to all 20 standard amino acids. These were developed from ff14SB and CHARMM36m, respectively. It was found that ff14IDPSFF performs very well in long-time simulations (i.e., microsecond time scales) and reproduces NMR observables.⁶⁰ CHARMM36IDPSFF force field also performs well in both multiple-trajectory simulations and replica-exchange simulations. Figure 1 illustrates their consistence with a well-studied IDP, Amyloid β protein 1–42 (Ab42). A recent comparison of multiple IDP force fields indicates that IDPs-specific force fields in general substantially improve the agreement of simulated observables with experiment. Interestingly CHARMM22*³⁸ performs better than CHARMM36m⁴⁸ for many observables, though it still has a preference toward helicity in simulations of short peptides.⁶¹

Figure 1.

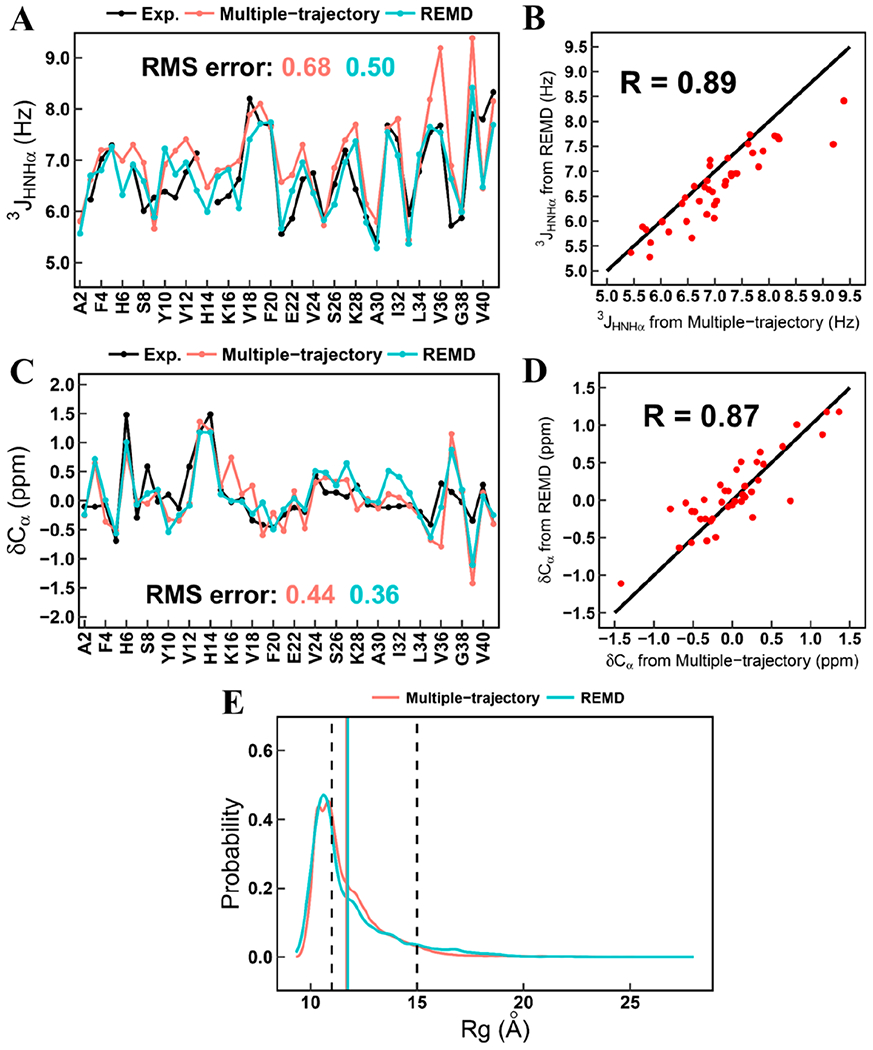
Comparison of ³J_HNHα couplings, chemical shift, and Rg between multiple-trajectory and REMD simulations. (a) Residual ³J_HNHα couplings. (b) Correlation of calculated ³J_HNHα couplings between multiple-trajectory and REMD simulations. (c) Residual chemical shifts of Cα atoms. (d) Correlation of calculated chemical shifts of Cα atoms between multiple-trajectory and REMD simulations. (e) Probability distribution of Rg from the simulated ensembles of Aβ42 generated by multiple-trajectory and REMD simulations. The range of experimental Rg is marked by two dash lines. The averaged Rg values from both simulation methods are marked by the solid lines and are labeled with the same colors of corresponding simulation methods.

A residue-specific OPLS force field, OPLSIDPSFF, was also proposed with a similar CMAP strategy to correct backbone torsion terms for all 20 standard residues.³¹ The OPLSIDPSFF was developed from OPLS-AA/L⁴² and was meant to combine with the TIP4P-D water.³¹ The OPLSIDPSFF force field can reproduce most experimental data for the tested proteins, especially for NMR chemical shifts and scalar couplings when combined with TIP4P-D water model.

To simulate biological molecules with folded and disordered regions, both folded and disordered conformations should be well reproduced with a given force field. The ff03CMAP is one example.³⁰ This is because its development was based on a different training set containing not only IDPs but also folded proteins. This demonstrates the significance of choosing training models. The ff03CMAP force field could be used in conjunction with TIP4P-Ew⁶² and TIP4P-D⁶³ water models. The ff03CMAP/TIP4P-Ew combination is especially suitable for folded protein simulation, while the ff03CMAP/TIP4P-D combination performs well in IDP simulations.³⁰

In addition, Wu and his co-workers developed a three-dimensional-CMAP force field called RSFF2C based on RSFF2, with correction not only in the backbone dihedrals (ϕ and ψ) but also in the side-chain dihedral (χ₁).⁶⁴ The RSFF2C force field significantly improves the backbone dihedral sampling of both folded and disordered proteins and ab initio folding of various fast-folding proteins.

A previous experiment of short peptides indicates that neighboring residues have a crucial effect on the stabilities of secondary structures by influencing their hydration environments.⁶⁵ Thus, the ESFF1 force field was developed by extending the residue-specific CMAP correction by considering the sequence environment of each residue.⁶⁶ The sequence environment of a residue is classified as polar if the residue’s neighbor is Gly, Ser, Tyr, Cys, Asn, Gln, Thr, His, Glu, Asp, Arg, and Lys. Its sequence environment is classified as nonpolar if its neighbor is Met, Trp, Phe, Val, Leu, Ile, Pro, and Ala. Subsequently, a total of four (polar/nonpolar-X-polar/nonpolar) sequence environments emerge for each of the 20 residues. Extensive simulation results show that ESFF1 can reproduce the NMR measurements of 61 short peptides and IDPs well. The ESFF1 also achieves a reasonable balance between the folded and disordered proteins by implementation of 71 well trained environmental CMAP parameters.

Refining Protein–Water Interactions.

In simulations of IDPs, the interaction between protein and water is particularly essential, because they do not have robust hydrophobic cores with many buried nonpolar residues. This shows the importance of selecting the right water model with the right force field. The nonbond interactions between protein and water can be divided into electrostatic and van der Waals components, which are represented by atomic partial charges and L-J parameters. The protein–water van der Waals interaction in particular was found to often influence the size of simulated IDPs as measured by the radius of gyration, Rg. In early MD simulations of IDPs, Rg is often a basic property to monitor as it can be readily inferred from experimental methods such as SAXS and FRET.⁶⁷ However, many early IDP force fields trained with NMR data cannot lead to IDPs extended enough to be consistent as observed in experiment. In many later generations of IDP force fields, this limitation was successfully addressed. For example, the CHARMM36m⁴⁸ and a99SB-disp⁴⁹ force fields discussed in the previous section on CMAP correction also includes refinement of the protein–water L-J potential parameters.

There are many approaches to refine the water–protein interaction, though the L-J potential is often adjusted^{48,49,63,68,69} The formula of L-J potential (also known as 12–6 potential) can be expressed as eq 6.

$$V_{ij,\mathrm{L}-\mathrm{J}}=4{\epsilon }_{ij}\left[{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^6\right]$$ (6)

The effects of improper coupling of water models and force fields and failures of current water models were discussed in detail by Shaw and co-workers.⁴⁹ The TIP4P-D water model was subsequently proposed with a larger oxygen value ε. This water model does improve the Rg values of some simulated IDPs but it also causes some α-helix to unfold and overestimates the Rg of several longer IDPs. This strategy has been adopted in the development of ff03ws based on ff03w and TIP4P/2005.⁶⁹ This force field, in a way, solved another big problem that exists among previous IDP force fields: the overstabilizing the protein–protein interaction, which often influences the aggregation behaviors of IDPs. On the contrary, a force field termed a99SB-UCB^68,70 that also modified the nonbonded and backbone parameter somehow can solve this problem. The CHARMM36m adjusts both oxygen and hydrogen atoms of water⁴⁸ to improve its performance in simulations of IDPs.

The Kirkwood–Buff (KB) solution theory offers another angle to quantify the protein–water interaction and have been utilized to develop nonprotein force fields.^71–73 An IDP force field was also developed based on the KB theory (termed KBFF).⁷⁴ In addition, an IDP force field utilizing the traditional nonbond fix strategy (NBFIX) was proposed (termed CUFIX).⁷⁵ The simulation results of proteins, nucleic acids, and lipids were found to have a remarkable agreement with experimental data by introducing these modifications.⁷⁵

Besides the explicit solvent model, the implicit solvent model is another way for IDP simulation. Compared with the explicit solvent models, the implicit solvent models use additional potentials rather than real water molecules to describe the influence of solvent. The general free energy of solvation is usually divided into three parts, shown as eq 7.

$$\mathrm{\Delta }{G}_{\text{sol}}=\mathrm{\Delta }{G}_{\text{cav}}+\mathrm{\Delta }{G}_{\text{vdW}}+\mathrm{\Delta }{G}_{\text{ele}}$$ (7)

Solvent-accessible surface area (SASA) methods model either the nonpolar terms ΔG_cav + ΔG_vdW or the entire ΔG_sol term, while Poisson–Boltzmann and Generalized-Born methods model the ΔG_ele term. Because they use much less computational resources, implicit models are used in large-scale screening⁷⁶ and large-system simulation,⁷⁷ which is important for IDP studies. Implicit solvent models are also applied to protein–surface research.⁷⁸ Some popular Generalized-Born solvent models are shown in this review.⁷⁹

Other Strategies.

Although the refinement of dihedral parameters and CMAP correction are the most common techniques for developing IDP force fields, IDP-specific force fields can also be configured in several other ways. Ramanathan and co-workers utilized small-angle scattering (SAS) data as their training set to develop a ForceBalance-SAS force field.⁸⁰ A key strategy in this effort is to rely on machine learning to optimize a set of force field parameters simultaneously. This approach could help us to avoid the issue of overcorrection that often appears early on.

Coarse-grained IDPs force fields are also available. AWSEM-IDP⁸¹ was also developed from the AWSEM force field.⁸² AWSEM has been successfully used to study protein folding, binding, and aggregation problems. The MOFF force field⁸³ is another coarse-grained IDP force field developed with the maximum entropy algorithm⁸⁴ with respect to a range of experimental data, and is used for successful simulation studies of IDPs.

Even with various improvements discussed above, limitations do exist as it is often very difficult to balance the performance between folded and disordered proteins with a given combination of force fields and water models. Apparently, there is a limit in refinement of dihedral terms and protein–water van der Waals interactions if we insist on a unified protein force field to be used for both folded and disordered proteins. The electrostatic and hydrogen-bonding interactions in IDPs may also play key roles in their structural preferences. Thus, the next step for improving the performance and accuracy of the IDP-specific force field might be on these polar interactions. Indeed, the charge distribution of a residue should be perturbed by its neighboring residues and solvent exposure, which in principle can be handled by the emerging polarizable force fields.

A great deal of effort has been devoted to developing modern polarizable force fields, including the fluctuating charge models^85,86 in the context of OPLS-AA, the fluctuating charge model and the Drude oscillator model^87–91 in the context of CHARMM, and detailed multipole expansions and more complicated MM potentials in the context of Amoeba.^92,93 In Amber, polarization was implemented with induced dipoles.⁹⁴ In Amber ff12pol, the induced dipoles are calculated using Thole models to avoid “polarization catastrophe”.^95–98 The latest efforts have shifted to the use of Gaussian models for more consistent treatment of electrostatics in Amber.^99–101 There has been encouraging applications of polarizable force fields in protein simulations. The CHARMM Drude force field is shown to be able to simulate the folding of the helical (AAQAA)3 peptide¹⁰² and the unfolding of a b-amyloid fragment.¹⁰³ It is clear that the limitation of polarizable force fields is their low efficiency. However, efficient software packages, particularly those that can best take advantage of the more efficient GPUs, are emerging and will positively impact molecular simulations of IDPs.

Enhanced Sampling Methods.

Unlike the folded proteins, either simulating equilibrium structures or studying the mechanism of interactions and aggregations of IDPs needs large-scale sampling. To facilitate the cost of computational resources, enhanced sampling methods are essential to IDPs. There are mainly three types of ideas. The first is by using additional potential energy term to overcome the energy barrier, which includes metadynamics^104,105 and umbrella sampling.¹⁰⁶ The former adds potential energy according to the chosen collective variables (CVs) while the latter adds potential energy in an elastic form. The second idea is to exchange replicas from parallel trajectories, including temperature replica exchange molecular dynamics (T-REMD),¹⁷ temperature cool walking (TCW),¹⁰⁷ and bias exchange metadynamics (BEMD).¹⁰⁸ The difference between these three is the T-REMD is based on MD simulation, while the TCW and BEMD are based on Monte Carlo simulation and metadynamics. The T-REMD, often referred to as REMD, is perhaps the most popular enhanced sampling method. The last idea is using both principle component analysis (PCA) and a kind of edge searching method to find the “edge structures” on the energy surface and running seed MDs based on the structures chosen. By circularly running this workflow, the sampling points will gradually escape from the initial potential energy trap. The structure dissimilarity sampling (SDS),¹⁰⁹ parallel cascade selection MD (PaCS-MD),^110–113 self-avoiding conformational sampling (SACS),¹¹⁴ complementary coordinates MD (CoCo-MD),¹¹⁵ and frontier expansion sampling (FES)¹¹⁶ all belongs to this type. The only difference between these methods is the algorithm they use to find the frontier structures, like the convex hull algorithm used in the FES method.

Force Field Benchmark.

The unification of simulation and experiment is the key point of force field benchmark. The most popular experimental data used are SAXS, FRET, and NMR data. The SAXS and FRET experimental data can tell detailed changes in the protein shapes. The NMR chemical shift and J-coupling data give information about the secondary information on each single residues while the NOE data show the long-range interactions between residues. Besides these statistical data, IDPs that already have prior knowledge may be the best systems for IDP force field benchmarking.

Aβ_16–22 and Aβ₄₀ are well-studied IDPs related to neuro-degenerative disease, of which the aggregation phenomenon is of great importance. Strodel and co-workers have compared many AMBER, CHARMM, OPLS, and GROMACS force fields on these IDPs.^51,52,117 For Aβ_16–22, Gromos54a7 and OPLS-AA overstabilized protein–protein interactions while AMBER99SB*ILDN and CHARMM22* also produce the oligomer formation too fast. The ff03ws may be the suitable force field for Aβ_16–22.⁵¹ Further study shows that CHARMM36m produced by Huang and co-workers⁴⁸ also performed well.¹¹⁷ For Aβ₄₀, MD simulation of a large time scale was produced, revealing that a99SB-UCB and ff99SB-IDLN (with TIP4P-D) have the best and the second-best performance. Meanwhile ff03ws gives too much helix conformation and ff99SB*-IDLN (with TIP3P) gives too much β-sheet conformation. ff99SB-disp, CHARMM22*, and CHARMM36m have acceptable results.⁵²

The RS peptide with repeating arginine and serine was sampled by Rauscher et al. using T-REMD.¹¹⁸ The CHARMM22* and CHARMM36m, both with TIP3P, performed the best. The ff03ws and CHARMM36m, both with TIP4P-D, get more expanded structures than expected.

For the α-synuclein that has a structural character of β hairpin fragment, six force fields were tested in a relatively short time scale (500 ns).⁴⁶ It was reported that the CHARMM27 and OPLS-AA did not stabilize the β-hairpin, while ff03 and GROMACS 43A1 generated a shorter hairpin compared with the native one. The ff99SB and GROMACS 53A6 gave a stable β-hairpin conformation, but the latter one was found to overestimate the β-strand conformation.

Histain5 is another typical 24 residues IDP used for comparing force fields. It was found that ff99SB-IDLN, ff99SBnmr-IDLN, GROMACS 53A6, and GROMACS 54A7 generate too collapsed ensembles compared with experimental results. By modifying protein–water interactions, the ff03ws and ff99SB-IDLN with TIP4P-D generate more expanded conformations.^119,120

Other protein systems, such as p53, polyQ, and hIAAP, were all tested in the previous studies. The system and used force field are all shown in Table 1, the force fields with good performances are labeled in bold.

Table 1.

Typical Systems for the Test of Force Field and Solvent Model

protein system	force field and solvent model	refs
Aβ16–22	ff99SB-disp(TIP4P-D), C36m(TIP3P), C36 mW, G54a7(SPC), OPLS-AA(TIP4P-D)	117
Aβ16–22 and its mutants	G54a7(SPC), ff03ws(TIP4P/2005), OPLS-AA(TIP4P), ff99SB*-IDLN(TIP4P-Ew), C22*(TIP4P-Ew)	51
Aβ40	ff03ws, ff99SB-IDLN(TIP4P-D), ff99SB-UCB, ff99SB-disp, C22*(TIP3P), C36m	52
RS peptide	ff99SB*-IDLN(TIP3P), ff03w(TIP4P/2005), ff03ws(TIP4P/2005), C22*(TIP3P modified), C22*(TIP4P-D), C36(TIP3P), C36(TIP3P modified), C36m(TIP3P modified), C36m(TIP4P-D)	118
Histain5	ff99SB-IDLN(TIP3P), ff99SB-IDLN(TIP4P-D), ff99SBnmr-IDLN(TIP3P), G53a6(SPC), G54a7(SPC), ff03ws(TIP4P-D)	119, 120
p53-TAD2(aa40-61)	ff03(TIP3P), C27(TIP3P), OPLS-AA/L(TIP3P), ff99SB-IDLN(TIP3P), C36m(TIP3P modified)	121
p53-TAD(aa1-61)	ff99SB-IDLN(TIP3P), ff99SB-IDLN(TIP4P-D), C36m, C36 mW, C22*, ff99SB-disp	122
polyQ	ff99(TIP3P), ff99SB(TIP3P), ff99SB*(TIP3P), ff03(TIP3P), ff03*(TIP3P), ff03w(TIP4P/2005), C27(TIP3P modified), C22*(TIP3P modified), C36(TIP3P), G53a6(SPC), G54a7(SPC), OPLS-AA/L(TIP4P), C36m(TIP3P modified)	123
hIAAP	ff99SB*-IDLN(TIP3P), ff99SB*-IDLN(TIP4P), ff03w(TIP4P/2005), ff03w(TIP4P), C27(TIP3P modified), C27(TIP4P), C22*(TIP3P modified), C22*(TIP4P), G53a6(SPC), OPLS-AA/L(TIP4P)	124

CONCLUSION

In this review, we have summarized various strategies for improving force fields for molecular simulations of IDPs in recently published IDP force fields. The two parameters most frequently revised for IDP force fields are the backbone dihedral parameters and the L-J potential parameters for protein–water interactions. Mostly the training data are from experimental observables and ab initio quantum mechanical calculations. Apparently both reparameterization strategies and training sets influence the final developed force field. The parent force fields and strategies are shown in Table 2.

Table 2.

Summary of Strategy and Tested Systems of Force Fields for IDPs

force field	parent FF	strategy	tested systems
ff03*	ff03	backbone reparameterization	dipeptides, tripeptides, Ac-(AAQAA)3-NH2, HEWL19, ubiquitin, GB1, Trp-cage, Villin, pin WW domain, polygutamine, etc.
ff99SB*	ff99SB	backbone reparameterization	dipeptides, tripeptides, Ac-(AAQAA)3NH2 HEWL19, ubiquitin, polygutamine, β-amyloid, etc.
ff03w	ff03*	slight backbone modification to fit TIP4P/2005	Ac-(AAQAA)3-NH2, GB1, Trp-cage, Villin, pin WW domain, RS peptide, polygutamine, hIAAP, HEWL19, HIV-rev, Aβ40, Aβ42 phosphodiesterase-γ, CspTm, ubiquitin, etc.
OPLS-AA/M	OPLS-AA	QM calculation of backbone and side-chain parameters	dipeptides, tripeptides, Ala5, ubiquitin, GB3, etc.
OPLS3	OPLS2.1	QM calculation of backbone and side-chain parameters	K19, Ac-(AAQAA)3-NH2, cln025, trpcage, GB3, ubiquitin, Sumo2, BPTI, crambin, lysozyme, BACE, CDK2, JNK1, MCL1, P38, PTP1B, thrombin, Tyk2, etc.
CHARMM22*	CHARMM22	backbone and side-chain reparameterization	Villin, RS peptide, polygutamine, β-amyloid, hIAAP, HEWL19, HIV-rev, Aβ16–22, Aβ40 Aβ42 phosphodiesterase-γ, CspTm, ubiquitin, PaaA2, α-synuclein, Ala5, ACTR, DrkN SH3, GCN4, GTT, Trp-cage, Villin, CLN025, etc.
RSFF1	OPLS-AA	residue-specific backbone modification	Coil Lib, Trp-cage, Trpzip-2, GB1, homeodomain, Ala14, WW domain, etc.
RSFF2	ff99SB	residue-specific backbone modification	Coil Lib, Trp-cage, Trpzip-2, GB1, homeodomain, Ala14, WW-domian, etc.
CHARMM27	CHARMM22	adding CMAP parameter	dipeptides, tripeptides, ubiquitin, 1GPR, 1HIJ, polygutamine, hIAAP, α-synuclein, etc.
CHARMM36	CHARMM27	modified CMAP based on NMR data	ubiquitin, GB1, CspA, apoCAM, IFABP, HEWL, RS peptide, polygutamine, FG-nucleoporin, etc.
CHARMM36m	CHARMM36	refined CMAP parameters + modified L-J potential	FG-nucleoporin, RS peptide, IN, HEWL, Ac-(AAQAA)3-NH2, GB1, chignolin, CLN02S, Nrf2, polygutamine, HIV-rev, Aβ40 Aβ42, phosphodiesterase-γ, CspTm, ubiquitin, etc.
a99SB-disp	a99SB-ILDN	modified CMAP parameters + modified L-J potential	Aβ40, Aβ42, NTAIL, PaaA2, α-synuclein, Ala5, ACTR, DrkN SH3, GCN4, GTT, Trp-cage, Villin, CLN02S, Ac-(AAQAA)3-NH2, calmodulin, HEWL, ubiquitin, BPTI, GB3, etc.
ff99IDPs	a99SB-ILDN	disordered promoting residue specific CMAP parameters	RS peptide, HIV-rev, Aβ40, Aβ42, phosphodiesterase-γ, CspTm, ubiquitin, RS peptide, HEWL, NTAIL p53, IA3, α-synuclein, etc.
ff14IDPs	ff14SB	disordered promoting residue specific CMAP parameters	RS peptide, HIV-rev, Aβ40, Aβ42, phosphodiesterase-γ, CspTm, ubiquitin, RS peptide, HEWL, NTAIL p53, IA3, α-synuclein, etc.
ff14IDPSFF	ff14SB	all residue specific CMAP parameters	RS peptide, HEWL19, HIV-rev, Aβ40, Aβ42, phosphodiesterase-γ, CspTm, ubiquitin, KID, c-Myb, Tau, IA3, α-synuclein, p53, iysozyme, etc.
CHARMM36IDPSFF	CHARMM36	all residue specific CMAP parameters	Ala5, Ala7, Aβ40, Aβ41, ACTR, DrkN SH3, hIAPP, Histain5, BPTI, GB3, CLN02S, Villin, Ac-(AAQAA)3-NH2, RS peptide, FG peptide, HEWL, HIV-rev, HP21, GB1, ubiquitin, c-Myb, IA3, p53, pKID, MeVN, Tau, α-synuclein, etc.
OPLSIDPSFF	OPLS-AA	all residue specific CMAP parameters	Ala5, Ala7, Aβ40, Aβ42 ACTR, RS peptide, GB3, Ac-(AAQAA)3-NH2, Mev-n, HIV-rev, HP21, GB1, ubiquitin, c-Myb, IA3, p53, pKID, MeVN, Tau, etc.
ff03CMAP	ff03	all residue specific CMAP parameters	Aβ40, Aβ42, ACTR, IA3, p53, Tau, RS peptide, HIV-rev, HEWL, GB3, BPTI, CspTm, ubiquitin, SPR17, etc.
ESFF1	ff14SB	environment specific CMAP parameters	Aβ40, Aβ42, ACTR, IA3, p53, Tau, RS peptide, Histain5, DrkN SH3, α-synuclein, MevN, KID, c-Myb, rIAPP, revARM, etc.
RSFF2C	RSFF2	three dimensional CMAP parameters	Ala14, Ac-(AAQAA)3-NH2, Trp-cage, Trpzip-2, GB1, WW domain, etc.
ff03ws	ff03w	modification of L-J potential	Ala5, Aβ16–22, Aβ40, Aβ42, Ac-(AAQAA)3-NH2, RS peptide, Histain5, Trp-cage, ACTR, Villin, CspTm, R1S, GB1, iysozyme, ubiquitin, etc.
a99SB-UCB	ff99SB	modification of nonbonded and backbone parameters	dipeptides, tripeptides, Ala5, Aβ40, Aβ42, ubiquitin, GXG peptides

It is subject to debate that the polarizable force fields may hold the key for more consistent simulations of both folded and disordered proteins. And their adoption will become more widespread as both software and hardware improve.

There are clearly many unresolved issues in force field strategies for IDPs. For example, the current IDP force fields are limited to simulations with standard amino acids. However, post-translation modifications (PTMs) are very common in IDPs. There were several PTM force field parameters available,^125–128 but IDP-specific parameters are still lacking for accurate simulations to study the effects of PTMs in IDPs. In addition, balancing local structural features (i.e., NMR chemical shift) and global structural features (i.e., Rg) is a more challenging problem to be solved in the years to come in molecular simulations of IDPs. Apparently molecular dynamics is not the only theoretical or computational approach in IDPs as recently reviewed.^11,129,130