Landmark-free morphometric analysis of knee osteoarthritis using joint statistical models of bone shape and articular space variability

Abstract.

Purpose: Osteoarthritis (OA) is a common degenerative disease involving a variety of structural changes in the affected joint. In addition to narrowing of the articular space, recent studies involving statistical shape analysis methods have suggested that specific bone shapes might be associated with the disease. We aim to investigate the feasibility of using the recently introduced framework of functional shapes (Fshape) to extract morphological features of OA that combine shape variability of articular surfaces of the tibia (or femur) together with the changes of the joint space.

Approach: Our study uses a dataset of three-dimensional cone-beam CT volumes of 17 knees without OA and 17 knees with OA. Each knee is then represented as an object (Fshape) consisting of a triangulated tibial (or femoral) articular surface and a map of joint space widths (JSWs) measured at the points of this surface (joint space map, JSM). We introduce a generative atlas model to estimate a template (mean) Fshape of the sample population together with template-centered variables that model the transformations from the template to each subject. This approach has two potential advantages compared with other statistical shape modeling methods that have been investigated in knee OA: (i) Fshapes simultaneously consider the variability in bone shape and JSW, and (ii) Fshape atlas estimation is based on a diffeomorphic transformation model of surfaces that does not require a priori landmark correspondences between the subjects. The estimated atlas-to-subject Fshape transformations were used as input to principal component analysis dimensionality reduction combined with a linear support vector machine (SVM) classifier to identify the morphological features of OA.

Results: Using tibial articular surface as the shape component of the Fshape, we found leave-one-out cross validation scores of $\approx 91.18\%$ for the classification based on the bone surface transformations alone, $\approx 91.18\%$ for the classification based on the residual JSM, and $\approx 85.29\%$ for the classification using both Fshape components. Similar results were obtained using femoral articular surfaces. The discriminant directions identified in the statistical analysis were associated with medial narrowing of the joint space, steeper intercondylar eminence, and relative deepening of the medial tibial plateau.

Conclusions: The proposed approach provides an integrated framework for combined statistical analysis of shape and JSPs. It can successfully extract features correlated to OA that appear consistent with previous studies in the field. Although future large-scale study is necessary to confirm the significance of these findings, our results suggest that the functional shape methodology is a promising new tool for morphological analysis of OA and orthopedics data in general.

1. Introduction

Osteoarthritis (OA) is currently the most common degenerative joint disease. The healthcare burden of OA is significant: it affects 30 million US adults¹ and is an indication for 95% of joint replacements at a total annual cost of 40 billion.² The disease is commonly assumed to develop in response to abnormal loading patterns in the joint.³ There is no single recognized cause of such mechanical derangement. Rather, OA is likely an end-product of a range of distinct anatomical and kinematic deficiencies—congenital, lifestyle-related, or post-traumatic (e.g., due to ligament tears). This complex, multifactorial etiology challenges early detection and diagnosis and is likely one of the reasons for the current lack of disease-modifying treatments for OA.

Because of the role of biomechanical factors in OA, it is hypothesized that the morphology of the joint—which affects its kinematics and load-distribution—might yield useful biomarkers for risk stratification, early detection, and staging of the disease. Such biomarkers might include variables representing the shape (geometry) of the bones of the joint and/or their relative alignment. For example, in knee and hip OA, a radiographic measurement of joint space width (JSW) is an FDA-recommended structural outcome in clinical trials of OA-modifying drugs.⁴ Recently, there has been an increasing interest in the application of statistical shape models (SSMs) as a promising approach to develop morphological biomarkers of OA. We review some of this work in the following paragraphs. [Here, we use the term SSM to describe statistical models of population shape variability, formed by analysis of two-dimensional (2D) or three-dimensional (3D) imaging datasets of a sample of subjects from the population.]

In OA of the knee, an early demonstration of SSM in identification of morphological variants associated with the disease came from models based on 2D radiographs. For example, Haverkamp et al.⁵ developed an SSM of the entire knee joint, accounting both for the geometry of the bones (tibia, patella, and femur) and their alignment. Three morphological modes—widening of the tibia and femur, flexion of the knee, and elevated lateral tibial plateau—were found to be significantly associated with established symptoms of OA, i.e., pain, cartilage defects on MRI, and Kellgren/Lawrence grade from radiographs. Recently, it has been shown that, when machine learning was used to derive OA prediction models from a large ensemble of clinical, lifestyle and imaging variables, the best-performing models often included radiographic SSMs.⁶

3D SSMs are a natural extension of the radiography-based approach, potentially enabling more precise assessment of shape variability due to the lack of anatomical overlap. In knee OA, 3D SSMs obtained from MRI identified a variety of morphological features that are likely to be associated with the disease, e.g., in studies of OA progression,^7,8 in at-risk population,⁹ and in patients awaiting total knee replacement due to OA.¹⁰ Importantly, certain articular surface geometries found through 3D SSM appear to be linked to significant increases in MRI signals of cartilage loss in patients with ACL tears (OA often develops secondary to ACL injuries).¹¹ Considering that cartilage loss is a hallmark of OA, this result further strengthens the case for using shape analysis to establish new biomarkers of the disease.

The majority of the works discussed above involve shape models developed by parameterizing bone surfaces using a set of landmarks, either placed manually or obtained through mesh generation. To form an SSM, one needs to first establish correspondences between the landmarks of the subjects contributing to the model. For relatively densely sampled surface meshes, this matching can in principle be achieved using a variety of automatic methods (including, e.g., point cloud registration¹² and analysis of local curvatures¹³). Along similar lines, the recent work of Ref. 14 using surface meshes from the Osteoarthritis Initiative (OAI) dataset involved a supervised postprocessing step to enforce a consistent number of vertices across the different subjects as well as correspondences between these vertices.

In contrast to the majority of the prior work in morphological analysis of OA, this article investigates an alternative shape modeling strategy that obviates the need for landmark extraction and correspondences. To that end, we follow the framework of generative surface atlas models.^15,16 Intuitively, we estimate a template bone surface, representing the “mean shape” of the subject sample, together with template-centered variables that model the transformations from this template to each subject, relying on a global and landmark-free measure of fidelity between surface meshes. The transformations describe shape variation in the population in a manner that does not explicitly require corresponding control points on the bone surfaces. To the best of our knowledge, this is one of the first illustrations of this methodology in application to knee OA.

Another important distinction with the prior work on 3D SSMs in knee OA is that we propose to jointly consider the distribution of bone shapes and joint space morphologies—in particular, JSW—in the population. To this end, we use a previously developed algorithm¹⁷ to equip each location on the tibial (or femoral) surface with a unique measurement of local distance to the femur (or tibia); the set of such measurements for all points on the articular surface forms a joint space map (JSM). To develop a statistical model combining bone shapes and JSMs, we interpret the JSMs as textures on each bone surface. We utilize the framework of functional shapes (Fshapes), introduced theoretically in Refs. ¹⁸ and ¹⁹ to perform atlas estimation on the population of such textured bone surfaces. Note that it shares some mathematical features with, but is conceptually distinct from, the setting of functional maps²⁰ as the latter approach uses artificially constructed functions chosen specifically to estimate the surface correspondences, whereas the FShape functions (here, the JSM) represent additional data measured on the surface that is not a priori directly correlated with the geometry of the surface.

It is important to note that the proposed application of Fshapes does not assume that the variations in surface geometry and JSM are necessarily correlated; for example, certain shape variants might predispose for OA and thus be present in a subject even if the JSM is fairly normal. Rather, the benefit of simultaneous modeling of both aspects of articular morphology is that it provides a rigorous approach to aligning the data for intersubject comparisons. This is especially important for JSM analysis, in which a conventional approach would require a deformable registration of the articular surfaces followed by deformations of the JSMs to ensure that the subsequent comparisons use corresponding regions of the joint. In our approach, the study sample is described in terms of geometric mappings of the shapes and functional transformations of the JSMs (e.g., local widening or narrowing of the articular space) that are automatically mapped onto a common atlas without the need for invoking a sequence of deformable registrations. As we show below, the statistical analysis can then be performed either jointly on both components of the Fshape transformations (geometry + JSM) or individually on each component.

We evaluate the ability of the Fshape framework to extract interpretable modes of variation in bone geometry and JSMs correlated with OA. Specifically, the proposed analysis was performed on volumetric images of weight-bearing knees acquired using a recently introduced extremity cone-beam CT (CBCT).²¹ Extremity CBCT is a dedicated orthopedic CT system with several features that are particularly attractive for evaluation of OA, including high isotropic spatial resolution and the unique capability for 3D imaging in a natural standing stance. Compared with MRI, which is often the only form of 3D imaging available in existing OA cohorts such as the OAI, CBCT is potentially better suited for the morphological modeling proposed in this work. First, MRI typically exhibits lower resolution in the longitudinal (slice) direction than in-plane; the isotropic resolution of CBCT may therefore be advantageous for the development of accurate models of articular surfaces. Perhaps more importantly, extremity CBCT enables weight-bearing 3D imaging, which is not available in conventional MRI. Since joint space narrowing is often accentuated under physiological load, CBCT might yield additional insights into the progression of OA. The work presented below is, therefore, not only a general contribution to the SSM methodologies in OA but is also partly motivated by the need to develop rigorous analysis of the new information provided by the extremity CBCT. While the Fshape model was previously applied for disease characterization in retinal data,²² the results presented in this paper are, to the best of our knowledge, the first demonstration of this integrated approach in the 3D assessment of the morphology of weight-bearing knee in OA.

2. Data Acquisition and Processing

2.1. Study Population and CBCT Imaging Protocols

The volumetric knee images used in this work were obtained in an Institutional Review Board-approved pilot study of the extremity CBCT system. Weight-bearing dominant knees of the participants were imaged at 80-kVp tube voltage and 10-mGy absolute dose.²¹ The scans were reconstructed using 3D-filtered backprojection to generate $20\times 20\times 20{\mathrm{cm}}^3$ volumes centered on the knee joints. Voxel size was 0.52 mm. Morphological analysis was performed on a sample of $N=34$ subjects; 17 of them were diagnosed with knee OA using clinical criteria consistent with the current standard of care, including symptoms and physical examination by an orthopedic specialist, as well as radiographic signs assessed by a musculoskeletal radiologist. The radiological evaluation considered the presence of joint space narrowing, osteophytes, and effusion. The remaining 17 subjects (referred to as “non-OA” or “normal”) had no known symptoms or history of OA. We note that this is the same study population that has been used in our previous publication introducing the JSM algorithm.¹⁷

2.2. Segmentation and Joint Space Map Estimation

For each subject, we first segmented the tibia and femur using a semiautomated pipeline implemented in Matlab (Mathworks, Natick, Massachusetts) and ImageJ (NIH, Bethesda, Maryland). The CBCT reconstructions were thresholded to identify bone voxels. Morphological opening and closing were performed on the bone volume to remove erroneously classified soft-tissue voxels and fill holes. Afterward, a connected components analysis was performed to identify the tibia and femur, and additional binary closing was applied to each bone individually.

The voxelized segmentations of the tibia and femur were input to a previously reported joint space mapping algorithm.¹⁷ Briefly, the segmented tibial and femoral articular surfaces were treated as two conductors of a capacitor. The capacitor model was applied within an ∼65 mm wide region of interest (ROI) centered on the knee joint. All tibial surface voxels within the ROI were assigned to $+1\mathrm{V}$ potential; the femoral surface voxels were assigned to $-1\mathrm{V}$. A numerical solution of the Gauss’s law yielded the electric field lines joining the two surfaces. The length of the field lines was then computed using Euler’s method to provide an estimate of the JSW at each articular surface voxel. Field lines longer than 35 mm were omitted from the subsequent analysis because their paths fell outside the tibio–femoral joint space.

The choice of polarity of the articular surfaces is not critical in the electrostatic joint space model since only the length (and not the direction) of the field lines is used as the measure of JSM. Furthermore, our procedure did not involve any registration steps to ensure that the polar regions were consistently aligned to specific aspects of knee anatomy. Rather, we relied on a simple manual selection of the ROI, where the capacitor model was applied, and on thresholding of very long field lines to ensure that each articular surface voxel was equipped with a JSW measurement.

The JSMs obtained through the procedure outlined above have certain attractive properties. First, they are symmetric, i.e., independent of whether they were measured from femur or tibia. Such symmetry appears to represent the intuitive notion of local joint spacing better than a mapping based on closest point (CP) distances between surfaces—similar to conventional distance fields—where the outcome depends on whether the joint width is estimated from tibia to femur or vice versa. This asymmetry emerges because the CP model is ambiguous—multiple points on a source surface might map onto one point on the target surface. The second important characteristic of the our approach is that it does not rely on an arbitrary choice of a common projection direction, in contrast to the conventional radiographic measurement that uses the longitudinal axis (LA) of the knee joint as a reference. It is important to recognize that there is currently no large-scale clinical data to establish whether the theoretical advantages of the electrostatic JSM translate to improved diagnostic performance compared with the CP-based mapping (which has also been employed in weight-bearing CBCT²³) or the radiographic LA-based definition. However, the Fshape methodology is agnostic to how the JSM was generated and can accommodate other models^23,24 if future clinical evaluations suggest that such methodologies are advantageous compared with the current approach.

Point clouds of the boundaries of the tibia and femur were extracted from the voxelized segmentations and triangulated into textured surface meshes using MATLAB. For the analysis, the surface meshes were manually truncated in the longitudinal direction. For the tibiae, the resulting mesh boundaries were $\sim 20\mathrm{mm}$ away from the tibial plateaus; for the femurs, the boundaries were $\sim 25\mathrm{mm}$ away from the most distal aspect of the condyles (the distances are reported as measured along the long axes of the bones). Since the surface fidelity metrics considered in this work are in our experience fairly robust to intersubject inconsistencies in the definition of mesh boundary, we did not attempt to standardize the depth of the longitudinal truncation beyond simple visual inspection.

The JSMs were interpolated from the original voxel grid onto the vertices of the bone surface mesh—i.e., each vertex was equipped with an estimate of the local distance to the opposite bone (note that the same JSM is used for both bones owing to the symmetry of the electrostatic model). By the construction of the mesh, its vertex density was comparable to the voxel sampling density of the volume used for computing the JSMs. This ensured that the interpolation step did not result in substantial smoothing of the JSMs. This study does not investigate the performance of our method for surface triangulations that are markedly sparser than the voxel grid. The primary justification for using such sparse surface meshes is to accelerate atlas estimation. Since processing speed is usually not a concern in statistical shape analysis, we believe that the triangulation density employed here represents a reasonable choice that guarantees high fidelity of the shape model and of the JSM texture on that model. Such relatively dense mesh representations are particularly appropriate in CBCT to capture fine surface details revealed by the high isotropic spatial resolution of this modality.

3. Atlas Estimation

The procedure described above yields a cohort of textured triangulated surfaces that combine the shape of each tibia (resp. femur) with functional information on relative alignment between femur and tibia given by the JSM at each vertex. To identify the morphometric features of OA, we model and analyze the morphological variability in this dataset, namely the variability of both the tibia (resp. femur) shapes and JSMs. As mentioned earlier, our approach involves automatically estimating an atlas from these textured surfaces, consisting of a template representing a mean shape and a mean JSM, together with template-centered variables that model the shape and JSM transformations from the template to each subject in the dataset. This is achieved using the Fshapes approach that provides a joint geometric-functional, landmark-free framework to process such objects. Below we summarize the atlas estimation process for tibia surfaces equipped with JSM textures (the same procedure applies to femur surfaces). A more detailed description of the Fshape model and related algorithms can be found in Ref. 18.

3.1. Hypertemplate and Rigid Prealignment

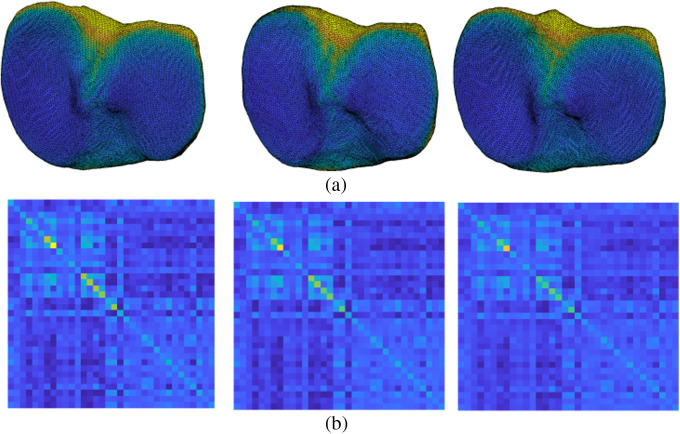
We start by defining a hypertemplate Fshape that will serve as an initial guess and reference for the atlas estimation process. (As a reminder, the term “functional shape” or Fshape refers to an object consisting of a triangulated surface and a texture on that surface, here, a JSM.) It was obtained by selecting a single subject from the population and applying three iterations of standard Laplace smoothing implemented in Meshlab to the triangulated bone surface mesh of that subject. (We confirmed that the number of smoothing iterations was sufficiently low to avoid selfintersections in the resulting hypertemplate.) The hypertemplate texture component was set to a constant equal to the average JSM value across all vertices of all subjects. This smooth initialization for the average Fshape will be later refined by the atlas estimation algorithm. Note that the choice of hypertemplate will still influence the estimated atlas at the output of the algorithm. As we will illustrate in Sec. 4.1 and Fig. 2, the eventual results remain fairly robust when other hypertemplates (based on different smoothed subjects from the population) are used instead.

Fig. 2.

(a) The template Fshapes as well as the $34\times 34$ Gram matrices of (b) the Fshape transformations $(v_i,h_i)$ for three estimated atlases corresponding to different choices of hypertemplate initializations.

Prior to atlas estimation, we performed a rigid alignment of each subject’s tibia to the tibia hypertemplate using the standard point cloud registration implemented in MATLAB. The same registration parameters were then applied to the femurs. This approach removed gross intersubject differences in the placement of the extremity within the scanner field-of-view—e.g., a rotation of the entire knee (i.e., only the transformation component that was common to the tibia and femur) with respect to the CBCT gantry. The JSMs were left unchanged on the new rotated/translated surfaces since the alignment step accounted for rigid displacements of the entire joint and the JSM is invariant to such transformations.

3.2. Atlas Problem Formulation

The atlas estimation problem is formulated a follows: consider a population of $N$ textured surfaces (Fshapes) $(S_i,f_i)$, where $S_i$ is the tibia surface of subject $i$, given as a triangluated set of vertices in ${\mathbb{R}}^3$, and $f_i$ is the JSM defined at each vertex of $S_i$. Our goal is to estimate a template Fshape $(\overline{S},\overline{f})$, representing the population mean surface-JSM object, together with a set of $N$ geometric–functional transformations mapping the template to each subject. Note that we do not assume any predefined correspondences between the vertices of the surfaces $S_i$ nor that the sampling density or number of vertices is the same for all $S_i$. The flexibility of this approach makes it well-suited for surfaces extracted from the CT images using the pipeline mentioned in Sec. 2. Furthermore, while in this study, the JSM textures were discretized at the vertices of the surface meshes $S_i$, a more finely sampled representation capturing the details of texture fluctuations within each triangle could also be incorporated into the atlas estimation algorithm as long as a reasonably efficient numerical differentiation scheme is available to compute gradients in this representation.

We now define a model of combined morphological and JSP transformations of these textured surfaces. Following the framework of Ref. 18, we first model the geometric deformation component of an Fshape transformation through a diffeomorphism of ${\mathbb{R}}^3$, namely a smooth and invertible mapping of the full 3D space that preserves the topology of the original surface. We estimate this deformation in the setting of large diffeomorphic deformation metric mapping (LDDMM).²⁵ Briefly, the diffeomorphisms are generated by flowing vector fields of ${\mathbb{R}}^3$. If $v(t,x)$, $t\in [\mathrm{0,1}]$, denotes an integrable time series of spatially smooth vector fields, the flow of $v$ is the mapping $(t,x)\mapsto {\phi }^v(t,x)$, where ${\phi }^v(t,x)$ is defined for all $x\in {\mathbb{R}}^3$ as the solution at time $t$ of the ODE $\dot{y}(t)=v(t,y(t))$ with initial condition $y(0)=x$. In integral from, this is written as

$${\phi }^v(t,x)=x+{\int }_0^{t}v(s,\phi (s,x))\mathrm{d}s.$$ (1)

Assuming that for each $t$, $v(t,·)$ belongs to a certain Hilbert space $V$ of sufficiently smooth vector fields (typically a Sobolev space of certain order), the results of Refs. ²⁵ and ²⁶ show that the transformations $\phi (t,·)$ are diffeomorphisms of ${\mathbb{R}}^3$. Furthermore, the quantity ${\int }_0^1{\Vert v(t,·)\Vert }_V^2\mathrm{d}t$, where ${\Vert ·\Vert }_V$ is a norm on the space $V$ of vector fields, is a natural metric or cost of the final deformation ${\phi }^v(1,·)$. This norm enforces spatial regularity of the field and resulting deformation and is typically defined based on a certain differential operator on the vector fields of $V$ (e.g., powers of the vector Laplacian of ${\mathbb{R}}^3$) that we write $L_V$. This results in the following energy associated with the deformation ${\phi }^v(1,·)$:

$$E_1(v)={\int }_0^1{\Vert v(t,·)\Vert }_V^2\mathrm{d}t={\int }_0^1{\int }_{{\mathbb{R}}^3}⟨v(t,x),(L_{V}v)(t,x)⟩\mathrm{d}x\mathrm{d}t.$$ (2)

Second, we define a model for variations in texture (i.e., JSM) of a generic Fshape $(S,f)$. We introduce a residual function $h:S\to \mathbb{R}$ also defined on the surface $S$. The residual modifies the JSM based on the simple relation $f+h$ (assuming for now that the shape $S$ is fixed). To regularize the transformation induced by the residual, we assume that the signal and residual are differentiable. Note that, in the discrete setting, this is not a restrictive assumption since the interpolation can be applied to obtain functions that are differentiable or at least differentiable almost everywhere; furthermore, the electrostatic joint model of Ref. 17 typically leads to smooth JSM functions. We then consider the following $H^1$ energy on $h$:

$$E_2(S,h)={\int }_S({|h(s)|}^2+{|{\nabla }_{S}h(s)|}^2)\mathrm{d}A(s),$$

where $dA$ denotes the area measure on the surface and ${\nabla }_{S}h$ is the surface gradient of $h$ along $S$. This extends the setting of Ref. 18 by adding a penalty on the gradient of the residual.

The combined transformation model of the Fshape $(S,f)$ is given by a pair $(v,h)$ of a deformation field $v$ (with associated deformation ${\phi }^v$) and a residual signal $h$. The transformed Fshape is $({\phi }^v,h)·(S,f)=({\phi }^v(S),(f+h)\circ {\phi }^{v,-1})$, where ${\phi }^v(S)$ is the surface transported by ${\phi }^v$ and ${\phi }^{v,-1}$ is the inverse of the mapping. The composition by ${\phi }^{v,-1}$ just means that the modified signal $f+h$ on $S$ is transported onto the new surface ${\phi }^v(S)$. The total energy of this transformation is defined as the sum of the energies of the shape and functional components:

$$E_S(v,h)=E_1(v)+\gamma E_2(S,h)={\int }_0^1{\Vert v(t,·)\Vert }_V^2\mathrm{d}t+\gamma {\int }_S({|h(s)|}^2+{|{\nabla }_{S}h(s)|}^2)\mathrm{d}A(s).$$ (3)

Note that we write $(v,h)$ as the only inputs of $E_S$, omitting the dependency on the surface $S$ on which we measure the variation of JSM. Moreover, we add a parameter $\gamma >0$, which acts as a balancing factor between these two energy terms. Indeed, these can have different ranges of values depending on the size of the shapes and amplitude of the signal functions. This parameter can be typically set through experimental calibration, for example, by running several one-to-one registrations using the representative Fshape pairs and comparing the values of the two energy terms after convergence. Based on such an optimization, we used $\gamma =0.1$ in the simulations of this paper.

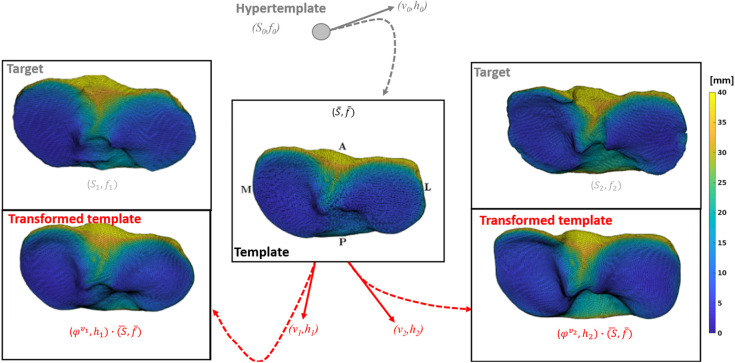
With the above model of Fshape transformation, we now return to the problem of atlas estimation from the set of $(S_i,f_i)$. Considering the hypertemplate Fshape $(S_0,f_0)$ as the starting point, we seek (i) a template (or average) Fshape $(\overline{S},\overline{f})$, which is itself a transformation of the hypertemplate given by the deformation field and residual $(v_0,h_0)$, as well as (ii) the transformations $\{(v_i,h_i)|i=1,\dots ,N\}$ that match the $(\overline{S},\overline{f})$ to the subjects of the population. The estimation, shown in Fig. 1, is formulated as the optimization problem:

$$\underset{(v_i,h_i{)}_{i=0,\dots ,N}}{\min }{E}_{S_0}(v_0,h_0)+\sum _{i=1}^N{E}_{\overline{S}}(v_i,f_i)\mathrm{subj.\; to}\{\begin{array}{l}(\overline{S},\overline{f})=({\phi }^{v_0},h_0)·(S_0,f_0)\\ ({\phi }^{v_i},h_i)·(\overline{S},\overline{f})\approx (S_i,f_i)\end{array},$$ (4)

where we point out that $h_0$ is by convention defined on the hypertemplate surface $S_0$, whereas the $h_i$ for $i=1,\dots ,N$ is defined on the template surface $\overline{S}={\phi }^{v_0}(S_0)$. We write $({\phi }^{v_i},h_i)·(\overline{S},\overline{f})\approx (S_i,f_i)$ since, in practice, we do not seek an exact matching to the subjects’ Fshapes and instead use relaxation fidelity metrics based on the framework of functional currents and varifolds. As detailed in Refs. ¹⁸ and ²⁷, where they were introduced, these fidelity metrics provide a measure of the proximity between two textured surfaces without the need to establish prior correspondences between their vertices. As a result, the atlas estimation procedure that we propose does not require establishing such landmark correspondences.

Fig. 1.

Overview of the atlas estimation setting. Starting from the initialization given by the hypertemplate Fshape $(S_0,f_0)$, the algorithm iteratively evolves the mean template together with the deformation fields $v_i$ and residual textures $h_i$ to generate template transformations approximately matching the respective textured surfaces in the dataset.

3.3. Algorithm

Equation (4) involves a high-dimensional and nonconvex optimization problem over the $N+1$ time-dependent deformation fields $v_i$ and residuals $h_i$. Except for $i=0$, the cost functional is a sum of independent terms on the $(v_i,h_i)\mathrm{s}$ for $i=1,\dots ,N$. We perform joint minimization over these variables using the quasi-Newton BFGS descent procedure and thus need to compute the gradient of the atlas estimation functional with respect to the different variables involved. For brevity, we leave the full details of these computations to Refs. ¹⁸ and ²² and only summarize the major points below.

The JSM residuals $h_i$ are defined on the vertices of $S_0$ (for $i=0$) or $\overline{S}$ (for $i=1,\dots ,N$). The gradient of the functional with respect to the $h_i\mathrm{s}$ is fairly straightforward to compute. We note that, compared with Ref. 18, we introduced the additional first-order term ${\nabla }_{S}h$ in the expression of $E_2$ that needs to be accounted for in the gradient. For the discretization of $E_2$, we introduce a usual ${\mathbb{P}}_1$ finite element scheme in which functions $h_{S,i}(s)$ are approximated by first-degree polynomial functions on each face of $S_0$ or $\overline{S}$ that interpolate the vertex values $h_i$. The entire cost functional becomes a function of the $h_i\mathrm{s}$ and is then differentiated accordingly.

The minimization over the deformation fields $v_i$ is more involved since these vector fields are defined at all times $t\in [\mathrm{0,1}]$ over the full space ${\mathbb{R}}^3$. Yet, as deformations are essentially acting on the (hyper-)template shape, the theory of optimal control for the LDDMM model²⁶ (see also Ref. 28) shows that one can limit the search to vector fields that can be more compactly represented by a finite set of momentum vectors attached to the vertices of the template surface. The dynamics of $v_i(t,·)$ with respect to the corresponding momenta is described by Hamiltonian equations. This allows for the implementation of a shooting strategy in which the optimization over the time-dependent vector fields is replaced by an optimization over the initial momentum vectors. The gradient of the cost functional with respect to the initial momenta is computed by backward integration of the adjoint Hamiltonian equations.

The atlas estimation algorithm was implemented as an extension of the FshapesTk MATLAB library²⁹ utilizing CUDA for the most numerically intensive operations. We performed two atlas estimations: one for the tibia and the other for the femur. As a reminder, the electrostatic JSM is symmetric, and thus the tibia and the femur were both equipped with the same JSM. The atlases were obtained for the combined population of OA and non-OA subjects (i.e., using a total of 34 textured surfaces as input). The surfaces had an average of 16k vertices, and the hypertemplates had $\sim 15\mathrm{k}$ vertices. The algorithm was run until convergence, which took 950 iterations and a total runtime of 50 h on one server node with a GeForce GTX 780 Ti graphics card.

3.4. Atlas Estimation Results

Figure 1 shows the template tibia surface and template JSM obtained from the atlas estimation algorithm applied to the entire population, i.e., jointly on the OA and non-OA subjects. The result $(\overline{S},\overline{f})$ is visually consistent with what would be expected of the mean shape and JSM, showing an increased joint space gap in the interchondylar notch area and narrower joint space on the tibial plateaus.

In addition to the template Fshape, the atlas estimation provides the deformation fields ${(v_i)}_{i=1,\dots ,N}$ and the residual JSMs ${(h_i)}_{i=1,\dots ,N}$ that transform the template to approximately match the shape and JSM of each subject. Figure 1 compares the result of applying this transformation to the template (labeled with red text) to the target tibia Fshapes of two subjects [labeled as $(S_1,f_1),(S_2,f_2)$]. To give a more quantitative assessment of this proximity, we computed the mean distance from each point on an articular surface of a subject to its CP on the corresponding transformed template (which gives a measure of proximity less sensitive to outliers than, e.g., the Hausdorff distance). Averaged across the whole population, we find an average distance of $1.15\pm 0.24\mathrm{mm}$ between the subjects and the initial (untransformed) tibia template versus $0.40\pm 0.011\mathrm{mm}$ for the distances between the subjects and the transformed template. The agreement between the transformed template and the measured shape is thus substantially improved compared with the initial undeformed template, suggesting that the proposed atlas estimation model is indeed able to capture the dominant aspects of morphological variability in the knee joint.

4. Statistical Analysis

The template transformations ${(v_i,h_i)}_{i=1,\dots ,N}$ shown in Fig. 1 provide a description of morphological variability of the dataset in the form of pairs of shape deformation fields and JSM residuals associated with each subject. These variables can be used to characterize the variance of the data around the template, and, perhaps more importantly, to discover statistically significant discriminative features between OA and non-OA subjects. Prior work has developed extensions of methods such as principal component analysis (PCA), support vector machines (SVM), linear discriminant analysis, or regression analysis for statistical analysis of purely geometric shape spaces.^30–34 Here, we adapt such methods to the present case involving joint consideration of shape and texture on that shape.

4.1. Dimensionality Reduction

The high dimensionality of variables $(v_i,h_i)$ poses a challenge for statistical analysis. As is quite common in biomedical datasets, the total number $N=34$ of subjects in the study sample is significantly smaller than the dimensions of the variables $v_i$ and $h_i$, which are respectively $n\times 3$ and $n$, where $n$ is the number of vertices of the template ($n=\mathrm{15,146}$ here). In Ref. 22, a similar two-class problem was tackled using the regularized linear discriminant analysis to prevent model overfitting. However, the choice and influence of the regularization parameter is challenging to analyze and interpret, particularly for the data structures at play in this work. Instead, we choose to proceed in two steps, as advocated in many data analysis studies: first, we perform feature selection to reduce the dimensionality of model variables, followed by classification (or discriminative analysis) on the reduced variable set.

Variables $v_i$ and $h_i$ are vector and scalar maps defined at all vertices of the template. We wish to preserve this global structure in the feature extraction step, as opposed to, e.g., extracting features defined at isolated vertices, which may not be relevant or easily interpretable in this context. To that end, we use PCA as an (unsupervised) approach for dimensionality reduction and variance analysis of the dataset. For statistical analysis of geometric deformations, prior publications have typically applied PCA to the corresponding Jacobian determinant maps or deformation gradient tensors.¹⁴ In our context, it is more natural to perform PCA directly on the Fshape transformations using the metric of transformation energy [Eq. (3)] rather than the standard (but meaningless here) Euclidean metric on the vectorized $(v_i,h_i)\mathrm{s}$. For this purpose, we only need to compute the Gram matrix $G={(⟨(v_i,h_i),(v_j,h_j)⟩)}_{i,j=1,\dots ,N}$, where

$$⟨(v_i,h_i),(v_j,h_j)⟩\doteq {\int }_0^1{⟨v_i(t,·),v_j(t,·)⟩}_V\mathrm{d}t+\gamma {\int }_{\overline{S}}(h_i(s)h_j(s)+{\nabla }_S{h}_i(s)·{\nabla }_S{h}_j(s))\mathrm{d}A(s),$$ (5)

and apply PCA to this transformed representation of the data. We show the profile of the Gram matrix in Fig. 2(left). It depends naturally on the parameters of the metric but can technically also vary with the choice of hyperparameters used in the atlas estimation process, in particular, the selection of the hypertemplate. To evaluate how robust the approach is in that regard, we also ran the atlas estimation for different choices of hypertemplates. (This experiment was performed only for the tibia). Figure 2 shows the resulting average shape + JSM templates [Fig. 2(a)] and the associated Gram matrices [Fig. 2(b)]. The average templates are relatively stable across the different instances: the mean JSWs of the three cases are 8.65, 9.39, and 9.82 mm (left to right), and the mean distance between pairs of template surfaces—taken as the mean distance of corresponding vertices—is 0.5 mm. Similarly, the Gram matrices for the three hypertemplates (essentially representing the distance between the resulting templates and each shape + JSM in the dataset) are also stable across the three initializations.

Note that the PCA analysis can be performed on the geometric (resp. texture) variation component only by considering the Gram matrix obtained with only the first (resp. second) term of Eq. (5). Importantly, in both approaches, the geometric and texture variability in the sample are jointly established through the atlas estimation process. Only the PCA and subsequent classification are restricted to one of the components (shape/geometry or texture/JSM). In the latter, we will refer to the three possible classification approaches as “modalities.”

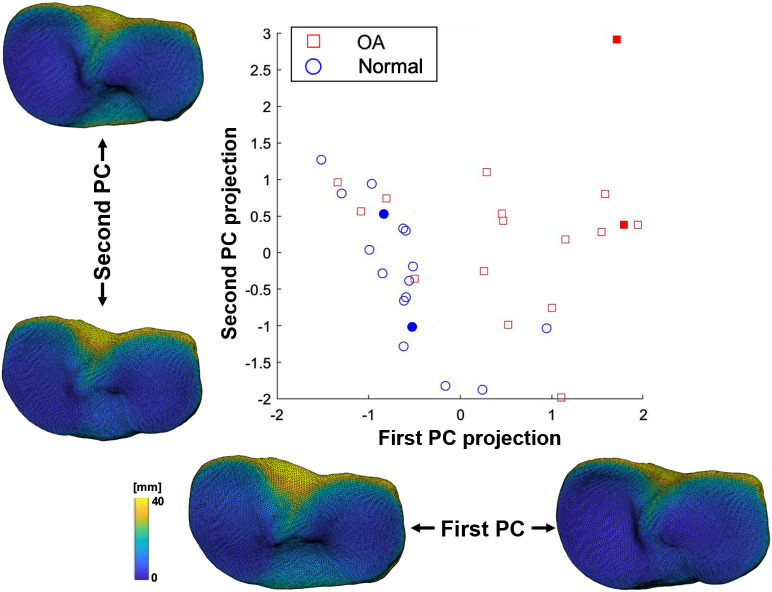
Figure 3 shows the projection of subject data in the 2D space given by the first two principal components (PCs) of the combined geometric-texture transformation of the tibia. The OA population exhibits higher variance of PC scores compared with non-OA, as well as a slight trend toward positive scores of the first PC. As PCA modes are linear combinations of the $(v_i,h_i)\mathrm{s}$, one can generate the corresponding Fshape transformations and visualize the effect of those PC transformations on the template, as shown in Fig. 3. The first PC appears to correspond to (i) a shape deformation resulting in deepening of the medial tibial plateau and (ii) a texture transformation resulting in shallower joint space.

Fig. 3.

Projection of the knee CBCT dataset on a 2D space defined by the fitst two PCs of the Fshape transformations. The tibial shapes and JSMs corresponding to the first two principal modes of variation are also illustrated. CBCT volumes of subjects indicated with filled markers are shown in Fig. 6.

4.2. Learning Discriminant Features

The PCA modes account for the variability across the full dataset, but they are not necessarily the most representative of the effect of OA on the shape and JSM of the tibio–femoral joint. To extract most discriminant features of OA, we now consider supervised machine learning techniques applied to the PCA representation of the data.

Specifically, for any predefined dimension $r$ of the PCA reduction (Sec. 4.1), we obtain projected coordinates (scores) $z_1,\dots ,z_N\in {\mathbb{R}}^r$ of the full dataset. A linear SVM classifier is trained on the PCA coordinates together with subjects’ labels (OA or non-OA).

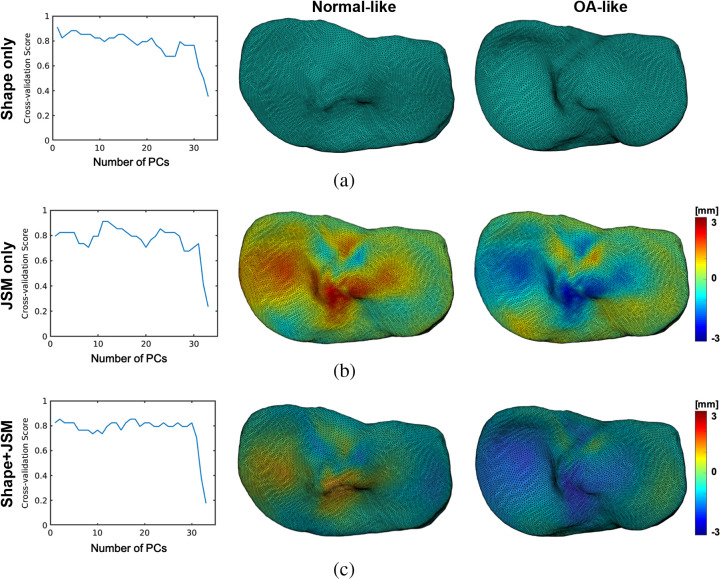
The choice of $r$ may have significant influence on the resulting classifier: a too low value of $r$ may not capture enough dimensions to recover discriminant features, whereas a too large $r$ may in turn incorporate noisy components and degrade the prediction accuracy. To optimize $r$, we perform leave-one-out cross validation for each choice of dimension $r$ to assess the classification accuracy of the corresponding linear SVM classifier. The cross-validation scores are plotted in Fig. 4 for three-dimensionality reduction modalities discussed in Sec. 4.1: pure geometric (shape) variations, pure texture variations, and geometry + texture combined [which only differ in the choice of the Gram matrix in Eq. (5), namely keeping only the first term, the second term, or both terms in the inner product, respectively].

Fig. 4.

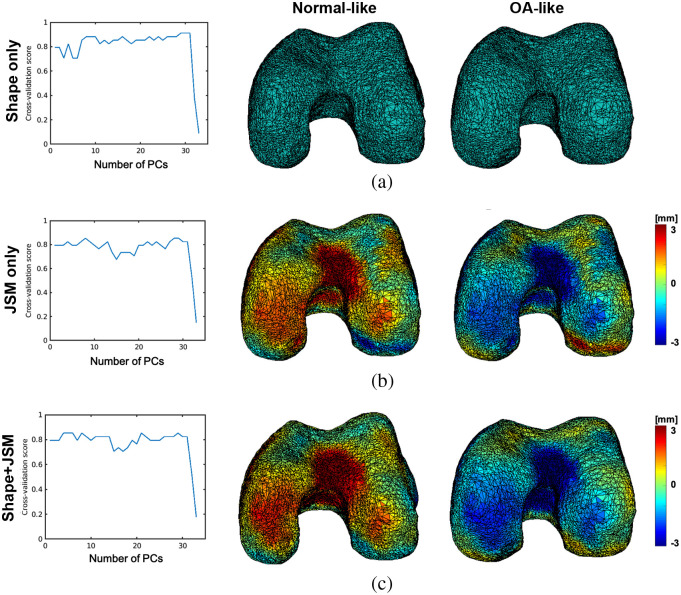
Leave-one-out cross-validation rates as a function of the PCA reduction space dimension $r$ for the SVM classifications based on (a) the geometric (shape) components of the Fshape atlas-to-subject transformations, based on (b) the JSM residual component of the transformations, and based on (c) the geometric and the JSM component. The effects of applying the discriminant vectors identified through this analysis to the template are shown on the right. The anatomical directions are consistent with Fig. 1: top is anterior, bottom is posterior, left is medial, and right is lateral. The colormaps in this and the following figures represent the residual JSM, that is the deviation from the template JSM. Negative values indicate narrowing of the joint space.

We obtain maximal scores of $31/34\approx 91.18\%$ for the classifications based on geometry PCs of the tibia [Fig. 4(a)] and residual JSM PCs [Fig. 4(b)]. In the first case, the highest score is obtained with $r=1$, meaning that the most discriminant direction coincides with the first PC of shape deformations. However, for the residual JSMs-based classification, the optimal score is obtained with $r=11$ or $r=12$ PCA modes. In both cases, we find three misclassified subjects, two of which are common to both modalities. The approach utilizing the entire Fshape transformation for classification [combined shape deformation and residual JSM, Fig. 4(c)] leads to slightly lower, but more stable with respect to $r$, cross-validation scores. The highest value of $29/34\approx 85.29\%$ is attained for $r=\mathrm{2,17},18$. We also provide in Table 1 the confusion scores for each case. The majority of misclassified subjects, in particular the ones misclassified by the shape only features, were found to be OA patients with only minimal radiographic joint space narrowing. The diagnosis of OA in these cases was based on the other clinical criteria stated in Sec. 2.1, such as symptoms or presence of osteophytes. It is plausible that these subjects represent a specific phenotype of the disease that was underepresented in our study sample and that has not been captured by the current statistical analysis of the Fshape transformations.

Table 1.

Confusion matrices for the different modalities (obtained with the optimal value of $r$ in each case).

	Normal	OA
Shape only
Normal	17	3
OA	0	14
JSM only
Normal	16	2
OA	1	15
Both
Normal	16	4
OA	1	13

As a reminder, the three classification modalities described earlier were based on the same set of shape and texture transformations, jointly established by the atlas estimation algorithm. Only the final PCA and SVM analyses were performed on a subset of those transformations. An alternative and more commonly used approach would be to only estimate the geometric registrations between the template and each of the subject surfaces, without considering the JSM match in atlas optimization. The registrations could then be used to map the raw JSMs back to the template surface. The dimensionality reduction and SVM could then be performed directly on the resulting pulled-back JSMs. In initial experiments, this leads to consistently worse cross-validation scores than our approach. We indeed found scores below 80% for all values of $r$ in this case. The proposed description of JSM variability in terms of residual transformations of a mean template estimated jointly with shape deformation appears to yield a more robust description of JSM features of OA.

To visualize and interpret the morphological and JSM changes underlying the estimated discriminant features of the tibia, we chose the optimal values of the dimensionality reduction parameter $r$ for each of the classification modalities and computed the corresponding linear SVM discriminant vectors over the entire dataset. The effects of applying the transformations associated with these vectors to the template shape and JSM are displayed in the right panel of Fig. 4. The top row illustrates the features identified using only the shape deformation component of the Fshape template-to-subject mappings provided by atlas estimation. OA-like morphology exhibits a deepening of the medial plateau combined with a narrowing of the interchondylar notch and deformation of the posterior tibia. The middle row shows non-OA and OA-like JSMs obtained by applying residuals representing the discriminant direction of only the texture component of the Fshape transformations. OA appears to be associated with a narrower joint space primarily in the areas of the medial plateau and interchondylar notch. Finally, Fig. 4(c) shows the combined shape-texture discriminant vectors given by PCA-SVM analysis of components of the template-to-subject Fshape mappings. We would like to re-emphasize here that the only difference between this modality and the classifications in Figs. 4(a) and 4(b) is in applying the PCA jointly (instead of individually) to the shape deformations and JSM changes obtained from the atlas estimation procedure. The atlas estimation itself was the same for all three modalities and was always informed by both the geometry and signal patterns of the Fshapes. It is indeed the case, though, that the combined classification of both components gives a slightly lower score ($29/34\approx 85.29\%$) than the other modalities, which appears to be the result of misclassified subjects for the shape and JSM modalities being all misclassified again when those are combined in the SVM analysis. However, the combined classification extracts similar features to those identified using the individual texture and shape modalities, namely deepening of the medial tibial plateau (a geometric effect) and narrowing of the joint space in the same region (a JSM/texture effect). Moreover, as mentioned earlier, the scores of the combined classifier appear more stable with the number of selected PCA modes $r$ than for the other modalities.

These observations are further confirmed by applying the same atlas estimation and statistical analysis of the Fshape transformations to the femur surfaces instead. Figure 5 shows the corresponding discriminant directions for each modality together with the leave-one-out cross-validation rates. Once again, these highlight a global narrowing of the knee combined with a compression of the intercondylar notch associated with OA patients compared with the controls.

Fig. 5.

Leave-one-out cross-validation rates as (a) a function of $r$ and (b) discriminant vectors for SVM classifications on distal femur data. Similar to Fig. 4, the top row shows the results for the classification based on the geometric components of the Fshape, the middle row uses the JSM residual, and the bottom row uses the geometric and the JSM components. Anatomical directions key: top is anterior, bottom is posterior, left is medial, and right is lateral.

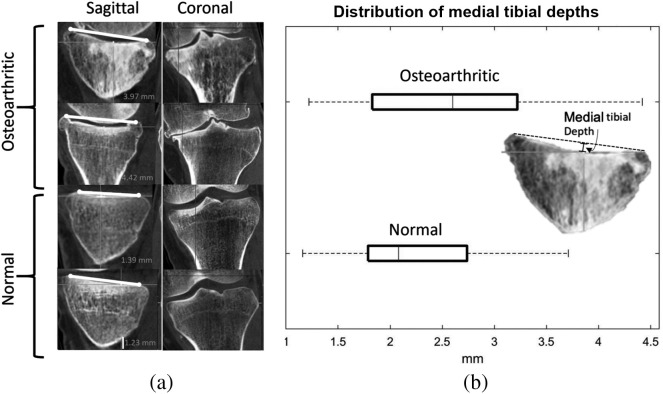
To illustrate how the OA features identified using the Fshape methodology relate to the findings of conventional joint space assessment, Fig. 6 shows the original CBCT images of two example OA cases and two example non-OA cases. The four cases are indicated with solid markers in the PCA projection graph of Fig. 3. The narrowing of the medial joint space in the example OA subjects is apparent in the coronal plane views (left side of the knees) and agrees with the JSM discriminant features of Fig. 4. Furthermore, the sagittal views reveal appreciable concavity of the medial tibial plateau in the OA knees compared with normals, as would be expected based on the shape features of OA identified in our analysis. To quantify this finding, we performed measurements of medial tibial depth (MTD)³⁵ across the entire study sample. The measurement involves drawing a line connecting the peak anterior and posterior points of the medial tibial plateau in its central sagittal plane and computing the distance from that line to the deepest point of the plateau, as shown in Fig. 6. The distribution of MTDs in the OA and non-OA subgroups, summarized with a box-and-whisker plot in Fig. 6, shows that the OA subjects indeed exhibit a somewhat deeper medial tibial compartment. Overall, the discriminant features of the Fshape transformations appear to agree with visual assessment and conventional anatomical measurements of the knee datasets.

Fig. 6.

(a) Example CBCT volumes of two OA subjects and two normal subjects, illustrating medial joint space narrowing and deepening of the medial tibial plateau consistent with the findings of the discriminative analysis of the Fshape model. In the coronal view, medial is to the left of the image. (b) Distribution of MTD measurements in the study population, further confirming the tendency toward increased concavity of the medial plateau.

5. Discussion

We demonstrated an application of the functional shape framework for statistical analysis of morphological variability in normal and osteoarthritic knees. The proposed approach models the knee as a combination of a geometric shape—the tibial surface—and a texture representing a map of JSWs at the points of the surface (theJSM). Indirectly, the texture component of the Fshape measures the relative position of the tibia and the femur. To our knowledge, this represents the first use of this mathematical model to describe the tibiofemoral joint.

Given the knee Fshapes of a study subject cohort, an atlas estimation algorithm was applied to yield a template describing the mean tibial (or femoral) surface and mean JSM in the cohort. The morphology of each subject was then summarized in terms of a transformation—consisting of a diffeomorphic shape deformation and a JSM residual—that mapped the template Fshape to the Fshape of the subject. Since the atlas estimation was performed jointly on the geometric and JSM components, our framework preserved the spatial relationships between major bone shape features and the corresponding local patterns of JSW. Initial results appear to suggest that this yields more robust morphological features than a multistage approach consisting of shape registration followed by remapping of the JSMs using the registration transformations.

Unlike the conventional statistical shape modeling (SSM) strategies commonly applied in OA, the proposed algorithm for Fshape matching does not require a priori point correspondences between the subjects’ tibial surfaces. It has to be recognized that some degree of internal consistency between the input datasets is still required, including a roughly matched selection and discretization of bone regions used to create the articular surface models and to compute the JSMs. Nevertheless, our results indicate that the desired data uniformity can be achieved through relatively straightforward manual preprocessing. Compared with shape modeling based on matching landmarks, which often relies on identifying vertex correspondences within densely sampled surface meshes, our framework might be potentially better suited for situations in which the datasets obtained at different resolutions or with different modalities are combined for morphological analysis. In such cases, the correspondence-based methods might be challenged by intersubject surface discretization mismatches caused by the variance in acquisition parameters. For datasets where spatial resolution and surface discretization density are roughly similar across all subjects, the landmark-free and landmark-based approaches are likely equally applicable, at least in practice (in fact, the generative atlas framework might incur a higher computational cost). However, we are not aware of any principled algorithms for combined analysis of the variability in shape (here, articular surface) and a texture on the shape (here, the JSM) using the conventional, landmark-based formulation. Therefore, the Fshapes offer a potentially valuable alternative to the current methods of morphological analysis in OA by providing such a combined model within the generative atlas setting. Furthermore, since the Fshapes use diffeomorphic mappings to describe shape variability, they might be sensitive to different aspects of the disease than the conventional approaches that examine statistical distributions of landmark locations. Further studies in large patient cohorts are needed to obtain a rigorous comparison of the two frameworks in the detection of morphological features of OA.

The template-to-subject Fshape mappings established through the atlas estimation serve as input variables for analysis of morphological variability in the sample set. Here, we performed such analysis to identify tibial shape and JSM features that are discriminative of OA. It is important to note that the primary goal of this work was to demonstrate the feasibility of the Fshape framework in application to 3D knee datasets. The OA classification experiments were not meant to yield generalizable conclusions regarding shape and JSM features of the disease. Rather, they provided a demonstration that the Fshape mappings obtained through atlas estimation do indeed reflect major patterns of morphological variability in the study sample. This is evidenced by the high rate of correct classifications ($>80\%$) obtained using the geometric and JSM features obtained through the Fshape atlas estimation framework. However, given the rather small number of subjects in the dataset and the simple structure of the disease group—consisting mainly of patients with fairly advanced diagnostic features of OA—the classification scores obtained in our analysis remain largely indicative at this point. Future work should involve more extensive classification experiments in larger and more diverse populations.

Recognizing the preliminary character of our classification study, we wish to discuss two additional considerations. First, while we chose a framework based on PCA of the Fshape mappings combined with linear SVM, other linear methods for dimensionality reduction and discriminant analysis are a priori also suitable, including linear discriminant analysis or LASSO.³⁶ Furthermore, the description of knee morphology using Fshape transformations also supports nonlinear classifiers such as kernel SVM or random forests³⁷ and/or a variety of alternative approaches for the feature reduction step, c.f., for instance the recent review.³⁸ We have tested some of those alternatives and found slightly higher significance of the discriminant features obtained from our proposed PCA/SVM approach. The reason for this finding might be that these more sophisticated classification approaches were overparametrized because of the relatively small sample size in this feasibility study, leading to potential overfitting. Since our objective was to illustrate the relevance of morphological features obtained through Fshape analysis and not to optimize OA classification, we concluded that the proposed PCA/SVM framework was sufficient for this goal. In this context, an additional advantage of linear SVM over nonlinear methods is that the direction that the separating hyperplane obtained from SVM can be directly viewed as a global deformation or change in JSM (see Figs. 4 and 5). Such a convenient visualization is more difficult to achieve for nonlinear classifiers.

Second, even though the OA features obtained in our analysis are not generalizable because of the small study sample in this work, a brief comparison with OA features identified in other SSM studies is in order. Recognizing the differences in study populations and analysis methodologies that make such a comparison very preliminary, we note a number of similarities between our findings and those of earlier SSM results. For example, Ref. 9 demonstrated regions of elevated tibial surface in the intercondylar eminence and a slight deepening of the tibial plateau in subjects at risk of OA compared with controls. Both of these features are also present in our discriminant vectors of Fig. 4. Lynch et al.¹⁰ compared mean normal and OA knee shapes obtained from SSM and reported, among other features, slightly depressed medial and lateral tibial plateaus and narrowing/elevation of proximal intercondylar eminence. Neogi et al.⁷ compared extreme examples of OA and non-OA knee models obtained from SSM and found a ridge of “osteophytic” growth around the perimeter of the articular surface of the tibia (which may correspond to apparent deepening of the tibial plateaus seen in our model) and narrowing/elevation of the intercondylar spine. Similar shape features of OA are present in the shape models of Bowes et. al.³⁹ Overall, the findings of steeper intercondylar eminence and relatively deeper tibial plateaus compared with the perimeter of the tibia appear to be shared by our model of OA discriminant features and prior work.

With respect to JSM (the texture component of the Fshape), the discriminant analysis of Fig. 4 indicated a narrower joint space in OA-like knees, in particular, in the medial aspect of the tibia. This finding is not unexpected in this study population consisting of symptomatic OA patients since (as mentioned in Sec. 1) joint space narrowing is a recognized diagnostic marker of OA. However, the proposed method enables simultaneous examination of the variability in bone shape and JSM, thus providing a unified mathematical framework to discover co-occurring features of those two aspects of knee morphology. For example, our findings show that the loss of joint space in the medial compartment of OA knees is accompanied by increased depth of the tibial plateau in this region, suggesting that the femur “sinks” into the eroded medial tibial condyle on that side.

The analysis of SVM discriminant directions raises an interesting point of whether such features can be converted into a simple numerical representation as a first step toward the development of quantitative biomarkers. SVM provides only a normalized discriminant vector representing the direction of the separating hyperplane in the space of Fshape transformations. It is challenging to convert this normalized vector representation into a direct estimate of, e.g., the amplitude of local joint narrowing or articular surface deepening. However, we believe that one could still obtain a quantitative metric of the interclass shape and JSM differences by computing the distance of each class center to the discriminant hyperplane. Such a distance could then be used as a potential estimate of the average intensity of the effect along the discriminant vector. The development and validation of such quantitative metrics is beyond the scope of the current feasibility study.

Another important direction for the future development of the FShape framework in orthopedic applications is an extension to joint space mapping approaches beyond the electrostatic formulation investigated here. As discussed in Sec. 2.2, the capacitor model has certain theoretical advantages—namely symmetry and not requiring a fixed reference axis—compared with other JSM estimation algorithms proposed for 3D analysis of OA.^23,24 In fact, these properties are attractive for thickness measurements in a variety of laminar structures. For example, similar methods based on the Laplace equation have been proposed for thickness calculations in the myocardium and brain cortex.^40,41 However, the electrostatic model results in long field lines at the periphery of the articular surface that do not accurately represent the JSW in this area. In our experience, such long field lines can be excluded from analysis (here using a >35-mm threshold) since they typically form a contiguous annulus outside the region affected by OA. However, a more robust JSM estimation method is desirable to avoid such arbitrary postprocessing. One potential alternative might involve adopting a definition of thickness developed for brain imaging in Refs. ⁴² to ⁴⁴. In these studies, signed 3D distance functions from the two surfaces bounding the volume of interest are first obtained. Next, 0-level-sets of a normalized weighted sum of the two distance functions are computed for a range of weight parameters $w$. In this manner, $w$ becomes a normalized depth coordinate within the volume of interest, with the length of streamlines of $w$ providing a measure local thickness. Since the pseudopotential $w$ represents a smooth evolution of one articular surface onto the other, its streamlines might yield a more accurate distance metric at the periphery of the joint compared with the electric field lines considered in our approach. Recognizing the potential benefits of translating these sophisticated thickness estimation strategies to orthopedic imaging, we note that the Fshape framework is agnostic of the procedure used to obtain the JSMs. While the current feasibility study used the capacitor model—primarily because it has been previously shown to be predictive of OA in CBCT images—the proposed methodology will be equally applicable to the level-set definition of thickness described earlier. Rigorous comparison of diagnostic performance of Fshapes utilizing various joint space mapping techniques is a promising area for future research.

In summary, we demonstrated the feasibility of statistical analysis of 3D knee morphology using the framework of functional shapes. The proposed methodology enables combined modeling of population variability in bone shape and in spatial maps of articular space width without the need for landmark correspondences between the members of the study sample. Preliminary results indicate that this approach is capable of identifying morphological features associated with joint degeneration in OA. Future work will establish the statistical significance of functional shape findings in OA using larger and more diverse populations.

Biography

Biographies of the authors are not available.

Disclosures

The authors declare no conflicts of interest.