Impact of Accelerating Insulin on an Artificial Pancreas System Without Meal Announcement: An In Silico Examination

Abstract

Background:

Controlling postprandial blood glucose without the benefit of an appropriately sized premeal insulin bolus has been challenging given the delays in absorption and action of subcutaneously injected insulin during conventional and artificial pancreas (AP) system diabetes treatment. We aim to understand the impact of accelerating insulin and increasing aggressiveness of the AP controller as potential solutions to address the postprandial hyperglycemia challenge posed by unannounced meals through a simulation study.

Methods:

Accelerated rapid-acting insulin analogue is modeled within the UVA/Padova simulation platform by uniformly reducing its pharmacokinetic time constants (α multiplier) and used with a model predictive control, where the controller’s aggressiveness depends on α. Two sets of single-meal simulations were performed: (1) where we only tune the controller’s aggressiveness and (2) where we also accelerate insulin absorption and action to assess postprandial glycemic control during each intervention.

Results:

Mean percent of time spent within the 70 to 180 mg/dL postprandial glycemic range is significantly higher in set (2) than in set (1): 79.9, 95% confidence interval [77.0, 82.7] vs 88.8 [86.8, 90.9] ([Note to typesetter: Set all unnecessary math in text format and insert appropriate spaces between operators.] P < .05) for α = 2, and 81.4 [78.6, 84.3] vs 94.1 [92.6, 95.6] (P < .05) for α = 3. A decrease in percent of time below 70 mg/dL is also detected: 0.9 [0.4, 2.2] vs 0.6 [0.2, 1.4] (P = .23) for α = 2 and 1.4 [0.7, 2.8] vs 0.4 [0.1, 1.4] (P < .05) for α = 3.

Conclusion:

These proof-of-concept simulations suggest that an AP without prandial insulin boluses combined with significantly faster insulin analogues could match the glycemic performance obtained with an optimal hybrid AP.

Introduction

Postprandial glycemia makes a substantial contribution to overall glycemic control in diabetes treatment. Unfortunately, meeting postprandial glycemic target values has been challenging due to slow absorption and action of subcutaneously injected insulins. Insulin secretion from a healthy β-cell is a highly dynamic process, where glucose is the main stimulator of insulin release, leading to the characteristic biphasic pattern consisting of a brief first phase of insulin secretion (~10 minutes), followed by a sustained second phase. The earliest secreted insulin is a necessary element to offset the rapid rise in postprandial blood glucose. Unlike the rapid physiologic action of insulin after its release from a healthy β-cell, the maximum glucose lowering action from a subcutaneously injected insulin could be observed as late as 90 minutes to two hours after its injection.^1,2 The underlying reasons for delay in insulin action are multifactorial, with chemical properties of insulin and factors concerning subcutaneous (SC) tissue being the principal contributors.³ Moreover, subcutaneously delivered insulin may pose additional glycemic risks due to its prolonged action (up to six hours), potentially increasing the risk of late postprandial hypoglycemia.

A single-hormonal artificial pancreas (AP) system optimizes insulin delivery in real time, every five minutes, based on changes in sensor glucose levels. While most current systems function best with a premeal insulin bolus (hybrid AP), a fully automated system would not benefit from this sharp and early increase in circulating insulin. Consequently, a fully automated AP insulin controller reacts to meals only after sensor glucose levels begin to rise. Besides, there is no insulin depot delivered in to the SC area as the insulin delivery is spread over hours in mini boluses; therefore, the delay in insulin absorption and action is further exacerbated during fully automated AP, representing one of the main barriers to its implementation.^4,5 Thus, the most common strategy is to define a single- or dual-hormone system with a hybrid controller, where feedforward insulin boluses are manually delivered at mealtimes, and the control law takes over the basal rate.^6-11 The drawback associated with this design is that manual priming requires user assessment of the total amount of carbohydrates for every meal, which is a burdensome and potentially inaccurate task for patients.^12,13

Other insulin delivery routes than SC have been explored to generate more physiological plasma insulin profiles. For example, inhaled human insulin has shown tangible benefits with respect to SC insulin injections.¹⁴ However, this scheme also depends on prandial manual doses. Another alternative is to deliver insulin into the intraperitoneal (IP) space to minimize delays.¹⁵ For instance, fully automated AP combined with IP insulin delivery provided superior glucose control to that with SC insulin delivery in a short demonstration study.¹⁶ Nevertheless, this approach’s clinical application is still limited by its inherent costs and risk profile.¹⁷

Although fully automated AP has been successfully deployed in clinical studies,^18-24 there is an undeniable compromise between the controller’s aggressiveness and insulin stacking due to the extended duration of insulin action (DIA). An ideal insulin analogue should mimic the pharmacokinetic (PK) and pharmacodynamic (PD) profiles of endogenous insulin to optimize exogenous insulin treatment. Rapid-acting insulin analogs with faster PK/PD profiles have been introduced recently toward this goal,^25-27 but a significant unmet need for more rapid insulin absorption that provides superior postprandial glucose control remains, particularly as new AP technology enters clinical care.^1,28

In this work, we delve into how much the analogue insulin lispro (LIS) glucodynamic action could be accelerated to safely increase the controller’s aggressiveness in a SC AP with a model predictive control (MPC) law. To this end, we leverage the UVA/Padova simulator²⁹ to test the performance of the proposed controller in scenarios that include both announced and unannounced meals and different synthetic insulins.

Methods

Model of Insulin Pharmacokinetics

In this article, we consider the two-compartment PK model of SC fast-acting insulin that was presented in Ref.³⁰ and later updated in Ref.³¹:

$${\stackrel{·}{I}}_{\mathrm{sc}1}\left(t\right)=-\left(k_{\mathrm{a}1}+k_{\mathrm{d}}\right)I_{\mathrm{sc}1}\left(t\right)+u\left(t-\mathrm{\tau }\right)$$ (1)

$${\stackrel{·}{I}}_{\mathrm{sc}2}\left(t\right)=-k_{\mathrm{a}2}{I}_{\mathrm{sc}2}\left(t\right)+k_{\mathrm{d}}{I}_{\mathrm{sc}1}\left(t\right)$$ (2)

$$R_{\mathrm{i}}\left(t\right)=k_{\mathrm{a}1}{I}_{\mathrm{sc}1}\left(t\right)+k_{\mathrm{a}2}{I}_{\mathrm{sc}2}\left(t\right)$$ (3)

where $I_{\mathrm{sc}1}$ and $I_{\mathrm{sc}2}$ (pmol/min) are, respectively, the amounts of monomeric and nonmonomeric insulin in the SC space, $k_{\mathrm{a}1}$ and $k_{\mathrm{a}2}$ (1/min) are the corresponding rate constants of absorption into plasma, $k_{\mathrm{d}}$ (1/min) is the diffusion rate from nonmonomeric to monomeric state, $u$ (pmol/kg/min) is the exogenous insulin infusion rate, $\mathrm{\tau }$ (min) is a subject-specific input delay, and $R_{\mathrm{i}}$ (pmol/kg/min) is the rate of insulin absorption into plasma. In Ref.³¹, the PK model was identified using insulin data collected from 116 adult subjects with type 1 diabetes (T1D) who underwent a SC injection of LIS. Individual sets of PK parameters were extracted from parameter distributions obtained from model identification that were then randomly assigned to each in silico subject of the simulator. Analysis of population sets indicate that all PK parameters follow a lognormal probability distribution and are uncorrelated from each other and from the other parameters of the UVA/Padova model.

In Silico Generation of Faster Insulin Analogues

The model described by Equations (1) to (3) is a second-order time-delay linear time-invariant system with the following transfer function:

$$G_{{\mathrm{i}}_{\mathrm{sc}}}\left(s\right)=\frac{k_{\mathrm{a}1}s+k_{\mathrm{a}2}\left(k_{\mathrm{a}1}+k_{\mathrm{d}}\right)}{\left(s+k_{\mathrm{d}}+k_{\mathrm{a}1}\right)\left(s+k_{\mathrm{a}2}\right)}{e}^{-\mathrm{\tau }s}$$ (4)

As shown, $G_{{\mathrm{i}}_{\mathrm{sc}}}$ has two poles located at $p_1=-(k_{\mathrm{d}}+k_{\mathrm{a}1})$ and $p_2=-k_{\mathrm{a}2}$. According to the parameter estimates reported in Ref.³¹, the mean value of $k_{\mathrm{a}1}$ is close to zero and negligible with respect to the mean values of both $k_{\mathrm{d}}$ and $k_{\mathrm{a}2}$. Thus, $G_{{\mathrm{i}}_{\mathrm{sc}}}\left(s\right)$ can be approximated as:

$$G_{{\mathrm{i}}_{\mathrm{sc}}}\left(s\right)\cong {\tilde{G}}_{{\mathrm{i}}_{\mathrm{sc}}}\left(s\right)=\frac{k_{\mathrm{a}2}{k}_{\mathrm{d}}}{\left(s+k_{\mathrm{d}}\right)\left(s+k_{\mathrm{a}2}\right)}{e}^{-\mathrm{\tau }s}$$ (5)

In order to define faster insulin analogues, we accelerate the insulin absorption from the SC tissue by manipulating only the poles of ${\tilde{G}}_{{\mathrm{i}}_{\mathrm{sc}}}\left(s\right)$ while keeping the other parameters unchanged. To this end, lognormal distributions were fitted to the vectors of parameters $k_{\mathrm{d}}$ and $k_{\mathrm{a}2}$ associated with LIS, and new sets were sampled from the fitted distributions, but with their mean values modified by a factor of $\mathrm{\alpha }>1$.

The bandwidth of a system is commonly defined as the lowest frequency satisfying −3 dB from its gain at zero frequency. Note that if the average bandwidth of the PK model for LIS is ${\mathrm{\omega }}_{\mathrm{l}}$, then the average bandwidth for the $\mathrm{\alpha }$-insulin analogue will be ${\mathrm{\omega }}_{\mathrm{f}}=\mathrm{\alpha }{\mathrm{\omega }}_{\mathrm{l}}$. In this way, the larger $\mathrm{\alpha }$ is, the faster the analogue becomes.

In order to determine the PK/PD properties of the $\mathrm{\alpha }$-insulins, a euglycemic clamp was performed in simulation. In this in silico procedure, a 0.2 U/kg single dose of $\mathrm{\alpha }$-insulin was administered to each of the 100 in silico adults of the UVA/Padova simulator and the simulated intravenous glucose infusion rates (GIR) were automatically adjusted by means of a proportional controller that maintained the glucose levels close to the basal values. Figures 1 and 2 illustrate the PK and GIR profiles, respectively, for different values of $\mathrm{\alpha }$.

Figure 1.

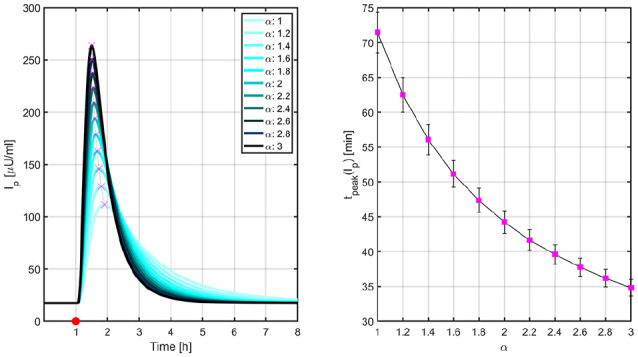
Mean PK profiles (left) and times to peak insulin levels (right) for different values of $\mathrm{\alpha }$.

Left: the red circle indicates the time that the 0.2 U/kg insulin bolus was administered and the magenta crosses, the peak levels. Right: vertical lines represent the standard error bars. PK, pharmacokinetic.

Figure 2.

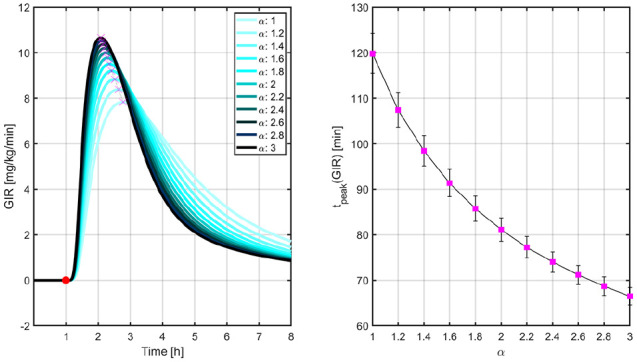
Mean GIR profiles (left) and times to peak GIR levels (right) for different values of $\mathrm{\alpha }$.

Left: The red circle indicates the time that the 0.2 U/kg insulin bolus was administered and the magenta crosses, the peak levels. Right: vertical lines represent the standard error bars. GIR, glucose infusion rate.

In Ref.³², this euglycemic glucose clamp was carried out on 38 adult patients with T1D to compare the PK/PD properties of LIS and ultra-rapid BioChaperone LIS²⁷ (BC-LIS). Results demonstrated that times to maximum insulin levels and GIR occur 20 and 30 min earlier, respectively, with BC-LIS. Bearing this in mind, and for merely illustrative purposes, we can associate BC-LIS with $\mathrm{\alpha }\cong 1.6$ in our approach.

MPC for Regulating the Blood Glucose Level

To assess the impact of faster insulins on the performance of an AP, we consider an originally hybrid MPC law as a baseline. This control strategy has been published by the authors elsewhere,³³ and a summary of its formulation is provided in the Appendix.

Detuning of the MPC controller aggressiveness ($Q$)

In a hybrid AP approach, it is assumed that meal disturbances are mostly mitigated by feedforward insulin boluses that are delivered at mealtimes. In this case, the user needs to calculate the prandial dose based on, among other factors, the meal size in grams of carbohydrates (gCHO) and his/her insulin-to-carbohydrate ratio (CR) in gCHO/U. In order to avoid a controller overreaction to postprandial glucose excursions, the scalar weight $Q$ that penalizes glucose deviations from target (see the Appendix for a description of $Q$ in the MPC formulation) is detuned as follows:

$$Q\left(\mathrm{IOB}\right)=\{\begin{array}{cc}{Q}_0& \mathrm{if}\mathrm{IOB}<0\\ \frac{{\mathrm{\beta }}_1\cdot \left(1-{\mathrm{\beta }}_2\right)\cdot Q_0}{{\mathrm{\beta }}_2\cdot TDI}\cdot \mathrm{IOB}+Q_0& \mathrm{if}\mathrm{IOB}\in \left[0,\mathrm{TDI}/{\mathrm{\beta }}_1\right]\\ Q_0/{\mathrm{\beta }}_2& \mathrm{if}\mathrm{IOB}>\mathrm{TDI}/{\mathrm{\beta }}_1\end{array}$$ (6)

where $Q_0$ is the value of $Q$ at steady state, TDI (U/day) denotes the subject-specific total daily insulin requirement, IOB (U) is the insulin-on-board relative to the expected IOB from basal delivery, and ${\mathrm{\beta }}_1$ and ${\mathrm{\beta }}_2$ are tuning parameters. In this way, when a meal bolus is delivered, the IOB estimate will have a peak, desensitizing the controller to glucose deviations from reference. The higher ${\mathrm{\beta }}_1$ and ${\mathrm{\beta }}_2$, the less responsive the controller at mealtimes.

Detuning of $\mathrm{\lambda }$ and $\mathrm{\Delta }{u}_{max}$

Long delays in insulin peak and duration substantially limit the achievable sensitivity of an AP to glucose deviations, because an aggressive control law can lead to late hypoglycemia due to insulin stacking. Here, we propose to re-tune the controller’s aggressiveness based on the dynamics of the insulin analogue: the faster the insulin analogue is, the more aggressive the controller can be. To this end, the average DIA was calculated for several $\mathrm{\alpha }$-insulins and fitted using a nonlinear least-squares approach by the following exponential function derived from the structure of Equation (5):

$$\mathrm{DIA}\left(\mathrm{\alpha }\right)={\mathrm{\gamma }}_1{e}^{{\mathrm{\gamma }}_2\mathrm{\alpha }}+{\mathrm{\gamma }}_3{e}^{{\mathrm{\gamma }}_4\mathrm{\alpha }}$$ (7)

with ${\mathrm{\gamma }}_1=13.83$, ${\mathrm{\gamma }}_2=-2.05$, ${\mathrm{\gamma }}_3=2.89$, and ${\mathrm{\gamma }}_4=-0.26$ (see Figure 3). To make the controller more aggressive for faster insulins, design parameters $\mathrm{\lambda }$ and $\mathrm{\Delta }{u}_{\max }$ are now defined as functions of the $\mathrm{DIA}$ as follows:

Figure 3.

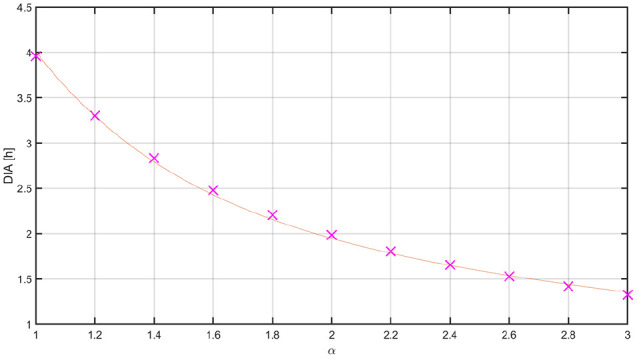
Mean DIA for different values of $\mathrm{\alpha }$.

The red line represents the fitted exponential function. DIA, duration of insulin action.

$$\mathrm{\lambda }\left(\mathrm{DIA}\right)=\{\begin{array}{cc}{\mathrm{\psi }}_1{e}^{{\mathrm{\psi }}_2\cdot \mathrm{DIA}}/u_b& \mathrm{if}\mathrm{DIA}<4h\\ {\mathrm{\psi }}_1{e}^{{\mathrm{\psi }}_2\cdot 4}/u_b& \mathrm{otherwise}\end{array}$$ (8)

$${\mathrm{\Delta }\mathrm{u}}_{\max }\left(\mathrm{DIA}\right)=\{\begin{array}{cc}-{\psi }_3\cdot \mathrm{DIA}+{\psi }_4& \mathrm{if}\mathrm{DIA}<4h\\ -{\psi }_3\cdot 4+{\psi }_4& \mathrm{otherwise}\end{array}$$ (9)

Numerical values of the tuning parameters ${\mathrm{\psi }}_i$ with $i=\left\{1,\dots ,4\right\}$ along with all the other parameters for the MPC are reported in Table 1. In this way, when the controller commands LIS (DIA = 4 hours), parameters $\mathrm{\lambda }$, which penalizes insulin deviations from basal rate, and $\mathrm{\Delta }{u}_{\max }$, which represents the difference between two consecutive insulin infusions (see the Appendix for the mathematical description of these two parameters in the MPC formulation), are set to their default values (${\mathrm{\lambda }}_0,{\mathrm{\Delta }\mathrm{u}}_{\max 0})$. However, their values decrease as the insulin is accelerated, allowing the controller to take more aggressive actions. Statistical comparisons between results obtained with the hybrid controller and LIS, and the fully automated controller and $\mathrm{\alpha }$-insulin were determined using a t-test of significance for means and a Mann-Whitney U-test for medians.

Table 1.

Tuning Parameters of the MPC Law.

Parameter	Value	Parameter	Value
N p	24	$y_{\min }$	70 mg/dL
N c	18	${\mathrm{\tau }}_r$	5
$Q_0$	10	${\mathrm{\beta }}_1$	20
$\kappa$	100	${\mathrm{\beta }}_2$	1000
${\mathrm{\lambda }}_0$	${\mathrm{\psi }}_1{e}^{{\mathrm{\psi }}_2\cdot 4}$/$u_b$	${\mathrm{\psi }}_1$	18
$u_{\min }$	-$u_b$	${\mathrm{\psi }}_2$	1.125
$u_{\max }$	1000 mU/mL-$u_b$	${\mathrm{\psi }}_3$	25
∆$u_{\max 0}$	50 mU/mL	${\mathrm{\psi }}_4$	150

Abbreviation: MPC, model predictive control.

Results

In this section, a battery of tests is presented to evidence the impact of accelerating insulin absorption and action on postmeal hyperglycemia mitigation with a fully automated AP controller. To this end, 12-hour simulations that include different $\mathrm{\alpha }$-insulins and one (un)announced meal challenge are performed considering the proposed MPC as the control law. In order to test robustness with respect to intersubject variability, simulations are run for all 100 adult subjects of the UVA/Padova simulator. Outcomes are computed over the eight hours following the meal so as to capture both early hyperglycemia and late hypoglycemia. Time responses are depicted in Figure 4, and numerical results, including average glucose values, time in ranges, and risk indices, are tabulated in Table 2. Both low blood glucose index (LBGI) and high blood glucose index (HBGI)³⁴ have been included in this analysis to quantify the risks of hypo- and hyperglycemia obtained with each closed-loop strategy.

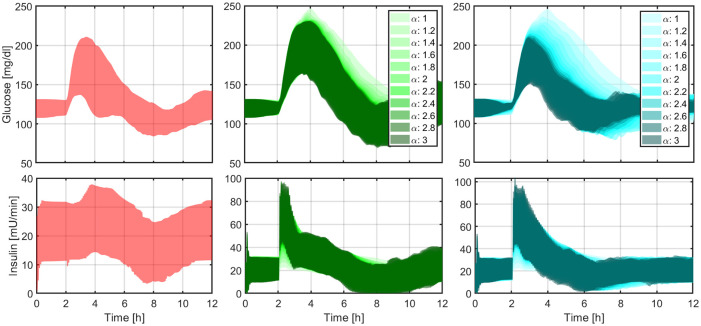
Figure 4.

Closed-loop responses obtained with LIS to an announced meal (left panel), with LIS and different levels of controller’s aggressiveness to an unannounced meal (middle panel), and with $\mathrm{\alpha }$-insulin and different levels of controller’s aggressiveness to an unannounced meal (right panel).

The boundaries of the filled areas represent the 5th and 95th percentiles. LIS, insulin lispro.

Table 2.

Comparison Between Numerical Results Related to Each Set of Closed-Loop Simulations.

	Announced		Unannounced meal						Unannounced meal
	Lispro		Lispro						$\mathrm{\alpha }$-Insulin
Insulin	1		1		2		3		1		2		3
$\mathrm{\alpha }$	Mean	Median [IQR]	Mean	Median [IQR]	Mean	Median [IQR]	Mean	Median [IQR]	Mean	Median [IQR]	Mean	Median [IQR]	Mean	Median [IQR]
Average glucose	130	128 [13]	157	155 [18]	141	140 [12]	138	138 [11]	157	155 [18]	135	135 [8]	131	130 [6]
% time < 50 mg/dL	0	0 [0]	0	0 [0]	0.1	0 [0]	0.2	0 [0]	0	0 [0]	0.1	0 [0]	0.1	0 [0]
% time < 70 mg/dL	0.1	0 [0]	0	0 [0]	0.9	0 [0]	1.4	0 [0]	0	0 [0]	0.6	0 [0]	0.4	0 [0]
% time in [70, 180]	92.9	100 [13]	70.1	67.0 [18]	79.9	77.8 [21]	81.4	79.4 [24]	70.1	67.0 [18]	88.8	88.2 [18]	94.1	100 [11]
% time > 180 mg/dL	7.0	0 [13]	29.9	33.0 [18]	19.2	22.2 [21]	17.2	20.1 [23]	29.9	33.0 [18]	10.6	11.3 [18]	5.5	0 [11]
% time > 250 mg/dL	0	0 [0]	0.6	0 [0]	0.3	0 [0]	0.2	0 [0]	0.6	0 [0]	0	0 [0]	0	0 [0]
LBGI	0.19	0.07 [0]	0.05	0 [0]	0.40	0.11 [0]	0.52	0.18 [1]	0.05	0 [0]	0.21	0.01 [0]	0.14	0 [0]
HBGI	1.83	1.54 [2]	5.29	5.26 [3]	3.56	3.57 [2]	3.28	3.26 [2]	5.29	5.26 [3]	2.4	2.40 [1]	1.66	1.65 [1]

Abbreviations: HBGI, high blood glucose index; IQR, interquartile range; LBGI, low blood glucose index.

Glycemic Control Using a Hybrid Approach

To define a baseline of hybrid glucose control, a first set of simulations is carried out with LIS and meal announcement, that is, delivering feedforward meal boluses at mealtimes. Given the meal size $\mathrm{M}=50$ g CHO and the subject’s CR, the bolus size is calculated as $\mathrm{M}/\mathrm{CR}$. Average time responses are depicted in Figure 4 (left panel) and numerical results are tabulated in the first set of columns of Table 2.

Glycemic Control With Unannounced Meals

Here, we eliminate the prandial bolus and gradually increase the controller’s aggressiveness. To this end, we tune the MPC using Equations (8) and (9) but keep using LIS in the simulations, that is, $\mathrm{\alpha }$ is only used to define the controller’s aggressiveness, but not to accelerate the insulin analogue. Average time responses are illustrated in Figure 4 (middle panel) and numerical results are tabulated in the second set of columns of Table 2. Note that not only the mean percentage of time in the range [70, 180] mg/dL increases (70.1, 95% confidence interval [66.9, 73.4] for $\mathrm{\alpha }=1$ vs 81.4 [78.6, 84.3] for $\mathrm{\alpha }=3$, P < .05), but also the mean percentage of time below 70 mg/dL (0.0 [0.0, 0.0] for $\mathrm{\alpha }=1$ vs 1.4 [0.7, 2.8] for $\mathrm{\alpha }=3$, P < .05). The same situation is observed with respect to the risk indices: LBGI 0.05 [0.03, 0.10] for $\mathrm{\alpha }=1$ vs 0.52 [0.36, 0.75] for $\mathrm{\alpha }=3$, P < .05; HBGI 5.29 [4.88, 5.71] for $\mathrm{\alpha }=1$ vs 3.28 [3.00, 3.56] for $\mathrm{\alpha }=3$, P < .05.

The final step is to repeat these simulations but switching from LIS to the corresponding accelerated $\mathrm{\alpha }$-insulin. Results are reported in Figure 4 (right panel) and the third set of columns of Table 2. In this case, a more marked increase in time in range is detected (70.1 [66.9, 73.4] for $\mathrm{\alpha }=1$ vs 94.1 [92.6, 95.6] for $\mathrm{\alpha }=3$, P < .05), with a slight nonsignificant increase in time below 70 mg/dL (0.0 [0.0, 0.0] for $\mathrm{\alpha }=1$ vs 0.4 [0.1, 1.4] for $\mathrm{\alpha }=3$, P = .13). Similarly for the risk indices: LBGI 0.05 [0.03, 0.10] for $\mathrm{\alpha }=1$ vs 0.14 [0.07, 0.30] for $\mathrm{\alpha }=3$, P = .09; HBGI 5.29 [4.88, 5.71] for $\mathrm{\alpha }=1$ vs 1.66 [1.52, 1.80] for $\mathrm{\alpha }=3$, P < .05.

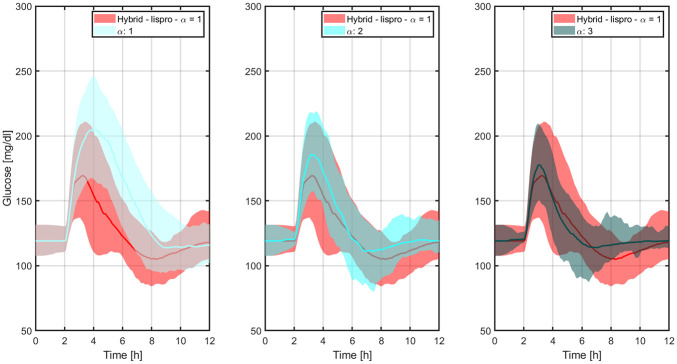
Figure 5 indicates how the percentages of time <70 mg/dL and >180 mg/dL evolve with LIS and the $\mathrm{\alpha }$-insulin analogues as the controller’s aggressiveness is increased. Glucose trajectories from Figure 4 are overlapped in Figure 6 to facilitate the comparison between both the hybrid and reactive AP approaches. Results indicate that nonsignificant difference between medians is obtained for $\mathrm{\alpha }\ge 2.4$. In this way, for a reactive AP that does not rely on manual insulin boluses at mealtimes to match the glucose control performance achievable by its hybrid version, times to maximum insulin levels and GIR obtained with BC-LIS ($\mathrm{\alpha }\cong 1.6$) have to occur 10 and 15 minutes earlier, respectively, according to Figures 1 and 2.

Figure 5.

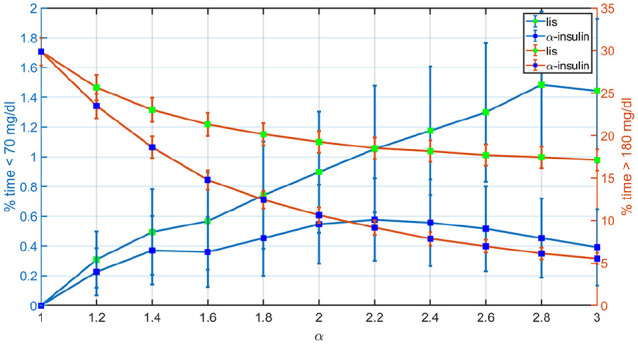
Comparison between the mean percentages of time <70 mg/dL and >180 mg/dL achieved with LIS and $\mathrm{\alpha }$-insulin for different levels of controller’s aggressiveness.

Vertical lines represent the standard error bars. LIS, insulin lispro.

Figure 6.

Comparison between the glucose trajectories obtained with LIS and the baseline hybrid controller, and the ones obtained with $\mathrm{\alpha }$-insulin and different levels of controller’s aggressiveness.

The thick lines are the median values, and the boundaries of the filled areas represent the 5th and 95th percentiles. LIS, insulin lispro.

It is important to emphasize that if the acceleration of the insulin analogue is not accompanied by an increase in the controller’s aggressiveness, then the benefits of faster insulins in glucose control are less noticeable. For instance, if $\mathrm{\alpha }$ is only used to accelerate the insulin analogue, but not to increase the controller’s aggressiveness, a less marked increase in time in range is observed (70.1 [66.9, 73.4] for $\mathrm{\alpha }=1$ vs 79.5 [76.5, 82.4] for $\mathrm{\alpha }=3$, $P<$.05), although with no increase in time below 70 mg/dL (0.0 [0.0, 0.0] for $\mathrm{\alpha }=1$ vs 0.0 [0.0, 0.0] for $\mathrm{\alpha }=3$).

Discussion

Hybrid AP systems rely on feedforward insulin boluses to manage postprandial glucose excursions and on the glucose controller to maintain normoglycemia by modulating the basal insulin delivery. Users play a key role in this scheme since carbohydrate counting is cornerstone for meal insulin bolus calculation. Although this method reduces the stress on the controller, it is burdensome for patients and prone to human errors that may affect the achievable glucose control performance. One alternative is to eliminate the meal announcement from the control structure and tune the controller to be more reactive to glucose deviations. The longer the time to peak, the more sensitive the controller needs to be to alleviate postprandial hyperglycemia. As evidenced in Figure 4, if the baseline hybrid MPC is used without meal boluses ($\mathrm{\alpha }=1$), large glucose excursions are manifested since the controller is purposely designed to perform only slight modifications to the basal rate. Having said that, increasing the controller’s aggressiveness to deliver an insulin “kick” at mealtimes is not an appropriate decision for a given insulin analogue, since it may contribute to the risk of hypoglycemic values toward the end of the meal response. In contrast, Figure 4 reveals that when the increase in the controller’s aggressiveness is accompanied by faster acting insulins, both a faster descend from peak to trough and a superior protection to late hypoglycemia are easily discernible. Above all, the takeaway message is that the controller should align the insulin and meal rates of appearance for effective postprandial glucose control (see Figure 7). With this in mind, faster insulin analogues could represent a critical means to achieve that goal in a SC AP approach. Besides, the proposed control strategy can still be applied in a hybrid scheme, because the controller is de-tuned for high IOB values (Equation 6).

Figure 7.

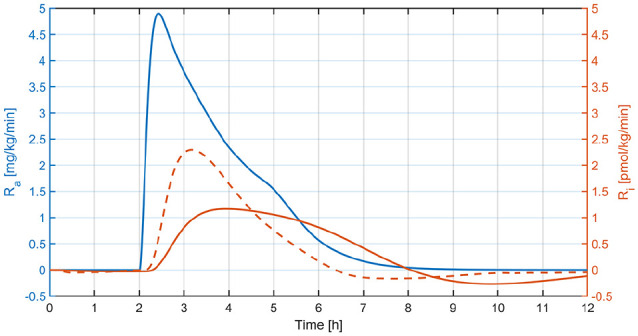
Mean glucose rate of appearance (R_a) vs mean insulin rate of appearance (R_i) relative to the basal value from Figure 4—middle panel (continuous line) and Figure 4—right panel (dashed line).

Finally, it is worth remarking that in this article, we have explored the impact of accelerating the insulin analogue on a predefined AP system, and consequently, results depend, to some extent, on the proposed baseline control scheme. In addition, further simulations should be carried out to test the robustness of the control strategy against, for example, variations in insulin sensitivity. Nevertheless, since this article discusses about fundamental limitations on control system performance, the same procedure could be applied to different control strategies, and general conclusions with respect to the benefits of using faster insulins in automatically controlling the blood glucose level in T1D will remain unaffected.

Conclusion

In this article, a methodological tuning of an MPC law for an AP was proposed to accommodate the controller’s aggressiveness according to the velocity of the insulin analogue glucodynamic action. In these proof-of-concept simulations, we evidenced that current fast-acting insulin analogues need to be further accelerated concerning their glucodynamic action for fully automated insulin treatment approaches to reach safely the glycemic performance of optimal hybrid strategies.

Appendix

The proposed MPC is based on the so-called Subcutaneous Oral Glucose Minimal Model.³⁵ To embed this model into the MPC formulation, it is first linearized at the steady state given by the subject-specific insulin basal rate u_b (mU/min) and a blood glucose setpoint of 120 mg/dL, and later discretized with a sampling period T_s = 5 min. In this way, a triplet $\left(A,B,C\right)$ that describes the insulin-glucose dynamics is obtained.

Let $u,y\in ℝ$ denote the insulin and glucose deviations from steady state, and $x\in {ℝ}^n$, the model state vector. Denoting the prediction and control horizons by N_p and N_c, respectively, we formulate the following MPC problem that is solved at each step $k$:

$$\left[{\tilde{u}}_k^{*},{\tilde{\mathrm{\eta }}}_k^{*}\right]=\underset{{\tilde{u}}_k,{\tilde{\mathrm{\eta }}}_k}{\mathrm{argmin}}J\left(x_k,{\tilde{u}}_k,{\tilde{\mathrm{\eta }}}_k\right)$$ (10)

with cost function

$$J(\cdot )=\sum _{j=k+1}^{k+N_{\mathrm{p}}}[Q{\left(y_j-r_j\right)}^2+\kappa {\mathrm{\eta }}_{j-1}^2]+\sum _{j=k}^{k+N_{\mathrm{c}}-1}\mathrm{\lambda }\mathrm{\Delta }{u}_j^2$$ (11)

subject to

$$x_k={\widehat{x}}_k$$ (12)

$$x_{j+1}=A{x}_j+B{u}_j\forall j\in {\mathbb{N}}_k^{k+N_{\mathrm{p}}-1}$$ (13)

$$y_j=C{x}_j\forall j\in {\mathbb{N}}_k^{k+N_{\mathrm{p}}}$$ (14)

$$u_{\min }\le u_j\le u_{\max }\forall j\in {\mathbb{N}}_k^{k+N_{\mathrm{c}}-1}$$ (15)

$$\mathrm{\Delta }{u}_j\le \mathrm{\Delta }{u}_{\max }\forall j\in {\mathbb{N}}_k^{k+N_{\mathrm{c}}-1}$$ (16)

$$y_{\min }-y_j\le {\mathrm{\eta }}_{j-1}\forall j\in {\mathbb{N}}_{k+1}^{k+N_{\mathrm{p}}}$$ (17)

$${\mathrm{\eta }}_j\ge 0\forall j\in {\mathbb{N}}_k^{k+N_{\mathrm{p}}-1}$$ (18)

$$r_j=\{\begin{array}{ll}{y}_k\cdot e^{-\left(j-k\right)/{\mathrm{\tau }}_r},\hfill & y_k\ge 0\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\forall j\in {\mathbb{N}}_k^{k+N_{\mathrm{p}}-1}$$ (19)

Predictions of the insulin-glucose dynamics are made using the obtained state-space realization $\left(A,B,C\right)$ (Equations 13 and 14) with the initial state x_k estimated by means of a Kalman filter (Equation 12). Equations (15) and (16) enforce that the insulin infusion lies in the interval $\left[u_{\min },u_{\max }\right]$, and the difference between two consecutive insulin infusions is not higher than $\mathrm{\Delta }{u}_{\max }$. Equations (17) and (18) enforce a soft constraint on the glucose lower bound $y_{\min }$ (hypoglycemic threshold). Three positive scalars are included in the cost function: (i) $\kappa$ that penalizes control actions that lead to low glucose levels, (ii) $\mathrm{\lambda }$ that weights $\mathrm{\Delta }u$, and (iii) $Q$ that penalizes glucose deviations from the asymmetric, time-varying, exponential reference signal $r$.³⁶

Sequence ${\tilde{u}}_k^{*}=\left\{u_k^{*},\dots ,u_{k+N_{\mathrm{c}}-1}^{*}\right\}$ contains the optimal control policy and sequence ${\tilde{\mathrm{\eta }}}_k^{*}=\left\{{\mathrm{\eta }}_k^{*},\dots ,{\mathrm{\eta }}_{k+N_{\mathrm{p}}-1}^{*}\right\}$ the optimal slack variables associated with the soft constraint. In this formulation, the control signal at step $k$ is defined as the first element of ${\tilde{u}}_k^{*}$, that is, $u_k=u_k^{*}$. In order to minimize the risk of hypoglycemia the controller is combined with an auxiliary module, the so-called Unified Safety System (USS Virginia) that enforces a limit to basal injections when low glucose values are predicted.³⁷