Deep neural maps for unsupervised visualization of high-grade cancer in prostate biopsies

Abstract

Prostate cancer (PCa) is the most frequent noncutaneous cancer in men. Early detection of PCa is essential for clinical decision making, and reducing metastasis and mortality rates. The current approach for PCa diagnosis is histopathologic analysis of core biopsies taken under transrectal ultrasound guidance (TRUS-guided). Both TRUS-guided systematic biopsy and MR-TRUS-guided fusion biopsy have limitations in accurately identifying PCa, intraoperatively. There is a need to augment this process by visualizing highly probable areas of PCa. Temporal enhanced ultrasound (TeUS) has emerged as a promising modality for PCa detection. Prior work focused on supervised classification of PCa verified by gold standard pathology. Pathology labels are noisy, and data from an entire core have a single label even when significantly heterogeneous. Additionally, supervised methods are limited by data from cores with known pathology, and a significant portion of prostate data is discarded without being used. We provide an end-to-end unsupervised solution to map PCa distribution from TeUS data using an innovative representation learning method, deep neural maps. TeUS data are transformed to a topologically arranged hyper-lattice, where similar samples are closer together in the lattice. Therefore, similar regions of malignant and benign tissue in the prostate are clustered together. Our proposed method increases the number of training samples by several orders of magnitude. Data from biopsy cores with known labels are used to associate the clusters with PCa. Cancer probability maps generated using the unsupervised clustering of TeUS data help intuitively visualize the distribution of abnormal tissue for augmenting TRUS-guided biopsies.

Introduction

Prostate cancer (PCa) is the most dominant noncutaneous cancer in men. Researchers have categorized PCa risk to show common clinical decision-making groups: low-risk group who are appropriate for active surveillance, intermediate-risk group for whom intervention is beneficial and high-risk group who will benefit from more aggressive intervention. Intermediate- and high-risk disease are referred to as clinically significant PCa (sPCa) [1]. Mortality often happens when cancer is metastasized beyond the prostate. This is the main motivation for early detection of sPCa to enable the best treatment decision for the patient.

The diagnosis of PCa involves immunoassay-based measurement of the blood levels of prostate-specific antigen (PSA) and digital rectal examination (DRE). PSA level, suspicious DRE, patients age and therapeutic consequences will determine the need for prostate biopsy [2]. The current gold standard for PCa diagnosis is histopathologic analysis of the specimen taken during the biopsy procedure guided by transrectal ultrasound (TRUS-guided biopsy), initially suggested by Hodge et al. [3]. The current biopsy protocol is not patient-specific and includes systematic sampling of 12–20 locations in the prostate gland [4]. Studies have shown low sensitivity in detection of sPCa for systematic (sextant) biopsies [5]; therefore, the conventional biopsy process is a blind approach resulting in a over- and underdiagnosis of PCa.

Fusion of multi-parametric MRI (mp-MRI) and ultrasound has been used to improve PCa detection [5] by enabling targeting of cancer foci predetermined in MRI during TRUS-guided biopsy. While mp-MRI has high sensitivity, it has low specificity for identifying intermediate-risk or low-volume disease [5–7]. In addition, registration of 3D TRUS to mp-MRI [8] is a complex task and it fails to fully account for patient motion or organ deformation occurring during the biopsy. The lower specificity of mp-MRI means that a biopsy is still required with a suspicious mp-MRI [9]. This emphasizes the need to augment the detection of sPCa in mp-MRI to reduce a very large number of false positives currently observed in fusion biopsy.

Several ultrasound-based approaches have been suggested to increase the cancer yield of TRUS-guided biopsy. Analysis of the absolute intensity of radio frequency signals [11] and observed mechanical response of tissue to external excitation (elastography) [12] are among these approaches. PCa is a multi-focal, heterogeneous disease in which microstructure and mechanical properties vary significantly across different grades of cancer and patients. Therefore, determining a consistent cancer-related tissue property has been proven to be difficult which limits clinical uptake of these methods. Analysis of time series of ultrasound data, temporal enhanced ultrasound (TeUS), has emerged as a promising modality for PCa detection. TeUS is comprised of a set of ultrasound frames captured over a short period of time from a stationary tissue location without mechanical excitation (Fig. 1). Previous ex vivo [13–15] and in vivo [16,17] studies have used machine learning techniques to show that TeUS information can be successfully used to determine discernible characteristic of cancer tissue.

Fig. 1.

a Temporal enhanced ultrasound (TeUS). The blue signal shows the variation of a pixel amplitude in ultrasound data over a sequence of imaging frames; b preprocessing and region of interest (ROI) selection. Eighty ROIs are selected along each biopsy core in TeUS data, centered on the biopsy target (b reprinted from [10])

Prior work using TeUS has focused on supervised classification verified by gold standard pathology of the cores. Reporting of pathology labels has a significant limitation as the location of cancerous tissue with respect to the entire core is not labeled. A core may also contain only a small percentage of cancer, while the entire core can be declared as cancer. Furthermore, cancer has different grades and normally contains several tissue types of substantially different microstructures. In other words, since the tissue in each core can be highly heterogeneous, labels for cores can be extremely noisy, which makes supervised training and classification highly challenging. Another shortcoming of previous work is that learning models of PCa is limited only to ultrasound data from the biopsy region where pathology labels are available. Ultrasound data from a significant portion of the prostate, beyond the biopsy needle, are therefore discarded.

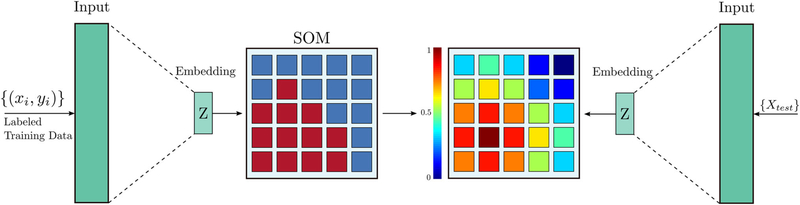
In this work, we provide an entirely novel approach to visualization of sPCa for biopsy guidance. We propose an end-to-end unsupervised solution based on a recent innovation in our group, deep neural maps (DNMs) [18], to provide a holistic map of cancer distribution using TeUS data. DNM is a representation learning method inspired by self-organizing maps (SOM), where data are mapped nonlinearly to a lower dimension, yielding a topologically arranged hyper-lattice, where similar samples are mapped close together in the map. TeUS data from entire imaging planes are clustered to the hyper-lattice, and areas of sPCa can be identified using the labels available for data from cores. Our key innovation is to enable learning from a significant number of unlabeled data that are often ignored in conventional machine learning. While classification of cancer tissue has not been the focus of this work, we demonstrate that our contribution enables high AUC values for aggressive cancer (> 0.8) using a simple classifier without any parameters, which is comparable to our prior contributions using supervised classification techniques [10,15,19]. This will help intuitively visualize the distribution of abnormal tissue for augmenting TRUS-guided biopsies.

The remainder of the paper is organized as follows. “Materials and methods” section provides an overview of the TeUS data and details our unsupervised end-to-end solution for visualization of sPCa maps. “Results and discussion” section presents the results and samples of these maps followed by discussions and conclusions in “Conclusion and future directions” section.

Materials and methods

Data

TeUS data were acquired from 255 biopsy cores of 157 subjects during MR-TRUS fusion prostate biopsy procedure. The study was approved by institutional research ethics boards, and patients provided informed consent to participate. The biopsy targets have been selected by a radiologist that has examined the mp-MRI sequences and marked the location highly likely to be cancer. UroNav (Invivo Corp., FL) was used for the MR–ultrasound fusion during the guided biopsy. Prior to firing the biopsy gun, the ultrasound transducer was held steady for about 5 s to acquire 100 frames of TeUS data, followed by firing the biopsy needle to collect a sample of the tissue. Gleason Score (GS) is the recommended method for grading PCa. The Gleason Grade (GG) refers to the aggressiveness of prostate cancer and is described using a scale of 1–5 with 5 representing aggressive cancer. The Gleason Score (GS) is the addition of the GGs of the dominant and the second dominant cancer components in a specimen regardless of the amount [2]. In our dataset, 83 biopsy cores are cancerous with GS 3 + 3 or higher (have GG of 4 and 5); 31 of them were clinically significant with GS 4 + 3 (5) GS 4 + 4 (21) and GS 4 + 5 (5). The rest of 172 cores are non-cancerous, which includes benign or fibromuscular tissue, chronic inflammation, atrophy and prostatic intraepithelial neoplasia (PIN).

Preprocessing

TeUS data are available from an entire imaging plane for every biopsy core. From this, TeUS data corresponding to the prostate gland are extracted by manually contouring the prostate boundaries. The frequency spectrum is computed for regions of interest (ROI) of 0.5 × 0.5 mm in the prostate area. Specifically, we calculate the discrete Fourier transform (DFT) of zero-mean ultrasound time series for each TeUS signal in the ROI (on average 27 time series in an ROI), normalized to the frame rate. DFT is a discrete transform to convert the time-domain, finite sequence of ultrasound time series data to frequency domain [20]. We generate inputs for DNM by averaging the absolute values of the DFT of TeUS signals in each ROI. Details of a similar process are discussed in [21]. We choose the first 25 average frequency components as the input for DNM. Previously [10,22,23], we investigated the physical phenomenon governing TeUS, suggesting that tissue micro-vibrations at low frequency, partly due to physiological motion and pulsation from the heart beat (~ 1Hz), are key contributors to its tissue typing capability. Therefore, for each ROI we represent TeUS data with the first 25 positive frequency components. The number of ROIs of size 0.5 × 0.5 mm from the prostate area results in roughly 100,000 regions for the training set, with 25 values for frequency components. Therefore, the size of the input matrix is roughly 100,000 × 25. Hereafter, we refer to these data as “unlabeled data,” which we use for learning the visualization of sPCa in an imaging plane.

We also generate “labeled data” from 32 benign cores, 14 cores with GS 4+4 and 12 with GS 3+3. For this purpose, an area of 2 × 10 mm along the projected needle path is selected (similar to [10]). We divide this area to 80 equally sized ROI of 0.5 × 0.5 mm and calculate the DFT components as stated earlier.

Unsupervised learning of PCa from unlabeled TeUS data

Pesteie et al. [18] proposed an unsupervised representation learning model, DNM, which transforms and embeds the input data to a latent variable and learns an N-dimensional hyper-lattice from the embedding space.

This is achieved via an auto-encoder (AE) neural network, which learns the transformation function between the input and the latent variables [24], along with a Kohonen map, also known as SOM [25]. SOMs are an unsupervised learning approach where neurons within the map compete between themselves to be activated. The outcome is an organized connection of neurons. SOMs are used to transform high-dimensional data to one or two-dimensional discrete maps. In our DNM architecture, the SOM learns representations from embedding space, as shown in Fig. 2. The DNM model preserves the topography of the data in a nonlinear lower dimension, yielding a semantic map of representations topologically arranged in a hyper-lattice, where similar samples are mapped close together in the map. Thus, the DNM yields a deterministic mapping between the data and the hyper-lattice and vice versa.

Fig. 2.

Architecture of the DNM. An AE neural network learns the input to latent variable transformation function, while a SOM learns representations from the embedding space

Training the DNM is a two-step process, namely pretraining and joint optimization. During pre-training, the AE is trained on the dataset via the conventional stochastic gradient descent algorithm. This builds a latent space from which the original data can be precisely reconstructed. Then, the SOM is trained on the latent variables of the data via the incremental learning algorithm. Incremental learning methods are referred to a set of algorithms that repeatedly train a model without forgetting the previously learned patterns. In SOM, the lattice is updated with respect to a time-decaying neighborhood function, which controls the size of the update region on the lattice. Hence, during the early stages of training, the model tries to learn global representations. As the size of the neighborhood decreases, the model starts to fine-tune its neurons locally, while preserving the global attributes of the learned representations [26]. The objective is to minimize the l₂ norm of the Euclidean distance between the embedding of a given input and its best matching neuron in the map. Once the AE and the SOM components are pre-trained, they are jointly optimized together, such that the distance between the best matching neuron of the map with its neighbors is maximized for all data points through optimizing the weights of the AE as well as SOM representations. Therefore, the DNM learns a set of feature extractors that map the data to a latent space, where the topology is still preserved.

To effectively capture the variation in the frequency spectrum of TeUS data associated with tissue type, we leverage abundant data from the prostate (“unlabeled data”) and use them as input to the DNM. We hypothesize that DNM is a viable solution to learn distinctive representations from unlabeled TeUS signals, which yield a similarity metric for cancerous and benign tissues. In order to test this hypothesis, we use an AE with fully connected layers of 25 → 14 → 25 along with a 25 × 25 lattice size of the SOM. We experimented with various dimensions of the AE for achieving the best reconstruction error. The AE and SOM are pre-trained for 2000 and 1000 iterations, respectively. Thereafter, the DNM is trained using the combination of AE and SOM loss functions for 1500 iterations. Batch size of 128 is used for the experiment.

Projection of labeled data on the 2D lattice

In the previous section, we explained the training process of DNM with data from all training patients that include various outcome classes such as benign and all available grades of cancer. As a result, a two-dimensional topographic lattice is generated from the entire unlabeled TeUS data. Following training, we identify the center of clusters for each outcome class (Benign, GG 3, GG 4) in the lattice. For this purpose, we use a subset of the data from biopsy cores with gold standard pathology outcomes. The subset includes benign patients and patients with PCa (consistently GG 4 and GG 3) in most of their biopsy sample. Figure 3 demonstrates the schematic diagram of our proposed approach for determining this association. In this section, we only use biopsy cores with homogeneous pathology, and samples with mixed Gleason Grades (GS 4 + 3 and GS 4 + 5) are not used for identifying center of clusters.

Fig. 3.

An illustration of our proposed approach for finding clusters representing cancer in the low-dimensional space of SOM. On the right, we calculate a similarity map based on the distance of lattice nodes to the center of the cluster

For each labeled ROI in a given class, we project its 25 frequency features on the lattice and obtain the corresponding best matching neuron to that ROI, on the map. Next, we use Gaussian kernels to smooth the projections. This leads to a projection map for each class, which can be used to identify the correspondence between a given class of outcome in TeUS data and regions of the lattice. Since the DNM model has separated latent signatures of the TeUS data for each class, the projection map indicates different clusters, where the center of each cluster corresponds to the highest majority of projection (see Fig. 4).

Fig. 4.

Projections of “labeled data” from the entire training set on the DNM lattice of size 25 × 25 for benign tissue, GG 4 and GG 3. Note that GG 4 shows a dominant cluster and a secondary cluster that is closer to the benign cluster center. We hypothesize that this secondary cluster reflects the benign tissue (in addition to cancerous tissue) present in majority of biopsy cores irrespective of their cancer grade. The lattice projection maps are then used to calculate a metric to determine the similarity of ROIs of a test case to each cluster center

Visualization of high-grade cancer

As explained in “Preprocessing” section, DNM learns a semantic map of representations in which similar ROIs from TeUS data are mapped closer together. We leverage this key property and calculate similarity values based on the Euclidean distance of lattice nodes to the GG 4 cluster (aka high-grade cancer) identified previously. Finally, we use these similarity values to generate colormaps that indicate the likelihood of sPCa and overlay them on TeUS imaging planes.

More specifically, for each case in the test data, we generate a frequency representation of TeUS data. This representation is calculated in neighborhoods of 0.5 × 0.5mm (ROI). We take the DFT of each RF time series in this neighborhood (on average 27 time series in an ROI) and average their first 25 frequency components. This generates 25 frequency representations for each ROI which are used as an input feature to the DNM to calculate their projections to the lattice space. Having obtained the center of the cluster for the high-grade cancer (GG 4) from training data, we assign a similarity value to the ROI (one color) based on the distance of its projection to the cluster center. We repeat these steps for all ROIs that cover the prostate area and create the final colormap.

Results and discussion

Figure 4 shows the projection results for different classes in the “labeled data.” As shown in this figure, the cluster centers corresponding to various classes in the lattice space are distant from each other. Most importantly, the projection of GG 4 cluster is farther away from Benign compared to those of GG 3 from Benign. This aligns well with transition of cell types in a continuum from benign tissue microstructure toward low-grade cancer to moderate- and high-grade cancerous tissue in histopathology.

Figure 5 shows visualization of a cancer and a benign case. Colormaps are generated following the process outlined in “Projection of labeled data on the 2D lattice” and “Visualization of high-grade cancer” sections and are overlaid on B-mode ultrasound images. The target was initially identified in mp-MRI and registered to TRUS images for biopsy guidance. We observe that for the cancer case (top row) the similarity to GG 4 is high (red) around the target, while the similarity to Benign is low (blue). Moreover, for the benign case (bottom row) the similarity to Benign is high (Red) around the target, while the similarity to GG 4 is low (blue).

Fig. 5.

Similarity map for different GG overlaid on B-mode ultrasound images. Red and blue indicate higher and lower similarity to the specific grade indicated at the bottom of each image. Top row: cancer case: (a) similarity map to GG 4, (b) similarity map to GG 3, (c) similarity to Benign. As shown, the biopsy-confirmed cancer patient is highly similar to the GG 4 map (red) in a. Bottom row: benign case: (a) similarity map to GG 4,(b) similarity map to GG 3, (c) similarity map to Benign. For the benign patient, similarity to GG 4 is lowest, as expected, in plot (a)

We also evaluate the performance of our approach for classification of TeUS data into sPCa and Benign. For each test patient, after projecting all ROIs (n = 80) along the biopsy track to the lattice coordinates, we determine the percentage of ROIs that project to the same coordinates within the GG 4 cluster. This is meant to be a measure of the agreement in projections of different ROIs of each sample. We use a simple classifier to declare a case as sPCa based on the similarity value of the ROI projections on the lattice. A linear relationship is observed (Fig. 6) by comparing the performance of the classifier and the percentage of the agreement in the projections of ROIs. For cores with high consensus in projection, we achieve an AUC > 0.8; however, the results suggest that the simple linear classifier does not perform well for cores with little consensus in the projection. For these cores, a more complex classifier will be needed with parameters to tune to take into account the dispersion and weighted distances of projections. From clinical point of view, significant prostate cancer is one that involves GG 4. Our reported AUC values indicate that our approach can be highly sensitive to the presence of GG 4 at a reasonable specificity, which is critical for clinical decision making. Future work will extend this classifier to further improve AUC.

Fig. 6.

a Similarity map calculated based on distance from the maximum peak in the GG 4 cluster; b performance of the classifier based on the percentage of agreement in projection among ROIs along each biopsy needle

In the SOM training algorithm, topological structures among data points are preserved. This ensures that similar inputs are projected to similar regions on the grid. Using this property, we defined the similarity metric based on the distances in the grid. The topology-preserving property of SOM retains neighborhood relationships of the neurons. Therefore, metrics that incorporate both the distance between the latent representations of the input data and the distance between the neurons in the 2D grid can be used for future work.

Previous studies have focused on supervised learning with recurrent neural networks for detection of prostate cancer using TeUS data [19]. Here, for the first time, we demonstrate the feasibility of unsupervised learning for prostate cancer detection with TeUS. Although classification algorithms based on supervised learning methods tend to have higher accuracy compared to those based on unsupervised learning, the number of labeled data points is several orders of magnitude lower than unlabeled data which we take advantage of in this paper.

Conclusion and future directions

In this paper, we proposed a new approach for identifying and visualizing benign and various grades of cancer in the prostate tissue from TeUS data. We utilized an unsupervised representation learning model, namely DNM, to obtain a topology-preserving mapping from the data space to a 2D lattice space from unlabeled data. Later, we used the pathology outcomes from a subset of TeUS data to identify representations in the lattice that correspond to each tissue category, i.e., Benign, GG 3 and GG 4. Finally, we used the distance from the center of GG 4 cluster as a similarity value to assign labels to ROIs in TeUS data.

Our approach is computationally efficient. The association between class labels and input data can be determined by projecting the input to the lattice space and using a lookup table. One of the limitations of our approach is that DFT computation is an additional step that needs to be performed for evaluation. Currently, we are exploring optimized solutions by using the temporal analysis of TeUS data using recurrent neural networks to eliminate the need for DFT.