Integration strategies of multi-omics data for machine learning analysis

Graphical abstract

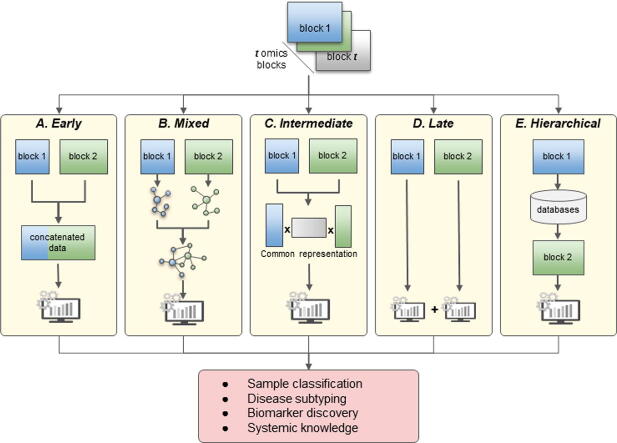
Schematic representation of the main strategies for multi-omics datasets integration. A) Early integration concatenates all omics datasets into a single matrix on which machine learning model can be applied. B) Mixed integration first independently transforms or maps each omics block into a new representation before combining them for downstream analysis. C) Intermediate integration simultaneously transforms the original datasets into common and omics-specific representations. D) Late integration analyses each omics separately and combines their final predictions. E) Hierarchical integration bases the integration of datasets on prior regulatory relationships between omics layers.

Abstract

Increased availability of high-throughput technologies has generated an ever-growing number of omics data that seek to portray many different but complementary biological layers including genomics, epigenomics, transcriptomics, proteomics, and metabolomics. New insight from these data have been obtained by machine learning algorithms that have produced diagnostic and classification biomarkers. Most biomarkers obtained to date however only include one omic measurement at a time and thus do not take full advantage of recent multi-omics experiments that now capture the entire complexity of biological systems.

Multi-omics data integration strategies are needed to combine the complementary knowledge brought by each omics layer. We have summarized the most recent data integration methods/ frameworks into five different integration strategies: early, mixed, intermediate, late and hierarchical. In this mini-review, we focus on challenges and existing multi-omics integration strategies by paying special attention to machine learning applications.

1. Introduction

The advent of powerful and inexpensive screening technologies [1] recently produced huge amounts of biological data that opened the way to a new era of therapeutics and personalized medicine [2]. Treatment efficiency and adverse effects can differ vastly between individuals due to differences in age, sex, genetics and environmental factors (e.g., anthropometric and metabolic statuses; dietary and lifestyle habits [3], [4]). The aim of precision medicine is thus to design the most appropriate intervention based on the biological information of each individual [5].

Clinical information and omics data can be directly retrieved from databases or collected with screening technologies for disease [6], class prediction [7], biomarkers discovery [8], disease subtyping [6], improved system biology knowledge [9], drug repurposing and so on. Each type of omics data is specific to a single “layer” of biological information such as genomics, epigenomics, transcriptomics, proteomics, metabolomics, and provides a complementary medical perspective of a biological system or an individual [1]. In the past, single-omics studies were done in hope of discovering the causes of pathologies and helping select an appropriate treatment. We now realize that such approaches are overly simplistic. Most diseases affect complex molecular pathways where different biological layers interact with each other. Hence the need for multi-omics studies that can encompass several layers at once and draw a more complete picture of a given phenotype [10]. With multiple omics, faint patterns in gene expression data can be reinforced with epigenomics [11] for example. Complementary information can be exploited to better explain classification results [12], improve prediction performances [13], [14] or understand complex molecular pathways [15] that would be out of grasp for single-omics studies. However, multi-omics studies include data that differ in type, scale and distribution, with often thousands of variables and only few samples. Additionally, biological datasets are complex, noisy, with potential errors due to measurement mistakes or unique biological deviations. Discovering pertinent information and integrating the omics into a meaningful model is therefore difficult and a great number of methods and strategies have been developed in recent years to tackle this challenge [6], [16]. If the integration is not done correctly, adding more omics might not result in a significant increase of performance, but will increase the complexity of the problem along with computational time.

A way to classify existing approaches is therefore needed in order to select appropriate methods and find good practices. Zitnik et al. (2019) [17] differentiated two types of integration. Either horizontal integration, which studies the same omics across different groups of samples or vertical integration, which examines multiple omics variables on the same samples. In this mini-review, we focus on vertical integration, where each omics dataset (or omics block) has the same rows (samples), but different variables (omics features). We also assume that the datasets are already processed, normalized or scaled depending on the omics’s type. In the current literature, general reviews on vertical integration [18], [19], [20], [21] often classify methods based on mathematical aspects, usually whether or not they are Bayesian, Network-based, deep learning-based, kernel-based, or matrix factorization-based methods. In this review, we are also interested in presenting general integration strategies for multi-omics datasets and sorting methods based on how they are used, which we believe to be more intuitive and practical than using their underlying mathematical basis as only classification. For that purpose, Ritchie et al. (2015) [22] introduced three integration approaches for vertical integration (called meta-dimensional in the review): concatenation-based integration combines datasets before analysis, transformation-based integration performs mapping or data transformation of each datasets before analysing the transformed datasets and model-based integration that performs analysis separately on each dataset before combining the results. Our work continues and extends those three categories to five distinct integration strategies and rename them to early (concatenation-based), mixed (transformation-based), late (model-based), intermediate and hierarchical. The names for the integration strategies are inspired from Zitnik et al. (2019) [17], but it is important to clarify that their classification (early, late and intermediate) is mainly different from ours.

This review presents the most recent advances in multi-omics analysis, with a special focus on the integration strategy. It is intended for computational biologists looking for general approaches and ideas in handling their omics datasets. For more specific reviews on multi-omics integration, we suggest several other reviews either methodologically oriented on subject such as variable selection [23], dimensionality reduction [24], autoencoders [25], clustering [26], [27] or network-based methods [10], [11], [28], [29], or biologically oriented on subjects like metabolomics [30], [31], phosphoproteomics [32], toxicology [33], host interactions [34], [35] and others [36], [37], [38], [39].

2. Challenges

Multiple challenges arise when integrating multi-omics datasets. Some are more general to machine learning analysis such as the presence of missing values or class imbalance and existing reviews already cover those subjects: Song et al. (2020) [40] and Mirza et al. (2019) [41].

Some are more specific and include the noisiness and complexity of omics datasets, which naturally occurs in biological data. Relevant patterns are sometimes subtles and involve many molecules from different omics layers. Finding those patterns across multiple datasets is therefore a difficult task. Moreover, when conducting omics or multi-omics experiments, the gathering of large amounts of biomedical data can often be done only on a small sample of patients for economical reasons, scarcity of the phenotype of interest, lack of volunteers, etc. This results in datasets with a number of variables greatly exceeding the number of samples. This issue is called the curse of dimensionality and machine learning algorithms tend to overfit these highly dimensional datasets, which decreases their generalizability on new data [42]. Another challenge is their heterogeneity which must be handled correctly as omics can have different data distribution or data types (e.g., numerical, categorical, continuous, discrete, etc.). Additionally, omics datasets can differ vastly in size (number of features), as a typical gene expression dataset will have tens of thousands of variables, while a metabolomics dataset can have a few thousands. Those discrepancies between omics can hinder their integration and produce an imbalance in the learning process. The different integration strategies presented in this mini-review address those problems differently by either reducing the number of variables, transforming the input data into a more exploitable representation, integrating at the end of the analysis, etc. More details about the strategies and tools available will be given in the next section of this review.

Class imbalance occurs when the distribution of classes in the learning data is biased, which can be a significant problem when working on rare events, such as an uncommon trait in a population. Several methods can be used to resolve this problem [14,15], such as sampling and cost-sensitive learning. Sampling tries to balance the dataset before the integration process, where either the majority class is randomly under sampled, or the minority class is oversampled by creating new artificial observations, or a combination of both methods. Cost-sensitive learning is directly integrated in the algorithm and balances the learning process by giving more weight to misclassified minority observations.

Missing data can take many forms ranging from variables with missing values to sample with missing omics data. If enough samples are available, removing the rows with missing data, namely listwise deletion, may be acceptable. If not, different statistical methods can be used to impute the missing values. A comprehensive review can be found in Song et al. (2020) [16]. Moreover, some machine learning methods can directly handle missing values like Random Forest 17 or K-Nearest Neighbor 18 or more recent methods [19,20].

3. Main integration strategies

From multiple omics datasets, each having the same rows representing samples (patients, cells) and different columns representing biological variables grouped by omics (gene expression, copy number variation, miRNA expression, etc.), different goals could be achieved such as sample classification, disease subtyping, biomarker discovery, etc. Machine learning (ML) models are commonly used to analyze complex data, but the integration of multiple noisy and highly dimensional datasets is not straightforward. Hence, multiple integration strategies have been developed, each one of them having pros and cons. Assuming each dataset has been pre-processed according to its omics data, the datasets could simply be assembled with sample wise concatenation and the resulting matrix used as input to ML models (Early integration, section 3.1). But in practice, most ML models will struggle to learn on such a complex dataset, particularly if the number of samples is low. Other strategies rely on transforming or mapping the datasets to reduce their complexity, either independently (Mixed integration, section 3.2) or jointly (Intermediate integration, section 3.3). An opposite strategy can also be adopted (Late integration, section 3.4), which does not combine data and analyzes each omics dataset separately. The prediction of each model is assembled afterward for a final decision. Finally, the hierarchical strategy (section 3.5) integrates the omics datasets by taking into account the known regulatory relationships between omics as presented by the central dogma of molecular biology [43]. In the next sections, we will first introduce dimensionality reduction methods (Section 3.0) as a powerful tool and secondary processing step and then present the different integration strategies in more detail (3.2, 3.3, 3.4, 3.5, 3.6).

3.1. Dimensionality reduction for multi-omic integration

A sometimes necessary step in multi-omics analysis is dimensionality reduction, that is the process of reducing the number of variables in order to decrease the dimensionality and noise of a dataset. It is an optional simplification step and can be used regardless of the chosen integration strategy, but some (early and intermediate integration) often require prior dimensionality reduction to be more effective.

Two distinct approaches exist: feature selection which simply removes noisy and redundant variables and feature extraction, which combines the original variables into new and more meaningful variables. With an early integration, dimensionality reduction should be done on the concatenated matrix in order to take into account all the omics during the process. If dimensionality reduction is carried out separately on each dataset, a potential loss of information could ensue by not including every feature, the approach would then fall under one of the other integration strategies. In the next two sections we will quickly outline the most commonly used methods in both approaches, specific reviews on the subject can be found here [23], [24].

3.1.1. Feature selection

Most omics datasets possess a high dimensionality which is in itself difficult to handle, but the problem is accentuated in multi-omics studies due to the number of datasets. One solution is to apply feature selection in order to simplify the integration process. Feature selection determines a smaller set of features which supposedly keeps most of the relevant information while reducing the dimensionality of the dataset. In addition to improving computing efficiency, removing features decreases complexity and noise which often results in higher performances and a reduced risk of overfitting for ML models. A low number of variables also makes the resulting models more interpretable. When a lot of variables are removed, feature selection can also deal on its own with the block scaling problem by evening out the number of features in each omics block [44].

Feature selection (FS) methods are organized into three classes, filter-based, wrapper-based and embedded methods. Filter-based methods are independent of any machine learning models and usually implement statistical analysis to find the most relevant variables while avoiding redundant features. They can be based on correlation (e.g., CFS [45], RCA [46]), distance (e.g., ReliefF [47]) or information gain [48] (e.g., mRMR [49]). Wrapper methods repeatedly apply a predictive ML model on different sets of features and those that improve the overall quality of the model are kept. Recursive feature elimination is the most common one, it starts by fitting a model with all the variables and gradually removes those which do not contribute to the model performances. These methods are focused on predictive power and can be used with any supervised ML models, but are limited by their computing efficiency if the dataset is large, which is often the case when studying omics. Finally, embedded methods are algorithms with feature selection built directly in the classifier. Among those embedded methods, the two most widely used are tree-based feature importance [50] and regularization. Regularization methods combine a loss function which evaluates the goodness of fit of the model, with a penalization function that punishes its complexity by favoring a smaller number of features. Compared to wrapper methods, they also resort to ML models, but are less computationally expensive. Due to the vast extent of regularization methods, we will not discuss it further and invite our reader to Wu et al. (2019) [23] and Vinga (2021) [51] for more information.

Feature selection can be applied to the separate omics datasets followed by concatenation. By definition it would no longer be an early integration as models would have been applied to each omics block independently. However, one might want to select variables while considering all omics together as it takes into account the redundancy of features across omics and might find more relevant features that single-omics studies will miss. The most straightforward way is to apply feature selection on the concatenated omics datasets. This strategy faces some of the same challenges described in the early integration section, that is balancing the influence of the different omics blocks, the increased complexity as well as additional computing time which would preclude the use of wrapper methods that are too computationally expensive.

3.1.2. Feature extraction

Feature extraction (FE) methods aim to transform the input features into another set of variables, that are linear or non-linear combinations of the original features. Their objective is to extract features in a way that the new variables keep the relevant information, while being less noisy and redundant. Learning from a smaller set of features also decreases complexity and improves computing efficiency. FE methods are often used in an exploratory manner to visualize data and expose important features, but they can also reduce the interpretability of a model as the extracted features are no longer biological measurements.

The most widely used FE method is Principal Component Analysis (PCA) [52]. PCA builds new variables called principal components, uncorrelated linear combinations of the original features that maximize the description of variance in the dataset. It is however sensitive to outliers and cannot handle non-linear trends in the data. Several extensions have thus been developed to correct those problems including Kernel PCA [53] or Bayesian PCA [54]. Other similar methods include Principal Coordinates Analysis (PCoA) [55], Correspondence Analysis (CA) [56] and Independent Component Analysis (ICA) [57] may answer some of the shortcomings of PCA. Most FE methods are also being developed with sparsity constraints, often integrating regularization methods such as LASSO or elastic net in order to remove useless or redundant features. Sparse FE methods can be used for feature selection and include Sparse PCA (sPCA) [58], Sparse Canonical Correlation Analysis (CCA) [59], Sparse Non-Negative Matrix Factorization (Sparse NMF) [60], Sparse CA [61], etc. For example, Park et al. (2020) [62] used sPCA on each omics dataset and concatenated the retrieved PCs as a new dataset used as input to a Cox regression analysis.

FE methods can be used separately on each omics dataset to facilitate integration and for block scaling [24], [63] in a mixed integration fashion, or applied on the concatenated multi-omics datasets (early integration). The extracted features are then useful as input to ML models or for clustering. However, those approaches often lead to unwanted redundancy and suboptimal results [64], [65]. Intermediate methods solve this problem by jointly analysing the datasets, resulting in FE methods capable of taking into account all variables simultaneously, more in Section 3.3.

However, those methods will struggle to explore multi-omics datasets as applying them on the concatenated omics usually gives poor results. Thus, feature extraction methods are often used on each omics dataset separately for either block scaling [24], [63], or after concatenation of the extracted features for clustering or other downstream analysis.

3.2. Early integration

The early integration is based on the concatenation of every datasets into a single large matrix. This process increases the number of variables, but the number of observations stays the same. Consequently, several integration challenges are exacerbated by this process resulting in a more complex, noisy and high dimensional matrix, which makes learning difficult. Additionally, the size difference between omics datasets can promote a learning imbalance as the algorithm spent more time learning on the omics with the biggest number of variables, overlooking the other omics [66], [67]. Early integration also ignores the specific data distribution of each omics, which can potentially misguide ML models into finding irrelevant patterns that simply reflect the features’ membership to the same omics. A conclusion found for example in a comparison study done by Spicker et al. (2008) [66]. Nevertheless, early integration is still commonly used as it has some clear advantages including its simplicity, easy implementation and mostly, combining variables from each omics allows ML models to directly uncover interactions between the different layers. It is also not known to what extent the aforementioned drawbacks influence the downstream analysis and it is possible that the performances of some ML models are not significantly lessened.

Approaches using the early integration strategy need at least to address the complexity of the composite matrix, often by reducing its number of variables through feature selection or dimensionality reduction methods. Then, most ML models can be used for analysis, but in recent years, Deep Learning (DL) [68] has been commonly used as it is flexible and powerful enough to accurately detect relevant patterns even from the concatenated data. For instance, Xie et al. (2019) [69] fed both multi-omics and clinical data to the input layer of an artificial neural network, itself linked to a Cox Proportional hazard model (Cox-PH) in order to predict survival of patients with cancer. For a similar goal, Chaudhary et al (2018) [70] implemented instead of the common fully connected neural network an autoencoder to reduce the dimensionality of the multi-omics matrix and extract meaningful and compact DL-based variables on which clustering was done with the k-mean algorithm.

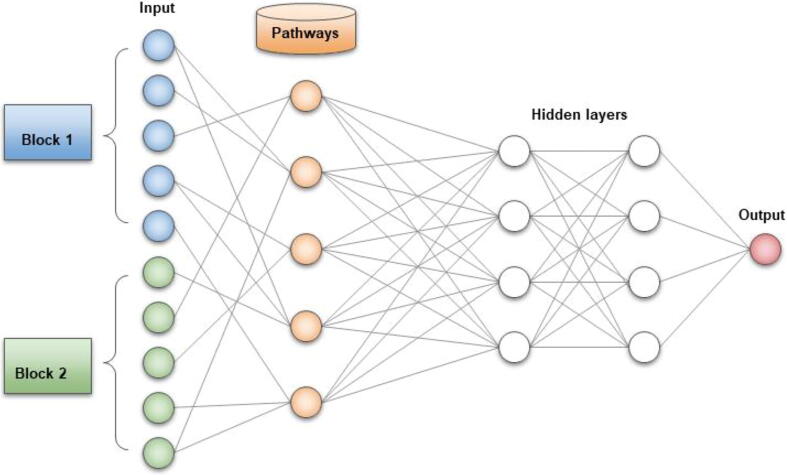
Although they are highly adaptive and often achieve superior performances with big datasets, one of the most challenging issues with neural networks is their black box nature, that is their lack of interpretability. Particularly in biomedical studies, having a good predictive model is not enough and an understanding on how genes and other molecules are implicated in the underlying biological process is necessary. The transparency of machine learning results may also lead to new biological discoveries. As several methods have been developed for interpreting neural networks models, we invite our reader to other reviews [71], [72]. Most of those strategies focus on explaining the final decision of the algorithm and identifying biomarkers, but some DL models [73], [74] can directly find relevant biological pathways during the learning process (Fig. 1). The basic idea behind this approach is to utilize known biological pathways to define the architecture of the neural network. The input layer representing biological entities (molecules, genes, proteins, etc.) is connected to a second layer where each node is a known molecular pathway. Connections between nodes are made only if the molecule is known to take part in the pathway, resulting in a sparse interaction between the first two layers. The pathway layer is then fully connected to hidden layers. When training the model, all the connections are updated and the final prediction of the network is directly interpretable by looking at which nodes are activated. The drawback of such methods is that they cannot discover new interactions or make use of little studied proteins or genes if their implication in a pathway has not yet been discovered.

Fig. 1.

Structure of an interpretable artificial neural network. The input layer is followed by an additional pathway layer, where each node corresponds to a known molecular pathway. If a molecule is known to be involved in a pathway, a connection is made between the two. Hence, important pathways implicated in the outcome are activated with bigger weights during training. Figure inspired from Deng et al. (2020)[73].

Additionally, the early strategy allows the inference of heterogeneous networks using methods such as Mixed Graphical Models (MGM) [75], [76], which expand from Gaussian Graphical Models that assume normal distribution of variables to a mixed model. MGM regresses each variable against every other using either linear regression or logistic regression depending on the type of variable (continuous or discrete/categorical). Another method, based on decision trees, is Graphical Random Forest [44], [77], which computes a Random Forest on each variable using every other feature as predictors. Features that are ranked as important by the importance measure of Random Forest are considered to interact with the selected variable. MGM as well as Graphical Random Forest can integrate prior knowledge [78], [79]. Additionally, Zhong et al. (2019) [80] developed mixed Directed Acyclic Graph (mDAG) which can infer causal interactions based on variables with different distributions and can potentially be used in multi-omics studies. More information on inferring heterogeneous networks from multi-omics data can be found in the reviews [76], [81].

3.3. Mixed integration

The mixed integration strategy addresses the shortcomings of the early integration by transforming independently each omics dataset into a simpler representation. The new representation can be less dimensional and less noisy which facilitates analysis. Moreover, most heterogeneities between omics datasets such as the data’s type or size differences are removed in the new representation. The combined representation can then be analysed by classical ML models. We will present three transformation methods, kernel-based methods, graph-based methods and Deep Learning (DL).

3.3.1. Kernel learning

Kernel models are powerful ML models able to implicitly operate in a high dimensional space in which linear relationships between observations can be found. Consequently, kernels can naturally be used to infer pairwise similarities of samples [82], taking the form of a similarity matrix that can be used for downstream analysis using ML models such as Support Vector Machines (SVM) [83], Partial Least Squares (fKPLS) [84] or a Cox model (kernel-fusion Cox) [85]. Different types of kernels exist such as linear, gaussian, polynomial, sigmoid, etc., thus providing different similarity measures for the same data. Because one of them can be more suitable than the other depending on the type of omics and its data distribution, the right kernel is often found with cross-validation. Multiple Kernel learning (MKL) [86] can integrate different omics blocks by first computing a kernel for each dataset (the kernel can be of different types), and combining them to produce a global similarity matrix which describes samples across all multi-omics datasets. The best way to combine the different kernels is found experimentally by learning their appropriate weights. Two different approaches exist [87], either using a wrapper strategy such as SimpleMKL [88] or using an optimization algorithm such as SpicyMKL [89] or SMO-MKL [90].

Recently, Zhang et al. (2016) [91] and He et al. (2021) [92] both used SimpleMKL on five different omics datasets, with a preliminary feature selection using mRMR [49] to increase performances. However, Zhang et al. applied for each dataset the same kernel type (Gaussian), whereas He et al. used two different types (Gaussian and Polynomial). On the other hand, SIMLR [93] and its multi-omics extension CIMLR [94] compute several gaussian kernels with varying hyperparameters for each omics and assume that the global kernel matrix better reflects similarity between samples and naturally reflects possible clusters. Wang et al. (2017) [93] shows that the constructed similarity measure outperforms standard similarity measures.

MKL can also be used in an unsupervised and exploratory manner [95], [96]. The resulting similarity space produced by the multi-omics kernel can be used as input by well-known algorithms such as PCA (kPCA) [53] or k-means (kernel Power k-means) [97]. Since the samples are no longer described by their input features, but by the new feature space describing their similarities, interpretation of the unsupervised model can be more challenging. For example, Speicher and Pfeifer (2015) [96] used unsupervised MKL on gene expression, methylation and copy number data for cancer subtype discovery, but could only assess for each cancer type the relative importance of each omics. Ideally, one would want to retrieve the importance of specific variables to better explain the results. Thus, a method based on random permutation and kPCA was introduced by Mariette and Villa-Vialaneix (2017) [95] to address this problem. The importance of a variable is measured by randomly permuting its value between samples and its influence can be estimated in the PCs space obtained with kPCA, in the same way as regular PCA.

3.3.2. Graph-based

A mixed strategy based on graphs consists of modelling each omics into a separate graph before analysis. Three approaches can consequently be used. The first one is to combine them into a single homogeneous network through fusion. The second approach is to build a multi-layer (or multiplex) network with inter-layer connections. Once a unique network is obtained, utilizing the principle of guilt-by-association, nodes close to each other are assumed to share related biological functions. Therefore, finding pertinent modules is often done in order to classify nodes with unknown functions or reveal activated pathways. In contrast to modules, random walks can connect distant nodes within the network to reveal potential long-distance interactions. Random walks simulate an imaginary particle starting at a seed node and moving randomly to other nodes in order to explore the network’s topology. After several iterations, a stationary probability distribution is obtained, which depicts the topological properties of the seed node and can be used to reveal its importance or its similarity to other nodes. Finally, the third approach does not rely on integrating several networks, but on learning graph-based variables from each of them, which can be used as input to other ML models.

The first approach of building homogeneous networks often relies on creating patient similarity networks for each omics, in which patients are nodes and weighted edges describe their similarities. Then, all networks are combined using a fusion method such as Similarity Network Fusion (SNF) [98] or its variation Affinity Fusion (ANF) [99] which is implemented with block normalization. Recently, Wen et al. (2021) [100] introduced Random Walk with Restart for multi-dimensional data Fusion (RWRF) which authors say is a more effective fusion method. One advantage of such methods is that the network doesn’t get more complex with additional omics as their overall size is based on the number of samples, not the number of features. The resulting integrated graph can then be used as input for ML models [99], [101], [102] for clustering, subtype discovery or survival prediction.

The second approach relies on building multi-layer networks, where each layer represents an omics and interactions between omics are either inferred or retrieved from interaction or pathways databases. We invite our readers to the review of Lee et al. (2019) [29] for more information on multi-layer networks inference. Studying the overall topology of the network can reveal important molecules and perturbed pathways leading to specific phenotypes. Several methods can explore the network’s topology including shortest paths, random walks and other variations for multi-layer networks. In order to do gene reprioritization, Valdeolivas et al. (2019) [103] for example recently developed two new algorithms based on random walks for multiplex networks that can explore the different layers of physical and functional interactions between omics. For a similar goal, Shang and Liu (2020) developed iRANK [104], a variation of the PageRank algorithm [105] that they utilized on a multi-layer network composed of epigenomics data, gene expression data and protein–protein interactions network. A different approach was used by Murodzhon et al. (2017) [15] who developed OmicsNet, a weighted multi-layer network made of omics layers as well as a biological concept layer and phenotype layers. Specific nodes can then be associated with phenotypes by calculating along the weighted path an integrated score which can model a plausible signaling cascade. The results can be used for biomarker discovery or predictive analysis. Moreover, Liu et al. (2013) [106] proposed an interesting method to inspect a multi-layer network, recently improved by others [107], [108], where the activity of known molecular pathways present in the network is assessed by random walks. Active pathways are predicted by their concentration of important nodes (differentially expressed, associated with disease, topological importance, etc.). New features are then constructed based on the activity values of pathways and used with ML models for subtype classification or survival prediction tasks.

The third approach utilizes graph embedding methods which can learn low dimensional representation of the nodes and their surroundings from each network. The new graph-based features are then combined and fed to other ML models for prediction, classification, etc. Existing reviews on graph embedding methods [109], [110] go into more details, we will only present some recent cases. For example, DTINet [111] used random walk-based embedding on multiple interaction and similarity networks of proteins, drugs and diseases in order to detect similar nodes and predict new drug-target interactions (DTI). DTInet uses a dimensionality reduction method (DCA [112]) to reduce the multiple embeddings to a unique embedding for drug features and target features. Xuan et al (2019) [113] used a similar approach, but showed that the dimensionality reduction might remove too much information and instead used an ensemble learning approach with Gradient Boosting Decision Tree, which also deals with class imbalance as the number of unknown DTIs is higher than the number of known DTIs. Additionally, the graph-based variables can be compacted even further using autoencoders [114], [115] (Deep Learning , section 3.2.5). DeepDR [115] for example combined the different features obtained for each graph with a multi-modal autoencoder. The bottleneck layer containing the integrated information was later fed to a collective Variational Autoencoder [116] (cVAE) for DTIs prediction.

Multiple Kernel Learning (MKL) (Section 3.2.4) can also be used as graph embedding methods. In order to establish which molecular pathways are involved in breast cancer, Manica et al. (2019) [117] developed PIMKL which combines MKL with prior knowledge in the form of interaction networks and annotated genes or pathways. Kernel functions were designed to encode the topological information of known pathways, which can also be combined with the multi-omics datasets. The overall process allows the mapping of samples from the omics space to an interaction space (edge space), which explicitly reveals the underlying biological mechanisms. Additionally, Tepeli et al. (2021) [118] developed PAMOGK which introduced a graph kernel to determine sample similarity from graph data and predict subgroups of patients.

Additionally, Graph Neural Networks (GNN) [119] and its upgrade Graph Convolutional Neural Networks (GCN), are specifically designed to receive graph data as input. GCNs have also been developed for DTIs prediction [120] or node classification [121]. Going further than simple link prediction, Zitnik et al. (2018) [122] have used a GCN called Decagon to predict the presence of side effects between two drugs as well as the side effects’ type. GCN can also embed entire networks, which is mostly applied on drugs (which can be considered as graphs of atoms) and the resulting molecular embedding can be combined with multi-omics datasets to increase prediction performances [123]. More information on deep learning for biological networks can be found in Muzio et al. (2021) [124]. General integration of multi-omics data with deep learning is the subject of the next section.

3.3.3. Artificial neural networks

Artificial neural networks (NN) are powerful ML models made of many neurons organized in layers. They can be used directly on the concatenated omics (Section 3.1 Early integration) or separately on each omics (Section 3.4 Late integration), but it can also be utilized to learn meaningful latent representations (deep learning-based features) from each datasets by processing them in separate layers. The latent representations can be seen as new deep variables learned by the different layers of the model, which can be easily concatenated or connected to other neural networks for more analysis. Thus, the hidden layers of a NN can be considered as successive feature extraction layers, while only the final output layer can produce a prediction. Some NN architectures are specialized in learning a pertinent latent representation, such as Autoencoders (AE) and Restricted Boltzmann Machines (RBM). Both models are unsupervised neural networks that reproduce the original data from a compressed representation encoded within the central or bottleneck layer of the network. The fewer neurons in this layer, the more compact the representation is. The new representation is then useful as input for other ML models and particularly for clustering [125].

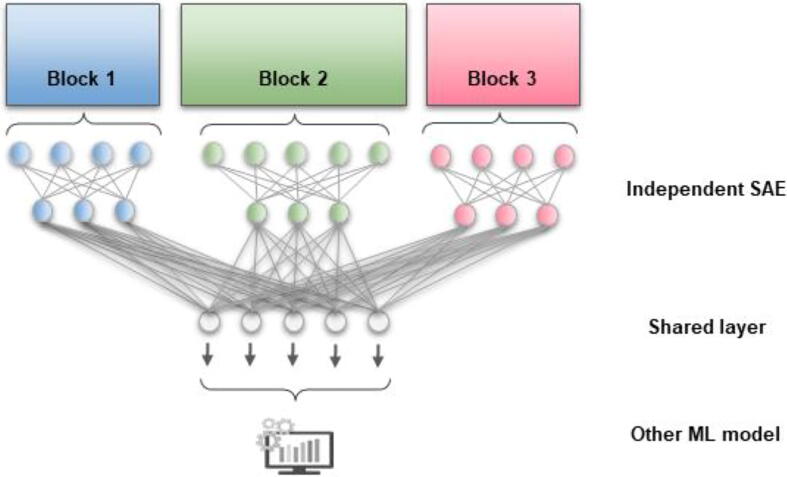
Among the deep learning models developed for multi-omics integration, we can present MOLI [13], [127], which retrieved DL-based features using subnetworks on each omics dataset and concatenate the obtained deep features. Then, a final neural network is used on the concatenated deep features for prediction of drug activity. Using a similar approach, Islam et al. (2020) [128] predicted breast cancer subtypes using the concatenated features, but they learned them through convolution neural networks applied on gene expression and copy number variation datasets. Instead of concatenating the deep features obtained for each omics block, another approach is to simply connect them to a shared layer. For example Xu et al. (2019) [126] (Fig. 2) first used stacked Sparse Autoencoders (SAE) on each omics dataset and integrated the results into a final layer. The resulting shared representation was fed to a deep flexible neural forest for predicting cancer subtypes. Similarly, Yang et al. (2021) [129] developed a multimodal autoencoder capable of taking all omics datasets as input, compacting them into the central layer, or bottle-neck layer of the autoencoder and reconstructing them at the end. The resulting deep features generated in that common layer take into account all omics and were also used for the discovery of cancer subtypes.

Fig. 2.

Example of a mixed artificial neural network. Each omics block is first reduced to a latent representation using independent Stacked Sparse Autoencoders (SAE). The new representations learned are integrated in a final shared layer. The common representation is used for downstream analysis such as prediction or clustering. Figure inspired from Xu et al. (2019) [126].

3.4. Intermediate strategies

We describe as intermediate integration any methods capable of jointly integrating the multi-omics datasets without needing prior transformation and without relying on a simple concatenation. They generally output new constructed representations, one common to all omics and some omics-specific, on which further analysis can be done. This step reduces the dimensionality and complexity of the multi-omics datasets. However, they are most often used after feature selection and robust pre-processing as the heterogeneity between datasets can prevent them from working correctly. Only a few methods were developed with the ability to find semi-shared structures, that is patterns shared between some omics but not all. Such methods include SLIDE [130] for example. Ideally, to limit the loss of information that occurs by selecting features independently for each omics, an intermediate feature selection method could be used such as the extension of mRMR developed by EL-Manzalawy et al. (2018) [65]. It selects features by taking into account their complementarity within and across omics blocks. The same results cannot be achieved by simply applying mRMR on each dataset, nor by applying mRMR on the concatenated dataset. Some intermediate strategies are also designed as multi-block feature extractions methods and can be utilized for exploratory purposes or as basis for downstream analysis, in the same way as a regular feature extraction (Section 3.0).

Intermediate methods are often formulated with the assumption that the different datasets share a common latent space, which can reveal the underlying biological mechanisms. Among those methods, extensions of the widely used Non-negative Matrix Factorization (NMF) [131] have been developed including joint NMF [132] and integrative NMF [133], [134]. Both methods infer a common matrix depicting the latent relationships between every omics dataset, but while joint NMF uses the common space to identify modules of correlated multi-omics data, integrative NMF implements sample clustering and subtype discovery. Other similar methods are presented in Table 1. The main advantage of such intermediate methods is their ability to discover the joint inter-omics structure, while also highlighting the complementary information contained in each omics. We won’t go into further details as the number of multi-block dimensionality reduction methods is substantial and still increasing, for more information, specific reviews have been written on the subject [14], [26], [135].

Table 1.

A non-exhaustive list of multi-block dimensionality reduction methods for multi-omics datasets. NMF: Non-negative Matrix Factorization, MOFA: Multi-Omics Factor Analysis, JIVE: Joint and Individual Variation Explained, MO: multi-omic.

Method	Principle	Purpose	Recent applications
jNMF/intNMF/nNMF [132], [133], [139]	Matrix factorization	Disease subtyping, module detection, biomarker discovery	jNMF found biomarkers in MO and pharmacological data connected to drug sensitivity in cancerous cell lines [140]. intNMF identified Glioblastoma and breast cancer subtypes from MO and clinical data [134].
MOFA/MOFA+ [141], [142]	Bayesian Factor Analysis	biomarker discovery, systemic knowledge	MOFA found new biomarkers and pathways associated with Alzeihmer’s disease based on MO data including proteomics, metabolomics, lipidomics [143].MOFA + found predictive biomarkers from DNA methylation and gene expression data in cardiovascular disease [144].
iCluster [145]	Gaussian latent variable model Generalized linear regression Bayesian integrative clustering	Disease subtyping, biomarker discovery	iCluster was used to identify subtypes of esophageal carcinoma from genomic, epigenomic and transcriptomic data [148].
iClusterPlus [146]			iClusterPlus was used to identify subtypes of non-responsive samples with ovarian cancer from different omics datasets [149].
iClusterBayes [147]			iClusterBayes was used to identify predictive biomarkers and clinically relevant subtypes on MIB cancer from 5 different omics [150].
JIVE/aJIVE [151], [152]	Matrix factorization	Disease subtyping, systemic knowledge, module detection	JIVE was used as a dimension reduction technique to improve survival prediction of patients with glioblastoma from mRNA, miRNA and methylation data [153].
Integrated PCA 64	Generalized PCA	Visualization, prediction	iPCA was used as a dimension reduction technique to improve prediction of outcome on lung cancer from CpG methylation data, mRNA and miRNA expression [154].
SLIDE [130]	Matrix factorization	Disease subtyping, module detection, biomarker discovery	SLIDE was used on DNA methylation data and gene, protein and miRNA expression for subtyping patients with breast cancer [130].

Other methods originally developed for two datasets were extended to multi-omics including Canonical Correlation Analysis (CCA) [136], [137] or Co-Inertia Analysis (CIA) [138]. The difference between them and the other presented in Table 1 is that they do not construct a common space, but infer omics specific factors while maximizing some joint measure such as correlation of co-inertia. We won’t go into further details as the number of multi-block dimensionality reduction methods is substantial and still increasing, for more information, specific reviews have been written on the subject [14], [26], [135].

3.5. Late integration

For handling multi-omics datasets, the most straightforward integration strategy is to apply machine learning models separately on each dataset and then combine their respective predictions, namely Late integration. Its strength relies on its capacity to use readily available tools designed specifically for each omics type, and compared to the other strategies, it does not suffer the challenges of trying to assemble different kinds of data. For example, Sun et al.(2019) [155] built neural networks for each dataset consisting of gene expression, copy number data and clinical information and linearly aggregated their predictions into a single final prediction for cancer prognosis. A more complex aggregation function was used by Wang et al. (2020) [156] where the authors trained Graph Convolutional Neural Networks on each omics (and their respective patient similarity networks) to recover initial classification predictions. The single-omics predictions were then utilized to construct a cross-omics tensor, which was forwarded to a View Correlation Discovery Network (VCDN) that makes a final class prediction based on the individual omics predictions and the latent cross-correlation between omics.

The shortcoming of such integration strategy is that it cannot capture inter-omics interactions and at no point in the learning process can the different machine learning models share knowledge and utilize the complementarity information between omics. Combining predictions is simply not enough to accurately exploit multi-omics data and understand the underlying biological mechanisms of diseases. For that reason, and because it boils down to multiple single-omics analysis, we will not discuss it further.

3.6. Hierarchical integration

A challenge in system biology is to understand the modular organization structured at the molecular level. A new trend is to incorporate these regulatory effects in the integration strategy to better reflect the nature of multidimensional data. Hierarchical strategy bases the multi-omics integration on the inclusion of the prior knowledge of regulatory relationships between the different layers. For example, a strategy for genotype-phenotype integration based on existing knowledge of cellular subsystems could follow this logic: genotypic variations in nucleotides can give rise to change in gene expression or functional changes in proteins which in turn could ultimately affect the phenotype. Therefore, hierarchical integration strategies often use external information from interaction databases and scientific literature. Moreover, because omics are organized in sequential fashion, the challenges of multi-omics integration are not exacerbated and can be dealt with separately for each dataset.

Some methods for supervised hierarchical integration include Bayesian analysis of genomics data (iBAG) [157], linear regulatory modules (LRMs) [158] and Assisted Robust Marker Identification (ARMI) [159] and Robust Network [160]. Hierarchical integration methods are often designed to study specific regulatory relationships. For example, iBAG has been developed to investigate associations between epigenetic and gene expression regulation. The framework uses hierarchical modeling to combine the data from methylation and gene expression to study the associations with patient survival. Robust Network has developed an approach for modeling the gene expression (GE) and copy number variation (CNV) regulation that describe the dominant cis-acting CNV effects compare to trans-acting CNVs. This approach could be extended to other regulation relationships such as gene expression by methylation and microRNAs. Additionally, hierarchical integration can be used to infer gene regulatory networks (GRN) from multi-omics datasets. For instance, Zarayeneh et al. (2016) [11] developed a GRN inference method by taking into account interaction effects between gene expression, Copy Number Variations (CNV) and DNA methylation. Their method utilized the epigenomic data to better predict regulatory interactions and achieved significantly better results on simulated data, compared to two other GRN inference methods SGRN [161] and DCGRN [162]. For more information on inference methods for GRN, we recommend Wani and Raza (2019) [28].

Finally, Fortelny and Bock (2020) [163] developed a neural network model in which each node corresponds to a biological entity such as a protein or a gene and each edge with a known interaction. The layout of the network follows the flow of information in the cell, with the input layer being gene expression and the following layers being transcription factors, signalling proteins, receptors, etc. The advantage of this DL model is that it is directly interpretable by looking at the activated nodes.

4. Summary and outlook

In this mini-review, we presented the different strategies available to handle multi-omics datasets integration. Most integration approaches developed in recent years tend to first modify and transform each dataset using different machine learning models known as Mixed integration, in order to reduce their complexities and heterogeneities and facilitate their subsequent integration and analysis. While it can give informative results, each dataset is transformed independently, potentially resulting in a loss of information and a final model that can still suffer from noise or redundant information. Ideally, at any point of the learning process, each omics dataset should be assessed while considering the other datasets, so that the complementary information could be best exploited. The early and intermediate integration strategies do solve this problem by integrating all datasets beforehand, but the large matrix resulting from an early integration is difficult to exploit by most ML models and intermediate integration often relies on unsupervised matrix factorization, which has difficulty incorporating the considerable amount of pre-existing biological knowledge. Another methodology, hierarchical integration, is explicitly designed with the prior understanding of how the different omics layers interact with each other. However, only few such methods have been developed and are often tailored for specific omics types, which makes them less generalizable than other approaches. Additionally, they are dependent on prior data, which prevents them from exploring and discovering new biological mechanisms and pathways.

Another issue to tackle is whether or not “More is better”, quoting from Huang et al. (2017)[19]. Adding omics datasets for the only sake of adding more data might not always be a good idea. They carry more information and can potentially reveal pathways from different biological layers, but the additional data could also bring more noise, redundancy and an increased computational time than relevant information. Additionally, while multi-omics integration often leads to better results [126], [154], [164], some have shown that it is not always the case [26], [165]. Worse performances could arise if the model is not suited for a particular goal or for particular multi-omics datasets. Some models cannot handle massive matrices, outliers, highly correlated variables, noise, etc., issues that are exacerbated in multi-omics studies. It is also possible that the omics are not correctly integrated [165]. We believe that if the machine learning model and the integration strategy are chosen judiciously, multi-omics should always surpass single-omics performances, but knowing in advance the proper integration strategy is not always feasible. There are not yet any general rules of thumb to foresee which method will achieve better results and most benchmarks generally conclude that the best approaches have to be chosen depending on the initial data. Nevertheless, based on recent trends, we can begin to notice effective approaches. For example, the early integration is being more and more outperformed when compared to other integration strategies [13], [65], [66], [164]. We believe that an early integration cannot handle too many datasets, especially when their heterogeneity is great and we suggest instead the mixed strategy which is tailored to deal with such challenges. The complementarity of datasets and their relative pertinence should also be taken into account, as some omics will contain less or possibly no useful information [153], [166]. Depending on the studied pathology, some omics will be more appropriate than others. In the same way, specific combinations of omics (metabolomics + proteomics, genetics + epigenetics, etc.) should be more fruitful than others and an understanding of those interactions is necessary. Based on the literature and biological knowledge collected on a specific topic, one could infer which omics layer should be retained or disregarded. Otherwise, the influence of each omics block should be determined during the analysis. For example, the mixed integration generally assumes equal importances and reshape the omics into similar representations. Thus in order to adjust their influences, their appropriate weights can usually be learned during training in the case of supervised learning. For unsupervised learning, it remains a challenge. This issue can be elegantly tackled by intermediate methods as they produce multi-omics and omics specific outputs which reveal the complementarity and benefits of each omics.

Furthermore, progress is continuously being made and new tools for multi-omics integration are continually being proposed. Network-based integrations are very promising, particularly for their ability to use pre-existing interaction networks and known molecular pathways as well as their straightforward interpretation. The exploration of multi-layer heterogeneous networks is just beginning and will surely continue to grow and gain in predictive and explanatory power as most of the tools currently used were designed for single-omics layers. The advances of deep learning are also quite compelling. Their flexible architectures facilitate the integration of multiple omics datasets, which can also be combined with biomedical images or other types of data, offering a better grasp of a patient's pathology. However, due to its large number of parameters, DL models are hard to train, must be tuned precisely and often experience overfitting. Their performances rely heavily on the availability of samples, which is still limited. An interesting way to deal with this issue is transfer learning [167], machine learning models are pretrained on larger and general datasets on which they can learn basic patterns and are then fine-tuned on the more specific dataset of interest. Transfer learning is widely used in image recognition, but is not yet regularly used in multi-omics studies. Deep learning also suffers from the reputation of not being easily interpretable, which is a major obstacle in biomedical studies. We have presented in this mini-review some examples of interpretable DL models, but more research must be done in order to confirm their capabilities and whether or not they can be adapted for different purposes.

With the ever-growing access to biological data, multi-omics research will be performed more and more often, and it is urgent that we identify the best practices, tools and strategies for their integration. In that aspect, benchmark studies are also particularly useful and should be done more frequently. With the notable exception of Herrmann et al. (2020) [168] which focused on survival prediction methods for multi-omics data, most benchmarks focus on clustering and dimensionality reduction methods [14], [26], [27], [135], [169], [170], [171]. Thorough comparisons of other ML models have not been made for multi-omics datasets, and we have yet to know if the deep learning prowess made in other fields of pattern recognition can be reproduced in bioinformatics [172].

4.1. Search strategy

This mini-review presents methods and strategies for multi-omics integration. The goal is not to produce an extensive list of articles and tools currently being used in the bioinformatic community, as the subject is too wide and not fit for a mini-review. The goal is more to display general trends and interesting ideas about the subject, with a particular focus on new and original methods developed in the past three years.

Articles and reviews were searched on PubMed with the keywords multi-omics / multiomics / machine learning multi-omics / deep learning multi-omics / network multi-omics / multi-omics integration / multi-block omics. Reviews published after 2015 were prioritized as well as methods and tools published after 2017, unless an older method was recently improved upon in a recent publication. This preliminary search produced approximately 1,000 results. Then, publications were kept only if the tool presented could manage at least two omics (exception was made for the hierarchical integration which is more specific). Additionally, we focused mostly on popular publications developing new approaches rather than on publications using existing tools to answer biological problems. In order to restrain the length of the mini-review and promote an easier reading experience, an effort was made not to include too similar articles. Altogether, these criteria resulted in the current publications presented in the mini-review.

5. Author statement

MP, AB and MPSB wrote the manuscript. AB and MPSB designed the figures. MP, MPSB, AB, OP revised the manuscript. AD supervised research.

Funding

This work was supported by Research and Innovation chair L’Oréal in Digital Biology.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.