Bayesian Structure Learning in Multi-layered Genomic Networks

Abstract

Integrative network modeling of data arising from multiple genomic platforms provides insight into the holistic picture of the interactive system, as well as the flow of information across many disease domains including cancer. The basic data structure consists of a sequence of hierarchically ordered datasets for each individual subject, which facilitates integration of diverse inputs, such as genomic, transcriptomic, and proteomic data. A primary analytical task in such contexts is to model the layered architecture of networks where the vertices can be naturally partitioned into ordered layers, dictated by multiple platforms, and exhibit both undirected and directed relationships. We propose a multi-layered Gaussian graphical model (mlGGM) to investigate conditional independence structures in such multi-level genomic networks in human cancers. We implement a Bayesian node-wise selection (BANS) approach based on variable selection techniques that coherently accounts for the multiple types of dependencies in mlGGM; this flexible strategy exploits edge-specific prior knowledge and selects sparse and interpretable models. Through simulated data generated under various scenarios, we demonstrate that BANS outperforms other existing multivariate regression-based methodologies. Our integrative genomic network analysis for key signaling pathways across multiple cancer types highlights commonalities and differences of p53 integrative networks and epigenetic effects of BRCA2 on p53 and its interaction with T68 phosphorylated CHK2, that may have translational utilities of finding biomarkers and therapeutic targets.

1. Introduction

Cancer is a complex disease that is caused by deregulation of several molecular processes and cellular pathways, usually triggered by genetic alterations in specific sets of genes (Hanahan and Weinberg, 2000, 2011; Creixell et al., 2012). Pathway and network analysis aim to gain insight into these underlying interactive mechanisms, and to reduce data involving thousands of altered genes and proteins to a smaller, and more interpretable set of functionally altered processes (Pe’er and Hacohen, 2011). The Cancer Genome Atlas (TCGA) has generated a rich source of multi-dimensional genomics (’omics for short) data for patients across multiple tumor types and their subtypes (http://cancergenome.nih.gov). More recently, The Cancer Proteome Atlas (TCPA) (http://bioinformatics.mdanderson.org/main/TCPA:Overview) has generated a complementary set of reverse phase protein array (RPPA)-based proteomic data across most of these patients’ samples, covering major oncogenic signaling pathways (Li et al., 2013; Akbani et al., 2014). Multi-level integration and processing of network information across these modalities is emerging, based on the principle that any biological mechanism is a systematic conflation of multiple molecular events and their interactions (Kristensen et al., 2014).

The basic data structure constitutes of a finite sequence of hierarchically-ordered datasets for each individual subject, which facilitates integration of diverse inputs such as genomic, transcriptomic, and proteomic data to investigate the unified regulatory mechanisms underlying the biology of various cancers. Figure 1 shows a conceptual data structure that allows for the characterization of dependencies within and between the datasets from the ordered layers. Two types of edges characterize the network structure: undirected edges within each layer, and directed edges to distinguish variables in a layer from variables in all the previous layers. Most integrative analyses rely on directed relationships between different data platforms based on the biological mechanisms (Wang et al., 2013), and the variables observed from each platform constitute a layer. For example, following the central dogma of biology, the first layer could constitute DNA-level data (copy number, methylation), the second layer the transcriptomic (mRNA expression), and the third layer proteomic data. In this context, the directed edges capture cross-platform (e.g., transcriptional, translational) dependencies, and the undirected edges capture the within-platform dependencies.

Fig. 1.

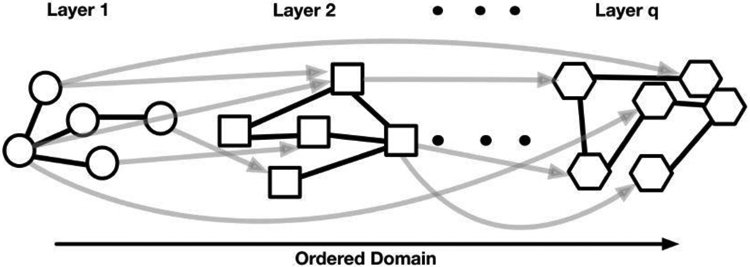
Example network for q ordered layers. In our application, we consider four layers corresponding to DNA methylation, Copy number aberration, gene expression and protein expression (see Section 7).

Modeling each of the layers independently does not account for the hierarchical multi-layered structure of the data, and can only provide information on how networks operate at a static point in time or under a static condition. A critical next step is to understand a holistic and dynamic picture of the interactive system and the information flow, which can only be achieved by simultaneously modeling multiple layers of data. Our objective is to investigate the conditional dependencies among the variables from multiple layers, while accounting for the order defined by the underlying layered structure of the data. Statistically, this translates to a structural estimation of graphs with a mixture of directed and undirected edges. This objective poses significant methodological and computational challenges, however, to building a single graphical model that includes hierarchical multiple graphs with directed edges for dependencies, constrained by orders between layers, as well as with undirected edges for unconstrained dependencies within layers.

Chain graphs have been used to model the layered architecture of networks, where the vertices can be naturally partitioned into ordered sets that exhibit undirected and directed acyclic relations within and between the sets. The conditional independencies that correspond to missing edges (i.e., Markov properties in the chain graphs) have been studied by Lauritzen and Wermuth (1989); Frydenberg (1990); Andersson et al. (2001). Drton and Eichler (2006) introduced a point-estimation approach to maximum likelihood estimation given the graph structure, and Drton and Perlman (2008) proposed a constraint-based method to estimate the structure. However, all of the above-mentioned methods for chain graphs are restricted to low-dimensional data with sample sizes larger than the number of vertices.

In its simplest form (two layers), a chain graph is equivalent to a multiple multivariate regression model. Multiple predictors affect multiple responses that exhibit a correlation structure, and both regression coefficients (for directed edges) and the error precision matrix (for undirected edges) are assumed to be typically sparse. Approaches based on the doubly-penalized joint likelihood have been proposed by Rothman et al. (2010); Yin and Li (2011). A joint L₁ penalty was imposed on both the regression coefficients and the precision matrix, resulting in a penalized likelihood that is bi-convex (but not convex), which implies that the optimization algorithm may be unstable and fail to converge (Lee and Liu, 2012). Cai et al. (2012); Chen et al. (2016) proposed a two-step approach, in which only regression coefficients are estimated in the first step, and then the error inverse covariance matrix is obtained in the second step, given the estimated regression parameters. To select good initial parameters for this bi-convex problem, Lin et al. (2016) proposed an L₁ penalized maximum likelihood estimation with prescreening of variables, and extended this methodology to multi-layered graphs with an arbitrary number of layers. In a Bayesian framework, Bhadra and Mallick (2013); Consonni et al. (2017) proposed a Bayesian model based on the hyper-inverse Wishart prior on the covariance matrix, which assumes that the UGs within each layer are decomposable. The decomposability assumption is generally restrictive, explores a smaller model space, and potentially provides misspecification of the structure for networks in many real applications.

In this article, we propose a novel approach for a multi-layered Gaussian graphical model (mlGGM) that accommodates data from an arbitrary number of layers. The mlGGM is a special case of the chain graph model, where the random variables that correspond to the vertices are assumed to follow a multivariate Gaussian distribution, and the zero structures of the mean parameter and the precision parameter directly link to the absence of the directed and undirected edges, respectively. We construct a regression-based formulation that converts the mlGGM into a more tractable node-wise multiple regression model. We generalize the node-wise multiple regression approach that coherently accounts for conditional independencies in mlGGMs. We jointly select both undirected and directed edges that point to a vertex via Bayesian variable selection priors for each of the regressions, allowing for a much larger graph space than that of decomposable graphs. Moreover, the prior formulation allows for the incorporation of relevant prior knowledge through the edge-specific informative prior, and provides a computationally more efficient procedure to estimate mlGGMs.

Through simulation studies under various settings of the mlGGMs, we demonstrate the utility of our node-wise regression framework in the structural recovery of the mlGGM, and compare its performance to those of related multivariate regression-based methods. We also numerically evaluate sign consistency (i.e., whether our univariate regression-based formulation correctly finds the signs of the undirected and directed dependencies when we have the known structure). We illustrate the applicability and versatility of mlGGMs to infer integrated genomic networks for multi-omic data, using biological hierarchies among the platforms across multiple cancers. The signed topological structure obtained from our method allows for more refined inference of both cross- and within-platform dependencies, including the inhibition/activation between platforms and positive/negative correlations within platforms. Furthermore, we investigate the commonalities and differences in their multi-layered network structures across cancer types, and show translational utilities of these integrative networks.

The rest of this article is organized as follows. Section 2 provides data structure and backgrounds on mlGGMs. Section 3 presents the joint model and the corresponding prior construction. We introduce our Bayesian node-wise selection (BANS) framework in Section 4. We discuss posterior inference on graphical structure estimation in Section 5. Simulation studies are carried out in Section 6. We demonstrate the utility of our method in multi-layered genomic network studies across cancer types in Section 7. Section 8 concludes the article.

2. Background

2.1. Data structure

We consider a graphical model over p biological units across multi-omic data, Y = (Y₁,…,Y_p)^T ∈ℝ ^p. Here p could constitute different platform-specific observations (e.g., genes, proteins, etc.), but for ease of conceptual and technical exposition, we use genes throughout. A graph of Y can be denoted by G = (V,E), where V = {1,…, p} includes all genes across platforms, and E may contain both directed (→) and undirected edges (–) between the genes. We assume to know a priori that a partitioning T = {τ_k ∣1 ≤ k ≤ q}, q ≤ p, is a family of pairwise disjoint ordered layers of p genes. The ordered partitioning T implies that any edges between the layers are directed. In other words, each layer t_k constitutes genes from a platform, and the layers are ordered according to a biological hierarchy. Formally, the partitioning T is called a dependence chain if k < l ⇒ v ½ u∀u ∈ τ_k, v ∈ τ_l. In other words, when k < l, any edges between t_k and t_l point from a vertex in t_k to a vertex in t_l. For each v ∈ V , let 1 ≤ t(v) ≤ q be the index, such that v ∈ τ_t(v). We assume without loss of generality that the vertices are labeled, such that, t(u) < t(v) ⇒ u < v. Factorization based on biological hierarchies. The integrative genomic analyses for multi-platform genomics data can be performed based on coherent biological justifications motivated by their hierarchical dependencies. Following the central dogma of biology, where the epigenetic and DNA level, such as methylation and copy number variation, potentially regulate mRNA expression (transcription regulation), which in turn is known to regulate protein expressions (translation regulation) (Morris and Baladandayuthapani, 2017). For our case study, we integrate four datasets from copy number aberration (CNA), methylation, mRNA expression, and protein expression, and the dependence chain (T ) constitutes four (q) disjoint sets that have their own unique order: (CNA, methylation) < mRNA < protein (see Figure S14)

Notationally, if u → v, the vertex u is a parent of v. Let pa_v = {u ∈V :u → v ∈ E} and pa_A = ∪_v∈Apa_v, A be the sets of parents of v and a subset A⊆V , respectively. We assume the dependence chain allows for factorization of DAGs at the layer level (i.e., the graph in Figure 1 is a DAG of the dependence chain, τ₁,…, τ_q). We denote the sub-vector of Y corresponding to a subset A⊂V by Y_A. The joint probability distribution of Y can be factorized as

$$P(\mathit{Y})=\prod _{\tau \in \mathrm{T}}P({\mathit{Y}}_{\tau }\mid {\mathit{Y}}_{{\text{pa}}_{\tau }})$$ (1)

(Lauritzen, 1996). Through factorization, the network structure in Figure 1 can be viewed as q − 1 two-layered models, such as {Y_τm : m = 1,…, k − 1} versus Y_τk for k > 1, plus a one-layered UG model for Y_τ1. In the example of using DNA methylation, CNA, mRNA expression and protein expression, the multi-layered networks can be constructed from two UG models for CNA and methylation, and two two-layered models for mRNA and protein expressions.

To complete our chain graph model, we specify the Markov property. For a dependence chain T , we define the cumulatives to be the set C_l = ∪_k≤l τ_k for 1 ≤ l ≤ q. Andersson et al. (2001) proposed a Markov property for chain graphs and set the pairwise Markov property for G as

$$\begin{gathered} u-v\notin E\Rightarrow Y_u\perp Y_v\mid {\mathit{Y}}_{C_{t(v)},\{u,v\}}\text{for}t(u)=t(v) \\ u\to v\notin E\Rightarrow Y_u\perp Y_v\mid {\mathit{Y}}_{C_{t(v)-1},\{u\}}\text{for}t(u)<t(v). \end{gathered}$$ (2)

A missing directed edge between two random variables Y_u and Y_v implies that they are conditionally independent, given all other variables in τ₁,…, τ_t(v)−1, while the conditional set of missing undirected edges is all other variables in τ₁,…, τ_t(v).

2.2. Multi-layered Gaussian graphical models

In this section, we specify each factor in (1). We assume that the p × 1 random vector Y follows the multivariate Gaussian distribution N(0,Ω⁻¹), with the positive definite precision matrix Ω. The mlGGM G = (V,E), following the Markov property stated in (2), is

$$\mathit{Y}=\mathbf{B}\mathit{Y}+\mathit{ò},\mathit{ò}\sim N(0,{\mathsf{K}}^{-1}),$$ (3)

where B = (b_vu) is a p × p matrix with u → v ∉ E ⇔ b_vu = 0, and K = (κ_vu) is a positive definite p × p matrix with v − u ∉ E ⇔ κ_uv = κ_vu = 0. Then the precision matrix of Y is

$$\Omega =(\mathbf{I}-\mathbf{B}{)}^{\mathrm{T}}\mathsf{K}(\mathbf{I}-\mathbf{B}),$$ (4)

where I is an identity matrix. B is a coefficient matrix for which the zero structures encode the directed edges between layers. The precision matrix of the error ò, K is a symmetric matrix, where the nonzero off-diagonal elements represent the undirected edges within a layer after taking out the effects from the directed edges, and the ith diagonal element is the inverse variance of Y_i.

The mlGGM in (3) for a dependence chain T with ∣T∣= q > 1 can be expressed as one GGM for t₁ and q − 1 two-layered GGMs by the factorization in (1). For a matrix A = (a_ij), we denote sub-matrices A_S1,S2 = (a_ij)_{i∈S1,j∈S2} and A_S = (a_ij)_i∈S,j∈S. We also denote the transpose of a sub-matrix, ${\mathbf{A}}_{{\mathsf{S}}_1,{\mathsf{S}}_2}^{\mathrm{T}}=({\mathbf{A}}_{{\mathsf{S}}_1,{\mathsf{S}}_2}{)}^{\mathrm{T}}$. Under the factorization in equation (1), the model in (3) can be re-expressed as the component-wise conditional distributions:

$${\mathit{Y}}_{\tau }\mid {\mathit{Y}}_{{\text{pa}}_{\tau }}\sim N({\mathbf{B}}_{\tau ,{\text{pa}}_{\tau }}{\mathit{Y}}_{{\text{pa}}_{\tau }},{\mathsf{K}}_{\tau }^{-1})\text{for all}\tau \in \mathsf{T}.$$ (5)

Because the first layer t₁ has an empty parent set, it has zero mean in (5) and is equivalent to the UG. The conditional distribution corresponds to a multivariate multiple regression, where the block of variables Y_τ is regressed on the parents Y_paτ.

There are other formulations of chain graphs based on the Lauritzen-Wermuth-Frydenberg (LWF) Markov property (Lauritzen and Wermuth, 1989; Frydenberg, 1990). In the case of continuous variables with a joint multivariate Gaussian distribution, the Markov property in (2) is coherent with data generated by the linear system in (5) (Cox and Wermuth, 1993; Andersson et al., 2001; Drton and Eichler, 2006). Further details on implication of Markov properties are in Section S1.

3. Joint model and prior construction

In this section, we discuss the estimation problem of the multi-layered graph structure that includes both directed and undirected edges, which induces network-based integration of multi-omic data. Under known T , our focus is to estimate the zero-structures of B and K that encode the directed edges and undirected edges between and within layers, respectively. For directed edges, the problem boils down to finding the parents, pa_v for v ∈ τ_k ⊆ V from the cumulative C_k−1, which is the union of all the preceding layers of t_k. The model corresponding to the first layer, t₁, is given by

$${\mathit{Y}}_{{\tau }_1}\sim N(0,{\mathsf{K}}_{{\tau }_1}^{-1}),$$ (6)

where there are no predictors. From the second component to the last component, τ₂,…τ_q with ∣T∣= q, the structure of the model is expressed by the following multivariate multiple regressions:

$${\mathit{Y}}_{{\tau }_k}={\mathbf{B}}_{{\tau }_k,C_{k-1}}{\mathit{Y}}_{C_{k-1}}+{\mathit{ò}}_{{\tau }_k},\text{and}{\mathit{ò}}_{{\tau }_k}\sim N(0,{\mathbf{K}}_{{\tau }_k}^{-1}),k=2,\dots ,q,$$ (7)

where C_k is the cumulative for the kth layer. The model for the first layer only involves the parameter for the precision matrix K_τ1 , which is a traditional model for UGs (Lauritzen, 1996). The parameters of interest are the coefficient matrices {B_τk,Ck−1 : k = 2,…, q}, which encode the directed edges across the layers, and {K_τk : k = 1,…, q}, which encode the conditional dependencies within the layers, after adjusting for the effects from the directed edges. Fitting the set of regression models can be performed independently and in parallel, assuming priors over the parameters that are independent across the regressions. Component-wise regressions. In this component-wise regression framework, we can use the Inverse Wishart prior for ${\mathsf{K}}_{{\tau }_k}^{-1}$ and the independent normal priors for elements of B_τk,Ck−1 : for all k = 1,…, q,

$$\begin{gathered} {\mathsf{K}}_{{\tau }_k}^{-1}\sim InverseWishar{t}_{\mid {\tau }_k\mid }({\delta }_{{\tau }_k},{\lambda }_{{\tau }_k}{\mathbf{I}}_{\mid {\tau }_k\mid }), \\ {b}_{vw}\sim N(0,c_{vw}^2∕{\kappa }_{vv})\text{forall}v\in {\tau }_k\text{and}w\in C_{k-1}, \end{gathered}$$ (8)

where λ_τk > 0 and δ_τk > 0 for all k = 1,…, q, and c_vw are constants. The prior of each regression coefficient b_vw is dependent on the precision k_vv of the variable Y_v (vth diagonal element of K).

In essence, we are able to divide the estimation problem of the mlGGM in (3) into smaller multivariate regression problems by specifying the priors that are independent across τ ∈ T in (8). The Inverse-Wishart distribution is the global conjugate prior for covariance matrices. However, the number of parameters greatly increases as the total number of variables from multiple layers increases. For estimating the two-layered GGM for the kth component, t_k, we have ∣τ_k∥C_k−1∣+∣τ_k∣(∣τ_k∣+1)/2 number of parameters for the directed edges, undirected edges, and the variances of the variables in t_k. The number of parameters is 3775, even for ∣τ_k∣= 50 and ∣C_k−1∣= 50. Moreover, the number of parameters becomes larger when we handle downstream layers, due to the increasing number of preceding layers. Bhadra and Mallick (2013) and Consonni et al. (2017) proposed a joint selection of the nonzero elements of B_τk,Ck−1 and K_τk, where the undirected relations encoded in K_τk correspond to the limited space of decomposable graphs using the hyper-inverse Wishart prior (Dawid and Lauritzen, 1993). Moreover, the method selects entire columns of the coefficient matrix B_τk,Ck−1, and fails to select single elements of this matrix (i.e., a variable in an upper layer is either connected to all variables in a lower layer or to none), and the same precision matrix K_τk informs the selection of the coefficient matrix B_τk,Ck−1. Assumptions on both B_τk,Ck−1 and K_τk, while improving computational efficiency due to conjugate formulation and allowing for the exact calculation of the marginal likelihood of the graph, impose the artificial restriction on both undirected and directed structures, and may potentially result in misspecification of the networks structures. In particular, the space of decomposable graphs corresponding to K_τk is increasingly sparse with the increasing size of t_k. For example, the percentages of graphs that are decomposable decrease as 95%, 80%, 55%, 29% and 12% for ∣τ_k∣= 4, 5, 6, 7, and 8, respectively (Armstrong, 2005).

4. Bayesian node-wise selection (BANS) framework

To circumvent the above-mentioned challenges, we develop a model selection procedure that allows for more general graph space than the procedures proposed by Bhadra and Mallick (2013); Consonni et al. (2017), as well as greater computational efficiency than the joint model formulation. We propose a Bayesian node-wise selection (BANS) method to jointly estimate undirected edges and directed edges of mlGGMs, using a node-wise regression framework. For a node, the Bayesian variable selection approach simultaneously finds its neighbors and parents, which are connected by undirected and directed edges, respectively.

4.1. Working model

For all v ∈ V, C_v and P_v are defined by the set of all other vertices in the same layer as v, τ_t(v), {v} and all the preceding vertices, C_t(v)−1, respectively. We consider multivariate regression between τ_t(v) as responses and P_v as predictors. Note that the sets in {P_v : v ∈ τ} are all the same, and we consider P_v = P_τ for v ∈ τ. We re-express models (6) and (7) to node-wise regressions:

$$Y_v={\mathit{Y}}_{{\mathsf{P}}_v}^{\mathrm{T}}{\mathbf{b}}_v+{\mathbf{ò}}_v\text{for all}v\in V,$$

where ò = (ò₁,…, ò_p)^T ~ N(0,K⁻¹) and b_v is a ∣P_v∣×1 vector of {b_vu : u ∈ P_v}. For the well-known conclusion that gives the relation between the concentration matrix of the multivariate normal distribution and the regression coefficients (Anderson, 1984), we have the following lemma.

Lemma 1. For all v ∈ V, ${\mathbf{ò}}_v={\mathit{ò}}_{{\mathrm{C}}_v}^{\mathrm{T}}{\alpha }_v+e_v$, where α_v = −K_Cv,v/κ_vv and e_v ~ N(0,1/κ_vv) is independent of ò_{V, {v}}.

The undirected edges encoded in the zero structures of the precision matrix K can be found by the zero structures of the regression coefficients obtained from regressing each residual ϵ_v to the residuals corresponding to the other vertices in the same layer.

Proposition 1. For all $v\in V,Y_v={\mathit{Y}}_{{\mathsf{P}}_v}^{\mathrm{T}}{\mathbf{b}}_v+{\mathit{Y}}_{{\mathsf{C}}_v}^{\mathrm{T}}{\alpha }_v-{\mathit{Y}}_{{\mathsf{P}}_v}^{\mathrm{T}}{\mathbf{B}}_{{\mathsf{C}}_v,{\mathsf{P}}_v}^{\mathrm{T}}{\alpha }_v+e_v$, where α_v = −K_Cv,v/κ_vv and e_v ~ N(0,1/κ_vv) is independent of ò_{V, {v}}.

The proof of Proposition 1 is provided in Section S2. From Proposition 1, we coherently convert the estimation problem of mlGGM in (3) to that of node-wise regressions. For a given node, both undirected edges between vertices in the same layer and directed edges toward the vertex can be jointly uncovered by model selection for a regression model. Our working model can be re-expressed as follows: for all v ∈ V ,

$$Y_v=\sum _{i\in {\mathsf{P}}_v}{\mathit{b}}_{vi}{Y}_i+\sum _{j\in {\mathrm{C}}_v}{\alpha }_{vj}{Y}_j+\sum _{j\in {\mathrm{C}}_v}{\alpha }_{vj}\sum _{i\in {\mathsf{P}}_v}-b_{ij}{Y}_i+e_v,$$ (9)

where e_v ~ N(0,1/κ_vv). Our model (9) for a vertex v ∈ V involves regression coefficients for the directed edges from the vertices in the preceding layers (P_v → v), undirected edges from the vertices in the same layer (C_v − v), and directed edges from the vertices in the preceding layers to the vertices in the same layer other than v(P_v → C_v).

A simple illustrative example.

Consider the linear model corresponding to the chain graph with two layers for genes {Y₁,Y₂} and proteins {Y₃,Y₄} described with solid lines in Figure 2 (a): Y₁ = ò₁, Y₂ = ò₂, Y₃ = b_3lY₁ + ò₃, and Y₄ = b₄₂Y₂ + ò₄, where ϵ₁ and ϵ₂ and (ò₃,ò₄) are mutually independent, and ϵ₃ and ϵ₄ (the residuals of proteins after taking out effects from genes) have bivariate normal distribution with an arbitrary covariance matrix. The undirected edge between proteins Y₃ and Y₄ is estimated by the regression coefficients, α₄₃ and α₃₄, from the two regressions for responses Y₃ and Y₄ in our working model with true nonzero regression coefficients, as shown in Figure 2 (b). For example, for the protein Y₃, our working model includes effects for the parent gene Y₁, the neighbor protein Y₄, and the indirect effect of the neighbor’s parent gene Y₂. Therefore, when we select directed and undirected edges for a biological unit v, the indirect effects of its neighbor’s parents are adjusted.

Fig. 2.

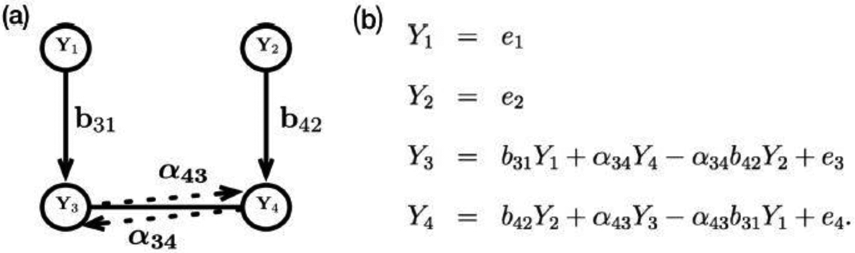
An example of a chain graph with layers {1, 2}, {3, 4}. (a) Solid lines represent the data generating structure and dotted lines display how we parameterize undirected edges in our neighborhood selection framework. (b) Our working model.

The next step is to deduce the prior distribution of {α_v∣v ∈ V} from the joint prior on the precision matrix K. The priors in (8) are re-expressed as follows: for all τ ∈ T,

$$\begin{gathered} {\alpha }_{vw}\mid {\kappa }_{vv}\sim N(0,1∕({\lambda }_{\tau }{\kappa }_{vv}))\text{forall}v\in \tau \text{and}w\in {\mathsf{C}}_v, \\ {\kappa }_{vv}\sim Gamma(\frac{{\delta }_{\tau }+\mid \tau \mid -1}{2},\frac{{\lambda }_{\tau }}{2})\text{forall}v\in \tau , \\ {b}_{vw}\sim N(0,c_{vw}^2∕{\kappa }_{vv})\text{forall}v\in \tau \text{and}w\in {\mathsf{P}}_v, \end{gathered}$$ (10)

where the Wishart prior on K_τ translates to normal and gamma priors on α_v and K_vv for v ∈ τ.

4.2. Model selection priors

Our goal is to infer the dependence structure of the underlying chain graph of the data Y. Using our framework, the undirected and directed edges of the chain graph can be selected using zero restrictions on the regression parameters, B and α. Based on the priors in (10), model selection is achieved through a mixture prior on the regression coefficients: for all v ∈ τ, w ∈ P_v, u ∈ C_v, and τ ∈ T ,

$$\begin{gathered} \text{Directed edges :}{b}_{vw}\mid {\gamma }_{vw},{\kappa }_{vv}\sim {\gamma }_{vw}N(0,c_{vw}^2∕{\kappa }_{vv})+(1-{\gamma }_{vw}){\delta }_0, \\ \text{Undirected edges :}{\alpha }_{vu}\mid {\eta }_{vu},{\kappa }_{vv}\sim {\eta }_{vu}N(0,1∕({\lambda }_{\tau }{\kappa }_{vv}))+(1-{\eta }_{vu}){\delta }_0, \\ \text{Variance parameters :}{\kappa }_{vv}\sim Gamma(\frac{{\delta }_{\tau }+\mid \tau \mid -1}{2},\frac{{\lambda }_{\tau }}{2}), \end{gathered}$$ (11)

where δ₀ is the Dirac delta function and c_vw, and λ_τ, and δ_τ are fixed hyperparameters. We complete the formulation of our model by specifying the prior on γ_vw and η_vw:

$$P({\gamma }_{vw}=1)=p_{vw}\text{and}P({\eta }_{vw}=1)=q_{vw},$$

where p_vw and q_vw are fixed hyperparameters. The binary indicators, γ_vw and η_vw, are latent variables that encode the directed structure between layers and the undirected structure within a layer. If γ_vw = 1, the arrow from w to v (w → v) is included in the graph, and γ_vw = 0 otherwise. If η_vw = 1, the undirected edge between v and w (v − w) is present in the graph.

5. Likelihood and posterior inference

For each vertex, we implement the Bayesian procedure to select the parents from the preceding layers and neighbors from the same layers as the vertex. Let Y = (y₁,…y_p) and Y_A for a set A ⊂ V be a n × p data matrix and n× ∣A∣ sub-matrix of Y for which the columns correspond to the set of vertices A. From Proposition 1, we have the following node-wise likelihood function:

$$\begin{gathered} L=\prod _{\tau }\prod _{v\in \tau }p({\mathbf{y}}_v\mid {\mathbf{Y}}_{{\mathsf{C}}_v\cup {\mathsf{P}}_v},{\alpha }_v,{\kappa }_{vv},{\mathbf{B}}_{\tau ,{\mathsf{P}}_v}) \\ =\prod _{\tau }\prod _{v\in \tau }{\left(\frac{{\kappa }_{vv}}{2\pi }\right)}^{n∕2}\text{exp}\left\{-\frac{{\kappa }_{vv}}{2}{\left({\mathbf{y}}_v-{\mathbf{Y}}_{{\mathsf{P}}_v}{\mathbf{b}}_v-{\mathbf{Y}}_{{\mathsf{C}}_v}{\alpha }_v+{\mathbf{Y}}_{{\mathsf{P}}_v}{\mathbf{B}}_{{\mathsf{C}}_v,{\mathsf{P}}_v}^{\mathrm{T}}{\alpha }_v\right)}^{\mathrm{T}}\left({\mathbf{y}}_v-{\mathbf{Y}}_{{\mathsf{P}}_v}{\mathbf{b}}_v-{\mathbf{Y}}_{{\mathsf{C}}_v}{\alpha }_v+{\mathbf{Y}}_{{\mathsf{P}}_v}{\mathbf{B}}_{{\mathsf{C}}_v,{\mathsf{P}}_v}^{\mathrm{T}}{\alpha }_v\right)\right\}, \end{gathered}$$

where α_v = −K_Cv,v/κ_vv. We construct the likelihood L by pooling conditional densities within each of the two-layer models. The inference using the likelihood L is not equivalent to the joint likelihood from our original model in (6) and (7), because the resulting local distributions are likely to be inconsistent in that there is no joint distribution p(Y_τ∣Y_Pτ) from each of the local distributions p(Y_v∣Y_Cv∪Pτ) (Heckerman et al., 2000). The results are asymmetry of the structure, magnitudes, and signs inferred from {α_v : v ∈ V} between α₄₃ and α₃₄ in Figure 2. The neighborhood selection approach (Meinshausen and Bϼhlmann, 2006) for UGs requires a symmetrization step after estimating the regression coefficients for all node-wise regressions. Similarly, in our model framework, the set of undirected edges can be defined by {v − w : η_vw = 1and η_wv = 1} or {v − w : η_vw = 1or η_wv = 1}. For more accurate inference on the graphical structure, instead of using the post-hoc symmetrization, we implement MCMC sampling (BANS) to estimate the posterior distributions with the symmetric constraint η_vw = η_wv and showed better accuracy in the structural learning than post-hoc symmetrization obtained from BANS-parallel (Section S7.5 in the Supplementary Materials). However, considering the gain in computation efficiency by using the node-wise parallelizable procedure, BANS-parallel is scalable and useful for high-dimensional problems.

5.1. MCMC Sampling

Our neighborhood selection approach for the chain graph model enables us to estimate the chain graph via a node-wise variable selection framework. Now we consider estimating the undirected edges and directed edges toward a vertex v. Since the parameter spaces for the binary indicators η and γ are enormous, computing the explicit posterior probabilities for all possible subsets poses computational challenges. Instead, we use a stochastic search variable selection (SSVS) to generate a Gibbs sequence for each vertex v(George and McCulloch, 1993). Our sampling scheme consists of two parts for updating undirected edges and directed edges. The symmetric constraints of the UG structure can be incorporated when sampling η by assuming η_vw = η_wv for v ≠ w. The MCMC algorithm, which is described in detail in Section S3 can be summarized as follows. For a vertex v ∈ τ ⊆ V at iteration t:

1. Undirected edges

   1.1 Set y_v = y_v − Y_Pvb_v and ${\mathbf{X}}_v={\mathbf{Y}}_{{\mathsf{C}}_v}-{\mathbf{Y}}_{{\mathsf{P}}_v}{\mathbf{B}}_{{\mathsf{C}}_v,{\mathsf{P}}_v}^{\mathrm{T}}$.

   1.2 Update {η_k : k ∈ τ} and set ${\text{ne}}_v^{(t)}=\{w\in \tau :{\eta }_{vw}\ne 0\}$.

   1.3 Update $\left\{{\alpha }_k:k\in \{v\}\cup {\text{ne}}_v^{(t)}\right\}$, and $\left\{{\kappa }_{kk}:k\in \{v\}\cup {\text{ne}}_v^{(t)}\right\}$.

2. Directed edges

   2.1. Set y_v = y_v − Y_Cvα_v and X_τ = (Y_Pv −α_vu1 Y_Pv −α_vu2 Y_Pv …), where u₁,u₂,… are vertices in ${\text{ne}}_v^{(t)}$.

   2.2. Update {γ_v : v ∈ τ}, B_τ,Pv, and κ_vv.

Sampling parameters that correspond to undirected edges are not independent among the vertices in the same layer, due to the imposed symmetric constraints. Thus, our MCMC sampling is performed for each layer. Within an MCMC sampling, steps 1 and 2 are repeated for all vertices in a layer. The mlGGM estimation using this MCMC sampling method is called BANS. We also implemented node-wise sampling scheme, called BANS-parallel in Section S6.

5.2. Graphical structure estimation

The posterior samples of the model parameters for undirected and directed edges obtained from our MCMC methods are used to perform Bayesian inference. The MCMC samples explore the distribution of possible graphs, with each graph leading to a different topology based on the model parameters. The maximum a posteriori (MAP) estimate represents the mode of the posterior distribution of possible graphs. This approach is not feasible, however, since the space of possible graphs is large and the most likely graph may still appear only in a very small proportion of MCMC samples. An alternative and practical solution is to select the edges marginally by using all of the MCMC samples and averaging the presence/absence of each edge over the MCMC samples (Hoeting et al., 1999).

We propose a false discovery rate (FDR)-based determination of significant networks. Our MCMC methods are applied to each of the layers as responses, with all the preceding layers as predictors. For each layer, suppose we have M posterior samples of the corresponding parameter set. From M MCMC iterations for all layers, we estimate the posterior marginal probability of edge inclusion for each edge g_vw as the proportion of MCMC iterations after the burn-in in which the edge v − w for t(v) = t(w) or w → v for t(w) < t(v) was selected in the graph. The values 1 − g_vw can be considered as Bayesian q-values, or estimates of the local FDR (Storey and Tibshirani, 2003; Newton et al., 2004), if the vwth edge is called a discovery. Given a desired FDR level α ∈ (0,1), we call the set of edges X_ϕα = {(v,w) : g_vw > ϕ_α discoveries. The significance threshold ϕ_α can be determined based on the approach of Baladandayuthapani et al. (2014). We first sort all {g_vw} in descending order to yield {g_(t)}. Then we set ϕ_α = g_{ξ), where $\xi =\max \{k\mid k^{-1}\sum _{j=1}^k(1-g_{(j)})<\alpha \}$. We expect that only 100α% of the discovered X_ϕα are false positives. An alternative approach is to select the set of edges that appear with marginal posterior probability of inclusion greater than ϕ_α = 0.5 (Barbieri and Berger, 2004). This rule results in an expected FDR for ${\varphi }_{\alpha },FDR=\frac{\sum _{(v,w)}(1-g_{vw})I(g_{vw}>{\varphi }_{\alpha })}{\sum _{(v,w)}I(g_{vw}>{\varphi }_{\alpha })}$, where I is the indicator function.

6. Simulations

The aim of our simulation study is to compare BANS with other joint estimation approaches under various simulation settings that generate high- and low-dimensional data under the mlGGM in (3) (Section 6.2). We perform sensitivity analysis of our model to hyperparameters and check the convergence of the proposed algorithm in Section S4 and S5 of the supplementary materials, respectively. Section S7 includes extensive simulation studies evaluating sign consistency of the estimated partial correlations for edges using structured sampling scheme and the performance of BANS and BANS-parallel with different types of priors under various simulation settings of non-Gaussian synthetic data.

6.1. Data generation with random chain graphs

To generate random chain graphs, we assume that the UGs within layers follow the Erdös and Rényi (ER) model (Erdős and Rényi, 1960). A graph that follows the ER model is constructed by randomly connecting the vertices. We assume that each undirected edge within a layer is included in the chain graph with probability p_E independent from all other edges. We also assume that each directed edge between two consecutive layers is independently linked with probability p_E / 2. Thus, the vertex i in the graph is almost surely connected to (∣τ_t(i)∣−1)p_E undirected edges and ∣τ_t(i)−1−1∣p_E / 2 directed edges. We generate an adjacency matrix A = (A_ij)_p×p that represents a random chain graph on V = {1,…, p} with A_ij = A_ji = 1 for i − j, and A_ij = 1 and A_ji = 0 for i → j. We use the random chain graph generation procedure as follows: (1) assign p vertices to the dependence chain T = {τ_k∣k = 1,…, q} so that the sizes of the layers are mostly the same; (2) set independent realizations of Bernoulli(p_E) in the lower triangular elements of the sub-matrix corresponding to each layer, then symmetrize it; and (3) set independent realizations of Bernoulli(p_E / 2) in the off-block diagonal elements between two consecutive layers. Given a randomly generated chain graph G with the dependence chain T , the observed data are simulated by the mlGGM in equation (3), after setting the intensities of the nonzero elements of B and K . The nonzero elements of B and K are randomly sampled from (−1.5,−0.5)∪(0.5,1.5). To guarantee the positive definiteness of K , their diagonal elements are filled by column-wise sums of absolute values, plus a small constant. Then we draw a random sample Y of size n from the distribution N(0,Ω⁻¹) with Ω in equation (4). In the additional simulation setting that emulates the DNA Damage response network estimated for 309 TCGA lung squamous cell carcinoma (LUSC) samples (Section S7.1), we used the parameter estimates B and K obtained from the real data application to generate simulation datasets.

6.2. Performance evaluation

We compare the performance of our BANS method against those of multivariate regression-based methods in learning the topologies of chain graphs under various simulation settings of mlGGMs according to the simulation parameters, the number of variables (p), sample size (n), number of layers (q), and degree of sparsity (p_E). We consider the following multivariate regression-based methods for two-layer models: multivariate regression with covariance estimation (MRCE) (Rothman et al., 2010), and covariate-adjusted precision matrix estimation (CAPME) (Cai et al., 2012), which are available in R packages mrce and capme, respectively. We apply glasso (Friedman et al., 2008) for MRCE and CLIME (Cai et al., 2011) for CAPME to estimate the UG for the first layer, as MRCE and CAPME are not applicable to UGs.

We investigate the performance of our method under different simulation settings by varying (p,n,q,p_E). Different measures of structural difference can be used to assess the performance of our method. We define TP, TN, FP, and FN as the total number of true positive, true negative, false positive, and false negative edges, respectively. For goodness of estimation, we use sensitivity TP/(TP+FN), specificity TN/(TN+FP), and Matthew’s correlation coefficient (MCC): {(TP × TN) − (FP × FN)} / {(TP + FP)(TP+FN)(TN + FP)(TN + FN)}^1/2 that ranges from −1 (total disagreement) to 1 (perfect classification), with a larger value corresponding to a better fit.

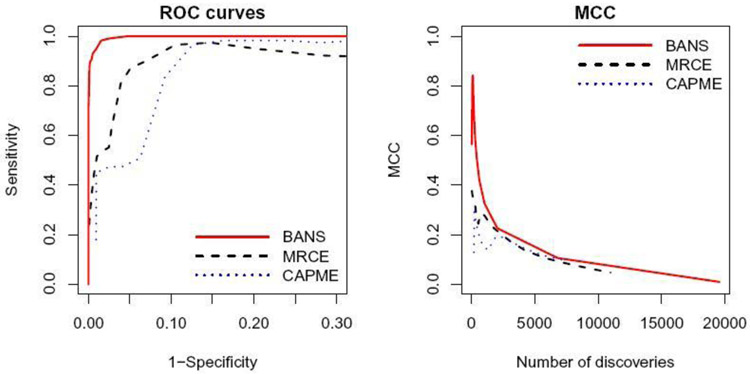
To evaluate the sensitivity, specificity, MCC, and number of discoveries, we determine the tuning parameters of glasso, MRCE, CLIME and CAPME using five-fold cross-validation, and control the FDR at 0.1 for BANS. To further compare the performance on graph structure recovery, we obtain the receiver operating characteristic (ROC) curve and the MCC curve as the function of the number of discoveries for each simulation dataset by varying the tuning parameters for MRCE and CAPME, as well as the cutoff for the posterior marginal probability of edge inclusion for BANS. The sensitivity, specificity, MCC, and number of discoveries for the selected tuning parameters, and pAUC and AUC obtained from the ROC curves, are shown in Table S1. In terms of graph structure recovery, our method yields better performance for all settings. The number of discoveries is very close to the number of edges in the true graph, while other methods tend to provide a much greater number of edges. The small standard errors for the number of discoveries suggest that our procedure is stable across simulation replicates. Figure 3 and Figure S11-S13 display the ROC curves and MCC curves averaged over 50 replications, which demonstrate that our method performs better than MRCE and CAPME. Our method shows better ROC curves and MCC curves for all four simulation settings across different tuning parameters. In the high-dimensional case, when p = 200 and n = 100 (Figure 3), the sensitivities of MRCE and CAPME are flattened for some intervals of 1-specificity, and MRCE shows unstable variable selection performance, because the curves show a decreasing pattern as the tuning parameters decrease.

Fig. 3.

ROC curves and MCC curves for graph structure learning for (p,n,q,p_E) = (200,100,10,0.03).

We evaluated the performance of BANS in simulation settings where data were generated from non-Gaussian, and the graphical structures were the same as the estimated DNA damage response network for 309 TCGA lung squamous cell carcinoma. We performed comparisons to (1) BANS-parallel (Section S6), (2) XMRF (Wan et al., 2016), that fits UGs to mixed data types, (3) Neighborhood selection of UGs using Florseshoe prior (Carvalho et al., 2010) and (4) objective Bayes fractional Bayes factor (OBFBF) (Consonni et al., 2017) using model averaging. Given the simulation settings where the data are generated from Poisson distribution, BANS showed better performance than XMRF (Section S7.2). For the evaluation of our prior choice, the point mass prior in equation (11) showed superior performance than Horseshoe prior and OBFBF in estimating UGs (Section S7.3 and Section S7.4). While BANS-parallel without symmetric constraint in the MCMC sampling showed smaller AUC and MCC values than BANS, it still performed better than other methods such as MRCE and CAPME (Figure S8). Considering the gain in computational efficiency (Section S7.5), BANS-parallel is potentially useful alternative in high-dimensional setting. Finally, we confirmed that posterior inference on signs of edges were accurately estimated from the structured MCMC algorithm given η and γ using BANS (Section S7.6).

7. Pan-Cancer Network Anaysis of Multi-platform Omic Data

Biological motivation

Crosstalk within signaling pathways and their perturbation by oncogenes limit single gene-based approaches to understanding cancer biology. Approaches have been developed for discovering mutations that perturb signaling networks (so-called network-attacking mutations) to understand how individual genomic variants initiate network perturbation (Creixell et al., 2012). Although genomic variants are critical to understanding functional cancer networks, it is well-established that complex molecular networks and systems are formed by a large number of interactions of genes and their products, which operate in response to different cellular conditions (Bandyopadhyay et al., 2010). Therefore, systematic approaches to unravelling cancer-specific rewiring of molecular networks are key to the successful identification of network-based drug targets for cancer treatment, in the paradigm of network medicine that acknowledges the application of network topology and dynamics towards identification of therapeutic targets (Barabási et al., 2011).

TCGA PanCancer Atlas initiative (Weinstein et al., 2013) built a uniformly-processed dataset and a unified data analysis pipeline to develop an integrated picture of commonalities and differences across tumor types. Recent studies (Hoadley et al., 2018; Sanchez-Vega et al., 2018) reclassified human tumor types based on molecular similarity and investigated co-occurence of alterations in tumor signaling pathways, which differentiate between individual tumors and tumor types using TCGA pan-cancer data. (Akbani et al., 2014) investigated correlations between protein and other data types, such as mRNA, copy number, and mutation data across cancer. (Gong et al., 2017) performed expression quantitative trait locus (eQTL) analysis that focuses on the links between genotypes and gene expression for pan-cancer TCGA data. These methods only consider links between two platforms; they do not incorporate within platform dependencies. Using our BANS method, graph-based multi-level integration approach, our goal is to understand unified interplay within and between genomic, epigenomic, transcriptomic, and proteomic platforms to elucidate the commonalities and differences in systems across cancer types.

Data structures

We applied our method to multi-omic datasets from the 7 TCGA tumor types, lung adenocarcinoma (LUAD, n=356), lung squamous cell carcinoma (LUSC, n=309), colon adenocarcinoma (COAD, n=338), rectum adenocarcinoma (READ, n=121), uterine corpus endometrial carcinoma (UCEC, n=393), ovarian serous cystadenocarcinoma (OV, n=227), and skin cutaneous melanoma (SKCM, n=333). For each of the tumor types, we included multi-platform data, DNA methylation, copy number alteration, mRNA expression data, and reverse phase protein array (RPPA)-based proteomic data. Genomic features from each data platform constitute a layer; the ordering of the layers follows biological justifications, because of the natural interplay among diverse genomic features: gene encoded by DNA is transcribed to mRNA, mRNA is translated to protein, and DNA methylation helps to regulate transcription (Morris and Baladandayuthapani, 2017) (Figure S14).

Based on the principle that within-platform interactions arise from pathway-based dependencies that are altered across different tumor types, we selected 10 key signaling pathways, based on emerging literature on RPPA-based proteomic profiling of various tumor types (Akbani et al., 2014; Cherniack et al., 2017; Li et al., 2017). The pathways and the gene membership for each pathway are listed in Table S2. We focus on building integrative networks for all combinations of the 10 pathways and the 7 cancer types. Using TCGA-Assembler (Zhu et al., 2014), we downloaded CNA, DNA methylation, mRNA expression, and protein expression data, then matched the samples across platforms. We applied BANS separately to each type of cancer and pathway combination (10×7=70 analyses). The MCMC sampler was run for 10,000 iterations of burn-in, followed by 20,000 iterations as the basis for inference. For each analysis, we estimated the graph structure at FDR 0.1 and obtained the signs of each nonzero coefficient using the cutoff ξ = 0.5 for the posterior probability of the signs from the structured estimation. Figures S15-S24 display the estimated networks for all pathways and cancer types.

7.1. Global commonalities and differences in mlGGMs

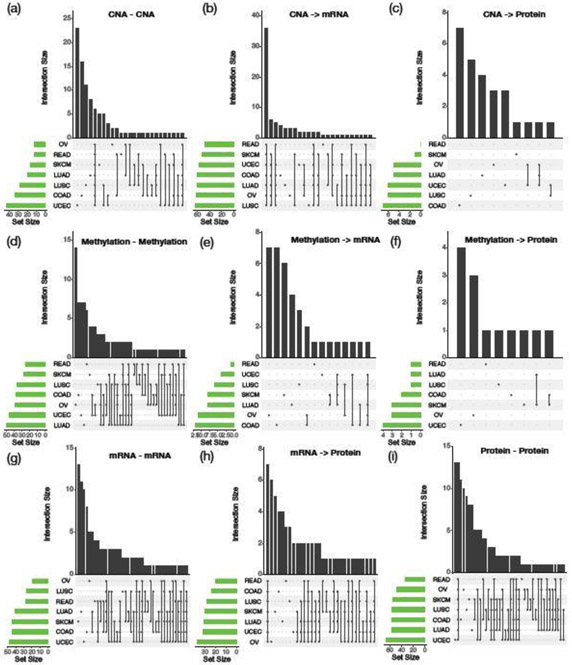
We first investigated the number of edges that are shared and differentiated across different cancer types for each of the possible edges at the platform level. For each combination of the cancer types and pathways, the mlGGM contains 4 layers at CNA, DNA methylation, mRNA expression, and protein expression, and allows 9 different types of dependencies, represented by the 4 types of undirected edges (i.e., CNA–CNA, methylation–methylation, mRNA–mRNA, and protein–protein) and the 5 types of directed edges (i.e., CNA →miRNA, CNA →protein, methylation → mRNA, methylation →protein, and mRNA →protein) (Figure S14). Across all pathways, our BANS method detected 433 (UCEC), 350 (SKCM), 328 (OV), 240 (READ), 391 (COAD), 394 (LUAD), and 361 (LUSC) directed/undirected edges in the estimated mlGGMs. Across all 10 pathways, we decomposed the edges by the aforementioned 9 types of dependences within and between the four layers, as well as the numbers of intersecting edges across the 7 cancer types are depicted using UpSet plots (shown in Figure 4). UpSet plot is an effective visualization of intersections for more than three sets, and a more-scalable approach than Euler diagrams (Lex and Gehlenborg, 2014). For each of the 9 possible relations within and between layers, the UpSet plot contains column and row bar plots. The column bar plot encodes all edge set intersections in the columns of a matrix using a binary pattern, and renders bars above the matrix columns to represent the number of exclusively intersecting edges that are shared by the corresponding cancer types to the column, but not of the others. The row bar plot displays the total number of edges for each cancer type.

Fig. 4.

UpSet plots showing relationships of mlGGMs across all 10 pathways between 7 cancer types. Each column-wise bar corresponds to the number of exclusively intersecting edges that are shared by the cancer types represented by the dark circles, but not of the others, and each row-wise bar displays the total number of edges for the corresponding cancer type.

Between platform regulatory relations:

Transcriptional and translational effects represented by directed edges CNA →mRNA (Figure 4-b) and mRNA → Protein (Figure 4-h) tend to be shared across cancer types, which is along expected lines of the basic biological mechanisms. For example, in Figure 4-b, 36 edges were shared by all 7 cancer types, and few unique edges to a cancer type were found. We found few regulatory edges from CNA to proteins, and from methylation to mRNA and Protein across cancer types (Figure 4-c,e,f). For example, for Methylation → mRNA in Figure 4-e, we found 7 edges unique to OV and COAD.

Within platform conditional dependencies:

The undirected edges represent dependencies within platform after taking out the regulatory effects from upstream platforms. The dependence structures within platforms tend to be unique to cancer type. For CNA (Figure 4-a), UCEC, COAD, LUSC, and LUAD had 23, 15, 11, and 7 edges that are not shared by any other cancer types, while 6 edges were shared across all cancer types. For Methylation (Figure 4-d), OV included 14 unique edges among 48 edges in total. For mRNA (Figure 4-g), SKCM had 13 of 45 edges that were unique. For protein (Figure 4-i), UCEC had the largest protein network, with 62 protein-protein interactions, 13 of which were unique to the cancer, while the same number of the edges were shared across all cancer types.

7.2. Pan-cancer network signaling

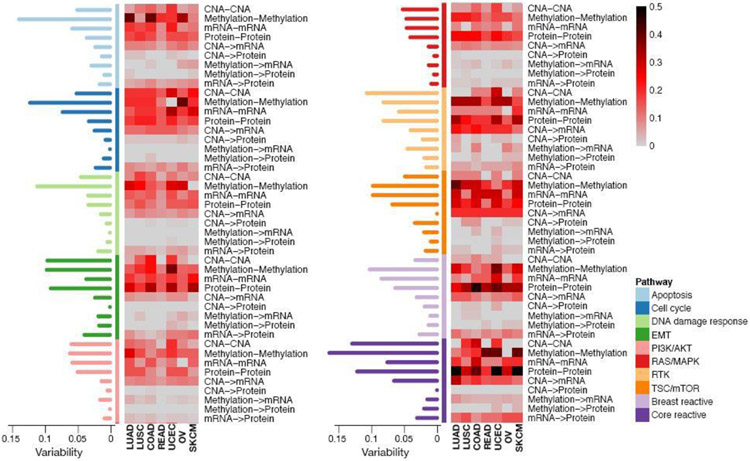
We investigate the extent of cross-signaling within- and between- layers for each pathway across tumor types. For a given network, we define the ratio of the observed number of edges to the total number of possible edges as connectivity score (CS): high (low) CS value indicates high (low) cross-signaling of the network. We also compute standard deviation of CS values across cancer types to represent that the levels of connectivity of the network are different across tumor types: the genes in the network are highly connected (high signaling) in some cancers, but have few connection (low signaling) in other cancers. Figure 5 displays the CS values and the variability are displayed: CS ranged from 0 to 0.5, and the variability ranged from 0 to 0.17. The overall pattern of the heat map suggests that the within-layer sub-networks had a higher level of signaling than between-layer sub-networks. The core reactive pathway showed a high level of network signaling within platforms, and the highest level of protein-protein signaling across tumor types, which suggests that our estimation aligns well with the a priori functional characteristics of this pathway, which was defined on the basis of all tumor types (Akbani et al., 2014). The CS was markedly different in methylation-methylation networks for most of the pathways, compared to other types of sub-networks: the apoptosis pathway for LUAD and COAD, cell cycle pathway for OV, EMT pathway for UCEC, TSC/mTOR pathway for LUAD, breast reactive pathway for UCEC, and core reactive pathway for READ, UCEC, and SKCM showed the high level of signaling for methylation-methylation. The transcriptional and translational effects that are represented by CNA →mRNA and mRNA →protein sub-networks showed the high-level of signaling across pathways and cancer types, compared to other between-layer networks, again following along expected lines of the biological hierarchy.

Fig. 5.

Heatmap depicting connectivity score (CS) of the within- and between-layer sub-networks of the estimated mlGGMs across the 7 cancer types and 10 pathways. The scores are indicated on a low-to-high scale (grey-red-black). The standard deviations of the CS values across cancer types are displayed in the barplots.

7.3. p53 Integrative Networks

In this section we focus on a gene/protein of particular interest (i.e., p53) across all tumor types. p53 is the most frequently mutated gene in human tumors, and has a central role as a tumor suppressor and novel therapeutic target (Bouchet et al., 2006; Levine, 2019). The transcription factor p53 is activated downstream of the DNA damage response (DDR) in reaction to cell stress, and mediates distinct outcomes of DDR signaling (Reinhardt and Schumacher, 2012). The TP53 gene encodes the p53 protein that targets a large set of genes associated to apoptosis and cell cycle pathways (Bouchet et al., 2006; Reinhardt and Schumacher, 2012). Due to the high level of inter-connectivity of the DDR with other signaling networks, predicting the efficacy of treatment and designing an optimal combination therapy to target multiple genes will require a detailed understanding of the tumor-specific signals of other molecules.

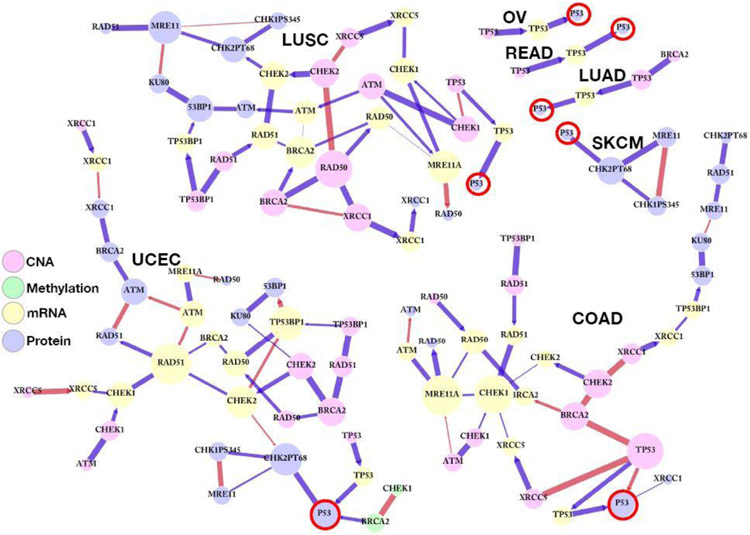
Let g_ij be the estimated posterior marginal probability of the edge (i − j or i → j) inclusion. We consider the estimated mlGGMs are weighted graphs, whose edges have been assigned the given posterior inclusion probabilities, and the degree of the nodes across all layers are defined as the summation of the weights for the edges that are connected to the node: $W_i=\sum _{j=1}^{p}I(i\to j\text{or}i\leftarrow j\text{or}i-j)g_{ij},\forall i\in V$. The degree of the nodes in a weighted mlGGM measures the strength of nodes in terms of the total weight of their directed and undirected connections. With the goal of studying the underlying mechanism of p53 protein, we focused on the sub-networks of the estimated mlGGMs, which include the nodes connected to the p53 protein by any lengths of paths including both undirected and directed edges. Figure 6 displays the p53 integrative networks, where the edges are colored and weighted by the signs and the posteriors, g_ij, and the sizes of nodes are weighted by their degrees, W_i.

Fig. 6.

Integrative sub-networks for the p53 protein (red circle), inferred from BANS for LUAD, LUSC, COAD, READ, UCEC, OV, and SKCM. Each connected component includes all nodes that are connected to the p53 protein by any lengths of paths, including both undirected and directed edges for each cancer. The colors of edges indicate the inferred signs of the edges: negative (red) and positive (blue). The sizes of nodes and the widths of edges are weighted by their degrees and posterior edge inclusion probabilities, respectively.

7.3.1. Translational findings

Our results confirm that the transcriptional effect from TP53 at CNA to TP53 gene expression, and translational effects from TP53 gene expression to the p53 protein across 6 tumor types (all except for SKCM), all with positive regulations. In contrast, the SKCM network included no upstream regulatory effects (from DNA and RNA) and only included protein-protein interactions. UCEC and SKCM shared the same protein-protein interactions between p53 protein expression and T68 phosphorylated CHK2 (CHK2PT68): CHK2 is a protein kinase that is activated in response to DNA damage and directly phosphorylated p53 on serine 20, which provides a mechanism for increased stability of p53 (Hirao et al., 2000) and has been suggested as an anticancer therapy target given its role as a tumor suppressor (Zannini et al., 2014). These findings prioritize UCEC and SKCM as potential cancer types for CHK2 targeting. We also found epigenetic effects in the p53 sub-networks: only UCEC had a positive regulatory effect from BRCA2 DNA methylation, which was correlated with CHEK1 DNA methylation. The physical and functional interactions between BRCA2 and TP53 have been reported and hypermethylation of the CpG island in the promotors of BRCA2 gene involve their inactivation and therefore a higher risk of developing a tumor including uterine cancer (Rajagopalan et al., 2010; Bosviel et al., 2012).

Epigenetic drugs have been developed and the anticancer effects are often tested using genome-editing technologies such as CRISPR-Cas9 systems, called Epigenome editing, which provides advantages over direct gene knockout based on RNA interference (Kungulovski and Jeltsch, 2016). Moreover, successes of epigenetic drugs have been reported by the important roles in synergy with other anticancer therapies or in reversing acquired therapy resistance (Morel et al., 2019). Our findings through this deeper investigation of underlying biological mechanisms of p53 networks across multiple molecular levels and cancer types have the potential to facilitate the development of novel therapeutic strategies, specifically gene-drug interactions for single and combination agents.

8. Discussion

We propose a unified Bayesian framework to model the layered architecture of networks from multiple omic data. We employ a multi-layered Gaussian graphical model (mlGGM) to investigate the conditional dependencies among the variables from multiple layers, while accounting for the order defined by biological hierarchies. The mlGGM is built upon a multivariate regression framework with mean and residual precision parameters, for which zero structures represent undirected and directed edges in the chain graph. Our fully probabilistic formulation coherently converts the complex mlGGM into more tractable, node-wise multiple regression models, wherein the zero structures of the regression coefficients encompass both the undirected and directed edges. Our edge-specific variable selection priors on node-wise regression models allow for flexible modeling of any type of graph, without restriction to decomposable graphs, as well as the incorporation of relevant prior knowledge, while maintaining computational efficiency. We applied our Bayesian node-wise selection (BANS) method to Pan-cancer integrative network analysis and found structural commonalities and differences across cancer types. We also identified underlying mechanisms of the p53 protein, which is a novel drug target for cancer treatment.

For identifiability, the main assumption in this article is that the layers have natural ordering. Ma et al. (2008) and Ha et al. (2015) proposed methods to estimate a Markov equivalence class of a chain graph and a DAG (as a special case of the chain graph model) by recovering skeletons on its subgraphs with no ordering information. In the absence of natural ordering, a chain graph is not identifiable and only its Markov equivalence class can be identified. In many applications, the vertices are naturally partitioned into multiple ordered layers, along with time points or the intrinsic biological mechanisms.

For chain graph models, there are two main types of conditional independencies implied by the LWF Markov property and the alternative Markov property (AMP). Through zero structures of the mean parameter B and the residual precision matrix K in the mlGGM in (3), we describe the AMP on chain graph models. For the LWF Markov property in high-dimensional Gaussian settings, Sohn and Kim (2012); McCarter and Kim (2014) made a convex formulation by using a conditional joint distribution given the predictors. The AMP Markov property is coherent, however, with data generation (as described in Section S1) by the direct link between the zero structure of the parameters in the multivariate linear regressions, and the presence/absence of edges in the graph.

For the resulting asymmetry of the structure, we impose the constraint on K during MCMC. Although most graphical model selection approaches based on node-wise regressions focus on estimating the structure, we showed the numerical performance of estimating signs of the directed edges and undirected edges, based on the structured estimation from the conditional posterior P(α,κ,B∣Y,η,γ) where η and γ are subjected to the structure G.

Our node-wise regression-based formulation, BANS to jointly estimate the undirected and directed edges to a node provides a flexible modeling framework. In particular, the proposed approach can be extended to allow nonlinear regulatory relations between layers, instead of the linearity assumption on the parameter B, and to infer multiple mlGGMs where some of the graphs may be unrelated, while others share common edges. BANS R codes implementing our method are available on https://github.com/***/BANS.