Analysis of waveform and amplitude of mouse rod and cone flash responses

Abstract

Vertebrate eyes have rod and cone photoreceptors, which use a complex transduction pathway comprising many biological processes to transform the absorption of light into an electrical response. A fundamental question in sensory transduction is how these processes contribute to the response. To study this question, we use a well-accepted phototransduction model, which we analyze with a novel method based on the log-transform of the current. We derive an analytical solution that describes the entire time course of the photoreceptor response to dim flashes of light. We use this solution to dissect and quantify the contribution of each process to the response. We find that the entire dim-flash response is proportional to the flash intensity. By normalizing responses to unit amplitude, we define a waveform that is independent of the light intensity and characterizes the invariant shape of dim-flash responses. We show that this waveform is exclusively determined by deactivation rates; activation rates only scale the waveform and affect the amplitude. This analysis corrects a previous assumption that the rising phase is determined entirely by activation rates. We further show that the rising phase depends on Ca²⁺ feedback to the cyclase, contrary to current belief. We identify the deactivation rates that control the recovery phase of the response, and we devise new methods to extract activation and deactivation rates from an analysis of response shape and response amplitude. In summary, we provide a comprehensive understanding of how the various transduction processes produce the cellular response.

INTRODUCTION

The signal transduction cascade of vertebrate rod and cone photoreceptors is a complex multistep process by which light-activation of a photopigment is transformed into a current response (see Burns & Pugh, 2010; Arshavsky & Burns, 2012; Reingruber et al., 2015; Fain, 2019). The photoreceptor response depends crucially on the interplay of two key molecules: the effector enzyme phosphodiesterase-6 (PDE), and the second messenger cyclic guanosine monophosphate (cGMP), which controls the opening of cyclic-nucleotide-gated (CNG) channels in the plasma membrane. Rhodopsin activation is coupled via a G-protein cascade to the activation of PDE, such that the number of activated PDE that are present in the outer segment at any time reflects the change in light intensity stimulating the photoreceptor. The light-signal encoded by the time course of light-activated PDE is then converted into a current response, because activated PDE hydrolyses cGMP and produces a net reduction in the number of open CNG channels. Finally, Ca²⁺-feedback modulates the transduction cascade, and this process is also light dependent because Ca²⁺ concentration is controlled by influx through CNG channels which close during the light response.

Experiments over the past 50 years have revealed many biological and biochemical details of this interconnected signaling pathway. More recently, considerable insight has come from experiments on genetically engineered photoreceptors, where specific components of the signaling cascade have been genetically modified. These findings have stimulated the development of sophisticated models, which we roughly classify into two main categories and which have different but complementary objectives. In the first category, modeling and mathematical analysis has been used to understand specific aspects of the photoreceptor response, for example (1) response amplification during the initial phase of the light response (Pugh & Lamb, 1993, 2000), (2) dark noise and the variability of the single-photon response (Rieke & Baylor, 1996; Rieke & Baylor, 1998; Holcman & Korenbrot, 2004; Reingruber & Holcman, 2008a; Caruso et al., 2011; Reingruber et al., 2013), (3) spatio-temporal properties of cGMP diffusion and GMP hydrolysis by activated PDE (Cameron & Pugh, 1990; Olson & Pugh, 1993; Dumke et al., 1994; Koutalos & Yau, 1996; Holcman & Korenbrot, 2004; Caruso et al., 2006; Reingruber & Holcman, 2008b; Gross et al., 2012b), or (4) analysis of Ca²⁺-feedback for light-adaptation and cGMP synthesis (Tranchina et al., 1991; Calvert et al., 1998; Burns et al., 2002; Chen et al., 2010c; Gross et al., 2012a). In the second category, highly complex models have been proposed to reproduce a large variety of experimental data including the effects of gene deletions and adaptation to background light (Field & Rieke, 2002; Andreucci et al., 2003; Hamer et al., 2003; Hamer et al., 2005; Reingruber & Holcman, 2008a; Shen et al., 2010; Korenbrot, 2012; Invergo et al., 2014; Astakhova et al., 2015; Lamb & Kraft, 2020).

Most recent models have been of this second category and have contained many equations and parameters that can be adjusted by numerical fitting procedures. These models attempt to describe the photoreceptor response in all of its intricacy, but because of this large parameter space, it is difficult to infer from simulations and fittings how individual parameters or parameter combinations affect various properties of the light response. For example, the recovery phase of flash responses can be fit with a single exponential, but because there are many deactivation rates it is not obvious how the fitted exponential time constant relates to the various rates of the model. Another drawback of complex models is that considerable effort is required to implement them in order to use them for data analysis. This may explain why simple concepts like amplification constant, recovery time, and dominant time constant are still frequently applied to analyze data and to extract parameter values: the amplification constant introduced by Pugh and Lamb (1993) can be determined by fitting the initial phase of a flash response with a quadratic function, the recovery time constant by fitting the recovery phase with a single exponential, and the dominant time constant from a Pepperberg plot (Pepperberg et al., 1992).

A closer examination, however, reveals that the mathematical expressions or procedures that relate these concepts to underlying model parameters are not derived from a precise analysis of a phototransduction model. For example, the formula for the amplification constant has been derived from an analysis of amphibian rod responses without taking deactivation processes into account (Lamb & Pugh, 1992), and this formula was then subsequently generalized to many other species (Pugh & Lamb, 1993, 2000). It still remains unclear exactly how deactivation processes affect the rising phase. As another example, in WT rods recovery and dominant time constants are both identified with the PDE deactivation rate (Krispel et al., 2006; Tsang et al., 2006; Chen et al., 2010a), which is based on empirical observations of how these values change between phenotypes but lacks a theoretical basis.

To be able to perform a comprehensive mathematical analysis that provides a mathematical foundation for these widespread concepts, we have focused on a simple but representative model that comprises all the relevant transduction processes that are known to be necessary for a realistic flash response. We use a new mathematical approach based on the log transform of the current normalized by the amplitude of saturating flash responses to derive analytic expressions for the entire dim-flash response. We then apply these analytic results to verify the validity of asymptotic expressions, and to dissect the contributions of individual processes of the transduction pathway to the various phases of a flash response. In this way, we obtain a comprehensive understanding of how the variety of biochemical processes synergize to determine the final response.

METHODS

ANIMALS AND RECORDINGS

The data we used to analyze photoreceptor responses came from experiments previously described (Ingram et al., 2019; Ingram et al., 2020; Reingruber et al., 2020). The recordings were taken from WT and GCAPs^−/− rods, and Gnat1^−/− and Gnat1^−/−;GCAPs^−/− cones. GCAPs^−/− mutants lack the guanylyl-cyclase activating proteins (GCAPs), which are closely associated with guanylyl cyclase in both rods and cones and mediate Ca²⁺-dependent modulation of the rate of the cyclase. In GCAPs^−/− mutants, Ca²⁺-dependent feedback to the cyclase is absent ($\widehat{\alpha }=1$, see below). Recordings from cones were made from Gnat1^−/− retinas lacking Gnat1, the alpha-subunit of the rod G protein transducin. Cones in the mouse retina receive input from rods through connexin-36 gap junctions (Asteriti et al., 2017; Jin et al., 2020), and this input is deleted in Gnat1^−/− cones. There is no effect on cone transduction, however, with the result that Gnat1^−/− cones essentially behave like WT cones (Ingram et al., 2019). As we have previously explained (Reingruber et al., 2020), rod WT and GCAPs^−/− responses had different collecting areas because GCAPs^−/− rod responses were recorded with suction electrodes, whereas WT rod (and cone) responses were recorded in retinal slices with voltage clamp.

MODEL

We used a simplified phototransduction model that has been previously described (Reingruber et al., 2020). Except for the activation of transducin and the inclusion of Ca²⁺ feedback, this model is similar to that used by Pugh and Lamb to analyze the rising phase of the light response (Lamb & Pugh, 1992; Pugh & Lamb, 1993). In brief, the photoreceptor current I as a function of the cyclic guanosine-nucleotide (cGMP) concentration c_cg is approximated as $I=I_d{\left(\frac{c_{cg}}{c_{cg,d}}\right)}^{n_{ch}}$, where I_d and c_cg,d are the current and cGMP concentration in darkness, and n_ch is the cooperativity constant of the channel. This approximation for the current assumes that the concentration of cGMP that half activates the channels is large in comparison to the basal cGMP concentration in darkness (Lamb & Pugh, 1992; Pugh & Lamb, 1993). The cGMP synthesis rate as a function of the Ca²⁺ concentration is $\alpha \left(c_{ca}\right)=\frac{{\alpha }_{max}}{c_{ca}^2+K_{\alpha }^2}={\alpha }_d\frac{c_{ca,d}^2+K_{\alpha }^2}{c_{ca}^2+K_{\alpha }^2}$, where c_ca,d is the calcium concentration in darkness, K_α determines the sensitivity of the rate to Ca²⁺ (Tranchina et al., 1991; Burns et al., 2002; Hamer et al., 2003; Gross et al., 2012b; Lamb et al, 2018), α_d = β_dc_cg,d is the synthesis rate in darkness that balances cGMP hydrolysis, and β_d is the rate constant of cGMP hydrolysis in darkness (dark cGMP turnover rate).

For the PDE activation cascade, we assumed that light-activated visual pigment activates the G-protein transducin, which activates cGMP phosphodiesterase-6 (PDE). We let R* be the number of pigment molecules activated by the flash, T* the number of activated transducins, and P* the number of light-activated PDEs. The parameter k_act is the rate of activation of transducin by a single activated visual pigment, μ_rh is the deactivation rate of a light-activated visual pigment molecule, and μ_pde is the deactivation rate of a light-activated PDE. The activation rate k_tr is the rate by which T* generates P*, and μ_tr is the deactivation rate of T* (the rate of decrease of T* concentration). Because the generation of a P* is accomplished by binding of T*, we have k_tr = μ_tr, such that a single T* generates a single light-activated PDE. The intermediate step by which T* activates PDE is often assumed to be fast and therefore omitted (Lamb & Pugh, 1992; Pugh & Lamb, 1993). We decided to keep this step as a representative reaction to study the effect of intermediate processes that delay the response without amplifying it. The value of μ_tr in Table 2 has been estimated in Reingruber et al. (2020) by fitting the model to the data. It therefore has to be considered as an effective value, which does not necessarily reflect the biological time scale by which T* activates PDE.

Table 2.

Parameter values for the rod and cone models.

Parameter	Rod	Cone
κ (μm2)	0.28 (WT) 0.42 (GCAPs−/−)	0.013
nch	2.5	2.5
ξ	0.45	0.0018
βd (s−1)	4.1	11.0
μpde (s−1)	5	37.8
μrh (s−1)	28	70.7
μtr (s−1)	23.8	70.7
${\widehat{K}}_{\alpha }$	0.87	0.84

With dimensionless quantities that are normalized with steady-state values in darkness, ${\widehat{c}}_{cg}=\frac{c_{cg}}{c_{cg,d}}$, ${\widehat{c}}_{ca}=\frac{c_{ca}}{c_{ca,d}}$, ${\widehat{K}}_{\alpha }=\frac{K_{\alpha }}{c_{ca,d}}$, $\widehat{\alpha }=\frac{\alpha }{{\alpha }_d}=\frac{1+ {\widehat{K}}_{\alpha }^2}{{\widehat{c}}_{ca}^2+{\widehat{K}}_{\alpha }^2}$, and $\widehat{I}=\frac{I}{I_d}={\widehat{c}}_{cg}{}^{n_{ch}}$, the transduction equations are

$$\frac{d}{dt}{R}^{*}=\varphi \left(t\right)\kappa -{\mu }_{rh}{R}^{*}$$

$$\frac{d}{dt}{T}^{*}=k_{act}{R}^{*}-{\mu }_{tr}{T}^{*}$$

$$\frac{d}{dt}{P}^{*}=k_{tr}{T}^{*}-{\mu }_{pde}{P}^{*}$$

$$\frac{d}{dt}{\widehat{c}}_{cg}={\beta }_d\widehat{\alpha }\left({\widehat{c}}_{ca}\right)-\left({\beta }_d+{\beta }_{sub}{P}^{*}\right){\widehat{c}}_{cg}$$

where ϕ(t) is the light intensity and κ is the collecting area.

It remains to provide an equation for the Ca²⁺ concentration ĉ_ca(t). As shown in Reingruber et al. (2013), the Ca²⁺ dynamics can be modelled as $\frac{d}{dt}{\widehat{c}}_{ca}={\mu }_{ca}\left(\widehat{I}-{\widehat{c}}_{ca}\right)$, where the rate constant μ_ca depends on the dark current, the outer segment volume, the buffering capacity B_ca, and the fraction of the CNG current that is carried by Ca²⁺ (see Eq. 33 in the SI of Reingruber et al., 2013). This equation further assumes that the half-saturating Ca²⁺ concentration K_ex of the exchanger is large compared to the dark Ca²⁺ concentration c_a,d (Pugh & Lamb, 2000). With B_ca = 80 we computed μ_ca ≈ 23s⁻¹ for a mouse rod (Reingruber et al., 2013), and with a smaller buffering capacity B_ca ~ 50 (Gross et al., 2012a), we would get μ_ca ≈ 37s⁻¹. For a mouse cone, due to the smaller volume, the value of μ_ca would be much higher. Because μ_ca is large and not rate limiting, we simplify and use the approximation ĉ_ca(t) ≈ Î(t), such that the Ca²⁺ concentration changes proportional to the current. This approximation becomes exact in the limit μ_ca → ∞.

With the new variables ${\tilde{P}}^{*}=n_{ch}{\beta }_{sub}{P}^{*}$, ${\tilde{T}}^{*}=\frac{n_{ch}{\beta }_{sub}{k}_{tr}}{{\mu }_{pde}}{T}^{*}$, ${\tilde{R}}^{*}=\frac{n_{ch}{\beta }_{sub}{k}_{tr}{k}_{act}}{{\mu }_{pde}{\mu }_{tr}}{R}^{*}$, y = −n_chlnĉ_cg = −lnÎ and ĉ_ca = e^−y, the previous system of equations becomes

$$\begin{array}{l}\frac{d}{dt}{\tilde{R}}^{*}={\mu }_{rh}\left(\varphi \left(t\right)\kappa \xi -{\tilde{R}}^{*}\right)\\ \frac{d}{dt}{\tilde{T}}^{*}={\mu }_{tr}({\tilde{R}}^{*}-{\tilde{T}}^{*})\\ \frac{d}{dt}{\tilde{P}}^{*}={\mu }_{pde}({\tilde{T}}^{*}-{\tilde{P}}^{*})\\ \frac{d}{dt}y={\tilde{P}}^{*}-{\beta }_{d}H\left(y\right),\end{array}$$ (1)

where the gain ξ is defined as

$$\xi =\frac{n_{ch}{k}_{act}{\beta }_{sub}{k}_{tr}}{{\mu }_{rh}{\mu }_{pde}{\mu }_{tr}}=\frac{n_{ch}{k}_{act}{\beta }_{sub}}{{\mu }_{rh}{\mu }_{pde}},$$ (2)

and

$$H\left(y\right)=n_{ch}\left(e^{\frac{y}{n_{ch}}}\widehat{\alpha }\left(e^{-y}\right)-1\right)=n_{ch}\left(e^{\frac{y}{n_{ch}}}\frac{1+{\widehat{K}}_{\alpha }^2}{e^{-2y}+{\widehat{K}}_{\alpha }^2}-1\right).$$ (3)

Eq. 1 shows that the activation rates affect the response only from the gain ξ by means of the product k_actβ_sub, which effectively modulates the flash intensity ϕ. In this respect, k_actβ_sub behaves similarly to the collecting area κ and could as well be incorporated into a modified collecting area $\tilde{\kappa }=\kappa k_{act}{\beta }_{sub}$. We have, however, elected to keep these variables separate for conceptional clarity. The parameter n_ch cannot be treated in this way, because it further affects the value of the function H(y) in Eq. 3.

Analytic results for PDE activation

The equations for PDE activation are linear and can be solved analytically,

$${\tilde{P}}^{*}\left(t\right)=\kappa \xi {\int }_0^t\varphi \left(s\right)g_p\left(t-s\right)ds$$ (4)

with Green’s function (also known as the impulse-response function) given by

$$g_p\left(t\right)={\mu }_{rh}{\mu }_{pde}{\mu }_{tr}\left(\frac{e^{-{\mu }_{rh}t}}{\left({\mu }_{rh}-{\mu }_{tr}\right)\left({\mu }_{rh}-{\mu }_{pde}\right)}+\frac{e^{-{\mu }_{tr}t}}{\left({\mu }_{tr}-{\mu }_{rh}\right)\left({\mu }_{tr}-{\mu }_{pde}\right)}+\frac{e^{-{\mu }_{pde}t}}{\left({\mu }_{pde}-{\mu }_{tr}\right)\left({\mu }_{pde}-{\mu }_{rh}\right)}\right)$$ (5)

The function g_p(t) is symmetric in μ_rh, μ_tr and μ_pde. For a flash at time t = 0 with intensity ϕ and duration Δt, we have ϕ(t) = ϕ(θ(t) – (t – Δt)), where θ is the Heaviside (or unit step) function. If the flash duration Δt is short and the flash produces $R_0^{*}=\kappa \varphi \Delta t$ photoisomerizations, we get from Eq. 4 the approximation ${\tilde{P}}^{*}\left(t\right)\approx R_0^{*}\xi g_p\left(t\right)$.

Analytic results for dim-flash responses

It is not possible to solve Eq. 1 analytically with the non-linear function H(y) from Eq. 3. For dim flashes where y ≪ 1, however, we can approximate H(y) by the leading-order term of its Taylor expansion. Because H(y) = 0 for y = 0, the leading order term is the linear expression $H\left(y\right)=y(1-n_{ch}{\widehat{\alpha }}^{\prime })$, where

$$\widehat{\alpha }\text{'}=\frac{d}{d{\widehat{c}}_{ca}}\widehat{\alpha }\left({\widehat{c}}_{ca}\right){|}_{{\widehat{c}}_{ca}=1}=-\frac{2}{1+{\widehat{K}}_{\alpha }^2}$$ (6)

The parameter α′ describes how strongly the dark cyclase activity is modulated by Ca²⁺. For GCAPs^−/− mutants we have α′ = 0. With the parameters in Table 2, we compute for a WT rod α′ ≈ −1.14, and for a WT (Gnat1^−/−) cone α′ ≈ −1.17, such that $1-n_{ch}{\widehat{\alpha }}^{\prime }\approx 3.8$ for rod or cone photoreceptors. In the leading order approximation, we have $\frac{d}{dt}y={\tilde{P}}^{*}-{\tilde{\beta }}_{d}y$, where we have introduced the effective dark turnover rate

$${\tilde{\beta }}_d={\beta }_d\left(1-n_{ch}{\widehat{\alpha }}^{\prime }\right).$$ (7)

We note that $\frac{d}{dt}y={\tilde{P}}^{*}-{\tilde{\beta }}_{d}y$ also corresponds to the first order approximation of a GCAPs^−/− photoreceptor with dark turnover rate ${\tilde{\beta }}_d$ and cyclase activity $\tilde{\alpha }={\tilde{\beta }}_d{c}_{cg,d}$ (we assume that the dark cGMP concentration is unchanged). Because ${\tilde{P}}^{*}\left(t\right)$ is the same for WT and GCAPs^−/− photoreceptors, we thus find that as a first approximation that a WT photoreceptor is described by the equations for a GCAPs^−/− photoreceptor with increased dark turnover rate $\begin{array}{r}\hfill {\tilde{\beta }}_d={\beta }_d\left(1-n_{ch}{\widehat{\alpha }}^{\prime }\right)\end{array}$ and increased cyclase activity $\tilde{\alpha }={\tilde{\beta }}_d{c}_{cg,d}$. This finding reveals a profound connection between the dim-flash responses of WT and GCAPs^−/− photoreceptors: the dim flash response (and also single-photon response) of a WT photoreceptor with dark turnover rate β_d is identical to the dim-flash response of a GCAPs^−/− photoreceptor with increased dark turnover rate ${\tilde{\beta }}_d$ given by Eq. 7, thus confirming the importance of the dark GMP turnover rate for the kinetics of the flash response (Nikonov et al., 2000).

With the linear approximation ${\beta }_{d}H\left(y\right)={\tilde{\beta }}_{d}y$, we obtain the solution

$$y\left(t\right)=\kappa \xi {\int }_0^t\varphi \left(s\right)g_y\left(t-s\right)ds,$$ (8)

with Green’s function

$$g_y\left(t\right)={\mu }_{rh}{\mu }_{pde}{\mu }_{tr}(-\frac{e^{-{\mu }_{rh}t}}{\left({\mu }_{rh}-{\mu }_{tr}\right)\left({\mu }_{rh}-{\mu }_{pde}\right)\left({\mu }_{rh}-{\tilde{\beta }}_d\right)}-\frac{e^{-{\mu }_{tr}t}}{\left({\mu }_{tr}-{\mu }_{rh}\right)\left({\mu }_{tr}-{\mu }_{pde}\right)\left({\mu }_{tr}-{\tilde{\beta }}_d\right)}-\frac{e^{-{\mu }_{pde}t}}{\left({\mu }_{pde}-{\mu }_{rh}\right)\left({\mu }_{pde}-{\mu }_{tr}\right)\left({\mu }_{pde}-{\tilde{\beta }}_d\right)}-\frac{e^{-{\tilde{\beta }}_{d}t}}{\left({\tilde{\beta }}_d-{\mu }_{rh}\right)\left({\tilde{\beta }}_d-{\mu }_{tr}\right)\left({\tilde{\beta }}_d-{\mu }_{pde}\right)}).$$ (9)

Note that ${\tilde{\beta }}_d{g}_y\left(t\right)$ is symmetric in μ_rh, μ_pde, μ_tr and ${\tilde{\beta }}_d$. For a short flash we have $y\left(t\right)\approx R_0^{*}\xi g_y\left(t\right)$. The time course of the normalized cGMP concentration is ${\widehat{c}}_{cg}\left(t\right)=e^{-\frac{y\left(t\right)}{n_{ch}}}=e^{-\frac{R_0^{*}\xi }{n_{ch}}{g}_y\left(t\right)}$.

If μ_rh and μ_tr are large compared to μ_pde and ${\tilde{\beta }}_d$, the response at its maximum amplitude is governed by

$$g_y\left(t\right)\approx {\mu }_{rh}{\mu }_{pde}{\mu }_{tr}\left(-\frac{e^{-{\mu }_{pde}t}}{\left({\mu }_{pde}-{\mu }_{rh}\right)\left({\mu }_{pde}-{\mu }_{tr}\right)\left({\mu }_{pde}-{\tilde{\beta }}_d\right)}-\frac{e^{-{\tilde{\beta }}_{d}t}}{\left({\tilde{\beta }}_d-{\mu }_{rh}\right)\left({\tilde{\beta }}_d-{\mu }_{tr}\right)\left({\tilde{\beta }}_d-{\mu }_{pde}\right)}\right).$$

From the condition for the derivative g_y′ (t_peak) = 0, we get for the time to peak

$$t_{\mathit{\text{peak}}}\approx \frac{1}{{\mu }_{pde}-{\tilde{\beta }}_d}\text{ln}\left(\frac{{\mu }_{pde}}{{\tilde{\beta }}_d}\frac{\left({\mu }_{rh}-{\tilde{\beta }}_d\right)\left({\mu }_{tr}-{\tilde{\beta }}_d\right)}{\left({\mu }_{rh}-{\mu }_{pde}\right)\left({\mu }_{tr}-{\mu }_{pde}\right)}\right).$$ (10)

The peak amplitude ${g_{y,\mathit{\text{peak}}}=g}_y\left(t_{\mathit{\text{peak}}}\right)$ is

$$g_{y,\mathit{\text{peak}}}\approx \frac{{\mu }_{pde}}{{\tilde{\beta }}_d-{\mu }_{pde}}\left({\left(\frac{{\mu }_{pde}}{{\tilde{\beta }}_d}\right)}^{\frac{{\mu }_{pde}}{{\tilde{\beta }}_d-{\mu }_{pde}}}-{\left(\frac{{\tilde{\beta }}_d}{{\mu }_{pde}}\right)}^{\frac{{\tilde{\beta }}_d}{{\mu }_{pde}-{\tilde{\beta }}_d}}\right).$$ (11)

Contrary to the time to peak, to compute the peak amplitude we can neglect the contributions from μ_rh and μ_tr

Dynamics of saturating flash responses during the saturation phase

For maximum-amplitude (saturating) responses with y ≫ 1 and ${\tilde{P}}^{*}\gg 1$, we have $H\left(y\right)\approx n_{ch}\widehat{\alpha }\left(y\right)e^{\frac{y}{n_{ch}}}$ and $\frac{\frac{d}{dt}y}{{\tilde{P}}^{*}}\ll 1$. With maximal cyclase activation, ${\alpha }_{max}={\widehat{\alpha }}_{max}{\beta }_d{c}_{cg,d}$, we find from Eq. 1 that during saturation

$$y\left(t\right)\approx n_{ch}\text{ln}\left(\frac{{\tilde{P}}^{\text{*}}\left(t\right)}{{\widehat{\alpha }}_{max}{\beta }_d{n}_{ch}}\right).$$ (12)

From this expression, we can obtain the GMP concentration as a function of the number of activated PDEs from:

$$c_{cg}\left(t\right)\approx \frac{{\alpha }_{max}}{{\beta }_{sub}{P}^{*}\left(t\right)}.$$ (13)

RESULTS

The signal transduction cascade of the vertebrate photoreceptor consists of an activation phase governed by excitation of rhodopsin, transducin, and cGMP phosphodiesterase-6 (PDE). Activated PDE increases the rate of hydrolysis of cGMP, which leads to a decline in the cGMP concentration, channel closure, and a reduction in Na⁺ and Ca²⁺ current entering the outer segment. Current recovery depends upon the deactivation of all of the activation steps.

We recently introduced a novel method of analysis of the photoreceptor response, where we used equations for the log transform of the cGMP concentration, y = −n_chlnĉ_c,g (Eq. 1), with the current given by Î = e^−y. We further introduce the more common current î = 1 – Î = 1 – e^−y which is zero in darkness. In Fig. 1, we compare the dim flash responses of rods (Figs. 1A and 1B) and cones (Figs. 1C and 1D) with and without the GCAP proteins (black) to simulations of y from Eqns. 1 – 3 (red), obtained with parameters from Table 2 which were derived in Reingruber et al. (2020), except for a slight modification in the values of the collecting areas to provide a better fit to the peak amplitudes. All the model parameters are defined in Table 1.

Figure 1.

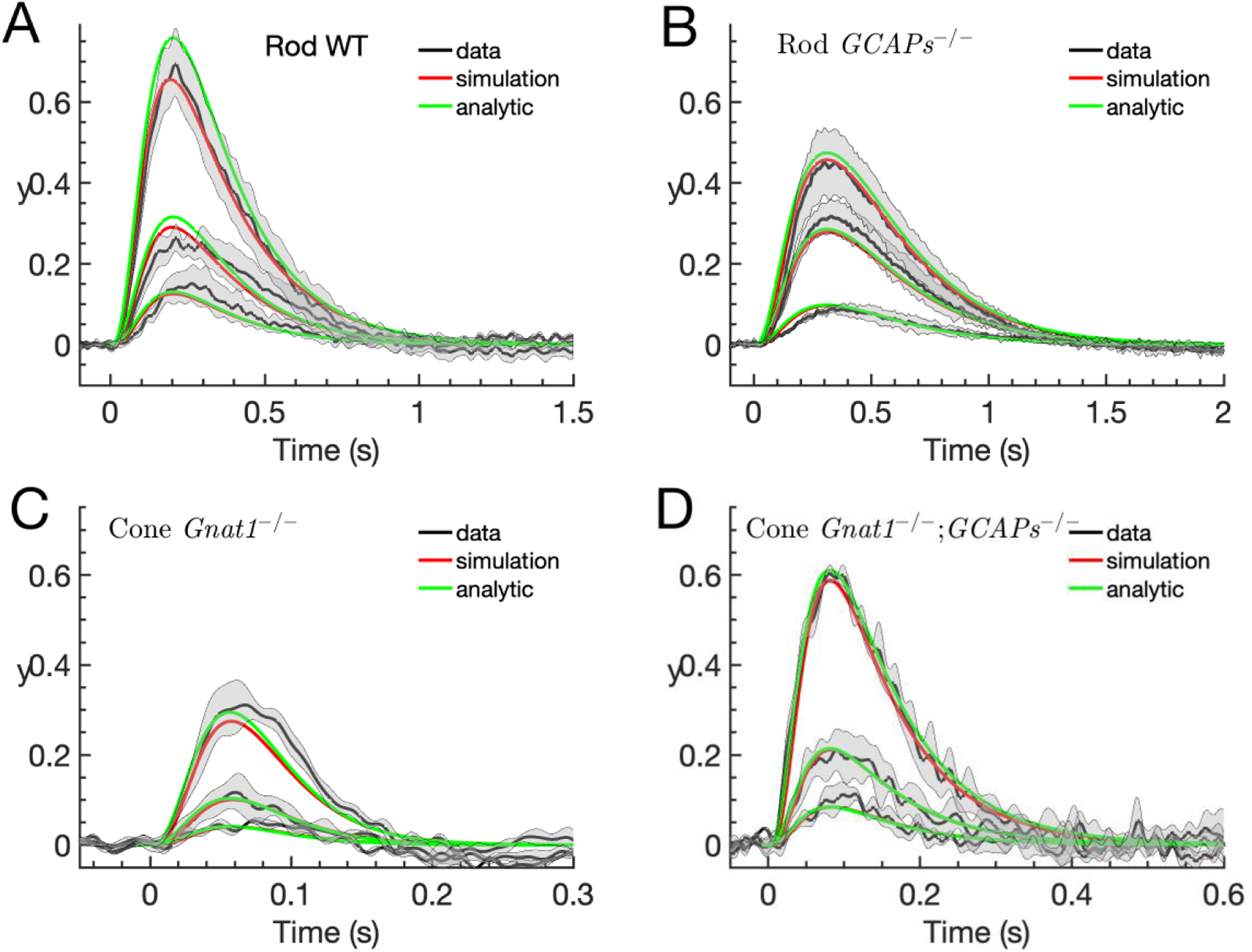
Log-transform of dim-flash responses. Experimental current recordings from mouse rods and cones have been normalized to their corresponding steady-state current in darkness I_d, with $\widehat{I}=\frac{I}{I_d}$ (such that Î = 1 in darkness), and then the log-transform of these normalized currents was computed according to y(t) = −lnÎ(t) (black curves). The experimental data is compared to simulations of y(t) (red curves) and the analytic results $y\left(t\right)=R_0^{\text{*}}\xi g_y\left(t\right)$ computed with Eq. 1 and Eq. 9 and parameters from Table 2. The expected number of pigment isomerizations $R_0^{\text{*}}=\kappa \varphi \Delta t$ are (1.8, 4.3, 10.3) for (A), (0.6, 1.6, 2.7) for (B), and (86, 220, 620) for (C-D). Flash durations are 10ms in (A), 20ms in (B) and 5ms in (C, D). (A) The rod WT data is computed with mean responses of 7 WT rods. (B) The rod GCAPs^−/− data is computed with mean responses of 5 rods from Chen et al. (2010c). (C) The Cone Gnat1^−/− (equivalent to WT or control, see text) data is obtained with responses from 3 cones. (D) The cone Gnat1^−/−;GCAPs^−/− (equivalent to cone GCAPs^−/−, see text) shows mean responses from 3 cones.

Table 1.

Parameter definitions and descriptions.

Parameter	Description
κ (μm2)	Collecting area
nch	CNG channel cooperativity
βd (s−1)	Rate constant of cGMP hydrolysis in darkness
μrh (s−1)	Rate of deactivation of an activated visual pigment
μpde (s−1)	Rate of deactivation of a light-activated PDE
μtr (s−1)	Rate of deactivation of activated transducin
${\widehat{K}}_{\alpha }$	Sensitivity of the cyclase activity on the Ca2+ concentration scaled by the dark Ca2+ concentration
ξ	$\text{Gain}\xi = \frac{n_{ch}{\beta }_{sub}{k}_{act}}{{\mu }_{pde} {\mu }_{rh}}$
kact (s−1)	Rate of transducin activation by an activated visual pigment
βsub (s−1)	Rate constant of cGMP hydrolysis by a light-activated PDE

We now extend the analysis of our model and show (see Methods) that, for dim flashes, we can solve the model equations analytically to derive an expression for y(t) for the entire current response, $y(t)=R_0^{*}\xi g_y(t)$, where g_y(t) is given by Eq. 9. The results of these calculations with parameters from Table 2 are shown as green curves in Fig. 1. In the following, we will use our analytic formulas to study in detail the kinetics of the dim flash responses in rods and cones in order to reveal how underlying biophysical processes and parameters determine the waveform and amplitude of flash responses. This analysis will help us extract biophysical parameters from experimental recordings and provide a better understanding of the transduction cascade.

Waveform of dim-flash responses

The analytical results $y(t)=R_0^{*}\xi g_y(t)$ provide the important demonstration that not only the initial phase, but the entire dim-flash response is linear with the flash intensity ϕ. We can then define the waveform of a dim-flash response as $\widehat{y}\left(t\right)= \frac{y\left(t\right)}{y_{\mathit{\text{peak}}}}$, which is independent of the flash intensity. With the analytic result ${\widehat{g}}_y\left(t\right)= \frac{g_y\left(t\right)}{g_{y,\mathit{\text{peak}}}}$, we have $y\left(t\right)=y_{\mathit{\text{peak}}}\widehat{g}\left(t\right)$, where $y_{\mathit{\text{peak}}}=R_0^{\text{*}}\xi g_{y,\mathit{\text{peak}}}$ is the amplitude of the response. Because the waveform is independent of the flash intensity, we can average over multiple waveforms to reduce experimental noise. In Fig. 2 we use the normalized rod and cone data from Fig. 1 (thin continuous lines) to compute the averaged waveform (thick continuous lines), which we compare with the analytic results ${\widehat{g}}_y\left(t\right)$ computed with Eq. 9 and parameters from Table 2 (green lines). The waveform is much faster in a cone compared to a rod due to more rapid rates of response decay. The difference in the waveform between WT and GCAPs^−/− is the result of Ca²⁺ feedback to the cyclase, which changes the value of ${\tilde{\beta }}_d$ defined in Eq. 7. The discrepancy between model and data, especially for rods, is more pronounced during the rising phase, where the computed waveform rises faster than the data. Because the response also rises faster in GCAPs^−/− rods where Ca²⁺ feedback is absent, the discrepancy between model and data is unlikely to result from our assumptions about Ca²⁺. Instead, we think that the main reason for the discrepancy is our neglect of fast and intermediate processes in our model, for example multiple steps of phosphorylation of rhodopsin, which would further slow down the initial rise (see also Discussion and the blue curve in Fig. 3B for large μ_tr).

Figure 2.

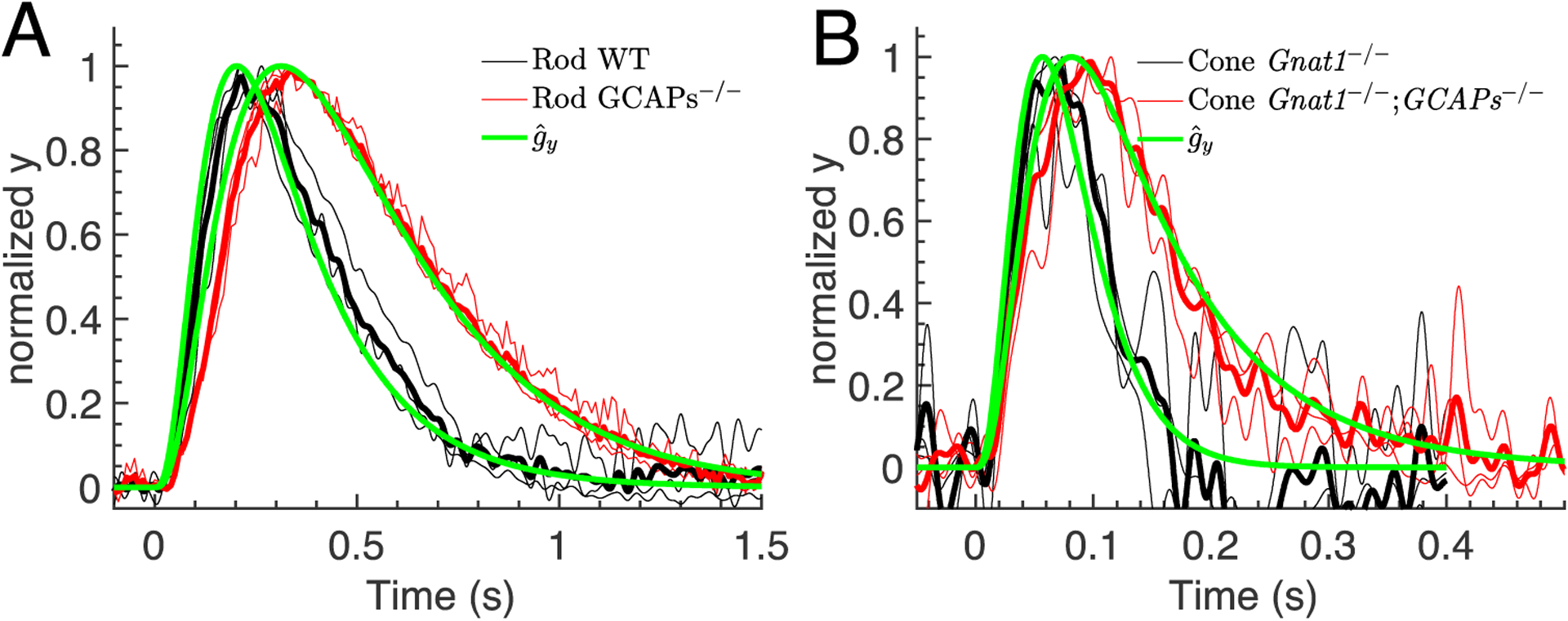
Waveform of dim-flash responses. The rod and cone waveforms $\widehat{y}\left(\text{t}\right)=\frac{y\left(t\right)}{y_{\mathit{\text{peak}}}}$ from Fig. 1 (thin continuous lines) were used to compute an averaged waveform (thick continuous lines). The averaged waveform is compared to the analytic result $\widehat{y}\left(t\right)={\widehat{g}}_y\left(t\right)$ computed with Eq. 9 and parameters from Table 2 (green lines). (A) Waveforms for rod WT (black curves) and GCAPs^−/− data (red curves) together with the corresponding analytic results (green curves). (B) Waveforms for cone WT (black curves) and GCAPs^−/− data (red curves) together with the corresponding analytic results (green curves).

Figure 3.

Rising phase of the waveform of a WT rod. (A) The curves show the first four terms of the Taylor series expansion of ${\widehat{g}}_y\left(t\right)$ computed with Eq. 9 and WT rod parameters from Table 2. The leading-order term is $\frac{1}{6}\frac{{\mu }_{rh}{\mu }_{pde}{\mu }_{tr}}{{\widehat{g}}_{y,\mathit{\text{peak}}}}{t}^3$. (B) The red curve shows the data for the averaged WT rod waveform from Fig. 2A. The green curves show quadratic fits to data and ${\widehat{g}}_y\left(t\right)$ performed with the fitting function $\frac{1}{2}\widehat{A}{\left(t-t_{eff}\right)}^2$. The fitted values for the waveform amplification constant are  ≈ 97s⁻² (data) and  ≈ 135s⁻² $\left({\widehat{g}}_y\right)$. The blue continuous curve displays ${\widehat{g}}_y\left(t\right)$ when the parameter μ_tr is assumed to be very large. The leading order term of the Taylor expansion of ${\widehat{g}}_y\left(t\right)$ for large μ_tr is $\frac{1}{2}\frac{{\mu }_{rh}{\mu }_{pde}}{{\widehat{g}}_{y,\mathit{\text{peak}}}}{t}^2$ (blue dashed curve).

This analysis shows that the waveform depends on ${\widehat{g}}_y\left(\text{t}\right)$, which in turn depends only on the dynamical parameters μ_rh, μ_tr, μ_pde and ${\tilde{\beta }}_d$ (see Methods, Eq. 9). We come to the surprising conclusion that the waveform of the photoreceptor response is determined exclusively by the deactivation rates μ_rh, μ_tr and μ_pde, together with the effective cGMP turnover rate ${\tilde{\beta }}_d$, which additionally depends on Ca²⁺ feedback to the cyclase (see Eq. 7). In the following we simplify the notation and we generally refer to the parameters μ_rh, μ_tr, μ_pde and ${\tilde{\beta }}_d$ as deactivation parameters or deactivation rates, although it is clear that ${\tilde{\beta }}_d$ is conceptually different from a deactivation rate like μ_rh. The activation parameters β_sub and k_act only scale the waveform by means of the gain ξ. We can therefore separate our analysis into two parts: (1), analysis of the rising and recovery phase of the waveform to extract information about the deactivation parameters; and (2), analysis of the peak amplitude $y_{\mathit{\text{peak}}}=R_0^{\text{*}}\xi g_{y,\mathit{\text{peak}}}$ to additionally infer information about the gain ξ and rates of activation. Whereas the peak amplitude y_peak depends on activation and deactivation parameters, the peak time is a property of the waveform and depends only on deactivation parameters (see Eq. 10).

Rising phase of dim-flash responses

Our analytic result for g_y(t) in Eq. 9 describes the dim-flash response as a sum of exponentials. To examine whether a simpler polynomial approximation of the waveform exists during the rising phase, we have expanded ${\widehat{g}}_y\left(t\right)= \frac{g_y\left(t\right)}{g_{y,\mathit{\text{peak}}}}$ for small values of the time t in a Taylor series using Eq. 9. Note that the following analysis does not require us to have an explicit analytic expression for g_y,_peak. The Taylor series expansion is alternating, ${\widehat{g}}_y\left(t\right)=a{t}^3-b{t}^4+c{t}^5-d{t}^6+\dots$ with the leading-order coefficient $a=\frac{1}{6}\frac{{\mu }_{rh}{\mu }_{pde}{\mu }_{tr}}{{\text{g}}_{y,\mathit{\text{peak}}}}$. Expressions for the higher order coefficients are lengthy, and we omit them; they can be computed with software like Maple or Mathematica.

In Fig. 3A we show the expansion for a WT rod; for GCAPS^−/− rods and for the cones, the analysis is similar. The Taylor expansion reveals that the leading order term is proportional to t³, which reflects the three processes in Eq. 1 that contribute to PDE activation. In general, if n first-order processes contribute to PDE activation, the leading order asymptotic is ~tⁿ (Baylor et al., 1974). For example, by assuming that the intermediate step by which a T* is transformed into a P* is very fast, corresponding to the limit μ_tr → ∞, the leading-order asymptotic changes to the quadratic polynomial ${\widehat{g}}_y\left(t\right)=\frac{1}{2}\frac{{\mu }_{rh}{\mu }_{pde}}{{\text{g}}_{y,\mathit{\text{peak}}}}{t}^2$. Since the waveform at short times depends on the number of intermediate processes that contribute to PDE activation, the larger this number, the longer the delay in the initial rise of the response. Thus, an analysis of the short-time waveform gives information about the effective number of intermediate processes that contribute to the early phase of PDE activation. That ${\widehat{g}}_y\left(t\right)$ for WT rod rises too fast in comparison to the data (Fig. 3B, red vs black curves) may be an indication that additional intermediate steps should be included (such as steps in rhodopsin phosphorylation) to delay the initial rise. We do not introduce such steps, because the kinetics and even number of phosphorylation steps required to extinguish R* activity are presently unknown, and the purpose of this work is to provide a comprehensive analysis by focusing on basic transduction processes rather than to obtain the best possible fit.

We next asked whether the leading-order term of the Taylor expansion can be used to fit the rising phase of the waveform up to larger times of the order the inflection time of the waveform. Fig. 3A and Fig. 3B for the limit μ_tr → ∞ show that the leading-order expression is a valid approximation only during a very short initial time period and fails at later times. We therefore conclude that the leading-order expansion is not suitable to describe the rising phase up to the inflection point. Nevertheless, many studies have shown that the quadratic approximation $y\left(t\right)= \frac{1}{2}{R}_0^{*}A{\left(t-t_{eff}\right)}^2$ gives a good fit to the rising phase of the light response up to this point (Pugh & Lamb, 1993). In this equation t_eff is an effective time delay that accounts for fast intermediate processes, and A is known as the amplification constant (Pugh & Lamb, 1993). We also find that the rising phase of the waveform data can be well fit by a quadratic function of the form $\widehat{y}\left(t\right)=\frac{1}{2}\widehat{A}{\left(t-t_{eff}\right)}^2$ (Fig. 3B green curves). This same equation also gives a good fit to ${\widehat{g}}_y\left(t\right)$ (Fig. 3B), which confirms that model and data are consistent.

Why does our leading-order expression proportional to t³ fail to fit the rising phase, whereas a lower order quadratic polynomial is well suited? The reason is that cancellations in the Taylor series due to the alternating summands produce an effective behavior of the response at later times that is very different from the leading order term. Whereas the leading-order behavior with many intermediate steps can be proportional to tⁿ, where n can be large, the effective behavior at later times might well be approximated by a polynomial of much lower order, e.g. by a quadratic function. The difficulty is that we cannot derive this effective polynomial starting from Eq. 9, and the polynomial fit has therefore no clear theoretical basis and must be considered as only empirical.

Because the amplification constant  was obtained by fitting of the waveform, its value can depend only on the deactivation parameters μ_rh, μ_tr, μ_pde, and ${\tilde{\beta }}_d$. Unfortunately, since we cannot mathematically derive the effective polynomial, we do not have an analytic formula for Â. It therefore remains unclear how  relates to the underlying deactivation parameters. Since the leading-order expansion with large μ_tr is also a quadratic polynomial, ${\widehat{g}}_y\left(t\right)=\frac{1}{2}\frac{{\mu }_{rh}{\mu }_{pde}}{{\text{g}}_{y,\mathit{\text{peak}}}}{t}^2$, we verified that this expression is not related to the quadratic fitting function (Fig. 3B dashed blue curve), and therefore it cannot be used to estimate $\widehat{A}=\frac{{\mu }_{rh}{\mu }_{pde}}{{\text{g}}_{y,\mathit{\text{peak}}}}$. We also note that the assumption that μ_tr is very large, corresponding to a model where R* directly activates P* (Lamb & Pugh, 1992; Pugh & Lamb, 1993), strongly increases the discrepancy between data and model during the rising phase (Fig. 3B blue vs red curve).

The amplification constant A defined by Lamb and Pugh is obtained by fitting the log-transform y(t) with the quadratic fitting function $\frac{1}{2}{R}_0^{*}A{\left(t-t_{eff}\right)}^2$ (Pugh & Lamb, 1993). In contrast, our amplification constant  is obtained by fitting the waveform $\widehat{y}\left(t\right)$ with this fitting function. With $y\left(t\right)=y_{\mathit{\text{peak}}} \widehat{y}\left(t\right)\approx y_{\mathit{\text{peak}}}\frac{1}{2}\widehat{A}{\left(t-t_{eff}\right)}^2=\frac{1}{2}{R}_0^{*}\frac{y_{\mathit{\text{peak}}}}{R_0^{*}} \widehat{A}{\left(t-t_{eff}\right)}^2$ we obtain the formula $A=\frac{y_{\mathit{\text{peak}}}}{R_0^{*}}\widehat{A}$, which relates the value of A to that of Â. With the dim-flash expression $y_{\mathit{\text{peak}}}=R_0^{*}\xi g_{y,\mathit{\text{peak}}}$ we further get $A=\xi g_{y,\mathit{\text{peak}}}\widehat{A}=n_{ch}{k}_{act}{\beta }_{sub}\frac{\widehat{A}{g}_{y,\mathit{\text{peak}}} }{{\mu }_{rh}{\mu }_{pde}}$. With the fitted values for  from Fig 3, with ξ from Table 2, and with g_y,_peak = 0.16 extracted from a numerical solution of Eq. 1, we compute for rods that A = ξg_y,_peak ≈ 7s⁻² (fit of data) and A ≈ 9.7s⁻² (fit of ${\widehat{g}}_y$), values that are within the wide range that can be found in the literature (Nikonov et al., 2006; Chen et al., 2010b; Majumder et al., 2013; Woodruff et al., 2014; Vinberg et al., 2015; Ingram et al., 2016). For a Gnat1^−/− cone we estimate  ≈ 2047s⁻² by fitting the waveform data in Fig 2B. With ξ from Table 2 and g_y,_peak = 0.26 (extracted from a numerical solution of Eq. 11), we compute A = ξg_y,_peak ≈ 0.95s⁻², less than for rods and similar to previous estimates (Nikonov et al., 2006;Ingram et al., 2019).

The value of A can also be computed by extracting $\frac{y_{\mathit{\text{peak}}}}{R_0^{*}}$ from the data (see also Fig. 5), and by using this value together with the fitted value for  to compute $A=\frac{y_{\mathit{\text{peak}}}}{R_0^{*}}\widehat{A}$; or, alternatively, from the frequently used procedure of fitting individual dim-flash responses y(t) (as in Pugh & Lamb, 1993). All of these methods are equivalent and necessarily give similar results for A (not shown) because, for dim flashes, $y\left(t\right)=y_{\mathit{\text{peak}}} \widehat{y}\left(t\right)$ and $y_{\mathit{\text{peak}}}=R_0^{*}\xi g_{y,\mathit{\text{peak}}}$. It is however advantageous to use  for the computation of A, because the recording noise can be reduced by averaging over multiple waveforms of individual responses.

Figure 5.

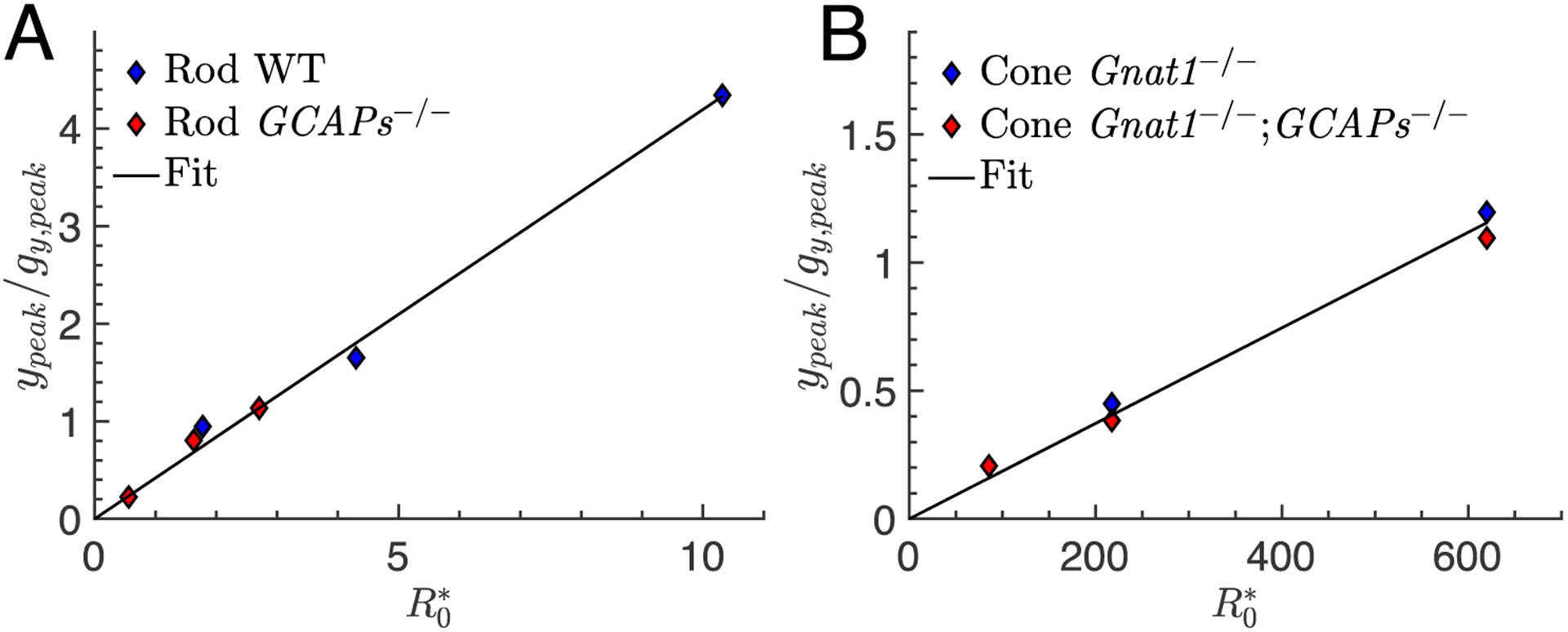
Estimation of the gain ξ from the peak amplitudes of dim-flash responses. (A) The peak amplitudes y_peak of the log-normal data for rods shown in Fig. 1 A–B together with g_y,peak computed with Eq. 1 and parameters from Table 2 are used to calculate $\frac{y_{\mathit{\text{peak}}}}{g_{y,\mathit{\text{peak}}}}$ for WT (blue diamonds) and GCAPs^−/− rod (red diamonds), and then plotted against the number of isomerizations $R_0^{*}$ specified in Fig. 1. The black curve is a linear fit to the combined datapoints with slope ξ = 0.42. (B) Same procedure as in (A) but for cones. The linear fit gives ξ = 0.0019.

In a previous analysis, Pugh and Lamb (1993) derived the expression A = n_chk_actβ_sub and inferred that A depends only on activation parameters. To derive their formula, they considered that the intermediate steps of transducin activation proceed very rapidly, corresponding to the limit μ_tr → ∞, and they further neglected all deactivation processes, corresponding to the limits μ_rh → 0, μ_pde → 0 and ${\tilde{\beta }}_d\to 0$. With these approximations, the rise of the waveform is given by the first order term ${\widehat{g}}_y\left(t\right)=\frac{1}{2}\frac{{\mu }_{rh}{\mu }_{pde}}{{\text{g}}_{y,\mathit{\text{peak}}}}{t}^2$ (blue dashed curve in Fig 3B) such that $\widehat{A}=\frac{{\mu }_{rh}{\mu }_{pde}}{{\text{g}}_{y,\mathit{\text{peak}}}}$. The corresponding expression for the log-normal response is $y\left(t\right)=R_0^{*}\xi g_{y,\mathit{\text{peak}}}{\widehat{g}}_y\left(t\right)= \frac{1}{2}{R}_0^{*} n_{ch}{k}_{act}{\beta }_{sub}{t}^2$. Hence, in the limit μ_tr → ∞ with vanishing deactivation rates, the rise of the response is described by a quadratic function with amplification constant A = n_chk_actβ_sub, just as Pugh and Lamb obtained. This result for A is a special case of our general formula $A=n_{ch}{k}_{act}{\beta }_{sub}\frac{\widehat{A}{g}_{y,\mathit{\text{peak}}} }{{\mu }_{rh}{\mu }_{pde}}$ for $\frac{\widehat{A}{g}_{y,\mathit{\text{peak}}} }{{\mu }_{rh}{\mu }_{pde}}=1$, which results from the first order expression $\widehat{A}=\frac{{\mu }_{rh}{\mu }_{pde}}{{\text{g}}_{y,\mathit{\text{peak}}}}$.

The amplification constant A = n_chk_actβ_sub faithfully characterizes the response for the case μ_tr → ∞ but only under two conditions. First, the deactivation rates must all be zero, in which case the response rises indefinitely as $y\left(t\right)=\frac{1}{2}{R}_0^{*} n_{ch}{k}_{act}{\beta }_{sub}{t}^2$. The value A = n_chk_actβ_sub therefore corresponds to the maximal amplification that this system would achieve if all deactivation processes are switched off. In this case, A necessarily depends only on activation rates. Second, during some very early phase of the response where the waveform can be approximated by the first order term of its Taylor expansion (Fig. 3A and 3B), the response rises with maximal amplification. The exact extent of this early phase depends on the deactivation rates. It is certainly not appropriate to fit the data up to the inflection point of the rising phase without considering deactivation processes, since the inflection point is a clear manifestation of the impact of the deactivation rates: without deactivation, this point would not exist and the response would rise indefinitely. If the data are fitted up to the inflection point, deactivation rates will necessarily affect the value of the amplification constant, which is quantified by our formula $\frac{\widehat{A}{g}_{y,\mathit{\text{peak}}} }{{\mu }_{rh}{\mu }_{pde}}$.

Our formula $A=n_{ch}{k}_{act}{\beta }_{sub}\frac{\widehat{A}{g}_{y,\mathit{\text{peak}}} }{{\mu }_{rh}{\mu }_{pde}}$ is valid for general μ_tr, and the latter affects the value of Âg_y,peak. By further considering the possibility that T* deactivation can occur also without activation of P*, in which case the values of k_tr and μ_tr would be different, our formula would generalize to $A=n_{ch}{k}_{act}{\beta }_{sub}{k}_{tr}\frac{\widehat{A}{g}_{y,\mathit{\text{peak}}} }{{\mu }_{rh}{\mu }_{pde}{\mu }_{tr}}$.

In summary, we conclude that fitting the rising phase of the waveform with a quadratic expression is empirical but provides no precise information about the underlying parameters because we do not have an analytic expression for Â. To estimate precise values for the deactivation rates from a waveform analysis, we must use Eq. 9. We return to the relationship between amplification and activation/inactivation rates in the Discussion.

Recovery phase of dim-flash responses

Both the rising and recovery phase of the waveform are governed by the same sum of exponentials given in Eq. 9. During the initial rising phase when time is small, all exponentials contribute to the waveform. Around peak time, the contributions from at least two exponentials are relevant, because a single exponential cannot generate a peak in the waveform. Finally, at larger times during the recovery phase, only the exponentials with the smallest rate constants (and slowest decay) contribute significantly to the waveform. For the values of parameters from Table 2, we have that μ_rh and μ_tr are much larger than μ_pde and ${\tilde{\beta }}_d$, where we can assume ${\tilde{\beta }}_d={\beta }_d$ for GCAPs^−/− and ${\tilde{\beta }}_d\approx 3.8{\beta }_d$ for WT photoreceptors (see Eq. 7). We conclude that the recovery phase of dim-flash responses in both rods and cones is governed primarily by the decay of light-activated μ_pde and the rate ${\tilde{\beta }}_d$ (note that ${\tilde{\beta }}_d$ depends on the dark turnover rate and degree of the cyclase activation). Moreover, from Table 2 we can compute for a WT rod that ${\tilde{\beta }}_d\approx 15.6s^{-1}$, and since this value is much larger than μ_pde = 5s⁻¹, it follows that the recovery of WT rod flash response is well approximated by a single exponential with decay rate μ_pde, as previous experiments have indicated (Krispel et al., 2006; Tsang et al., 2006; Chen et al., 2010a). Similarly, for a GCAPs^−/− cone with β_d = 11s⁻¹ and μ_pde = 37.8s⁻¹, we conclude that the recovery is governed by a single exponential with rate β_d.

To verify these conclusions, we fitted the recovery phase of the averaged waveform derived from the WT rod and the Gnat1^−/−;GCAPs^−/− cone from Fig 1 (black), with a single exponential (red) to estimate the decay rate μ_rec (Fig. 4A–B). From the fitting of the averaged waveform, we obtained μ_rec = 4.9s⁻¹ for the WT rod and μ_rec = 11.9⁻¹ for the Gnat1^−/−;GCAPs^−/− cone, which are both similar to the values in Table 2 that were obtained by fitting entire responses in Reingruber et al. (2020). By fitting the recovery of the three individual traces that were used to generate the averaged waveform, we get μ_rec = 4.9 ± 0.8s⁻¹ and μ_rec = 12.4 ± 1.2s⁻¹ (mean ± S.E.). In contrast, for a GCAPs^−/− rod the parameters β_d = 4.1s⁻¹ and μ_pde = 5s⁻¹ have very similar values, with the consequence that the recovery depends upon a sum of two exponentials. That is also true for a WT cone where ${\tilde{\beta }}_d\approx 41.8s^{-1}$ is similar to μ_pde = 37.8s⁻¹.

Figure 4.

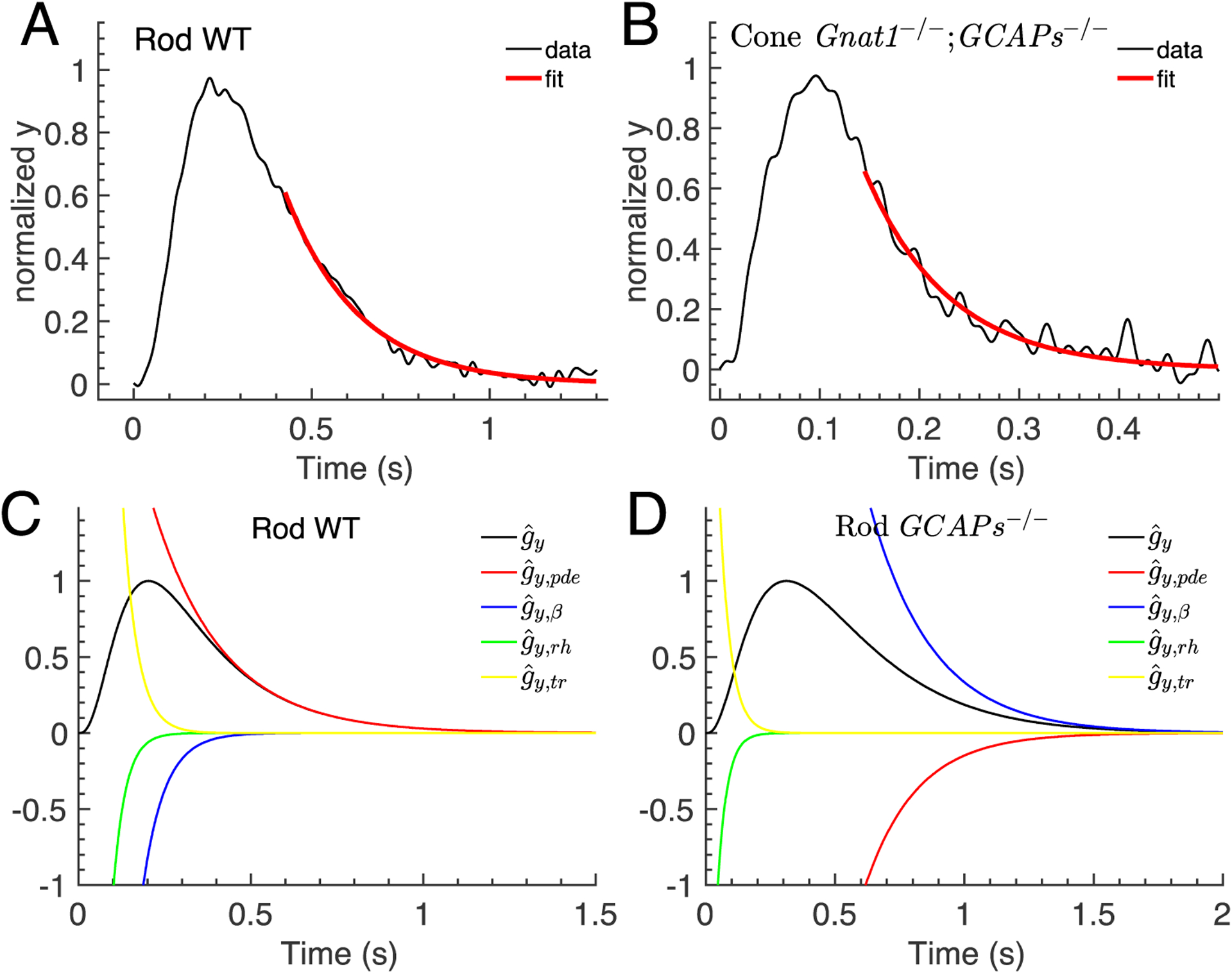
Recovery phase of the waveform. (A-B) The recovery phase of the averaged waveform data for WT rod and Gnat1^−/−;GCAPs^−/− cone from Fig. 2 (black curves) were fitted with a single exponential function to extract the recovery rates constants μ_rec (red curves). The fitted values are μ_rec = 4.9s⁻¹ for WT rod, and μ_rec = 11.9⁻¹ for Gnat1^−/−;GCAPs^−/− cone. (C-D) The curves show the individual single exponentials related to rhodopsin decay, transducin decay, PDE decay and the cyclase rate constant β that contribute to the waveform ${\widehat{g}}_y= {\widehat{g}}_{y,rh}+{\widehat{g}}_{y,tr}+{\widehat{g}}_{y,pde}+{\widehat{g}}_{y,\beta }$ computed with Eq. 9 for a WT rod (C) and a GCAPs^−/− rod (D) .

To illustrate these findings, we compare the recovery between a WT and GCAPs^−/− rod (Fig. 4C–D). We use Eq. 9 to extract the different exponential contributions to the waveform related to rhodopsin decay, transducin decay, PDE decay and the cyclase, ${\widehat{g}}_y= {\widehat{g}}_{y,rh}+{\widehat{g}}_{y,tr}+{\widehat{g}}_{y,pde}+{\widehat{g}}_{y,\beta }$ (Fig. 4C–D). Whereas the recovery of a WT rod (Fig. 4C, black curve) is dominated by a single exponential related to PDE decay (Fig. 4C, red curve), the recovery of a GCAPs^−/− rod (Fig. 4D, black curve) is the sum of two exponentials with decay rates μ_pde (Fig. 4D, red curve) and β_d (Fig. 4D, blue curve).

Peak amplitude, gain and sensitivity of dim-flash responses

The waveform analysis provides information about the dynamical parameters μ_rh, μ_tr, μ_pde, and ${\tilde{\beta }}_d$. The activation parameters β_sub and k_act can be extracted from the gain ξ. Since $y_{\mathit{\text{peak}}}=R_0^{*}\xi g_{y,\mathit{\text{peak}}}$, we can learn about ξ from the peak amplitude of the responses. The values y_peak can be extracted from the data, and if the collecting area κ is known, the expected number of activated rhodopsin molecules can be computed as $R_0^{*}=\kappa \varphi \Delta t$. To complete this calculation, however, we need to estimate g_y,peak.

Because we cannot extract g_y,peak directly from the data, we need additional information about the dynamical parameters in order to compute g_y,peak either from Eq. 9 or Eq. 11, or from a simulation obtained with Eq. 1. If the waveform around peak time is governed by μ_pde and ${\tilde{\beta }}_d$, we can use Eq. 11 to compute g_y,peak as a function of $\frac{{\mu }_{pde}}{{\tilde{\beta }}_d}$. Because the value of g_y,peak changes only slowly as a function of the dynamical parameters, acceptable values for g_y,peak can be computed even if the dynamical parameters are not known precisely. With Eq. 11 and parameters from Table 2, we obtain g_y,peak = 0.19 (rod WT), g_y,peak = 0.40 (rod GCAPs^−/−), g_y,peak = 0.34 (cone Gnat1^−/−), g_y,peak = 0.60 (cone Gnat1^−/−;GCAPs^−/−). For comparison, from a numerical simulation of Eq. 1, we find g_y,peak = 0.16 (rod WT), g_y,peak = 0.39 (rod GCAPs^−/−), g_y,peak = 0.26 (cone Gnat1^−/−), g_y,peak = 0.55 (cone Gnat1^−/−;GCAPs^−/−). Because the values of g_y,peak are similar between rods and cones, the large difference in the response amplitude between rods and cones is primarily generated by the difference in the gain ξ, which is of the order 0.45/0.0018 ≈ 250 (see Table 2).

In Fig. 5, we plot $\frac{y_{\mathit{\text{peak}}}}{g_{y,\mathit{\text{peak}}}}$ against $R_0^{*}$ for rods and cones, with g_y,peak computed from Eq. 1 and the parameters in Table 2. Because ξ is the same for WT and GCAPs^−/− photoreceptors, we can combine their data to estimate ξ. For a rod we obtain ξ = 0.42 (Fig. 5A), and for cone we get ξ = 0.0019 (Fig. 5B), which are both close to the values in Table 2 obtained by collective fitting of all of the responses. The gain is closely connected to the flash sensitivity. If we define the flash sensitivity S_F of a dark-adapted photoreceptor as the derivative of the normalized peak-response amplitude with respect to the number of photoisomerizations $R_0^{*}$, then for dim flashes with î_peak ≈ y_peak we have S_F ≈ ξg_y,peak. With the approximation g_y,peak,rod ≈ g_y,peak,cone, the sensitivity ratio between rods and cones is given simply the ratio of the gain, $\frac{S_{f,rod}}{S_{f,\mathit{\text{cone}}}}\approx \frac{{\xi }_{rod}}{{\xi }_{\mathit{\text{cone}}}}$. Hence to first estimation, the gain difference between rods and cones can be obtained from the ratio of the flash sensitivities, which can be extracted from the data. This conclusion is more important than it may seem, because it implies that the sensitivity of the photoreceptor is determined by the ratio $\frac{n_{ch}{\beta }_{sub}{k}_{act}}{{\mu }_{pde} {\mu }_{rh}}$. Assuming that the channel cooperativity n_ch is the same for rods and cones, the difference in sensitivity of the two kinds of photoreceptors can then be seen to depend only on the properties of the three proteins rhodopsin, transducin and PDE, which are all present as different isoforms in rods and cones (see Ingram et al., 2016).

Dynamics of saturating flash responses

So far, we have focused on dim-flash responses where we made use of our analytic result in Eq. 9. We do not use our model to fit brighter-light and saturating flash responses, because the model does not incorporate adaptation processes. It is nevertheless insightful to discover what the model predicts for saturating flashes. To study the responses to bright flashes we start from Eq. 1. Since for saturating flashes the normalized current î is close to one and almost constant during the saturation phase, the current does not reveal much information about the dynamics of PDE activity and cGMP concentration during this phase. We therefore focus on the dynamics of the log-transform y(t).

In Fig. 6 we compare the time course of y(t) computed from Eq. 1 for saturating-flash responses for WT and GCAPs^−/− rods (Fig. 6A), and Gnat1^−/− (effectively WT) and Gnat1^−/−;GCAPs^−/− cones (Fig. 6B). Whereas for dim flashes the responses are different between WT and GCAPs^−/− photoreceptors due to the cyclase, the kinetics during the saturation period become similar because the cyclase is maximally activated and constant and therefore does not affect the time dependency of the response. From Eq. 13, we find that the cGMP dynamics during saturation are determined by the PDE dynamics such that the product of the cGMP concentration and the number of activated PDEs is approximately constant with time. The magnitude of cyclase activation modulates the level of cGMP synthesis and thereby affects the extent by which the cGMP concentration is depleted by activated PDE (cGMP becomes less depleted in a WT photoreceptor due to higher cyclase activity). The level of cyclase activation affects the maximum of y that is attained during saturation. However, the shape of the responses, which can be found by normalizing the response to the maximum, is governed by PDE dynamics which are the same in both photoreceptors. This is the reason why in Figs. 6A and 6B we can adjust the flash intensity to superimpose responses for WT and GCAPs^−/− photoreceptors during the saturation phase.

Figure 6.

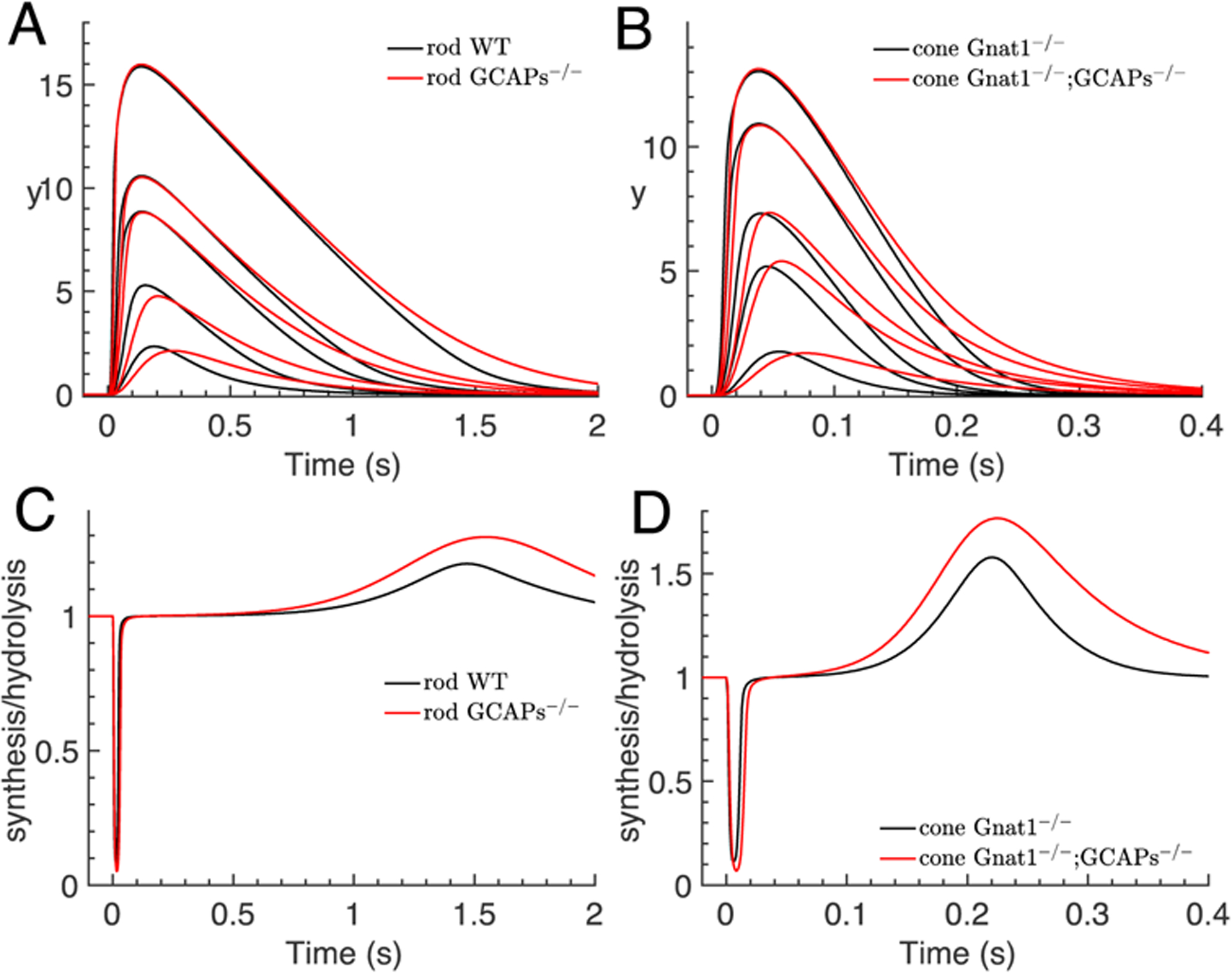
Simulations of saturating flash responses for rods and cones. The number of isomerizations $R_0^{\text{*}}=\kappa \varphi \Delta t$ that were used for the simulations are: (A) WT rod (40,140,600,1200,10000), GCAPs^−/− rod (15,50,250,500,4500); (B) Gnat1^−/− cone 10³x(4.55,1.95,45.5,19.5,455), Gnat1^−/−;GCAPs^−/− cone 10³x(1.95,9.75,19.5,78,195). (A) Comparison of the dynamics of the log-normal y(t) computed with Eq. 1 for saturating flashes for WT (black) and GCAPs^−/− rods (red). Flash intensities for WT and GCAPs^−/− rods are not the same but were chosen to obtain similar peak amplitudes in order to facilitate the comparison of the kinetics. Parameters are from Table 2. (B) Same procedure as in (A) but for cones. (C) The time course of the ratio r of the rod cGMP synthesis to hydrolysis rate (Eq. 14) for the two strongest flashes in (A) is depicted. (D) Same procedure as in (C) but for cone.

Eq. 13 predicts that during the saturation phase, the cGMP concentration adapts to PDE activation such that the hydrolysis rate matches the synthesis rate, β_subP*(t)c_cg(t) ≈ α_max. More generally, the ratio of the synthesis to hydrolysis rate during a flash response evolves according to

$$r=\frac{\alpha }{{\beta }_d{c}_{cg}+{\beta }_{sub}{P}^{*}{c}_{cg}}=\frac{\widehat{\alpha }}{\widehat{\alpha }+\frac{{\widehat{c}}_{cg}}{n_{ch}{\beta }_d}\frac{dy}{dt}}=\frac{\widehat{\alpha }}{\widehat{\alpha }-\frac{1}{{\beta }_d}\frac{d{\widehat{c}}_{cg}}{dt}}.$$ (14)

At peak time we have $\frac{dy}{dt}=0$ and r = 1. In Figs. 6C and 6D, we show r from Eq. 14 for the two strongest flashes from Figs. 6A and 6B. At the beginning,r quickly decreases due an increase in cGMP hydrolysis rate driven by PDE activation. This decrease in r produces rapid cGMP depletion, which in turn decreases the hydrolysis rate so that r starts to increase again even for GCAPs^−/− photoreceptors in the absence of cyclase feedback. At the time-to-peak of the response, the synthesis and hydrolysis of cGMP are the same, and r = 1. The value of r stays close to one during the saturation phase (Figs. 6C and 6D), which can be inferred from Eq. 14 because $\left|\frac{{\widehat{c}}_{cg}}{n_{ch}{\beta }_d}\frac{dy}{dt}\right|\ll 1$ when ĉ_c,g is small. Finally, during the recovery phase, r increases because the cyclase rate is greater than the PDE rate, and r returns to its equilibrium value as the response decays to baseline.

Figs. 6A and 6B show that during saturation, y(t) decreases almost linearly as a function of time. To explain this quasi-linearity, we assume that PDE recovery is governed by μ_pde such that $g_p\left(t\right)\approx \eta e^{-{\mu }_{pde}t}$ (Eq. 5). With ${\tilde{P}}^{\text{*}}\left(t\right)\approx R_0^{\text{*}}\xi \eta e^{-{\mu }_{pde}t}={\tilde{P}}_{max}^{\text{*}}{e}^{-{\mu }_{pde}t}$ we obtain from Eq. 12 during saturation

$$\frac{y\left(t\right)}{n_{ch}}\approx \text{ln}\left(\frac{{\tilde{P}}_{max}^{\text{*}}}{{\widehat{\alpha }}_{max}{\beta }_d{n}_{ch}}\right)-{\mu }_{pde}t= \text{ln}\left(\frac{R_0^{\text{*}}\xi \eta }{{\widehat{\alpha }}_{max}{\beta }_d{n}_{ch}}\right)-{\mu }_{pde}t.$$ (15)

Eq. 15 reveals that y(t)/n_ch decreases linearly with time with a slope given by μ_pde. Unfortunately, it is difficult to exploit Eq. 15 to estimate μ_pde by fitting the decay of y(t), because we cannot reliably compute y(t) from the data when the current is close to 1 as a result of noise and the singularity of the logarithm at zero. Instead, to extract μ_pde we can use information from multiple flash responses to measure the time t_D when the recovering current crosses a fixed threshold î_D, corresponding to the fixed value y_D = −ln(1 − î_D). With Eq. 15 we find that t_D satisfies $-\frac{y_D}{n_{ch}}+\text{ln}\left(\frac{\xi \eta }{{\widehat{\alpha }}_{max}{\beta }_d{n}_{ch}}\right)+\text{ln}{R}_0^{\text{*}}-{\mu }_{pde}{t}_D\approx 0$. Since the first two terms in this expression are constants, one can extract μ_pde by fitting the slope of t_D as a function of $\text{ln}{R}_0^{\text{*}}$, which is called a Pepperberg plot after the late David Pepperberg (Pepperberg et al., 1992). This analysis shows that the dominant time constant in this model is given by the PDE deactivation rate, τ_D = μ_pde⁻¹, and that a Pepperberg analysis can in principle be performed with both WT and GCAPs^−/− responses.

DISCUSSION

The signal transduction pathway of the vertebrate rod and cone photoreceptor consists of a series of biochemical and biophysical processes that transform the absorption of a photon into a change in membrane current. Despite many sophisticated mathematical models, a precise conceptual understanding of how all these interconnected processes work together to generate the response remains challenging. To obtain such an understanding, we derived an analytic solution for the entire dim-flash response based on a representative model that comprises the most important transduction processes. We applied this solution to dissect the flash response and to investigate its characteristic phases: the activation phase where the current rises, the intermediate peak or saturation phase, and the recovery phase where the photoreceptor returns to its initial state. Our novel analysis provides a detailed characterization of these phases.

Our analytic result $y\left(t\right)=R_0^{\text{*}}\xi g_y\left(t\right)$ shows that the entire log-transform of the dim-flash response is linear with the number of photoisomerizations $R_0^{\text{*}}$ generated by the flash. Since for dim flashes we have î(t) = 1 – e^−y(t) ≈ y(t), to a first approximation the current is also linear with $R_0^{\text{*}}$. The analytic function g_y(t) (Eq. 9) depends entirely on the deactivation parameters μ_rh, μ_tr, μ_pde and ${\tilde{\beta }}_d$, where ${\tilde{\beta }}_d$ can be seen as an effective dark cGMP turnover rate that also depends on Ca²⁺-feedback to the cyclase (Eq. 7). The activation parameters β_sub and k_act affect the response by means of the gain $\xi =\frac{n_{ch}{k}_{act}{\beta }_{sub}}{{\mu }_{rh}{\mu }_{pde}}$ (Eq. 2). We used this analytic result to separate the response into the waveform $\widehat{y}\left(t\right)={\text{g}}_y\left(t\right)/g_{y,\mathit{\text{peak}}}$, which is independent of the flash intensity and is normalized to amplitude one (Fig. 2); and the amplitude $y_{\mathit{\text{peak}}}=R_0^{\text{*}}\xi g_{y,\mathit{\text{peak}}}$, such that $y\left(t\right)=y_{\mathit{\text{peak}}}\widehat{y}\left(t\right)$. It follows that the dim-flash waveform $\widehat{y}\left(t\right)$ depends entirely on the deactivation parameters μ_rh, μ_tr, μ_pde and ${\tilde{\beta }}_d$, whereas the activation parameters β_sub and k_act only affect the response amplitude y_peak.

In a previous attempt to analyze the rising phase of dim flashes, Pugh and Lamb (1993) found that the quadratic expression $y\left(t\right)=\frac{1}{2}{R}_0^{\text{*}}A{\left(t-t_{eff}\right)}^2$ gives a reasonable fit to the rising phase of the log-transform of the current. They called the parameter A the amplification constant. By neglecting deactivation processes, Pugh and Lamb derived the formula A = n_chβ_subk_act. This formula relates the fitted value of A entirely to the activation rates and the channel cooperativity. This equation for A has since been widely used to evaluate the initial activation process and to extract values for the rates β_sub and k_act (see for example Pugh & Lamb, 2000; Kawamura & Tachibanaki, 2008; Invergo et al., 2014; Astakhova et al., 2015; Lamb et al., 2018).

From our analysis of the rising phase, we have derived the new formula $A=\frac{y_{\mathit{\text{peak}}}}{R_0^{*}}\widehat{A}$, where the amplification constant  can be obtained by fitting the rising phase of the waveform $\widehat{y}\left(t\right)$ with the quadratic fitting function $\frac{1}{2}\widehat{A}{\left(t-t_{eff}\right)}^2$ (Fig 3B). With our analytic result $y_{\mathit{\text{peak}}}=R_0^{\text{*}}\xi g_{y,\mathit{\text{peak}}}$, we obtain $A=\xi g_{y,\mathit{\text{peak }}}\widehat{A}=n_{ch}{k}_{act}{\beta }_{sub}\frac{\widehat{A}{g}_{y,\mathit{\text{peak}}}}{{\mu }_{rh}{\mu }_{pde}}$, where $\frac{\widehat{A}{g}_{y,\mathit{\text{peak}}} }{{\mu }_{rh}{\mu }_{pde}}$ depends only on the deactivation parameters. Our analysis thus reveals that the amplification constant A of Pugh and Lamb depends on both activation and deactivation parameters, and the impact of the deactivation parameters is quantified by $\frac{\widehat{A}{g}_{y,\mathit{\text{peak}}} }{{\mu }_{rh}{\mu }_{pde}}$. For example, for a WT mouse rod with the fitted value  = 97s⁻² (Fig 3B), g_y,peak = 0.16 (from a numerical solution of Eq. 11), μ_rh = 28s⁻¹ and μ_pde = 5s⁻¹ (from Table 2), we estimate $\frac{\widehat{A}{g}_{y,\mathit{\text{peak}}}}{{\mu }_{rh}{\mu }_{pde}}\approx 0.11$. For the Gnat1^−/− cone with Â=2047s⁻² (by fitting the data in Fig. 2B, not shown) and g_y,peak = 0.26, we find $\frac{\widehat{A}{g}_{y,\mathit{\text{peak}}}}{{\mu }_{rh}{\mu }_{pde}}\approx 0.2$. Hence, by assuming that n_ch ≈ 2.5, we conclude that the incorrect formula A = n_chk_actβ_sub would underestimate k_actβ_sub in a mouse rod by a factor of around 9, and in a mouse cone by a factor of around 5. A similar underestimation by factors of around 4 and 1.6 have been inferred for a carp cone and a frog rod from simulations where the deactivation processes have been switched off (Astakhova et al., 2015).

The results of Pugh and Lamb (1993) were derived from a first-order analysis of model equations, which is unaffected by deactivation processes. As suggested by the frog result from (Astakhova et al., 2015), deactivation processes might have only a reduced impact in amphibian rods, which were used for the initial analysis of Pugh and Lamb (1993). Nevertheless, based on the observation that the rising phase of many rod and cone photoreceptors can be well approximated by the quadratic fitting function $y\left(t\right)=\frac{1}{2}{R}_0^{\text{*}}A{\left(t-t_{eff}\right)}^2$, Pugh and Lamb generalized their result without performing a mathematical validation (Pugh & Lamb, 1993, 2000).

We derived an analytic solution for the dim-flash response that provided the basis for our analysis, and which revealed that the contribution of deactivation processes to the rising phase cannot be neglected. Moreover, we find that the fitting function $y\left(t\right)=\frac{1}{2}{R}_0^{\text{*}}A{\left(t-t_{eff}\right)}^2$ has to be considered as empirical because it is not derived from an analysis of the underlying model equations. Although our formula $A=\frac{y_{\mathit{\text{peak}}}}{R_0^{*}}\widehat{A}$ shows that the amplification constant defined by Pugh and Lamb depends on activation and deactivation parameters, we do not have an analytic expression for Â. It is therefore unclear how to extract deactivation rates from the fitted value of Â. To estimate such values, one has to use Eq. 9 for a fitting procedure. Alternatively, in more complex models where no such analytic result is available, deactivation rates have to be estimated from the underlying model equations with numerical fitting procedures (see e.g. Hamer et al., 2005; Invergo et al., 2014).

The formula A = n_chk_actβ_sub predicts that Ca²⁺-feedback does not affect the rising phase of dim-flash responses, which seems to be consistent with experimental data showing that the initial rise of the response is not much different between WT and GCAP^−/− photoreceptors (Burns et al., 2002). In contrast, in our model Ca²⁺-feedback to the cyclase affects the rising phase of the waveform via the effective parameter ${\tilde{\beta }}_d$ (Eq. 7), and also affects the fitted value of the amplification constant Â. Since the time to peak is larger in a GCAPs^−/− photoreceptors, the amplification constant  is necessarily smaller in a GCAP^−/− photoreceptor. For example, by fitting the rod GCAPs^−/− data from Fig. 2A, we find Â≈42s⁻² (not shown), contrary to Â≈97s⁻² for a WT rod (Fig. 3). Since however the response amplitude y_peak is larger in a GCAPs^−/− photoreceptor, the value of the amplification constant $A=\frac{y_{\mathit{\text{peak}}}}{R_0^{*}}\widehat{A}=n_{ch}{k}_{act}{\beta }_{sub}\frac{\widehat{A}{g}_{y,\mathit{\text{peak}}}}{{\mu }_{rh}{\mu }_{pde}}$ remains largely unchanged between WT and GCAPs^−/− photoreceptors. For example, for a WT rod we have Âg_y,peak ≈ 15.5s⁻², and for a GCAPs^−/− rod Âg_y,peak ≈ 16.4s⁻². We thus find that the experimental result that the initial rise of the response is not much different between WT and GCAP^−/− photoreceptors does not imply that Ca²⁺-feedback does not affect the rising phase of dim-flash responses. We show that the initial rise of the response remains almost unchanged because Ca²⁺-feedback affects both response amplitude and response dynamics. Lamb and Pugh derived their formula A = n_chk_actβ_sub by arguing that the Ca²⁺ dynamics is slow and therefore does not affect the initial rising phase. In contrast, we assume that Ca²⁺-dynamics is determined by the current dynamics, in which case Ca²⁺ feedback gradually modulates the response. By performing simulations with an additional equation for the Ca²⁺concentration, we checked that our assumption is justified to model the rising phase of dim-flash responses where the rise of the current is sufficiently slow. For strong flashes, where the current rises very fast, the initial Ca²⁺ dynamics is slightly delayed with respect to the current.

Because activation rates affect the gain ξ (Eq. 2), analysis of the gain is a more effective way to extract information about activation parameters. We show that the gain can be estimated either from an analysis of the rising phase with the formula ξ = A/(Âg_y,peak), or by fitting entire flash responses as shown in Reingruber et al. (2020), or from an analysis of the response amplitude (Fig. 5). For example, for a WT rod, with the gain and deactivation parameters from Table 2 together with the assumption β_sub~0.02s⁻¹, we find $k_{act}=\xi \frac{{\mu }_{rh}{\mu }_{pde}}{n_{ch}{\beta }_{sub}} \approx 1260s^{-1}$. With the amplification constant A=7.1s⁻² (estimated from Fig 3) together with the formula $A=n_{ch}{k}_{act}{\beta }_{sub}\frac{\widehat{A}{g}_{y,\mathit{\text{peak}}}}{{\mu }_{rh}{\mu }_{pde}}$, we obtain $k_{act}=\frac{\text{A}}{n_{ch}{\beta }_{sub}} \frac{1}{0.11}\approx 1290s^{-1}$, which is consistent with the value estimated from the gain. In contrast, the Pugh and Lamb formula predicts a value $k_{act}=\frac{A}{n_{ch}{\beta }_{sub}}\approx 142s^{-1}$. Because our estimation of the transducin activation rate is similar to the values of Heck and Hofmann (2001) and Lamb and Kraft (2020), and because we have used a conventional model of single-transducin activation for PDE, our calculations indicate that a high transducin activation rate cannot be used as unambiguous evidence for a dimeric transducin activation of PDE (Lamb & Kraft, 2020).

The recovery phase of the current is frequently fitted with a single exponential to extract the recovery rate constant μ_rec (or its inverse τ_rec) In WT rods this value is usually identified with the PDE deactivation rate μ_pde (Krispel et al., 2006; Tsang et al., 2006; Chen et al., 2010a). We have shown, however, that a more accurate procedure is to fit the recovery of the log-transform of the current, which is more directly governed by exponential decays (Eq. 9). Moreover, because the recovery of the response depends on a sum of exponentials (Eq. 9), careful analysis is needed to interpret the fitted value for the recovery rate correctly. We show that fitting the recovery phase with a single exponential is justified only for WT rod and GCAPs^−/− cone responses, where the fitted recovery rates correspond to μ_pde (rod) and β_d (cone). In contrast, for WT cone and GCAPs^−/− rod responses (Fig. 4C–D), the recovery phase is governed by a sum of two exponentials, and in this circumstance it is not appropriate to extract parameters by fitting the recovery phase with a single exponential decay function. For example, when Gross et al. (2012b) determined the widely accepted value β_d = 4.1s⁻¹, they claimed that PDE decay does not affect the recovery of GCAPs^−/− rod responses. Although the latter is not correct, their estimation for β_d seems still to be justified because it was apparently derived from GCAPs^{−/− RGS9-ox} rod responses with overexpressed GAP proteins, where PDE decay is accelerated to a value μ_pde ≈ 12.5s⁻¹.

Finally, we used the log-transform of the current to analyze response dynamics during saturation. Whereas the current reaches a maximal value and is almost constant during the saturation period, the log-transform of the current is not constant and can be used to study dynamics during saturation (Fig. 6). Although our model does not include mechanisms of adaptation and cannot be used to fit responses to brighter light intensities, the model predictions for saturating flashes are nevertheless interesting because they provide insight into the dynamics during the saturation period when cyclase is maximally activated.

We find that during saturation, response dynamics are determined by a close interplay between PDE activation and cGMP depletion, such that the product of GMP concentration and the number of activated PDEs is approximately constant with time (Eq. 13). The extent of cyclase activation modulates the minimal level of the cGMP concentration that is attained, as a result of hydrolysis by activated PDE; but cyclase activity does not otherwise affect the dynamics of the response. This finding might have important implications for adaptation, because it suggests that modulation of PDE deactivation is a powerful means to control the cGMP concentration at high light intensities when the cyclase rate is at a maximal value.

Our results for saturating flashes further provide a mathematical explanation for Pepperberg plots (Pepperberg et al., 1992). Eq. 15 predicts that the dominant time constant for a WT rod will be determined by the PDE deactivation rate, τ_D = μ_pde⁻¹, which agrees with experimental observations (Krispel et al., 2006; Tsang et al., 2006; Chen et al., 2010a). If PDE activation were super-linear due to the necessity of binding of two transducins such that ${\tilde{P}}_{max}^{\text{*}}~R_0^{\text{*}}{e}^{\rho R_0^{\text{*}}}$ (Lamb & Kraft, 2020), Eq. 15 predicts ${\tau }_D=\frac{1+\rho R_0^{\text{*}}}{{\mu }_{pde}}$, which agrees with the formula from Lamb and Kraft (2020). However, more precise analysis of a model that additionally incorporates adaptation processes is needed to clarify whether the observed increases of the dominant time constant with brighter flash intensity are a sign of dimeric PDE activation (Lamb & Kraft, 2020), or of some other process (Martemyanov et al., 2008; Burns & Pugh, 2010).

Whereas our model faithfully reproduces cone data, the discrepancy between model and data is larger for rods, especially during the initial phase where the simulations rise faster than the data (Fig. 2A and Fig. 3B). Fig. 2A shows that the initial rise of the simulated waveform is faster in a GCAPs^−/− rod where Ca²⁺ feedback is absent, which suggests that the main reason for the discrepancy between data and simulations is not related to our assumptions about Ca²⁺ feedback. A possible reason for this difference could be due to the neglect of multiple phosphorylation steps, which are likely to have a larger impact on rods than cones. Multiple phosphorylations are known to be important for the rod single-photon response (Field & Rieke, 2002; Hamer et al., 2003; Reingruber & Holcman, 2008a) and are therefore likely also relevant for dim-flash responses. On the assumption that the intermediate step involving transducin activation proceeds very rapidly, corresponding to a high rate μ_tr, the discrepancy between data and model increases because a faster intermediate step accelerates the initial rise of the simulated response (see Fig. 3B). The inclusion of multiple phosphorylation steps would have the opposite effect and would slow down the initial rise of the response, which would lead to a better agreement between data and model.

With our parsimonious model, we are the first to provide a comprehensive mathematical analysis for the whole of the dim-flash response. Our analysis dissects the response dynamics to identify how parameters or parameter combinations govern various phases of the response. This analysis provides a more precise conceptual understanding of how transduction processes determine the dynamics of the photocurrent. We hope that this new insight will lead to the design of new experiments to test these findings in more detail. We hope that this work will serve as a template to derive more refined analytic expressions with more complex models and will help to revitalize the analytic analysis of phototransduction models that was pioneered by Lamb and Pugh (Lamb & Pugh, 1992; Pugh & Lamb, 1993). In addition, our approach may also be useful in understanding other G-protein signaling cascades, for example in olfaction (see for example Reisert & Reingruber, 2019).

Key Points Summary.

• Most vertebrate eyes have rod and cone photoreceptors, which use a signal transduction pathway consisting of many biological processes to transform light into an electrical response.

• We dissect and quantify the contribution of each of these processes to the photoreceptor light response by using a novel method of analysis that provides an analytical solution for the entire time course of the dim-flash light response.

• We find that the shape of the light response is exclusively controlled by deactivation parameters. Activation parameters scale this shape and alter response amplitude.

• We show that that rising phase of the response depends on Ca²⁺ feedback, and we identify the deactivation parameters that control the recovery phase of the response.

• We devise new methods to extract values for deactivation and activation parameters from a separate analysis of response shape and response amplitude.