Multi-modal latent space inducing ensemble SVM classifier for early dementia diagnosis with neuroimaging data

Abstract

Fusing multi-modality data is crucial for accurate identification of brain disorder as different modalities can provide complementary perspectives of complex neurodegenerative disease. However, there are at least four common issues associated with the existing fusion methods. First, many existing fusion methods simply concatenate features from each modality without considering the correlations among different modalities. Second, most existing methods often make prediction based on a single classifier, which might not be able to address the heterogeneity of the Alzheimer’s disease (AD) progression. Third, many existing methods often employ feature selection (or reduction) and classifier training in two independent steps, without considering the fact that the two pipelined steps are highly related to each other. Forth, there are missing neuroimaging data for some of the participants (e.g., missing PET data), due to the participants’ “no-show” or dropout. In this paper, to address the above issues, we propose an early AD diagnosis framework via novel multi-modality latent space inducing ensemble SVM classifier. Specifically, we first project the neuroimaging data from different modalities into a latent space, and then map the learned latent representations into the label space to learn multiple diversified classifiers. Finally, we obtain the more reliable classification results by using an ensemble strategy. More importantly, we present a Complete Multi-modality Latent Space (CMLS) learning model for complete multi-modality data and also an Incomplete Multi-modality Latent Space (IMLS) learning model for incomplete multi-modality data. Extensive experiments using the Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset have demonstrated that our proposed models outperform other state-of-the-art methods.

1. Introduction

Alzheimer’s Disease (AD) is the most common form of dementia, which is characterized as a genetically complex and irreversible neurodegenerative disorder and often found in people over 65 years old (Alzheimer’s, 2015). Recent studies have demonstrated that there are about 26.6 million AD patients worldwide, and 1 out of 85 people will be affected by AD by 2050 (Palmer, 2011). Since there is no cure for AD, the timely and accurate diagnosis of AD and its prodromal stage (i.e., Mild Cognitive Impairment (MCI)) is clinically important (Zhou et al., 2019a; Lu et al., 2018; Long et al., 2018; Thung et al., 2018; Zhou et al., 2019c; Long, 2016; Wee et al., 2014).

Neuroimaging techniques, such as magnetic resonance imaging (MRI) (Wolz et al., 2012; Chen et al., 2019; Vemuri et al., 2008; Liu et al., 2018; Fan et al., 2019; Lian et al., 2018) and positron emission tomography (PET) (Herholz et al., 2002; Fan et al., 2008), are powerful tools that are able to measure different yet complementary information, and thus provide unprecedented opportunities for dementia study. As neuroimaging data are very high-dimensional, existing methods often use region-of-interest (ROI) based features, instead of the original voxel based features, for analysis (Chaves and et al., 2009; Magnin et al., 2009; Tong et al., 2014). In this context, many machine learning algorithms have been developed to utilize neuroimaging data for AD diagnosis. A conventional machine learning framework concatenates these features from multiple modalities into a long vector, and subsequently employs feature selection and classification. While this framework is easy to implement, it ignores many prior knowledge of the data that could be beneficial to the study. To exploit the correlation among multi-modalities, some studies have been developed to fuse the complementary information from multi-modality data for accurate AD diagnosis. For example, Zhu et al. (2016b) use Canonical Correlation Analysis (CCA) to first transform multi-modality data into a common CCA space, and then use the transformed features for classification. Hinrichs et al. (2009) use Multiple Kernel Learning (MKL) to fuse multi-modality data by learning an optimal linearly combined kernels for classification. Zhang et al. (2012) introduce a multi-modality multi-task learning based method by jointly using clinical scores and label information. A multi-task learning based feature selection method with inter-modality relationship preserving constraint is proposed in Liu et al. (2014).

Currently, some multi-modality fusion studies first employ feature selection or multi-modality fusion, and then the selected or fusion features are fed to train a classifier (e.g., Support Vector Machine (SVM)) (Zhu et al., 2016b; Zhang et al., 2012; Lei et al., 2017). It is a popular two-step strategy in AD diagnosis framework. However, the feature selection in the first step may not be the best to the classifier training in the second step, thus this separated pipeline could degrade the final classification performance. Moreover, some existing methods (Zhu et al., 2016b; Lei et al., 2017) often focus on learning a single classifier (e.g., SVM classifier) for AD diagnosis, which is difficult to address the heterogeneity of complex brain disorder. As in many recognition and classification tasks, ensemble approaches can obtain more promising performance (Freund and Schapire, 1997), which can reduce the variance of the base classifiers. More importantly, ensemble classifiers can obtain more promising performance if they have different decision boundaries, allowing for more flexibility through imposing diversity among the all models (Brown et al., 2005). Thus, to deal with this disease heterogeneity issue, it is more reasonable to train a set of diversified classifiers and ensemble them (i.e., instead of training a single classifier), which has been shown effective in previous studies (Freund and Schapire, 1997; Brown et al., 2005; Liu et al., 2016).

In addition, it is unavoidable to have missing data, i.e., some subjects have missing PET in the Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset, due to the participants’ no show-up or dropout. Generally, there are two approaches to deal with missing data issue (Thung et al., 2014), i.e., (1) discard the subjects with missing data, and (2) impute the missing data. Most existing approaches discard subjects with at least one missing modality and perform disease identification based on the remainder of the subjects with complete multi-modalities. In this case, this approach discards a lot of information that is potentially useful, which could not learn a reliable diagnostic model. Besides, imputation methods estimate missing values based on available data using specific imputation techniques, e.g., expectation maximization (EM) (Schneider, 2001), singular value decomposition (SVD) (Hastie et al., 2015), and matrix completion method (Thung et al., 2014). However, the effectiveness of these approaches can be affected by imputation artifacts. Moreover, several recently developed multi-view learning methods (Yuan et al., 2012; Liu et al., 2017) and multi-task learning based methods (Thung et al., 2014) demonstrate greater accuracies in AD diagnosis.

In general, most of the existing approaches suffer from the following challenges. First, some traditional multi-modal fusion methods simply concatenate features from each modality without considering the correlations among different modalities. Second, existing methods often make prediction based on a single classifier, which could not be able to address the heterogeneity of the Alzheimer’s disease (AD) progression. Third, most existing methods often employ feature selection (or reduction) and classifier training in two independent steps, without considering the fact that these two pipelined steps are highly related to each other. Forth, the missing data issue is commonly existing in multi-modality setting, thus, how to make use of all available subjects to train a more reliable model is critical for early AD diagnosis.

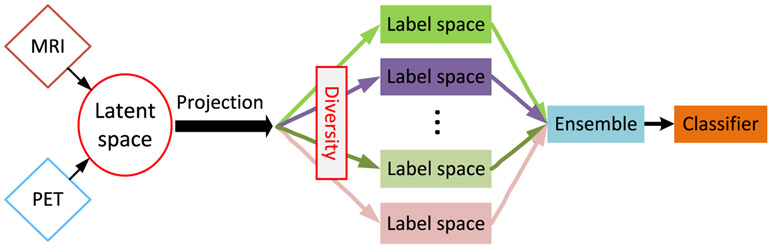
To this end, we propose a novel AD diagnosis framework via multi-modal latent space inducing ensemble SVM classifier, which can seamlessly perform latent space learning and ensemble of diversified classifiers learning in a unified framework (as shown in Fig. 1). Specifically, we first project neuroimaging features from different modalities (i.e., MRI and PET in our study) into a common latent space, to exploit the cross-modality correlations while learning their latent representations. Besides, to address the heterogeneity of AD progression, we learn multiple diversified classifiers by mapping the latent representations into multiple label spaces, and use an ensemble strategy to obtain a more robust classification result. Furthermore, we integrate latent space learning and classifier training into a unified framework, so that all the components in the framework can work together to achieve a better AD diagnostic model. More importantly, our proposed framework can address missing data issue and make use of all samples to train a reliable prediction model. We conducted experiments on the ADNI database, and the results have demonstrated the superiority of the proposed method over state-of-the-art methods.

Fig. 1.

The flow diagram of our proposed AD diagnosis framework. We project multi-modality data (i.e., MRI and PET in our case) into a common latent space to exploit the correlation among multi-modal neuroimaging data. Then, multiple classifiers with diversity constraint are trained and an ensemble strategy is used to obtain the final classification results.

Compared with previous AD diagnostic models, the main contributions of our work are four-fold, as described below.

• Our proposed AD diagnosis method seamlessly integrates the latent representations learning and multiple diversified classifiers learning into a unified framework, while previous methods often employ feature selection and classifier training in two separate steps. Thus, the features selected would be optimal to the classifier in our proposed method.

• We learn common latent representation for neuroimaging data from different modalities to better exploit the intrinsic correlations among them. In contrast, previous methods often fuse features from different modalities in their original forms and ignore the correlations among different modalities.

• Unlike existing diagnosis methods that often train a single classifier for model prediction, our proposed method learns multiple diversified classifiers and obtain the final result via an ensemble strategy. In this way, our model can better address the heterogeneity of neurodegenerative disease.

• Last but not least, our proposed method is also able to handle the missing data issue. Specifically, when a subject is associated with one or more missing modalities, instead of excluding this subject from the analysis, our model will project only the available modalities into the latent space. In this way, our proposed method will make use of all available subjects to train a more reliable prediction model. In addition, our method does not need to impute the missing data, which may introduce unnecessary noise into the data that subsequently reduces the classification performance.

A preliminary version of complete multi-modal latent space learning framework was presented in Zhou et al. (2018). This paper extends it and proposes a novel incomplete multi-modal latent space learning framework for incomplete multi-modal datset. We implement disease diagnosis on both complete and incomplete multi-modal dataset in this study.

The rest of this paper is organized as follows. Section 2 describes the materials and neuroimage preprocessing steps. Section 3 gives the details of the proposed approach. The experimental results are reported in Section 4. Finally, Section 5 concludes this paper.

2. Materials and neuroimage preprocessing

In this study, we used data from the public ADNI database (Jack, 2008) for performance evaluation. The ADNI dataset had been launched in 2003 by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, the Food and Drug Administration, private pharmaceutical companies and nonprofit organizations with a five-year public private partnership. The main goal of ADNI is to investigate if MRI, PET and other biological markers, together with clinical and neuropsychological assessments can be combined to measure the progression of AD −.

2.1. Subjects

In this study, we used 774 subjects from ADNI-1, including 226 normal controls (NC), 362 MCI and 186 AD subjects. In addition, there are only 379 subjects with complete MRI and PET data, including 101 NC, 185 MCI, and 93 -AD. Moreover, 362 MCI subjects included 205 stable MCI (sMCI) subjects and 157 progressive MCI (pMCI) subjects. In this study, we defined progressive MCI (pMCI) subjects as MCI subjects that will progress to AD within 24 months, while sMCI subjects as MCI subjects that remain stable at all available time points (0 – 96 months). The demographic and clinical information of all subjects used in this study are summarized in Table 1.

Table 1.

Demographic information of the used subjects (MMSE: mini-mental state examination).

	Female / male	Education	Age	MMSE
NC	108 / 118	16.0 ± 2.9	75.8 ± 5.0	29.1 ± 1.0
sMCI	68 / 137	15.7 ± 3.1	75.1 ± 7.6	27.4 ± 1.7
pMCI	62 / 95	15.6 ± 2.9	74.7 ± 6.9	26.6 ± 1.7
AD	87 / 99	14.7 ± 3.1	75.3 ± 7.6	23.3 ± 2.0

2.2. Neuroimage preprocessing

In this study, we downloaded ADNI preprocessed 1.5T T1-weighted MR images from the ADNI website.¹ All structural MR images were acquired from 1.5T scanners. These MR images were reviewed for quality and automatically corrected for spatial distortion, which were caused by gradient nonlinearity and B1 field inhomogeneity. Further, all PET images (i.e., FDG-PET scans) were collected from a variety of scanners with protocols individualized for each scanner. Following previous works (Zhang et al., 2012; Xue et al., 2006), we further processed the MR images using a standard pipeline including the following steps: (1) anterior commissure-posterior commissure (AC-PC) correction by using MI-PAV software,² (2) intensity inhomogeneity correction by using N3 algorithm (Sled et al., 1998), (3) brain extraction on all structural MR images by using a robust skull-stripping method (Wang et al., 2014), (4) cerebellum removal based on based on registration and intensity inhomogeneity correction, (5) tissues segmentation by using FAST method in FSL package (Zhang et al., 2001), obtaining three different tissues (i.e., white matter (WM), gray matter (GM), and cerebrospinal fluid), and (6) registration to a template (Kabani, 1998; Wu et al., 2006) by using HAMMER algorithm (Shen and Davatzikos, 2002), and then dissecting images into 93 regions-of-interest (ROIs) by labeling them based on the Jacob template (Kabani, 1998). In detail, we computed the GM tissue volume of each ROI in the labeled image, and then normalized them with the intracranial volume, thus the ROI-based feature was used to represent each subject. Besides, for each subject, we first aligned PET images to their corresponding T1-weighted MR images by using affine registration, and then computed the average PET intensity value of each ROI as PET feature. Thus, in our study, we have 93-dimensional ROI-based features from both the MRI and PET data, respectively.

3. Proposed method

3.1. Preliminary

An SVM (Vapnik, 2013) is a discriminative classifier formally defined by a separating hyperplane, which has been widely used in many fields such as pattern recognition and machine learning. Generally, the primal SVM can be formulated as

$$\underset{\mathbf{w},b}{\text{min}}\sum _{i=1}^{N}f\left(y_i,{\mathbf{x}}_i^{\mathsf{T}}\mathbf{w}+b\right)+\lambda \Psi (\mathbf{w}),$$ (1)

where f( · ) is a penalty function, w and b are the weight vector and bias, respectively, (x_i, y_i) is the i-th sample of input-output pair, (${\mathbf{x}}_i^{\mathsf{T}}\mathbf{w}+b$) is the predicted output for the i-th sample, N is the number of samples, and Ψ(w) is a regularizer term imposed on w, Besides, λ is a non-negative parameter used to balance between the data fitting loss term and the regularizer term.

3.2. Common latent space learning for multi-modality data

For a multi-modality data set X = (X₁, … , X_M}, where ${\mathbf{X}}_m\in {\mathbb{R}}^{d_m\times N}$ denotes the feature matrix for the mth modality with d_m features and N subjects, and M denotes the number of modalities, we exploit the correlations among different modalities by projecting different modalities into a common latent space, as given below:

$$\underset{{\mathbf{V}}_m,\mathbf{H}}{\text{min}}\sum _{m=1}^M\left(\Vert {\mathbf{V}}_m^{\mathsf{T}}{\mathbf{X}}_m-\mathbf{H}{\Vert }_F^2+\gamma \Vert {\mathbf{V}}_m{\Vert }_{2,1}\right),$$ (2)

where $\mathbf{H}\in {\mathbb{R}}^{h\times N}$ denotes the common latent representation, ${\mathbf{V}}_m\in {\mathbb{R}}^{d_m\times h}$ denotes the projection matrix that project X_m to H, γ denotes the regularization parameter, and h denotes the dimension of the latent space. The ℓ_2,1-norm regularizer (i.e., $\Vert {\mathbf{V}}_m{\Vert }_{2,1}={\sum }_{i=1}^{d_m}\sqrt{{\sum }_{j=1}^h{v}_{m,ij}^2}$) has been widely applied to multi-task feature learning (Wang et al., 2017; Zhou et al., 2019b; Zhang et al., 2018; Thung and Wee, 2018), and we use it to collectively penalize the coefficients in each row of V_m, and enforce row-wise sparsity in V_m. Consequently, the ℓ_2,1-norm on V_m encourages the selection of useful (ROI-based) features from X_m during the latent space learning in Eq. (2). In the next section, we will give the details of our proposed AD diagnosis model by integrating the latent space learning and classifier training into a unified framework.

3.3. Proposed dementia diagnosis framework

Combining Eqs. (1) and (2), and using the latent features instead of the original features for classifier training, we have a unified framework of latent space learning and classifier training, as given by

$$\begin{gathered} \underset{{\mathbf{V}}_m,\mathbf{w},\mathbf{H},b}{\text{min}}\sum _{i=1}^{N}f\left(y_{i,}{\mathbf{h}}_i^{\mathsf{T}}\mathbf{w}+b\right)+\lambda \Psi (\mathbf{w}) \\ +\beta \sum _{m=1}^M\Vert {\mathbf{V}}_m^{\mathsf{T}}{\mathbf{X}}_m-\mathbf{H}{\Vert }_F^2+\gamma \sum _{m=1}^M\Vert {\mathbf{V}}_m{\Vert }_{2,1}, \end{gathered}$$ (3)

where $\mathbf{H}=[{\mathbf{h}}_1,{\mathbf{h}}_2,\dots ,{\mathbf{h}}_N]\in {\mathbb{R}}^{h\times N}$ with ${\mathbf{h}}_i\in {\mathbb{R}}^{h\times 1}$ denoting the latent representation of the ith sample (i.e., the ith column of H ), and y_i ∈ {−1, 1} is the corresponding label for the ith sample. Besides, λ, β and γ are the regularization parameters that control the contribution of each term in Eq. (3). If we use hinge loss function for f ( · ), the first term in Eq. (3) is given as

$$\sum _{i=1}^{N}f\left(y_{i,}{\mathbf{h}}_i^{\mathsf{T}}\mathbf{w}+b\right)=\sum _{i=1}^N{\left(1-({\mathbf{h}}_i^{\mathsf{T}}\mathbf{w}+b)y_i\right)}_{+}^p,$$ (4)

where operation (·)₊ is defined as (x)₊ := max (x, 0), which returns x if it is non-negative, and returns zero otherwise. Besides, p is a constant, which is normally set to value 1 or 2 (Guo et al., 2017).

Eq. (3) consists of only a single SVM classifier with hinge loss function, which may not be able to address the heterogeneity of AD progression. Previous works such as Freund and Schapire (1997), Brown et al. (2005) have indicated that the ensemble of multiple classifiers could be a better and more reliable prediction model. Thus, in this study, following the work in Guo et al. (2017), we extend the single classifier training in Eq. (3) into the following framework of multiple classifiers training, given as

$$\begin{gathered} \underset{{\mathbf{V}}_m,\mathbf{W},\mathbf{H},\mathbf{b}}{\text{min}}\sum _{c=1}^C\sum _{i=1}^N{\left(1-({\mathbf{h}}_i^{\mathsf{T}}{\mathbf{w}}_c+b_c)y_i\right)}_{+}^p+\lambda \Psi (\mathbf{W}) \\ +\beta \sum _{m=1}^M\Vert {\mathbf{V}}_m^{\mathsf{T}}{\mathbf{X}}_m-\mathbf{H}{\Vert }_F^2+\gamma \sum _{m=1}^M\Vert {\mathbf{V}}_m{\Vert }_{2,1}, \end{gathered}$$ (5)

where $\mathbf{W}=[{\mathbf{w}}_1,{\mathbf{w}}_2,\dots ,{\mathbf{w}}_C]\in {\mathbb{R}}^{h\times C}$ is the weight matrix with each column (i.e., w_i) denoting the weight vector for one classifier, $\mathbf{b}=[b_1,b_2,\dots ,b_C]\in {\mathbb{R}}^{C\times 1}$ is the corresponding bias vector, and C is the number of classifiers. By using the model in Eq. (5), we can learn multiple classifiers, and obtain the final result by devising an ensemble strategy.

However, if there is no constraint on the weight matrix W that encourages diversity of classifiers, the performance of ensemble strategy will be limited. For example, if we choose $\Psi (\mathbf{W})=\frac{1}{2}\Vert \mathbf{W}{\Vert }_F^2$, the weight vectors of the classifiers (i.e., columns in W) may end up similar to each other, thus defeating the purpose of ensembling the results of multiple classifiers. To have a more meaningful ensemble classifier that can better address the heterogeneity of the AD progression, we would like to learn a set of diversified classifiers that have weight vectors (e.g., W_i, w_j) very different from each other. There are many ways to enforce diversity for a set of classifiers (Brown et al., 2005), but we choose method described in Guo et al. (2017) for its good performance. That is, we enforce the diversity of classifiers by minimizing the following function between each pair of classifier weight vectors, i.e., {min ∥w_i ⊙ w_j∥₀ = min ∑_k(w_i(k) · w_j(k) ≠ 0), i ≠ j), where ⊙ denotes Hadamard product, ∥ · ∥₀ denotes ℓ₀-norm, and w_i(k) denotes the k th element in w_i. This minimization will enforce the column weight vectors (e.g., w_i and w_j, i ≠ j) in W to be as orthogonal as possible, so that the classifiers learnt would be diversified. However, as it is difficult to directly optimize the ℓ₀-norm problem, we choose to minimize the relaxed exclusivity function instead, i.e., {min ∥w_i ⊙ w_j∥₁ = min ∑_k∣w_i(k)∣ · ∣w_j(k)∣, i ≠ j}, where ∣ · ∣ denotes the absolute operator. To guarantee the convexity of the regularizer Ψ(W), we combine the relaxed exclusivity function and the Frobenius norm of W to obtain the following regularizer (Guo et al., 2017):

$$\begin{gathered} \Psi (\mathbf{W})=\frac{1}{2}\Vert \mathbf{W}{\Vert }_F^2+\sum _{i,j\ne i}\Vert {\mathbf{w}}_i\odot {\mathbf{w}}_j{\Vert }_1 \\ =\frac{1}{2}\sum _{k=1}^h{\left(\sum _{c=1}^C\mid {\mathbf{w}}_c(k)\mid \right)}^2 \\ =\frac{1}{2}\Vert {\mathbf{W}}^{\mathsf{T}}{\Vert }_{1,2}^2. \end{gathered}$$ (6)

The derivation of Eq. (6) is discussed in details in Guo et al. (2017). In summary, we use the $\text{min}\frac{1}{2}\Vert {\mathbf{W}}^{\mathsf{T}}{\Vert }_{1,2}^2$ as a regularizer for W to encourage diversity of classifiers in our framework.

Finally, by substituting Eq. (6) into Eq. (5), we obtain a unified framework of latent space learning and multiple diversified classifiers training, where the final objective function is given as

$$\begin{gathered} \underset{{\mathbf{V}}_m,\mathbf{W},\mathbf{H},\mathbf{b}}{\text{min}}\sum _{c=1}^C\sum _{i=1}^N{\left(1-({\mathbf{h}}_i^{\mathsf{T}}{\mathbf{w}}_c+b_c)y_i\right)}_{+}^p+\frac{\lambda }{2}\Vert {\mathbf{W}}^{\mathsf{T}}{\Vert }_{1,2}^2 \\ +\beta \sum _{m=1}^M\Vert {\mathbf{V}}_m^{\mathsf{T}}{\mathbf{X}}_m-\mathbf{H}{\Vert }_F^2+\gamma \sum _{m=1}^M\Vert {\mathbf{V}}_m{\Vert }_{2,1}. \end{gathered}$$ (7)

Note that this framework assumes that all samples consist of complete multi modality data, thus we call our proposed method in Eq. (7) as Complete Multi-modal Latent Space (CMLS) learning model.

Remarks. In CMLS model, 1) each modality in multi-modality data is projected into a common latent space to exploit the correlations among different modalities; 2) the common latent representations are used to train multiple diversified classifiers to address heterogeneity issue of AD progression, so that an ensemble strategy can be used to improve the classification performance.

However, the applicability of the CMLS model is limited if it can only use samples with complete multi-modality data, as missing data is ubiquitous in multi-modality dataset. To address the missing data issue, we extend our framework in Eq. (7) into an Incomplete Multi-modal Latent Space (IMLS) learning model as

$$\begin{gathered} \underset{{\mathbf{V}}_m,\mathbf{W},\mathbf{H},\mathbf{b}}{\text{min}}\sum _{c=1}^C\sum _{i=1}^N{\left(1-({\mathbf{h}}_i^{\mathsf{T}}{\mathbf{w}}_c+b_c)y_i\right)}_{+}^p+\frac{\lambda }{2}\Vert {\mathbf{W}}^{\mathsf{T}}{\Vert }_{1,2}^2 \\ +\beta \sum _{m=1}^M\Vert {\mathbb{P}}_{{\mathbf{O}}_m}(\mathbf{H}-{\mathbf{V}}_m^{\mathsf{T}}{\mathbf{X}}_m){\Vert }_F^2+\gamma \sum _{m=1}^M\Vert {\mathbf{V}}_m{\Vert }_{2,1}, \end{gathered}$$ (8)

where ${\mathbb{P}}_{{\mathbf{O}}_m}(\mathbf{X})=\mathbf{X}\cdot {\mathbf{O}}_m$ is a mask operation that filters out missing data component (indicated by O_m) in X, and O_m is a diagonal matrix with its ith diagonal element indicating the existence of the mth modality data for the ith subject, i.e., value of 1 when we have the data available, and 0 otherwise. For the convenience of our readers to comprehend the proposed models in Eqs. (7) and (8), we have listed the main notations used in Table 2.

Table 2.

The main notations used in Eqs. (7) and (8).

Notation	Size	Description
Xm	dm × N	Feature matrix for the mth modality.
Vm	dm × h	Projection matrix for the mth modality.
H	h × N	Latent representation matrix.
W	h × C	Weight matrix for SVM classifiers, each column representing a classifier.
b	C × 1	Bias vector for SVM classifiers, each element representing the bias of a classifier.
Om	N × N	Filter matrix for the mth modality. The value of its ith diagonal element indicates the availability of the mth modality data for the i-th subject.
dm	–	Number of features for the mth modality data.
C	–	Number of classifiers.
N	–	Number of subjects (or samples).
h	–	Feature dimension in the latent feature representation.
M	–	Number of modalities in multi-modality data.
λ, β, γ	–	Regularization parameters

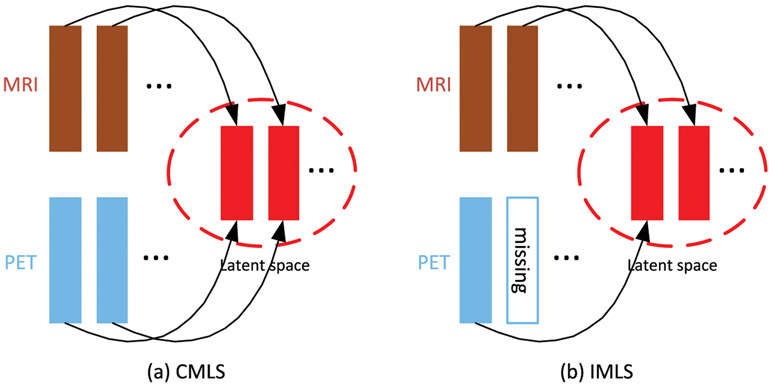
Remarks. As shown in Fig. 2, it is worth noting that our IMLS model addresses the missing data issue by making use of all the available samples to train the prediction model. When a sample has the complete multi-modality data, our IMLS model will project all the modality data into a latent space; when one or more modalities are missing, our IMLS model will project only the available modality (or modalities) into the latent space.

Fig. 2.

Comparison of CMLS and IMLS models. Both CMLS and IMLS models project different modalities of multi-modality data into a common latent space, but CMLS model is only applicable if the multi-modality data is complete, while IMLS model is applicable even when the multi-modality data is incomplete. As shown in the figure, IMLS model only projects the existing modality into the common latent space.

3.4. Optimization

The problems in Eqs. (7) and (8) can be solved via the Augmented Lagrange Multiplier (ALM) (Lin et al., 2011) algorithm, which alternatively optimizes the variables, i.e., optimizing one variable at a time with the other variables being fixed. We first provide the details for solving our CMLS model in Eq. (7). With consideration of $1-({\mathbf{h}}_i^{\mathsf{T}}{\mathbf{w}}_c+b_c)y_i=y_i{y}_i-({\mathbf{h}}_i^{\mathsf{T}}{\mathbf{w}}_c+b_c)y_i=y_i(y_i-({\mathbf{h}}_i^{\mathsf{T}}{\mathbf{w}}_c+b_c))$, we introduce an auxiliary variable $z_i^c≔y_i-({\mathbf{h}}_i^{\mathsf{T}}{\mathbf{w}}_c+b_c)$. Besides, we also introduce an auxiliary matrix Q = W to make the problem separable. Subsequently, we have the following equivalent problem

$$\begin{gathered} \underset{{\mathbf{V}}_m,\mathbf{W},\mathbf{H},\mathbf{Q},\mathbf{Z},\mathbf{b}}{\text{min}}(\mathbf{Y}\odot \mathbf{Z}{)}_{+}^p+\frac{\lambda }{2}\Vert {\mathbf{W}}^{\mathsf{T}}{\Vert }_{1,2}^2 \\ +\beta \sum _{m=1}^M\Vert {\mathbf{V}}_m^{\mathsf{T}}{\mathbf{X}}_m-\mathbf{H}{\Vert }_F^2+\gamma \sum _{m=1}^M\Vert {\mathbf{V}}_m{\Vert }_{2,1}, \\ s.t\mathbf{Q}=\mathbf{W},\mathbf{Z}=\mathbf{Y}-({\mathbf{H}}^{\mathsf{T}}\mathbf{Q}+1_N{\mathbf{b}}^{\mathsf{T}}), \end{gathered}$$ (9)

where $\mathbf{Y}\in {\mathbb{R}}^{N\times C}$ is the matrix of ground-truth labels with each of its column equivalent to the vector of ground-truth labels for N samples, 1_N is an all-one column vector of dimension N, and $\mathbf{Z}\in {\mathbb{R}}^{N\times C}$ is the corresponding matrix of prediction differences between the ground-truth labels and the label predictions from diversified classifiers.

The above objective function can be solved by minimizing the following ALM problem

$$\begin{gathered} \mathcal{L}({\mathbf{V}}_m,\mathbf{W},\mathbf{H},\mathbf{Q},\mathbf{Z},\mathbf{b},{\mathbf{P}}_1,{\mathbf{P}}_2) \\ =(\mathbf{Y}\odot \mathbf{Z}{)}_{+}^p+\frac{\lambda }{2}\Vert {\mathbf{W}}^{\mathsf{T}}{\Vert }_{1,2}^2 \\ +\beta \sum _{m=1}^M\Vert {\mathbf{V}}_m^{\mathsf{T}}{\mathbf{X}}_m-\mathbf{H}{\Vert }_F^2+\gamma \sum _{m=1}^M\Vert {\mathbf{V}}_m{\Vert }_{2,1} \\ +\Phi ({\mathbf{P}}_1,\mathbf{Q}-\mathbf{W})+\Phi \left({\mathbf{P}}_2,\mathbf{Z}-\mathbf{Y}+\left({\mathbf{H}}^{\mathsf{T}}\mathbf{Q}+1_N{\mathbf{b}}^{\mathsf{T}}\right)\right), \end{gathered}$$ (10)

where $\Phi (\mathbf{P},\Delta )=\frac{\mu }{2}\Vert \Delta {\Vert }_F^2+\langle \mathbf{P},\Delta \rangle$, with ⟨ · , · ⟩ denoting the matrix inner product, μ is a positive penalty scalar, and P₁ and P₂ are Lagrangian multipliers. To find a minimal point for $\mathcal{L}$, we update one variable while keeping the other variables fixed. Thus, we split the above optimization problem into the following multiple subproblems.

V_m -subproblem: The associated optimization problem with respect to Vm can be written as

$$\underset{{\mathbf{V}}_m}{\text{min}}\beta \Vert {\mathbf{V}}_m^{\mathsf{T}}{\mathbf{X}}_m-\mathbf{H}{\Vert }_F^2+\gamma \Vert {\mathbf{V}}_m{\Vert }_{2,1}.$$ (11)

We can solve problem (11) by taking the derivative of the objective function with respect to V_m, and set it to zero (Nie et al., 2010; 2016). We first compute the derivative of the term ∥V_m∥_{2, 1} w.r.t. V_m, i.e., $\frac{\partial \Vert {\mathbf{V}}_m{\Vert }_{2,1}}{\partial {\mathbf{V}}_m}=\Lambda {\mathbf{V}}_m$, where $\Lambda \in {\mathbb{R}}^{d_m\times d_m}$ is a diagonal matrix with its ith diagonal element given as ${\Lambda }_{ii}=\frac{1}{2\Vert {\mathbf{V}}_{m,i:}{\Vert }_2^2}$, and V_m,i: denotes the ith row of V_m. Then, taking the derivative of the objective function in Eq. (11) and set it to zero, we have the following close-form solution

$${\mathbf{V}}_m={\left({\mathbf{X}}_m{\mathbf{X}}_m^{\mathsf{T}}+\frac{\gamma }{\beta }\Lambda \right)}^{-1}{\mathbf{X}}_m{\mathbf{H}}^{\mathsf{T}}.$$ (12)

Note that, Λ is dependent on V_m, thus we can use an iterative optimization step to update V_m and Λ until convergence.

W -subproblem: When other variables are fixed except W, the minization of objective function in Eq. (10) is equivalent to

$$\underset{\mathbf{W}}{\text{min}}\frac{\lambda }{2}\Vert {\mathbf{W}}^{\mathsf{T}}{\Vert }_{1,2}^2+\Phi ({\mathbf{P}}_1,\mathbf{Q}-\mathbf{W}).$$ (13)

The optimization problem in Eq. (13) can be split into a set of subproblems. We optimize each row of W, i.e., W_i:, by solving

$$\underset{{\mathbf{W}}_{i:}}{\text{min}}\frac{\lambda }{2}{\mathbf{W}}_{i:}\mathbf{G}{\mathbf{W}}_{i:}^{\mathsf{T}}+\Phi ({\mathbf{P}}_{1,i:},{\mathbf{Q}}_{i:}-{\mathbf{W}}_{i:}),$$ (14)

where $\mathbf{G}≔\text{diag}([\frac{\Vert {\mathbf{W}}_{\mathrm{i}:}{\Vert }_1}{\mid {\mathbf{W}}_{\mathrm{i}:}(1)\mid +\xi },\dots ,\frac{\Vert {\mathbf{W}}_{\mathrm{i}:}{\Vert }_1}{\mid {\mathbf{w}}_{\mathrm{i}:}(\mathrm{C})\mid +\xi }])$, and ξ is a small constant to avoid zero denominator. Then, an iterative strategy can be adopted to update W_i: and G. When G is fixed, we update W_i: by using

$${\mathbf{W}}_{i:}=(\mu {\mathbf{Q}}_{i:}+{\mathbf{P}}_{1,i:})(\lambda \mathbf{G}+\mu \mathbf{I}{)}^{-1}.$$ (15)

H -subproblem: Dropping all unrelated terms with respect to H yields

$$\begin{gathered} \underset{\mathbf{H}}{\text{min}}\beta \sum _{m=1}^M\Vert {\mathbf{V}}_m^{\mathsf{T}}{\mathbf{X}}_m-\mathbf{H}{\Vert }_F^2 \\ +\Phi \left({\mathbf{P}}_2,\mathbf{Z}-\mathbf{Y}+({\mathbf{H}}^{\mathsf{T}}\mathbf{Q}+1_N{\mathbf{b}}^{\mathsf{T}})\right). \end{gathered}$$ (16)

Taking the derivative of the above objective with respect to H and setting it to zero, we get the following close-form solution

$$\begin{gathered} \mathbf{H}={\left(\frac{2\beta }{\mu }M\mathbf{I}+{\mathbf{QQ}}^{\mathsf{T}}\right)}^{-1} \\ \times \left(\frac{2\beta }{\mu }\sum _{m=1}^M{\mathbf{V}}_m^{\mathsf{T}}{\mathbf{X}}_m-\mathbf{Q}(\mathbf{Z}-\mathbf{Y}+1_N{\mathbf{b}}^{\mathsf{T}}+{\mathbf{P}}_2∕\mu {)}^{\mathsf{T}}\right), \end{gathered}$$ (17)

where I is an identity matrix.

Q -subproblem: The associated optimization problem with respect to Q can be written as

$$\underset{\mathbf{Q}}{\text{min}}\Phi ({\mathbf{P}}_1,\mathbf{Q}-\mathbf{W})+\Phi ({\mathbf{P}}_2,\mathbf{Z}-\mathbf{Y}+({\mathbf{H}}^{\mathsf{T}}\mathbf{Q}+1_N{\mathbf{b}}^{\mathsf{T}})).$$ (18)

Taking the derivative of the above objective with respect to Q and setting it to zero, we obtain the following close-form solution

$$\mathbf{Q}=(\mathbf{I}+{\mathbf{HH}}^{\mathsf{T}}{)}^{-1}(\mathbf{W}-{\mathbf{P}}_1∕\mu -\mathbf{H}(\mathbf{Z}-\mathbf{Y}+1_N{\mathbf{b}}^{\mathsf{T}}+{\mathbf{P}}_2∕\mu )),$$ (19)

where I is an identity matrix.

Z -subproblem: When other variables are fixed except Z, the minimization of objective function in Eq. (10) is equivalent to

$$\begin{gathered} \underset{\mathbf{Z}}{\text{min}}(\mathbf{Y}\odot \mathbf{Z}{)}_{+}^p+\Phi ({\mathbf{P}}_2,\mathbf{Z}-\mathbf{Y}+({\mathbf{H}}^{\mathsf{T}}\mathbf{Q}+1_N{\mathbf{b}}^{\mathsf{T}})) \\ \iff \underset{\mathbf{Z}}{\text{min}}(\mathbf{Y}\odot \mathbf{Z}{)}_{+}^p+\frac{\mu }{2}\Vert \mathbf{Z}-\mathbf{S}{\Vert }_F^2, \end{gathered}$$ (20)

where S = Y – H^⊤ Q – 1_Nb^⊤ – P₂/μ. In our study, we set p = 2. Following Guo et al. (2017), we have the following close-form solution

$$\mathbf{Z}=\Omega \odot \mathbf{S}∕\left(1+\frac{2}{\mu }\right)+\overline{\Omega }\odot \mathbf{S},$$ (21)

where Ω := (Y ⊙ S > 0) is an indicator matrix, and $\overline{\Omega }$ is the complementary support of Ω.

b -subproblem: The optimization problem associated with b can be written as

$$\begin{gathered} \underset{\mathbf{b}}{\text{min}}\Phi ({\mathbf{P}}_2,\mathbf{Z}-\mathbf{Y}+({\mathbf{H}}^{\mathsf{T}}\mathbf{Q}+1_N{\mathbf{b}}^{\mathsf{T}})) \\ \iff \underset{\mathbf{b}}{\text{min}}{\Vert \left(\mathbf{Z}-\mathbf{Y}+{\mathbf{H}}^{\mathsf{T}}\mathbf{Q}+{\mathbf{P}}_2∕\mu \right)+1_N{\mathbf{b}}^{\mathsf{T}}\Vert }_F^2. \end{gathered}$$ (22)

The close-form solution for the above problem is given as

$$\mathbf{b}=\frac{1}{N}(\mathbf{Y}-\mathbf{Z}-{\mathbf{H}}^{\mathsf{T}}\mathbf{Q}-{\mathbf{P}}_2∕\mu {)}^{\mathsf{T}}{1}_N.$$ (23)

Multipliers: The multipliers P₁ and P₂ can be updated by

$$\{\begin{array}{c}{\mathbf{P}}_1≔{\mathbf{P}}_1+\mu (\mathbf{Q}-\mathbf{W})\hfill \\ {\mathbf{P}}_2≔{\mathbf{P}}_2+\mu (\mathbf{Z}-\mathbf{Y}+({\mathbf{H}}^{\mathsf{T}}\mathbf{Q}+1_N{\mathbf{b}}^{\mathsf{T}})).\hfill \end{array}\phantom{\}}$$ (24)

We repeat the above updating steps iteratively until convergence. Similar with solving CMLS model, we can also use ALM algorithm to solve our IMLS model efficiently. Note that, the multimodality data set X only consists of these subjects with complete multi-modalities in CMLS, while the multi-modality data set X consists of the all subjects with complete an incomplete multi-modalities in IMLS.

3.5. Prediction

After training our model, we can obtain the ensemble classifier weight w and bias b, which are the average of weight vectors and biases of all the diversified classifiers, respectively, i.e., $\mathbf{w}=\frac{1}{C}{\sum }_{c=1}^C{\mathbf{w}}_c$, and $b=\frac{1}{C}{\sum }_{c=1}^C{b}_c$. Then, for a testing sample x^te with Θ available modalities, its latent representation is computed by averaging the feature projections from each available modality, i.e., ${\mathbf{h}}_{te}=\frac{1}{\mid \Theta \mid }{\sum }_{m\in \Theta }{\mathbf{V}}_m^{\mathsf{T}}{\mathbf{x}}_m^{te}$, where ∣Θ∣ ( ≤ M) denotes the number of modalities in Θ. Finally, the classification label for this test sample is given as ${\mathbf{y}}_{te}=\text{sign}({\mathbf{h}}_{te}^{\mathsf{T}}\mathbf{w}+b)$.

4. Experiments

4.1. Experimental setup

We evaluate the effectiveness of the proposed model by conducting the following three binary classification tasks: i.e., MCI vs. NC, MCI vs. AD, sMCI vs. pMCI classifications. We use classification accuracy (ACC) and Area Under Curve (AUC) as performance metrics to compare our proposed method with the other comparison methods.

We perform 10-fold cross validation for all the methods under comparison, and report the means and standard deviations of the experimental results with ten repetitions. For parameter setting of our method, we determine the regularization parameter values (i.e., (λ, β, γ} ∈ {10⁻⁶ , … , 10³}) and the dimension of the latent space (i.e., h ∈ {10, 20, … , 80}) via an inner cross-validation search on the training data, and searched the number of classifiers C in the range {10, 20, … , 80}. We also use inner cross-validation to select hyper-parameter values for all the comparison methods. Besides, the soft margin parameter of SVM is determined via grid search in the range of {10⁻⁵, 10⁻⁴, … , 10²}.

4.2. Comparison results on complete multi-modality data

Comparison methods.

In this subsection, we compare our proposed method (i.e., CMLS) with other classification methods that use complete multi-modality data, as listed below.

• Baseline method. We include the result for the experiment by using the original features to train a SVM classifier, without performing any feature selection or reduction operation (denoted as “ORI”).

• Feature reduction (or selection) methods. Two methods are compared in this category, namely 1) Principal Component Analysis (PCA) (Jolliffe, 2002), and 2) ℓ₁-norm based feature selection method, which is denoted as “Lasso”. For PCA, we determine the optimal dimensionality of the data based on their respective eigenvalues computed by the generalized eigen-decomposition method according to Zhu et al. (2016a). For Lasso method, we optimize its sparsity parameter (λ) by cross-validating its value in the range of {10⁻⁴, … , 10²}.

• Multi-modality fusion methods. Four multi-modality/view learning methods are compared in this category, i.e., (1) CCA (Hardoon et al., 2004); (2) Multi-view Learning with Adaptive Neighbours (MLAN) method (Nie et al., 2018), which performs clustering/semi-supervised classification and local structure learning simultaneously; (3) Deep Matrix Factorization (DMF) method (Zhao et al., 2017), which conducts deep semi-nonnegative matrix factorization (NMF) to seek a common representation for multi-view clustering task; and 4) Multi-view Dimensionality Co-Reduction (MDCR) method (Zhang et al., 2017), which adopts kernel matching to regularize the dependencies across multiple views and projects each view into a low-dimensional space. For CCA method, we optimize its regularization parameter by cross-validating its value in the range of {10⁻⁴ , … , 10²}. For MLAN method, the parameter λ is determined in the range of {0, 0.02, … , 1}. For DMF method, the parameters β and γ are searched in the range of {10⁻⁵, 10⁻⁴, … , 10²}. For MDCR method, the parameter λ is determined in the range of {0, 0.5, … , 4}. Note that we use MLAN method to directly perform disease prediction, while resorting to SVM classifier to perform disease prediction for the other methods.

• Deep learning based feature representation method. In this category, we compare our CMLS model with Stacked AutoEncoder (SAE) (Suk et al., 2015) method. In SAE, the main parameter is the number of hidden units. Following Suk et al. (2015), we use a three-layer network for multimodality data by using a grid search from [100, 300, 500] – [50, 100] – [10, 20, 30] (bottom-top).

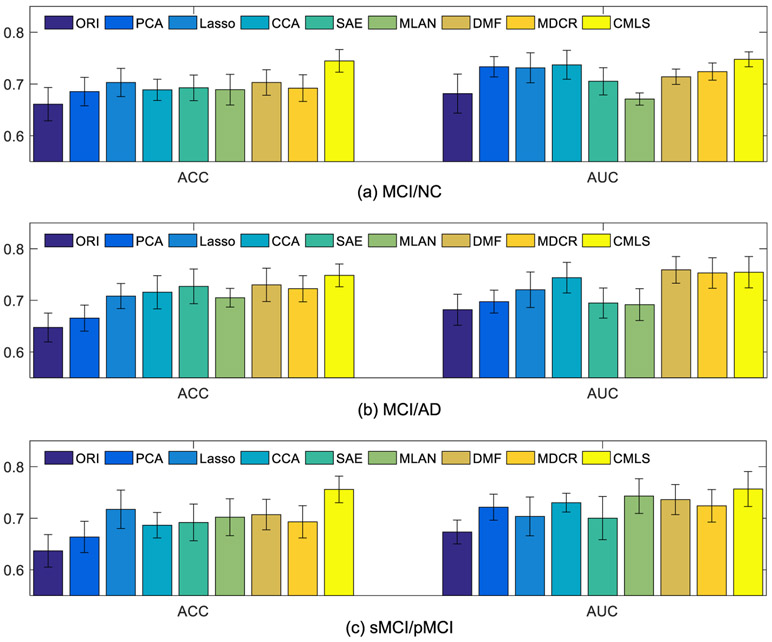
Results.

Fig. 3 shows the comparison results between our proposed method and all the comparison methods. From Fig. 3, it can be observed that our proposed method obtains better classification performance in terms of ACC and AUC than all the comparison methods. Specifically, comparing with the Lasso based feature selection method, which fuses multi-modality data without the consideration of correlations between MRI and PET data, our method performs significantly better. For CCA method, we can see that it obtains relatively better AUC performance. This is possibly because the multimodal fusion can better exploit the complementary information and correlation between different modalities, which led to the improved classification performance. Besides, though the SAE method uses high-level features learned from auto-encoder for classification, it has low performance, probably because it is an unsupervised feature learning method that does not consider label information. In addition, when compared with the three state-of-the-art multi-view learning methods, our method still obtains better performance. It is worth noting that the DMF and MDCR methods use two independent steps for dementia diagnosis, while our method fuses them into a unified framework. Thus, the results also verify the effectiveness of our unified framework.

Fig. 3.

Comparison of classification results using two evaluation metrics (i.e., ACC and AUC) for three classification tasks: (a) MCI/NC, (b) MCI/AD, and (c) sMCI/pMCI, using complete multi-modality dataset.

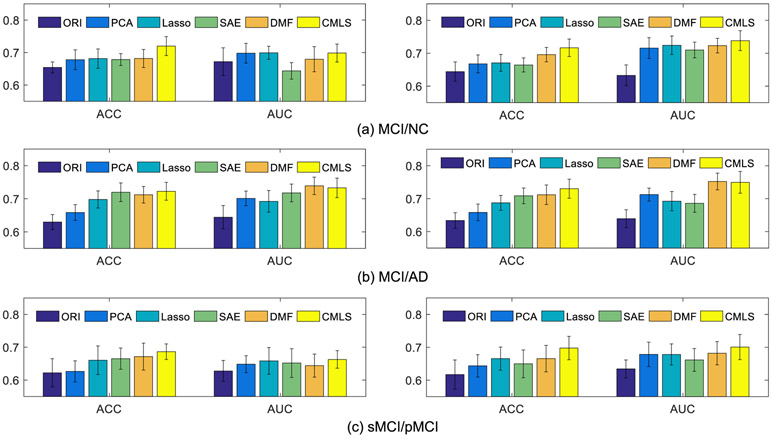
To investigate the benefit of multi-modality fusion, we also shows classification results that used only single modality. Fig. 4 shows the performance comparison of different methods using single modality (i.e., MRI or PET). Note that, multi-modality fusion methods (i.e., CCA, MLAN and MDCR) are excluded in this experiment. From Fig. 4, it can be observed that the degraded version of our method that uses only single modality (i.e., MRI data or PET data) still outperforms other comparison methods. Besides, comparing Figs. 3 and 4, we can see that all the methods perform better when using multi-modality data, if compared with the case of using only single modality data.

Fig. 4.

Comparison of results for three classification tasks, i.e., (a) MCI/NC, (b) MCI/AD, and (c) sMCI/pMCI, using single modality data: MRI (left) and PET (right).

4.3. Comparison results using incomplete multi-modality data

Comparison methods.

In this subsection, we compare our proposed method (i.e., IMLS) with some state-of-the-art methods that are applicable to incomplete multi-modality data, as listed below.

• Data imputation methods, including (1) Zero value imputation, and (2) k-Nearest Neighbor (KNN) (Hastie et al., 1999; Keller et al., 1985). Specifically, for Zero imputation method, the missing values in all samples are filled with zeros. Since all the features are z-normalized (i.e., minus mean and divide by standard deviation) before the imputation process, thus this imputation method is equivalent to filling the missing feature values with the average observed feature values. For KNN imputation method, the missing values in all samples are filled with the weighted mean of the k nearest-neighbor samples. In addition, we search the parameter k in the range of {5, 10, 15, 20, 25}.

• iMSF method (Yuan et al., 2012). This method is a multi-view based method, which first partitions subjects into several views, and a specific classifier is constructed for each view. Then, a structural sparse learning model is employed to select a common set of features among these tasks. There are two versions of iMSF that use different loss functions, i.e., the least square loss (denoted as “iMSF-R”) and the logistic loss (denoted as “iMSF-L”).

• Matrix Shrinkage and Completion method (MSC) (Thung et al., 2014). This method can handle classification problem with incomplete multimodality data. Specifically, MSC method first partitions the combined matrix (e.g., features and targets) into sub-matrices, and each sub-matrix consists of samples with complete features from multi-modality data (i.e., corresponding to a certain combination of modalities) and target outputs. Following that, a multi-task sparse learning framework is used to select informative features and samples. Subsequently, the shrunk combined matrix with missing features and unknown target outputs is imputed, which is realized via low-rank matrix completion algorithm by using a fixed-point continuation method (Ma et al., 2011).

• State-of-the-art incomplete multi-view learning methods, including (1) Doubly Aligned Incomplete Multi-view Clustering (DAIMC) method (Hu and Chen, 2018), and (2) Incomplete Multi-View Weak-label Learning (iMVWL) method (Tan et al., 2018). DAIMC is a clustering method that is designed for incomplete multi-modality data using weighted semi-nonnegative matrix factorization. To apply this method for classification task, we train a SVM classifier using the learned common latent features in DAIMC. On the other hand, iMVWL learns a shared subspace from incomplete views, local label correlations, and a predictor in this subspace, simultaneously.

Results.

Fig. 5 shows the comparison results between our proposed method and all the comparison methods by using incomplete multi-modality data. From Fig. 5, we have the following observations: (1) Our proposed method performs better than all the comparison methods. (2) The MSC method obtains relatively better AUC performance in the three classification tasks. (3) The DAMIC method also obtains relatively better performance in terms of ACC and AUC than other comparison methods. Overall, our method obtains some improvements over other existing methods and several state-of-the-art methods.

Fig. 5.

Comparison of classification results using two evaluation metrics (i.e., ACC and AUC) for three classification tasks: (a) MCI/NC, (b) MCI/AD, and (c) sMCI/pMCI) on the incomplete multi-modal dataset.

Further, to verify the benefit of multi-modality data fusion, Fig. 6 shows the classification results of different methods. Note that, in this comparison experiment, the subjects have complete MRI data but with incomplete PET data, thus, we compare the methods (i.e., ORI, PCA, Lasso, SAE) using complete MRI data with the methods (i.e., MSC and Ours) using complete MRI data and partial PET data. From Fig. 6, it can be observed that our proposed method performs better than other methods in term of ACC on three classification tasks, and also in term of AUC on MCI/NC and sMCI/pMCI task. Besides, it is also worth noting that the MSC obtains relative classification performance than the remaining methods. More importantly, from Figs. 5 to 6, we can see that all methods perform better by combing MRI and PET data than the case of only using MRI data. Thus, these results have verified the effectiveness of our proposed method by fusing incomplete multi-modalities.

Fig. 6.

Comparison of results for three classification tasks (i.e., (a) MCI/NC, (b) MCI/AD, and (c) sMCI/pMCI) using MRI data on the incomplete dataset.

4.4. Ablation study

To validate the effectiveness of the common latent space learning, we conduct an experiment by comparing our method with our degraded method that does not use latent space learning. Specifically, we denote our degraded method as FeatConcate+ensemble, which directly concatenates the original features from the two modalities (MRI and PET), and feed them into the learning framework of multiple diversified classifiers. The comparison results are shown in Fig. 7. From the results, it can be observed that our method with using latent space learning performs better than our model without using it.

Fig. 7.

Comparison between our CMLS model and its degraded counterpart âǣFeatConcate+ensembleâǥ without using common latent space learning.

To verify the effectiveness of ensemble of diversified classifiers, we compare the performance of our proposed methods for the cases of using single classifier (i.e., C = 1) and multi-classifiers, where “CMLS_s” denotes our complete multi-modality latent space learning model using a single classifier and “IMLS_s” denotes our incomplete multi-modality latent space learning model using a single classifier. The comparison results are shown in Fig. 8. From the results, it can be seen that our proposed two models using the ensemble of diversified classifiers perform better than the case of using only a single classifier. Thus, these results validate the superiority of ensembling multiple diversified models for classification.

Fig. 8.

Comparison between our proposed models (left: CMLS; right: IMLS) and their counterparts using only a single classifier (left: CMLS_s; right: IMLS_s).

4.5. Parameter analysis

It is critical to select a set of robust parameters for our proposed models, so that our proposed methods can work well in most situations. Thus, in this section, we study the effects of different hyper-parameter (i.e., λ, β, γ, C, and h) values to the performance metrics. First, for the three regularization parameters (i.e., λ, β, and γ), we fix the value for one parameter and tune the other two parameters in the range of {10⁻⁶, 10⁻⁵, … , 10³}. Then, we tune the parameters C and h in the range of {10, 20, … , 80}. Fig. 9 shows the effect of the parameter changes by using our proposed CMLS for three classification tasks (from top to bottom: MCI/NC, MCI/AD, and sMCI/pMCI) in terms of classification accuracy (i.e., ACC). Specifically, for MCI/NC classification task, when λ and β are within [10⁻³, 10⁻¹] and γ ≥ 1, our proposed method has better classification performance. For MCI/AD classification task, when λ is within [10⁻², 1], and β ≥ 0.1 and γ ≥ 1, our proposed method achieves better classification results. For sMCI/pMCI classification task, when λ is within [10⁻², 1] and γ ≥ 1, our proposed method achieves reasonably good performance. Besides, for the parameters C and h, our method obtains reasonably betetr classification results when C ∈ [30, 60] and h ∈ [40, 50].

Fig. 9.

Effect of the parameter changes for our proposed method (i.e., CMLS) in response to three classification tasks (from top to bottom: MCI/NC, MCI/AD, and sMCI/pMCI) in terms of accuracy (ACC).

4.6. Most related brain regions

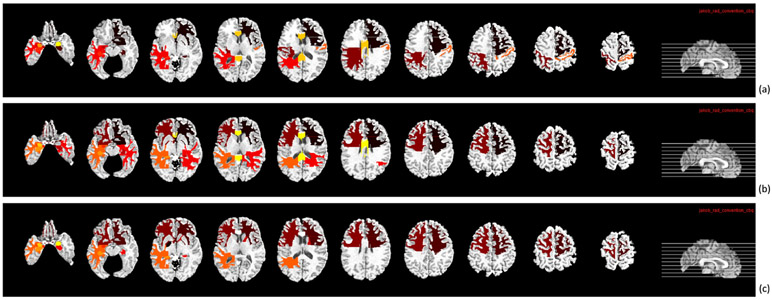
Furthermore, we also identified the potential brain regions that can be used as biomarkers in AD and its early stage diagnosis. We computed the frequency of the ROIs and reported the ten most related ROIs in Figs. 10 and 11 for three classification tasks. Generally, these identified ROIs are in agreement with many previous studies about AD and its early stage diagnosis (Thung et al., 2014; Zhu et al., 2016a; Misra et al., 2009). Specifically, in MRI data, the top selected ROIs common to three classification tasks are the frontal lobe WM right, hippocampal formation right, uncus left, temporal lobe WM left, hippocampal formation left, and amygdala left. In PET data, the top selected ROIs common to three classification tasks are the globus palladus left, frontal lobe WM right, precuneus right, parietal lobe WM left, temporal lobe WM left, and precuneus left, which are the altered regions in AD reported in some previous studies (Jie et al., 2013; Zhu et al., 2016a; Hua et al., 2008; Chételat, 2005). Thus, in future work, these brain regions can be used as potential biomarkers for AD diagnosis.

Fig. 10.

Top selected regions from MRI data for three classification tasks: (a) MCI/NC, (b) MCI/AD, and (c) sMCI/pMCI.

Fig. 11.

Top selected regions from PET data for three classification tasks: (a) MCI/NC, (b) MCI/AD, and (c) sMCI/pMCI.

5. Conclusion

In this paper, we propose a multi-modality latent space inducing ensemble SVM classifier for early AD diagnosis framework. Specifically, we first project the original ROIs-based features into a latent space to effectively exploit the correlations among modalities in multi-modality data. Then, by using the learnt latent representations, we learn multiple diversified classifiers and use an ensemble strategy to obtain the final result, so that our proposed model is more robust to disease heterogeneity. Furthermore, we extend our AD diagnosis framework to address the missing data issue which is common in multi-modality dataset. Experimental results using the ADNI dataset demonstrate that our proposed method outperforms other state-of-the-art methods in early AD diagnosis. In future work, we could extend the proposed model using a deep learning framework to improve the classification performance, since features learned from deep networks are typically more discriminative than the hand-crafted features (Fan et al., 2018; Bernard et al., 2018; Shen et al., 2017).