Only the Fastest Corticospinal Fibers Contribute to β Corticomuscular Coherence

Abstract

Human corticospinal transmission is commonly studied using brain stimulation. However, this approach is biased to activity in the fastest conducting axons. It is unclear whether conclusions obtained in this context are representative of volitional activity in mild-to-moderate contractions. An alternative to overcome this limitation may be to study the corticospinal transmission of endogenously generated brain activity. Here, we investigate in humans (N = 19; of either sex), the transmission speeds of cortical β rhythms (∼20 Hz) traveling to arm (first dorsal interosseous) and leg (tibialis anterior; TA) muscles during tonic mild contractions. For this purpose, we propose two improvements for the estimation of corticomuscular β transmission delays. First, we show that the cumulant density (cross-covariance) is more accurate than the commonly-used directed coherence to estimate transmission delays in bidirectional systems transmitting band-limited signals. Second, we show that when spiking motor unit activity is used instead of interference electromyography, corticomuscular transmission delay estimates are unaffected by the shapes of the motor unit action potentials (MUAPs). Applying these improvements, we show that descending corticomuscular β transmission is only 1–2 ms slower than expected from the fastest corticospinal pathways. In the last part of our work, we show results from simulations using estimated distributions of the conduction velocities for descending axons projecting to lower motoneurons (from macaque histologic measurements) to suggest two scenarios that can explain fast corticomuscular transmission: either only the fastest corticospinal axons selectively transmit β activity, or else the entire pool does. The implications of these two scenarios for our understanding of corticomuscular interactions are discussed.

SIGNIFICANCE STATEMENT We present and validate an improved methodology to measure the delay in the transmission of cortical β activity to tonically-active muscles. The estimated corticomuscular β transmission delays obtained with this approach are remarkably similar to those expected from transmission in the fastest corticospinal axons. A simulation of β transmission along a pool of corticospinal axons using an estimated distribution of fiber diameters suggests two possible mechanisms by which fast corticomuscular transmission is achieved: either a very small fraction of the fastest descending axons transmits β activity to the muscles or, alternatively, the entire population does and natural cancellation of slow channels occurs because of the distribution of axon diameters in the corticospinal tract.

Introduction

The corticospinal tract plays a fundamental role in dexterous movements in primates (Lemon, 2008). To date, studies of corticospinal function have relied on microelectrode recording or stimulation in animals, and non-invasive stimulation in humans (Rothwell, 2007, 2012; Lemon, 2008). Both of these approaches are biased toward the largest cells with the fastest conducting axons; by contrast little is known of the contribution of slower fibers, although these make up the overwhelming majority of the corticospinal tract (Kraskov et al., 2019). One way to overcome this limitation might be to study the transmission of endogenous motor commands from cortex to muscle, since the different corticospinal axon calibers will impose their own characteristic conduction times on the signal propagation.

A particularly advantageous state to examine slow and fast corticospinal transmission to motoneurons might be during voluntary tonic contractions, when motor cortical circuits generate oscillatory activity in the β band (15–30 Hz; Baker et al., 1997). These oscillations are known to be carried by fast corticospinal cells (Baker et al., 2003), and to synchronize motoneurons (Williams and Baker, 2009; Negro and Farina, 2011) leading to significant corticomuscular coherence (Conway et al., 1995; Baker et al., 1997; Salenius et al., 1997). Reliable characterization of β time delays between cortex and muscles could quantify how oscillations are carried by the different conduction velocity divisions of the corticospinal tract.

Many previous works have studied the delay between coherent cortical and muscle β activity (Brown et al., 1998; Halliday et al., 1998; Gross et al., 2000; Mima et al., 2000; Riddle and Baker, 2005; Govindan et al., 2006). Determining oscillatory delays is relatively straightforward if there is transmission in only one direction (Halliday et al., 1995). However, the motor cortex not only sends oscillations down to the spinal cord (Baker et al., 2003), but also receives ascending oscillatory input over afferent pathways (Hansen and Nielsen, 2004; Baker et al., 2006; Baker, 2007). Such bidirectional coupling can generate erroneous estimates using simple correlational measures like coherence (Cassidy and Brown, 2003; Witham and Baker, 2012; Campfens et al., 2013). In modeled data, delay estimates closer to the known “ground truth” are generated by approaches such as Granger causality (directed coherence; Witham et al., 2010). When applied to physiological recordings, directed coherence measures longer delays than those expected from the fastest corticospinal axons, suggesting that both fast and slow axons conduct the β oscillations (Witham et al., 2010, 2011). However, there is considerable intersubject variability, a factor of ∼2-fold between the slowest and fastest delay estimates (Witham et al., 2011). The large variability of β transmission speeds found across individuals may have two explanations: either the contributions of slow and fast fibers to signal transmission are highly variable across individuals (Witham et al., 2011), or else, the variability is generated artifactually because of methodological issues in the current approaches used to characterize corticomuscular transmission of oscillatory activity (Witham and Baker, 2012; Campfens et al., 2014).

Here, we study the contribution of fast and slow corticospinal fibers to corticomuscular β transmission. To do this, we first propose and validate two critical improvements to measuring corticomuscular delays. First, we previously showed that directed coherence extracts accurate delay estimates using simulated data with a broad range of spectral frequencies (Witham et al., 2010). However, corticomuscular β coherence only involves transmission of signals within a relatively narrow band. Surprisingly, here we find that this can impact delay measures, and that an alternative approach in the time domain (cumulant density; Halliday et al., 1995) is more reliable than directed coherence. Second, past work used the interference electromyogram (EMG) to represent peripheral activity; this will incorporate a dependence on the shape of motor unit action potential (MUAP) waveforms (Williams and Baker, 2009), which is a source of spurious variability. Here, we instead used the spiking activity of pools of motor units blindly extracted from surface recordings (Farina and Holobar, 2016). The resulting improved corticomuscular transmission delay estimates are compared with conduction times for fast corticospinal transmission determined by noninvasive brain stimulation. Finally, we use a model to understand the implications of our results for passage of motor commands over both fast and slow corticospinal axons.

Materials and Methods

This work presents data from three experiments. Experiment 1 involves simulations of bidirectional β transmission between two sources (Fig. 1A). The aim of this experiment was to test the reliability of the directed coherence and the cumulant density function to estimate temporal delays between coherent band-limited signals.

Figure 1.

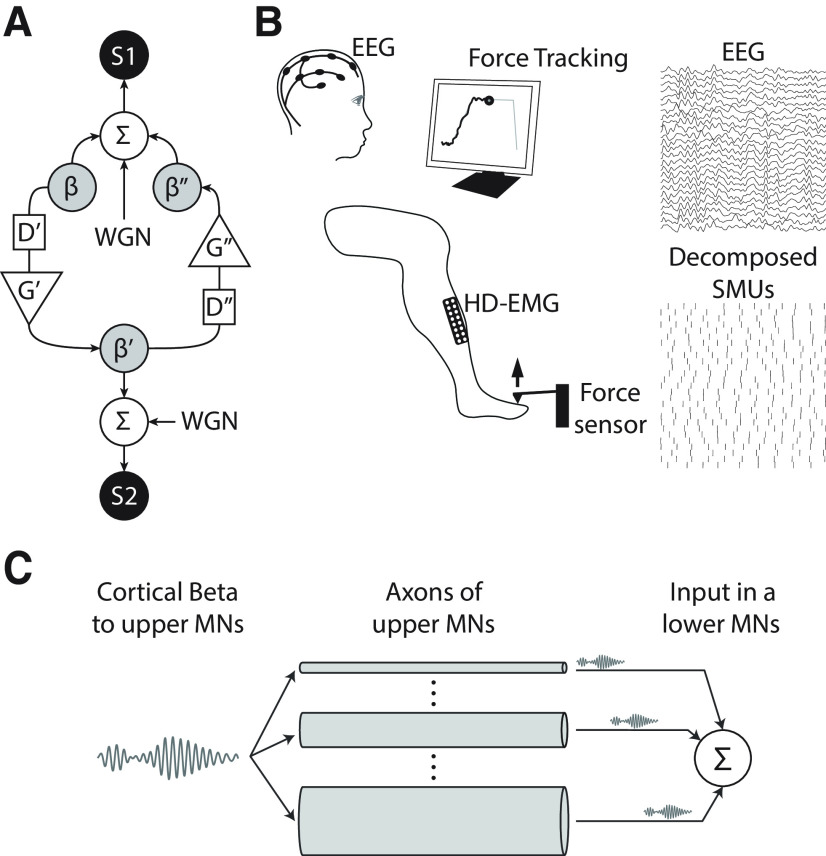
The study presented here is based on data from three experiments. A, Schematic of the simulation used in experiment 1 to test the reliability of the cumulant density and directed coherence methods to estimate interaction delays in a bidirectional system in which only a limited band of frequencies is transmitted between sources S1 (simulating a cortical source) and S2 (simulating a muscle source). WGN stands for white Gaussian noise; ∑ indicates the summation of input signals; D'/D'' and G'/G'' represent the delays and gains in the S1→S2 and S2→S1 directions. Delays were generated with bandpass filters that restricted the transmitted signal (β/β'/β'') to a specific frequency band centered around 21 Hz. B, Schematic representation of the set-up in the main recording in experiment 2 (contraction of the TA). During the recording blocks, subjects were asked to track a ramp-and-hold force trace on a screen by producing torques with their ankle (for experiments with the TA) or with their index finger (for experiments with the FDI). In all cases, the hold part was set at 10% of the MVC level. HD-EMG and EEG were recorded and offline processed to study the characteristics of the interactions between scalp signals and the composite spike train resulting from combining the information of all the identified SMUs from the recorded muscle. M1→muscle β transmission delay estimates were the main outcome measure. C, Simulation run in experiment 3 to analyze the conditions that can explain the observed β transmission delays in experiment 2, in the light of what is known about the distribution of axon diameters in upper motoneurons (MNs) projecting to the lower MN pool.

In experiment 2, electroencephalography (EEG) and high-density electromyography (HD-EMG) of the tibialis anterior muscle (TA) or the first dorsal interoseous muscle (FDI) were acquired concurrently in human subjects during sustained muscle contractions (an example of the simultaneous recording of EEG and TA HD-EMG is shown in Fig. 1B). Additionally, in a subset of subjects, motor-evoked potentials (MEPs) in the TA induced by transcranial magnetic stimulation (TMS) were measured to estimate the minimum corticomuscular transmission delays (Day et al., 1989). Recordings in experiment 2 are used for three purposes. First, they are used to confirm the results obtained by simulation in experiment 1 regarding the comparison between β transmission delay estimates using the directed coherence and the cumulant density function. Second, recordings are used to compare corticomuscular β transmission delays obtained using single motor unit (SMU) activity and the interference EMG obtained using standard surface montages. This allows us to determine the influence of the shapes of MUAPs on β transmission delay estimates. Finally, data from experiment 2 are also used to test the relation between β transmission delays and subjects' heights, and to compare transmission delays with MEP latencies to infer the conduction velocity of the descending pathways transmitting β activity to the muscles.

Finally, in experiment 3, we simulate the propagation of β activity along the axons of upper motoneurons with realistic distributions of axon diameters (and conduction velocities), and the subsequent summation of the delayed signals in the soma of lower motoneurons of a muscle (Fig. 1C). We use the results from this analysis to infer, in the light of the results from experiment 2, how β may be transmitted to the muscles by populations of upper motoneurons.

Experiment 1: simulation of a bidirectional system transmitting band-limited signals

We simulated a bidirectional system with two sources (S1 and S2) generated by combining independent white Gaussian noise with a shared β signal constrained in a specific frequency band around 21 Hz (Fig. 1A). Simulations were meant to resemble bidirectional corticomuscular interactions that are typically constrained within the β band (Baker, 2007), and used a sampling rate of 256 Hz and a duration of 120 s. To simulate cortical β projections to muscles, β was transmitted from S1 to S2 (β') with a delay (D') of 19.5 ms and a gain (G') of 0.2. Then, to simulate afferent projections to the brain, β' was transmitted from S1 to S2 (β'') with a delay (D'') of 31.3 ms and a gain (G'') of 0.2. The delays here were defined to make the simulated system comparable to previous similar works (Witham et al., 2010). Gains were empirically chosen to obtain coherence results similar to those obtained with experimental data from humans (e.g., results obtained in experiment 2 here). To understand the influence of the bandwidth of the β signals, we ran different simulations with β signals being bandpass filtered within frequency bandwidths between 4 and 40 Hz, in incremental steps of 2 Hz, and centered around 20–22 Hz (Kilner et al., 1999). Signal-to-noise ratios (SNRs) of the β contributions to S1 and S2 between 0 and 12 dB (in steps of 1 dB) were tested for each bandwidth considered. All the parameters in the model were determined empirically to make the results obtained from simulations match the average results with real human data (i.e., results obtained in experiment 2).

Experiment 2: recordings of EEG and HD-EMG during tonic contractions

Nineteen healthy subjects (two females; age range 23–35 years) were recruited. The average height was 178 ± 6 cm (range 165–187 cm). This sample size is larger than in most previous studies on corticomuscular coherence to adequately represent known intersubject variation. All subjects gave their informed consent before participating in the study. The study was approved by the University College London Ethics Committee (Ethics Application 10037/001) and conducted in accordance with the Declaration of Helsinki.

Recordings of EEG and HD-EMG

We measured brain and muscle electrical signals during sustained contractions of either the TA (all subjects) or the FDI (12 subjects). For the experiments with the TA, subjects were asked to sit on a straight chair with their knees flexed at a 90° angle and their right foot placed beneath a custom-made lever measuring ankle dorsiflexion forces during isometric contractions (Fig. 1B). The ankle forces together with HD-EMG recordings of the TA were acquired by a multichannel EMG amplifier (Quattrocento, OT Bioelettronica). The sampling frequency was 2048 Hz. HD-EMG grids (five columns and 13 rows; gold coated; 1 mm in diameter; 8-mm interelectrode distance) recorded the myoelectrical activity of the TA.

For the experiments with the FDI, subjects were asked to sit on a chair with their dominant arm placed on a planar surface on the side of the chair. The hand was placed with the palm facing down, and all fingers except for the index finger were immobilized with a strap. The index finger was attached to a force transducer (BTP 200; Biometrics Ltd.) placed medially to the lateral margin of the distal phalanx. Subjects were instructed to push against the surface of the transducer by abducting the index finger. The force measurements together with HD-EMG recordings of the FDI were acquired by a multichannel EMG amplifier as in the experiments with the TA. In this case, the HD-EMG grids used were analogous to the ones used for the TA but with an interelectrode distance of 4 mm. In all the recordings, the HD-EMG grids were centered around the muscle belly and oriented in parallel with the muscle fibers so that the maximum skin area over the muscle was covered. Before placing the grids, the skin was shaved and cleansed with a 70% alcohol solution. HD-EMG signals were acquired in monopolar mode.

Synchronously with HD-EMG measurements, EEG was recorded using an ActiChamp amplifier (63 channels, polarity defined as negative upwards; BrainProducts). Active Ag/AgCl scalp electrodes were used for the recordings, with electrodes arranged according to a 10/10 layout. Recordings were referenced to POz and the ground electrode was placed on AFz. Electrode impedances were maintained below 10 kΩ. A sampling frequency of 1 kHz was used to acquire the data.

A common digital signal was used to synchronize HD-EMG and EEG data offline.

Experimental paradigm

After a standardized warm up, subjects performed three maximal voluntary isometric contractions (MVCs) with the recorded muscle in each session that were separated by at least 30 s. During the MVCs, subjects were instructed to contract as much as possible for at least 3 s. The peak force value across the MVCs corresponded to the final MVC value and was digitally recorded. For the main recordings, subjects were asked to follow ramp-and-hold force trajectories displayed on a monitor. The trajectories consisted of 2-s ramp contractions from 0% to 10% MVC followed by a 60-s holding phase at 10% MVC. During the holding phase, subjects were instructed to keep an isometric force of 10% MVC. The ramp-and-hold contractions were repeated twice by each subject, with a 2-min rest in between.

Recording of MEP latencies

Five subjects recruited for experiment 2 (average height 179 ± 4 cm) took part in a second experiment performed on a different day, which measured the latencies of MEPs in the TA following TMS over M1. For this experiment, bipolar EMG from the TA was recorded with two surface Ag-AgCl electrodes 2 cm apart (WhiteSensor 40 713, Ambu). The ground electrode was placed on the right ankle. EMG signals were amplified, bandpass filtered between (20–2000 kHz, Digitimer D360 amplifier, Digitimer Ltd, United Kingdom) and acquired at 5-kHz sampling rate with a data acquisition board (CED Power1401, Cambridge Electronic Design Ltd) connected to a PC and controlled with Signal V6 software (also CED). A standard TMS device connected to a 110-mm double-cone coil (Magstim 200², The Magstim Company) was used to stimulate the TA representation of the left M1. The coil was held tangentially on the scalp at an angle of 0° to the mid-sagittal plane to induce a posterior–anterior current across the central sulcus. The motor hotspot was determined by searching for the position where consistent MEPs could be seen in the TA at rest. Active motor threshold (AMT) was defined as the lowest intensity to evoke a MEP of at least 0.2-mV peak-to-peak amplitude in five of 10 consecutive trials while subjects gently contracted their muscles (around 0.15-mV peak-to-peak background activation). Thereafter, 15 TMS pulses with an intensity of 1.4× AMT were delivered while subjects maintained contraction. This gave clear MEPs in the TA. In offline analysis, MEP onset latency was determined via visual inspection on a trial by trial basis from the raw EMG traces and the average latency was determined (Rocchi et al., 2018; Ibáñez et al., 2020).

Experiment 3: simulation of corticospinal β transmission to lower motor neurons through multiple axons with different conduction velocities

We simulated the transmission of β activity along the descending axons of upper motoneurons directly innervating cells in the motoneuron pool of a muscle. Specifically, we simulated how cortical β inputs would be summated at the soma of lower motoneurons when considering a distribution of transmission delays across the descending axons of the upper neurons based on previously published results (Firmin et al., 2014). Therefore, we used the list of observed axon diameters from Firmin's paper (monkey CS28; raw data kindly provided by RN Lemon) and converted them into axon transmission delays using a Hursh factor of 6. In our tests here, we assumed axon lengths from 400 to 1000 mm. Previous reports give estimated central motor conduction time for the TA as ∼14.5 ms (Jaiser et al., 2015). Allowing 3–4 ms for transsynaptic depolarizations at the cortical and spinal levels leaves ∼11 ms for axonal conduction. Considering that the fastest corticospinal conduction velocity is 76.2 m/s (Firmin et al., 2014) gives an axon length of 840 mm. Our simulated length range therefore includes the best estimate of the actual length relevant for the TA muscle. A lognormal function was fitted to the transmission delays calculated from Firmin and colleagues' data; a Kolmogorov–Smirnov test failed to reject the null hypothesis that the experimental data comes from a lognormal distribution (p = 0.056). Our model considered 10⁶ descending axons. The β input to the descending axons was modeled as 20 s of white Gaussian noise bandpass filtered in the β band (Butterworth, third order, band 20–30 Hz). Delays according to the distribution of descending axons were applied to the simulated β input in the frequency domain (McGill and Dorfman, 1984). Finally, all the delayed versions of the simulated β input were summed and the group delay between the resulting signal and the input was estimated from the phase-frequency regression in the coherence function (obtained using the periodogram method with 1-s segments, and discarding the first 1-s segment containing a transitory period). Note that this way of estimating delays is the most suitable one for unidirectional transmission of sinusoidal signals (Rosenberg et al., 1989). Simulations were performed using a sampling rate of 256 Hz.

The above simulation was run first by simulating the transmission of the input β signal through all the axons (100% of the axons) generated by the fitted lognormal distribution. Then, the same simulation was repeated after applying a set of thresholds to the axon diameters that could transmit β rhythms. Each threshold was used as a lower bound applied to axon diameters, so that only a certain percentage of the fastest axons (with diameters above a given threshold) contributed to β transmission. The following percentages were tested: 0.1%, 0.5%, 1%, 5%, 10%, 25%, 50%, and 50%.

Together with group delays, normalized amplitudes of the resulting signals after combining all the delayed versions of the simulated β input were estimated to measure the strength of the transmitted information. This was done by obtaining the root-mean-square (rms) amplitude of the signals resulting from summing the contributions of all the axons transmitting the β input, and dividing the resulting value by the total number of axons considered (10⁶) and by the rms amplitude of the simulated input (as with the delay estimates, the first 1-s segment was ignored here). These amplitudes thus depended on the amount of cancellation among the channels transmitting β activity and on the number of axons included by each diameter threshold.

Finally, in addition to the simulations run testing how β inputs were transmitted, additional equivalent simulations were performed with input signals bandpass filtered between 8 and 10 Hz (Butterworth, third order, band 8–12 Hz). This was done to compare how transmission delays and amplitudes changed for input signals contained within different frequency bands.

Data analysis

HD-EMG decomposition into motor unit spike trains

The main results in experiment 2 were obtained using spiking activity of SMUs instead of the interference EMG. In offline analysis, the HD-EMG signals were first bandpass filtered (20 to 500-Hz band, second order zero-lag Butterworth filter) and subsequently decomposed into SMU spike trains by blind source separation techniques described in previous works (Holobar et al., 2014; Negro et al., 2016). The accuracy of the decomposition algorithm used has been previously demonstrated both by simulations and experimentally over the full recruitment range of the recorded muscles (Farina and Holobar, 2016; Del Vecchio and Farina, 2019; Del Vecchio et al., 2019, 2020). SMUs recruited >10 s after subjects reached the 10% MVC level in each recorded block and SMUs with a standard deviation in instantaneous firing rate higher than 20 Hz were discarded. The remaining SMUs were used to construct a composite spike train to be used in subsequent connectivity analyses. This was done by summing the binary activity of all the trains of pulses from the valid SMUs. The spike time of each SMU corresponded to the onset of its MUAP. To estimate this onset, double differential signals were obtained from the monopolar HD-EMG recordings along the columns of the electrodes grid (i.e., approximately along the longitudinal direction of muscle fibers). Then MUAPs were obtained via spike-triggered averaging (Farina and Holobar, 2016) and the channel in the recording grid showing the largest ratio between the peak-to-peak amplitudes of the MUAP and preceding noise (in the interval [−40, −20] ms before the peak time of the MUAP) was selected to estimate the MUAP onset time. Using this channel, the time at which the average MUAP first crossed a threshold set at five standard deviations above the mean basal activity was defined as the MUAP onset time. Onset estimates were checked visually, and any errors from this automated approach corrected manually.

Derivation of monopolar and bipolar EMG from HD-EMG recordings

To study how MUAPs affect corticomuscular delay estimates, we compared EEG→SMU and EEG→EMG β transmission delays estimates. Bipolar and single channel monopolar recordings were derived from the originally recorded monopolar HD-EMG signals to simulate the recordings that would have been obtained using typical EMG montages. To derive the bipolar EMG, two sets of five neighboring electrodes in the electrodes grid (with the central electrode of the grid corresponding to the belly of the muscle) were averaged, the difference of these averages was then computed to derive EMG signals recorded by large (standard) electrodes having an interelectrode distance of 1.6 cm (Del Vecchio et al., 2017). Single channel monopolar EMG was obtained by averaging the recordings of the five central positions in the recording grid. Both bipolar and monopolar EMG derivations were then analyzed both with and without rectification (Negro et al., 2015).

EMG synthesis using motor unit activity

To study whether differences between EEG→SMU and EEG→EMG β transmission delay estimates were only because of the filtering effect of MUAPs, we synthetized EMG signals from the decomposed SMU activity and compared the estimates of β delays with the ones obtained using the real EMG (Del Vecchio and Farina, 2019). For this purpose, synthesized signals were obtained from the identified SMU activity by convolving the spiking activity with the estimated shapes of MUAPs (i.e., using the MUAPs shapes as filters). These shapes were obtained using spike-triggered averaging (Farina and Holobar, 2016). The used window to extract peri-spike segments had the following expression:

$$w\left(n\right)=\{\begin{array}{cc}{e}^{-\frac{1}{2}{\left(\alpha \frac{n}{\left(N-1\right)/2}\right)}^2}& 0\le n<N/2\\ 1& N/2\le n<3*N/2\\ e^{-\frac{1}{2}{\left(\alpha \frac{\left(n-N\right)}{\left(N-1\right)/2}\right)}^2}& 3*N/2\le n<2*N\\ 0& otherwise\end{array},$$

where N is the length of the central flat part of the window (set to 50 ms), n is the sample index, and α is a constant set to 2.5. This window tapered the extracted MUAP shapes at the onset and offset so that the estimated MUAP shapes used as filters to synthetize EMG activity did not present any sharp transitions. Individual MUAP shapes were extracted by multiplying w(n) with EMG segments around the estimated spike times. The MUAP shape of for each SMU was then obtained by averaging all the individual MUAPs of the corresponding unit.

EEG preprocessing

EEGLAB toolbox for MATLAB was used for the EEG preprocessing (Delorme and Makeig, 2004). First, EEG signals were bandpass filtered between 0.5 and 45 Hz (Butterworth IIR filter, third order). An independent component analysis algorithm (BINICA) was used to visually identify and remove artefacts because of electrical noise, muscle activity, eyeblinks, eye movements or noisy electrodes (on average, 78 ± 45% of the components were kept). Laplacian derivations (subtracting the average activity of neighboring equidistant channels) were computed for electrodes C1, Cz, and C2 for the TA and C5, C3, and C1 for the FDI. The resulting signals from these derivations were used for the connectivity analysis described below. Specifically, the channel with which corticomuscular coherence amplitude was highest in the β band in each case was selected for further analysis (Ibáñez et al., 2014). As expected, the channels most frequently selected were Cz for the TA and C1 or C3 for the FDI (16/19 subjects for the TA and 10/12 for the FDI, in the analysis using SMUs; Petersen et al., 2012; Vidaurre et al., 2019).

Connectivity analysis

A key part of our study is the analysis of the connectivity between continuous (EEG) and spiking (SMUs) signals. The main results presented here were obtained using the previously validated Neurospec 2.11 toolbox for MATLAB (MathWorks Inc.) aimed to analyze nonparametric directional connectivity between time series and point process data (www.neurospec.org; Halliday, 2015). In brief, this framework uses a combined time and frequency domain approach to decompose the standard coherence function by direction. Here, this directional coherence estimation method is used to extract, from the conventional EEG-SMU (or EEG-EMG) coherence function, the part resulting from cortical projections to muscles (EEG→SMU or EEG→EMG coherence). For the identification of significant coherences, we use Neurospec's estimates for the upper 95% confidence limit (Rosenberg et al., 1989), defined as $1-{0.05}^{1/\left(L-1\right)}$, where L is the number of segments from which the Fourier transform is computed. In all cases, coherence analysis with Neurospec was done using segments of 1 s and multitapers (three tapers) for spectral estimation.

The Neurospec 2.11 framework also allows the characterization of corticomuscular interactions in the time domain by estimating the cumulant density function (cross-covariance) together with upper and lower 95% confidence lmits to determine significant peaks based on the assumption of uncorrelated processes. These confidence limits are set as $\pm \frac{1.96}{\sqrt{R}}$, where R is the number of data points considered. The cumulant density function and the confidence limits are used here to estimate the lag with which the possible correlation existing between EEG and muscle activity is strongest and to assess its significance. To focus on the delays of corticomuscular transmissions descending from the brain (EEG→SMU/EMG transmission delays), the time point with the largest peak found at positive lags was determined. Peak time was used because EEG recordings were performed with an inverted polarity (negative upward), implying that positive deflections relate to periods during which dendritic trees of pyramidal cells in the motor cortex receive predominating excitatory input (Baker et al., 2003; Farmer et al., 2004; Zrenner et al., 2018).

Directed coherence (spectral Granger causality) was also used to replicate results obtained in previous studies of transmission delays in corticomuscular β interactions. Specifically, we used the same implementation of directed coherence as in Witham et al. (2010, 2011). In brief, the studied signals were down-sampled to 512 Hz and autoregressive models of order 256 were fitted to blocks of 10 s, followed by averaging of model coefficients (Witham et al., 2010). Geweke's normalization of directed coherence was used (Geweke, 1982). The 95% confidence intervals for significance assessment were obtained using Monte Carlo simulation as in previous studies (Witham et al., 2010, 2011). β Transmission (group) delays were determined from the slopes of the linear functions fitted to phase values corresponding to frequencies at which directed coherence was significant in the range between 12 and 30 Hz. Delay estimates were only considered reliable if four or more phase points could be used for linear fitting.

Finally, in the analysis of the simulated data in experiment 1, apart from using the cumulant density function and the directed coherence, β transmission delays were also estimated using the phase of the spectral coherence (obtained using the coherence estimate calculated using Neurospec211 toolbox as explained above). This provided results that could be compared with previous simulation studies (Witham et al., 2010).

Statistics

Statistical analyses of results in experiment 2 were performed using SPSS (version 22.0; IBM). All results are reported as the mean ± SD (unless specified otherwise) and considered significant if p < 0.05. Normality of data distribution was assessed using Lilliefors tests. Comparison of means and variances of EEG→SMUs delay estimates based on the cumulant density function and the directed coherence was done using a paired t test and an F test. Paired t tests were run between delay estimates obtained with SMU activity and with each of the considered EMG recording configurations (monopolar or bipolar; rectified or unrectified). Pearson's correlation (one-tailed) was used to study the possible relationship between corticomuscular β transmission delay estimates and subjects' heights. Finally, Pearson's correlation (one-tailed) was used to measure the correlation between delay estimates obtained using real EMG and the EMG synthesized from the spiking trains of the decomposed SMUs as explained in previous sections. For this analysis, we rejected data points which were two standard deviations above or below the mean delays combining the results from real and synthesized data. This led to the removal of five (TA) and nine (FDI) points before testing the correlation, and it was done to disregard possible wrong delay estimates from the cumulant density function either using the real or synthetized EMG (because of spurious peaks in the cumulant density; see, for example, the extreme values with the monopolar unrectified configuration in Results).

Results

This section is divided into two parts. In the first part, results from experiments 1 and 2 are used to indicate several factors that need to be considered to estimate corticomuscular β transmission delays reliably. This allows us to measure the delay in cortical β transmission to muscles during mild contractions. The second part then uses results from experiment 3 to infer, in light of the experimental results from part 1, which fibers of the corticospinal tract may contribute to corticomuscular β transmission.

Part I, reliably estimating β corticomuscular transmission delays

Part IA, the cumulant density provides more reliable corticomuscular β transmission delay estimates than the directed coherence

In this section, we first use simulations of a bidirectional system transmitting signals with different bandwidths and signal-to-noise levels to explore the measurement of β transmission delays by different methods. Then, we repeat this comparison with experimental data from healthy subjects.

Figure 2A shows the total coherence (black lines) and the directed coherence in the S1→S2 direction (gray shaded areas) for representative simulations with different bandwidth and SNR levels. Transmission delays were estimated using three methods. First, delays were obtained from a regression line fitted to the phase of the standard coherence function, which is a common approach in studies of corticomuscular coherence (Pogosyan et al., 2009; Petersen et al., 2012). Estimates in this case were in the range [−0.1, +0.1] ms for all bandwidths and SNR levels tested, representing a consistent underestimate of the true value by ∼20 ms (results not plotted in a figure). This is in line with previous work: the coherence spectrum does not estimate delay well in systems with bidirectional interactions (Witham et al., 2010).

Figure 2.

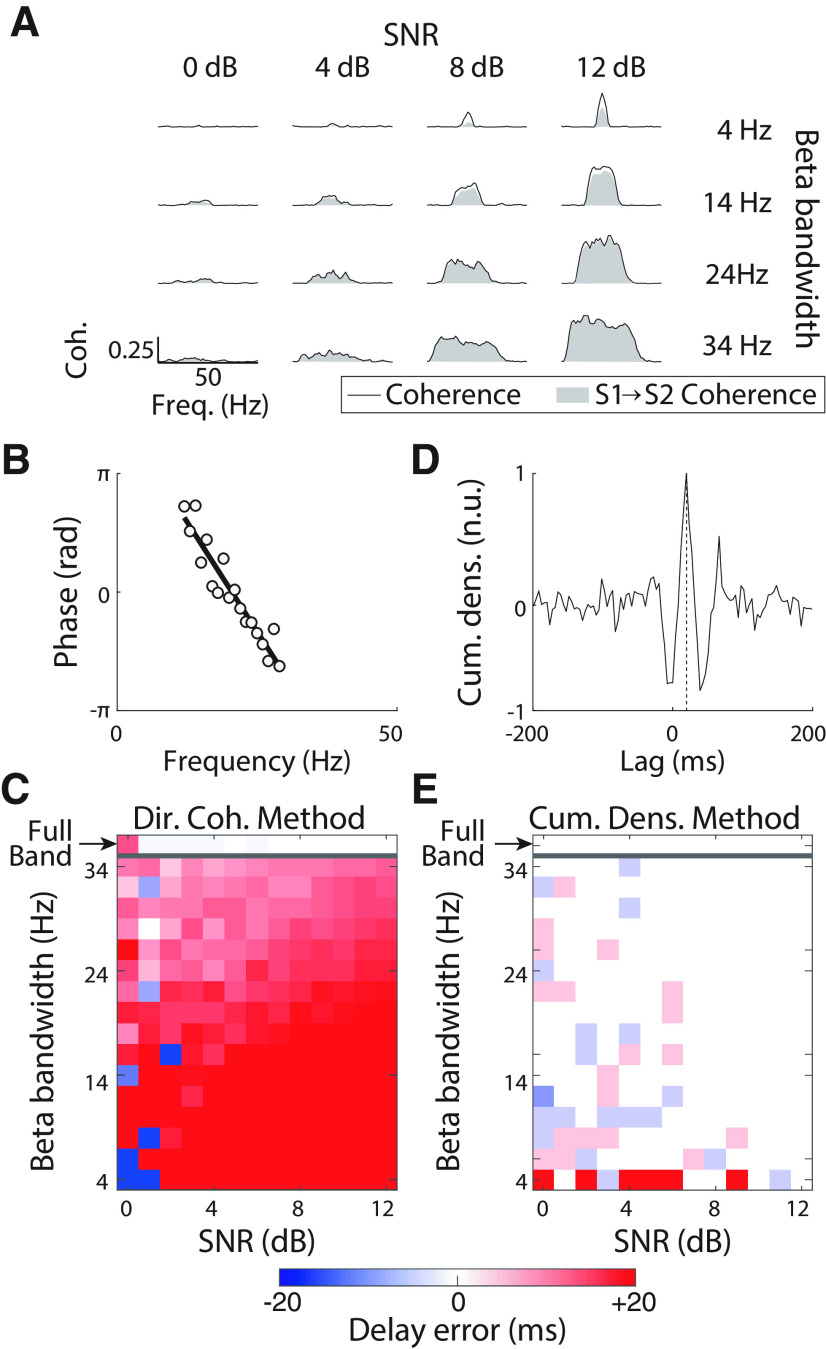
β Transmission delay estimates using the directed coherence and the cumulant density function with data from experiment 1. A, Coherence (black lines) and S1→S2 coherence (gray areas) for different simulated conditions. From top to bottom rows, results for different β bandwidths of the transmitted signals are plotted: 4, 14, 24, and 34 Hz. From left to right column, results for different SNRs of the transmitted signals: 0, 4, 8, and 12 dB. B, Example of linear regression of the directed coherence phase–frequency relationship in the S1→S2 direction used to estimate the β transmission (group) delay. C, Errors in the transmission delay estimates in the S1→S2 direction based on the directed coherence. D, Example of β transmission delay estimation based on the cumulant density. The vertical dashed line indicates the transmission delay with which the maximum peak is found in the cumulant density. E, Errors in the transmission delay estimates in the S1→S2 direction based on the cumulant density.

The second method tested was directed coherence (Witham et al., 2011; Witham and Baker, 2012). An example (for 18-Hz bandwidth, SNR 2 dB) of a linear fit to the phase-frequency spectrum for directed coherence is shown in Figure 2B. Figure 2C shows the error in delay estimate (relative to the known ground truth of the simulation), for varying levels of bandwidth and SNR. When the transmitted signal covered the full spectrum of frequencies (white noise), delay estimates based on the directed coherence were accurate for SNR > 0 dB (Fig. 2C, white shading, top row), as reported by previous work (Witham et al., 2010). However, when the transmitted signals had more limited bandwidth, estimates at high SNR were biased toward delays longer than the true values. Measurements for SNR = 0 dB were variable and unreliable.

Finally, the cumulant density was used to estimate delay in the time domain, by finding the latency of the positive peak (see example in Fig. 2D). These delays estimates were accurate for a wide range of parameters, and only showed appreciable errors for bandwidths of 4 Hz (Fig. 2E). This lack of reliability for narrow band signals is because of the large oscillations appearing in the cumulant density in these cases, which has been previously noted to introduce errors (Halliday, 2015).

Experimentally-recorded measurements from experiment 2 were analyzed to obtain β transmission delay estimates for comparison with the simulations in experiment 1. To obtain reliable corticomuscular transmission delays, spiking activity of pools of SMUs was used. On average, 18 ± 8 SMUs (TA) and 7 ± 2 SMUs (FDI) were extracted per subject from HD-EMG (range of SMUs: 5:29 for TA, 4:11 for FDI). The average discharge rate across all SMUs was 11.0 ± 1.6 pps for the TA and 13.4 ± 1.5 pps for the FDI.

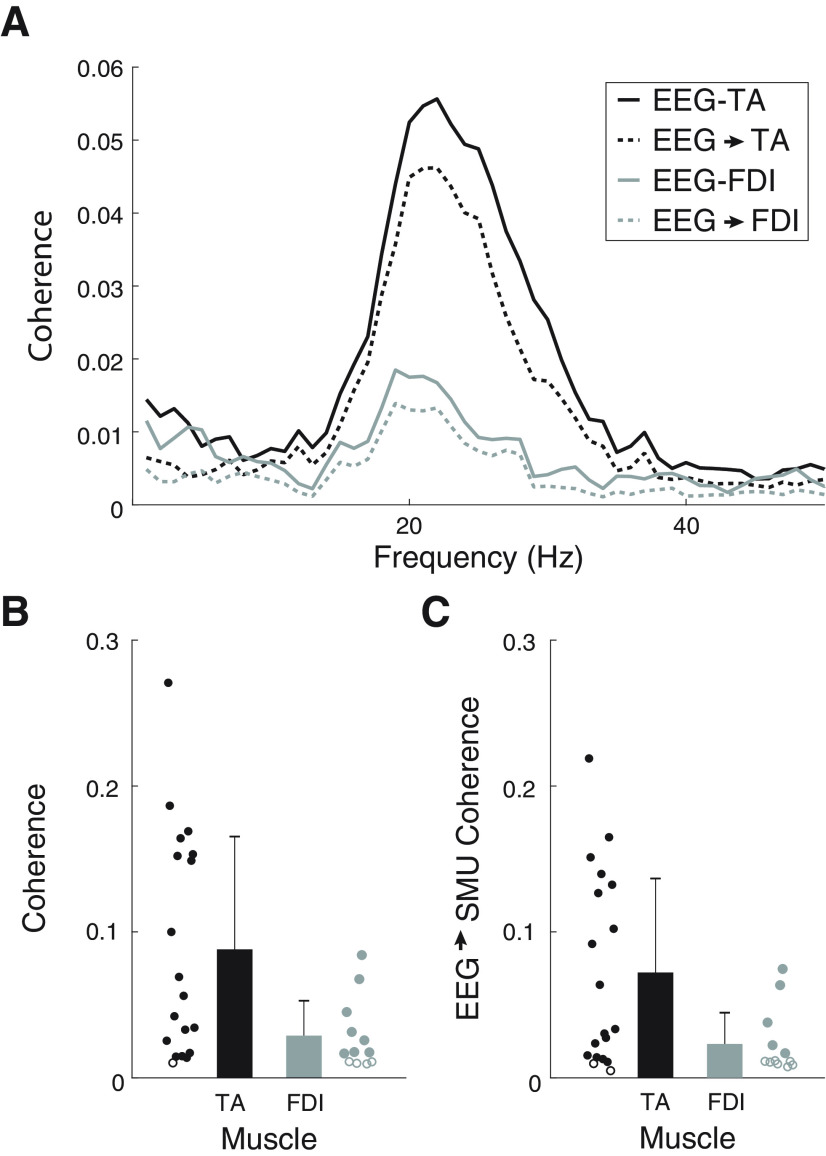
Figure 3 summarizes the coherence results obtained with the two muscles measured in experiment 2. Figure 3A shows the average corticomuscular and descending (EEG→SMUs) coherence estimates with the TA and FDI. In line with previous studies (Ushiyama et al., 2010), stronger coherence was observed with the TA than with the FDI. Significant EEG-SMUs coherence in the β band was observed in 18 out of the 19 subjects with the TA and in eight out of 12 subjects with the FDI (Fig. 3B). The corticomuscular coherence peak was 0.09 ± 0.08 for the TA and 0.03 ± 0.02 for the FDI. The limit used to define significant coherence peaks was 0.01 ± 0.00. With the TA, the average peak amplitude of the EEG→SMUs coherence was 0.07 ± 0.06, and it was significant in 16 cases (Fig. 3C). With the FDI, the average peak amplitude of the EEG→SMUs coherence was 0.02 ± 0.02, and it was only significant in five cases. We did not find clear coherence peaks at other frequencies outside the β band across subjects. In addition, coherence in the SMUs→ EEG direction was generally smaller and more variable than in the descending direction (on average it was 0.02 ± 0.02 with the TA and below 0.01 with the FDI). These results indicate that, in the context of sustained mild contractions, β is the only frequency band within which rhythmic cortical signals are consistently transmitted to the muscle, and that the contribution of descending projections to the total coherence is stronger than the contribution of ascending projections.

Figure 3.

Corticomuscular coherence and EEG→SMU coherence results. A, Average coherence (solid) and EEG→SMU coherence (dashed) obtained with the TA (black) and FDI (gray). B, Peak corticomuscular coherence in the β band with the TA (black) and FDI (gray). C, Peak EEG→SMU coherence in the β band with the TA (black) and FDI (gray). Circles represent individual results. Open circles represent subjects with no significant coherence.

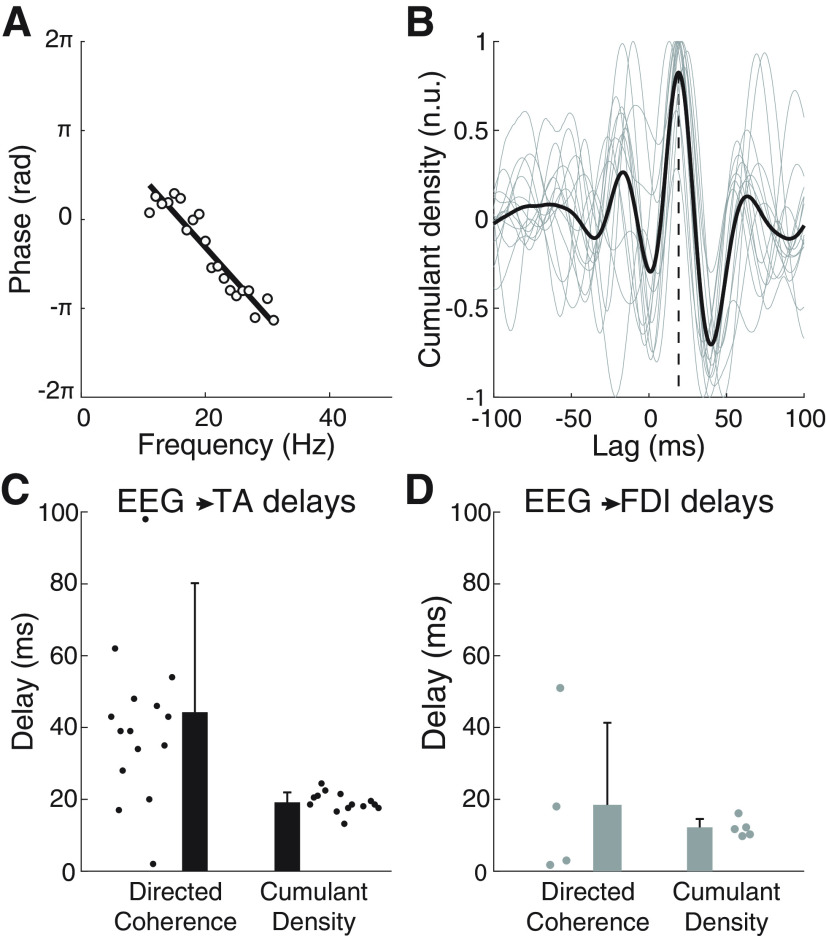
Figure 4A shows the linear fit to the EEG→SMUs directed coherence phase for a representative subject; the slope indicated a 38.8-ms delay for this example. The average cumulant density with data from the TA (Fig. 4B) showed a positive peak for most individual traces at a positive time lag. Significant cumulant density peaks at positive lags were seen in 14 subjects for the TA and in five subjects for the FDI. Using the directed coherence, significant delay estimates could be obtained from 15 (TA) and three (FDI) subjects. Average EEG→SMUs delays based on these two methods were 19.1 ± 2.7 ms (cumulant density) and 44.2 ± 35.9 ms (directed coherence) with the TA, and 12.0 ± 2.5 ms (cumulant density) and 18.5 ± 22.9 ms (directed coherence) with the FDI (Fig. 4C,D). These differences between the delay estimation methods are in line with those from simulated data in experiment 1. In the group of subjects from whom significant EEG→SMUs delay estimates with the TA could be obtained using both, the cumulant density and directed coherence, the mean and variance of delays were significantly larger with the directed coherence than with the cumulant densities (t₍₁₂₎ = −3.556, p = 0.004; F_(1,12) = 12.645, p = 0.004). This comparison was not performed for delays in the FDI because of the small number of significant estimates.

Figure 4.

β Transmission delay estimates using the directed coherence and the cumulant density function using data from experiment 2. A, Example of the phase spectrum from the directed coherence in the EEG→SMU direction to estimate transmission delays. Data from the TA experiment done by one subject (white circles) and linear fit to estimate the delay (black line). B, Average (black) and single-subject (gray) normalized cumulant densities obtained between the EEG and SMU data (TA experiments). A vertical dashed line is used to indicate the lag at which the average peak in the cumulant density is found. C, D, β EEG→SMU transmission delay estimates using the directed coherence and the cumulant density function for experiments with the TA (C) and the FDI (D). Circles represent individual results.

PART IB, pooled SMU activity gives better delay estimates than EMG

Surface EMG signals are the result of convolving spike trains with the corresponding MUAPs at the skin surface (Farina and Merletti, 2001). To study the influence of the filtering effect of MUAPs on descending spike trains, EEG→SMUs β transmission delay estimates were compared with those obtained using monopolar and bipolar EMG signals with and without rectification using data from experiment 2.

Figure 5A,B shows the individual and group results of β transmission delay estimates using the decomposed spiking activity of SMUs or different configurations for recording surface EMG. For experiments with the TA, delay estimates based on SMUs (19.1 ± 2.7 ms; average of 14 subjects with significant delay estimates) were significantly lower (p < 0.001) than with any EMG-based configuration: 25.1 ± 4.6 ms using bipolar EMG and rectification (12 subjects with significant estimates), 36.1 ± 8.7 ms using bipolar EMG and no rectification (10 subjects with significant estimates), 24.6 ± 3.2 ms using monopolar EMG and rectification (14 subjects with significant delay estimates), 38.9 ± 18.7 ms using monopolar EMG and no rectification (17 subjects with significant estimates). An analogous trend of the group results could be observed in the data from the experiments with the FDI: delay estimates based on SMUs (12.0 ± 2.5 ms; average of five subjects with significant delay estimates) were lower than with any EMG-based configuration: 22.7 ± 18.0 ms using bipolar EMG and rectification (seven subjects with significant estimates), 39.0 ± 31.8 ms using bipolar EMG and no rectification (six subjects with significant estimates), 13.5 ± 3.9 ms using monopolar EMG and rectification (three subjects with significant delay estimates), 25.3 ± 6.2 ms using monopolar EMG and no rectification (five subjects with significant estimates). Because of the small number of subjects with significant delay estimates in FDI, no statistical comparisons were run in this case.

Figure 5.

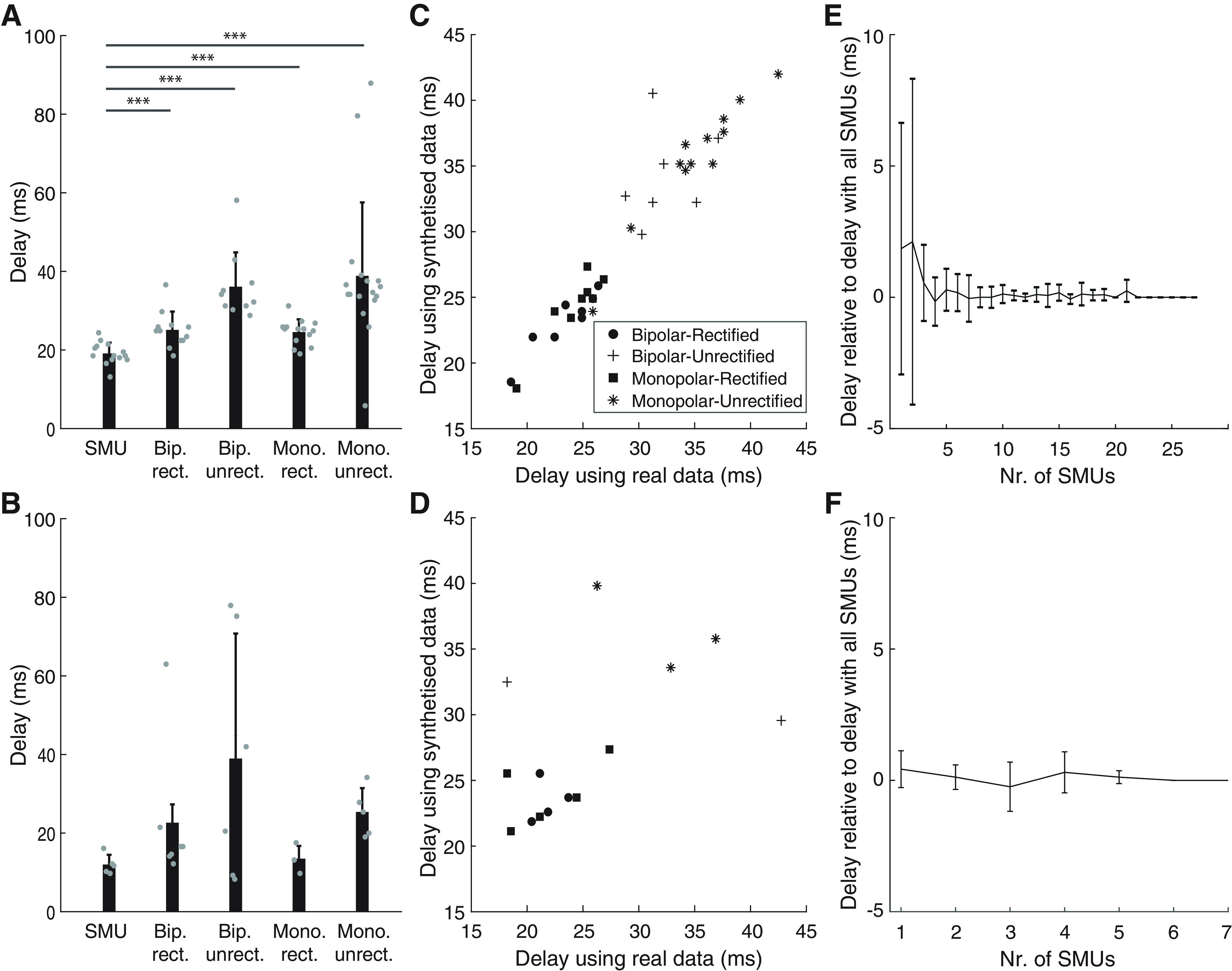
Comparison between EEG→SMU and EEG→EMG β transmission delay estimates in Part 2. A, B, β Transmission delay estimates with data from the TA (A) and FDI (B) using SMUs activity and four different EMG montages: bipolar rectified (Bip. rect.), bipolar unrectified (Bip. unrect.), monopolar rectified (Mono. rect.), monopolar unrectified (Mono. unrect.). Gray circles represent individual data; ***p < 0.001. C, D, β EEG→EMG delay estimates (C, TA; D, FDI) using real (x-axis) versus synthetized EMG from the decomposed SMUs (y-axis). E, F, Group results (E, TA; F, FDI) of the EEG→SMU β delay estimates obtained using increasing numbers of SMUs relative to estimates obtained considering all the decomposed SMUs in each subject.

To ensure that differences in the results with SMUs and EMG were solely because of the effect of the MUAPs, we synthetized EMG signals from the spiking SMU activity. Delay estimates with synthesized EMG of the TA were strongly correlated with delays obtained using real EMG data (R = 0.964; p < 0.001; Fig. 5B). Estimates using synthesized EMG of the FDI were also correlated with estimates using the actual recordings but less strongly, likely because of the presence of inaccurate delay estimates in some subjects and with some of the surface EMG configurations (R = 0.541; p = 0.023; Fig. 5D). The observed correlations (specially with the data from the TA experiments) indicate that differences observed between EEG→SMU and EEG→EMG delay estimates are largely explained by the filtering effect of MUAPs. They also suggest that decomposed SMUs contain the majority of the relevant information in the EMG.

Finally, we also measured how EEG→SMU β transmission delay estimates change with increasing samples of SMUs considered. This was done to assess whether the activity extracted from the decomposed SMUs sufficiently describes the information of the entire pool of active motoneurons innervating the muscle. Results of this analysis show that stable EEG→SMUs delay estimates could be obtained in all subjects when activity of just three or more decomposed SMUs were combined (Fig. 5E,F). Therefore, the numbers of decomposed SMUs per subject obtained in this study should be sufficient to yield accurate delay estimates.

PART IC, integrated EEG gives better delay estimates than raw EEG

In the previous sections, EEG→SMU β transmission delay estimates are obtained assuming that the descending β activity does not undergo any phase delays between the point where EEG is recorded and the measurement point at the muscle. However, this is not correct, since pyramidal tract neuron spiking is related to the integral of nearby recordings of local field potential (Baker et al., 2003). This implies that EEG signals (recorded here with a polarity defined as negative upward) undergo a phase shift of π/2 in their integration by the pyramidal neurons. This phase shift must be taken into account as it affects β transmission delay estimates obtained using the cumulant density function, which works in the time domain and is blind to phase delays.

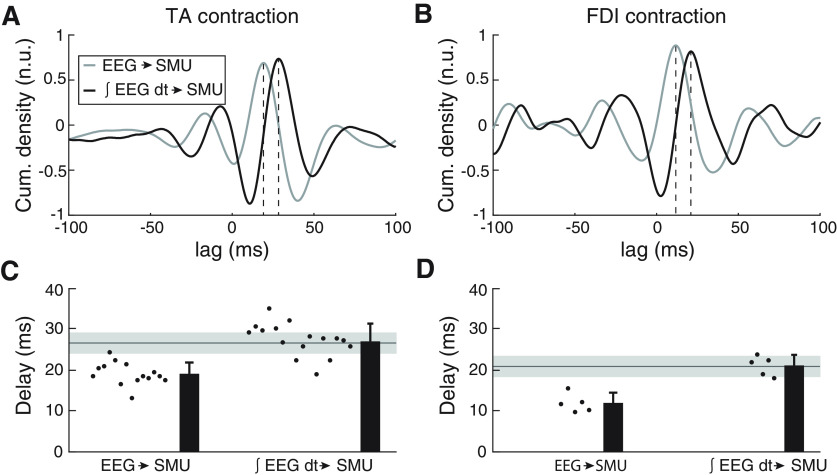
Figure 6A,B illustrates the average cumulants between raw EEG and pooled SMU activity across subjects (gray trace; data from the experiments with the TA and FDI are shown on panels A and B, respectively). To correct for the phase shift between EEG and corticospinal neuron activity, we integrated the EEG by replacing each value with its cumulate sum up to that point; the cumulant determined with integrated EEG (∫ EEG dt) is illustrated with the black track in Figure 6A,B. The delay estimated from the average cumulant peak shifted later (see dotted vertical lines): from 19.0 to 28.3 ms for the TA data and from 11.7 to 21.0 ms for the FDI data.

Figure 6.

A, B, Average normalized cumulant densities obtained between the EEG and SMU activity (gray line) and between the integrated EEG (∫ EEG dt) and SMU activity (black line). Panels A, B show data from the experiments with the TA and FDI, respectively. C, D, β Transmission delay estimates when based on EEG without phase modifications (left) versus when considering that spike trains in pyramidal tract neurons relate to ∫ EEG dt (right). The horizontal solid line and gray area on each panel indicate the mean and SD of TA MEP latencies in previous studies using large sets of healthy individuals (Rossini et al., 1999). Panels C, D show data from the experiments with the TA and FDI, respectively.

Figure 6C,D present individual and average results across subjects. By taking into account the phase shift caused by integrating EEG activity, the average cortical→SMU β transmission delay to the TA and FDI became 28.6 ± 3.1 and 21.2 ± 2.6 ms, respectively. This was 9.4 ± 1.0 ms (TA data) and 9.2 ± 1.1 ms (FDI data) longer than if the phase shifts were not accounted for.

Compared with EEG→SMU delay estimates, cortical→SMU delay estimates including the integration of EEG were much closer to previously reported measures of MEP latency for TA and FDI, based on recordings from large samples of subjects (26.7 ± 2.6 ms for the TA and 20.7 ± 0.8 ms for the FDI; horizontal line and shading show mean ± SD in Fig. 5C,D; Rossini et al., 1999). This is further confirmed when comparing estimated β transmission delays to the TA with the MEP latencies measured in five subjects in our study: the difference between the two measures was 1.14 ± 1.60 ms. Overall, this suggests that β is transmitted to the muscles through the fastest corticospinal axons. If Cortical→SMU β coherence is determined by the most direct and fast descending projections (and not by varying groups of descending axons across individuals), assuming that conduction velocities of these fastest projections is comparable across subjects, then it is expected that β transmission delays correlate with the traveled distances to the muscles (Jaiser et al., 2015). Indeed, this was the case in our experiments with the TA: a significant correlation was found between cortical→SMU β transmission delay estimates and subjects' heights (R = 0.651, p = 0.006). This analysis could not be performed with the data from the experiments with the FDI because of the limited number of significant transmission delay estimates obtained with our sample.

PART II, corticomuscular transmission is determined by the fastest descending axons

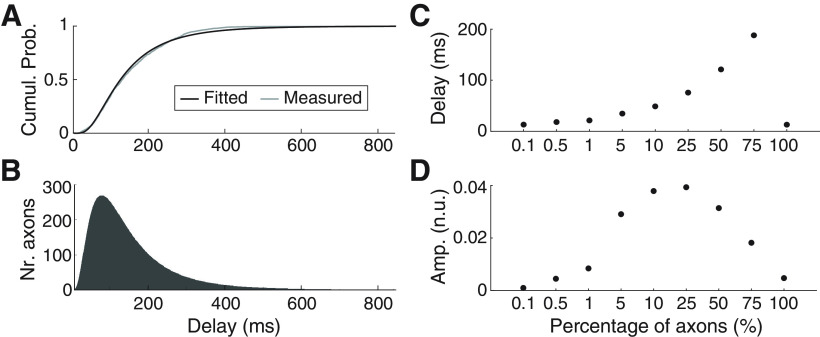
Having removed methodological confounding factors from estimates of corticomuscular β transmission delay, we found delays close to the fastest descending pathways as assessed by TMS. This is somewhat unexpected, given the large preponderance of slow fibers in the corticospinal tract. We explored how selective transmission by the fastest routes can be achieved in experiment 3 by simulation. The distribution of axon diameters from a previous careful anatomic study in monkeys (Firmin et al., 2014) was modeled using a lognormal function, which provided a good fit (Fig. 7A, compare gray and black lines). The fitted lognormal function was then used to generate distributions of axon diameters, which were converted to conduction velocities assuming a Hursh factor of 6, and to transmission delays by assuming a given axon length. Figure 7B illustrates the distribution of transmission delays of the simulated axons for a distance of 800 mm, estimate to be close to the value for the human TA motoneuron pool (Jaiser et al., 2015). Using this distribution, we then simulated different scenarios in which β activity was restricted to axons conducting faster than a certain threshold.

Figure 7.

Results of the transmission and posterior summation of β signals (band pass-filtered noise within 20–30 Hz) simulating the propagation of β activity through the corticospinal tract to lower motoneurons. Simulations use a population of 10⁶ axons of 800 mm of length (similar to the estimated length of corticomotoneural cells to the TA) and axon diameters (and conduction velocities) based on previously published work (Firmin et al., 2014). A, Cumulative probability function of delay estimates considering the measured axon diameters in Monkey CS28 in Firmin's article (gray line) and the axon diameter distribution obtained by fitting a lognormal function to actual data (black line). B, Histogram of the distribution of transmission delays used for the simulation (obtained using the fitted lognormal function shown on panel A). C, D, Transmission delays and normalized rms amplitudes for different scenarios simulated in which different percentages of the fastest axons transmit the (cortical) β signal. Amplitudes panel D result from summing the contributions of all axons transmitting β and dividing by the total number of axons simulated (10⁶) and by the rms amplitude of the input signal.

Figure 7C shows how the estimated transmission delay changed as the conduction velocity threshold altered. Unsurprisingly, when only the fastest 0.1% of the axons were allowed to transmit the β oscillations, the measured conduction delay was short (13 ms), implying a conduction velocity of ∼62 m/s. As more and more slow axons were included in the transmission of β, the estimated delay rose. However, surprisingly when all axons were included, the delay dropped again to be the same as in the case where only the fastest 0.1% axons transmitted β oscillations. This is because cancellation occurs over such a wide delay range; for a delayed version of the input oscillation, phase cancellation occurs because of the summation with other delayed versions of the same signal that arrive earlier and later to the end of the transmission channel. In this context, the only signals that are not cancelled are those transmitted at the fastest possible speeds. As a result, only the fastest axons (those not resulting in relevant phase shifts of the oscillations transmitted along the whole axon length) can transmit an uncancelled signal. Figure 7D plots the corresponding normalized rms amplitude of the transmitted β oscillation. Again, the amplitude rises with the inclusion of slower axons, but then falls as cancellation begins to influence the transmission. Note however that the amplitude when all axons contributed was 5 × 10⁻³ (normalized units), compared with 0.9 × 10⁻³ when only the fastest 0.1% of axons contributed.

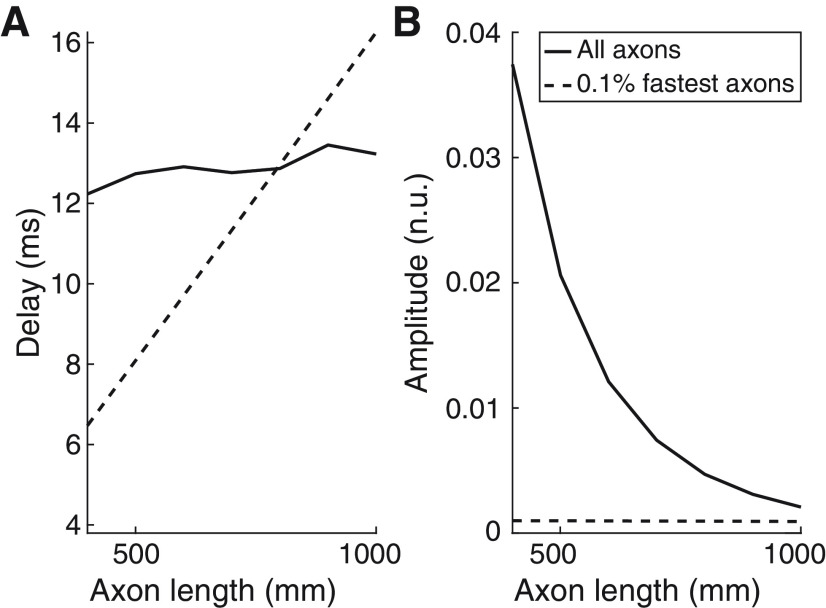
Figure 8 shows how transmission delays (Fig. 8A) and normalized rms amplitudes of the transmitted signals (Fig. 8B) change as a function of the length of the axons transporting β. Results shown are for two extreme cases where either all axons or only the 0.1% fastest axons transmit β inputs. In the case where all axons transmit β activity and contributions from slow axons are mutually cancelled, transmission delays remain relatively stable with small increases while amplitudes decay exponentially as axon lengths increase. This implies that longer transmission channels intrinsically lead to increasingly more selective transmissions involving only the fastest axons. By contrast, when only the 0.1% fastest axons transmit β activity, delays relative to the fastest axons increase linearly with the simulated axon lengths, which reflects a relatively stable conduction speed in this scenario. In this case, amplitudes remain relatively unchanged at very low levels since only a small number of axons contribute to β transmission.

Figure 8.

Changes as a function of the lengths of the axons of (A) β transmission delays; (B) normalized rms amplitudes of the transmitted signals. These amplitudes resulted from summing the contributions of all axons transmitting β and dividing by the total number of axons simulated (10⁶) and by the rms amplitude of the input signal. Results for two cases are plotted: all axons transmit β activity (solid lines); only the 0.1% fastest axons transmit β activity (dashed lines).

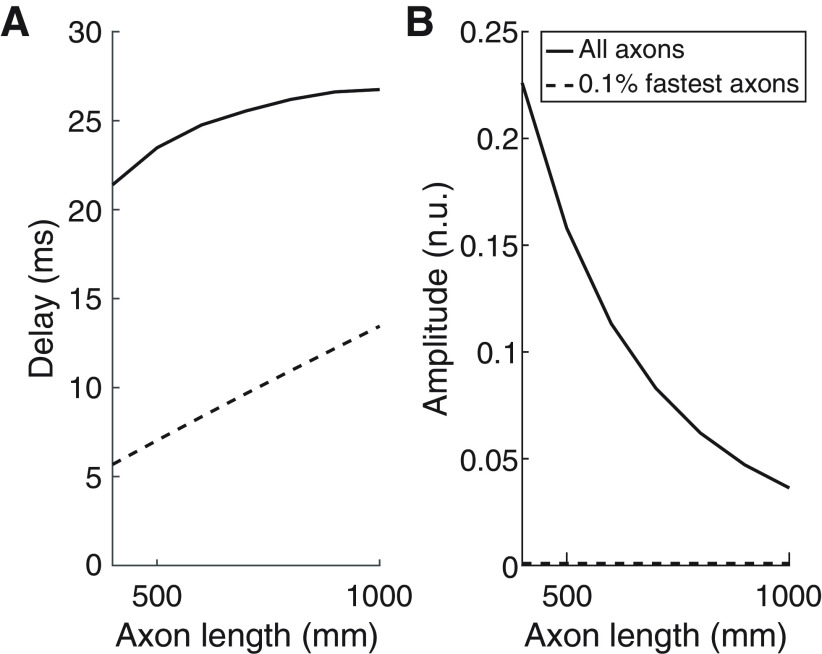
Finally, we studied how the frequency of the signals traveling through the simulated axons affected their transmission. Figure 9 shows transmission delays and amplitude of the transmitted signals through the simulated set of axons for the case in which the inputs are at frequencies within 8–12 Hz. In this case, the transmission delays when only the 0.1% fastest axons transmit signals are ∼15 ms shorter than in the scenario where all axons contribute to transmission. In terms of the amplitude of the transmitted signals, results do not change compared with when β activity is transmitted when only the 0.1% fastest axons transmit signals (amplitudes of ∼0.9 × 10⁻³). However, in the case where all axons contribute to signal transmission, amplitudes are nearly one order of magnitude higher than in the case where β is transmitted, which reflects that less signal cancellation is given when the transmitted signals are at lower frequencies.

Figure 9.

Changes as a function of the lengths of the axons of (A) transmission delays and (B) normalized rms amplitudes of the transmitted signals when white Gaussian noise bandpass-filtered between 8 and 12 Hz is transmitted. Results for two cases are plotted: all axons transmit alpha activity (solid lines); only the 0.1% fastest axons transmit alpha activity (dashed lines).

Discussion

Here, we propose and validate methods to improve delay estimates in the corticomuscular transmission of β rhythms. Applying these approaches to experimental data from human subjects revealed delays only a little greater than expected from the fastest corticospinal pathway. Most previous animal and human studies have worked exclusively on fast corticospinal transmission, because of unavoidable biases introduced by available recording and stimulation methods. Because much more is known about fast-conducting corticospinal components, it may be tempting to view our results as fitting comfortably with current knowledge. However, measuring propagation of endogenous β oscillations is not inherently biased according to conduction velocity. Recent studies have emphasized that fast-conducting fibers make up only a tiny fraction of the corticospinal tract (Firmin et al., 2014; Kraskov et al., 2019, 2020). We might expect corticomuscular coherence delays to be much longer, perhaps close to the average conduction delay across all corticospinal fibers, and indeed long corticomuscular delays have been reported previously, but using approaches which we show here can yield overestimates (Witham et al., 2010, 2011). The finding that delays using improved methods actually match those from the fastest fibers is an unexpected result, which provides an important insight into motor control.

Reliable estimates of cortical β transmission delay to muscles

We found three factors which could lead to erroneous delay estimates in previous studies, and showed using simulated and experimental data how to compensate for them to produce reliable measures. The first is the nature of the analysis applied to extract delays in a bidirectional system, such as between the cortex and muscles (Riddle and Baker, 2005; Baker, 2007). A common approach is to use directed coherence (Granger causality; Granger, 1969), and to measure the slope of the phase-frequency relationship (Witham et al., 2010, 2011). However, for bidirectional communication over a restricted bandwidth, delays are overestimated (Fig. 2). The peak time of the cumulant density yields unbiased delays, so long as the bandwidth is not very narrow (close to a pure sinusoid), a condition met by experimental data (Fig. 3).

When using directed coherence to estimate delays, constant phase shifts in one of the signals alter the offset of the regression line fitted to the phase-frequency relationship. This has no impact on delays, which are extracted from the regression slope. By contrast, a disadvantage of the cumulant density is that constant phase shifts change the peak time and hence the estimated delay. We know that corticospinal cells discharge with a ∼90° phase shift relative to local field potential oscillations (Baker et al., 2003), this phase shift can be corrected for by using the mathematical integral of the EEG (Baker et al., 2003).

A final relevant factor, often not considered previously, is the influence of the EMG. Surface EMG can be modeled using a cascade of multidimensional filters in time and space that replicate how the motor unit transforms motoneuron spiking to signals at the skin (Farina et al., 2002). The duration of the MUAP affects corticomuscular delay estimates (Williams and Baker, 2009). This can be avoided by decomposing EMG to SMUs, and instead using the pooled SMU spike train in analysis.

Corticomuscular β transmission is determined by the fastest corticospinal neurons

Our results indicate that corticomuscular β transmission delays are 1–2 ms longer than the onset latencies of MEPs evoked by TMS. It is a familiar argument when studying stimulus-evoked electrophysiological responses that the earliest responses must reflect the action of the fastest conducting pathway, with the smallest number of interposed synapses (Witham et al., 2016). The close match of MEP and β delays suggests that transmission is dominated by the fastest corticospinal neurons. The predominance of the fastest projections is unexpected, given that slowly-conducting neurons (<20 m/s) greatly outnumber fast ones (<3% of the population; Firmin et al., 2014). By simulating the summation of β signals transmitted with transmission delays distributed according to the neuroanatomical data of Firmin et al., (2014), we conclude that there are two different scenarios which might explain the results.

In the first scenario, all corticospinal neurons transmit β activity equally, but phase cancellation occurs between the contributions of slow corticospinal axons. This results from the characteristics of the delay distribution resulting from the axon diameter distribution (Fig. 7B). There is a sharp increase at short delays, and a long tail which declines gradually with long delays. While consistent with the delay estimates, this scenario has associated implications. Phase cancellation will also occur for transmission of frequencies outside the β band, but the extent will depend on an interaction of the oscillation frequency, conduction velocity distribution and conduction distance. This is observed when comparing transmission delays for β inputs and inputs in the 8- to 12-Hz band (Figs. 8, 9). Even slower delays would occur for the frequencies below 5 Hz, which typically characterize voluntary movements (Churchland et al., 2012). It seems implausible that the motor system could operate effectively with such long and frequency-dependent delays, unless descending motor commands to muscles were modulated at higher frequencies (Watanabe and Kohn, 2015).

A second implication of this possibility is that the amplitude of β activity reaching motoneurons should exponentially decay as the length of corticospinal axons increases (Fig. 8). This is at odds with empirical observations that corticomuscular coherence is larger in lower than upper limb muscles, although the central conduction distances are greater to lumbar than cervical spinal segments (Ushiyama et al., 2010).

An alternative scenario consistent with our results is that only a small proportion of corticospinal neurons with the fastest conduction velocity is effectively involved in transmitting β activity. In this case, β transmission delays would change proportionally to the axon lengths, and the β amplitudes of motoneuron inputs would be determined by the number of axons involved, with little appreciable cancellation. This seems more plausible, and better fits experimental data. Such selective β transmission could occur in two ways (which are not exclusive). First, β could only be carried down the corticospinal tract by fast axons. This would require that slow neurons are excluded from participating in the cortical circuitry which generates β oscillations. It is known that fast corticospinal cells do not just read out the activity of a cortical oscillator (Baker et al., 2003) but are an integral part of the oscillatory generator (Jackson et al., 2002). It is possible that the intracortical connections of slowly-conducting corticospinal cells do not place them within this network. Even if connections are not so specifically organized, aspects of the single cell physiology might have a similar effect. Low neural firing rates reduce the efficiency with which β oscillations are encoded in spike discharge (Baker et al., 2003; Lepage et al., 2011). Slowly conducting cells might have lower firing rates, although to date there is no data available to address this. In primate motor cortex, a wide range of pyramidal cells express the Kv3.1b channel (Soares et al., 2017). This could support more rapid repolarization after an action potential and hence higher firing rates, but does not seem to be restricted to only large cells which might contribute fast corticospinal axons.

Second, it is possible that, although slow corticospinal axons carry β oscillations to the cord, they do not make connections capable of propagating this activity to motoneurons. Spike triggered averaging in awake monkey suggests that some corticospinal fibers with slower conduction velocities can make monosynaptic connections to motoneurons [down to an estimated 12 m/s, applying the conduction distances quoted in Firmin et al. (2014) and Kraskov et al. (2019) to antidromic latencies in Lemon et al. (1986), a conclusion which is supported by work in anesthetized animals (Witham et al., 2016)]. However, whether the very slowest fibers make such contacts, and whether these are as strong or as frequent as for the fast fibers, remains unknown. In the corpus callosum, larger diameter axons give off larger synaptic boutons (Innocenti and Caminiti, 2017), suggesting that they generate stronger inputs in their target neurons; it is not known whether this correlation also exists for cortico-motoneuronal connections. The situation regarding indirect, oligosynaptic influences on motoneurons, and the relative balance there between fast and slow corticospinal inputs, is similarly lacking in experimental data at present.

The observation that only the fastest corticospinal projections are responsible for corticomuscular β coherence may allow a better understanding about how coherence is altered in certain conditions. For example, in humans with a stroke or with motor neuron disease, β corticomuscular coherence is reduced (Fisher et al., 2012; von Carlowitz-Ghori et al., 2014; Proudfoot et al., 2018). This may be because large corticospinal neurons are most vulnerable in these pathologies, and their loss leads to less reliable cortical transmission to muscles (Brownell et al., 1970; Kraskov et al., 2019).

Limitations

One limitation of the present study is that we used data on axon diameters at the level of the medullary pyramid and from macaque monkeys to approximate the distribution of fiber diameters in corticospinal projections to human motoneuron pools. The precise conclusions from our simulations will depend on how well this approximation holds. Additionally, our study only includes results for two muscles receiving a large amount of direct corticospinal contributions (Ushiyama et al., 2010), a generalization to other muscles with different proportions of efferent and afferent connections with cortex is unproven and should be tested in future works.