Abstract
Tau neurofibrillary tangles, a pathophysiological hallmark of Alzheimer’s disease (AD), exhibit a stereotypical spatiotemporal trajectory that is strongly correlated with disease progression and cognitive decline. Personalized prediction of tau progression is, therefore, vital for the early diagnosis and prognosis of AD. Evidence from both animal and human studies is suggestive of tau transmission along the brain’s preexisting neural connectivity conduits. We present here an analytic graph diffusion framework for individualized predictive modeling of tau progression along the structural connectome. To account for physiological processes that lead to active generation and clearance of tau alongside passive diffusion, our model uses an inhomogenous graph diffusion equation with a source term and provides closed-form solutions to this equation for linear and exponential source functionals. Longitudinal imaging data from two cohorts, the Harvard Aging Brain Study (HABS) and the Alzheimer’s Disease Neuroimaging Initiative (ADNI), were used to validate the model. The clinical data used for developing and validating the model include regional tau measures extracted from longitudinal positron emission tomography (PET) scans based on the 18F-Flortaucipir radiotracer and individual structural connectivity maps computed from diffusion tensor imaging (DTI) by means of tractography and streamline counting. Two-timepoint tau PET scans were used to assess the goodness of model fit. Three-timepoint tau PET scans were used to assess predictive accuracy via comparison of predicted and observed tau measures at the third timepoint. Our results show high consistency between predicted and observed tau and differential tau from region-based analysis. While the prognostic value of this approach needs to be validated in a larger cohort, our preliminary results suggest that our longitudinal predictive model, which offers an in vivo macroscopic perspective on tau progression in the brain, is potentially promising as a personalizable predictive framework for AD.
Keywords: Alzheimer’s disease, tau tangles, positron emission tomography, structural connectome, diffusion tensor imaging
1. Introduction
Alzheimer’s disease (AD) is a progressive neurodegenerative disorder which is the most prevalent form of dementia and is a looming public health challenge [1]. Extracellular amyloid-β (Aβ) plaques and intracellular tau neurofibrillary tangles are two misfolded protein aggregates implicated in AD pathophysiology [2]. These pathological proteins are known to appear in the brain long before the manifestation of clinical and cognitive symptoms and are key to the early diagnosis of AD during its preclinical (asymptomatic) phase [3–5]. Positron emission tomography (PET) radioligands that avidly and selectively bind to misfolded Aβ and tau have enabled 3D visualization and longitudinal quantitation of these proteins and catalyzed in vivo investigations on the biological underpinnings of this complex and heterogeneous disorder [6–9]. While the mechanistic basis of AD and the precise links between Aβ and tau aggregation remain unclear, key differences have been noted between the natures of these two underlying proteinopathies. Unlike Aβ, tau aggregation is strongly correlated with neurodegeneration and cognitive impairment [10–17]. The two proteins exhibit distinct trajectories of spatial spread as the disease progresses. Whereas Aβ travels from the neocortex to the brainstem and cerebellum, tau first appears in the locus coeruleus and the transentorhinal cortex, spreads to the entorhinal cortex and hippocampus, and finally ascends to the neocortex [18, 19]. While tau accumulation in the medial temporal lobe (MTL) is recognized as a feature of normal aging, its spread outside the MTL in conjunction with elevated Aβ is thought to mark the transition from the asymptomatic to the symptomatic phase of AD and the onset of cognitive impairment [20]. Methods to model and predict the spatiotemporal spread of tau are, therefore, vital for the early diagnosis and prognosis of AD.
The spatiotemporal propagation pattern of tau lies at the heart of the seminal Braak staging scheme for AD [2]. Recent studies using the PET radiotracer 18F-Flortaucipir have successfully recapitulated histopathological Braak staging in vivo both cross-sectionally [21–26] and longitudinally [27–29]. The stereotypic spatial topography and temporal trajectory of tau have led to the idea that tau may spread from cell to cell via anatomical or synaptic connectivity in a prion-like fashion [30–33]. Initial evidence for this hypothesis emerged from animal models [34–36]. In vivo imaging studies in humans using 18F-Flortaucipir PET have lent further support to this idea by demonstrating strong region-specific associations between regional mean or covariance measures derived from tau PET and localized measures of structural [37] or functional [38–40] connectivity. Graph theory metrics have been used to investigate the temporal directionality in longitudinal Aβ and tau datasets [41]. Building on seminal work on network diffusion models (NDMs) for neuropathological spread [42, 43], we published, as part of our prior work, a proof of concept of structural connectivity dependent tau spread using human 18F-Flortaucipir PET and diffusion tensor imaging (DTI) data from the Harvard Aging Brain Study [44]. Very recently, a landmark paper featuring an epidemic spread model (ESM) for tau provided rigorous clinical validation of a connectivity-based approach for tau prediction [45]. Underlying both NDM and ESM is the idea of propagation of pathophysiological entities along the brain’s preexisting, stereotyped neural connectivity conduits captured mathematically by a graph Laplacian matrix (in NDMs) or an equivalent anatomical connection probability matrix (in ESMs). Compared to the ESM [46], which is a probabilistic model, the NDM [42, 43, 47] takes an analytic and deterministic approach based on graph-domain partial differential equations (PDEs) and, therefore, is more intuitive and computationally efficient. Existing literature on NDMs, however, is based either on PDEs that are homogeneous (source-free) and rely on passive diffusion or on PDEs with impulse sources sporadically distributed in time. While these frameworks provide qualitative explanations for disease spread and enable source inference, they are less suitable for modeling the simultaneous accretion and propagation of tau for quantitative prediction. Here, we use an analytic graph diffusion approach to quantitatively model the aggregation and propagation of tau along the structural network of the brain.
While passive diffusion from localized sources can qualitatively characterize the spread of misfolded proteins or surrogate measures like atrophy [47, 48], spatiotemporal impulses do not capture the continuous proteopathic seeding processes that underlie tau aggregation [49, 50]. Tau molecular “seeds” are thought to be monomeric or oligomeric forms of the protein that recruit monomeric tau and facilitate misfolding [51]. Recent histological data suggest high expression of seed proteins in the entorhinal cortex, some downstream sites along the Braak pathway, and some white matter tracts [52]. New studies have also emphasized the role of Aβ in potentiating the seeding processes that lead to misfolding [53, 54]. Evidence from cell lines suggests a sigmoidal evolution of tau seeding featuring an exponential growth phase [49]. Concomitantly with seeding that leads to misfolded tau accretion, tau clearance is mediated by a combination of proteasomal and autophagic degradative processes [55, 56] with increased emphasis being placed on peripheral pathways and the glymphatic system [57, 58]. While the exact mechanisms of tau clearance remain an active area of research, they are a key therapeutic target for tauopathies [59]. Clearance mechanisms have been previously incorporated in spread models for misfolded proteins [46, 60]. To accommodate the cumulative effects of tau seeding and removal, our model is based on an inhomogeneous PDE that includes a source term capturing local trends of active generation and clearance alongside passive diffusion along the structural network of the brain.
In this work, we use regional tau measures derived from longitudinal 18F-Flortaucipir tau PET data collected at two and three timepoints as part of the Harvard Aging Brain Study [61, 22]. We perform additional validation on three-timepoint 18F-Flortaucipir tau PET scans from the Alzheimer’s Disease Neuroimaging Initiative database. Unlike previous works that have modeled misfolded protein dynamics starting from one or more focal point sources and tested the goodness of fit using single-timepoint observations, we model tau seeding and clearance as a continuous-time process and quantitatively validate our model predictions using 18F-Flortaucipir PET measures at a future timepoint. Instead of a population-level healthy structural or functional connectome as used in most prior studies on neuropathological spread, we use structural connectivity information extracted from individual diffusion-weighted magnetic resonance imaging (MRI) scans. Our model allows us to separate passive diffusion trends from active generation/clearance trends for each anatomical region-of-interest (ROI). In section 2, we derive closed-form analytic solutions for two inhomogeneous graph diffusion PDEs both based on continuous-time source functionals – one linear in time and another exponential. We then present data acquisition and processing details. Our main findings are reported in section 3. We demonstrate model fitting using two-timepoint data and validate the model in three-timepoint datasets. Finally, in sections 4 and 5, we summarize this work, discuss its strengths and limitations, and present our envisioned future directions.
2. Methods
2.1. Theory
The spread of a physiological variable can be modeled as a diffusion process along the brain’s structural connectome using a graph diffusion equation. The network underlying the diffusion process is defined as a graph where the ith node, , represents the ith gray matter parcellation or anatomical ROI, is the number of ROIs, and represents the connectivity strength between node νi and node νj. To model the spread of pathological tau species along the brain’s structural network, we represent the regional tau burden as a time-varying graph signal vector , , where t is a scalar time variable. x(t) is the solution to a first-order PDE, usually referred to as the network diffusion equation:
| (1) |
where is the normalized graph Laplacian matrix. Solutions to the homogeneous PDE shown in (1) are of the form:
| (2) |
where x(t0) is the initial tau burden at time t0. To model active generation or clearance alongside passive spread, a source term, s(t), can be added to (1) leading to an inhomogeneous PDE:
| (3) |
Analytic graph diffusion models have evolved from purely qualitative models based on passive diffusion [42] to those that incorporate impulse sources of brain atrophy [47, 62]. While past work on NDMs has reported high correlations between observed atrophy and predicted atrophy based on inferred point sources earlier in time, quantitative predictions using serialized measures entails modeling of seeding and clearance processes between timepoints. The first model tested here assumes a spatially heterogeneous source linearly varying in time. Building on empirical evidence that tau seeding is a sigmoidal process with an exponential phase after an initial lag, the second model is based on an exponential source term. For both models, the solution to (3) can be computed as a sum of the solution to the homogeneous counterpart and an integral that is derived from the source term as follows:
| (4) |
2.1.1. Linear Source Model
The first model assumes that tau model production and clearance follow a spatially heterogeneous and temporally linear source term s(t) formulated as:
| (5) |
Here is a linear rate vector. The corresponding PDE is given by:
| (6) |
The integrand in (4) for the source term in (5) is:
| (7) |
Using the matrix integration by parts formula, we get the following solution to the inhomogeneous PDE in (6):
| (8) |
We use the eigenvalue decomposition of the Laplacian, L = QΛQ−1 and utilize special properties of products of matrix exponentials to simplify the terms as follows:
| (9) |
The time gap between two sequential PET scans in the HABS cohort is about 2 years. Accounting for the slow pace of tau accumulation in this time frame, we linearize this equation to obtain:
| (10) |
where Δt = t − t0 and is the identity matrix. The inter-scan time, Δt, is a known entity for each individual. To fit the resultant model to a two-timepoint dataset, we solve for the model parameters β and r by minimizing the following cost function:
| (11) |
where we denote x(t0) as x0 and x(t) as xt and summarize the model as a function f(x0, β, r) of the unknown parameters. We adopt a gradient descent strategy to solve the optimization problem. The gradient derivation is provided in the appendix. To ensure that we have reached the global minimum, we use a multi-start approach with random initializations.
2.1.2. Exponential Source Model
The second model seeks to emulate an exponential seeding profile by defining a source term featuring a global parameter σ governing the rate of production/clearance and a spatially heterogeneous entity , which captures production or clearance of tau at different ROIs. The resultant source term is formulated as:
| (12) |
The corresponding PDE is given by:
| (13) |
We computed the solution to this equation in closed form from (4) and (12) as:
| (14) |
As with the linear source model, given the proximity of serial scans, we approximate this model and express it in terms of Δt = t − t0 as follows:
| (15) |
To fit this model to a two-timepoint dataset, we solve for the model parameters β, α, and r by minimizing the following cost function:
| (16) |
where we denote x(t0) as x0 and x(t) as xt and summarize the model as a function f(x0, β, α, σ) of the unknown parameters. Once again, we use gradient descent to minimize the cost function. The gradient derivation is provided in the appendix. We used a multi-start approach with random initializations to attain global minima.
2.2. Data Description
2.2.1. Participants
The overall workflow is summarized in Fig. 1. Our model validation relies on two independent data sources: the Harvard Aging Brain Study (HABS) and the Alzheimer’s Disease Neuroimaging Initiative (ADNI). We use longitudinal structural MRI, diffusion MRI, and 18F-Flortaucipir PET imaging for tau from both repositories. Additionally, for each HABS data sample, we utilize our knowledge of each individual’s Aβ-status derived from 11C-Pittsburgh Compound-B (PiB) PET imaging.
Figure 1:
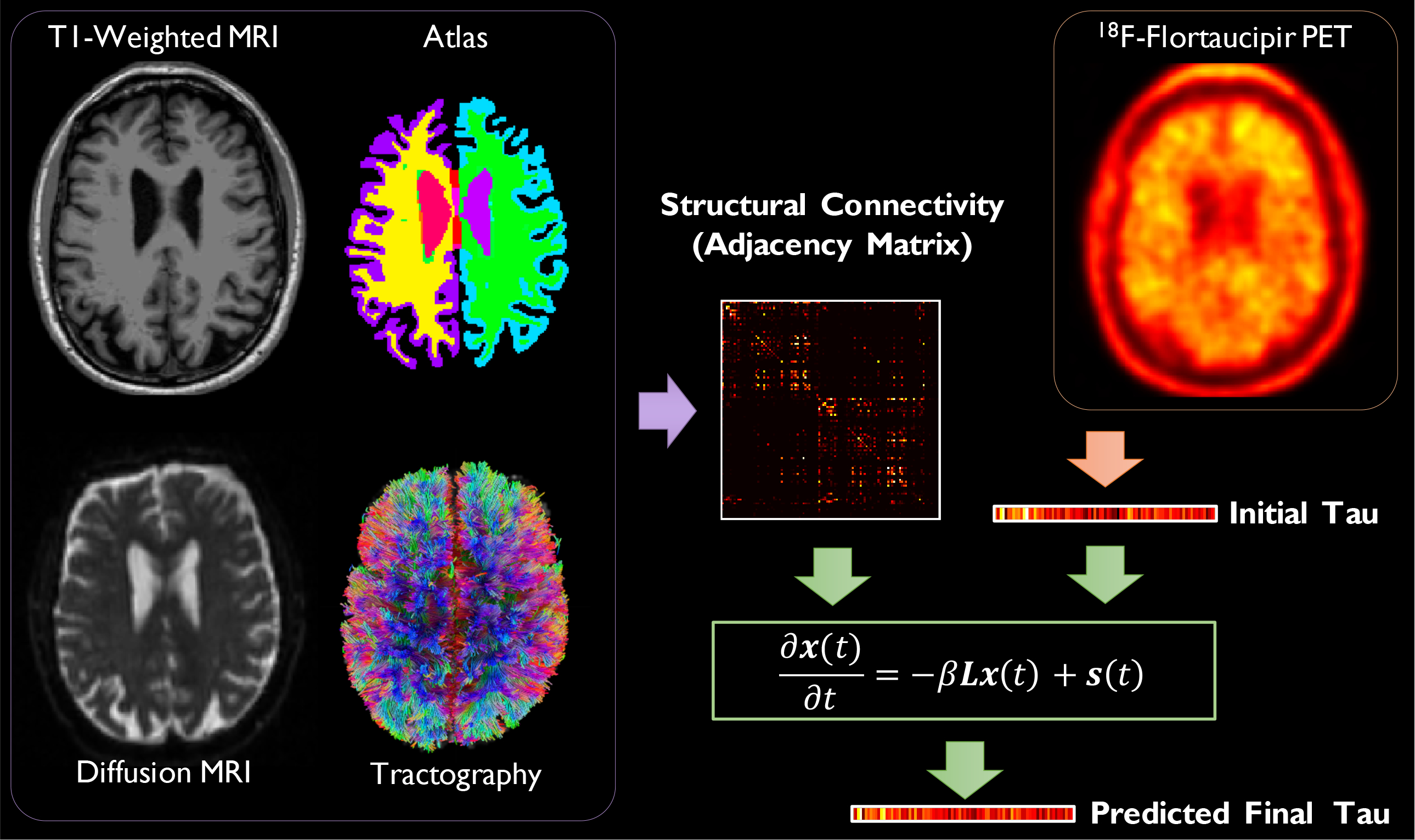
Overall workflow showing sample images: T1-weighted MRI, the warped anatomical atlas, diffusion MRI, white matter fiber tracts, and 18F-Flortaucipir PET. The atlas is generated from FreeSurfer parcellation of the T1-weighted MR image. White matter fiber tracts are reconstructed from diffusion MRI via tractography. Fiber counting is performed on the segmented diffusion image volumes to derive pairwise inter-ROI connection strengths thereby yielding a graph adjacency matrix, from which a weighted Laplacian is computed. ROI means from 18F-Flortaucipir PET constitute the initial regional tau burden at baseline and are represented as a graph signal vector. The predicted final tau at follow-up is computed by solving an inhomogeneous PDE.
HABS is an ongoing longitudinal study designed to further our understanding of what differentiates normal aging from preclinical AD. Preclinical AD refers to the presymptomatic stage of AD which is usually tracked using pathophysiological biomarkers, e.g., Aβ and tau measures from PET or cerebrospinal fluid [63]. HABS participants who underwent 3T diffusion-weighted MRI scans at baseline and subsequently underwent serial 18F-Flortaucipir PET scans at two or three timepoints were included in our data analysis. All participants were cognitively normal (CN) elderly individuals. Of the n = 68 HABS participants used in this work, 59 had only two 18F-Flortaucipir scans (baseline and follow-up), while the remaining nine had a third 18F-Flortaucipir scan (baseline and two follow-ups). Henceforth, we will refer to these two subsets as the HABS-2TP (two-timepoint) and HABS-3TP (three-timepoint) datasets respectively. The HABS-2TP dataset is used for parameter computation and assessing the goodness of model fitting while the HABS-3TP dataset is utilized for validation of downstream prediction of tau.
ADNI is a multisite study that features serial collection of neuroimaging, neuropsychological, biochemical, genetic, and other measures from cognitively normal and impaired human subjects (http://adni.loni.usc.edu/). In our work, we use data from n = 22 ADNI3 participants who underwent 3T MRI and 18F-Flortaucipir PET scans at baseline and subsequently underwent serial MRI and 18F-Flortaucipir PET scans after 24- and 48-month followup timepoints. 10 of these subjects are elderly CN individuals, 7 had mild cognitive impairment (MCI), and 5 were AD patients. Henceforth, we will refer to this dataset as the ADNI-3TP (three-timepoint) dataset. Aβ PET scans are not available for all subjects in the ADNI-3TP dataset. Therefore, we do not consider ADNI Aβ-status in our analysis.
Table 1 presents a summary of participant demographics. The time gap between the DTI scan and the baseline 18F-Flortaucipir PET is indicated as ΔtDTI-PET. HABS uses the average PiB distribution volume ratio in frontal, lateral temporoparietal, and retrosplenial (FLR) ROIs for Aβ quantitation. This measure is reported in the “PiB FLR” column.
Table 1:
Participant demographics*
| Dataset | n (female) | Age (yrs.) | ΔtDTI-PET (yrs.) | MMSE | CDR | PiB FLR |
|---|---|---|---|---|---|---|
| HABS-2TP | 59 (35) | 76.07 ± 6.22 | 2.27 ± 1.03 | 29.29 ± 1.05 | 0 ± 0.07 | 1.48 ± 0.50 |
| HABS-3TP | 9 (1) | 74.19 ± 5.08 | 2.37 ± 0.46 | 28.67 ± 1.58 | 0 ± 0 | 1.48 ± 0.28 |
| ADNI-3TP | 22 (17) | 73.80 ± 9.55 | −0.05 ± 0.23 | 27.55 ± 3.43 | 0.20 ± 0.33 | N/A |
Values are in the format mean ± standard deviation
MMSE: Mini-Mental State Examination
CDR: Clinical Dementia Rating
2.2.2. Data Acquisition
For the HABS dataset, all MRI scanning was performed on a Siemens Tim Trio 3T imaging system with a 12-channel phased-array head coil. T1-weighted scans were based on a Magnetization Prepared Rapid Gradient-Echo (MPRAGE) sequence with a voxel size of 1.05×1.05×1.2 mm3. The diffusion-weighted scans were acquired using a spin-echo echo-planar imaging sequence: echo time (TE) 84 ms, repetition time (TR) 8,040 ms, field-of-view (FOV) 256×256×128, voxel size 2 mm isotropic with 30 isotropically distributed orientations for the diffusion-sensitizing gradients at a b-value of 700 s/mm2. PET scans were performed on a Siemens ECAT PET HR+ scanner (3D mode, 63 image planes, 15.2 cm axial FOV, 5.6 mm transaxial resolution, and 2.4 mm slice interval). For PiB PET scans, an 8.5–15 mCi bolus injection was immediately followed by a 60-minute dynamic acquisition. 18F-Flortaucipir PET data were acquired for the 80 to 100 minute time window following a 10 ± 1 mCi bolus injection. Serial tau PET imaging was conducted with intervals of 25.5 ± 8.4 months between consecutive scans.
For the ADNI dataset, all MRI data was obtained on Siemens Prisma 3T scanners. T1-weighted anatomical scans were based on an MPRAGE sequence with voxel size 1×1×1 mm3, FOV 208×240×256, TE 3 ms, TR 2,300 ms, and inversion time (TI) 900 ms. The diffusion-weighted scans were acquired with TE 56 ms, TR 7,200 ms, FOV 232×232×160, voxel size 2 mm, and diffusion-sensitizing gradients at a b-value of 1000 s/mm2. 18F-Flortaucipir PET data were acquired for the 75 to 105 minute time window following a 10±1 mCi bolus injection. Serial tau PET imaging was conducted with intervals of 24 months between consecutive scans.
2.3. Data Processing
2.3.1. Computation of Tau Measures
T1-weighted MRI preprocessing was performed using FreeSurfer v6.0 [64, 65]. We utilized the FreeSurfer based auto-reconstruction process that incorporates motion correction, intensity normalization, skull stripping, and linear and nonlinear volumetric registration leading to anatomical (cortical and subcortical) parcellations.
PET images were rigidly coregistered to the T1 MR images using FSL [66–68]. FreeSurfer ROIs defined by MR as described above were transformed into the PET native space. For both HABS and ADNI, standardized uptake value ratios (SUVRs; cerebellar gray matter reference) were computed for 18F-Flortaucipir PET. For HABS PiB PET scans, and distribution volume ratios (DVRs; cerebellar reference) were computed, and Aβ+/− status was determined by using a cutoff of 1.20 on the PiB FLR DVR.
85 ROIs were retained from the 112 regions defined by the FreeSurfer Desikan-Killiany atlas after discarding white matter ROIs and ROIs that are known to have high off-target binding. We extracted mean SUVRs for the 85 ROIs to form an 85 × 1 intensity vector from each 18F-Flortaucipir PET image.
2.3.2. Structural Connectome Computation
The diffusion MRI scans were preprocessed using FSL to correct discrepancies arising from subject motion, eddy current distortion, and susceptibility. Diffusion tensors were reconstructed using DSI Studio, and deterministic fiber tracking was performed to obtain the streamlines between different brain regions. Whole-brain seeding was used. The termination criterion was decided by fractional anisotropy. An “end in region” criterion was applied to retain only those streamlines that end in an ROI thereby ensuring that the final set of streamlines are representative of the actual inter-ROI connectivity. We used an angular threshold of 45°, an anisotropy threshold of 0.6 times Otsu’s threshold (effective range of 0.14 to 0.45 across the subjects), a total of 50,000 seeds, and a fiber length range of 30 to 300 mm. The fiber trajectories were smoothed by averaging the propagation direction with 40% of the previous direction. We used identical parameter settings for all participants.
The tracts were normalized by length, and only those ending in the 85 retained gray-matter ROIs from the FreeSurfer Desikan-Killiany atlas were considered. The streamlines between each pair of ROIs were counted to generate pairwise inter-ROI connection strengths. Individual 85×85 adjacency matrices were thus created for ROI-based analysis to capture individualized structural connectivity profiles for each human subject. Normalized weighted Laplacian matrices were computed from the adjacency matrices.
2.3.3. Model Implementation and Validation
Model parameters for both the linear and exponential source models were fitted by minimizing the cost functions in (11) and (16) respectively. The cost functions were iteratively minimized using an alternating gradient strategy with the linear parameters (e.g., the vector parameters α and r) and the nonlinear parameters (e.g., the scalar parameters β and σ) updated in sequential sub-iterations. All gradients were computed analytically as described in the appendix. The HABS-2TP dataset was used to demonstrate model fitting performance. The HABS-3TP and ADNI-3TP datasets were used for independent validation at the third timepoint. For assessment of model fitting in the HABS-2TP dataset and prediction accuracy in the HABS-3TP and ADNI-3TP datasets, we compare predicted and observed SUVRs and differential SUVRs (dSUVRs). We use the normalized root-mean-square error (NRMSE) and the normalized mean absolute error (NMAE) between the observed and predicted SUVRs and dSUVRs as quantitative and objective figures-of-merit to assess model performance. The NRMSE is based on an L2 norm of the differences between observed and predicted measures, while the NMAE is based on the L1 norm. While both metrics are quantitative in nature, they penalize larger and smaller errors to different relative extents. Both metrics are, therefore, used for robust assessment of model accuracy.
3. Results
3.1. Goodness of Fit in HABS-2TP Data
Parameter fitting was done for individual subjects in the HABS-2TP dataset using the linear and exponential source models. Recent literature highlights the predictive value of tracking the longitudinal change in inferior temporal lobe (IFT) tau [29]. Accordingly, in our analysis, we separate individuals with more than 1% increase in IFT tau burden from baseline to follow-up (tau ↑) from those with no discernible increase (< 1%) in IFT tau burden from baseline to follow-up (tau ).
We also separate the subjects based on their Aβ status into Aβ+ and Aβ− categories. Furthermore, since tau evolution can be conceptualized as a slow-moving process, a high degree of correlation could exist between the two timepoints. Therefore, alongside computing ROI mean SUVRs to assess goodness of fit, we also computed dSUVRs. Fig. 2 depicts observed and predicted mean SUVRs and dSUVRs in 10 ROIs deemed critical for tau in preclinical AD for two representative individuals – a tau ↑ subject and a tau subject. These ROIs were selected for visualization based on recent literature that identified several regions in the brain that optimally capture longitudinal change early in the Alzheimer’s continuum [27, 69]. While there is good agreement between observed and predicted SUVRs for both the linear and exponential source models, the latter more robustly estimates dSUVRs. Table 2 shows quantitative metrics for the goodness of fit, namely the NRMSE and NMAE between the observed and predicted SUVRs and dSUVRs for all ROIs. Consistent trends for the two metrics, as observed here, are indicative of robustness, as the two metrics penalize larger and smaller errors to different extents. The exponential source model led to smaller errors in dSUVRs than the linear model for all subjects and for the tau ↑ and tau subgroups. We also separately report performance for Aβ+ and Aβ− cases. The exponential source model performed better in the tau ↑ subgroup, which features a greater proportion of signal over noise in the dSUVRs, compared to the tau subgroup, which exhibits relatively subtle longitudinal changes that are more susceptible to noise-induced variations. The reverse was true for the linear source model. In comparison, there was a smaller difference in the data fidelity metrics between the Aβ+ and Aβ− groups. This could be explained by the fact that the Aβ+ subgroup in our cohort includes many tau subjects, while the Aβ− subgroup includes many tau ↑ subjects.
Figure 2:
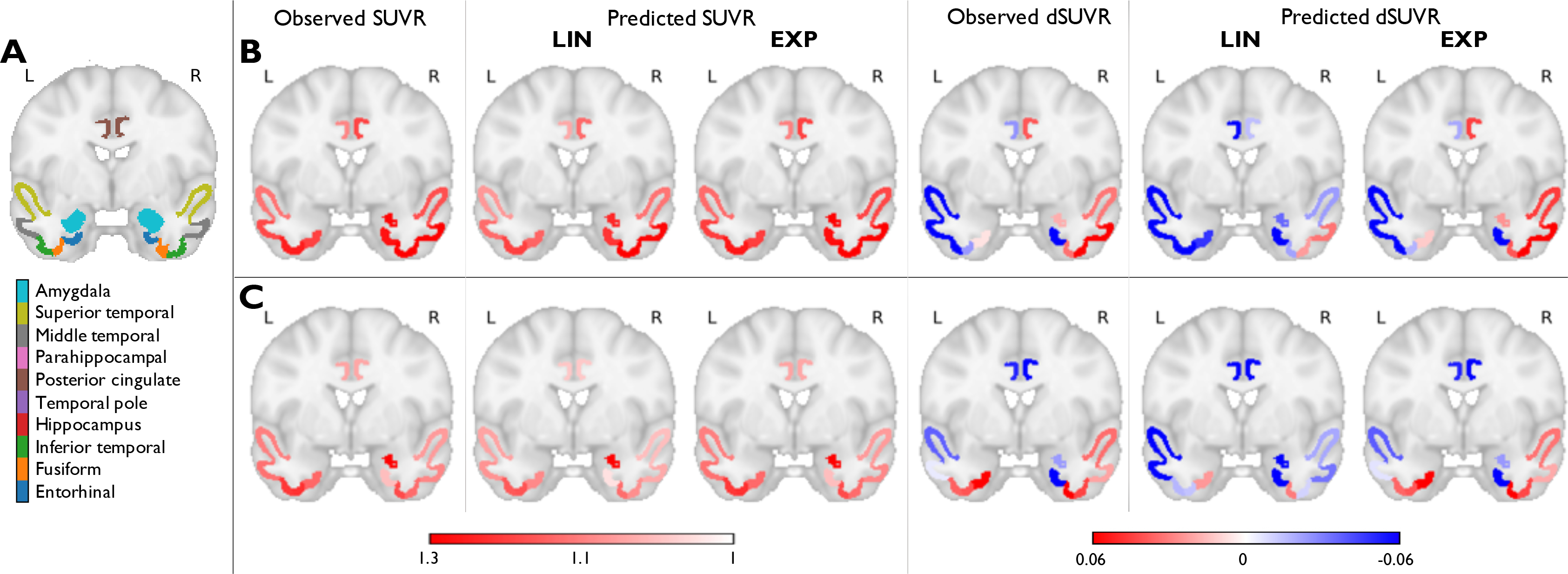
Fitting results using the linear (LIN) and exponential (EXP) source models in the HABS-2TP dataset. (A) A coronal slice in MNI152 space showing 10 ROIs deemed critical for tau in early AD. The ROIs (based on the FreeSurfer Desikan-Killiany atlas) are overlaid on the MNI template. Observed and predicted ROI mean SUVRs and dSUVRs in (B) A subject with increasing IFT tau between baseline and follow-up and (C) A subject with no significant increase in IFT tau between baseline and follow-up.
Table 2:
Model fitting accuracy in the HABS-2TP dataset*
| Metrics | NRMSE | NMAE | ||||||
|---|---|---|---|---|---|---|---|---|
| Model | LIN | EXP | LIN | EXP | ||||
| Group (n) | SUVR | dSUVR | SUVR | dSUVR | SUVR | dSUVR | SUVR | dSUVR |
| All (59) | 0.0370 | 0.0869 | 0.0227 | 0.0532 | 0.0365 | 0.0857 | 0.0147 | 0.0345 |
| Tau ↑ (27) | 0.0412 | 0.1011 | 0.0171 | 0.0421 | 0.0407 | 0.0999 | 0.0106 | 0.0260 |
| Tau (32) | 0.0365 | 0.0859 | 0.0272 | 0.0639 | 0.0360 | 0.0846 | 0.0189 | 0.0444 |
| Aβ+ (21) | 0.0391 | 0.0966 | 0.0247 | 0.0612 | 0.0388 | 0.0959 | 0.0149 | 0.0369 |
| Aβ− (38) | 0.0378 | 0.0998 | 0.0227 | 0.0599 | 0.0372 | 0.0981 | 0.0153 | 0.0404 |
LIN: linear source model; EXP: exponential source model
3.2. Model Interpretation
To facilitate model interpretation, we separately examine the propagative and generative components for the exponential source model. Fig. 3 shows a connectogram summarizing the results of model fitting. The plot uses a circular layout with all fitted ROIs indicated on the outer annulus (Annulus 4). The inter-ROI links in the center offer a population-level snapshot of structural connectivity with the link thickness commensurate with pairwise connection strengths scaled by the reciprocal of the ROI size (scaling done for improved visibility). The critical ROIs highlighted in Fig. 2 and their connectivities are indicated in red. In a graph diffusion model, −Lx(t) is proportional to the rate of aggregation in each ROI purely due to passive diffusion from its connected neighbors. Annulus 1 depicts for each ROI a bar graph of the distribution of Lx(t) across subjects sorted from most negative (inward diffusion or accumulation – yellow) to most positive (outward diffusion or dissipation – green). Based on the sign of the median value of this measure, each ROI can be determined to be either a dissipator or an accumulator. In the exponential source model in (13), the vector α acts as a source/producer or sink/remover depending on its sign and could be linked to the physiological processes of seeding or clearance. Annulus 2 depicts for each ROI a bar graph of the distribution of α across subjects sorted from most negative (remover or sink – blue) to most positive (producer or source – red). Based on the sign of the median value of this measure, each ROI can be determined to be either a source or a sink. All ROIs can be placed into one of four classes depending on its source/sink and accumulator/dissipator status based on medians. This overall classification is indicated in Annulus 4 for four cross-sectional subgroups: (1) Tau , Aβ−, n = 21, (2) Tau , Aβ+, n = 11, (3) Tau ↑, Aβ−, n = 17, and (4) Tau ↑, Aβ+, n = 10. This analysis suggests that several of the ROIs critical in early AD switch classes from sink+dissipator to source+dissipator when the tau or Aβ status changes.
Figure 3:
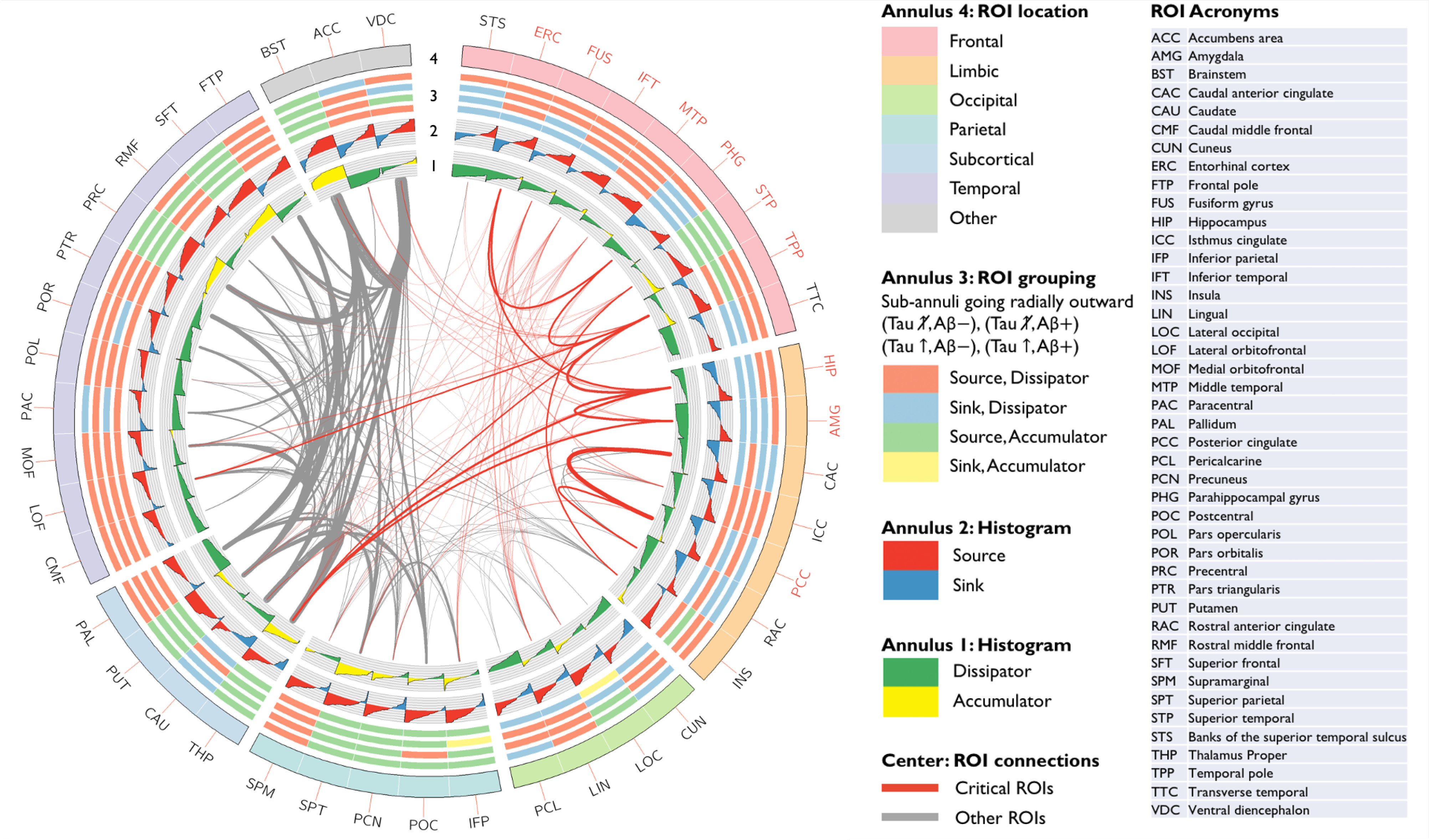
A connectogram summarizing model-fitting results. All ROIs are indicated on the outer annulus (Annulus 4) and color-coded based on their anatomical location. The inter-ROI links in the center offer a population-level snapshot of structural connectivity with the link thickness commensurate with pairwise connection strengths scaled by the reciprocal of the ROI size (scaling done for improved visibility). All fibers connected to the critical ROIs indicated in Fig. 2 are shown in red. Annulus 1 shows for each ROI a bar graph of the distribution of a diffusion measure across subjects sorted from most negative (inward diffusion or accumulation – yellow) to most positive (outward diffusion or dissipation – green). Annulus 2 shows for each ROI a bar graph of the distribution of the source/sink strength across subjects sorted from most negative (sink/remover – blue) to most positive (source/producer – red). All ROIs can be placed into one of four classes depending on its source/sink and accumulator/dissipator status. Annulus 3 shows this overall classification for four subject groups corresponding to the sub-annuli going radially outward: (Tau , Aβ−), (Tau , Aβ+), (Tau ↑, Aβ−), (Tau ↑, Aβ+).
Whereas the entorhinal cortex (ERC) and the IFT regions are a source+dissipator in all but the tau , Aβ− subgroup, the hippocampus (HIP) is a source+dissipator only for tau ↑ cases while the the amygdala (AMG) and the parahippocampal gyrus (PHG) are a source+dissipator only for the tau ↑, Aβ+ subgroup. While these groupings are cross-sectional, the sequence is consistent with a recently reported tau seeding assay suggesting that the HIP and PHG are prominent downstream sites of seeding following the ERC [52]. This sequence of seeding sites is also consistent with the Braak pathway. As per the histological evidence underlying Braak’s landmark paper [2], whereas stage I is associated with isolated or low levels of neurofibrillary tangles in the trans-ERC and ERC sub-regions, the new areas recruited in stage II include pyramidal cells in the HIP and the AMG. The connectivity profile in our data also confirms strong ERC-HIP, ERC-PHG, and HIP-AMG connectivity.
3.3. Model Validation with HABS-3TP Data
To test the model’s predictive capability of downstream tau aggregation from baseline, we validated the model using the HABS-3TP cohort. The model parameters are fitted by utilizing the first two timepoints, while prediction accuracy is assessed at the third timepoint. It should be noted that the parameter fitting step is not allowed access to any data from the third timepoint.
Fig. 4 shows observed and predicted mean SUVRs and dSUVRs in the 10 ROIs that are critical for tau in preclinical AD for two representative individuals – a tau ↑ subject and a tau subject from the HABS-3TP cohort. Table 3 presents NRMSE and NMAE between the observed and predicted SUVRs and dSUVRs for all ROIs.
Figure 4:
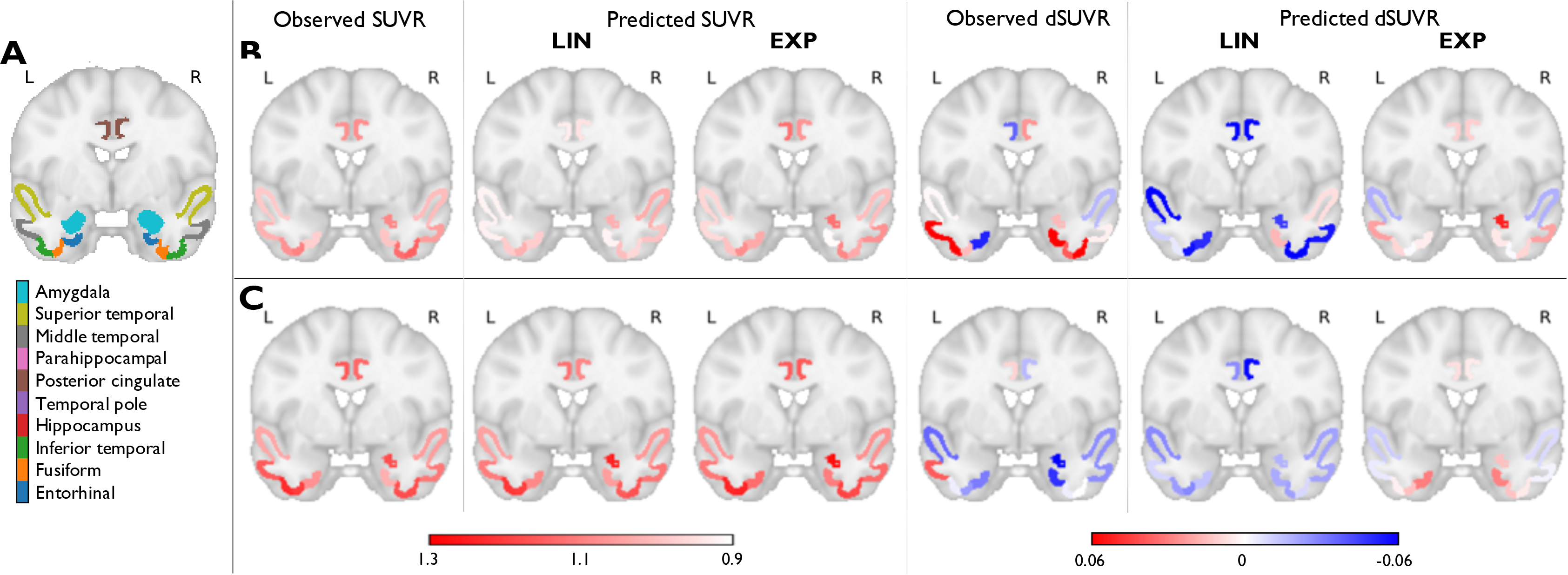
Prediction results using linear (LIN) and exponential (EXP) source models in the HABS-3TP dataset. (A) A coronal slice in MNI152 space showing 10 ROIs deemed critical for tau in early AD. The ROIs (based on the FreeSurfer Desikan-Killiany atlas) are overlaid on the MNI template. Observed and predicted ROI mean SUVRs and dSUVRs in (B) A subject with increasing IFT tau between baseline and follow-up and (C) A subject with no significant increase in IFT tau between baseline and follow-up.
Table 3:
Prediction accuracy in the HABS-3TP dataset
| Metrics | NRMSE | NMAE | ||||||
|---|---|---|---|---|---|---|---|---|
| Model | LIN | EXP | LIN | EXP | ||||
| Group (n) | SUVR | dSUVR | SUVR | dSUVR | SUVR | dSUVR | SUVR | dSUVR |
| All (9) | 0.1722 | 0.1804 | 0.0941 | 0.0985 | 0.1217 | 0.1274 | 0.0635 | 0.0665 |
| Tau ↑ (6) | 0.1785 | 0.1869 | 0.1195 | 0.1113 | 0.1287 | 0.1349 | 0.0778 | 0.0725 |
| Tau (3) | 0.1813 | 0.4610 | 0.0644 | 0.1610 | 0.1183 | 0.3009 | 0.0489 | 0.1222 |
| Aβ+ (6) | 0.1913 | 0.2004 | 0.0876 | 0.0918 | 0.1418 | 0.1486 | 0.0753 | 0.0789 |
| Aβ− (3) | 0.1503 | 0.3417 | 0.0633 | 0.1439 | 0.0972 | 0.2210 | 0.0474 | 0.1078 |
LIN: linear source model; EXP: exponential source model
The degradation of performance from the model fitting task to the prediction task is an expected outcome as the third timepoint is not previously seen by the model and also because, in many regions, the differential fitted by the model is dominated by noise. The relative performance of the exponential and linear source models at the prediction task is consistent with the model fitting results.
3.4. Secondary Validation with ADNI-3TP Data
For additional validation, we tested the predictive capability of our model on the ADNI-3TP dataset. Model fitting and prediction steps similar to those performed for HABS were repeated on this cohort. Fig. 5 shows observed and predicted mean SUVRs and dSUVRs in the 10 tau-critical ROIs for two representative individuals – a tau ↑ subject and a tau subject from the ADNI-3TP cohort. Table 4 presents NRMSE and NMAE between the observed and predicted SUVRs and dSUVRs for all ROIs. The trends in the ADNI results are consistent with those in HABS results that confirming the overall robustness of the predictive model.
Figure 5:
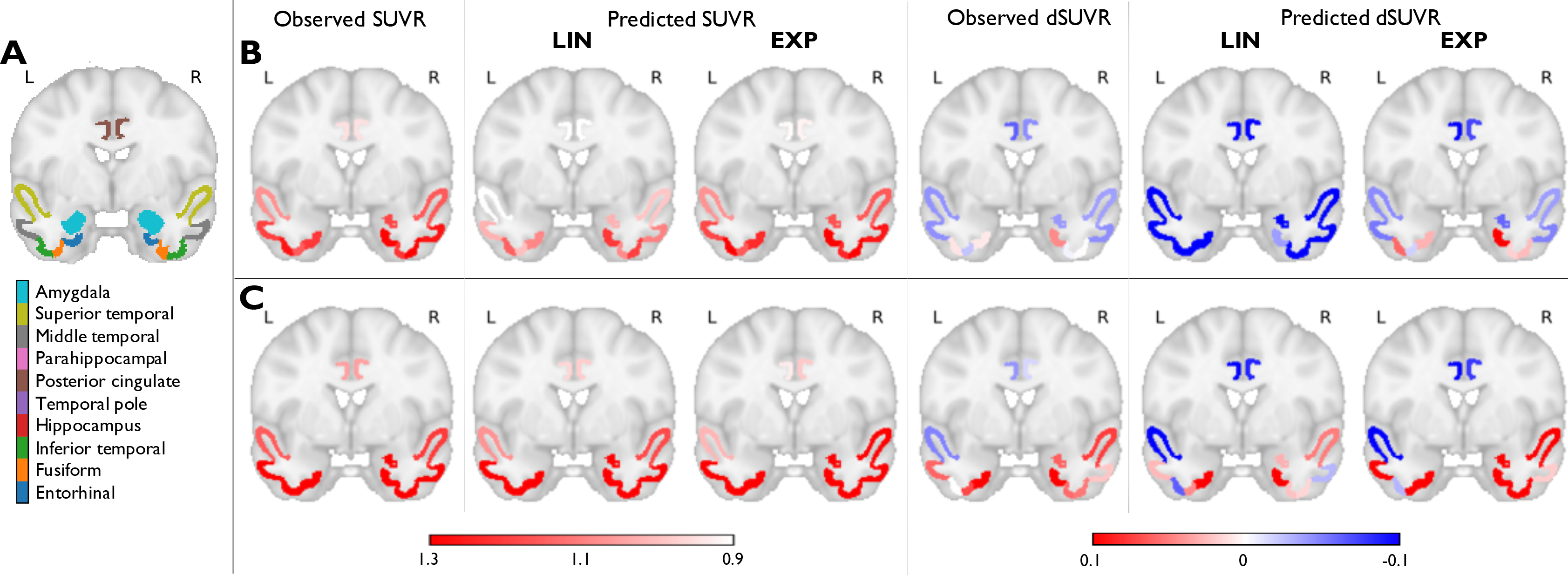
Prediction results using linear (LIN) and exponential (EXP) source models in the ADNI-3TP dataset. (A) A coronal slice in MNI152 space showing 10 ROIs deemed critical for tau in early AD. The ROIs (based on the FreeSurfer Desikan-Killiany atlas) are overlaid on the MNI template. Observed and predicted ROI mean SUVRs and dSUVRs in (B) A subject with increasing IFT tau between baseline and follow-up and (C) A subject with no significant increase in IFT tau between baseline and follow-up.
Table 4:
Prediction accuracy in the ADNI-3TP dataset
| Metrics | NRMSE | NMAE | ||||||
|---|---|---|---|---|---|---|---|---|
| Model | LIN | EXP | LIN | EXP | ||||
| Group (n) | SUVR | dSUVR | SUVR | dSUVR | SUVR | dSUVR | SUVR | dSUVR |
| All (22) | 0.0829 | 0.2754 | 0.0442 | 0.1470 | 0.0724 | 0.2406 | 0.0308 | 0.1023 |
| Tau ↑ (10) | 0.1006 | 0.3883 | 0.0566 | 0.2185 | 0.0889 | 0.3431 | 0.0393 | 0.1515 |
| Tau (12) | 0.0799 | 0.2341 | 0.0384 | 0.1125 | 0.0712 | 0.2086 | 0.0289 | 0.0847 |
| MCI (7) | 0.0672 | 0.2662 | 0.0363 | 0.1438 | 0.0600 | 0.2378 | 0.0270 | 0.1069 |
| CN (12) | 0.1395 | 0.3697 | 0.0640 | 0.1695 | 0.1230 | 0.3258 | 0.0458 | 0.1214 |
| AD (3) | 0.1204 | 0.3418 | 0.0871 | 0.2473 | 0.1038 | 0.2949 | 0.0603 | 0.1712 |
LIN: linear source model; EXP: exponential source model
4. Discussion
Motivated by literary evidence that the spatiotemporal trajectory of misfolded tau protein may provide clues to the course of AD, we modeled pathological tau spread via an inhomogeneous PDE. This equation builds on the well-established NDM that portrays tau propagation as a passive diffusion process along conduits determined by the brain’s structural network. Though we recognize the role that diffusion plays in modeling the transmission of tau across brain regions, passive diffusion cannot alone explain the escalation in tau burden that is a signature of AD progression. We thus assign to the NDM an additional source term thereby creating an inhomogeneous PDE. We generated closed-form solutions to this equation for linear and exponential source functionals. The resultant parametric models were fitted by iterative computation of the model parameters using tau PET data at two timepoints. To test the model’s accuracy, we compared predicted and observed tau at a third timepoint. For this comparison, we used ROI mean SUVRs as measures of localized tau burden and additionally used dSUVRs to quantify the change across timepoints. As quantitative figures of merit, we use the NRMSE and NMAE error measures. The exponential source model outperformed the linear source for all data groupings.
Source modeling allows us to examine the source/sink and accumulator/dissipator status of each ROI based on the medians. Many ROIs considered critical in early AD were classified as sink+dissipator for the tau , Aβ− subgroup and switched to source+dissipator when the tau or Aβ status changed. The posterior cingulate cortex (PCC) showed a reverse transition from source+dissipator to sink+dissipator from the Aβ− to the Aβ+ subgroups. The latter observation is interesting since prior work in both cross-sectional [70] and longitudinal [37] cohorts suggests the PCC region to be an important site of interaction between Aβ and tau.
A key challenge toward capturing in vivo tau measures using PET is the off-target binding of 18F-Flortaucipir in several ROIs, including the basal ganglia, choroid plexus, and the meninges. At the ROI level, we circumvented this impediment by removing several ROIs that exhibit high off-target binding. As future work, we will address off-target effects enhanced by spillover by partial volume correcting our data via image deblurring [71] and examine the impact of this on model fitting and prediction. Consistent with the focus of the HABS cohort for preclinical AD, we centered our attention on ROIs that exhibit pathological tau in the early and asymptomatic disease stages. While the subtle but detectable changes in in vivo tau burden in the preclinical stage are of particular significance in the early diagnosis and prognosis of AD, a major challenge is posed by the noise susceptibility of the differential tau PET signals. For more robust interpretation, our future work will involve validation at multiple timepoints, which will be achievable within a few years as more three-timepoint and some four-timepoint datasets become available in the HABS cohort. While, due to the availability of only two timepoints for fitting, we have restricted ourselves to linearized source models, as more timepoints are available, we will be able to investigate fully nonlinear solutions and explore more sophisticated source functionals.
A key limitation of the current study is the small size of our dataset. 18F-Flortaucipir PET is a relatively recent technology, which makes the cohort sizes for serial datasets too small for robust statistical analyses. But, as more data become available in the HABS and ADNI cohorts, the increased statistical power may be harnessed to more robustly validate longitudinal tau progression models.
Very recent literature suggests the superiority of probabilistic tractography over the deterministic approach used in this paper [72]. As future work, we will use probabilistic and anatomically corrected tractography to create structural connectomes and compare the relative merits of probabilistic and deterministic tractography in the context of tau progression modeling.
It should be noted that neurodegenerative diseases like AD lead to gradual changes in the structural connectome. Similar to past efforts by other research groups on spread models for neurodegenerative diseases, we consider a static structural connectivity profile in our model. As future research, we will investigate models that accommodate an evolving differential operator.
5. Conclusion
We presented here a model to capture the spatiotemporal evolution of tau and validated it using data from the HABS and ADNI cohorts. By combining PET and DTI, we offered a macroscopic perspective on tau propagation along neural pathways. The structural network of the brain was reconstructed via a tractography-derived connectome while longitudinal tau measures based on 18F-Flortaucipir PET scans were used to capture the temporal evolution of misfolded tau. We performed quantitative assessment of model fitting and prediction accuracy based on both SUVRs and dSUVRs. To our knowledge, this is the first attempt to model tau progression in an individualized manner with model validation performed using longitudinal observations. Our approach is distinct from prior efforts in that it is data-driven and does not start with a (hypothetical) focal seed. As an analytic model, this approach is more intuitive and computationally efficient than alternative probabilistic models of protein dynamics. Our model lays the groundwork for an analytic framework for personalized prediction of disease progression based on individual (rather than group-level) connectivity graphs. At a preliminary level, our model appears promising as a tool for longitudinal tracking of tau aggregation. Since the model has only been tested for a small number of subjects, studies in larger cohorts need to be performed to assess its full prognostic potential.
Acknowledgments
This work was supported in part by the NIH grants K01AG050711 and R03AG070750.
Appendix
Gradient Computation for the Linear Source Model
Minimization of the cost function in (11) requires the computation of gradients of f(x0, β, r) with respect to β and r. These can be computed as follows:
| (17) |
| (18) |
Gradient Computation for the Exponential Source Model
Minimization of the cost function in (16) requires the computation of the gradients of f(x0, β, α, σ) with respect to β, α, and r. The gradient of the data-fit cost ΦEXP(β, α, σ) with respect to an arbitrary parameter vector (M = 1 for β and σ, M = N for α) can be computed from the gradient ∇zf using:
| (19) |
This would require us to tackle the matrix inverse in (15). To this end, we use the eigenvalue decomposition of the Laplacian given by L = QΛQ−1, where QT = Q−1 due to the symmetry of L. The matrix inverse term can then be written as:
| (20) |
The derivatives of M(β, σ) with respect to the unknowns β and σ can be obtained as follows:
| (21) |
The required gradients can then be computed as follows:
| (22) |
References
- 1.Hebert LE, Weuve J, Scherr PA, Evans DA. Alzheimer disease in the United States (2010–2050) estimated using the 2010 census. Neurology 2013;80(19):1778–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Braak H, Braak E. Neuropathological stageing of Alzheimer-related changes. Acta Neuropathol 1991;82(4):239–59. [DOI] [PubMed] [Google Scholar]
- 3.Dubois B, Hampel H, Feldman HH, Scheltens P, Aisen P, Andrieu S, Bakardjian H, Benali H, Bertram L, Blennow K, Broich K, Cavedo E, Crutch S, Dartigues JF, Duyckaerts C, Epelbaum S, Frisoni GB, Gauthier S, Genthon R, Gouw AA, Habert MO, Holtzman DM, Kivipelto M, Lista S, Molinuevo JL, O’Bryant SE, Rabinovici GD, Rowe C, Salloway S, Schneider LS, Sperling R, Teichmann M, Carrillo MC, Cummings J, Jack CR. Preclinical Alzheimer’s disease: Definition, natural history, and diagnostic criteria. Alzheimers Dement 2016;12(3):292–323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sperling RA, Aisen PS, Beckett LA, Bennett DA, Craft S, Fagan AM, Iwatsubo T, Jack CR, Kaye J, Montine TJ, Park DC, Reiman EM, Rowe CC, Siemers E, Stern Y, Yaffe K, Carrillo MC, Thies B, Morrison-Bogorad M, Wagster MV, Phelps CH. Toward defining the preclinical stages of Alzheimer’s disease: recommendations from the National Institute on Aging-Alzheimer’s Association workgroups on diagnostic guidelines for Alzheimer’s disease. Alzheimers Dement 2011;7(3):280–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Jack CR, Knopman DS, Jagust WJ, Shaw LM, Aisen PS, Weiner MW, Petersen RC, Trojanowski JQ. Hypothetical model of dynamic biomarkers of the Alzheimer’s pathological cascade. Lancet Neurol 2010;9(1):119–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lois C, Gonzalez I, Johnson KA, Price JC. PET imaging of tau protein targets: a methodology perspective. Brain Imaging Behav 2019;13(2):333–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Saint-Aubert L, Lemoine L, Chiotis K, Leuzy A, Rodriguez-Vieitez E, Nordberg A. Tau PET imaging: present and future directions. Mol Neurodegener 2017;12(1):19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jack CR, Barrio JR, Kepe V. Cerebral amyloid PET imaging in Alzheimer’s disease. Acta Neuropathol 2013;126(5):643–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Herholz K, Ebmeier K. Clinical amyloid imaging in Alzheimer’s disease. Lancet Neurol 2011;10(7):667–70. [DOI] [PubMed] [Google Scholar]
- 10.La Joie R, Visani AV, Baker SL, Brown JA, Bourakova V, Cha J, Chaudhary K, Edwards L, Iaccarino L, Janabi M, Lesman-Segev OH, Miller ZA, Perry DC, O’Neil JP, Pham J, Rojas JC, Rosen HJ, Seeley WW, Tsai RM, Miller BL, Jagust WJ, Rabinovici GD. Prospective longitudinal atrophy in Alzheimer’s disease correlates with the intensity and topography of baseline tau-PET. Sci Transl Med 2020;12(524). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hedden T, Oh H, Younger AP, Patel TA. Meta-analysis of amyloidcognition relations in cognitively normal older adults. Neurology 2013;80(14):1341–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Donohue MC, Sperling RA, Petersen R, Sun CK, Weiner MW, Aisen PS. Association Between Elevated Brain Amyloid and Subsequent Cognitive Decline Among Cognitively Normal Persons. JAMA 2017;317(22):2305–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Palmqvist S, Sch?ll M, Strandberg O, Mattsson N, Stomrud E, Zetterberg H, Blennow K, Landau S, Jagust W, Hansson O. Earliest accumulation of -amyloid occurs within the default-mode network and concurrently affects brain connectivity. Nat Commun 2017;8(1):1214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gordon BA, McCullough A, Mishra S, Blazey TM, Su Y, Christensen J, Dincer A, Jackson K, Hornbeck RC, Morris JC, Ances BM, Benzinger TLS. Cross-sectional and longitudinal atrophy is preferentially associated with tau rather than amyloid positron emission tomography pathology. Alzheimers Dement (Amst) 2018;10:245–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Strain JF, Smith RX, Beaumont H, Roe CM, Gordon BA, Mishra S, Adeyemo B, Christensen JJ, Su Y, Morris JC, Benzinger TLS, Ances BM. Loss of white matter integrity reflects tau accumulation in Alzheimer disease defined regions. Neurology 2018;91(4):e313–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Xia C, Makaretz SJ, Caso C, McGinnis S, Gomperts SN, Sepulcre J, Gomez-Isla T, Hyman BT, Schultz A, Vasdev N, Johnson KA, Dickerson BC. Association of In Vivo [18F]AV-1451 Tau PET Imaging Results With Cortical Atrophy and Symptoms in Typical and Atypical Alzheimer Disease. JAMA Neurol 2017;74(4):427–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bejanin A, Schonhaut DR, La Joie R, Kramer JH, Baker SL, Sosa N, Ayakta N, Cantwell A, Janabi M, Lauriola M, O’Neil JP, Gorno-Tempini ML, Miller ZA, Rosen HJ, Miller BL, Jagust WJ, Rabinovici GD. Tau pathology and neurodegeneration contribute to cognitive impairment in Alzheimer’s disease. Brain 2017;140(12):3286–300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cho H, Choi JY, Hwang MS, Kim YJ, Lee HM, Lee HS, Lee JH, Ryu YH, Lee MS, Lyoo CH. In vivo cortical spreading pattern of tau and amyloid in the Alzheimer disease spectrum. Ann Neurol 2016;80(2):247–58. [DOI] [PubMed] [Google Scholar]
- 19.Sepulcre J, Grothe MJ, Sabuncu M, Chhatwal J, Schultz AP, Hanseeuw B, El Fakhri G, Sperling R, Johnson KA. Hierarchical Organization of Tau and Amyloid Deposits in the Cerebral Cortex. JAMA Neurol 2017;74(7):813–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sperling R, Mormino E, Johnson K. The evolution of preclinical Alzheimer’s disease: implications for prevention trials. Neuron 2014;84(3):608–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Schwarz AJ, Yu P, Miller BB, Shcherbinin S, Dickson J, Navitsky M, Joshi AD, Devous MD, Mintun MS. Regional profiles of the candidate tau PET ligand 18F-AV-1451 recapitulate key features of Braak histopathological stages. Brain 2016;139(Pt 5):1539–50. [DOI] [PubMed] [Google Scholar]
- 22.Johnson KA, Schultz A, Betensky RA, Becker JA, Sepulcre J, Rentz D, Mormino E, Chhatwal J, Amariglio R, Papp K, Marshall G, Albers M, Mauro S, Pepin L, Alverio J, Judge K, Philiossaint M, Shoup T, Yokell D, Dickerson B, Gomez-Isla T, Hyman B, Vasdev N, Sperling R. Tau positron emission tomographic imaging in aging and early Alzheimer disease. Ann Neurol 2016;79(1):110–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ossenkoppele R, Schonhaut DR, Sch?ll M, Lockhart SN, Ayakta N, Baker SL, O’Neil JP, Janabi M, Lazaris A, Cantwell A, Vogel J, Santos M, Miller ZA, Bettcher BM, Vossel KA, Kramer JH, Gorno-Tempini ML, Miller BL, Jagust WJ, Rabinovici GD. Tau PET patterns mirror clinical and neuroanatomical variability in Alzheimer’s disease. Brain 2016;139(Pt 5):1551–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Scholl M, Lockhart SN, Schonhaut DR, O’Neil JP, Janabi M, Ossenkoppele R, Baker SL, Vogel JW, Faria J, Schwimmer HD, Rabinovici GD, Jagust WJ. PET Imaging of Tau Deposition in the Aging Human Brain. Neuron 2016;89(5):971–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Marquie M, Siao Tick Chong M, Anton-Fernandez A, Verwer EE, Saez-Calveras N, Meltzer AC, Ramanan P, Amaral AC, Gonzalez J, Normandin MD, Frosch MP, Gomez-Isla T. [F-18]-AV-1451 binding correlates with postmortem neurofibrillary tangle Braak staging. Acta Neuropathol 2017;134(4):619–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Schwarz AJ, Shcherbinin S, Slieker LJ, Risacher SL, Charil A, Irizarry MC, Fleisher AS, Southekal S, Joshi AD, Devous MD, Miller BB, Saykin AJ. Topographic staging of tau positron emission tomography images. Alzheimers Dement (Amst) 2018;10:221–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jack CR, Wiste HJ, Schwarz CG, Lowe VJ, Senjem ML, Vemuri P, Weigand SD, Therneau TM, Knopman DS, Gunter JL, Jones DT, Graff-Radford J, Kantarci K, Roberts RO, Mielke MM, Machulda MM, Petersen RC. Longitudinal tau PET in ageing and Alzheimer’s disease. Brain 2018;141(5):1517–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Harrison TM, La Joie R, Maass A, Baker SL, Swinnerton K, Fenton L, Mellinger TJ, Edwards L, Pham J, Miller BL, Rabinovici GD, Jagust WJ. Longitudinal tau accumulation and atrophy in aging and Alzheimer disease. Ann Neurol 2019;85(2):229–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hanseeuw BJ, Betensky RA, Jacobs HIL, Schultz AP, Sepulcre J, Becker JA, Cosio DMO, Farrell M, Quiroz YT, Mormino EC, Buckley RF, Papp KV, Amariglio RA, Dewachter I, Ivanoiu A, Huijbers W, Hedden T, Marshall GA, Chhatwal JP, Rentz DM, Sperling RA, Johnson K. Association of amyloid and tau with cognition in preclinical Alzheimer disease: A longitudinal study. JAMA Neurol 2019;76(8):915–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lee SJ, Desplats P, Sigurdson C, Tsigelny I, Masliah E. Cell-to-cell transmission of non-prion protein aggregates. Nat Rev Neurol 2010;6(12):702–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Frost B, Diamond MI. Prion-like mechanisms in neurodegenerative diseases. Nat Rev Neurosci 2010;11(3):155–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nussbaum JM, Schilling S, Cynis H, Silva A, Swanson E, Wangsanut T, Tayler K, Wiltgen B, Hatami A, Ronicke R, Reymann K, Hutter-Paier B, Alexandru A, Jagla W, Graubner S, Glabe CG, Demuth HU, Bloom GS. Prion-like behaviour and tau-dependent cytotoxicity of pyroglutamylated amyloid-β. Nature 2012;485(7400):651–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nussbaum JM, Seward ME, Bloom GS. Alzheimer disease: a tale of two prions. Prion 2013;7(1):14–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.de Calignon A, Polydoro M, Su?rez-Calvet M, William C, Adamowicz DH, Kopeikina KJ, Pitstick R, Sahara N, Ashe KH, Carlson GA, Spires-Jones TL, Hyman BT. Propagation of tau pathology in a model of early Alzheimer’s disease. Neuron 2012;73(4):685–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Boluda S, Iba M, Zhang B, Raible KM, Lee VM, Trojanowski JQ. Differential induction and spread of tau pathology in young PS19 tau transgenic mice following intracerebral injections of pathological tau from Alzheimer’s disease or corticobasal degeneration brains. Acta Neuropathol 2015;129(2):221–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ahmed Z, Cooper J, Murray TK, Garn K, McNaughton E, Clarke H, Parhizkar S, Ward MA, Cavallini A, Jackson S, Bose S, Clavaguera F, Tolnay M, Lavenir I, Goedert M, Hutton ML, O’Neill MJ. A novel in vivo model of tau propagation with rapid and progressive neurofibrillary tangle pathology: the pattern of spread is determined by connectivity, not proximity. Acta Neuropathol 2014;127(5):667–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Jacobs HIL, Hedden T, Schultz AP, Sepulcre J, Perea RD, Amariglio RE, Papp KV, Rentz DM, Sperling RA, Johnson KA. Structural tract alterations predict downstream tau accumulation in amyloid-positive older individuals. Nat Neurosci 2018;21(3):424–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Franzmeier N, Rubinski A, Neitzel J, Kim Y, Damm A, Na DL, Kim HJ, Lyoo CH, Cho H, Finsterwalder S, Duering M, Seo SW, Ewers M. Functional connectivity associated with tau levels in ageing, Alzheimer’s, and small vessel disease. Brain 2019;142(4):1093–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Adams JN, Maass A, Harrison TM, Baker SL, Jagust WJ. Cortical tau deposition follows patterns of entorhinal functional connectivity in aging. Elife 2019;8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Franzmeier N, Dewenter A, Frontzkowski L, Dichgans M, Rubinski A, Neitzel J, Smith R, Strandberg O, Ossenkoppele R, Buerger K, Duering M, Hansson O, Ewers M. Patient-centered connectivity-based prediction of tau pathology spread in Alzheimer’s disease. Sci Adv 2020;6(48). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sepulcre J, Grothe MJ, Uquillas F, Ortiz-Teran L, Diez I, Yang HS, Jacobs H, Hanseeuw B, Li Q, El Fakhri G, Sperling R, Johnson KA. Neurogenetic contributions to amyloid beta and tau spreading in the human cortex. Nat Med 208;24(12):1910–1918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Raj A, Kuceyeski A, Weiner M. A network diffusion model of disease progression in dementia. Neuron 2012;73(6):1204–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Raj A, LoCastro E, Kuceyeski A, Tosun D, Relkin N, Weiner M. Network Diffusion Model of Progression Predicts Longitudinal Patterns of Atrophy and Metabolism in Alzheimer’s Disease. Cell Rep 2015;10(3):359–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Yang F, Chowdhury SR, Jacobs HIL, Johnson KA, Dutta J. A longitudinal model for tau aggregation in Alzheimer’s disease based on structural connectivity. Inf Process Med Imaging 2019;11492:384–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Vogel JW, Iturria-Medina Y, Strandberg OT, Smith R, Levitis E, Evans AC, Hansson O, Alzheimer’s Disease Neuroimaging Initiative, Swedish BioFinder Study. Spread of pathological tau proteins through communicating neurons in human Alzheimer’s disease. Nature Communications 2020;11(1):1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Iturria-Medina Y, Sotero RC, Toussaint PJ, Evans AC, Alzheimer’s Disease Neuroimaging Initiative. Epidemic spreading model to characterize misfolded proteins propagation in aging and associated neurodegenerative disorders. PLoS Comput Biol 2014;10(11):e1003956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Hu C, Hua X, Ying J, Thompson PM, Fakhri GE, Li Q. Localizing sources of brain disease progression with network diffusion model. IEEE J Sel Top Signal Process 2016;10(7):1214–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Torok J, Maia PD, Powell F, Pandya S, Raj A. A method for inferring regional origins of neurodegeneration. Brain 2018;141(3):863–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Holmes BB, Furman JL, Mahan TE, Yamasaki TR, Mirbaha H, Eades WC, Belaygorod L, Cairns NJ, Holtzman DM, Diamond MI. Proteopathic tau seeding predicts tauopathy in vivo. Proc Natl Acad Sci USA 2014;111(41):E4376–4385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kaufman SK, Del Tredici K, Thomas TL, Braak H, Diamond MI. Tau seeding activity begins in the transentorhinal/entorhinal regions and anticipates phospho-tau pathology in Alzheimer’s disease and PART. Acta Neuropathol 2018;136(1):57–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Shafiei SS, Guerrero-Munoz MJ, Castillo-Carranza DL. Tau oligomers: Cytotoxicity, propagation, and mitochondrial damage. Front Aging Neurosci 2017;9:83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.DeVos SL, Corjuc BT, Oakley DH, Nobuhara CK, Bannon RN, Chase A, Commins C, Gonzalez JA, Dooley PM, Frosch MP, Hyman BT. Synaptic tau seeding precedes tau pathology in human Alzheimer’s disease brain. Front Neurosci 2018;12:267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Bassil F, Brown HJ, Pattabhiraman S, Iwasyk JE, Maghames CM, Meymand ES, Cox TO, Riddle DM, Zhang B, Trojanowski JQ, Lee VM. Amyloid-Beta (Aβ) plaques promote seeding and spreading of alph-asynuclein and tau in a mouse model of Lewy body disorders with Aβpathology. Neuron 2020;105(2):260–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.He Z, Guo JL, McBride JD, Narasimhan S, Kim H, Changolkar L, Zhang B, Gathagan RJ, Yue C, Dengler C, Stieber A, Nitla M, Coulter DA, Abel T, Brunden KR, Trojanowski JQ, Lee VM. Amyloid-βplaques enhance Alzheimer’s brain tau-seeded pathologies by facilitating neuritic plaque tau aggregation. Nat Med 2018;24(1):29–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Lee MJ, Lee JH, Rubinsztein DC. Tau degradation: the ubiquitin-proteasome system versus the autophagy-lysosome system. Prog Neurobiol 2013;105:49–59. [DOI] [PubMed] [Google Scholar]
- 56.Hyttinen JM, Amadio M, Viiri J, Pascale A, Salminen A, Kaarniranta K. Clearance of misfolded and aggregated proteins by aggrephagy and implications for aggregation diseases. Ageing Res Rev 2014;18:16–28. [DOI] [PubMed] [Google Scholar]
- 57.Woo JA, Liu T, Fang CC, Casta?o MA, Kee T, Yrigoin K, Yan Y, Cazzaro S, Matlack J, Wang X, Zhao X, Kang DE, Liggett SB. β-Arrestin2 oligomers impair the clearance of pathological tau and increase tau aggregates. Proc Natl Acad Sci USA 2020;117(9):5006–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Hauglund NL, Pavan C, Nedergaard M. Cleaning the sleeping brain – the potential restorative function of the glymphatic system. Current Opinion in Physiology 2020;15:1–6. [Google Scholar]
- 59.de Leon MJ, Blennow K. Therapeutic potential for peripheral clearance of misfolded brain proteins. Nat Rev Neurol 2018;14(11):637–8. [DOI] [PubMed] [Google Scholar]
- 60.Garbarino S, Lorenzi M. Modeling and inference of spatio-temporal protein dynamics across brain networks. Inf Process Med Imaging 2019;11492:57–69. [Google Scholar]
- 61.Dagley A, LaPoint M, Huijbers W, Hedden T, McLaren DG, Chatwal JP, Papp KV, Amariglio RE, Blacker D, Rentz DM, Johnson KA, Sperling RA, Schultz AP. Harvard Aging Brain Study: Dataset and accessibility. Neuroimage 2017;144(Pt B):255–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Kim HR, Lee P, Seo SW, Roh JH, Oh M, Oh JS, Oh SJ, Kim JS, Jeong Y. Comparison of Amyloid Aβ and Tau Spread Models in Alzheimer’s Disease. Cereb Cortex 2019;29(10):4291–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Jack CR, Bennett DA, Blennow K, Carrillo MC, Dunn B, Haeberlein SB, Holtzman DM, Jagust W, Jessen F, Karlawish J, Liu E, Molinuevo JL, Montine T, Phelps C, Rankin KP, Rowe CC, Scheltens P, Siemers E, Snyder HM, Sperling R, Elliott C, Masliah E, Ryan L, Silverberg N. NIA-AA Research Framework: Toward a biological definition of Alzheimer’s disease. Alzheimers Dement 2018;14(4):535–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis. I. Segmentation and surface reconstruction. Neuroimage 1999;9(2):179–94. [DOI] [PubMed] [Google Scholar]
- 65.Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis. II: Inflation, flattening, and a surface-based coordinate system. Neuroimage 1999;9(2):195–207. [DOI] [PubMed] [Google Scholar]
- 66.Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, Niazy RK, Saunders J, Vickers J, Zhang Y, De Stefano N, Brady JM, Matthews PM. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 2004;23 Suppl 1:S208–219. [DOI] [PubMed] [Google Scholar]
- 67.Woolrich MW, Jbabdi S, Patenaude B, Chappell M, Makni S, Behrens T, Beckmann C, Jenkinson M, Smith SM. Bayesian analysis of neuroimaging data in FSL. Neuroimage 2009;45(1 Suppl):S173–186. [DOI] [PubMed] [Google Scholar]
- 68.Jenkinson M, Beckmann CF, Behrens TE, Woolrich MW, Smith SM. FSL. Neuroimage 2012;62(2):782–90. [DOI] [PubMed] [Google Scholar]
- 69.Sanchez JS, Becker JA, Jacobs HIL, Hanseeuw BJ, Jiang S, Schultz AP, Properzi MJ, Katz SR, Beiser A, Satizabal CL, O’Donnell A, DeCarli C, Killiany R, El Fakhri G, Normandin MD, Gómez-Isla T, Quiroz YT, Rentz DM, Sperling RA, Seshadri S, Augustinack J, Price JC, Johnson KA. The cortical origin and initial spread of medial temporal tauopathy in Alzheimer’s disease assessed with positron emission tomography. Sci Transl Med 2021;13(577). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Sepulcre J, Schultz AP, Sabuncu M, Gomez-Isla T, Chhatwal J, Becker A, Sperling R, Johnson KA. In Vivo Tau, Amyloid, and Gray Matter Profiles in the Aging Brain. J Neurosci 2016;36(28):7364–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Song TA, Yang F, Chowdhury S, Kim K, Johnson K, El Fakhri G, Li Q, Dutta J. PET image deblurring and super-resolution with an MR-based joint entropy prior. IEEE Trans Comput Imaging 2019;5(4):530–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Girard G, Caminiti R, Battaglia-Mayer A, St-Onge E, Ambrosen KS, Eskildsen SF, Krug K, Dyrby TB, Descoteaux M, Thiran JP, Innocenti GM. On the cortical connectivity in the macaque brain: A comparison of diffusion tractography and histological tracing data. Neuroimage 2020;221:117201. [DOI] [PubMed] [Google Scholar]


