Grappling with COVID-19 by imposing and lifting non-pharmaceutical interventions in Sri Lanka: A modeling perspective

Abstract

The imposition and lifting of non-pharmaceutical interventions (NPIs) to avert the COVID-19 pandemic have gained popularity worldwide and will continue to be enforced until herd immunity is achieved. We developed a linear regression model to ascertain the nexus between the time-varying reproduction number averaged over a time window of six days (R_ts) and seven NPIs: contact tracing, quarantine efforts, social distancing and health checks, hand hygiene, wearing of facemasks, lockdown and isolation, and health-related supports. Our analysis suggests that the second wave that emerged in Sri Lanka in early October 2020 continued despite numerous NPIs.

The model indicates that the most effective single NPI was lockdown and isolation. Conversely, the least effective individual NPIs were hand hygiene and wearing of facemasks. The model also demonstrates that to mitigate the second wave to a satisfactory level (R_ts<1), the best single NPI was the contact tracing with stringent imposition (% of improvement of R_ts was 69.43 against the base case). By contrast, the best combination of two NPIs was the lockdown & isolation with health-related supports (% of improvement was 31.92 against the base case). As such, many health authorities worldwide can use this model to successfully strategize the imposition and lifting of NPIs for averting the COVID-19 pandemic.

Graphical abstract

1. Introduction

COVID-19, caused by the 2019 novel coronavirus (SARS-CoV-2), was first reported in Wuhan, China, in late December 2019 (Chen et al., 2020; Huang et al., 2020). On November 12, 2020, the World Health Organization COVID-19 Situation Dashboard (https://coronavirus.jhu.edu/map.html) reported 53.141 million confirmed COVID-19 cases and 1.299 million deaths globally, and those in Sri Lanka accounted for 15,350 and 46, respectively.

The rapid transmission of COVID-19 across countries and regions and the non-availability of an effective vaccine or treatment have spurred many countries to introduce various strategies for preventing the spread of COVID-19 (Bo et al., 2020). Many policymakers have imposed non-pharmaceutical interventions (NPIs) as effective and efficient mitigation strategies to reduce the daily case numbers within the susceptible population by cutting off the transmission modes (Bo et al., 2020, Ferguson et al., 2020, p. 20; Hellewell et al., 2020). As of November 2020, NPIs continue to be the leading public health tool worldwide against the spread of this virus. The NPIs adopted worldwide include contact tracing, quarantine, social distancing and health screening, hand hygiene, wearing of facemasks, lockdown and isolations, and health-related supports (reverse transcription-polymerase chain reaction or RT-PCR testing, provision of free medical services, and establishment of adequate makeshift hospitals) (Bouchnita & Jebrane, 2020; Brauner et al., 2020; ECDC, 2020; Flaxman et al., 2020; Li et al., 2020; Patiño-Lugo et al., 2020). Lai et al. (2020) demonstrated that without NPIs, the number of COVID-19 cases would have increased by 51-fold in Wuhan, 92-fold in other Hubei cities, and 125-fold in other provinces of China. Ferguson et al. (2020), in their simulation study for the United Kingdom and the United States, showed that the peak demand for intensive-care beds would be 30 times the availability if the epidemic had not been controlled through NPIs.

Even after the peak of the disease transmission is curtailed, several NPIs must be maintained to control the reemergence of the disease. Several simulations have shown that failure to do so could give rise to a devastating second wave (Ngonghala et al., 2020; Davies et al., 2020; Flaxman et al., 2020). Moreover, Patiño-Lugo et al. (2020) recommended the continued implementation of several NPIs, including social distancing, for several months and possibly until a vaccine is made available. Thus, implementing efficient and effective NPIs contributes to controlling the factors that determine the time-varying effective reproduction number (R_ts), thereby helping prevent the spread of the COVID-19 pandemic (Cori et al., 2013). However, the imposition and lifting of NPIs may be influenced by political, social, and cultural factors despite the behavior of the disease (ECDC, 2020; Iezadi et al., 2020). Furthermore, restricting NPIs to the shortest possible time is essential because the long-term imposition of NPIs is likely to cause significant adverse psychological, social, and economic consequences (Rawaf et al., 2020). Thus, NPIs are often imposed and lifted individually or in combinations at varying levels of intensities at different times. As a result, analyzing their effectiveness is challenging. Nevertheless, the findings of such an analysis may provide decision-makers useful insights into the imposition and lifting frequencies of NPIs that have a notable contribution to reducing the daily number of COVID-19 cases (Li et al., 2020).

The policy decisions taken by government authorities for reopening a country for day-to-day activities with the imposition/strengthening and lifting of NPIs dictate a new normal that people have to embrace. Most countries are prepared, although reluctantly, to enter a new normal lifestyle with the introduction of a set of NPIs, which may prevail over a short or long period depending on R_ts (Pragholapati et al., 2020). Several computer simulations have assessed the effectiveness of NPIs by simulating scenarios with and without the imposition of NPIs against R_ts (Min et al., 2020; Flaxman et al., 2020; Bajiya et al., 2020) or by investigating previously pooled data from various countries before and after the implementation of NPIs (Davies et al., 2020). Although these models estimate the number of cases under various NPIs, they do not consider the effects of imposing, intensifying, and lifting NPIs. Thus, their applicability to the forecasting of such scenarios is limited. However, by applying the linear regression method with grid search for parameter optimization, we can use previous results to make decisions. In contrast, traditional computer models use input values and given decisions to produce a result. To our knowledge, limited studies have been conducted worldwide to explore such scenarios and computational tools that help usher in a new normal with the imposition and lifting of NPIs. Therefore, in this study, we attempted to understand how NPIs should be or could have been implemented to reduce the case numbers of COVID-19 to levels that do not qualify as an epidemic. We applied a linear regression model, incorporated the imposition and lifting of NPIs to predict the temporal variation of R_ts with training and testing efforts, and used case data from Sri Lanka. We adopted a linear regression model because it is a well-accepted method to assess the temporal variations of epidemiological parameters worldwide (Ceylan, 2020; Ghosal et al., 2020; Maul, 1992; Ogundokun et al., 2020). Furthermore, we believe that such a model can be applied to any other country or situation to predict the transmission behavior in terms of R_ts by using the country's own NPIs. These predictions provide insights into adopting new strategies to overcome challenges and how and when to impose or lift NPIs effectively and efficiently to cultivate a safe culture in society.

2. Data and methods

2.1. Epidemiological data retrieval and comparison

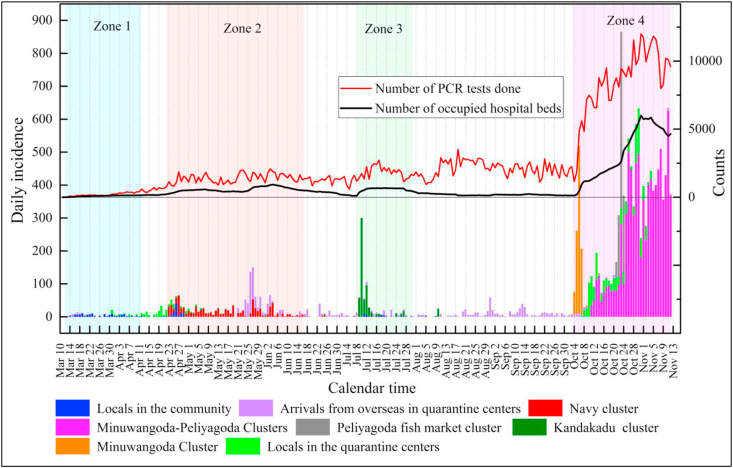
We retrieved the available epidemiological data on COVID-19 in Sri Lanka for a period commencing from the first day of a case reported on March 11, 2020, to November 12, 2020, as daily records. We divided this period into four zones based on the potential transmissibility of COVID-19 (Fig. 1). Zone 1, called the “locals in the community cluster,” is from March 11 to April 12, 2020. Zone 2, called the “navy cluster,” is from April 22 to June 17, 2020. We disregarded the area between Zones 1 and 2 because it did not contribute to the transmission of COVID-19 cases (Fig. 1). All daily cases reported during this period were reported to be locals isolated at quarantine centers, and their contribution to the transmission of COVID-19 was negligible. Similarly, Zone 3, called the “Kandakadu cluster,” is from July 8 to July 31, 2020. Zone 4, which is called the “Minuwangoda-Peliyagoda cluster,” covers the period between October 3 and November 12, 2020. The areas between Zones 2 and 3 and between Zones 3 and 4 were disregarded because these zones were attributed to arrivals from overseas in quarantine centers, whose contribution to the transmission of COVID-19 was inconsequential.

Fig. 1.

Daily incidences of COVID-19 in clusters recorded in Sri Lanka (These incidences were recorded with data collected from different government sources and their accuracy was checked and corrected with the other secondary sources) and the number of RT-PCR tests carried out and number of hospital bed occupied in makeshift hospitals (sources:www.covid.iq.lk;www.epid.gov.lk;www.hpb.health.gov.lk); Y axis indicated with counts refer to the number of RT-PCR tests carried out and the number of beds occupied by COVID-19 patients in the makeshift hospitals.

Zone 1 – Locals in the community cluster made up the first COVID-19 cluster of the country because of the transmission of COVID-19 for the first time in Sri Lanka from a Chinese tourist. The transmission subsequently died down at the end of Zone 1. Zone 2 – The navy cluster resulted from the transmission of COVID-19 cases by navy personnel at work in Welisara Navy Base. Zone 3 – The Kandakadu cluster emerged with the transmission of COVID-19 cases in Kandakadu rehabilitation center, Polonnaruwa, with many inmates becoming sick. Zone 4 – The Minuwangoda–Peliyagoda cluster, the country's largest cluster, began with two new epicenters emerging from an apparel factory in Minuwangoda and the main fish market in Peliyagoda. As of November 12, 2020, it continued with daily case numbers at a high rate.

We collected temporal epidemiological data, such as COVID-19 daily incidences in the different clusters mentioned above, number of infector–infected pairs, number of daily RT-PCR tests carried out, number of daily beds provided and occupied in makeshift hospitals, and number of daily NPIs adopted or implemented from known COVID-19 dashboards [COVID-19 (Sri Lanka) - Analytical Dashboard - www.covid.iq.lk; Epidemiology Unit, Ministry of Health - www.epid.gov.lk; Health Promotion Bureau - www.hpb.health.gov.lk]. We verified the data collected through other secondary sources, such as daily news alerts, newspaper articles, and other authentic websites. The descriptive statistics of the data collected (daily incidences, RT-PCR tests, and bed occupancy) are presented in Table S1 (Supplementary Materials). Moreover, we grouped all specific NPIs into seven, and their imposition and lifting over time with their intensity (in a normalized form) were recorded using published references in different articles listed in Table S2 (Supplementary Materials).

We conducted the student t-test to determine the significant differences between the respective means of all epidemiological parameters among the four zones (Table S3 in Supplementary Materials), and the differences were considered significant when p < 0.05.

2.2. Estimation of diagnostic serial intervals (SI_d)

The estimation of R_t depends on the generation interval (GI; the interval of onset of infection between two consecutive generations), and GI is approximated from the serial interval (SI; the interval of onset of symptoms between two successive generations) (Wang et al., 2020, Zhao, 2020; Zhao et al., 2020). However, given that COVID-19 cases are detected during pre-symptomatic and asymptomatic periods, the use of SI is questionable, and it cannot be estimated accurately (Mettler et al., 2020). A properly organized contact tracing system can estimate a new epidemiological parameter called diagnostic serial interval (SI_d), which is the time between the diagnosis dates of the infector and the infected (Mettler et al., 2020). We estimated SI_d by using the relationships of the infector and the infected. Moreover, diagnosis for pre-symptomatic patients was carried out via RT-PCR testing before the onset of symptoms. We calculated SI_d instead of SI because of these proxies mentioned above. We selected the possible infector–infected pairs to calculate SI_d, with the number of pairs being 41, 9, 12, and 10 for Zones 1 to 4, respectively (Table S4 in Supplementary Materials). Following Mettler et al. (2020), we applied the bootstrap method with the normal approximated bootstrapped confidence interval (CI of 95%) to calculate the mean and standard deviation (SD) of SI_d for each zone. We corrected the individual SI_d values using trimmed means with 5% trimming to eliminate outliers (Mettler et al., 2020). We determined the mean and SD of SI_d by using the statistical software MATLAB (Version 2017a). Additional data (100,000 pairs) on infector–infected pairs were generated using the bootstrap method for all four zones because the actual numbers of pairs were limited. Fig. S1 (Supplementary Materials) depicts the distribution of the frequency of the mean of SI_d over time for all four zones. We estimated the mean and SD of SI_d for all four zones by using these density functions with a 95% CI.

2.3. Estimation of R_t and R_ts

Although the basic reproduction number (R₀) of an infectious disease is the initial average number of secondary cases produced by a primary case in a susceptible population, it is prudent to estimate the time-dependent instantaneous reproduction number R_t with the imposition of NPIs to forecast the transmission potential over time. We, therefore, estimated R_t. With the imposition of effective NPIs, R_t can be < 1 so that the epidemic abates or is controlled. R_t depends on contact rates, population density, immunity level, and movement restrictions imposed among susceptible people (Cori et al., 2013).

R_t can be numerically calculated using the discretized renewal equation developed by Nishiura and Chowell (2009), as follows:

$$R_t\left(t_i\right)=\frac{I_i}{{\sum }_{j=1}^i{I}_{(i-j)}{\rho }_j},$$ (1)

where $I_i$ is the local incidence at time $t_i$ and ${\rho }_j$ is the discretized probability distribution of the generation interval, which is assumed to be gamma-distributed. Usually, ${\rho }_j$ is estimated using SI, which is not easily predictable because most cases were asymptomatic or pre-symptomatic. We, therefore, approximated SI with SI_d because daily incidences were identified through RT-PCR tests carried out via contact tracing rather than waiting for the onset of symptoms. Next, we calculated the mean and SD of the discretized probability distribution of GI by using the SI_d distribution values for each zone. We also computed the mean and SD of GI using the statistical software R (Version 4.0.3). Moreover, the gamma distribution values for ${\rho }_j$ were estimated by applying GI data using MATLAB software (Version 2017a). Fig. S2 (Supplementary Materials) depicts the gamma-distributed discretized probability distribution of the GI for all four zones. Then, R_t values were estimated with the MATLAB software by using Equation (1) (Version 2017a).

However, R_t estimates appear to be highly variable over time; hence, interpretation in small time steps with elevated levels is difficult (Fraser et al., 2011). Therefore, we estimated R_t (mean value) over a long time window lagged by a couple of days by averaging R_t values over the entire time window. At time t, we calculated the mean and SD of R_t with a CI of 95% over a time window with length s ending at time t. These estimates, denoted as time-varying reproduction number R_ts, quantify the average transmissibility over a time window of length s ending at time t. The time window of s was varied as 5, 6, and 10 days to obtain the data points with the best fit.

In our analysis, when R_ts>1, the pandemic tends to spread through a large part of the population over time, whereas R_ts<1 indicates an effective control of the spread of the pandemic before many people become infected (Cori et al., 2013).

2.4. Linear regression model for the nexus between R_ts and NPIs

We proposed that R_ts has a linear relationship with NPIs, and by using linear regression modeling, it can be predicted as follows:

$$\left[R_{t,s}\right]=\alpha -\left\{\sum _{j=1}^n{\beta }_j\left(\frac{1}{s}\right)\sum _{i=t-\left(s-1\right)}^t{\left(NPI\right)}_{i,j}\right\}+\epsilon ,$$ (2)

where $\alpha$ and ${\beta }_j$ are the constants to be determined by solving Equation (2) and j varies to up to 7 (n = 7) because seven NPIs are considered for the model. In the model, ${\beta }_1$ to ${\beta }_7$ represent the weighing factors for the seven NPIs, namely, (i) contact tracing, (ii) quarantine efforts, (iii) social distancing and health screening, (iv) hand hygiene, (v) wearing of facemasks, (vi) lockdown and isolation, and (vii) health-related benefits, respectively. The algorithm calculates the alpha and beta values in equation (2) by employing a grid search method. Here, the initial parameters for the grid were assigned on a trial and error manner after which a grid was created for a range as indicated in the MATLAB code we have provided (Please refer to Fig. S3, for the parameter range we have considered). The algorithm assigns alpha and beta values from the grid to equation (2) and by comparing the mean-squared errors with the estimated R_ts values for Zone 1, Zone 2, and Zone 3 the alpha and beta values were optimized. s is the sliding window time (5 days), and ${\left(NPI\right)}_{i,j}$ is represented by the normalized values (varies between 0 and 1) assigned for every NPI over time (the values assigned are indicated in Table S5 in the Supplementary Materials). $\epsilon$ is the error term defined by the minimum square root of squares of the differences between actual and predicted values.

The typical normalized values for NPIs over time for all four zones must be decided based on the actual applications of NPIs by the government authorities. Table S5 (Supplementary Materials) shows the list of NPIs with their specific and normalized numbers used for modeling purposes. We analyzed the linear regression model described in Equation (2) by using the MATLAB software (Version 2017a). Fig. S3 (Supplementary Materials) shows the MATLAB code generated to solve Equation (2). We used the R_ts estimated values of Zones 1 to 3 for model training, and Zone 4 was utilized for model testing. Once the testing was done, we changed the different plausible individual NPIs to explore the possibilities of obtaining R_ts predicted <1. We implemented the same exercise with different plausible combinations of two NPIs instead of individual NPIs. We critically evaluated the possible caveats for a new normal to be adopted with these predicted scenarios in the future.

3. Results and discussion

3.1. Comparison of basic epidemiological parameters of four zones

The means of daily incidences of COVID-19 cases for Zones 1 to 4 were 3.79 ± 2.96, 16.04 ± 14.68, 26.48 ± 64.13, and 268.76 ± 200.38, respectively. We found that the means of daily incidences of Zones 1 and 2 were significantly different (p < 0.05), and those of Zones 1 and 4, 2 and 4, and 3 and 4 were also significantly different (p < 0.05) (Table S3 in Supplementary Materials). The means of the daily number of beds occupied for Zones 1 to 4 were 89.94 ± 45.72, 561.18 ± 173.04, 594.74 ± 97.77, and 3184.00 ± 1937.84, respectively. The means of daily beds occupied for all four zones were significantly different from one another (p < 0.05), except for the means between Zones 2 and 3. Similarly, the means of daily RT-PCR tests in Zones 1 to 4 were 203.21 ± 134.58, 1396.58 ± 337.51, 1855.17 ± 421.43, and 8374.80 ± 2618.54, respectively. The means of RT-PCR tests for all four zones were significantly different from one another (p < 0.05) (Tables S1 and S3 in Supplementary Materials show the descriptive statistics and p-values). These comparison scenarios indicate that health authorities have significantly improved the number of beds in makeshift hospitals and the RT-PCR tests conducted against daily incidences from Zones 1 to 4.

We estimated SI_d by using infector–infected relationships for Zones 1 to 4, and the means were 2.98 days (95% CI: 2.40, 3.56), 3.11 days (95% CI: 2.17, 4.16), 2.66 days (95% CI: 2.08, 3.25), and 5.00 days (95% CI: 3.62, 6.38), respectively. The mean of SI_d of Zone 4 was significantly different (p < 0.05) from the means of the three other zones. Similar to Mettler and et al. (2020), we also experienced skewed biases toward the early part of each zone when estimating SI_d because we identified the infector-infected pairs only at the early part of each zone. Moreover, no such relationships were formally available from government sources covering the entire periods of the zones. Nevertheless, the noticeable delay in carrying out RT-PCR testing (mean SI_d = 5.00 days) was the primary reason for recording high numbers of daily cases in Zone 4 in certain days. Mettler et al. (2020) estimated SI_d for COVID-19 for two data sets, namely, Data A and Data B in South Korea, and obtained the result of 3.63 days (95% CI: 3.24, 4.01) and 2.31 days (95% CI: 1.48, 3.14), respectively. They reported that the SI for Data B (3.43 days with 95% CI: 2.62, 4.24) is relatively longer than SI_d. Evidently, the high mean value recorded for SI_d (5.00 days) in Zone 4 prompted the onset of the second wave in Sri Lanka.

3.2. Estimated levels of R_t and R_ts of the four zones

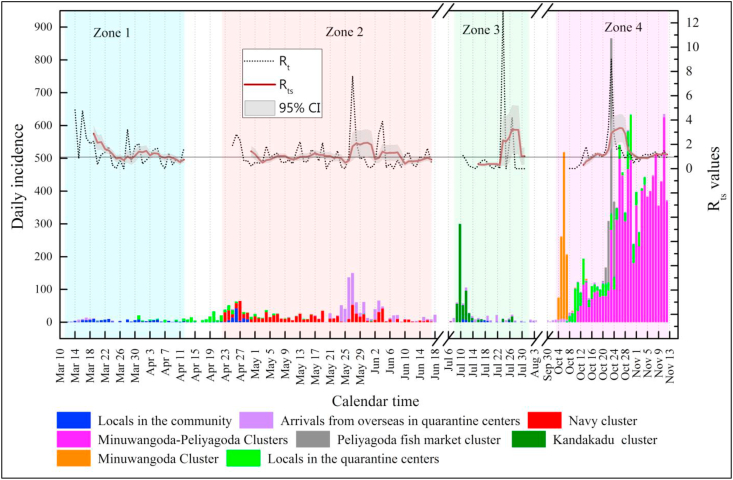
As proposed by Nishiura and Chowell (2009), we estimated R_t for each zone by considering the gamma-distributed discretized probability distribution of GI. In estimating R_t, we surmised that no contribution was derived from daily cases in quarantine centers or home quarantine because these cases were not exposed to the locals in the community. Fig. 2 depicts the variation of R_ts lagged by six days. Zone 1 had a high value of R_ts on March 20, 2020 (2.88, 95% CI: 1.21, 4.56), but the value decreased to <1 on April 12, 2020 (0.74, 95% CI: 0.10, 1.38), indicating the absence of a pandemic situation at the latter date. The initial higher value of R_ts for Zone 1 was merely attributed to lack of NPIs, but as the time passed with the enforcement of several NPIs (main drivers were health-related supports, lockdown and isolation, social distancing and health screening), R_ts dropped. However, by April 30, 2020, with the occurrence of Zone 2, a high value greater than 1 (1.43, 95% CI: 0.31, 2.55) was reported because of navy personnel contracting COVID-19. By June 17, 2020, the situation was improved with a reduced R_ts of less than 1 (0.75, 95% CI: 0.18, 1.32), indicating that the navy cluster was subdued without continuing the pandemic further. The main drivers for reducing R_ts towards the latter part of Zone 2 were the strengthening of NPIs, namely, wearing facemasks, quarantine efforts, hand hygiene, social distancing & health screening, and contact tracing. Conversely, Zone 3 began with a low value of R_ts <1, increased in the middle part (July 29, 2020; 3.19, 95% CI: 0.00, 8.51), and decreased to 1.00 (95% CI: 0.00, 2.86) by July 31, 2020. In Sri Lanka, the pandemic was under control until October 03, 2020, and Zone 4 commenced with the maximum R_ts value reported on October 26, 2020 (3.35, 95% CI: 0.33, 6.37). With the emergence of very high case numbers (after July 12) in Zone 3, all NPIs were tightened so that R_ts dropped drastically towards the end. With the sharp decrease of R_ts at the end of Zone 3, NPIs were relaxed, allowing the general public to engage in normal activities. However, with the astounding case numbers reported at the beginning of Zone 4, all NPIs were again imposed. In contrast to the situation in the other zones, R_ts continued to increase to slightly above 1 until November 12, 2020, the date on which we stopped collecting data for practical reasons; however, the pandemic was continuing. Therefore, we prove based on the estimates of R_ts values that although the health authorities managed the pandemic situation in the first three zones, they were unsuccessful in combating it in Zone 4; hence, the second wave of COVID-19 commenced on October 03, 2020, in Sri Lanka.

Fig. 2.

Variation of estimated R_t and R_ts in all four zones (Note: R_t is estimated following Nishiura and Chowell (2009) based on the daily incidences; R_ts values were estimated taking average of 6-day R_t values with 6-day lagging ending at time t. 95% CI for R_ts were shaded in the figure.).

Cori et al. (2013) estimated the R_ts values for measles, pandemic influenza, smallpox, and SARS by adopting a lagging window of 7 days for the general prediction of pandemic situations of different countries. Lessler et al. (2009) estimated R_ts for an outbreak of H1N1 in New York School, the USA, by adopting a time window of 6 days; the same was estimated for the Ebola outbreak in Liberia with a time window of 27 days (International Ebola Response Team, 2016). We assumed a time window of 6 days for Sri Lanka in estimating the R_ts for the COVID-19 outbreak at time t because the NPIs that are responsible for reducing or enhancing the pandemic situation are directly attributed to the disease transmission in about six days (before which NPIs are assumed to have little contribution to the control efforts for COVID-19 at time t).

3.3. Model-based parameterization and performance of the linear regression model against NPIs

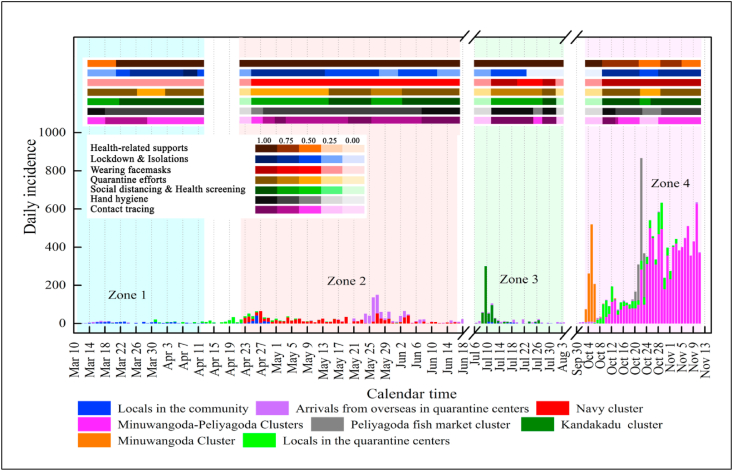
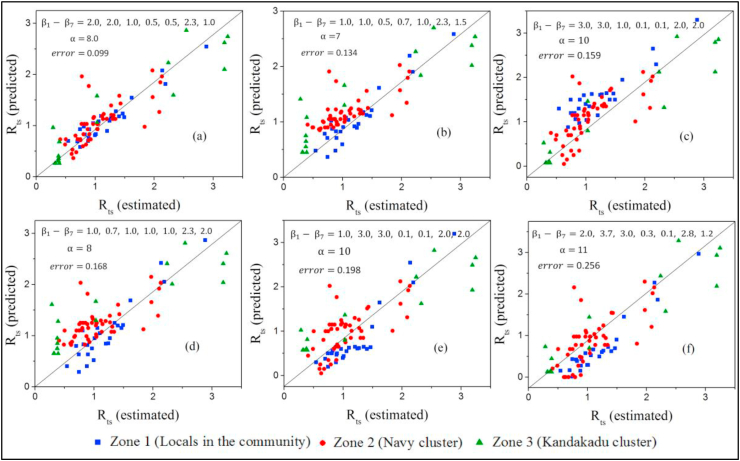
NPIs play a pivotal role in lowering R_ts. Fig. 3 shows how the imposition and lifting of NPIs occurred in Sri Lanka, and Table S5 (Supplementary Materials) indicates the degree to which the imposition or lifting of NPIs was carried out in the form of normalized transformation scores. The scores obtained for Zones 1, 2, and 3 were applied for the model containing Equation (2) as the model training step, and the constant parameters of $\alpha$ and ${\beta }_1$ to ${\beta }_7$ were estimated in a manner where $\epsilon$ was minimal. Fig. 4 shows plots of the predicted R_ts versus the estimated R_ts for different combinations of $\alpha$ and ${\beta }_1$ to ${\beta }_7$ values in an ascending order of $\epsilon$. The best-fitted plot (Fig. 4(a)) determines the most probable constant parameters of $\alpha$ and ${\beta }_1$ to ${\beta }_7$, and they were 8.0, 2.0, 2.0, 1.0, 0.5, 0.5, 2.3, and 1.0, respectively. The parameter estimation indicated that the highest impact (${\beta }_6$ = 2.3) was from the NPI of lockdown and isolation. In contrast, the minimal impact (${\beta }_4$ and ${\beta }_5$ = 0.5) was from the NPIs of hand hygiene and wearing of facemasks.

Fig. 3.

Imposition and lifting of seven NPIs in all zones over time in Sri Lanka; the degree of imposition intensities is marked in different shades of the same color and is depicted in the legend; evidence of such implementation arrangements was given in Table S2 in Supplementary Materials.

Fig. 4.

R_ts (predicted) vs. R_ts (estimated) plots for different combinations of α and ${\beta }_1$ - ${\beta }_7$ values; the plots are arranged in an ascending order (a to f) as the error increases.

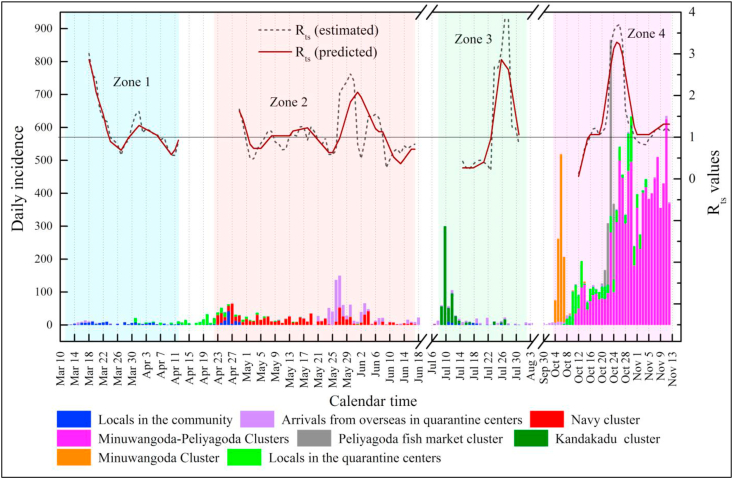
Patiño-Lugo et al. (2020) obtained similar observations, wherein lockdown and its combinations with other NPIs were determined to be more efficient than hand hygiene and wearing of facemasks. Davies et al. (2020) demonstrated through their stochastic model that R₀ can be reduced by the application of various NPIs. However, they predicted that the situation in the UK could not be prevented sufficiently to manage the ICU demand. The effective reproduction number R_t starts at R₀ and decreases monotonically because the number of individuals susceptible to the infection but are not yet infected declines as the virus spreads. The function R(t) can be influenced by NPIs and voluntary behavioral changes. However, in the case of a finite population, the effective reproduction number decreases automatically and necessarily over time because the number of infections would diverge otherwise (Kuhbandner & Homburg, 2020). The model was run for the data obtained for Zone 4 as a model-testing step by keeping the trained parameters unchanged. Fig. 5 depicts the trained and tested plots of R_ts over time, and the results suggest that the model fits reasonably well with R_ts estimated data. Alternatively, Li et al. (2020) analyzed the temporal association of R_ts with the imposition and lifting of NPIs for 131 countries by using a similar model and assumed that the first 28 days after the imposition of a particular NPI is effective in controlling the pandemic. The majority of similar model applications carried out worldwide do not attempt to check their validity by performing training and testing with known data sets having a reasonable accuracy, unlike our modeling effort. Therefore, this is the first time worldwide that such modeling with training and testing before any prediction is conducted, and the model parameters can be easily adjusted to any setting of a country whose NPIs are known.

Fig. 5.

Predicted R_ts values with linear regression modeling for four zones based on the normalized values assigned for all seven NPIs over time; R_ts estimated data of Zones 1, 2, and 3 are used for the training of the model while data of Zone 4 is utilized for the testing the model; Daily incidences of all four zones are also shown for reference.

3.4. Temporal predictions of R_ts with impositions of plausible improved individual and combinations of two NPIs for Zone 4

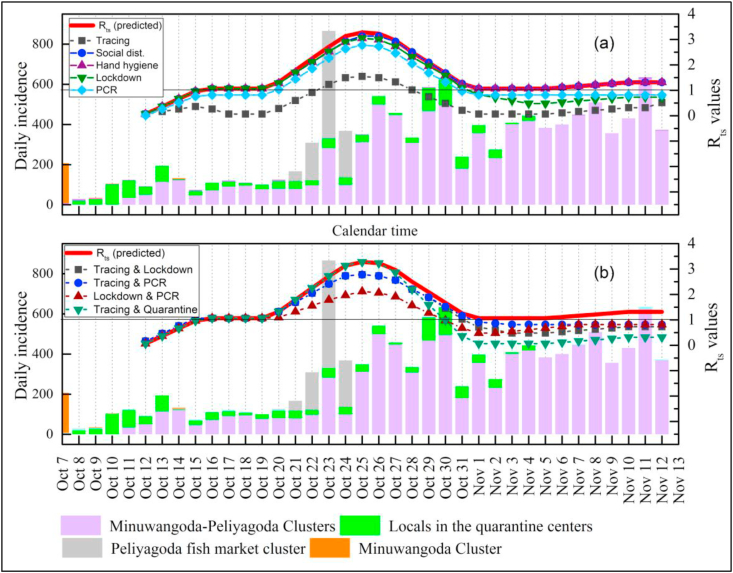
Our modeling showed that the second wave of the COVID-19 pandemic has begun, as depicted in Zone 4, and continues to be persistent (R_ts>1), although several NPIs have been imposed. The degree to which the combinations of NPIs have been adopted appears inadequate to avert the pandemic in Sri Lanka. Such inadequacies are due to economic reasons in the country. Sri Lanka did not opt for very stringent impositions of several NPIs, particularly during the second wave, because such drastic interventions could have crippled the lifestyle of people critically, as reported elsewhere (The Lancet, 2020). Hence, we used the model to study the plausible options that could have been practiced to avert the pandemic situation with more individual and combinations of two NPIs for Zone 4. Fig. 6 shows the comparisons of predicted R_ts for Zone 4 obtained by using the linear regression model with one NPI intensified or improved, and the same was done with the most probable combinations of two NPIs intensified. We analyzed five plausible individual and four twin cases, and their information is presented in Tables S6(a) and S6(b) in the Supplementary Materials. The individual cases encompassed contact tracing, social distancing and health screening, hand hygiene, lockdown and isolation, and health-related supports, with their normalized values intensified to their maximum potential. Table 1 shows the percentage of improvements that could have been obtained by imposing stringent individual and combinations of twin NPIs. Our model indicates that the most effective individual NPI was contact tracing that could have been mobilized with an improved workforce (% of improvement of R_ts was 69.43 compared with that of the baseline). However, improvement of contact tracing to the level expected, as indicated by the model, may not be practically feasible because the daily cases of COVID-19 are reported in many parts of the country. Another two individual NPIs, namely, lockdown and isolation and health-related supports, managed to bring the pandemic situation under control in Sri Lanka when applied with improved impositions (% of improvements of R_ts were 17.08 and 22.16, respectively). However, we believe that the two individual NPIs are extremely difficult to be practiced with improved impositions unless the country comes back to a deadlock; hence, they are unsuitable in terms of economic and social gains. Conversely, further improvements in social distancing with health screening and hand hygiene showed only marginal improvements of settings (% of improvements of R_ts were 2.06 and 3.88, respectively), indicating that further improvement of these two NPIs is insufficient to reduce R_ts to an acceptable level (<1). De Visscher A. (2020), in his simulations, used an extended SIR model and observed a similar trend. His study demonstrated that lifting extreme NPIs, such as lockdowns, can lead to increased mortality rates even though other NPIs, such as wearing of facemasks and hand hygiene, are maintained.

Fig. 6.

(a) Comparison of predicted R_ts for Zone 4 using the linear regression model for Zone 4 with one NPI intensified at any given time; (b) the same comparison with most probable combinations of two NPIs intensified at a given time; Red line (R_ts predicted) indicates the base case on temporal R_ts against NPIs adopted by the authorities and all other lines represent the same for intensified NPIs.

Table 1.

Percentage improvements obtained by different plausible individual NPIs and combinations of two NPIs that should have been made stringent for the control of virulent COVID-19 pandemic with lowering R_ts; Percentage improvements are calculated comparing the mean of R_ts of ‘base case’ (mean = 1.52) with the means of improved cases given in the table.

	Case #	Type of NPI made stringent	Mean of Rts	% Improvement achieved
Individual NPIs made stringent	Case 1	NPI 1 (Contact tracing)	0.46	69.43
	Case 2	NPI 3 (Social distancing and health screening)	1.48	2.06
	Case 3	NPI 4 (Hand hygiene)	1.46	3.88
	Case 4	NPI 6 (Lockdown and isolation)	1.26	17.08
	Case 5	NPI 7 (Health-related supports)	1.18	22.16
Combinations of twin NPIs made stringent	Case 1	NPI 1 (Contact tracing)	1.22	19.77
		NPI 6 (Lockdown and Isolation)
	Case 2	NPI 1 (Contact tracing)	1.30	14.12
		NPI 7 (Health-related supports)
	Case 3	NPI 6 (Lockdown and isolation)	1.01	31.92
		NPI 7 (Health-related supports)
	Case 4	NPI 1 (Contact tracing)	1.06	29.89
		NPI 2 (Quarantine efforts)

We report that instead of an individual NPI being enhanced to its highest possible degree, a combination of two NPIs with moderate improvements yields improved results in reducing R_ts. Plausible combinations of two NPIs consist of (1) improved contact tracing and lockdown and isolation, (2) contact tracing and health-related supports, (3) lockdown and isolation and health-related supports, and (4) contact tracing and quarantine efforts. Our finding corroborates that of Min et al. (2020), who reported that a combination of strict contact tracing, strict social distancing, and provision of health-related supports has reduced the transmission of COVID-19 drastically in South Korea. When plausible combinations of two NPIs were imposed with a decreased degree of intensification in the current study, the expected level of satisfaction toward the end of Zone 4 (R_ts<1) was achieved easily (Fig. 6(b)). The model results indicate that the imposition of any of the four combinations over time has managed to bring down the pandemic situation to a non-virulent setting. Case 3 in Table 1 (lockdown and isolation and health-related supports) shows the most significant improvement (% of improvement of R_ts was 31.92), and Case 2 (contact tracing and health-related supports) exhibits the lowest (% of improvement was 14.12).

Perkins and España (2020) demonstrated how the transmission of COVID-19 is mitigated by the adoption of combinations, such as case 3, in several countries. Li et al. (2020), who performed a similar type of modeling, suggested that a decreasing trend of R_ts is possible following improved efforts of lockdown and isolation and quarantine. A study conducted in Canada by using Oxford Stringency Index (OSI) scores recommended robust modeling studies to be undertaken with additional data to interpret the effectiveness of NPIs successfully (McCoy et al., 2020). Another study that covered 11 European countries reported that the major NPI responsible for controlling the transmission of COVID-19 is the lockdown, and its continued imposition should be considered to keep the transmission of the disease under control (Flaxman et al., 2020). Bouchnita and Jebrane (2020), who performed NPI modeling, suggested that measures that are stricter than social distancing and lockdown over a long time should have been used to control the COVID-19 pandemic in Wuhan, China. Many of the modeling efforts carried out worldwide, including ours, infer one common premise indicating that the optimum use of plausible combinations of NPIs would flatten R_ts to levels <1, and their imposition and lifting need to be carefully organized to produce maximum results on the control of the transmission of COVID-19. Moreover, their continued promulgation over time in critical settings is mandatory in the future. The time intervals during which these NPIs are to be implemented are not easily conceivable with the present scale of the transmission of the COVID-19 virus worldwide. Therefore, we surmise that combinations of NPIs will be in force in many countries until an effective, reliable vaccine reduces the daily incidences. Such episodes of imposition and lifting of NPIs invariably cause inconvenience, discomfort, displeasure, and inconsistency in the day-to-day activities of many people. However, we need to develop cognitive skills to adapt to this new lifestyle called new normal. Nevertheless, we notice that this model could not be applied with the rollout of the vaccine program, and we declare that it is an inherent limitation of our approach. We believe that machine-learning algorithms are more appropriate in such complex scenarios.

3.5. Expected role of the government

Our model studies confirmed that all seven NPIs with episodes of different scales of imposition and lifting over extended periods are essential in continuously suppressing the transmission of COVID-19 in Sri Lanka. Therefore, we have adopted a new normal, but the experience may differ from person to person. However, the continuation of the new normal is a daunting task because many people are unwilling to change their normal lifestyles. With regard to the creation of a healthy new normal for the general public, the government's role in the future would be somewhat different, and new opportunities will need to be unfolded in many lifestyle areas. By imposing and lifting efficient NPIs in the future, government authorities may engage in many tasks that are previously unknown but pertinently crucial in the new normal for averting COVID-19.

4. Conclusion

Our analysis implies that the first three zones of the COVID-19 pandemic were under control (R_ts<1), whereas Zone 4 (Minuwangoda and Peliyagoda) emerged uncontrollably (R_ts>1), indicating that the second wave has begun. The linear regression model developed for R_ts against NPIs was trained and tested successfully. Our model suggests that the most effective individual NPI was lockdown and isolation, and the least effective ones were hand hygiene and wearing of facemasks. The model also indicates that the stringent imposition of contact tracing as a single NPI could have brought the second wave under control (% of improvement of R_ts was 69.43). However, none of the individual NPIs was easy to be improved. By contrast, the intensified scale of applying a combination of lockdown and isolation and health-related supports could have brought the second wave to a satisfactory level (% of improvement of R_ts was 31.92). Our results confirm that the imposition of all seven NPIs with varying degrees of intensifications over an extended period is essential in averting the COVID-19 pandemic in Sri Lanka. This model can be replicated worldwide for numerous health authorities to strategize the imposition and lifting of NPIs and thus avert the COVID-19 pandemic.

CRediT authorship contribution statement

Mahesh Jayaweera: conceptualization, methodology, investigation, writing – original draft, visualization, supervision, project administration. Chamath Dannangoda: conceptualization, methodology, data curation, model formulation. Dilum Dilshan: methodology, resources, investigation, formal analysis, data curation. Janith Dissanayake: writing – review and editing, data curation. Hasini Perera: resources, validation, investigation, data curation, writing – original draft. Jagath Manatunge: validation, resources, writing – review and editing. Buddhika Gunawardana: validation, resources, writing – review and editing.

Declaration of competing interest

The authors declare that they have no known conflict of interests or personal relationships that could have appeared to influence the work reported in this paper.

Handling Editor: Dr HE DAIHAI HE

Funding

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Appendix A. Supplementary data

The following is the Supplementary data to this article: