Peptide bond planarity constrains hydrogen bond geometry and influences secondary structure conformations

Abstract

An extensive database study of hydrogen bonds in different protein environments showed systematic variations in donor-acceptor-acceptor antecedent angle (Ĥ) and donor-acceptor distance. Protein environments were characterized by depth (distance of amino acids from bulk solvent), secondary structure, and whether the donor/acceptor belongs to the main chain (MC) or side chain (SC) of amino acids. The MC-MC hydrogen bonds (whether in secondary structures or not) have Ĥ angles tightly restricted to a value of around 155°, which was distinctly different from other Ĥ angles. Quantum chemical calculations attribute this characteristic MC-MC Ĥ angle to the nature of the electron density distribution around the planar peptide bond. Additional classical simulations suggest a causal link between MC-MC Ĥ angle and the conformation of secondary structures in proteins. We also showed that donor-acceptor distances are environment dependent, which has implications on protein stability. Our results redefine hydrogen bond geometries in proteins and suggest useful refinements to existing molecular mechanics force fields.

Graphical abstract

Highlights

• •Hydrogen bonds are known to stabilize the structures of proteins.
• •We investigated the hydrogen bond types involving the main and side chains of amino acids and their environments.
• •The different types have unique preferences for donor-acceptor distances as well as for the donor-acceptor-acceptor antecedent (Ĥ) angles.
• •Classical and quantum calculations implicate the electronic structure of the peptide bond as the origin of these differences.
• •This study explains the origin of secondary structures and is important for protein characterization and design.

1. Introduction

Hydrogen bonding is an attractive force between an electronegative acceptor atom and a hydrogen atom, which is in turn covalently bound to an electronegative donor atom (Arunan et al., 2011a, 2011b). It is prominent among non-covalent interactions as it is directional, atom-specific and acts in the length scale of ~2.5 ​Å – 3.5 ​Å between donor and acceptor atoms with an estimated energy of ~1.3–9 ​kcal/mol (Pace, 2009; Pace et al., 2014). The physical nature of hydrogen bonding however is complex. While it is largely electrostatic in nature, it also possesses some covalent bonding features (Cordier et al., 1999; Isaacs et al., 1999). It has been established that in proteins, hydrogen bonds contribute to structural integrity and stability (Eswar and Ramakrishnan, 2000; Myers and Pace, 1996), secondary structures formation (Bordo and Argos, 1994; Eswar and Ramakrishnan, 1999), folding (Ben-Naim, 1991; Deechongkit et al., 2004; Rose et al., 2006; Chatterjee et al., 2009), molecular recognition (Fersht, 1987), pK_as of ionizable amino acid residues (Tan et al., 2013; Thurlkill et al., 2006), atomic packing (Kurochkina and Privalov, 1998) etc. Given its importance in proteins, much effort has been spent in characterizing the energetics and stereochemistry of hydrogen bonding (Fersht, 1987; Byrne et al., 1995; Connelly et al., 1994; Eberhardt and Raines, 1994; Habermann and Murphy, 1996; Honig and Yang, 1995; Nick Pace et al., 2014; Sheu et al., 2003; Shirley et al., 1992). Despite claims to the contrary (Campos et al., 2005), experimental evidence demonstrates the net stabilizing effect of hydrogen bonds in proteins (Pace, 2009; Deechongkit et al., 2004; Nick Pace et al., 2014; Cao and JU, 2014). The strength of protein hydrogen bonds is context-specific, and could vary with features such as polarity of its environment, contact order, temperature etc (Pace, 2009; Cordier and Grzesiek, 2002; Nisius and Grzesiek, 2012). Hydrogen bonding could also indirectly stabilize proteins by enhancing van der Waals interaction through increased packing density in the interior of proteins (Honig, 1999; Lazaridis et al., 1995; Schell et al., 2006).

The geometric parameters of hydrogen bonds in proteins can be learned from statistical analyses of known protein structures. Such analyses have been extensively documented earlier and have provided crucial insights into protein structural stability and function (Baker and Hubbard, 1984; McDonald and Thornton, 1994; Sticke et al., 1992). However, these studies were performed over small datasets (e.g. n ​= ​15 in the study by Baker and Hubbard) of known structures and the protein data bank (PDB) has since grown exponentially (Berman, 2000). Not only do we have a larger number of high-resolution structures, we also have different means of characterizing protein environments (Deechongkit et al., 2004; Chakravarty and Varadarajan, 1999). In this study we characterized protein residues by an established, concise descriptor of protein environment – depth (Tan et al., 2011, 2013; Chakravarty and Varadarajan, 1999). Our analyses supplement and update older studies of hydrogen bond parameterization (Baker and Hubbard, 1984; McDonald and Thornton, 1994; Sticke et al., 1992; Fabiola et al., 2002; Grzybowski et al., 2000; Ippolito et al., 1990; Kortemme et al., 2003; Lommerse et al., 1997; Taylor and Kennard, 1984; Taylor et al., 1983). We have compared statistical analyses with quantum mechanical calculations. An earlier study had shown good correlation in such comparisons on hydrogen bonds in model systems (Morozov et al., 2004). Further, we use such calculations to obtain valuable insights on the different types of hydrogen bonds in proteins.

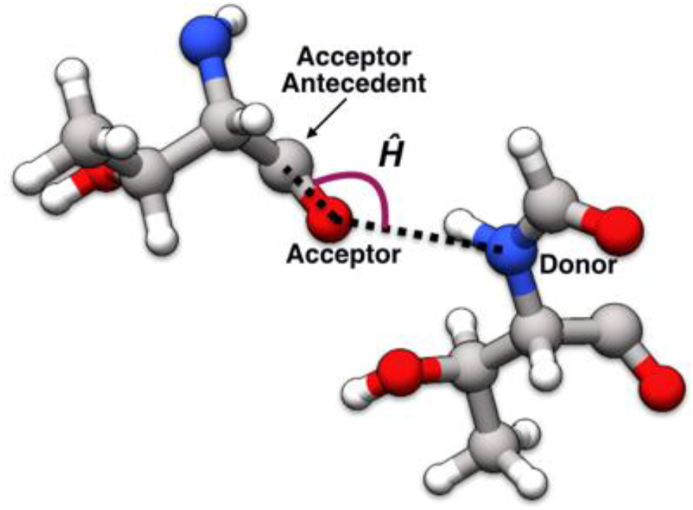
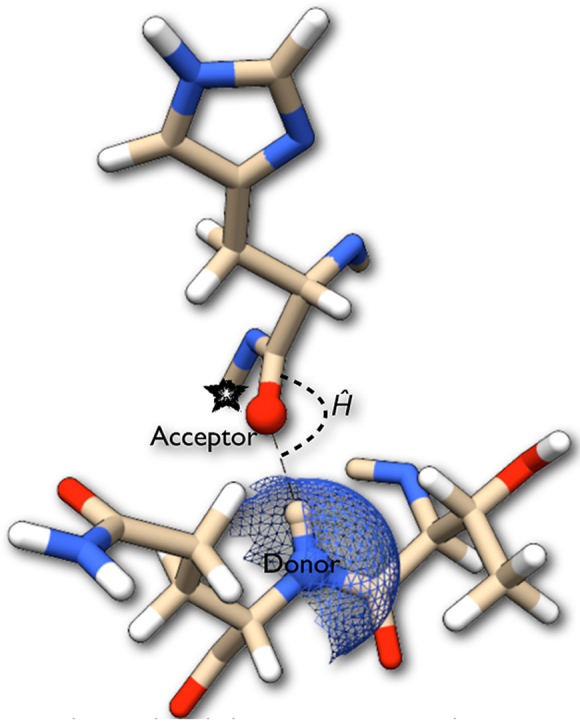
We have carried out a detailed analysis of different types of hydrogen bonds and their preferences of geometry in different environments. The geometry here is characterized by the donor-acceptor distance and donor-acceptor-acceptor antecedent angle (Ĥ angle, Fig. 1). We attempted to rationalize the Ĥ angle preferences by two complementary methods — (a) comparing to data obtained from small molecules and (b) by performing quantum chemical calculations on model systems that mimicked hydrogen bonded peptide units. Other simulations were performed to study the connection between hydrogen bond geometry and protein secondary structure. Taken together, these studies suggest a likely causal connection between peptide bond planarity and the formation of secondary structures. Our findings suggest the means of creating a hydrogen bond potential that could be used in refining protein structures/models, especially if they are of low resolution. Such potentials could also be incorporated in existing molecular mechanics force fields.

Fig. 1.

The Ĥ angle in proteins is between the hydrogen bond donor, acceptor and acceptor antecedent.

2. Results

2.1. Geometry of Protein Hydrogen Bonds

The geometry of hydrogen bonds is dependent on the types of donor/acceptor atoms and the protein environment. To investigate these dependencies, we studied the frequency of occurrence of different types of hydrogen bonds and their geometries in different environments. In the sections below, the residue environment is parameterized using the depth measure.

First we investigate the geometries of hydrogen bonds. From the high-resolution, single domain data training set, the statistics of donor-acceptor distance (within a cutoff of 4.0 ​Å) and Ĥ angle were collected. These data were compared to a reference state where there is no angular preference of donor/acceptors. In this reference state, the atoms were randomly distributed as if they were non-interacting entities, akin to molecules of an ideal gas. The reference state distribution is described as -

$$N^{exp}(r)=N_0\cdot 4\pi r^2\cdot dr$$ (Equation 1)

where N^exp(r) is the expected number of donor-acceptor pairs at a distance r, and dr is the bin size for collecting statistics (20 equally sized bins spanning the range 2.3–4.1 ​Å). N₀ is the background density of donor/acceptor pairs at a cut-off distance and is given by –

$$N_0=\frac{N^{obs}(r_{cut})}{4\pi r_{cut}^2\cdot dr}$$ (Equation 2)

where r_cut ​= ​4 ​Å and N^obs(r) is the observed number of donor-acceptor pairs at a distance r. We only considered the geometries of those hydrogen bonds that had log-odds ratio values of 4 or higher. This confines the donor-acceptor distance to less than 3.5 ​Å and the Ĥ angle to lie between 100 and 180°. Most hydrogen bonds are concentrated at donor-acceptor distances of 2.9 ​Å and Ĥ angles of 155° (Supplementary Fig. S3). Note, our Ĥ angle range decreases the lower bound to 100° from the previously established 120° (Baker and Hubbard, 1984). We believe that this expansion in the definition is a better description of hydrogen bonds. For instance, it better explains amide protections in hydrogen exchange experiments as evidenced in a case study of hen egg white lysozyme. Residue 23, 42 and 78 have Ĥ angles of 119°, 118° and 112° respectively and are known to exchange slowly, an indication of their status as being hydrogen bonded (Supplementary data 4). The composition of hydrogen bonds at different geometries is further discussed in the following sections.

2.2. Type-specific donor-acceptor distance and Ĥ angle

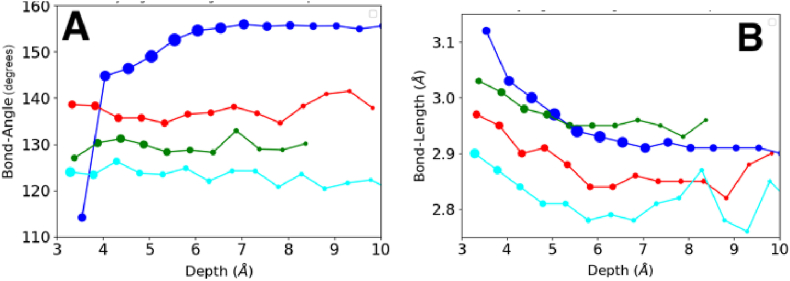
The different hydrogen bond types (MC-MC, MC-SC, SC-MC and SC-SC, as defined in the methods section) have slightly different preferred donor-acceptor distances and average Ĥ angles and are distinct from one another. MC-MC bonds typically occur with the highest Ĥ angle values of ~155°. MC-MC bonds however tend to have lower Ĥ angles, ~105°, when exposed at the protein surface. The other hydrogen bond types, MC-SC, SC-MC and SC-SC all have their distinct Ĥ angle preferences of ~130°, ~135° and ~125° respectively. These preferences do not change with change in residue environment (Fig. 2A).

Fig. 2.

The average geometry (A) Ĥ angle and (B) donor-acceptor distance of different hydrogen bond types at different solvation environments measured by depth. For a description of the different types of hydrogen bonds, MC-MC (blue), MC-SC (green), SC-MC (red), SC-SC (cyan), refer to the methods section. The sizes of the symbols are proportional to the log_e of data sampled.

The mean donor-acceptor distances of the different hydrogen bond types, while distinct from one another, all show a tendency to decrease as they occur in increasingly buried environments (Fig. 2B). The MC-MC bonds and MC-SC bonds are the longest bonds (ranging from ~3.1 ​Å when exposed to ~2.9 ​Å when buried) while the SC-SC bonds are the shortest (~2.9 ​Å - ~2.8 ​Å). The MC-MC type has the largest donor-acceptor distance and Ĥ angles while the SC-SC type has the smallest of both.

To test the statistical significance of the difference in geometries (Ĥ angle and donor-acceptor distance) in the different hydrogen bond types, the hydrogen bonds were categorized by type and depth. Depth values ranged from 3.0 ​Å to 10.0 ​Å and were binned at intervals of 0.5 ​Å. Statistical significance was established using a Welch's t-test in each of the bins. Most of the differences in donor-acceptor distances and Ĥ angles between different types of hydrogen bonds were statistically significant (p ​< ​0.05). Some exceptions were at the protein surface (depth ​< ​4 ​Å) where there are large structural/geometrical fluctuations. Statistical differences could also not be detected in the protein core (depth ​> ​8 ​Å) because of sparse data (Supplementary data 5).

2.3. Ĥ angle distribution in small organic molecules

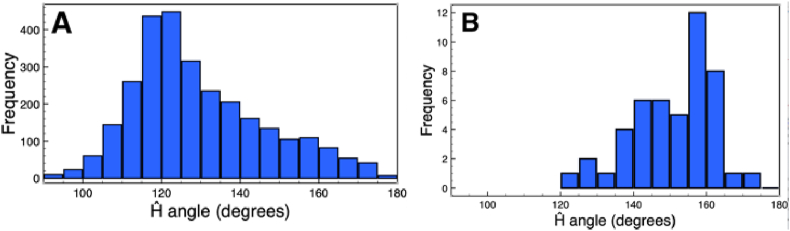
To investigate the hydrogen bond geometry when it is devoid of all possible structural and environment constraints, we surveyed the Crystallography Open Database (Gražulis et al., 2012; Graulis et al., 2009) for statistics on donor-acceptor distance and Ĥ angle in small organic molecules. In this dataset, only hydrogen bonds constituted by a nitrogen donor, an oxygen acceptor and a carbon acceptor antecedent were considered. We also required that the hydrogen atom be explicitly present for a hydrogen bond to be detected. 2886 hydrogen bonds from 1922 small molecules were found in the dataset (Supplementary data 1B). From the distribution of hydrogen Ĥ angle (Fig. 3A) we made two observations:

• (1)The mean Ĥ angle in small organic molecules is ~125° (+-16.5°). This value is similar to hydrogen Ĥ angle of SC-SC hydrogen bonds in protein (Fig. 2A).
• (2)More than one third of hydrogen bonds would have been missed if an Ĥ angle threshold of 120° was used. This is in contrast to ~3% if a threshold of 100° were used.

Fig. 3.

Histograms of Ĥ angle in (A) small organic molecules (B) dipeptide and tripeptides with Gly contributions coloured in red.

Next, we similarly surveyed the Crystallography Open Database and the Cambridge structural database (Allen, 2002) for MC-MC hydrogen bonds in dipeptides and tripeptides. A total of 48 hydrogen bonds were found in 22 structures (Supplementary data 7). It was observed that hydrogen Ĥ angle also has a mean value of ~153.5° (+-8.6°) if 5 GLYs were excluded (Fig. 3B). Ĥ angles of hydrogen bonds involving GLY residue typically are ~140° or smaller.

2.4. Donor-acceptor distance and Ĥ angle in protein secondary structures

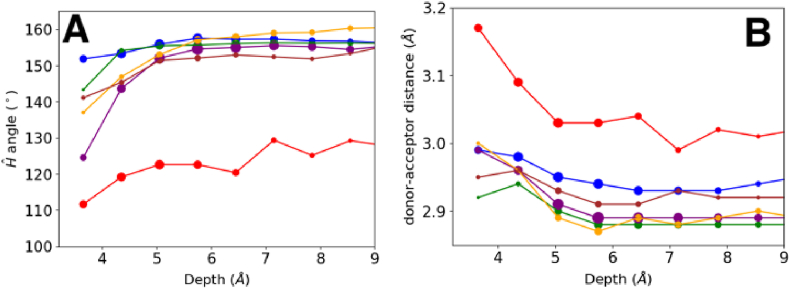
We investigated the environmental variation of MC-MC type hydrogen bonds as they are crucial to the formation of secondary structures. MC-MC hydrogen bonds were sub-classified into alpha-helical, beta-strand and non-secondary structure. The non-secondary structure classification here is more precisely conformations that are not beta strands or 4₁₃ alpha helices. 3₁₀ helices for instance also form a part of the non-secondary structure type. The 3 sub-classes have slightly different geometry preferences (Fig. 4). Ĥ angles in secondary structures have a mean of ~155° (the angle is slightly higher in case of parallel beta sheets), and do not vary with residue depth except at the protein surface. The Ĥ angles in regions without secondary structure ranges from ~110° to ~130° at different levels of depth (red line in Fig. 4A). Interestingly, when (i, i+3) hydrogen bonds are excluded from the non-secondary structure hydrogen bonds, the Ĥ angle values tend towards 150°. Clearly, MC-MC hydrogen bonds in non-secondary structures (with the exception of (i, i+3) associations) also display the same geometry as their secondary structure counterparts.

Fig. 4.

The donor-acceptor distance (A) and Ĥ angle (B) of different MC-MC hydrogen bond types at different depths. The hydrogen bond of the MC-MC type includes alpha helix (blue), anti-parallel beta-strand (purple), parallel beta-strand (orange), beta-strand excluding GLY and termini (green), non-secondary structure (red), and non-secondary structure excluding (i, i+3) hydrogen bond (brown). The sizes of the symbols are proportional to the log_e of the data points sampled, normalized by colour.

Of the 3 sub-classes, donor-acceptor distances in beta strands are the shortest (Fig. 4B). On the surface (depth ​< ​6 ​Å) they are slightly longer than 3.0 ​Å and this value converges to a little under 2.9 ​Å ​at a depth of ~6 ​Å and remains steadily at this value for all higher depths. The donor-acceptor distances of helices and non-secondary structures converge to a value ~2.95 ​Å only at depth of about 8 ​Å. The donor-acceptor distances of these 2 sub-classes at the surface are ~3.0 ​Å and ~3.2 ​Å respectively.

Earlier studies have established that shorter donor-acceptor distances imply stronger binding (for a review on the subject see (Arunan et al., 2011b)) and that donor-acceptor distances are correlated to the charge on the donor atom (Raghavendra et al., 2006). Our database analysis fortifies both of these established results. Beta sheet proteins in general tend to have higher melting temperatures (Supplementary data 8) and the correlation coefficient between donor atom partial charge and donor-acceptor distance ~ ​= ​0.75 (as opposed to ~0.11 for partial charge on the acceptor atom). More interestingly, when the data presented in Fig. 4 is studied amino acid wise, one can make a clear distinction between the residues that have strong preferences for beta sheet and alpha helices (supplementary data 9).

The deviations from the mean hydrogen Ĥ angle are greater at the surface (depth ​< ​6 ​Å) than in the interior (depth ​> ​6 ​Å) for beta sheets (~15.5° on surface, ~9.1° in protein interior). The deviation from the average at lower depths is less pronounced in cases where glycine residues and terminal residues (1 residue at the N and C termini of strands) are not included in the computation. The deviation of hydrogen Ĥ angles in alpha helices and non-secondary structure regions are ~8.8° and ~15.5° respectively and do not change with depth. Interestingly, H-bonds connecting non-secondary structure regions are seldom found at depths >7 ​Å. Small deviations notwithstanding, all MC-MC Ĥ angles fluctuate about ~155° regardless of depth levels.

It is interesting to note that the Ĥ angle of MC-MC hydrogen bonds regardless of secondary structure converges to the same value of ~155°. To get an insight into these Ĥ angle preferences, QM calculations were performed on small molecules and peptide systems.

2.5. Quantum chemical studies of the Ĥ angle explains its characteristic values in protein main and side chains

Quantum mechanical calculations were performed on small molecule models of proteins with two objectives: (a) to compare trends of the calculated Ĥ angle with those obtained from the statistical analysis, and more importantly (b) to rationalize the structural differences between the different types of hydrogen bonds. The Ĥ angles from quantum mechanical simulations on model systems (Supplementary data 2A) were found to be 138.0°, 112.8°, 112.5° and 100.0° for the MC-MC, SC-MC, MC-SC and SC-SC types of hydrogen bonds respectively (Supplementary data 2B). The trend in the Ĥ angle (MC-MC ​> ​SC-MC ​> ​MC-SC ​> ​SC-SC) is consistent with the database study. The actual calculated numbers do not exactly match the corresponding observed ones, a difference that can be attributed to several factors such as oversimplified model systems, absence of any secondary interactions besides the primary hydrogen bond interaction, and lack of incorporation of the complex environment that is present in the actual protein. Nevertheless, the Ĥ angle values being so significantly different depending on whether the donor/acceptor belongs to the MC or SC of the amino acids, hints at a fundamental basis for it, which we have investigated. Interestingly, in our more realistic models, i.e., di-glycine models 1 and 2, the MC-MC Ĥ angle are closer to observed values at 150.3° and 147.8° respectively (Supplementary data 2C).

To understand the striking change in Ĥ angle between the MC-MC and SC-MC type of hydrogen bonds, we performed a quantitative study using atomic partial charges. We started with three different MC-MC hydrogen bond models and through a sequence of steps modified these to corresponding models of SC-MC type of hydrogen bonds (see the methods section for details). In each of the three cases, the essential difference between the MC-MC (original molecule) and its corresponding SC-MC (saturated molecule) counterpart is only the changed hybridization of the hydrogen bond donor atom. This permits a clear and unambiguous analysis of the effect of the type of hydrogen bond on structure.

Based on the above analysis we can explain the decrease in Ĥ angle going from MC-MC type to systems where the hydrogen bond involves a side chain. The first interesting result is that in all the three models, the hydrogen bond angle (the angle between the donor-proton-acceptor, not to be confused with Ĥ) changes only slightly (by ​~ ​5°) going from the original to the saturated molecule (Supplementary table S2.2). The hydrogen bond angle is almost linear in the original molecule (model for MC-MC hydrogen bond) and continues to be almost linear in the saturated molecule (model for SC-MC hydrogen bond). However, the striking result is that the Ĥ angle in the NMA dimer and the di-glycine dimer models decrease significantly going from the original to the saturated molecule by 14° – 19° (Supplementary table S2.2). This is consistent with statistical observations (see section Type-specific donor-acceptor distance and Ĥ angle) for the MC-MC and SC-MC hydrogen bond types discussed above.

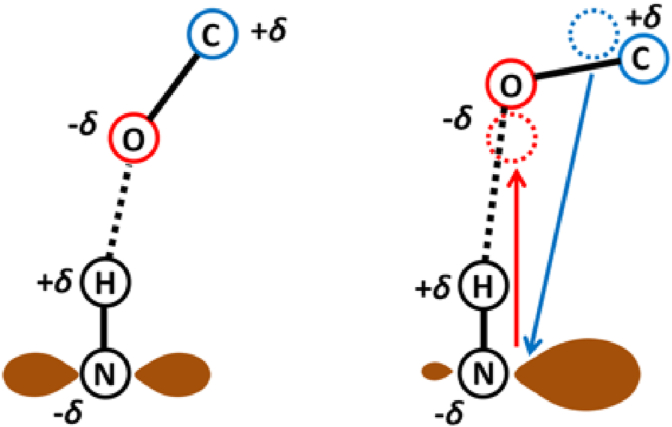
We can understand these structural differences in terms of the partial charges and electrostatic interaction between the hydrogen bond donor, and the acceptor and acceptor antecedent. The partial charge on the nitrogen does not change significantly from the original to the saturated molecule (Supplementary Table S2.2). The significant change, however, is the distribution of this charge — in the original molecule the three bonds of N are planar (sp² hybridized) and the p-orbital density is almost equally dispersed below and above the plane, whereas in the saturated molecule, the p-orbital density is in the form of a lone pair and is relatively more concentrated around the N (Fig. 5). This concentrated negative charge repels the negative charge of the acceptor O, increasing the N–O distance, and consequently increasing the distance between the two dimers. The concentrated negative charge also interacts with the O C dipole (O is the acceptor and C is the acceptor antecedent with negative and positive partial charges respectively), which causes it to rotate such that the C moves towards the N due to attraction, even as the O moves away from the N due to repulsion.

Fig. 5.

Schematic representation showing the decrease in Ĥ angle going from a MC-MC to SC-MC type of hydrogen bond. The atoms N and O are negatively charged (-δ), while H and C are positively charged (+δ). The red arrow indicates repulsion between the negative charges while the blue arrow indicates an attraction between opposite charges. The brown cloud represents the electronic charge density on the N atom.

In all models the N–O distance increases going from the original to the saturated molecule (Supplementary table 2.2). In the NMA dimer model and di-glycine model 1, the N–C distance decreases, while in di-glycine dimer model 2 the N–C distance increases. Though there is a slight increase of 0.05 ​Å in the N–C distance in di-glycine model2, the N–O distance increases by 0.2 ​Å, which is still consistent with the rotation of the O C dipole. In all three models, the effect of the rotation of the O C dipole, with the O remaining almost along the N–H–O straight line and C coming closer to the N, is that the Ĥ angle decreases.

2.6. Linking Ĥ angles to secondary structure

We next investigated the link between secondary structure formation and Ĥ angle variation by two different methods A) Empirical modeling and B) Molecular dynamics simulations – to study the geometries of helical peptides with different Ĥ angles.

The empirical modeling follows the general principle of constructing the 3D structures of molecules by satisfying spatial restraints. The spatial restraints are of two major types. 1) Stereochemical restraints, to ensure proper bonded parameters. 2) Spatial restraints between non-bonded atoms of the molecule (poly-peptide) including restraints on distances, angles, torsion angles etc. to give the overall conformation of the polymeric system. In our model systems, we have restrained the Ĥ angles to different values while the polypeptide as a whole is restrained to an alpha helix or beta sheet.

2.6.1. Restraining Ĥ angles in alpha-helices

A set of simulations was performed to fold a 24-mer poly-Ala peptide from an extended conformation to an alpha helix. The simulations were carried out using the refine_slow option of MODELLER (Šali and Blundell, 1993) that optimizes structure by satisfying spatial restraints. All the (i ​+ ​4, i) hydrogen bonding pairs of amides and carbonyl oxygens in an alpha helix were restrained to donor-acceptor distance of 2.9 ​Å with a standard deviation of 0.2 ​Å. In each simulation, the corresponding Ĥ angles were restrained to one of 11 different values ranging from 100° to 180° in steps of 10°, and the values 125° and 155°. In addition to the hydrogen bond restraints, stereo-chemistry of all amino acids were appropriately restrained (Restraints:STEREO module of MODELLER) while considering L-J and electrostatics over the entire system.

Alpha helices were successfully generated in 7 of the 11 restraining attempts. When the helices were formed, the hydrogen Ĥ angle lies in a narrow range of 145–160°, regardless of the initial restraining angles. In the 4 cases that alpha helices were not formed, the restraints caused several atomic clashes in the system (violation of the Ramachandran map) (supplementary data 10). An atomic clash is defined when two atoms are separated by a distance of 0.25 ​Å less than the sum of their van der Waal's radii.

2.6.2. Sampling Ĥ angles in beta sheets

We next examined the range of allowed Ĥ angles that would result in parallel and anti-parallel beta sheets. Our model systems consisted of two 6-residue strands that formed parallel and anti-parallel sheets in an almost planar configuration (the dihedral angle formed by the first and last C^α atoms on both strands ​~ ​9.3°). For the parallel and anti-parallel sheets, templates were extracted from PDB:3AUM (residues 111–115, 121–125) and PDB:2PEC (residues 204–208, 226–230) respectively. To each strand in both systems an extra residue was engineered so as to maintain the relative planarity of the system.

To simulate sheets with different Ĥ angles, we sheared one strand with respect to other by 3.5 ​Å, in steps of 0.1 ​Å, in both directions so as to maintain the overall planarity of the sheet (Supplementary Figure S11.1). In addition to shearing along the length of the sheet, the two strands were also laterally separated (from −0.75 ​Å to 0.75 ​Å in steps of 0.1 ​Å) so as to sample different hydrogen bond distances. After every step, we computed the donor-acceptor distances, Ĥ angles and atomic clashes in the 4 central residues of each strand.

In both sets of shearing simulations, clash-free sheets were formed when Ĥ angles lay within a narrow range of ~10° with a mean close to ~155° (Supplementary Figure S11.2), with the parallel system having a slightly more permissive upper bound. Interestingly, the lower bound for the Ĥ angle was ~150° regardless of donor-acceptor distance.

2.6.3. Molecular dynamics simulations of poly-alanine helices

We performed three different sets of replicate molecular dynamics simulations on a 16-mer poly-alanine ɑ-helix. The first simulation was a constraint free control. The second and third sets had repulsive and attractive potentials at Ĥ angles of 155° respectively.

In the free simulation, all (i+4 - i) hydrogen bonds remain intact but the Ĥ angles are ​~ ​170°–175°. There is a small distortion of the ideal alpha helical geometry as evidenced by the spread in the Ramachandran angles (Supplementary figure S12.2A). This is perhaps indicative of the force field parameters confining the donor-acceptor-acceptor antecedent atoms to a near-linear geometry. This discrepancy in the force field is perhaps also responsible for the helix to explore regions of the Ramachandran map that are slightly away from the centre of the “ideal” helix location (Supplementary figure S12.2A).

In the second simulation, when there was an energy barrier placed at 155°, the Ĥ angle sampled the 110°–140° (on average 127°) region. But more importantly, the donor acceptor distances all exceeded 3.2 ​Å. In this simulation the helix was observed to melt, with around half of all the hydrogen bonds breaking during the simulation (Supplementary Figure S12.1 and S12.2B).

In the third simulation the Ĥ angles all had values ~155° (Supplementary figure S12.1). Note that the distribution of Ĥ angles now mimics our database observations. In this simulation, the Ramachandran angles correspond to that of ideal ɑ-helix (Supplementary figure S12.2C). Note that the ϕ and ψ angle values in this simulation are less spread than in the free simulation. The restraining force at 155°, which was applied to the structures taken from the second set of simulations restores ideal helical geometry. This Ĥ angle value results in idealised secondary structure geometry.

3. Discussion

Hydrogen bonds and their role in protein structural stability and function have been extensively studied. Our study supplements these findings by investigating the variation of hydrogen bond donor-acceptor distance and the Ĥ angle with respect to protein environment, which we characterized by residue depth.

The most surprising of our results concerns the Ĥ angle. There are very few mentions of the preferred values of the Ĥ angle in earlier studies and most of them contend that it should be≥120° (Baker and Hubbard, 1984; Torshin et al., 2002). Our analysis of a set of high-resolution crystal structures revealed that the different types of hydrogen bonds had specific preferred values of this Ĥ angle. That the deviations to these preferred angles were small led us to investigate further.

We devoted most of our attention to the MC-MC Ĥ angle, which regardless of amino acid depth, consistently maintains a value of ~155°. This invariance in value is also seen in hydrogen bonds across alpha helices and beta strands. The trivial explanation that the formation of secondary structures “constrains” the Ĥ angle to ~155° does not hold because hydrogen bonds between residues in non-secondary structure regions also have the same value. Even small molecules, such as dipeptides devoid of protein environment context, whose structures are deposited in the Cambridge and Crystallography Open databases, show the same preferred value for MC-MC hydrogen bonds. Clearly secondary structures do not influence the Ĥ angle preference.

To investigate the genesis of the angle preference we carried out empirical, molecular mechanics and quantum chemical simulations. The empirical and molecular mechanics simulations attempted to constrain MC-MC Ĥ angles to values other than 155° (ranging from 100° to 180°). In each of these simulations, the values either reverted to ~155° on optimization or else the final models had a) steric clashes or b) when the starting structure was of regular secondary structure – the final model developed characteristics that deviated significantly from the starting secondary structure.

QM studies convincingly establish that the planar nature of the peptide bond and the electron density distributed about such a bond is instrumental in confining the MC-MC hydrogen bond to ~155°. The QM computations also reveal that this peptide bond planarity and the corresponding electron density explains the decreasing Ĥ angle trend amongst the different hydrogen bond types (MC-MC ​> ​SC-MC ​> ​MC-SC ​> ​SC-SC; with rigorous comparisons done to show MC-MC ​> ​SC-MC).

We noted two exceptions to the MC-MC Ĥ angle at ~155° trend. First, hydrogen bonds in beta strands close to the protein surface tend to have smaller Ĥ values. These outliers are typically beta sheet termini and glycine residues. If these residues were excluded, the Ĥ angle values were back to ~155°. The Ĥ angle of MC-MC hydrogen bonds involving glycine residues (either as acceptor or donor) in secondary structures and coils buck this trend and have an average value ~142°. No other amino acid shows this tendency suggesting that the asymmetric substitution around the alpha carbon plays an important role in determining the electron density of the peptide bond. The second exception was (i, i+3) hydrogen bonds that have a preferred Ĥ angle ~130°. Omitting these (7.4% of all hydrogen bond observations) from the dataset of non-secondary structure hydrogen bonds restores the average value to ~155°. The precise nature of the (i, i+3) hydrogen bonds warrants investigation and is beyond the scope of this study.

Database analysis results show that secondary structure and protein environment do not play a significant role in determining MC-MC Ĥ values. The value of ~155° for the MC-MC hydrogen bond arises instead from the planar nature of the peptide bond. The electron density around the peptide bond makes other Ĥ angle values sterically infeasible. The Ramachandran angles at which alpha helices and beta strands are formed are those where the Ĥ angle of ~155° is satisfied between hydrogen bonding partners. Repetitive Ramachandran angles lead to the formation of secondary structures that are stabilised by hydrogen bonds. Given the restrictions placed on the Ĥ angle by the peptide bond, such Ramachandran angles are restricted to the current ideal values for alpha helices and beta sheets. The planar peptide bond hence influences the nature and types of secondary structures in proteins.

In addition to the Ĥ angles, we also studied the variation of donor-acceptor distance in the different types and in different environments. We observed that donor-acceptor distances in all types of hydrogen bonds, except those in alpha helices, decrease with increasing depth. As small donor-acceptor distances are symptomatic of stronger hydrogen bonds, this trend is in accordance with the established fact that buried hydrogen bonds are stronger than their counterpart on the protein surface. Among different types of hydrogen bonds also, there are minute (~0.1–0.2 ​Å), but nevertheless statistically significant differences. MC-SC hydrogen bonds have the longest bond donor-acceptor distances (average value 3.1 ​Å) while SC-SC distances are the shortest (average value 2.9 ​Å).

It is of some importance that SC-SC hydrogen bonds are the shortest. We believe that this is indicative of interactions between residues that are likely to be highly conserved or between residue positions whose hydrogen bonding confers structural stability to the protein.

Interestingly, our results also showed that donor-acceptor distance correlates with partial charge on the donor, but not the acceptor. This unintuitive result is nonetheless in agreement with a previous ab-initio quantum mechanical computation (Raghavendra et al., 2006). Additionally, donor-acceptor distances in beta sheets are shorter than in helices and coils (Supplementary data 4). As donor-acceptor distance is correlated with partial charge distribution on the donor group, we hypothesized that amino acids with high propensity for beta-sheets could have more polarized amide groups. Evidence supporting this hypothesis is the observation that amino acids with high propensity for beta sheet formation (e.g. isoleucine, leucine, valine) are beta branched. A previous study showed that beta-branched carbons could increase the dipole moment of adjacent atoms (in this case, the amide group) by hyperconjugation (Alabugin et al., 2011). As beta sheets have stronger hydrogen bonds, it stands to reason that all-beta proteins would generally melt at higher temperatures in comparison to all-alpha proteins. This is borne out by a cursory analysis of melting temperatures of different types of proteins (Supplementary data 7).

As asparagine and glutamine side chains contain peptide-bond like chemical structure, we expect that the MC-MC Ĥ angle preferences also hold for such SC-SC interactions. This could enable crystallographers in resolving the identities of the amide and carbonyl groups in asparagine and glutamine, which is often an issue given the similarity of their electron densities.

Future structure refinement and force field developments should take into account the findings from this study and suitably amend parameter values, particularly, the partial charges of main chain amides. An explicit hydrogen bonding term should be (re-)introduced in the potential to account for the different hydrogen bond types and their corresponding Ĥ values. In an associated study, we explored the refining of low resolution X-ray and NMR structures that had several broken hydrogen bonds. The data obtained in this study helped build a refinement protocol that not only restores a large fraction of the missing hydrogen bonds but also improves on overall structural accuracy (data not shown).

In this study, we have demonstrated that hydrogen bonds in proteins do not belong to one homogeneous class. Different hydrogen bonds have distinctively different geometry and strength under different environmental conditions. These variations are important considerations in constructing, refining or engineering protein and peptide structures.

4. Methods

4.1. Hydrogen bond criteria

To qualify as a hydrogen bond the hydrogen bond donor and acceptor atoms should be separated by 3.5 ​Å or less and the donor-acceptor-acceptor antecedent angle (Ĥ) should be larger than 100°. This definition is an amendment from the one proposed earlier (Baker and Hubbard, 1984). Our motivation for making this amendment is described in the Results section under “Geometry of Protein Hydrogen Bond”. In this study, hydrogen atoms were not considered, as their precise positioning in many of the analyzed structures is not known.

4.2. Data sets

561 high-resolution (resolution 1.7 ​Å or better; R-free 0.2 or better), non-redundant (at 30% sequence identity), single domain protein structures (chain lengths between 80 and 180 amino acids) were extracted from the PDB to study hydrogen bond frequencies and geometries. The list of PDB entries corresponding to the different data sets mentioned below can be found in the Supplementary material (Supplementary data 1a). The data set consists of a total of 67563 hydrogen bonds.

4.3. Classification of hydrogen bonds

In this study, we empirically classified hydrogen bonds into 4 types based on whether the donor/acceptor atoms are from the main-chain/side-chain: (i) donor: main-chain; acceptor: main-chain (MC-MC), (ii) donor: main-chain; acceptor: side-chain (MC-SC), (iii) donor: side-chain; acceptor: main-chain (SC-MC) and (iv) donor: side-chain; acceptor: side-chain (SC-SC). MC-MC hydrogen bonds are further divided into 3 sub-types based on secondary structure: (i) alpha helix (ii) beta strand and (iii) non-secondary structure.

4.4. Hydrogen bond parameters

The strength and geometry of hydrogen bonds vary with the environment. To investigate this dependence, correlations were drawn between hydrogen bond geometry and several environment parameters of the donor/acceptor atoms including (1) whether they belong to the main-chain or side-chain (2) atomic depth (3) secondary structure (4) partial charge. Values of partial charge were extracted from the GROMOS96 force field (Van Gunsteren et al., 1996).

4.5. Atom/residue depth computation

Atom/residue depth is defined as the distance of an atom/residue to its closest bulk water.

(Tan et al., 2011, 2013; Chakravarty and Varadarajan, 1999). In this study, bulk water is defined as those solvent molecules that have 4 or more other solvent molecules as neighbors (within a distance of 4.2 ​Å). Residue depth stratifies the protein interior and is hence a concise descriptor of residue environment. The depth of a hydrogen bond is defined as the average of depths of its donor and acceptor.

4.6. Secondary structure assignment

Secondary structure was assigned using the write_data module of MODELLER that in turn uses the distance matrix idea (Richards and Kundrot, 1988) and DSSP (Kabsch and Sander, 1983).

4.7. Quantum mechanical calculations

To compare trends of the calculated Ĥ angle the model systems used and the details of the methods are provided in Supplementary data 2A and 2B. Note that our model systems of amino side chains are representative of most side chains, with the exception of side chains such as asparagine or glutamine that resemble the main chain.

The calculations to rationalize the structural differences between MC-MC and SC-MC type of hydrogen bonds were performed on three model systems -

• 1)The simplest model for a hydrogen bond between two main chains that we have used is the N-methylacetamide (NMA) dimer (Supplementary figure S2.4). This has been widely used to model hydrogen bonds in proteins (Buck and Karplus, 2001; Miller and Lisy, 2007) and is referred to as the NMA dimer model in this study. We performed geometry optimization of the dimer using second order Møller-Plesset perturbation theory (MP2) and the 6-31G(d, p)++ basis set. Since there are several local energy minima corresponding to different geometries, the optimized structure depends on the choice of the initial structure. To ensure adequate sampling of the coordinate space, we constrained the Ĥ angle to six different values (from 85° to 160° in steps of 15°) and optimized the rest of the molecule, and then released the constraints and performed a full optimization. The hydrogen bond angles and Ĥ angles obtained from this systematic sampling and from several other random initial geometries are given in Supplementary table S2.1. For our analysis, we considered the structure that has the greatest hydrogen bond angle and a trans peptide bond (referred to as original structure in Supplementary table S2.2 and shown in Supplementary figure S2.5a). We then added two hydrogen atoms to saturate the C O bond on the NMA molecule, which acts as the hydrogen bond donor and optimized the modified dimer structure in three steps: one, constraining the position of all atoms except the two hydrogen atoms attached to the C and O; two, constraining all the atoms on the donor NMA including the two H atoms at the positions obtained in step one (Saturated planar structure shown in Supplementary figure S2.5b); and three, removing all constraints. The final saturated structure is a model for a SC-MC type of hydrogen bond (referred to as Saturated optimized structure in Supplementary table S2.2 and shown in Supplementary figure S2.5c). The three-step procedure, where the structure is allowed to relax in parts, is required to arrive at a saturated optimized structure that is close to the original structure. This allows for a meaningful comparison of the Ĥ angle between these two structures. If instead, all atoms are allowed to relax at once after adding the hydrogen atoms, the structure tends to optimize to an arbitrary local minimum on the potential energy surface, which in general can be completely different from the original structure.
• 2)& 3) To check the robustness of our analysis and to have more realistic models, we also considered dimers of glycine dipeptide with two different sets of Ramachandran angles (Supplementary table S2.2). Here we optimized the geometry of two sets of glycine dipeptide dimers orienting them in an anti-parallel beta sheet manner and constraining the (Ψ, Φ) angles to be (140°, −120°) and (140°, −100°) to eliminate multiple local minima. These 2 systems are referred to as di-glycine dimer models 1 and 2 in this study. For these larger sized molecules compared to NMA, for reasons of computational efficiency, we used density functional theory (DFT) with the B3LYP exchange-correlation energy functional and the same 6-31G(d,p)++ basis set. We then added two hydrogen atoms to the C O bond adjacent to the central N in the dipeptide which is a hydrogen bond donor in a manner similar to NMA, to obtain a model for a SC-MC type of hydrogen bond (Supplementary figure S2.6). All the calculations were performed using the GAMESS program package (Schmidt et al., 1993).

4.8. Molecular dynamics simulations

A 16-mer poly-alanine ɑ-helix was constructed using the secondary_structure module in MODELLER. The average ϕ and ψ angles of all the residues in the starting structure were −64° and −42° respectively. The average value of the Ĥ angle of the (i+4, i) hydrogen bond in starting structure was ~154°. The helical peptide was placed at the center of a dodecahedron box such that the distance from the peptide to the walls of the box was at least 10 ​Å. The simulation set up consists of 7228 atoms, including 7065 SPC216 water molecules.

Three sets of 10 ​ns (ns) molecular dynamic (MD) simulations were performed on the system described above. The system was energy minimized until the maximum force on the system was less than 1000 ​kJ/mol/nm. Before the 10ns production run, the system was subjected to 100 ​ps (ps) of canonical ensemble (NVT) simulation, followed by another 100ps of isothermal-isobaric ensemble (NPT) simulation. In the production run of the simulation in the NPT ensemble temperature was maintained at 300 ​K using a Berendsen's thermostat.

In the first simulation that acts as a control, the helix was subjected to free MD for 10 ​ns (ns) without any external constraints. In the second 10ns MD simulation, a repulsive potential at 155° was applied (using a cosine functional form similar to that of a dihedral rotation and a force constant of 40 ​kJ/mol, see supplementary data 13) to all (i+4, i) hydrogen bond Ĥ angles. This energy barrier was applied to force the system to explore Ĥ angles other than what it was in the initial structure. In the third simulation, the last frame of the second simulation was used as the starting structure. The repulsive potential was replaced by a constraining potential at 155° (using the same cosine functional form as the second simulation but changing the sign of the 40 ​kJ/mol force constant, see supplementary data 13) was applied to all (i+4, i) hydrogen bond donor-acceptor pairs. This was done to increase the sampling rate at the ~155° region. All simulations and constraint manipulations were performed with the Gromacs (ver 5.1) software suite, using the CHARMM36 force field.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary data to this article: