Advances, Interactions, and Future Developments in the CNS, Phenix, and Rosetta Structural Biology Software Systems

Abstract

Advances in our understanding of macromolecular structure come from experimental methods, such as X-ray crystallography, and also computational analysis of the growing number of atomic models obtained from such experiments. The later analyses have made it possible to develop powerful tools for structure prediction and optimization in the absence of experimental data. In recent years, a synergy between these computational methods for crystallographic structure determination and structure prediction and optimization has begun to be exploited. We review some of the advances in the algorithms used for crystallographic structure determination in the Phenix and Crystallography & NMR System software packages and describe how methods from ab initio structure prediction and refinement in Rosetta have been applied to challenging crystallographic problems. The prospects for future improvement of these methods are discussed.

INTRODUCTION

X-Ray Crystallographic Structure Determination

X-ray crystallography is a critical tool in the study of biological systems. It provides atomic resolution information that is a prerequisite to understanding the fundamentals of life, from the structure of the double helix (99) to the structure of the intact 70S ribosome (50). It is also a method central to the development of new therapeutics for human disease, in both commercial and academic settings. The technique has matured over the last 100 years, with a rapid increase in the number of macromolecular structures solved worldwide annually, increasing from less than 1,000 per year in 1995 to over 8,000 per year in 2011 (http://biosync.sbkb.org). This remarkable productivity has been a result of constant improvement in the technology for protein production, crystallization, data collection, and data analysis. A major driver of this technology development has been multiple large-scale structural genomics efforts that have been funded in several countries (43).

Advances in computational methods for the analysis of diffraction data (2) have greatly improved the crystallographic process, introducing more automation and ultimately leading to better atomic models. More recently, algorithms, in particular maximum likelihood, have been introduced that improve the generation of structure factor phases using either anomalous diffraction methods (24, 63) or molecular replacement methods (62). Automation of model building, pioneered in the ARP/wARP system (71), has dramatically reduced the manual effort required for many crystallographic projects, and efforts continue to push the resolution limits of successful model building. Methods for refining atomic models based on experimental diffraction data have improved, with multiple methods being introduced to make it possible to optimize models even when only low-resolution (lower than 3 Å) data are available. These methods make it possible to generate atomic models of a quality previously only attainable with higher-resolution data. Finally, the tools for validating crystallographic models have improved to a point that many errors in models are readily detectible and can be corrected early in the structure solution process (14).

Low resolution:

resolution of diffraction lower than where present crystallographic methods break down

Ab Initio Modeling and Model Improvement

In parallel with advances in crystallographic methods, there have been significant advances in the methods for protein and RNA structure prediction and refinement (19, 65). Recently, these latter methods have been applied to problems of crystallographic model building and refinement (16, 20, 30). These approaches use knowledge-based sampling of protein conformations and torsion-space minimization to identify the positions of all protein and RNA atoms that minimize a physically realistic energy function. The force fields used by such approaches are often able to identify near-native conformations within the necessarily very-low-free-energy native basin, but computational sampling is intractable in all but the smallest of cases. Although these sampling methods and force fields are unable to consistently solve structures on their own, they can be very powerful when coupled with weak experimental data. For example, the incorporation of diffraction data in molecular replacement (MR)-Rosetta has made it possible to solve challenging molecular replacement problems, and the incorporation of sparse NMR data in CS-Rosetta has allowed accurate NMR structure determination from data sets too sparse for structure determination using conventional methods.

Refinement:

iterative modification of the model’s parameter values using computational optimization algorithms to improve the fit of the model to a target function

MR:

molecular replacement

The development of MR-Rosetta and CS-Rosetta illustrates an important theme, revisited below, of connecting experimental structural biology with high-accuracy structure prediction. Present force fields and sampling methods in prediction tools like Rosetta are unable to solve structures on their own but can become powerful with constraints from even limited data, such as unphased structure factors. Conversely, structural biology methods have not historically made extensive or routine use of physically realistic force fields to break degeneracies in crystallographic data sets, e.g., in solving the phase problem. Problems at the interface between structural biology and structure prediction are exciting for practitioners of both fields as they provide puzzles that are just now becoming solvable, rigorous tests of available methods, and practically useful outcomes.

ADVANCES IN CRYSTALLOGRAPHIC STRUCTURE SOLUTION

Experimental Phasing

The classical problem in crystallography is the phase problem: Without knowing the unmeasured phase angles corresponding to the measured diffraction spots, an electron density map cannot be computed. The multiple isomorphous replacement experiment used to solve the phase problem for the earliest protein crystal structures is almost obsolete in its original form, in which the anomalous scattering effect was ignored. Indeed, there is now a very heavy reliance on anomalous scattering alone, sometimes in the form of multiwavelength anomalous diffraction (MAD), which directly exploits the wavelength dependence of the anomalous scattering effect, but increasingly using just single-wavelength anomalous diffraction (SAD).

MAD:

multiwavelength anomalous diffraction

SAD:

single-wavelength anomalous diffraction

Several trends have driven the increased reliance on anomalous scattering methods for experimental phasing. Anomalous scattering depends sensitively on the X-ray wavelength, so the now-ubiquitous availability of tunable synchrotron X-radiation has been essential to optimizing the relative size of the anomalous signal (SAD) or resolving the remaining phase ambiguity by adding information from multiple wavelengths (MAD). Another breakthrough was the development of a method to stably and reproducibly incorporate intrinsic anomalous scatterers by replacing methionine residues with selenomethionine (41). The application of maximum likelihood methods to MAD (24) and SAD phasing (63, 70) allows small phasing signals to be exploited robustly. Finally, density modification methods allow weak phase information from MAD or, especially, SAD experiments to be improved significantly.

In recent years, SAD phasing has achieved greater prominence (21) and now accounts for approximately half of the structures determined by experimental phasing methods (79). One of the main reasons for the popularity of SAD phasing is that it requires the collection of only a single data set from a single crystal; because only one crystal is used, there is no danger of nonisomorphism, and often the required single data set can be collected before significant radiation damage has set in. Nonetheless, radiation damage becomes more of a problem as new microbeam sources make it possible to collect data from smaller crystals or if the even weaker anomalous signal from intrinsic sulfur atoms is exploited. Fortunately, it has been demonstrated convincingly that SAD phasing can be carried out with data merged from multiple crystals, as long as sufficient care is taken to ensure that only data from isomorphous crystals are combined (56).

Molecular Replacement

In molecular replacement, the phase problem is solved by calculating phases from a similar structure placed in the position of the unknown molecule in the crystallographic unit cell. As the Protein Data Bank (PDB; 6) grows (>84,000 entries to date), it becomes ever more likely that a suitable template model exists. Presently, approximately two-thirds of protein structures deposited in the PDB are solved by molecular replacement (57); even if there were no further improvements in the molecular replacement method, the growth of the PDB would ensure that this proportion would increase.

PDB:

Protein Data Bank

Nonetheless, the rise of molecular replacement also owes a great deal to developments in methodology. The introduction of maximum likelihood targets for molecular replacement (62) has increased the signal in molecular replacement searches. Chances of success can be increased substantially if a variety of models is tested, differing in the starting template structures or the ways in which poorly conserved regions are trimmed off or different parts of the model are weighted (12, 47). Further gains can be made by piecing together larger structures using known fragments from a comprehensive domain library (57).

Two developments have converged to create a new approach for the ab initio solution of protein structures termed ARCIMBOLDO (82). First, the increased sensitivity of likelihood targets for molecular replacement searches has made it possible to find smaller fragments, as small as single helices for proteins of moderate size, given data to 2–2.5 Å resolution. Second, advances in automated model building have made it possible to complete a structure from a starting point as small as a few isolated helices. This new approach has already been applied to solve a number of novel structures.

Until recently, molecular replacement could not be applied if a sufficiently close template was not available. However, as the modeling field has matured, it has become possible to improve templates derived from distant homologs or even to employ ab initio models.

Use of Ab Initio Modeling Methods

Crystallographic phasing of diffraction data sets has provided an early and important nexus of practical structural biology and de novo structure prediction tools. Phasing can be carried out rapidly by molecular replacement if a model with high structural similarity to the crystallized macromolecule (typically, higher than 2 Å RMSD over the majority of the structure) is available. However, for targets with low-homology templates (or with no identifiable homologs), molecular replacement provides a highly stringent and practical challenge for structure prediction (72). Indeed, phasing experiments have been carried out in several community-wide blind trials (38, 61, 78) to assess whether models have achieved a high enough accuracy to be practically useful. Successful molecular replacement with models has been achieved in cases of high symmetry (89), in “simple” protein and nucleic acid structures (52, 90), and in targets modeled from homologs followed by all-atom refinement (75). Fully de novo modeling (20, 75) and even crowd-sourced model refinement (interactive 3D optimization by large communities of nonexperts) (48) have given successful molecular replacement solutions, but successes in these more difficult problems remain rare. However, recent years have seen accelerating developments in phasing with predicted structures.

MR-Rosetta

Rosetta is a protein structure modeling suite that combines a physically realistic all-atom potential function together with various conformational sampling methods to predict the structure of a protein given its amino acid sequence. Although originally developed for predicting protein conformations in the absence of experimental data, there has been recent success in using sparse or noisy experimental data to guide conformational sampling, providing more accurate and better converged solutions than using the force field or data alone.

In difficult molecular replacement cases, one problem that arises is that the initial molecular replacement search may succeed—finding the correct placement of the molecule—but the resulting model-phased density map is too noisy to interpret. MR-Rosetta (30) makes use of Rosetta’s underlying sampling methods and force field in order to refine structures guided by this noisy density data: Rosetta’s standard comparative modeling protocol is performed with an additional score term that maintains agreement between the model and density data (31). The approach begins with a sequence alignment to a homologous structure, as well as the (possibly ambiguous) molecular replacement solution using the homolog. Conformations are sampled by first threading the sequence onto the homolog and then using fragment assembly to rebuild unaligned regions of the protein. Finally, iterative optimization of both side chain and backbone coordinates is then carried out by gradient-based optimization of the Rosetta energy function supplemented by the fit-to-density score term.

MR-Rosetta can contribute to solving difficult MR problems in two ways. First, it can identify the correct molecular replacement solution in cases where the solution may be ambiguous. Second, it can improve models to the point that the resulting density is interpretable; most MR-Rosetta-improved maps can be automatically solved by Phenix autobuild (94). On a variety of data sets on which previous molecular replacement and refinement methods failed, the MR-Rosetta approach correctly identified a molecular replacement solution from among a set of several candidates that was not otherwise distinguishable and was in most cases able to improve these models to the point that the resulting density maps were automatically interpretable. One such example is illustrated in Figure 1.

Figure 1.

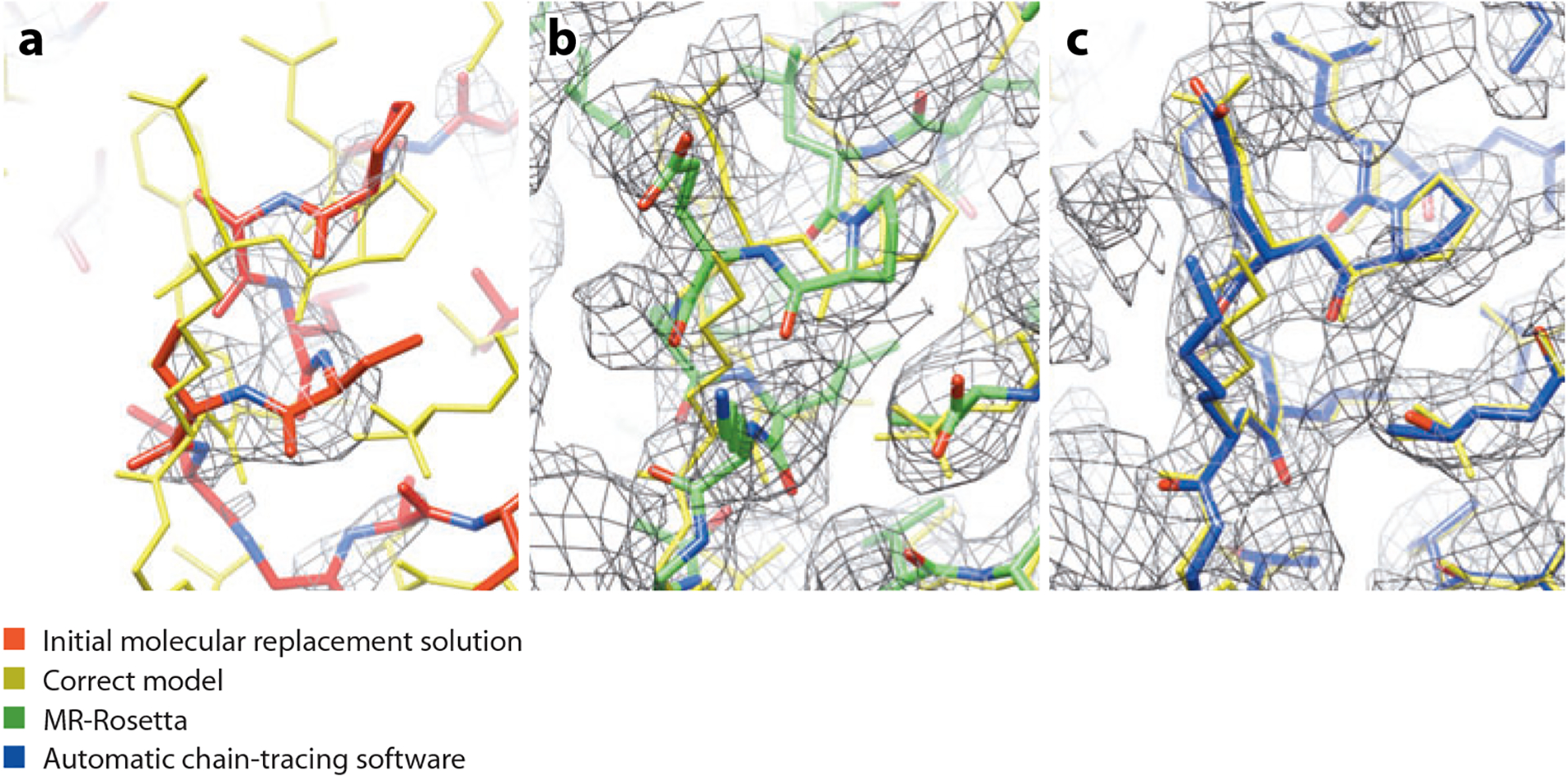
Rebuilding and refinement of a weak molecular replacement solution using MR-Rosetta. (a) The initial molecular replacement solution (red) is incomplete and deviates from the correct model (gold); weak density information and model bias lead to the inability of automatic chain-tracing software to find a solution. (b) After application of MR-Rosetta, the solution is much closer to correct (green). (c) Automatic chain-tracing software quickly finds a high-accuracy model (blue).

Phenix:

Python-based Hierarchical ENvironment for Integrated Crystallography

Morphing

It is common in molecular replacement to find a template structure in the PDB similar enough to the structure to be solved that the template can be positioned correctly in the unit cell yet different enough that this correctly positioned structure cannot be used to generate a map of high enough quality to rebuild successfully. The case described above where Rosetta modeling was useful in structure determination fell into this category. After the structures are finally completed, the difficulty of rebuilding these models can seem surprising in retrospect, given that the template structure was, in fact, remarkably similar in local detail to the structure to be rebuilt. The reason that these structures could not be rebuilt starting from these templates was that the templates and structures differ by 2–3 Å because of overall shifts that move large parts of the structures relative to one another. Figure 2 illustrates this with an example of a template used in molecular replacement: Chain A of the HIV-1 protease structure 2hs1 (51) is optimally superimposed on its corresponding final structure, XMRV PR protease (55). It can be seen that various parts of the final structure are in large part simply offset (in different ways) from the template.

Figure 2.

Comparison of XMRV PR protease structure (yellow; 55) with template used in molecular replacement, and chain A of the HIV-1 protease structure 2hs1 (blue; 51). Note the much higher degree of local similarity (individual segments are simply translated from each other) compared with the overall large coordinate differences. Figure created with PyMol (25). Data taken from Reference 95.

Morphing (95) is a procedure designed to take advantage of this local similarity of template and target structure. The basic idea is to distort the template in a simple way to make it more similar to the target. The information used to carry out this distortion is an electron density map. The main hypothesis in this method is that any local region of the template is related to the corresponding region of the target structure by a translation in the range of approximately 0–2 Å. This translation is found for a group of atoms in a 12-Å-diameter sphere by finding the shift that maximizes the correlation between the electron density map and the density calculated from the shifted atoms. Secondarily, it is hypothesized that these translations are smoothly varying along the polypeptide chain. Accordingly, the shifts found by optimizing map–model correlation are smoothed. One shift is then applied to all the atoms in each residue, yielding a new model in which each residue is shifted as a unit. The resulting model can then be refined and used in additional cycles of morphing.

Figure 3 shows how this morphing procedure can work. The glucuronoyl esterase Cip2 (PDB ID: 3pic; 73) is used as a template for determining the structure of Cgl1109 (10). In the region shown, the Cip2 template is offset from the target structure by a shift of approximately 1.4 Å. Morphing the Cip2 template six times yields a model much more similar to the target structure (Figure 4). A key element in the utility of morphing is that each application of morphing can lead to a model more similar to the target structure; this in turn can lead to an improved electron density map; this in turn can lead to an improved model on the next cycle. Figure 5 illustrates how much the maps can improve by serial application of morphing in the cases of several structures (95). The serial application of morphing often yields substantial improvements over simple refinement (three cycles of Phenix refinement) and in several cases major improvement over extensive refinement procedures (100 cycles of refinement).

Figure 3.

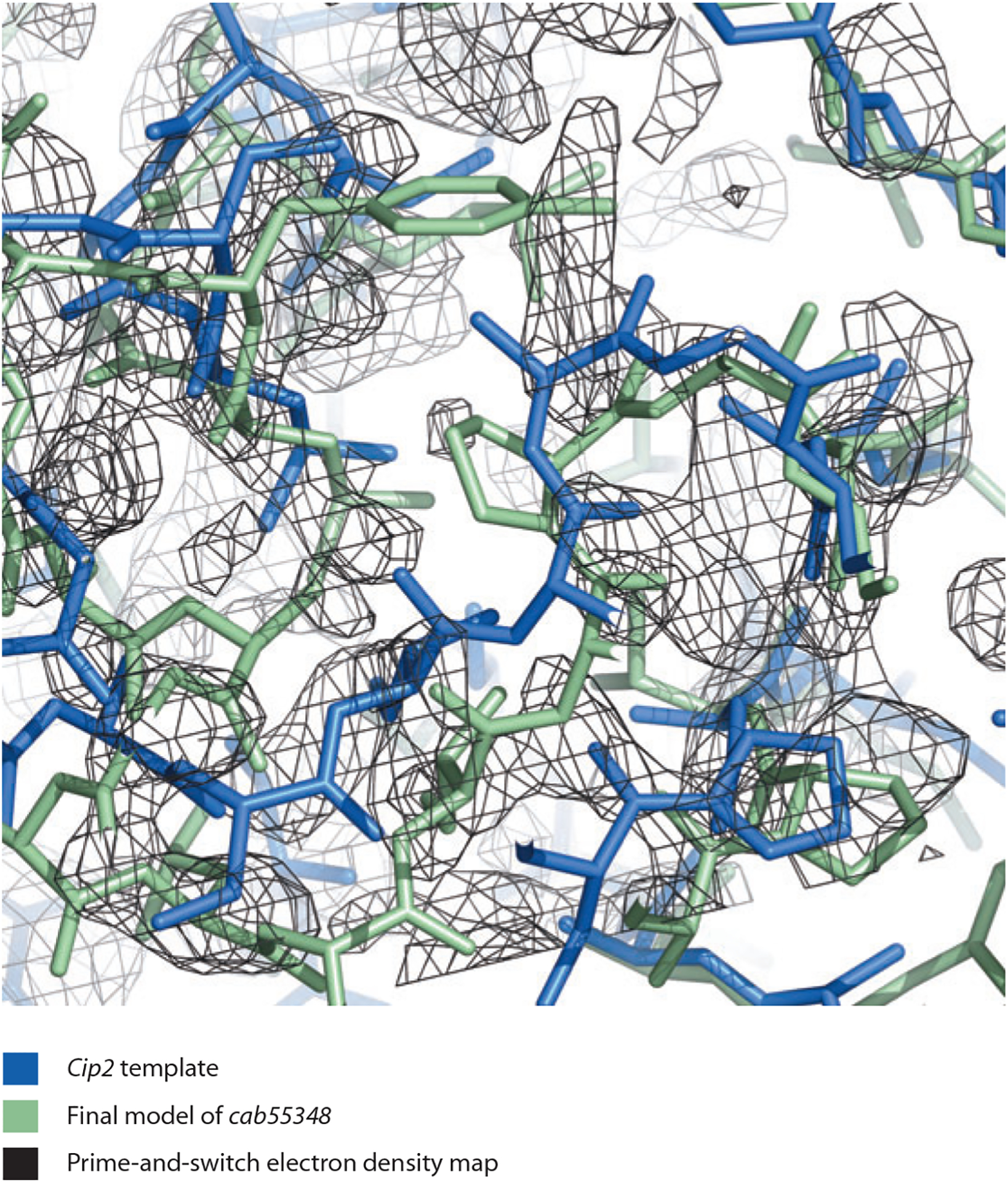
Cip2 template (blue; 73), final model of cab55348 (green), and prime-and-switch electron density map based on the template structure (black). Figure created with PyMol (25). Data taken from Reference 95.

Figure 4.

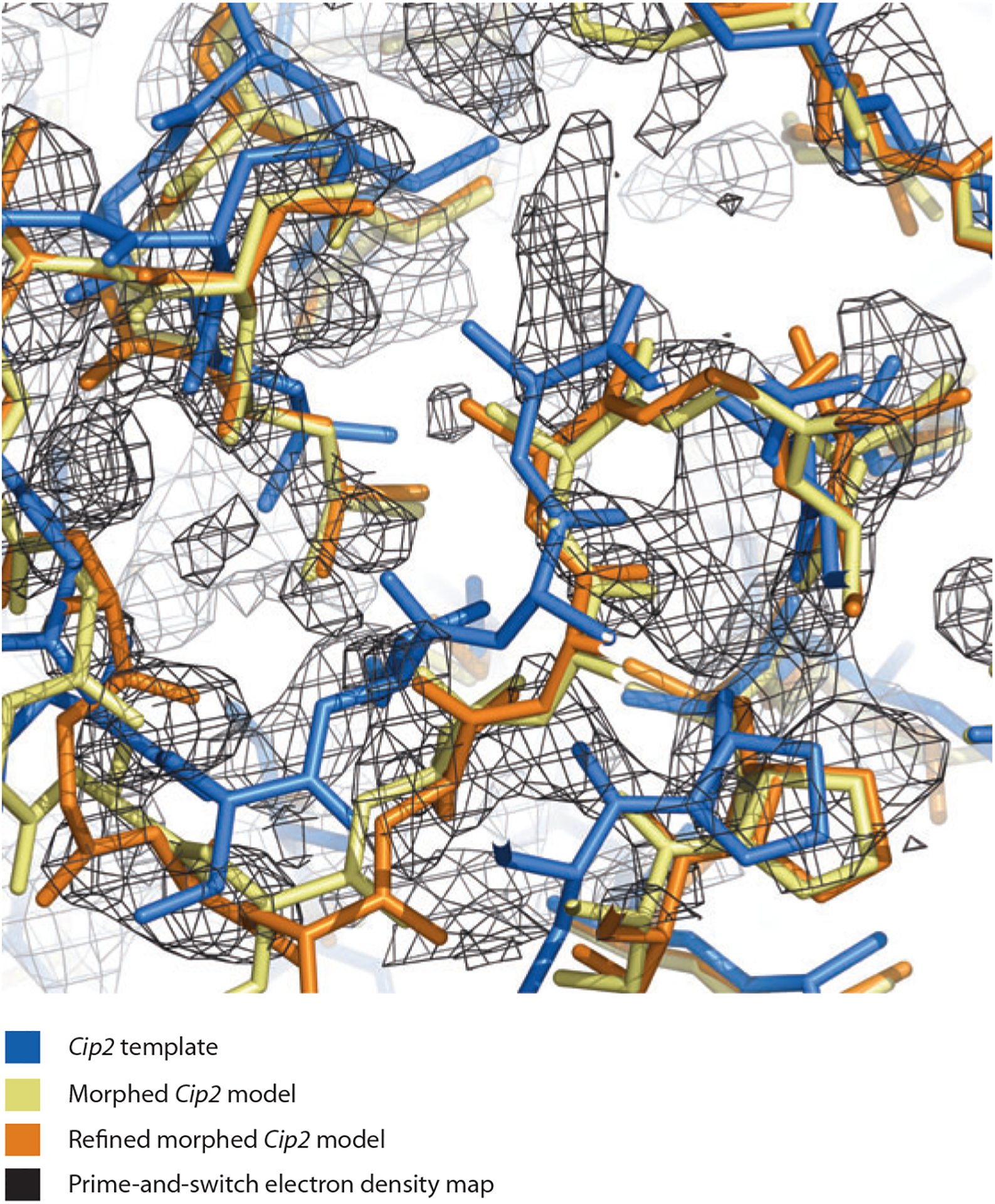
Cip2 template (blue), morphed Cip2 model (yellow), refined morphed Cip2 model (orange), and prime-and-switch electron density map based on the template structure (black). Figure created with PyMol (25). Data taken from Reference 95.

Figure 5.

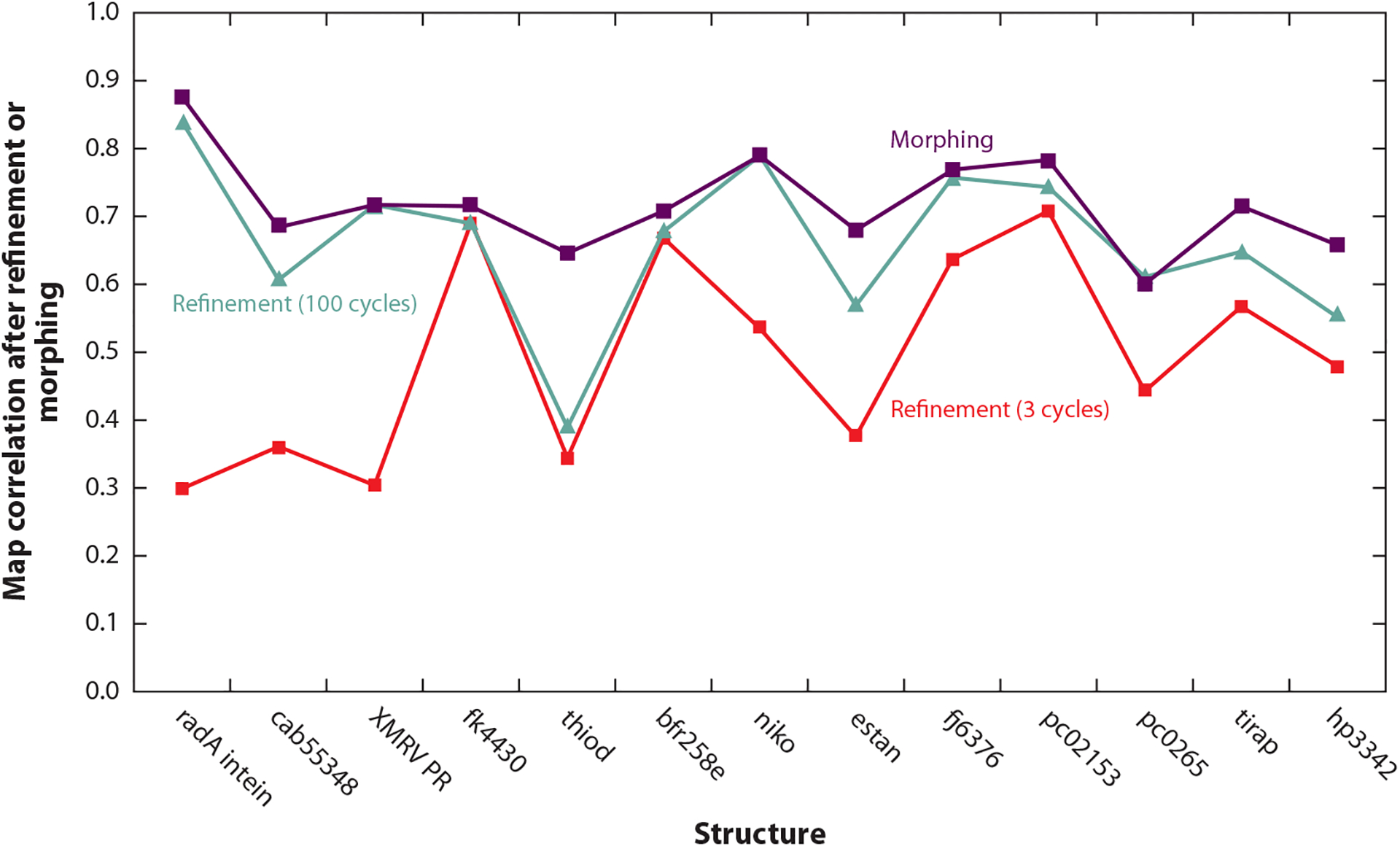
Morphing using prime-and-switch maps and a total of six cycles for structures at resolutions of 1.7–3.2 Å. The map correlation between 2mFo-DFc maps (from refinement or morphing) and the final electron density maps for each structure are shown. Data taken from Reference 95.

Morphing can be thought of as an automated way of using an electron density map to find regions of a template structure that are very similar to the target structure and offsetting each such region by an appropriate translation, yielding a composite structure that can be very close to the target structure. Morphing can be of utility in molecular replacement and also potentially in other structure determination methods where only a poor map and template are available.

ADVANCES IN BUILDING AND REFINEMENT OF CRYSTALLOGRAPHIC STRUCTURES, ESPECIALLY AT LOW RESOLUTION

Estimating Uncertainties in Automated Model Building

The development of methods for automated iterative model building, refinement, and density modification as implemented in Phenix (phenix.autobuild; 94) and of related approaches in other applications [e.g., ARP/wARP (71, 53); BUCCANEER (17); RAPPER (28); HipHop Refinement (68)] has made it feasible to carry out the entire process of structure determination many times. This in turn has made it feasible to carry out extensive error analyses of crystallographic models (27, 68, 69, 92) and to calculate maps that have essentially no model bias (93).

It is difficult to accurately estimate the uncertainties in atomic coordinates for models of protein structures. An important general approach is to use the agreement of model and data to estimate coordinate errors (18, 60, 67, 76, 86, 96). An advantage of this approach is that a simple description of the uncertainty in each atomic coordinate can be generated. On the other hand, a limitation of the approach is that it is only fully applicable if the coordinate errors have a distribution that is approximately Gaussian. In macromolecular crystallography, it is possible to have several or even many discrete possibilities for side chains and for segments of main chain (e.g., loops) so that this assumption may not always be valid.

Recently, a different kind of approach to describing the uncertainties in macromolecular crystallographic models has been developed. In this new formulation, a group of models is generated. Each individual model is constructed in the same way but independently, using a different random seed in model building, and each is individually refined to be compatible with the data (27, 68, 69, 92). In this way, the entire model-building and refinement process can be performed a number of times in parallel, generating a group of models, each obtained with the same process. Then, assuming that all the models have similar quality measures, each structure obtained is more or less equally likely to be correct, and variation among members of the group represents a lower bound on the uncertainty in the models. Ideally, all the final steps that a crystallographer would normally carry out (final validation, examination in comparison to an electron density map) would be applied (independently) to each of these models as well (74), though this has not normally been carried out in these analyses.

Ten structures, selected from the PDB, were modified by random coordinate shifts and rebuilt 20 times, using different random seeds and automated model-building procedures in Phenix. It was seen that, particularly at higher resolution, many of the rebuilt models have free R-values at least as low as the original structures. However, the rebuilt models are not all the same; in the 2.6 Å resolution structure 1CQP (44), it is seen that for residues in the core of the structure, all 20 models superimpose very closely. However, many side chains on the surface are represented differently in the 20 models (see figure 2 in Reference 92). This means that, using this procedure for model building, the positions of these side chains are not known precisely, and the group of models represents this uncertainty. Note that the multimodel representation of uncertainties differs in a fundamental way from individual estimates of coordinate error: In the multimodel representation, it can be seen that relationships between atomic positions (e.g., the shape of part of a side chain) can be retained, whereas the coordinates of each atom are uncertain. In effect, the multimodel description is a way of representing the correlations of errors in atomic positions.

Free R-value:

application of standard statistical cross-validation methods to the crystallographic R-factor; typically used to measure the fit of a model to the experimental data

Optimization of RNA Structures Using ERRASER

The last decade has seen accelerating efforts to crystallize functional RNA molecules and complexes from the ribosome to riboswitches. Nevertheless, most of the resulting diffraction data sets continue to give resolutions lower than 2.5 Å. At this resolution, the positions of all atoms aside from the electron-dense phosphate and the nucleobase are ambiguous. As reported by automated validation tools like MolProbity, most RNA crystallographic models are thus rife with atom–atom clashes, outlier bond lengths and angles, dubious ribose puckers, and suspicious backbone conformers. As with MR-Rosetta (and other examples) above, structure prediction methods can help resolve these ambiguities. For example, since 2008, there has been available a set of 54 community-consensus RNA backbone conformers, each named by a two-character string such as 1a for A-form, 1g for the start of a GNRA (Guanosine, any Nucleotide, puRine, Adenosine) tetraloop, and !! for an unfavorable outlier (81). Targeting favorable backbone conformers with the RCrane system (45, 46) can aid in interactive RNA fitting, as is now available in Coot (33). Enumerative Refinement of RNA ASsisted by Electron density in Rosetta (ERRASER; 16) leverages an exhaustive search method [step-wise assembly (SWA)] developed for high-resolution de novo RNA structure prediction (88) and a combined Rosetta/electron-density scoring function to rebuild and refine single nucleotides (16). The procedure first runs a simple Phenix RNA refinement against the structure factors, then several cycles of a protocol making use of the Rosetta RNA energy function supplemented with the electron density map. This protocol consists of Rosetta real-space refinement of the global structure, followed by SWA exhaustive conformational sampling and evaluation for all nucleotides that had MolProbity clash, backbone conformer, or pucker problems or large movement in the refinements. The protocol is iterated until convergence, and then a final Phenix RNA refinement helps ensure agreement with the structure factors.

ERRASER:

Enumerative Refinement of RNA ASsisted by Electron density in Rosetta

In a recent benchmark, ERRASER automatically eliminated the majority of steric or conformational errors identified by MolProbity and improved the geometry, while retaining or lowering free R-values. Improvements in accuracy were confirmed in several cases by low-resolution/high-resolution data set comparisons, a detailed manual inspection by the Richardson lab, and independent validation from functional measurements (16). Figure 6 shows overall score changes and a local example, from the SAM-I riboswitch at 2.9 Å resolution (PDB ID: 2GIS; 64). The kink-turn as deposited has bond angle, clash, pucker, and backbone conformer outliers (denoted by the two-character code !!), all but one of which is corrected by ERRASER. The resulting sequence of conformers (7r-6p-!!−0a) matches that in the later 2.6 Å structure (PDB ID: 2YGH), confirming that the protocol has added correct information. When that higher-resolution model is analyzed with ERRASER, it corrects the last outlier to a valid conformer (two-character code 2[). This is especially notable because ERRASER does not use the 54 community-consensus backbone conformers in sampling or scoring conformations.

Figure 6.

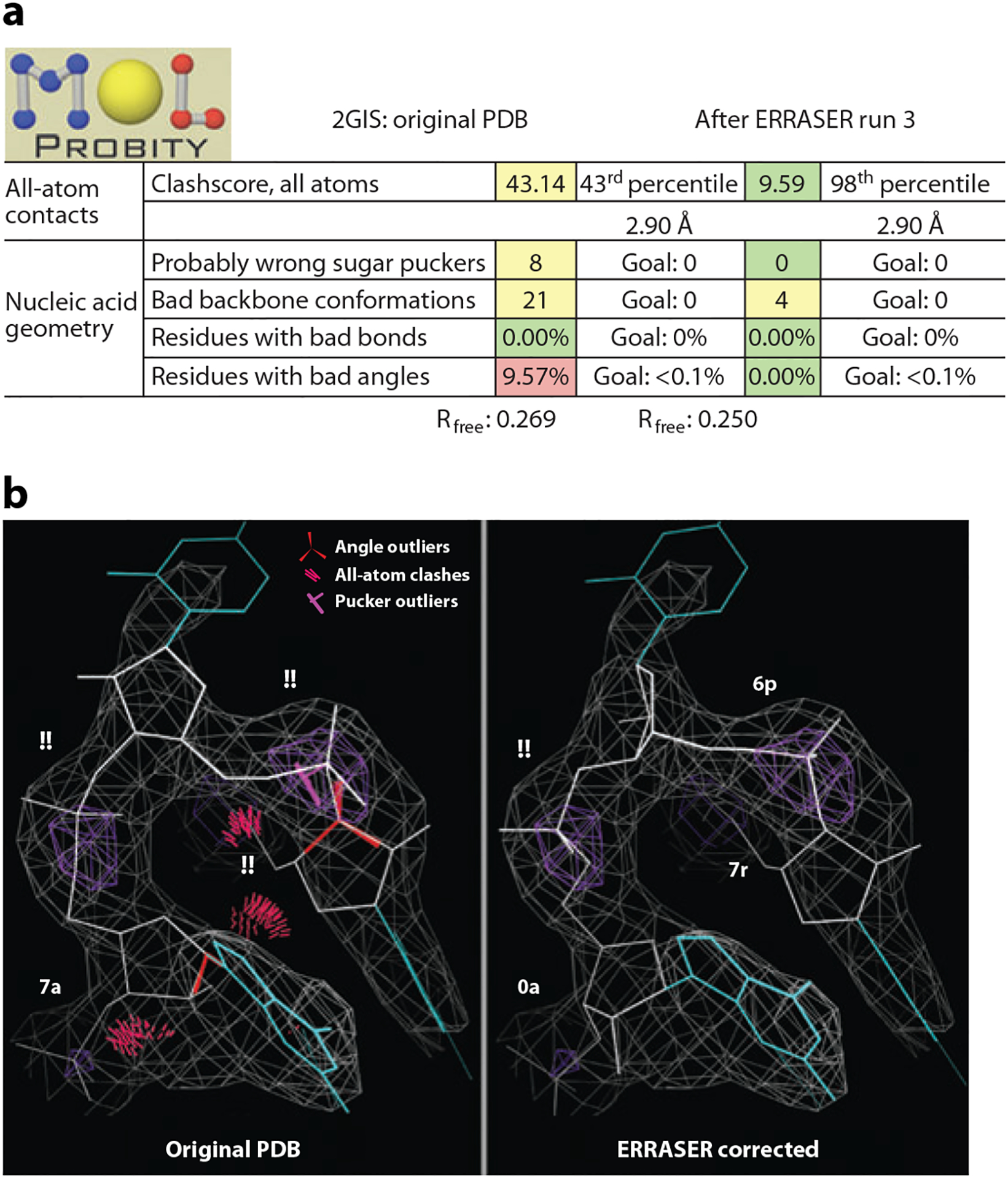
ERRASERcorrection of the SAM-I riboswitch mRNA structure (2GIS). (a) MolProbity summary report and free R-values before and after. (b) Kink-turn region before and after. (Backbone conformers are depicted in two-character codes, angle outliers as red fans, all-atom clashes as clusters of hot pink spikes, and pucker outliers as magenta crosses on the 3′P-to-base perpendicular.)

If Rosetta is installed locally, Phenix scripts can invoke the ERRASER protocol. Generally, the use and further development of these automated tools should ease the painstaking efforts required of RNA crystallographers to derive models with reasonable stereochemistry and torsional geometry from low- or medium-resolution data and should also help improve the quality of their results.

Stereochemistry:

prior knowledge of ideal protein geometry or other biophysical factors; often used during crystallographic structure refinement as restraints, or for validation purposes

Use of Prior Information in Structure Refinement

Two approaches have been developed to include external information about macromolecular structures into refinement: DEN refinement and reference restraint refinement.

DEN refinement.

Low-resolution X-ray diffraction data at 5 Å contain, in principle, sufficient information to determine the true structure as the number of observable diffracted intensities exceeds the number of torsion-angle degrees of freedom of a macromolecule (9). Although an exhaustive conformational search in torsion-angle space against the diffraction data should lead to an accurate structure at 5 Å resolution, such a search is at present computationally intractable. A recent approach implemented in the Crystallography & NMR System (CNS) aids the search by adding known information to the observed data at low resolution. Instead of just adding generic information about macromolecular stereochemistry [idealized chemical bond lengths, bond angles, and atom sizes that heralded the era of reciprocal space restrained refinement (40, 42)], specific information for the particular macromolecule(s) or complex is added in the form of deformable elastic network (DEN) restraints, this information being derived from known structures of homologous proteins or domains (the reference model) (84, 85).

CNS:

Crystallography & NMR System

DEN:

deformable elastic network

The true structure often differs from the reference model by large-scale deformations, whereas the polypeptide geometry is approximately conserved. How can such deformations be mathematically described? An early approach (29) used low-frequency normal modes shown to reproduce large-scale collective changes in structures with very few degrees of freedom (54); this approach has been used to refine protein structures with low-resolution X-ray or cryoelectron microscopy data (26, 91). DEN has been shown to fit models into cryoelectron density maps, allowing large deformations such as hinge bending (84).

DEN defines harmonic “springs” between selected atom pairs using the reference model as the template. The equilibrium distance (at which its potential energy is minimum) of each spring is initially set to the distance between these atoms in the starting structure for refinement. As torsion-angle molecular dynamics against a combined target function (comprising diffraction data, DEN, and empirical energy function) proceeds, the equilibrium lengths of the DEN network are adjusted to incorporate the distance information from the reference model. The degree of this adjustment is controlled by a unitless parameter, γ. The optimum value for γ and for the weight, w_DEN, of the DEN energy term is obtained empirically by performing a series of DEN refinements with different combinations of these parameters and then selecting the DEN refinement with the best free R-value. To further increase the chances of obtaining an optimum solution, multiple trials must be performed for each parameter pair (85) to ensure optimal performance.

DEN refinement has been implemented by performing torsion-angle molecular dynamics refinement (80), interspersed with individual restrained B-factor refinement in the presence of a sparse set of distance restraints that are initially obtained from a reference model (85). Typically, random distances between pairs of atoms are drawn within a specified distance range and a primary sequence separation range. The number of selected distance restraints is set equal to the number of atoms. Therefore, on average, one distance restraint is selected per atom.

The reference model can be simply the starting model for refinement or a homology or predicted model that provides external information. In this respect, DEN refinement is a general refinement method, so it is not restricted to cases with a high-resolution homology model, but rather any starting model can be used as the reference. Furthermore, the method can be applied to any macromolecular structure, including those involving nonprotein components. DEN refinement can also be used to re-refine a structure when a new high-resolution structure has become available for parts of a low-resolution complex; in that case, the reference model will be different from the starting model.

As mentioned above, for the success of DEN refinement it is essential to perform a global search for an optimum parameter pair (γ, w_DEN). Furthermore, for each adjustable parameter pair tested, multiple refinements should be performed with different initial random number seeds for the velocity assignments of the torsion-angle molecular dynamics method and different randomly selected DEN distance restraints. The globally optimal model (in terms of minimum free R-value), possibly augmented by geometric validation criteria, is then used for further analysis. By default, the last two macrocycles of the DEN refinement protocol are performed without any DEN restraints. For refinements at very low resolution, DEN restraints may be retained throughout the entire refinement process.

For test cases with diffraction data sets at 3.5–5 Å resolution with portions of the structure also being known structures at higher resolution, DEN refinement produced significant improvements in the model over conventional refinement as monitored by coordinate accuracy, the definition of secondary structure, and the quality of electron density maps. Similar improvements were found for re-refinements of a representative set of 19 low-resolution crystal structures from the PDB (85). Subsequent applications of the DEN method have shown the technique to be a viable alternative to the MR-Rosetta approach (10) and a powerful tool when refining models against very-low-resolution data; e.g., DEN-refinement of the photosystem I complex using synchrotron data at 7.4 Å resolution produced a better model than all other refinement methods tested, including segmented rigid body refinement (9).

Reference models.

Other methods for including additional information in structure refinement have recently been developed that are complementary to the DEN approach. Basic knowledge of molecular chemistry has been used as a source of information for geometric restraints in macromolecular refinement, e.g., target bond and angle values (34) and related libraries that include additional terms for torsion angles, planes, and chiral centers (98). However, it has long been observed that this information is insufficient to maintain reasonable stereochemistry in the absence of sufficient experimental diffraction data, resulting in atomic models with poor geometry and poor fit to the experimental data. For structures with low-resolution data, a number of methods have been developed that incorporate information from related higher-resolution models into the refinement target, thereby improving the data-to-parameters ratio. These include the DEN method described above (85), local structure similarity restraints in Buster (87), and external structure restraints in REFMAC (66), all of which use elastic-network distance restraints between nearby atoms derived from a reference model to provide additional restraints. A related, but in detail different, approach has been developed within the Phenix structure refinement program, phenix.refine (4).

In phenix.refine, a related model, ideally one solved at higher resolution, is used to generate a set of torsion restraints that add a new restraint term into the optimization function (39). This approach is conceptually similar to the local noncrystallographic symmetry restraints described by Sheldrick et al. (97). In phenix.refine, restraints for proteins are generated for side chain χ angles and backbone torsion angles (φ, ψ, ω). Additionally, if the corresponding residue in the reference model has suitable Cβ geometry, torsion angle restraints for the Cβ-Cα-C-N and C-N-Cα-Cβ angles are generated to preserve reasonable Cβ geometry for each residue (58). For RNA and DNA, restraints are generated for all proper torsions involving heavy atoms. The torsion restraints are described using a “top-out” function, which allows the restraints to function as a simple harmonic restraint when near the target value, while smoothly tapering off to have zero influence at larger deviations of the torsion from the target. The top-out function is based on an inverted normal distribution that is parameterized to be compatible with the conventional harmonic potential at values close to the minimum, similar to the Geman-McClure robust estimator function (37) used in REFMAC5 (66) for interatomic distances. This allows for differences between the working and reference models, such as hinge motions or local changes in backbone and/or side chain rotamer conformations. Torsion restraints were chosen for their direct relationship to the fold of the macromolecule, the strong correlation between torsion values and a wide range of validation criteria (14), and to allow for easy restraint calculation without the need for structural alignment of the reference model to the target model in Cartesian space. Unlike simple distance restraints, torsion angles can also be readily interpreted in the light of complex prior chemical knowledge, such as rotamer and Ramachandran distributions. Thus, a routine is also used for automated correction of rotamer outliers in the working model, by comparison with the reference model, prior to refinement.

The reference model torsion restraint method in phenix.refine was used and tested in the refinement of a cyclic GMP-dependent kinase (49). This kinase was crystallized with cGMP (PDB ID: 3OD0), cAMP (3OCP), and as a partial apo structure (3OGJ). The cAMP-bound data set was collected to 2.49 Å, and a high-quality model for that resolution was determined. The cGMP (2.9 Å) and partial apo (2.75 Å) data sets were of lower quality, and standard refinement resulted in poor models with below-average validation statistics for their respective resolutions. To improve the quality of these refined models, reference model restraints derived from the cAMP-bound model were applied to cGMP-bound and partial apo refinements. Following the introduction of the reference model restraints, the models of the cGMP-bound and the partial apo forms show substantial improvement in MolProbity validation criteria, including increasing the clashscore percentile from 15th to 87th and from 46th to 80th for the cGMP-bound and partial apo structures, respectively, while decreasing the free R-value in both cases (0.2389 from 0.2582, and 0.2543 from 0.2612, respectively).

Clashscore:

number of serious all-atom clashes (bad overlap ≥ 0.4 Å) per thousand atoms in MolProbity

Comparison of the reference model method with structures used for testing the DEN method indicates that it is able, in several cases, to produce models with decreased overfitting and improved geometry as judged by Ramachandran statistics (39). In contrast, DEN refinement may have a larger radius of convergence when there are larger concerted differences between the working model and its reference. The two methods are complementary and provide powerful tools for optimizing models against low-resolution data, making substantial conformational changes to better fit the data and maintaining good geometry.

ADVANCES IN STRUCTURE VALIDATION

MolProbity

MolProbity (14, 23) is a suite of model validation programs freely available as a web service or for separate installation. Its unique features are the sterics of all-atom contacts (101) using explicit hydrogen atoms added and optimized by Reduce (102) and the validation of RNA backbone conformers and ribose puckers (81). It also provides updated versions of traditional geometry (58), rotamer (59), and Ramachandran (58) criteria and presents the results as scores, percentiles, charts, and online 3D graphics in KiNG (15). From a decade of use, it has proved effective in guiding correction of the diagnosed problems (5), and both clashscore (number of steric overlaps ≥ 0.4 Å per 1,000 atoms) and incorrect 180° flips of Asn/Gln/His side chains have decreased by approximately 30% in wwPDB depositions (14).

All-atom contacts:

atom–atom noncovalent interactions calculated with all explicit hydrogen atoms; evaluated at the atomic surfaces

To enable even greater improvements with less manual effort, the separate modules of MolProbity have been rewritten as Python toolbox utilities or otherwise integrated into Phenix, providing local or global evaluations as low-level calls to guide choices in automated chain tracing, refinement, or rebuilding. For example, rotamer scores and “backrub” adjustments (22) can be used along with real-space refinement to optimize side chain conformations (1, 39). In addition, essentially all MolProbity-style evaluations are available within the Phenix GUI after each refinement macrocycle as plots, outlier lists, and 3D graphics in KiNG or Coot (33) for monitoring progress in overview or in detail. Clicking on an individual outlier takes the user to the spot in Coot, for man–machine collaboration on model correction.

A number of the worldwide PDB X-ray Validation Task Force recommendations (77) (see below) come from aspects of data, model, and model-to-data validation already present in Phenix or MolProbity, but treatment and presentation will be modified to match what depositors and users see at the PDB in the future. The first such change to be implemented is the new six-category Ramachandran system (adding Ile/Val and cisPro), now available in both Phenix and MolProbity as derived from 1.6 million residues of quality-filtered data. Figure 7 compares the new Ile/Val reference distribution to the new general-case distribution. Present validation research emphasizes the development of new criteria, tools, and strategies to enable reliable validation-based model correction at lower resolutions, as outlined in the final section.

Figure 7.

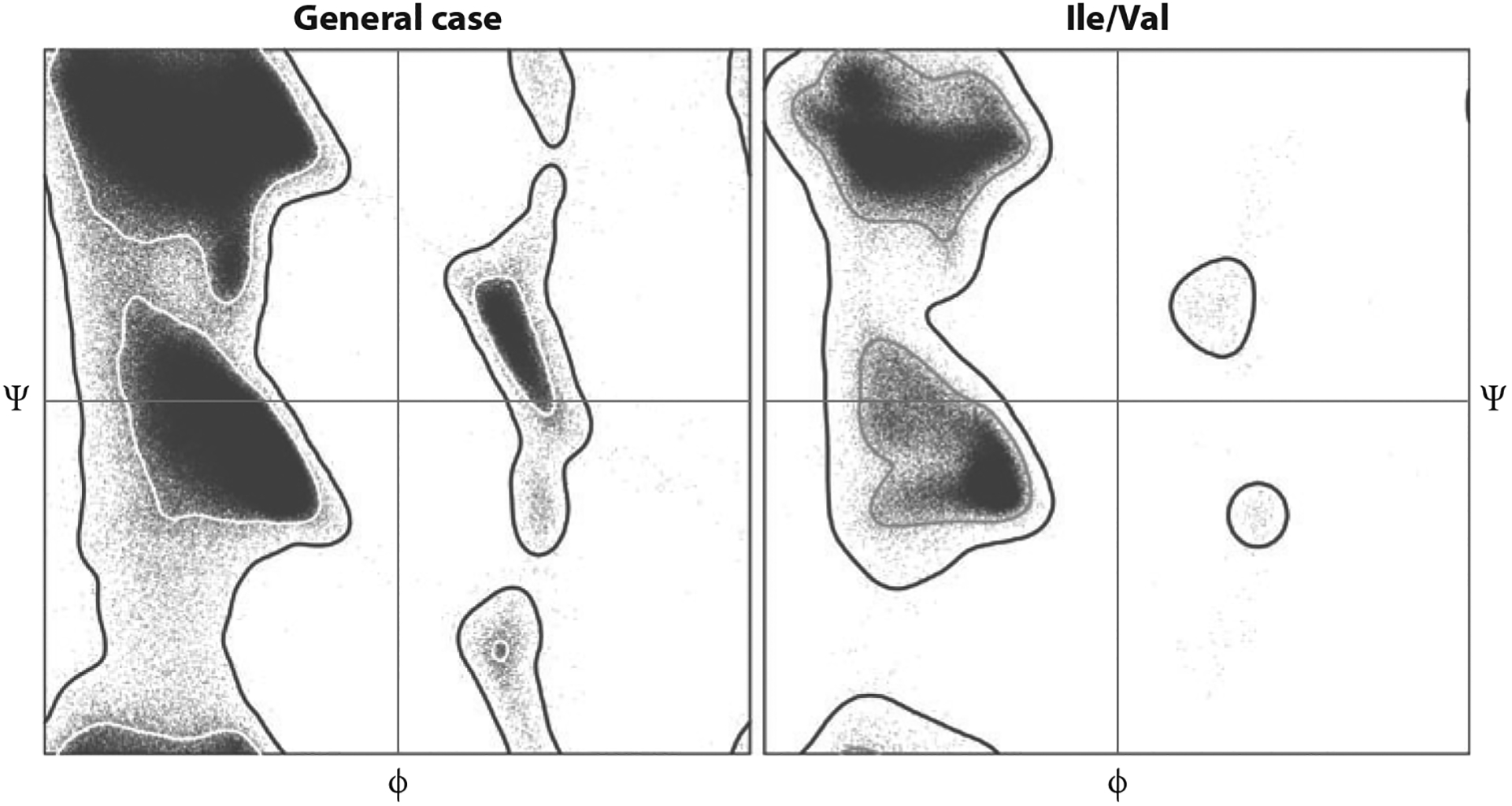
Ramachandran-plot validation distributions from the Top8000 data set showing difference of the newly separated Ile/Val category from the general case. Inner contour encloses 98% of the filtered reference data; outer contour encloses 99.95% and divides allowed from outlier conformations.

X-Ray Validation Task Force

The improvements in methods and the automation available for routine structure determination have been a great boon to structural biology, but the increased speed and ease of structure determination has been a double-edged sword. Structural biology is now accessible to researchers with very limited training, and with pressure to produce results quickly, it is not surprising that errors are introduced. Many errors are small and have little effect on biological interpretation, but some are catastrophic, such as forcing the chain tracing to fit into a map computed in the wrong hand (13).

Such problems were apparent even in the early 1990s, so the PDB introduced into its deposition pipeline a number of validation tools to check the consistency of structures with prior knowledge about geometry and stereochemistry. However, with the rapid expansion of the PDB, these tools became outdated, and the recent decision to make the deposition of the diffraction data mandatory created new opportunities for more thorough validation. For these reasons, the worldwide PDB (6) established the X-ray Validation Task Force to expand the suite of validation tools and to bring them up to date. The report of this task force (77) suggested a wide range of tools to check the quality of structures, associated experimental data, and agreement of the structures with the data.

Once these tools have been implemented fully by the worldwide PDB, fewer serious errors should reach the public databases. Importantly, the Validation Task Force suggested that the validation report for a new structure be made available to referees considering publications describing new structures. The availability of such reports should help to prevent many erroneous structures from reaching the published literature.

POTENTIAL IMPROVEMENTS TO STRUCTURE REFINEMENT USING PHYSICS-BASED POTENTIALS

The main difficulty encountered in low-resolution refinement is a low observation-to-parameters ratio. The relative lack of observations makes it difficult to optimize a structure to maintain good agreement with the experimental data while maintaining reasonable geometry. This is partially due to the fact that the only structural restraints generally used in refinement are based on simple stereochemistry and sterics.

Recently, efforts have been made to decrease the effective degrees of freedom of refinement by adding additional physical or statistical terms as restraints during crystallographic refinement. Some of the terms employed include restraints on hydrogen-bonding geometry (35), Ramachandran-based backbone torsional potentials (39), and electrostatics (36). Indeed, the initial implementation of crystallographic refinement by simulated annealing (11) used an early version of the CHARMM20 force field (7) that included electrostatics. The benefits of including electrostatics with respect to hydrogen bonding in crystallographic refinement were noted in the refinement of influenza virus hemagglutinin (100), although incorrect hydrogen bonds were observed when electrostatics were used during the simulated annealing stages, especially for charged groups such as the head groups of arginine residues. For simplicity, it then became the practice in most refinement programs to exclude electrostatics during all refinement stages and assume the diffraction data is capable of supplying this excluded a priori information (3). However, recent joint X-ray and neutron refinements with a modified version of CNS (8) demonstrated that hydrogen bond orientation/geometry was improved by the inclusion of electrostatics in the force field (36), suggesting that inclusion of electrostatics in macromolecular structure refinement should be revisited.

Similarly, structure prediction methods such as Rosetta (83) that utilize potential functions developed for accurate structure recapitulation in the absence of experimental data (incorporating, e.g., a full orientation-dependent hydrogen bonding potential) could be quite powerful in combination with experimental X-ray data for refining structures. By using these richer, more physically realistic force fields during low-resolution refinement, we may reduce the effective degrees of freedom describing motion of the protein. This will reduce the number of experimental measurements needed in crystallographic refinement to uniquely identify a solution with both good agreement with experimental data and physically realistic geometry. The use of such force fields will be key in extending crystallographic refinement methods to handle data whose highest-resolution reflections are 4 Å or lower. Presently, in such data sets we are mostly restricted to rigid-body-only or highly restrained refinement. These problems similarly arise in refinement of structures into cryoelectron microscopy single-particle reconstructions.

FUTURE CHALLENGES

Model Building in Low-Resolution Maps

A variety of automated protein model-building tools is now available, and given sufficiently high-resolution data (3.0 Å or higher) and reasonably accurate initial phase information, automated interpretation is typically straightforward. However, with lower-resolution data, automatic interpretation generally fails, and manual building—when even possible—is difficult and prone to introduce errors that may be difficult to correct in refinement. Similarly, for RNA and DNA modeling, tools for autofitting coordinates into maps have been developed (see, e.g., ARP/wARP version 7.2) but will likely suffer from the same problems encountered in interpreting low-resolution data.

Drawing from structure prediction methods could be powerful in extending the resolution at which automatic model building may be applied. Knowledge-based sampling, used by structure prediction methods, can expand the conformational space that is feasible to explore as well as eliminate physically impossible conformations that fortuitously agree with the experimental data. Physically realistic force fields can be used to choose between alternate conformations that appear equally good using the experimental data alone.

Use of All Available Information to Generate Optimal Models at Low Resolution

As the new generation of structure prediction tools becomes more integrated into model building, the stereochemical and geometric qualities of the models are markedly improving, as assessed by automated validation tools such as MolProbity and cross-validation measures such as free R-value. Such improvements are, in many or most cases, expected to correlate with more accurate models. Nevertheless, with fewer obvious model errors introduced from manual interpretation, a new question arises: How can one falsify or derive strong support for each amino acid and nucleotide in a macromolecule structure? Could methods such as DEN, MR-Rosetta, phenix.autobuild, or ERRASER be systematically introducing other errors—e.g., allowed but entirely incorrect backbone conformations—that are not yet straightforward to diagnose? Indeed, exercises involving the intentional introduction of errors (incorrect protein homology templates, syn/anti nucleobase flips in RNA) followed by refinement do not always remove the errors, especially in data sets with low-resolution diffraction data. In these cases, there is presumably not enough information in the diffraction data or the energy function to return a single correct model. Ideally, refinement or building algorithms should be able to report a local uncertainty measure for the final models. Perhaps methods that permit enumerative sampling of segments of the macromolecule can flag whether multiple conformations with similar scores (e.g., within 1 k_BT) are viable. Alternatively, applying refinement/correction tools after perturbations of the initial structures, as described above for automated building tools, may help bracket systematic errors. Making such local assessment of confidence straightforward and routine is an important challenge for this new generation of structural biology tools.

Other strategies being explored for avoiding, detecting, and correcting such problems include explicit tests for likely issues such as sequence misalignment, as done by Dunkle et al. (32); new shortcuts to permit integration of nonpairwise steric terms into inner-loop calculations; and new validation measures specifically designed for effectiveness at lower resolutions by incorporating knowledge of common systematic errors and assessing combined patterns of multiple criteria across larger regions of sequence and space.

Such examples illustrate several problems characteristic of model fitting at low resolution. Due to the high ambiguity, local regions of the model are often caught in a local minimum rather far from the correct one, so that rebuilding techniques need to be capable of making large and concerted changes. Contrary to usual expectations, at low resolution the slow spatial change of density mixes contributions from backbone and side chain, so that a β-sheet may have different density connectivity in regions with small versus large side chains. That slower variation also makes difference maps less useful at the single-residue level. Many atoms should genuinely lie outside density, and both fitting and refinement need to avoid moving them into it more aggressively than is warranted. In the molecular core, it is likely that methods can be developed to identify the correct answer by adding more external information in addition to the experimental data. However, at the surface, acceptable answers will surely require sophisticated treatment of multimodel ensembles that jointly rather than individually fit the data and that make use of all the weapons of both energy calculations and empirical rules.

SUMMARY POINTS.

1. There have been advances in all areas of computational methods for crystallographic structure solution.

2. There have been advances in the methods for protein and RNA structure prediction and refinement in the absence of experimental data.

3. A powerful synergy has emerged between methods for protein and RNA structure prediction and refinement and those used for crystallographic structure solution.

4. The success rate of molecular replacement phasing has been improved by the introduction of ab initio modeling and the use of physically realistic force fields to improve models.

5. Powerful new methods have been developed for refinement of models with respect to crystallographic data at low-resolution limits (3.5 Å or lower).

6. Structure validation methods have advanced for both proteins and nucleic acids, and they are now routinely applied as part of the structure solution process, leading to better atomic models.