Recall of Speech is Impaired by Subsequent Masking Noise: A Replication of ^{Experiment 2}

Abstract

Introduction:

The presence of masking noise can impair speech intelligibility and increase the attentional and cognitive resources necessary to understand speech. The first study to demonstrate the negative cognitive effects of noisy speech found that participants had poorer recall for aurally-presented digits early in a list when later digits were presented in noise relative to quiet (Rabbitt, 1968). However, despite being cited nearly 500 times and providing the foundation for a wealth of subsequent research on the topic, the original study has never been directly replicated.

Methods:

This study replicated Rabbitt (1968) with a large online sample and tested its robustness to a variety of analytical and scoring techniques.

Results:

We replicated Rabbitt’s key finding that listening to speech in noise impairs recall for items that came earlier in the list. The results were consistent when we used the original analytical technique (an ANOVA) and a more powerful analytical technique (generalized linear mixed effects models) that was not available when the original paper was published.

Discussion:

These findings support the claim that effortful listening can interfere with encoding or rehearsal of previously presented information.

A robust finding in the speech perception literature is that increasing the level of the background noise—regardless of the nature of the noise—tends to impair speech intelligibility (e.g., Miller & Nicely, 1955; Sumby & Pollack, 1954) and increase the amount of effort listeners must expend to identify the speech (Sarampalis et al., 2009; Strand et al., 2018). This concept, which is typically referred to as “listening effort,” rests on the assumption that listeners have a limited pool of cognitive resources (Kahneman, 1973), so as the speech identification task becomes more difficult, listeners must recruit additional resources to complete that task and therefore have fewer resources available to complete other tasks (Gagné et al., 2017) or encode what was heard into memory (e.g., McCoy et al., 2005; Sommers & Phelps, 2016).

One of the earliest studies to demonstrate that background noise can impair cognitive processes associated with identifying speech was conducted over 50 years ago (Rabbitt, 1968). Although Rabbitt (1968) did not use the term “listening effort,” the study has formed the basis for much of the work on the topic and is often cited as the theoretical basis for listening effort research (e.g., Piquado et al., 2010; Sarampalis et al., 2009). Rabbitt conducted three experiments that employed free recall measures to investigate the effect of background noise on retention of aurally-presented digits. The second of these experiments has been particularly influential in shaping our understanding of listening effort.

In Experiment 2, Rabbitt (1968) aurally presented lists of eight digits, with the first half and second half presented either in masking noise or in silence (“clear”). Following presentation of the eight digits, participants were instructed to recall the digits in the first half or second half of the list (see Figure 1). The key finding was that recall of digits in the first half was better when items in the second half were presented in the clear rather than in noise. That is, subsequent noise impaired recall for previously presented items, regardless of whether those items were themselves presented in noise.

Figure 1:

Left: Design schematic of the four noise conditions (clear/clear, noise/clear, clear/noise, noise/noise) in Rabbitt (1968). On each trial, participants heard the first half and the second half of each list in either noise or silence (“clear”) and were then cued to recall one or the other. Right: Example “clear-noise” trial in which participants heard the first half of the list without masking noise and the second half with noise and were then asked to recall the first half.

These findings are particularly informative because recall for the words in the first half of the list was impaired as a result of a noise manipulation that occurred after those words were presented (see also Cousins et al., 2014; Piquado et al., 2010). Thus, the impaired recall of first-half items cannot be attributed to noise obscuring the intelligibility of the to-be-remembered items. Instead, these findings suggest that the additional listening effort required to recognize speech in noise in the second half of the list interfered with rehearsing or encoding the digits from the first half, thereby leading to poorer subsequent recall. Despite its consequential impact on the field, this experiment has never been directly replicated.

In the current study, we replicated the methods of Rabbitt (1968) Experiment 2 to test whether noise impairs recall of previously heard items. In addition, we assessed whether the negative effects of noise in the second half of the list on recall of the first half were more pronounced when the first half of the list was also presented in noise. We hypothesized that when individuals are already expending high levels of listening effort to parse noisy speech in the first half of the list, then the detrimental effects of noise in the second half should be particularly pronounced. Rabbitt’s original study showed a pattern of data that was numerically consistent with this hypothesis, but the interaction was not directly tested, so we assess that interaction here. Finally, we tested the robustness of the findings to several methods of scoring participant responses—including the strict scoring criteria Rabbitt employed as well as a more lenient, partial-credit approach—and analytical techniques, including the ANOVA used by Rabbitt and generalized linear mixed effects models.

Methods

We attempted to match the methods of Rabbitt (1968) as closely as possible; deviations from the original experiment are explicitly noted below. Stimuli, raw data, code for analysis, and the preregistration documentation can be found at https://osf.io/qjbxw/.

Participants

Participants (ages 25–69, M = 35.7 years, SD = 10.2 years; 54% male, 44% female; 79% White, 10% Black or African-American; 9% Asian; 3% Native American or Alaskan Native; note that percentages may not sum to 100% because participants were allowed to select multiple or no options) were recruited from the online participant recruitment platform Prolific (www.prolific.co). Our participant group matched Rabbitt’s with regard to age (25–69 years old, mean = 45.3). Rabbit did not report demographic details of participants, but we only recruited native English speakers located in the United States who reported having normal hearing. Data collection occurred between September 18 and September 28, 2020. Rabbitt tested 11–21 participants at the same time, but given our online sample, participants in this replication study were tested individually. Participants provided consent and received $4 for 25 minutes of participation. Carleton College’s Institutional Review Board approved all research procedures.

In order to reach a preregistered sample of 200 participants, we ran a total of 290 participants. Participants were excluded based on the following preregistered criteria: if they did not complete the full study (N = 22); if their recall of words in the second half of the list in the clear was below 80%, indicating they were not fully attending to the task (N = 0); or if they reported using external memory aids (e.g., writing numbers down during presentation in lieu of remembering them) after completing the study (N = 59). Nine additional participants regularly reported more than four digits, rather than following the instructions to only recall the four digits in the first or second half of the list. We had not anticipated this being an issue so did not preregister excluding those participants, but opted to exclude them because they were not completing the task as instructed and reporting more than four digits leads to artificially inflated recall rates given that there are only eight possible digits.

Stimuli

Stimuli consisted of the numbers one through nine, excluding seven. Rabbitt (1968) reported that stimuli consisted of eight digits, but did not specify which digits; we excluded seven so all the digits were monosyllabic. The stimuli were recorded by a female native English speaker without a strong regional accent using a Blue Yeti microphone in Audacity (version 2.4.2). Stimuli were matched on root-mean-square amplitude and were between 415 and 630 ms long. Rabbitt generated noise via a “simulated GPO telephone line with a Modulated Noise Reference Unit” (Rabbitt, 1968, p. 242) that maintained a constant signal-to-noise ratio. To attempt to replicate this as closely as possible without the original technology, we first generated speech-shaped noise in Praat to match the long term average spectrum of the speech stimuli (Winn, 2018). Words were then edited using Python (Python Software Foundation., 2017 version 3.6.4) to introduce speech-shaped noise that modulated with the amplitude of the target speech, thereby maintaining a constant signal-to-noise ratio. Rabbitt (1968) did not report the signal-to-noise ratio used, so we conducted a brief pilot study to determine the most difficult noise level that would result in 99% speech intelligibility, which was equivalent to intelligibility in the clear: −3 dB.

Random sequences of the eight digits were generated using a custom Python script to replicate Rabbitt’s method of drawing lists from random number tables. The speech tokens were then joined together in Audacity, presented at one digit per second (with silence occupying the remaining time) and with a two second pause between the first and second half of the list, followed by a target grouping cue (“Group 1” or “Group 2”). Each half of the list was presented either in noise or in the clear. There were 14 lists of each of the four compositions (clear/clear, clear/noise, noise/clear, noise/noise) for a total of 56 experimental trials. Participants were prompted to recall the first half and second half an equal number of times (seven times for each of the four compositions).

Procedure

We programmed the experiment using Gorilla Experiment Builder (Anwyl-Irvine et al., 2020). Participants were instructed to use headphones and complete the task in a quiet space with minimal visual distractions. They first completed a browser sound check (Milne et al., 2020) to ensure they could hear presented audio and were then instructed to adjust their audio to a comfortable volume and to not change it during the experiment. Next, participants completed a headphone screening (Milne et al., 2020) that required them to listen to three brief stimuli and identify which of the three contained a Huggins’ Pitch (one white noise signal presented in each ear which, when combined, produce the perception of hearing a tone). These pitches can only be perceived when headphones are used in both ears, and are weak or absent when played over loudspeakers. The non-Huggins’ Pitch stimuli were white noise, and the three stimuli were randomly ordered within each trial. Participants completed six of these trials and could only complete the experiment if they correctly identified which of the three stimuli contained the Huggins’ pitch on all of the six trials. If they failed the task the first time, they were given a chance to try again. Trials were presented in a randomized order.

Next, participants read instructions for the main task and completed five practice trials, followed by the 56 experimental trials. After each list, participants were prompted to type either the first half or the second half of the list. Participants had 10 seconds to enter their responses in a textbox, at which point the next trial began. Following Rabbitt’s methods, the 56 lists were presented in the same randomized order for all participants. Thus, on any trial, participants could not predict ahead of time the composition of the list (e.g., clear/noise) or the cuing instructions (e.g., recalling the first or second half).

After the participants completed the experiment, they were asked if they used any outside help, such as writing the numbers down, and if so, what they did. They then were asked demographic questions which included age, whether English was their first language, race, and biological sex. These questions were not included in Rabbitt (1968) but were included here given the online setting and modern expectations for reporting participant demographic data.

Results

Data analysis was conducted in R version 4.0.3, (R Core Team, 2020). The first analysis matched the one used in Rabbitt (1968). Half lists were scored as correct if participants reported all four digits of the cued half correctly and in order. This method of scoring (referred to here as “absolute scoring”) is a rather coarse measure of recall, as participants who recalled all four items in the wrong order received the same score (0) as those who did not recall any of the items. Therefore, in addition to Rabbitt’s original method, we also calculated accuracy using a more lenient scoring method (“partial scoring”), in which individual digits (as opposed to half lists) were scored as correct if the reported digit occurred in the cued set of digits, regardless of order. Thus, items recalled out of order received the same score as those recalled in order, and recalling some but not all of the items resulted in partial credit. The average number of first-half items recalled using absolute scoring as well as the average number of digits recalled using partial scoring in each of the four noise conditions are reported in Table 1.

Table 1.

By-participant mean number of first-half lists correctly recalled using absolute scoring (out of 7) and mean number of first-half digits correctly recalled using partial scoring (out of 28), grouped by noise condition

	C/C	C/N	N/C	N/N
Absolute Score (SD)	5.11 (1.84)	4.75 (2.04)	4.96 (1.98)	4.59 (1.82)
Partial Score (SD)	25.82 (3.47)	25.15 (3.66)	25.31 (3.49)	24.98 (3.40)

A repeated-measures ANOVA using the absolute scores on each half of the list combined demonstrated a significant effect of noise on recall, F(1, 199) = 5.07, p = 0.03, indicating that digits presented in noise were recalled less accurately than those in the clear. There was also a significant effect of recall group, F(1, 199) = 102, p < 0.001, indicating that first-half items were recalled less accurately than second-half items. Following the conventions of Rabbitt (1968), our next analysis was conducted only on the first half of the list, and demonstrated that the presence of noise in the second half significantly impaired recall the first half, F(1, 199) = 22.4, p < 0.001. This result replicates the key finding reported in Rabbitt (1968)—indeed, the magnitude of the effect of noise in the second half of the list on recall of the first half of the list in our study was identical to that in Rabbitt’s original experiment (Cohen’s d = 0.19 for both; see Figure 2).

Figure 2.

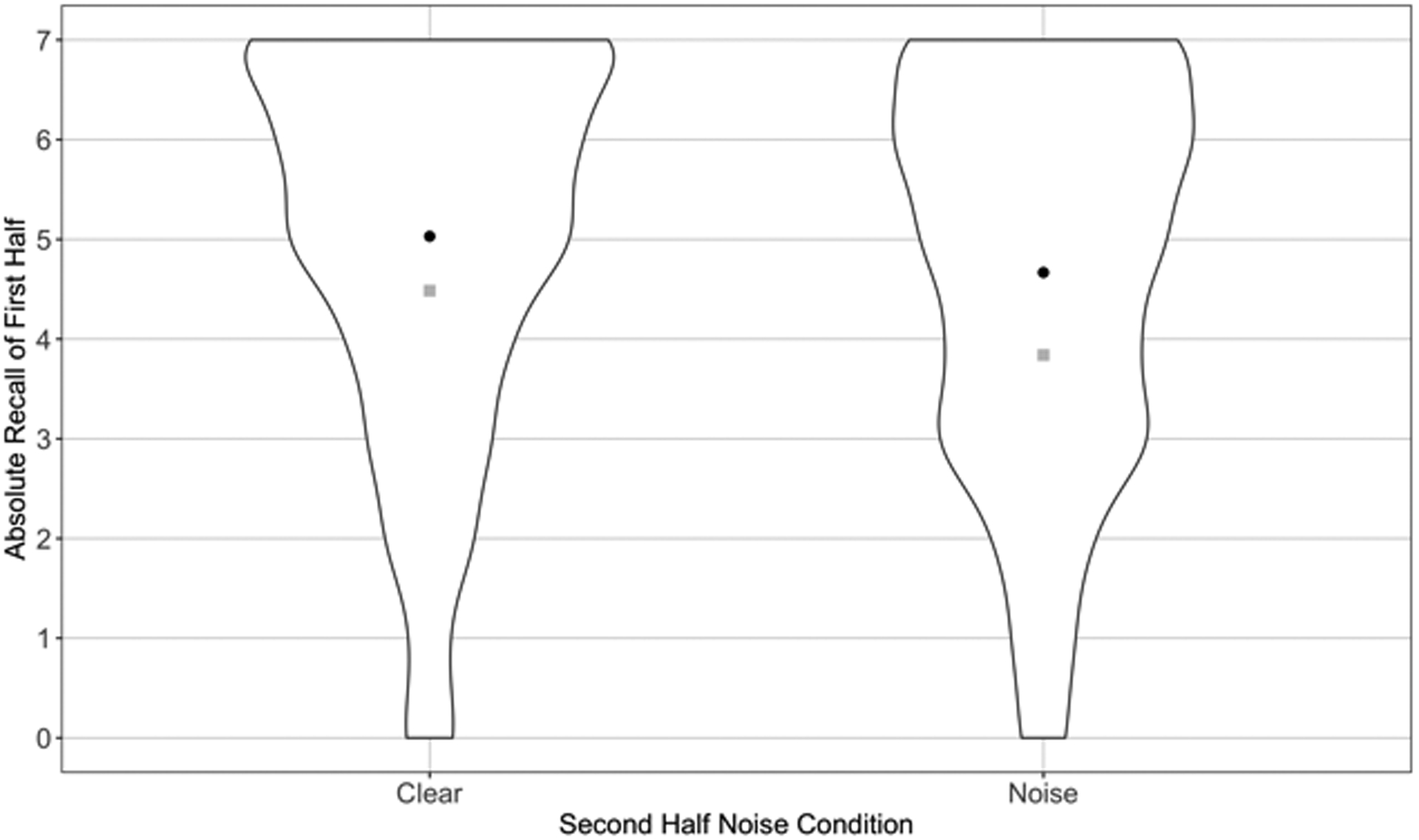
Violin plot depicting distribution of absolute recall of first-half lists (out of 7) by noise condition of second-half list. Black points indicate means for each condition, grey squares indicate the mean values reported in Rabbitt (1968).

The pattern of results was consistent when the same analyses were run using the partial scoring method: the presence of noise impaired recall overall, F(1, 199) = 16.71, p < .001, and second-half items were recalled better than first-half items, F(1, 199) = 64.29, p < 0.001. Critically, the presence of noise in the second half of the list impaired recall of items in the first half of the list, F(1, 199) = 15.41, p < 0.001 (Cohen’s d = .14).

We also tested for an interaction between the presence of noise in first-half lists and second-half lists. This analysis assessed whether recall of first-half items was more impaired by noise in the second half when the first half also had noise. Rabbitt’s data showed this pattern numerically—the change from noise/clear to noise/noise resulted in participants recalling .9 fewer lists on average, whereas the change from clear/clear to clear/noise resulted in a change of only .39 lists—but the original study did not test for this interaction. Contrary to our hypothesis, the effect did not emerge in our dataset: the interaction between noise in first- and second-half lists was not significant when using either absolute F(1, 199) = 0.001, p = 0.97 or partial F(1, 199) = 2.14, p = 0.15 scoring.

The ANOVAs above were conducted to enable us to match the methods that Rabbitt employed as closely as possible, but statistical advances since 1968 allow us to use a more powerful analytical tool: generalized linear mixed effects models (see Jaeger, 2008 for a discussion of the benefits of this approach over ANOVAs). For the mixed effects analysis reported below, accuracy was determined at the item level such that a particular digit was recalled either correctly or incorrectly. Given the binary nature of the outcome, we used generalized linear mixed effects models with a logit link function via the lme4 package (version 1.1.26) in R (Bates et al., 2014). Significance was determined by comparing nested models via likelihood ratio tests. Mirroring the key comparison in Rabbitt’s Experiment 2, we first tested whether noise in the second half of the list affected recall of items in the first half. The full model included a fixed effect indicating whether noise was present in the second half of the list (dummy coded such that quiet was the reference level), and the reduced model lacked this effect but was otherwise identical to the full model. The random effects structure for both models included random intercepts for participants and items, and by-participant random slopes for noise in the second half of the list. The likelihood ratio test indicated that the presence of noise in the second half of the list was significant (χ²₁ = 6.34, p = .01), and examination of the summary output for the full model indicated that recall of words in the first half was better when the second half was presented in the clear than when it was presented in noise (B = −.32, SE = .12, z = −2.64, p = .008).

Next, we tested whether noise in the second half impaired recall of items in the first half to a greater extent when those first-half items were also presented in noise (i.e., an interaction between noise in the first half and noise in the second half). The fixed effects in the full model included this interaction term and both lower-order terms, and the random effects included by-participant and by-item random intercepts, as well as by-participant random slopes for both first and second half noise. A likelihood ratio test comparing this model to a model lacking the interaction term indicated that the interaction was not significant (χ²₁ = 1.28, p = .26). Thus, the three sets of analyses (ANOVA with absolute scoring, ANOVA with partial scoring, and mixed effects analyses) converge on the same result: items in the first half of the list are recalled less accurately when the second half is presented in noise than in the clear, regardless of the presence of noise in the first half.

Discussion

In this study, we attempted to replicate Rabbitt (1968) in a large online sample using the original method of absolute scoring as well as a partial scoring method. The results robustly support Rabbitt’s main finding: the presence of noise disrupts recall of previously heard information. Notably, the results also replicated when we analyzed the data with generalized linear mixed effects models, which are more powerful than ANOVAs but were not available when the paper was published. Thus, it appears that Rabbitt’s original finding is robust to a variety of scoring and analytical techniques.

Although the finding that noise impairs recall of previously presented information is robust to replication, the mechanisms underlying the effect remain unclear. Rabbitt explained that the finding may have occurred because the task of listening to speech in noise occupied “channel capacity,” thereby inhibiting rehearsal. However, there exist multiple possible mechanisms by which noise could interfere with recall (e.g., perhaps subsequent noise interferes with sensory memory rather than rehearsal). The experiments presented in Rabbitt (1968)—and the current replication—cannot adjudicate between these possibilities, but future experiments could be designed with the intention of clarifying the stage in the encoding process that is disrupted by the presence of noise.

In addition to testing for a main effect of second-half noise on recall, we tested for an interaction between first-half noise and second-half noise. These novel analyses did not provide any evidence that the presence of noise in the second half was more detrimental to first-half recall when the first half was presented in noise than in the clear. We had hypothesized that noise in the first half of the list would increase listening effort, and participants would therefore be nearer the capacity of their cognitive resources than when the first half of the list was presented in the clear. In this case, the addition of noise in the second half should be particularly detrimental for recall of first-half items. We did not find support for this hypothesis: the effects of noise in the second half were consistent regardless of whether the first half was presented in noise. This may have occurred because participants could complete the task relatively easily even in the most difficult condition—indeed, recall accuracy was 92.4% across all conditions. Therefore, even when both half-lists were presented in noise, participants may not have been near the limits of their cognitive capacity, so adding noise to the first half did not affect recall above and beyond the presence of noise in the second half. The high level of accuracy across conditions may also explain why the observed effect size was relatively small (Cohen’s d = 0.19). Presenting the digits in more difficult levels of background noise or asking participants to recall more than four digits would likely increase the magnitude of the effect, but we opted to follow Rabbit’s methodology as closely as possible in this replication study. Future work could test participants under more difficult conditions to assess whether the interaction between first and second half noise may emerge and whether the magnitude of the effect may increase, or perhaps test these effects in older adults, who tend to have poorer recall and expend greater listening effort compared to young adults (Sommers & Phelps, 2016).

Although we attempted to follow Rabbitt’s original methods as closely as possible, the study deviated in several ways; most notably, participants were tested individually and online rather than in groups in a lab setting. Previous research (Bentley et al., 2017; Crump et al., 2013; Leding, 2019) has replicated a variety of classic psychology findings—including those related to memory and recall (e.g., Bentley et al., 2017)—through online data collection, and some work has also indicated that classic findings in spoken word recognition emerge in online samples (Slote & Strand, 2016). Despite the possibility of additional variability in online settings, the effect size in this replication experiment was identical to that reported by Rabbitt. Thus, the current research provides further support for the claim that despite environmental variability of online studies and variability in participants’ hardware and software, at least in some cases online experiments can demonstrate the same effects as in-lab experiments.