Abstract
Directed evolution has been used for decades to engineer biological systems at or below the organismal level. Above the organismal level, a small number of studies have attempted to artificially select microbial ecosystems, with uneven and generally modest success. Our theoretical understanding of artificial ecosystem selection is limited, particularly for large assemblages of asexual organisms, and we know little about designing efficient methods to direct their evolution. Here, we have developed a flexible modeling framework that allows us to systematically probe any arbitrary selection strategy on any arbitrary set of communities and selected functions. By artificially selecting hundreds of in-silico microbial metacommunities under identical conditions, we first show that the main breeding methods used to date, which do not necessarily let communities to reach their ecological equilibrium, are outperformed by a simple screen of sufficiently mature communities. We then identify a range of alternative directed evolution strategies that, particularly when applied in combination, are well suited for the top-down engineering of large, diverse, and stable microbial consortia. Our results emphasize that directed evolution allows an ecological structure-function landscape to be navigated in search for dynamically stable and ecologically resilient communities with desired quantitative attributes.
INTRODUCTION
Harnessing microbial communities is a major aspiration of modern biology, with implications in fields as diverse as medicine, biotechnology, and agriculture 1. Several groups have demonstrated that small synthetic communities can be engineered to carry out functions such as biodegrading environmental contaminants 2–4, manipulating plant phenotypes 5, or producing biofuels 6,7, among others 8,9. Despite these success stories, engineering consortia from the bottom-up (i.e. “rational design”) remains challenging. The function of a consortium is generally affected by species interactions, which are difficult to predict from first principles and expand rapidly with species richness 10–16. Perhaps more importantly, microbial communities are rapidly evolving ecological systems, and their engineered functions can be disrupted by environmental fluctuations, invasive species, species extinctions, or the fixation of mutant genotypes 17–20.
Rather than fighting these eco-evolutionary forces, an alternative “top-down engineering” approach seeks to leverage ecology and evolution to find microbial consortia with desirable attributes 20–26. Most work has focused on enrichment approaches 22,25–28, but a small number of studies have gone further and empirically demonstrated that ecological communities can respond to artificial selection applied at the level of the community itself 29,30. This strategy has been deployed to iteratively optimize complex microbial communities that modulate plant phenotypes 1,30–34, animal development 35, or the physico-chemical composition of the environment 36–40. Despite its conceptual elegance, the success of artificial selection at the microbiome level has been mixed and generally modest, and artificial selection has not yet been widely adopted in microbiome engineering 1,41.
A limiting factor is that we do not know how to design efficient artificial selection protocols at the microbial community level. The selection methods used in early studies (e.g. 30,42) were inspired by even earlier work on artificial group selection of either single-species populations 43–45, or two-species communities of sexually reproducing animals 29,46. In these studies, new generations of communities were created through either: (i) a sexual reproduction-like “migrant-pool” strategy, where the communities with the highest function were mixed together and then used to inoculate a new generation, or (ii): an asexual-like “propagule” reproduction strategy, where the best communities were selected and then propagated without mixing 29,30,36. All subsequent microbial ecosystem-selection studies followed suit and employed variations of those two methods.
But are selection strategies originally developed for small populations of sexually reproducing organisms well suited to efficiently direct the evolution of much larger and diverse communities of generally asexual microbes? Are there other alternatives? To address these questions, we set out to explore the effectiveness of all previous selection strategies we could find in the literature. To do this, we evaluated them in parallel on the same set of in-silico microbial communities and for a number of different functions. We show that all of these protocols do worse than a simple screen, a no-selection control that has been largely missing from previous microbiome selection experiments. The limitations of past protocols led us to propose an alternative framework for top-down microbial community engineering that is based on the directed exploration of the ecological structure-function landscape (i.e. the map between community composition and community function), through iterated rounds of randomization and selection 10–12,15,47,48. This approach is inspired by the directed evolution field, where proteins and RNA molecules are evolved in the laboratory through a guided random exploration of their genotype-phenotype maps 49,50. In the second part of this paper, we address how these structure-function landscapes can be systematically navigated in search for stable communities of high function.
RESULTS
Migrant-pool and propagule breeding strategies are limited in their ability to breed high-functioning microbial communities.
A small number of studies have attempted to breed ecological communities (including two from our own group), using different variations of the migrant-pool and propagule methods of selection 30,32,33,36–38,51. To better understand the limitations of the empirical strategies used in the literature, we first set out to systematically evaluate them under identical conditions. To do this empirically, one would have to apply all protocols in parallel to the same set of communities (hereafter the “metacommunity”29), ideally, in replicate experiments and for various different metacommunities. This would require a prohibitively large number of experiments, each with its own control lines. We therefore resorted to in silico communities, which can provide the required throughput and allow us to rigorously compare a large number of selection strategies. For that purpose, and inspired by the work of Lenton and Williams 51,52 and others 53–55, we have constructed a flexible computational modeling framework (implemented through a Python package, ecoprospector; Fig. 1A, Methods) that allows us to implement arbitrary community-level selection strategies on arbitrarily large populations of arbitrarily diverse in silico communities (Methods). Microbes within a community grow and interact with each other via resource competition following the Microbial Consumer Resource Model (MiCRM) 56–59 (Methods). Despite its simplicity, the MiCRM exhibits emergent functional and dynamical behaviors that recapitulate those observed in both natural 58 and experimental communities 60,61.
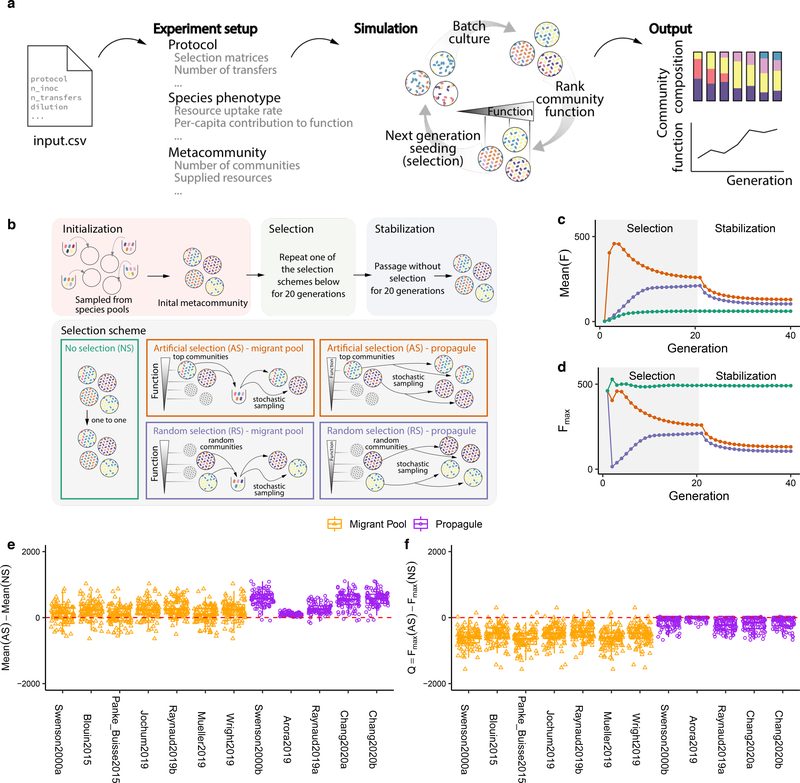
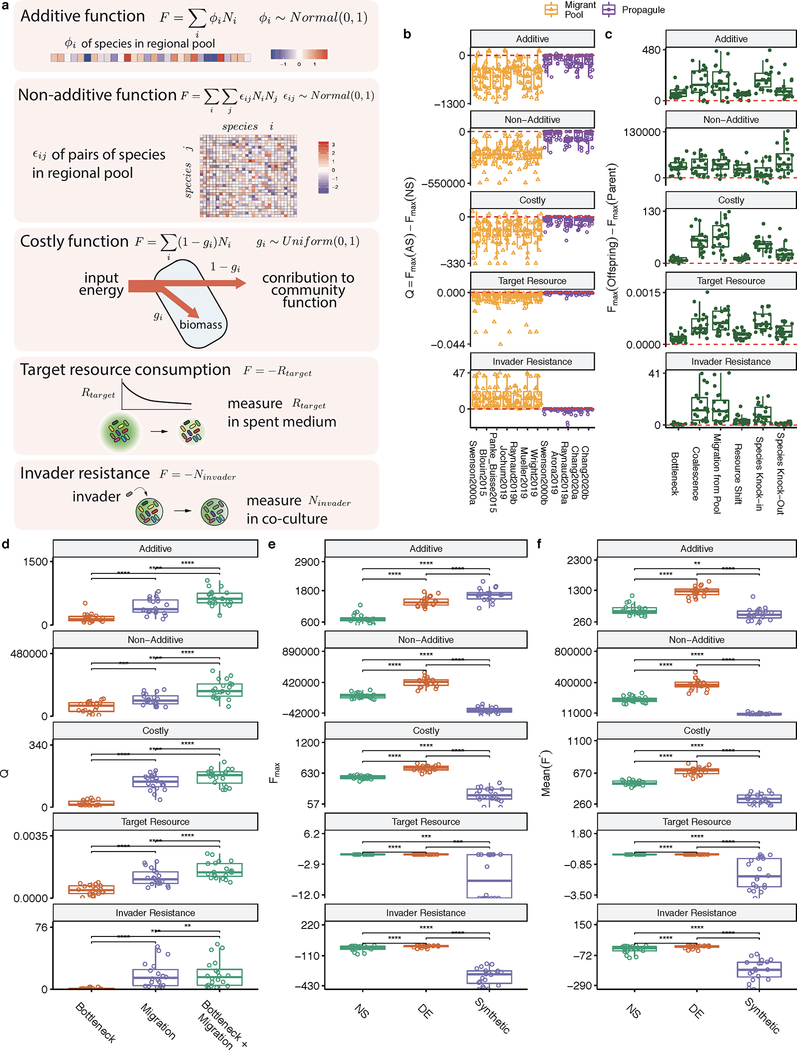
Figure 1. Migrant-pool and propagule strategies are limited in their ability to find new, high-functioning microbial communities.
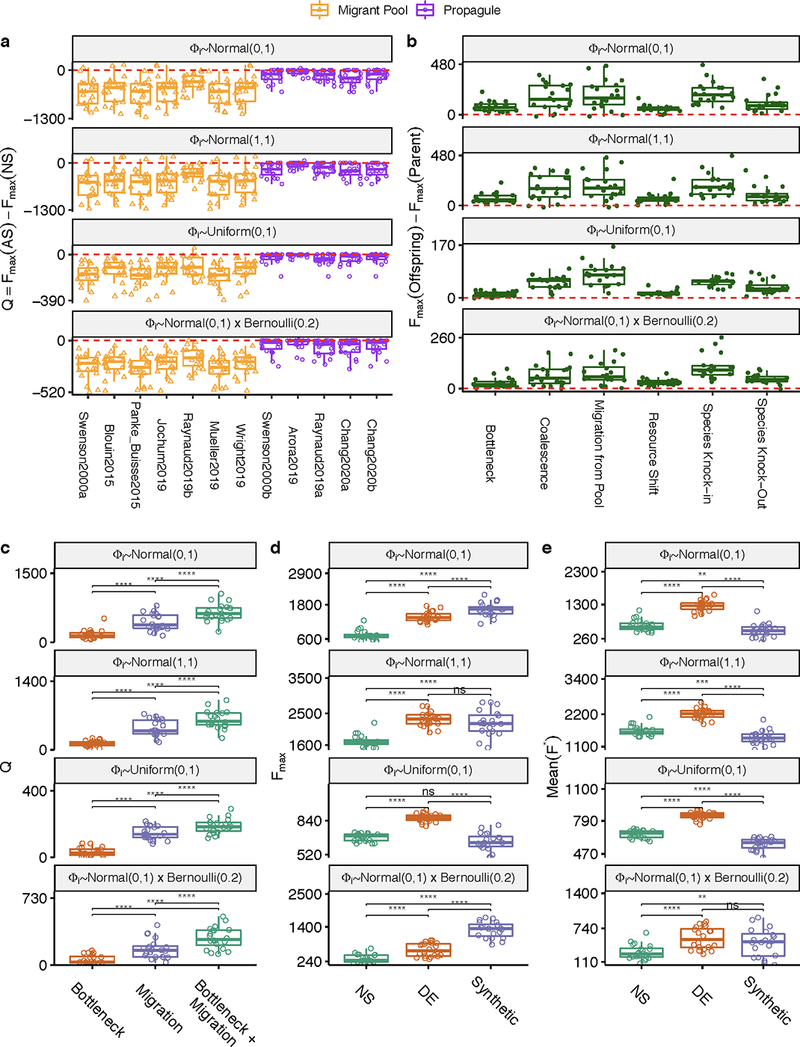
(A) We constructed a Python package, ecoprospector, which allows us to artificially select arbitrarily large and diverse in silico communities. The experimental design of a selection protocol (e.g., number of communities, growth medium, method of artificial selection, function under selection, etc.) is entered in a single input .csv file (Methods). Communities are grown in serial batch-culture, where each transfer into a new habitat is referred to as a community “generation”. Within each batch incubation, species compete for nutrients from the supplied medium. At the end of the incubation period, communities are selected according to the specified, protocol-specific selection scheme, and the selected group is used to seed the communities in the offspring generation. Once the protocol is carried out to completion, ecoprospector outputs a simple text format for later analysis on community function and composition. (B) Illustration of previously used migrant pool and propagule selection schemes (AS) as well as the corresponding randomized controls (RS) 29,43. We also consider a no-selection ‘control’ scheme (NS). All protocols are applied at the end of each community generation and are implemented using a matrix representation depicted in Supplementary Fig. 1. A representative outcome of one community-level selection experiment is shown in (C-D), where we adapted the selection protocol from the migrant-pool strategy in ref 30. A metacommunity is seeded by inoculating ninoc = 106 randomly drawn cells from a species pool into each of 96 identical habitats and allowing them to grow (Methods). The metacommunity was then subject to 20 rounds of selection (generations), and then allowed to stabilize without selection for another 20 generations. The function maximized under selection F is additive on species contributions, whose per-capita species contribution to function is randomly generated (see main text). In each selection round, the top 20% communities with highest F (AS; red) (or a randomly chosen set in (RS; blue)) are selected and mixed into a single pool which is then used to seed all communities in the next generation by randomly sampling 106 cells into them. The NS protocol (green) simply propagates the communities in batch mode without selection. The changes in overall function over the generations is shown in (C) (average F) and (D) (maximum function Fmax). (E) Selection strategies were adapted from twelve experimental protocols in previous studies (see Supplementary Table 1; Methods). All were applied to standard metacommunity sizes (96 communities), for the same number of generations (20 selection generations + 20 stabilization generations). All protocols have a significantly greater mean function in the AS than in the NS line (two-sided paired t-test, P < 0.01) as well as the RS lines (Supplementary Fig. 4). (F) The difference in Fmax between the AS and NS lines (Q). All protocols show a Mean Q < 0 (two-sided Welch’s t-test, P < 0.01), indicating that they did not succeed at improving the function of the best stabilized community in the ancestral population.
Each simulation considers a metacommunity of 96 replicate habitats, all containing the same initial composition of 90 resources (Methods). Each of these habitats is seeded with ninoc = 106 cells, randomly drawn from a regional pool of 2100 species that is unique for each habitat (Methods and Supplementary Methods). Each species is represented by a different randomly sampled vector of nutrient utilization parameters (Methods). A typical community is seeded with 228±14 (Mean±SD) species. The inoculum size and species richness we used are a lower bound for most microbiome enrichment communities (Supplementary Methods) 60.
Once inoculated, all 96 communities in the metacommunity are allowed to grow for a fixed batch-incubation time t (Methods), at the end of which we measure their function F. We have tested several functions of varying complexity (Supplementary Methods), and the majority of our findings are consistent throughout. For that reason, we focus on the simplest function and discuss the rest in the Supplementary Methods. The simplest case is a community function that is additive on species contributions: F = ∑iϕiNi, where ϕi and Ni are the per-capita contribution of species i and its abundance, respectively (Methods). This function is by assumption redundantly distributed in the community and can be carried out by all species in isolation. In the Supplement, we show that eliminating this redundancy assumption does not qualitatively change our results. Also for simplicity, we assume that the per-capita contribution of a species is fitness neutral, an assumption that is relaxed in the supplement.
At the end of each batch-incubation a subset of those communities with highest F are selected to breed the next generation, according to the selection strategy that is being evaluated (Fig. 1A–B). This involves transferring cells and leftover nutrients into new habitats with all nutrients replenished (Methods). In addition, for the migrant-pool strategies, each offspring community is seeded by multiple parents, and so we also have dispersal. Because cells are randomly sampled, this step introduces stochasticity in the population dynamics that may cause fluctuations around any dynamical attractor. We also note that species are not allowed to evolve (i.e. change their uptake rates) at any point during the simulations.
Strategies from previous experimental work were adapted to our specific standardized conditions (e.g. 96 communities, incubation time, dilution factor, etc.) from the papers where they were originally used (Methods; Supplementary Table 1). To evaluate the effectiveness of these adapted strategies under our in silico conditions, we applied each of the twelve selection protocols to the same starting metacommunity for a total of 20 rounds of artificial selection (i.e. community “generations”). To evaluate the stability of the selected function when community-level selection is not constantly applied, we passaged all communities without selection for an additional 20 transfers, giving them time to reach equilibrium (Fig. 1B).
To illustrate a typical outcome, we plot in Fig. 1C–D a representative artificial selection (AS) line where we used the original migrant-pool strategy introduced in ref 30. For reference, we also show the outcome of a random selection (RS) control, where communities were chosen randomly for reproduction (also adapted from that used in 30). As shown in Fig. 1C, the mean function in the AS line increases more than in the RS control, indicating a positive response to selection. Importantly, however, the function of the highest-performing community (Fmax) in the AS line is lower than in a third “no selection” (NS) control line 43, where each community in the starting metacommunity is passaged without community-level selection (Fig. 1D; Supplementary Fig. 1). In other words, a simple “ecological prospecting” procedure, where we screen 96 stable enrichment communities for function and select the best (e.g. 62) would have found a better community than the multiple rounds of artificial selection we applied at the community level. We note that a NS control line has been missing in all microbiome selection experiments we are aware of.
This experiment illustrates that the mean function in the metacommunity can increase simply because of selection against the worst-performing communities. Importantly, the goal of top-down microbiome engineering is not to improve the mean function, but to find communities with higher functions. Therefore, we propose that the difference between the function Fmax of the highest-performing community (hereafter referred to as the “top community”) in the artificial selection line relative to a no selection control (Q=Fmax[AS]-Fmax[NS]) is a better metric to quantify the success of a selection strategy for top-down engineering purposes. Values of Q>0 indicate a successful selection experiment, whereas Q<0 indicates an unsuccessful one. Using this metric, we evaluated the success of the twelve propagule and mixed-pool protocols used in previous empirical studies, including our own (Fig. 1E–F) 30–33,35–40. To obtain a statistically sound assessment, we applied each selection method to N=100 independent artificial selection lines, each with their own NS and RS controls (where applicable; Methods). All randomly sampled parameters, including the per-capita species contribution (ϕi), 96 regional species pools, the initial resource environment (Rɑ) and the initial species abundances (Ni) were resampled for each of the 100 replicates but were kept constant across selection methods (and so the statistical analysis is always pairwise). For all twelve protocols, the mean function increased in response to selection relative to the NS control (the enrichment screen; Fig. 1E) and the RS control (Supplementary Fig. 2). Yet, in line with what we observed in Fig. 1D, all protocols failed to improve Fmax relative to the NS control (Fig. 1F)
Selecting communities before they are stable is inefficient.
As is the case in all previous artificial selection experiments, our communities are propagated in serial batch-culture. Within each batch incubation, the community goes through an ecological succession. At the end of each batch, a small number of cells are randomly drawn from the community and used to seed a new habitat where all nutrients have been replenished, starting a new batch. Inspired by Doulcier et al, we may see each succession as a “developmental” process at the community level. Communities at the end of a batch incubation can be thought of being in an “adult state” and ready for reproduction, whereas communities at the beginning of an incubation are in an “infant state” 53. In absence of artificial community-level selection, our in silico enrichment communities eventually self-assemble into a dynamical state where successions are identical every generation (Supplementary Fig. 3). Note that this is due exclusively to population dynamics, and that no evolution or migration is necessary 60,63–65. We say that communities are “generationally stable” when the successions are identical across community generations and, therefore, the composition of an adult “offspring” community is the same as that of its adult “parent”. In our simulations, we typically need >5 generations to approach a generationally stable state (Methods).
We speculated that a reason why the selection strategies we evaluated above may be failing to improve Fmax is that, following the original protocols, we started selection at the end of the first batch when the communities are not yet generationally stable. Consistent with this hypothesis, we found that the community rank (from the highest to lowest function) in the first generation is a poor predictor of the rank of generationally stable communities (Supplementary Fig. 4; Spearman’s ρ=0.423, p < 0.01, N=96). In other words, artificial selection in early generations favors communities that had a high function early on, but which end up having mediocre functions once they are generationally stable (Supplementary Fig. 4). This explains why Q<0 for the vast majority of strategies. In Supplementary Figs. 5–7, we further show that the large population sizes (N=106) of the infant communities in our simulations (which are in the lower end of what is common in experimental microbiome selection) and the lack of heritability away from equilibrium also contribute to the failure of the propagule and mixed pool methods to improve Fmax. Both of these methods represent a small subset of all possible ways one could generate an offspring population from the selected members of the parent population. Therefore, we asked if other methods could be used that would increase the success of artificial selection to engineer communities from the top-down.
An artificial community-level selection strategy inspired by directed evolution of biomolecules.
Directed evolution is a form of artificial selection that has been applied for decades to optimize molecular and cellular phenotypes 49,66,67. In its most common implementation, directed evolution is an iterative process that navigates the genotype-phenotype map in search of a genetic variant of high function 50,68,69. The process starts by screening a library of genetic variants. Those that are closest to the desired phenotype are selected and their mutational neighborhood is then randomly explored through mutagenesis or recombination, in search of new variants with even higher function. The best among those are selected, and the process can be continued as many times as needed 68. We reasoned that generationally stable communities of high function can be similarly found through an iterative, guided exploration of their ecological structure-function landscape (Fig. 2A).
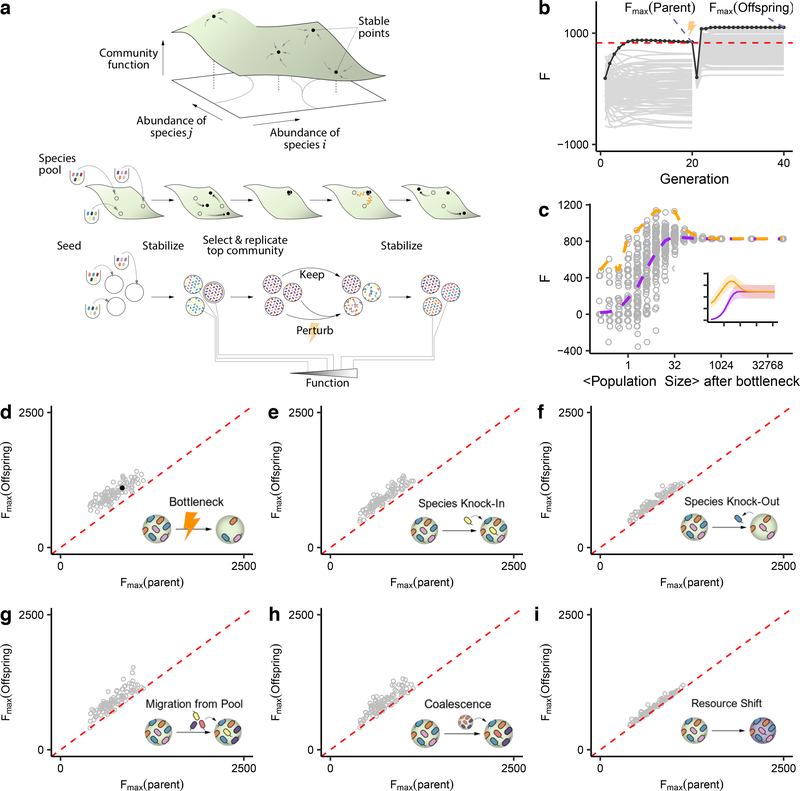
Figure 2. Directed evolution as an artificial selection strategy for high-performing communities.
(A) Directed evolution of microbial communities can be represented as a guided navigation of a dynamic structure-function landscape, which contains several stable fixed points with different community functions. Community states are given by the abundances of species i,j in the “adult” population at the end of a batch. Each of the stable fixed points represents a “generationally stable” equilibrium, as defined in the main text. A library of communities is generated by inoculating from a set of different species pools, followed by stabilization without selection before being scored for function. The top-performing community is selected and either passaged intact into the new generation, or subject to ecological perturbations to generate compositional variants, thereby “exploring” the neighboring stable equilibria in the structure-function landscape. We note that this panel is only a cartoon, the true structure-function landscape is multi-dimensional, and the dynamical stability of equilibria can be significantly more complex than illustrated here. None of those details are critical for our results or discussion. (B) A representative outcome of directed evolution of in silico microbial communities. N=96 communities are first stabilized by serially passaging without selection with a dilution factor of 103× for 20 generations. The community with the highest function Fmax(parent) (black dots and line) is selected and used to seed the new generation. To that end, the selected community is either passaged intact with the same dilution factor of 103× (N=1), or subject to 95 dilution shocks (108×) to generate variants. The 96 offspring communities are then propagated for another 20 generations until they stabilize. The top offspring variant Fmax(offspring) is highlighted with black dots and line. The red dashed line denotes the Fmax of a no-selection line. (C) Sampling the optimal bottleneck size by subjecting a single parent community to bottlenecks of different intensity. Each bottleneck is applied 95 times. In orange, we trace the Fmax for the highest-function variants for each bottleneck size. In purple, we track the mean function. Inset shows the outcome of repeating this experiment 100 times with different starting communities (Mean±SD). This shows that intermediate bottlenecks maximize the Fmax. (D-I) Fmax of 95 stable offspring variants generated through a variety of methods (see text for details), as a function of the Fmax of the (stable) parental community from which all variants were generated. Points above the red dashed line indicated an increase in Fmax from parent to offspring. The filled black circle in panel D marks the representative example shown in panel B.
To that end, we designed a directed evolution approach which consists of the following sequence of steps (Fig. 2A): (i) An initial library of communities is created by inoculating identical habitats from different species pools, and serially passaged in the absence of (community-level) artificial selection to allow all communities to stabilize. (ii) The generationally stable communities are then screened for a community-level function of interest, and the highest-performing community is selected. (iii) The selected generationally stable community continues to be passaged intact into the offspring generation, retaining its function and composition. The rest of the offspring generation will consist of proximal “compositional variants”, which have been subject to some perturbation (using one of a variety of possible methods presented below) in order to generate random differences in community composition relative to their ancestor. (iv) The offspring communities are allowed to reach their own generationally stable equilibria; and (v) the now generationally stable offspring communities are scored for function (Fig. 2A). The process can be repeated as many times as needed.
How may we generate proximal compositional variants of the best parental community? Various approaches are available including adding or removing species, in bulk or in isolation. In Fig. 1, the large population sizes of infant communities (n~106) led to a low between-population variation in the selected function (see Supplementary Discussion), thus failing to generate a diverse enough pool of proximal compositional variants (Supplementary Fig. 5). We reasoned that a more stringent propagule bottleneck may be able to better explore the structure-function landscape, a process that has been successfully applied in the past to converge on simpler, functional consortia by dilution-to-extinction 70. To test this idea, the top community from a stable parent metacommunity was selected after 20 serial transfers (with dilution factor = 103×), and then used to seed a new generation by subjecting it to 95 separate harsh dilution shocks (dilution factor = 108×), which led to a mean bottlenecked “infant” population size of n=9.76±3.12 cells (Mean±SD) (Fig. 2B). The 95 resulting “offspring” communities differed from each other in which species from the parental community were randomly sampled in the dilution shock. When subject to serial batch culture, they converged to different generationally stable compositions after 20 additional generations (Supplementary Fig. 8). Since they vary in their composition (they are compositional variants), the stable offspring communities also had different functions and some were higher than their parent’s (Fig. 2B).
Consistent with our hypothesis, (Fig. 2C), the propagule method works best at exploring the structure-function landscape and improving Fmax when we use harsh bottlenecks (starting population sizes of order n~10) but it fails at exploring the landscape when the number of cells after the bottleneck is above n~103. For mean bottleneck sizes around n~1, community diversity is too low and the function diminishes. The hump-shaped dependence of Fmax on the dilution strength shown in Fig. 2C is consistent with the findings of dilution-to-stimulation experiments 70.
Besides bottlenecks, many other community perturbations can be applied to explore the proximal ecological space in search for compositional variants with high function. For instance, we could create these variants by invading the top parental community with a single, high-ϕi species (i.e. a “knock-in”) (Fig. 2E) 71. One could also create variants of a community by selectively eliminating (“knocking-out”) one of its members (e.g. a species with low-ϕi, or one which competes with a higher-contributing species) (Fig. 2F). In practice, entirely knocking out a species from a natural habitat is challenging, but tools exist for the depletion or knock-down of species from natural and synthetic communities 72–76. Larger and more blunt perturbations are also possible: for instance, we could create a library of variants by invading the top parental community with a randomly sampled set of species from multiple different regional pools (i.e. a set of migration events) (Fig. 2G), or by coalescing the top parental community with a library of other generationally stable communities 77,78 (which is a form of migrant-pool method) (Fig. 2H). Another approach is to introduce a library of small random shifts to the nutrient composition, which leads to a rearrangement in species composition and therefore to different functions (Fig. 2I). We have applied all of these perturbations to N=100 independent lines (Methods), and in all cases they were successful at producing one or more dynamically stable community variants with higher function than the best member of the parent population (Figs 2D–I).
Iteratively combining bottlenecks and migrations to optimize community function selects for high-functioning communities that are ecologically stable.
Some of the perturbations in Fig. 2 work by eliminating taxa that are deleterious to community function (e.g. the single species knockouts or the dilution shocks). Others work by adding taxa that are beneficial to community function (e.g. single species knock-ins, or multi-species invasion from the regional pool). We hypothesized that a method that combines random elimination of resident strains with random addition of new strains could help us find high-function variants, as such a method could simultaneously eliminate deleterious species and add beneficial ones. Although random deletion can also eliminate beneficial strains and random addition may contribute deleterious ones, by “tossing the dice” a sufficiently large number of times we have a chance to find one or more variants where the combined effects aligns in the same beneficial direction, reaching high-function regions of the ecological space inaccessible through either method alone.
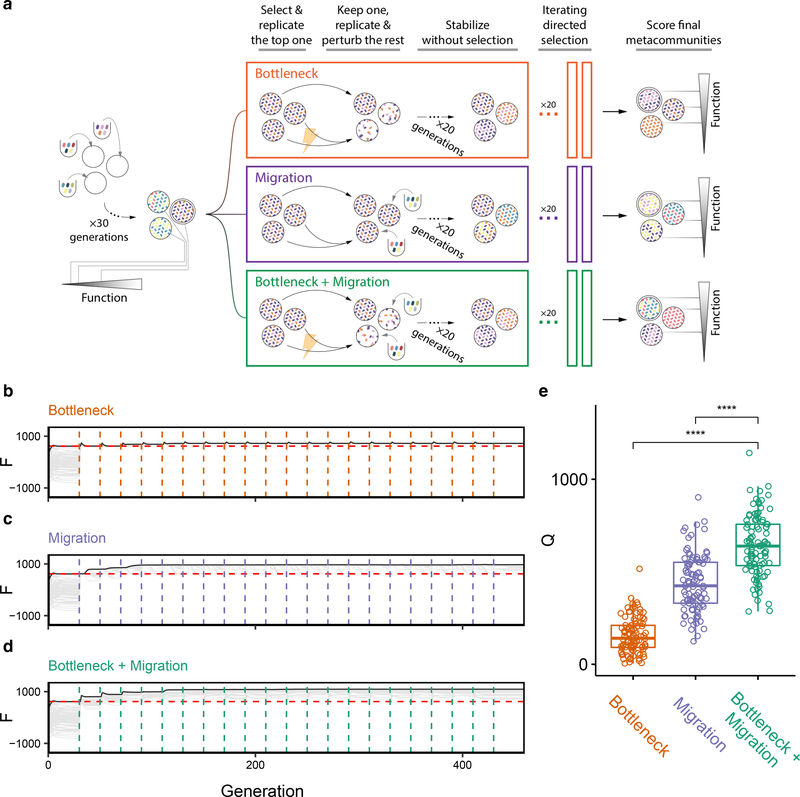
To test this hypothesis, we directed the evolution of a metacommunity (N=96 communities) using either a species deletion protocol (the dilution bottleneck in Fig. 2D), a species addition protocol (the migration we introduced in Fig. 2G), or a protocol that combined both perturbations simultaneously (Fig. 3A; Methods). As we show in Fig. 3B–D, the strategy that combines both perturbations finds a higher-function community than the two perturbations alone. When we replicated this experiment 100 times with different metacommunities, we found that the combination of both perturbations produced a significantly higher Q than either the dilution shock (Q = 641±163 vs 155±95, Mean±SD, two-sided paired t-test, p<0.01, N=100) or the migration protocol (Q = 641±163 vs 438±152, Mean±SD, two-sided paired t-test, p<0.01, N=100) (Fig. 3E).
Figure 3. Iteratively combining bottlenecks and migrations to optimize community function selects for high-functioning communities.
(A) Schematic of iterative protocols of directed evolution. A metacommunity of 96 communities was stabilized for 30 generations by serial batch-culture with dilution factor 103×(Methods). The top community after 30 generations was selected, and either passaged intact to the offspring generation, or used to generate 95 new variants by three different means: (red) in addition to the regular dilution factor (103×), we applied a harsh bottleneck (104×); (purple) we applied a migration event where 102 cells (~45 species; Methods) were randomly sampled from the regional pool and added to each community immediately after passaging them with the regular dilution factor of 103×; (green) a combination of both: after the passage with regular dilution factor (103×), communities are first bottlenecked with a dilution factor (104×), followed by migration from the regional pool (102 cells of ~45 species). The 96 offspring communities are stabilized for an additional 20 transfers, following which they are scored for function. The process can be iterated at this point (B-D) F for all communities in each generation as a function of time. Each vertical dashed line marks the time points at which the metacommunities experience selection followed by generation of new variants (color represents perturbation type). Red horizontal lines represent the Fmax of a no-selection line. (E) Q obtained from each of the three protocols at the final time point (generation 460) in N=100 independent selection lines. Each point represents the outcome of a different directed evolution experiment. Brackets represent two-sided paired t-tests (N=100 for each test). ****:p<0.0001.
An important strength of using directed evolution to engineer microbial communities from the top-down is that we find high-functioning communities that are dynamically stable. Because, by design, the function we are selecting for is additive and the per-capita contribution of each species (ϕi) is not affected by other species, one could argue that a “synthetic” bottom-up approach where we just mix high-contributing taxa would have worked equally well (if not better) than our artificial selection protocols. This ‘rational design’ is intuitively appealing given that the directed evolution protocol used in Fig. 3D selects for communities enriched with high ϕi species (Supplementary Fig. 9–10). While this may be true, since the communities in Fig. 3 have been formed by recurrent invasions from the regional species pool, they are likely to be more robust to external invasions than “synthetic” bottom-up consortia. To test this hypothesis, we went back to the artificial selection line shown in Fig. 3D, and created a “bottom-up” synthetic consortium by mixing together the n species with the highest ϕi in the regional pool (where n is the number of taxa in our artificially selected community, allowing us to control for the effect of biodiversity on functional stability 79) (Fig. 4A; Methods). We then allowed this synthetic community to stabilize in the same environment and propagation conditions that were used in the artificial selection line.
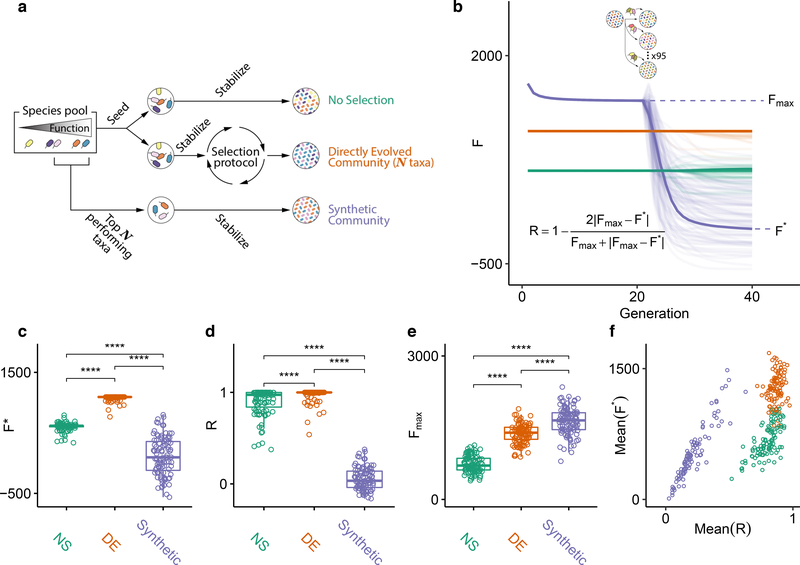
Figure 4. Directed evolution produces communities that are resistant to ecological perturbations.
(A) We compare the function and ecological stability of communities engineered from the top-down by directed evolution (DE; red), with a synthetic bottom-up consortium (purple). A no-selection (NS; green) control is also provided for reference. The DE community was found by multiple rounds of selection using a protocol that combines bottleneck and migration to generate variants. The synthetic community of equal diversity (species richness) was assembled by mixing together high-ϕi species from the regional pool (Methods). The top community of the NS control was also chosen as reference. (B) The three communities were stabilized for 20 generations (note that the DE and NS were already in equilibrium at the start, but the synthetic community was not). After that, each community was subject to invasion by a randomly sampled set of species from the regional species pool (Methods). This process was repeated 95 independent times for each community. The perturbed communities (lighter-color lines) were allowed to equilibrate by passaging for an additional 20 generations without artificial selection. Following the perturbation, communities reached a new state with function F*, and from the changes in function before and after the perturbation we compute the resistance R (inset equation) 80. (C-D) The values of F* and R resulting from panel (B) are plotted. Values above brackets represent p-values of paired t-tests (N = 95 each test). (E-F) The experiment in (B) was repeated 100 times with as many different initial DE, NS, and synthetic consortia. (E) shows Fmax of 100 independent experiments. Values above brackets represent p-values of two-sided paired t-tests (N=100 each test) (F) Mean(R) vs Mean(F*) for all 100 independent experiments. *:p<0.05, ****:p<0.0001.
As shown in Fig. 4B, the generationally stable synthetic community has indeed higher function than the directed evolution experiment. Yet, when we invaded both communities with the same random sample of species from the regional pool (containing 100 cells and, on average, 45 species; Methods), the function of the synthetic community collapsed below the artificially selected community (Fig. 4B). By averaging over 95 independent invasion experiments, we obtained the average Resistance (R) (a metric of ecological stability, which we calculated as in Shade et al 80), as well as the average community function after invasion (F*) (Supplementary Methods). As we anticipated, the artificially selected community was more resistant to invasion (considering either metric) than the synthetic consortium (F*=1077±48 vs 114±314, and R=0.974±0.072 vs 0.054±0.122, respectively; Mean±SE, p<0.01 in both cases; two-sided paired t-test, N=95) (Fig. 4C–D). The synthetic consortium also has lower resistance than the one found by an enrichment screen (the top community in the NS line: R=0.898±0.150 vs 0.054±0.122, respectively; Mean±SE, p<0.01; two-sided paired t-test, N=95) (Fig. 4C–D).
When we repeated every step of this experiment for the remaining 99 artificial selection lines in Fig. 3E, we found that these results were generic. The function of the bottom-up synthetic consortia (Fsyn) is generally higher than the Fmax found through directed evolution and enrichment screens (Fig. 4E). However, the synthetic communities are less resistant to invasion than the artificially selected communities (Mean(R)=0.867±0.045 vs 0.217±0.119, and Mean(F*)=1261±190 vs 530±309 (Mean±SE) respectively, p<0.01 in both cases, two-sided paired t-test, N=100) (Fig. 4F). Importantly, the directed evolution communities were more resistant to invasion, on average, than those found through enrichment screens, even though resistance to invasion was not directly selected for (R = 0.867±0.045 vs 0.793±0.087 and Mean(F*) =1261±190 vs 660±180 (Mean±SE), p<0.01 in both cases, two-sided paired t-test, N=100) (Fig. 4F). This indicates that the repeated migrations that are part of the protocol in the directed evolution experiment confer the selected communities with higher stability to this perturbation (though not necessarily to other perturbations, Supplementary Fig. 9). Our results also suggest that a simple screen may allow us to find a more ecologically stable (if also lower functioning) community than a synthetic consortium, at least when ecological stability is not engineered into the consortium.
DISCUSSION
Directed evolution can be used to iteratively optimize the function of microbial communities, through sequential rounds of exploration and selection. Previous approaches to engineer communities from the top-down include enrichment (which is often followed by a perturbation such as a bottleneck, to reduce community complexity) 20,22–24,28,81,82, and selective breeding by artificial selection 1,30–33,35–41. The directed evolution approach we have studied here combines components of both approaches: the iterative search that is inherent of the latter, with the idea of building stable consortia and exploring compositional variants of the former. In addition to inducing evolutionary changes in the resident species, the methods to generate compositional variants and explore the ecological structure-function landscape include many ecological perturbations that randomly sample new species in and out of the community. For instance, bottlenecking (also known as dilution-to-extinction 21,22,27,70,81,83) is a blunt method for randomly removing “deleterious” taxa, which has the cost of also eliminating potentially beneficial species. Horizontal immigration from the regional pool may create variants that contain new and potentially “beneficial” species, but it has the cost of potentially adding species with deleterious effects. A selection method that combines the two with strong selection is able to compensate for the specific weaknesses of each, leading us to high-function regions of the ecological structure-function landscape that were not reached by any of the two individual strategies alone (Fig. 4). These communities are also ecologically resistant to invasions compared to both enrichment and synthetic communities assembled by artificially mixing together species with high per-capita function.
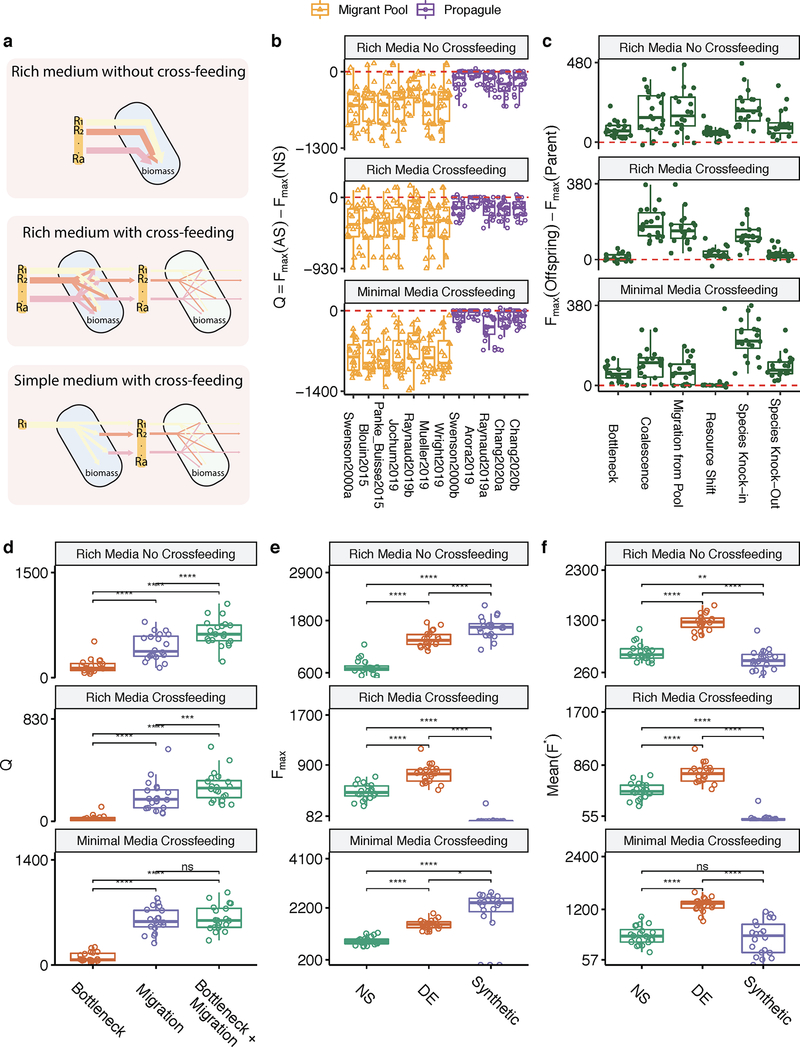
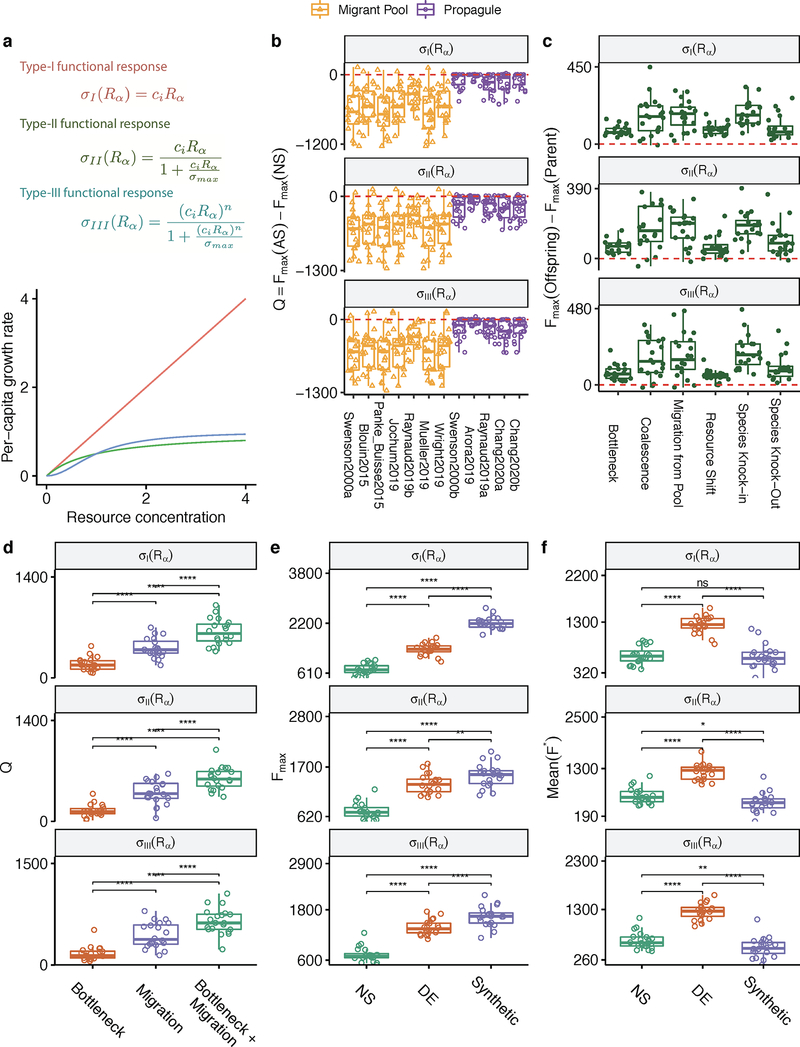
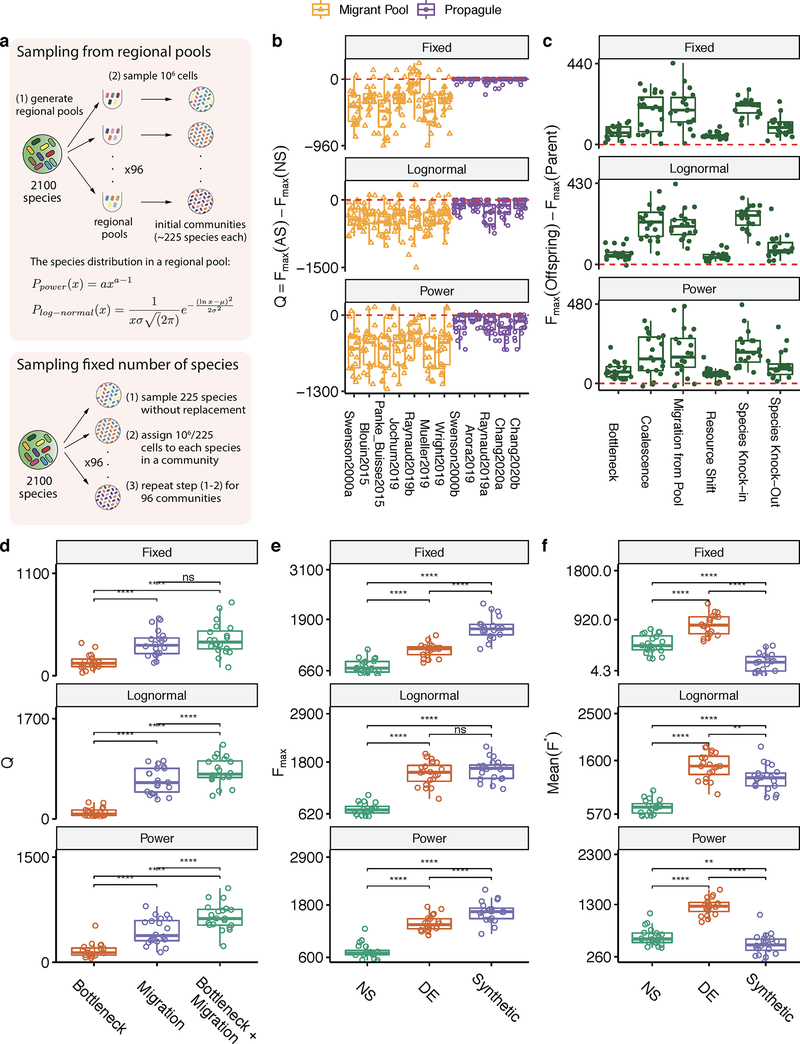
As is the case for any computational model, ours has simplifying assumptions and, therefore, limitations. We discuss them at length in the Supplementary Discussion. Perhaps the most notable one is that, for simplicity, we have focused on a function that is additive on the species contributions and which carries no cost at the individual level. We relax both these assumptions in the Supplementary Methods. We show that our main findings also hold when we work with non-additive functions, including those modeling realistic community objectives such as resisting invasion from an undesired organism or the elimination of a specific metabolite (Extended Data Fig. 1). In addition, our main results were found to hold true under alternative ecological scenarios, which include growth media of different richness and interactions ranging from pure nutrient competition to cross-feeding (Extended Data Fig. 2); alternative functional responses by the species in our communities (Extended Data Fig. 3); different methods of sampling taxa from the environment (Extended Data Fig. 4); and various distributions of per-capita species contributions to the community function: from highly redundant to rarefied (Extended Data Fig. 5). Finally, we also show that our results hold true when species contributions to the function under selection are not fitness neutral (Extended Data Fig. 1). Although many microbial functions, such as the secretion of metabolic byproducts and overflow metabolites do not incur any cost to their producer 84, many other functions are costly for the contributing cell 85.
On this note, it is important to note that our simulations do not include within-species evolution. It is thus possible that, on an evolutionary timescale, the directly evolved communities would be vulnerable to “cheater” mutants which forgo the cost of functional contributions in favour of faster growth, outcompeting their direct ancestors as would be predicated by social evolution theory 85. The timescale over which evolution would degrade community function is unknown, through recent community evolution experiments suggest that evolution is heavily constrained when species are embedded within a complex community 86. Furthermore, recent artificial community-level selection experiments suggest that one may be able to preserve a costly community function that may be prone to exploitation by cheaters (the expression of an extracellular enzyme) by continuously purging those communities where cheating phenotypes arise (i.e. purifying selection at the community-level)40.
It is important to highlight that the mechanisms we have considered here to generate variation between communities are all purely ecological, as we do not allow evolution within species. Taken as a unit, one can consider communities to be evolving: we are introducing heritable variation between them and then selecting upon that variation, and this results in changes in the genetic makeup of the communities (i.e. their metagenomes) as well as in their attributes 55,87. Explicitly incorporating within-species evolution into our framework (for example by allowing new mutants to arise within each growth cycle) represents an exciting future direction for this work and would allow us to explicitly explore the complex trade-offs between community function, ecological stability and evolutionary resilience. We hope that our results will not only clarify the limitations of previous approaches to artificially selecting communities, but also motivate the development of new empirical methods for the directed evolution of microbial communities.
METHODS
The ecoprospector package.
All the results presented in this paper are generated using ecoprospector, a new freely available Python package for implementing artificial selection of microbial communities using customisable protocols. The package builds off the recently published community-simulator package (which is a dependency of ecoprospector) 88 and implements protocols in a modular manner that allows an extremely large parameter space of possible protocols to be explored. The parameters for all simulations implemented in this paper are stored in csv files (Methods).
Microbial Consumer-Resource Simulations:
We model microbial community dynamics using the Microbial Consumer Resource Model (MiCRM) 56–59 (See Supplementary Methods). The MiCRM is a minimal model for microbial communities growing in well-mixed resource limited environments (such as in batch culture or in a chemostat). Briefly,the MiCRM models the change through time in i) the abundance of a set of consumer species denoted by Ni and ii) the concentration of a set of resources denoted by Rα. In the simulations presented in the main text of this paper consumer and resource dynamics can be described by the following sets of equations:
| (Eq.1) |
| (Eq. 2) |
In this version of the MiCRM ecological interactions between species arise from the uptake of resources to the environment and the dependence of resource import rate on resource concentration follows a Hill (type-III) function: where ciα is the uptake rate of species i for resource α, σmax is the maximum resource uptake rate and n is the hill coefficient for the functional response. For all simulations in the main text we have set σmax = 1 and n = 2. A more general version of this model can be found in the Supplementary Methods and the full list of parameters are in Supplementary Table 2. There we also show that our results are not limited to the simplification presented here but hold true for different functional responses (Extended Figs. 1–5).
Initial conditions:
All simulations are done considering a metacommunity made up of multiple independent communities each of which is simulated using the MiCRM. In order to set the consumer uptake rates across the metacommunity and the initial resource and species compositions of each community, we have adapted the method for constructing random ecosystems from community-simulator. The parameters associated with this and the values we used are outlined in Supplementary Table 3 (adapted and expanded from Marsland et al 2020) and Supplementary Table 4. Unless otherwise specified these values are set to the default values used in the community-simulator package. These parameters will be referenced throughout the rest of the methods section.
Uptake rates:
In our simulations of consumer-resource dynamics, species differ solely in the uptake rate for different resources ciα. All ciα are sampled from the same probability distribution. In community-simulator ciα can be sampled from one of three different distributions: i) a Gaussian distribution ii) a Gamma distribution, or iii) a Bernoulli distribution with binary preference levels set by c0 and c1 (referred to as the binary model). Denoting the total uptake capacity of species i by Ci = ∑α ciα, these distributions are parameterized in terms of mean and variance in total uptake rate: μc = <Ci> and σc2 = Var(Ci).
For our purposes none of these distributions were suitable because i) we wanted all ciα to be positive (unlike the gaussian distribution) ii) we wanted ciα of some resources to be 0 (unlike the gamma distribution) and iii) we wanted more than two possible values of ciα (unlike the binary model), To address these limitations, we introduced a new sampling method that combines the gamma distribution and the binary model. Under this approach ciα can be written as the product of X and Y, where X is sampled using the binary model and Y is sampled from a gamma distribution. The mean and variance of Y is constrained to values that ensure that mean and variance of Ci are still μc and σc2.
Specifically, under the binary model:
| (Eq.3) |
Where Z is sampled from the Bernoulli distribution with , where M is the total number of resources (Supplementary Table 3). Therefore
| (Eq.4) |
| (Eq.5) |
Because ciα = XY, to ensure that μc = <Ci> and σc2 = Var(Ci) we set:
| (Eq.6) |
| (Eq.7) |
Initial resource conditions
All communities within a metacommunity are grown on the same set of M = 90 resources. In order to generate an arbitrary ‘rich’ medium, the initial abundance of each resource () is obtained by first sampling it from a uniform distribution between 0 and 1 and then normalizing so that the total resource concentration is equal to Rtot = 1000. All communities within a metacommunity have the same for all α.
Initial consumer conditions.
Each simulation of a single metacommunity starts with H = 2100 possible species. Each of the 96 communities in a metacommunity is inoculated from a different regional species pool, by sampling ninoc cells from it. All species pools contain the same set of 2100 species but differ from each other in the distribution of species abundances (i.e., the ranks of species abundance differ across pools). As such, some taxa will be exceedingly rare in some species pools (and are therefore extremely unlikely to be sampled into that well during inoculation), while being common in others (making it more likely that they will be sampled in the wells inoculated from those). In practice this can be done experimentally by inoculating each well of a 96-well plate from a different environmental inoculum (i.e different aquatic and terrestrial communities from various natural and artificial sources: leaf litters, sewage, soil samples, or the built environment). We have shown in previous work that this strategy generates widely different starting communities at the species level 60, which exhibit sufficient functional variation to elicit a strong response to artificial community-level selection 40.
The abundance of each species i (where i ranges from 1–2100) in any one of the species pools (Ui) follows a power-law distribution with exponent a and probability density function:
| (Eq. 8) |
We use a power law distribution as natural microbial communities often follow power-law like abundance distributions 89. We set a to 0.01 as for our ninoc value this gives us communities at the start of our simulations with 225±12 (Mean±SD, for 96 communities) species, which is comparable to previous work (i.e 110–1290 ESVs in 60). In addition the rarefaction curves for our initial communities are qualitatively similar to rarefaction curves obtained from experimental studies (Supplementary Fig. 11). We have also confirmed that our results are robust to alternative methods for seeding the initial metacommunity (Supplementary Methods, Extended Fig. 4). Cell counts are converted into initial species abundances Ni through a conversion factor ψ which we set at 106. This means that a value of ninoc = 106 cells is equivalent to a total abundance Ninoc = 1 (arbitrary units) in the initial inoculum. Because each community is inoculated from a different species pool (each with its own abundance distribution), the abundance of each of the H species differs across communities ensuring that our simulations start with compositional and functional variability (Fig. 2B).
Incubation.
Once the initial resource and consumer abundance has been set and the MiCRM parameters have been sampled a single community-level ‘generation’ is simulated by propagating the system forward for an incubation time t via numerical integration of dynamical equations (Eq. 1–2). During a batch incubation, resources are depleted (and not replenished) as the consumers increase in density. At the end of each batch incubation at time t the function of each community in the metacommunity is quantified (see following section) and the communities are ranked in terms of their function.
Serial Passaging.
During a single batch incubation, resources are depleted (but not replenished) as consumers grow on them. We do not impose any mortality within each batch period, consistent with recent empirical findings 60, and neither species nor resources are externally removed or supplied during an incubation period (as they would, for instance, in a chemostat). The batches are incubated for a period of time t, which, consistent with experimental practice, does not necessarily correspond to the time required to deplete all of the supplied nutrients. Rather, the length of the incubation time is a free parameter in our simulations, and it can be altered to improve the outcome of artificial selection, reflecting empirical practice 37. Within each batch period the community undergoes an ecological succession which is truncated at time t. With exception of the limit case when t goes to infinity and all resources are depleted (so growth stops), the species and resources do not reach a fixed stable equilibrium or climax within a batch. Nonetheless, when communities are subject to multiple rounds of passaging and incubation communities do converge to a batch or ‘generational’ equilibrium characterized by repeatable community dynamics following each round of dilution (Supplementary Fig. 3). We refer to this repeatable ecological succession as “generational stability” as it reflects convergence of communities to an identical composition at equivalent time-point within a batch (i.e. a community generation), without them being a climax community.
Community function.
The function F of each community is measured at the end of each generation In principle, any arbitrary community function can be chosen as the “phenotype” under selection. For example, one could consider the total biomass of the community, the species richness of the community, the distance of the abiotic environment from some target state, the resistance to invasion etc. In the main text of this paper, we have limited our analysis to a simple additive case:
| (Eq. 9) |
where ϕi is the per-capita contribution of species i and Ni is its population size. We sampled ϕi from a normal distribution of mean 0 and standard deviation σ = 1 so species can have both positive and negative effects on the function of interest. An example of a function that may be modeled in this manner is the production of vitamin B12 by the gut microbiome, which often benefits the host animal 90,91. Some species in the microbiome produce this vitamin, whereas others are known to degrade or uptake those beneficial molecules, competing with the host.
The choice of this sampling distribution for ϕi does not qualitatively impact our findings. For instance, in Extended Data Fig. 5 we repeat all of our simulations for other sampling methods where all ϕi are ≥ 0. These could correspond to other biologically realistic additive functions such as the total biomass of the community 38, the amount of light scattered on a specific wavelength 53, or the amount of an enzyme secreted into the environment 10. As we show on Extended Fig. 5, using this and other sampling distributions does not alter our findings in any significant manner. For each independent metacommunity simulation we sampled ϕi at the start of the experiment and then held the values constant (i.e. species were not “evolving” their ϕi trait).
Selection matrix.
After the function of each community has been measured, the ‘parental’ communities are ‘passaged’ to produce a new set of ‘offspring’ communities. The metacommunity size is kept constant (so the number of offspring communities is equal to the number of parent communities). Passaging simulates the pipetting of bacterial culture into wells containing fresh media (such as from one 96-well plate into another). Which parental communities are selected to contribute species to each offspring community depends on its ranked function. This is specified by a selection matrix S whose element Suv determines the fraction of cells from the parental community of rank function v that are used to inoculate offspring community u (Supplementary Fig. 1).
In principle any arbitrary fraction of a parent community of rank v can be transferred to offspring community u. For the simulations presented in this paper we have set a standard dilution factor d and all non-zero elements of the S matrix are set to 1/d. Note that the selection matrix S is similar to the transfer matrix f used in the community-simulator package 88 except the indices of the parent community are based on the ranked function of the community rather than being positional.
We also note that whilst for most protocols rank function is determined across the entire metacommunity, for a few simulations we carried out here we used block designs. In these cases a metacommunity is divided into multiple sub-metacommunities (sublines) and the rank function is quantified within each sub-metacommunity. The rank function within each sub-metacommunity is then used to determine which parents are selected. For these cases the selection matrix is divided into blocks along the v axis with each sub-metacommunity being allocated one block. Communities are then sorted by rank along the v axis within each block. See 35,39 in Supplementary Table 1 for examples.
Passaging:
The passaging algorithm considers the transfer of both resources and species. Resource concentrations Rα are treated as continuous, and we assume they are transferred without any noise. Let be the concentration of resource α (ranging from 1–90) in offspring community at position u (ranging from 1–96) and be the concentration of resource α in parent community with rank v (ranging from 1–96). We can then write
| (Eq. 10) |
Where (the initial resource condition), denotes the amount of Rα in the freshly supplied medium. The term captures the resources that are passed from either one or multiple parent communities (depending on the selection matrix S) to the offspring community.
Species abundances Ni are treated as discrete in order to incorporate demographic noise. Let be the abundance of species i in offspring community u and be the abundance of species i in parent community with rank v. The total number of cells of all species (z) that are passaged from parent community with rank v to offspring community u is distributed according to a Poisson distribution:
| (Eq. 11) |
Note that ψ is the conversion factor that determines the amounts of cells equivalent to Ni = 1, in this case ψ=106. The species identity of each cell transferred to community u is then determined by multinomial sampling with the probability of any one cell belonging to species i being equal to the relative abundance of species i in the parent community (). This procedure is repeated for every pair of parent (v) and offspring community (u). After this has been completed, the total number of cells of each species transferred to each offspring community is converted back into abundances () using the conversion factor ψ.
Aside from the introduction of Poisson sampling for the total cell number, this procedure is identical to the one used in the community-simulator package. Poisson sampling accounts for variability in total number of cells transferred after each generation, an important source of error (compositional variation) in the batch culture lab experiments we are modelling here.
Random seed.
A single random seed is used to uniquely determine the initial abundance condition of metacommunity, the species features ciα and ϕi, and resource composition in the medium Rα0. Whilst each community in the metacommunity will have different initial species abundances, each random seed is associated with a unique set of initial species abundances across the entire metacommunity. As well as ensuring that our results are reproducible, this allows us to carry out different protocols on identical sets of starting communities. For this reason most statistical comparisons in this paper are paired, reflecting the fact that the results are non-independent when different protocols are tested using the same random seed. All simulations throughout the main text were run for 100 unique seeds and those in the Extended Figs. 1–5 were run for 20 unique seeds.
Directed evolution.
After seeding the metacommunity, we allow all 96 communities to stabilize by propagating them for 20 transfers without selection (using S=(1/d)I, as we do in the no-selection control). Then the highest functioning community is selected and passaged into 96 fresh habitats with a dilution factor of d=103× (the same one that had been used during the 20 previous transfers). One of these new communities is left unperturbed. The other 95 copies are all perturbed as described below in an attempt to push the community to a new stable state. After the perturbation, all communities, including the unperturbed community, are grown for 20 generations without selection (S=(1/d)I) to let them reach a stable state.
In Figures 2D–I, we consider six different types of perturbation and their magnitudes that are applied to the 95 copies of the top-performing community (Supplementary Table 5):
Bottleneck perturbation. This approach involves subjecting the 95 communities to an additional dilution step. This is done by repeating the passaging protocol described previously using S=(1/dbot)I where dbot is the bottleneck dilution factor. For figures 2B and 2D the dbot=105. An average of N=9.76±3.12 (Mean±SD) cells remain in the community after a bottleneck of this magnitude. In figure 2C we carried out this procedure multiple independent times using a gradient of bottleneck dilution factors (ranging from dbot=10, to dbot=8×105).
Species knock-in. This approach involves introducing a different high-functioning species from the regional pool into each of the 95 communities. A collection of candidate high-performing species is first prepared by growing every single species from the regional pool in monoculture, passaging them in the same batch condition as the communities for 20 serial transfers, and then identifying the top 5% of species (threshold percentile θ=0.95) according to their rank function. This gives us a collection of 105 candidate species from the pool of H = 2100. We then invaded each of the 95 communities with a different randomly chosen candidate from this set. This is done by introducing 103 cells of the chosen species into each community after they have been diluted. 103 is chosen to minimize the probability of stochastic extinction of the invader.
Knock out. This approach involves eliminating one of the species in the community, so that all offspring communities have n-1 species (whereas the parent had n). In each community we delete a different taxa. When n <95 (as is the case for our simulations) the number of perturbed offspring communities is equal to n. The 95-n ‘spare’ communities are left unperturbed.
Migration. This approach involves perturbing the communities by invading with them a random set of species sampled from different regional pools. We use the same approach that we used to initially inoculate the communities. To recap, for each community we added nmig=106 cells randomly sampled from different regional species pools, in which the species abundances are distributed according to Eq. 5. The number of cells introduced via migration is comparable to the number of cells in the communities after the regular batch dilution (~106)
- Coalescence. This approach involves coalescencing the copies of top-performing communities with the other stable communities in the metacommunity before selection. To do this, the parents metacommunity is not discarded at the point of directed evolution. Instead, it is kept and the offspring metacommunity is grown for a single generation (so that both the parent and offspring metacommunities are in stationary phase). The two metacommunities are then mixed, generating a new metacommunity of coalesced communities. Let J be the resource and consumer abundance of the offspring metacommunity and K be the resource and consumer abundance of the parent metacommunity. The consumer and resource abundance of the mixed metacommunity L is simply:
For our simulations we use a fcoa = 0.5, equivalent to mixing equal volumes. To inoculate into the offspring community, the coalesced communities are then diluted with a dilution factor d=103× (using S = I/d).(Eq. 12) Resource shift. This approach involves introducing a different random change to the ‘media’ (Rα0) of each of the 95 communities. We have a complex media of M=90 Resources. We first select the most abundant resource in the media and reduce its abundance by δR1. This amount of resource is then added to one of the other 89 resources chosen at random. For our simulations we set δ = 1. Unlike other perturbations mentioned above that only happen in the short term (pulse perturbation), the changes in nutrient composition is permanent and persists for the rest of the simulation (press perturbation) 80.
Note that whether a type of perturbation performs better than others depends on its magnitude (e.q., dilution factor in bottleneck, or amount of resource being shifted), which we have not systematically explored except for the bottleneck (Figure 2B). We chose the parameter values so that the effect sizes shown in Figures 2D–I all have a similar magnitude, but quantitative comparisons among them should be avoided.
Code Availability.
All simulations were conducted in python using ecoprospector (https://github.com/Chang-Yu-Chang/ecoprospector). All the data analysis was conducted in R. The complete code used for this paper including the ecoprospector package can be found in the Zenodo repository (https://doi.org/10.5281/zenodo.4608427).
Data Availability.
All data generated and analyzed in this paper can be found at https://doi.org/10.5281/zenodo.4608427
Extended Data
Extended Data Figure 1. Non-additive function, costly function, and two empirically motivated functions.
(A) Illustration of the different types of community function we have considered. In addition to the additive function used in the main text we have simulated four other community functions: a non-additive pairwise function, a costly function, a function that maximises the consumption of a target resource, and a function that maximizes resistance to an invader. Panels B-F reproduce the main results reported in Figures 1–4. (B) Difference in Fmax between the artificial selection line (AS) and no-selection line (NS) for all previously published protocols, corresponding to Fig. 1F. (C) Difference in Fmax between parent (before directed evolution) and offspring (after directed evolution) for the 6 types of perturbation considered in figure 2, this plot aggregates the results shown in Fig. 2D–I. (D) Reproduction of Fig. 3E, to show that iteratively combining migrations and bottlenecks does better than either alone. Q is obtained from each of the three iterative protocols at generation 460 (E) Reproduction of Fig. 4E, where we compare Fmax of the no-selection (NS), directed evolution (DE), and synthetic communities; (F) Mean function (F*) of the DE, NS and Synthetic communities following an ecological perturbation (migration). This corresponds to the y-axis of Fig. 4F.
Extended Data Figure 2. Alternative ecological scenarios with metabolic cross-feeding.
Besides the rich medium without cross-feeding shown in the main text, we have included two other ecological scenarios: i) rich medium with cross-feeding and ii) simple minimal medium with cross-feeding. The layout of (B-F) follows Extended Data Fig. 1B–F, reproducing the main results from Fig. 1–4.
Extended Data Figure 3. Functional responses.
The resource import rate depends on its concentration in the environments, which can take a linear (type I), Monod (type II), or Hill (type III) form. A Type-III functional response is used in the simulation presented in the main text. The layout of (B-F) follows Extended Data Fig. 1B–F, reproducing the main results from Fig. 1–4.
Extended Data Figure 4. Alternative Metacommunity sampling approaches.
We simulate three metacommunity sampling approaches: i) Each community is seeded with 106 cells drawn from a different regional pool, where the species abundances in each regional pool are drawn from a power-law distribution with a = 0.01, ii) Each community is seeded with 106 cells drawn from a different regional, where the species abundances in each regional pool are drawn from a log-normal distribution with mean μ = 8 and standard deviation σ = 8, iii) Each community is seeded with a randomly chosen set of 225 species and they are all set to have the same initial abundance. The simulation in the main text adopts the power-law distribution approach. The layout of (B-F) follows Extended Data Fig. 1B–F, reproducing the main results from Fig. 1–4.
Extended Data Figure 5. Different distributions of per capita species contribution to additive community function.
Per capita species contribution drawn from i) normal distribution centered around 0 with standard deviation sd=1, ii) normal distribution with mean=11 and sd=1, iii) uniform distribution ranged from min=0 to max=1, iiii) a sparse additive function where 20% of the species contribute to community function.In the main text, per capita species contribution uses normal distribution with mean=0 and sd=1. The layout of (B-F) follows Extended Data Fig. 1B–F, reproducing the main results from Fig. 1–4.
Supplementary Material
ACKNOWLEDGMENTS:
The authors wish to thank Hernan Garcia and Rob Phillips for inviting most of us, either as instructors or as students, to the Physical Biology of the Cell summer course a the Marine Biology Laboratory in Woods Hole, MA, where this project was started and the first version of the ecoprospector package was coded. We also wish to thank Brian Von Herzen for his input and discussion while we were at MBL. This work was supported by the National Institutes of Health through grant 1R35 GM133467-01, and by a Packard Foundation Fellowship to AS. C-YC was supported by a graduate fellowship Government Scholarship to Study Abroad by the Government of Taiwan. MR-G was supported by a Gaylord Donnelley postdoctoral fellowship through the Yale Institute for Biospheric Studies.
Footnotes
COMPETING INTERESTS. The authors declare no competing interests
REFERENCES
- 1.Mueller UG & Sachs JL Engineering Microbiomes to Improve Plant and Animal Health. Trends Microbiol 23, 606–617 (2015). [DOI] [PubMed] [Google Scholar]
- 2.Gilbert ES, Walker AW & Keasling JD A constructed microbial consortium for biodegradation of the organophosphorus insecticide parathion. Appl. Microbiol. Biotechnol 61, 77–81 (2003). [DOI] [PubMed] [Google Scholar]
- 3.Yoshida S, Ogawa N, Fujii T & Tsushima S Enhanced biofilm formation and 3-chlorobenzoate degrading activity by the bacterial consortium of Burkholderia sp. NK8 and Pseudomonas aeruginosa PAO1. J. Appl. Microbiol 106, 790–800 (2009). [DOI] [PubMed] [Google Scholar]
- 4.Piccardi P, Vessman B & Mitri S Toxicity drives facilitation between 4 bacterial species. Proc. Natl. Acad. Sci. U. S. A 116, 15979–15984 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Herrera Paredes S et al. Design of synthetic bacterial communities for predictable plant phenotypes. PLoS Biol 16, e2003962 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Minty JJ et al. Design and characterization of synthetic fungal-bacterial consortia for direct production of isobutanol from cellulosic biomass. Proc. Natl. Acad. Sci. U. S. A 110, 14592–14597 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Jiang Y, Dong W, Xin F & Jiang M Designing Synthetic Microbial Consortia for Biofuel Production. Trends Biotechnol 0, (2020). [DOI] [PubMed] [Google Scholar]
- 8.Eng A & Borenstein E Microbial community design: methods, applications, and opportunities. Curr. Opin. Biotechnol 58, 117–128 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fredrickson JK ECOLOGY. Ecological communities by design. Science 348, 1425–1427 (2015). [DOI] [PubMed] [Google Scholar]
- 10.Sanchez-Gorostiaga A, Bajić D, Osborne ML, Poyatos JF & Sanchez A High-order interactions distort the functional landscape of microbial consortia. PLoS Biol 17, e3000550 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Senay Y, John G, Knutie SA & Brandon Ogbunugafor C Deconstructing higher-order interactions in the microbiota: A theoretical examination. bioRxiv 647156 (2019) doi: 10.1101/647156. [DOI] [Google Scholar]
- 12.Gould AL et al. Microbiome interactions shape host fitness. Proc. Natl. Acad. Sci. U. S. A 115, E11951–E11960 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mickalide H & Kuehn S Higher-Order Interaction between Species Inhibits Bacterial Invasion of a Phototroph-Predator Microbial Community. Cell Syst 9, 521–533.e10 (2019). [DOI] [PubMed] [Google Scholar]
- 14.Sanchez A Defining Higher-Order Interactions in Synthetic Ecology: Lessons from Physics and Quantitative Genetics. Cell systems vol. 9 519–520 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Guo X & Boedicker JQ The Contribution of High-Order Metabolic Interactions to the Global Activity of a Four-Species Microbial Community. PLoS Comput. Biol 12, e1005079 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sundarraman D et al. Higher-Order Interactions Dampen Pairwise Competition in the Zebrafish Gut Microbiome. MBio 11, (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Goldman RP & Brown SP Making sense of microbial consortia using ecology and evolution. Trends Biotechnol vol. 27 3–4, author reply 4 (2009). [DOI] [PubMed] [Google Scholar]
- 18.Brenner K, You L & Arnold FH Response to Goldman and Brown: Making sense of microbial consortia using ecology and evolution. Trends Biotechnol 27, 4 (2009). [DOI] [PubMed] [Google Scholar]
- 19.Escalante AE, Rebolleda-Gómez M, Benítez M & Travisano M Ecological perspectives on synthetic biology: insights from microbial population biology. Front. Microbiol 6, 143 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gilmore SP et al. Top-Down Enrichment Guides in Formation of Synthetic Microbial Consortia for Biomass Degradation. ACS Synth. Biol 8, 2174–2185 (2019). [DOI] [PubMed] [Google Scholar]
- 21.Cortes-Tolalpa L, Jiménez DJ, de Lima Brossi MJ, Salles JF & van Elsas JD Different inocula produce distinctive microbial consortia with similar lignocellulose degradation capacity. Appl. Microbiol. Biotechnol (2016) doi: 10.1007/s00253-016-7516-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lee D-J, Show K-Y & Wang A Unconventional approaches to isolation and enrichment of functional microbial consortium--a review. Bioresour. Technol 136, 697–706 (2013). [DOI] [PubMed] [Google Scholar]
- 23.Lazuka A, Auer L, O’Donohue M & Hernandez-Raquet G Anaerobic lignocellulolytic microbial consortium derived from termite gut: enrichment, lignocellulose degradation and community dynamics. Biotechnol. Biofuels 11, 284 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Puentes-Téllez PE & Falcao Salles J Construction of Effective Minimal Active Microbial Consortia for Lignocellulose Degradation. Microb. Ecol 76, 419–429 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.He X, McLean JS, Guo L, Lux R & Shi W The social structure of microbial community involved in colonization resistance. ISME J 8, 564–574 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jung J, Philippot L & Park W Metagenomic and functional analyses of the consequences of reduction of bacterial diversity on soil functions and bioremediation in diesel-contaminated microcosms. Sci. Rep 6, 23012 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Franklin RB & Mills AL Structural and functional responses of a sewage microbial community to dilution-induced reductions in diversity. Microb. Ecol 52, 280–288 (2006). [DOI] [PubMed] [Google Scholar]
- 28.Kang D et al. Enrichment and characterization of an environmental microbial consortium displaying efficient keratinolytic activity. Bioresour. Technol 270, 303–310 (2018). [DOI] [PubMed] [Google Scholar]
- 29.Goodnight CJ Evolution in metacommunities. Philos. Trans. R. Soc. Lond. B Biol. Sci 366, 1401–1409 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Swenson W, Wilson DS & Elias R Artificial ecosystem selection. Proc. Natl. Acad. Sci. U. S. A 97, 9110–9114 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Jochum MD, McWilliams KL, Pierson EA & Jo Y-K Host-mediated microbiome engineering (HMME) of drought tolerance in the wheat rhizosphere. PLoS One 14, e0225933 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mueller UG et al. Artificial Microbiome-Selection to Engineer Microbiomes That Confer Salt-Tolerance to Plants. bioRxiv 081521 (2016) doi: 10.1101/081521. [DOI] [Google Scholar]
- 33.Panke-Buisse K, Poole AC, Goodrich JK, Ley RE & Kao-Kniffin J Selection on soil microbiomes reveals reproducible impacts on plant function. ISME J 9, 980–989 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Panke-Buisse K, Lee S & Kao-Kniffin J Cultivated Sub-Populations of Soil Microbiomes Retain Early Flowering Plant Trait. Microb. Ecol (2016) doi: 10.1007/s00248-016-0846-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Arora J, Mars Brisbin MA & Mikheyev AS Effects of microbial evolution dominate those of experimental host-mediated indirect selection. PeerJ 8, e9350 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Swenson W, Arendt J & Wilson DS Artificial selection of microbial ecosystems for 3-chloroaniline biodegradation. Environ. Microbiol 2, 564–571 (2000). [DOI] [PubMed] [Google Scholar]
- 37.Wright RJ, Gibson MI & Christie-Oleza JA Understanding microbial community dynamics to improve optimal microbiome selection. Microbiome 7, 85 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Blouin M, Karimi B, Mathieu J & Lerch TZ Levels and limits in artificial selection of communities. Ecol. Lett 18, 1040–1048 (2015). [DOI] [PubMed] [Google Scholar]
- 39.Raynaud T, Devers M, Spor A & Blouin M Effect of the Reproduction Method in an Artificial Selection Experiment at the Community Level. Frontiers in Ecology and Evolution 7, 416 (2019). [Google Scholar]
- 40.Chang C-Y, Osborne ML, Bajic D & Sanchez A Artificially selecting bacterial communities using propagule strategies. Evolution (2020) doi: 10.1111/evo.14092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Arias-Sánchez FI, Vessman B & Mitri S Artificially selecting microbial communities: If we can breed dogs, why not microbiomes? PLoS Biol. 17, e3000356 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Day MD, Beck D & Foster JA Microbial Communities as Experimental Units. Bioscience 61, 398–406 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Wade MJ Group selections among laboratory populations of Tribolium. Proc. Natl. Acad. Sci. U. S. A 73, 4604–4607 (1976). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wade MJ An experimental study of group selection. Evolution 31, 134–153 (1977). [DOI] [PubMed] [Google Scholar]
- 45.Wade MJ A Critical Review of the Models of Group Selection. Q. Rev. Biol 53, 101–114 (1978). [Google Scholar]
- 46.Goodnight CJ Experimental Studies of Community Evolution I: The Response to Selection at the Community Level. Evolution 44, 1614–1624 (1990). [DOI] [PubMed] [Google Scholar]
- 47.Guo X & Boedicker J High-Order Interactions between Species Strongly Influence the Activity of Microbial Communities. Biophys. J 110, 143a (2016). [Google Scholar]
- 48.Stein RR et al. Computer-guided design of optimal microbial consortia for immune system modulation. Elife 7, (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Arnold FH Innovation by Evolution: Bringing New Chemistry to Life (Nobel Lecture). Angew. Chem. Int. Ed Engl 58, 14420–14426 (2019). [DOI] [PubMed] [Google Scholar]
- 50.Tracewell CA & Arnold FH Directed enzyme evolution: climbing fitness peaks one amino acid at a time. Curr. Opin. Chem. Biol 13, 3–9 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Williams HTP & Lenton TM Artificial selection of simulated microbial ecosystems. Proc. Natl. Acad. Sci. U. S. A 104, 8918–8923 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Williams HTP & Lenton TM Artificial Ecosystem Selection for Evolutionary Optimisation. in Advances in Artificial Life 93–102 (Springer Berlin Heidelberg, 2007). [Google Scholar]
- 53.Doulcier G, Lambert A, De Monte S & Rainey PB Eco-evolutionary dynamics of nested Darwinian populations and the emergence of community-level heredity. Elife 53433 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Xie L, Yuan AE & Shou W Simulations reveal challenges to artificial community selection and possible strategies for success. PLoS Biol 17, e3000295 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Wilson DS Complex Interactions in Metacommunities, with Implications for Biodiversity and Higher Levels of Selection. Ecology 73, 1984–2000 (1992). [Google Scholar]
- 56.Marsland R 3rd et al. Available energy fluxes drive a transition in the diversity, stability, and functional structure of microbial communities. PLoS Comput. Biol 15, e1006793 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Marsland R, Cui W, Goldford J & Mehta P The Community Simulator: A Python package for microbial ecology. bioRxiv 613836 (2019) doi: 10.1101/613836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Marsland R, Cui W & Mehta P A minimal model for microbial biodiversity can reproduce experimentally observed ecological patterns. bioRxiv 622829 (2019) doi: 10.1101/622829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Advani M, Bunin G & Mehta P Statistical physics of community ecology: a cavity solution to MacArthur’s consumer resource model. J. Stat. Mech 2018, 033406 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Goldford JE et al. Emergent simplicity in microbial community assembly. Science 361, 469–474 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Lu N, Sanchez-Gorostiaga A, Tikhonov M & Sanchez A Cohesiveness in microbial community coalescence. bioRxiv 282723 (2018) doi: 10.1101/282723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Faith JJ, Ahern PP, Ridaura VK, Cheng J & Gordon JI Identifying gut microbe-host phenotype relationships using combinatorial communities in gnotobiotic mice. Sci. Transl. Med 6, 220ra11 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Estrela S et al. Metabolic rules of microbial community assembly. bioRxiv 2020.03.09.984278 (2020) doi: 10.1101/2020.03.09.984278. [DOI] [Google Scholar]
- 64.Friedman J, Higgins LM & Gore J Community structure follows simple assembly rules in microbial microcosms. Nat Ecol Evol 1, 109 (2017). [DOI] [PubMed] [Google Scholar]
- 65.Venturelli OS et al. Deciphering microbial interactions in synthetic human gut microbiome communities. Mol. Syst. Biol 14, e8157 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Hall BG Experimental evolution of a new enzymatic function. II. Evolution of multiple functions for ebg enzyme in E. coli. Genetics 89, 453–465 (1978). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Smith GP & Petrenko VA Phage Display. Chem. Rev 97, 391–410 (1997). [DOI] [PubMed] [Google Scholar]
- 68.Bloom JD & Arnold FH In the light of directed evolution: pathways of adaptive protein evolution. Proc. Natl. Acad. Sci. U. S. A 106 Suppl 1, 9995–10000 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Romero PA, Krause A & Arnold FH Navigating the protein fitness landscape with Gaussian processes. Proc. Natl. Acad. Sci. U. S. A 110, E193–201 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Ho K-L, Lee D-J, Su A & Chang J-S Biohydrogen from cellulosic feedstock: Dilution-to-stimulation approach. Int. J. Hydrogen Energy 37, 15582–15587 (2012). [Google Scholar]
- 71.Shepherd ES, DeLoache WC, Pruss KM, Whitaker WR & Sonnenburg JL An exclusive metabolic niche enables strain engraftment in the gut microbiota. Nature 557, 434–438 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Ting S-Y et al. Targeted Depletion of Bacteria from Mixed Populations by Programmable Adhesion with Antagonistic Competitor Cells. Cell Host Microbe (2020) doi: 10.1016/j.chom.2020.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Sheth RU, Cabral V, Chen SP & Wang HH Manipulating Bacterial Communities by in situ Microbiome Engineering. Trends Genet 32, 189–200 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Lemon KP, Armitage GC, Relman DA & Fischbach MA Microbiota-targeted therapies: an ecological perspective. Sci. Transl. Med 4, 137rv5 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Harcombe WR & Bull JJ Impact of phages on two-species bacterial communities. Appl. Environ. Microbiol 71, 5254–5259 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Chan BK et al. Phage treatment of an aortic graft infected with Pseudomonas aeruginosa. Evol Med Public Health 2018, 60–66 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Rillig MC, Tsang A & Roy J Microbial Community Coalescence for Microbiome Engineering. Front. Microbiol 7, 1967 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Sierocinski P et al. A Single Community Dominates Structure and Function of a Mixture of Multiple Methanogenic Communities. Curr. Biol 27, 3390–3395.e4 (2017). [DOI] [PubMed] [Google Scholar]
- 79.Tilman D The ecological consequences of changes in biodiversity: A search for general principles. Ecology 80, 1455–1474 (1999). [Google Scholar]
- 80.Shade A et al. Fundamentals of microbial community resistance and resilience. Front. Microbiol 3, 417 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Kang D et al. Construction of Simplified Microbial Consortia to Degrade Recalcitrant Materials Based on Enrichment and Dilution-to-Extinction Cultures. Front. Microbiol 10, 3010 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Zanaroli G et al. Characterization of two diesel fuel degrading microbial consortia enriched from a non acclimated, complex source of microorganisms. Microb. Cell Fact 9, 10 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Peter H et al. Function-specific response to depletion of microbial diversity. ISME J 5, 351–361 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Pacheco AR, Moel M & Segrè D Costless metabolic secretions as drivers of interspecies interactions in microbial ecosystems. Nat. Commun 10, 103 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.West SA, Griffin AS, Gardner A & Diggle SP Social evolution theory for microorganisms. Nat. Rev. Microbiol 4, 597–607 (2006). [DOI] [PubMed] [Google Scholar]
- 86.Scheuerl T et al. Bacterial adaptation is constrained in complex communities. Nat. Commun 11, 754 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Lewontin RC The Units of Selection. Annu. Rev. Ecol. Syst 1, 1–18 (1970). [Google Scholar]
- 88.Marsland R, Cui W, Goldford J & Mehta P The Community Simulator: A Python package for microbial ecology. PLoS One 15, e0230430 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Shoemaker WR, Locey KJ & Lennon JT A macroecological theory of microbial biodiversity. Nat Ecol Evol 1, 107 (2017). [DOI] [PubMed] [Google Scholar]
- 90.Degnan PH, Taga ME & Goodman AL Vitamin B12 as a modulator of gut microbial ecology. Cell Metab 20, 769–778 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Degnan PH, Barry NA, Mok KC, Taga ME & Goodman AL Human gut microbes use multiple transporters to distinguish vitamin B₁₂ analogs and compete in the gut. Cell Host Microbe 15, 47–57 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data generated and analyzed in this paper can be found at https://doi.org/10.5281/zenodo.4608427