A theoretical approach for the acylation/deacylation mechanisms of avibactam in the reversible inhibition of KPC-2

Abstract

Klebsiella pneumoniae carbapenemase (KPC-2) is the most commonly encountered class A β-lactamase variant worldwide, which confer high-level resistance to most available antibiotics. In this article we address the issue by a combined approach involving molecular dynamics simulations and hybrid quantum mechanics/molecular mechanics calculations. The study contributes to improve the understanding, at molecular level, of the acylation and deacylation stages of avibactam involved in the inhibition of KPC-2. The results show that both mechanisms, acylation and deacylation, the reaction occur via the formation of a tetrahedral intermediate. The formation of this intermediate corresponds to the rate limiting stage. The activation barriers are 19.5 kcal/mol and 23.0 kcal/mol for the acylation and deacylation stages, respectively. The associated rate constants calculated, using the Eyring equation, are 1.2 × 10⁻¹ and 3.9 × 10⁻⁴ (s⁻¹). These values allow estimating a value of 3.3 × 10⁻³ for the inhibition constant, in good agreement with the experimental value.

Supplementary Information

The online version contains supplementary material available at 10.1007/s10822-021-00408-3.

Introduction

The World Health Organization (WHO) [1–4] has warned about the absence of novel antibiotics to fight the propagation of drug resistant bacteria, which kill tens of thousands of people/year. Two reports reveal that there are few new effective antibiotics in development, meaning that the world has very few options to fight the so-called superbacteria. Antibiotic resistance appears when bacteria become immune to existing drugs, entailing that minor wounds and common infections become potentially deadly.

Antibiotics, discovered in the 1920s, have saved millions of lives by overcoming bacterial diseases such as pneumonia, tuberculosis and meningitis. However the continuous use of these drugs over the decades, have allowed bacteria to develop resistance to the same drugs that once reliably defeated them turning into so-called superbugs [5–8].

To face the bacteria's ability to become resistant to known drugs, a steady production of new antibiotics is required, but for pharmaceutical companies the development of new products is limited by cost reasons mainly, usually they are prescribed for just few days or weeks, in contrast to medicines for chronic diseases like diabetes or rheumatoid arthritis.

The ongoing COVID-19 pandemic stresses the critical need for rapid development of vaccines and antiviral treatments to reduce the number of hospitalizations and deaths caused by this dangerous new coronavirus, SARS-CoV-2. The laboratories have responded quickly and at least about four vaccines are already in use. But there exist an even higher threat behind the current outbreak, one that is already killing thousands of people around the world and that complicate the care of many COVID-19 patients. It is the hidden threat from antibiotic resistance—bacteria that are not killed by standard antibiotics. The patients at greatest risk from superbugs are the ones who are already more vulnerable to illness from viral lung infections like influenza, severe acute respiratory syndrome (SARS), and COVID-19. The year 2009 influenza H1N1 pandemic, for example, killed about 300,000 people around the world. Many of those deaths—between 29 and 55%—were actually caused by secondary infections.

The production of class A β-lactamases belonging to the Klebsiella pneumoniae carbapenemase (KPC) kind is responsible for the resistance to carbapenems. Avibactam [9–11], Figure S4 of Supplementary information, is a diazobicyclooctanone β-lactamase inhibitor which in conjunction with ceftazidime deliver effective protection against strains producing serine carbapenemases, including KPC- and OXA-type enzymes. In this study we address the acylation and deacylation stages of avibactam with KPC-2 from a theoretical point view, by molecular dynamic (MD) simulations, along with hybrid quantum mechanics/molecular mechanics (QM/MM) calculations.

Methodology

The methodology used is the same of previous studies [12–15]; namely, the crystal structure of KPC-2 in complex with avibactam determined at 1.80 Å (PDB code 4ZBE) [11] was taken as the initial structure. All ionizable residues were set to the states corresponding to pH 7.0 using PROPKA 3.0, and all crystalline waters were included [16]. A cubic box of dimensions (90 × 80 × 90) ų of water molecules was used for the system. The box was centered in the enzyme-inhibitor complex. The system contains a total of 49,352 atoms, of which 45,396 atoms correspond to water molecules, and the difference corresponds to the protein, avibactam, and ion atoms.

The molecular dynamics simulations were accomplished with the NAMD [17] program using the CHARMM36 [18] force field and the TIP3P [19] water model. The simulations were carried without constraints using the NPT ensemble with a time step of 2 fs, and periodic boundary conditions were applied. The NAMD Nosé–Hoover implementations were used to maintain the temperature and pressure (1 atm) [20]. Long-range electrostatic effects were taken into account by the particle mesh Ewald summation method [21], whereas short-range interactions were calculated directly within a cutoff of 12 Å. Energy minimization was carried out using the conjugate gradients algorithm. Thereafter, MD simulations of 1 ns with 2-fs time steps at 310 K were performed to equilibrate the system. Production MD simulations of 100 ns and 2-fs time steps at 310 K were carried out without harmonic restrictions. The starting configuration was trimmed to a sphere of 30 Å, centered at the carbonyl carbon of avibactam, consisting of a mobile part of 25 Å (active site and surroundings), a buffer zone of 2 Å, and a reservoir of 3 Å. During the simulation, all intramolecular motions involving hydrogen atoms were frozen using the SHAKE algorithm [22] with a tolerance of 10⁻⁸. Snapshots were saved every 20 ps for a total of 5000 structures. The VMD [23] was used for the trajectory analysis.

The system was partitioned into a QM region consisting of avibactam, Ser69, Lys72, Ser129, Glu165 and Lys233 side chains using the link atom approach to the boundary atoms, whereas the MM region consisted of the rest of the system. Computations were carried out at M06-2X/6-31+G(d,p) [24] level of theory with the Q-Chem/CHARMM interface [25]. The PES was explored in terms of the reaction coordinates defined below.

The Q-Chem program was employed to carry out the PES exploration by a series of geometry optimizations of the mobile part of the system in the presence of harmonic restrains applied (RESDmodule) on the reaction coordinates. Each energy minimization was carried out with a gradient tolerance of 0.001 kcal/mol by the ABNR algorithm. The search of the transition states was accomplished on a clusterized model comprising avibactam and those residues in the QM zone. The level of theory used is the same mentioned above, and Jaguar [26] was used for the respective characterization. NBO analysis [27], to characterize the intermediate and transition states, was performed using NBO6 as implemented in Jaguar.

Results and discussion

Acylation of avibactam

MD simulations were performed considering two forms of the complex enzyme-inhibitor, namely, the charged and neutral forms. The first one considers the Glu165 and Lys72 residues in their ionic forms, while the second form considers these residues in their neutral form. We followed this procedure because the protonation states of these residues have not been clearly established, thus different protonation states for these residues have been proposed in literature for the diverse postulated mechanisms [28, 29].

The obtained plots of root-mean-square deviation (RMSD) and root mean square fluctuation (RMSF) for the active site along the simulation are shown in Figures S1 and S2 of Supplementary information.

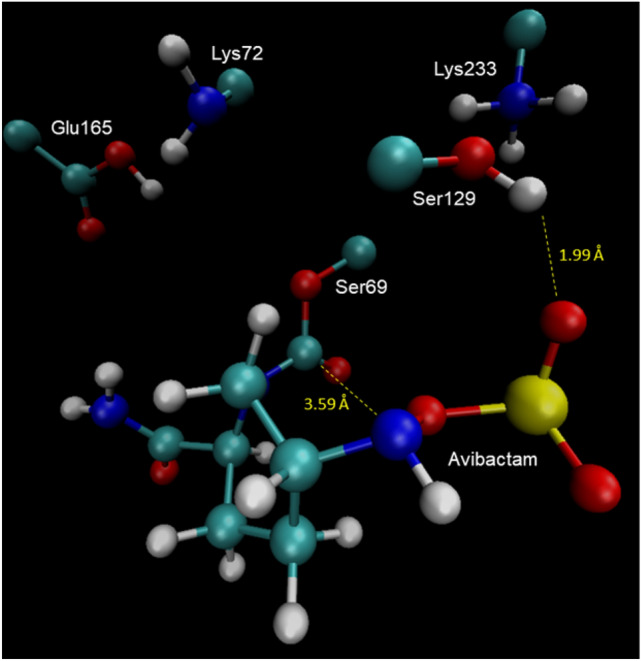
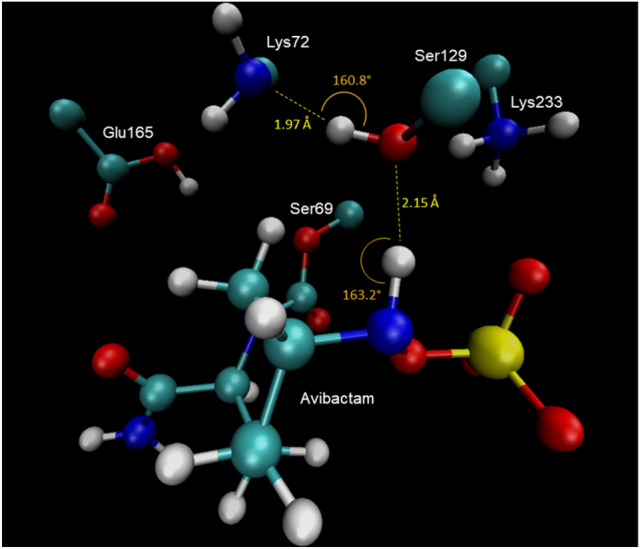
A more stable behavior is observed for the neutral in comparison to the ionic form along the simulation. The same tendency is observed in the RMSF results, in agreement with results reported in literature. In consequence, in this study we consider the neutral form of the active site. The structure of the system was taken at 65 ns, Fig. 1, as a single representative configuration to model the reaction pathway. In this structure is observed that the sulfate group of avibactam interacts with Lys233 and Ser129, while the carboxamide group of avibactam interacts with Glu165, which in turn also interacts with Lys72. This optimal conformation favors the nucleophilic attack of the Ser69–hydroxyl oxygen on the carbonyl carbon of avibactam, and also exposes the lone pair of electrons of the N6 atom to perform the nucleophilic attack on the Ser69-hydroxyl proton. This concerted event leads to the ring opening and consequently the acylation of avibactam, i.e. the inactivation of the enzyme. We have considered only the neutral form of the residues because of the empirical evidence based on neutron and high-resolution x-ray crystallography showing that during the acylation, the residues Glu165 and Lys72 should be in their ionic form in contrast to that observed during the deacylation step in which these residues should be in their neutral form [30–32].

Fig. 1.

Representative structure of the active site taken at 65 ns for the neutral form

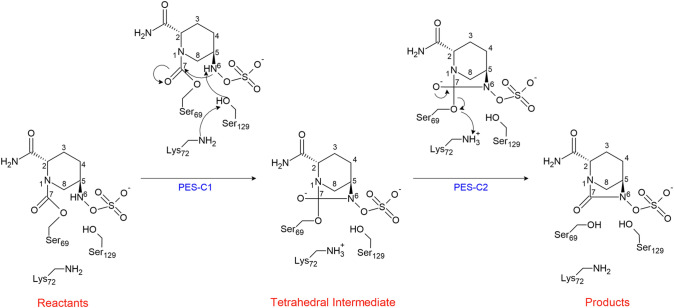
To study the acylation mechanism, inhibition, of avibactam by KPC-2, we have considered the following two approaches reported in literature for other class A β-lactamases. In the mechanism A, the Ser69 residue is activated by Lys72, which in turn performs a nucleophilic attack on the C7 carbon of avibactam, entailing the formation of the tetrahedral intermediate, step A₁. Once formed the intermediate, the reaction continues with the protonation of the N6 atom by Lys72 through Ser129, step A₂. These concerted stages lead to the ring opening of avibactam [28], Scheme 1.

Scheme 1.

Proposed inhibition mechanisms for class A β-lactamases

On the other hand, the mechanism B, considers only one reacting residue, Ser69; i.e., itself play the role of the acid–base species required for the enzyme inhibition, while the other residues located in the active site participate in the positioning of avibactam in the right conformation to allow the attack of Ser69, in addition to their participation in the stabilization of the transition states by electrostatic interactions with avibactam [13], Scheme 1.

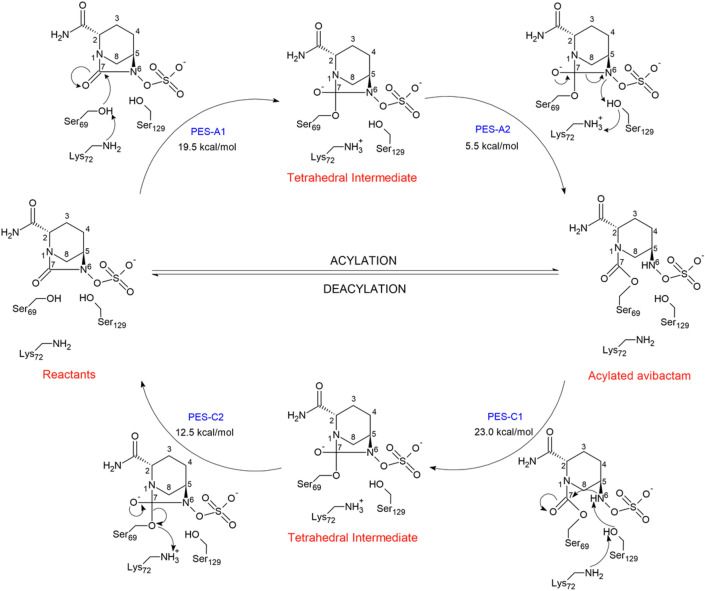
Mechanism A

The mechanism A was addressed by means of two potential energy surface (PES), one for each mechanistic step. The first step, represented by PES-A1, was explored in terms of two symmetric coordinates, R₁ and R₂. The coordinate R₁, is defined as the distance between the hydroxyl proton of Ser69 and the nitrogen atom of Lys72, while R₂ is defined as the distance between the C7 atom and the O_s atom of Ser69. The second step, represented by PES-A2, was investigated in terms of the reaction coordinates R₃ and R₄; where R₃ is defined as the distance between hydroxyl proton of Ser129 and the N6 atom, and R₄ instead is defined as the distance between the amine hydrogen of Lys72 and the oxygen of Ser129. The obtained PES-A1 is shown in Fig. 2. The topology of the surface suggests a synchronous concerted mechanism, in which both reaction coordinates change nearly symmetrically when the reaction path goes from R to the tetrahedral intermediate INT, via the occurrence of the transition state TS-A1, whose structure is shown in Fig. 3. The calculated activation barrier for this stage is 19.5 kcal/mol. The structure of the tetrahedral intermediate INT is shown in Fig. 4.

Fig. 2.

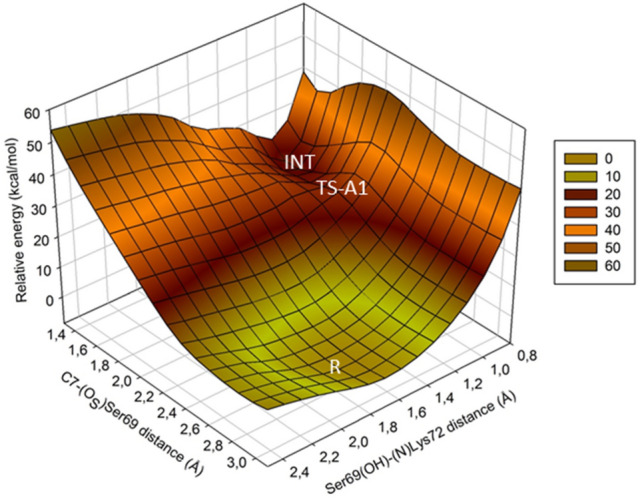
3-D view of the potential energy surface for the first stage of mechanism A

Fig. 3.

Structure of the transition state TS-A1 in the active site

Fig. 4.

Structure of the tetrahedral intermediate INT

The PES-A2, corresponding to the second stage involving the transformation of the just formed tetrahedral intermediate to the acylated avibactam, Fig. 5. The activation barrier for this stage is 5.5 kcal/mol.

Fig. 5.

3-D view of the PES-A2 corresponding to the second stage of the mechanism A

Mechanism B

The exploration of this mechanism was carried out in terms of the following two symmetrical reaction coordinates: R₅ is defined as the distance between the hydroxyl oxygen of Ser69 and the carbonyl carbon of avibactam, while the coordinate R₆ is defined as the distance between the hydroxyl proton of Ser69 and the N6 nitrogen atom of avibactam. These coordinates account for the acylation and proton transference events, respectively. The obtained PES-B shows that the reaction starts with the variation almost symmetrical of both coordinates when going from the reactant R to the transition state TS-B, Fig. 6. During this stage the proton transference from the hydroxyl proton of Ser69 toward the N6 atom of avibactam is almost completed. This event increases the nucleophilic character of the hydroxyl oxygen of Ser69, triggering its nucleophilic attack on the C7 atom de avibactam, producing its acylation. This last attack occurs at coordinate R₆ almost constant, and whose calculated activation barrier is 25.0 kcal/mol. The structure of the transition state is shown in Fig. 7, while the structure of the acylated product is shown in Fig. 8.

Fig. 6.

3-D view of the PES-B for the acylation of avibactam according to the mechanism B

Fig. 7.

Structure of the transition state for the acylation of avibactam according to the mechanism B

Fig. 8.

Structure of the acylated avibactam in the active site

The potential energy profile along the acylation reaction pathway for the two mechanism considered in this study is shown in Fig. 9.

Fig. 9.

Potential energy profile for the avibactam acylation pathway. Green: mechanism A; light blue: mechanism B

Deacylation of avibactam

Figure S3 of Supplementary information shows the results of the molecular dynamics simulations and the root-mean-square fluctuation (RMSF) for the acylated avibactam. Both plots show a very stable behavior along the simulation. During the dynamics, two relevant angles N6–H–(O)Ser129 and Ser129(O–H)–(N)Lys72 fluctuate between two possible orientations as shown in Fig. 10. Those conformations having angle values greater than 120° are those allowing the proton shuttle among avibactam, Ser129 and Lys72, entailing the deprotonation of the N6 atom by Ser129. This concerted event triggers of recyclization and liberation of avibactam.

Fig. 10.

Orientations of the Ser129(O–H)–(N)Lys72 and N6–H–(O)Ser129 angles during the simulation

In order to choose a representative structure from the dynamics, cluster analysis was performed in terms of the dihedral angles α, β and γ, defined as follows: α = C8–C5–N6–H_A, β = C4–C5–N6–H_A, and γ = C5–N6–O–S.; the first two dihedrals account for the orientation of the proton attached to the N6 atom, while the last one reflects the orientation of the sulfate moiety. In clustering analyses, data is segregated in descriptive groups based on common features. The elements of each group share more common characteristics among them than with those of other groups. The most representative component of each group is known as centroid of the cluster. The results of this analysis are shown in Fig. 11. In this figure, the red dot represents the centroid of the cluster.

Fig. 11.

Clustering analysis in terms of the dihedral angles α, β and γ. The red dot represents the centroids

This centroid corresponds to the structure at 29 ns of the simulation, whose structure is shown in Fig. 12. It is possible to observe the perfect alignment of the N₆H-Ser129-Lys72 hydrogen bonding interactions. This conformation favors the deprotonation of the avibactam N6 atom by Lys72 through Ser129.

Fig. 12.

Structure corresponding to the centroid taken at 29 ns

In consideration to the above MD results, we postulate that the deacylation mechanism involves two stages, which may be described by two potential energy surfaces, PES-C1 and PES-C2, according to Scheme 2.

Scheme 2.

Mechanism of recyclization of avibactam from its complex with KPC-2

PES-C1 accounts for the abstraction of the proton from the N6 atom by Lys72 through Ser129; while PES-C2 accounts for the protonation of the Ser69´s oxygen atom by Lys72, along with the concomitant cleavage of the bond between the C7 atom of avibactam and the oxygen atom of Ser69, i.e., the reciclyzation of avibactam. For the PES-C1, the following reaction coordinates were defined, R₇ is defined as the distance between the hydroxyl proton of Ser129 and the nitrogen atom of Lys72, and R₈ is defined as the distance between the C7 and N6 atoms. For the second stage, PES-C2, the reaction coordinates are: R₉ is the distance between the C7 atom and the O_S atom of Ser69, while R₁₀ is defined as the distance between amine proton of Lys72 and the O_S atom of Ser69.

The obtained PES-C1 is shown in Fig. 13 The topology of the PES suggest a two-stage reaction path, in which the first one corresponds to an approaching between the C7 and N6 atoms of avibactam, to form the Michaelis complex MC-C1. From this point the reaction continues with the protonation of the Lys72-N atom by Ser129, along with the simultaneous nucleophilic attack of the N6 atom on the C7 carbon. This event leads to the formation of the tetrahedral intermediate INT, Fig. 14, via the transition state TS-C1, Fig. 15. The calculated energy barriers are the following, 12 kcal/mol for the conformational rearrangement between the reactant state R and the Michaelis complex MC-C1; while 23.0 kcal/mol for the formation of the tetrahedral intermediate INT.

Fig. 13.

3-D view of the PES-C1, corresponding to the formation of the tetrahedral intermediate

Fig. 14.

3-D view of the tetrahedral intermediate INT

Fig. 15.

3-D view of the transition state TS-C1

From the so formed tetrahedral intermediate INT, the reaction continues according the reaction pathway shown in PES-C2, Fig. 16. In this stage, both reaction coordinates vary in an asymmetrical way, i.e., while the Lys72(NH)–(O_s)Ser69 distance decreases the C7–(O_s)Ser69 distance increases. This reaction path leads finally to the product P, i.e., the recyclization of avibactam, along with the recovery of the enzyme. This last step occurs via the formation of a transition state TS-C2 whose structure is shown in, Fig. 17, and the respective calculated activation barrier is 12.5 kcal/mol.

Fig. 16.

2-D view of the PES-C2, corresponding to the recyclization of avibactam

Fig. 17.

3-D view of the transition state TS-C2

The potential energy profile along the deacylation pathway is shown in Fig. 18.

Fig. 18.

Potential energy profile along the avibactam deacylation pathway

Once determined the values of the activation barriers for both, acylation and deacylation, stages we estimated the values of the rate constants using the Eyring equation. Then these calculated values were used to estimate the inhibition constant according the following equation: k_inhibition = k_deacylation/k_acylation. The calculated value is very good agreement with the value reported in literature [28] of 2.7 × 10⁻⁴, Table 1.

Table 1.

Calculated and experimental values of the inhibition constant of avibactam for KPC-2

	kacyl (s−1)	kdeacyl (s−1)	k2/k1
This work	1.2 × 10−1	3.9 × 10−4	3.3 × 10−3
Experimental	5.2 × 10−1	1.4 × 10−4	2.7 × 10−4

In closing, we can say that during the acylation and deacylation stages the reaction follows the same pathway, but in reverse sense, as shown in Scheme 3. Thus, the observed tetrahedral intermediates are the same in both stages.

Scheme 3.

Representation of the acylation/deacylation cycle of avibactam with KPC-2

Conclusions

In this article the acylation and deacylation stages of avibactam with KPC-2 is addressed by means of molecular dynamic simulations and hybrid QM/MM calculations. The results show that during the first step of the acylation reaction, Ser69 is activated by Lys72 allowing in this way the nucleophilic attack of the hydroxyl oxygen on the carbonyl carbon C7 of avibactam, entailing the formation of a tetrahedral intermediate. Afterwards, the reaction continues with the nucpleophilic attack of the N6 atom of this intermediate on the hydroxyl group of Ser129, leading to the acylated avibactam formation. The rate limiting stage for the acylation is the first one corresponding to the formation of a tetrahedral intermediate whose activation barrier is 19.5 kcal/mol; the corresponding rate constant calculated by the Eyring equation results to be 1.2 × 10⁻¹ (s⁻¹). The deacylation mechanism, proceeds also in two steps, the first one corresponds to the formation a tetrahedral intermediate, via the occurrence of the TS-C1 transition state, whose calculated barrier for this step is 23.0 kcal/mol. The second step corresponds to the recyclization of avibactam to allow its liberation and the enzyme recovery. For this step the calculated activation barrier is 12.5 kcal/mol. The respective rate constant is 3.9 × 10⁻⁴ (s⁻¹). These rate constant values allow estimating a value of 3.3 × 10⁻³ for the inhibition constant, in good agreement with the empirical evidence.

Supplementary Information

Below is the link to the electronic supplementary material.