Atomistic Polarizable Embeddings: Energy, Dynamics, Spectroscopy, and Reactivity

Conspectus

The computational modeling of realistic extended systems, relevant in, e.g., Chemistry and Biophysics, is a fundamental problem of paramount importance in contemporary research. Enzymatic catalysis and photoinduced processes in pigment–protein complexes are typical problems targeted by computer-aided approaches, to complement experiments as interpretative tools at a molecular scale. The daunting complexity of this task lies in between the opposite stringent requirements of results’ reliability for structural/dynamical properties and related intermolecular interactions, and a mandatory principle of realism in the modeling strategy. Therefore, in practice, a truly realistic computational model of a biologically relevant system can easily fail to meet the accuracy requirement, in order to balance the excessive computational cost necessary to reach the desired precision.

To address such an “accuracy vs reality” dualistic requirement, mixed quantum mechanics/classical mechanics approaches within Atomistic (i.e., preserving the discrete particle configuration) Polarizable Embeddings (QM/APEs) methods have been proposed over the years. In this Account, we review recent developments in the design and application of general QM/APE methods, targeting situations where a local intrinsically quantum behavior is coupled to a large molecular system (i.e., an environment), often involving processes with different dynamical time scales, in order to avoid brute-force, unpractical quantum chemistry calculations on the complete system.

In the first place, our interest is devoted to the available APEs models presently implemented in computational software, highlighting the quantum chemistry methods that can be used to treat the QM subsystem. We review the coupling strategy between the QM subsystem and the APE, which requires to examine the way the QM/MM mutual interactions are accounted for and how the polarization of the classical environment is considered with respect to (wrt) the quantum variables. Because of the need of reliable molecular and macromolecular structures, a pivotal aspect to address here is the handling of the system dynamics (i.e., gradients wrt nuclear positions are required), especially for large molecular assemblies composed by an overwhelming number of atoms, exploring many conformations on a complex energy landscape.

Alongside, we highlight our views on the necessary steps to take toward more accurate general-purposes and transferable explicit embeddings. The main objective to achieve here is to design a more physically grounded multiscale approach. To do so, one should apply advanced new generation classical models to account for refined induction effects that are able to (i) improve the quality of QM/MM interaction energies; (ii) enhance transferability by avoiding the compulsory partial (or total) reparameterization of the classical model. Moreover, the extension of recent developments originating from the field of advanced classical molecular dynamics (MD) to the realm of QM/APE methods is a key direction to improve both speed and efficiency for the phase space exploration of systems of growing size and complexity.

Lastly, we point out specific research topics where an advanced QM/APE dynamics can certainly shed some light. For example, we discuss chemical reactions in “harsh” environments and the case of spectroscopic theoretical modeling where the inclusion of refined environment effects is often mandatory.

Key References

• Loco D.; Polack É.; Caprasecca S.; Lagardère L.; Lipparini F.; Piquemal J.-P.; Mennucci B.. A QM/MM approach using the AMOEBA polarizable embedding: from ground state energies to electronic excitations J. Chem. Theory Comput. 2016, 12, 3654–3661.¹ The QM/AMOEBA QM/APE model is presented, the working equations are presented as well as its extension to compute excitation properties. Its viability is shown predicting the hypsochromic shift in the first absorption band of the Reichardt’s ET30 dye.

• Loco D.; Lagardère L.; Cisneros G. A.; Scalmani G.; Frisch M.; Lipparini F.; Mennucci B.; Piquemal J.-P.. Towards large scale hybrid QM/MM dynamics of complex systems with advanced point dipole polarizable embeddings Chem. Sci. 2019, 10, 7200–7211.² The QM/AMOEBA model is extended to treat QM regions covalently bonded to the environment. Dynamics is shown to be stable even with rough QM/MM partitions, while excitation properties are not affected by including portions of the environment in the QM region.

• Gökcan H.; Kratz E.; Darden T. A.; Piquemal J.-P.; Cisneros G. A.. QM/MM Simulations with the Gaussian Electrostatic Model: A Density-based Polarizable Potential J. Phys. Chem. Lett. 2018, 9, 3062–3067.³ The Gaussian Electrostatic Model (GEM) is a polarizable potential based on electron density that has been shown to provide very accurate environments for QM/MM computations. The QM/GEM approach includes Coulomb, exchange–repulsion, polarization and dispersion interactions in the QM/MM energy, only missing the charge-transfer term.

• Loco D.; Spezia R.; Cartier F.; Chataigner I.; Piquemal J.-P.. Solvation effects drive the selectivity in Diels–Alder reaction under hyperbaric conditions Chem. Commun. 2020, 56, 6632–6635.⁴ QM/APE dynamics is applied to model high-pressure effects on a Diels–Alder reaction. The more favorable kinetics at high pressure is rationalized through stabilizing polarization interactions in the denser packing of the solvation shells.

Introduction

Intrinsically quantum phenomena such as chemical transformations or photophysical processes are common in Nature. However, when dealing with extended molecular aggregates, they typically occur only within a limited portion of the system.^5,6 This is a justification to reduce the complexity of a computational model designed to address those kind of events by partitioning the whole system (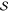) (see Figure 1) into a small chemically active one (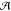), requiring quantum chemistry (QC) methods, and a much larger, inactive (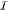) one, later defined as the environment, treated with a cheaper classical description.

Figure 1.

QM/MM partitioning scheme for a complex system as defined by eq 1. 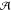is represented together with its HOMO (isovalue = 0.035). The corresponding components of the effective Hamiltonian of eq 4 are also depicted.

These are the initial assumptions defining a general quantum mechanics/molecular mechanics (QM/MM) model, whose main concern is to achieve realistic and reliable modeling of the interaction between and 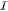. The leading terms of this interaction, which are thus mandatory to be accurately taken into account, are electrostatic in nature.^7,8

QM/MM static and dynamical approaches have currently diffused in various fields where the atomistic structure of an extended realistic system needs to be taken into account, e.g., photoinduced processes in biomolecules, nanomaterials, and, more generally, composite systems.⁶ Most of the applications are rooted in the QM/MM electrostatic embedding scheme,^7,8 where the environment does polarize the QM subsystem but cannot respond to the modified QM electronic structure.

However, researchers working independently have since reported more and more examples of the relevance of including explicitly polarization effects in general purposes FF-based models. These allow for a more realistic modeling of the different properties without exhibiting the common issue of reparameterization thanks to an enhance transferability.⁹⁻¹⁷ An effective way to achieve this goal is to formulate the classical potential from an energy decomposition analysis of the QM reference intermolecular interaction energy. This offers the opportunity to build a model potential on solid grounds in order to obtain a meaningful physically based partition of the interaction energy. A sounder representation of the QM/MM interactions can be then achieved using these classical models, providing a mechanistic insights to the relevant environment effects.

This topic is currently attracting increasing attention thanks to the growing availability of computational power, nowadays offered by GPUs¹⁸⁻²⁰ and supercomputer centers,^21,22 which is extremely relevant for the application and development of more accurate, but more computationally demanding, transferable classical models and, consequently, embedding schemes.

Despite the fact that QM/APEs are not standard yet, early fundamental works already employed a polarizable embedding to deal with complex systems.²³⁻²⁵ In their seminal paper, Warshel and Levitt employed a polarizable Force Field (FF), since environment polarization effects are non-negligible for realistic simulations carried out beyond the vacuum conditions, e.g.: to account for considerable charges-redistribution effects around protein active sites.²³ An early, more complete and detailed presentation of a QM/APE has been given by Thompson and Schenter,²⁴ and Gao.²⁵

Following this path, many efforts have been performed in the last 20 years both in modeling development and in designing highly efficient codes, both in the realm of classical molecular dynamics (MD) and in mixed quantum classical methods.

Mathematically, the many-body polarization problem is translated into a nonlinear system of equations, which are in practice solved with a self-consistent field (SCF) procedure. Popular approximate methods to solve the QM many-body problem (e.g., Hartree–Fock (HF) or Kohn–Sham (KS) density functional theory (DFT)) also require one to solve an SCF procedure. It is then natural to develop variational formulations of QM/APE methods, which is a very consistent and convenient framework to treat energy derivatives, e.g., to compute nuclear gradients and molecular properties.

To illustrate the effect of variational APEs on the main QM/MM coupling contribution to the system–environment interactions, which, as mentioned before, is electrostatic in nature, we report here two simple examples. First we compare in Figure 2 (top) the electrostatic interactions between a ±1 bare charge and one water molecule treated either with the AMOEBA²⁶ or the TIP3P²⁷ FFs. These interactions should be considered as the “building blocks” of the QM/MM coupling and as a quality measure of the embedding only, not for the classical models by themselves. Both FFs have in fact not been conceived to model these kind of situations, but the explicit treatment of polarization in AMOEBA is expected to improve the adaptability/tranferability of the model and thus the interactions’ quality. The ±1 charge interactions with a CCSD(T)/CBS (Complete Basis Set) QM water are used as reference and exhibit a good agreement with the AMOEBA embedding, which presents qualitative improvements over TIP3P.

Figure 2.

Top: ±1 charge–water electrostatic interactions (water structure’s parameters: HÔ = 104.48◦ and OH = 0.9578 Å): the CCSD(T)/CBS has been extrapolated according to ref (28) from aug-cc-pV5 and 6z basis sets. Bottom: gas-phase-to-water full DFT (ωB97X/6-311+G(d,p)) shifts for pNA in three minimal two waters (2w) clusters (Clst) and a larger one (7w_Clst) are compared with the QM/AMOEBA and QM/TIP3P ones. For two of the small clusters, EOM-CCSD/cc-pVDZ shifts are also reported.

A second example is drawn in Figure 2 (bottom) from the bathochromic shift of p-nitroaniline (pNA) in small water clusters. Full time-dependent (TD)DFT calculations are taken as reference for the environment effects, which are accounted in these calculations at the DFT level. A reference EOM-CCSD shift is also computed for two small clusters to roughly estimate the TDDFT performance in the description of the excitation process, which is a ππ* charge transfer, known to be problematic for TDDFT. Nevertheless, the chosen long-range corrected functional (ωB97X) qualitatively reproduces the reference data. The QM/TIP3P results always find a reduced shift and, in some cases, significant differences with the full DFT reference values. On the contrary, QM/AMOEBA results are always very close to full TDDFT treatment.

The different formulations of the electrostatic QM/MM coupling is the core subject of this Account, which is first devoted to review the currently available polarizable embeddings and to describe in a coherent manner the different flavours of QM/APE arising from different classical models that explicitly account for polarization. An overview is dedicated to the coupling strategies of the electronic structure theory with polarizable environments, and to QC methods themselves that have been specifically combined to APEs. A perspective is also given on recent developments in hybrid QM/APE dynamics implementations and on the major improvements in the field that could be brought by modern molecular dynamics techniques and advanced embeddings, going beyond polarization. Lastly, examples of applications which can benefit of accurate QM/APE methods are discussed.

QM/APE Mutual Polarization in a Variational Formulation

Let us define, in the canonical QM/MM “additive scheme”^7,8 fashion, the global energy of the whole embedded system 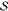of Figure 1 as

1

where E^MM is the classical FF energy for 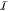and E^QM depends on the QC approach applied to 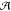. The last term represents the interaction energy between the two subsystems:

2

3

E_Bond^QM/MM collects bonding interaction crossing the QM/MM boundaries,^2,7,8 while E_vdW accounts for dispersion–repulsion.

E_El^QM/MM in eq 3 accounts for the QM/MM electrostatic coupling, which is often the leading interaction term, and it includes the self-consistent mutual polarization between the QM and the classical APE. The E_Fix-El term defines pure fixed-electrostatic Coulomb interactions, while E_Pol^QM/MM is an induction term modeling the environment polarization response.^25,29

With the formulation of an SCF-base variational QM/APE method, we aim to find an approximated solution to the following Shrödinger equation:

4

An effective Hamiltonian (see also Figure 1) is defined, composed of 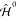, the in vacuo QM Hamiltonian, 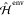, the classical environmental one, and 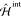arising from the QM/MM interactions.

Within HF/KS-DFT approximation, the energy functional describing the energy of the whole system 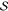(see Figure 1), including the APE contributions, reads as

5

E₀ in eq 5 is the variational energy to be minimized in an SCF procedure, where the QM density D and the environment polarization Ξ[D] are treated in the same footage in the hybrid variational problem. In practice, this means that D and Ξ[D] are not optimized altogether, so that the resulting minimized energy E₀ accounts for the complete and reciprocal relaxation of both the electron density and of the polarizable environment. The last two terms of eq 5 are characteristic of the APE of choice: E^El(Ξ,D) is the explicit QM/APE electrostatic coupling, while V^FF is a purely classical, FF-related contribution. As opposed to E^El(Ξ,D), V^FF does not explicitly affect the description of the environment effects in the variational picture, since it does not contribute to the SCF equations, as detailed in the reference literature^1,30 The quality reached in the description of environment effects is instead related to the complexity of the embedding contributions to the QM/APE electrostatic coupling and how this coupling is treated, as we will later discuss.

A modified HF/KS operator is also a required ingredient to solve the variational embedding problem, and it is defined by imposing 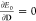, so that it can be expressed as

6

and applied in the Roothaan equations. μ, ν are atomic basis functions indexes, while the first three terms in eq 6

7

8

9

are, respectively, the usual elements of the one- and two-electron integrals matrices and of the exchange-correlation kernel.

Lastly f_μν^El(Ξ[D]) accounts for the QM/APE and classical subsystem polarization. Polarization is a many-body problem in nature, and in a QM/APE model the sources of polarization are (i) the classical electrostatic model used for the environment and (ii) the QM nuclei and electrons, which are in turn polarized back by the environment, which brings in the so-called mutual polarization effect.

By imposing the stationary condition 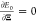, we can write the last ingredient of the coupled QM/APE equations, the polarization problem

10

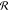is a general response matrix, and 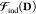is the inducing electrostatic field, which is also a function of D, including the QM induction effect. Solving the Roothaan equations, coupled to eqs 6 and 10, the QM/APE energy can be computed within an SCF-based algorithm. Thanks to the stationary conditions imposed to the coupled QM/APE equations, the clear advantage of the variational formulation is that the derivation of analytical derivatives of eq 5 does not require one to compute additional, expensive, chain rule terms.

To develop more advanced embedding schemes and to go beyond polarization, accounting for higher-order induction effects, is in our opinion a prominent frontier for embedding modeling and theory. Nowadays this objective is reachable thanks to the development of many advanced FFs.^3,31−33 Before moving to this subject, we report an overview on the main QM/APE models developed from quite different formulations of the polarizable embedding, to highlight the very close resemblance of the polarization equations in each of them, despite their apparent differences. After focusing on the modeling aspects, we discuss different approaches to solve the coupled SCF procedures associated with the QM problem, and to the polarization energy.

Embedding from a Molecular Mechanics Perspective

Different APEs have been developed, corresponding to different strategies that were proposed to model polarization effects. The specific expressions of their electrostatic terms (see eq 5) have been already detailed elsewhere.^{1−3,30,32,34−39} For all these models, the equations used to compute the polarization interactions in a variational fashion appear very close to each other. For this reason, we compare only this component of the QM/APE interaction energy in order to offer to the reader a unified view on the representation of the polarization problem.

Induced Point Dipole

Induced point-dipole models (IPDMs) have been used in a variety of QM/APE implementations.^{1,2,32,34−36} In this context, the molecular charge density is generally represented through a set of static atomic multipoles, truncating the expansion at some multipole order. To account for polarization, localized isotropic or anisotropic³⁵ dipole–dipole polarizabilities are also assigned generally to each classical atom, allowing the classical environment to respond to the presence of an applied electric field through a set of induced point-dipoles.

The electrostatic interaction term of eq 5 collects then the Coulomb interaction between multipoles and QM nuclei and electronic density D, the letter represented through the potential, electric field, its gradient, etc., generated by the QM subsystem and evaluated at the classical sites.^{1,2,32,34,35,40,41} The term of eq 5 related to polarization is written as a set of classical linear response equations, representing the linear response of the environment to any applied electric field. The associated energy, including the induction effect due to both QM electrons and nuclei, equals half the interaction energy with the induced dipole moments:

11

where μ collects the induced dipoles at each classical site. The inducing field 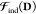is the sum of the different sources of polarization related to the static-multipoles and the QM nuclei and electrons. The last two contributions effectively couple the QM subsystem with the polarization of the classical one. T is the classical linear response or interaction matrix, which accounts for induced dipole–induced dipole interactions, including Thole damping^1,32,34 and for the polarization self-energy. The T matrix thus only accounts for dipole–dipole polarization effects, neglecting higher order polarizabilities that would require additional formalism.

E^Pol is nonadditive due to the mutual polarization and therefore has to be solved for self-consistently. Imposing 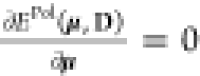, the induced dipoles are thus computed as

12

The problem can be solved within an iterative procedure or, for small systems, by direct inversion of the T matrix.

Here and in the following, we refer the reader to the literature for the HF/KS operator of eq 6 corresponding to the specific embedding.

Fluctuating Charges

Fluctuating charges (FQ) models assign electronegativity and hardness parameters at each atom, determining the corresponding atomic charge according to the electronegativity equalization principle through a constrained minimization procedure. As for induced dipole models, QM/FQ approaches have been coupled to HF/DFT SCF schemes.^38,42,43 Contrary to IPDM, no formal distinction exists between fixed and induced terms: they are both embodied by the product between the QM electrostatic potential and the FQs q[D]. Due to the variational approach, this latter quantity depends upon the QM density and needs to stay consistent with it along the way of the variational procedure. FQs are then computed as

13

with Lagrangian multiplier (λ) constraints.^38,43 The QM/FQ polarization formulated in this way closely resembles the induced dipole models formulation. The interaction matrix T(43) accounts for FQs–FQs induction contribution and the polarization self-energy. V(D) is the potential due to the QM subsystem, and it is the origin of QM/APE mutual polarization, while C relates to purely classical contributions.

To the best of our knowledge, this approach is currently mainly available to treat QM/MM systems in water solution. This fact represents a limitation when compared to the other polarizable models presented in this Account.

Drude Oscillators

The Drude oscillator (DO) model formulation is closely related to the IPD one, since each polarizable atom is endowed by a fixed charge q and connected, through an harmonic spring with defined force constant k_D, to a mobile (Drude) charge q_D. A Drude particle with initial position r_D is displaced at some distance d = |r_D – r| from the atom when subject to any applied electric field, so that one can define the Drude atomic induced dipole as μ_D = q_Dd.⁴⁴

The QM/DO polarization energy can be simply written as the interaction of point-charges with the inclusion of: (i) an additional effect of the potential due to the QM nuclei and to the electron density; (ii) the DOs’ polarization self-energy.^44,45

The solution of the polarization problem corresponds then to the optimization of the displacement d, whose value is certainly affected by the presence of the QM density. In this case, by imposing 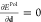:^37,44,46

14

Writing r_D[D] highlights the fact that the Drude particle position is the classical quantity directly affected by the interactions with the QM subsystem. Moreover, in this model, 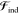collects the classical and QM sources of polarization. Exploiting the known relation with the atomic polarizability (α = q_D²/k_D) and the expression for μ_D, eq 14 corresponds then to the classical dipole linear equation.⁴⁶

Next Generation Force Fields: Beyond Polarization

In the near future, QM/APE hybrid approaches will likely benefit more and more from efficient implementations of FFs^3,31−33 even more refined than the polarizable ones, designed to explicitly capture more physics in the coupling Hamiltonian, so to, e.g., encompass QM density-dependent dispersion, charge penetration, and higher-order induction interactions as exchange–repulsion and charge transfer (see Figure 3).

Figure 3.

Pictorial representation of a water dimer, surrounded by monomer charge densities, to represent charge penetration (CP) and charge transfer (CT) interactions, typically missing in classical FF.

Such short-range interactions are mostly neglected in classical embedding schemes, whose reliability is indeed due to the general predominance of long-range electrostatics. Nevertheless, short-range nonelectrostatic effects have been shown to prevent unphysical electron spill-out toward the classical subsystem when diffuse basis functions are employed to predict excitation properties.³⁶

The EFP2 FF^32,47 has been developed to include all these interactions and hybrid methods exist including QM/EFP exchange repulsion and dispersion terms in the effective Hamiltonian.

On the same line, in the QM/GEM (Gaussian Electrostatic Model) method, an improved environment representation is achieved describing the classical fragment’s electrostatics through a frozen electron density.⁴⁸⁻⁵⁰ In practice, the GEM formalism provides a description of electrostatic properties at a high resolution, compared to conventional point charges or distributed multipoles, by fitting reference QM molecular densities through a continuous auxiliary Gaussian hermite basis to reproduce gas phase ab initio intermolecular interactions, in the spirit of polarizable force fields such as SIBFA.⁵¹ It naturally includes short-range penetration effects^48,49,52 and density-based approximation of exchange-repulsion.⁴⁸

In terms of QM/APE, GEM embedding goes beyond classical electrostatics as the polarizable GEM densities interact with the QM subsystem through short-range electrostatics, density overlap-based exchange-repulsion, and dispersion terms.^3,52 The frozen densities can be used efficiently thanks to a generalization of the particle mesh Ewald to hermite Gaussian densities⁴⁹ and are suitable for MD simulations. Various GEM models exist. For example, it has been combined to AMOEBA’s bonding and polarization terms to perform MD simulations at a reduced computational cost (GEM*).⁵³

GEM can thus be seen as a hybrid method that uses some ingredients of the classical polarizable FF approaches (it uses the induced dipole formalism) and some features of the fragment-based methods⁵⁴ (i.e., the frozen densities). In that connection, going one step further toward the QM fragmentation methods, it is also important to discuss the X-Pol³¹ strategy and its variations.⁵⁵

Instead of fitting energy components to reference QM data, the X-Pol method computes the energies and properties of a molecular system through an effective Hamiltonian. Each monomer is treated with a QC approach and embedded in the external potential due to all the other fragments whose electronic densities are represented through partial atomic charges. The appropriate Fock operator is constructed to include such embedding effects in the optimization of the monomer wave function. Additional terms also account for exchange-repulsion, dispersion, and other interfragment correlation energy contributions.⁵⁵ The variational X-Pol method,⁵⁵ in particular, offers an efficient and accurate embedding naturally including polarization effects. It has been used to develop quantum mechanical FF to perform accurate simulations of liquid water and hydrogen fluoride as well as small proteins.⁵⁵ As for GEM, complex systems are made tractable applying practical and parametrizable procedures to model interfragment electrostatic and exchange-dispersion interactions, together with an efficient QC method for each monomer.

The Coupling Scheme

To account for the complete environment relaxation, the total energy of the system given in eq 5 is computed from the solution of the QM/APE coupled equations. It requires one to solve the modified HF/KS equations exploiting the solution for eqs 6 and 10 and terminating the procedure when a convergence on both D and Ξ[D] is reached. In practice, such coupled equations can be solved simultaneously, as is normally done in the so-called “microiterative coupling scheme”.^37,44 Simplified QM/APE coupling schemes have also been devised, and some are highlighted in Figure 4. The dual-SCF (or double-SCF) procedure^24,25 involves an inner MM cycle to first converge the environment polarization response and an external one to account for environment polarization effects on the QM electronic density.

Figure 4.

QM/APE coupling schemes.

In multipurpose implementations,³⁷ interfacing the general QC and MM suite of programs, this strategy is advantageous, as it is equivalent to an electrostatic embedding. FQ and DO models can be adapted to this strategy, since in practice they involve point-charges interactions, while for IPDMs and multipoles-base FFs the adaptation is less straightforward and the advantages less obvious.

A sequential approach is instead adopted by the LICHEM package: QM/MM electrostatic embedding calculations are performed after solving the polarization SCF, for which a point-charges representation of the QM subsystem is adopted. .⁵⁶ A similar strategy is followed in the QM/AMOEBA implementation in Tinktep, transforming the QM electron density in point-multipoles up to quadrupoles to treat the QM/MM polarization.³⁹

The calculation of QM/APE coupling terms can be improved by more efficient polarization solvers such as the Truncated Conjugate Gradient (TCG) class of methods, applied in classical dynamics with the AMOEBA potential.^57,58 On the same line, predictor-corrector schemes (see Figure 4) represent a valuable mean to avoid expensive repeated SCF calculations in QM/APE MD. It has been applied in the context of Drude models, implementing the time-reversible scheme developed by Niklasson and co-workers.⁴⁴ For the time being, no detailed comparison of these different possible treatments of the QM/APE coupling is available in the literature.

From a Dynamics Perspective

Starting from the variational energy defined in eq 5, analytical nuclear gradients with respect to either QM or MM coordinates can be conveniently computed, according to the Hellmann–Feynman theorem. The exact expressions vary for the different QM/APE schemes, but a common aspect is that the gradient contributions due to the polarization response matrix only concern displacements of classical atoms.³⁰ We have recently presented the implementation of a Born–Oppenheimer (BO) QM/AMOEBA MD, where the force expressions are described in detail.³⁰ The QM/AMOEBA MD has been also coupled with the Niklasson’s extended Lagrangian method⁵⁹ to alleviate the computational cost of the SCF procedure.^2,30 An improved electronic density guess is formally derived from the extended BO Lagrangian, storing densities computed in few prior MD steps, and used as a new guess density for the QM/APE SCF.³⁰ This approach has been tested by some of the authors on simple systems, showing an improved energy conservation even under unfavorable SCF convergence criteria and a noticeable reduction of the computational time required for the SCF. As a general comment, we note here that the time step used in QM/APE dynamics does not differ from that used in fully ab initio MD, ranging roughly from 0.1 to 1 fs, depending on the system.

Other strategies to improve the sampling in MD simulations are related to new generation integrators such as BOUNCE⁶⁰ or BAOAB-RESPA(1),⁶¹ which require one to evaluate expensive interactions more rarely than standard integrators. They rely on the partitioning of the interparticle interactions between a slow and more expensive component (V_slow) and a faster varying one (V_fast). In more detail, BAOAB-RESPA(1) arises from the combination of the BAOAB discretization of the Langevin process⁶² within a RESPA(1) framework associated with this separation of the potential.⁶¹ The BOUNCE integrator is built on the same roots but evaluating the slowly varying interactions through jump processes.⁶⁰ These interactions are computed only at random and optimal time steps depending on the upper bound of ∇V_slow when the system jumps. It means that the momenta follow the reflection:

15

The adaptation of such procedures to QM/APE dynamics is under an active investigation in our group.

Embedding from a Quantum Chemistry Perspective

We find it useful to recall here the main QC methods going beyond HF/KS-DFT to improve the treatment of electron correlation, or dealing with excited states (ESs) properties, that have been coupled to APE models. Such a rapid overview can help the interested reader to have insight on the relatively fragmented literature, mainly reporting method implementations that in some cases, unfortunately, have never been further developed.

Both IPD and FQ models have been extended to the linear response (LR-)TDDFT theory exploiting the Casida formalism;^{1,34,38,43,63} a response theory formulation has also been developed up to a quadratic response for DFT³⁵ and linear response for PE-MCSCF.⁴¹ It is well-known that the nonlinearity in the QM/APE model equations induce a discrepancy between LR and state specific (SS) methods, so that SS corrections have been implemented in different QM/APE.^1,64 Among SS approaches, we highlight here that Density Matrix Renormalization Group⁶⁵ has been coupled to IPDM, exploiting a range-separation approach. This model has been tested to efficiently and accurately deal with the retinylidene electronic excitation in proteins.⁶⁶

Different flavors of coupled cluster theory coupled to IPDMs, both SS versions⁶⁷ or within a linear or quadratic response theory,⁶⁸ do exist. As an aside, we mention QM/APE implementations within the more and more popular GW–Bethe–Salpeter equation approach.^69,70

Exploiting a response theory formulation, different QM/APE models have been extended to the simulation of spectroscopic observables, such as vibrational and electronic circular dichroism¹⁴ or two photon absorption.⁷¹ In the near future, further work will be required to empower such advanced QC/APEs and broaden their range of applicability to extended systems, because of the design of more specific and efficient codes.

From a Chemical Perspective

In conclusion, we first review a recent computational study carried out in our Laboratory to report an example of application for some of the methodologies discussed in this Account. Our application focuses on the effect of high-pressure conditions on the kinetics of a Diels–Alder reaction between cyclopentadiene and acrylonitrile in dichloromethane solution.⁴ The high-pressure conditions are of great interest as a green physical catalysis method in organic chemistry.

We applied a sequential approach based on polarizable MDs to equilibrate the solvent with frozen optimized reactants, followed by full QM/APE MDs, in order to improve the description of system-environment interactions. The reacting species (RS) representing the main step of the reaction (see Figure 5) are treated at the M06-2X/3-21G level, and during the QM/APE dynamics they mainly vibrate around their optimized geometries, mutually interacting with the solvent, modeled by the AMOEBA FF, according to the variational embedding scheme discussed in this Account. The QM level of theory has been selected to reproduce the reference MP2 activation energies,⁴ ensuring an affordable cost for the molecular dynamics simulation. The good performance of the QM level of choice⁴ can be ascribed to a fortuitous error compensation between the functional behavior and the basis set superposition error due to the small basis. Since during the QM/AMOEBA dynamics the RS mainly fluctuates around their optimized conformation, this is not expected to have a negative impact on the values of the predicted barriers, allowing for a reasonable MD sampling.

Figure 5.

Structures of the different species involved in the reaction and energy diagram from QM/AMOEBA simulations for the two different pressure regimes explored. Data taken from ref (4).

In Figure 5, we depict the different energy landscapes for the 1 atm and 10 Katm reactions, each in both the exo and endo configurations. The Tinker-HP²¹/Gaussian09⁷² coupled suite of software was used for all the QM/APE MDs, with a 0.5 fs time step in the NVE ensemble. An enhanced diastereoselectivity toward the endo product is predicted under high pressure due to the balance between a differential solvation, mostly due to solvent polarization, between endo and exo pre-TS and an inverse stability of their respective TS. As a result, the reaction is kinetically favored by high-pressure conditions, in particular for the endo diastereomer where the kinetics is diffusion controlled.⁴

X-ray spectroscopies are another interesting example of a rather unexplored field of application for computational studies based on QM/APE MD. The great advances recently performed in X-ray-based studies of chemical and biological processes call for the aid from computational methods as interpretative tools. TDDFTs⁷³ as well as different wave-function-based methods⁷⁴ have been applied to study core-excitation processes. Through X-ray spectroscopies, liquid systems⁷⁵ and systems in condensed phase⁷⁶ are explored by probing the local atomic chemical environment, eventually extracting structural information.

In addition environment effects, an aspect little explored or uexplored in the simulation of X-ray spectroscopies is the effect of ultrafast nuclear dynamics in the short-living core-excited states, as schematically exemplified in Figure 6. Despite the short time period involved, the development or extension of theoretical methods either treating the nuclear motion at classical or quantum level could be relevant and it is worth further investments.

Figure 6.

Pictorial representation of possible events following the absorption of an X-ray photon.⁷³

A major challenge is the simulation of resonant inelastic soft X-ray scattering (RIXS)⁷³ consisting of a photon-in-photon-out Raman scattering process, potentially giving access to ultrafast nonadiabatic processes, to study the electronic structure of liquids and solutions under ambient conditions.⁷⁴ RIXS is computed from transition energies and dipole moments of the excitation and emission processes and does not involve ionization processes, so that it is well suited for, e.g., TDDFT-based QM/APE-MD methods.

Conclusions

In summary, this Account sorts through the recent fundamental developments in QM/APE approaches, offering a global vision for their main theoretical and computational aspects. We also include a look at their past progress and a perspective of their evolution toward advanced molecular dynamics and spectroscopic techniques. The convergence of such approaches with modern software and algorithms^21,77 able to efficiently solve both the MM polarization equations and the QM/APE coupling will be an additional step forward in the diffusion of such techniques.

To improve the simulation predictive power of QM/APE methods, two ingredients are required: the implementation of new generation FFs increasingly oriented toward a physically motivated description of molecular interactions and the coupling with advanced electronic structure models for the QM region. Such improvements call for a global effort to develop efficient implementations to deal with real-life chemical systems for daily research problems. It will complement and aid the rationalization of the experimental scientist’s work in different research fields involving concepts such as molecular interactions in condensed phase and complex systems.

Biographies

Daniele Loco received his PhD in Chemistry from the University of Pisa in 2018, and since then he has been a Postdoctoral Fellow at Sorbonne Université under the supervision of Prof. Jean-Philip Piquemal. His main interest is to develop models suited for systems in complex environments to be applied in computational chemistry problems.

Olivier Adjoua obtained a Master of Science in Applied Mathematics at the University of Paris-Saclay in 2018. He is an engineer at Sorbonne Université in the group of Prof. Jean-Philip Piquemal and started a PhD. His interests concerns High Performance Computing with a special focus on Graphic Processing Units (GPUs) acceleration.

Louis Lagardère obtained a Master of Science in Applied Mathematics (2012) then received his PhD in Computational Chemistry (2017) from Université Paris 6, Pierre et Marie Curie. Since then he holds a permanent research engineer position at Sorbonne Université. His interest lies in interdisciplinary work at the crossroads between computational chemistry, high performance computing and applied mathematics.

Jean-Philip Piquemal (b. 1976) received his PhD in 2004 from Université Paris 6, Pierre et Marie Curie (UPMC). As a National Institutes of Health Postdoctoral Fellow, he performed research at NIEHS in the group of Dr. Thomas A. Darden at NIEHS from 2004 to 2006. In 2006, he came back to Paris as an Assistant Professor, to become Professor in 2011. Since 2019 he is Distinguished Professor of Theoretical Chemistry at Sorbonne Université. He is junior Member of the Institut Universitaire de France and Adjunct Professor of Biomedical Engineering at UT Austin. His interest lies in interdisciplinary work at the crossroads between computational chemistry, high performance computing, applied mathematics, and biology.

The authors declare no competing financial interest.