Coupled oscillators coordinate collective germline growth

SUMMARY

Developing oocytes need large supplies of macromolecules and organelles. A conserved strategy for accumulating these products is to pool resources of oocyte-associated germline nurse cells. In Drosophila, these cells grow more than 100-fold to boost their biosynthetic capacity. No previously known mechanism explains how nurse cells coordinate growth collectively. Here, we report a cell cycle-regulating mechanism that depends on bidirectional communication between the oocyte and nurse cells, revealing the oocyte as a critical regulator of germline cyst growth. Transcripts encoding the cyclin-dependent kinase inhibitor, Dacapo, are synthesized by the nurse cells and actively localized to the oocyte. Retrograde movement of the oocyte-synthesized Dacapo protein to the nurse cells generates a network of coupled oscillators that controls the cell cycle of the nurse cells to regulate cyst growth. We propose that bidirectional nurse cell-oocyte communication establishes a growth-sensing feedback mechanism that regulates the quantity of maternal resources loaded into the oocyte.

Graphical Abstract

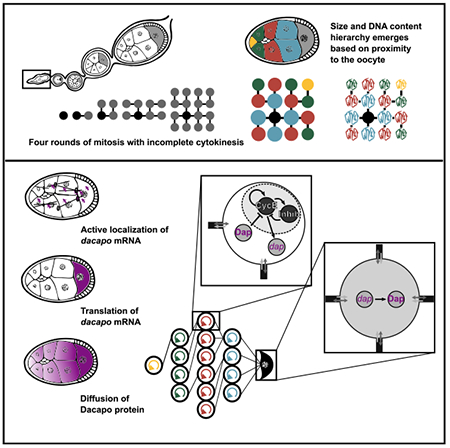
In brief

Doherty et al. uncover a mechanism whereby oocyte-mediated cell cycle regulation controls the collective growth of supporting nurse cells within the Drosophila ovarian cyst. This mechanism fits the framework of coupled oscillators that undergo synchronization and has widespread implications for other similar dynamical systems in biology.

INTRODUCTION

In many species, oocyte development depends on the donation of organelles and macromolecules synthesized in connected sister germline cells (Haglund et al., 2011; Lei and Spradling, 2016). In Drosophila, the oocyte and its 15 sister nurse cells (NCs) arise from a germline precursor cell that divides synchronously four times with incomplete cytokinesis. All 16 cells of this germline cyst remain connected to each other by stalled cytokinetic furrows called ring canals (RCs). One cell, thought to be predetermined from the first division (Barr et al., 2019; Spradling, 1993), is specified as the oocyte, whereas the other 15 become NCs. Over the course of oogenesis, the oocyte grows at the expense of the NCs, with mRNAs, proteins, and organelles transported from the NCs into the oocyte through the RCs. Although there is no known barrier to diffusion among the germline cells (Shimada et al., 2011), NC size is not uniform, suggesting that NC growth is regulated (Imran Alsous et al., 2017). Despite the importance of NCs to oocyte development, little is known about what regulates their growth and, consequently, their collective biosynthetic capacity.

In contrast to the meiotic oocyte, NCs enter the endocycle –a modified cell cycle of alternating G- and S-phases without intervening mitoses (Spradling, 1993; Figure 1A)– and become highly polyploid (King, 1970). The NC endocycle is controlled by the S-phase promoting cyclin, cyclin E (CycE) (Lilly and Spradling, 1996). The CDK inhibitor Dacapo (Dap) is an important regulator of CycE during NC endocycles (de Nooij et al., 2000). Although Dap is not required for NC polyploidization, NC endocycles in dap-null egg chambers have compromised replication licensing and improper extensions of S-phase (Narbonne-Reveau and Lilly, 2009). In addition, Dap is crucial to prevent CycE-mediated S-phase entry by the oocyte nucleus (Hong et al., 2003).

Figure 1. Groups identified in volume hierarchy are also observed in DNA content hierarchy.

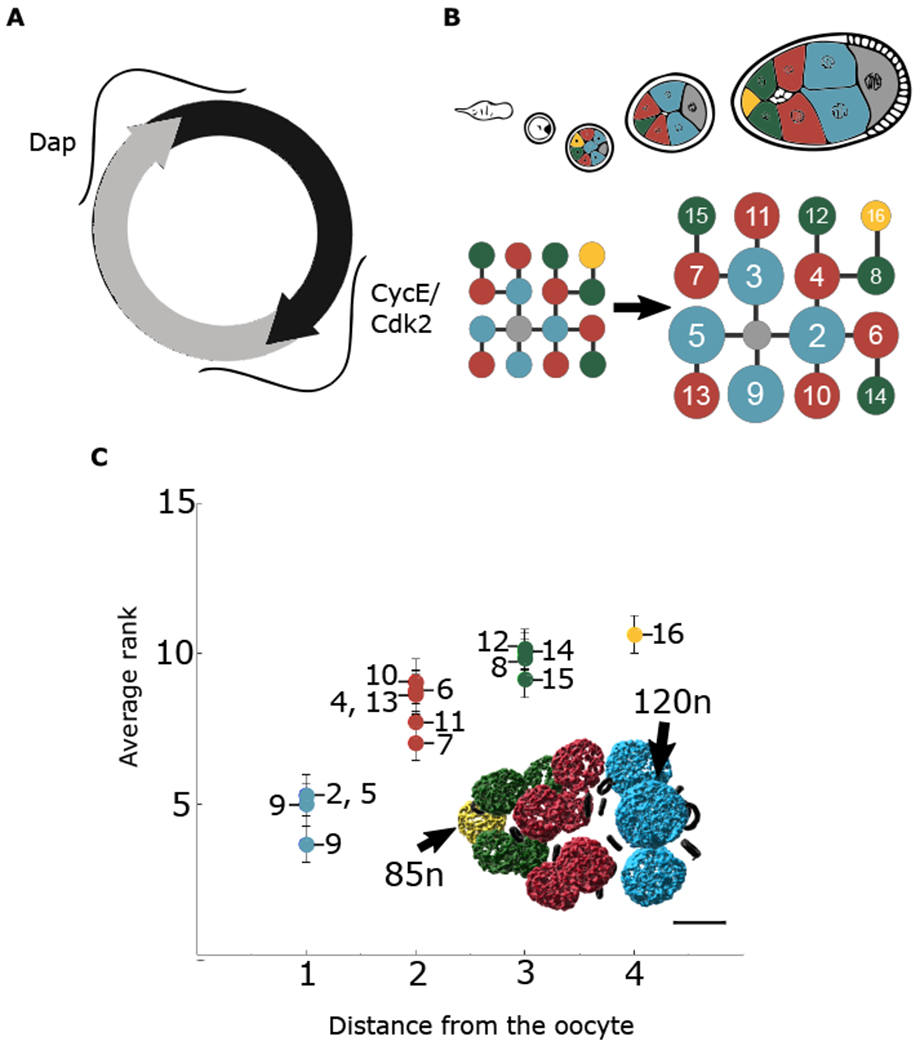
(A) Schematic of CycE/Cdk2 and Dap during NC endocycles.

(B) Representation of NC groups based on proximity to the oocyte. Blue cells are directly connected to the oocyte and have the largest volume on average. Red cells are two ring canal connections away and next largest on average. Green cells are three ring canal connections away and third largest on average. The single yellow cell is four ring canal connections away and smallest on average. Numbering is assigned based on the initial pattern of four incomplete mitotic divisions that give rise to the cyst. Each NC is uniquely identifiable within the lineage tree.

(C) Averaged ranking of DNA content (highest = rank 1, lowest = rank 15) from stages 2–9; n = 33 egg chambers. The same groups emerge as with volume measurements. Reconstruction of DAPI signal reveals hierarchy of DNA content within an egg chamber. Error bars represent standard error. Scale bar, 20 μm

Here, we show that the Drosophila oocyte acts as an organizing center that regulates NC growth, indicating that the oocyte plays an active role in the development of the germline cyst. We further show that this oocyte-imposed control is mediated by Dap. Transcripts encoding the Dap protein are synthesized by the NCs and are localized to the oocyte (de Nooij et al., 2000). Oocyte-derived Dap protein then diffuses to the NCs, where it acts to couple NC endoreplication cycles, thereby coordinating their collective growth. Thus, the coordination of NC growth is likely the result of a universal phenomenon in which coupled oscillators synchronize to a common frequency (Pikovsky et al., 2001). We propose that this growth-regulating circuit acts as a feedback mechanism to control the quantity of maternal components loaded into the oocyte.

RESULTS

NC endocycles are synchronized based on proximity to the oocyte

The invariant division pattern of the 16-cell germline cyst — which, together with the surrounding somatic follicle cells constitutes an egg chamber— creates a lineage tree that allows for the unique identification of each NC (King, 1970) (Figure 1B). Thus, the same NC can be compared among different egg chambers across all stages of oogenesis. NCs that reside the same number of ring canal connections away from the oocyte are of similar size, constituting a “coordination group” (Figure 1B). NCs in groups closer to the oocyte are larger (Imran Alsous et al., 2017). As a result of endocycling, NC ploidy reachesapproximately 500–2,000n (King, 1970) (Data S1). Increased DNA content is well-correlated with increased cell size (Orr-Weaver, 2015; Øvrebø and Edgar, 2018). Consistent with this, there is a hierarchy of DNA content among NCs, whereby NCs closer to the oocyte have more DNA (Figure 1C). Furthermore, ploidy follows the same coordination groups as cell size. We therefore hypothesized that the regulation of NC cell cycles could function to create coordination groups.

To investigate endocycle dynamics, we used CRISPR to endogenously tag CycE with superfolder green fluorescent protein (sfGFP) and imaged live egg chambers. Reconstruction of the pattern of CycE within the NC lineage tree showed that S-phase entry and exit appear to occur synchronously among subsets of NCs based on their proximity to the oocyte (Figure 2A). Notably, while cell cycles within coordination groups were largely synchronized, there was usually a marked difference between cell cycle stages of different coordination groups. These spatial NC groupings are consequently predictive of the DNA and cell size groups.

Figure 2. Groups identified in volume hierarchy are also observed in endocycle progression.

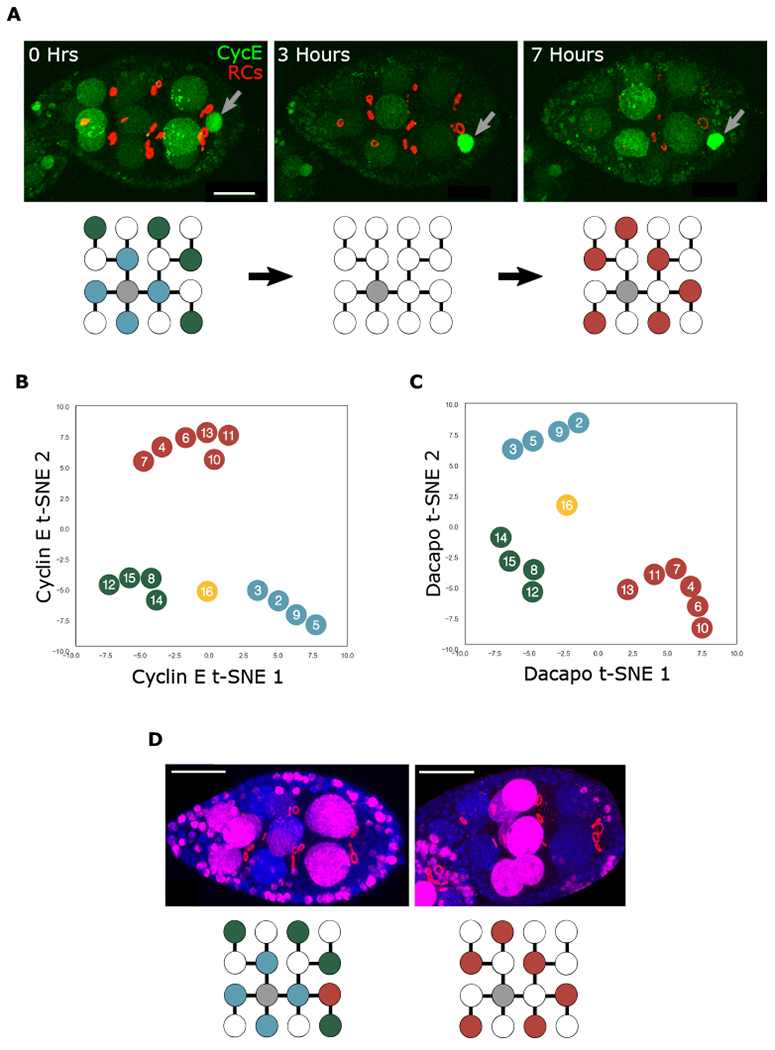
(A) Snapshots of a CycE-sfGFP (CycE) egg cultured ex vivo for 7 h. Ring canals (RCs) are marked with Pavarotti-mCherry. The red channel was generated from reconstruction of RCs. The signal from follicle cell RCs was removed for clarity. High levels of CycE are detected in the oocyte nucleus (gray arrows). Below is a visual representation of NC groups, with high levels of nuclear CycE indicated with colored circles and low levels with white circles.

(B and C) t-SNE representation of CycE (B) and Dap (C) NC nuclear localization patterns from stages 2–9; n = 52 egg chambers (B), n = 80 egg chambers (C).

(D) Egg chambers cultured ex vivo in EdU for 1 h (magenta). RCs are marked with phosphotyrosine antibody (red). DNA is stained with DAPI. NC nuclei with incorporation are marked below. Scale bars, 20 μm.

Limitations on culturing ovaries ex vivo preclude capturing the full extent of endocycles over the course of oogenesis. Thus, we fixed and imaged a population of CycE-sfGFP egg chambers spanning approximately 42 h (stages 2–9 of oogenesis) in order to better probe the grouped behavior. Nonlinear dimensionality reduction analysis of the imaging data (t-SNE) revealed the emergence of the same coordination groups (Figures 2B and S1A). Together, these results show that NCs in the same coordination group synchronously enter and exit S-phase.

We then sought to better understand how this distinct pattern of CycE emerges. CycE is inhibited by Dap to reset the replication cycle (Hong et al., 2003; Narbonne-Reveau and Lilly, 2009). We therefore immunostained egg chambers with an anti-Dap antibody and performed the same t-SNE analysis as done for CycE-sfGFP. Once again, the same groups emerged (Figures 2C and S1B). Based on the behavior of CycE and Dap, we conclude that NCs progress through endocycles in synchronized coordination groups. Furthermore, since CycE and Dap control endoreplication, their grouped dynamics suggest a grouped pattern of DNA replication. To test this prediction, we performed EdU incorporation experiments for 1 h and again observed the same grouped pattern (Figure 1D). Thus, coordinated group progression through endocycles is a general characteristic of Drosophila NCs during oogenesis.

Dacapo protein moves from the oocyte to the NCs

We next sought to understand how NCs that share no direct cytoplasmic connection endocycle together. Within the NC lineage tree, groups emerge solely based on one metric –the number of cytoplasmic bridges that separate them from the oocyte. Therefore, we predicted that the oocyte plays a central role in coordinating NC growth.

Previous studies showed that dap mRNA, but not cycE mRNA, is enriched in the oocyte (de Nooij et al., 2000; Shcherbata et al., 2004). We hypothesized that dap mRNA transcribed in the NCs is actively localized to the oocyte by transport on the polarized microtubule network within the cyst. Once in the oocyte, it is then translated, and Dap protein diffuses to the NCs (Figure 3A). This retrograde Dap movement would generate the NC endocycle coordination groups on the basis of oocyte proximity.

Figure 3. Dap can move from the oocyte to the NCs.

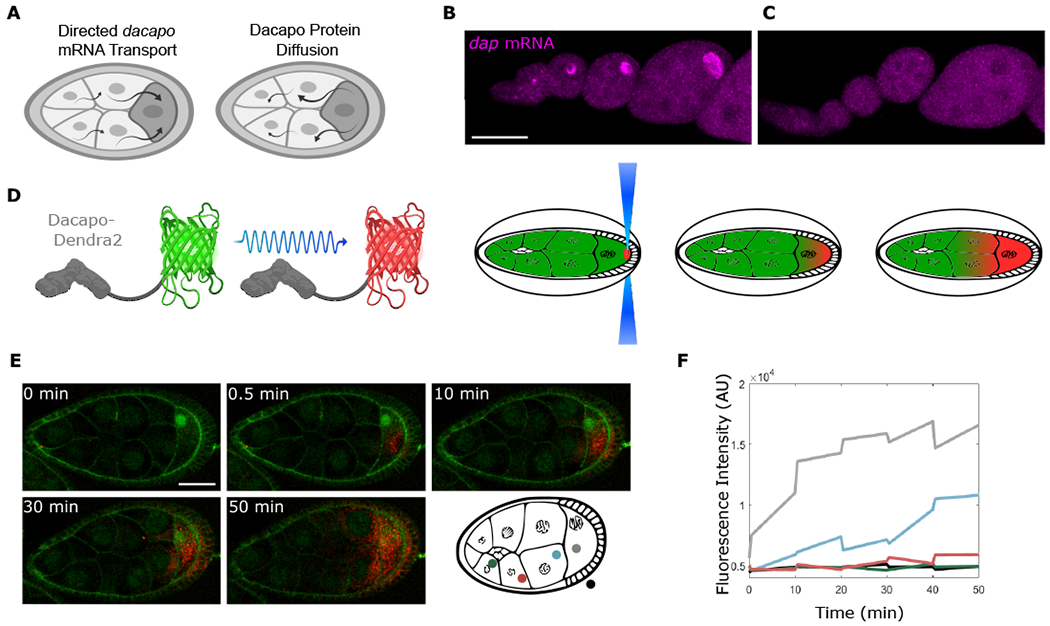
(A) Model predicts that the localized dap mRNA creates a pool of Dap protein that moves to the NCs.

(B and C) Single molecule fluorescence in situ hybridization (smFISH) for sfGFP mRNA performed on egg chambers from control Dap-sfGFP females (B) or from Dap-sfGFP females fed with yeast containing colchicine (C). ANOVA performed on fluorescence intensity collected from an ROI within the oocyte for stages 4-8 egg chambers, F value = 32.71, p value = 2.08 × 10⁻⁵; n = 10 egg chambers for each condition.

(D) Dap-Dendra2 photoversion scheme.

(E) Time sequence of Dap-Dendra2 photoconversion of region shown in (D). Photoconversion performed every 10 min. First photoconversion event (between t = 0 min and t = 0.5 min) was performed 3× to bleach Dendra2 in ROI, intended to mark region of excitation and confirm that nonspecific photoconversion does not occur in adjacent NCs. Successive photoconversion events were performed once. Membranes were stained with CellMask green plasma membrane stain.

(F) The graph shows fluorescence intensity quantified before and after each photoconversion event. Colors correspond to measurements in different regions of the egg chamber. Scale bars, 50 μm (B) and (C), 40 μm (E).

To test whether dap mRNA is actively localized to the oocyte, we fed females with yeast supplemented with colchicine to disrupt the microtubule network. In oocytes produced by these females, dap mRNA was no longer enriched in the oocyte, confirming microtubule-dependent transport (Figures 3B and 3C). Next, we investigated whether Dap protein can diffuse from the oocyte to the NCs. We endogenously tagged Dap with the photoconvertible protein Dendra2 and monitored its movement using live imaging (Figure 3D). Prior to photoconversion, green fluorescent Dap-Dendra2 was detected in the oocyte. After photoconversion of Dap-Dendra2 from green to red in a small region of the oocyte cytoplasm, red fluorescence was detected in the NCs (Figures 3E and S2; Video S2). The appearance of photoconverted Dap in the NCs was no faster than the expected rates of diffusion of the mammalian homolog of Dap, p27, when tagged with GFP, and was possibly slower (Figures 3E and 3F) (Molatore et al., 2010). Thus, Dap protein can move from the oocyte to the NCs.

Our data support a model in which Dap protein is produced in the oocyte from oocyte-localized dap mRNA and then diffuses to the NCs to regulate endocycles (Figure 3A). This model predicts that the oocyte-sourced Dap should be the major contributor of Dap protein in the NCs. To test this, we trapped Dap protein in the oocyte using an oocyte-localized GFP-recognizing nanobody, VhhGFP4 (Rothbauer et al., 2006). To restrict VhhGFP4 to the oocyte, we fused it to Oskar (Osk), which is translated exclusively at the posterior of the oocyte and accumulates there from the end of stage 8 onward (Rongo et al., 1995) (Figures 4A and S3). A transgene expressing Osk-VhhGFP4 was then introduced into females expressing endogenously tagged Dap-sfGFP. In the resulting egg chambers, Dap-sfGFP was highly enriched at the posterior of the oocyte and depleted from the NC nuclei as compared with Dap-sfGFP in egg chambers without Osk-VhhGFP4 (Figures 4B and 4C). This result supports the idea that Dap protein present in the NCs is produced in the oocyte.

Figure 4. Oocyte-sourced Dap constitutes a major proportion of Dap in the NCs.

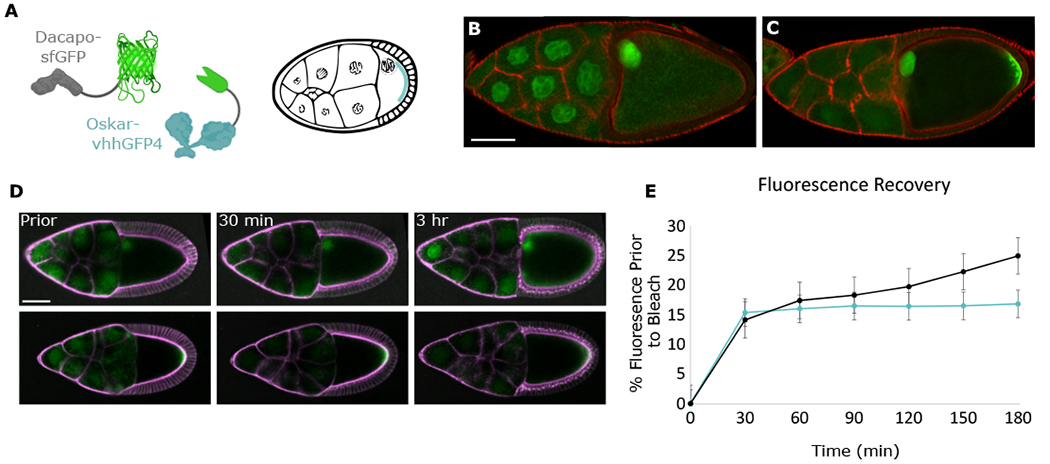
(A) Schematic of Osk-vhhGFP4 localized at the posterior of the egg chamber where it traps Dap-sfGFP.

(B and C) Confocal images of stage-10 Dap-sfGFP egg chambers without (B) or with (C) Osk-vhhGFP4. At this stage, Dap-sfGFP, like wild-type Dap (data not shown), has uniform levels in all NCs. Actin is stained with phalloidin (red).

(D) Time sequence of photobleach of NC region in Dap-sfGFP or Dap-sfGFP; Osk-vhhGFP4 egg chambers. Membranes were stained with CellMask Deep Red Plasma membrane Stain. Egg chambers were imaged prior to photobleaching of NC region and then imaged every 10 min for the next 3 h.

(E) Quantification of FRAP. Measurements of average sfGFP intensity of NC region, taken as percentage of average sfGFP intensity of NC region prior to bleach; n = 3 egg chambers for each condition. Error bars represent standard error. Scale bars, 70 μm (B) and (C), 50 μm (D).

To further test whether Dap is produced in the NCs or oocyte, we performed FRAP (fluorescence recovery after photobleaching) experiments on Dap-sfGFP egg chambers with or without Osk-VhhGFP4. We photobleached the entire NC area of stage-9 egg chambers and imaged fluorescence recovery over the next 3 h (Figure 4D). Within the first 30 min after photobleaching, both Dap-sfGFP and Dap-sfGFP; Osk-vhhGFP4 NC area recovered approximately 15% of the original mean fluorescence intensity. However, over the next 2.5 h, fluorescence recovery in the Dap-sfGFP; Osk-vhhGFP4 NCs plateaued, while the fluorescence of Dap-sfGFP NCs continued to increase by an additional 10% (Figure 4E). The initial 30 min fluorescence recovery in both cases is likely due to redistribution of fluorescent protein not within the plane of photobleaching. However, the continued fluorescence recovery by Dap-sfGFP NCs but not by Dap-sfGFP; Osk-vhhGFP4 NCs during the subsequent 30–180 min time period shows that when Dap protein is trapped in the oocyte, new Dap does not appear in the NCs. Thus, Dap protein originating in the oocyte is the major source of Dap protein in the NCs.

NC endocycles fit a model of coupled nonlinear oscillators

Since live imaging of egg chambers cannot capture the dynamics of more than one endocycle, we turned to modeling to provide a framework for understanding the system. To determine whether the oocyte-provided Dap regulates CycE dynamics among NC coordination groups, we modeled a network of asymmetrically coupled oscillators interconnected in the same way as the 16-cell cyst, with a transcriptionally quiescent oocyte and fifteen auxiliary NCs. Our goal in performing this analysis was to implement a coarse-grained model of our experimental system using a set of ordinary differential equations (ODEs) that could be used to propose a mechanism sufficient to explain our experimental observations and provide further insights that are not easily tested in an experimental setting. The results of our model’s predictions provide further proof of principle for our hypothesis that the oocyte plays a direct role in regulating NC coordination and is responsible for the observed groupwise structure within the developing cyst.

Assuming the contents of cells are well-mixed, the germline cell cluster can be modeled using a system of coupled ODEs. Within each NC, we modeled two components, X and Y, which generate a pattern of self-sustained nonlinear oscillations. Since Dap is not required for NC endocycles, and thus is not required as part of the minimal oscillatory circuit (Hong et al., 2003), component Y represents other negative regulators of CycE (Morgan, 2007). Though other negative regulators of CycE have been identified in different types of Drosophila endocycles, such as the salivary gland (Zielke et al., 2011), a comparable definitive characterization of the NC endocycle has not been performed. Thus, Y is left as a generalized term. The component X, which represents CycE, promotes its own production and, additionally, promotes the production of Y (Siu et al., 2012). In addition, X induces the production of a third component, W, a proxy for dap mRNA, which is directly transported to the oocyte. Once localized to the oocyte, dap mRNA produces a fourth component, Z, representing Dap protein, which is transported throughout the network diffusively, where it inhibits the autocatalytic component (X) of endocycles (Figure 5A). The details of this model are provided in the STAR methods.

Figure 5. Endocycling groups emerge from a model based on retrograde transport.

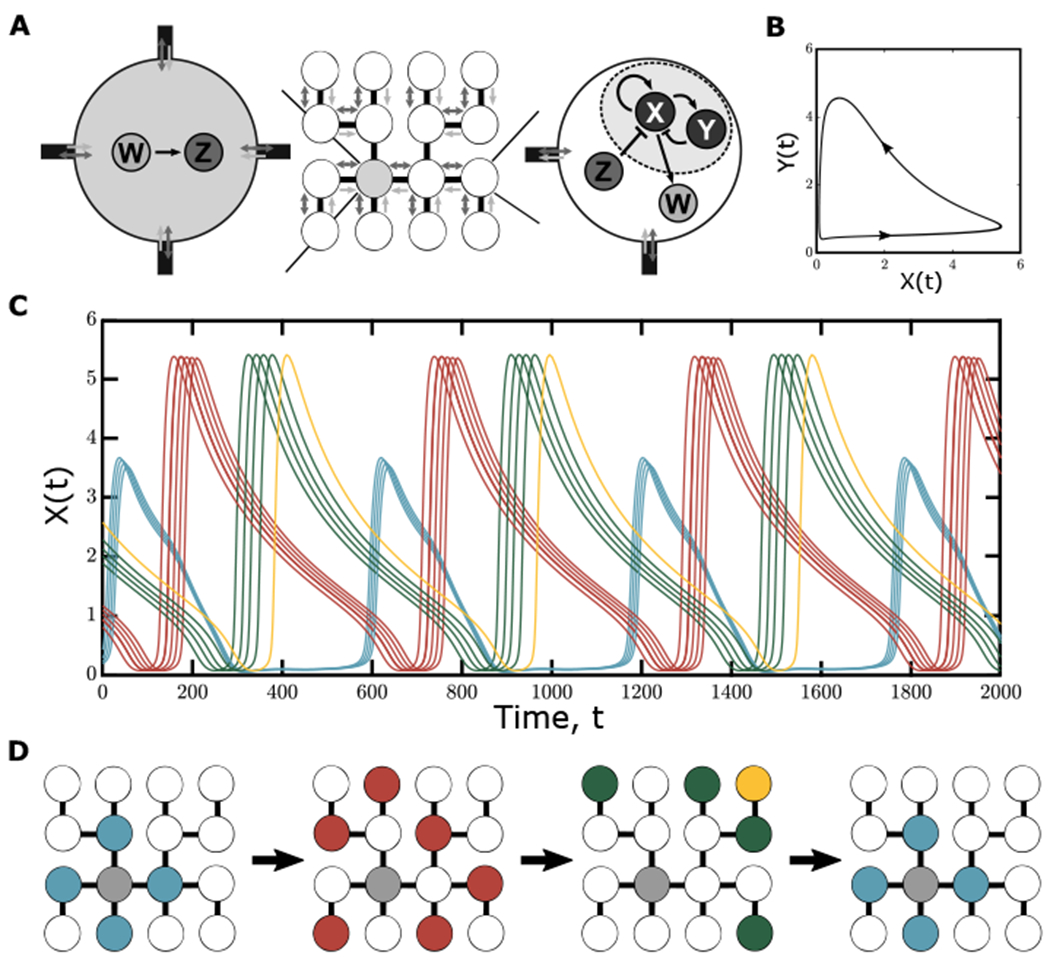
(A) Representation of the proposed reaction scheme and transport within the egg chamber: each NC contains two components, X (CycE) and Y (Negative regulators of CycE), which interact in a nonlinear way to produce oscillatory behavior. Additionally, X produces a component W (dap mRNA), which is directly localized to the oocyte. In the oocyte, W produces component Z (Dap protein), which passively diffuses back to the NCs, where it further inhibits the production of X. This transport-based model proves sufficient for the emergence of endocycling groups based on distance from the oocyte.

(B) The limit cycle behavior based on nonlinear interactions between X and Y within each NC.

(C) Temporal dynamics of component X in each NC taken after an initial transient. From randomized initial conditions, groups of NCs oscillate in synchrony when directed transport is present within the system.

(D) Schematic of dynamics of component X over time on the NC tree, as in Figure 1D.

We identified sets of model parameters such that the asymmetrically coupled oscillators in the network recapitulate the groupwise oscillatory structure based on the distance from the oocyte observed in our previous experimental observations of CycE. That is, the differences in cell cycle phase observed in the model are the result of network connectivity with respect to the source of the inhibitor (in this case, the quiescent oocyte). In addition, this model provides further insight into the mechanism responsible for the emergence of groups within the network system. In particular, the presence of the diffusible inhibitor is the driving factor in creating the groupwise hierarchy within the network of coupled oscillators. This is most apparent when the degradation rate of either Z or W is decreased, leading to less effective inhibition. In these cases, the oscillations within each group can be disrupted or altogether destroyed. This oscillator death starts from the cells connected directly to the oocyte, then spreads to cells two, three, and four connections away (Figures S4 and S5). The propagation of this behavior based on the diffusion of the inhibitory factor from the oocyte provides further evidence that the oocyte plays a direct role in establishing the oscillatory pattern seen within the network of coupled oscillators. We therefore conclude that the regulatory interactions present in this minimal model are sufficient to explain the emergence of grouped CycE patterns in the developing egg chambers (Figure 5).

NC volume regulation is lost when Dap is removed

If oocyte-supplied Dap is necessary for timing NC endocycles, then depleting Dap should disrupt the group coordination, and therefore the NC size hierarchy. Complete elimination of Dap mRNA and protein from the germline disrupts cyst patterning because the oocyte nucleus enters S-phase and loses specification (Hong et al., 2003). To overcome this problem and deplete Dap protein after specification of the oocyte, we took advantage of the deGradFP method, which targets GFP-tagged proteins for degradation (Caussinus and Affolter, 2016). We introduced a UASp-deGradFP transgene into Dap-sfGFP females and activated expression after oocyte specification using the otu-Gal4 driver (Figures 6A, 6B, S6A, and S6B). Consistent with our prediction, we found that these egg chambers maintain oocyte specification but lose the clear NC size and DNA content hierarchy (Figures 6C–6F), while maintaining a positive correlation between DNA content and NC volume (Figures 6G and 6H). The loss of the NC size hierarchy demonstrates a role for the cell cycle regulator Dap in the regulation of NC size, establishing a direct link between endocycle regulation and collective growth. This is consistent with our hypothesis that Dap protein is the coupling factor that regulates the timing of NC endocycles and allows for the coordination of collective NC growth.

Figure 6. Post-translational degradation of Dap disrupts cyst volume hierarchy.

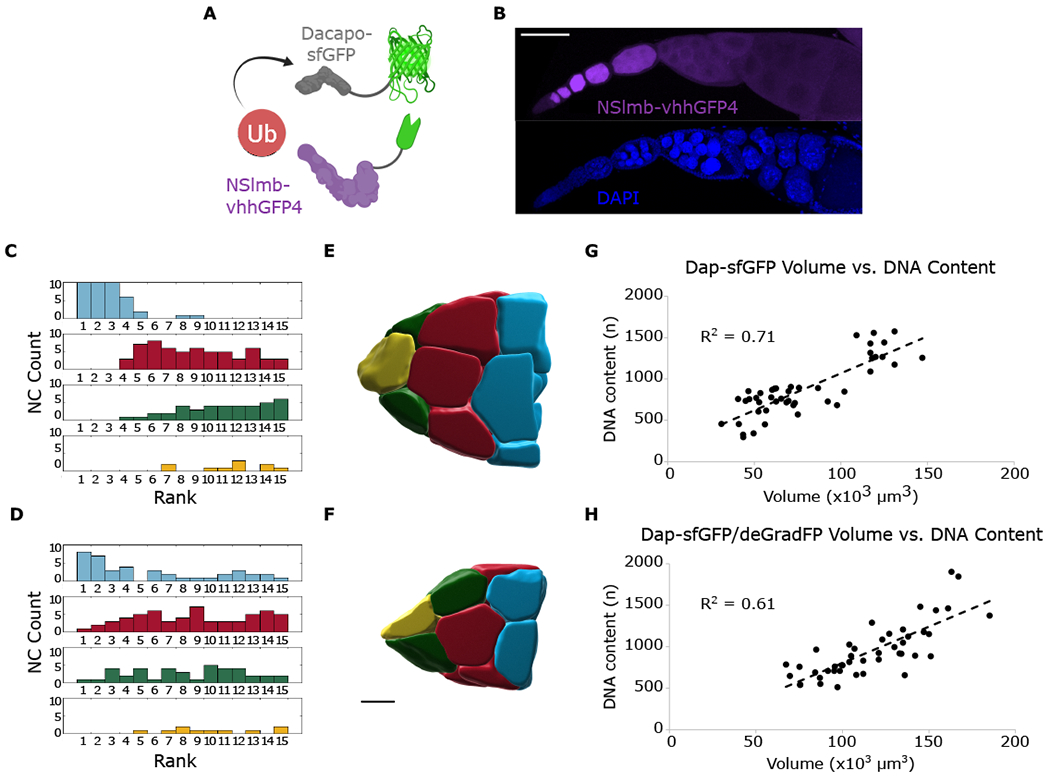
(A) Schematic showing ubiquitination of Dap-sfGFP targeted by interaction with deGradFP.

(B) Confocal z series projection of deGradFP (purple) and DAPI (blue) localization. Localization of deGradFP is uniform within cysts after oocyte specification and tapers off at later stages.

(C and D) Group histograms of ranked volumes for Dap-sfGFP (C) and Dap-sfGFP; deGradFP (D). Brown-Forsythe test for equality of variances for blue group, p = 5.6 × 10⁻⁰⁶, indicating difference in variance is statistically significant.

(E) Reconstruction of Dap-sfGFP NCs. Size hierarchy is observed.

(F) Reconstruction of Dap-sfGFP; deGradFP NCs. Size hierarchy is disrupted.

(G and H) Quantification of NC volume and DNA content from stage 9 egg chambers for Dap-sfGFP (G) and Dap-sfGFP; deGradFP (H); n = 3 for each condition. Scale bars, 100 μm (B), 40 μm (E) and (F).

In systems of coupled oscillators, synchronization may occur spontaneously (Pikovsky et al., 2001). This results in the emergence of a common frequency of oscillation, though not all oscillations are necessarily in phase. Out-of-phase synchronization of groups is consistent with our observations and models for NCs that are not directly connected to the oocyte (Figures 2A and 5C). Therefore, synchronization of the endocycles in these more distant cells would result in a common frequency of oscillation. Further analysis of the data from fixed samples analyzed in Figures 2B and 2C supports this conclusion: using egg-chamber volume as a proxy for time, we performed least-squares spectral analysis (see STAR methods) to estimate the frequency of CycE and Dap oscillations over the course of oogenesis. For both the CycE and Dap, the same common frequency of approximately 0.15 endocycles/h –or about one endocycle every 6.5–7 h– emerged for all groups (Figure S7). This rate of endocycling is consistent with our measurements of DNA content, which show that NCs have undergone 9–10 endocycles during this 2.5-day period of oogenesis (King, 1970; Spradling, 1993, Data S1). Since the oocyte-proximal cells have roughly the same period as the other NCs during these stages of oogenesis, any oocyte-proximal group advantage would have been acquired prior to synchronization. This advantage is likely due to an asymmetric distribution of factors within the cyst (Huynh and St Johnston, 2004) that induce the NCs closer to the oocyte to enter the endocycle sooner than NCs farther from the oocyte. Since DNA replication is an exponential process, this advantage would be exponentially reinforced over time, and NCs closer to the oocyte would grow faster. Thus, we propose the NC volume hierarchy is established initially and maintained by the coupling of NC endocycles.

DISCUSSION

Our genetic and imaging data provide clear evidence of bidirectional cell communication within the ovarian germline cluster: a product of the NCs (dap mRNA) is converted to a product of the oocyte (Dap protein), which then regulates the growth timing of the very cells in which the first product was created. It is important to note, however, that other spatially regulated elements may contribute as well. We propose that as the NCs grow and become more biosynthetically active, production of dap transcripts that are then supplied to the oocyte increases, leading to more Dap protein diffusing within the system. However, based on the effect of Dap depletion on NC volume and DNA content and on modeling of the CycE/Dap circuit, this feedback must be tuned within a specific range in order for proper NC growth regulation to occur. To the best of our knowledge, this is the first demonstration of a growth-regulating bidirectional feedback mechanism between the Drosophila oocyte and its support cells.

The regulatory logic established here has much in common with the regulatory strategies emerging from studies of mammalian oogenesis, where somatic granulosa cells supply the oocyte with regulatory molecules and metabolic precursors (Clarke, 2018). First, the growth of granulosa cells relies on signals originating from the oocyte. The granulosa cells fail to enter mitosis and proliferate in the absence of an oocyte. Thus, oocyte-derived proteins control cell cycle dynamics (either endocycles or mitotic divisions) in both Drosophila and mammalian oogenesis. Second, similar to the Drosophila germline cluster, where the oocyte controls endocycles in both directly attached and distant NCs, mammalian oocytes influence the growth of both directly attached and distant granulosa cells. This depends on the long-range effects of the oocyte-derived paracrine signals, most notably growth differentiation factor 9 (GDF9) (Clarke, 2018). While the predominant view is that these signals arrive at their target cells by diffusion through transzonal projections and a series of gap junctions (Kidder and Vanderhyden, 2010), a recent study suggests that they can also move through cytoplasmic bridges, which are similar to the RCs in the Drosophila germline cluster (Komatsu and Masubuchi, 2018) (Figure 7).

Figure 7. Bidirectional communication between oocyte and support cells occurs in both mammals and flies.

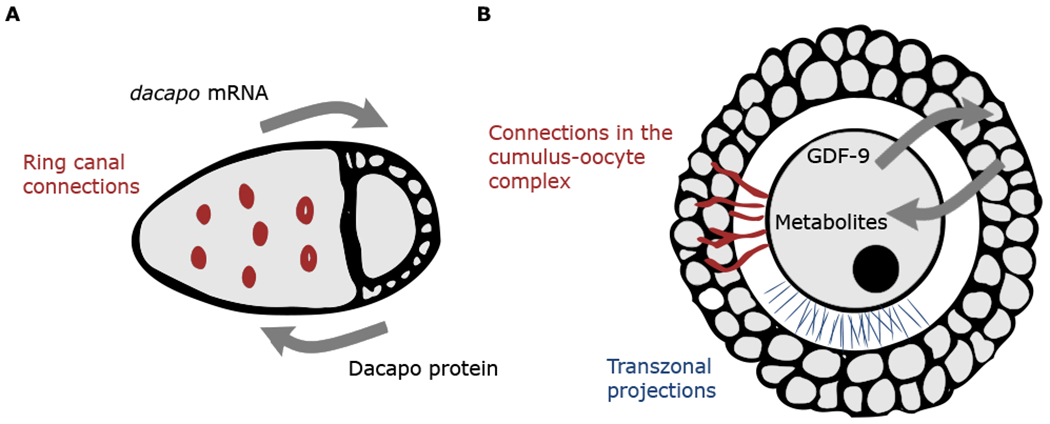
(A) Schematic of a Drosophila egg chamber. Exchange of molecules occurs via physical connections through RCs.

(B) Schematic of a secondary mammalian follicle. Exchange of molecules is thought to occur via physical connections, including transzonal projections and connections in the cumulus-oocyte complex.

Third, and perhaps most significantly, the diffusion of oocyte-derived factors is part of a feedback loop between the oocyte and cells needed for its growth. In Drosophila, a direct read out of the NC biosynthetic capacity (dap transcript) is a precursor for the signal that in turn regulates NC growth (Dap protein). This allows for regulation of NC growth at the tissue level and, indirectly, regulates oocyte growth, as the contents of the NCs are eventually transported into the oocyte. In mammals, GDF9 and bone morphogenetic protein 15 (BMP15) control the production and oocyte-directed flux of glycolytic precursors, cyclic nucleotides, and amino acids that are synthesized by the granulosa cells and are essential for oocyte development and growth (Clarke, 2018). This spatially distributed feedback strategy may determine the “stop” condition for the growth of supporting cells, ensuring robust loading of the oocyte with factors essential for its development (Jones and Shikanov, 2019). In parallel, we speculate that Dap may play a role in the exit of NCs from the endocycle, which is consistent with the role of Dap in terminal differentiation of many different cell types. Interestingly, the mammalian homolog of Dap, p27, has a similar localization pattern in the mammalian follicle as it does in the Drosophila germline. Nuclear protein levels of p27 are consistently high within the oocyte nucleus, while levels oscillate in nuclei of the growing granulosa cells (Pérez-Sanz et al., 2013).

In conclusion, the structural simplicity of the Drosophila germline cluster and its amenability to live imaging and sophisticated genetic perturbations make it an attractive model for exploring the systems-level properties of collective dynamics of the oocyte and supporting cells. Our computational modeling suggests that these dynamics can be interpreted within the framework of nonlinear oscillators coupled on a tree-like network, a mathematical structure that poses a wealth of interesting questions, such as the emergence of synchronized regimes and their dependence on the network topology (Golubitsky and Stewart, 2016; Pikovsky et al., 2001; Strogatz, 2003). These questions are especially interesting given a plethora of network structures revealed by studies on female germline clusters in different organisms (Kloc et al., 2004; Lei and Spradling, 2016; Świątek and Urbisz, 2019).

STAR★METHODS

RESOURCE AVAILABILITY

Lead contact

Additional information and requests may be directed to Stanislav Y. Shvartsman (stas@princeton.edu).

Materials availability

Materials or fly strains available upon request.

Data and code availability

Data and code are available upon request.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Fly lines and crosses

y¹ w^67c23 (Bloomington Drosophila Stock Center [BDSC] 6599) flies were used as the wild-type for DNA content quantifications. CycE-sfGFP (this paper) was used for CycE reconstructions/t-SNE analysis. CycE-sfGFP was crossed with mCherry-Pavarotti (marking ring canals) (Derivery et al., 2015) to make stable lines used for live imaging. Dap-sfGFP flies were crossed to Osk-vhhGFP4 to create flies homozygous for both genetic elements. Dap-sfGFP was crossed with either UASp-deGradFP (BDSC 58739) or otu-Gal4 (BDSC 58424) to make two different stable lines that were then crossed together at 25 ° C. Crosses for CRISPR DsRed positive selection removal were done at 25 °C. All other crosses were done at 23 °C. Stocks were maintained at 23 °C on standard cornmeal/agar media.

METHOD DETAILS

Design of endogenously tagged and transgenic flies

Endogenously tagged fly lines were created using the flyCRISPR scarless gene editing method (flycrispr.molbio.wisc.edu) Bier et al., 2018). Constructs were designed to insert superfolder GFP or Dendra2 at the C-terminus of Dap or CycE. Primer sequences are listed in the key resources table.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Rabbit anti-Phosphotyrosine	Abcam	Cat# ab179530
Goat anti-Rabbit Alexa Fluor 568	Invitrogen	Cat# A-11036
Donkey anti-Rabbit Alexa Fluor 647	Invitrogen	Cat# A-31573
Mouse anti-Dap	DSHB	NP1
Goat anti-mouse Alexa Fluor 568	Invitrogen	Cat# A-11004
Chemicals, peptides, and recombinant proteins
Ni-NTA agarose resin (Qiagen)	Qiagen	Cat# 30210
Pierce BCA Protein Assay Kit	Thermo Scientific	Cat# 23227
Alexa Fluor 568 phalloidin	Thermo Scientific	Cat# A12380
RapiClear 1.47	SUNJin Lab	Cat# RC147001
Aqua-Poly/Mount	Polysciences	Cat# 18606
CellMask green plasma membrane stain	Invitrogen	Cat# C37608
CellMask far red plasma membrane stain	Invitrogen	Cat# C10046
Colchicine	Sigma-Aldrich	Cat# PHR1764
sfGFP smFISH Probes	(Eichler et al., 2020)	N/A
Critical commercial assays
Click-iT Plus EdU Alex Fluor 647 Flow Cytometry Assay Kit	Invitrogen	Cat# C10634
Experimental models: organisms/strains
y[1] w[67c23]	Bloomington Drosophila Stock Center	BDSC 6599
CycE-sfGFP	This paper	N/A
Dap-sfGFP	This paper	N/A
Dap-Dendra2	This paper	N/A
Ubi > mCherry-Pavarotti	Gift of Emmanuel Derivery	N/A
P{nos-Cas9.R}attP2	Bloomington Drosophila Stock Center	BDSC 78782
P{nos-Pbac}attP2	(Keenan et al., 2020)	N/A
UASp-deGradFP	Bloomington Drosophila Stock Center	BDSC 58739
P{otu-GAL4::VP16.R}1	Bloomington Drosophila Stock Center	BDSC 58424
P{osk-vhhGFP4}VK33	This paper	N/A
PBac{yellow[+]-attP-3B}VK00033	Bloomington Drosophila Stock Center	BDSC 9750
Oligonucleotides
(1) Dacapo-chiRNA-F	CTTCGCTTTGGGGCGATGTTGAAG	N/A
(2) Dacapo-chiRNA-R	AAACCTTCAACATCGCCCCAAAGC	N/A
(3) CyclinE-chiRNA-F	CTTCGGGTGAGTGTGAGAGGATGA	N/A
(4) CyclinE-chiRNA-R	AAACTCATCCTCTCTCACTCACCC	N/A
(5) dsRed-side-F	GGTGGATCTGGAGGTTCC	N/A
(6) sfGFP-side-R	CGCGGCCGCTAAATTCAATTC	N/A
(7) sfGFP-side-F	AATTCGTTTAAACCTGCAGGAC	N/A
(8) dsRed-side-R	GGAACCTCCTGAACCACC	N/A
(9) Dacapo-LF	ggcgaattgaatttagcggccgcgCTCCATAAGGGGTTGTTTGATTGGTTTTAAGTCCAC	N/A
(10) Dacapo-LR	agccgccggaacctccagatccaccGTTGTGGCGCGGCCGCTTCAACAT	N/A
(11) Dacapo-RF	aggttctggtggttcaggaggttccTAATGCTCCAGATTCGCT	N/A
(12) Dacapo-RR	ctagtcctgcaggtttaaacgaattTTGATGTATGAGTTGAAT	N/A
(13) CyclinE-LF	gggcgaattgaatttagcggccgcgCTGCACAGAGCGGGACAT	N/A
(14) CyclinE-LR	agccgccggaacctccagatccaccGGGATTGCTTCTACTGCT	N/A
(15) CyclinE-RF	aggttctggtggttcaggaggttccTGAGAGATTCGCCTCACT	N/A
(16) CyclinE-RR	ctagtcctgcaggtttaaacgaattCCTTTTGAATGTACATAA	N/A
(17) Dacapo PAM F	TGTTGAAGCGtCCGCGCCACAA	N/A
(18) Dacapo PAM R	TCGCCCCAAAGTGTGCCC	N/A
(19) CyclinE PAM F	TGCTCTTGGCtATCATCCTCT	N/A
(20) CyclinE PAM R	GTGAGGCGAATCTCTCAG	N/A
(21) Scarless Dendra Adaptor F	ccaggtgtggATTAACCCTAGAAAGATAATCATATTGTGACGTACGTTAAA	N/A
(22) Scarless Dendra Adaptor R	gggtgttcatACTACCCCCTGAGCCGCC	N/A
(23) Dendra Scarless Adaptor F	agggggtagtATGAACACCCCGGGAATTAACCTG	N/A
(24) Dendra Scarless Adaptor R	tagggttaatCCACACCTGGCTGGGCAG	N/A
(25) White gene side_fwd	accgggcccctagtatgtatgtaagttaataaaaccc	N/A
(26) White gene side-rev	ccagttggacggtaccctgatactccag	N/A
(27) Amp Side_fwd	ctccagctaaggatccgagcttgaatcaagatacatatatgcaaattttg	N/A
(28) Amp Side_rev	atacatactaggggcccggtacgtaccc	N/A
(29) nanobody + stop_fwd	tcagggtaccgtccaactggtggagtctg	N/A
(30) nanobody + stop_rev	gctcggatccttagctggagacggtgac	N/A
Recombinant DNA
PQE80 vector	E. Goldsmith UT Southwestern	N/A
pU6-BbsI-chiRNA	(Gratz et al., 2013)	Addgene plasmid # 45946
pScarlessHD-sfGFP-DsRed	Gift from Kate O’Connor-Giles	Addgene plasmid # 80811
Dendra2-H3.3-N-14	Gift from Michael Davidson	Addgene plasmid # 57725
pcDNA3_NSlmb-vhhGFP4	(Caussinus et al., 2011)	Addgene plasmid # 35579
pattB-Osk-sfGFP	(Eichler et al., 2020)	Gavis Lab
Software and algorithms
Imaris	Bitplane	http://www.bitplane.com
MATLAB	Mathworks	https://www.mathworks.com
Jupyter Notebook	Project Jupyter	https://jupyter.org/
NumPy	(Harris et al., 2020)	https://numpy.org/
Pandas	(McKinney, 2010)	https://pandas.pydata.org/
Matplotlib	(Hunter, 2007)	https://matplotlib.org/
Seaborn	(Waskom et al., 2017)	https://seaborn.pydata.org/
Scikit-Learn library	(Pedregosa et al., 2011)	https://scikit-learn.org/

The guide RNA plasmid pU6-BbsI-chiRNA (Gratz et al., 2013) was digested with BbsI and then annealed primers (1) and (2) or (3) and (4) were cloned into the cut vector via T4 ligation.

The homology-directed repair plasmid pHD-sfGFP-ScarlessDsRed was amplified with two sets of primers (5) and (6), and (7) and (8). 1 kb of genomic DNA on both sides of the targeted region was amplified with PCR from the genomic DNA of flies expressing Cas9 (BDSC 78782). Primers used for flanking regions of Dap were (9) and (10), and (11) and (12). Primers used for flanking regions of CycE were (13) and (14), and (15) and (16). For both pHD-sfGFP-ScarlessDsRed-Dap and pHD-sfGFP-ScarlessDsRed-CycE, a four-piece Gibson assembly was performed with both pHD-sfGFP-ScarlessDsRed PCR products and the two corresponding PCRs of the flanking genomic regions. In order to avoid re-cutting, Q5 Site-Directed Mutagenesis (NEB) of the PAM regions was performed either with primers (17) and (18) for Dap, or primers (19) and (20) for CycE.

For insertion of Dendra2 at the C-terminus of Dap, pHD-sfGFP-ScarlessDsRed-Dap-PAM_Mut was amplified with primers (21) and (22). The Dendra2-H3.3-N-14 plasmid was amplified with primers (23) and (24). A two-piece Gibson assembly was then performed. The same guide RNA plasmid as above was used.

Following transgenesis and removal of the Cas9 by crossing, flies were then crossed to a line containing nos-pBac transposase (Keenan et al., 2020) to flip out the DsRed selection cassette. F1s that had lost DsRed expression were sequenced and used to establish a stable line.

For creation of the pattB-osk-vhhGFP4 plasmid, the pattB-osk-sfGFP plasmid from (Eichler et al., 2020) amplified using primer pairs (25) and (26), and (27) and (28). The pcDNA3_NSlmb-vhhGFP4 plasmid (Caussinus et al., 2011) was amplified with primers (29) and (30). A three piece Gibson assembly was then performed.

All CRISPR engineering and transgenesis was conducted by BestGene Inc. CRISPR plasmids were injected into Cas9-expressing flies (BDSC 78782). pattB-osk-vhhGFP4 DNA was injected into flies containing the attP site VK33 (BDSC 9750). All endogenously tagged and transgenic flies created for this paper are homozygous viable and fertile.

sfGFP expression and purification

The sfGFP coding sequence was cloned into BamH and HindIII sites of the pQE80 vector. Protein expression was induced with 1 mM IPTG at OD₆₀₀=0.6-0.8, and cultures were grown at 22 °C for 6 h with agitation at 250 rpm. Cell pellets were collected and stored at −20 °C. Cell pellets were then resuspended in 40 ml Lysis buffer (10 mM imidazole, 300 mM NaCl, 50 mM NaH2PO4, pH 8), and treated with lysozyme. The lysate was sonicated on ice and cleared by centrifugation. The supernatant was sterile filtered and sfGFP were purified using Ni-NTA agarose resin (Qiagen) following the manufacturer’s recommendations. Aliquots were snap frozen in liquid nitrogen and stored at −80 °C. The concentration of the purified sfGFP was estimated by Pierce BCA Protein Assay Kit (Thermo Scientific).

Immunofluorescence and stains

Ovaries from females fed for two days on standard Drosophila food supplemented with baker’s yeast were dissected in PBS and fixed at room temperature in 4% formaldehyde in PBS for 20 minutes. All wash steps were performed in 0.1% Tween-20 in PBS and antibodies were diluted in blocking solution (1% BSA in PBS). Unless otherwise mentioned below, ovaries were permeabilized for an hour in 1% Triton-X100 in PBS, blocked for 2 hours, and then stained with rabbit anti-phosphotyrosine (1:500) (Abcam) at 4 °C. Ovaries were then washed and stained with goat anti-rabbit Alexa Fluor 568 (1:400) (Invitrogen) or donkey anti-rabbit Alexa Fluor 647 (1:400) (Invitrogen) for two hours at room temperature. Egg chambers were subsequently washed and stained with 250 ng/mL DAPI for 5 minutes.

For DNA quantifications, egg chambers were washed and stained with 50 ng/mL DAPI for 15 minutes and then washed overnight again.

For anti-Dap immunofluorescence, egg chambers were blocked in both 1% BSA and 5% NGS in PBS and then stained overnight at 4 °C with mouse anti-Dap (1:250) (DSHB) and the rabbit anti-phosphotyrosine mentioned above. All subsequent wash steps were performed with the PBS-Tween buffer kept at an ice-cold temperature. The secondary antibody wash was also performed overnight at 4 °C with goat anti-mouse Alexa Fluor 568 (1:400) (Invitrogen) and the donkey anti-rabbit mentioned above.

To visualize Osk-vhhGFP4 localization and DegradFP expression, egg chambers underwent standard permeabilization and blocking and were then incubated overnight at 4 °C with 6.3 μg/mL purified sfGFP in blocking medium.

For visualization of membranes, fixed egg chambers were stained with Alexa Fluor 568 phalloidin (1:1000) (Thermo) for 2 hours. This step was sometimes substituted for the anti-phosphotyrosine immunostaining because it also allows for visualization of ring canals.

Optical clearing and mounting

To mitigate the drop in fluorescence signal that can occur when imaging thick samples and ensure accurate quantification of fluorescence in all NCs in an egg chambers, egg chambers were “fully cleared.” An egg chamber was determined to be fully cleared if the fluorescence intensity of follicle cell DAPI signal was the same at both the top and bottom of the Z-stacks. Clearing was achieved by mounting egg chambers in a mixture of 75:25 RapiClear 1.47 (SUNJin Lab):Aqua-Poly/Mount (Polysciences). For larger egg chambers that are much thicker, a pre-clearing step was performed by washing overnight at 4 °C in 75:25 RapiClear:PBS, then rinsing very quickly with 500 μl PBS before mounting in 100% RapiClear. Slides were stored at 4 °C.

Ex-vivo ovary culture for live-imaging

Ovaries from well-fed females were dissected in growth media consisting of Schneider’s medium supplemented with fetal bovine serum, insulin, and streptomycin/penicillin (Prasad and Montell, 2007). Ovaries were then transferred to a MatTek dish and large drops of media were added around the rim of the dish to combat the effects of evaporation. Egg chambers were then imaged for 6-8 hours.

For photoconversion experiments, dissected ovaries were transferred to growth media with CellMask green plasma membrane stain (1:1000) (Invitrogen). After 30 minutes the media was removed and fresh growth media was added to dilute out the stain. Ovaries were then transferred to a MatTek dish for imaging. Egg chambers were imaged for 50 minutes.

For FRAP, dissected ovaries were transferred to growth media with CellMask far red plasma membrane stain (1:1000) (Invitrogen). After 30 minutes the media was removed and fresh media added and transferred to a MatTek dish. Photobleaching was performed on the entire NC region as marked by the membrane signal. Egg chambers were imaged for 3 hours.

EdU incorporation

All steps were performed using reagents from the Click-iT Plus EdU Alex Fluor 647 Flow Cytometry Assay Kit (Invitrogen). Egg chambers were cultured in growth media with 10 μm EdU for 1 hour. Mixing/wash steps were scaled up from the manufacturer’s instructions to 500 μl per sample and performed by rocking egg chambers on a nutator. Egg chambers were then fixed and stained with the standard immunofluorence protocol listed above for visualization of ring canals and DNA.

Colchicine feeding experiments

Dap-sfGFP females were fed yeast paste containing 50 mg/mL colchicine for 48 hours prior to dissection. Ovaries were fixed and hydridized with smFISH probes for sfGFP according to (Eichler et al., 2020).

Microscopy

Imaging was performed on a Nikon A1R scanning confocal microscope. The 60x 1.4/NA Plan-Apo oil and 40x 1.3/NA Plan-Apo oil objectives were used for both live and fixed imaging. Z-stacks of fixed samples were captured with a step size of 400 nm. For live imaging Z-stacks were captured with a z-step of 1.5 μm. For photoconversion experiments, Dap-Dendra2 was converted from 507 nm emitting to 573 nm emitting fluor in the posterior region of the oocyte using a focused 405 nm laser beam. For FRAP experiments, the 488 nm laser was used to bleach the entire NC area.

Image processing

For movies of CycE-sfGFP; mCherry-Pavarotti egg chambers, signal from the TRITC channel was processed with the automatic surfaces creation in Imaris (v9.2.1). “Objects” from the follicle cells were removed so only signal from NC ring canals remained. A new channel was then created from a mask of this remaining signal. Egg chambers not of interest were masked for clarity of presentation in figures.

Network transport model

We modeled the concentrations of nuclear and cytoplasmic components within the NCs and oocyte using a set of ordinary differential equations (ODEs). These equations describe the temporal rate of change of cell cycle regulator CycE (X) and some undefined inhibitor of this regulator (Y), Dap mRNA (W), and Dap protein (Z). In this model, X and Y create a limit cycle within each NC nucleus in the network (Ferrell et al., 2011; Novák and Tyson, 2008). The production of component W is induced by X, which is shuttled into the NC’s cytoplasm and asymmetrically localized via active transport to the oocyte through connections of the network. Only within the oocyte, W induces production of component Z, which then passively diffuses throughout the cell cluster. Once Z has diffused back to a NC, it is able to shuttle into the nucleus and inhibit further production of component X.

Model equations

The interaction of the nuclear components X and Y in each NC are taken from a previously established model for an activator-inhibitor oscillator (Fall et al., 2005). This choice of model is appropriate as CycE is a known auto-promoter and can promote the production of some of its inhibitors (Siu et al., 2012). Thus, the first rational function in Equation 1 highlights the autocatalytic nature of CycE, while the second function represents the inhibitory nature of generalized component Y. Additionally, we assume that X is further inhibited by Z as it flows back from the oocyte into NCs, yielding the final inhibitory function in Equation 1. Both of these inhibitors are assumed to affect the production rate of X. Finally, the component X can also degrade linearly with rate k₂.

The production of the general inhibitor Y is assumed to occur at some basal rate k₃. In addition, the component X acts to inhibit the degradation of Y, yielding the second term in Equation 2. That is, presence of X helps to reduce the effective degradation of component Y in each cell. As this model is used to demonstrate the ability of a diffusive inhibitor to perturb oscillations in a coupled network based on network structure, these interactions are sufficient to induce oscillations in an uncoupled system.

The production of W is dependent on the presence of X and occurs at some rate k₅, and this W is degraded at some rate k₆. Similarly, W produces Z at a rate k₇ only in the oocyte, though Z is degraded in all cells at a rate k₈. Both W and Z can be transported throughout the network at rates v₂ and v₃, respectively, although W is transported unidirectionally toward the oocyte while Z is purely diffusive. The general set of ODEs within each cell can therefore be written as:

$$\frac{d{X}_i}{dt}={\left[v_1\left(\frac{{\epsilon }^2+{\left(\frac{X_i}{K_m}\right)}^2}{1+{\left(\frac{X_i}{K_m}\right)}^2}\right)\left(\frac{1}{1+\left(\frac{Y_i}{K_n}\right)}\right)\left(\frac{1}{1+\left(\frac{Z_i}{K_z}\right)}\right)-k_2{X}_i\right]}_{i>1},$$ (Equation 1)

$$\frac{d{Y}_i}{dt}={\left[k_3-\frac{k_4{Y}_i}{1+{\left(\frac{X_i}{K_j}\right)}^2}\right]}_{i>1},$$ (Equation 2)

$$\frac{d{W}_i}{dt}=k_5{X}_i-k_6{W}_i+v_2{\left[\underset{\_}{\mathit{A}}(\alpha )\underset{\_}{\mathit{W}}\right]}_i,$$ (Equation 3)

$$\frac{d{Z}_i}{dt}=F(i)-k_8{Z}_i+v_3{\left[\underset{\_}{\mathit{A}}(\beta )\underset{\_}{\mathit{Z}}\right]}_i,$$ (Equation 4)

where i = 1 is the oocyte and all i> 1 are the supporting NCs, F(i) is a piecewise function whose value is k₇W₁ when i = 1 and 0 otherwise, and A(x) is the adjacency matrix that describes the asymmetric transport present within the connected network of cells. For the 16-cell network we seek to model, the adjacency matrix can represented as follows:

$$\underset{\_}{\mathit{A}}\left(x\right)=\left(\begin{array}{cccccccccccccccc}-4x\hfill & (1-x)-(1+2x)\hfill & (1-x)\hfill & 0\hfill & (1-x)\hfill & 0\hfill & 0\hfill & 0\hfill & (1-x)\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ x\hfill & 0\hfill & 0\hfill & (1-x)\hfill & 0\hfill & (1-x)\hfill & 0\hfill & 0\hfill & 0\hfill & (1-x)\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ x\hfill & 0\hfill & -(1+x)\hfill & 0\hfill & 0\hfill & 0\hfill & (1-x)\hfill & 0\hfill & 0\hfill & 0\hfill & (1-x)\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & x\hfill & 0\hfill & -(1+x)\hfill & 0\hfill & 0\hfill & 0\hfill & (1-x)\hfill & 0\hfill & 0\hfill & 0\hfill & (1-x)\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ x\hfill & 0\hfill & 0\hfill & 0\hfill & -1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & (1-x)\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & x\hfill & 0\hfill & 0\hfill & 0\hfill & -1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & (1-x)\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & x\hfill & 0\hfill & 0\hfill & 0\hfill & -1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & (1-x)\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & x\hfill & 0\hfill & 0\hfill & 0\hfill & -1\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & (1-x)\hfill \\ x\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & (x-1)\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & x\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & (x-1)\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & x\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & (x-1)\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & x\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & (x-1)\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & x\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & (x-1)\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & x\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & (x-1)\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & x\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & (x-1)\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & x\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill & (x-1)\hfill \end{array}\right).$$

This adjacency matrix is enumerated based on the unique label that can be given to each cell in our 16-cell cyst, as shown in previous work (Imran Alsous et al., 2017). The argument for this function represents the bias in cell-cell transport between adjacent cells. For example, x = 1 corresponds to pure transport away from the oocyte, which can be seen by the first row in the matrix correspond to having things only leaving cell 1. On the other hand, a similar argument can be used to see that x = 0 corresponds to pure transport toward cell 1 (the oocyte). Again, this can be seen most readily by noticing that the first row contains terms that serve only to “feed” the oocyte. Because the transport of W is unidirectional toward the oocyte, α = 0; in contrast for the simple diffusion of Z, β = 0.5. These equations can be rescaled by ${\widehat{X}}_i=X_i/K_m$, ${\widehat{Y}}_i=Y_i/K_n$, ${\widehat{W}}_i=W_i{v}_1/k_5{K}_m^2$, ${\widehat{Z}}_i=Z_i{v}_1^2/k_5{k}_7{K}_m^3$, and $\tau =t{v}_1/K_m$, yielding the following set of ODEs:

$$\frac{d{\widehat{X}}_i}{d\tau }={\left[\left(\frac{a+{\widehat{X}}_i^2}{1+{\widehat{X}}_i^2}\right)\left(\frac{1}{1+{\widehat{Y}}_i}\right)\left(\frac{1}{1+f{\widehat{Z}}_i}\right)-b{\widehat{X}}_i\right]}_{i\ne 1},$$ (Equation 5)

$$\frac{d{\widehat{Y}}_i}{d\tau }={\left[c-d\frac{{\widehat{Y}}_i}{1+e{\widehat{X}}_i^2}\right]}_{i\ne 1},$$ (Equation 6)

$$\frac{d{\widehat{W}}_i}{d\tau }={\widehat{X}}_i-g{\widehat{W}}_i+\sigma {\left[\underset{\_}{\mathit{A}}(\alpha )\underset{\_}{\widehat{\mathit{W}}}\right]}_i,$$ (Equation 7)

$$\frac{d{\widehat{Z}}_i}{d\tau }=\widehat{F}(i)-h{\widehat{Z}}_i+\gamma {\left[\underset{\_}{\mathit{A}}(\beta )\underset{\_}{\widehat{\mathit{Z}}}\right]}_i,$$ (Equation 8)

where $\widehat{F}\left(i\right)$ is now ${\widehat{W}}_1$ when i = 1 and 0 otherwise. We are now left with 10 parameters, (a,b,c,d,e, f ,g,h,σ,γ), whose definitions are given (See table below). Throughout our analysis, the parameters (a, b, c, d, e) are taken to be (0.01, 0.1, 0.01,0.1, 100), as this set of values is sufficient to create a limit cycle between X and Y in the absence of all other components. This leaves five other parameters:(f ,g,h,σ, γ).

Nondimensionalized parameters for the system of ODEs in Equations 5, 6, 7, and 8

Name	Definition	Name	Definition
a	ε2	f	$k_5{k}_7{k}_m^3/v_1^2{k}_z$
b	k2Km/v1	g	k6Km/v1
c	k2Km/v1Kn	h	k8Km/v1
d	k4Km/v1	σ	v2Km/v1
e	$k_m^2/k_j^2$	γ	v3Km/v1

Oscillatory behavior and emergence of groups in 16-cell system

Within the vastly complex system represented by Equations 5, 6, 7, and 8, we seek to probe the various groupwise behavior, with respect to the nuclear component X, that may exist depending on the differential rates of transport σ and γ, as well as the how Z may skew the oscillations within the NCs as it flows back from the oocyte via diffusion. In all cases, we continue to assume that (a, b, c, d, e, α, β) = (0.01, 0.1, 0.01, 0.1, 100, 0, 0.5) are fixed.

When the amounts of X and Y are started from randomized initial conditions within the NC, and the concentrations of all other components are initially set to zero, certain sets in the 5-D parameter space (f , g, h, σ, γ) cause the emergence of distinct groups of oscillating NCs. Notably, these emerging groups appear to synchronize their phase based on network distance from the oocyte, in a similar fashion to the structure observed for NC volumes in the developing Drosophila egg chamber (Imran Alsous et al., 2017). One such example is the parameter set (f , g, h, σ, γ) = (0.02, 0.02, 0.85, 2, 0.035), which after an initial transient produces dynamics of component X as shown (Figure 3C). This is just one example of a parameter set that shows the feasibility of our minimal model to explain the behavior seen in developing egg chambers.

Computation

All of the systems of ODEs were written in MATLAB and simulated using the ode23s routine. Relevant parameter sets (above) were chosen to highlight the emergence of groupwise oscillations in the 16-cell system. Initial conditions were selected such that the initial amount of W and Z in all cells was 0, and the initial amounts of X and Y in each NC was taken from the offset uniform distribution U(0, 1) + 1.25 and run for a long transient to allow for the emergence of groups.

QUANTIFICATION AND STATISTICAL ANALYSIS

Quantification of NC DNA content

To quantify NC DNA content, DAPI signal from Z-stacks of cleared egg chambers were analyzed using the automatic surfaces creation in Imaris. Integrated intensity was collected for each generated NC nucleus “object.” Signals from NC nuclei were then normalized to the average signal of pre-stage 6, diploid follicle cell nuclei to determine raw DNA content for NC.

Quantification of NC nuclear CyclinE and Dap content

To quantify the nuclear localization of CycE-sfGFP or antibody-stained Dap in each NC, we used manual surface creation in Imaris. We identified NC by their unique position in the cell tree, and then determined a fluorescence region of interest (ROI) for each NC nucleus identified by DAPI signal in each NC. We then recorded the relative fluorescence inside each ROI. To account for divergence among nuclear volumes in egg chambers, we divided each fluorescence value by the volume of its ROI. To compare NC fluorescence values across multiple egg chambers, we then converted these values to pseudo-t-scores, by normalizing each value by the mean and standard deviation of all the NC fluorescence values of the corresponding egg chamber. For our analyses, we expressed the normalized fluorescence data of each NC i as a vector $v_i\in {ℝ}^n$ for i = 2, 3, …16, where n is the number of egg chambers analyzed for the data.

Generation of t-SNE plots and Pearson Correlation heatmaps

To generate the t-SNE plots, the following workflow was used: first, we used MATLAB to implement an algorithm for automatic selection of the t-SNE input parameter perplexity; we obtained a perplexity value of 2. Next, we used Python to format our raw data into the data matrix [v₂ v₃… v₁₆]^T = M∈ ℝ^{15 x n} using the NumPy (v1.15.1) and Pandas (v0.23.4) libraries. After this, we performed Principal Component Analysis using the Scikit-Learn library for linear dimensionality reduction of M∈ ℝ^{15 x n} into X∈ ℝ^{15 x 15} for input into the t-SNE algorithm, since the t-SNE algorithm is slow to implement as the number of dimensions increases, and, by definition, a matrix of rank 15 cannot have greater than 15 independent vectors in its basis. Finally, we performed t-SNE using the Scikit-Learn library for non-linear dimensionality reduction of X∈ ℝ^{15 x 15} into Y∈ ℝ^{15 x 2}, using a perplexity value of 2 and the range of learning rates 0.001 to 1000, for 1000 iterations.

Correlation heatmaps were generated with the Jupyter Notebook and Python packages Matplotlib (v3.0.0) and Seaborn (v0.9.0). For each data set, we used the M matrix as input and calculated pairwise similarity between column vectors using the Pearson Correlation Coefficient (PCC) metric, although other measures of similarity (e.g. Cosine Similarity, Euclidean Distance, etc.) gave similar results.

Colchicine effect quantification

Analysis of variance (ANOVA) was performed on the fluorescence intensity collected from an ROI within the oocyte for stage 4-8 egg chambers. 10 egg chambers from colchicine-fed females were compared to 10 egg chambers from females fed regular yeast paste.

Quantification of FRAP signal

For each time point, mean fluorescence intensity of the 488 channel for the NC cell region was collected Data collected after photobleaching were converted to percentage of the mean fluorescence intensity prior to photobleaching Error bars represent standard error.

Generation of ranked NC volume histograms

NC volume measurements were taken from egg chambers where the oocyte occupied approximately half of the total volume (stage 9/10). Individual NC volume measurements were collected from phalloidin-based Imaris reconstructions of 10 Dap-sfGFP and 10 otu-Gal4/+; Dap-sfGFP; UASp-deGradFP/+ egg chambers. For each egg chamber, all NCs were ranked according to volume (1 being largest, 15 being smallest). For each 10-egg chamber set, the ranks for all NCs in a group were combined into one dataset. For example, the ranks for Dap-sfGFP NCs, 2,3,5 and 9 were combined into the blue Dap-sfGFP dataset. The 8 datasets were graphed in MATLAB (R2019a) using the histogram() function. The Brown-Forsythe test for equality of variances was performed to compare the two different blue group conditions using the MATLAB vartestn() function.

GENERATION OF LOMB-SCARGLE PERIODOGRAMS

To observe the temporal dynamics of CycE and Dap nuclear localization, it was necessary to first associate our fluorescence values with discrete time points in development. To do so, we first calculated the volume of each fixed egg chamber by measuring each of principal semi-axes from its 3-D reconstruction and approximating its volume as that of an ellipsoid. From a variety of previous studies on the timing of oogenesis (Shimada et al., 2011; Spradling, 1993) and our own data analyzing egg chamber volume, we performed logarithmic regression on time vs. egg chamber volume. This provided us with the following formula to compute time in development for each egg chamber based on its volume:

$$t_j=9.9657\ln (V_j)-76.601$$

Having associated each egg chamber and its corresponding normalized fluorescence values with a developmental time, we then sorted our data matrix M row-wise in order of increasing developmental time to generate time series data. Next, we generated group time series data vectors v_Blue, v_Red, v_Green, and v_Yellow ∈ ℝⁿ by averaging the fluorescence values of the NCs belonging to a coordination group. For example, for egg chamber j,

$$v_{Blue}(t_j)=\frac{1}{4}(v_2(t_j)+v_3(t_j)+v_5(t_j)+v_9(t_j))$$

Finally, we implemented the Lomb-Scargle algorithm in MATLAB and generated periodograms of power density with normalized spectrum scaling for each group time series vector. From the periodograms, the highest peaks corresponded to the main contributing frequencies in the Dap and CycE nuclear localization oscillations. To distinguish peaks resulting from Dap and CycE oscillations from peaks resulting from noise, we first assumed that no single coordination group had a source of noise that was unique to that group. Next, we summed the areas under the peaks of each of the group time series periodograms to construct a single periodogram; this would allow peaks that are significant across all of the four group time series periodograms to become stronger while simultaneously preserving noisy peaks unique to coordination groups.

Highlights.

• Oocyte-nurse cell communication controls collective Drosophila germline growth

• Dacapo mediates bidirectional communication between the oocyte and nurse cells

• Nurse cell endocycles fit a model of synchronized coupled oscillators